Mapping Monomeric Threading to Protein–Protein Structure Prediction

Abstract

The key step of template-based protein–protein structure prediction is the recognition of complexes from experimental structure libraries that have similar quaternary fold. Maintaining two monomer and dimer structure libraries is however laborious, and inappropriate library construction can degrade template recognition coverage. We propose a novel strategy SPRING to identify complexes by mapping monomeric threading alignments to protein–protein interactions based on the original oligomer entries in the PDB, which does not rely on library construction and increases the efficiency and quality of complex template recognitions. SPRING is tested on 1838 nonhomologous protein complexes which can recognize correct quaternary template structures with a TM score >0.5 in 1115 cases after excluding homologous proteins. The average TM score of the first model is 60% and 17% higher than that by HHsearch and COTH, respectively, while the number of targets with an interface RMSD <2.5 Å by SPRING is 134% and 167% higher than these competing methods. SPRING is controlled with ZDOCK on 77 docking benchmark proteins. Although the relative performance of SPRING and ZDOCK depends on the level of homology filters, a combination of the two methods can result in a significantly higher model quality than ZDOCK at all homology thresholds. These data demonstrate a new efficient approach to quaternary structure recognition that is ready to use for genome-scale modeling of protein–protein interactions due to the high speed and accuracy.

INTRODUCTION

The number of possible protein–protein complexes scales in principle as the square of the number of monomer protein chains in genomes, with estimates of the possible number of distinct protein complexes in the order of millions.¹ Although the currently available high-throughput experimental methods have been employed to identify putative interacting protein pairs on proteome scales, the estimated error rates range from 41% to 90%.² These high-throughput methods do not provide structural information, i.e., where and how the proteins interact. Structural determination methods, such as X-ray and NMR techniques, could provide such information but are too costly and labor intensive to be applied on the proteome scale.

To address these issues, many computational approaches have been proposed for predicting the quaternary structures of proteins, which can be categorized as template-based and template-free approaches.³ In the template-based approaches as applied to dimers,^4–10 the quaternary model is constructed by matching a pair of monomer target sequences to a library of related template protein complexes which have the structure experimentally solved. In the template-free approaches,^11–18 also known as protein–protein docking, the target protein complex structure is predicted by scoring a large set of protein–protein orientations which are generated by assembling known monomer structure models.

Both methods have advantages and disadvantages. The template-free approaches can in principle treat any protein targets whose monomer structures are known. However, there is no guarantee of a high-quality structural prediction, particularly when bound structures undergo conformational changes from the unbound structures.¹⁹ These usually involve side-chain readjustments and sometimes backbone rearrangements. Furthermore, the docking methods require the information that the two proteins interact; this restriction is largely due to the limitations of the force fields used for evaluating the interaction energy.²⁰

Template-based (or homologous modeling) approaches generally have a higher accuracy than docking when homologous templates are available, but the alignment accuracy decreases sharply when the evolutionary relationship between target and template proteins becomes ambiguous, which generally corresponds to the scope of a target–template sequence identity <30%. Recently it was recognized that the structural space of protein–protein interfaces is highly degenerate,^21,22 which implies that the template-based approach can in principle be used to deal with any protein. In practice, the identification of the analogous protein complex pairs is highly challenging because the majority of the neighboring structure pairs have no obvious evolutionary relationship. Thus, development of new approaches to detect distantly homologous protein complex pairs is essential.

Partly toward this goal, we recently developed a method called COTH⁹ which first threads both target sequences to a representative complex structure library. The monomer template structures identified by single-chain threading are then shifted to the dimeric framework that was identified by multiple-chain threading. The combination of the tertiary and quaternary libraries demonstrates a significant increase of the alignment coverage from the original complex structure templates, compared with other multiple-chain threading methods. However, the COTH procedure can be laborious since two template libraries (one for monomer and one for dimer) need to be maintained and updated. It is quite often that we found some interactions have been missed in the dimeric library even though we increased the sequence identity cutoff up to 90%. More importantly, the structural superposition can shift the complex structure to a wrong orientation especially when the structural similarity between the monomer structures in the two threading steps is low.

In this work, we address these issues by developing a new single-chain-based threading and mapping method for complex structure prediction, called SPRING (single-chain-based prediction of interactions and geometries). Since in most cases one chain structure is taken directly from the original oligomer structure in the PDB, the alignment loss from the monomer-to-dimer superimposition is kept minimal. Second, the close match of the interface areas from the same oligomers helps improve the coverage and accuracy of interface contact predictions which aims to solve a major issue in previous multiple-threading approaches.^8,9,23 Third, since a one-step single-chain threading is conducted, only the monomer structure library is needed in SPRING. It is therefore faster than COTH and other threading approaches, and the library is easier to maintain and update. Meanwhile, a precalculated lookup table is exploited to quickly exclude most of the complex frameworks that have no homologous association to the binding sequences. This is particularly important for speeding up the genome-scale modeling of protein–protein interactions, since only a small subset of interactions need to be pursued after this filtering step. Moreover, the complex template coverage is significantly maximized since there is no sequence cutoff for constructing the library. To examine the efficiency and generality, we will carefully test the method in control with other state-of-the-art template-based methods in large-scale benchmarks. The SPRING algorithm is freely available at http://zhanglab.ccmb.med.umich.edu/spring/.

MATERIALS AND METHODS

SPRING Algorithm

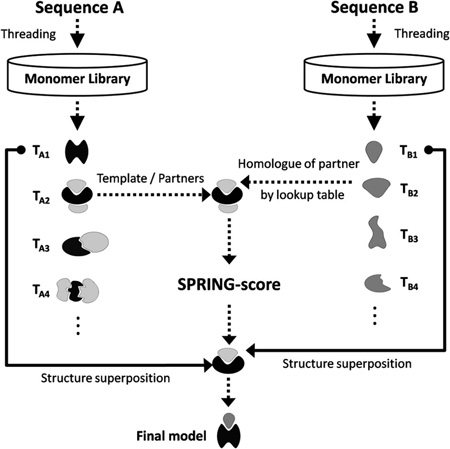
SPRING constructs the structure of protein complexes starting from two input chain sequences A and B (Figure 1). At first, a list of putative monomer templates (T_A) for sequence A is identified from the monomeric template library using a threading approach, e.g., MUSTER,²⁴ HHsearch,²⁵ or both. The threading provides a template alignment and a Z-score (Z_A) for the input sequence A. Here, the Z-score is defined as the difference between the raw alignment scores and the mean in the unit of variations, which has been widely used to assess the significance of the threading alignments, i.e., a higher Z-score means a higher significance and usually corresponds to a better quality of the alignment. The top template of the highest Z-score (T_A1) will be used to construct a monomer model for chain A.

Figure 1.

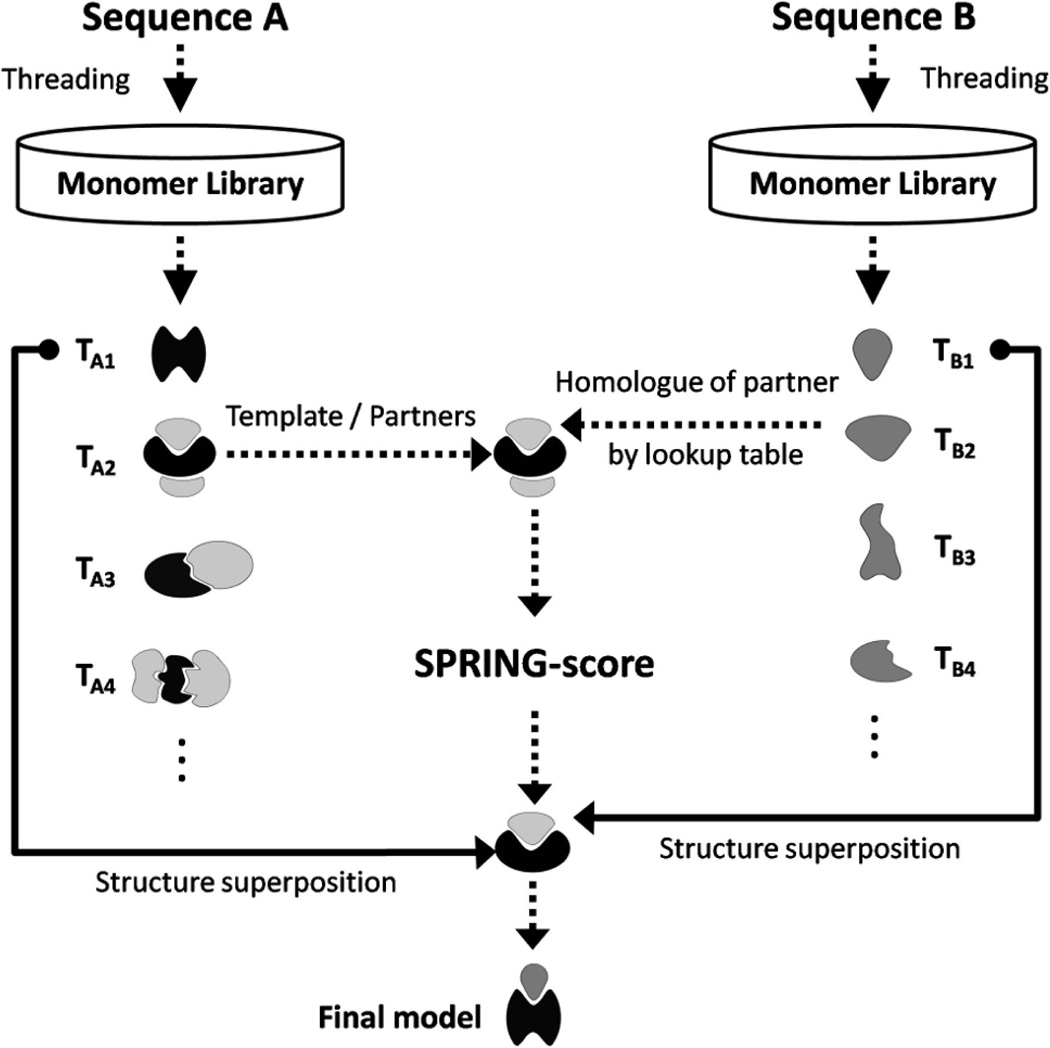
Flowchart of SPRING pipeline. Target sequences A and B are first threaded against the monomer template library, which yields two lists of templates T_A (black) and T_B (gray). For chain A, we retrieve all binding partners P_A (light gray) from the original template entry in the PDB. Each binding partner is associated to its closest homologue (e.g., P₂ and B₂) by a precalculated look-up table using PSI-BLAST. The complex models are then constructed by structurally aligning the top-rank monomer models to the template/binding partner and ranked by SPRING-score (eq 1).

Meanwhile, we thread the sequence of chain B through the monomeric structure library to identify another set of putative templates (T_B) with associated Z-scores (Z_B) (right column of Figure 1). Analogous to chain A, we derive a top-ranked monomer model for chain B using the template with the highest Z-score (T_B1).

To construct structure models of the complex, we now gather a set of template/partner frameworks by using the (top- and lower-ranking) monomer templates of chain A (T_A). Therefore we retrieve the corresponding oligomer file of each monomer template T_A from the PDB. Then, all binding partners of the templates T_A are collected from the oligomers (labeled as P_A). These also include binding partners and their respective orientations as deposited by the remark “350” of the PDB file. Template/partner frameworks can only be derived from monomer templates T_A with at least one binding partner.

Using the identified template/partner frameworks, we start by structurally aligning the top-ranked monomer model of chain A to all templates (T_A), where the alignment is built on the subset of interface residues. Additionally, we align the top-ranked monomer model of chain B to all binding partner structures of chain A that were retrieved from the PDB oligomers (P_A); the alignment is based on the subset of interface residues. These two monomer-to-oligomer superimpositions yield a dimeric model, consisting of the reoriented top monomer models for chains A and B based on each of the oligomer frameworks. Here, we note that the tertiary structures of two components are both from the top threading template, although the oligomer frameworks can come from the lower-rank threading templates. Based on our training results, using the top-rank monomer templates can generate on average better quality of complex models than using lower-rank monomer templates based on both global and interface scores. This is because the top monomer templates have generally a higher accuracy of alignments than lower-rank ones. Moreover, for reasonable frameworks the structures of component chains and the top monomer templates are often close, and the alignment loss from the superimpositions is minimal. Nevertheless, most of the top complex models by SPRING are built from the top oligomer frameworks. In these cases, the component models of the probe chain are taken directly from the oligomers, and no structural superimposition is needed.

To improve the efficiency, we exclude template/partner frameworks if the corresponding binding partner is not homologues to any of the monomer templates (T_B) identified for chain B. The homology can be quickly verified through our precalculated look-up table, which is essentially a one-to-one PDB ID map to associate every binding partner in the oligomers to its closest homologues monomer structure from our tertiary template library (middle column of Figure 1). The look-up table was pregenerated by an all-against-all PSI-BLAST search²⁶ of the PDB library, where the partner/homologue association with the lowest E-value was selected for each binding partner. The look-up table is particularly useful to increase the efficiency for genome-wide all-against-all modeling studies, since only a small subset (~1%) of protein pairs that can find putative template/partner frameworks is needed for the consequent model construction.

The models constructed from monomer-to-oligomer mappings are evaluated by the SPRING-score which is a linear combination of three terms:

$$\text{SPRING-score}=\text{min}(Z_{\mathrm{A}},Z_{\mathrm{B}})+w_1\mathrm{T}\mathrm{M}+w_2\text{contact}$$ (1)

where the first term is the smaller Z-score of threading of the two target sequences; the second is the TM-score returned by TM-align²⁷ when aligning the top-ranked monomer model for B to the subset of interface residues of the selected binding partners of chain A (P_A); the third counts for a distance-specific interface contact potential, which was derived from 3897 nonredundant dimeric protein structures with a sequence identity <30% to each other.²² It uses a formula similar as Zhou et al. but with the atomic distances taken from residues in separate chains,²⁸ and w₁ = 12.4 and w₂ = −0.2 are the weight factors balancing the terms. We determine the weighting parameters through a grid search on a separate training set of 200 randomly selected protein complexes by maximizing the number of ‘acceptable’ models, where an acceptable model refers to the top-ranked models with >30% of correctly predicted C_α-atom contacts in the interface.

For heterodimer proteins, this process is repeated using B as probe to identify binding partners for the complex template identification and model construction. The models of the highest SPRING-score in the two processes are finally selected as predicted models. For homodimer proteins, a single threading starting on one chain is sufficient due to the symmetry of the complex structures.

Libraries of Protein Structure Templates

SPRING is based on monomer threading, and we constructed from the PDB a representative set of 43 571 monomeric protein structures, sharing a pairwise sequence identity of <70%. Obsolete structures and theoretical models were removed. For multiple-domain proteins, both individual domains and whole proteins are included in the library, which has been proven to increase the alignment accuracy of single domain proteins.²⁴

For benchmarking SPRING with other methods, we also constructed a set of nonredundant dimeric complex structures that is needed by COTH and the naïve complex threader using MUSTER, HHsearch, and PSI-BLAST. This library was derived from DOCKGROUND²⁹ with a filter of pairwise sequence identity <70%. In addition, irregular structures, transmembrane complexes, and complexes with alternate binding modes were removed. To rule out crystallization artifacts, complexes with <30 interface residues or with a buried surface area <250 Ų were not included. It finally contains 7404 dimeric protein structure templates at the same date cutoff of the monomer library.

Test Set of Protein–Protein Complexes

The evaluation of prediction performance was conducted using a set of 1838 nonhomologous protein–protein complexes from the PDB, including dimers derived from higher order oligomers, similar to that used by Lu et al.⁸ Each of the 3676 monomer structures from the dimers contains at least 40 interface residues with at least 30 interface residue–residue contacts, where a contact is defined as a pair of residues from different chains with at least one pair of side-chain heavy atoms within 4.5 Å. In addition, the dimers have a sequence identity <35% to each other (i.e., at most one chain in a dimer can have >35% sequence identity to any of the chains in another dimer so that homodimers are included).

Measures of Dimer Model Quality

The global model qualities are evaluated using TM-score,³⁰ the global complex RMSD, and the sequence-template alignment coverage. Local model qualities are measured using the fraction of native C_α- atom contacts (fnat) in the interface, the interface RMSD (I-RMSD), and the interface alignment coverage, where interface residues are defined as those with a heavy atom distance of <10 Å to any residue of the other chain.

TM-score has been extensively used to assess the quality of monomeric protein structure predictions, because of its attribute to balance alignment accuracy and coverage. In order to calculate TM-score of dimeric models, we convert the dimer into an artificial monomer by connecting the C-terminal of the first chain with the N-terminal of the second and then run TM-score program, using the length of the query complex as normalization scale. This definition of complex TM-score is sensitive to the topology of individual chains and their relative orientation. A high complex TM-score indicates the correct modeling of both individual chain structures and their relative orientation.³¹

RESULTS

Control of SPRING with Competing Threading Methods

SPRING derives complex structure by mapping monomer alignments as identified by single-chain threading algorithms, e.g., MUSTER²⁴ and HHsearch²⁵ (Figure 1). To examine the gain of the threading and mapping procedure over the traditional dimeric or monomeric threading procedures, we implement SPRING using the monomer alignments from MUSTER (called SPRING-M), in control with COTH (threading and superposition) and a naïve implementation of MUSTER (called NAIVE-M). In NAIVE-M, MUSTER is used to align every chain of the target complex with that of known proteins in the complex template library. A template model is obtained if both chains from a template are aligned with the target. This procedure is identical to the strategy that was used by several authors in the former studies.^8,23,32

Figure 2 shows a comparison of the three methods on a set of 1838 interacting protein–protein sequence pairs, based on the global TM-score, the fraction of correctly predicted interface contacts (fnat), the interface RMSD, and the global RMSD, respectively. To rule out contamination from close homologous templates which are easy to identify by sequence comparisons, any templates which have a sequence identity >30% to target proteins in the testing set have been excluded from the template libraries. This filter is implemented in all the following threading calculations unless noted specifically.

Figure 2.

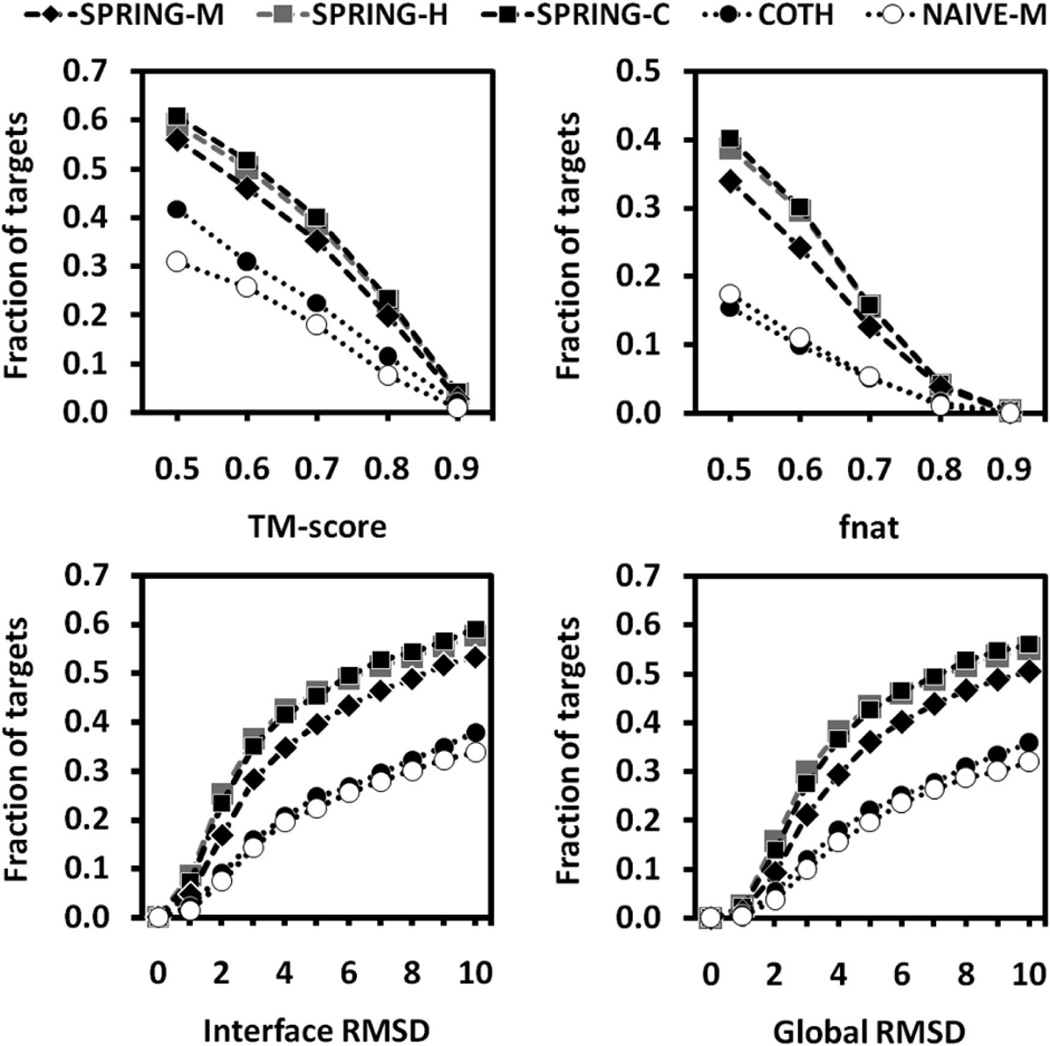
Cumulative fraction of TM-score, native contacts, and interface and global RMSD at different threshold cutoffs, for models on 1838 proteins predicted by SPRING-M, SPRING-H, SPRING-C, COTH, and NAIVE-M, respectively. The shown data are from the best out of five top-ranked models for each protein target.

Overall, the number of successful predictions by SPRING-M is the highest among all methods in each of the TM-score ranges. The same is true for the fraction of interface C_α-atom contacts and the interface and global RMSD results. For instance, if we consider a TM-score threshold of >0.5, SPRING-M, COTH, and NAIVE-M generated valid dimeric models for 1029 (56%), 767 (42%), and 568 (31%) out of the 1838 protein targets, respectively. Similarly, if we count for the number of cases which have an I-RMSD <5 Å and with at least 50% interface residues aligned, the number for SPRING-M, COTH, and NAIVE-M is 638 (35%), 381 (21%), and 359 (20%), respectively.

To further examine the detailed difference between the algorithms, in Figure 3A,B we present a head-to-head comparison of dimeric models predicted by SPRING-M and COTH, with regard to the TM-score and contact accuracy (fnat). There are 1023 cases where SPRING-M generates models of a higher TM-score than COTH, where COTH does so in 539 cases. Overall, the average TM-score of the predicted SPRING-M models is 13% higher than that of COTH. For interface structure modeling, SPRING-M models preserve 31% of the native contacts, whereas in COTH it does so in only 17% of cases (see Figure 3B). Since both methods used the top-ranked monomeric models to form the dimer models, their global alignment coverage is close (~88%). Thus, this TM-score increase is purely due to the identification of better dimer templates from the SPRING-M threading mapping, which results in more precise chain orientations. This is further manifested by the modeling quality at the interface structures. If we defined a high-quality hit as that with an I-RMSD <2.5 Å on >90% of interface residues aligned, SPRING-M produced 162 hits compared to 89 by COTH, which corresponds to an increase of 82%.

Figure 3.

Head-to-head comparisons of 1838 SPRING-M models with that by the control methods. The left column shows TM-score of the best in top-five complex models, and the right column is the fraction of the correctly predicted interface contacts. (A,B) SPRING-M vs COTH and (C,D) SPRING-M vs NAIVE-M.

In Figure 3C,D, we present a similar head-to-head comparison of SPRING-M with NAIVE-M, where the TM-scores of the dimeric models predicted by SPRING-M are on average 40% higher than that of NAIVE-M. The major reason for the TM-score increase in SPRING-M is due to the boost of template libraries because SPRING-M has the monomer structures built from the tertiary template library (43 571 entries) which is much larger than the quaternary template library (7404 entries), while the latter was the only source used by NAIVE-M for building the complex models. For interface structure, the NAIVE-M alignments conserve 17% of native contacts (see Figure 3D), which is similar to that of COTH but 45% lower than that of SPRING-M. Here, although the individual COTH models are on average of higher TM-score, they do not contain more correct interface contacts than NAIVE-M. The poor performance of COTH relative to SPRING-M is mainly due to the alignment strategy that COTH employs to combine the monomers of the identified dimeric template. Since COTH uses a full-length global superposition strategy, it focuses less on the interface conservation, rather than the global topology of the complexes. In contrast, SPRING-M maps the monomer alignment using a subset of interface residues, which guarantee a better match in the interface regions. Meanwhile, many of the top alignments have the partner chain directly coming from the original oligomer entry which helps enhance the shape match of the interfaces. Third, the quaternary chain orientation of the complexes as identified by SPRING-M mapping has a better quality than that by monomeric or dimeric threading, which further contributes to the interface contacts.

The observed performance differences of SPRING-M from COTH and NAIVE-M with regard to the TM-scores are statistically significant, which have the p-values from the pairwise student t tests of 10^–72 and 10^–166, respectively. In Table 1, we summarize the overall model qualities for each method, according to the average TM-score, the fraction of native C_α-atom contacts, the number of hits with an I-RMSD <2.5 Å, and the global alignment coverage, respectively. The results are shown from both the first model and the best in top-five models, where SPRING-M clearly outperforms the control methods in all the criterions.

Table 1.

Comparison of Different Threading Methods on 1838 Nonhomologous Targets

		top 1/5
methods	TM-scorea	fnatb	hitsc	coveraged
NAIVE-Pe	0.25/0.26	0.10/0.11	42/47	45/47%
NAIVE-Hf	0.35/0.37	0.15/0.17	80/93	56/58%
NAIVE-Mg	0.38/0.40	0.15/0.17	60/67	87/88%
COTH	0.48/0.50	0.15/0.17	70/89	88/88%
SPRING-M	0.54/0.56	0.26/0.31	133/162	88/88%
SPRING-H	0.55/0.57	0.29/0.33	211/246	81/81%
SPRING-C	0.56/0.58	0.29/0.34	187/219	86/83%

^aAverage TM-score of predicted complex models.

^bAverage fraction of conserved interface native contacts.

^cNumber of targets with model of I-RMSD <2.5 Å and >90% interface covered.

^dAverage fraction of aligned complex residues.

^eNaïve implementation of PSI-BLAST.

^fNaïve implementation of HHsearch.

^gNaïve implementation of MUSTER.

Illustrative Examples of Dimeric Threading

To further analyze the strength and weakness of SPRING-M in comparison with the other methods, we dissect in detail several typical examples. Figure 4 presents the model predictions for the 1-Cys peroxiredoxin complex (PDB ID: 1XCC), which is a typical homodimer complex. First, NAIVE-M identified a template from the glutathione peroxidase-5 (PDB ID: 2P5Q) with a sequence identity of 11% to the target. The predicted model has a TM-score = 0.37 and an I-RMSD = 12 Å, covering 64% of interface residues. The model predicted by COTH uses the same complex (PDB ID: 2P5Q) as the global template. However, COTH derives both monomer models from the peroxiredoxin-4 protein (PDB ID: 2PN8). The combination of the monomer templates on the dimer framework increases the TM-score from 0.37 to 0.52, which has an I-RMSD of 7.1 Å to the native crystal structure complex. In total, it has 376 residues aligned, which are much higher than that in the NAIVE-M alignment.

Figure 4.

Predicted dimer models (dark color) of NAIVE-M, COTH, and SPRING-M for target protein superposed with the native structure of the 1-Cys peroxiredoxin complex (light color, PDB ID: 1XCC). The values below each superposition are TM-score, I-RMSD, and fraction of aligned interface residues.

Finally, SPRING-M derives the orientation based on the single-chain MUSTER threading, which retrieves the dimer template from the tryparedoxin (PDB ID: 1UUL). The individual monomers of this dimer template are structurally similar (TM-score = 0.67) to the monomers of the template (PDB ID: 2P5Q) as identified by COTH and NAIVE-M, but the chain orientation in 1UUL is much closer to the native than that in 2P5Q. The closer orientation of the framework allows SPRING-M to generate a dimer model of higher quality after the mapping of monomer structures (see Figure 4).

An interesting question is why 1UUL was only successfully identified by SPRING-M but not other methods since both COTH and NAIVE-M use MUSTER for monomer threading. A closer analysis showed that this template is not included in the nonredundant dimer structural library since the complex structure contains a single decamer and thereby multiple alternative binding modes for the homologue chain pairs. Since the other two algorithms did not select particular binding modes from a set of alternatives, none of the putative orientations could be detected. As an essential advantage, however, SPRING-M considers all alternative binding modes from all complexes of the oligomer structure, since it starts from monomer threading with the composite SPRING-score selecting the most suitable pair. In this example, although all monomer templates have a low sequence identity to the target (<30%), the SPRING-score is high (27.5), which gives us a high confidence on the prediction. The overall TM-score of the mapped dimer model is 0.75 with an I-RMSD of 3.0 Å. Again, the fraction of aligned interface residues of both SPRING-M and COTH models is the same (= 83%), where the improvement of SPRING-M is on the choice of the better template framework and the closer mapping of monomer structures in the individual domains.

Figure 5 presents another example from the putative kinase complex (PDB ID: 2AN1, chains A and D). In this example, the best template (PDB ID: 1YT5) is included in the dimeric structural library. But the oligomer complex includes 8 biomolecules based on 4 homologues chains; these correspond to 48 dimeric alternative binding modes. The COTH library can chose only one binding mode from the dimeric pair of chains A and D that has the lowest solvent free energy (–183 kcal/mol) as defined in the PDB; this template results in an incorrect orientation for this target (fnat = 0.09 and I-RMSD = 14.2 Å), although the individual monomer models are similar to native (TM-scores >0.77).

Figure 5.

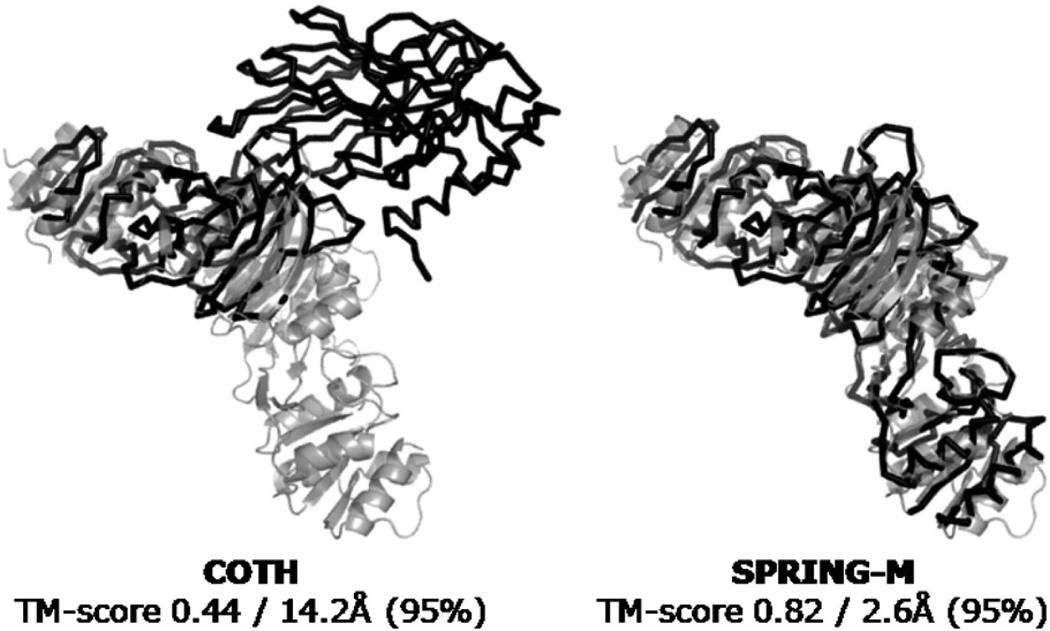
Complex models (dark color) are superposed with the native crystal structure of putative kinase complex (light color, PDB ID: 2AN1). (A) COTH and (B) SPRING-M.

In contrast, since SPRING-M retrieves partners from original oligomer complex structure, it naturally considers all 48 putative binding modes in the look-up table. Despite the slightly higher solvent free energy (–139 kcal/mol), the complex of biomolecules 3 and 5 with chains A and B was selected by SPRING-M as the most suitable framework, since the TM-score from TM-align superposition (0.82) and the contact potential (–41) are both better than all other partnerships (TM-score and contact potential values for the A/D pair template are 0.44 and –22, respectively). The choice of this A/B template results in a complex model with much better quality (fnat = 0.70 and I-RMSD = 2.6 Å) than that by COTH (see Figure 5). Meanwhile, since only one chain was required for other proteins (instead of both chains in COTH) to be superimposed on the framework, the interface shape match is another contribution to the quality of the interface structures of the SPRING-M models in this example.

Performance of SPRING Using Different Monomeric Threading Algorithms

In the previous sections, we compared SPRING-M, COTH, and NAIVE-M with all three algorithms based on MUSTER to ensure a fair comparison of different template identification and complex construction strategies. However, neither SPRING mapping nor the SPRING-score is restricted to specific monomeric threading algorithms. An interesting question is whether and how the SPRING pipeline benefits from choosing different target-template alignment algorithms. Here we test the performance of SPRING using another threading program, HHsearch²⁵ (SPRING-H). While MUSTER generates the target-template alignment based on a composite sequence and structural profiles, HHsearch uses the hidden Markov models. They can have significantly different results on template selection and target-template alignment for specific cases, although the overall performance in the tertiary template identification was shown comparable in previous benchmark tests.³³

Based on the data of the 1838 protein complexes, we found that SPRING-H identifies on average better quality quaternary templates than that by SPRING-M. For instance, if we consider a TM-score threshold >0.5, SPRING-H and SPRING-M generated valid dimeric models for 1082 (59%) and 1029 (56%) protein targets, respectively, after excluding homologous templates (see Figure 2). Similar conclusion is obtained, regarding the average TM-score, contact accuracy, interface, and global RMSDs. In particular, if we count the number of correct models with an I-RMSD <2.5 Å and >90% interface coverage, SPRING-H has about 1.5 times more hits than SPRING-M (see Table 1).

This difference is quite striking since MUSTER and HHsearch alignments have about the same TM-score on the tertiary template recognitions (i.e., 〈TM-score〉 = 0.57 for both alignments in our test). A detail analysis showed that the alignment coverage of the MUSTER alignments is ~8% higher than that of HHsearch. These extra residues of alignments have resulted in a higher overall RMSD in the MUSTER alignment (8.1 vs 5.8 Å in HHsearch). Since SPRING aligns monomeric models to the interfaces of the dimeric frameworks (see Figure 1), a high monomeric RMSD can easily shift the alignment into less favorable orientations. Thus, SPRING-H profits from the more accurate target-template alignments although HHsearch provided a lower coverage of aligned residues.

Nevertheless, when combining the alignments HHsearch and MUSTER, SPRING (called SPRING-C) yields a slightly but significant (pairwise student t test <10^–7) improvement of 1.4 and 3.1% compared to SPRING-H, in the average TM-score and fnat, respectively (see Figure 6A,B). Additionally the number of acceptable models (TM-score >0.5) increases from 1082 (59%) in SPRING-H to 1115 (61%) in SPRING-C. In Figure 6C,D, we also present a head-to-head comparison of SPRING-M with SPRING-C, where the TM-scores of dimeric models predicted by SPRING-C are on average 4% higher than that of SPRING-M. Considering the contact accuracy, SPRING-M preserves 31% of native contacts (see Figure 6D) compared to 34% by SPRING-C. The overall results of the comparisons are summarized in Table 1. These data demonstrate that a complementary alignment from different threading algorithms can further improve the yields of SPRING.

Figure 6.

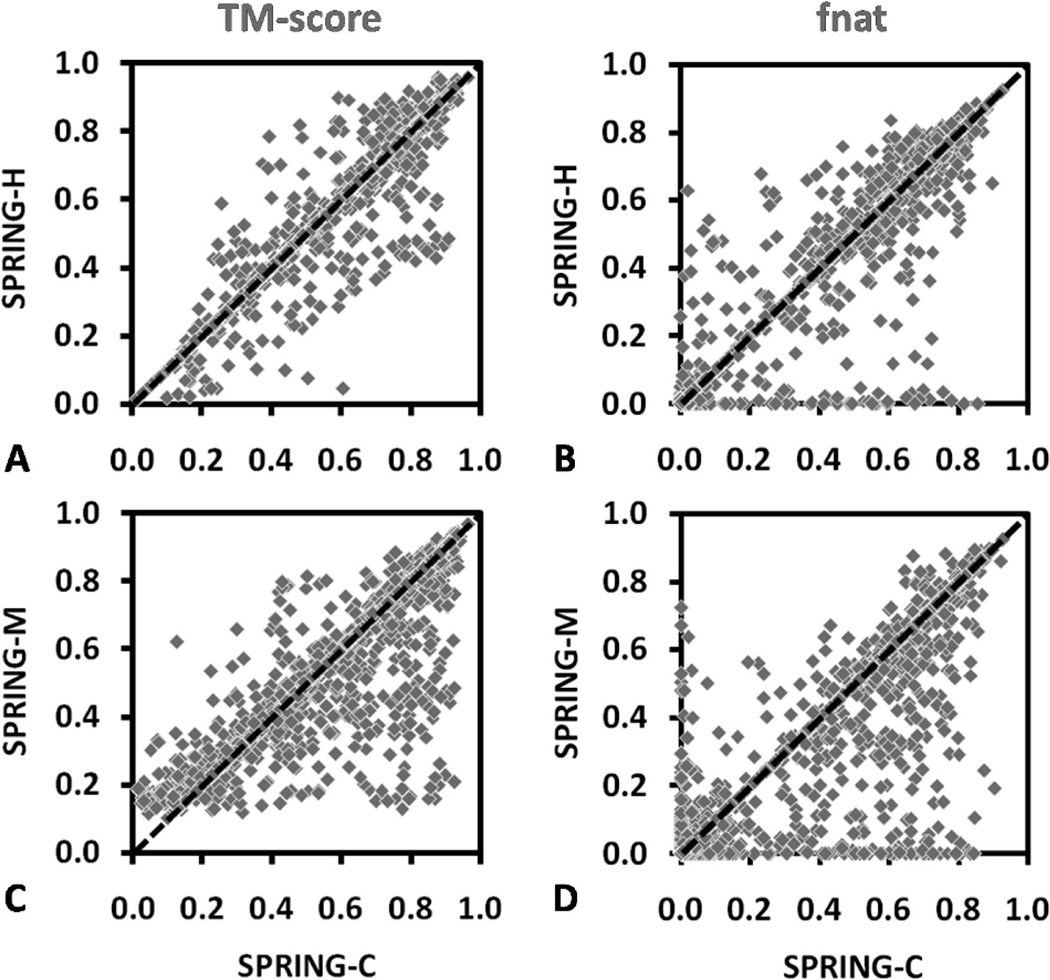
Head-to-head comparisons of the SPRING models using different monomeric threading methods on 1838 test proteins. The left column shows TM-score of the best in top-five complex models, and the right column is the fraction of the correctly predicted interface contacts. (A,B) SPRING-C vs SPRING-H and (C,D) SPRING-C vs SPRING-M.

Specificity of SPRING Predictions

The confidence of the SPRING method is assessed by the SPRING-score, which is a combination of threading Z-score, structural mapping TM-score, and interface contact potential (see eq 1). In this section, we examine whether the SPRING-score is able to distinguish correct from incorrect SPRING predictions, which is important in practical applications since confidence scores of predictions essentially decide how the models should be used by biologist users. We use SPRING-C for the illustration.

Figure 7 presents TM-score, fnat, and interface and global RMSDs of the predicted models to the native complexes in different SPRING-score interval. Considering the first models for the 1838 cases, SPRING-C made 987 (54%) predictions with a SPRING-score >13. In 774 (78%), 579 (59%), 601 (61%), and 519 (53%) cases, the predicted models have a TM-score >0.5, a fnat >0.5, and interface and global RMSDs <5 Å (see the dark regions in Figure 7). Apparently, when SPRING-score is higher, there is a higher fraction of protein targets that have models with a better quality and vice versa. For example, when considering TM-score >0.5 as a threshold, the fraction of successful modeling is 60, 80, and 88% for the targets in the SPRING-score interval of [13, 15], [15, 20], and >20, respectively. If we use a threshold of SPRING-score >13 to predict the correct template alignments, the false-positive and false-negative rates for TM-score >0.5 are 0.22 and 0.27, respectively. A similar tendency was also seen when using other criterions (see Figure 7).

Figure 7.

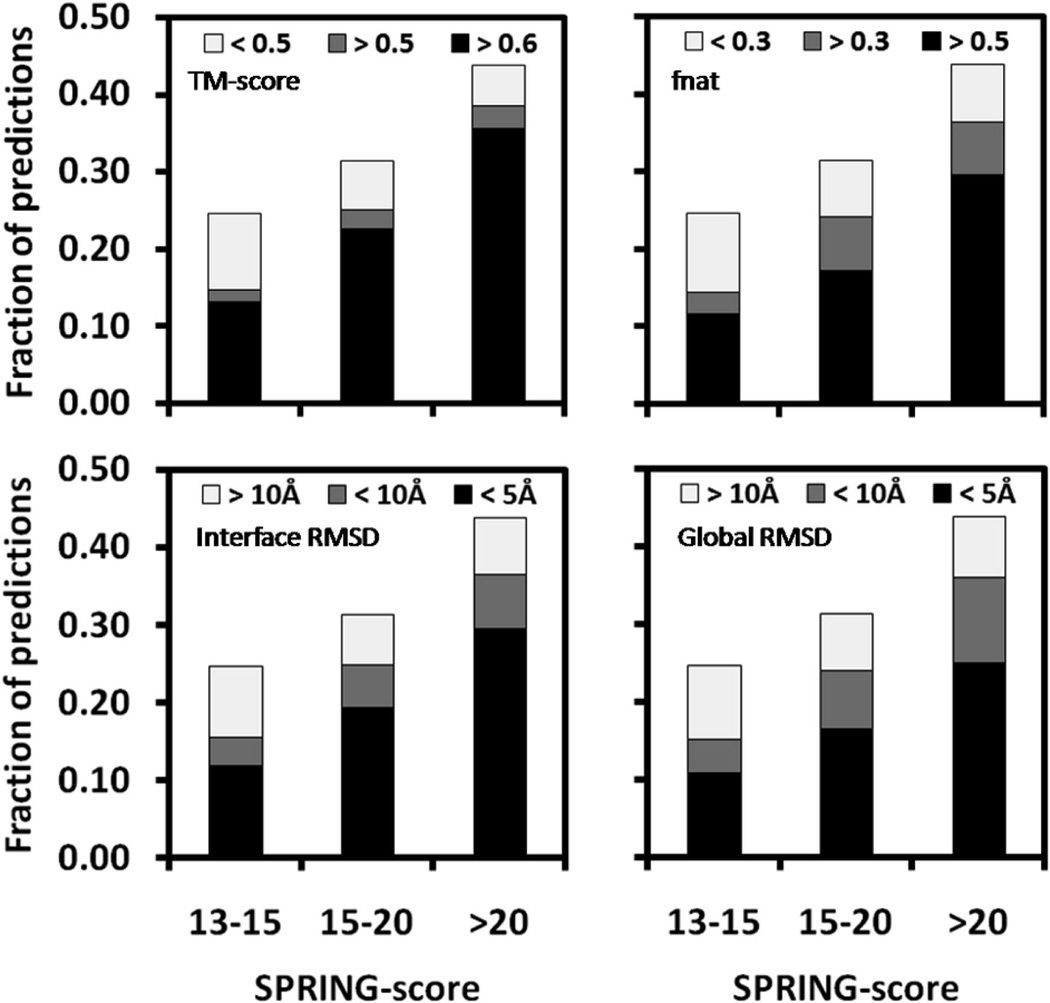
Fraction of predicted models above and below specific quality thresholds within a given SPRING-score interval for the top-ranked models. The depicted quality measures are TM-score, fraction of native interface contacts, interface, and global RMSD. Models with <50% of aligned interface residues are included in the RMSD category >10 Å.

Nevertheless, there is a considerable fraction of proteins which have low specificity, i.e., the proteins that have a high-scoring prediction but with poor model qualities when compared to the native or vice versa. For instance, we identified overall 53 structures which have a SPRING-score >20 but with a TM-score <0.5. In the majority of these cases, we found that SPRING ranks the templates of alternative binding modes as the highest score templates. Incorporation of specific binding affinity energy terms, such as the binding predictions by BSpred,⁹ can be a possible solution to further improve the specificity of SPRING.

Comparison of SPRING with Other Conventional Threading Strategies

The majority of above SPRING benchmark data are controlled with our internal algorithms of COTH⁹ and MUSTER.²⁴ To have a general control with other external threading algorithms, we implement two additional procedures of the naïve extension of PSI-BLAST (NAIVE-P) and HHsearch (NAIVE-H) for complex modeling. Following the traditional homology-based multimeric threading strategy, ^8,23,32 these procedures first match the monomer chains through the dimer template library by PSI-BLAST or HHsearch. If the two target chains hit the monomers from the same complex template, the aligned regions isolated from the template constitute the complex models.

As shown in Table 1, SPRING significantly outperforms NAIVE-P and NAIVE-H, in terms of global and local quality of the models. For example, the TM-score and the number of native contacts in the first model of SPRING-C is 124 and 190% higher than that of NAIVE-P and 60 and 93% higher than that of NAIVE-H. Among the naïve extensions of the monomer threading algorithms, NAIVE-M has a slightly higher TM-score than NAIVE-H due to the higher alignment coverage but with a lower number of hits considering the I-RMSD cutoffs. Both algorithms have a significantly better model quality than NAIVE-P, which stems from the improved sensitivity of profile–profile alignments by MUSTER and HHsearch on monomer threading over the sequence-profile alignment by PSI-BLAST.

Control of SPRING with Rigid-Body Docking Algorithms

To have a control of SPRING with the rigid-body docking methods,^11–18 we implement SPRING-H on the dimer complexes of the protein docking benchmark set³⁴ 3.0, which have both complex and unbound monomer structures solved in the PDB. Since SPRING has often partial structure aligned, we implement another version of SPRING-UB which superimposes the unbound monomer structures to the SPRING-H models after threading.

In Figure 8, we present the modeling results of SPRING-H and SPRING-UB in terms of the number of targets with an IRMSD <5 Å in the top-five models. As expected, the SPRING algorithm strongly depends on the level of filters for excluding homologous templates. At the sequence identity cutoffs of 30, 50, and 70%, SPRING-H generated models with I-RMSD <5 Å for 16, 23, and 28 targets, respectively. SPRING-UB has a slightly better result (with 17, 24, and 31 targets, respectively) due to the better model of the monomer structures.

Figure 8.

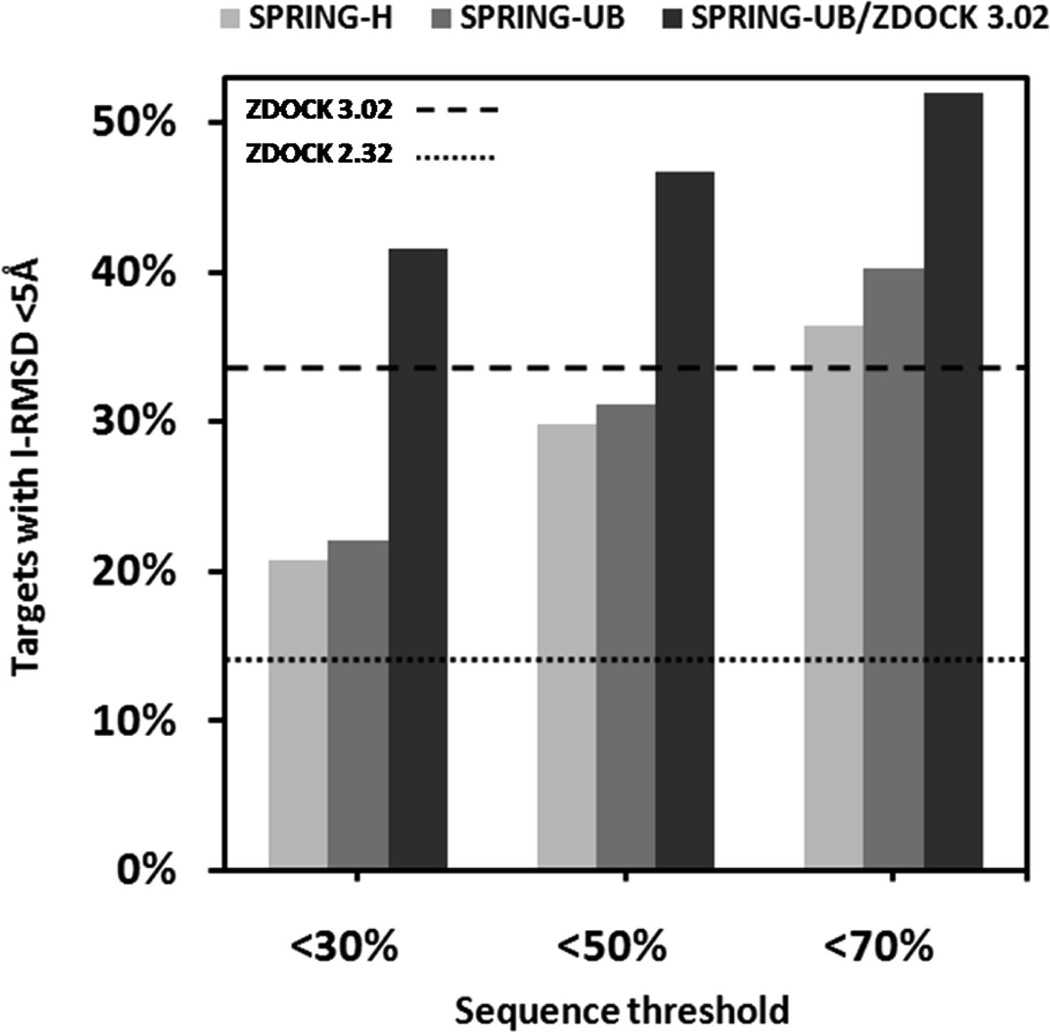
Comparison of SPRING and ZDOCK models at different target-template sequence similarity thresholds (30, 50, and 70%) on 77 heterodimeric protein complexes. The number of correct predictions, i.e., with I-RMSD <5 Å, is shown for SPRING-H, SPRING-UB, ZDOCK (V2.32 and V3.02) and a combination of SPRING-UB and ZDOCK V3.02.

As a control, two ZDOCK programs (V2.32 and V3.02) are implemented, which represent one of best rigid-body algorithms according to the CAPRI experiments.³⁵ While both ZDOCK programs use the fast Fourier transformation technique to sample the conformation space of docking, ZDOCK V3.02 incorporates a new statistical pairwise potential to improve modeling selections.³⁶ ZDOCK V2.32 generates models of I-RMSD <5 Å for 11 targets, which is lower than both SPRING-H and SPRING-UB. However, the new pairwise potential significantly improves the ZDOCK V3.02 program with models of I-RMSD <5 Å for 26 targets, where SPRING could produce a similar number of correct models only if the homologue filter cutoff increases up to 50–70%.

In the right column of Figure 8, we also show the results of a hybrid modeling which has two models selected from SPRING-UB and three from ZDOCK V3.02. This combined approach outperformed all the four individual methods at different sequence identity thresholds (30, 50, and 70%) with correct models in the top five for 32, 36, and 40 targets, respectively. The results illustrate that the approaches of SPRING and ZDOCK are complementary to each other and a combination can lead to improved prediction accuracy.

CONCLUSION

We presented SPRING, a new method to identify protein complex structural templates by mapping single-chain-based threading alignments with complex frameworks. Large-scale benchmark testing was performed in control with a recently developed cothreading method COTH⁹ and the naïve extension of three monomer threading algorithms (MUSTER, HHsearch and PSI-BLAST), where the latter strategy is identical to that used by other authors in former template identification studies.^8,23,32

Based on a large test set of 1838 nonhomologous protein complexes, we showed that SPRING can produce models in the top five for 1115 (61%) targets with a TM-score >0.5, after all homologous template with a sequence identity >30% are excluded. The average TM-score for all targets is 0.58 with 34% of native interface contacts correctly predicted. In our recent studies, we have demonstrated that a TM-score >0.5 is statistically significant, which corresponds to a model of the correct fold in tertiary structure prediction³⁷ and in quaternary structure comparisons.²² These data demonstrate that SPRING has the ability to generate reasonably correct complex models for more than half of nonhomologous targets.

On the same benchmark protein set with same homology filter, the TM-score of the SPRING models is 16, 45, 57, and 123% higher than that by COTH, MUSTER, HHsearch, and PSI-BLAST, respectively. The differences are statistically significant and all with p-values <10^–76 in the pairwise student t test. Considering the fraction of correctly predicted interface contacts, the SPRING models preserve at least twice as many native contacts compared to the competing methods. The corresponding p-values of the pairwise student t test are below 10^–103 in all the comparisons. The number of targets with high-quality models (i.e., with an I-RMSD <2.5 Å and >90% of interface residues aligned) was 219 in SPRING, compared to 89/67/93/47 in the competing methods, respectively.

Compared to COTH, a method that is conceptually closest to SPRING among the control methods, the major advantage of SPRING is the employment of the monomer-to-oligomer mapping which allows the use of entire PDB library for complex frame derivation, while COTH exploits only a subset of complex structures at certain sequence identity cutoff which renders a loss of template frameworks; in particular the different binding modes from same monomer sequences (see the example in Figure 5). Such loss cannot be recovered by improving the scoring function of ranking. Indeed, we have tried to immigrate the SPRING-score (another major difference of SPRING) to COTH, but this change does not make a significant difference on the overall TM-score of COTH threading alignments.

We also control SPRING with the rigid-body docking algorithms on the docking benchmark databases.³⁴ As expected, the relative performance of algorithms strongly relies on the thresholds that are used to filter out homologous templates. However, a combination of the two approaches outperforms individual ones at all homologous cutoffs, which demonstrates the complementarities of the algorithms. Thus, a combination of both threading and rigid-body docking methods should represent a promising and reliable approach to the genome-wide structure modeling, where various targets with different levels of homology and difficulty need to be modeled.

For the evaluation of model qualities, we illustrated that there is a strong correlation between SPRING-score and the quality of the predicted models. If we consider a cutoff of good quality models of TM-score >0.5, the false-positive and false-negative rates for a SPRING-score >13 are 0.22 and 0.27, respectively. These data not only underline the high specificity of the SPRING predictions but also highlight the limitation of current threading-based approaches, since SPRING does not have high confidence predictions in nearly 50% of testing cases. This is partly due to the limited availability of analogous template structures since all homologous templates with a sequence identity >30% have been excluded in the test. Nevertheless, considering the large number of possible protein–protein interactions in genomes, high accuracy predictions for even less than half of all interactions would yield highly valuable new insights, not saying that a higher successful rate should not be possible if homologous templates are included.

As a threading-based modeling approach, SPRING only provides partial structures on the target sequences, with C_α structural models derived from the complex templates. The full-length atomic structural models need to be generated using separate assembly and refinement procedures, such as TACOS (http://zhanglab.ccmb.med.umich.edu/TACOS/). Moreover, in the presented version, SPRING only considers pairwise protein sequences known to interact. The extension of the method to the high-order complex prediction is straightforward since no additional template library and monomer complex lookup table are needed. We are working on addressing these issues and plan to apply the SPRING mapping technique to the construction of genome-wide structural networks.