Distinct regions of anterior cingulate cortex signal prediction and outcome evaluation

Abstract

A number of theories have been proposed to account for the role of anterior cingulate cortex (ACC) and the broader medial prefrontal cortex (mPFC) in cognition. The recent Prediction of Response Outcome (PRO) computational model casts the mPFC in part as performing two theoretically distinct functions: learning to predict the various possible outcomes of actions, and then evaluating those predictions against the actual outcomes. Simulations have shown that this new model can account for an unprecedented range of known mPFC effects, but the central theory of distinct prediction and evaluation mechanisms within ACC remains untested. Using combined computational neural modeling and fMRI, we show here that prediction and evaluation signals are indeed each represented in the ACC, and furthermore, they are represented in distinct regions within ACC.

Our task independently manipulated both the number of predicted outcomes and the degree to which outcomes violated expectancies, the former providing assessment of regions sensitive to prediction and the latter providing assessment of regions sensitive to evaluation. Using quantitative regressors derived from the PRO computational model, we show that prediction-based model signals load on a network including the posterior and perigenual ACC, but outcome evaluation model signals load on the mid-dorsal ACC. These findings are consistent with distinct prediction and evaluation signals as posited by the PRO model and provide new perspective on a large set of known effects within ACC.

1 Introduction

The medial prefrontal cortex (mPFC), and especially the anterior cingulate cortex (ACC), is one of the most commonly identified regions of activation across studies of cognition (Yarkoni et al., 2011). Numerous models have attempted to describe the functions of the ACC, including conflict monitoring (Botvinick et al., 2004; Carter et al., 1998) error likelihood (Brown and Braver, 2007, 2005), outcome unexpectedness (Oliveira et al., 2007; Jessup et al., 2010), volatility (Behrens et al., 2007), error monitoring (Holroyd and Coles, 2002; Steinhauser et al., 2008) and simple time-on-task (Carp et al., 2010; Grinband et al., 2010). While each of these theories has accounted for certain aspects of ACC function, each fails to account for certain important phenomena. As a result, there remains considerable current debate over exactly what is computed within the mPFC (Brown, 2011; Cole et al., 2009; Yeung and Nieuwenhuis, 2009).

We have recently proposed a model that accounts for an unprecedented range of effects observed in the mPFC: the predicted response outcome (PRO) model (Alexander & Brown, 2011; see also Silvetti et al., 2011). According to the PRO model (Figure 1), the mPFC learns to predict the outcomes of actions. Actual outcomes are then compared against predicted outcomes, generating a discrepancy or surprise signal that updates predictions. As a result, the PRO model provides a unifying account of prediction, error, and learning effects that have been localized to the mPFC (Alexander and Brown, 2011). This model is consistent with a number of studies arguing that mPFC represents action values (Croxson et al., 2009; Gläscher et al., 2009; Hayden et al., 2011; Kennerley et al., 2006) and is able to simulate the various effects described above.

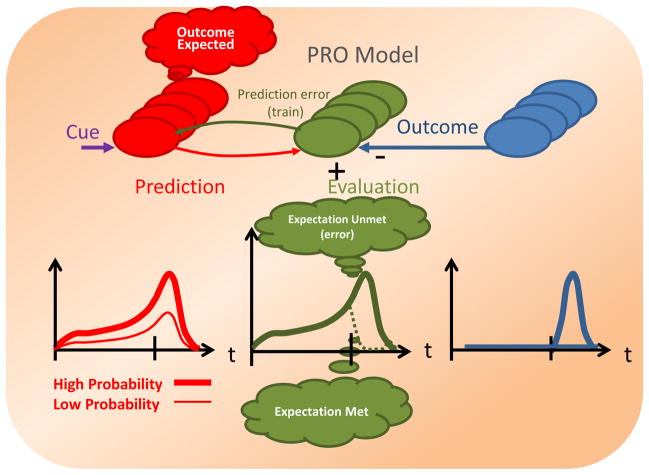
Figure 1.

A general conceptual illustration of the Predicted Response Outcome (PRO) model of anterior cingulate cortex. Left: The Prediction units (red) generate a timed prediction of what outcomes are expected, with what probability, and when. There are four Prediction units (ellipses) shown here for illustration purposes, corresponding to four predicted outcomes, although the number of Prediction units will vary in general with different tasks so that there is one Prediction unit for each corresponding possible outcome. Lower left: Greater probabilities (y-axis) are associated with greater prediction activity, which peaks at the time when the outcome is expected due to the temporal discounting of the probability. Middle: The evaluation units compute negative surprise, i.e. they detect when an expected outcome fails to occur. This is simply the difference between the predicted and actual outcomes and represents how improbable the negative surprise was. The green arc from Evaluation to Prediction indicates that prediction errors from the Evaluation units train and update the prediction signals. Lower middle: Events that are predicted with a high probability yield greater surprise signals (Expectation Unmet) when they fail to occur, but a weaker surprise signal when they do occur (Expectation met). Right: Outcomes occur (i.e. Outcome value rises rapidly and transiently to 1) or fail to occur (i.e. Outcome value is 0) at specific times.

While the PRO model provides a compelling unified theory of ACC function, its main proposal remains untested, namely whether distinct prediction-related and outcome-related signals exist within the ACC. If so, a related question is whether the distinct prediction and outcome signals are found in overlapping regions of ACC, or whether they are largely segregated within different subregions of ACC. The PRO model predicts only that the two signals will exist; it does not predict whether or not they will overlap within regions of the ACC. The current evidence of regional distinctions within the ACC suggests that these two signals may not only exist within ACC but also be spatially distinct. For example, several recent studies have outlined distinct subregions of the ACC based on probabilistic connectivity (Beckmann et al, 2009), dynamic causal modeling (Fan et al, 2008), motor representations (Amiez and Petrides, 2012), neural deficits in schizophrenia (Krawitz et al., 2011), and experimental paradigms incorporating error, conflict, and task-switching effects into a single design (Nee et al., 2011), highlighting the anatomical and functional heterogeneity of the ACC. The current study was designed to test whether a model-based analysis could identify these prediction and outcome processes in the ACC, and if so, whether these processes are spatially distinct or overlapping.

Here we find that distinct regions of the ACC are involved in generating prediction and outcome (i.e. prediction error) signals, in line with the PRO model. To investigate this, we use a task which parametrically manipulates both the number of predictions subjects make and the number of surprising outcomes. We present the same behavioral sequence to both the PRO model and human subjects, and we derive model-based regressors from the PRO model. These are entered as covariates in the fMRI analysis to identify regions that correspond to the theoretical components of the PRO model.

2 Materials and Methods

The Institutional Review Board of Indiana University approved the experimental procedures reported here.

2.1 Participants

Data from 14 right-handed participants (9 female) were collected (mean age = 24.93, SD = 2.92). Participants reported no history of psychiatric or neurological disorder, and reported no current use of psychoactive medications. Participants were compensated $25/hour for their time, in addition to a performance bonus based on how many correct responses they made during the task. Participants were trained on the task on a computer outside of the scanner until they gave verbal confirmation that they understood the task.

2.2 Procedure

2.2.1 fMRI Paradigm

The task was designed to manipulate the neural activity related to predicting and evaluating outcomes. To achieve this, we manipulated the number of outcomes subjects had to predict as consequences of their actions, as well as the degree to which the actual outcomes differed from the predicted outcomes. Subjects were instructed to make two choices regarding a pair of options, and then they were required to predict the outcomes of the choices. Critically, for some trials, participants were required to maintain predictions about each outcome from their pair of choices (Predict2 condition), while on other trials, participants were required to maintain a prediction about only one outcome from their pair of choices (Predict1 condition). These conditions were later contrasted to test for an effect of an increasing number of maintained predictions. Thereafter, the subjects were informed of the outcomes of their choices. Outcomes could violate zero, one, or two predictions thereby providing a parametric effect of expectancy violation. Each participant underwent a behavioral session outside of the scanner consisting of 100 trials. If the participant felt that they understood the task and consented to undergo the scanning paradigm at a later time, each participant completed another 50 trials immediately before scanning to refresh their memory of the task. During scanning each participant underwent 5 runs of 100 trials each, with each run lasting 8 minutes and 40 seconds.

The task consisted of three phases: A choice phase, a prediction phase, and an outcome phase (See Figure 2). During the choice phase, participants were presented with two rows of two boxes, forming a pair of boxes for each row. The two rows of boxes were separated by a white horizontal line. A question mark (“?”) placed in between a row of boxes prompted subjects to choose one box from the row. Choices were to be based on prior outcomes (described below). After choosing between boxes in one row, the question mark moved to the other row. The placement of the first prompt (top or bottom) was randomly counterbalanced across trials.

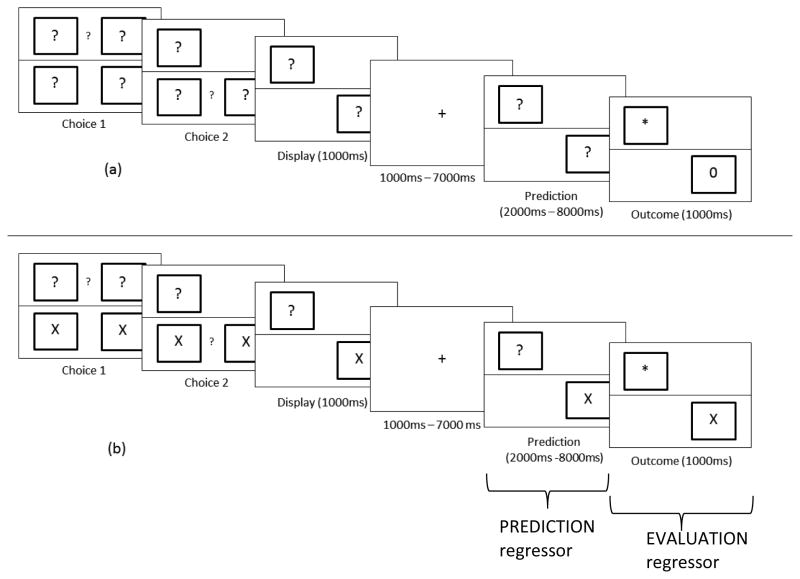
Figure 2.

Task design. Dissociation of decision, prediction, and outcome effects. In each trial, the question mark between the two upper or two lower boxes prompted a choice between the adjacent boxes. After a delay to separate out the decision and motor-related activities, subjects were re-presented with their choices, at which point they could predict the impending feedback to be delivered in the Outcome phase of the trial. Outcomes (“*” and “0”) shown later in the chosen boxes indicated that subjects should choose the same box again on the next trial (stay) or, less commonly, choose a different box on the next trial (switch). (a) In the Predict2 condition, participants made a series of two choices and later received outcome feedback for each choice. During the prediction phase of the task, participants could predict the impending outcome(s). (b) In the Predict1 condition, participants also made two choices, but they knew that they would receive only a single outcome cue. No feedback was given for boxes containing an “X”. Instead, participants were told to repeat their previous choice in the next trial. Hence, there was only a single outcome to predict and evaluate in the Predict1 condition. Overall, the task affords distinct activity estimates of decisions, of predicting 1 vs. 2 outcomes, and of receiving 0, 1, or 2 rare switch feedback cues. The actual stimuli were shown to subjects with the colors inverted, i.e. white stimuli on black background.

During the choice phase, participants chose one box from each row. In the Predict2 condition, all boxes contained a question mark (“?”) which informed the subject that a chosen box would yield an outcome cue (described below). In the Predict1 condition, one of the rows contained boxes with “X”s, which indicated that the chosen box would not yield an outcome. The other row of boxes contained question marks and thus yielded outcomes. As a result, in the Predict2 condition, subjects made two choices that yielded outcomes, while in the Predict1 condition, subjects made two choices, only one of which yielded an outcome. Outcome cues informed subjects whether to choose that row’s box again on the next trial (i.e., a “stay” cue), or to choose the other box in that row on the next trial (i.e., a “switch” cue). Hence, the results of outcomes had to be maintained in order to inform future choices. After the participants made their choices, they were presented with their choices for 1000ms, followed by a fixation cross of a jittered duration, before beginning the prediction phase.

During the prediction phase, participants were re-presented with their choices. This phase signaled to the subject that outcomes would soon be presented and provided a cue for the prediction of those outcomes. Hence, the prediction phase was used to model prediction. Although prediction of outcomes may begin immediately after choices are made, because of the prediction phase’s closer temporal proximity to the actual outcome received by the participants, the PRO model expects prediction-related cells to ramp up during the prediction phase (Alexander & Brown, 2011), a phenomenon that has also been observed empirically (Amador et al., 2000; Hayden et al., 2009; Shidara and Richmond, 2002). Furthermore, this was designated as the prediction phase because it was dissociated from the motor activity preceding it. In the Predict2 condition, both boxes had question marks in the center, signaling that there would be two outcome cues, and that the participant should maintain two separate outcome predictions. In the Predict1 condition, only one box had a question mark in the center while the other box had an “X” in the center, signaling that there would be only one outcome cue and that the participant should therefore maintain one outcome prediction. The prediction phase lasted for a jittered duration up to 7500ms, and was followed by the outcome phase. The condition of predicting two outcomes instead of one outcome was not confounded with working memory load, because even in the Predict1 condition, subjects had to remember the location of the unpredicted outcome in order to choose it correctly in subsequent trials.

Outcomes of the participants’ choices were revealed in the outcome phase. In the Predict2 condition, both of the chosen boxes revealed an outcome cue. In the Predict1 condition, only one of the chosen boxes revealed an outcome cue. Subjects were instructed that in the Predict1 condition, the box with the “X” in the center would not reveal an outcome cue. Subjects were instructed that the outcome of their choices would inform what decision to make on the next trial. Outcomes informed subjects whether to choose the same box as the current trial (stay) or choose the other box (switch). In this way, subjects were motivated to attend to the feedback and update their choices accordingly in subsequent trials. Stay and Switch cues were denoted by “*” and “0” with stay/switch to character mappings counter-balanced across subjects. If subjects performed the task correctly, they would expect to find a stay cue most of the time (p=0.6) in all chosen boxes, and in at least one box if two outcomes were predicted (p=0.8). As a result, we expected that participants would predict a stay cue and that a switch cue would be a violation of that prediction.

Subjects were told that they would receive a reward of $0.05 on every trial if they correctly followed the outcome cue (either switching their response or making the same response on the next trial), and that they would not receive any reward if they failed to follow the outcome cue. This dissociation of receiving either a switch or stay cue and earning reward ensured that the observed effects were not confounded with reward anticipation or error likelihood

Feedback provided information for what options to choose on the next trial. Of particular interest was the phase following the choice phase. During this prediction phase, subjects maintained predictions about the outcome of their choice(s), affording the assessment of prediction-related neural activation. The task was designed to separate these phases of prediction and evaluation so that BOLD responses to each could be estimated independently.

2.2.2 Control paradigm

Thirteen (13) of the participants also underwent a control run before performing the experimental task (one participant failed to complete the control run due to technical issues). During this run, participants were presented with the different combinations of box locations as they would see during the Prediction phase of the experiment (see Figure 2). These were the only stimuli presented during the control block. The presentations of the boxes were separated by a jittered interval with a similar distribution to the jitters during the actual experiment. Participants were instructed to attend to the boxes as they normally would during the experiment and to remain focused. In contrast with the experimental condition described above, they were not otherwise required to respond, and participants were instructed not to form predictions as they would in the experimental task because the computer automatically made choices for the subjects.

The purpose of this control run was to determine whether brain activation for the contrast of predicting two outcomes vs. predicting one outcome (see Imaging Results below) could be explained by visual, eye movement, or attention factors instead of monitoring for multiple action outcomes.

2.3 fMRI analysis

2.3.1 Image acquisition and preprocessing

The experiment was conducted with a 3 Tesla Siemens Trio scanner using a 32-channel head coil. Foam padding was inserted around the sides of the head to increase participant comfort and reduce head motion. Imaging data was acquired at a 30° angle from the anterior commissure-posterior commissure line in order to maximize signal-to-noise ratio in the orbital and ventral regions of the brain (Deichmann et al., 2003). Functional T2* weighted images were acquired using a gradient echo planar imaging sequence [30 × 3.8mm interleaved slices; TE = 25ms; TR = 2000ms; 64×64 voxel matrix; 220×220mm field of view]. For the experimental condition, five runs of data were collected with 240 functional scans each. For the control condition, one run of data was collected with 145 functional scans. High resolution T1-weighted images for anatomical data [256×256 voxel matrix] were collected at the end of each session.

SPM5 (Wellcome Department of Imaging Neuroscience, London, UK; www.fil.ion.ucl.ac.uk/spm) was used for preprocessing and data analysis. The functional data for each run for each participant was slice-time corrected and realigned to each run’s mean functional image using a 6 degree-of-freedom rigid body spatial transformation. The resulting images were then coregistered to the participant’s structural image. The structural image was normalized to standard Montreal Neurological Institute (MNI) space and the warps were applied to the functional images. The functional images were then spatially smoothed using an 8mm Gaussian kernel.

2.3.2 Model-Based Analysis

The PRO model characterizes dACC/mPFC as a region involved with learning to predict likely outcomes and signaling unexpected deviations from predicted outcomes. The model learns temporally discounted estimates of the likelihood of possible outcomes using a temporal difference (TD) learning algorithm (Sutton & Barto, 1990) that has been extended in the following ways. First, the PRO model learns predictions for multiple, independent outcomes, regardless of their affective valence, in contrast to TD learning which learns the aggregate reward value of outcomes weighted by the frequency with which those outcomes are observed. Second, the PRO model generates a vector-valued error signal in order to update model predictions regarding likely outcomes according to the following equation:

$${\delta }_{i,t}=O_{i,t+1}+\gamma P_{i,t+1}-P_{i,t}$$ (1)

where O is a vector reflecting the occurrence of outcomes i at time t+1, P reflects outcome predictions, and γ is a discount factor (γ = 0.95). Model predictions were computed as

$$P_{i,t}={\sum }_j{I}_{j,t}{W}_{i,j,t}$$ (2)

where I is a vector of binary values reflecting the presence (1) or absence (0) of a particular input j at time t, and W is the matrix of weights indicating the discounted estimate of the likelihood of an outcome i for all inputs. Model weights are updated according to

$$W_{i,j,t}=W_{i,j,t}+\alpha {\delta }_{i,t}{\overline{I}}_{j,t}$$ (3)

where α is a learning rate parameter (α = 0.1) and Ī is an eligibility trace computed as

$${\overline{I}}_{j,t}=I_{j,t}+0.95{\overline{I}}_{j,t}$$ (4)

In previously published simulations, the error signal δ was used to dynamically adjust the rate at which new information (in the form of unexpected deviations from expectations) was integrated into the model to allocate top-down control of behavior, allowing the PRO model to fit observed, aggregate behavioral data. For our current analysis, our aim is different in that, rather than fitting behavioral data, we seek to generate trial-by-trial predictions of ACC activity for individual subjects using the sequence of outcomes observed by those subjects in the course of the task. Accordingly, we simulate the PRO model during the period in each trial following the presentation of the predict cue and terminating following feedback. There were two model inputs used during simulations, corresponding with cues given to the subject instructing them to predict the outcome of the top or bottom set of boxes, while four possible outcomes were model, corresponding with feedback to the subject indicating that they should stay or switch for the top and bottom sets.

Four regressors and two parametric modulators were used in GLMs for our model-based analyses. Two regressors modeled left vs. right button presses, as described above. A third regressor, PREDICTION, was modeled as a series of impulse functions at each TR in the interval from the onset of the prediction cue to the delivery of feedback. Finally, the EVALUATION regressor was modeled as an impulse function at the time feedback was delivered. In addition, model-based predictions of neural activity derived from simulations of the PRO model were used to create parametrically modulated PREDICTION and EVALUATION regressors. Participants who committed any errors (N = 8) had two additional regressors included in their analysis – one for the prediction phase on error trials, and one for the outcome phase on error trials. Note that the capitalized words “PREDICTION” and “EVALUATION” refer to different periods within a trial during which subjects will likely be engaging in, respectively, predicting likely outcomes and evaluating observed outcomes. Also, the PREDICTION and EVALUATION regressors are parametrically modulated by the PRO model output, as described below.

Parametric modulators for our model-based analysis were derived from simulations of the PRO model using parameters that were identical to those published previously (Alexander & Brown, 2011), with the exception that each model iteration was interpreted as lasting 100ms, (i.e., each TR corresponded to 20 model iterations). The reason for this change from the original PRO model (Alexander & Brown, 2011) was to allow the model to converge on appropriate predictions given the limited amount of training data (see below). The model was simulated only for the PREDICTION and EVALUATION phases of each trial. Input to the model consisted of two stimuli, corresponding to task cues indicating that the subject would receive feedback related to the top or bottom boxes as described in section 2.2.1. A total of four possible outcomes were modeled: Top/Switch, Top/Stay, Bottom/Switch and Bottom/Stay.

In order to generate parametric modulators for trial-by-trial activity in the behavioral task for a single subject, the PRO model was initially trained on a randomly selected subset of 50 trials (out of 100) that the subject had experienced during scanning. During the training period, weights in the model representing outcome predictions were updated to reflect the model’s estimation of the likelihood of observing specific outcomes (see Figure 1 for a conceptual framework of this process). The intended purpose of the training phase was to faithfully replicate the circumstances of our experimental setup in which subjects completed a control run prior to scanning. Following this initial training phase, the model, using the prediction weights obtained during training, was presented with the complete sequence of 100 trials experienced by that subject during scanning in the order in which the subject experienced them. During this sequence, all model learning rules remained in effect. Model activity was recorded on each 100 ms simulation iteration, and was calculated as the rectified value of current, learned predictions of likely outcomes minus actual outcomes, i.e., negative surprise (Alexander & Brown, 2011), summed over all outcome predictions according to the following equation:

$${\mathit{Activity}}_t={\mathrm{\sum }}_i{\lfloor \mathit{Predicted}{\mathit{Outcome}}_{i,t}-\mathit{Actual}{\mathit{Outcome}}_{i,t}\rfloor }^{+}$$ (5)

where t is the current model iteration, and the superscript “+” indicates positive rectification, i.e. that negative values are evaluated as zero. Note that equation (5) is used to compute model activity for both PREDICTION and EVALUATION parametric modulators in the GLM. In the current analyses, we do not model the complement of negative surprise (positive surprise: observed outcomes minus learned predictions) for two reasons. First, a wide range of activity observed in dACC/mPFC has been accounted for using only the notion of negative surprise (Alexander & Brown, 2011); incorporating only the negative component of surprise, therefore, is a more direct test of one of the central claims of the PRO model. Second, positive and negative surprise tend to be directly (though not perfectly) correlated; the absence of a predicted stimulus is often accompanied by the occurrence of an unpredicted stimulus. In the current study, outcomes are binary and are always presented, and so the values obtained from modeling only negative surprise vs. the combination of negative and positive surprise are correlated perfectly. The value of a Predicted Outcome is a temporally discounted function reflecting both the learned likelihood of a particular outcome i occurring as well as the amount of time until that outcome is expected to occur. On each model iteration, the Predicted Outcome is updated to reflect the current time-discounted predicted likelihood of a predicted outcome occurring. The Actual Outcome is binary, taking the value of 1 on the model iteration t in which a particular outcome is observed, and 0 at all other times. Equation (5) was used to derive parametric modulators for both the PREDICTION and EVALUATION regressors. The parametric modulator for the PREDICTION regressor was calculated for each two second TR as the average model activity of the 20 iterations starting from the TR onset and ending at the iteration immediately preceding the onset of the next TR. The number of TRs per trial varied due to jitter between the onsets of the PREDICTION phase and EVALUATION phase, ranging from 3 to 7. It may seem counter-intuitive that equation (5) can be used to generate both the PREDICTION and EVALUATION signals, but note that during the PREDICTION interval (prior to the occurrence of an outcome, the value for the Actual Outcome is 0 for all i, indicating that an outcome has not yet occurred. Model activity during this period therefore reflects only the time-discounted outcome prediction. In this way, equation (5) reflects the PREDICTION signal prior to the outcome, and the EVALUATION signal afterward. The parametric modulator for the EVALUATION phase was calculated as the average activity from equation (5) during the 20 iterations following the delivery of feedback to the model. The procedure described above was conducted twice for each subject’s data, once in order to generate PREDICTION modulators, and once in order to generate EVALUATION modulators. The independent simulations were identical with the exception that, for the EVALUATION simulations, the time interval between the beginning of the prediction phase and the delivery of feedback was held constant, while simulations used to generate PREDICTION modulators simulated the jittered interval between the onset of the PREDICTION phase and the EVALUATION phase. The rationale for this is that, due to the procedure used to generate jitter intervals, trials with especially long intervals were severely undersampled due to the relative infrequency of long jitter intervals, resulting in a failure of the model to converge on appropriate predictions regarding outcomes at those times. Additional analysis using EVALUATION modulators generated using simulations incorporating jittered intervals showed effects similar to those reported below, albeit with a substantial loss in power due to the unreliability of model predictions regarding outcomes following prolonged jitter intervals.

Unless otherwise stated, all results were thresholded at the voxel-level at p < 0.005. Cluster extent provided corrections for multiple comparisons (p < 0.05 corrected) through AlphaSim (http://afni.nimh.gov/afni/). Based on AlphaSim, whole-brain analyses included a 144 voxel extent criterion.

3 Results

3.1 Behavioral Results

All participants performed the task at a satisfactory level (≥ 95% correct responses per participant, collapsed across correct switches and correct stays). When errors did occur, there was no significant difference between incorrect switches and incorrect stays (t(13)=0.849, P = 0.404). However, participants did commit significantly more errors in the Predict1 condition compared to the Predict2 condition (t(13) = 2.09, P < 0.05). Participants were verbally debriefed after the task, and each participant reported that they had understood the task.

3.2. Model-Based Results

The PRO model postulates that the mPFC/ACC generates predictions of outcomes, which are then compared against actual outcomes to produce a discrepancy signal that drives future learning (Figure 1). Simulations of the PRO model indicate that the mPFC/ACC should be sensitive to the number of predictions, as well as the degree to which predictions are violated. Here, we explore these effects.

3.2.1. Effect of Prediction

In order to determine whether the mPFC/ACC is sensitive to the number of predictions as anticipated by the PRO model, we regressed neural activity onto the model-based PREDICTION regressors generated by the PRO model, and entered these into the GLM as parametric modulators. A one-sample t-test was then carried out on these (mean-centered) parametric modulators, comparing the effect to a population mean of zero. Confirming model predictions, significant loading on the model PREDICTION signal was found in the left anterior portion of the ACC (MNI −6, 26, 26; k = 484 voxels; peak voxel z-value = 3.49; P < 0.001), as well as the caudal cingulate zone (CCZ; MNI −6, −26, 40; k = 12077 voxels; peak voxel z-value = 4.66; P < 0.001), as shown in Figure 3. In addition to the ACC, a network of other regions also showed activity consistent with outcome predictions, including the bilateral insula, which has been implicated in outcome prediction (Preuschoff et al., 2008); (Table 1).

Figure 3.

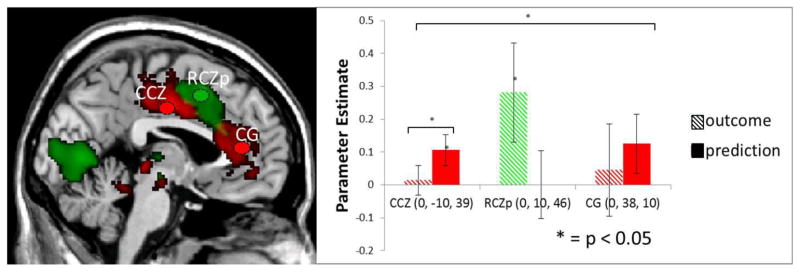
Regions of the CCZ/ACC showing increased activation in response to prediction- and outcome-related effects as predicted by the PRO model, presented at a cluster corrected threshold of p < 0.05. The RCZp and CG ROIs were taken from Nee et al (2011), while the CCZ ROI was created from coordinates reported in Drabant et al (2011). Red: Prediction-related effects; Green: Outcome-related effects.

Table 1.

Activation clusters loading onto the PREDICTION parametric modulators generated by the PRO model. See Results section 3.3.1.

Brain Region (TD)	X	Y	Z	Z-score	Cluster Corrected p-value	Cluster Size
	(MNI)
Effect of model PREDICTION regressor
Left Supramarginal Gyrus	−56	−24	42	5.75	<0.001	12077
Caudal Cingulate Zone*	−6	−26	40	4.66	<0.001
Left Thalamus	−14	−32	0	4.66	<0.001	399
Right Anterior Insula	34	32	−12	4.58	<0.001	929
Left Insula	−48	22	2	3.83	<0.001	950
Left Rostral ACC	−6	26	26	3.49	<0.001	484
Left Inferior Parietal Lobe	−46	−60	10	3.42	<0.05	173

An asterisk (“*”) denotes a sub-cluster of the above cluster.

3.2.2. Effect of Outcome

Similarly, in order to test which cortical areas are associated with violations of predictions, we tested for areas loading onto the model-based EVALUATION (mean-centered) parametrically modulated regressors generated by the PRO model. Signification loading on the model EVALUATION signal was found in the dorsal ACC (MNI 2, 18, 48; k = 671 voxels; peak voxel z-value = 4.17; P < 0.001, cluster corrected). This region was situated in-between areas sensitive to predictions described above, but did not overlap with them (see Figure 3). Other regions loading on the EVALUATION regressors included visual cortex, bilateral insula, bilateral middle frontal gyrus, and left superior frontal sulcus (Table 2). These areas may carry out separate evaluations of prediction error, as has been shown, for example, in the insula (Preuschoff et al., 2008) and visual cortex (Egner et al., 2010).

Table 2.

Activation clusters loading onto the EVALUATION parametric modulators generated by the PRO model. See Results section 3.3.2.

Brain Region (TD)	X	Y	Z	Z-score	Cluster Corrected p-value	Cluster Size
	(MNI)
Effect of model EVALUATION regressor
Visual Cortex	6	−64	0	4.85	<0.001	2509
Left Superior Frontal Sulcus	−26	0	52	4.36	<0.05	202
Dorsal ACC	2	18	48	4.17	<0.001	671
Right Hippocampus	18	−26	−8	4.12	<0.001	531
Left Anterior Insula	−32	22	−6	4.08	<0.01	271
Right Frontal Middle Gyrus	46	6	30	3.99	<0.01	311
Left Frontal Middle Gyrus	−42	−2	24	3.96	<0.05	189
Right Thalamus	10	−20	14	3.92	<0.01	288
Right Anterior Insula	36	18	2	3.59	<0.05	168
Left Parietal Inferior Lobe	−48	−38	38	3.24	<0.05	149

3.2.3. Comparison of prediction and surprise effects

It is also possible that the various dorsal ACC regions were simply more active during different phases of the trial as main effects, independent of any parametric modulation by model-based signals. To explore this possibility, an additional contrast was carried out on the un-modulated PREDICTION and EVALUATION regressors to test the overlap of main effects with the parametric modulators. No overlap was found between the un-modulated, main effect of activity during the PREDICTION phase of the trial vs. the parametric modulator for PREDICTION. For the un-modulated, main effect of EVALUATION, overlap was found with the parametric modulator in the dorsal anterior cingulate cortex with the parametric effect of EVALUATION (significant effect of un-modulated EVALUATION REGRESSOR, MNI −2, 6, 48; k = 3854 voxels; peak voxel z-value = 5.47; P < 0.001). This overlap is expected because multiple predictions are made in a given trial, so one of them is likely to be violated, which would generally elevate activity in regions that compute prediction error and specifically negative surprise. Nevertheless, the parametrically modulated regressors were mean-centered and orthogonal to the corresponding un-modulated regressors, so logically it is possible to see a main effect but not a loading on the parametric modulator in a given region, and vice versa. The results overall suggest some main effect of activation in the dorsal ACC during the EVALUATION phase, but this is not confounded with the distinct loading on the PREDICTION and EVALUATION parametrically modulated regressors.

To test furthermore whether specific brain areas were more responsive overall to the unmodulated PREDICTION regressor as opposed to the un-modulated EVALUATION regressor, a paired t-test was carried out to compare beta estimates for EVALUATION relative to PREDICTION. This comparison revealed significantly greater activity during the EVALUATION phase in the dorsal ACC (MNI 4, 12, 46; k = 4133 voxels; peak voxel z-value = 5.29; P < 0.001), consistent with previous results showing generally strong activity in this region during outcome relative to prediction (Brown, 2009; Jahn et al., 2011). The opposite contrast of PREDICTION minus EVALUATION showed activation mainly in white matter regions.

3.2.4. Dissociation of prediction and surprise effects

In order to test whether each of the ACC regions were preferentially activated to only one of the contrasts and not the other, unbiased ROIs were created in order to test for a significant ROI x Contrast interaction (Nieuwenhuis et al., 2011). Two spherical ROIs (5mm each) were placed in distinct ACC subregions outlined by Nee et al (2011) to demarcate the structural and functional heterogeneity of the ACC without being near enough to have parameter estimates from each ROI unduly affected by smoothing (Figure 3). The first ROI was placed in the posterior rostral cingulate zone (RCZp; MNI center 0, 10, 46). The second spherical ROI was placed in the rostral cingulate gyrus (CG; MNI center 0, 38, 10). An additional 5mm spherical ROI was placed in the caudal cingulate zone (CCZ; MNI center, 0, −10, 39), in order to extend the coverage of our analysis to the posterior regions of the cingulate. The location of this ROI was taken from peak voxel coordinates for a contrast of strong vs. medium anticipation (Drabant et al., 2011). These three regions were selected to serve as unbiased ROIs corresponding to known functional and anatomical subdivisions within the ACC (Fan et al., 2008; Paus, 2001)

A significant ROI x Condition interaction was found (F(2, 26) = 3.75, P < 0.05), driven by greater effects for EVALUATION than PREDICTION in region RCZp, and the reverse pattern (greater effects for PREDICTION than EVALUATION) in both CG and CCZ (Figure 3). Within each ROI, paired-t-tests were conducted to test for significant differences between the effects of PREDICTION and EVALUATION. Bonferroni correction for multiple comparisons was used when comparing mean differences, resulting in a corrected critical t-value of 2.75. Within RCZp there was a significant effect of EVALUATION (t(13) = 3.54, P < 0.01) and a non-significant result of PREDICTION (t(13) = 0.34, P > 0.05), with a paired t-test between the conditions showing no significant difference (t(13) = 2.32, P < 0.05). The opposite pattern was found within CCZ with a significant effect of PREDICTION greater than EVALUATION (t(13) = 3.13, P < 0.01), driven by a significant effect of PREDICTION (t(13) = 4.30, P < 0.01) and a non-significant result of EVALUATION (t(13) = 0.45, P > 0.05). Within CG, there was a trend towards a significant effect of PREDICTION (t(13) = 2.37, P < 0.1) but no effect of EVALUATION (t(13) = 0.76, P > 0.05), although a paired t-test revealed no significant difference between the parameter estimates (t(13) = 1.31, P > 0.05). Overall, these results lend support to the proposal that distinct sub-regions of the ACC are involved in prediction and outcome calculations, which is consistent with the PRO model.

3.3. Control Analysis

A control run was presented to thirteen subjects, in which the same prediction phase images were presented to the subjects, but no responses were made and no predictions formed. Within the independent ROIs of CCZ and CG, parameter estimates were extracted for the contrast Predict2-Predict1 of the control run, and compared to parameter estimates for Predict2-Predict1 of the experimental runs. Within CCZ, the Predict2-Predict1 contrast for the experimental runs was significantly greater than zero (t(12) = 3.49, P < 0.01), while the same contrast for the control run was not significantly greater than zero (t(12) = −0.29, P = 0.77). For region CG, on the other hand, the Predict2-Predict1 contrast was significantly greater than zero (t(12) = 3.27, P < 0.01), while prediction-related activity for the control run was significantly less than zero (t(12) = −3.59, P < 0.01; Figure 4). These results suggest that prediction-related activity was not solely driven by oculomotor or attention-related processes.

Figure 4.

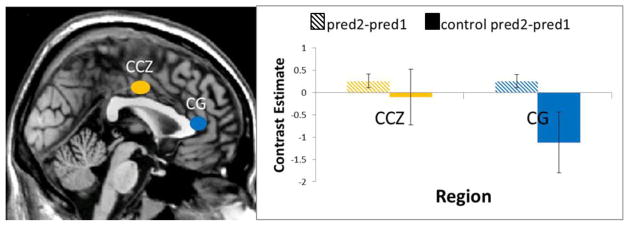
Regions of the posterior cingulate (CCZ) and anterior cingulate (CG) showing increased activation for predicting 2 outcomes (Predict2) as opposed to predicting 1 outcome (Predict1). Within these independent ROIs, parameter estimates were extracted for the control condition. A paired t-test in both regions revealed that the parameter estimates for the Predict2-Predict1 contrast were significantly greater than for the control contrast. The control condition did not pass any corrected thresholds in a whole-brain analysis.

4. Discussion

4.1 Model-based regressors reveal anatomically distinct areas of ACC in prediction and outcome

Using model-based regressors generated by the PRO model, we found that prediction-related signals loaded onto posterior and perigenual portions of the ACC. This prediction effect did not overlap with a medial supracollosal region of the ACC that showed a complementary effect of outcome evaluation (Figure 3). The finding of distinct prediction and evaluation regions within mPFC is consistent with the corresponding theoretically distinct prediction and evaluation mechanisms of the PRO model. Previous studies have shown anticipatory signals in ACC (Aarts et al., 2008; Sohn et al., 2007), but it has been unclear whether these areas of the ACC were the same as those that generate outcome-related signals (Dehaene et al., 1994; Gehring et al., 1993; Holroyd and Coles, 2002). Here, we found that the regions in mPFC encoding prediction signals are distinct from other regions of the mPFC that encode outcomes.

Other studies have suggested regional dissociations within the ACC in cognitive tasks, and our findings account for earlier regional dissociations in the framework of the PRO model. Behrens et al. (2007) reported distinct social vs. reward learning volatility effects in the anterior cingulate gyrus and sulcus, respectively. We previously demonstrated that volatility effects could be understood as reflecting an outcome evaluation signal in the PRO model (Alexander & Brown, 2011). The current results show that the region with EVALUATION effects includes both of the regions where reward and social volatility effects have been reported (Behrens et al., 2007). Also, three distinct cingulate motor areas have recently been reported in the human (Amiez et al., 2012). Interestingly, the three human cingulate motor areas show substantial overlap with the corresponding three PREDICTION and EVALUATION regions found here in the ACC. The EVALUATION region in particular coincides with a region that has topographic connections with widespread regions of lateral prefrontal cortex (Beckmann et al., 2009; Blumenfeld et al., 2012; Taren et al., 2011).

Our results challenge other theories of ACC function, in particular conflict monitoring theory (Botvinick et al., 2001). Conflict monitoring theory posits that mutually incompatible response processes can account for greater activation within ACC. However, it is unclear how the conflict model could account for the observed PREDICTION regressor effects, because the time period of prediction is separate from the action periods when conflict might be present. Similarly, it is unclear how the conflict model could account for the EVALUATION regressor effects, as again there is no overt action associated with learning the outcome.

In contrast, the present results add to a growing body of findings that are consistent with the ACC as a region that predicts and evaluates outcomes, as exemplified in the PRO model. We have previously demonstrated that apparent conflict effects in ACC can be found even when the task is manipulated such that the responses are not in conflict with each other, although our previous design did not distinguish prediction vs. outcome signals (Brown, 2009). Nevertheless, such data cannot be accommodated by the conflict monitoring model, but according to the PRO model, apparent conflict effects may instead result from a prediction of multiple possible responses on conflict trials (i.e. both correct and incorrect outcomes are possible with incongruent trials), vs. a single predicted outcome (i.e. correct on congruent trials). The present results now suggest that such a prediction signal may be presented in the posterior and perigenual ACC. Likewise, we and others have found that error effects (Gehring et al., 1993), which have been argued to represent conflict (Yeung et al., 2004), may instead represent surprise. In particular, error effects reverse when errors are more common than correct trials (Ferdinand et al., 2012; Jessup et al., 2010; Oliveira et al., 2007). The PRO model simulates both error and surprising correct outcome effects in a single EVALUATION regressor (Alexander and Brown, 2011), and the present results now suggest that such a signal is represented specifically in the mid-dorsal cingulate.

The results are consistent with a growing body of literature suggesting that ACC is involved in representing action values (Kennerley et al., 2006; Croxson et al., 2009; Glascher et al., 2009; Hayden et al., 2011). In addition, these results are consistent with other neuroimaging and modeling work of the mPFC, including Bayesian modeling of absolute prediction error between expectation and outcome phases (Ide et al., 2013), Bayesian modeling of hierarchical prediction errors (Iglesias et al., 2013), and updating one’s prior beliefs about the environment in order to form more accurate predictions about response-outcome associations (O’Reilly et al., 2013). Notably, the prediction and outcome effects discussed in these studies show similar patterns of brain activity as shown in the current paper. Furthermore, the results provide empirical support for the theoretical prediction of two interacting prediction and evaluation components that subserve performance monitoring: predicted action values are represented in a network of regions including the ACC, and these in turn provide a basis against which other regions of the ACC evaluate ongoing behavior. Actions that fail to yield an expected level of reward at the time of outcome may be evaluated within the ACC as requiring corrective action, such as a change in strategy (Hayden et al., 2011; Kennerley et al., 2006) or an impetus to forage in order to find a more valuable action (Kolling et al., 2012).

One potential issue with our model-based analysis is that outcomes presented at especially long jitter intervals are undersampled in our design, resulting in a failure of the PRO model to converge on appropriate predictions for outcomes presented following infrequent long intervals. In order to address this issue, we simulated the PRO model twice for each subject, once in order to generate parametric modulators for the PREDICTION regressor during which jittered intervals were simulated as they were experienced by the subject, and once in order to generate EVALUATION modulators, during which intervals were set to the most common jitter interval (60 model iterations). This approach ensured that model predictions at the time of feedback converged on the likelihood of observing the various outcomes associated with the task. Other possible strategies for addressing this issue are possible. One such strategy for generating parametric modulators might involve more extensive training of the model on synthetic data in order to resolve the problem with undersampling long-jitter trials in order to allow the model to converge on appropriate predictions. An additional option would be to model only those trials in our GLM with the most frequently observed jitter intervals. Finally, in order to prevent undersampling of specific intervals during the experiment, jitter intervals might be sampled from a uniform distribution of possible jitter intervals (rather than an exponential distribution), although this approach would impact overall efficiency of the experimental design (Dale, 1999).

4.2 Ruling Out Alternative Explanations

One potential explanation for the prediction results is that the dual-task nature of making two predictions could drive ACC activity. A previous study of dual-task performance found activation in perigenual ACC (Dreher and Grafman, 2003), and that region overlaps with the region found here in response to prediction. However, this previous study used a block design that did not distinguish response, prediction, and outcome feedback conditions as we have done here. Our results show that the ACC region with multiple outcome prediction effects is specifically active during the prediction phase of a trial as distinct from the response or outcome phase. Thus, is it likely that if the same region is active during dual-task performance, such activity may reflect predictions of the outcomes associated with performing each of the two tasks rather than task responses or feedback evaluation (Brown, 2009; Jahn et al., 2011).

One particularly interesting result of the EVALUATION analysis was a significant cluster of activation in the visual cortex, in addition to the observed dorsal ACC cluster. Surprising outcomes may call for increased attention to inputs reflected here in greater visual activity. By increasing the activity of inputs, the cognitive system may be better suited to gather contextual information that can account for discrepancies between expectations and outcomes thereby minimizing future prediction errors. While increased attention may explain both visual and ACC activation, it is unclear how such an account could explain the various effects ascribed to the ACC that are predicted by the PRO model. Instead, we suggest that distinct mechanisms govern the ACC and visual activations.

Another set of confounding factors to be ruled out is the potential effect of errors or error likelihood. In the Predict2 condition, there were two opportunities to fail at finding the stay cue, which in principle might lead to greater error likelihood effects in the Predict2 vs. Predict1 conditions, as well as potentially greater error effects. However, we designed the task to dissociate errors vs. the absence of one or both stay cues. Subjects were given a monetary incentive to perform the task correctly. Crucially, the reward was given for following the win-stay/lose-shift strategy, and this contingency was explained explicitly to the participants as part of the task instructions. The reward available did not differ between Predict1 vs. Predict2 trials, nor was the reward reduced if subjects received a switch cue, provided that they followed the task rules. In this way, even though receiving a switch cue was unexpected, it was not to be considered an error provided that subjects followed the task rules. Thus, the effects of one or two switch cues can be attributed to surprise or switching, but not to errors in terms of gaining reward. Furthermore, the error rates were low overall, so the effects are not likely to be attributable to differences in error likelihood across conditions. If anything, participants were more likely to commit error in the Predict1 condition compared to the Predict2 condition, which would argue against an interpretation of this effect in terms of error likelihood. Thus, it is unlikely that the observed effects represent error-related processes.

Although several other computational models of mPFC function could be considered, the task design makes it difficult to carry out a quantitative model comparison. As the current paradigm modeled both prediction and outcome phases, it would not be a direct comparison to include models for which model behavior is undefined for prediction (e.g., reinforcement learning; Holroyd & Coles, 2002), undefined for outcome (e.g., error likelihood; Brown & Braver, 2005), or undefined for both prediction and outcome (e.g., conflict monitoring or time on task; Botvinick et al, 2004; Grinband et al, 2010). Furthermore, a model of mPFC activity such as the reward value and prediction model (RVPM; Silvetti et al, 2011) is too similar to the model used here to serve as a viable alternative model.

Overall, it is unclear how existing theories other than the PRO model could account for the present results. Other proposed theories cast ACC as computing error likelihood (Brown and Braver, 2005), volatility (Behrens et al., 2007), time-on-task (Carp et al., 2010; Grinband et al., 2011), differences between actual vs. intended responses (Scheffers and Coles, 2000), differences between actual vs. intended outcomes (Holroyd and Coles, 2002; Ito et al., 2003), and predicted action values (Scheffers and Coles, 2000; Walton et al., 2004). The prediction effect occurs at a time that is temporally dissociated from response processes, so it is unlikely to involve response conflict. The interval between prediction and outcome has the same distribution in the Predict1 and Predict2 conditions, so it is unclear how a time-on-task account could explain the prediction effect. Furthermore, the outcome events are modeled separately from the prediction events and with a variable interval between them, so the prediction and outcome events can be estimated independently of each other. Lastly, the nature of the task contingencies does not change throughout the course of the experiment, so volatility differences are unlikely to play a role. To the best of our knowledge, the PRO model is the only existing framework that can account for the multiple outcome prediction effect found here. Furthermore, we have recently shown that a computational simulation of the PRO model can reproduce the various effects that have been cited as evidence for all of these various theories of ACC function above (Alexander and Brown, 2011), as well as generating the regressors used to model the prediction and outcome effects identified here. Thus, our results are consistent with the PRO model as a unifying theory of ACC function.

Highlights.

• The PRO model predicts that prediction and outcome signals are in mPFC.

• Model-based regressors for prediction and outcome were applied to FMRI data.

• We found distinct regions of ACC associated with prediction and outcome processes.