Abstract
This paper outlines the first attempt to segment the boundary of preclinical subcutaneous tumors, which are frequently used in cancer research, from micro-Computed Tomography (microCT) image data. MicroCT images provide low tissue contrast, and the tumor-to-muscle interface is hard to determine, however faint features exist which enable the boundary to be located. These are used as the basis of our semi-automatic segmentation algorithm. Local phase feature detection is used to highlight the faint boundary features, and a level set-based active contour is used to generate smooth contours that fit the sparse boundary features. The algorithm is validated against manually drawn contours and microPET images. When compared against manual expert segmentations, it was consistently able to segment at least 70% of the tumor region (n=39) in both easy and difficult cases, and over a broad range of tumor volumes. When compared against tumor microPET data, it was able to capture over 80% of the functional microPET volume. Based on these results, we demonstrate the feasibility of subcutaneous tumor segmentation from microCT image data without the assistance of exogenous contrast agents. Our approach is a proof-of-concept that can be used as the foundation for further research, and to facilitate this, the code is open-source and available from www.setuvo.com.
1. Introduction
X-Ray Computed Tomography (CT) is a commonly used technique for acquiring in vivo 3D volumetric images. The images are formed by the attenuation of x-rays as they pass through the object, and provide clear information regarding internal anatomical structures wherever there are strong differences in linear attenuation coefficient (which is dependent on material density and atomic number). CT images are able to identify certain types of pathology such as lung tumors, where the tumors are clearly visible against a background of air-filled lung tissue, but they are well known to lack soft tissue contrast, and this limits its ability to differentiate most internal tissues.
Murine subcutaneous tumor models are a mainstay of preclinical oncology research. They involve solid tumors grown between the skin and muscle, and provide simple models for evaluating the efficacy of new therapeutics. Subcutaneous tumors are frequently imaged with a combination of Positron Emission Tomography (PET) and CT using integrated PET/CT scanners. The PET image data provides in vivo images of specific biological processes, such as metabolism or hypoxia, occurring within the tumor. Tumor-specific PET signals are frequently produced by a biologically active subset of cells within the tumor, but the biologically inactive cells are indistinguishable from normal tissue, and this makes it difficult to quantify the proportion of PET-positive and negative tumor cells within the tumor. The CT data provides an anatomic reference for the PET data, and in theory it could yield an accurate tumor boundary to superimpose over the PET data. In practice the tumor-muscle interface is hard to delineate due to the lack of soft tissue contrast, and as a result this is rarely done except by manually performed segmentations. Partially automated subcutaneous tumor segmentation has been demonstrated using contrast-enhanced flat-panel detector CT (Missbach-Guentner et al. 2008) and T2-weighted MRI (Montelius et al. 2012), however to our knowledge, there has been no prior work on using image processing to segment subcutaneous tumors using non-contrast CT images.
In this paper we describe a semi-automatic algorithm for segmenting the boundary of murine subcutaneous tumors from microCT image data, which is able to locate the tumor-muscle interface. Our method does not use any exogenous contrast agent, and can work using attenuation corrections CT scans which accompany PET images on integrated PET/CT scanners. It relies on the presence of faint features at the tumor-muscle interface which are a result of the tumor being separated from the muscle by a thin layer of blood vessels and connective membranes. This layer, which is less dense than the surrounding tissue, can be observed as slightly dark regions in microCT images (Figure 1). By using an intensity-invariant feature detection method to emphasize these features, along with an active contour with a strong smoothness constraint, it is possible to develop an algorithm that can automatically segment the tumor boundary.
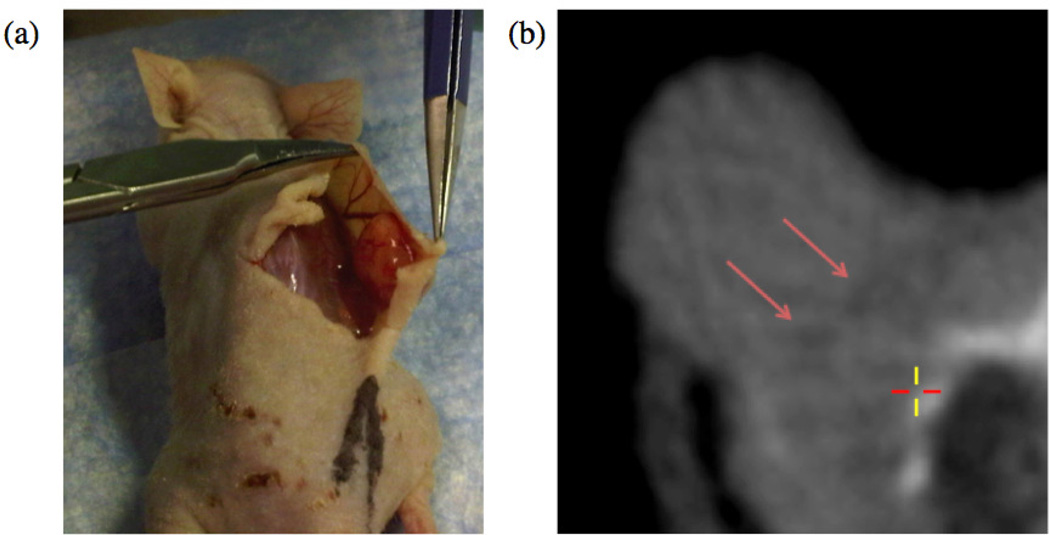
Figure 1.
(a) A shoulder-borne subcutaneous tumor being cut away from the mouse body. The tumor is a self-contained mass which does not invade into the underlying muscle. (b) An axial microCT slice of the tumor exhibiting faint dark features at the tumor-muscle boundary (highlighted with red arrows).
The algorithm described in this paper is validated against manual segmentations and microPET images. The complete open-sourced application, along with videos demonstrating the method, can be found at www.setuvo.com.
2. Materials and Methods
2.1. Image Acquisition
Animal studies were approved by the Administrative Panel for Lab Animal Care (APLAC) at Stanford University. For subcutaneous tumors, 6 week old male nude mice were injected with 1 million A549 human lung carcinoma tumor cells under the skin of each shoulder, and tumors were grown for six weeks. For orthotopic breast tumors, 1 million MDA-MB-231 human breast adenocarcinoma cells were injected into the mammary fat pads of 6 week old female mice. Tumors were grown for eight weeks prior to imaging.
For imaging, animals were injected with 7.5MBq of 18F-EF5 or 18F-FAZA via tail vein injection and imaged three hours later. Following anaesthetization using 2% isofluorane, mice were imaged with a Siemens Inveon microPET/CT. An attenuation correction CT scan was first acquired, followed by a 10 minute PET scan. The microCT datasets were reconstructed using a Filtered Back Projection algorithm to a resolution of 480 × 480 × 632, with a voxel length of 0.21mm in each axis. The PET list mode data was binned into a single frame and reconstructed using an OSEM (Ordered-Subsets Expectation Maximization) algorithm to a resolution of 128 × 128 × 159, with a voxel length of 0.77 mm in the x and y axes, and 0.79 mm in the z axis.
2.2. Pre-Processing
Two thresholds were applied to the microCT data I(x, y). The threshold ta to separate tissue from air, and tb to separate tissue from bone. The bone map obtained by thresholding with tb was subjected to a morphological dilation which expanded the bone regions by 2 voxels in all directions, yielding a binary map Ibone. An exclusion map, Iex, is constructed using the equation
| (1) |
A sample exclusion map is shown in Figure 2b.
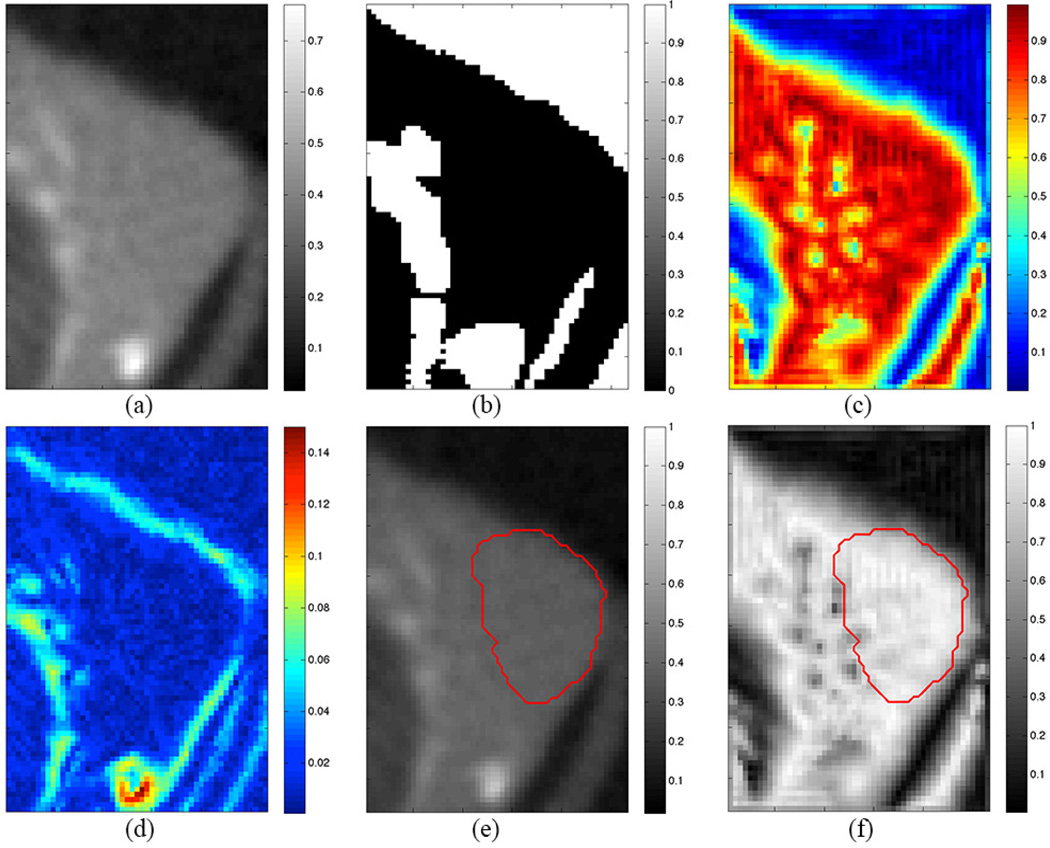
Figure 2.
(a) Axial microCT slice of subcutaneous tumor. (b) Exclusion map highlighting air and bone (white regions). (c) Local phase map highlighting faint boundary features (yellow spots). (d) Gradient map. (e,f) Segmentation result from algorithm (red contour) superimposed on microCT image (e) and local phase map (f).
2.3. Local Phase Feature Detection
Local phase is a commonly used concept for detecting features in 1D signal processing in an intensity-invariant manner. A suitably chosen even bandpass filter, be(t), and its Hilbert Transform, bo(t), which is odd, can be applied to a signal f(t) to yield information on its shape (local phase, φ) and magnitude (local energy) at any given point. The local phase of a 1D signal f(t) is defined in (Boukerroui et al. 2004) as
| (2) |
and describes the differential response of the signal to the odd and even filters (Figure 3). The result is a measure of the odd or even symmetry of the localized signal feature. This principle can be extended to multiple dimensions using Felsberg's Monogenic Signal framework (Felsberg & Sommer 2001), where it is used as an intensity-invariant image-based feature detector.
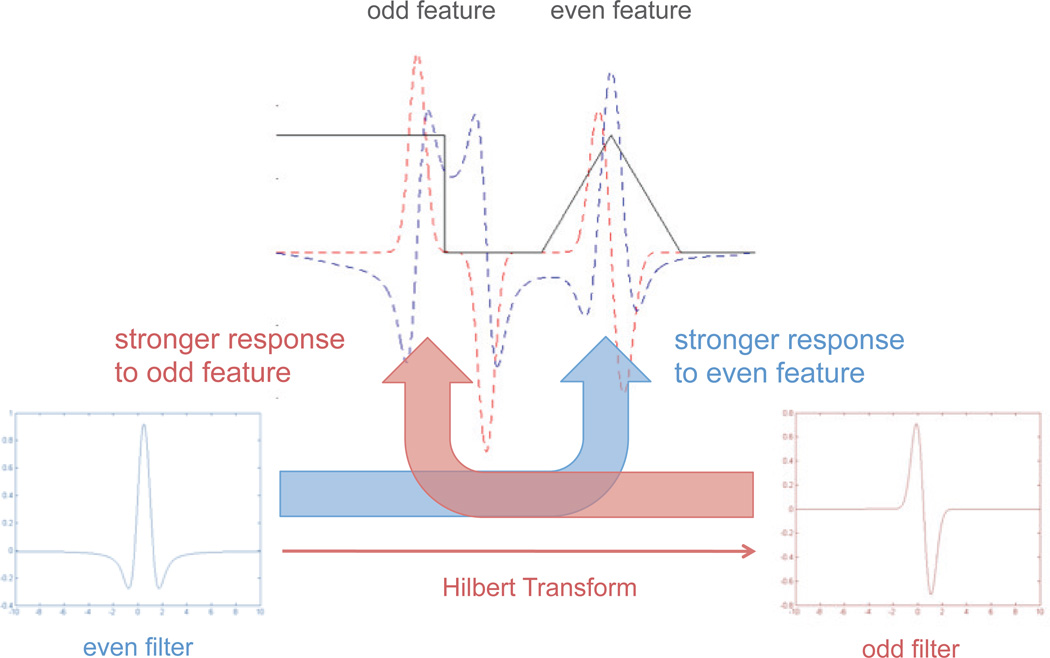
Figure 3.
Local phase relies on the differential response of odd and even filters to odd and even symmetric features. A 1D signal (black line) is shown containing an odd feature (step function) and an even feature (triangle function). When an even 1D Difference of Gaussians filter is convolved with the signal, the output (blue dashed line) is stronger for the even feature. The Hilbert Transform is used to generate a quadrature odd filter from the initial even filter, and this yields a stronger response to the odd feature (red dashed line).
The bandpass filter is generated using a rotationally invariant filter (Mellor & Brady 2005),
| (3) |
where α = 3.25 and β = 0.25. Using this, local phase φ is computed as described in (Mellor & Brady 2005), using the equation
| (4) |
where I is the image, be is the even bandpass filter, and h1, h2 are vector-valued filters which generate a quadrature pair of odd filters when convolved with the even bandpass filter. These vector-valued filters are generated using an extension of the Hilbert Transform known as the Reisz Transform (Felsberg & Sommer 2001), and they enable the generation of higher dimension odd filters. In the 2D frequency domain, these filters are defined as
| (5) |
| (6) |
where u1, u2 are the spatial frequencies resulting from the 2D Fourier Transform of I(x, y).
The Felsberg formalism is naturally extensible to higher dimensions, which is useful for our current application. Wang et al. defined 3D local phase as
| (7) |
where h1, h2, h3 are the transfer functions of
| (8) |
| (9) |
| (10) |
thus allowing local phase to be computed on volumetric data (Wang et al. 2009). Figure 4 shows the local phase map for a single slice from a microCT volume, and it can be seen that faint features at the interface between the tumor and body are highlighted in blue.
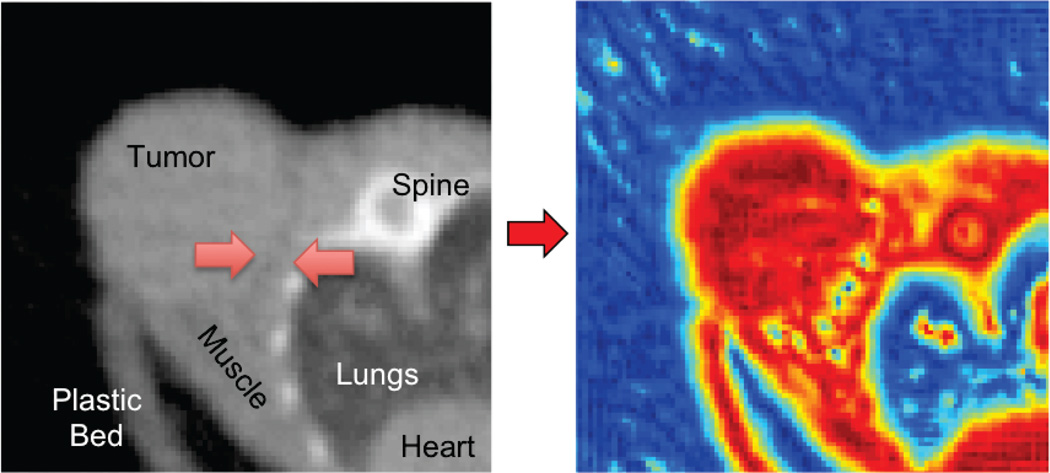
Figure 4.
An axial microCT slice of a subcutaneous tumor (left), and its corresponding local phase map (right). The faint interface features highlighted with red arrows on the microCT image are emphasized in the local phase image as yellow/blue dots.
2.4. Level Set Segmentation
A 3D level set is used to segment the tumor boundary using a combination of the local phase and exclusion maps, based on the implementations described in (Lefohn et al. 2004) (Mostofi 2009). A signed distance function ϕ is initialized using a user input click within the tumor volume, and this is evolved using the level set PDE
| (11) |
where α is a weighting coefficient for the two terms. The second term defines the regularizing curvature term, which enforces a smoothness constraint on the boundary. The F term within the bracket describes an image-based speed term where
| (12) |
where φ is the local phase map (Equation 7), T defines a target threshold local phase value, ε defines a margin around that threshold, Iex is the thresholded microCT image defined in Equation 1 and β is a weighting factor for the gradient term. If the level set boundary lies on a voxel whose local phase value lies within (T – ε) < T < (T + ε) then it will experience a positive growth force at that point, otherwise it will experience a negative shrinking force. The exclusion map Iex causes the level set to experience no force if it ventures out into the excluded regions (air and bone). In these instances, it will undergo smoothing (and a slight amount of shrinkage) due to the curvature term. The gradient term is used because the local phase of the tumor-muscle interface features are of a similar value to the tumor-air perimeter voxels, and therefore the speed term is boosted in this region to encourage the level set to extend to the tumor-air boundary. A sample gradient map is shown in Figure 2d.
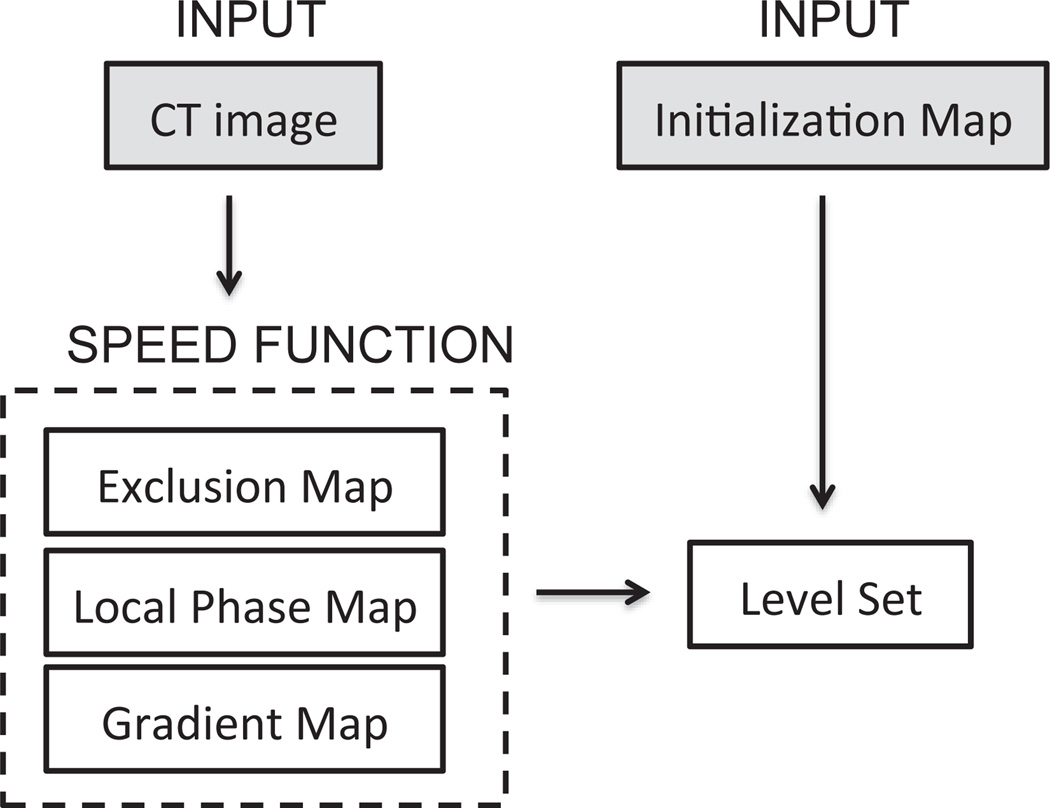
The level set equation is solved in C using upwind differencing (Osher & Fedkiw 2002) and the narrow-band implementation described by (Lefohn et al. 2004). The parameters used are shown in Table 1. Most of the parameters are determined via observation of the microCT image and local phase data values for the boundary features, however optimization is performed for α and β by comparing outputs for a range of values (0.55 < α < 0.75 and 0 < β < 10). The segmentation algorithm is written in Matlab using a GUIDE-based interface for simple user operation, and the level set is called through a MEX function. The whole algorithm is summarized in Figure 5.
Table 1.
Summary of parameters for the CT tumor segmentation algorithm. MicroCT data and local phase maps are normalized to range 0–1.
| Parameter | Symbol | Approximate Value |
|---|---|---|
| CT air threshold | ta | 0.1 |
| CT bone threshold | tb | 0.9 |
| Level set weighting | α | 0.65 |
| Local phase margin | ε | 0.15 |
| Local phase threshold | T | 0.9 |
| Gradient map contribution | β | 5.0 |
Figure 5.
Outline of segmentation algorithm.
2.5. Validation
The segmentation results are assessed by comparison against manually segmented tumors. The manual contours were drawn by a radiation oncology resident with experience in CT tumor segmentation, using image features that defined the surgical flat plane (the interface between the tumor and muscle tissue layers). Each manual segmentation is accompanied with a confidence value between 1–5 which represents the resident's confidence in identifying the correct boundary. Low confidence values of 1–2 were due to small or irregular tumors with few flat plane features, or tumors that were proximal to a forelimb. High values of 4–5 were due to large tumors and/or excellent flat plane features. The software used for manual contouring was Amira 5.4.3 software (Visualization Sciences Group, Burlington, MA).
The Dice similarity metric (Dice 1945) is computed to determine the level of agreement between the algorithm output and the manually drawn tumor boundaries. Given two segmentation regions A and B, the Dice measure is given by
| (13) |
where n(·) represents the number of voxels included in a region. The Dice measure produces values between 0 and 1, where 1 represents perfect overlap.
Segmentation boundaries were also compared against co-acquired (and co-registered) 18F-EF5 microPET images. The tumor microPET signal was automatically segmented by a 3D region growing algorithm. A manually placed seed point was used to grow out a continuous region up to a fixed intensity threshold TPET = 1.5(Imuscle), where Imuscle is by the mean PET intensity (defined as % injected dose per unit volume) in a reference muscle. This approach mimics the approach used clinically in defining hypoxic regions from hypoxia PET tracer data using a tumor-muscle ratio of 1.5 (Komar et al. 2008).
3. Results
Figure 2 shows the output from each step of the algorithm. The white regions in the exclusion map (Figure 2b) dictate no-go areas for the level set. The local phase map (Figure 2c) shows the tumor and tissue in red (0.8 ≤ φ ≤0.95), and the level set parameters ε and T are set to grow in these regions. The interface features are represented in the local phase map as blue regions (φ ≤ 0.6). The tumor-air boundary voxels have similar local phase values (0.5 ≤ φ ≤ 0.7), corresponding to the relatively dark layer of tumor voxels on the air boundary due to partial volume effect, and this causes the level set to terminate early. To counteract this, the gradient map (Figure 2d) is added to the local phase map to raise the values of the air boundary voxels, thus encouraging the level set to propagate to the true boundary.
Figures 2e shows the results of the level set (red contour) superimposed over the original microCT image, and Figure 2f shows the level set result superimposed on the local phase map. The level set is clearly arrested when it encounters the local phase boundary features, and the curvature term prevents it from leaking out from the edges where fewer features are available.
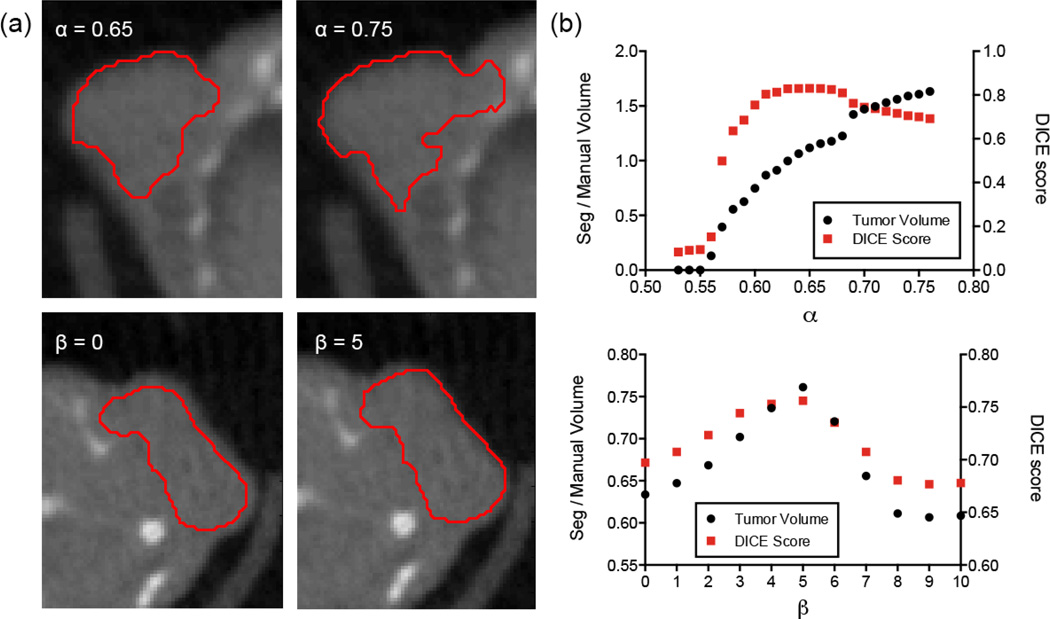
The effect of the key parameters is shown in Figure 6. Two parameters are optimized, α in Equation 11 and β in Equation 12. The most important term is α, the speed function tuning parameter which determines the relative contribution of the local phase map and the curvature term. When α is too high, the local phase term dominates and the level set spills out into the neighboring tissues. Conversely, when α is too low, the curvature term dominates and the level set undergoes a net shrinkage. The plot in Figure 6b shows that α is relatively insensitive to small variations around the optimal value (α ± 0.05), but the segmentation quality degrades rapidly outside this range. The second term, β, controls the gradient map weight. When β is close to zero, the level set doesn't reach the tumor-air boundary. The optimum value is found around β = 5, although the algorithm is relatively insensitive to variations in β. The parameter values in Table 1 were found to work with most of the analysed tumors, with minor variations in α yielding improvements in some cases.
Figure 6.
(a) Images showing the effect of varying α and β. (top row) Effect of varying α in Equation 11. If α is too high then the level set spills out into the neighboring tissue. (bottom row) Effect of varying β in Equation 12. If β is too low then the level set doesn't extend all the way to the tumor-air boundary. (b) Plots of α and β against relative tumor volume (segmentation volume/manually drawn volume) and Dice score for parameter optimization.
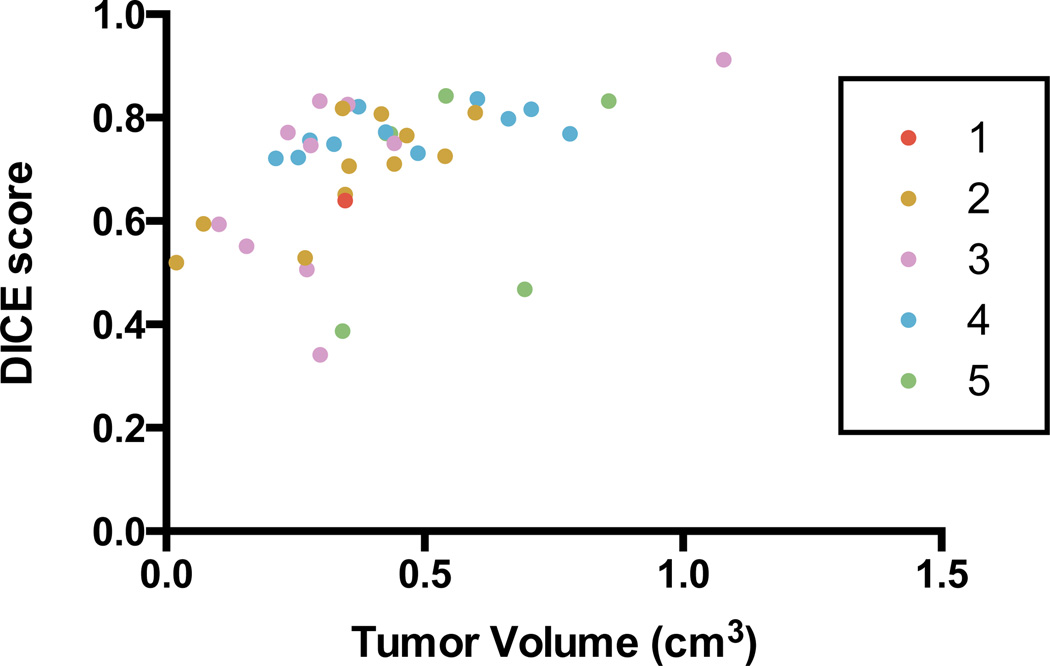
Figure 7 summarizes the segmentation results against manual segmentations (n = 39) for A549 subcutaneous tumors. When compared against manual segmentations, the algorithm achieves consistently high Dice scores (mean Dice score is 0.71; 95% confidence interval is 0.67–0.75) across a range of tumor volumes (range 0.1 – 1.1 cm3). The algorithm is able to perform well in simple and difficult cases (as determined by the resident's confidence in each contour). Six tumors obtain Dice scores less than 0.5. Examination of these tumors reveals two causes of the low scores. The first is that the algorithm underestimates the manually drawn boundary, and in the case of small tumors, this results in a higher proportion of false-negative voxels which impacts the score. The second is that the level set overshot the true boundary due to a lack of strong tumor-tissue interface features to constrain it.
Figure 7.
Evaluation of segmentation results against manual segmentations using DICE scores. Each tumor is colour-coded according to the confidence of the resident in drawing the boundaries. Scores range from 1 (low confidence) to 5 (high confidence).
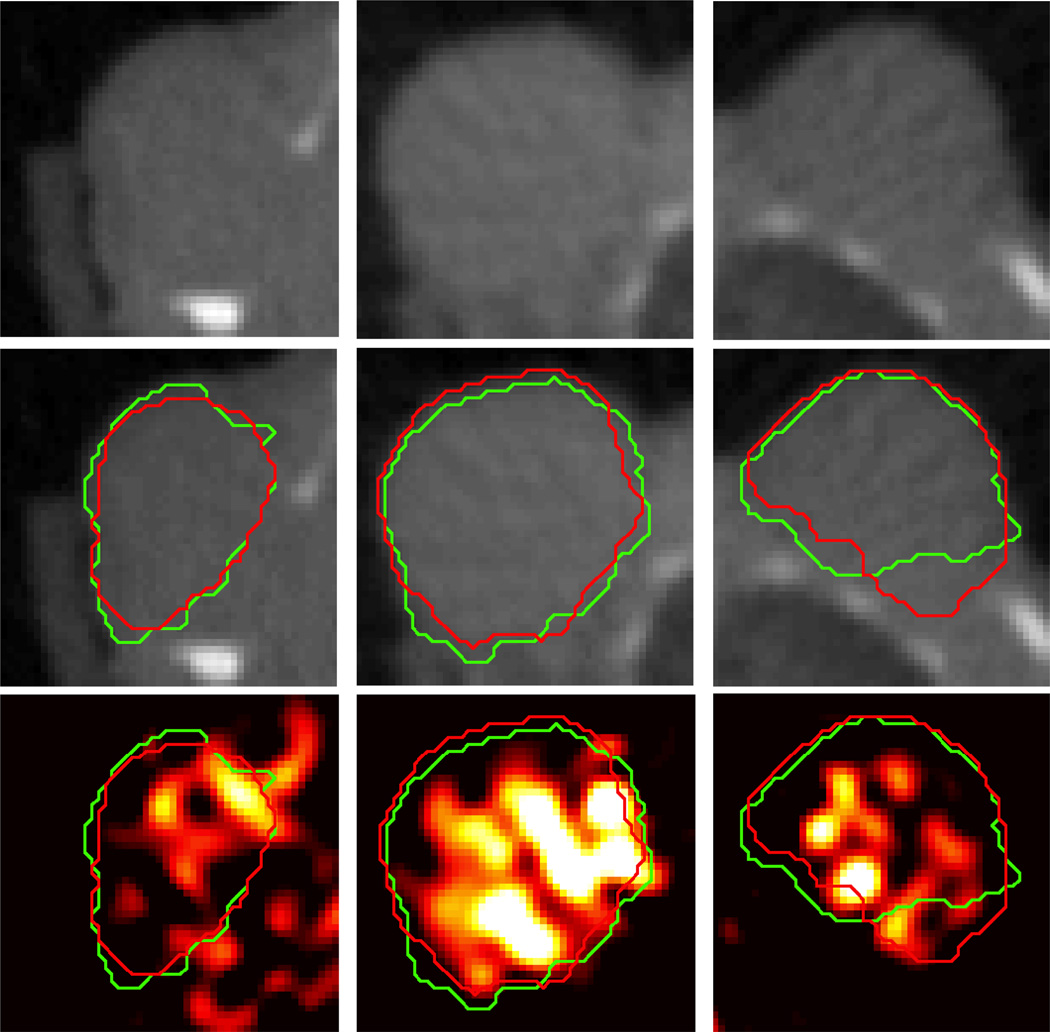
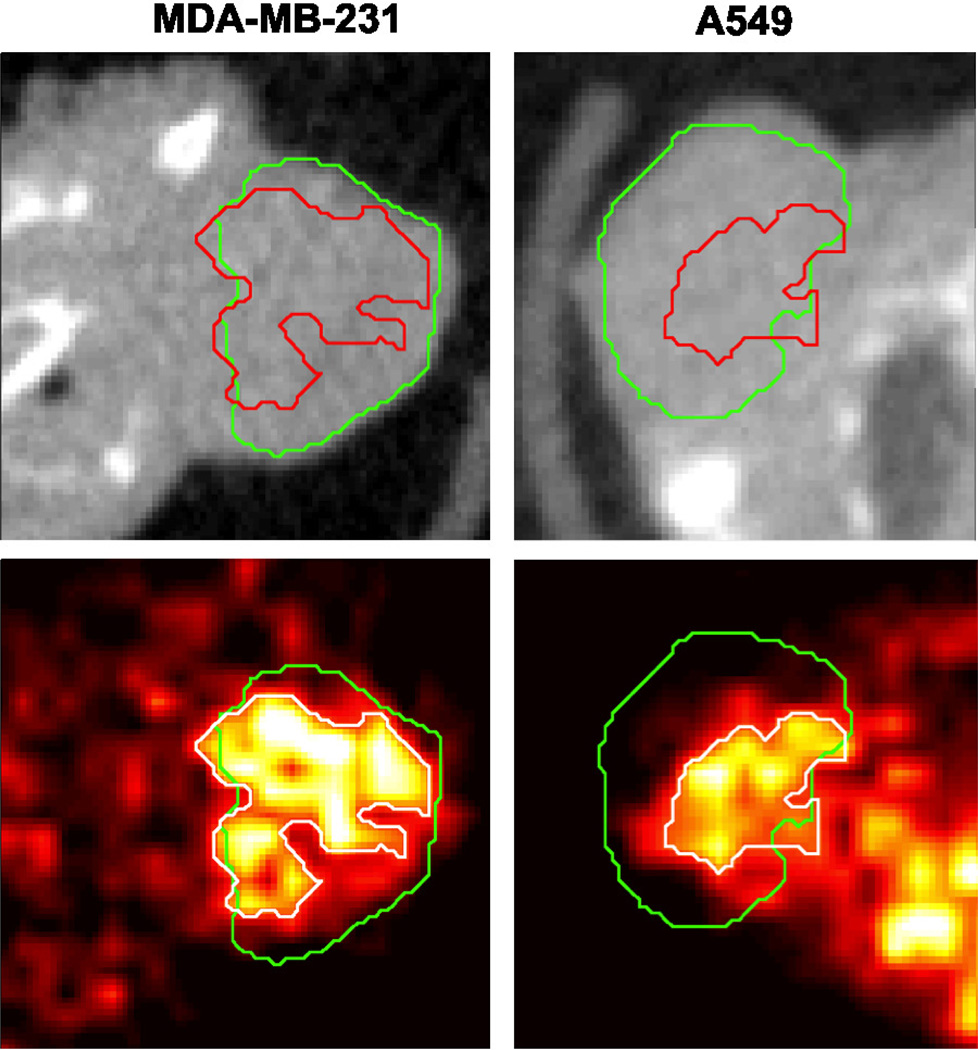
Figure 8 shows the manual and level set boundaries compared for three different tumors, against both the microCT and the 18F-EF5 microPET image data. The manual and level set boundaries show good overall agreement, and both are able to capture most of the tumor-specific microPET tracer signal. Figure 9 shows a comparison between the level set contour and a region growing algorithm boundary designed to capture the functional tumor microPET signal. The hypoxia microPET signal highlights a functional subvolume of the tumor, however the microCT tumor algorithm is able to capture most of this subvolume. Table 2 summarises the extent to which the microCT boundary is able to capture the tumor microPET functional volume. The algorithm is able to capture 88% of tumor microPET signal in A549 tumors, which tend to have small functional volumes (38% of the overall tumor volume), and slightly less (82%) for orthotopic MDA-MB-231 tumors which have larger functional volumes (63% of the overall tumor volume).
Figure 8.
Comparison between segmentation results (red contour) against manual segmentations (green contour) and tumor PET tracer uptake for three different A549 subcutaneous tumors (one per column). Top row shows axial microCT slices of the tumor. Middle row shows the same slice with the segmentation contours superimposed. Bottom row shows co-registered PET image of 18F-EF5 uptake in the tumors, with segmentation contours superimposed.
Figure 9.
Comparison between the CT tumor segmentation result (green contour) and a region growing algorithm for segmenting the tumor PET signal (red contour in top CT image, white contour in bottom PET image). Top row shows axial microCT slices of the tumor, and bottom row shows co-registered PET image. Left column shows 18F-FAZA uptake in an orthotopic MDA-MB-231 tumor, and right column shows 18F-EF5 uptake in an A549 subcutaneous tumor.
Table 2.
Quantitation of percentage of functional tumor microPET region captured by CT tumor segmentation, and size of tumor microPET region as a percentage of the microCT-derived volume. n represents number of tumors analysed.
| Tumor Type | Tracer | % PET Region Captured | Fraction of CT Volume | n |
|---|---|---|---|---|
| A549 | 18F-EF5 | 87.9 ± 2.7 | 37.8 ± 13.7 | 15 |
| MDA-MB-231 | 18F-FAZA | 81.8 ± 15.1 | 63.1 ± 24.1 | 8 |
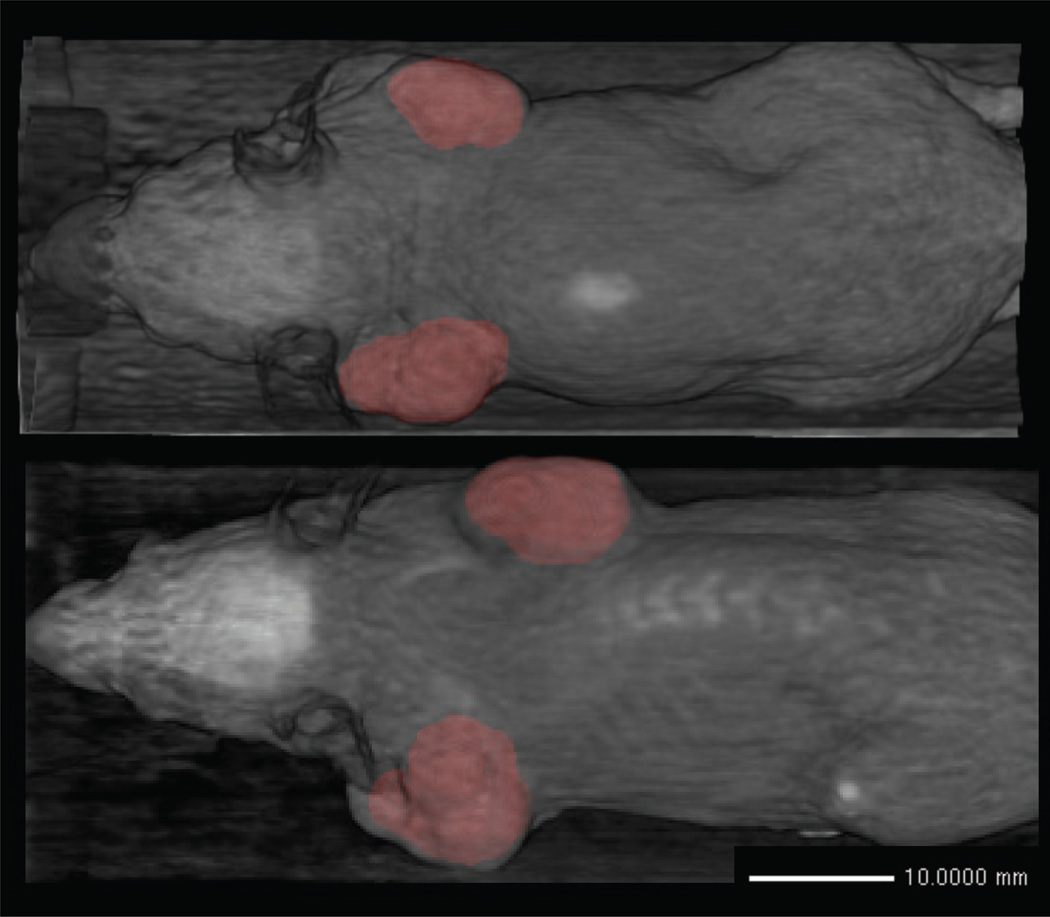
Figure 10 shows a 3D rendering of mice with multiple segmented tumors. The level set takes 30 seconds to compute 1000 iterations on a 2010 Macbook Pro with a 2.4 GHz Intel Core i5 and 4GB DDR3 RAM. It typically takes 1500–1800 iterations to reach convergence for a single tumor.
Figure 10.
Birds-eye view 3D volume rendering of the segmentation results (red) superimposed on the microCT image (grey) for two mice.
4. Discussion
PET images require some form of anatomic reference in order to make full use of the available biological information. Modern PET/CT scanners produce high resolution anatomic CT images which are co-registered with the PET images, and such scanners are becoming widely used for animal research. For certain types of tumors, particularly lung tumors, CT images allow tumors boundaries to be directly observed and segmented (Fushiki et al. 2009). Subcutaneous tumors are one of the most widely used preclinical cancer models (Sausville & Burger 2006), however the boundary at the muscle interface is hard to discern due to the low soft tissue contrast in CT. Other modalities such as MRI and ultrasound are better able to distinguish tumor tissue from the neighboring muscle, and these methods are sufficient for measuring tumor volumes (Montelius et al. 2012)(Ayers et al. 2010), however they are difficult to register to PET data.
Segmenting subcutaneous tumor boundaries from microCT images is a difficult image processing problem, and there exists little prior work in this area. (Missbach-Guentner et al. 2008) proposed a method which used intravenous contrast to highlight the tumor vasculature, which in subcutaneous tumors is peripheral to the tumor tissue. This would make segmentation more amenable to straightforward image processing techniques. To our knowledge, there exists no partially automated method for segmenting such tumors from microCT images without any exogenous contrast. Our work provides a first proof-of-principle to demonstrate the feasibility of solving this problem.
Our approach uses a biological feature of subcutaneous tumors, namely their inability to invade into the underlying tissue. They form compact solid blocks of tissue which are fed by the host's vascular system, and the development of these peripheral blood vessels results in the formation of a thin membrane which separates the tumor from the muscle. This can be observed in microCT images in the form of sparse faint dark features. In order to utilize these features, we employ two techniques. The first is local phase based feature detection which emphasizes the faint boundary features in a way that is insensitive to variations in image intensity/contrast (by focusing on the line symmetry of the local signal). The second is a level set active contour which regularizes the problem through the use of a smoothness constraint, thus overcoming the feature sparsity problem. The method shows promising results on two tumor types (human A549 lung carcinoma cell and MDA-MB-231 breast adenocarcinoma xenografts) and a single scanner (a Siemens Inveon microPET/CT). Further development of this method will require testing on different tumor types and images from different scanners.
The algorithm is available as open-source software from www.setuvo.com. There exists considerable scope for improvements. GPU-based techniques can be used to improve the speed of the level set computation, and the initialization methods can also be improved (using, for example, co-acquired PET data). The accuracy can be improved through the incorporation of additional prior information based on an improved understanding of the tumor models being imaged. Our future work involves using the segmentation boundaries as an input for mathematical models of tumor growth, thus providing tumor boundary conditions for the models. Other uses can include the development of PET tumor quantification metrics which include the contribution from PET-negative tumor voxels, for example tumor hypoxic fraction when imaging with hypoxia-specific PET tracers.
Acknowledgements
The authors would like to thank the funding providers which include the Stanford Molecular Imaging Scholars program (NIH/NCI R25 CA118681-06) which funded RA, and NIH/NCI R01 CA131199 which funded the imaging studies.
References
- Ayers GD, Mckinley ET, Zhao P, Fritz JM, Metry RE, Deal BC, Adlerz KM, Coffrey R, Mannng C, Coffey RJ, Manning HC, Ph D. Volume of preclinical xenograft tumors is more accurately assessed by ultrasound imaging than manual caliper measurements. J Ultrasound Med. 2010;29(6):891–901. doi: 10.7863/jum.2010.29.6.891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boukerroui D, Brady M, Noble A. On the choice of band-pass quadrature filters. J Math Imaging Vis. 2004;21(4):53–80. [Google Scholar]
- Dice L. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- Felsberg M, Sommer G. The monogenic signal. IEEE Trans Sig Proc. 2001;49(12):3136–3144. [Google Scholar]
- Fushiki H, Kanoh-Azuma T, Katoh M, Kawabata K, Jiang J, Tsuchiya N, Satow A, Tamai Y, Hayakawa Y. Quantification of mouse pulmonary cancer models by microcomputed tomography imaging. Cancer Sci. 2009;100(8):1544–1549. doi: 10.1111/j.1349-7006.2009.01199.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komar G, Seppänen M, Eskola O, Lindholm P, Grönroos TJ, Forsback S, Sipilä H, Evans SM, Solin O, Minn H. 18F-EF5: a new PET tracer for imaging hypoxia in head and neck cancer. J Nucl Med. 2008;49(12):1944–1951. doi: 10.2967/jnumed.108.053785. [DOI] [PubMed] [Google Scholar]
- Lefohn AE, Kniss JM, Hansen CD, Whitaker RT. A streaming narrow-band algorithm: interactive computation and visualization of level sets. IEEE Trans Vis Comput Gr. 2004;10(4):422–433. doi: 10.1109/TVCG.2004.2. [DOI] [PubMed] [Google Scholar]
- Mellor M, Brady M. Phase mutual information as a similarity measure for registration. Med Image Anal. 2005;9(4):330–343. doi: 10.1016/j.media.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Missbach-Guentner J, Dullin C, Tomography C, Kimmina S, Zientkowska M, Domeyer-Missbach M, Malz C. Morphologic changes of mammary carcinomas in mice over time as monitored by at-panel detector volume. Neoplasia. 2008;10(7):663–673. doi: 10.1593/neo.08270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montelius M, Ljungberg M, Horn M, Forssell-Aronsson E. Tumour size measurement in a mouse model using high resolution MRI. BMC Med Imaging. 2012;12(1):12. doi: 10.1186/1471-2342-12-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostofi H. PhD thesis. UK: University of Oxford; 2009. Fast level set segmentation of biomedical images using graphics processing units. [Google Scholar]
- Osher S, Fedkiw R. Level Set Methods and Dynamic Implicit Surfaces. Springer; 2002. [Google Scholar]
- Sausville Ea, Burger AM. Contributions of human tumor xenografts to anticancer drug development. Cancer Res. 2006;66(7):3351–3354. doi: 10.1158/0008-5472.CAN-05-3627. discussion 3354. [DOI] [PubMed] [Google Scholar]
- Wang P, Kelly C, Brady M. 2009 6th IEEE International Symposium on Biomedical Imaging. 2009:1174–1177. [Google Scholar]