On the interfacial fracture of porcelain/zirconia and graded zirconia dental structures

Abstract

Porcelain fused to zirconia (PFZ) restorations are widely used in prosthetic dentistry. However, their susceptibility to fracture remains a practical problem. The failure of PFZ prostheses often involves crack initiation and growth in the porcelain, which may be followed by fracture along the porcelain/zirconia (P/Z) interface. In this work, we characterized the process of fracture in two PFZ systems, as well as a newly developed graded glass-zirconia structure with emphases placed on resistance to interfacial cracking. Thin porcelain layers were fused onto Y-TZP plates with or without the presence of a glass binder. The specimens were loaded in a four-point-bend fixture with the thin porcelain veneer in tension, simulating the lower portion of the connectors and marginal areas of a fixed dental prosthesis (FDP) during occlusal loading. The evolution of damage was observed by a video camera. The fracture was characterized by unstable growth of cracks perpendicular to the P/Z interface (channel cracks) in the porcelain layer, which was followed by stable cracking along the P/Z interface. The interfacial fracture energy G_C was determined by a FEA taking into account stress shielding effects due to the presence of adjacent channel cracks. The resulting G_C was well less than commonly reported values for similar systems. Fracture in the graded Y-TZP samples occurred by a single channel crack at a much greater stress than for PFZ. No delamination between the residual glass layer and graded zirconia occurred in any of the tests. Combined with its enhanced resistance to edge chipping and good esthetic quality, graded Y-TZP emerges as a viable material concept for dental restorations.

1. Introduction

Posterior dental prostheses are commonly made of porcelain veneer fused to metal (PFM) or zirconia (PFZ) framework. Porcelain has good esthetic qualities, but is susceptible to premature fracture. Although the reported incidence of porcelain fracture is higher in PFZ relative to PFM [1–6], the two systems share similar damage forms. Fracture may occur from edge chipping (“cohesive” failure) [1, 6–9] or interfacial fracture (“delamination”) [10–12]. The higher porcelain chipping and delamination rates observed in PFZ are due to the development of deleterious tensile residual stresses [13–17] and the low interfacial fracture energy G_C of PFZ relative to PFM [18, 19]. The residual thermal stress occurs during heat treatment due to the mismatch in thermal expansion coefficient between veneer and core as well as the low thermal diffusivities characterizing most ceramics. It is pointed out that any crown or FPD failure other than edge chipping must involve a crack reaching the interface between veneer and core. Indeed, this has been demonstrated in several in vitro studies on fatigue of PFZ restorations [20–23]. Hence, assessing and improving interfacial strength is an important aspect of material design.

There have been several approaches for preventing the delamination problem of PFZs. One such approach is to use a glass bonding layer to improve the adhesion of porcelain to zirconia. Unfortunately, this can only marginally, if at all, increase the resistance to delamination. This is because when cracks in the porcelain veneer reach the veneer/core interface, they tend to graze along the weak interface or deflect into the porcelain veneer rather than penetrate the stiffer and tougher zirconia core. A much more effective strategy is to alter the crack growth route so that it penetrates into the zirconia framework via proper engineering of the interfacial microstructure [24, 25]. This way, the superior strength and toughness of zirconia could effectively hold off the crack, adverting porcelain delamination altogether. Using a glass-ceramic infiltration technique, a functionally graded glass-zirconia material has been developed [25]. Previously, we have examined the fracture resistance of this material, including subsurface flexural fracture [26–28] and edge chipping resistance [29, 30]. The results showed that this material retains the proven strength benefit of Y-TZP, yet it has a superior esthetic quality [24]. Here, we examine the fracture resistance of its interface.

Considerable work has been devoted to assessing the interfacial adhesive strength of porcelain-veneered zirconia restorations. This is generally done by subjecting the material to some form of external forces and examining the ensuing fracture pattern [31–34]. While useful for routine screening, this approach yields no direct information on the interfacial fracture energy G_C. A simple means for evaluating G_C for dental restorations is the four-point-bend bilayer configuration. Several studies have used this method to determine the interfacial energy of PFM with various metal copings [19, 35] or different porcelain-veneered zirconia systems [18]. However, the fracture process in such tests can be complex; even simple configurations such as thin-film bilayers under tension are known to fail in an intricate process involving multiple channel cracks in the hard film and delamination between film and substrate (e.g., [36, 37]). In addition, the multiple channel cracks may greatly alter the fracture resistance as well as the calculations of interfacial fracture energy [38, 39].

In this study, we elucidate the fracture process and fracture resistance of some PFZ systems as well as a newly-developed graded Y-TZP coated by a glass layer (hereafter, we designate this material as graded Y-TZP) due to tensile loading. Special emphasis is placed on resistance to interfacial fracture. Porcelain/zirconia bilayers and graded Y-TZP samples are loaded in the four-point-bend fixture shown in Fig. 1. Two PFZ systems are considered: porcelain fused directly onto zirconia and porcelain fused to zirconia in the presence of a glass binder. The latter is motivated by works showing that binders may greatly enhance interfacial fracture resistance [35]. The fracture process is observed from the specimen edge using a video camera equipped with a telescopic lens. The tests are supplemented by a 2D FEA for calculating interfacial fracture energy, taking into account the evolving fracture morphology. Section 2 describes the materials and methods used while Section 3 presents the test results. The latter is discussed in Section 4 in relation to dental restorations.

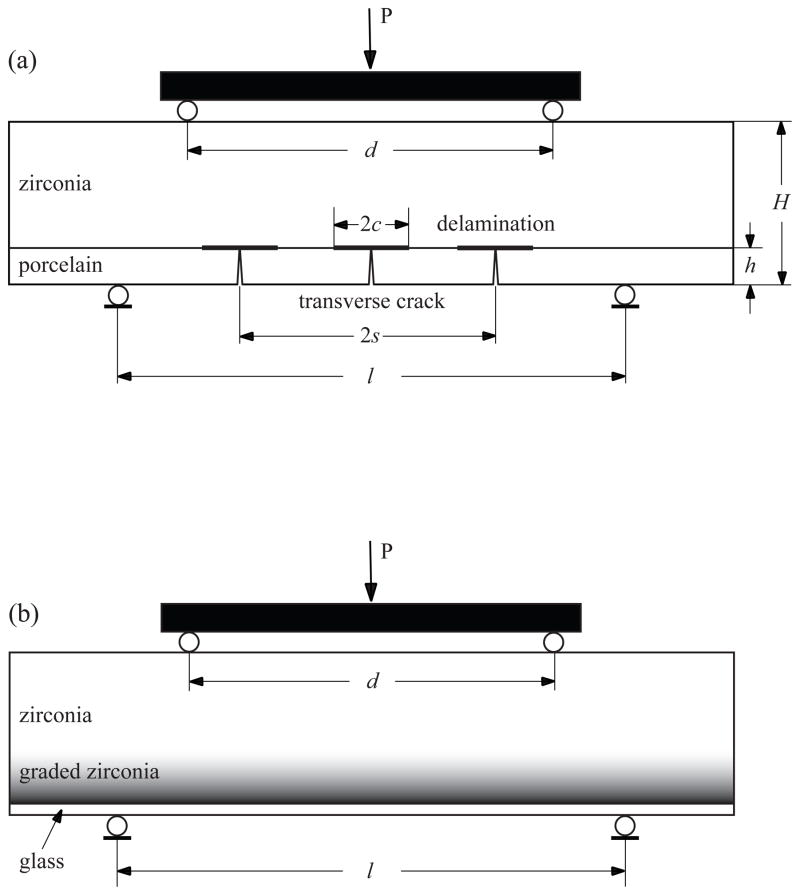
Fig. 1.

The porcelain/Y-TZP bilayer specimen (a) and graded Y-TZP specimen (b) used, shown in the four-point-bend fixture. Illustration (a) contains channel and delamination cracks used in the FEM model.

2. Materials and methods

The materials used were porcelain fused to zirconia (PFZ) and graded Y-TZP. For PFZ, two configurations were studied: porcelain fused directly onto zirconia (P group) and porcelain fused to zirconia in the presence of a thin glass binder (Y group). Prior to veneering, the zirconia (Tosoh Y-TZP, CTE = 10.5 x 10⁻⁶ K⁻¹) surface was sandblasted with 50 μm Al₂O₃ particles for 5 s at a standoff distance of 10 mm and a compressed air pressure of 2 bars. The P group was produced by laying porcelain powder (Heraceram Zirconia, leucite-reinforced porcelain, CTE = 10.5 x 10⁻⁶ K⁻¹, Heraeus Kulzer GmbH, Hanau, Germany) onto zirconia and heating to 870 °C with a dwell time of 1 min. For the Y group, an adhesive paste having a thickness of approximately 0.1 mm (Heraceram ZR-Adhesive paste, Heraeus Kulzer GmbH, CTE = 10.5 x 10⁻⁶ K⁻¹) was first applied to the zirconia veneering surface and fired at 1050 °C for 20 min to help wet the zirconia surface. Upon cooling to room temperature, the same porcelain used for the P group was applied and fired. Examination of the interface region in the Y specimens with a high-resolution optical microscope revealed no visible sign of interlaminar glass adhesive, indicating good interdiffusion between glass and porcelain. Hence, both P and Y groups could be characterized by a single veneer layer. The graded Y-TZP was prepared as described earlier [25, 40]. Briefly, an in-house prepared glass with composition similar to dental porcelain in the form of powder slurry was first applied on pre-sintered Y-TZP (1350 °C for 1 hour). Glass infiltration and densification occurred in a single process at 1450 °C for 2 hours, resulting in a structure consisting of a 15 to 40 μm thick residual glass layer followed by a 120 μm thick graded layer and finally a bulk Y-TZP. Fig. 2a shows a micrograph of a graded Y-TZP sample broken by bending. One observes a uniform residual glass layer without large voids or flaws. The glass layer is attached to the Y-TZP core through a graded glass-zirconia layer where the content of intergranular glass is gradually diminishing.

Fig. 2.

Micrographs for graded Y-TZP loaded in the four-point-bend fixture: (a) SEM image of a fractured bar showing a thin (25 μm) residual glass layer on a graded Y-TZP and no delamination crack, (b) A video frame taken right after fracture showing a single channel crack, (c) Post-mortem optical image of the sample in (b) taken normal to the surface of the glass layer showing no multiple channel cracks, and (d) Fracture surface in graded zirconia, revealing that fracture initiates from the graded Y-TZP layer below the interface with the glass layer. The dark spot in (b) indicates the location of Vickers indentation.

All specimens were fabricated in the desired form: length L = 30 mm, total thickness H = 2.7 mm and specimen width b = 2.5 mm, see Fig. 1. At least 7 specimens were prepared for each group. The porcelain thickness h for both PFZ groups is 0.4 mm. The fracture tests were conducted using the four-point-bend test [41]. Fig. 1 shows the PFZ (a) and graded Y-TZP (b) specimens in their loading fixture. The distances between lower and upper supporting pins, l and d, were 20 and 10 mm, respectively. Prior to testing, the tensile surfaces of the PFZ samples were polished down to a 1 μm diamond suspension finish and then indented at their center points by a Vickers indenter at a load of 5 N to introduce an artificial flaw for crack initiation (crack length of ~ 45 μm). In the case of graded Y-TZP, some specimens (n = 10) were tested as fabricated, while in others (n = 7), the tensile surface was indented with a Vickers tool at 10 N load (crack length of ~ 70 μm). The specimens were loaded in a standard universal testing machine at a rate of 0.1 mm/min. One specimen side face, polished to mirror surface quality, was observed by a video camera (Canon EOS-7D) equipped with a high-power zoom lens (Optem, Inc.).

Referring to Fig. 1, the load P produces bending moment M = P(l − d)/4 in the beam portion bounded by the upper pins. The tensile stress at the lower surface of the PFZ bilayer, σ_p, where fracture initiates, is easily found from beam theory as [38]

$${\mathrm{\sigma }}_{\mathrm{p}}=1.5P(1-d)/[{bH}^2(E_2/E_1+6h/H)],$$ (1a)

where E and ν denote Young’s modulus and Poisson’s ratio, and subscript 1 and 2 indicate porcelain and Y-TZP (Fig. 1a). For the graded material, the tensile stress at the lower surface of the residual glass layer, σ_g, and at the adjacent Y-TZP surface, σ_y, are found from Eq. 1a. Noting that the thicknesses of the graded zirconia layer and glass layer are very small compared to the total specimen thickness, and that the modulus of the glass layer is small compared to that of zirconia. Hence, the prevalent condition (6h/H)/(E₂/E₁) ≪ 1 yields:

$${\mathrm{\sigma }}_{\mathrm{g}}=1.5P(l-d)E_1/(E_2{bH}^2)$$ (1b)

$${\mathrm{\sigma }}_{\mathrm{y}}=1.5P(l-d)/({bH}^2)$$ (1c)

The following elastic properties were used in these calculations: (E₁, E₂, E_g) = (70, 210, 70) GPa, (ν₁, ν₂, ν_g) = (0.20, 0.32, 0.22), where “g” stands for glass. The energy release rate (ERR) for interfacial cracking in the PFZ samples was determined by a 2D FEA. The calculations were performed with the aid of a commercial FEM code (Abaqus, Inc.) as described earlier [38].

3. Results

3.1 Porcelain/Y-TZP

Fig. 3 shows select frames from a video sequence for a porcelain/zirconia bilayer (P group). A channel crack popped in from the lower surface at stress σ_p = 93.1 MPa, arresting at the interface (a). Interestingly, this crack did not initiate from the Vickers indent (located in the specimen’s plane of symmetry passing through the dark spot). At slightly greater loads, channel cracks, spaced about 3 times layer thickness apart, popped in (b). Cracking along the P/Z interface initiated nearly spontaneously from every tip of the channel cracks starting at stress σ_p = 128.4 MPa (c). With increasing load, the interface cracks grew stably in a rather symmetric fashion [(d) and (e)].

Fig. 3.

Select frames from a video sequence for porcelain/Y-TZP (P group): (a) Onset of first channel crack (σ_p = 93.1 MPa), (b) A lower magnification at a slightly larger load showing nearly evenly spaced channel cracks (σ_p = 102 MPa), (c) Onset of delamination from the tips of the channel cracks (σ_p = 124.8 MPa), (d) and (e) Images taken during the (stable) delamination growth (σ_p = 163.2 MPa and 184.8 MPa, respectively). σ_p denotes the tensile stress at the lower surface of the porcelain layer as evaluated from Eq. 1(a). The thickness of the porcelain layer 0.4 mm.

Fig. 4 is a magnified view of a typical crack path in the Y group. The channel crack had split into two horizontal cracks that grew along a rather wavy interface [18]. No glass adhesive at the interface was evident, indicating good interdiffusion between glass and porcelain. The tensile stress needed to initiate a channel crack in the porcelain layer was calculated from Eq. 1a using corresponding loads recorded during the experiments. The combined data yielded mean and SD values of 90.3 and 15.2 MPa, respectively.

Fig. 4.

Optical microscope image of porcelain/glass/Y-TZP (Y group) specimen after unloading. The channel crack in the porcelain branches out into two delamination cracks. No glass adhesive layer is visible at the interface.

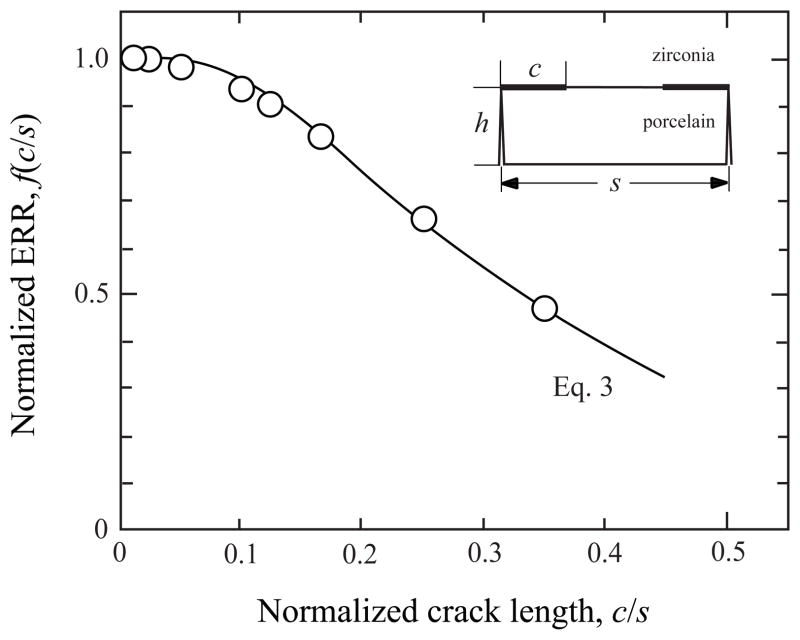
The fracture morphology was modelled as shown in Fig. 1a. The specimen consisted of an array of channel cracks, spaced in intervals of distance s, which extended across the full veneer thickness and width. Interface cracks of length c extended from the tip of each channel crack in both directions. Because of the relative smallness of the veneer layer, only a cell element as shown in the inset in Fig. 5 was modelled. Additionally, taking advantage of symmetry, the loading was represented by a uniform bending strain applied along the midsection. The energy release rate G = G(c/s) for a given crack length c is found from

Fig. 5.

Normalized energy release rate f vs. normalized delamination length c/s for the four-point-bend porcelain/Y-TZP specimen (Fig. 1a). Symbols are from the FEM analysis. Solid line is an empirical fit to the FEM data (Eq. 3).

$$G=G^{\text{ss}}f(c/s)$$ (2a)

$$\begin{array}{l}{G}^{\text{ss}}\equiv 1.5(1-{{\mathrm{\nu }}_2}^2){[P(l-d)/2b]}^2(1/E_2{H}^3)[1/{(1-h/H)}^3-\mathrm{\gamma }/Q]\\ \mathrm{\gamma }\equiv E_2(1-{{\mathrm{\nu }}_1}^2)/E_1(1-{{\mathrm{\nu }}_2}^2)\\ Q\equiv {(h/H)}^3+\mathrm{\gamma }{(1-h/H)}^3+3\mathrm{\gamma }/[\mathrm{\gamma }{(h/H)}^{-1}+{(1-h/H)}^{-1}],\end{array}$$ (2b)

where G^ss is the interfacial ERR for the limit case c/s ≪ 1 or a single channel crack [41], while f(c/s) is a certain function of c/s which we add here in order to account for the presence of adjacent channel cracks. This function depends on Dundur’s parameters α and β [37, 39].

Fig. 5 (symbols) shows the variation of f(c/s) or normalized ERR with normalized delamination length for the present porcelain/YTZ-P system (α = −0.47, β = 0.35) as obtained from our FEA. (The calculations are similar to those described in [38] and hence not repeated here.) The ERR rapidly diminishes with normalized crack length, which highlights the need to account for stress shielding from multiple channel cracks in the fracture analysis. The behavior near c/s = 0.5 (complete delamination) varied greatly. To help in routine calculations, the FEM data are empirically fitted by a function f (solid line in Fig. 5):

$$f(c/s)=1.0-1.5{\mathrm{e}}^{-0.37s/c}$$ (3)

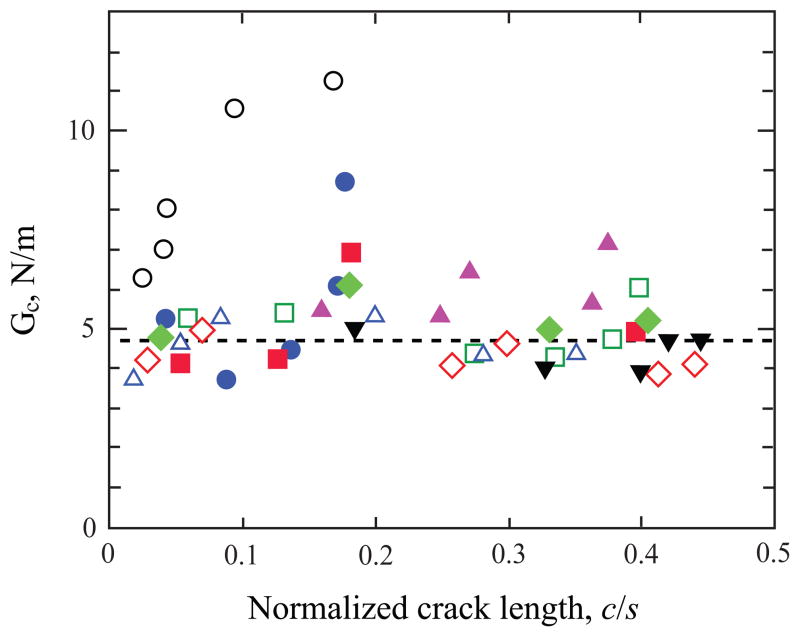
Using this in Eq. 2 together with concurrent test data for P, c and s and the (fixed) geometric and materials variables, the variation of critical energy release rate G_C with normalized crack length c/s can be found. The results are shown in Fig. 6, where different symbols represent different test specimens. The values of G_C for the Y (filled circles) and P (unfilled circles) groups seems indistinguishable, in line with the good diffusion of the glass adhesive into porcelain as evident from Fig. 4. Notwithstanding the large scatter, G_C seems independent of crack length, which would confirm it as a material property. It should be noted that this quantity is a mixed-mode type with nearly equal parts of mode I and mode II ERR components [42]. The average and standard deviation values of G_C are 4.8 N/m and 1.4 N/m, respectively. This is well below the pure mode I value for porcelain of 11.0 N/m (e.g., [26]), indicating a very small mode II fracture energy.

Fig. 6.

Variation of interfacial energy release rate with normalized delamination length c/s for all porcelain-veneered zirconia samples tested. The fracture energy is obtained from Eqs. 2 and 3; the mean value is represented by a dashed line. Open and filled symbols correspond to porcelain fused onto zirconia directly (P group) or in the presence of a thin glass binder (Y group), respectively. Different symbols are used to represent different samples.

3.2 Graded Y-TZP

As exemplified in Fig. 2b, the graded Y-TZP fractured by a single channel crack. This is confirmed in Fig. 2c, which shows no other cracks on the surface of the residual glass. It is also apparent from Fig. 2a that no delamination occurred along the glass/graded Y-TZP interface. For this reason the ERR was not calculated for this material. As is apparent from Fig. 2d, the crack has initiated in the graded Y-TZP, somewhat below the interface with the glass layer, consistent with the lack of multiple cracks in the glass layer. From Eq. 1c, the corresponding mean (SD) tensile stress is found as 820 (120) MPa. The stress values for the samples which were pre-indented by a 10 N Vickers indentation were slightly smaller, i.e. 685 (102) MPa, consistent with the presence of an initial crack extending deeper into the graded Y-TZP. Using Eq. 1b, the mean (SD) tensile stress at the outer surface of the residual glass layer is found to be 261 (38) MPa. This level is believed to be insufficient to induce a crack in the glass layer; as shown in Chai et al. [43], the failure stress for a mirror-like glass surface is several times larger.

4. Discussion

The fracture process in a thin porcelain layer fused onto zirconia with or without an intermittent glass binder and in a graded Y-TZP was determined using the four-point-bend specimen. For the PFZ systems channel cracks initiated and grew in the porcelain layer nearly simultaneously. For this reason the stress at which this occurred must reflect failure stress, σ_F, a quantity controlled by material microstructure rather than external flaws. Further support for this is given by the fact that our data are fairly close to the 77 to 85 MPa figure reported by White et al. [44] in testing porcelain bars. The channel cracks grew unstably before arresting at the P/Z interface. Delamination along the veneering interface grew stably from the tips of these cracks, roughly in a symmetric fashion. Our FEA showed that shielding afforded by adjacent channel cracks considerably enhanced the fracture resistance while at the same time altered the calculations of energy release rate. It is interesting to note that such mechanism for enhancing fracture resistance is also provided by enamel tufts in natural teeth [45], where the inner enamel layers are populated with filled fissures that appear to provide stress shielding, and in the fracture of canine teeth of wild animals, where multiple cracks in the enamel coat act to delay crack growth into the dentin substrate [46]. In the case of graded Y-TZP, no delamination occurred. Instead, the fracture was limited to a single surface normal crack that was initiated at a much greater stress than for PFZ. Adding this to its proven strength and fracture resistance characteristics [47], graded Y-TZP with the porcelain-like residual glass coating emerges as a viable concept for dental restoration.

It is interesting to examine interfacial fracture data obtained in similar works. Göstemeyer et al. [18] determined G_C for four different porcelains veneered to a common Y-TZP. Both rapid and slow cooling rates were employed during specimen fabrication. The values for VM9, Triceram, Zirox and Lava for the rapid/slow cooling rates are 17.1/13.0, 13.3/9.8, 12.8/11.6, and 8.2/7.5 N/m, in that order. Le Thanh [48] studied porcelain veneered to zirconia and found G_C-value of 12.4 N/m. The range of G_C values in these two sources, which employed similar material combination as used here, well exceeds the present G_C-value of 4.8 N/m. This departure may be partially attributed to the effect of stress shielding discussed above, which has not been considered in those studies. According to this work the onset of multiple channel cracks is governed by the veneer thickness to load span ratio, which was about 0.4 (e.g., Fig. 3b). It is possible that multiple channel cracks may have occurred in Refs. 20 and 44 (although this was not reported) given that the veneer thickness to load span ratio was less than 0.15. It should be noted that the stress decay controlling multiple cracking also depend on the veneer/core modulus mismatch; stiffer cores would reduce the distance between channel cracks [38, 39].

Our analysis involves several approximations that need be elaborated. (a) Eq. 1a is derived based on beam theory. With a span to beam thickness ratio about 4, our FEA shows that the error in calculating surface stress is less than 2% percent. The term E₁/E₂ in Eq. 1b represents a modulus correction over the monolith zirconia case E₁/E₂ = 1. Eq. 1b is a consequence of the minor effect on specimen curvature caused by the relative thinness of the glass and graded zirconia layers. For this reason the error in calculating σ_g from Eq. 1b and σ_y from Eq. 1b are also small, estimated to be less than 2%. (b) Our delamination analysis is based on a 2D model. This is justified since after the crack reaches the interface, it extends along the entire beam width before delamination can take place. Our FEM model is limited to a single cell element (see insert in Fig. 5). This is quite justified given the numerous vertical cracks present in the samples (e.g., about 10 cracks in the loading span of 10 mm, see Fig. 3b). (c) The scatter in Fig. 6 is believed to reflect material variations rather than measurement inaccuracies; the quantities c and s are determined from images such as shown in Fig. 3, with the error less than a few percent. The load P is obtained from a standard load cell, with typical error less than 1%. Since the stress at the lower specimen surface σ_p is proportional to load P, with error in σ_p on the order of 2%, the error in G_C from Eq. 2 is estimated to be less than 5%.

It is interesting to comment on how the present study may relate to dental restorations. Interfacial cracks in this case may initiate after channel cracks forming at the occlusal surface reach the veneer/core interface. Although our study was concerned with PFZ systems, delamination may also occur in other systems, e.g., PFM. Syabsuwan and Swain [19] tested porcelain veneered to gold, palladium, nickel-chromium alloy or titanium copings. Prior to loading a channel crack was introduced over the entire porcelain layer. The fracture energy was calculated based on the load needed to cause a stable growth of the delamination, as deduced from changes in the system compliance. The reported G_C-value ranged from 72.7 N/m for gold to 16.6 N/m for titanium coping. Tholey et al. [35] conducted a similar study for porcelain/titanium, in which the titanium interface was subjected to different surface treatments. The reported G_C-values for titanium-Rocatec and titanium-sandblasted (10.8 and 12.6 N/m, respectively) are similar to the 16.6 N/m figure for porcelain/titanium reported in [19]. Such higher G_C-values may increase the density of channel cracks. Once formed, the interface cracks may graze along the interface or deflect toward the free surface to form a chip; the specifics which are governed by the mode mix of the ERR and the interface toughness law. The former is controlled by such factors as local crown geometry and loading manner, as well as by residual stresses caused by mismatch in thermal expansion coefficients between veneer and core [13–17]. As for the toughness law, the fracture energy G_C associated with a four-point-bend test is a mixed-mode type with nearly equal parts of mode I and mode II ERR. For general applications, the full mode mix toughness spectrum would be needed. Nevertheless, it may be assumed that material systems having small G_C-values such as PFZ would favor interfacial fracture, while those with large G_C-value such as PFM may fail by edge chipping. Multiple channel cracks may be expected only in those regions where the veneer layer can be considered thin, as in the connectors of FDP subject to intraoral loading.

5. Conclusions

When determining interfacial fracture energy using flexure of thin-film bilayers with the film being under tension, care must be taken to account for the formation of multiple channel cracks. Neglecting the stress shielding effect afforded by such cracks can lead to gross overestimates of interfacial fracture energy. Such a test configuration is most pertinent to the connector fracture or margin fracture of porcelain-veneered zirconia restorations, where the porcelain veneer is relatively thin. The present work shows that an effective way to circumvent the deleterious delamination problem in PFZ systems is to utilize a compositionally graded interlayer between the glass overlay and zirconia core.