Passive Diffusion as a Mechanism Underlying Ribbon Synapse Vesicle Release and Resupply

Abstract

Synaptic ribbons are presynaptic protein structures found at many synapses that convey graded, “analog” sensory signals in the visual, auditory, and vestibular pathways. Ribbons, typically anchored to the presynaptic membrane and surrounded by tethered synaptic vesicles, are thought to regulate or facilitate vesicle delivery to the presynaptic membrane. No direct evidence exists, however, to indicate how vesicles interact with the ribbon or, once attached, move along the ribbon's surface to reach the presynaptic release sites at its base. To address these questions, we have created, validated, and tested a passive vesicle diffusion model of retinal rod bipolar cell ribbon synapses. We used axial (bright-field) electron tomography in the scanning transmission electron microscopy to obtain 3D structures of rat rod bipolar cell terminals in 1-μm-thick sections of retinal tissue at an isotropic spatial resolution of ∼3 nm. The resulting structures were then incorporated with previously published estimates of vesicle diffusion dynamics into numerical simulations that accurately reproduced electrophysiologically measured vesicle release/replenishment rates and vesicle pool sizes. The simulations suggest that, under physiologically realistic conditions, diffusion of vesicles crowded on the ribbon surface gives rise to a flow field that enhances delivery of vesicles to the presynaptic membrane without requiring an active transport mechanism. Numerical simulations of ribbon–vesicle interactions predict that transient binding and unbinding of multiple tethers to each synaptic vesicle may achieve sufficiently tight association of vesicles to the ribbon while permitting the fast diffusion along the ribbon that is required to sustain high release rates.

Introduction

Ribbon synapses mediate vesicle release in response to graded changes in membrane potential in numerous sensory cells (e.g., retinal photoreceptors, hair cells of the inner ear). In the retina, these synapses exhibit a disk-shaped (ribbon-like) presynaptic organelle covered with synaptic vesicles that are individually tethered to the ribbon by 3–5 filaments each (Usukura and Yamada, 1987). Although the vesicles in these terminals are highly mobile (Holt et al., 2004; Rea et al., 2004), ribbon-attached vesicles rarely exchange with the cytoplasmic pool of vesicles and leave the ribbon only after fusion with the plasma membrane (Holt et al., 2004; LoGiudice et al., 2008).

Neurotransmitter release from retinal bipolar cell ribbon synapses has been thoroughly characterized electrophysiologically (Heidelberger et al., 1994; von Gersdorff et al., 1996; Singer et al., 2004; Singer and Diamond, 2006; Oesch and Diamond, 2011) and with total internal reflection (TIRF) microscopy (Zenisek et al., 2000; Holt et al., 2004; Chen et al., 2013), but the specific roles for ribbons in synaptic transmission remain debated. Different experimental approaches suggest that synaptic ribbons may either shuttle attached vesicles to the presynaptic membrane for release (i.e., a “conveyor belt”) (Bunt, 1971; von Gersdorff, 2001) or perhaps slow the diffusion of vesicles, possibly enabling them to fuse with each other before fusing with the presynaptic membrane (i.e., a “safety belt”) (Parsons and Sterling, 2003; Matthews and Sterling, 2008). More recent experiments suggest a role for the ribbon in vesicle priming (Snellman et al., 2011). Although simple kinetic models closely recapitulate electrophysiologically measured release dynamics (Schnee et al., 2005; Oesch and Diamond, 2011), the simplicity of these models does not yield any mechanistic information about vesicle dynamics on the ribbon.

Here, we have used axial (bright-field) scanning transmission electron microscopy (STEM) tomography (Hohmann-Marriott et al., 2009; Sousa et al., 2011) to reconstruct rat rod bipolar cell (RBC) ribbon synapses and characterize synaptic ultrastructure and vesicle pools. This structural approach provides an isotropic voxel size of ∼3 nm in tissue sections that are 1 μm in thickness, thus avoiding the need for serial sectioning, for which the resolution normal to the plane of the specimen is limited to minimum section thickness of ∼25 nm. Passive vesicle diffusion simulations, based on these reconstructions, were then calibrated to reproduce electrophysiologically determined release/replenishment rates (Oesch and Diamond, 2011). Further refinement of the simulation parameters to reproduce the reported membrane approach speed of vesicles (Zenisek et al., 2000; Chen et al., 2013) suggested a vesicle priming time constant of ∼150 ms. Our simulations argue that passive diffusion of densely packed vesicles on the ribbon contributes to a flow field directed toward the presynaptic membrane, thereby achieving apparent “conveyor belt” behavior in the absence of molecular motors. Vesicle pool sizes predicted in the simulations match those observed in electron micrographs and electrophysiological data. Other Monte Carlo simulations of vesicle tethering suggest that transient, stochastic binding and unbinding of individual tethers permit sufficiently fast vesicle diffusion along the ribbon, whereas multiple (∼2–5) tethers prevent each vesicle from dissociating completely from the ribbon.

Materials and Methods

STEM tomography.

Animal procedures followed National Institutes of Health guidelines, as approved by the National Institute of Neurological Disorders and Stroke Animal Care and Use Committee. Retinas were collected during the day under ambient laboratory lighting from P18 Sprague Dawley rats (6 rats total, from either sex) that were housed on a 12:12 light-dark cycle. Subsequently, retinas were fixed with 2% PFA/2% glutaraldehyde at room temperature for 2 h (then overnight at 4°C) and embedded in EMbed-812 (Electron Microscopy Sciences). Sections were collected on formvar-coated slot grids, poststained with 1% aqueous uranyl acetate (15 min)/0.5% lead citrate (5 min), coated with an evaporated carbon support film, and 20 nm gold particles were applied as fiducial markers. Dual-axis tilt series of selected RBC ribbon synapses were acquired on an FEI Tecnai TF30 TEM/STEM operating at 300 kV. For ribbon reconstruction, the tilt increment for 1-μm-thick sections was 1.5°, extending from 55° to −55°, and pixel size was 1.4 nm. For tether analysis, the tilt increment for 200-nm-thick sections was 2°, extending from 65° to −65°, and pixel size was 0.75 nm. Tilt series processing and tomogram generation were performed using IMOD (version 4.1.10; http://bio3d.colorado.edu/imod/). Subsequent segmentation, reconstruction, and analysis were performed in Amira 5 (Mercury Computer Systems). All ultrastructural measurements were made in Amira, with statistical analysis in Excel, and are presented as mean ± SD. A vesicle was considered attached if it was tethered to the ribbon by a fine filament. A ribbon-associated vesicle was considered docked if it touched the presynaptic membrane or was tethered to the presynaptic membrane by fine filaments. Vesicle diameters were measured from the center of the lipid bilayer.

Determination of the vesicle diffusion coefficient.

A vesicle was placed at the center of a 0.4 × 0.4 × 0.4 μm box, and the average time required to travel 125 nm in any direction was calculated (n = 1000 trials). The value of 125 nm was chosen because it was contained within the simulation box, but much greater than the average vesicle diffusion distance in a single time step. The diffusion coefficient (D) was then calculated from the average time (t) and distance (r) as follows: D = r²/6t. After 1000 trials, the effective diffusion coefficient of a solitary vesicle with a diffusion coefficient of 1.5 × 10⁻² μm²s⁻¹ was calculated to be 1.47 × 10⁻² μm²s⁻¹, within ∼2% of the true value. Repeating the simulations with 160 vesicles (the observed density of free cytoplasmic vesicles, i.e., excluding the ∼40 vesicles typically attached to the ribbon; see Fig. 1) yielded a calculated effective diffusion coefficient of 1.20 × 10⁻² μm²s⁻¹, which could be corrected back to an effective diffusion coefficient of 1.52 × 10⁻² μm²s⁻¹ by increasing the vesicle diffusion coefficient to 1.875 × 10⁻² μm²s⁻¹ (see Fig. 2C).

Figure 1.

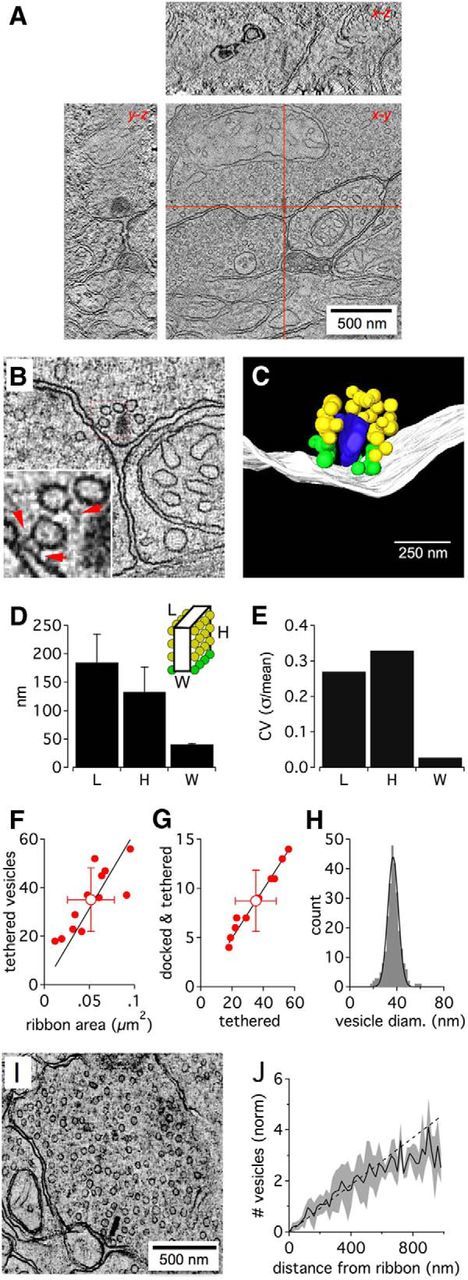
Tomography of the rat rod bipolar ribbon synapse. A, Example tomographic reconstruction of a rod bipolar terminal. STEM tomography allowed reconstruction of 1-μm-thick sections, containing entire ribbon synapses (as shown in x-z and y-z planes represented by red lines in x-y plane). Scale bar, 250 nm. B, Slice from a tomogram of a ribbon synapse. Inset, Red arrows indicate tethers between vesicles and the ribbon (classified as “attached” vesicles) and between vesicles and the presynaptic membrane (classified as “docked” vesicles). C, Reconstruction showing the ribbon (blue), presynaptic membrane (white), docked vesicles (green), and attached vesicles (yellow). Scale bars: B, C, 250 nm. D, Length of the ribbon along the membrane, height of the ribbon away from the membrane, and width across the ribbon for 12 reconstructions. Error bars indicate SD. E, Coefficient of variation in the length, height, and thickness of reconstructed ribbons. F, Linear relationship between the number of ribbon-attached vesicles versus the ribbon area: regression (n = 12): 630 ± 49 vesicles μm⁻²; r = 0.82 (p = 0.0006). G, Linear relationship between the number of “docked and tethered” vesicles versus the total population of ribbon-attached vesicles: regression (n = 12): 24.8 ± 0.4%; r = 0.99 (p = 9 E−10). H, Distribution of diameters calculated from ribbon-attached vesicles (n = 266 vesicles from 8 ribbon synapses; black represents Gaussian fit). I, Slice from a tomogram showing the terminal and cytoplasmic vesicles. J, Normalized count of vesicles in tomographic reconstructions as a function of distance from the center of the ribbon. The number of vesicles was normalized to account for different vesicle densities between terminals. Black line indicates average from 5 terminals; gray area represents SD; bin width = 20 nm.

Figure 2.

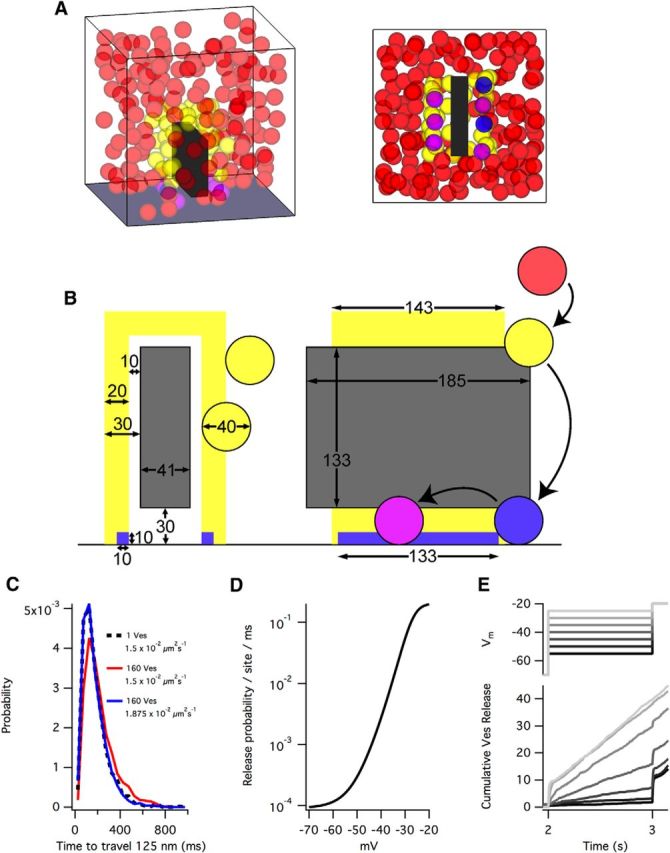
A model based on passive diffusion recapitulates electrophysiology. A, Example side and bottom views of a simulation. Simulations were enclosed in a 0.4 μm × 0.4 μm × 0.4 μm box and contained 200 vesicles. Upon release, vesicles were added back into the simulation at a random location. B, Schematic of parameters (in nm) used in the model. Vesicles (40 nm diameter) were: (1) not attached to the ribbon (red); (2) attached to the ribbon but not docked (yellow, must be within yellow attachment region); (3) attached and docked at the base of the ribbon (blue, must be within blue docking region); or (4) attached, docked, and primed (pink, must be within blue docking region). C, The effective diffusion coefficient is lowered by high concentrations of free vesicles. In our simulations, with ∼160 free vesicles, the influence of vesicle concentration lowered the effective diffusion coefficient 20%. Therefore, to achieve an effective diffusion coefficient of 1.5 × 10⁻² μm²s⁻¹, we used a vesicle diffusion coefficient of 1.875 × 1.5 × 10⁻² μm²s⁻¹. Dashed line indicates the distribution of times taken for a single vesicle to travel 125 nm in free space with a diffusion coefficient of 1.5 × 10⁻² μm²s⁻¹. Red represents the distribution of times in simulations with 160 free vesicles. Blue represents the distribution of times in simulations with 160 free vesicles with a diffusion coefficient of 1.875 × 10⁻² μm²s⁻¹ (n = 1000 for each distribution). D, Each primed vesicle had a release probability commensurate with the membrane voltage as in Oesch et al. (2011). E, Membrane voltage (V_m) step protocols (2 s at −70 mV, then a 1 s step ranging from −55 to −25 mV, then a step to −20 mV; top) reproduced the vesicle release rates derived from integrated EPSCs in Oesch et al. (2011). Traces represent averages of 20 simulations. Simulation parameters: D_ribbon/D = 0.5 and priming = 150 ms.

We considered that the size of our simulation box might influence the diffusion of vesicles because of boundary effects. Indeed, in exploratory simulations, doubling or tripling the simulation volume (but maintaining the same concentration of vesicles) did lower the rate of vesicle collisions with an artificially denuded ribbon (i.e., no attached vesicles) but did not change the vesicle pools or release rates of simulated voltage step protocols (as shown in Fig. 5). Because this suggests that release rate is not limited by the collision rate of cytoplasmic vesicles with the ribbon, higher hit rates resulting from greater cytoplasmic diffusion coefficients (e.g., 0.11 μm²s⁻¹, as observed at lizard cone terminals) (Rea et al., 2004) would presumably have little overall effect on release rate.

Figure 5.

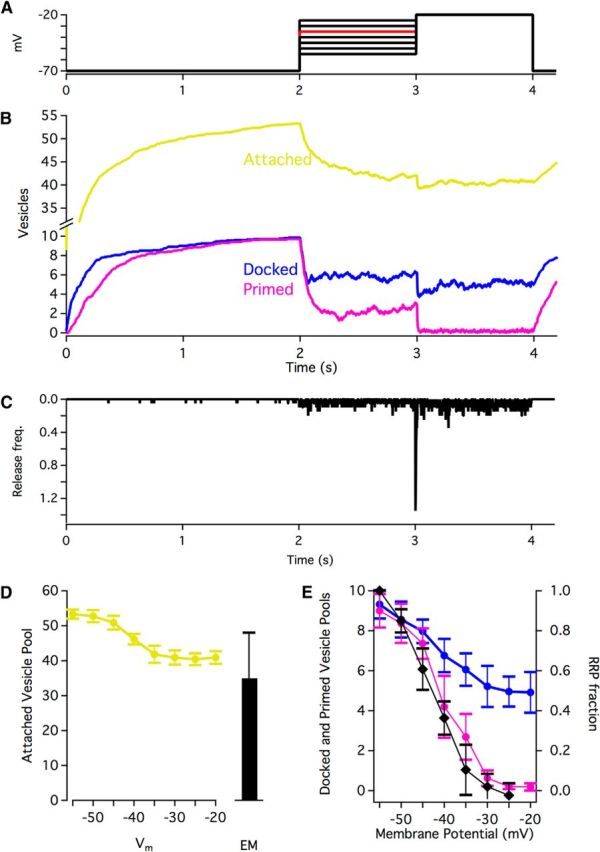
Vesicle pool occupancy. A, Step protocol for simulations. B, Example traces (step to −35 mV shown) of pool occupancy throughout a simulation. Traces are average of 20 simulations. C, Vesicle release as a result of the voltage protocol shown in B. Average of 20 simulations. Bin width = 2 ms. D, Attached vesicle pools during steps to different membrane potentials compared with the counts of attached vesicles in electron micrographs (n = 12 reconstructed ribbons). Averages of 20 simulations. Error bars indicate SD. E, Docked and primed vesicle pools during steps to different membrane potentials. Black represents readily releasable pool available during electrophysiological recordings with the same step protocol (Oesch et al., 2011). Averages of 20 simulations. Error bars indicate SD.

Ribbon synapse simulations.

All simulations were performed using IgorPro6.3 (WaveMetrics). The total number of vesicles (40 nm diameter) in the 0.4 μm × 0.4 μm × 0.4 μm (0.064 μm³) simulation was 200, in accordance with the vesicle density (∼2100/μm³) observed in tomographic reconstruction (see Fig. 1), and a maximum of ∼60–70 vesicles attached to the ribbon. Vesicle diffusion was represented as a random walk, where steps in x, y, and z dimensions were randomly drawn from a Gaussian distribution with variance of 2Dt (Berg, 1983), where D is the diffusion coefficient (1.875 × 10⁻²μm²s⁻¹; see Fig. 2) and t is the time step (0.1 ms for all simulations). The nature of vesicle collisions is poorly constrained by existing data. As collisions are likely to be highly inelastic and, therefore, computationally complex, vesicle collisions were not calculated: diffusion steps that resulted in spatial overlap with a neighboring vesicle were discarded and recalculated. Once freely diffusing vesicles entered the tethering region of the ribbon (see Fig. 2), vesicles were confined to the tethering region and did not dissociate from the ribbon (i.e., the attachment probability for vesicles entering the region was 100%). Similarly, docked vesicles never “undocked” but were always confined to the docking region, and primed vesicles always remained primed until release. Upon release, vesicles were replaced in the cytoplasm at a random location to avoid rundown of vesicle concentration. Simulation of voltage step protocols used vesicle release rates for primed vesicles based on membrane potentials ranging from −70 mV to −20 mV drawn from a continuous fit of observed release probabilities (Oesch and Diamond, 2011). For comparisons of simulations with a ribbon versus no ribbon (see Fig. 6), sustained release rate was calculated over 2 s starting 3 s after a step. “Subtraction” calculations (see Fig. 6C,D) at a given membrane potential (V_m) were calculated as the normalized sustained rate at V_t minus the normalized sustained rate at V_b, which was then scaled to the maximum transient size. For simulations of fluorophore-assisted light inactivation (FALI) (see Fig. 8), attached vesicles were prohibited from moving along the side of the ribbon but were not completely static. To preserve their jittery behavior after FALI, vesicles made steps in x, y, and z dimensions (as described above), but always relative to the same point in space (determined at the onset of FALI). For 25% of primed vesicles, FALI also prohibited movement but allowed jittering around a set point in space. These primed vesicles were also prohibited from release. Although this prohibition of release for a subset of the primed vesicles was incorporated specifically to reproduce the ∼25% reduction observed experimentally (Snellman et al., 2011), the logic is not entirely arbitrary as we observed tethers between docked vesicles and the ribbon.

Figure 6.

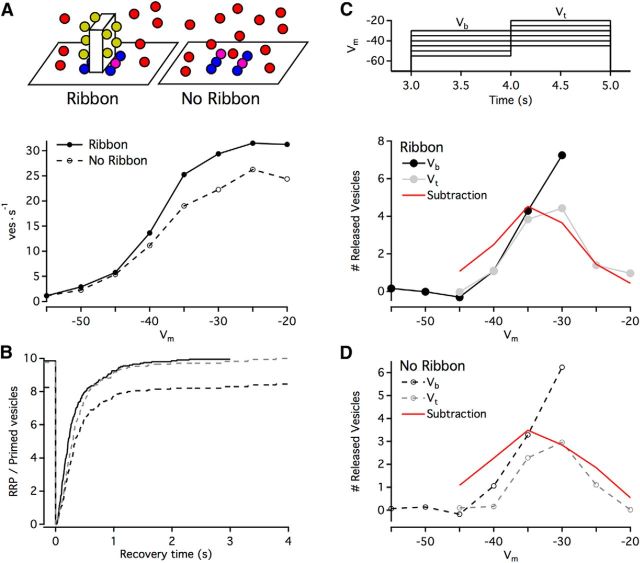
Removing the ribbon. A, Top, Schematic of simulations. Other than the presence or absence of the ribbon, simulation parameters were identical. Bottom, Sustained release rates in simulations as a function of membrane potential (V_m). Release rates were collected across 2 s of simulation time (beginning 3 s after step to V_m); points indicate averages of 4 simulations. B, Time course of recovery of primed vesicles after instantaneous depletion (at 0 s; other than the instant of depletion, release probability was 0). Solid line indicates ribbon present; dashed line indicates ribbon absent; gray dashed line is normalized to the ribbon present condition (i.e., 10 vesicles, a full recovery). Trace represents the average of 20 simulations. C, Top, Voltage step protocol for simulations. A 1 s background step (V_b, range: −55 mV to −30 mV) was followed by a 1 s test step (V_t) that was 10 mV larger. Bottom, Plotted is the number of released vesicles in ribbon simulations during the first 0.1 s after a step minus the sustained rate of release over that time period. Each point is an average of 11 simulations. The subtraction was calculated as the sustained rate (A, bottom) at V_t minus the sustained rate at V_b, normalized to maximum RRP size. D, Same as C, but with no ribbon present in the simulations.

Figure 8.

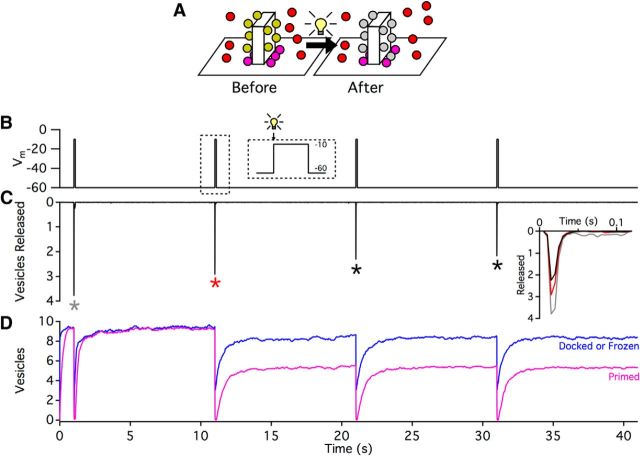
Simulation of FALI-mediated tether disruption. A, Schematic of simulations. During simulations of FALI (represented as a light bulb), all attached vesicles and 25% of primed vesicles (gray in schematic) were prohibited from moving along the side of the ribbon. In addition, the affected primed vesicles were unable to be released, removing them from the RRP but not the base of the ribbon. B, Voltage step protocol for simulations, with a holding V_m = −60 mV followed by a 100 ms step to −10 mV every 10 s. Immediately before the onset of the second step, FALI-mediated tether disruption was simulated (dashed inset). C, The number of vesicles released (during 5 ms bins) as a function of simulation time. Trace is an average of 53 simulations. Inset, Comparison of responses to V_m step (to −10 mV), colors corresponding to steps indicated by asterisks. D, The changes in vesicle pools at the base of the ribbon that occurred during the simulation. Although the simulated FALI only immobilized 25% of primed vesicles, the primed pool only recovered to ∼5 vesicles. Alternatively, the total number of vesicles at the base of the ribbon (i.e., those either docked or frozen by FALI) was not substantially reduced. Primed trace represents the average of 53 simulations. Docked or frozen trace represents the average of 35 simulations.

Calculation of vesicle diffusion along ribbon side.

To quantify and compare vesicle motion down the side of the ribbon (see Fig. 4), we calculated the z-dimensional effective diffusion coefficient (D_z-axis) of vesicle movements orthogonal to the membrane (Berg, 1983) as follows:

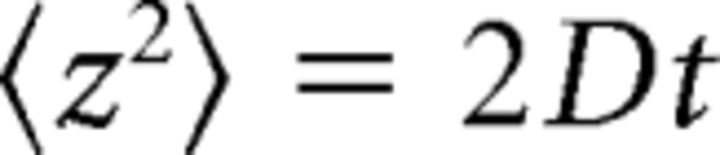where 〈z²〉 is the average squared distance (i.e., attachment height on the ribbon) and t is the time taken to reach the membrane. Plots were fit by the following:

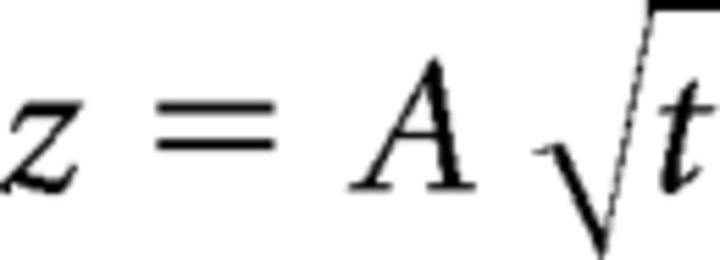where A represents the free parameter in the fitting procedure, followed by the calculation of the diffusion coefficient as follows:

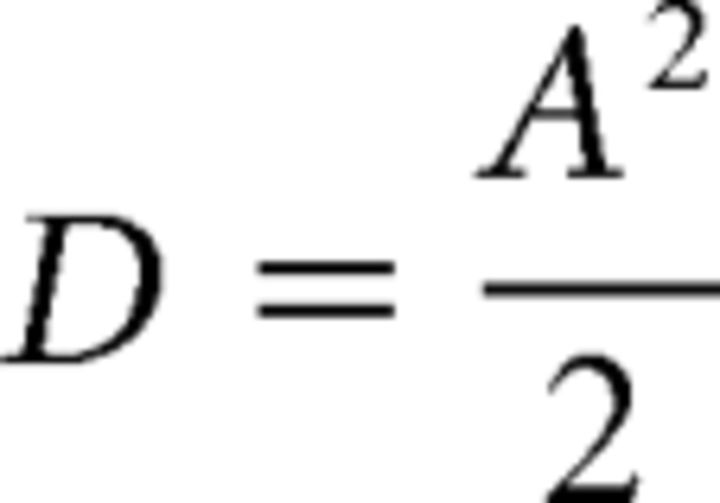Some vesicles residing in the top, curved attachment region (e.g., as shown in Fig. 4Dii,Eii) were hindered from moving in the z-axis, manifesting as a skew in measurements toward longer times (e.g., the spread in points at ∼185 nm attachment height in Fig. 4A,Di,Ei). To limit the bias of this skew on calculation of D_z-axis, times and distances from vesicles attaching at the top of the ribbon (>160 nm away from the membrane; see Fig. 4) were excluded from fits.

Figure 4.

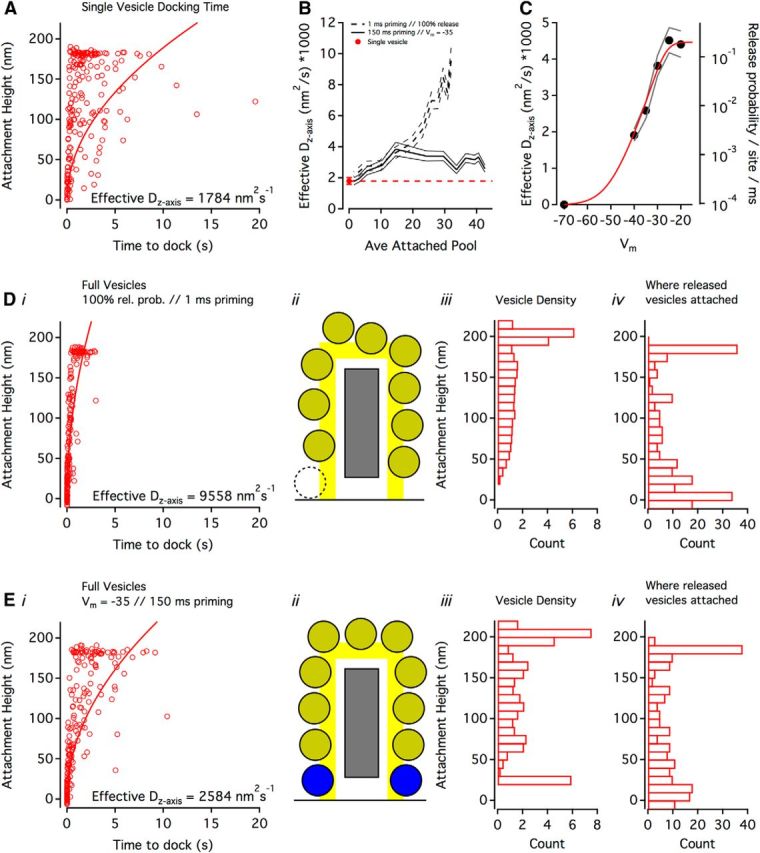
Diffusion of attached vesicles toward the base of the ribbon. A, The relationship between vesicle attachment height on the ribbon and the time taken for that vesicle to dock when the simulation only contained a single vesicle (i.e., there were no other vesicles on the ribbon). Individual trials are shown (open circles, n = 200), with a fit (solid curve) used to calculate the effective D_z-axis of vesicles attaching <160 nm (to avoid the geometric effects of the curved attachment region, see schematic in E). B, Effective D_z-axis values as a function of the average attached vesicle pool size for two conditions: a release-maximizing condition (dashed line indicates SD) and a physiologically relevant condition (solid line). Single-vesicle D_z-axis (from A, red circle and dashed line) shown for comparison. C, With anatomically accurate numbers of vesicles in the simulation (i.e., same density as in reconstructions), changes in D_z-axis were proportional to release probability. Di, Same as A, but showing the release-maximizing condition: simulations contained anatomically accurate concentrations of vesicles, priming was 1 ms for docked vesicles, and primed vesicles were released with 100% probability. Dii, Ribbon schematic of release-maximizing condition with same scale as Di. Dashed vesicle outline: because priming and release were essentially instantaneous, on average, there were no docked vesicles at the base of the ribbon. Diii, Vesicle density (bin width = 10 nm) along the side of the ribbon in the release-maximizing condition. Height was determined from the vesicle center. Div, The z-distance traveled by a released vesicle (bin width = 10 nm, n = 200 released vesicles). Because this was calculated as (attached height − docking height), and the docking region extended 10 nm away from the membrane (Fig. 2B), some values were negative. Ei, Same as A and D, but showing a physiologically relevant condition: simulations contained anatomically accurate concentrations of vesicles, priming was 150 ms for docked vesicles, and primed vesicles were released with probability approximating V_m = −35 mV. Eii–iv, Same as Dii-iv, but showing the physiologically relevant condition.

Vesicle tethering simulations.

Random walk diffusion calculations were performed as in the ribbon synapse simulations, but along an array of tethers (see Fig. 7A,B). For each set of conditions, diffusion coefficients were calculated based on fits of the average time taken for a vesicle to diffuse 50 nm (n = 100 trials; see Fig. 7B). The binding probability during each time step (0.1 ms) was a constant 0.7 for all simulations, with the unbinding probability modulated proportionally (e.g., a binding:unbinding ratio of 2.0 had a binding probability of 0.7 and an unbinding probability of 0.35). Over a range, the absolute value of the binding probability appeared to be irrelevant as long as the binding:unbinding ratio was maintained: halving the magnitude of the probabilities made little difference. If one interprets the binding/unbinding probabilities as “on rates” (K_ON) and “off rates” (K_OFF), respectively, then this suggests that the dissociation constant (K_D = K_OFF/K_ON) is more important than the absolute value of K_ON. Loss rates (the rate at which completely unbound vesicles diffuse into the open space away from the tether binding region, in vesicles⁻¹s⁻¹) were calculated by simulating 20 vesicles on the tether array simultaneously. The duration of these simulations was important to accurately calculate very low loss rates: for the conditions with very low loss rates, our longest simulations could detect loss rates of 0.0125 vesicles⁻¹s⁻¹ (20 vesicles, 4 s of simulated time). The range of tether densities incorporated into the simulations (2304–4624 μm⁻²) provided 4 (minimum) to 7 (maximum) tethers under the footprint of a vesicle at any given time. Combined with varying binding:unbinding ratios, this resulted in an average of ∼2 (minimum) to ∼5.5 (maximum) bound tethers per vesicle.

Figure 7.

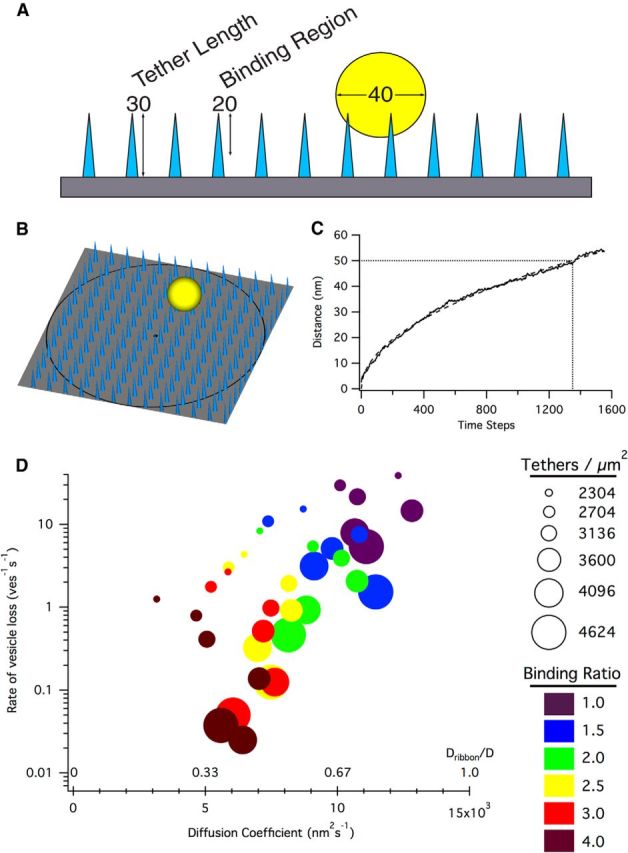
Crowd surfing of vesicles. A, Schematic of tether simulations. Vesicles (yellow, 40 nm diameter) could interact with tethers (light blue, 30 nm in length) within a 20 nm binding region offset 10 nm from the surface of the ribbon (gray). Vesicles that were unbound to tethers and diffused outside of the binding region were considered lost and were used to calculate the rate of vesicle loss from the ribbon. B, Example view of a simulation. Vesicles were created in the center (black dot) of an array of tethers, and the distance versus time of the vesicle was tracked for each trial until the vesicle had diffused 125 nm (black ring). C, Example diffusion coefficient calculation for a binding:unbinding ratio of 4.0 and a tether density of 2704 tethers/μm². Trace represents the average of 100 trials; dashed curve represents fit; dotted lines indicate the number of time steps (1350) to diffuse 50 nm. Using the diffusion equation r² = 4Dt, D = (50 nm)²/4(.135 s) = 4630 nm² /s. D, The diffusion coefficient of a vesicle crowd surfing along tethers was dependent on the density of tethers and their binding:unbinding ratio. Relatively low binding ratios (e.g., ∼3) were capable of maintaining low vesicle off rates (equivalent to ∼2 vesicles per ribbon per second) while still allowing sufficiently fast diffusion (D_ribbon/D = ∼0.5).

Results

Tomography of RBC ribbon synapses

To obtain accurate anatomical parameters for our ribbon simulations, we reconstructed 12 full-length rat RBC ribbon synapses in 1-μm-thick sections using dual-axis STEM tomography (Fig. 1A,B). Reconstructed ribbons exhibited a plate-like structure 41 ± 1 nm thick, 185 ± 50 nm long, and extending 133 ± 44 nm away from its attachment at the presynaptic membrane (i.e., height, Fig. 1C,D). Most ribbons were approximately rectangular in shape; and although the length and height of ribbons varied substantially, ribbon thickness (width) was extremely consistent across ribbons (Fig. 1E).

We counted 35.1 ± 13.1 synaptic vesicles tethered to each reconstructed ribbon (n = 12); 8.8 ± 3.1 of these tethered vesicles were “docked” (i.e., they also touched the presynaptic membrane directly or were tethered by fine filaments; Fig. 1B, inset, red arrows). The number of vesicles attached to the entire ribbon varied in proportion to the area of the ribbon (Fig. 1F), but the fraction of docked vesicles was consistent across ribbons (25 ± 2%; Fig. 1G). Tethered vesicles were 38 ± 6 nm in diameter (n = 266 from 8 ribbons, coefficient of variation: 0.16; Fig. 1H).

Reconstructions showed ∼3–5 filamentous tethers per ribbon-attached vesicle (Fig. 1B, inset). These tethers were 29.5 ± 8.5 nm (n = 32 tethers) in length, consistent with freeze-fracture experiments in frog retina (30–50 nm) (Usukura and Yamada, 1987). Using tether lengths of 30 nm and average values for ribbon dimensions to approximate the ribbon's area available to bind vesicles, we estimated the density of the vesicles attached to our reconstructed ribbons at ∼45% of hexagonal close packing, similar to that observed at stimulated frog hair cell ribbon synapses (∼50%) (Lenzi et al., 2002). Notably, tethers linking docked synaptic vesicles to the base of the ribbon were shorter (20.3 ± 8.3 nm; n = 32 tethers; p = 5.6E−5, two-tailed Student's t test).

The average density of vesicles in the cytoplasm surrounding ribbons was 1933 ± 720 vesicles/μm³ (n = 6), measured by counting the number of vesicles in tomographic reconstructions that were <1 μm from the center of the ribbon. In contrast to goldfish retinal bipolar cell terminals, where cytoplasmic vesicles density is lower in the central region of the terminal (Holt et al., 2004), vesicle density was evenly distributed throughout RBC terminals (Fig. 1I,J).

Simulations based on anatomical parameters and passive vesicle diffusion reproduce electrophysiological data

Synaptic vesicles in bipolar cell terminals are highly mobile and move throughout the terminal unconstrained by connection to the actin cytoskeleton (perhaps because of a lack of synapsin) (Mandell et al., 1990), suggesting that a simple diffusion mechanism may provide an ample supply of synaptic vesicles to the ribbon during continuous bouts of release (Holt et al., 2004). No direct evidence exists, however, to support any particular hypotheses of how vesicles interact with and move along the ribbon. Electron microscopy has provided evidence for compound fusion of ribbon-tethered vesicles (Matthews and Sterling, 2008), and TIRF microscopy has enabled vesicles to be tracked to the plasma membrane with relatively high temporal and spatial resolution (Zenisek et al., 2000; Holt et al., 2004; Chen et al., 2013), but neither approach has revealed the physiological consequence of ribbon vesicle interactions. In lieu of such evidence, we chose at the outset to consider the simple hypothesis that vesicles “slide” along the side of the ribbon (Bunt, 1971; von Gersdorff et al., 1996), without explicitly specifying the underlying mechanism.

We created a Monte Carlo diffusion simulation of a single ribbon synapse enclosed in a 0.4 μm × 0.4 μm × 0.4 μm (0.064 μm³) box (Fig. 2A). The ribbon dimensions and vesicle density in the cytoplasm were chosen to reflect the average values measured in our tomographic reconstructions. In this simulation, cytoplasmic vesicles (Fig. 2B, red) diffused freely within the box until entering a tethering region surrounding the ribbon (yellow). Once “tethered,” vesicles (now yellow) could diffuse in any direction within the tethering region, allowing them to “slide” along the ribbon. Tethered vesicles that diffused to within 10 nm of the membrane at the base of the ribbon (blue region) became “docked” (blue) and could not leave that region. The docking region extended only 20 nm away from the ribbon, as opposed to the 30 nm of the tethering region, to reflect the shorter tethers of docked vesicles measured in reconstructions. Docked vesicles became “primed” (i.e., release competent, magenta) randomly in accordance with a specified time constant, and primed vesicles underwent release with a probability that depended on presynaptic membrane potential (Oesch and Diamond, 2011).

The effective diffusion coefficient of free cytoplasmic vesicles in bipolar cell terminals measured via fluorescence recovery after photobleaching (FRAP) experiments is 1.5 × 10⁻² μm²s⁻¹ (Zenisek et al., 2000; Holt et al., 2004). This number, however, reflects slowed diffusion resulting from high concentrations of free vesicles within the terminal (Gaffield et al., 2006). By calculating the time taken for vesicles to travel 125 nm, we determined that the influence of vesicle concentrations observed in our reconstructions should reduce the effective diffusion coefficient by ∼20% in our model (Fig. 2C). We therefore used a diffusion coefficient of 1.875 × 10⁻² μm²s⁻¹ to overcome this reduction and reproduce the effective diffusion coefficient previously reported.

To re-create release rate data obtained with electrophysiological membrane voltage step protocols (Oesch and Diamond, 2011), the release probability for “primed” vesicles was determined as a function of presynaptic membrane potential according to previous results (Fig. 2D, reproduced from Oesch and Diamond, 2011). Recordings from AII amacrine cells postsynaptic to RBCs indicated a readily releasable vesicle pool (RRP) comprising ∼55 docked, primed vesicles at multiple ribbon synapses connecting an RBC and AII amacrine cell and the release of 219 ± 28 vesicles in 1 s after a step of the presynaptic RBC to −25 mV from −70 mV (Oesch and Diamond, 2011). In our simulations, random vesicle diffusion, docking, and priming gave rise to a maximal RRP of 10 vesicles, close to electrophysiological (Singer and Diamond, 2006) and anatomical (Fig. 1) measures. Moreover, the simulations reproduced a comparable release rate (39.7 vesicles released in 1 s following step to −25 mV) by assuming a priming time constant of 150 ms (Fig. 2E).

During simulations of high release probability (i.e., strong membrane depolarization steps), the vesicle priming time constant and diffusion coefficient on the ribbon (D_ribbon) collectively determined the maximum release rate of the synapse (Fig. 3A). If priming occurred at the presynaptic membrane, then it would occur during the 60–250 ms interval that vesicles dwell at the membrane before being released (“a few hundred milliseconds”: Betz and Bewick, 1993; 250 ± 30 ms, 210 ± 30 ms: Zenisek et al., 2000; 61 ± 7 ms, 69 ± 8 ms: Chen et al., 2013). We chose 250 ms as an upper limit for the priming time constant because, with 10 docked vesicles per ribbon, slower priming could not achieve the observed rate of ∼40 vesicles per second per ribbon. Different combinations of priming time constants and diffusion coefficients for vesicles on the ribbon yielded simulated release rates comparable with those observed electrophysiologically (Oesch and Diamond, 2011) (Fig. 3A).

Figure 3.

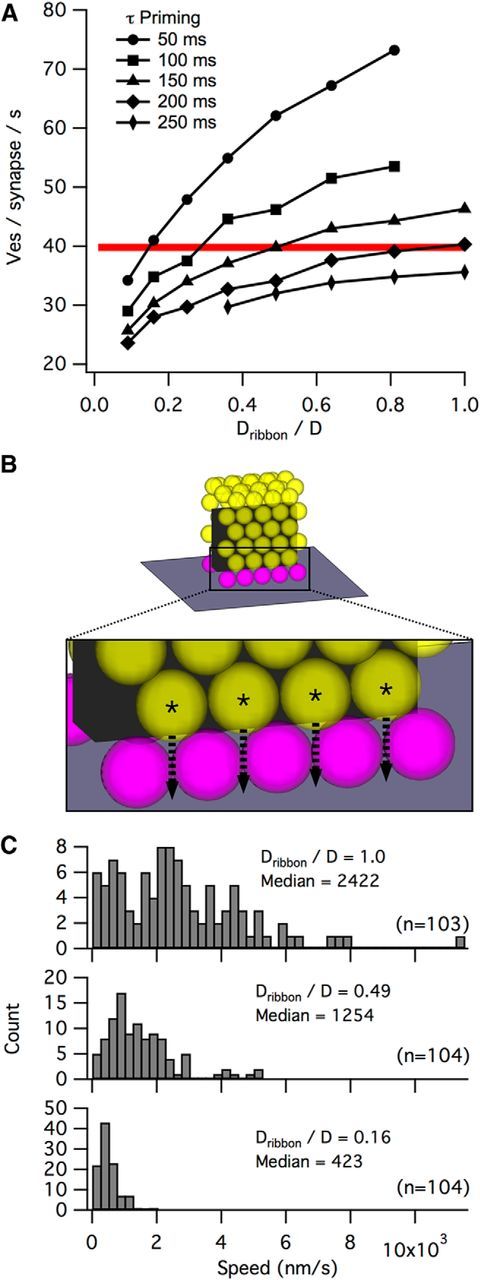
The relationship between priming and diffusion on the ribbon. A, Sensitivity of synapse release rate (during 1 s step to −25 mV) to changes in the priming time constant or the diffusion coefficient of vesicles on the ribbon (D_ribbon, as a fraction of the effective diffusion coefficient of free vesicles, D). Red line indicates release rate per ribbon synapse calculated from electrophysiological recordings (Oesch et al., 2011). Each point is the average of 20 simulations. B, Full ribbons (68 attached vesicles, top) were stepped to −25 mV from −70 mV while the times taken for vesicles the second row (asterisks, bottom) to dock was recorded. C, Distributions of vesicle approach speeds for D_ribbon/D = 1 (top), 0.49 (middle), or 0.16 (bottom). The mode of the D_ribbon/D = 0.49 distribution at ∼700 nm/s is consistent with previous approach speeds determined with pHrodo and Fm1–43 (∼800 nm/s) (Chen et al., 2013; Zenisek et al., 2000).

Nearly the entire range of reported values for priming (∼50–200 ms) was capable of reproducing the experimental release rate, although this required wide variation in D_ribbon values (Fig. 3A). To identify a realistic combination to use in the simulations, we compared the refilling rate of vesicles in the simulation using different D_ribbon values against the known membrane approach speed, determined by TIRF microscropy (∼800 nm/s) (Zenisek et al., 2000; Chen et al., 2013), that more likely depends on diffusion rather than priming. To do this, we measured the time required for vesicles in the second row on a full ribbon to dock following a step from −70 mV to −25 mV (Fig. 3B). Because the mode of the distribution of membrane approaches speeds with a D_ribbon value of 0.49 was ∼700 nm/s (Fig. 3C), close to the experimentally determined value, we used a priming time constant of 150 ms and a ribbon diffusion coefficient (D_ribbon) that was 49% of free diffusion in the cytoplasm (Fig. 3D, unless otherwise noted).

Diffusion of vesicles along the ribbon creates a passive conveyor belt

One challenge to the idea that the ribbon serves as a vesicle conveyor belt is the observation that vesicle movement on the ribbon occurs in the presence of a poorly hydrolyzable ATP analog (Heidelberger et al., 2002) and does not, therefore, use motor proteins or some other form of active transport (Parsons and Sterling, 2003). Furthermore, the idea of a conveyor belt seems to imply a regular, processional advance of vesicles from the far reaches of the ribbon toward its base. Our simulations suggest that passive diffusion of vesicles along the ribbon is sufficient to reproduce release rates from electrophysiological recordings, but to what degree do the vesicles attached to the ribbon in our simulations resemble coherent motion, as on a conveyor belt, and how does this relate to the geometry of the ribbon?

To predict the time course of a single vesicle diffusing along the side of the ribbon and the source of released vesicles, we recorded in our simulations the following: (1) the height at which a vesicle first attached to an otherwise vacant ribbon and (2) the time required for the vesicle to dock at the base of the ribbon (n = 200 trials; Fig. 4A). Vesicles became attached along the length of the ribbon, with a prominent cluster at the top reflecting the increased surface area of attachment at the ribbon's crest. Fitting the data (see Materials and Methods) allowed us to estimate an effective diffusion coefficient for the axis extending away from the membrane (D_z-axis) at 1784 nm²s⁻¹.

We next sought to determine how multiple attached vesicles might influence the diffusion of each other by comparing D_z-axis values across a range of attached pool sizes (Fig. 4B) for two scenarios: (1) a release-maximizing scenario where priming was extremely short (τ = 1 ms) and all primed vesicles were immediately released (dashed lines); (2) a more physiologically realistic scenario in which priming τ = 150 ms and vesicles released with a probability approximated by a voltage step to −35 mV (solid lines). For both scenarios, increasing the average number of attached vesicles yielded larger D_z-axis values, suggesting a synergy whereby additional vesicles mutually speed their own resupply to the presynaptic membrane. Curiously, the physiologically relevant scenario plateaued at ∼15 attached vesicles and an average D_z-axis of 3185 nm²s⁻¹ (Fig. 4B).

This plateau may reflect a rate limit imposed either by the longer priming or lower release probability in the physiologically relevant scenario (i.e., vesicles may be unable to dock because all available docking sites are occupied by vesicles either waiting for release or in the process of priming). Consistent with this idea, the calculated D_z-axis varied proportionately with release probability over the range of −40 mV to −20 mV in simulations with anatomically accurate vesicle densities (Fig. 4C), suggesting that the plateau is a result of a rate-limiting release probability. For simulations with ultrastructurally observed vesicle density (Fig. 4D,E), the effective D_z-axis was ∼5.4 and ∼1.4 times greater than the effective D_z-axis of single vesicle simulations, indicating that passive diffusion of crowded vesicles can give rise to “conveyor belt”-like coherent motion.

Stimulation has been shown to alter the distribution of synaptic vesicles along the length of the ribbon (Lenzi et al., 2002; Jackman et al., 2009). We monitored the density of attached synaptic vesicles as a function of ribbon height (see ribbon schematics in Fig. 4Dii,Eii, drawn on the same spatial scale as plots in Fig. 4D,E). Vesicle density tapered toward the membrane in the release-maximizing scenario (Fig. 4Diii), whereas the vesicle density of the physiologically relevant scenario exhibited peaks along the side of the ribbon that were spaced ∼40 nm apart (Fig. 4Eiii). The large peaks of vesicle density at the curved crest of the ribbon reflect the ∼3.5 times greater surface area available for attaching vesicles. We also determined the net z-axis distance that released vesicles traveled before docking, allowing us to calculate how far up the side of the ribbon released vesicles first attached (Fig. 4Div,Eiv). In the release-maximizing scenario, most released vesicles first attached at the base of the ribbon (Fig. 4Div), corresponding to the region of the ribbon with the lowest vesicle density (Fig. 4Diii). In the physiologically relevant scenario, however, vesicle attachment was more uniformly distributed across the surface of the ribbon (Fig. 4Eiv).

Collectively, these simulations demonstrate the dynamics of attached vesicles that diffuse passively along the ribbon. How do these results compare with the concept of a conveyor belt? The velocity of vesicle flow is positively correlated with vesicle density (Fig. 4B) and is modulated by release probability/release rate (Fig. 4C). Under realistic release conditions, priming of docked vesicles takes a sufficiently long time that an orderly queue of vesicles appears to stack up (Fig. 4Eiii, peaks), suggesting that passive diffusion can produce “convective” vesicle flow down a concentration gradient that resembles a directed, active transport process. Under unrealistically fast release conditions (Fig. 4D), however, this process appears to break down, as attached vesicles are more randomly distributed (no peaks in Fig. 4Diii), and a larger fraction of vesicles bypass other attached vesicles by attaching very low on the ribbon (Fig. 4Div).

Dynamic vesicle pool sizes are similar to those measured experimentally

Vesicle pools are dynamic and vary with stimulation (Lenzi et al., 2002; Jackman et al., 2009; Oesch and Diamond, 2011). We tracked the changes in the size of different vesicle pools during simulated voltage step protocols (Fig. 5A). During an initial 2 s equilibration time (membrane potential = −70 mV), vesicles in the cytoplasm attached to the ribbon, docked at its base, and became primed for release (Fig. 5B). At t = 2 s, the membrane potential was stepped to an intermediate voltage (−55 mV to −25 mV) for 1 s before stepping to −20 mV for an additional 1 s. Examples of the vesicle pool changes and release frequency through time for the −35 mV step protocol are shown in Figure 5B and Figure 5C, respectively. Across the stepped membrane potentials, the simulated attached vesicle pool varied from 53 vesicles to 40 vesicles, or ∼68% to 51% hexagonal packing density of the model ribbon (Fig. 5D). A comparison of the attached pools in the simulation and those reconstructed by electron tomography suggests that the reconstructed ribbons may have been releasing vesicles at a high rate when fixed, perhaps as a result of the fixative itself (Smith and Reese, 1980). If this were true, then one might expect the docked pool in reconstructions to be small; however, at 9 vesicles, the reconstructed docked pool occupied almost all of the 10 possible spots at the base of the model ribbon. Interestingly, the simulated docked pool never dipped below ∼50% occupancy, even with strong stimulation (Fig. 5E, blue), whereas the primed pool (magenta) closely mirrored the RRP fraction remaining at a given membrane potential during electrophysiological recordings (Oesch and Diamond, 2011; black).

Ribbons may not be required for certain synaptic computations

To examine the impact of the ribbon on synaptic transmission at RBC synapses, we simulated vesicle release and replenishment in the presence and absence of the ribbon (Fig. 6). In both conditions,we maintained observed vesicle density, a realistic priming time constant (τ = 150 ms), and the same geometric arrangement of docking/release sites. The maximum sustained release rate for simulations without ribbons was 83% of simulations with ribbons (at V_m = −25; Fig. 6A). Similarly, following instantaneous depletion of the primed vesicle pool at t = 0, the primed pool in ribbon-free simulations recovered to only ∼85% of the levels reached in the presence of a ribbon within 4 s (Fig. 6B, compare solid and dashed black lines), although the time course of this recovery was similar (Fig. 6B, gray dashed line indicates ribbon-free recovery normalized to recovery with ribbon). For our model ribbon synapse, which can dock 5 vesicles on each side at its base, the lack of a ribbon appears to limit the docking to ∼4 vesicles on each side (at least on the time scale of several seconds). Although this suggests that the ribbon facilitates slightly more efficient packing at the docking sites, the benefit is relatively minor and could potentially be “rescued” by a small (a few tens of nanometers) increase in extent of the docking region/active zone.

Following an abrupt change in luminance, RBC ribbon synapses exhibit transient and sustained release components that encode temporal contrast and luminance, respectively (Oesch and Diamond, 2011) (Fig. 5C). Paired recordings between RBCs and AII amacrine cells have indicated that ribbon synapses accurately calculate the difference in sustained release during a “background” presynaptic membrane potential (V_b) and a “test” potential (V_t) and encode this difference in the transient release component occurring at the transition between V_b and V_t (Fig. 5B,C). Because RBC membrane potential encodes luminance, ϕ, logarithmically, the transient response evoked by a step between two luminance levels ϕ_b and ϕ_t corresponds to the Weber contrast between them (dϕ/ϕ_b) (Oesch and Diamond, 2011). To determine the ribbon's role in this computation, we simulated a membrane voltage step protocol (Fig. 6C, top) in which the simulation was first equilibrated at −70 mV, followed by a 1 s step to V_b, then a 1 s step to V_t (10 mV more depolarized than V_b), and finally a step back down to −70 mV. For each step (either V_b or V_t), we calculated the magnitude of the transient component of release as the number of vesicles released during the first 0.1 s of the step in excess of the sustained release rate expected during that period (Fig. 6C, bottom). In our simulations, the transient release elicited by the step from V_b to V_t was generally proportional to the difference in sustained release rate at the two potentials regardless of whether a ribbon was present (compare Fig. 6C, bottom and Fig. 6D). This suggests that the subtraction operation that underlies the computation of Weber contrast does not require the synaptic ribbon.

Crowd surfing: a viable mechanism for vesicle movement along the ribbon

The simulations presented above suggest that passive vesicle diffusion along the side of the ribbon sufficiently recapitulates experimental observations, but they do not provide any mechanistic insight into how vesicles actually move along the ribbon surface. A plausible mechanism must prevent vesicles from detaching completely from the ribbon (Holt et al., 2004) yet still permit sufficiently fast diffusion along the ribbon (i.e., D_ribbon). To examine this question, we designed a new simulation to test how tethers might interact with vesicles and the ribbon (Fig. 7). The surface of a simulated ribbon was tiled with an array of 30-nm-long rigid tethers that could bind to vesicles that were within a 20 nm binding region (Fig. 7A). During each simulation time step (0.1 ms), the vesicle probabilistically bound or unbound tethers that lay beneath the footprint of the vesicle. In this way, the vesicle “crowd surfed” along the surface of the ribbon, passed between tethers. Because vesicles were not allowed to diffuse out of the range of a bound tether, their movement was slower than that permitted by free diffusion. In the simulation, a vesicle was considered “lost” when a completely unbound vesicle diffused beyond the binding region for tethers. To calculate diffusion along the tethers, vesicles were placed at the center of the tether array (Fig. 7B, black dot) and traveled 125 nm away from the starting point (Fig. 7B, black circle) before initiating a new trial. After 100 trials, the average time taken to diffuse 50 nm was used to calculate D_ribbon, using D_ribbon = (50²)/(4t) (example shown in Fig. 7C).

We systematically varied the binding:unbinding probability ratio (from 1.0 to 4) and the density of tethers along the ribbon surface (from 2304 to 4624 tethers/μm²) to determine the vesicle loss rate and diffusion coefficient across a range of parameter combinations (Fig. 7D). As expected, lower binding:unbinding ratios gave rise to relatively fast diffusion (D_ribbon/D as high as 0.85) but also high vesicle loss rates (e.g., >1 vesicles⁻¹s⁻¹) that were exacerbated at lower tether densities. Higher binding:unbinding ratios, however, achieved very low loss rates (as low as 0.025 vesicles⁻¹s⁻¹) without a severe reduction in diffusion coefficient (D_ribbon/D ≈ 0.37 to 0.51 for loss rates <0.14 vesicles⁻¹s⁻¹). Together, the crowd surfing model, whereby the vesicle is borne along the surface of the ribbon by transient interactions with multiple tethers, suggests a specific, anatomically feasible mechanism that yields realistic vesicle loss rates and diffusion coefficients.

Insights into ribbon disruption experiments

Although far from comprehensive, the general mechanistic underpinning of the tether-centric model presented here permits interesting and potentially informative comparisons to recent experiments. For example, a recent investigation in which ribbons were photodamaged with fluorophore-assisted light inactivation (FALI) of a ribbon-targeted, fluorescein-labeled peptide suggested that ribbons facilitate vesicle priming (Snellman et al., 2011). In particular, the authors found that, although voltage step-evoked release at mouse RBC ribbons was only slightly reduced (by ∼25%) during the first step immediately following FALI, release evoked by subsequent steps was reduced to a much greater extent (by ∼70%). The number of vesicles at the base of the ribbon was not reduced substantially by FALI, suggesting that vesicles could move along the ribbon and dock at release sites but not undergo priming (Snellman et al., 2011).

Using our vesicle release model (Fig. 2), we considered an alternative possibility that FALI may have disrupted tether interactions with vesicles without affecting priming (Fig. 8A). In our “virtual experiment,” simulations were designed to mimic the original step protocol used by Snellman et al. (2011) (100 ms step in V_m from −60 mV to −10 mV performed every 10 s for 40 s; Fig. 8B). Just before the second step, we simulated tether damage by prohibiting attached vesicles from moving along the side of the ribbon. In addition, a small subset of primed vesicles (25%) was immobilized and prohibited from releasing, effectively removing them from the releasable pool. The intrinsic properties of the remaining vesicle docking sites were unaffected: they remained capable of docking, priming, releasing, and replenishing. Access to these sites by free synaptic vesicles in the terminal was, however, restricted by the immobilized vesicles on the ribbon and damaged release sites.

The number of vesicles released during the simulated voltage step protocol mimicked qualitatively the results of the original experiment (Fig. 8C): FALI caused only a mild reduction in release in response to the first step, but release was reduced to a greater extent during subsequent steps (for a comparison of release evoked by 100 ms steps before and after FALI, see Fig. 8C, inset). Although in our simulations the maximum possible RRP was reduced after FALI by 25% (from 10 to 7.5 vesicles), the RRP post-FALI recovered only to 5 vesicles on average, despite the fact that the total number of vesicles at the base of the ribbon (including docked, primed, and FALI-immobilized vesicles) remained fairly constant (Fig. 8D). Although these simulations do not exclude a role for the ribbon in vesicle priming (Snellman et al., 2011), they do suggest an alternate explanation that is consistent with the experimental data, and they also demonstrate the potential insights that may be gained from a more mechanistic model of a ribbon synapse.

Discussion

Several roles have been proposed for ribbon synapses: neurotransmitter store (Osborne and Thornhill, 1972), diffusion barrier (Sjöstrand, 1958; Bartoletti et al., 2011; Graydon et al., 2011), vesicle conveyor belt (Bunt, 1971), and scaffold for compound fusion (Parsons and Sterling, 2003). However, a mechanistic explanation of how the ribbon accomplishes any of these tasks has remained elusive. Although recent studies have progressively catalogued the molecular constituents of synaptic ribbons (Schmitz et al., 2000; tom Dieck et al., 2005; Uthaiah and Hudspeth, 2010), their precise molecular structure and function remain unclear. Here, we tested the feasibility of a passive, diffusion-based mechanism by incorporating detailed ultrastructure (Fig. 1) into simulations constrained by experimentally observed parameters (e.g., release and replenishment rates, vesicle dwell times, membrane approach speeds; Figs. 2 and 3).

Using axial STEM tomography, we visualized the precise 3D organization of every vesicle associated with entire ribbons within 1-μm-thick sections. Importantly, axial STEM tomography yields much higher z-resolution than achieved by serial section TEM or serial block face scanning electron microscopy, techniques that are both limited by the minimum slicing thickness (∼25 nm). Axial STEM tomography also has advantages over focused ion beam scanning electron microscopy, for which it can be difficult to maintain an isotropic spatial resolution in the range of a few nanometers. Our analysis did not require large specimen volumes (e.g., 10³–10⁶ μm³) that can be successfully analyzed by focused ion beam scanning electron microscopy and serial block face scanning electron microscopy (Denk and Horstmann, 2004; Heymann et al., 2009).

Our simulated ribbon emulated a passive conveyor belt that was positively influenced by the packing density of attached vesicles and stimulus intensity (Fig. 4). The vesicle pools that developed during simulations resembled those observed ultrastructurally and electrophysiologically (Fig. 5). Rapid binding and unbinding of vesicles to the ribbon via tethers appeared sufficient to maintain low vesicle loss rates while permitting sufficient vesicle mobility along the ribbon surface (Fig. 7).

Photoreceptor ribbon synapses have been reconstructed tomographically (Sato et al., 2008; Zampighi et al., 2011; Omori et al., 2012), but we think that this is the first tomographic reconstruction of bipolar cell ribbons. The ultrastructural dimensions and associated vesicle pools of these ribbons match closely with goldfish bipolar cell ribbon synapses reconstructed with serial section EM (von Gersdorff et al., 1996). Notably, our reconstructions show that the pool of docked vesicles constitutes a highly consistent fraction (25 ± 2%) of the total attached pool (Fig. 1C,F). This is surprising given the variability in ribbon height (Fig. 1D), the geometric parameter likely to dictate the fraction of docked vesicles (tom Dieck et al., 2012), although our reconstructed ribbons exhibited no significant correlation between height and the fraction of docked vesicles (p = 0.54). If vesicles, despite diffusing freely along the ribbon, tend to form evenly spaced rows along the ribbon (Fig. 4Eiii), larger variations in height may be required to influence significantly the number of rows of attached vesicles. Larger rod photoreceptor ribbons (∼130 docking sites in cat) have been proposed to minimize pauses in ongoing vesicle release that could be mistaken for responses to photoisomerizations (Rao-Mirotznik et al., 1995). However, filtering at the rod–rod bipolar synapse, which optimizes signal-to-noise (Field and Rieke, 2002), may obviate the need for such large vesicle pools at RBC synapses.

Perhaps the largest assumption that the model makes is that vesicles can diffuse along the side of the ribbon. This seems a reasonable supposition, however, because vesicles that attach to the ribbon are subsequently released during stimulation (LoGiudice et al., 2008), and labeled vesicles (i.e., those containing recently endocytosed membrane) have been found attached to the ribbon some distance away from the plasma membrane (Paillart et al., 2003; LoGiudice et al., 2008), suggesting diffusion along the side of the ribbon (but not excluding the possibility of compound fusion; see below). Moreover, vesicles at ribbon synapses have been observed to approach the presynaptic membrane before their evoked release (Zenisek et al., 2000; Chen et al., 2013), although it has not been shown explicitly that these vesicles are tethered to the ribbon during their approach.

Importantly, these simulations reproduced several experimentally observed phenomena that they were not explicitly designed to reproduce. This was particularly evident for vesicle pool dynamics, which play a critical role in how the ribbon synapse transmits information. At the rod bipolar ribbon synapse, luminance and contrast are encoded in the occupancy of the readily releasable vesicle pool and changes in occupancy, respectively (Oesch and Diamond, 2011). The primed vesicle pools and release rates of the simulations presented here provide similar information (Figs. 5E and 6C). In addition, the vesicle density profile in simulations of a maximally releasing ribbon (with short priming; Fig. 4Diii) tapers toward very low occupancy at the membrane, similar to dark-adapted lizard cone ribbons (Jackman et al., 2009) and strongly stimulated bullfrog saccular hair cell ribbons (Lenzi et al., 2002). Similarly, despite the capacity of the model ribbon to accumulate a much larger attached pool, steady-state attached pools matched the attached pools in our EM reconstructions (Fig. 5C).

Our simulations demonstrate the plausibility of a functional conveyor belt that does not necessarily require ATP (Heidelberger et al., 2002; Parsons and Sterling, 2003) or even particularly fast vesicle movement along the ribbon. Indeed, effective D_z-axis was limited not by diffusion itself, but by stimulus intensity (i.e., release probability; Fig. 4C) because the docked pool of vesicles remained relatively full (Fig. 4Eiii). A side effect of this appears to be a plateau effect with respect to the attached pool occupancy (Fig. 4B). One of the benefits of having a plateau in vesicle resupply to the presynaptic membrane across a range of attached pool sizes is that it might help to keep resupply speeds relatively consistent despite rundown of vesicles that may occur during sustained release. Furthermore, by tracking vesicle attachment heights and density along the ribbon during a simulation, the simulations conveyed interesting nuances of how a passive conveyor belt might perform under various stimulus conditions. For example, in our release-maximizing conditions, one might presume that the conveyor belt would simply “treadmill” faster and that the process mediating vesicle translocation would increase turnover in proportion. Contrary to this idea, during simulated maximal release rates, a larger fraction of released vesicles attached at the base of the ribbon (Fig. 4Div), thereby leapfrogging other vesicles in queue and avoiding the conveyor belt altogether.

Three topics not addressed by the model are as follows: (1) the effects of presynaptic calcium on vesicle dynamics, (2) multivesicular release, and (3) nonribbon release. Resupply of vesicles at ribbon synapses has been shown to be calcium dependent (Mennerick and Matthews, 1996; Gomis et al., 1999; Cho et al., 2011; Schnee et al., 2011), although it remains unclear which aspect(s) of resupply (vesicle mobility in the terminal, ribbon attachment rate, docking rate, priming rate) is modulated. Ribbon synapses also can release multiple synaptic vesicles simultaneously (Glowatzki and Fuchs, 2002; Singer et al., 2004; Mehta et al., 2013), and the ribbon itself may be critical in the coordination of vesicle release (Mehta et al., 2013). Electron microscopic evidence of membranous tubules tethered to goldfish retinal bipolar ribbons after prolonged stimulation suggests that the ribbon may organize this synchronous release of vesicles via compound fusion (Matthews and Sterling, 2008). It may be the case that these stronger or longer stimuli enact additional mechanisms (e.g., calcium-induced calcium release) (Cadetti et al., 2006; Babai et al., 2010) or change the mode of release at these synapses. Last, although vesicles in the model must be docked at the base of the ribbon to be released, docking and release of vesicles at nonribbon sites may also participate in transmission from RBCs (Zenisek et al., 2000; Chen et al., 2013; Kantardzhieva et al., 2013; Mehta et al., 2014).

The simulations presented here make a number of predictions that can be tested with future experiments. The model suggests specific relationships between RRP refilling speed (e.g., D_ribbon), priming/vesicle dwell times, and vesicle release rate (Fig. 3A). A wide range of vesicle dwell times has been reported (60–250 ms) (Zenisek et al., 2000; Chen et al., 2013), suggesting a wide range of priming rates. The model presented here can operate within this range of priming values and allows one to predict vesicle diffusion along the ribbon (D_ribbon), provided one knows the release rate of the synapse. D_ribbon is a complicated parameter, though, and an understanding of the relationship between priming/vesicle dwell time and stimulus conditions is crucial. More useful, perhaps, is the prediction that effective D_z-axis of attached vesicles, and consequently membrane approach speed, should vary in accordance to release probability (Fig. 4C). This is unlikely to be the case for proposed ribbon models where the ribbon acts as a stable vesicle scaffold (i.e., “safety belt”) for compound fusion (Parsons and Sterling, 2003). Both vesicle dwell time and membrane approach speed can be measured with TIRF (Chen et al., 2013) and might be experimentally manipulated. Further experiments, using increasingly sophisticated measurement techniques, stimulation protocols, and molecular manipulations, will constrain further our conceptual and numerical models of ribbon synapse function.