A modeling analysis of the effects of molecular size and binding affinity on tumor targeting

Abstract

A diverse array of tumor targeting agents ranging in size from peptides to nanoparticles is currently under development for applications in cancer imaging and therapy. However, it remains largely unclear how size differences among these molecules influence their targeting properties. Here we develop a simple, mechanistic model that can be used to understand and predict the complex interplay between molecular size, affinity, and tumor uptake. Empirical relationships between molecular radius and capillary permeability, interstitial diffusivity, available volume fraction, and plasma clearance were obtained using data in the literature. These relationships were incorporated into a compartmental model of tumor targeting using MATLAB to predict the magnitude, specificity, time dependence, and affinity dependence of tumor uptake for molecules across a broad size spectrum. In the typical size range for proteins, the model uncovers a complex trend in which intermediate sized targeting agents (MW ~ 25 kDa) have the lowest tumor uptake, while higher tumor uptake levels are achieved by smaller and larger agents. Small peptides accumulate rapidly in the tumor but require high affinity to be retained, while larger proteins can achieve similar retention with >100 fold weaker binding. For molecules in the size range of liposomes, the model predicts that antigen targeting will not significantly increase tumor uptake relative to untargeted molecules. All model predictions are shown to be consistent with experimental observations from published targeting studies. The results and techniques have implications for drug development, imaging, and therapeutic dosing.

Introduction

Traditional small molecule cancer therapeutics suffer from limited selectivity between tumor and healthy tissues, leading to marginal therapeutic indices. One approach for improving diagnostic or therapeutic specificity is to utilize targeting molecules capable of selectively binding antigens overexpressed in the tumor (1). Such agents can deliver payloads such as toxins, radiometals, or imaging agents to the tumor, or may induce cell death in a more direct manner by blocking proliferative signaling or recruiting immune effectors.

Traditionally, tumor targeting has focused on the use of IgG monoclonal antibodies due to their high functional affinity for the target antigen and favorable pharmacokinetic profile. However, effective antibody treatment of many solid tumors remains limited by an inability of the drugs to completely penetrate the tumor tissue leaving regions of untargeted cells (2,3). Additionally, slow plasma clearance of IgGs due to active recycling by the neonatal Fc receptor maintains high drug levels in the blood that complicate imaging or therapy.

With these limitations in mind, a number of alternative tumor targeting molecules have been developed with unique physical properties. Initial development of novel targeting agents focused on making smaller fragments of the full IgG that retain antigen binding properties, including 27 kDa scFvs, 50 kDa Fabs, 80 kDa minibodies, and various scFv and Fab based multimers (4). More recently, alternative binding scaffolds including 14 kDa DARPins and 7 kDa affibodies have been engineered that bind antigens with high affinity despite their small size (5,6). At the other end of the size spectrum, nanoparticles and liposomes with molecular radii ranging from 10–100 nm have been developed that incorporate targeting, imaging, and therapeutic functionalities (7). Chemical conjugation approaches such as PEGylation have allowed for further tailoring of molecular size (8).

While these diverse molecules vary in a number of properties including valency, geometry, stability, and surface charge, the most obvious difference is a wide range of molecular radii. Despite several experimental comparisons, however, the exact effects of these size differences on tumor targeting remain unclear. This confusion arises largely from the fact that size influences several distinct transport parameters relevant to tumor targeting including permeability across the tumor capillary wall (P), diffusivity within the tumor interstitium (D), available volume fraction in the tumor (ε), and rate of plasma clearance (k_clear) (8–11). These parameters counteract each other in a manner that makes predicting the effects of size difficult a priori. For instance, small molecules have increased rates of transport across the capillary wall and within the tumor but are also rapidly cleared from the plasma, eliminating the diffusive gradient into the tumor. In contrast, large molecules are cleared from the blood more slowly, but simultaneously suffer from slower rates of transcapillary and interstitial transport.

Due to the complexity of these tradeoffs, computational tools are needed to accurately predict the effects of molecular size on tumor transport. Such models have previously been used to predict antibody microdistribution and macrodistribution within tumors and examine the effect of parameters such as tumor physiology, dose, binding affinity, and antigen turnover (12,13). Here we extend these models to predict the magnitude and specificity of tumor uptake for molecules covering the continuum of sizes from small peptides to liposomes by incorporating derived empirical relationships for the effect of hydrodynamic radius on the parameters P, D, ε, and k_clear. Our predictions are consistent with published biodistribution studies targeting HER2 expressing xenografts in mice, as well as clinical data from targeting CEA expressing tumors in humans, and shed light on the complex interplay of size and binding affinity in tumor targeting.

Methods

Previously reported experimental measurements of capillary permeability (P), interstitial diffusivity (D), available volume fraction (ε), and plasma clearance (k_clear) for molecules of various sizes in tumor tissues were collected from the literature (Supplemental Tables 1–4). The data sets include studies on proteins, small molecule tracers, dextrans, PEG chains, and liposomes primarily in mouse xenograft models. Mathematical equations describing the relationship between these parameters and molecular radius (R_mol) over a broad continuum of sizes were derived by fitting structural and empirical models of the capillary wall, tumor interstitial space, and renal and non-renal routes of plasma clearance. Implicit in all of these descriptions is the assumption that these are hydrophilic molecules that are not sequestered in membranes or fatty tissue. Fitting was performed using the non-linear least squares method in MATLAB.

The effect of molecular radius on diffusivity (D) and available volume fraction (ε) within the tumor can be described by modeling the tumor interstitial space as a series of small and large right circular cylindrical pores. Using this framework, the molecular diffusivity within each pore can be described as D_pore = D_free * (D_pore/D_free), where D_free is the diffusivity of the molecule in solution (cm²/s) and D_pore/D_free is the fractional reduction in free diffusion within the pores (14). D_free can be estimated using the relationship D_free = (3×10⁻⁶ cm²/s)/R_mol, where R_mol is the molecular radius in nm, while D_pore/D_free can be solved as:

$$\frac{D_{\mathit{pore}}}{D_{\mathit{free}}}=\frac{(1-2.105\lambda +2.0865{\lambda }^3-1.7068{\lambda }^5+0.72603{\lambda }^6)}{\left(1-0.75857{\lambda }^5\right)}$$ (1)

for values of λ < 0.6 where λ is defined as the ratio of molecular radius (R_mol) to pore radius (R_pore) (14). For 0.6 < λ < 1, numerical values of D_pore/D_free were determined from previously described lookup tables (15). For λ > 1, D_pore/D_free = 0. To account for diffusion through small and large pores in the tumor, diffusivity over the entire tumor space was defined as D = (A*D_{pore_small} + B*D_{pore_large}) where D_{pore_small} and D_{pore_large} are the diffusivities in the small and large pores respectively, and A and B are the relative amounts of diffusion that take place through each pore size (A + B = 1).

Using the same self-consistent two pore representation of the tumor interstitial space, the available volume fraction can be described using the equation:

$$\epsilon =V_i\left(A\ast {\phi }_{\mathit{pore}\_\mathit{small}}+B\ast {\phi }_{\mathit{pore}\_\mathit{l}arg\mathit{e}}\right)$$ (2)

where V_i is the interstitial fluid volume fraction, A and B are the ratios of small and large pores, and φ_{pore_small} and φ_{pore_large} are the partition coefficients of molecules in each pore size defined as φ = (1 − λ)² for λ < 1, and φ = 0 for λ > 1 (16). From small molecule tracer studies, V_i was approximated as 0.5 (10). Since both the interstitial diffusivity and void fraction are described by the same model of the interstitial space, data sets describing each parameter (Supplemental Tables 1–2) were simultaneously fit to the respective equations to determine values for R_{pore_small}, R_{pore_large}, A, and B.

The effect of molecular radius on vascular permeability was similarly modeled using a two-pore representation of the tumor capillary wall. Transport was assumed to be primarily diffusive in nature due to high interstitial fluid pressure in tumors (17), such that permeability across a pore (cm²/s) can be modeled as:

$$P_{\mathit{pore}}=D_{\mathit{free}}\ast \left(\frac{D_{\mathit{pore}}}{D_{\mathit{free}}}\right)\ast \phi$$ (3)

where D_free, (D_pore/D_free), and φ are defined as above (16). Total permeability through small and large pores was defined as P = A_cap*P_{cap_pore_small} + B_cap*P_{cap_pore_large} where A_cap and B_cap are the fractional capillary pore areas per unit membrane thickness (cm⁻¹) for small and large pores respectively. As above, the model was fit to experimentally determined P values (Supplemental Table 3) to estimate A_cap, B_cap, R_{cap_pore_small}, and R_{cap_pore_large}. While these parameters are similar to those used to describe D and ε, here they are describing pores in the capillary wall versus pores in the interstitial space of the tumor.

Due to the various routes and complexities inherent in plasma clearance, there are no simple structural models to describe the size dependency of the clearance term k_clear. Instead a largely empirical model was utilized for the renal and non-renal routes of clearance. For renal clearance, macromolecular filtration can be described as Cl_R = GFR*Θ, where Cl_R is the renal clearance in mL/hr, GFR is the rate of fluid filtration across the glomerular wall estimated at 10 mL/hr in female mice (18), and Θ is the macromolecular sieving coefficient. The sieving coefficient depends on molecular size and can be described as (19):

$$\mathrm{\Theta }=\frac{\mathrm{\Phi }{K}_{\mathit{conv}}}{1-e^{-\sigma Pe}+\mathrm{\Phi }{K}_{\mathit{conv}}{e}^{-\sigma Pe}}$$ (4)

where Φ is the equilibrium partition coefficient, σ is a correction term for the geometry of the glomerular slits approximately equal to 2 for baseline glomeruli, K_conv is the solute hindrance factor for convection, and Pe is the Péclet number defined as:

$$Pe=\frac{(\mathrm{\Phi }{K}_{\mathit{conv}})vL}{(\mathrm{\Phi }{K}_{\mathit{diff}})D_{\mathit{free}}}$$ (5)

In this description, v is the fluid velocity vector estimated at 0.001 cm/s, L is the membrane thickness approximated at 100 nm in mice (20), D_free is the diffusivity in solution discussed above, and K_diff is the diffusive hindrance factor. Since there are limited mechanistic models for the effect of size on the hindrance factors K_conv and K_diff, they, along with the partition coefficient, are defined using empirical terms as reported previously (21):

$$\mathrm{\Phi }{K}_{\mathit{diff}}=exp(-\alpha R_{\mathit{mol}})$$ (6)

$$\mathrm{\Phi }{K}_{\mathit{conv}}=exp(-\beta R_{\mathit{mol}})$$ (7)

where R_mol is the molecular radius of the targeting agent and α and β are empirical constants fit to the data (units nm⁻¹).

Non-renal clearance was incorporated to account for plasma loss of molecules above the cutoff size for glomerular filtration. With several route of clearance and no structural models a fully empirical model was used with the form:

$${Cl}_{NR}={Cl}_{NR,0}-\delta \left(\frac{r_{\mathit{mol}}}{r_{\mathit{mol}}+\gamma }\right)$$ (8)

where Cl_NR,0 is the non-renal clearance for small molecule tracers (mL/hr), and δ (mL/hr) and γ (nm) are empirical constants fit to the data. While this equation has no physiological significance, it is consistent with experimental observations of decreasing non-renal clearance with increasing molecular size down to a constant level for large molecules (22). Cl_NR,0 was arbitrarily set to 2 mL/hr to account for the dominance of renal clearance in the size range of small peptides.

The single exponential plasma clearance term k_clear (units hr⁻¹) was then defined as:

$$k_{\mathit{clear}}=\frac{{Cl}_R+{Cl}_{NR}}{V_{\mathit{plasma}}}$$ (9)

where V_plasma is the plasma volume estimated in mice as 2 mL (23). For predictions of tumor uptake in human patients, the plasma volume was increased to 3 L. This equation was fit to experimental measurements of k_clear for molecules of various sizes (Supplemental Table 4) to determine the constants α, β, δ, and γ. Although a biexponential description of plasma clearance is more physiologically accurate, the single exponential term is a reasonable approximation that allows us to better describe the broad features of size dependent clearance over the entire continuum of molecular radii using a single parameter.

Tumor uptake of targeting molecules was simulated using a mechanistic compartmental model of antibody uptake in tumors¹ (Supplemental Figure 1), in which tumor concentration following a sub-saturating bolus iv injection can be described as:

$${[Ab]}_{\mathit{tumor}}=\left(\frac{2{PR}_{\mathit{cap}}}{R_{\mathit{Krogh}}^2}\right)\left(\frac{{[Ab]}_{\mathit{plasma},0}\left(e^{-k_{\mathit{clear}}t}-e^{-\mathrm{\Omega }t}\right)}{(\mathrm{\Omega }-k_{\mathit{clear}})}\right)$$ (10)

$$\mathrm{\Omega }=\frac{2{PR}_{\mathit{cap}}}{\epsilon R_{\mathit{Krogh}}^2}\left(\frac{K_d}{\left(\frac{[Ag]}{\epsilon }\right)+K_d}\right)+k_e\left(\frac{\left(\frac{[Ag]}{\epsilon }\right)}{\left(\frac{[Ag]}{\epsilon }\right)+K_d}\right)$$ (11)

where [Ab]_plasma,0 is the initial plasma concentration of the targeting agent (%ID/mL), t is the time, [Ag] is the target antigen concentration (M), k_e is the rate of endocytic clearance (sec⁻¹), K_d is the targeting molecule’s affinity for the antigen (M), R_cap is the capillary radius (μm), and R_Krogh is the average radius of tissue surrounding each blood vessel (μm). P, ε, and k_clear represent permeability, available volume fraction, and plasma clearance rate, respectively, with values for each sized molecule taken from the fits described above. The diffusivity term (D) does not appear in the above equations as Thurber et al. demonstrated in the model derivation that antibody uptake from the tumor surface is negligible relative to vascular uptake for most experimentally or clinically relevant tumor types and sizes, and that the permeability term is the rate limiting step in vascular uptake. The diffusivity term is still included in the methods for fitting interstitial pore size, however, as it provides a check for self-consistency with the size-dependent trends in available volume fraction. Size-independent parameter values were estimated from the literature or were varied as described in each simulation. For figures plotted as a function of effective molecular weight, estimates were made from radius using the relationship MW = 1.32*R_mol³ (fit from data in reference (24)).

Using the above model, the time of peak tumor uptake following bolus injection can be defined as:

$$t_{\mathit{opt}}=\frac{ln\left(\frac{k_{\mathit{clear}}}{\mathrm{\Omega }}\right)}{\left(k_{\mathit{clear}}-\mathrm{\Omega }\right)}$$ (12)

where Ω is defined in Equation 11.

Results

Relationship of size to transport parameters

The molecular size of a tumor targeting agent influences four parameters involved in tumor uptake: plasma clearance (k_clear), capillary permeability (P), interstitial diffusivity (D), and available volume fraction in the tumor (ε). Values of these parameters for molecules of different sizes were collected from experimental studies reported in the literature (Supplemental Tables 1–4) and used to fit models of the capillary wall, tumor interstitial space, and renal and non-renal routes of plasma clearance. While these models may not fully represent the physiological phenomena behind each parameter, they provide a reasonable framework for describing experimental trends in these parameters over the range of targeting agent sizes.

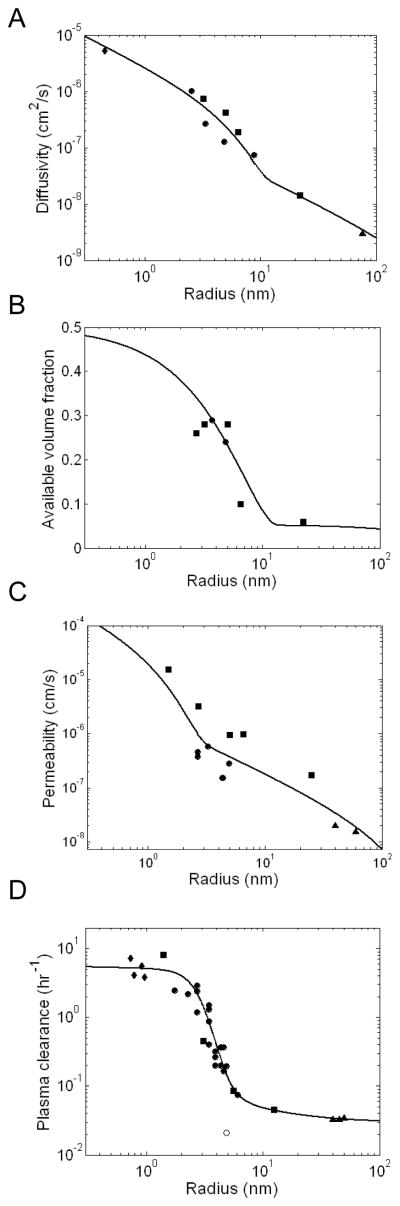
The interstitial diffusivity and available volume fraction data sets are best described by a two-pore model of the tumor interstitial space with pore radii of 13.8 nm and 1 μm at a ratio of 9 to 1 (Figure 1A,B). The small pore size is consistent with previous descriptions of size dependent transport in the tumor interstitial space (14), while the large pores are necessary to account for the observed diffusion of 2 MDa dextran and liposomes. Similarly, the relationship between molecular radius and transcapillary permeability was well fit by a two-pore model of the capillary wall with 4.5 nm and 500 nm radius pores with fractional area to thickness ratios of 17.6 cm⁻¹ and 0.65 cm⁻¹, respectively (Figure 1C). These values are again physiologically reasonable as ~5 nm pores are typical of healthy vasculature (16), and larger pores with 500 nm radii have been observed in leaky tumor vessels due to overexpression of VEGF and other hyperpermeability factors (24).

Figure 1.

Size dependent transport parameters. A, B. Relationship between molecular radius and effective diffusivity (D) and available volume fraction (ε) in the tumor. Data points were simultaneously fit to a two pore model of the tumor interstitial space. C. Relationship between molecular radius (R) and effective molecular permeability across the tumor vasculature (P). Data points were fit to a two pore model of the capillary wall. D. Relationship between molecular radius and plasma clearance rate (k_clear). Data points were fit to an empirical model of renal and non-renal clearance. IgG clearance is denoted by an open circle and was not included in the fit. All data fitting was performed using a non-linear least squares method. Data points were collected from experimental results reported in the literature and include measurements of proteins (circles), dextran and PEG polymers (squares), small molecule tracers (diamonds), and liposomes (triangles). Additional descriptions of the experimental data are presented in Supplemental Tables 1–4.

The effect of size on plasma clearance is difficult to model as it is influenced by both renal and non-renal routes of clearance. As such, a largely empirical model of plasma clearance was derived with resulting parameters of α = 1.6 nm⁻¹, β = 0.95 nm⁻¹, δ = 1.94 mL/hr, and γ = 0.20 nm (Figure 1D). While these parameters have no physiological significance, they produce a fit that closely resembles the trend in the data and is similar to previous empirical descriptions of size dependent clearance (25). Plasma clearance data for IgGs are displayed separately and not included in the fit as the Fc domain significantly reduces clearance through interactions with endothelial FcRn receptors (26).

Predicted maximum tumor uptake

A previously described compartmental model of tumor uptake was used to predict the peak tumor concentration achieved for radiolabeled HER2 targeting molecules of various sizes following a bolus iv injection. Values for P, ε, and k_clear were determined for each size using the relationships derived above. Size-independent model parameters were estimated for a well-vascularized HER2 expressing xenograft model from values in the literature and are presented in Table 1. While molecules bound to HER2 typically undergo net cellular internalization with a half time of ~6–8 hours ( ref (27) and unpublished results) endocytic clearance in the context of measured total tumor uptake of radiolabel depends also on the rate at which degraded label is cleared from the cell. Therefore we simulated two different radiolabels, faster-clearing ¹²⁵I and residualizing ^99mTc (28).

Table 1.

Size independent parameter values

Parameter	Value	Reference
[Ab]plasma,0	50 %ID/mL	Assuming 2 mL plasma volume in mice
[Ag]	150 nM	(13)
Rcap	8 μm	(46)
RKrogh	75 μm (50–100 μm)	(47,48)
ke (125I)	1.6E-5 sec−1	(49)
ke (99mTc)	4.8E-6 sec−1	(28,50)

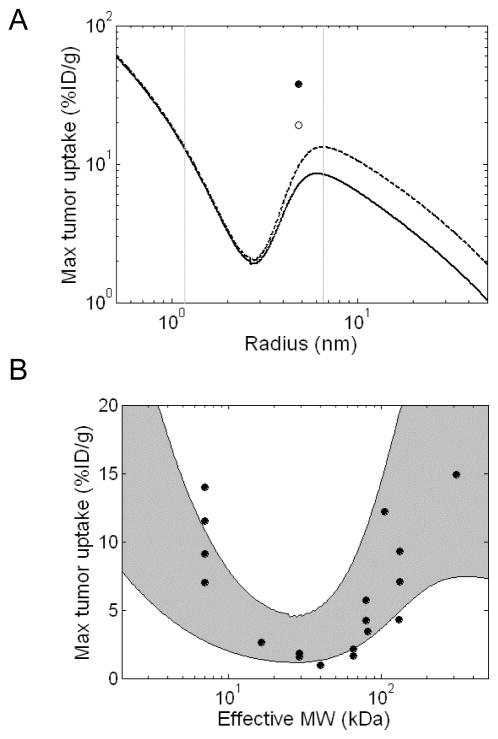
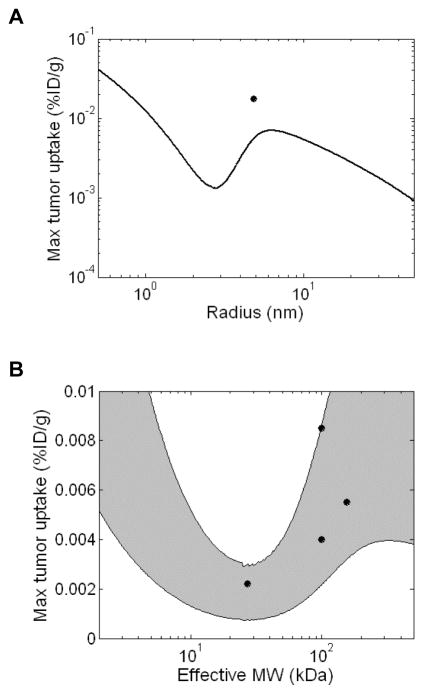
The simulations predict a complex relationship between peak tumor accumulation and size (Figure 2A). In general, predicted tumor uptake is highest for small targeting agents and decreases with increasing molecular radius due to the size-dependent decrease in tumor capillary permeability and available volume fraction reflected in Figures 1B and 1C. However, this trend briefly reverses in the size range typical of proteins producing a local minimum for tumor uptake at a radius of ~2.8 nm and a local maximum at ~6.5 nm. The existence of the minimum and maximum in this curve can be attributed primarily to the sigmoid dependence of renal clearance on size (Figure 1D). Molecules in this size range start to become larger than the kidney filtration cutoff leading to sustained circulation in the plasma which provides increased chances for extravasation into the tumor. Although capillary permeability and available volume fraction are still decreasing in this size range, the decrease in systemic clearance is greater, producing a net increase in tumor uptake. IgGs are predicted to achieve significantly higher tumor uptake than other molecules of equivalent size as a result of their slower plasma clearance due to size-independent FcRn-mediated salvage. The use of residualizing ^99mTc is predicted to increase peak tumor uptake relative to ¹²⁵I labeled molecules when used with large molecules.

Figure 2.

Predicted effect of molecular size on maximum tumor uptake. Simulations were performed using a compartmental model of tumor transport and size-dependent values of P, ε, and k_clear. All size-independent parameters are reported in Table 1. Tumor concentrations are reported as %ID/g. A. Predicted peak tumor concentrations of HER2 binding molecules (K_d = 1 nM) labeled with ¹²⁵I (solid line) or residualizing ^99mTc (dashed line). IgG uptake was simulated independently (open circle - ¹²⁵I, solid circle – ^99mTc) and is predicted to be higher due to FcRn mediated reduction in plasma clearance. The vertical grey lines highlight the size range typical of protein therapeutics that is further analyzed in Figure 2B. B. Comparison to experimental data. Peak uptake simulations were performed as above and plotted as a function of effective molecular weight. The predicted uptake trends for R_Krogh = 50 μm and R_Krogh = 100 μm form the upper and lower bounds respectively of the shaded grey area. Data points were collected from HER2 targeting experiments in the literature including ^99mTc, ¹¹¹In, and ⁶⁴Cu labeled molecules of various sizes. References and additional details for each experimental data point are presented in Supplemental Table 5. The units of radius and effective MW used in panel A and B, respectively, can be related using the relationship MW = 1.32*R_mol³ (for example 7 kDa affibodies, 27 kDa scFvs, 50 kDa Fabs, and 150 kDa IgGs have radii of 1.74 nm, 2.74 nm, 3.47 nm, and 4.86 nm, respectively.)

Model predictions for ^99mTc labeled targeting agents in the size range typical of proteins (2–500 kDa) were compared to data from experimental HER2 targeting studies in the literature (Figure 2B). Each data point represents the highest tumor concentration achieved by a given targeting agent over an experimental time course (Supplemental Table 5). Since the R_Krogh value for intercapillary spacing is the least well-characterized parameter in the model and depends on the extent of vascularization and necrosis within the tumor, simulations were performed for a range of values between 50 and 100 μm. While the computational predictions differ quantitatively from the experimental uptake for several molecules in this size range, the overall trends are consistent. In both the simulations and experimental precedents, intermediate sized proteins (~25 kDa) have the lowest tumor uptake while higher levels of targeting are achieved by smaller or larger agents. Higher predicted IgG uptake in the range of 30–40 %ID/g is also consistent with experimental precedents (Supplemental Table 5).

Time dependence of tumor uptake

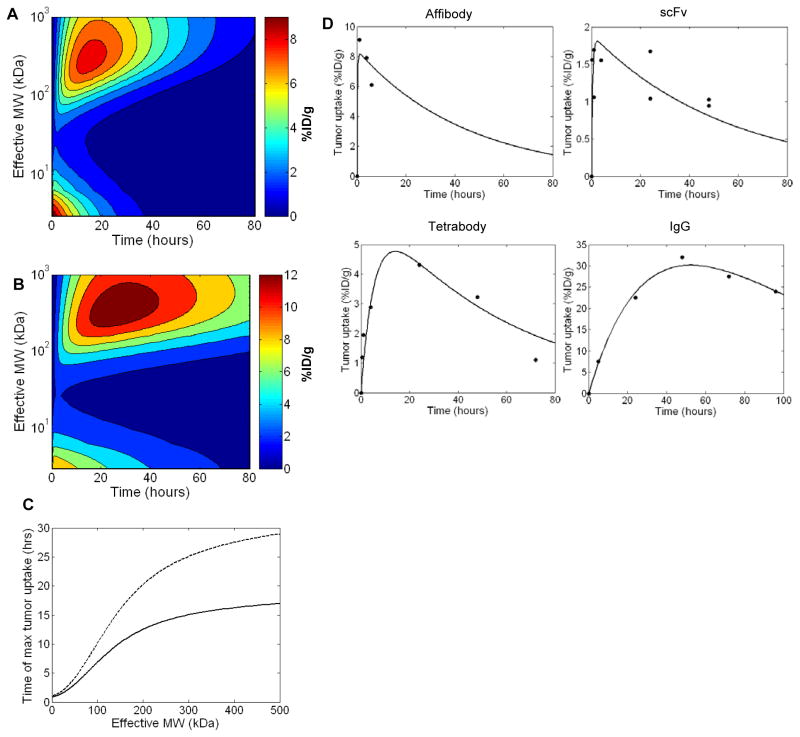
The time of peak tumor uptake and length of tumor retention also have important implications for imaging and therapy. Therefore, full time course simulations were performed for ¹²⁵I or ^99mTc labeled HER2 targeting molecules (K_d = 1 nM) ranging in size from 2–1000 kDa. As reported above, peak tumor levels are similar for proteins at the small and large ends of this size range with a local uptake minimum in between (Figure 3A,B). The time at which peak uptake occurs, however, differs significantly as small macromolecules reach their maximum tumor level within minutes, while uptake of larger molecules occurs on the time scale of hours to days (Figure 3C). Targeting agents labeled with residualizing ^99mTc are predicted to achieve peak tumor uptake at later time points and display significantly greater tumor retention than those labeled with ¹²⁵I as expected given their differences in cellular clearance. The predictions in Figures 3A–C are valid only for molecules lacking Fc domains or other active trafficking as FcRn mediated salvage increases the time until peak tumor uptake by increasing serum persistence.

Figure 3.

Predicted effect of molecular size on time course of tumor uptake. Tumor uptake over time was simulated for ¹²⁵I (A) or ^99mTc (B) labeled non-Fc domain containing HER2 binding molecules (K_d = 1 nM) ranging in size from 2–1000 kDa. C. Effect of molecular size on the time of maximum tumor uptake for ¹²⁵I (solid line) or ^99mTc (dashed line) labeled molecules. D. Comparison to experimental data. Tumor uptake simulations were performed for affibodies (MW = 7 kDa), scFvs (27 kDa), tetrabodies (130 kDa), and IgGs (150 kDa) and compared to experimentally measured time courses for ^99mTc labeled HER2 targeting molecules (29–32). R_Krogh values were fit to the experimental data for each molecule using the least squares method with results of 57, 80, 101, and 84 μm for the affibody, scFv, tetrabody, and IgG data sets respectively. These values are all in a physiologically reasonable range.

Computational predictions were compared to published biodistribution time courses for anti-HER2 proteins labeled with ^99mTc (Figure 3D) (29–32). In order to more directly compare the time-dependency of the predicted uptake, the magnitude of uptake (%ID/g) was adjusted in each case by fitting the R_Krogh value to the experimental data. For high affinity targeting molecules (K_d ≪ [Ag]) as is the case here, the R_Krogh term impacts the height of the curve but has no influence on the shape or time of peak uptake. In all cases, the computationally predicted time course of tumor loading and retention matches the experimental results well. Affibodies and scFvs achieve peak uptake within the first few hours while larger tetramer and IgG molecules achieve tumor uptake more slowly. IgGs in particular have very slow tumor accumulation with peak uptake after days due to the slow rate of plasma clearance driven by FcRn mediated salvage.

Affinity dependence of tumor uptake

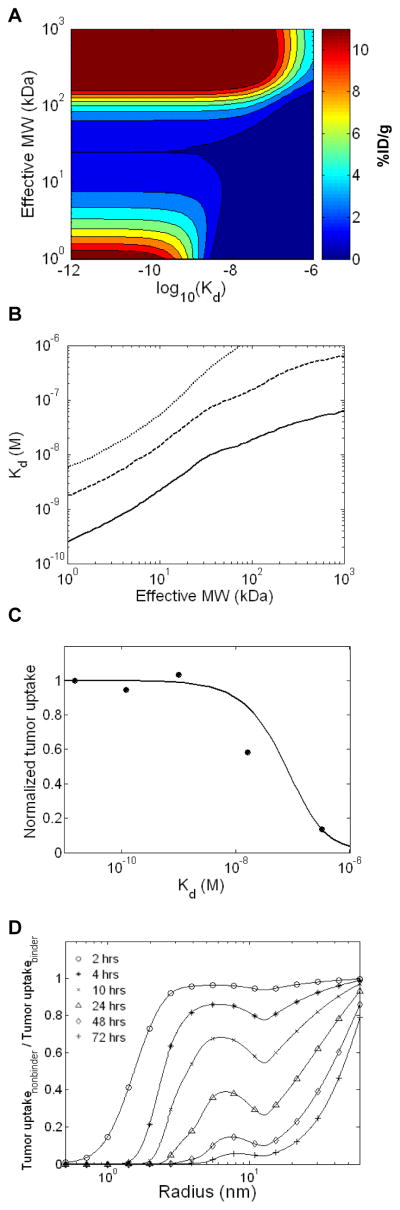
Experimental and theoretical analyses suggest that increasing the affinity of a targeting molecule for its antigen will increase tumor localization up to a point at which tumor levels plateau (12,33). However, the precise affinity at which maximum tumor uptake is achieved depends on the targeting molecule’s size. To examine this relationship in more detail, calculations were performed to predict the tumor uptake at 24 hours for macromolecules varying in both molecular size and affinity. For all sizes in the range of 1–1000 kDa, the expected improvement in tumor uptake with increasing affinity was observed up to a plateau at high affinities (Figure 4A). The threshold affinity of this plateau was size dependent, however, as smaller proteins require tighter binding on the order of 10⁻¹⁰ to 10⁻⁸ M K_d values to maintain significant tumor uptake, while large molecules are able to achieve similar uptake levels at much lower affinities in the 10⁻⁸ to 10⁻⁶ M K_d range (Figure 4A, B). IgGs, for instance, require only a 6×10⁻⁷ M affinity to achieve 50% of their peak tumor uptake at 24 hours. The differences in affinity dependence are due to the fact that small, unbound molecules are cleared rapidly from the tumor through vascular intravasation due to their high capillary permeability. As such, small proteins must be anchored to the antigen through high affinity interactions to be retained. In contrast, large, unbound molecules intravasate slowly such that moderate affinity molecules are able to rebind repeatedly and remain in the tumor.

Figure 4.

Binding and affinity dependence. A. Predicted tumor uptake at 24 hours for ^99mTc labeled HER2 targeting molecules varying in both size and affinity for the target antigen. B. Affinity necessary to achieve 10% (small dashes), 50% (large dashes), or 90% (solid line) of the maximum tumor uptake at 24 hours as a function of molecular size. C. Comparison to experimental data. The predicted 24 hour tumor concentration for HER2 targeting scFvs (MW = 27 kDa) of various affinities were compared to experimental uptake measurements for affinity variants of the C6.5 scFv (33). Model predictions and experimental data are normalized by their respective uptake values for the highest affinity case. D. EPR mediated non-specific uptake. Predicted tumor concentrations of non-targeted molecules (K_d = 1 M) ranging in radii from 0.5–60 nm were calculated for various times and normalized by the predicted uptake of size matched antigen binding molecules with a K_d of 1 nM (untargeted to targeted uptake ratio). A value of 0 represents fully binding mediated tumor retention, while a value of 1 represents equivalent uptake of targeted and non-targeted molecules. R_Krogh = 100 μm.

Computational predictions were compared to experimentally reported tumor uptake data for anti-HER2 scFvs ranging in affinity from 15 pM to 320 nM (33). The model accurately predicts the experimental trend in which the three highest affinity scFvs have similar uptake while lower tumor uptake levels are observed for the 16 nM and 320 nM K_d molecules (Figure 4C).

Non-binding mediated uptake: size dependence of the enhanced permeability and retention (EPR) effect

Experimental studies have suggested that significant tumor accumulation of large macromolecules may occur even in the absence of tumor-specific binding due to the EPR effect (34). We therefore calculated the uptake of untargeted macromolecules relative to the tumor levels of size-matched molecules that bind the target antigen with a 1 nM K_d (Figure 4D). The simulations demonstrate that at early time points uptake is similar for non-targeted and targeted molecules for all but the smallest peptides. Following this initial uptake phase, unbound molecules are cleared rapidly from the tumor while bound molecules are retained, producing a high level of specificity of targeting at later time points for molecules in the size range of most proteins (radius < 10 nm). In contrast, larger molecules in the size range of liposomes (~50 nm) are predicted to have similar tumor levels of targeted and non-targeted molecules even at later time points, as uptake is dominated by EPR effects. This situation arises as the slow clearance of large, unbound molecules by vascular intravasation occurs at the same rate as clearance of antigen-bound molecules by cellular internalization and degradation. These model predictions are consistent with experimentally measured values of tumor uptake specificity (Supplemental Figure 2).

Predicted uptake in human tumors

While comparisons to mouse xenograft studies are a useful validation for model predictions of size dependent trends, the true utility of a model depends on its ability to predict tumor uptake in human patients. Therefore, simulations were performed for tumor uptake of targeting agents of various sizes in human subjects and compared to clinical data for uptake of anti-carcinoembryonic antigen (CEA) scFv, F(ab′)₂, DFM, and IgG molecules labeled with ¹³¹I (35). [Ab]_plasma,0 was reduced from 50 %ID/mL to 0.033 %ID/mL due to the increase in plasma volume from 2 mL to 3 L, and the [Ag] and k_e values were changed to 300 nM and 9.6E-6 sec⁻¹ to reflect the different expression and trafficking properties of CEA (36). All other parameter values were left the same as used in the mouse studies as they should be relatively independent of animal species or body weight in their stated form and few measured values are available for human patients. The predicted max tumor level for molecules ranging in size from peptides to liposomes is presented in Figure 5A. The size-dependent trends are identical to those observed in the mouse simulations, while the absolute values are significantly reduced due to the increased plasma volume. The predicted uptake levels in the size range of proteins match closely with the clinically measured tumor concentrations (Figure 5B).

Figure 5.

Predicted tumor uptake in humans. Simulations were performed as described in Figure 2 except with V_plasma = 3L, and [Ag] and k_e adjusted for targeting CEA. A. Predicted peak tumor concentrations in humans of CEA binding molecules (K_d = 1 nM) labeled with ¹²⁵I. IgG uptake was simulated independently and denoted by the solid circle. B. Comparison to clinical data. Peak uptake simulations were performed as above and plotted as a function of effective molecular weight in the size range typical of proteins (2–500 kDa). The predicted uptake trends for R_Krogh = 50 μm and R_Krogh = 100 μm form the upper and lower bounds respectively of the shaded grey area. The data points represent clinically measured tumor concentrations for scFv, F(ab′)₂, DFM, and IgG molecules targeting CEA expressing tumors in humans (35).

Discussion

The increased development of novel tumor binding agents for applications in cancer therapy and imaging has raised the question of how size differences among these molecules impact their targeting properties. Here we incorporate derived relationships between molecular radius and the transport parameters permeability, available volume, and plasma clearance into a compartmental model of tumor uptake to quantitatively assess the effect of molecular size on the magnitude and specificity of tumor localization. Despite the simplicity of the model, we are able to accurately predict several experimental trends for HER2 targeting molecules in mice and CEA targeting molecules in humans, suggesting that size and affinity alone can largely account for the targeting properties of most macromolecules. The modeling framework presented here can also be applied to other tumor types and antigens by simply altering the relevant parameters, which can be independently measured.

While several groups have experimentally or computationally compared tumor uptake for small sets of different sized molecules (30,37,38), here we compare molecules across a broad continuum of molecular radii uncovering complex trends of size dependency. In particular, the model predicts that in the size range of most protein agents, there is a local uptake minimum at ~25 kDa while larger and smaller agents achieve higher tumor levels. This prediction is consistent with experimental measurements of HER2 targeting molecules and suggests that small proteins such as affibodies and DARPins, along with larger molecules including multimers and PEGylated proteins should be superior targeting agents compared to scFvs. For large molecules, uptake can be further increased by incorporation of Fc or albumin binding domains to actively reduce plasma clearance (26,39).

Although small and large proteins are predicted to have similar peak tumor levels, they differ significantly in the time and affinity dependence of uptake. Small proteins achieve high tumor levels rapidly but require high affinity to be retained, as unbound molecules clear from the tumor rapidly. The rapid uptake of small proteins combined with their efficient clearance from the plasma and normal tissues may make them ideally suited for imaging applications (6). In contrast, large molecules can achieve high uptake at comparatively low affinities but accumulate in the tumor on a much slower time scale. These molecules may be best suited for multi-step pretargeting strategies in which the slow clearance from the plasma can be augmented by clearing agents (40).

Outside the size range of typical protein agents, the model predicts very high tumor uptake for small, hydrophilic, high affinity peptides. While high affinity peptides of this size are rare, there are some experimental precedents supporting the prediction. Somatostatin antagonists and glucagon-like peptide analogues have been shown to achieve tumor levels of 61 and 287% ID/g, respectively, in mouse tumor models (41,42). While these high tumor levels may be partially attributable to differences among the tumor models or target antigens, they provide enticing precedents that may motivate future development of targeting agents in this size range. At the other end of the size spectrum, the model predicts lower tumor uptake levels on the order of 1–2 %ID/g for liposomes and other large targeting agents. There are several caveats for making general predictions about liposome and nanoparticle uptake including molecular radii close to the capillary cut-off and greater variation in molecular geometry and chemical structure relative to proteins. Nevertheless, the model predictions are consistent with experimentally measured uptake values of 1–8 %ID/g for a majority of liposomes and nanoparticles (43–45).

One of the more intriguing predictions from the model is that for molecules beyond a certain size there is little to no increase in tumor uptake from antigen targeting. The precise size at which this targeting independent uptake dominates depends on several parameters, but is generally predicted to occur in the ~50 nm size range typical of liposomes and nanoparticles. These predictions are consistent with several experimental reports of insignificant differences in tumor levels of liposomes and nanoparticles with or without targeting ligands (43,44). In contrast, antigen specific targeting may be observed with smaller particles, in tumors with high vascular permeability, or by targeting antigens on the luminal side of the tumor vasculature. For vascular targeting agents in particular, the entire analysis of extravasation and diffusion presented here is irrelevant. It is also important to note that antigen targeting may still improve the therapeutic efficacy of liposomes and nanoparticles even without altering the total tumor concentration by increasing the amount of drug internalized by cells within the tumor (44).

Given the large number of parameters used in the model and the inherent variability in these parameter values due to tumor heterogeneity and experimental error, it is inevitable that there will be some variation or error in the tumor uptake predictions presented here for specific molecules in a given tumor. We believe, however, that the overall trends predicted by the model including predominance of EPR in liposome targeting, and the greater importance of high affinity for small binding molecules should be relatively consistent as they are well supported by published experimental evidence. Better understanding of these trends through the modeling framework presented here should aid in the future design of targeting agents with improved uptake and specificity.

Appendix

Definition of parameter values

D

Diffusion coefficient in tumor (cm²/s)

P

Tumor capillary permeability (cm/s)

ε

Available volume fraction in the tumor

k_clear

Single exponential plasma clearance rate (hr⁻¹)

R_cap

Capillary radius (μm)

R_Krogh

Radius of tissue surrounding capillary (μm)

[Ab]_plasma0

Initial plasma antibody concentration (%ID/mL)

[Ab]_tumor

Average concentration of total antibody (bound + free) in tumor (%ID/g)

[Ag]

Antigen concentration in tumor (M)

K_d

Antibody dissociation constant (M) = k_off/k_on

k_e

Internalization/degradation rate of bound antibody (sec⁻¹)

D_free

Diffusion coefficient in solution (cm²/s)

D_pore

Diffusion coefficient in cylindrical pore (cm²/s)

R_mol

Hydrodynamic radius of the targeting molecule (nm)

R_pore

Radius of the pore (nm)

λ

Ratio of molecular radius to pore radius

V_i

Interstitial fluid volume fraction in tumor

φ

Partition coefficient in pore

A, B

Relative amounts of diffusion through small and large pores, respectively

A_cap, B_cap

Fractional capillary pore areas per unit membrane thickness through small and large pores, respectively (cm⁻¹)

Cl_R

Renal clearance (mL/hr)

GFR

Glomerular filtration rate (mL/hr)

Θ

Macromolecular sieving coefficient

Φ

Equilibrium partition coefficient at glomerular wall

σ

Correction term for geometry of glomerular slits

K_conv

Solute hindrance factor for convection

K_diff

Diffusive hindrance factor

Pe

Péclet number, ratio of convection to diffusion

v

Fluid velocity vector (cm/s)

L

Membrane thickness (nm)

α, β

Empirical constants for describing kidney filtration (nm⁻¹)

Cl_NR

Non-renal clearance (mL/hr)

δ, γ

Empirical constants for non-renal clearance (units mL/hr and nm, respectively)

V_plasma

Plasma volume (mL)