Evidence for two-dimensional solitary sound waves in a lipid controlled interface and its implications for biological signalling

Abstract

Biological membranes by virtue of their elastic properties should be capable of propagating localized perturbations analogous to sound waves. However, the existence and the possible role of such waves in communication in biology remain unexplored. Here, we report the first observations of two-dimensional solitary elastic pulses in lipid interfaces, excited mechanically and detected by FRET. We demonstrate that the nonlinearity near a maximum in the susceptibility of the lipid monolayer results in solitary pulses that also have a threshold for excitation. These experiments clearly demonstrate that the state of the interface regulates the propagation of pulses both qualitatively and quantitatively. Finally, we elaborate on the striking similarity of the observed phenomenon to nerve pulse propagation and a thermodynamic basis of cell signalling in general.

1. Introduction

In a living system, hydration shells around membranes, biomacromolecules (e.g. proteins, DNA, etc.) and ions form quasi-two-dimensional interfacial zones that account for most of the interstitial water. Such an interface can be characterized thermodynamically by its state diagrams [1] that map the interrelationships of physical variables (lateral pressure surface density, surface potential charge, etc.). These state diagrams can be obtained experimentally from macroscopic measurements on the interface. One of us has previously established that the state of the interface is a crucial determinant for equilibrium and non-equilibrium events at the interface [2–4]. For instance, heat capacity or compressibility of the interface [2–4] has been shown to regulate transmembrane current fluctuations or two-dimensional pulse propagation, during which all the variables of interface (pressure, temperature, surface potential, fluorescence, density, charge, etc.) are affected simultaneously as required by Maxwell's relations [3,5,6]. Such events derived from fundamental physical principles may imply certain biological functions (e.g. local membrane transport and communication) and this relationship between state and function can be tested experimentally. For example, sound waves at the membrane interface have been proposed as the physical basis of nerve pulses and it is believed that key features of action potentials (shape stability, all-or-none nature, etc.) result from nonlinear properties of cell membranes [7–11], an idea first put forward by Kaufmann [10]. Theoretically, it is not the complexity of membrane composition, which includes proteins (ion channels and pumps), lipid heterogeneity, etc., but the nonlinearity in the elasticity of the interface that is necessary to support such sound waves. Although such conditions on elasticity are met even in a single or multiple component lipid system, the existence of nonlinear sound waves, also known as solitary elastic waves, which resemble action potentials, has not been demonstrated in a hydrated lipid interface, yet.

This study reports the first observation of ‘solitary’ elastic waves in lipid monolayers. Propagating waves were excited mechanically and the resulting propagating variations in state were detected by fluorescence energy transfer (FRET) measurements. The relationship between the thermodynamic state and velocities of the propagating waves confirmed that they indeed travel within the lipid interface [4]. Most importantly, only when the system was close to the nonlinear regime of the state diagram, sharp localized pulses with large amplitudes were observed. Furthermore, these pulses were excitable only above a critical state-dependent threshold. These self-supporting solitary wave packets propagating in the interface bear striking resemblances to action potentials in living systems.

2. Opto-mechanical experiments on a lipid interface

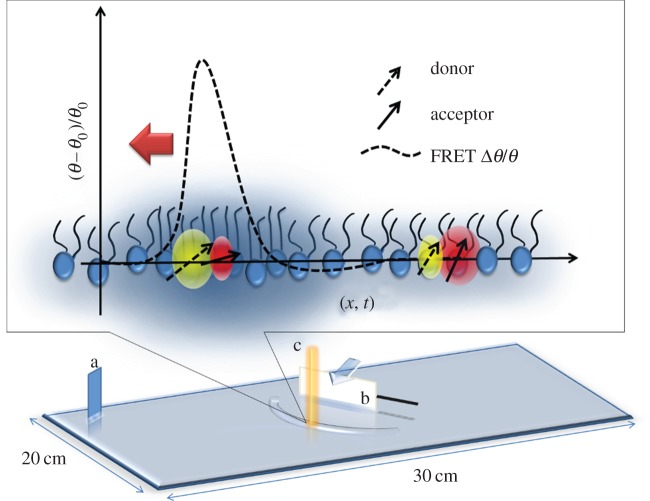
From an experimental point of view, the ability to control and monitor the state of an interface is crucial for a thermodynamic approach. This is easily achieved in lipid monolayers where the diagrams of state, for instance lateral pressure or surface potential versus area, can be obtained at various bulk pH and temperature conditions [12,13]. We recently showed that the fluorescence intensity of dye molecules embedded in the lipid monolayer is also a thermodynamic observable of the interface [6], meaning that it can be analysed as any other thermodynamic property of the interface (such as surface potential, density, etc.) once the equation of state in terms of fluorescence emission is known. Fluorescence measurements provide a fast and non-contact means for measuring state changes associated with propagating pulses. In this study, we use FRET between a pair of dye molecules, which has two major advantages over standard fluorescence intensity measurements: (i) ratiometric measurements provide significantly better signal-to-noise ratios [14], and (ii) one can distinguish between longitudinal (compressional) and transversal (capillary) components of a pulse [15] (figure 1 and electronic supplementary material, S1 Comment). The experimental set-up shown in figure 1 was used to control and monitor the state of the lipid monolayer at the air/water interface. A chloroform solution, containing lipids dipalmitoylphosphatidylcholine (DPPC), the donor N-(7-nitrobenz-2-oxa-1,3-diazol-4-yl)-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethylammonium salt (NBD-PE) and acceptor dye molecules Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethylammonium salt (Texas Red DHPE) from Invitrogen (100 : 1 : 1) was spread on the water surface of a Langmuir trough. The mean lateral pressure (π) of the monolayer was measured using a Wilhelmy plate. FRET between donor and acceptor dye molecules embedded in the lipid monolayer was measured ratiometrically (20 kS s⁻¹) by the FRET parameter defined as

2.1

Figure 1.

Experimental set-up. The state of the interface was controlled by titrating a lipid-dye solution on a Langmuir trough while measuring the lateral pressure (at a). A razor blade (b) was actuated horizontally by a piezoelectric element (black stripe) in order to excite longitudinal pulses that were detected by FRET at c, where the distance b ↔ c = 1 cm. The cartoon represents a microscopic interpretation of FRET at an interface. In an ordered two-dimensional medium, the FRET efficiency is ∼f(r, μ₁ · μ₂), where r is the distance and μ represent the emission or adsorption dipole, respectively. Therefore along with distance, the relative orientation of absorption and emission dipoles is also relevant (as opposed to their absolute orientation with respect to the interface). As the pulse arrives the relative distance and orientation of the transition dipoles of the donor and acceptor molecule change as a function of state represented by (θ,π) [6]. Correspondingly, the FRET efficiency changes that leads to anticorrelated changes in the intensity of donor signal and acceptor signal. On the other hand, any motion of the interface due to capillary modes of the water waves travelling simultaneously with the longitudinal modes will change the donor and acceptor signal in a correlated manner. The FRET parameter Δθ/θ₀ amplifies the anticorrelated parts of the signal while filtering out the correlated parts. Finally, it is the relationship of the observed velocities to the compressibility of the interface that confirms the compressional nature of the waves (figure 4). (Online version in colour.)

For this, emission intensities were acquired simultaneously at two wavelengths (535 and 605 nm), while fluorescence was excited at 465 nm and the FRET parameter was characterized as a function of state (π) using the opto-mechanical set-up described in our previous work [6]. For wave experiments, a razor blade attached to a piezo cantilever (American Piezo Company no. 40–2040) was arranged such that the long edge of the blade touches the air–water interface forming a meniscus, while the motion of the cantilever moves the blade horizontally along the interface. The pulses were excited by using controlled mechanical impulses (Δt ∼ 10 ms) of the piezo cantilever (figure 1 and electronic supplementary material, figure S1). The maximum displacement (approx. 1 mm) of the blade represents the upper bound for the amplitude on a relative scale of 0–1A which can be tuned using the power supply (Grass Instruments S88E) for the piezo element. This technique has previously been shown to ensure maximum coupling to the longitudinal mode [16]. The ensuing changes in state were quantified optically via the relative changes in FRET parameter derived from equation (2.1) (figure 1)

2.2

In order to understand the state dependence, the pulses were excited at different mean surface pressures.

3. Localized nonlinear pulses controlled by state of the interface

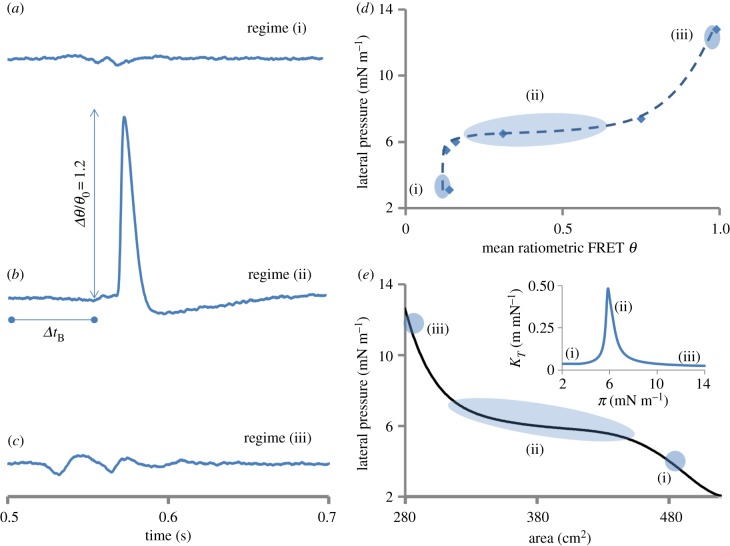
Figure 2 presents the first observations of nonlinear pulses propagating along a lipid monolayer. The pulses were measured optically using equation (2.2) (see also the electronic supplementary material, figure S1) in fundamentally different regimes of the state diagram (marked in figure 2d,e). The regimes differ in terms of their isothermal compressibility κ_T = −(1/A)(∂A/(∂π)_T that can be obtained from the π ↔ A isotherm (inset figure 2e). κ_T has a sharp peak in the transition region around π = 6 mN m⁻¹ marked as regime (ii), while regime (i) at π = 3.2 mN m⁻¹ and regime (iii) at π = 12.8 mN m⁻¹ represent the two states that lie far on either side of the peak in κ_T. Comparing the pulse shapes in these three different states reveals at least two striking differences: (i) for the same strength of excitation the amplitude increases by one to two orders of magnitude (approx. 40 times) when excited in the transition regime, and (ii) a significant temporal confinement or steepening of the pulse appears simultaneously (figure 2a–c). The latter can be better appreciated in the frequency domain representation where the temporal confinement inversely results in a significant spectral broadening (Δω ∼ 1/Δt), as will be discussed below. In our recent work, on opto-mechanical coupling [6], it was shown that Δθ/θ ∼ ΔA/A ∼ ΔV/V in the transition region at the interface, where A and V are the surface area and surface potential respectively. Based on this correspondence, the solitary waves excited in the transition regime with a relative FRET amplitude Δθ/θ of 1.2 units are estimated to measure approximately 200 mV in surface potential while sub-threshold pulses measured outside this region will correspond to a surface potential of approximately 5 mV [5]. The pulse shape varies strongly as a function of state near the transition and can be resolved further (electronic supplementary material, figure S2). The pulses remain highly localized and deform gradually while they propagate before eventual decay as discussed later. The exact details of the pulse shape (extent of sharpness and the prominence of long tail below baseline) depend on the boundary conditions (distance from edges of the trough, figure 1) and the choice of piezo cantilever (blocking force, resonance frequency, etc.) to a certain extent.

Figure 2.

State dependence of pulse shapes in a lipid interface. Elastic interfacial pulses (a–c) were excited in fundamentally different regimes (i, ii and iii) of the state diagram (d,e) [6] at π(A) = 3.2, 6 and 12.8 mN m⁻¹, respectively. The inset in (e) shows the three regimes on the isothermal compressibility κ_T(π) curve calculated from π(A). A distinct pulse (b) only appears near or in the plateau (regime ii) of the state diagram and is an order of magnitude stronger in amplitude (approx. 40 times) than pulses in regimes (i) and (iii) (see the electronic supplementary material, figure S1 for individual donor and acceptor signals). Although the sharp pulse as in (b) only appears near the nonlinear regime of the state diagram, the absolute shape is very sensitive to the precise state along (i) to (ii) (see the electronic supplementary material, figure S2). In these experiments, the state was altered by changing the surface density of lipid molecules but it can equally well be varied by changing other physical parameters (temperature, pH, lipid-type, ion or protein adsorption, solvent incorporation, etc.). The delay Δt was used to calculate the experimental propagation velocity c_exp. Experimental details: pulses measured via FRET (see equation (2.2) and electronic supplementary material, figure S1), lipid (DPPC) monolayer at 19°C for the excitation resulting from a piezo amplitude of approximately 1 mm (1 A), distance between excitation and detection was 1 cm. The dashed line in (d) is a guide to the eye. The similarity of the pulses in the nonlinear regime (ii) with action potentials (see fig. 13 in [17]) is striking. (Online version in colour.)

4. Threshold amplitude and ‘all-or-none’ nature

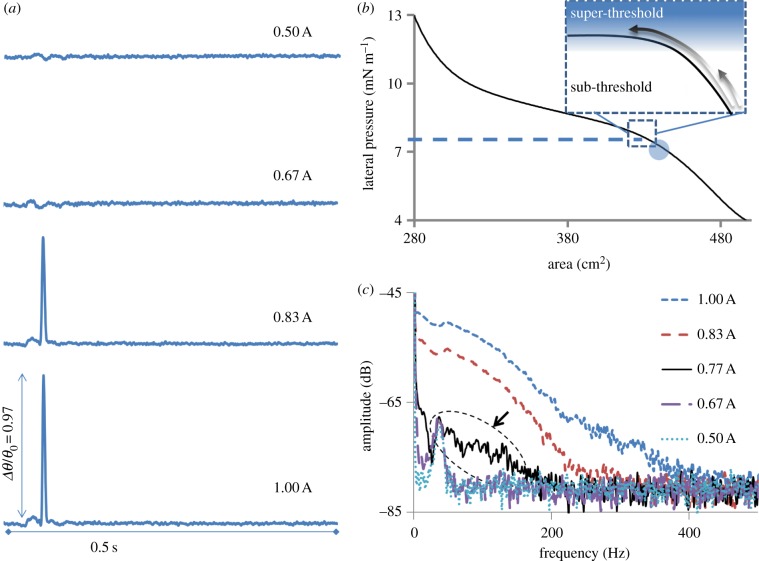
The sensitive dependence of pulse's shape on state combined with the abrupt increase in its amplitude and confinement indicates that the observed phenomenon is of nonlinear nature. To analyse this nonlinearity further, pulse amplitude Δθ and shape (frequency spectrum) were obtained as a function of excitation strength (peizo amplitude). This experiment presented another remarkable feature of the observed solitary pulses, the presence of a threshold. Only excitations of amplitude above a certain threshold could excite solitary pulses (figure 3). On zooming into the pulse shape, it is observed that near the threshold the increased excitation strength is temporally focused onto certain regions along the pulse shape (electronic supplementary material, figure S4). This results in excitation dependent steepening and confinement of the pulse's shape along with a nonlinear increase in its amplitude. This is better represented by the broadening of the corresponding frequency spectrums (fast Fourier transform; figure 3c). In a linear system, stronger excitations simply cause elevations or rescaling of spectral features to higher amplitudes [18]. However, clear qualitative changes in the spectrum are observed for the pulses presented herein, which underline the impact of nonlinear effects. The higher frequencies (100–300 Hz), present at an excitation of 0.83 A, are practically absent at 0.67 A, where A is an arbitrary scale between 0 and 1 representing the strength of excitation. However, a similar rise in excitation strength from 0.50 to 0.67 A had practically no effect, as represented by near complete overlap of the corresponding spectrums. The onset of higher frequency components near 0.77 A (see also the electronic supplementary material, figure S3) and subsequent strong spectral broadening indicate the existence of a threshold. Although the amplitude-dependent spectral broadening observed here is typical of systems with nonlinear susceptibilities [18,19], the precise control over the degree of nonlinearity is an extraordinary advantage of this set-up.

Figure 3.

Threshold for excitation of solitary waves. (a) The pulses resulting from varying the excitation strength are shown for a fixed state marked by the circle in (b). Clearly, a ‘threshold’ for the onset of solitary behaviour exists between excitation strength of 0.67 and 0.83 A in this state, where maximum displacement amplitude of approximately 1 mm corresponds to 1 A. The inset in (b) represents the idea of a threshold on a generalized state diagram where solitary pulses can be excited by super-threshold excitation. (c) The corresponding average frequency spectrums of the pulses are shown. The arrow points to the onset of nonlinear behaviour (see the electronic supplementary material, figure S4). All the pulses in (a) are plotted on same scale for the y-axis representing the variations in FRET parameter. Experiments were performed on a lipid (DPPC) monolayer at a lateral pressure of 7.2 mN m⁻¹ and 21°C. (Online version in colour.)

5. Theoretical considerations

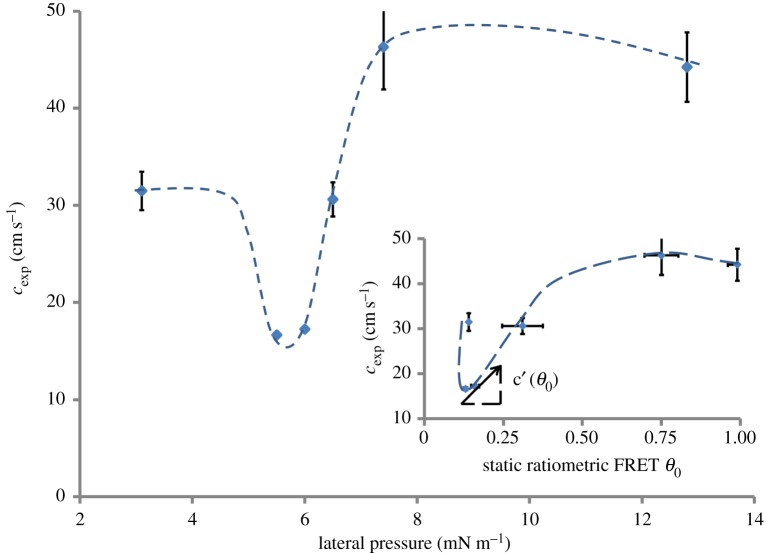
Theoretically, the nonlinearity in the adiabatic compressibility κ_s of the interface relates to the evolution of a propagating pulse at the interface [4,6]. κ_s is related to the velocity of propagation c_g, which has been measured (c_exp) and plotted as a function of mean pressure and mean FRET parameter θ₀ (figure 4). The minimum in c_exp is related to a maximum in κ_s (figures 2e and 4) [4,6] confirming the compressional nature of the optically observed pulses. The propagation velocity of a wave packet is represented by the group velocity c_g(θ,ω) ≡ ∂ω/∂k which in general is a function of both the amplitude θ and frequency ω, k being the wavenumber. The time delay Δt, measured experimentally, is inversely related to c_g and in a dispersive nonlinear system Δt varies within a single pulse Δθ(t), which usually leads to broadening of the pulse shape as it travels. For a pulse of amplitude Δθ and spectral width Δω, the broadening scales as

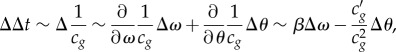5.1

where β ≡ ∂²κ/∂ω² is known as the group velocity dispersion parameter [20] and 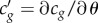represents the nonlinearity in compressibility. Qualitatively 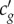can be estimated from the phenomenological dependence c_g(θ)(≈c_exp(θ)) (figure 4), where the tangent on any point along the curve would be directly related to c′_g. For a preserved pulse shape (ΔΔt → 0) a simple relation, representing the balance between nonlinearity and dispersion, can be derived as 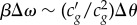. This relationship can be compared with experiments to test whether the observed nonlinear pulses are indeed of solitary nature. In figure 3a, it is reasonable to assume that the values for β and 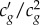do not change significantly between the two super-threshold pulses. On comparing the spectral half widths (figure 3c) and amplitudes (figure 3a) of these two pulses |Δθ/Δω|_0.83 ∼ |Δθ/Δω|_1.00 = 0.0045, indicating that the pulse shape is indeed conserved as the nonlinearity and dispersion balance each other. In addition to the solitary nature of the observed pulses, the relation between dispersion and nonlinearity also explains the origin of the threshold. The slope c′_g of the phenomenological curve c_g(θ) (figure 4) changes sign (negative to positive) on increasing pressure across the minimum in c_g(θ). Assuming β does not change its sign, the dispersion and the nonlinearity can only be balanced on one side of the minimum, while on the other side the two effects would rather reinforce each other, smearing out any pulse propagation immediately (note that Δθ is observed to be positive in this region). This is further supported by resolving the state dependence of the pulse shape more sensitively (electronic supplementary material, figure S2). Upon a small increment in π(A) from 5.1 to π(A) = 5.3 mN m⁻¹ the signal shoots up nonlinearly, indicating a strong threshold when approaching the transition from the liquid expanded side. In conclusion, not only the observed pulses are of solitary nature, they also have a clear threshold for excitation due to the second-order nonlinear effects at the minimum in c_g near the transition.

Figure 4.

Non-equilibrium opto-mechanical state diagram. Mean velocities are plotted as a function of lateral pressure. The minimum in velocity near 6 mN m⁻¹ corresponds to a maximum in the compressibility of the lipid monolayer. This justifies the interpretation that the pulses measured via FRET are of compressional nature. The inset plots the same data with respect to the equilibrium value of θ₀ = (I₅₃₅/I₆₀₅ nm) at which the pulse was excited. The slope along any point on this curve is related to the local nonlinearity in the system (see equation (5.1)). The experimental velocities were obtained by dividing the distance between excitation and detection (d = 1 cm) by the time of flight marked by the first deviation in the FRET signal. The pulses were excited at the maximum amplitude of 1 A approximately 1 mm. The dashed and dotted lines are guides to the eye. Pulses were measured via FRET (see equation (2.2) and the electronic supplementary material, figure S1) in a lipid (DPPC) monolayer at 19°C and the error bars represent standard deviation over n = 10 measurements. (Online version in colour.)

Further experiments in different lipid systems are required for a deeper understanding of the observed nonlinearity and threshold. Threshold, dispersion and viscosity, which all depend on state [21,22], affect the evolution of pulse (shape) and hence need to be systematically examined. As discussed for a solitary pulse of given amplitude, the width is conserved despite dispersion when nonlinear effects of the medium counteract sufficiently. However in a dissipating medium, the decay in amplitude will result in a corresponding broadening of the pulse to the point where the nonlinearity cannot balance the dispersion anymore, i.e. that during propagation the amplitude will eventually ‘slip’ below the threshold due to dissipation. This is clearly observed for the solitary pulses reported in this study (electronic supplementary material, figure S5), although at this point the primary reason for decay in amplitude is not clear (we imagine dissipative or geometrical effects as a possible source; figure 1). The role of spatial confinements [23,24] is currently being explored to understand the geometrical effects which according to our preliminary analysis seem to be important for the biphasic nature of the pulse shape.

6. Biological implications

So far, we have tried to emphasize that the solitary pulses with a threshold for excitation result from a peak in compressibility and we have shown this systematically for a lipid monolayer. However, the same line of arguments applies for lipid bilayers and real biological membranes as long as their equation(s) of state give rise to nonlinearities [12,25–28]. The latter is experimentally well established in living cells and single neurons [25,28] and as the measurement of the susceptibilities (c_p,κ_T, etc.) of living systems (single cells) improve, their relevance for many nonlinear phenomena in biology will be better established [29,30]. The obvious differences between mono- and bilayer—although highly important for a detailed analysis—are therefore irrelevant from a fundamental point of view. Nevertheless, a brief discussion on mono- versus bilayer as acoustic mediums may be helpful. The problem of mono- and bilayer correspondence is steeped in rich literature [31–33], but its most important aspect relevant to sound propagation is probably the role of surface tension which is significantly high (γ ∼ 30 ↔ 72 mN m⁻¹) in monolayers at air/water compared with a leaflet in a bilayer where γ → 0. This has direct implications for capillary (transversal) modes which scale with γ and are therefore almost unavoidable in monolayers but are likely to be absent in a bilayer [16,34]. Excitation of longitudinal waves is therefore expected to be more efficient in lipid bilayers. Still, the crucial difference in boundary conditions in the two systems and the role of chemical gradient across the membrane and its integration into a propagating state change need to be further investigated [3].

Finally, based on the general role of nonlinear state diagrams in our study and given the recent discussion on the thermodynamic foundation of nerve pulses, we would like to discuss the biological relevance of our findings. The shape of the solitary pulses in lipid monolayers and action potentials in cell membranes can be directly compared because fluorescence reports membrane potential in both cases [6,35,36]. There are several striking similarities between our results on lipid monolayers and the data on nerve pulses: (i) both systems support ‘all-or-none’ pulses which propagate as solitary waves and exist only in a narrow window bound by certain nonlinearities in their respective state diagrams [28,37,38], (ii) the pulses in both systems represent an adiabatic phenomenon [39,40] and are not only electrical but are also inseparably mechanical (deflection and volume), optical (polarization, chirality, fluorescence, turbidity) and thermal (temperature, enthalpy) pulses [5,6,36,37,39,41–46].

The velocities of the pulses reported herein are in the same order of magnitude as those reported for action potentials in plant cells as well as non-myelinated animal cells [47–49]. Similarly, the biphasic shape (figure 2b) is quite characteristic of action potentials and its similarity to the observed pulses in this study is striking and should be compared with fig. 13 in Hodgkin and Huxley's famous work [17]. Interestingly, the biphasic pulse shape obtained in the monolayer does not require separate proteins and accompanying ion fluxes to explain different phases (rising, falling, undershoot) as in an action potential. Despite these similarities, however, we believe that absolute velocity and pulse shape are not proper criteria for testing a new theory of nerve pulse propagation as both vary tremendously, in cells and as well as in lipid monolayers, depending on composition, excitation and state of the membrane interface [50–52]. Rather, it is the variation in velocity as a function of state c_g(π, T), variation in pulse shape as a function of degree of nonlinearity 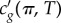and the existence of a threshold that can be explained thermodynamically [22,53–55], as seen in this study. But before making further such comparisons, the amplitude velocity relation [56,57], the existence of refractory period [58] and the behaviour of two pulses under collision need to be explored for a comprehensive understanding of these nonlinear effects. For example in nonlinear systems, two pulses might change or annihilate in general on collision (like action potentials) or remain unaffected like solitons under special circumstances [7,57,59–62].

Finally, given that the state of the interface has been shown to strongly correlate with the activity of membrane-bound proteins and enzymes [63–65], we are also looking at the effect of these pulses on protein and enzyme kinetics as a new mechanism in biological signalling. Further studies will show whether the solitary elastic pulses as reported here are indeed a physical basis of nerve pulses and cellular communication in general [66,67].

Funding statement

Financial support by BU-ENG-ME and BU-XTNC is acknowledged. M.F.S. appreciates funds for guest professorship from the German research foundation (DFG), SHENC-research unit FOR 1543.