Abstract
The goal of this paper is to make modeling and quantitative testing accessible to behavioral decision researchers interested in substantive questions. We provide a novel, rigorous, yet very general, quantitative diagnostic framework for testing theories of binary choice. This permits the nontechnical scholar to proceed far beyond traditionally rather superficial methods of analysis, and it permits the quantitatively savvy scholar to triage theoretical proposals before investing effort into complex and specialized quantitative analyses. Our theoretical framework links static algebraic decision theory with observed variability in behavioral binary choice data. The paper is supplemented with a custom-designed public-domain statistical analysis package, the QTest software. We illustrate our approach with a quantitative analysis using published laboratory data, including tests of novel versions of “Random Cumulative Prospect Theory.” A major asset of the approach is the potential to distinguish decision makers who have a fixed preference and commit errors in observed choices from decision makers who waver in their preferences.
Keywords: Behavioral decision research, order-constrained likelihood-based inference, Luce's challenge, probabilistic specification, theory testing
1 Introduction
Behavioral decision researchers in the social and behavioral sciences, who are interested in choice under risk or uncertainty, in intertemporal choice, in probabilistic inference, or many other research areas, invest much effort into proposing, testing, and discussing descriptive theories of pairwise preference. This article provides the theoretical and conceptual framework underlying a new, general purpose, public-domain tool set, the QTest software.1 QTest leverages high-level quantitative methodology through mathematical modeling and state-of-the-art, maximum likelihood based, statistics. Yet, it automates enough of the process that many of its features require no more than relatively basic skills in math and statistics. The program features a simple Graphical User Interface and is general enough that it can be applied to a large number of substantive domains.
Consider a motivating analogy between theory testing and diagnostics in daily life. Imagine that you experience intense abdominal pain. You consider three methods of diagnostics:
You may seek diagnostic information from another lay person and/or a fever thermometer.
You may seek diagnostic information from a nurse practitioner.
You may seek diagnostic information from a radiologist.
Over recent decades, the behavioral sciences have experienced an explosion in theoretical proposals to explain one or the other phenomenon in choice behavior across a variety of substantive areas. In our view, the typical approach to diagnosing the empirical validity of such proposals tends to fall into either of two extreme categories, similar to the patient either consulting with a lay person (and maybe a thermometer) or with a radiologist. The overwhelming majority of ‘tests’ of decision theories either employ very simple descriptive measures (akin to asking a lay person), such as counting the number of choices consistent with a theoretical prediction; possibly augmented by a basic general purpose statistical test (akin to checking for a fever), such as a t-test; or proceed straight to a highly specialized, sometimes restrictive, and oftentimes rather sophisticated, quantitative test (akin to consulting with a radiologist), such as a “Logit” specification of a particular functional form of a theory. The present paper offers the counterpart to the triage nurse: We provide a novel, rigorous, yet very general, quantitative diagnostic framework for testing theories of binary choice. This permits the nontechnical scholar to proceed far beyond very superficial methods of analysis, and it permits the quantitatively savvy scholar to triage theoretical proposals before investing effort into complicated, restrictive, and specialized quantitative analyses. A basic underlying assumption, throughout the paper, is that a decision maker, who faces a pairwise choice among two choice options, behaves probabilistically (like the realization of a single Bernoulli trial), including the possibility of degenerate probabilities where the person picks one option with certainty. While the paper is written in a ‘tutorial’ style to make the material maximally broadly accessible, it also offers several novel theoretical contributions and it asks important new theoretical questions.
2 Motivating Example and Illustration
We explain some basic concepts using a motivating example that also serves as an illustration throughout the paper. In the interest of brevity and accessibility, we cast the example in terms of the most famous contemporary theory of risky choice, Cumulative Prospect Theory (Tversky and Kahneman 1992). However, since our empirical illustration only considers gambles in which one can win but not lose money, one can think of the predictions as derived from certain, more general, forms of “rank-dependent utility” theories.
Imagine an experiment on “choice under risk,” in which each participant makes choices among pairs of lotteries. We concentrate on a case where we aim to analyze data separately for each participant, and where each individual repeats each pairwise choice multiple times. Table 1 shows 25 trials of such an experiment for one participant. These data are from a published experiment on risky choice (Regenwetter et al. 2010, 2011a,b) that we use for illustration throughout the paper.
Table 1.
First 25 out of 800 pairwise choices of DM1.
| Trial | Stimulus Set | Gamble 1 | Gamble 0 | Observed Choice | KT-V4 Prediction |
|---|---|---|---|---|---|
| 1 | Cash I | 33.3% chance of $26.6 (R) | 41.7% chance of $23.8 (L) | 1 | |
| 2 | Distractor | 12% chance of $31.43 (R) | 18% chance of $27.5 (L) | 0 | |
| 3 | Noncash | 20% chance of ∼ 7 paperbacks (R) | 24% chance of ∼ 4 music CDs (L) | 1 | |
|
| |||||
| 4 | Cash II | 28% chance of $31.43 (R) | 36% chance of $24.44 (L) | 1 | 1 |
|
| |||||
| 5 | Cash I | 37.5% chance of $25.2 (L) | 45.8% chance of $22.4 (R) | 0 | |
| 6 | Distractor | 16% chance of $22 (R) | 24% chance of $22 (L) | 0 | |
| 7 | Noncash | 22% chance of ∼ 40 movie rentals (L) | 26% chance of ∼ 40 coffees (R) | 1 | |
|
| |||||
| 8 | Cash II | 32% chance of $27.5 (R) | 40% chance of $22 (L) | 1 | 0 |
|
| |||||
| 9 | Cash I | 29.2% chance of $28 (R) | 41.7% chance of $23.8 (L) | 0 | |
| 10 | Distractor | 4% chance of ∼ 40 coffees (L) | 20% chance of ∼ 4 music CDs (R) | 0 | |
| 11 | Noncash | 18% chance of ∼ 15 sandwiches (L) | 24% chance of ∼ 4 music CDs (R) | 1 | |
|
| |||||
| 12 | Cash II | 36% chance of $24.44 (L) | 44% chance of $20 (R) | 0 | 0 |
|
| |||||
| 13 | Cash I | 33.3% chance of $26.6 (R) | 37.5% chance of $25.2 (L) | 0 | |
| 14 | Distractor | 6% chance of ∼ 40 coffees (L) | 16% chance of ∼ 7 paperbacks (R) | 0 | |
| 15 | Noncash | 20% chance of ∼ 7 paperbacks (L) | 22% chance of ∼ 40 movie rentals (R) | 1 | |
|
| |||||
| 16 | Cash II | 28% chance of $31.43 (L) | 40% chance of $22 (R) | 1 | 0 |
|
| |||||
| 17 | Cash I | 29.2% chance of $28 (R) | 45.8% chance of $22.4 (L) | 0 | |
| 18 | Distractor | 8% chance of ∼ 7 paperbacks (L) | 16% chance of ∼ 40 coffees (R) | 1 | |
| 19 | Noncash | 18% chance of ∼ 15 sandwiches (R) | 26% chance of ∼ 40 coffees (L) | 1 | |
|
| |||||
| 20 | Cash II | 32% chance of $27.5 (R) | 36% chance of $24.44 (L) | 1 | 1 |
|
| |||||
| 21 | Cash I | 37.5% chance of $25.2 (L) | 41.7% chance of $23.8 (R) | 0 | |
| 22 | Distractor | 14% chance of $22 (L) | 26% chance of $22 (R) | 0 | |
| 23 | Noncash | 22% chance of ∼ 40 movie rentals (L) | 24% chance of ∼ 4 music CDs (R) | 1 | |
|
| |||||
| 24 | Cash II | 28% chance of $31.43 (R) | 44% chance of $20 (L) | 0 | 0 |
|
| |||||
| 25 | Cash I | 33.3% chance of $26.6 (R) | 45.8% chance of $22.4 (L) | 0 | |
Note: The symbol ∼ stands for “approximately.” (L) means that the gamble was presented on the left screen side, (R) means it was presented on the right. An entry of 1 under “Observed Choice” means that the respondent chose Gamble 1, whereas 0 means that he chose Gamble 0. The last column gives the Cash II predictions of KT-V4, i.e., Cumulative Prospect Theory with power utility (e.g., α = 0.79) and “Kahneman-Tversky” weighting (e.g., γ = 0.83).
In this experiment, which built on a very similar, seminal experiment by Tversky (1969), each of 18 participants made 20 repeated pairwise choices among each of 10 pairs of lotteries for each of three sets of stimuli (plus distractors). Participants carried out 18 warm-up trials, followed by 800 two-alternative forced choices that, unbeknownst to the participant, rotated through what we label ‘Cash I,’ ‘Distractor,’ ‘Noncash,’ and ‘Cash II’ (see Table 1 for 25 of the trials). The 200 choices for each stimulus set consisted of 20 repetitions of every pair of gambles among five gambles in that stimulus set, as was the case in the original study by Tversky (1969). The distractors varied widely. We will only consider ‘Cash I’ and ‘Cash II’ that both involved cash lotteries. Table 2 shows abbreviated versions of the “Cash II” gambles: For example, in Gamble A the decision maker has a 28% chance of winning $31.43, nothing otherwise (see Appendix A for the other cash stimulus set). The participant in Table 1 made a choice between two Cash II gambles for the first time on Trial 4, namely, she chose a 28% chance of winning $31.43 over a 36% chance of winning $24.44. The Cash II gambles are set apart by horizontal lines in Table 1. All gambles were displayed as “wheels of chance” on a computer screen. Participants earned a $10.00 base fee and one of their choices was randomly selected at the end of the experiment for real play using an urn with marbles instead of the probability wheel.
Table 2.
Illustrative motivating example. The 10 gamble pairs are the Cash II stimulus set of Regenwetter et al. (2010, 2011a). KT-V4 denotes a specific theoretical prediction made by Kahneman and Tversky's Cumulative Prospect Theory. HDM is an illustrative hypothetical decision maker, and DM1 and DM13 are Participants 1 and 13 in Regenwetter et al. (2010, 2011a). The right three columns show the frequencies, out of 20 repetitions, and corresponding percentages, that each decision maker chose the cash lottery coded as Gamble 1. Frequencies where the modal choice is consistent with KT-V4 are marked in typewriter style, cases where the modal choice is inconsistent with KT-V4 are underlined, unmarked choice frequencies are exactly at the 50% boundary. Significant violations (α = 0.05) are marked in bold font.
| Pair | Monetary gamble coded as Gamble 1 | Monetary gamble coded as Gamble 0 | KT-V4 Preferred | HDM # choices | DM1 # choices | DM13 # choices | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Chance | Gain | Chance | Gain | Gamble | Gamble 1 | Gamble 1 | Gamble 1 | ||||
| 1 | A: 28% | $31.43 | B: 32% | $27.50 | 1 | 18 | 90% | 17 | 85% | 16 | 80% |
| 2 ◊ | A: 28% | $31.43 | C: 36% | $24.44 | 1 | 19 | 95% | 13 | 65% | 9 | 45% |
| 3 ⊕ | A: 28% | $31.43 | D: 40% | $22 | 0 | 1 | 5% | 5 | 25% | 12 | 60% |
| 4 | A: 28% | $31.43 | E: 44% | $20 | 0 | 0 | 0% | 4 | 20% | 7 | 35% |
| 5 | B: 32% | $27.50 | C: 36% | $24.44 | 1 | 20 | 100% | 17 | 85% | 10 | 50% |
| 6 | B: 32% | $27.50 | D: 40% | $22 | 0 | 3 | 15% | 8 | 40% | 8 | 40% |
| 7 | B: 32% | $27.50 | E: 44% | $20 | 0 | 0 | 0% | 3 | 15% | 9 | 45% |
| 8 ◁ | C: 36% | $24.44 | D: 40% | $22 | 0 | 2 | 10% | 15 | 75% | 12 | 60% |
| 9 | C: 36% | $24.44 | E: 44% | $20 | 0 | 1 | 5% | 9 | 45% | 11 | 55% |
| 10 | D: 40% | $22 | E: 44% | $20 | 0 | 0 | 0% | 10 | 50% | 10 | 50% |
|
| |||||||||||
| Descriptive Analysis: | |||||||||||
| Total number of choices matching KT-V4 | 190 | 95% | 133 | 67% | 106 | 53% | |||||
| Number of modal choices matching KT-V4 | 10 | 8 (or 9) | 4 (or 6) | ||||||||
|
| |||||||||||
| Semi-quantitative Analysis (α = .05): | |||||||||||
| Number of signif. 2-sided Binomial tests for/against KT-V4 | 10 / 0 | 5 / 1 | 1 / 0 | ||||||||
|
| |||||||||||
| QTest (p-values) for KT-V4: | |||||||||||
| Modal Choice (Permit up to 50% error rate in each pair): | 1 | 0.03 | .55 | ||||||||
| 0.75-supermajority (Permit up to 25% error rate in each pair): | 1 | < 0.00001 | < 0.00001 | ||||||||
| 0.50-city-block .50 (Sum of 10 error rates may be at most .50): | 1 | < 0.00001 | < 0.00001 | ||||||||
|
| |||||||||||
|
|
|||||||||||
| “Kahneman-Tversky” (12 possible preference states): | 0.045 | 0.0002 | 0.36 | ||||||||
| “Goldstein-Einhorn” (43 possible preference states): | 0.25 | 0.01 | 0.20 | ||||||||
For this first illustration, we also consider a specific theoretical prediction derivable from Cumulative Prospect Theory. We will use the label
 to refer to Cumulative Prospect Theory with a “power” utility function with “risk attitude” α and a “Kahneman-Tversky weighting function” with weighting parameter γ (Stott 2006), according to which a binary gamble with a P chance of winning X (and nothing otherwise) has a subjective (numerical) value of
to refer to Cumulative Prospect Theory with a “power” utility function with “risk attitude” α and a “Kahneman-Tversky weighting function” with weighting parameter γ (Stott 2006), according to which a binary gamble with a P chance of winning X (and nothing otherwise) has a subjective (numerical) value of
| (1) |
For this paper, the exact details of this function are not important, other than to note that it depends on two parameters, γ and α. For some of the points we will make, it is useful to pay close attention to a specific prediction under
 . We consider the weighting function
and the utility function X.79, where we substituted γ = 0.83 and α = 0.79. These are displayed in Figure 1. We chose these values because that case allows us to highlight some important insights about quantitative testing. According to this model, the subjective value attached to Gamble 1 in Pair 1 of Table 2 is
. We consider the weighting function
and the utility function X.79, where we substituted γ = 0.83 and α = 0.79. These are displayed in Figure 1. We chose these values because that case allows us to highlight some important insights about quantitative testing. According to this model, the subjective value attached to Gamble 1 in Pair 1 of Table 2 is
Figure 1.
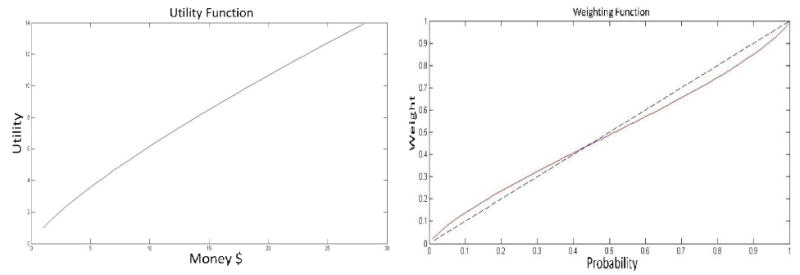
Example of a “power” utility function for money, with α = .79 (left) and a “Kahneman-Tversky” probability weighting function, with γ = 0.83 (red solid curve on the right) that generate KT-V4. (The blue dashed diagonal line in the right hand side is given for visual reference.)
| (2) |
whereas the subjective value attached to Gamble 0 in Pair 1 of Table 2 is
| (3) |
Therefore, Gamble 1 is preferred to Gamble 0 in Pair 1, according to
 with α = 0.79, γ = 0.83. A decision maker who satisfies
with α = 0.79, γ = 0.83. A decision maker who satisfies
 with α = 0.79, γ = 0.83 ranks the gambles EDABC from best to worst, i.e., prefers Gamble 1 to Gamble 0 in Pair 1, in Pair 2 and in Pair 5, whereas he prefers Gamble 0 to Gamble 1 in each of the other 7 lottery pairs, as shown in Table 2 under the header “KT-V4 Preferred Gamble.” We refer to such a pattern of zeros and ones as a preference pattern. The corresponding binary preferences are shown in the last column of Table 1.
with α = 0.79, γ = 0.83 ranks the gambles EDABC from best to worst, i.e., prefers Gamble 1 to Gamble 0 in Pair 1, in Pair 2 and in Pair 5, whereas he prefers Gamble 0 to Gamble 1 in each of the other 7 lottery pairs, as shown in Table 2 under the header “KT-V4 Preferred Gamble.” We refer to such a pattern of zeros and ones as a preference pattern. The corresponding binary preferences are shown in the last column of Table 1.
The values α = 0.79, γ = 0.83 are not the only values that predict the preference pattern EDABC in
 . We computed all preference patterns for values of α, γ that are multiples of 0.01 and in the range α, γ ε [0.01,1]. We consider α ≤ 1, i.e., only “risk averse” cases, for the sake of simplicity. Table 3 lists the patterns, the corresponding rankings, and the portion of the algebraic parameter space (the proportion of values of α, γ in our grid search) associated with each pattern.2 We labeled the pattern that gives the ranking EDABC as KT-V4 here and elsewhere. The complete list of values of α, γ yielding KT-V4 (i.e., ranking EDABC) is:
. We computed all preference patterns for values of α, γ that are multiples of 0.01 and in the range α, γ ε [0.01,1]. We consider α ≤ 1, i.e., only “risk averse” cases, for the sake of simplicity. Table 3 lists the patterns, the corresponding rankings, and the portion of the algebraic parameter space (the proportion of values of α, γ in our grid search) associated with each pattern.2 We labeled the pattern that gives the ranking EDABC as KT-V4 here and elsewhere. The complete list of values of α, γ yielding KT-V4 (i.e., ranking EDABC) is:
Table 3.
Predicted preference patterns under
 for Cash II. The pattern for KT-V4, marked in bold font here, was also given in Table 2. The proportions of occurrence for rankings of all five gambles out of 9899 value combinations of α,γ in the grid search, rounded to the closest
. The proportions of occurrence in the grid search for rankings of A, C, and D are a rounded to the closest
.
for Cash II. The pattern for KT-V4, marked in bold font here, was also given in Table 2. The proportions of occurrence for rankings of all five gambles out of 9899 value combinations of α,γ in the grid search, rounded to the closest
. The proportions of occurrence in the grid search for rankings of A, C, and D are a rounded to the closest
.
| Vertices for Cash II (with “Kahneman-Tversky” weighting and “power” utility) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| KT-V1 | KT-V2 | KT-V3 | KT-V4 | KT-V5 | KT-V6 | KT-V7 | KT-V8 | KT-V9 | KT-V10 | KT-V11 | KT-V12 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
|
| |||||||||||
| Ranking of A, B, C, D, E (and associated portion of the algebraic space): | |||||||||||
| EDCBA | EDCAB | EDACB | EDABC | EADCB | EADBC | AEDBC | AEBDC | ABEDC | ABECD | ABCED | ABCDE |
| 0.3974 | 0.0051 | 0.0061 | 0.0005 | 0.0002 | 0.0069 | 0.0005 | 0.0080 | 0.0007 | 0.0089 | 0.0106 | 0.5552 |
|
| |||||||||||
| Ranking of A, C, and D (and associated portion in the algebraic space) : | |||||||||||
| DCA | DAC | ADC | ACD | ||||||||
| .40 | .01 | .02 | .57 | ||||||||
Since 5 values of α, γ yield this predicted preference, Table 3 reports that the proportion of the algebraic space for
 that predicts preference pattern KT-V4 is 0.0005. Clearly, only decision makers with very specific weighting and utility functions are predicted to have preference EDABC according to
that predicts preference pattern KT-V4 is 0.0005. Clearly, only decision makers with very specific weighting and utility functions are predicted to have preference EDABC according to
 , for example.
, for example.
How can one test a theory like Cumulative Prospect Theory, or one of its specific predictions, such as the one instantiated in KT-V4, empirically? If empirical data had no variability, it would be natural to treat them as algebraic. But if there is variability in empirical data, a probabilistic framework is more appropriate. In particular, it is common to interpret algebraic models of behavior as assuming that behavior is deterministic, which may be too strong an assumption. Table 2 shows the binary choice frequencies of a hypothetical decision maker (HDM), as well as those of Participant 1 (DM1) and of Participant 13 (DM13) of Regenwetter et al. (2010, 2011a). We created the data of the hypothetical decision maker to look as though she acted in a ‘nearly deterministic’ way, with virtually every binary choice matching the prediction of KT-V4: In Pair 1 she chooses the ‘correct’ option 18 out of 20 times, in Pairs 2 and 3, she chooses the ‘correct’ option 19 out of 20 times. While some decision makers display relatively small amounts of variability in their binary choices, the typical picture for actual participants in the Tversky study and the Regenwetter et al. study was more like the data in the two right-most columns of Table 2. But we will see that even data like those of HDM warrant quantitative testing.
What are some common descriptive approaches in the literature to diagnose the behavior of the three decision makers? Table 2 shows various summary measures.
First, consider the total number of choices of a given decision maker that match KT-V4. HDM almost perfectly matches the prediction and only picks the ‘wrong’ gamble in 5% of all choices. The two real decision makers, DM1 and DM2 are not as clear cut. They chose the ‘correct’ option about two-thirds of the time. Many authors would consider this a decent performance of KT-V4.
Second, consider the number of pairs on which the decision maker chose the ‘correct’ option more often than the ‘wrong’ option, i.e., the number of pairs on which the observed modal choice matched the prediction of KT-V4. HDM's modal choice matches KT-V4 in every pair, hence HDM has 10 correct modal choices. The modal choices of DM1 match KT-V4 in 8 or 9 pairs. It depends on whether “modal choice” does or does not include the knife-edge case where a person chooses either option equally often, as DM1 does in Pair 10. Table 2 shows those choice frequencies in typewriter style where the strict modal choice matches KT-V4, and those choice frequencies underlined where the strict modal choice disagrees with KT-V4, whereas frequencies at the 50% level are neither in typewriter style nor underlined. DM13's strict modal choice matches KT-V4 only in four out of 10 gamble pairs. In the literature, many authors would interpret this finding as indicating a poorer performance of KT-V4 for DM13 than for DM1, and an inadequate performance for DM13 overall.
A major complication with the analysis so far is that it ignores the magnitude of the disagreement between KT-V4 and the observed choice frequencies. For instance, even though DM1 only had one ‘incorrect’ modal choice (in Pair 8), we should also ask whether 15 out of 20 choices inconsistent with KT-V4 in Pair 8 might be too much of a disagreement to be attributable to error and/or sampling variability. Likewise, while DM13 shows many ‘incorrect’ modal choices, it may be important to take into account that none of these involve frequencies that seem very different from 10 (i.e., 50%). Could they have occurred accidentally by sampling variability, if the decision maker, in fact, tends to choose consistently with KT-V4 more often than not, in every gamble pair?
Some scholars take a semi-quantitative approach by carrying out a Binomial test for each gamble pair. A common approach is to consider the Null Hypothesis that the person acts “randomly” and flips a fair coin for each gamble pair. We report such an analysis in Table 2. This Null is rejected for all 10 pairs for HDM, it is rejected for 5 pairs in DM1, and it is rejected in one pair in DM13. Scholars who take this approach, often proceed next to see whether the pattern of ‘significant’ binary choices is consistent with the theory in question, here KT-V4. For the hypothetical decision maker, all 10 Binomial tests come out significant and in favor of KT-V4. For DM1, five significant Binomial tests are supportive of KT-V4, but one test, the one for Pair 8, suggests that KT-V4 must be wrong, because the decision maker chooses the ‘wrong’ option in Pair 8 ‘more often than expected by chance.’ For DM13, this analysis draws a completely new picture: The Null Hypothesis that this decision maker flips coins is retained in 9 of 10 gamble pairs, with the remaining test result (Pair 1) supporting KT-V4.
This type of analysis, while taking some quantitative information into account, is problematic nonetheless: Since this analysis involved 10 distinct Binomial tests, Type-I errors may proliferate, i.e., we may accumulate false significant results. For example, if these 10 tests commit Type-I errors independently, and if we use α = .05 for each test (as in Table 2), then the overall combined Type-I error rate becomes 1 − (.95)10 = .40 after running 10 separate tests. A “Bonferroni correction” would, instead, reduce the power dramatically. The second problem arises when we move from testing a single prediction to multiple predictions (we will later consider 12 distinct predictions, KT-V1 through KT-V12).
Scholars with advanced expertise in quantitative testing rarely use the descriptive or semi-quantitative approaches we summarized in Table 2. Instead, they tend to consider primarily either of two approaches:
Tremble, or constant error, models (e.g., Birnbaum and Chavez 1997, Birnbaum and Gutierrez 2007, Birnbaum and Bahra 2012, Harless and Camerer 1994) assume that a person facing a pairwise choice will make an incorrect choice with some fixed probability ε and choose the preferred option with a fixed probability 1 − ε. According to these models, a decision maker satisfying
 with γ = 0.83 and α = 0.79 will choose Gamble 1 in Pair 1 of Table 2 with probability 1 − ε because the value of Gamble 1 is higher than that of Gamble 0 (see Equations 2 and 3). Generally, scholars in this branch of the literature consider error rates around 20 – 25%, i.e., values of ε around 0.20 – 0.25, to be reasonable. So, a tremble model of
with γ = 0.83 and α = 0.79 will choose Gamble 1 in Pair 1 of Table 2 with probability 1 − ε because the value of Gamble 1 is higher than that of Gamble 0 (see Equations 2 and 3). Generally, scholars in this branch of the literature consider error rates around 20 – 25%, i.e., values of ε around 0.20 – 0.25, to be reasonable. So, a tremble model of
 with γ = 0.83 and α = 0.79 would typically predict that, in Pair 1 of Table 2, Gamble 1 should be chosen with probability exceeding 0.75. In particular, constant error models predict that the preferred option in any lottery pair is the modal choice (up to sampling variability).
with γ = 0.83 and α = 0.79 would typically predict that, in Pair 1 of Table 2, Gamble 1 should be chosen with probability exceeding 0.75. In particular, constant error models predict that the preferred option in any lottery pair is the modal choice (up to sampling variability).Econometric models (which we use as a generic term to include, e.g., “Fechnerian,” “Thurstonian,” “Luce choice,” “Logit,” and “Probit” models) assume that the probability of selecting one gamble over the other is a function of the “strength of preference.” There are many sophisticated models in this domain (see, e.g., Blavatskyy and Pogrebna 2010, Hey and Orme 1994, Loomes et al. 2002, Luce 1959, McFadden 1998, Stott 2006, Wilcox 2008, 2011, Yellott 1977, for discussions and additional references). According to these models, the strength of preference, according to
 with γ = 0.83 and α = 0.79, favoring Gamble 1 over Gamble 0 in Pair 1 of Table 2 is
with γ = 0.83 and α = 0.79, favoring Gamble 1 over Gamble 0 in Pair 1 of Table 2 is
| (4) |
In these models, this strength of preference is perturbed by random noise of one kind or another. If the median noise is zero and the noise overwhelms the strength of preference, then these models predict choice probabilities near 0.50: A person with a very weak strength of preference will act similarly to someone flipping a fair coin. If the noise is almost negligible, then choice behavior becomes nearly deterministic. The vast majority of such models share the feature that whenever the strength of preference for one option over another is positive, then the ‘preferred’ option is chosen with probability greater than . In other words, they predict that the preferred option in any lottery pair is the modal choice (up to sampling variability).
While the “Descriptive Analysis” and “Semi-quantitative Analysis” in Table 2 resemble the patient who asks a lay person for diagnostic help, possibly supplemented with a simple quantitative measurement of body temperature, the alternative route of tremble and, especially econometric, models resembles the patient seeking diagnostics from the radiologist, with different models corresponding to different specialized, and often highly technical, medical diagnostics. Just like different medical diagnostic methods vary dramatically in the skill set they require and in the assumptions they make about the likely state of health, so do different ways to test theories of decision making vary in the mathematical and statistical skill set they demand of the scientist, and in the technical “convenience” assumptions they make for mathematical and computational tractability.
The questions and puzzles we just discussed illustrate a notorious challenge to meaningful testing of decision theories (e.g., Luce 1959, 1995, 1997): There is a conceptual gap between the algebraic nature of the theory and the probabilistic nature of the data, especially since algebraic models are most naturally interpreted as static and deterministic, whereas behavior is most naturally viewed as dynamic and not fully deterministic. Luce's challenge is two-fold: 1. Recast an algebraic theory as a probabilistic model. 2. Use the appropriate statistical methodology for testing that probabilistic model. The first challenge has been recognized, sometimes independently, by other leading scholars (see, e.g., Blavatskyy 2007, Blavatskyy and Pogrebna 2010, Harless and Camerer 1994, Hey 1995, 2005, Hey and Orme 1994, Loomes and Sugden 1995, Starmer 2000, Stott 2006, Tversky 1969, Wilcox 2008, 2011). Some of these researchers have further cautioned that different probabilistic specifications of the same core algebraic theory may lead to dramatically different quantitative predictions, a notion that we will very much reinforce further. Others have warned that many probabilistic specifications require difficult “order-constrained” statistical inference (Iverson and Falmagne 1985). Both components of Luce's challenge are nontrivial. From the outside, one can easily get the impression that virtually any level of rigorous probabilistic modeling and testing of decision theories requires advanced quantitative skills.
QTest solves many of the problems we reviewed. For example, it lets us formally test the Null Hypothesis that a decision maker's modal choices match KT-V4, via a single test on all of a person's binary choice data at once, provided that we have multiple observations for each choice pair. Table 2 shows the p-values of that test. A standard criterion is to reject a model or Null Hypothesis when the p-value is smaller than 0.05, the usual significance level. Hence, small p-values are indications of poor model performance. A p-value of 1 means that a model cannot be rejected on a given set of data, no matter what the significance level of the statistical test. Here, HDM fits this Null Hypothesis perfectly because in each row where KT-V4 predicts preference for Gamble 1, the hypothetical decision maker chose Gamble 1 more often than not, and in each row where KT-V4 predicts preference for Gamble 0, the hypothetical decision maker chose Gamble 0 more often than not. Hence the modal choice test of KT-V4 for HDM has a p-value of 1. It is quite notable that DM1 rejects the Null Hypothesis with a p-value of 0.03. QTest trades-off between the excellent fit of the modal choices in eight lottery pairs and the one big discrepancy between modal choice and KT-V4 in Pair 8, and rejects the Null Hypothesis. On the other hand, QTest does not reject KT-V4 by modal choice on DM13. The p-value of .55 takes into account that, despite the large number of observed ‘incorrect’ modal choices, none of these were substantial deviations.
The quantitative modal choice analysis contrasts sharply with the descriptive modal choice analysis and depicts a different picture. If we count observed ‘correct’ modal choices, then KT-V4 appears to be better supported by DM 1 than DM13. Only a quantitative analysis, such as that offered by QTest, reveals that DM1's single violation of modal choice is more serious than DM13's four violations combined. This teaches us that superficial descriptive indices are not even monotonically related to quantitative goodness-of-fit, hence can be very misleading. Note that QTest is also designed to avoid the proliferation of Type-I errors that a series of separate Binomial tests creates, since it tests all constraints of a given probability model jointly in one test.
The modal choice test is also useful for the quantitative decision scientist: Since the modal choice prediction is rejected for DM1, we can conclude that constant error models and a very general class of econometric models of
 with γ = 0.83 and α = 0.79 are likewise rejected, because the modal choice prediction is a relaxation of their vastly more restrictive (i.e., specific) predictions.
with γ = 0.83 and α = 0.79 are likewise rejected, because the modal choice prediction is a relaxation of their vastly more restrictive (i.e., specific) predictions.
Table 2 illustrates two more QTest analyses for KT-V4. We tested the Null Hypothesis that the decision maker satisfies KT-V4 and, in each gamble pair, chooses ‘incorrectly’ at most 25% of the time, as is required by the common rule of thumb for constant error models. Again, HDM fits perfectly. However, both DM1 and DM13 reject that Null Hypothesis with small p-values. We also included another example, more closely related to the first descriptive approach of counting ‘incorrect’ choices across all gamble pairs. For example, QTest can estimate binary choice probabilities subject to the constraint that the error probabilities, summed over all gamble pairs, are limited to some maximum amount, say 0.5 (this is a restrictive model allowing at most an average error rate of 5% per gamble pair), and provide a goodness-of-fit for KT-V4. Again, HDM fits perfectly, but DM1 and DM13 reject that model with small p-values.
The bottom panel of the table illustrates a very different class of models and their test. In the first model, the parameters α and γ of
 have become random variables, i.e., the utility and weighting functions of a decision maker are, themselves, no longer deterministic concepts. This captures the idea that a decision maker satisfying
have become random variables, i.e., the utility and weighting functions of a decision maker are, themselves, no longer deterministic concepts. This captures the idea that a decision maker satisfying
 could waver in his risk attitude α and in his weighting of probabilities. This model is rejected for DM1 and yields an adequate fit on the Cash II stimuli for DM13. At a significance level of 5%, the HDM is also rejected by Random
could waver in his risk attitude α and in his weighting of probabilities. This model is rejected for DM1 and yields an adequate fit on the Cash II stimuli for DM13. At a significance level of 5%, the HDM is also rejected by Random
 , even though that model permits, as one of its allowable preference states, the pattern labeled KT-V4 in the table, that HDM appears, descriptively, to satisfy nearly perfectly. However, as we move to Cumulative Prospect Theory with a two-parameter “Goldstein-Einhorn” weighting function, the data of HDM do not reject the Random
, even though that model permits, as one of its allowable preference states, the pattern labeled KT-V4 in the table, that HDM appears, descriptively, to satisfy nearly perfectly. However, as we move to Cumulative Prospect Theory with a two-parameter “Goldstein-Einhorn” weighting function, the data of HDM do not reject the Random
 model. In Random
model. In Random
 , variability of choices is modeled as variability in preferences. The rejection of the Random
, variability of choices is modeled as variability in preferences. The rejection of the Random
 model with “Kahneman-Tversky” weighting function means that the slight variability in the choice behavior of HDM cannot be explained by assuming that this decision maker wavers between different “Kahneman-Tversky” weighting functions!3
model with “Kahneman-Tversky” weighting function means that the slight variability in the choice behavior of HDM cannot be explained by assuming that this decision maker wavers between different “Kahneman-Tversky” weighting functions!3
The table shows that DM1 is consistent neither with the deterministic preference KT-V4 perturbed by random error, nor with two Random
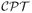 models. DM13 is consistent with both kinds of models, but the deterministic preference KT-V4 is significantly rejected if we limit error rates ≤ 25% on each gamble pair. The hypothetical decision maker is perfectly consistent with errorperturbed deterministic preference KT-V4, even with very small error rates, leading to a perfect fit (p-value = 1) for those models. The fit of Random
models. DM13 is consistent with both kinds of models, but the deterministic preference KT-V4 is significantly rejected if we limit error rates ≤ 25% on each gamble pair. The hypothetical decision maker is perfectly consistent with errorperturbed deterministic preference KT-V4, even with very small error rates, leading to a perfect fit (p-value = 1) for those models. The fit of Random
 is marginal for HDM and the “Kahneman-Tversky” version is, in fact, significantly rejected for HDM and DM1. This illustration documents the formidable power of quantitative testing. It also illustrates how QTest provides very general tests that lie in the open space between descriptive or semi-quantitative analyses on the one hand and highly specialized classic quantitative ‘error’ models on the other hand. QTest can serve as the ‘triage nurse’ of theory testing.
is marginal for HDM and the “Kahneman-Tversky” version is, in fact, significantly rejected for HDM and DM1. This illustration documents the formidable power of quantitative testing. It also illustrates how QTest provides very general tests that lie in the open space between descriptive or semi-quantitative analyses on the one hand and highly specialized classic quantitative ‘error’ models on the other hand. QTest can serve as the ‘triage nurse’ of theory testing.
This completes our motivating example.
3 The Geometry of Binary Choice
We now introduce a geometric framework within which we can simultaneously represent algebraic binary preference, binary choice probabilities, as well as empirically observed binary choice proportions all within one and the same geometric space4. For the time being, we are interested in three-dimensional visualizations, but we will later move to high-dimensional abstract models.
We start with lotteries A, B, C of Table 2. There are eight possible preference patterns among these gambles: the six rankings (each from best to worst): ABC, ACB, BAC, BCA, CAB, CBA, and two intransitive cycles that we label ABCA and ACBA. Using the binary 0/1 coding of the gambles given in Table 2, we can represent each of these 8 preference patterns as a corner (called a vertex) of a three-dimensional cube of length 1 (called the unit cube) in Figure 2. For example, ranking ABC is the point (1,1,1) in the space with coordinate system (A,B), (A,C), and (B,C)5. The cycle ABCA is the point (1,0,1). The axes of the geometric space are indexed by gamble pairs and, for representing algebraic preferences, simply represent the 0/1 coding of gambles in Tables 1 and 2. Note that “preference patterns” are (deterministic) models of preference, not empirical data.
Figure 2.

Two different views of the same geometric representation of eight algebraic and one probabilistic model(s) for Gambles A, B, C. Each of the eight possible preference patterns forms a vertex of the unit cube. Modal choice consistent with preference ranking ABC (choose A over B at least 50%, A over C at least 50%, and B over C at least 50% of the time) forms the smaller shaded cube.
If we move beyond just the 0/1 coordinates and consider also the interior of the cube, we can represent probabilities and proportions (observed data). Each axis continues to represent a gamble pair. For example, Figure 2 also shows a probability model, namely the modal choice consistent with the ranking ABC: If a person chooses A over B at least 50%, B over C at least 50%, and A over C at least 50% of the time, then their binary choice probabilities must lie somewhere in the smaller shaded cube attached to the vertex ABC. In particular, if a person acts deterministically and chooses A over B 100%, B over C 100%, and A over C 100% of the time, then this person's (degenerate) choice probabilities coincide with the vertex ABC that has coordinates (1,1,1) and that also represents the deterministic preference ABC.
Next, we proceed to a joint visualization of an algebraic model (KT-V4), a probability model (theoretical modal choice consistent with KT-V4), and empirical data (the observed choice proportions of HDM, DM1, and DM13), again in 3D. Now, and for our later visualizations, we concentrate on Gambles A, C, and D from Table 2 because they continue to be particularly informative.
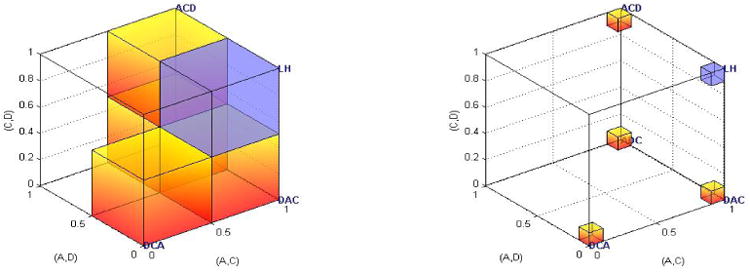
Figure 3 shows KT-V4 as the point (1,0,0) in 3D space, consistent with Table 2 which shows Gamble 1 as the preferred gamble in Pair 2 (A versus C, marked ◊), Gamble 0 as the preferred gamble in Pair 3 (A versus D, marked ⊕), and Gamble 0 as the preferred gamble in Pair 8 (C versus D, marked ◁). Hence, the three coordinates are the gamble pairs (A,C), (A,D), and (C,D). If a decision maker acted deterministically and in accordance with KT-V4, this person would choose A over C 100%, A over D 0%, and C over D 0% of the time, represented by the point (1,0,0). This point represents both a deterministic preference and a degenerate case where a person always chooses in a way consistent with that preference. Our hypothetical decision maker comes very close to such behavior: HDM's choice proportions were 95% A over C, 5% A over D, and 10% C over D, which corresponds to the point with coordinates (.95, .05, .10) marked with a star next to the vertex KT-V4 in Figure 3. DM1 has choice proportions giving the star with coordinates (.65, .25, .75). If we use modal choice as a criterion, a decision maker who satisfies KT-V4 should choose A over C at least 50%, A over D at most 50%, and C over D at most 50% of the time, as indicated by the shaded smaller cube attached to the vertex KT-V4. DM1 has two ‘correct’ out of three observed modal choices. Geometrically, this means that the data are represented by a star located above the shaded cube in Figure 3. Intuitively speaking, the 15 out of 20 choices in Pair 8 mean that the data point is somewhat ‘far away’ from the shaded cube but has two coordinates that are consistent with the shaded cube. On the other hand, DM13 translates into a star ‘very close’ to the shaded cube, at coordinates (.45, .60, .60), even though each observed modal choice is the opposite of what KT-V4 predicts (i.e., each coordinate has a value on ‘the wrong side’ of ).
Figure 3.
Three different angles of view of the same three-dimensional geometric visualization for Gamble Pairs 2 (A,C), 3 (A,D) and 8 (C,D). KT-V4 predicts the preference ranking DAC, i.e., the point with coordinates (1, 0, 0) in the space spanned by (A, C), (A, D), and (C, D). The shaded cube shows the binary choice probabilities consistent with the modal choice predictions for KT-V4 (choose A over C at least 50%, A over D at most 50%, and C over D at most 50% of the time). The three stars are the data sets for HDM, DM1, and DM13.
Figure 3 shows that counting ‘correct’ or ‘incorrect’ modal choices is tantamount to counting the number of coordinates that match the modal choice prediction. This makes it also obvious why the descriptive tally of ‘correct modal choices,’ while common in the literature, is not a useful measure of model performance. It is analogous to the patient counting the number of symptoms present while discarding all information about the intensity or importance of any symptoms. We can encounter data like those of DM1 that have 2 out of 3 coordinates in the correct range, yet the data are ‘far away’ from the modal choice predictions, while we can also collect data like those of DM13 that have 3 out of 3 coordinates slightly out of range without statistically violating the modal choice predictions. Figure 3 only depicts three dimensions. Going back to Table 2, DM1 has 9 out of 10 coordinates in the correct range, yet the data are ‘far away’ from the modal choice predictions, while DM13 has 4 out of 10 coordinates slightly out of range without statistically violating the predictions. Note that DM1 and DM13 are real study participants, not hypothetical persons custom-created to make a theoretical point.
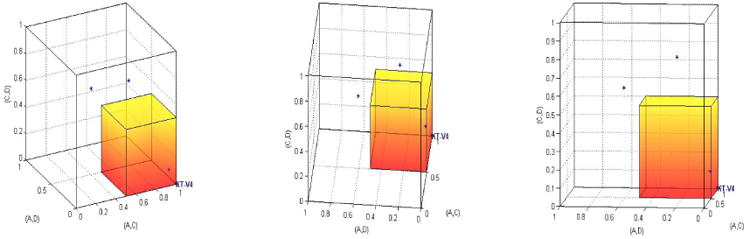
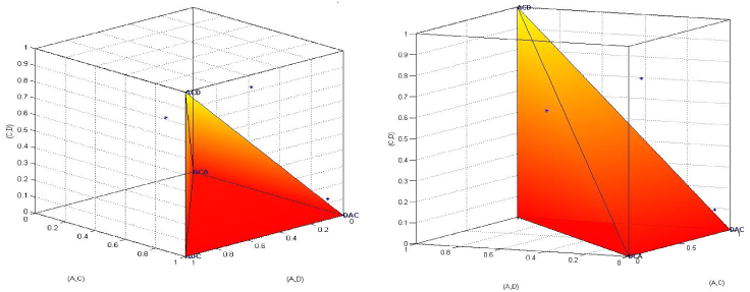
Table 2 provides two other quantitative test results for KT-V4 from QTest. We now illustrate these geometrically as well. Again, we project from a 10D space down to 3D space by concentrating on the same three gamble pairs. Figure 4 shows the three data sets with a probabilistic model that limits the error rates for each gamble pair to at most 25%. Hence, the permissible binary choice probability for A over C must be at least .75, the probability of choosing A over D must be .25 or lower, and the binary choice probability of C over D is likewise limited to at most .25. Again, HDM has data inside the shaded small cube, indicating a perfect fit. DM1 and DM13 are located ‘far away’ from the shaded cube, which is reflected in the rejection of the model on both data sets in Table 2, with very small p-values. This is the so-called 0.75-supermajority specification. An upper bound of 25% errors per gamble pair per person is consistent with a general rule of thumb that has been explored in the literature (see, e.g., Camerer 1989, Harless and Camerer 1994, Starmer and Sugden 1989). In fact, one can set the supermajority specification level anywhere from .5 to .999 in the QTest program.
Figure 4.
Two different angles of view of the same geometric visualization of HDM, DM1, DM13 and a supermajority model of KT-V4 (the shaded cube), where the choice probability of A over C is at least .75, the choice probability of A over D is at most .25, and the choice probability of C over D is at most .25.
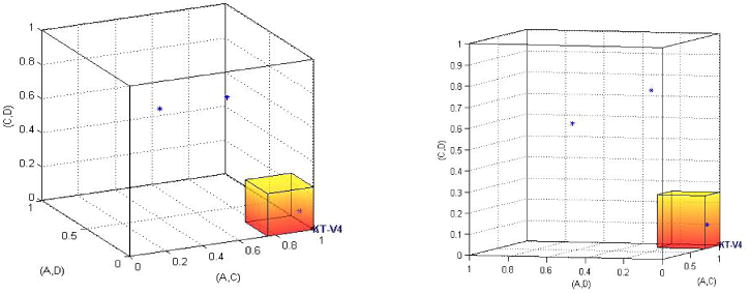
The last QTest analysis for KT-V4 we reported in Table 2 considers a different probability model. Instead of limiting the error rate for each gamble pair individually, we limit the sum of all error rates, added over all gamble pairs. This allows a decision maker to have a higher error rate on one gamble pair as long as they have a lower error rate on another gamble pair. Figure 5 illustrates, how, once again, HDM fits such a model perfectly because HDM's data lie inside the shaded pyramid, whereas DM1 and DM13 are again ‘far away’ from the model. Note that the tests in Table 2 are carried out in a 10D space whose coordinates are the 10 gamble pairs, whereas we only consider the 3D projection for Gambles Pairs 2, 3, and 8 in these figures. In other words, the tests in Table 2 are somewhat more complicated than the illustrative figures convey.
Figure 5.
Two different angles of view of the same geometric visualization of HDM, DM1, DM13 and the city-block model of KT-V4 (the shaded pyramid), where the sum of error probabilities can be at most 0.5.
Once we have moved to the geometric representation where algebraic models are vertices of a unit cube whose axes are formed by gamble pairs, where probability models are permissible ‘regions’ inside a unit cube (viewed as a space of binary choice probabilities), and where data sets are points in the same unit cube (viewed as a space of choice proportions), it appears that quantitative theory testing should be almost trivial. We have also seen how some data sets are ‘far away’ from some models, others are ‘nearby’ some models, and some are even inside (and hence “perfect fits” for) some models. However, as we discuss next, the intuitive interpretation of ‘distance’ between theory and data is an oversimplification. Each of the models in Figures 3-5 can be characterized mathematically as a probability model with so-called “order-constraints” on the parameters (say, each choice probability is < 1/2). We discuss these models informally here. Appendix B gives formal details and Davis-Stober (2009) provides the likelihood-based statistical inference framework for binary choice data that we build on.6
Maximum-likelihood estimation and goodness-of-fit analysis, say, of the best fitting binary choice probabilities for DM13, subject to the modal choice specification of KT-V4, as QTest provides in Figure 3, is nontrivial, for several reasons. For one thing, there are equally many parameters (binary choice probabilities) as there are empirical cells (binary choice proportions), yet we can tell from the figures that the models can be extremely restrictive, especially in highdimensional spaces, and hence, must be testable. As explained in Davis-Stober and Brown (2011) one cannot simply count parameters to evaluate the complexity of these types of models. The second reason, returning to data like those of DM1 and DM 13 in Figure 3 is that the best fitting parameters, i.e., the maximum-likelihood estimate, satisfying an order-constrained model may lie on a face, an edge, or even a vertex of the shaded modal choice cube. This becomes even more complicated in higher dimensional spaces, where the modal choice model has surfaces of many different dimensions. Standard likelihood methods will break down when the best-fitting parameter values are on the boundary of the model, because the log-likelihood goodness-of-fit statistic will not have the usual and familiar asymptotic χ2 distribution. Rather, the distribution depends on the geometry of the model in question. The best fitting model parameters also need not be the orthogonal projection of the data onto the model in the geometric space. In sum, statistical testing of these models is difficult. QTest is specifically designed to carry out the appropriate “order-constrained” maximum-likelihood estimation and goodness-of-fit tests for virtually all of the models we discuss.7
Another unusual, and possibly confusing, feature of these models is that they can allow for a “perfect fit” where, on certain sets of data, a model cannot be rejected no matter how large the significance level. This is because many of these models do not make “point predictions.” Rather they make predictions that occupy a volume in the unit cube of binary choice probabilities. When a point representing a set of choice proportions (data) is inside such a model, then the best-fitting choice probabilities are literally equal to the observed choice proportions, hence giving a perfect fit.
We now move to the full-fledged abstract models and their tests.
4 Aggregation- and Distance-based (Error) Models
Aggregation-based specifications8 of a theory
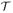 require that aggregated data should be consistent with the theoretical predictions of
require that aggregated data should be consistent with the theoretical predictions of
 , while also accounting for sample size. The prototypical case is majority/modal choice, which requires that the modal choice for each gamble pair be consistent with the theoretical prediction (up to sampling variability). To consider KT-V4 in Table 2 again, the theoretical majority/modal choice specification requires that the choice probability for Gamble 1 must be higher than that of Gamble 0 in Pairs 1, 2, and 5, whereas Gamble 0 must be chosen with higher probability than Gamble 1 in all remaining pairs.
, while also accounting for sample size. The prototypical case is majority/modal choice, which requires that the modal choice for each gamble pair be consistent with the theoretical prediction (up to sampling variability). To consider KT-V4 in Table 2 again, the theoretical majority/modal choice specification requires that the choice probability for Gamble 1 must be higher than that of Gamble 0 in Pairs 1, 2, and 5, whereas Gamble 0 must be chosen with higher probability than Gamble 1 in all remaining pairs.
So far we have focussed on the majority specification of a numerical theory like Cumulative Prospect Theory. To illustrate how the same approach can apply to theories that do not rely on numerical utility values, let us consider a simple “lexicographic heuristic” (see, e.g., Tversky, 1969):
ℒℋ: Prefer the gamble with the higher chance of winning unless the probabilities of winning are within 5 percentage points of each other. If the chance of winning is similar in both gambles (within 5 percentage points), prefer the gamble with the higher gain.
A decision maker who satisfies ℒℋ prefers Gamble 1 to Gamble 0 for Gamble Pairs 1, 5, 8, and 10 of Table 2, whereas he prefers Gamble 0 to Gamble 1 in Gamble Pairs 2, 3, 4, 6, 7, and 9 of Table 2. In particular, this decision maker violates transitivity, because, considering again the three gambles, A, C, D, we see that he prefers A to C, C to D, but D to A. The majority/modal choice specification of ℒℋ is illustrated in Figure 6. If we only considered Gambles A, C, and D, DM1 would fit perfectly, since the data point is inside the shaded cube attached to ℒℋ in Figure 6. However, we will see in Section 7 that ℒℋ is rejected on the full data in 10D space.
Figure 6.
Two different angles of view of the same geometric visualization of HDM, DM1, DM13, the modal choice models of KT-V4 (orange) and ℒℋ (blue). In this 3D figure, HDM is inside the orange cube for KT-V4, and DM1 is inside the blue cube attached to ℒℋ (the latter does not hold in 10D space).
If we think of majority/modal choice specifications as permitting up to 50% errors or noise in each binary choice, then we are allowing up to 50% of all data to be discarded as noise (even more, when we take into account sampling variability in finite samples). From that vantage point, we may want to place stronger constraints on the binary choice probabilities, so that we do not end up overfitting data by accommodating models that really are poor approximations of the cognitive process of interest. In a supermajority specification, we specify a lower bound on the rate, i.e., the minimum probability with which a decision maker must choose consistently with their preference, for each gamble pair. For example, in the data analysis of Section 7 we will consider a supermajority level of 0.9, according to which a person must choose the preferred gamble in a pair with probability at least 0.9, i.e., we permit up to 10% errors (up to sampling variability) for each gamble pair.
As we have seen in Figures 2-6, majority and supermajority specifications require the binary choice probabilities to be within some range of the vertex that represents the algebraic theory in question. Distance-based specifications of a theory
 generalize that idea. They constrain the choice probabilities to lie within some specified distance of the vertex that represents
generalize that idea. They constrain the choice probabilities to lie within some specified distance of the vertex that represents
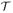 . Appendix B provides a formal summary of such models for three different distance measures.
. Appendix B provides a formal summary of such models for three different distance measures.
5 Distance-based Models for Theories with Multiple Predictions
There is no reason why we should limit ourselves to theories that only predict a single binary preference pattern like KT-V4 in Table 2. If a theory permits a variety of preference patterns, we can build a probabilistic model by combining the various probabilistic models for all of the permitted patterns. For example, for Gambles A, C, D in Table 2, we can consider all six possible rankings (each from best to worst): ACD, ADC, CAD, CDA, DAC, DCA. Figure 7 considers the majority/modal choice specification of that model on the left, and the supermajority specification of that model with a 0.90-supermajority level on the right hand side. In these models, the decision maker is allowed to rank order the gambles from best to worst according to any fixed ranking that is unknown to the researcher, then choose the preferred gamble in each gamble pair at least 50% (left hand side of Figure 7) or at least 90% (right hand side of Figure 7) of the time.
Figure 7.
Majority model (left) and 0.90-supermajority model (right) of the collection of all six rankings of lotteries A, C, and D. The left-hand side is also known as “weak stochastic transitivity.”
The 0.90-supermajority model in the right-hand side of Figure 7 can be interpreted to state that the decision maker is allowed to have any one of preference states ACD, ADC, CAD, CDA, DAC, DCA, and for that preference state, chooses the ‘correct’ object in any pair with probability 0.90 or higher. QTest finds the best fitting vertex and simultaneously tests whether the data are compatible with the constraints on binary choice probabilities. The left hand side of Figure 7 is a property that has received much attention in the literature under the label of weak stochastic transitivity (WST). WST is the majority/modal choice specification of the collection of all transitive complete rankings of a set of choice alternatives. Regenwetter et al. (2010, 2011a) dedicated much attention to the discussion of this property.9 WST was one of the earliest probabilistic choice models that became known to require order-constrained inference: Tversky (1969) attempted to test WST but acknowledged that appropriate order-constrained inference methods were unavailable. Iverson and Falmagne (1985) derived an order-constrained test for WST and showed that Tversky's data yielded little evidence for systematic violations. Regenwetter et al. (2010) provided a complete order-constrained test (using a similar algorithm as that in QTest) of WST and found no systematic violations. Returning to the data of our Table 2 in 10D space, HDM yields a perfect fit of WST. DM1 significantly violates WST with a p-value of 0.02 and DM13 yields a perfect fit (see also Table 2 of Regenwetter et al. 2010, for details). Note that the 3D figure of WST in Figure 7 gives the misleading impression that this might not be a restrictive property. In 10D space, the set of six shaded cubes in the left of Figure 7 becomes a collection of 120 such “hypercubes.” The two clear regions become 904 different such regions associated with 904 intransitive 0/1 patterns.
While weak stochastic transitivity provides a very general level of triage, in which all possible transitive complete rankings are permissible preference states and in which we employ a modal choice specification, we could alternatively consider only those transitive complete rankings as permissible preference patterns that are compatible with
 , but we could augment that list of preference states by other preference patterns, such as ℒℋ, to form a new, and also very general, Null Hypothesis. As an example, if we focus again on the three lotteries A, C, D, then there are only four possible preference patterns, namely ACD, ADC, DAC, and DCA permitted by
, but we could augment that list of preference states by other preference patterns, such as ℒℋ, to form a new, and also very general, Null Hypothesis. As an example, if we focus again on the three lotteries A, C, D, then there are only four possible preference patterns, namely ACD, ADC, DAC, and DCA permitted by
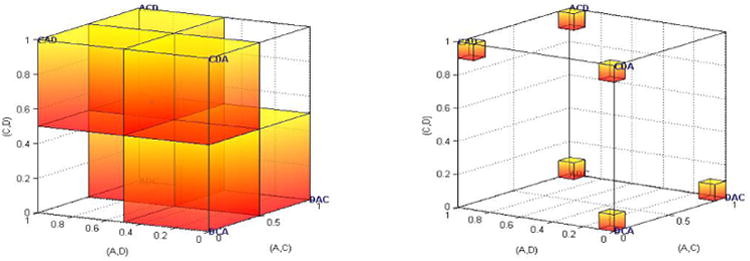
 . The left panel of Figure 8 shows the modal/majority choice specification of ℒℋ in blue in the upper left back corner of the probability cube, and the specification of Cumulative Prospect Theory, with “Kahneman-Tversky” probability weighting functions and risk averse “power” utility functions, that is, the majority/modal choice specifications of the rankings ACD, ADC, DAC, and DCA in orange. The entire collection forms an extremely general Null Hypothesis that QTest can test, similarly to weak stochastic transitivity, namely that the person is satisfying
. The left panel of Figure 8 shows the modal/majority choice specification of ℒℋ in blue in the upper left back corner of the probability cube, and the specification of Cumulative Prospect Theory, with “Kahneman-Tversky” probability weighting functions and risk averse “power” utility functions, that is, the majority/modal choice specifications of the rankings ACD, ADC, DAC, and DCA in orange. The entire collection forms an extremely general Null Hypothesis that QTest can test, similarly to weak stochastic transitivity, namely that the person is satisfying
 or ℒℋ, with an upper bound of 50% on theoretical error rates. The right hand side of Fig. 8 shows the 0.90-supermajority specification, where we limit error rates to 10% per lottery pair.
or ℒℋ, with an upper bound of 50% on theoretical error rates. The right hand side of Fig. 8 shows the 0.90-supermajority specification, where we limit error rates to 10% per lottery pair.
Figure 8.
Null Hypothesis that a person “satisfies
 or ℒℋ.” Majority/modal choice specification (left) and 0.90-supermajority specification (right) of ℒℋ (in blue) and the four rankings ACD, ADC, DAC, and DCA of
or ℒℋ.” Majority/modal choice specification (left) and 0.90-supermajority specification (right) of ℒℋ (in blue) and the four rankings ACD, ADC, DAC, and DCA of
 for A, C, D of Cash II (in orange).
for A, C, D of Cash II (in orange).
In this context, it is important to see that algebraic parameter counts and probability parameter counts do not match up at all. The algebraic version of
 has two free parameters, α and γ, that determine the shapes of the weighting and utility function, whereas ℒℋ has no free parameters. But, as we see in Figure 8, the probabilistic specifications of the two theories have the same number of parameters: If we consider the blue cube as representing one theory (ℒℋ), and the orange shaded region as representing another theory (
has two free parameters, α and γ, that determine the shapes of the weighting and utility function, whereas ℒℋ has no free parameters. But, as we see in Figure 8, the probabilistic specifications of the two theories have the same number of parameters: If we consider the blue cube as representing one theory (ℒℋ), and the orange shaded region as representing another theory (
 ), even though the two theories occupy vastly different volumes in the cube, and even though one is more flexible by virtue of allowing 4 different rankings of the gambles (12 rankings in 10D), they have the same numbers of parameters because they predict behavior by using the same number of binary choice probabilities (in the figure, we show three choice probabilities.) In other words, the usual rule of thumb that counting parameters determines the ‘complexity’ of a probability model, simply does not apply here. Furthermore, the Null Hypothesis that a decision maker “satisfies
), even though the two theories occupy vastly different volumes in the cube, and even though one is more flexible by virtue of allowing 4 different rankings of the gambles (12 rankings in 10D), they have the same numbers of parameters because they predict behavior by using the same number of binary choice probabilities (in the figure, we show three choice probabilities.) In other words, the usual rule of thumb that counting parameters determines the ‘complexity’ of a probability model, simply does not apply here. Furthermore, the Null Hypothesis that a decision maker “satisfies
 or ℒℋ” has the same number of parameters as the two nested Null Hypotheses 1) that a decision maker “satisfies
or ℒℋ” has the same number of parameters as the two nested Null Hypotheses 1) that a decision maker “satisfies
 ” and 2) a decision maker “satisfies ℒℋ.” The QTest user can build compound Null Hypotheses like the one in Figure 8, but should be aware that model competitions, e.g., selecting between
” and 2) a decision maker “satisfies ℒℋ.” The QTest user can build compound Null Hypotheses like the one in Figure 8, but should be aware that model competitions, e.g., selecting between
 and ℒℋ would ideally employ suitable methods for penalizing more complex (flexible) models. Unfortunately, for direct model selection/competition, classical (“frequentist”) statistical approaches, including the current version of QTest, are not well-suited (although, see Vuong 1989, for a method to carry out certain nonnested likelihood ratio tests).
and ℒℋ would ideally employ suitable methods for penalizing more complex (flexible) models. Unfortunately, for direct model selection/competition, classical (“frequentist”) statistical approaches, including the current version of QTest, are not well-suited (although, see Vuong 1989, for a method to carry out certain nonnested likelihood ratio tests).
For direct comparisons of the models we consider within QTest, one could calculate Bayes factors (e.g., Klugkist and Hoijtink 2007) or Deviance Information Criterion (DIC) values (Myung et al. 2005). Alternatively, one could carry out model selection via normalized maximum likelihood (see Davis-Stober and Brown 2011, for an application to order-restricted binomial models similar to those we consider here). All three of these are under development for a future version of QTest.
To this point, we have considered a variety of models that can formally capture the idea that a decision maker has a (possibly unknown) fixed preference and makes errors in her individual choices. In each model, the ‘true’ preference of a person is a vertex of the probability cube, and the shape attached to each vertex provides constraints on binary choice probabilities to represent the variable choice behavior that is deemed consistent with that deterministic preference.
6 Random Preference and Random Utility Models
We now consider models that radically differ from the ones we considered so far. Here, preferences are not treated as static like they are in aggregation- and distance-based specifications. In this approach, preferences themselves are modeled as probabilistic in nature. Here, variability in observed choice behavior is not due to noise/errors in the responses. Rather, such variability reflects substantive variation and/or uncertainty in the decision maker's evaluation process. We will see that this type of model is not just different conceptually, it is also quite different geometrically, from models that assume constant deterministic preferences (or utilities) perturbed by random errors.
In the introduction, we reviewed
 , according to which a binary gamble with a chance P of winning X (and nothing otherwise) has a subjective numerical value of
. How can we model a decision maker, who acts in accordance with this model, but who is uncertain about his risk attitude α and his γ in the weighting function? How can we model decision makers who, when asked to make a choice, sample values of α, γ according to some unknown probability distribution over the possible values of these algebraic parameters and then make a choice consistent with the
, according to which a binary gamble with a chance P of winning X (and nothing otherwise) has a subjective numerical value of
. How can we model a decision maker, who acts in accordance with this model, but who is uncertain about his risk attitude α and his γ in the weighting function? How can we model decision makers who, when asked to make a choice, sample values of α, γ according to some unknown probability distribution over the possible values of these algebraic parameters and then make a choice consistent with the
 representation? We will discuss a new Random
representation? We will discuss a new Random
 model, in which α, γ are allowed to be random variables with an unknown joint distribution. In order to keep this paper as nontechnical as possible, we consider a discretized model, in which α and γ only take values that are multiples of 0.01 in the range [0.01,1]. In other words, for simplicity, we consider an unknown distribution over finitely many possible value combinations of α, γ.
model, in which α, γ are allowed to be random variables with an unknown joint distribution. In order to keep this paper as nontechnical as possible, we consider a discretized model, in which α and γ only take values that are multiples of 0.01 in the range [0.01,1]. In other words, for simplicity, we consider an unknown distribution over finitely many possible value combinations of α, γ.
According to Random
 the probability that a respondent chooses Gamble 1 over Gamble 0 in Pair 1 of Table 2 is the probability that he uses values of α, γ for which
the probability that a respondent chooses Gamble 1 over Gamble 0 in Pair 1 of Table 2 is the probability that he uses values of α, γ for which
Can we test such a model without assuming a particular distribution over the values for α and γ? If we can communicate to QTest what constraints this model imposes on binary choice probabilities, then the program can carry out a quantitative test. We can derive, for example, that
no matter which values of α, γ we consider (in the specified range). Therefore, no matter what joint distribution we consider for α, γ (in that range), writing PXY for the binary choice probability that X is chosen over Y, it must be the case that, 0 ≤ PDE ≤ PAB ≤ 1. We discuss in the Online Supplement how one can find a complete and nonredundant list of such constraints. At present this task is technically challenging. For Random
 and Cash II, such a complete list is
and Cash II, such a complete list is
| (5) |
In other words, Random
 for Cash II is the collection of all binary choice probabilities PAB, PAC, PAD, PAE, PBC, PBD, PBE, PCD, PCE, PDE, for which the constraints (5) hold. (There is no constraint regarding whether PAD is greater, equal, or smaller than PBC, i.e., all three cases are permissible solutions, as long as the two quantities are greater than PAE and smaller than PAC.)
for Cash II is the collection of all binary choice probabilities PAB, PAC, PAD, PAE, PBC, PBD, PBE, PCD, PCE, PDE, for which the constraints (5) hold. (There is no constraint regarding whether PAD is greater, equal, or smaller than PBC, i.e., all three cases are permissible solutions, as long as the two quantities are greater than PAE and smaller than PAC.)
Consider Gambles A, C, D in Table 2 once again. Consider the possibility that the decision maker, at any point in time, rank orders the gambles from best to worst in a fashion consistent with
 , i.e., the ranking at any moment is one of ACD, ADC, DAC, DCA, and when asked to choose among two gambles, picks the better one in the current preference ranking. However, that ranking is uncertain and/or allowed to vary. Mixture, aka, random preference models quantify this variability with a probability distribution over preference patterns such as, in this case, the four rankings ACD, ADC, DAC, DCA. Figure 9 shows the binary choice probabilities if a person's preferences fluctuate or if the person is uncertain about their preference ranking, but permissible preference rankings are limited to the rankings ACD, ADC, DAC, DCA consistent with
, i.e., the ranking at any moment is one of ACD, ADC, DAC, DCA, and when asked to choose among two gambles, picks the better one in the current preference ranking. However, that ranking is uncertain and/or allowed to vary. Mixture, aka, random preference models quantify this variability with a probability distribution over preference patterns such as, in this case, the four rankings ACD, ADC, DAC, DCA. Figure 9 shows the binary choice probabilities if a person's preferences fluctuate or if the person is uncertain about their preference ranking, but permissible preference rankings are limited to the rankings ACD, ADC, DAC, DCA consistent with
 .
.
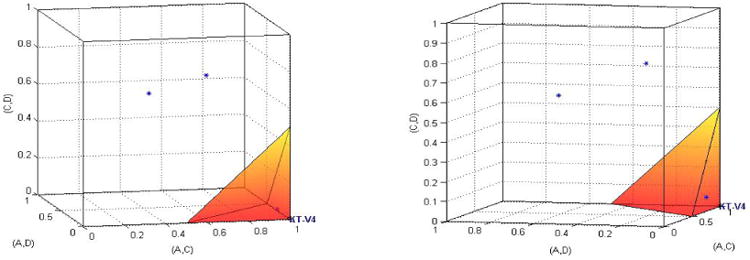
Figure 9.
Two different views of Random
 on gambles A, C, D. The four vertices ACD, ADC, DAC, DCA that are allowable preference patterns under
on gambles A, C, D. The four vertices ACD, ADC, DAC, DCA that are allowable preference patterns under
 . Every point in the shaded region has coordinates representing binary choice probabilities consistent with Random
. Every point in the shaded region has coordinates representing binary choice probabilities consistent with Random
 where α and γ have some unknown joint distribution (within the stated range).
where α and γ have some unknown joint distribution (within the stated range).
The shaded region in Figure 9, that forms an irregular pyramid in 3D space, is called a convex polytope (see the Online Supplement for more details). QTest is able to evaluate the maximum-likelihood based goodness-of-fit of any such convex polytope, within numerical accuracy, provided that 1) the polytope is full-dimensional in that it has the same dimension as the full probability space (in Figure 9, the 3D pyramid is full-dimensional in the 3D cube; see the Online Supplement for nonfull-dimensional examples), and provided that 2) the user gives the program a complete mathematical characterization of the polytope's mathematical structure. In practice, this means that the researcher who wants to test a random preference model will first have to determine the geometric description of the model. If the polytope is full-dimensional, then they can test the model using QTest up to computational accuracy. The characterization of Random
 on Cash II via the System of Constraints (5) happens to be fairly simple (it involves 12 nonredundant “≤” constraints). In the Online Supplement, we provide the corresponding complete system of 784 nonredundant constraints for Random
on Cash II via the System of Constraints (5) happens to be fairly simple (it involves 12 nonredundant “≤” constraints). In the Online Supplement, we provide the corresponding complete system of 784 nonredundant constraints for Random
 on Cash I. We also consider Random
on Cash I. We also consider Random
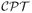 with “Goldstein-Einhorn” weighting functions and provide a complete system of 11 nonredundant constraints on Cash I, as well as 487 nonredundant constraints on Cash II in the Online Supplement.
with “Goldstein-Einhorn” weighting functions and provide a complete system of 11 nonredundant constraints on Cash I, as well as 487 nonredundant constraints on Cash II in the Online Supplement.
In Figure 9, the shaded region is an irregular pyramid characterized by the constraints
For example, the second to last inequality gives the shaded triangle in the (A, D) × (A, C) plane forming the base of the pyramid in the right side display, whereas the second inequality gives the triangle in the (C, D) × (A, D) plane forming the “back wall” of the pyramid in the right side display. The left hand display is rotated and oriented so as to show that the data sets of all three decision makers in Table 2 lie outside the Random
 model.10
model.10
Notice how strongly random preference models differ geometrically from aggregation- and distance-based specifications. The aggregation- and distance-based models are a collection of disjoint geometric objects that are attached to the vertices representing permissible preference states: e.g., four disconnected cubes in Figure 8 for distance-based specifications of
 on Cash II gamble pairs (A,C), (A,D), (C,D). A random preference model is always a single polytope whose vertices are the permissible preference states: e.g., the irregular pyramid in Figure 9, for Random
on Cash II gamble pairs (A,C), (A,D), (C,D). A random preference model is always a single polytope whose vertices are the permissible preference states: e.g., the irregular pyramid in Figure 9, for Random
 on Cash II gamble pairs (A,C), (A,D), (C,D). This makes it clear that fixed preference perturbed by error and variable/uncertain preferences can be distinguished mathematically and experimentally and at a very general level! In its current classical (“frequentist”) form, QTest can test each of these models, stated as a Null Hypothesis, provided that, in the random preference and random utility case, the user provides the mathematical description of the relevant polytope and that the latter is full-dimensional.
on Cash II gamble pairs (A,C), (A,D), (C,D). This makes it clear that fixed preference perturbed by error and variable/uncertain preferences can be distinguished mathematically and experimentally and at a very general level! In its current classical (“frequentist”) form, QTest can test each of these models, stated as a Null Hypothesis, provided that, in the random preference and random utility case, the user provides the mathematical description of the relevant polytope and that the latter is full-dimensional.
In the Online Supplement, we discuss a variety of technical issues, including sample size requirements, assumptions about iid sampling, and conditions under which data can be pooled across multiple participants.
7 Testing Cumulative Prospect Theory and ℒℋ
To illustrate some applications of QTest using the Cash I and Cash II data of Regenwetter et al. (2010, 2011a,b) we consider three different theories: ℒℋ,
 , and
, and
 . Theory ℒℋ is the lexicographic heuristic we introduced earlier and illustrated in several figures. The main purpose of including ℒℋ is to show that QTest is not limited to numerical utility theories, and to illustrate how it can represent and test even intransitive predictions. We have also seen
. Theory ℒℋ is the lexicographic heuristic we introduced earlier and illustrated in several figures. The main purpose of including ℒℋ is to show that QTest is not limited to numerical utility theories, and to illustrate how it can represent and test even intransitive predictions. We have also seen
 earlier. We now add a competing functional form that we label
earlier. We now add a competing functional form that we label
 because it uses a “Goldstein-Einhorn” weighting function (Stott 2006) with weighting parameters γ ∈ [0,1] and s ∈ [0,10]. According to
because it uses a “Goldstein-Einhorn” weighting function (Stott 2006) with weighting parameters γ ∈ [0,1] and s ∈ [0,10]. According to
 a gamble with a P chance of winning X (and nothing otherwise) has a subjective numerical value of
a gamble with a P chance of winning X (and nothing otherwise) has a subjective numerical value of
| (6) |
We use α ∈ [0,1] as in
 .
.
Table 4 shows the predicted preference patterns according to
 and
and
 for Cash I and Cash II. For Cash I, there are 22 different rankings possible according to
for Cash I and Cash II. For Cash I, there are 22 different rankings possible according to
 , whereas there are only 11 different rankings possible according to
, whereas there are only 11 different rankings possible according to
 . In contrast, in Cash II, there are altogether 43 different preference patterns for
. In contrast, in Cash II, there are altogether 43 different preference patterns for
 and only 12 predicted rankings for
and only 12 predicted rankings for
 . This means that either functional form of Cumulative Prospect Theory can be more or less restrictive for a given experiment, depending on the stimuli used. In particular,
. This means that either functional form of Cumulative Prospect Theory can be more or less restrictive for a given experiment, depending on the stimuli used. In particular,
 , which has one more algebraic parameter than
, which has one more algebraic parameter than
 (but does not contain
(but does not contain
 as a nested subtheory), is actually more parsimonious than
as a nested subtheory), is actually more parsimonious than
 in Cash I. Notice also that there are altogether 210 = 1024 different conceivable 0/1-coded preference patterns, of which 120 are rankings. Of those 120, the rankings predicted by either version of Cumulative Prospect Theory are only a fraction. This table also shows that some of the rankings predicted by
in Cash I. Notice also that there are altogether 210 = 1024 different conceivable 0/1-coded preference patterns, of which 120 are rankings. Of those 120, the rankings predicted by either version of Cumulative Prospect Theory are only a fraction. This table also shows that some of the rankings predicted by
 and/or
and/or
 only occur with a very specific set of parameter values in the weighting and utility functions. For example, it is very difficult to find a weighting function and a utility function within “Goldstein-Einhorn” that will give us a preference ranking ABDCE (GE-V40): only one in the two million combinations of parameter values that we checked in our grid search of the parameter space for
only occur with a very specific set of parameter values in the weighting and utility functions. For example, it is very difficult to find a weighting function and a utility function within “Goldstein-Einhorn” that will give us a preference ranking ABDCE (GE-V40): only one in the two million combinations of parameter values that we checked in our grid search of the parameter space for
 actually gave this ranking, namely α = 0.911, γ = 0.941 and s = 1.06. That particular ranking never occurred in our grid search for
actually gave this ranking, namely α = 0.911, γ = 0.941 and s = 1.06. That particular ranking never occurred in our grid search for
 .
.
Table 4.
Predicted preference patterns according to
 and
and
 for Cash I and Cash II. For each pattern, we provide the corresponding ranking of gambles (from best to worst), and the portion of the algebraic parameter space corresponding to each preference (based on a grid search), up to and rounded to the first significant nonzero digit. The precision and range of our grid search were as follows:
for Cash I and Cash II. For each pattern, we provide the corresponding ranking of gambles (from best to worst), and the portion of the algebraic parameter space corresponding to each preference (based on a grid search), up to and rounded to the first significant nonzero digit. The precision and range of our grid search were as follows:
 : α, γ ∈ [0.01, 1], step size 0.01.
: α, γ ∈ [0.01, 1], step size 0.01.
 : α, γ ∈ [0.001, 0.991], step size 0.01; s ∈ [0.01, 9.96], step size 0.05. When two gambles were assigned numerical values differing by less than 10−20, no prediction was made (100 cases of Cash I and 101 cases of Cash II, this occurred in
: α, γ ∈ [0.001, 0.991], step size 0.01; s ∈ [0.01, 9.96], step size 0.05. When two gambles were assigned numerical values differing by less than 10−20, no prediction was made (100 cases of Cash I and 101 cases of Cash II, this occurred in
 only).
only).
| Cash I | Cash II | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predicted Preference Patterns | Predicted Preference Patterns | ||||||||
|
|
|
|
|
||||||
| Vertex | Portion | Ranking | Vertex | Portion | Vertex | Portion | Ranking | Vertex | Portion |
| KT-v1 | 0.6 | edcba | GE-v1 | 0.3 | KT-V1 | 0.4 | EDCBA | GE-V1 | 0.2 |
| KT-v2 | 0.01 | decba | GE-v2 | 0.02 | DECBA | GE-V2 | 0.002 | ||
| KT-v3 | 0.009 | dceba | GE-v3 | 0.02 | DCEBA | GE-V3 | 0.002 | ||
| KT-v4 | 0.001 | cdeba | GE-v4 | 0.002 | CDEBA | GE-V4 | 0.0003 | ||
| KT-v5 | 0.008 | cdbea | GE-v5 | 0.02 | DCBEA | GE-V5 | 0.000007 | ||
| KT-v6 | 0.002 | cbdea | GE-v6 | 0.004 | CDBEA | GE-V6 | 0.002 | ||
| KT-v7 | 0.006 | cbdae | GE-v7 | 0.02 | CBDEA | GE-V7 | 0.0009 | ||
| KT-v8 | 0.0008 | bcdae | GE-v8 | 0.004 | EDBCA | GE-V8 | 0.00002 | ||
| KT-v9 | 0.007 | bcade | GE-v9 | 0.03 | DBCEA | GE-V9 | 0.0000005 | ||
| KT-v10 | 0.006 | bacde | GE-v10 | 0.03 | EBDCA | GE-V10 | 0.000005 | ||
| KT-v11 | 0.003 | edcab | EBCDA | GE-V11 | 0.0000005 | ||||
| KT-v12 | 0.003 | edacb | BDCEA | GE-V12 | 0.0000005 | ||||
| KT-v13 | 0.0001 | edabc | BECDA | GE-V13 | 0.000001 | ||||
| KT-v14 | 0.0001 | eadcb | BCEDA | GE-V14 | 0.0000005 | ||||
| KT-v15 | 0.003 | eadbc | BCDEA | GE-V15 | 0.00002 | ||||
| KT-v16 | 0.0003 | aedbc | CBDAE | GE-V16 | 0.001 | ||||
| KT-v17 | 0.004 | aebdc | BCDAE | GE-V17 | 0.0008 | ||||
| KT-v18 | 0.0001 | aebcd | BCAED | GE-V18 | 0.0000005 | ||||
| KT-v19 | 0.0002 | abedc | BCADE | GE-V19 | 0.002 | ||||
| KT-v20 | 0.004 | abecd | EDBAC | GE-V20 | 0.000008 | ||||
| KT-v21 | 0.005 | abced | EBDAC | GE-V21 | 0.000002 | ||||
| KT-v22 | 0.3 | abcde | GE-v11 | 0.5 | BEDAC | GE-V22 | 0.0000005 | ||
| BDAEC | GE-V23 | 0.0000005 | |||||||
| EBADC | GE-V24 | 0.000004 | |||||||
| BEADC | GE-V25 | 0.0000005 | |||||||
| BEACD | GE-V26 | 0.0000005 | |||||||
| BAEDC | GE-V27 | 0.0000005 | |||||||
| BAECD | GE-V28 | 0.000005 | |||||||
| BACED | GE-V29 | 0.000003 | |||||||
| BACDE | GE-V30 | 0.003 | |||||||
| KT-V2 | 0.005 | EDCAB | GE-V31 | 0.0009 | |||||
| KT-V3 | 0.006 | EDACB | GE-V32 | 0.001 | |||||
| KT-V4 | 0.0005 | EDABC | GE-V33 | 0.00007 | |||||
| KT-V5 | 0.0002 | EADCB | GE-V34 | 0.000007 | |||||
| KT-V6 | 0.007 | EADBC | GE-V35 | 0.001 | |||||
| EABDC | GE-V36 | 0.00002 | |||||||
| KT-V7 | 0.0005 | AEDBC | GE-V37 | 0.00009 | |||||
| KT-V8 | 0.008 | AEBDC | GE-V38 | 0.001 | |||||
| KT-V9 | 0.0007 | ABEDC | GE-V39 | 0.0002 | |||||
| ABDCE | GE-V40 | 0.0000005 | |||||||
| KT-V10 | 0.009 | ABECD | GE-V41 | 0.001 | |||||
| KT-V11 | 0.01 | ABCED | GE-V42 | 0.001 | |||||
| KT-V12 | 0.6 | ABCDE | GE-V43 | 0.8 | |||||
On the other hand, each of the two theories can very easily explain two prominent rankings of both stimulus sets, namely the ranking of the gambles from largest to smallest winning amount (abcde in Cash I and ABCDE in Cash II) and the ranking of the gambles from highest to lowest probability of winning (edcba in Cash I and EDCBA in Cash II). These two rankings combined correspond to almost all parameter values that we have considered in the grid search. The fact that two rankings are compatible with virtually all parameter values means that we may not be able to identify the parameter values at all precisely whenever the data are in line with one of these two prominent rankings. This is an accident of reusing published data. On the other hand, this example also shows that it is possible, in principle, to make extremely specific predictions that could narrow down the possible weighting and utility functions underlying binary choices. If a participant were to reliably provide data consistent with the preference ranking ABDCE (GE-V40) in Cash II, we would have a very precise idea of this decision maker's weighting and utility function as suggested by
 and we would have evidence in favor of
and we would have evidence in favor of
 and against
and against
 .
.
Table 5 shows our analysis results for modal choice and supermajority. The top panel provides the results for the majority/modal choice specification of
 ,
,
 , and ℒℋ. At first sight,
, and ℒℋ. At first sight,
 fits perfectly for 11 participants in Cash I and for 12 participants in Cash II, as indicated by ✓ in the corresponding columns. In each case that we find a theory to fit the data, we provide the label of the best fitting vertex. Since the Cash I and Cash II stimuli were intermixed in the experiment, any model that assumes a decision maker to use a fixed weighting and a fixed utility function and to make choices based on just those two functions, plus commit random errors, should be able to account for the Cash I and Cash II data jointly without requiring different weighting and utility functions for the two stimulus sets. In other words, a person's Cash I and Cash II responses can serve as each others' replications. When a theory consistently fitted the data of a person for both stimulus sets with the same weighting and the same utility function, then we marked the vertex labels in italics to indicate that they are mutually consistent. Whenever a theory is rejected on a given stimulus set for a given participant, we mark this with “−” and provide the p-value in bold faced font. The table can be read as follows: For Respondent 1, we find
fits perfectly for 11 participants in Cash I and for 12 participants in Cash II, as indicated by ✓ in the corresponding columns. In each case that we find a theory to fit the data, we provide the label of the best fitting vertex. Since the Cash I and Cash II stimuli were intermixed in the experiment, any model that assumes a decision maker to use a fixed weighting and a fixed utility function and to make choices based on just those two functions, plus commit random errors, should be able to account for the Cash I and Cash II data jointly without requiring different weighting and utility functions for the two stimulus sets. In other words, a person's Cash I and Cash II responses can serve as each others' replications. When a theory consistently fitted the data of a person for both stimulus sets with the same weighting and the same utility function, then we marked the vertex labels in italics to indicate that they are mutually consistent. Whenever a theory is rejected on a given stimulus set for a given participant, we mark this with “−” and provide the p-value in bold faced font. The table can be read as follows: For Respondent 1, we find
 and
and
 to fit the Cash I responses, but both theories are rejected on the Cash II data, whereas ℒℋ fits on both data sets. The column marked “Performance Summary” shows for each theory whether it is rejected (marked −), whether it fits consistently across the two stimulus sets (marked
to fit the Cash I responses, but both theories are rejected on the Cash II data, whereas ℒℋ fits on both data sets. The column marked “Performance Summary” shows for each theory whether it is rejected (marked −), whether it fits consistently across the two stimulus sets (marked
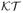 ,
,
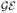 , or ℒℋ), or whether, even though it fits, it fails to do so consistently across the two stimulus sets (marked ↭).
, or ℒℋ), or whether, even though it fits, it fails to do so consistently across the two stimulus sets (marked ↭).
Table 5.
Results for modal (0.50-majority) and 0.90-supermajority specifications of Cumulative Prospect Theory with “Kahneman-Tversky” or “Goldstein-Einhorn” weighting functions and the Lexicographic Heuristic ℒℋ for 18 participants. Rejections have boldface p-values (rounded to nearest percent). Perfect fits are checkmarks (✓). Nonsignificant violations have their p-values listed (rounded to nearest percent). When a theory fits consistently in Cash I and Cash II, it is in italics. If it fits both stimulus sets, but there is no weighting function that yields the best fitting vertex for both stimulus sets, then the fitting vertices are in smaller font. In Performance Summary – means rejected,
 means CPT-KT fits consistently,
means CPT-KT fits consistently,
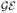 means CPT-GE fits consistently, and ↭means that two fits are mutually inconsistent.
means CPT-GE fits consistently, and ↭means that two fits are mutually inconsistent.
| 0.50-Majority/Modal Choice Specification | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| Performance | “Kahneman-Tversky” | “Goldstein-Einhorn” | ℒℋ | ||||||||||
| Summary | Cash I | Cash II | Cash I | Cash II | Cash I | Cash II | |||||||
| 1 | - | - | ℒℋ | v1 | 0.13 | - | 0.03 | v1 | 0.13 | - | 0.03 | 0.18 | 0.18 |
| 2 |
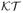
|
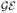
|
- | v22 | ✓ | V12 | ✓ | v11 | ✓ | V43 | ✓ | 0.00 | 0.00 |
| 3 |
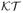
|
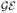
|
- | v1 | ✓ | V1 | ✓ | v1 | ✓ | V1 | ✓ | 0.00 | 0.00 |
| 4 | - | - | - | - | 0.01 | V11,12 | ✓ | - | 0.00 | V42,43 | ✓ | 0.00 | 0.00 |
| 5 |
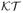
|
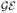
|
- | v1 | ✓ | V1 | ✓ | v1 | ✓ | V1 | ✓ | 0.00 | 0.00 |
| 6 | ↭ | ↭ | ↭ | v1 | 0.26 | V8 | 0.40 | v1 | 0.26 | V38 | 0.40 | 0.21 | 0.01 |
| 7 | ↭ | ↭ | - | v1 | ✓ | V2 | ✓ | v1 | ✓ | V31 | ✓ | 0.00 | 0.01 |
| 8 |
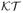
|
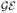
|
- | v1 | ✓ | V1 | ✓ | v1 | ✓ | V1 | ✓ | 0.00 | 0.00 |
| 9 | ↭ | ↭ | - | v1 | 0.09 | V10,11 | ✓ | v1 | 0.09 | V41,42 | ✓ | 0.00 | 0.00 |
| 10 |
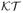
|
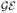
|
- | v1 | ✓ | V1 | ✓ | v1 | ✓ | V1 | ✓ | 0.00 | 0.00 |
| 11 |
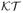
|
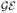
|
- | v1 | ✓ | V1 | ✓ | v1 | ✓ | V1 | ✓ | 0.00 | 0.00 |
| 12 | ↭ | - | ↭ | v13 | 0.26 | V10 | 0.12 | - | 0.01 | V26 | 0.17 | ✓ | 0.00 |
| 13 | ↭ | ↭ | ℒℋ | v11 | 0.67 | V5 | 0.62 | v1 | 0.67 | V34 | 0.70 | 0.08 | 0.56 |
| 14 |
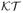
|
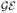
|
- | v22 | ✓ | V12 | ✓ | v11 | ✓ | V43 | ✓ | 0.00 | 0.00 |
| 15 | ↭ | ↭ | - | v1 | ✓ | V9,10 | ✓ | v1 | ✓ | V39,41 | ✓ | 0.02 | 0.00 |
| 16 | - | - | - | v1 | ✓ | - | 0.01 | v1 | ✓ | - | 0.02 | 0.00 | 0.00 |
| 17 |
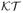
|
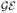
|
- | v22 | 0.31 | V12 | ✓ | v11 | 0.31 | V43 | ✓ | 0.05 | 0.00 |
| 18 | - | ↭ | ℒℋ | v1,2,3 | ✓ | - | 0.01 | v1,2,3 | ✓ | V4 | 0.23 | 0.4 | 0.47 |
| 0.90-Supermajority Specification | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| Performance Summary |
“Kahneman-Tversky” | “Goldstein-Einhorn” | ℒℋ | ||||||||||
| Cash I | Cash II | Cash I | Cash II | Cash I | Cash II | ||||||||
| 1 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 2 | - | - | - | - | 0.00 | V12 | 0.51 | - | 0.00 | V43 | 0.51 | 0.00 | 0.00 |
| 3 |
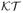
|
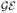
|
- | v1 | ✓ | V1 | 0.73 | v1 | ✓ | V1 | 0.73 | 0.00 | 0.00 |
| 4 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 5 |
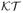
|
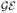
|
- | v1 | ✓ | V1 | 0.57 | v1 | ✓ | V1 | 0.58 | 0.00 | 0.00 |
| 6 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 7 | - | - | - | v1 | 0.81 | - | 0.00 | v1 | 0.81 | - | 0.00 | 0.00 | 0.00 |
| 8 |
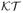
|
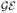
|
- | v1 | 0.95 | V1 | 0.90 | v1 | 0.95 | V1 | 0.90 | 0.00 | 0.00 |
| 9 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 10 |
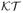
|
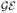
|
- | v1 | 0.72 | V1 | 0.30 | v1 | 0.72 | V1 | 0.30 | 0.00 | 0.00 |
| 11 |
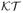
|
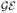
|
- | v1 | 0.95 | V1 | ✓ | v1 | 0.95 | V1 | ✓ | 0.00 | 0.00 |
| 12 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 13 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 14 |
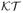
|
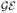
|
- | v22 | ✓ | V12 | ✓ | v11 | ✓ | V43 | ✓ | 0.00 | 0.00 |
| 15 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 16 | - | - | - | - | 0.02 | - | 0.00 | - | 0.02 | - | 0.00 | 0.00 | 0.00 |
| 17 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
| 18 | - | - | - | - | 0.00 | - | 0.00 | - | 0.00 | - | 0.00 | 0.00 | 0.00 |
In the lower part of Table 5, we report the 0.90-supermajority specification of
 and
and
 . The heuristic ℒℋ is now rejected on every data set. With supermajority of 0.90, both
. The heuristic ℒℋ is now rejected on every data set. With supermajority of 0.90, both
 and
and
 fit on the exact same data sets, namely, participants 3, 5, 8, 10, 11, and 14. The analysis in the lower half of the table strongly suggests that the inconsistent fits in the modal choice analysis that we found for Participants 6, 7, 9, 12, 13, 15, and 18 were examples of ‘overfitting,’ that is ‘accidental’ fits of the models. When we are interested in modeling true preference perturbed by random error, we may want to limit error rates far below 50% to avoid ‘overfitting.’ (Note, however, that econometric models will oftentimes predict choice probabilities close to
, notably whenever the strength of preference is negligible relative to the noise. In such models, choice proportions far from 50% would be reason for rejection.)
fit on the exact same data sets, namely, participants 3, 5, 8, 10, 11, and 14. The analysis in the lower half of the table strongly suggests that the inconsistent fits in the modal choice analysis that we found for Participants 6, 7, 9, 12, 13, 15, and 18 were examples of ‘overfitting,’ that is ‘accidental’ fits of the models. When we are interested in modeling true preference perturbed by random error, we may want to limit error rates far below 50% to avoid ‘overfitting.’ (Note, however, that econometric models will oftentimes predict choice probabilities close to
, notably whenever the strength of preference is negligible relative to the noise. In such models, choice proportions far from 50% would be reason for rejection.)
The lower half of Table 5 offers three important insights: First, both versions of Cumulative Prospect Theory are rejected on two thirds of the participants. Second, in those cases where either of these versions of Cumulative Prospect Theory fits a participant for one stimulus set, it does so also in the other stimulus set, hence, the successful fits are highly replicable. Third, the only predicted preference patterns that are not rejected, are the ranking of the gambles by decreasing winning amount (abcde in Cash I and ABCDE in Cash II), and the ranking of the gambles by increasing probability of winning (edcba in Cash I and EDCBA in Cash II). These two rankings are also consistent with simple heuristics according to which decision makers either ignore probabilities or outcomes for lotteries like these. The Cash I and Cash II stimulus sets were not originally designed to be diagnostic for a full-fledged test of Cumulative Prospect Theory, hence, we leave it for future work to determine the performance of
 and
and
 more systematically.
more systematically.
While we leave a full formal and theoretical discussion of the relationship among different types of probabilistic choice models for a different paper, we have mentioned that many econometric models make predictions that are nested in the majority/modal choice specification. For example, “Logit,” “Probit,” and “Contextual Utility” models, as well as a broad range of related econometric models (Blavatskyy 2007, Blavatskyy and Pogrebna 2010, Stott 2006, Wilcox 2008, 2011) are all nested in the modal choice specification. So are the choice probabilities under “decision field theory” (Busemeyer and Townsend 1992, 1993) in the case of deliberation with no initial bias. All of these models imply that an option with higher utility has a probability ≥ 1/2 of being chosen. If one were to apply any one of these probabilistic models to
 and
and
 , for example, then the resulting binary choice probabilities would lie inside the majority/modal choice model of
, for example, then the resulting binary choice probabilities would lie inside the majority/modal choice model of
 and
and
 .
.
This is an example of how QTest can serve as a screening device for the quantitatively savvy decision scientist: It follows from our analyses that these parametric probabilistic models, when applied to
 and
and
 , would probably also fit poorly for those five participants (1, 4, 12, 16, and 18) where we rejected the majority specification of
, would probably also fit poorly for those five participants (1, 4, 12, 16, and 18) where we rejected the majority specification of
 and
and
 . Likewise, in those 7 cases where the modal choice specification fit inconsistently, many econometric models of
. Likewise, in those 7 cases where the modal choice specification fit inconsistently, many econometric models of
 and
and
 would probably yield different, hence mutually inconsistent, parameter estimates on the Cash I and Cash II stimuli as well. Majority/modal choice specifications in QTest can serve as a triage for deciding whether or not it is worth applying one of these econometric models to a given set of data and for a given theory. Note that, unlike these econometric models, modal choice models do not require numerical strength of preference as input. For example, we have illustrated a modal choice specification of an intransitive model ℒℋ for which there is no “Logit” or “Probit” formulation.
would probably yield different, hence mutually inconsistent, parameter estimates on the Cash I and Cash II stimuli as well. Majority/modal choice specifications in QTest can serve as a triage for deciding whether or not it is worth applying one of these econometric models to a given set of data and for a given theory. Note that, unlike these econometric models, modal choice models do not require numerical strength of preference as input. For example, we have illustrated a modal choice specification of an intransitive model ℒℋ for which there is no “Logit” or “Probit” formulation.
Table 6 shows the results of fitting Random
 and Random
and Random
 on the same data. There are two noteworthy findings: First, while the full linear order model was very successfully fit to these data by Regenwetter et al. (2011a), the more restrictive, nested, Random
on the same data. There are two noteworthy findings: First, while the full linear order model was very successfully fit to these data by Regenwetter et al. (2011a), the more restrictive, nested, Random
 and
and
 models, in which only linear orders compatible with Cumulative Prospect Theory are allowed, are both rejected on two-thirds of the participants. Second, for Participant 7, we find evidence in favor of Random
models, in which only linear orders compatible with Cumulative Prospect Theory are allowed, are both rejected on two-thirds of the participants. Second, for Participant 7, we find evidence in favor of Random
 and against Random
and against Random
 , whereas for Participant 13, we find evidence in favor of Random
, whereas for Participant 13, we find evidence in favor of Random
 and against Random
and against Random
 . This documents that the quantitative analysis has the ability to let these theories compete. A more targeted experiment in the future could allow a stronger model competition. Full-fledged model competition and model selection, beyond mere rejections/retentions of Null Hypotheses, also requires a future extension of QTest, e.g., to Bayesian analysis methods that naturally trade-off between competing models based on their complexity (flexibility).
. This documents that the quantitative analysis has the ability to let these theories compete. A more targeted experiment in the future could allow a stronger model competition. Full-fledged model competition and model selection, beyond mere rejections/retentions of Null Hypotheses, also requires a future extension of QTest, e.g., to Bayesian analysis methods that naturally trade-off between competing models based on their complexity (flexibility).
Table 6.
Results for random preference models, Random
 and Random
and Random
 . Rejections have boldface p-values (rounded to nearest percent, except 0.045, 0.047, which are rounded to nearest permille). Perfect fits are checkmarks (✓). Nonsignificant violations have their p-values listed (rounded to nearest percent). In Performance Summary, – means rejected, “Random
. Rejections have boldface p-values (rounded to nearest percent, except 0.045, 0.047, which are rounded to nearest permille). Perfect fits are checkmarks (✓). Nonsignificant violations have their p-values listed (rounded to nearest percent). In Performance Summary, – means rejected, “Random
 ” means “Random
” means “Random
 fits consistently, “Random
fits consistently, “Random
 ” means “Random
” means “Random
 fits consistently.”
fits consistently.”
| Random Preference Model | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| Performance |
|
|
||||
| Summary | Cash I | Cash II | Cash I | Cash II | ||
| 1 | - | - | 0.00 | 0.00 | 0.00 | 0.01 |
| 2 | - | - | 0.01 | 0.07 | 0.01 | 0.04 |
| 3 |
|
|
0.39 | 0.09 | 0.49 | 0.95 |
| 4 | - | - | 0.00 | 0.05 | 0.00 | 0.13 |
| 5 |
|
|
0.44 | 0.38 | 0.11 | ✓ |
| 6 | - | - | 0.00 | 0.06 | 0.00 | 0.35 |
| 7 | - |
|
0.41 | 0.00 | 0.82 | 0.16 |
| 8 |
|
|
0.39 | 0.07 | 0.05 | ✓ |
| 9 |
|
- | 0.10 | 0.12 | 0.04 | 0.15 |
| 10 | - |
|
0.045 | 0.34 | 0.12 | 0.48 |
| 11 | - | - | 0.00 | 0.24 | 0.02 | 0.02 |
| 12 | - | - | 0.00 | 0.00 | 0.00 | 0.07 |
| 13 |
|
|
✓ | 0.36 | 0.06 | 0.20 |
| 14 |
|
|
✓ | ✓ | 0.63 | ✓ |
| 15 | - | - | 0.19 | 0.00 | 0.02 | 0.00 |
| 16 | - | - | 0.00 | 0.00 | 0.00 | 0.00 |
| 17 | - | - | 0.047 | 0.17 | 0.00 | 0.19 |
| 18 | - |
|
0.15 | 0.01 | 0.08 | 0.05 |
8 QTest as a triage method
Figure 10 gives an overview of how QTest operates as a triage method. The scholar first needs to determine all permissible preference patterns according to the theory or theories at hand.
Figure 10.
Summary graph.
Note: “RDDS 11” is Regenwetter et al. (2011a) who tested the linear ordering polytope on these data. “RDDSG 11” is Regenwetter et al. (2011b), who tested some lexicographic semiorder polytopes on these data. Regenwetter et al. (2010) tested weak stochastic transitivity on these data.
To model a decision maker who has a fixed preference or utility function perturbed by error (Sections 4 & 5), QTest provides highly automated tools to generate and test distance-based specifications (left column of Fig. 10). For example, weak stochastic transitivity (shown on the left of Fig. 7) is the majority/modal choice specification of the collection of all linear orders. Regenwetter et al. (2010) previously ran a test of weak stochastic transitivity using the computer code underlying QTest. Similarly, Fig. 8 gives majority/modal choice and supermajority specifications of
 (orange) and ℒℋ (blue). For any theory of pairwise preference (that does not predict indifference among any of the stimuli under consideration), whether it involves highly specified numerical functional forms like
(orange) and ℒℋ (blue). For any theory of pairwise preference (that does not predict indifference among any of the stimuli under consideration), whether it involves highly specified numerical functional forms like
 and
and
 , or whether it is characterized by some general property like ℒℋ, QTest only needs to know the permissible preference patterns to proceed. Scholars interested in a very general and abstract, say, ‘nonparametric rank-dependent’ theory (of which
, or whether it is characterized by some general property like ℒℋ, QTest only needs to know the permissible preference patterns to proceed. Scholars interested in a very general and abstract, say, ‘nonparametric rank-dependent’ theory (of which
 and
and
 are highly specialized refinements) can likewise use QTest as long as they specify all permissible preference patterns according to such a theory. For example, the permissible preference states may be specified through a list of general “axioms” (rules defining the mathematical representation of preferences). When a theory predicts a strength of preference (similar to our Eq. 4), there automatically exist a large number of econometric specifications, but some theories, such as ℒℋ, are not compatible with an econometric specification because they provide no strength of preference input to such models. Because tremble and most econometric models (when they exist) are nested in the majority/modal choice specification, a rejection of the modal choice specification is a strong argument against applying any such nested error models to those data (lower left of Fig. 10).11
are highly specialized refinements) can likewise use QTest as long as they specify all permissible preference patterns according to such a theory. For example, the permissible preference states may be specified through a list of general “axioms” (rules defining the mathematical representation of preferences). When a theory predicts a strength of preference (similar to our Eq. 4), there automatically exist a large number of econometric specifications, but some theories, such as ℒℋ, are not compatible with an econometric specification because they provide no strength of preference input to such models. Because tremble and most econometric models (when they exist) are nested in the majority/modal choice specification, a rejection of the modal choice specification is a strong argument against applying any such nested error models to those data (lower left of Fig. 10).11To model a decision maker who wavers in his preference or utility function (Section 6), QTest provides a suitable test, provided that the user enters a complete mathematical description of the relevant polytope (right column in Fig. 10). The Random
 polytope is illustrated in Fig. 9. The polytope for all linear orders was previously tested by Regenwetter et al. (2011a) and some lexicographic semiorder polytopes were tested by Regenwetter et al. (2011b), on these same data. The linear ordering polytope contains many econometric models as special cases, but it generally does not contain tremble models, hence a rejection of the linear ordering polytope would imply rejection of many econometric models (lower right of Fig. 10).
polytope is illustrated in Fig. 9. The polytope for all linear orders was previously tested by Regenwetter et al. (2011a) and some lexicographic semiorder polytopes were tested by Regenwetter et al. (2011b), on these same data. The linear ordering polytope contains many econometric models as special cases, but it generally does not contain tremble models, hence a rejection of the linear ordering polytope would imply rejection of many econometric models (lower right of Fig. 10).
We leave a much more extensive classification of probabilistic models, as well as many new theoretical developments connecting naturally to QTest, for future work.
9 Conclusions
QTest provides a highly versatile, yet accessible, quantitative testing environment for preferential binary choice. We have discussed aggregation- and distance-based specifications of algebraic theories that encapsulate the notion that the decision maker has a fixed binary preference and makes occasional erroneous choices, with error rates being constrained in a variety of ways. This type of model makes it possible to develop probabilistic specifications of theories that are numerical or nonnumerical, that allow a single preference pattern or multiple preference patterns. We also reviewed random preference models including two new probabilistic formulations of Cumulative Prospect Theory: Random
 and Random
and Random
 . Last, but not least, we have shown an application of some QTest analyses on previously published laboratory choice data. We illustrated how a simple lexicographic heuristic was rejected on (almost) every data set (even at the modal choice level). We provided tests of
. Last, but not least, we have shown an application of some QTest analyses on previously published laboratory choice data. We illustrated how a simple lexicographic heuristic was rejected on (almost) every data set (even at the modal choice level). We provided tests of
 and
and
 and concluded for the supermajority specification that both versions of Cumulative Prospect Theory account for the exact same six participants, who acted in a fashion consistent with two very simple heuristics, namely to prefer gambles with higher amounts or to prefer gambles with higher probabilities of winning. We also documented how QTest was ‘diagnostic’ between Random
and concluded for the supermajority specification that both versions of Cumulative Prospect Theory account for the exact same six participants, who acted in a fashion consistent with two very simple heuristics, namely to prefer gambles with higher amounts or to prefer gambles with higher probabilities of winning. We also documented how QTest was ‘diagnostic’ between Random
 and Random CPT − GE in retaining one while rejecting the other as a Null Hypothesis. A full model selection framework, however, will require further refinements, such as Bayesian extensions, for example. As we saw in Table 2, Random
and Random CPT − GE in retaining one while rejecting the other as a Null Hypothesis. A full model selection framework, however, will require further refinements, such as Bayesian extensions, for example. As we saw in Table 2, Random
 is even rejected on the data of the hypothetical decision maker HDM whose data appeared to be nearly in perfect agreement with KT-V4.
is even rejected on the data of the hypothetical decision maker HDM whose data appeared to be nearly in perfect agreement with KT-V4.
Since the Regenwetter et al. stimuli were designed as a replication of Tversky (1969), to test transitivity, not to be diagnostic among competing theories, we leave it for follow-up work to carry out more direct tests and comparisons of decision making theories using QTest. Likewise, work is under way to test theories on other domains, such as in intertemporal choice and probabilistic inference, using the same modeling and analysis framework. Furthermore, Bayesian extensions and parallelized versions of QTest for multicore computer systems are under development.
Supplementary Material
Acknowledgments
Shiau Hong Lim programmed most of QTest while at the Department of Computer Science, University of Illinois and while at the Department of Mathematics and Information Technology, University of Leoben, Austria. Yun-Shil Cha, Ying Guo, William Messner, Anna Popova, Chris Zwilling contributed to the program debugging, interface design, miscellaneous computation and carried out the data analyses. Cha and Messner have graduated from the University of Illinois since working on this project, and now work in industry. Regenwetter developed initial drafts of this article while a 2008-09 sabbatical Fellow of the Max Planck Institute for Human Development, Berlin. He thanks the Adaptive Behavior and Cognition group for many stimulating interactions. A number of colleagues have provided helpful comments at various presentations and discussion of this work. These include M. Birnbaum, P. Blavatskyy, M. Brown, E. Bokhari, D. Cavagnaro, J. Busemeyer, A. Glöckner, A. Bröder, G. Harrison, K. Katsikopoulos, G. Loomes, R.D. Luce, A.A.J. Marley, G. Pogrebna, J. Stevens, N. Wilcox, and attendees at the 2010 and 2011 meetings of the Society for Mathematical Psychology, the 2010 and 2011 meetings of the Society for Judgment and Decision Making, and the 2011 European Mathematical Psychology Group meeting, the 2011 Georgia State CEAR workshop on structural modeling of heterogeneity in discrete choice under risk and uncertainty, and the 2012 Warwick workshop on noise and imprecision in individual and interactive decision-making, the 2012 FUR XV meeting and the 2012 SJDM meeting. Regenwetter acknowledges funding under AFOSR grant # FA9550-05-1-0356, NIMH Training Grant PHS 2 T32 MH014257, NSF grant SES # 08-20009, NSF grant SES # 10-62045, and an Arnold O. Beckman Research Award from the University of Illinois at Urbana-Champaign. Davis-Stober was supported by a Dissertation Completion Fellowship of the University of Illinois when working on the theoretical and statistical models. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of colleagues, funding agencies, or employers.
Appendix
A Cash I lotteries in Regenwetter et al. (2010, 2011a,b)
Gamble a: 7/24 chance of gaining $28, gain or lose nothing otherwise.
Gamble b: 8/24 chance of gaining $26.60, gain or lose nothing otherwise.
Gamble c: 9/24 chance of gaining $25.20, gain or lose nothing otherwise.
Gamble d: 10/24 chance of gaining $23.80, gain or lose nothing otherwise.
Gamble e: 11/24 chance of gaining $22.40, gain or lose nothing otherwise.
For ease of notation we use small letters for Cash I and capital letters for Cash II (see Table 2).
B Probabilistic Specification
We introduce minimal mathematical notation to be concise. For a (deterministic) decision theory
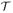 , and for each pair of choice alternatives, f, g, write
, and for each pair of choice alternatives, f, g, write
| (7) |
For KT-V4 of Table 2, we have
and thus (we also have the redundant information),
We call the vector
the vertex representation of
 . Leaving out the redundant coordinates above, the vertex representation of KT-V4 yields the following “vertex” of the unit “hypercube” in 10-space:
. Leaving out the redundant coordinates above, the vertex representation of KT-V4 yields the following “vertex” of the unit “hypercube” in 10-space:
| (8) |
Our first step in probabilizing theories about binary choice is to replace each coordinate by a parameter θfg ∈ [0,1] of a Bernoulli process. The Bernoulli process could model the random selection of a respondent, in which case the parameter θfg denotes the probability that such a respondent chooses f over g. Alternatively, the Bernoulli process could model a fixed respondent's selection of a choice alternative in a randomly sampled observation. In that case, θfg denotes the probability that the respondent chooses f over g in such an observation. With multiple paired comparisons, under certain iid sampling assumptions, the θfg form the parameters of a product of binomial distributions. Throughout, we assume a two-alternative forced choice paradigm where each θfg = 1 − θgf (and, for consistency, .)
Taking θfg(
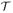 ) as
, the vertex representation embeds the deterministic theories as extreme points in a probability space. To paraphrase: “f is strictly preferred to g in theory
) as
, the vertex representation embeds the deterministic theories as extreme points in a probability space. To paraphrase: “f is strictly preferred to g in theory
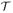 if and only if f is chosen over g with probability one in
if and only if f is chosen over g with probability one in
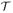 .” The purpose of probabilistic specifications is to extend the range of choice probabilities to values between zero and one. Our various probabilistic specifications achieve this goal by expanding the vertex representations into different types of geometric regions within the probability space.
.” The purpose of probabilistic specifications is to extend the range of choice probabilities to values between zero and one. Our various probabilistic specifications achieve this goal by expanding the vertex representations into different types of geometric regions within the probability space.
Probabilistic Specification by Majority and Supermajority Rules
Let
be a supermajority level. Supermajority specification of a deterministic theory
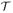 states a system of inequality constraints on the binary choice probabilities θfg(
states a system of inequality constraints on the binary choice probabilities θfg(
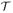 ), according to which, ∀ f ≠ g,
), according to which, ∀ f ≠ g,
| (9) |
When
, this is just a formal representation of the requirement that the modal pairwise choices in the population must match the binary preferences of theory
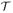 . The modal choice specification was illustrated in 3D-Figure 3, and the supermajority specification was illustrated in 3D-Figure 4 with λ = .75.
. The modal choice specification was illustrated in 3D-Figure 3, and the supermajority specification was illustrated in 3D-Figure 4 with λ = .75.
Distance-Based Specification
Let Δ be a distance measure (in the appropriate space). Let U > 0 be an upper bound on the permissible distance between choice probabilities and vertex representation. A distance-based probabilistic specification of a deterministic theory
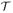 , with distance Δ and upper bound U, states that the vector θ(
, with distance Δ and upper bound U, states that the vector θ(
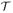 ) of binary choice probabilities that are allowable under
) of binary choice probabilities that are allowable under
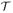 must satisfy
must satisfy
| (10) |
Three examples of Δ are as follows (using nonredundant choice probabilities):
| (11) |
| (12) |
| (13) |
The supremum-distance specification can be reformulated as a supermajority specification with λ = 1 − U. Figures 2 and 3 hence gave an illustration of distance-based specification with an upper bound U = 0.5 on the supremum distance. Figure 4 gave an illustration of distance-based specification with an upper bound U = 0.25 on the supremum distance. The city-block specification was illustrated in Figure 5 with U = 0.50.
Footnotes
QTest is funded by NSF-DRMS SES 08-20009 (Regenwetter, PI). While a Bayesian extension is under development, we concentrate on a frequentist likelihood based approach here. QTest, together with installation instructions, a detailed step-by-step tutorial, and some example data, are available from http://internal.psychology.illinois.edu/labs/DecisionMakingLab/. An Online Tutorial explains step-by-step how a novice user can replicate each QTest analysis using the original data, and generate three-dimensional QTest figures similar to those in the paper. The original Regenwetter et al. data are provided with the software in a file format that QTest can read directly.
There were 101 parameter combinations, among the 10,000, where the values associated to two gambles differed by less than 10−20. For reasons of numerical accuracy, we did not make a pairwise preference prediction in those cases. We also omit the technical details of how to expand the QTest analyses to incorporate “indifference” among pairs of objects, since we focus on two-alternative forced choice, where a decision maker cannot express “indifference” among pairs of lotteries.
More precisely, the HDM data are not statistically consistent with having been generated by a random sample from an unknown probability distribution over preference states consistent with
 with “Kahneman-Tversky” weighting functions and “power” utility functions, where α, γ are multiples of 0.01 and in a certain range.
with “Kahneman-Tversky” weighting functions and “power” utility functions, where α, γ are multiples of 0.01 and in a certain range.
In this paper, we concentrate on asymmetric and complete preferences only. Likewise, empirical data are assumed to be from a two-alternative forced choice paradigm, where, on each trial one and only one option must be chosen. QTest is flexible enough to handle other models but does not currently automate as much for the modeling and analysis processes for such cases. In particular, an extension of the Graphical User Interface for more general cases is not yet available. Regenwetter and Davis-Stober (2012) used the MATLAB© core underlying QTest to test models on ternary paired comparison data where respondents could state indifference among pairs of gambles.
The gamble pair (A,B) gives the x-axis, the pair (A,C) gives the y-axis, and (B,C) gives the z-axis in 3D space.
Myung et al. (2005) provide a corresponding Bayesian framework.
A prerequisite is that the model in question must be full-dimensional, which holds automatically for “distance-based” specifications. QTest also assumes an iid sample. Since QTest tests hypotheses about Binomial distributions, we recommend ≥ 20 observations per gamble pair. We discuss these topics in more detail in the Online Supplement.
We will keep the discussion here nontechnical in the interest of making QTest as approachable as possible. Appendix B provides some formally precise details. We leave a much more general theory for a different paper.
In particular, they explained why it is misleading to think of this as a probabilistic model of transitivity per se, since there are many more transitive preferences than there are rankings for any given set of objects. As Regenwetter and Davis-Stober (2012) discuss, if we moved beyond two-alternative forced choice, i.e., beyond 0/1 patterns, then there would be very many more pairwise preference relations to consider. For instance, while there are 5! = 120 rankings for five choice alternatives, there are about 150 thousand transitive binary preferences and about 33 million intransitive binary preferences for five choice alternatives.
Finding a nonredundant minimal complete list of constraints characterizing a random preference model can be very difficult. There are several public domain programs for this task, such as, e.g., PORTA (http://typo.zib.de/opt-long_projects/Software/Porta) and lrs (http://cgm.cs.mcgill.ca/$∼avis/C/lrs.html).
A referee pointed out that an econometric model could be a lower dimensional nested model of a modal choice specification. A rejection of the majority/modal choice specification still implies rejection of that nested econometric model, because the modal choice specification in such a case remains a generalization of the latter.
Dedicated to R. Duncan Luce (May 1925 - August 2012), whose amazing work provided much inspiration and motivation for this program of research.
References
- 1.Birnbaum M, Bahra J. Separating response variability from structural inconsistency to test models of risky decision making. Judgment and Decision Making. 2012;7:402–426. [Google Scholar]
- 2.Birnbaum M, Gutierrez R. Testing for intransitivity of preferences predicted by a lexicographic semiorder. Organizational Behavior and Human Decision Processes. 2007;104:96–112. [Google Scholar]
- 3.Birnbaum MH, Chavez A. Tests of theories of decision making: Violations of branch independence and distribution independence. Organizational Behavior and Human Decision Processes. 1997;71:161–194. [Google Scholar]
- 4.Blavatskyy P. Stochastic expected utility theory. Journal of Risk and Uncertainty. 2007;34:259–286. [Google Scholar]
- 5.Blavatskyy PR, Pogrebna G. Models of stochastic choice and decision theories: why both are important for analyzing decisions. Journal of Applied Econometrics. 2010;25(6):963–986. [Google Scholar]
- 6.Busemeyer JR, Townsend JT. Fundamental derivations from decision field theory. Mathematical Social Sciences. 1992;23:255–282. [Google Scholar]
- 7.Busemeyer JR, Townsend JT. Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review. 1993;100:432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- 8.Camerer CF. An experimental test of several generalized utility theories. Journal of Risk and Uncertainty. 1989;2:61–104. [Google Scholar]
- 9.Davis-Stober C, Brown N. A shift in strategy or “error”? strategy classification over multiple stochastic specifications. Judgment and Decision Making. 2011;6:800–813. [Google Scholar]
- 10.Davis-Stober CP. Analysis of multinomial models under inequality constraints: Applications to measurement theory. Journal of Mathematical Psychology. 2009;53:1–13. [Google Scholar]
- 11.Harless DW, Camerer CF. The predictive utility of generalized expected utility theories. Econometrica. 1994;62(6):1251–89. [Google Scholar]
- 12.Hey JD. Experimental investigations of errors in decision making under risk. European Economic Review. 1995;39(3-4):633–640. [Google Scholar]
- 13.Hey JD. Why we should not be silent about noise. Experimental Economics. 2005;8:325–345. [Google Scholar]
- 14.Hey JD, Orme C. Investigating generalizations of expected utility theory using experimental data. Econometrica. 1994;62(6):1291–1326. [Google Scholar]
- 15.Iverson GJ, Falmagne JC. Statistical issues in measurement. Mathematical Social Sciences. 1985;10:131–153. [Google Scholar]
- 16.Klugkist I, Hoijtink H. The bayes factor for inequality and about equality constrained models. Computational Statistics & Data Analysi. 2007;51:6367–6379. [Google Scholar]
- 17.Loomes G, Moffatt PG, Sugden R. A microeconometric test of alternative stochastic theories of risky choice. Journal of Risk and Uncertainty. 2002;24:103–130. [Google Scholar]
- 18.Loomes G, Sugden R. Incorporating a stochastic element into decision theories. European Economic Review. 1995;39:641–648. [Google Scholar]
- 19.Luce RD. Individual Choice Behavior: A Theoretical Analysis. John Wiley; New York: 1959. [Google Scholar]
- 20.Luce RD. Four tensions concerning mathematical modeling in psychology. Annual Review of Psychology. 1995;46:1–26. doi: 10.1146/annurev.ps.46.020195.000245. [DOI] [PubMed] [Google Scholar]
- 21.Luce RD. Several unresolved conceptual problems of mathematical psychology. Journal of Mathematical Psychology. 1997;41:79–87. [Google Scholar]
- 22.McFadden D. Specification of econometric models. Econometrica. 1998 forthcoming. [Google Scholar]
- 23.Myung J, Karabatsos G, Iverson G. A Bayesian approach to testing decision making axioms. Journal of Mathematical Psychology. 2005:205–225. [Google Scholar]
- 24.Regenwetter M, Dana J, Davis-Stober CP. Testing transitivity of preferences on two-alternative forced choice data. Frontiers in Quantitative Psychology and Measurement. 2010 doi: 10.3389/fpsyg.2010.00148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Regenwetter M, Dana J, Davis-Stober CP. Transitivity of preferences. Psychological Review. 2011a;118:42–56. doi: 10.1037/a0021150. [DOI] [PubMed] [Google Scholar]
- 26.Regenwetter M, Dana J, Davis-Stober CP, Guo Y. Parsimonious testing of transitive or intransitive preferences: Reply to Birnbaum (2011) Psychological Review 2011b [Google Scholar]
- 27.Regenwetter M, Davis-Stober CP. Choice variability versus structural inconsistency of preferences. Psychological Review. 2012;119:408–416. doi: 10.1037/a0027372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Starmer C. Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. Journal of Economic Literature. 2000;38:332–382. [Google Scholar]
- 29.Starmer C, Sugden R. Probability and juxtaposition effects: An experimental investigation of the common ratio effect. Journal of Risk and Uncertainty. 1989;2:159–17. [Google Scholar]
- 30.Stott H. Cumulative prospect theory's functional menagerie. Journal of Risk and Uncertainty. 2006;32:101–130. [Google Scholar]
- 31.Tversky A. Intransitivity of preferences. Psychological Review. 1969;76:31–48. [Google Scholar]
- 32.Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty. 1992;5:297–323. [Google Scholar]
- 33.Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 1989;57:307–333. [Google Scholar]
- 34.Wilcox N. Stochastic models for binary discrete choice under risk: A critical primer and econometric comparison. In: Cox J, Harrison G, editors. Risk Aversion in Experiments. Vol. 12. Emerald, Research in Experimental Economics; Bingley, UK: 2008. pp. 197–292. [Google Scholar]
- 35.Wilcox N. Stochastically more risk averse: A contextual theory of stochastic discrete choice under risk. Journal of Econometrics. 2011;162:89–104. [Google Scholar]
- 36.Yellott JIJ. The relationship between Luce's choice axiom, Thurstone's theory of comparative judgement, and the double exponential distribution. Journal of Mathematical Psychology. 1977;15:109–144. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


