Abstract
Modern molecular biology has always been a great source of inspiration for computational science. Half a century ago, the challenge from understanding macromolecular dynamics has led the way for computations to be part of the tool set to study molecular biology. Twenty-five years ago, the demand from genome science has inspired an entire generation of computer scientists with an interest in discrete mathematics to join the field that is now called bioinformatics. In this paper, we shall lay out a new mathematical theory for dynamics of biochemical reaction systems in a small volume (i.e., mesoscopic) in terms of a stochastic, discrete-state continuous-time formulation, called the chemical master equation (CME). Similar to the wavefunction in quantum mechanics, the dynamically changing probability landscape associated with the state space provides a fundamental characterization of the biochemical reaction system. The stochastic trajectories of the dynamics are best known through the simulations using the Gillespie algorithm. In contrast to the Metropolis algorithm, this Monte Carlo sampling technique does not follow a process with detailed balance. We shall show several examples how CMEs are used to model cellular biochemical systems. We shall also illustrate the computational challenges involved: multiscale phenomena, the interplay between stochasticity and nonlinearity, and how macroscopic determinism arises from mesoscopic dynamics. We point out recent advances in computing solutions to the CME, including exact solution of the steady state landscape and stochastic differential equations that offer alternatives to the Gilespie algorithm. We argue that the CME is an ideal system from which one can learn to understand “complex behavior” and complexity theory, and from which important biological insight can be gained.
Keywords: biochemical networks, cellular signaling, epigenetics, master equation, nonlinear reactions, stochastic modeling
1 Introduction
Cellular biology has two important foundations: genomics focuses on DNA sequences and their evolutionary dynamics; and biochemistry studies molecular reaction kinetics that involve both small metabolites and large macromolecules. Computational science has been an essential component of genomics. In recent years, cellular biochemistry is also increasingly relying on mathematical models for biochemical reaction networks. Two approaches have been particularly prominent: the Law of Mass Action for deterministic nonlinear chemical reactions in terms of the concentrations of chemical species, and the Chemical Master Equation (CME) for stochastic reactions in terms of the numbers of reaction species.
The Law of Mass Action and the CME are two parts of a single mathematical theory of chemical reaction systems, with the latter being fundamental. When the number of molecules in a reaction system are large, stochasticity in the CME disappears and the Law of Mass Action can be shown, mathematically, to arise as the limit[1–2].
In this article, we shall introduce the CME approach to biochemical reaction kinetics. We use simply examples to illustrate some of the salient features of this yet to be fully developed theory. We then discuss the challenges one faces in applying this theory to computational cellular biology. There have been several recent texts which cover some of the materials we discuss. See [2–3].
2 A System of Nonlinear Reactions
To illustrate the theory of the CME and the Law of Mass Action, let us first consider a simple system of nonlinear chemical reactions first proposed by Schlögl[4]
| (1) |
in which species A, B and C are at fixed concentrations a, b and c, respectively. The traditional, macroscopic kinetics of the system (1), according to the Law of Mass Action, is described by a deterministic ordinary differential equation (ODE)[5]
| (2) |
where x represents the concentration of X. It is straightforward to show that (2) exhibits bistability (via the so called pitchfork bifurcation) when α2β1b/(α1a)2 = 1/3[4–5]: that is, the polynomial on the right-hand-side switches from having only one positive root to have three positive roots. The system also shows another bifurcations when varying another lumped parameter (this time via the so called saddle-node bifurcation).
We now turn to the CME approach to this reaction system (1). If in a small volume such as that of a cell, the number of X is sufficiently small, its concentration fluctuations become significant[6]. The dynamics of reaction (1) then is stochastic, which should be described in terms of a master equation, also known as a birth-death process in the theory of Markov processes[7].
The system is represented by a discrete random variable nX(t): the number of X at time t (0 ≤ nX < ∞). Let P(k, t) = Pr{nX(t) = k}, and we have
| (3) |
where
and
Here V is the volume of the reaction system. It is a very important parameter of the model. The basic rule is still the Law of Mass Action: the rate of one step reaction , when there are k + 1 number of X molecules, is β1b(k + 1)/V. This gives the above last term. Similarly, the rate of one step reaction , when there are k number of X molecules, is α1ak(k − 1)/V2.
For complex biochemical reactions, master equation like this in general cannot be solved analytically. Various algorithms exist for simulating its stochastic trajectories[8]. For the above specific example, however, the exact stationary probability distribution to (3), i.e., after the system reaches stationarity, can be found as [9–10]:
| (4) |
where C0 is a normalization constant such that . The number of X molecules still fluctuates in the steady state. We note that for large V,
in which
μ = α2β1b/(α1a)2, , and C1 = ln C0. Therefore in terms of the concentration x = k/V, we have the probability distribution f(x) = V P(Vx):
| (5) |
| (6) |
Therefore, the stationary probability distribution of the concentration of X:
| (7) |
where
| (8) |
is independent of V. It is easy to verify that φ(x) is at its extrema exactly when the ODE (2) is at its fixed points. The function φ(x) can be thought as a “landscape” for the nonlinear chemical reaction system.
Closed System, Detailed Balance and Chemical Equilibrium
A chemical equilibrium is reached in the reaction system (1) when
| (9) |
This leads to the equilibrium condition that
| (10) |
In term of the two model parameters μ and σ introduced above, this equilibrium (also called detailed balance) condition is expressed as
| (11) |
This equation has a very strong thermodynamic meaning: the term ln(σ/μ) = ΔG/(kBT) is the chemical potential difference between A + B and C. If one considers A + B and C as two nodes in a circuit, then ΔG is the potential between them. When ΔG ≠ 0, there exists a nonequilibrium chemical driving force exerted on the reaction system.
Mathematically, the ODE (2) can be simplified. Let u = α2x/(α1a) and τ = (α1a)2t/α2, then (2) becomes
| (12) |
in which μ, σ > 0. If σ = μ, the right-hand-side of (12) becomes −(u2+μ)(u−1). There is only one unique fixed point, i.e., ueq = 1, the equilibrium point. This result is general. For equilibrium system, the steady state distribution obtained from the CME is always uni-modal, corresponding to the unique fixed point obtained from the Law of Mass Action ODE[9,11].
Nonequilibrium Steady State, Gaussian Approximation, and Multiscale Dynamics
When σ ≠ μ, the chemical reaction system is not in detailed balance. In this case, there is a continuous conversion of chemical energy to heat, even in the steady state. Therefore, there is a continuous production of entropy due to the conversion of more useful chemical energy to less useful heat. The entropy production rate
| (13) |
The nonequilibrium steady-state (NESS) has a net flux in the overall reaction A + B → C:
| (14) |
It is easy to show that the epr in (13) is always positive in the NESS. This result should be compared with “power = current × voltage” being always positive in a stationary electrical circuit.
For certain parameter values, say μ = 0.25 and σ = 0.01, the landscape function φ(x) in (8) has two minima and one maximum in-between:
| (15) |
It is easy to see that the root of u3 + μu = u2 + σ is precisely the extrema of φ(x) where
| (16) |
Therefore, the nonlinear chemical reaction system is bistable. The dynamics of the system exhibits multiple time scale: the relaxation within each “well” and transitions between the two wells. The former can be accurately described by a Gaussian (linear) random process. The latter, as two-state transitions, is on a much longer time scale.
It can be shown, according to the CME, that for a closed nonlinear chemical reaction system, its stationary distribution has a unique peak, the equilibrium[9,11]. Furthermore, the fluctuating dynamics, i.e., the stationary stochastic process in equilibrium is statistically time reversible[12]. These theoretical results indicate that complex behavior such as chemical bistability indeed can only occur in a “living system” with dissipation, i.e., useful chemical energy is converted into heat, and the process sustains a self-organizing complex dynamical system[13–14].
Multiscale Dynamics and the Keizer’s Paradox
Every CME model contains the parameter V, the volume of the reaction system. When the number of molecules, N, and V → ∞, the mathematical solution to the CME agrees with that from the Law of Mass Action which describes concentration x = N/V[1–2]. For most biochemical models, one might also be interested in the stationary behavior of the solution to the CME. This represents all the numbers of molecules in a reaction system, which are statistically independent of time, with stationary number fluctuations due to the biochemical reactions. One naturally identifies this with the homeostasis of a cell. Mathematically, this means one is interested in the limit of t → ∞. Hänggi et al.[15] and Baras et al.[16] correctly pointed out, however, there is a delicate computational issue of V (and N) → ∞ and t → ∞ and changing the order of the limits can lead to different mathematical predictions. This non-exchangability between V → ∞ and t → ∞ has been named Keizer’s paradox. One needs to be extra careful in dealing with the steady state behavior of a CME model.
This issue has been re-examined recently[11,17] in more details. It is shown to be intimately related to the multiple time scales of the bistability. The transition rates between the two states of a bistable system are exponentially small with increasing V: ∝ e−αV where α is a positive constant.
One naturally would like to approximate the CME in terms of a Fokker-Planck equation (second order PDE). The Fokker-Planck approximation of the CME has been discussed in several treatises (e.g., p. 116 of [18]). The approach is similar to the diffusion approximation theory for Boltzmann equation (Subsections 3.2 and 3.3 of [18]). Keizer also discussed multiple steady-states in biochemical reaction systems. However, the consequence of the multi-stability with diffusion approximation has not been fully discussed. van Kampen has repeatedly emphasized that the Fokker-Planck approximation can be obtained for master equations only with small individual jumps. A more sophisticated treatment of the Fokker-Planck approximation for master equation was given in terms of the Ω-expansion (Ch. 10 of [10]). This theory provides a more satisfying approximation for the stochastic relaxation in the limit of large V. However, it does not address how to obtain the stationary distribution with multistability. Computing such a stationary distribution is a major challenge.
3 Stochastic Bistability in the CME
In the previous section we stated that for sufficiently large V, the CME gives a stationary probability distribution for the numbers of all the dynamical species, which is in complete agreement with the prediction from the Law of Mass Action. A bistable system according to the Law of Mass Action, thus, corresponds to a bimodal distribution in the CME. The converse is not true, however. In recent years, there have been increasingly more examples showing that nonlinear biochemical reaction systems with macroscopic unistability can exhibit bistable behavior in a small volume. These results have important implications to cellular biochemistry. We shall give one example: the phosphorylation-dephosphorylation cycle (PdPC) with autocatalytic kinase[19]:
| (17) |
If we use x to denote the fraction of the phosphorylated E*, then according to the Law of Mass Action:
| (18) |
where k̃1 = k1EtcT, k̃−1 = k−1EtcD, Et is the total concentration of E and E*, cT and cD are ATP and ADP concentrations. (18) has two steady states, only one is positive and chemically meaningful. Hence there is no bistability in macroscopic size reaction system, with any parameters.
However, if the exactly same nonlinear PdPC is in a small reaction volume such as a cell, then according to the CME, the stationary probability distribution for the number of E* is
| (19) |
where k̂i = k̃i/V, i = ±1. C is a normalization factor.
It is easy to check that the distribution in (19) has two peaks, one at and the other at :
| (20) |
It is usually not an integer. Hence it exhibits stochastic bistability in a small volume.
4 Biochemical Bistability in a Cell and Epigenetic Inheritance with a Distributive Code
Since the discovery of DNA double helix, it has been well understood that DNA replication is the molecular basis of biological inheritance. However, in addition to DNA based inheritance, epigenetic inheritance has become an increasingly important concept in cell differentiation, stem cell research, as well as bacterial persistence[20]. Current research has been focusing on several specific molecular processes as the possible “code” for epigenetics, e.g., histone acetylation[21] and DNA methylation[22–23]. One of the key issues is that the code has to be sufficiently stable. This leads researchers to look for specific covalent modifications of transcriptional regulation apparatus.
However, specific covalent modifications might not be necessary in some cases. According to the theory of the CME, the stability of a state of a biochemical reaction system, i.e., the peak in the stationary distribution, is due to the biochemical reaction network[24]. In other words, the epigenetic code could be distributive, namely, properties such as state stabilities are the outcome of the collective behavior of many components of a biochemical network[23]. Therefore, detailed molecular mechanism(s) aside, the nonlinear biochemical reaction network(s) as the foundation of cellular epigenetics has to be valid.
Ptashne has recently re-emphasized the importance of heritability in the term of “epigenetics”[25]. We shall point out that the states of bi- or multistable nonlinear biochemical reaction systems, as defined above, naturally give rise to heritability. It is important to recall that the function φ(x) above is independent of V, and the variable x is the concentration. Hence, assuming there is no specific mechanism of regulating the production of molecule X, if the system’s volume is increased, the concentration x will go down. However, the nonlinear dynamic nature of the network automatically regulates the system and the steady state concentration of X is regained. Thus, as long as the volume of the system is slowly increasing in the synthesis phase of the cell cycle, the concentrations of all the key biochemical species (i.e., transcriptional regulators) are always maintained at its steady state value. Only when the volume change occurs in short time period and the amount of change is sufficiently large, there would be a chance that the system “jumps” into another basin of attraction (Fig. 1). If the basins of attraction of states are broad, then a daughter cell will still be in the same state as the parent cell without the need for any additional signal and regulation.
Fig. 1.
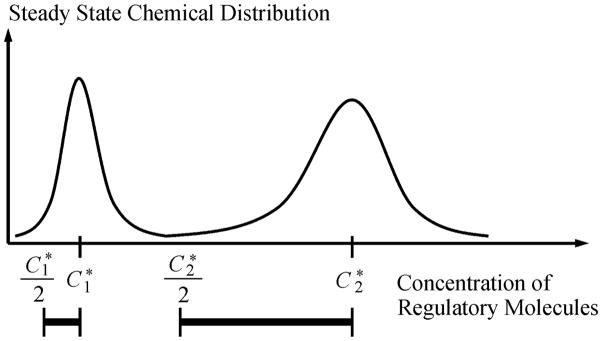
Schematics showing how two biochemical states of a nonlinear biochemical reaction system can be inheritable if the volume of the reaction system is increased, and then divided into two. Note that the abscissa is concentration, not number of molecules. In the figure, an increase in volume with a factor of 2, corresponding to a decrease of concentration to one half, will still maintain the system in its original attractors. Division does not change the concentration.
5 Computational Challenges from the Chemical Master Equation
In the theory of the CME, the dynamics of a biochemical reaction system, in a small volume, is represented by a multi-dimensional, integer-valued stochastic jump process in 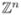 . The process is a discrete-state, continuous-time Markov process. As any Markov process, it can be mathematically characterized either in terms of its ensemble of stochastic trajectories, or by its probability distribution as function of time. These correspond to the stochastic differential equation and the Fokker-Planck equation representations of a Brownian dynamics. The CME is the differential equation for the probability distribution; the stochastic trajectory is defined by the well-known Gillespie algorithm. In analyzing a CME model, these two approach complement to each other.
. The process is a discrete-state, continuous-time Markov process. As any Markov process, it can be mathematically characterized either in terms of its ensemble of stochastic trajectories, or by its probability distribution as function of time. These correspond to the stochastic differential equation and the Fokker-Planck equation representations of a Brownian dynamics. The CME is the differential equation for the probability distribution; the stochastic trajectory is defined by the well-known Gillespie algorithm. In analyzing a CME model, these two approach complement to each other.
One type of chemical reaction systems, the single molecules or uni-molecular reaction system, has been extensively studied in the past. It is important to note that such systems are linear chemical reaction systems. Since all the molecules in uni-molecular reaction systems are statistically independent, it can be represented by either the particle-state-tracking (PST) algorithm or particle-number-tracking (PNT) algorithm[26]. The simulation can also be carried out approximately, but satisfactorily, by a continuous model of Langevin dynamics[27]. There is no multistability in such systems; nor complex dynamics.
The difference between PST and PNT is as follows: one either considers the discrete states of the particles in the simulation, or considers the number of particles in a particular state. These two approaches correspond precisely to the Lagrangian and Euler descriptions of fluid particles — in terms of trajectories of particles and in terms of the density[28]. In the current research on stochastic simulation of biochemical reaction systems, these correspond to the StochSim/MCell[29] and the StochKit, respectively. The Langevin approximated algorithm is closely related to the linear noise approximation (LNA)[30]. The LNA can be only valid within each “peak” region, i.e., a basin of attraction, of the CME. For nonlinear reaction systems with multi-stability, the Keizer’s paradox can occur which invalidates the Langevin approximation for the longer time scale dynamics.
On more general terms, there are many reasons to seek accurate solution to the CME directly, although much has been learned about the overall probabilistic landscape of many biochemical networks through stochastic simulations (Gillespie, StochSim/MCell, and StochKit) and approximated continuous models based on stochastic differential equations. First, details of the topological features and their quantification such as the existence and location of basins of attraction, craters, peaks, and saddle points of various dimensions, their widths, breadth, and depths on the probabilistic landscape, as well as their possible biological implications such as the inheritable epigenetic state arising from the properties of the network are largely unexplored. This is true even for simple reaction systems such as the 2-dimensional Schnakenberg model[31], which is only slightly more complex than the 1-dimensional Schlögl model discussed above, as there are no general exact probabilistic solutions available yet. Second, accurate solution to the CME problems can facilitate development of approximation methods that are capable of solving large-size problems. There is a large body of studies on theoretical approaches approximating the CME through the Fokker-Planck, and equivalently Langevin, equations. For effective design of these models and efficient computations of accurate solutions to large biochemical systems, it is essential to have some a priori knowledge of the ground truth. Third, perhaps most importantly, an accurate solution to the CME of simpler model systems can reveal important insights into basic principles on how biological networks function and how they respond to various environmental perturbations. A shining example of studying complex systems using manageably simple models is the study of protein folding. Models such as two- and three-dimensional lattice self-avoiding walks with only hydrophobic and polar (HP) interactions allow complete enumeration of all feasible conformations and calculation of exact thermodynamic parameters for molecules with short chain lengths. They have played important roles in elucidating the principles of protein folding[32], including collapse and folding transitions[33–40], influence of packing on secondary structure and void formation[41–44], the evolution of protein function[45–46], nascent chain folding[47], and the effects of chirality and side chains[44].
6 State Space of the Chemical Master Equation and Exact Calculation of Steady State Probability Landscape
The state space of the CME is that of M-dimensional vectors with non-negative integers, which represents the copy numbers of molecular species in a network; M is the number of dynamic species. These states are microscopic in nature, as they provide a detailed, chemical amount of each and every molecular species. An important advantage of treating these microscopic states of copy numbers explicitly is that both linear and nonlinear reactions (such as synthesis, degradation, bimolecular association, and polymerization) can be modeled as Markovian transitions between two microstates, one reaction at a time. Here the transition rates between states are determined by the intrinsic propensities of the reaction, and the copy numbers of molecules involved.
For any biochemical systems beyond the simplest toy problems, a challenging issue in obtaining an accurate solution to the CME is the characterization of the state space. That is, what are all the possible combinations of concentrations (or copy numbers) of the molecular species for a given set of reactions represented by a network? An accurate description of the state space is a prerequisite for computationally obtaining solutions to the CME. In principle, the size of the state space grows exponentially with the number of molecular species and the copy numbers of molecules in the system. For example, if there are 16 molecular species in a network, and there are only a total of 33 copies of molecules in the whole system, one can estimate somewhat naively the upper bound of the state space as (33 + 1)16 = 3.19 × 1024. Note the +1 counts the zero copy as a state. This is an astronomic number that is well beyond what can be computed with current and for-seeable future computing technology.
Below we discuss the enumeration of the state space of CME and exam how to obtain exact steady state solutions to the CME for biochemical systems with small and moderate sizes.
Optimal Enumeration of State Space
Although in principle the size of the state space grows exponentially with the number of molecular species and the copy numbers of molecules in the system, all is not lost. There are two important observations about general biochemical networks. First, the Markovian transition matrix is very sparse. For any given microstate, the number of reactions that could occur in a short time interval is small, which could be bounded by the total number of possible reactions in a biochemical network. Second, as an open system, molecules are synthesized and degraded constantly. However, the number of molecules that can be synthesized is never infinite, as synthesis is constrained by the time and resources required. With these two considerations, an algorithm to enumerate the state space of CME has recently been developed[48]. The algorithm is optimal in memory requirement, as it allows the enumeration of all states that can be reached from a given initial state, without including any irrelevant states. In addition, all possible transitions are recorded, and no infeasible transitions are attempted. The resulting transition matrix based on the enumerated state space is compact without redundant information, and is minimal in size. In addition, its computational time is also optimal[48].
Exact Calculation of Probability Distribution of the Steady State
Once the states reachable from a given initial state are enumerated, the rates of chemical reactions connecting two of these states can be computed. For example, we can study a simplified model of protein-DNA interaction. For the process of two protein monomer (ProteinA) dimerize and bind to a segment of DNA (GeneB), we can use the simplified model below. If we denote the rate of the reaction that brings the before-state i to the after-state j as aj,i, we have for the third order reaction:
with the following reaction rate coefficient aj,i:
where b is the intrinsic reaction rate which contains hidden systems volume V, npA, i is the copy number of protein A in state i, and ngB, i is the copy number of unbound gene B. Here the combination number of the protein for this second order reaction is . Note that in addition to the volume V, there is a factor of 2 difference between the intrinsic reaction rate here and the macroscopic rate constant discussed in Section 2.
Once the full reaction rate matrix A = {aj,i} ∈ ℝn×n is filled with computed rates, the chemical master equation can be written in a matrix-vector form as:
| (21) |
Here the matrix A represents the infinitesimal generator of a continuous time Markov process. The diagonal elements aii is set as: aii = − Σi≠j aj,i, and all off-diagonal elements are nonnegative. The analytical solution at time t to (21) can be written as a matrix exponential:
| (22) |
The matrix eAt is the Markovian state transition probability matrix with time duration t. We can also obtain its discrete equivalent M as[40]:
| (23) |
where I is the identity matrix, Δt is a small time interval during which one reaction occurs. When the system has reached the steady state, the probability landscape over the enumerated states P can be computed by solving the equation:
Here P can be obtained with an iterative solver such as that based on the successive over-relaxation (SOR) technique[49]. Alternatively, since P for the steady state corresponds to the eigenvector of M with eigenvalue 1.0, one can obtain P by using eigenvector method such as the Arnoldi method[50], as done in [48].
By examining computationally the stochastic behavior of genetic circuits for wild type and mutant networks, and by studying the probabilities of rare events, one can gain further understanding of the regulation mechanism of genetic circuits, its system stability against perturbation (such as fluctuations in nutritional conditions), and its robustness against genetic mutations (such as those due to DNA damage)[51].
7 Two Examples of Stochastic Biochemical Systems and Their CMEs
In this section we give two examples on how exact stationary probability landscapes of a biochemical network can be computed from its CME. The CME, of course, gives more than just a stationary distribution, but solving the steady state is almost obligatory in any analysis of mathematical models.
Toggle Switch
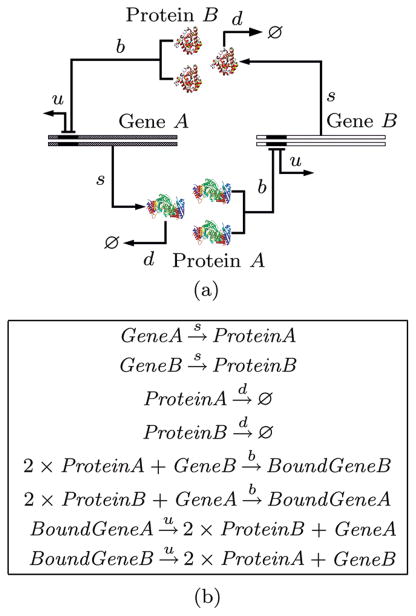
In Section 3, we already discussed how bistability arises from stochasticity. Another example is the well studied genetic toggle-switch system. This is a small network consisting of two genes, A and B, each inhibits the other (Fig. 2). It was the first synthetic network constructed in a wet lab from two repressible promoters arranged in a mutually inhibitory network in Escherichia coli by Gardner et al.[52]. It is flippable between two stable states by chemical or thermal induction and exhibits an ideal switching threshold. This toggle switch forms a synthetic cellular memory unit[52]. Although this is the simplest network with bistability that can already be identified from ODE models based on the Law of Mass Action, important questions such as switching probability between the “on” and “off” states requires a treatment of the stochasticity. Although there have been great recent progresses in deriving analytical solutions[53–56], they are applicable under special conditions, such as fast transition between the on- and off-states, or overall small noise associated with high concentrations. With the algorithm for state enumeration, the steady state landscape probability of the toggle-switch can be solved exactly for models with arbitrary parameter specifications.
Fig. 2.
Model of a toggle switch. (a) The network model and the reaction rates. Single copies of gene A and gene B encode protein products. Two protein monomers can repress the transcription of the other gene. The synthesis of protein product of gene A and gene B depends on the bound or unbound state of the gene. (b) The chemical reactions of the 8 stochastic processes involved in the toggle-switch system. The reaction rates include s for protein synthesis, d for protein degradation, b for protein-gene binding, and u for protein-gene unbinding (adapted from [48]).
Epigenetic Switch in Phage Lambda
Exact solution of the CME can also be obtained for larger systems in which biological phenomenon are modeled more realistically. An example is the epigenetic switch of phage lambda. Phage lambda is a virus that infects E. coli bacteria. It is the system in which gene regulation was first studied. Upon infection, phage lambda can choose two different life styles. In the lysogenic pathway, the DNA of phage lambda becomes integrated into the chromosome of the host, and can replicate for many generations along with the host. Upon adverse environmental perturbations such as UV irradiation, phage lambda switches from the lysogenic pathway to the lytic pathway, in which it uses the protein synthesis machinery of the host, and replicate to 100s of copies, which leads to the burst of the host cell. The lytic pathway offers critical evolutionary advantage for phage lambda to survive, as it allows phage to escape from hopelessly distressed E. coli host cells. In phage lambda, a gene regulatory circuit controls the switching between the maintenance of the lysogenic state and the induction of the lytic state. The CME model analysis clearly demonstrates the idea of a distributive epigenetic code. As a paradigm for understanding cell development, phage lambda has been extensively studied, with the molecular components and reaction rates well characterized (see the seminal book by Ptashne[57]). The key components of the switch of the genetic circuits and their wirings can be summarized in Fig. 3. There are three operators (OR1, OR2, and OR3) and two promoters (Pr and Prm). These are used to control the transcription of CI and Cro proteins, which dimerize and bind to the operator sites with different affinity and inhibit the expression of each other[57].
Fig. 3.
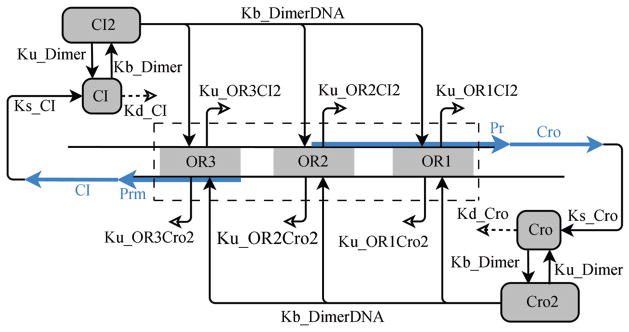
Phage λ switching network. Reactions including binding and unbinding, synthesis and degradation, dimerization are labeled as arrows, along with the corresponding kinetic constants (adapted from [51]).
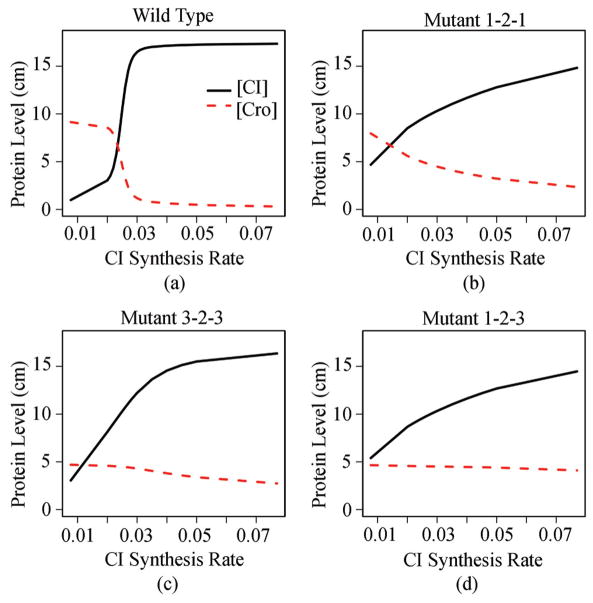
The importance of stochasticity in the genetic circuit of lambda phage is well recognized, and its effects have been studied using stochastic simulations[58] and stochastic differential equations[24,59]. The steady state probability landscape of the CME model based on the network depicted in Fig. 3 can be solved directly[51]. Fig. 4 shows the probability landscape under several physiological conditions when the system is in the lysogenic state, in transitory switching state, and in lytic state[51]. Fig. 5 shows the phase diagram of concentrations of CI and Cro at different CI synthesis rate.
Fig. 4.
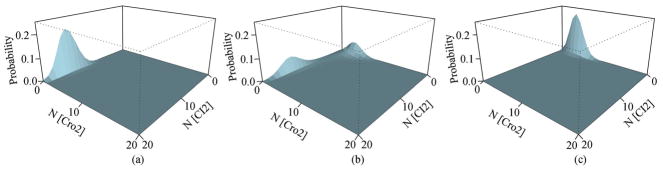
Lysogenic and lytic states and CI synthesis rate. (a) Lysogenic state, Ks CI=0.045/s. (b) The switching state, Ks CI=0.0245/s. (c) Lytic state, Ks CI=0.0077/s. X and Y axes are copy numbers of CI and Cro dimers; and Z axis is the marginal probability (adapted from [51]).
Fig. 5.
Relative CI and Cro dimer levels for wild type and mutant lambda phage. The lysogenic state has high CI (solid line) concentration, and the lytic state has high Cro (dashed line) concentration. Wild type lambda phage has a well-behaving switch, while mutants are all leaky (adapted from [51]).
By examining computationally the stochastic behavior of genetic circuits for wild type and mutant network, and by studying the probabilities of rare events, one can gain further understanding of the regulation mechanism of genetic circuits, its system stability against perturbation (such as fluctuations in nutritional conditions), and its robustness against genetic mutations (such as those due to DNA damage)[51].
8 Methods for State Space Simplification
For large systems in which enumeration is no longer feasible, one approach for numerical computation is to reduce the large number of microstates to a smaller finite number[60].
Finite State Projection
Munsky and Khammash made two key observations about projecting the high dimensional state space to a lower dimensional finite space by including only a subset of the original states. Denote two sets of indice of the states being chosen as J1 and J2, and assume J1 ⊆ J2. The reduced rate matrix obtained by selecting states in J1 and J2 are AJ1 and AJ2, respectively. The first observation is:
| (24) |
This relation implies that by increasing the size of the selected subset of states, the approximation improves monotonically. Second, if one obtains a reduced state space by selecting states contained in the index set J and if 1T etAJPJ (0) ≥ 1 − ε for ε > 0 and t ≥0, then:
| (25) |
That is, starting with the initial probability of the reduced vector PJ(0), compute the probability vector in the reduced space etAJPJ(0) at time t using the reduced rate matrix AJ. If the inner-product of this vector for time t with 1 is no less than 1 − ε, then the error of this vector with the projected true vector PJ(t) from the true probability P(t) is no more than εI. This inequality guarantees that the approximation obtained with reduced state space will never exceed the actual solution, and its error is bounded by ε[60].
These key observations led to the Finite State Project Algorithm, which iteratively adds new states to an initial reduced state space, until the approximation error is within a prescribed bound[60]. Munsky and Khammash further extended the original Finite State Projection method[61], and recommends running a few steps of stochastic simulation to obtain the initial probability vector P(0) that is non-sparse. However, there are no generally applicable strategies as to what states to add to a finite projection to most efficiently improve the approximation accuracy.
Krylov Subspace Method
The analytical solution to the CME can be expressed in the form of a matrix exponential P(t) = eAtP(0). As discussed before, the rate matrix A has a very large dimension but is sparse. An alternative approach to reduced the state space is to convert the problem of exponentiating a large sparse matrix to that of exponentiating a small dense matrix in the Krylov subspace 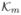 [62]:
[62]:
| (26) |
The idea is that the Krylov subspace used is of a very small dimension of m = 30–60. Denoting ||·||2 as the 2-norm of a vector or matrix, the approximation then becomes P(t) ≈ ||P(0)||2Vm+1 exp(tH̄m+1)e1, where e1 is the first unit basis vector, Vm+1 is a (m +1)×(m +1) matrix formed by the orthonormal basis of the Krylov subspace, and H̄m+1 the upper Hessenberg matrix, both computed from an Arnoldi algorithm[63]. The error can be bounded by
One only needs to compute explicitly exp(H̄m+1t). This is a simpler problem as m is much smaller. A special form of the well-known Padé rational of polynomials instead of Taylor expansion is used[64–65]:
where and . The Expokit software by Sidje provides an excellent implementation of this method[65]. This approach has been shown to be very effective in studying large dynamic system (n = 8.0 × 105) such as protein folding[40] and signaling transmission in macro-molecular assembly of GroEL-GroES[66].
The Krylov subspace method concurrently evaluate the matrix exponential. The overall scheme can be expressed as follows:
| (27) |
in which the evaluation is from right to left. Here {τi} are size of time steps, and K is the total number of time steps[62].
MacNamara et al. further extends the Krylov subspace method by splitting the rate matrix A. Based on the reachability criteria, one can divide the states into the “fast partition” and the “slow partition”[67]. Here the condition is that two states belong to the same subset of the fast partition if and only if one can be reached from the other via a sequence of finite fast reactions[67]. Correspondingly, the matrix can be splitted into two:
where Af corresponds to the fast CME, and As corresponds to the slow CME, and one has:
and
With this deliberate separation, both Af and As maintain the important property of being infinitesimal generators of continuous time Markov processes by themselves[67]. With more elaborated splitting scheme for aggregation of Markov processes, the Krylov subspace projection method have been shown to be computationally very efficient[62].
Approximation by Continuous Stochastic Differential Equation
An effective approach to study biochemical networks whose chemical master equations cannot be solved directly is to approximate them with stochastic differential equations. One widely used approach is that of the Fokker-Planck-Langevin model[10]. The Langevin equation for concentration flux consists of a drift term and a diffusion term. The drift term models the macroscopic deterministic component of the system. It reflects the time-dependent evolution of the mean concentrations of the molecular species. The diffusion term models the intrinsic stochasticity of the system. The basic form of a Langevin, stochastic differential equation is:
| (28) |
Here X is the vector of concentrations of molecular species in the reaction system, μ(X) the drift term, and the second term is the diffusion term. Here 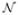 (0, 1/dt) is a vector of one-dimensional Gaussians, with zero mean and 1/dt variance. The coefficient σ(X) controls the amplitude of the Gaussian noise. It can be either a function of X or a constant. The key issue in developing Langevin models for biochemical networks is to determine μ(X) and σ(X). When σ(X) is a vector of constants, one adjusts its values so the variance of the Gaussian noise produce the correct fluctuations in the system[10].
(0, 1/dt) is a vector of one-dimensional Gaussians, with zero mean and 1/dt variance. The coefficient σ(X) controls the amplitude of the Gaussian noise. It can be either a function of X or a constant. The key issue in developing Langevin models for biochemical networks is to determine μ(X) and σ(X). When σ(X) is a vector of constants, one adjusts its values so the variance of the Gaussian noise produce the correct fluctuations in the system[10].
One of the most important issues to keep in mind when developing Fokker-Planck-Langevin approximations for a CME is the Keizer’s paradox previously discussed. For dynamical system with a single, globally attracting attractor, however, this is not an issue. We shall use the Schnakenberg model to demonstrate how well the Langevin approach works. Originally developed for studying the limit cycle behavior in a simple chemical reaction system[31,69], the Schnakenberg model is a simple system with two reacting components and three reversible reactions:
| (29) |
where X and Y are reacting species of the system, and A and B are external reactants whose concentrations (or copy numbers) are fixed constants. Each reaction has a corresponding microscopic reaction rate. The fixed copy numbers or concentrations of A and B can be adjusted, which lead to different behavior of the system. This simple system already produces complex behavior such as oscillation and has a single stable limit cycle (see [6, 70] for recent examples).
The macroscopic concentration obtained by solving the corresponding ODE model, the approximated steady state probability distribution obtained by integrating the Langevin model, and the exact probability distributions obtained by solving the chemical master equation[48] are shown in Fig. 6. At the parameter values of A = 10 and B = 50, the well-known oscillating limit cycle behavior of the Schnakenberg model can be seen in Fig. 6(a). At A = 20 and B = 40, the behavior of the system converges towards a fixed point (Fig. 6(b)). The landscapes of the steady state probability distributions obtained from solving the Langevin equation (Fig. 6(c)) and the chemical master equation (Fig. 6(e)) all show a crater, or a basin surrounded by a mountainous ridge for the parameter set of A = 10 and B = 50 (details not shown). This corresponds well with the limit cycle behavior observed in the ODE model. At A = 20 and B = 40, the landscapes show a single peak (Figs. 6(c) and 6(d)), which again corresponds well with the fixed-point behavior observed in the ODE model.
Fig. 6.
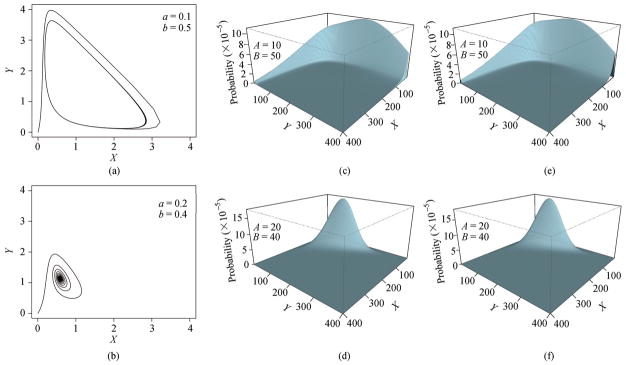
Calculated steady state probability distributions over different copy numbers of X and Y and the trajectories of evolving concentrations of X and Y of the Schnakenberg model. (a) and (b): Trajectories of evolving concentrations of X and Y according to the deterministic ordinary differential equation (ODE). Here (a) shows the well-known oscillating limit cycle behavior of the Schnakenberg model, and (b) shows the convergence towards a fixed point. The concentrations of A and B are set at values equivalent to the copy numbers used in stochastic models. (c) and (d): Reconstructed probability distributions over X and Y obtained from 200 000 simulations of the Langevin equation (LE). (e) and (f): Exact probability distributions over copy numbers X and Y obtained by solving the chemical master equation (CME). Two sets of copy numbers of (A, B) at (10, 50) and (20, 40) are used for the fixed parameters A and B (adapted from [68]).
As can be seen in Figs. 6, and 7, the model of Langevin equation approximates well the true probability landscape of the chemical master equation. This demonstrates that the diffusion term models the intrinsic stochasticity of the Schnakenberg model well.
Fig. 7.
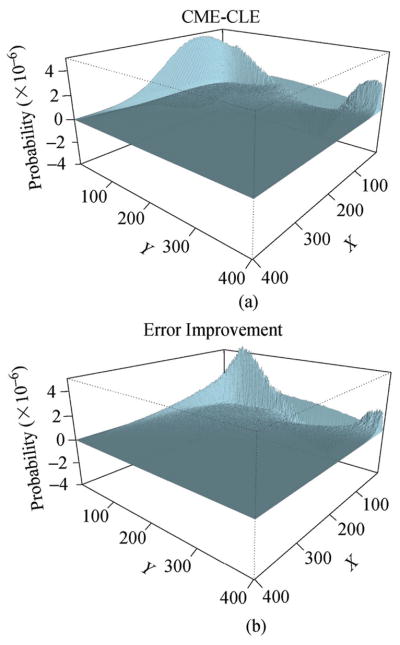
Comparison of errors between different steady state solutions of the Schnakenberg model. (a) Difference between the probability landscapes of the Langevin equation and that of the chemical master equation. This represents errors in the Langevin model. (b) The amount of the errors in (a) that are corrected by introducing explicitly a coupling term between X and Y (adapted from [68]).
Alternative models account for the stochasticity by replacing the diffusion term with a term for the variance-covariance between pairs of the molecular reactions[71], or between concentrations of different molecular species, without the explicit inclusion of a random process[72]. The magnitude of the covariance is determined by the Hessian matrix of the second-order partial derivative of the propensity functions of the reactions[71–72]. This inclusion of the second moments to account for the stochasticity is the basis of the stochastic kinetic model[71] and the mass fluctuation kinetic model (MFK)[72]. These models can model reactions involving one or two molecules well[71–72]. They are similar in spirit to the Fokker-Planck equation model of the CME as described in [73] by including a second moment term for better approximation, but are different from that of [73] as they are macroscopic in nature and do not involve any random processes.
Yet another approach is to directly model explicitly the stochastic coupling of the macroscopic concentrations of molecular species, in addition to the Gaussian noise of the original Langevin model[68]. The steady state probability landscape of the Schnakenberg model resulting from this approach is shown in Fig. 7. Significant improvement after incorporating the coupling term can be seen in Fig. 7.
Remark
The complex nature of the stochastic dynamics arising from biochemical networks bears much resemblance to another complex system, namely, that of protein folding. Both have very large space of micro-states, and both can be modeled by transitions between micro-states using master equations (for master equation approach in protein folding studies, see [37, 39–40]). However, these two systems differ in several important aspects. First, while protein folding can be modeled as a relaxation process towards the equilibrium state, biochemical networks are intrinsically open, with synthesis and degradation of molecules an integral part of the system, hence there are no equilibrium states. Instead, one frequently seeks to study the non-equilibrium steady state. Second, once the energy of a protein conformation is known, the relative probability of its sequence adopting this conformation in the equilibrium state can be calculated from the Boltzmann distribution, without the need of knowing all other possible conformations and their associated probabilities. In other words, the protein folding problem is local in the energy landscape. In contrast, it is not possible to calculate the relative probability of a specific microstate of copy numbers a priori without solving the entire CME, as the probability distribution of network states do not generally follow any specific analytical forms (no detailed balance and the existence of cycle fluxes). Third, transitions between microstates are clearly defined in biochemical networks by the reactions, whereas transitions between different protein conformations often technically depend on specific move sets, which are different in terms of allowable transitions between states and transition rates, although all such move-sets are developed with the goal to mimic physical movement of molecules.
9 Discussions and Outlooks
In this review, we have discussed the significance of the chemical master equation (CME) as a theoretical framework for modeling nonlinear, biochemical reaction networks inside cells, and the possible mechanism of cellular states, or attractors, as the inheritable phenotypes with a distributive epigenetic code. The validity of such a grand theory requires close comparisons between theoretical predictions with experiments. Solving a given CME, however, is a computationally challenging task at the present time. We have outlined several key difficulties, as well as some of the progresses that have been made so far.
In addition to the subject of studying algorithmic complexity, complex system, in a broady sense, is a major scientific problem of computer science and computational science[74]. One needs not to be reminded of the complex phenomena exhibited in the natural world of her/his surroundings. How to characterize and quantify such complex behavior is of great interests for understanding our physical and biological worlds. But what is complexity and how to define complex behaviors? Through studies of the CME, one seems to be able to gain some deeper understanding of the issues involved through concrete physical and biology examples. Recently, one of us has suggested that a key to mesoscopic complexity[75] is in the multi-stability with multiple time scale dynamics[76]. Nonlinear biochemical reaction systems in a cell-size volume can be a prototype for studying complexity.
Acknowledgments
We thank Professors Ping Ao, Bai-Lin Hao, Shou-Dan Liang, Kim Sneppen, Jin Wang, and Peter Wolynes for helpful discussions, and Youfang Cao for reading a draft of the manuscript.
This work is supported by US NIH under Grant Nos. GM079804, GM081682, GM086145, GM068610, NSF of USA under Grant Nos. DBI-0646035 and DMS-0800257, and ‘985’ Phase II Grant of Shanghai Jiao Tong University under Grant No. T226208001.
Biographies
 Jie Liang is a professor in the Department of Bioengineering at the University of Illinois at Chicago, and holds a visiting position at Shanghai Jiao Tong University. He received his B.S. degree from Fudan University (1986), MCS and Ph.D. degree from the University of Illinois at Urbana-Champaign (1994). He was an NSF CISE postdoctoral research associate (1994~1996) at the Beckman Institute and National Center for Supercomputing and its Applications (NCSA) in Urbana, Illinois. He was a visiting fellow at the Institute of Mathematics and Applications at Minneapolis, Minnesota in 1996, and an Investigator at SmithKline Beecham Pharmaceuticals in Philadelphia from 1997 to 1999. He was a recipient of the NSF CAREER award in 2003. He is a fellow of American Institute of Medical and Biological Engineering, and served as regular member of the NIH Biological Data Management and Analysis study section. His research interests are in biogeometry, biophysics, computational proteomics, stochastic molecular networks, and cellular pattern formation. His recent work can be accessed at (http://www.uic.edu/~jliang).
Jie Liang is a professor in the Department of Bioengineering at the University of Illinois at Chicago, and holds a visiting position at Shanghai Jiao Tong University. He received his B.S. degree from Fudan University (1986), MCS and Ph.D. degree from the University of Illinois at Urbana-Champaign (1994). He was an NSF CISE postdoctoral research associate (1994~1996) at the Beckman Institute and National Center for Supercomputing and its Applications (NCSA) in Urbana, Illinois. He was a visiting fellow at the Institute of Mathematics and Applications at Minneapolis, Minnesota in 1996, and an Investigator at SmithKline Beecham Pharmaceuticals in Philadelphia from 1997 to 1999. He was a recipient of the NSF CAREER award in 2003. He is a fellow of American Institute of Medical and Biological Engineering, and served as regular member of the NIH Biological Data Management and Analysis study section. His research interests are in biogeometry, biophysics, computational proteomics, stochastic molecular networks, and cellular pattern formation. His recent work can be accessed at (http://www.uic.edu/~jliang).
 Hong Qian received his B.S. degree in astrophysics from Peking University. He worked on fluorescence correlation spectroscopy (FCS) and single-particle tracking (SPT) and obtained his Ph.D. degree in biochemistry from Washington University (St. Louis). His research interests turned to theoretical biophysical chemistry and mathematical biology when he was a postdoctoral fellow at the University of Oregon and at the California Institute of Technology. In that period of time, he worked on protein thermodynamics, fluctuations and folding. Between 1994 and 1997, he was with the Department of Biomathematics at the UCLA School of Medicine, where he worked on the theory of motor proteins and single-molecule biophysics. This work led to his current interest in mesoscopic open chemical systems. He joined the University of Washington (Seattle) in 1997 and is now professor of applied mathematics, and an adjunct professor of bioengineering. His current research is in stochastic analysis and statistical physics of cellular systems. His recent book “Chemical Biophysics: Quantitative Analysis of Cellular Systems”, co-authored with Daniel A. Beard, has been published by the Cambridge University Press.
Hong Qian received his B.S. degree in astrophysics from Peking University. He worked on fluorescence correlation spectroscopy (FCS) and single-particle tracking (SPT) and obtained his Ph.D. degree in biochemistry from Washington University (St. Louis). His research interests turned to theoretical biophysical chemistry and mathematical biology when he was a postdoctoral fellow at the University of Oregon and at the California Institute of Technology. In that period of time, he worked on protein thermodynamics, fluctuations and folding. Between 1994 and 1997, he was with the Department of Biomathematics at the UCLA School of Medicine, where he worked on the theory of motor proteins and single-molecule biophysics. This work led to his current interest in mesoscopic open chemical systems. He joined the University of Washington (Seattle) in 1997 and is now professor of applied mathematics, and an adjunct professor of bioengineering. His current research is in stochastic analysis and statistical physics of cellular systems. His recent book “Chemical Biophysics: Quantitative Analysis of Cellular Systems”, co-authored with Daniel A. Beard, has been published by the Cambridge University Press.
Contributor Information
Jie Liang, Email: jliang@uic.edu.
Hong Qian, Email: qian@amath.washington.edu.
References
- 1.Kurtz TG. The relationship between stochastic and deterministic models for chemical reactions. J Chem Phys. 1972;57(7):2976–2978. [Google Scholar]
- 2.Beard DA, Qian H. Chemical Biophysics: Quantitative Analysis of Cellular Systems. London: Cambridge Univ. Press; 2008. [Google Scholar]
- 3.Wilkinson DJ. Stochastic Modeling for Systems Biology. New York: Chapman & Hall/CRC; 2006. [Google Scholar]
- 4.Schlögl F. Chemical reaction models for non-equilibrium phase transition. Z Physik. 1972;253(2):147–161. [Google Scholar]
- 5.Murray JD. Mathematical Biology: An Introduction. 3. New York: Springer; 2002. [Google Scholar]
- 6.Qian H, Saffarian S, Elson EL. Concentration fluctuations in a mesoscopic oscillating chemical reaction system. Proc Natl Acad Sci USA. 2002;99(16):10376–10381. doi: 10.1073/pnas.152007599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taylor HM, Karlin SK. An Introduction to Stochastic Modeling. 3. New York: Academic Press; 1998. [Google Scholar]
- 8.Resat H, Wiley HS, Dixon DA. Probability-weighted dynamic Monte Carlo method for reaction kinetics simulations. J Phys Chem B. 2001;105(44):11026–11034. [Google Scholar]
- 9.Gardiner CW. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. 3. New York: Springer; 2004. [Google Scholar]
- 10.van Kampen NG. Stochastic Processes in Physics and Chemistry. 3. Amsterdam: Elsevier Science; 2007. [Google Scholar]
- 11.Vellela M, Qian H. Stochastic dynamics and nonequilibrium thermodynamics of a bistable chemical system: The Schlögl model revisited. J R Soc Interf. 2009;6(39):925–940. doi: 10.1098/rsif.2008.0476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Qian H, Qian M, Tang X. Thermodynamics of the general diffusion process: Time-reversibility and entropy production. J Stat Phys. 2002;107(5/6):1129–1141. [Google Scholar]
- 13.Schrödinger E. The Physical Aspect of the Living Cell. New York: Cambridge Univ. Press; 1944. What Is Life? [Google Scholar]
- 14.Nicolis G, Prigogine I. Self-Organization in Nonequilibrium Systems. New York: Wiley-Interscience; 1977. [Google Scholar]
- 15.Hänggi P, Grabert H, Talkner P, Thomas H. Bistable systems: Master equation versus Fokker-Planck modeling. Phys Rev A. 1984;29(1):371–378. [Google Scholar]
- 16.Baras F, Mansour MM, Pearson JE. Microscopic simulation of chemical bistability in homogeneous systems. J Chem Phys. 1996;105(18):8257–8261. [Google Scholar]
- 17.Vellela M, Qian H. A quasistationary analysis of a stochastic chemical reaction: Keizer’s paradox. Bull Math Biol. 2007;69(5):1727–1746. doi: 10.1007/s11538-006-9188-3. [DOI] [PubMed] [Google Scholar]
- 18.Keizer J. Statistical Thermodynamics of Nonequilibrium Processes. New York: Springer-Verlag; 1987. [Google Scholar]
- 19.Bishop L, Qian H. Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase. Biophys J. 2010 doi: 10.1016/j.bpj.2009.09.055. (in the press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kussell E, Kishony R, Balaban NQ, Leibler S. Bacterial persistence: A model of survival in changing environments. Genetics. 2005;169(4):1804–1807. doi: 10.1534/genetics.104.035352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Turner BM. Histone acetylation and an epigenetic code. Bioessays. 2000;22(9):836–845. doi: 10.1002/1521-1878(200009)22:9<836::AID-BIES9>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 22.Jones PA, Takai D. The role of DNA methylation in mammalian epigenetics. Science. 2001;293(5532):1068–1070. doi: 10.1126/science.1063852. [DOI] [PubMed] [Google Scholar]
- 23.Dodd IB, Micheelsen MA, Sneppen K, Thon G. Theoretical analysis of epigenetic cell memory by nucleosome modification. Cell. 2007;129(4):813–822. doi: 10.1016/j.cell.2007.02.053. [DOI] [PubMed] [Google Scholar]
- 24.Zhu XM, Yin L, Hood L, Ao P. Robustness, stability and efficiency of phage λ genetic switch: Dynamical structure analysis. J Bioinf Compt Biol. 2004;2(4):785–817. doi: 10.1142/s0219720004000946. [DOI] [PubMed] [Google Scholar]
- 25.Ptashne M. On the use of the word “epigenetic”. Curr Biol. 2007;17(7):R233–R236. doi: 10.1016/j.cub.2007.02.030. [DOI] [PubMed] [Google Scholar]
- 26.Mino H, Rubinstein JT, White JA. Comparison of algorithms for the simulation of action potentials with stochastic sodium channels. Ann Biomed Eng. 2002;30(4):578–587. doi: 10.1114/1.1475343. [DOI] [PubMed] [Google Scholar]
- 27.Fox RF. Stochastic versions of the Hodgkin-Huxley equations. Biophys J. 1997;72(5):2069–2074. doi: 10.1016/S0006-3495(97)78850-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lamb H. Hydrodynamic. New York: Dover; 1945. [Google Scholar]
- 29.Morton-Firth CJ, Bray D. Predicting temporal fluctuations in an intracellular signalling pathway. J Theoret Biol. 1998;192(1):117–128. doi: 10.1006/jtbi.1997.0651. [DOI] [PubMed] [Google Scholar]
- 30.Elf J, Ehrenberg M. Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Res. 2003;13(11):2475–2484. doi: 10.1101/gr.1196503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vellela M, Qian H. On Poincaré-Hill cycle map of rotational random walk: Locating stochastic limit cycle in reversible Schnakenberg model. Proc Roy Soc A: Math Phys Engr Sci. 2009 (in the press) [Google Scholar]
- 32.Dill KA, Bromberg S, Yue K, Fiebig KM, Yee DP, Thomas PD, Chan HS. Principles of protein-folding — A perspective from simple exact models. Prot Sci. 1995;4(4):561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Šali A, Shakhnovich EI, Karplus M. How does a protein fold? Nature. 1994;369(6477):248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
- 34.Socci ND, Onuchic JN. Folding kinetics of protein like heteropolymer. J Chem Phys. 1994;101:1519–1528. [Google Scholar]
- 35.Shrivastava I, Vishveshwara S, Cieplak M, Maritan A, Banavar JR. Lattice model for rapidly folding protein-like heteropolymers. Proc Natl Acad Sci USA. 1995;92(20):9206–9209. doi: 10.1073/pnas.92.20.9206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Klimov DK, Thirumalai D. Criterion that determines the foldability of proteins. Phys Rev Lett. 1996;76(21):4070–4073. doi: 10.1103/PhysRevLett.76.4070. [DOI] [PubMed] [Google Scholar]
- 37.Cieplak M, Henkel M, Karbowski J, Banavar JR. Master equation approach to protein folding and kinetic traps. Phys Rev Lett. 1998;80(16):3654–3657. [Google Scholar]
- 38.Mélin R, Li H, Wingreen N, Tang C. Designability, thermodynamic stability, and dynamics in protein folding: A lattice model study. J Chem Phys. 1999;110(2):1252–1262. [Google Scholar]
- 39.Ozkan SB, Bahar I, Dill KA. Transition states and the meaning of φ-values in protein folding kinetics. Nature Struct Biol. 2001;8(9):765–769. doi: 10.1038/nsb0901-765. [DOI] [PubMed] [Google Scholar]
- 40.Kachalo S, Lu H, Liang J. Protein folding dynamics via quantification of kinematic energy landscape. Phys Rev Lett. 2006;96(5):058106. doi: 10.1103/PhysRevLett.96.058106. [DOI] [PubMed] [Google Scholar]
- 41.Chan HS, Dill KA. Compact polymers. Macromolecules. 1989;22(12):4559–4573. [Google Scholar]
- 42.Chan HS, Dill KA. The effects of internal constraints on the configurations of chain molecules. J Chem Phys. 1990;92(5):3118–3135. [Google Scholar]
- 43.Liang J, Zhang J, Chen R. Statistical geometry of packing defects of lattice chain polymer from enumeration and sequential Monte Carlo method. J Chem Phys. 2002;117(7):3511–3521. [Google Scholar]
- 44.Zhang J, Chen Y, Chen R, Liang J. Importance of chirality and reduced flexibility of protein side chains: A study with square and tetrahedral lattice models. J Chem Phys. 2004;121(1):592–603. doi: 10.1063/1.1756573. [DOI] [PubMed] [Google Scholar]
- 45.Williams PD, Pollock DD, Goldstein RA. Evolution of functionality in lattice proteins. J Mole Graph Modelling. 2001;19(1):150–156. doi: 10.1016/s1093-3263(00)00125-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bloom JD, Wilke CO, Arnold FH, Adami C. Stability and the evolvability of function in a model protein. Biophys J. 2004;86(5):2758–2764. doi: 10.1016/S0006-3495(04)74329-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lu HM, Liang J. A model study of protein nascent chain and cotranslational folding using hydrophobic-polar residues. Prot Struct Funct Bioinf. 2008;70(2):442–449. doi: 10.1002/prot.21575. [DOI] [PubMed] [Google Scholar]
- 48.Cao Y, Liang J. Optimal enumeration of state space of finitely buffered stochastic molecular networks and exact computation of steady state landscape probability. BMC Syst Biol. 2008;2:30. doi: 10.1186/1752-0509-2-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Barrett R, Berry M, Chan TF, Demmel J, Donato J, Dongarra J, Eijkhout V, Pozo R, Romine C, van der Vorst H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. 2. Philadelphia, PA: SIAM; 1994. [Google Scholar]
- 50.Lehoucq R, Sorensen D, Yang C. Arpack Users’ Guide: Solution of Large Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. Philadelphia, PA: SIAM; 1998. [Google Scholar]
- 51.Cao Y, Lu HM, Liang J. Stochastic probability landscape model for switching efficiency, robustness, and differential threshold for induction of genetic circuit in phage λ. Proc. the 30th Annual Int. Conf. IEEE Eng. Med. Biol. Soc.; Vancouver, Canada. Aug. 20–24, 2008; pp. 611–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gardner TS, Canter CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403(6767):339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 53.Kepler TB, Elston TC. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys J. 2001;81(6):3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Schultz D, Onuchic JN, Wolynes PG. Understanding stochastic simulations of the smallest genetic networks. J Chem Phys. 2007;126(24):245102. doi: 10.1063/1.2741544. [DOI] [PubMed] [Google Scholar]
- 55.Kim KY, Wang J. Potential energy landscape and robustness of a gene regulatory network: Toggle Switch. PLoS Comput Biol. 2007;3(3):e60. doi: 10.1371/journal.pcbi.0030060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wang J, Xu L, Wang E. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc Natl Acad Sci US A. 2008;105(34):12271–12276. doi: 10.1073/pnas.0800579105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ptashne M. Genetic Switch: Phage Lambda Revisited. New York: Cold Spring Harbor Laboratory Press; 2004. [Google Scholar]
- 58.Arkin A, Ross J, McAdams HH. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics. 1998;149(44):1633–1648. doi: 10.1093/genetics/149.4.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Aurell E, Brown S, Johanson J, Sneppen K. Stability puzzles in phage λ. Phys Rev E. 2002;65(5):051914. doi: 10.1103/PhysRevE.65.051914. [DOI] [PubMed] [Google Scholar]
- 60.Munsky B, Khammash M. The finite state projection algorithm for the solution of the chemical master equation. J Chem Phys. 2006;124(4):044104. doi: 10.1063/1.2145882. [DOI] [PubMed] [Google Scholar]
- 61.Munsky B, Khammash M. A multiple time interval finite state projection algorithm for the solution to the chemical master equation. J Comput Phys. 2007;226(1):818–835. [Google Scholar]
- 62.Macnamara S, Bersani AM, Burrage K, Sidje RB. Stochastic chemical kinetics and the total quasi-steady-state assumption: Application to the stochastic simulation algorithm and chemical master equation. J Chem Phys. 2008;129(9):095105. doi: 10.1063/1.2971036. [DOI] [PubMed] [Google Scholar]
- 63.Datta BN. Numerical Linear Algebra and Applications. Brooks/Cole Pub. Co; 1995. [Google Scholar]
- 64.Golub GH, van Loan CF. Matrix Computations. Johns Hopkins Univ. Press; 1996. [Google Scholar]
- 65.Sidje RB. Expokit: A software package for computing matrix exponentials. ACM Trans Math Softw. 1998;24(1):130–156. [Google Scholar]
- 66.Lu HM, Liang J. Perturbation-based Markovian transmission model for probing allosteric dynamics of large macromolecular assembling: A study of GroEL-GroES. PLoS Comput Biol. 2009;5(10):e1000526. doi: 10.1371/journal.pcbi.1000526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Cao Y, Gillespie DT, Petzold LR. The slow-scale stochastic simulation algorithm. J Chem Phys. 2005;122(1):14116. doi: 10.1063/1.1824902. [DOI] [PubMed] [Google Scholar]
- 68.Cao Y, Liang J. Nonlinear coupling for improved stochastic network model: A study of Schnakenberg model. Proc. the 3rd Symp. Optimiz. Syst. Biol; Zhangjiajie, China. Sept. 20–22, 2009; pp. 379–386. [Google Scholar]
- 69.Schnakenberg J. Simple chemical reaction systems with limit cycle behaviour. J Theoret Biol. 1979;81(3):389–400. doi: 10.1016/0022-5193(79)90042-0. [DOI] [PubMed] [Google Scholar]
- 70.Qian H. Open-system nonequilibrium steady state: Statistical thermodynamics, fluctuations, and chemical oscillations. J Phys Chem B. 2006;110(31):15063–15074. doi: 10.1021/jp061858z. [DOI] [PubMed] [Google Scholar]
- 71.Goutsias J. Classical versus stochastic kinetics modeling of biochemical reaction systems. Biophys J. 2007;92(7):2350–2365. doi: 10.1529/biophysj.106.093781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Uribe CA, Verghese GC. Mass fluctuation kinetics: Capturing stochastic effects in systems of chemical reactions through coupled mean-variance computations. J Chem Phys. 2007;126(2):024109. doi: 10.1063/1.2408422. [DOI] [PubMed] [Google Scholar]
- 73.Keizer J. On the macroscopi equivalence of descriptions of fluctuations for chemical reactions. J Math Phys. 1977;18:1316–1321. [Google Scholar]
- 74.Mitchell M. Complexity: A Guided Tour. London: Oxford Univ. Press; 2009. [Google Scholar]
- 75.Laughlin RB, Pines D, Schmalian J, Stojković BP, Wolynes PG. The middle way. Proc Natl Acad Sci USA. 2000;97(1):32–37. doi: 10.1073/pnas.97.1.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Qian H, Shi PZ, Xing J. Stochastic bifurcation, slow fluctuations, and bistability as an origin of biochemical complexity. Physical Chemistry Chemical Physics. 2009;11(24):4861–4870. doi: 10.1039/b900335p. [DOI] [PubMed] [Google Scholar]