Universal Pacemaker of Genome Evolution in Animals and Fungi and Variation of Evolutionary Rates in Diverse Organisms

Abstract

Gene evolution is traditionally considered within the framework of the molecular clock (MC) model whereby each gene is characterized by an approximately constant rate of evolution. Recent comparative analysis of numerous phylogenies of prokaryotic genes has shown that a different model of evolution, denoted the Universal PaceMaker (UPM), which postulates conservation of relative, rather than absolute evolutionary rates, yields a better fit to the phylogenetic data. Here, we show that the UPM model is a better fit than the MC for genome wide sets of phylogenetic trees from six species of Drosophila and nine species of yeast, with extremely high statistical significance. Unlike the prokaryotic phylogenies that include distant organisms and multiple horizontal gene transfers, these are simple data sets that cover groups of closely related organisms and consist of gene trees with the same topology as the species tree. The results indicate that both lineage-specific and gene-specific rates are important in genome evolution but the lineage-specific contribution is greater. Similar to the MC, the gene evolution rates under the UPM are strongly overdispersed, approximately 2-fold compared with the expectation from sampling error alone. However, we show that neither Drosophila nor yeast genes form distinct clusters in the tree space. Thus, the gene-specific deviations from the UPM, although substantial, are uncorrelated and most likely depend on selective factors that are largely unique to individual genes. Thus, the UPM appears to be a key feature of genome evolution across the history of cellular life.

Introduction

Molecular clock (MC) is one of the central concepts of molecular evolution. The MC was discovered in 1962 by Zuckerkandl and Pauling who observed that the number of amino acid differences between the sequences of homologous proteins was roughly proportional to the time that elapsed since the radiation of the corresponding species from their last common ancestor (Zuckerkandl and Pauling 1962, 1965). The MC became the foundation of molecular dating whereby the age of an evolutionary event, usually the radiation of two evolutionary lineages from the common ancestor, is estimated from the sequence divergence using dates known from the fossil record as calibration points (Kumar and Hedges 1998; Hedges 2002; Graur and Martin 2004; Welch and Bromham 2005). In phylogenetic terms, when genes evolve along a rooted tree under the MC, branch lengths are proportional to the time between speciation (or duplication) events and the distances from each internal tree node to all the descendant leaves are the same (ultrametric tree), up to the sampling error.

The general validity of the MC was supported by numerous independent subsequent studies (Kimura 1987; Zuckerkandl 1987; Bromham and Penny 2003; Lanfear et al. 2010). However, the MC has been shown to be strongly overdispersed, that is, the differences between the root to tip distances in most subtrees of a given phylogenetic tree typically greatly exceed the expectation from sampling error, under the assumption of a Poisson mutational process (Takahata 1987; Cutler 2000; Wilke 2004; Bedford and Hartl 2008) (more precisely, the rates on individual tree branches are overdispersed relative to the expectation but the phrase “overdispersed clock” has become common). The overdispersion of the MC appears to be lineage-specific: In lineages with large effective population sizes, the MC is overdispersed to a significantly greater extent than the MC in lineages with small populations, with the implication that deviations from the MC are at least partially caused by selection (Bedford et al. 2008). The demonstration of the overdispersion of the MC inspired the various flavors of relaxed MC model under which the gene-specific evolutionary rate is allowed to differ between branches, either in a correlated manner or through independent sampling from a prior distribution. However, in both cases, the variance of the rates is constrained by design, for the uncorrelated models by the choice of the prior distribution (Thorne et al. 1998; Drummond et al. 2006; Drummond and Suchard 2010). The relaxed MC models underlie most of the modern methods of molecular dating.

An important evolutionary phenomenon that can be viewed as being complementary to the MC is lineage-specific change of gene evolutionary rates. For example, genes of rodents in many cases evolve substantially faster than the orthologous genes in primates (Bromham 2009, 2011). Similarly, a genome-wide analysis of ratios between the evolutionary rates of orthologous genes in triplets of related bacterial, archaeal, and mammalian species revealed near constancy of these ratios, with only a small percentage of gene-specific deviations that were attributed to functional diversification of individual genes (Jordan et al. 2001). Analysis of phylogenetic trees for 44 mammalian genes demonstrated that lineage-specific slowdown of evolution occurred independently in several orders including primates and whales (Bininda-Emonds 2007). Phylogenetic analysis of mitochondrial DNA that extensively sampled numerous taxa also detected robust lineage-specific rates that differed by up to an order of magnitude between animal taxa (Martin et al. 1992; Nabholz et al. 2009). However, several studies have revealed major differences between lineages in the relative rates of evolution of different genes; these findings put the validity of lineage-specific rates into question and led to the concept of “erratic evolution” (Ayala 2000; Rodriguez-Trelles et al. 2001).

The ultimate causes of lineage-specific accelerations or decelerations of evolution rates are not well understood and could be extremely diverse. However, the universal proximal cause, most likely, is the increase or decrease of the effective population size of the corresponding organisms that affects the strength of selection and modulates the selection-dependent components of the evolution rate. Accordingly, one could expect that such changes of gene-specific evolutionary rates apply to all genes in the evolving genomes. This expectation is compatible with the observation that the shape of the distribution of evolution rates across the complete sets of orthologous genes in pairs of related genomes remains virtually unchanged throughout the evolution of life, from bacteria to mammals (Grishin et al. 2000; Wolf et al. 2009).

Together, the remarkable conservation of evolutionary rate distribution across the entire spectrum of life and the observations on lineage-specific changes of evolutionary rates prompted us to develop a new model of gene and genome evolution that is more general than the MC and that we denoted Universal PaceMaker (UPM) of Genome Evolution (Snir et al. 2012). Under the UPM model, all genes evolve at approximately constant rates relative to each other, that is, the changes in the gene-specific rates of evolution are strongly correlated genome wide. Clearly, this model of evolution implies the conservation of the genome-wide distribution of evolutionary rates without requiring that the absolute evolutionary rates remain constant (the definition of the MC). However, relative rates of evolution would remain approximately constant under the MC model as well.

To determine which model, MC or UPM, better fits the available data on genome evolution, we devised a test that involved fitting phylogenetic trees for individual genes to the species tree constrained according to each of the two models (Snir et al. 2012). Specifically, under the MC, the branch lengths are constrained by the requirement for ultrametricity, that is, the distances from each internal tree node to all its descendant leaves are required to be the same (up to the estimate precision determined by sampling error). There are no such constraints under the UPM model, so the fit of each branch in each gene tree (GT) to the respective branch in the species tree can be optimized separately. Using the appropriate information criteria to account for the different number of degrees of freedom, we showed that for a set of several thousand trees of conserved archaeal and bacterial genes, the UPM model yielded a significantly better fit than the MC model to the supertree (ST) that was employed to approximate the species tree of prokaryotes.

Although a better fit to the data on the evolution of numerous genes than the MC, the UPM is itself strongly overdispersed (Snir et al. 2012). By comparing the positions (ranks) of individual genes in the rate distributions for multiple, diverse groups of closely related organisms, we showed that, although the gene-specific relative rate is an important feature of genome evolution that explains more than half of the evolutionary distance variation, the ranges of relative rate variability are extremely broad even for universal genes (Wolf et al. 2013).

In our previous analysis, the advantage of the UPM model over the MC was demonstrated for a data set that included genes of archaea and bacteria that are separated by billions of years of evolution and for which the tree topologies are strongly affected by extensive horizontal gene transfer. Furthermore, there is no species tree in the strict sense for prokaryotes, so the ST that appeared to reflect a central trend of vertical evolution was used as a surrogate. We sought to compare the UPM and MC models on simpler, more robust data sets of eukaryotic genes for which the topology is in agreement with an unequivocally defined species tree. Using such robust data sets for Drosophila and yeast species, we show here that the UPM model in each case gives a superior fit to the data compared with the MC model. We further develop a general theory that combines the two models of evolution. The results indicate that the UPM model reflects a pervasive aspect of genome evolution.

Materials and Methods

Analysis of Drosophila Gene Families

Aligned sequences of Drosophila gene families and corresponding tree topologies were obtained from the Dfam database (http://www.indiana.edu/∼hahnlab/fly/DfamDB, last accessed May 22, 2014) (Clark et al. 2007; Hahn et al. 2007). Alignment positions with more than 50% of gap characters were removed. Tree edge lengths for the given topology were calculated using the RAxML program under PROTGAMMALG evolution model (Stamatakis 2006). The phylogenetic tree topology for 12 Drosophila species was obtained from Clark et al. (2007). The data on the abundances of protein and mRNA products of Drosophila melanogaster genes were obtained from Laurent et al. (2010). The “evolutionary age” of D. melanogaster genes was obtained from Wolf et al. (2009).

Analysis of Saccharomycetales Gene Families

Sequences of the gene complements of Saccharomycetales and their assignments to families were obtained from the Génolevures site (http://www.genolevures.org/, last accessed May 22, 2014) (Sherman et al. 2009). Sequence alignments were generated using the MUSCLE program (Edgar 2004). Alignment positions with more than 50% of gap characters were removed. Phylogenetic tree reconstruction, tree edge length calculation, and tree topology testing were performed using the RAxML program under the PROTGAMMALG evolution model (Stamatakis 2006). The abundances of protein and mRNA products of Saccharomyces cerevisiae genes were obtained from Laurent et al. (2010). The “evolutionary age” of Aspergillus fumigatus orthologs of S. cerevisiae genes was obtained from Wolf et al. (2009).

ST Edges, Evolution Rates, and Model Comparison

As described previously (Snir et al. 2012), we assume that all deviations of the observed GT edge lengths from their expectations can be expressed as a single factor ε, which assumes independent randomly distributed values (eq. 5). Under the further assumption that ε comes from a normal distribution, the maximum-likelihood solution for b and r is equivalent to finding the minimum of the Euclidean norm for the deviation of the observed edge lengths from the expected lengths:

(1)

where the summation for i is done over the ST edges and the summation for k is done over all GTs.

For the case analyzed here, that of a 1:1 mapping between GT and ST edges, an analytical, closed form solution to equation (1) can be obtained using a linear algebraic approach (Strang 2005). However, this operation turned to be infeasible for the amount of data handled in this work. We therefore resorted to a numerical solution as follows.

For a given b, one can easily obtain optimal values for r as a closed form solution by minimizing E_k² individually for each gene g. Therefore, we employed a numerical optimization program “fmin_slsqp” from the Python scipy.optimize package to search for the optimum values of b and used analytically computed values of r for each state of b to estimate the corresponding value of E². Typically, numerical approaches use multiple starting points to avoid being trapped at local, suboptimal maxima. However, as shown in our previous work (Wolf et al. 2013), the surface under study has a unique local (and hence also global) optimum point. Therefore, we pursued the following approach. We sampled a small (∼100) random set of genes G′ and analytically found the optimum of b over G′. Given the obtained optimal values of b (for the subset G′), we infer the optimal values for the entire gene set G and used these values as a starting point for the search described above (the Python code implementing this algorithm is available from the authors upon request).

Optimization under the UPM model used unconstrained values of b; for the MC model, ultrametricity constraints were applied (Snir et al. 2012), again using the constrained optimization program fmin_slsqp. The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) were used to compare the goodness of fit of the MC and UPM models:

(2)

(3)

where 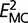and 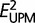E_{{\rm UPM}}^2 are the deviation norms for the MC and UPM models, n is the total number of edges in GTs, and Δd is the number of constraints in the MC model (five and eight for Drosophila and Saccharomycetales, respectively).

Results

The Universal Genome Pacemaker and MC

In multicellular eukaryotes with a clear separation between the germline and the soma, the histories of most of the individual genes agree with each other, and their common topology represents the species tree. For organisms whose history includes extensive horizontal gene exchange, all individual gene phylogenies could, in principle, be different, so instead of the species tree, the dominant vertical trend of evolution can be represented by a ST. For the sake of generality, we will refer to the rooted tree topology that is assumed to represent the history of the given set of organisms as the “supertree” (fig. 1).

Fig. 1.—

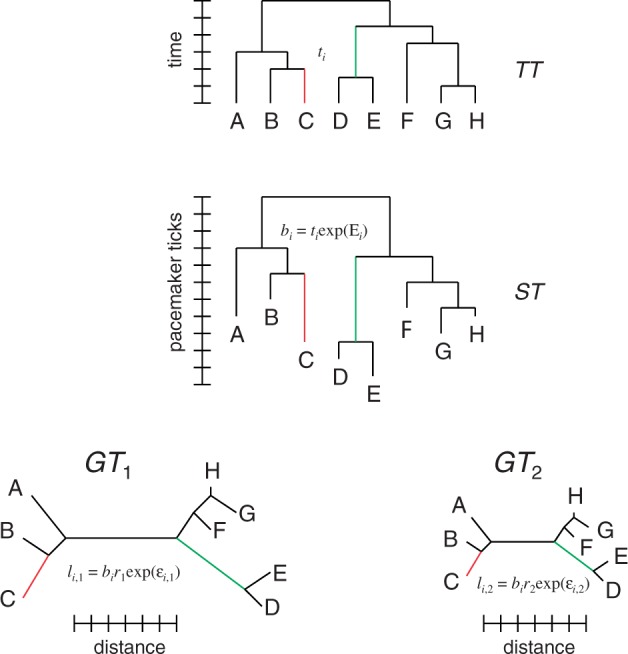
Relationships between the TT, ST, and GTs. Examples of edges corresponding to each other in TT, ST, and GTs are highlighted in the same color.

As the ST is assumed to reflect the history of organisms (to the extent the concept is applicable), its internal nodes (including the root) represent speciation events. Excluding cases of extreme compressed cladogenesis, where the new lineages arise at such short intervals that the emerging clades inherit nonsegregated polymorphisms from the ancestral population, speciation events correspond to time points in the past. Thus, the ST can be mapped to an ultrametric tree of the same topology where the distances between each internal node and each of its descendant leaves are equal to each other and to the time elapsed since speciation. The lengths of the edges in this tree also can be expressed in time units as the duration of intervals between the speciation events. We will refer to this tree as the “time tree” (TT; fig. 1).

Consider a set of “gene trees” (fig. 1) that reflect the (reconstructed) phylogenetic history of individual genes. In general, the GT topology may be different from that of the ST because of artifacts of phylogenetic reconstruction, gene loss, gene duplication, and horizontal gene transfer. Thus, the mapping between each GT and the ST involves the correspondence between a path (a set of consecutive edges) in the GT and a path in the ST, and some of the leaves in both GT and ST might have to be omitted to obtain the maximum agreement subtree (MAST). However, for the purpose of this work, we will consider only “perfect” GTs that contain exactly one leaf from each of the organisms in ST and the GT topology is the same as the ST topology. In this case, each GT is isomorphic to the ST, and there exists an unambiguous one-to-one mapping between the GT and ST edges.

Now consider a particular kth GT. For each ith edge of this GT, the relationship between its length and the corresponding ST and TT edges can be expressed as:

(4)

where l_i,k is the length of the ith edge of the kth GT, b_i is the length of the ith edge of the ST, and t_i is the length of the ith edge of the TT. The length of the GT edge differs from the length of the corresponding ST edge by a factor that can be decomposed into two components, r_i, which is common to all edges in the kth GT, and δ_i,k, specific to this particular edge. The lengths of the corresponding GT and TT edges (the latter subject to ultrametricity constraints) differ by a factor Δ_i. For convenience, we will represent Δ_i and δ_i,k in an exponential form:

(5)

In these terms, the expected length of the ith edge of the kth GT is given by the product of the length of the ith ST edge b_i and the relative evolution rate of the kth gene r_i. The deviation of the observed length l_i,k from this expectation, δ_i,k = exp(ε_i,k), can be attributed to multiple causes including the error of edge length estimation and local change of evolution rate. Here, we assume that all these factors can be represented by a single combined random variable ε_i,k with the expectation of 0. This assumption allows us to obtain the best estimate for the unknown lengths of ST edges (vector b) and unknown relative evolution rates for the genes (vector r) from the observed GT edge lengths by minimization of the apparent variance of ε. In particular, under the assumption of a normal distribution of ε, the minimum deviation between the l_i,k from its expectation b_ir_i (minimum variance of ε) corresponds to the maximum-likelihood solution for b and r.

The relationships between the ST and TT edges, b_i = t_i, exp(Ε_i), can be described in the following terms. If Var(Ε) = 0 for all edges, b_i is proportional to t_i (i.e., all lineages evolve at the same rate relative to each other) and the ST is also ultrametric. In this case, when one finds the solution for b and r, one would need to apply ultrametricity constraints on the values of b. In the opposite case of Var(Ε) → ∞, there is no relation between the ST edge length and the duration of time for which the (ancestral) lineage existed. In this case, one would solve for the minimum variance of ε with unconstrained values of b.

The two extreme cases (Var(Ε) → 0 and Var(Ε) → ∞) describe the two opposing modalities of molecular evolution: MC and unconstrained UPM. The range of intermediate regimes can be referred to as “constrained universal pacemaker” or “relaxed molecular clock” (e.g., as described in Renner [2005]). Under these models, the evolution rates relative to time can differ between lineages, but abrupt rate changes are penalized in likelihood computation.

Analysis under the most general constrained UPM model requires disentangling the contributions from lineage-specific rate variations among multiple genes and rate variations in individual genes to the deviation of the observed GT edge lengths from the TT edge lengths. Because the level of constraint is not known beforehand, such an analysis is subject to much uncertainty. Thus, we use the simplifying assumption of the strict MC and the unconstrained UPM as two alternative, extreme regimes of evolution and seek to determine which of these regimes yields a better fit to the genome-wide phylogenetic data.

UPM and MC in Drosophila

The initial data set consisted of 6,698 gene families that contained exactly one gene from each of the 12 Drosophila species in the Dfam database. Of these, 2,900 families have Dfam tree topology that agrees with the known species tree topology. We calculated the tree edge lengths for these families and used them to find the maximum-likelihood estimates for the ST edge lengths (b) and gene evolution rates (r) under the UPM model.

The solution thus obtained shows an extremely high level of deviation of the estimated edge lengths from the observed values. The root mean square deviation (RMSD) for this set of 60,900 tree edges (21 edge in each of the 2,900 trees) was 1.66 natural log units (RMSD factor of 5.24×), compared with the RMSD of 0.76 natural log units in our earlier published estimates for prokaryotic gene families (Snir et al. 2012). At face value, this result implies that the evolution of genes within a single genus of insects is subject to a much greater variability of evolution rates than the evolution of diverse gene families that span the entire depth of the history of cellular life. However, we suspected that the observed high variability in these data was primarily an artifact caused by the presence of numerous short edges in the GTs. Obviously, the lengths of short edges are estimated from a small number of inferred substitutions and thus are subject to a high uncertainty. We tested this possibility using two approaches. First, from the reconstructed UPM ST edge lengths, we selected 10 tree edges that typically are longer than the other 11 edges and repeated the UPM optimization with only these 29,000 edges. Second, we discarded all trees that either include the shortest edge with less than 0.0005 substitutions per site or the longest edge with more than 3 substitutions per site. The 16,422 edges of the remaining 783 trees were used to find the optimal UPM solution. The two procedures indeed reduced the RMSD to 0.80 and 0.59 log units, respectively, in agreement with our expectations.

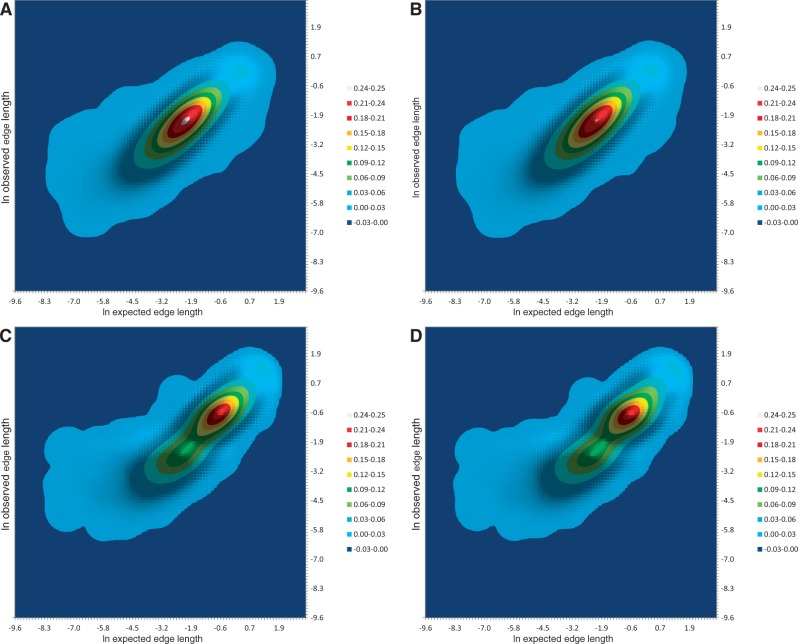
To minimize the effect of short edges, we reduced the original Drosophila data set to six species that are widely separated in the original 12-species tree: Drosophila ananassae, D. grimshawi, D. melanogaster, D. mojavensis, D. pseudoobscura, and D. willistoni. Gene families with exactly one gene from each of these species, and GT topology matching that of the species tree were selected, and the edge lengths calculated. After removing trees with excessively long or short edges (using the thresholds of 3 and 0.0005 substitutions per site, respectively), 6,989 GTs were used for the subsequent analysis (62,901 tree edges with nine edges in each tree). In this data set, the deviation of observed edge lengths from the expected edge lengths is reduced dramatically (table 1 and fig. 2A) to 0.47 log units (RMSD factor of 1.61×). This is considerably less deviation than previously found in the nearly universally conserved genes of prokaryotes estimated across the whole tree of life (0.76 log units; Snir et al. [2012]) and is comparable to the deviation that was previously obtained for selected, optimally spaced pairs of genomes (0.41 log units; Wolf et al. [2013]).

Table 1.

Comparison of the MC and UPM Models for “Perfect” GTs of Drosophila and Yeast

Variable	Drosophila		Yeast
	UPM	MC	UPM	MC
Number of trees	6,989		1,005
Number of species	6		9
Number of edges	62,901		15,075
Variance per edge	0.22	0.23	0.24	0.28
RMSD, ln units	0.47	0.48	0.49	0.53
RMSD factor	1.61	1.61	1.64	1.70
Number of constraints	0	5	0	8
Delta AIC	0	1,359.0	0	2,005.4
Delta BIC	0	1,313.7	0	1,944.4
Sampling variance per edge	0.10	—	0.14	—

Fig. 2.—

Distribution of expected versus observed tree edge lengths in Drosophila and Saccharomycetales GTs under the UPM and MC models. Probability density is shown by color. (A) Drosophila, UPM; (B) Drosophila, MC; (C) Saccharomycetales, UPM; and (D) Saccharomycetales, MC.

In contrast to the UPM, the MC model implies an ultrametric ST. Ultrametricity constraints necessarily increase the deviation of the observed edge lengths from the expected values. For the six Drosophila species data set, the optimization under the MC constraints increases the per-edge variance by 2.2% (0.23 vs. 0.22) compared with the optimization under the UPM (table 1 and fig. 2B). The better fit of the UPM model is achieved at the expense of extra degrees of freedom (5 for a six-species tree). We employed the AIC and BIC to compare the quality of fit for the two models. Despite the small difference in the variance, both comparisons indicate strong support for the UPM model (table 1), with relative likelihood weights of 10⁺²⁹⁵:1 and 10⁺²⁸⁵:1, respectively.

To test whether the advantage of the UPM over the MC is a characteristic of the majority of gene families rather than an artifact of selecting the “perfect” six-species trees, we performed the analysis on a much wider set of genes (11,005 vs. 6,989) using the previously described approach (Snir et al. 2012). If paralogs were present, the orthologs with the highest similarity to other family members were selected to represent each of the six species. For GTs reconstructed without constraints, the MAST was by comparing the GT with the ST; the MASTs with four or more species were analyzed with and without the ultrametricity constraints. Both AIC and BIC indicate an overwhelming preference for the UPM model (table 2) despite the substantial increase in the residual variance (2.8×).

Table 2.

Comparison of the MC and UPM Models for the MASTs from Drosophila and Yeast

Variable	Drosophila		Yeast
	UPM	MC	UPM	MC
Number of trees	11,005		3,865
Number of species	4–6		4–9
Number of edges	87,321		37,148
Variance per edge	0.62	0.63	0.40	0.43
RMSD, ln units	0.79	0.79	0.63	0.66
RMSD factor	2.20	2.21	1.89	1.93
Number of constraints	0	5	0	8
Delta AIC	0	687.9	0	2,661.5
Delta BIC	0	641.0	0	2,593.4

UPM and MC in Saccharomycetales Yeast

The Génolevures database contains 1,689 gene families with exactly one gene from each of the nine species of Saccharomycetales (Candida glabrata, Debaryomyces hansenii, Eremothecium [Ashbya] gossypii, Kluyveromyces lactis, K. thermotolerans, S. cerevisiae, S. kluyveri, Yarrowia lipolytica, and Zygosaccharomyces rouxii). We reconstructed multiple alignments and phylogenetic trees for all these families. There seems to be a broad consensus on the species phylogeny among these nine yeast species although two distinct placements of E. gossypii have been proposed, namely as a sister group to K. thermotolerans (Scannell et al. 2007) or as an outgroup to the branch that encompasses Saccharomyces, Candida, Zygosaccharomyces, and Kluyveromyces (Dujon 2010). We found that our reconstructed trees better agreed with the former topology and used it throughout this work.

There are 1,005 Saccharomycetales gene families that satisfy the following criteria: 1) exactly one gene from each of the nine species; 2) sequence alignment is compatible with the species tree topology (i.e., the species tree topology is not rejected by the Shimodaira–Hasegawa test compared with the maximum-likelihood topology at 0.05 significance level); and 3) all tree edge lengths are between 0.0005 and 3 substitutions per site. This set containing 15,075 tree edges (15 per tree) was used for the subsequent analysis.

For these trees, the RMSD of observed edge lengths from their expectations under the UPM model was 0.49 natural log units (RMSD factor of 1.64×), nearly the same as in Drosophila species (table 1 and fig. 2C). Analysis under the MC constraints resulted in the per-edge variance increase by 14% (0.28 vs. 0.24, table 1 and fig. 2D), indicating an overwhelming support for the UPM model (AIC and BIC relative likelihood weights of 10⁺⁴³⁵:1 and 10⁺⁴²²:1, respectively).

As with Drosophila, analysis of the wider set of genes (3,865 genes with no requirement for single orthologs and no constraints on reconstructed topology) reveals that the support for the UPM over the MC is robust and is not an artifact of the tree selection (table 2).

Sources of Evolutionary Rate Variation

There seem to be two major causes of the deviation of the observed tree edge lengths from the expected values. One cause is purely technical: Distances are estimated using a finite number of amino acid replacements that is inferred for a particular edge under a particular evolutionary model using an imperfect algorithm. The other source of variation is rooted in biology: Changes in the selection pressure and mutational context cause changes in the evolution rates of particular genes on particular edges relative to the genome-average rate in the course of evolution, resulting in changing positions of the respective genes in the distributions of evolutionary rates.

We sought to disentangle these sources of evolutionary rate variation by creating artificial gene sets that are devoid of biological variation. To this end, we employed the following procedure separately with the Drosophila and Saccharomycetales sets of 6,989 and 1,005 genes, respectively: First, all genes were ranked by the lengths of their sequence alignments. We selected 400 genes around the 75th length percentile, ranked them by their inferred relative evolution rates (r), and selected 100 genes around the median rate. The alignment columns in the alignments of each of these 100 genes were sampled with replacement to create a set of artificial alignments with the same lengths as the original alignments. Thus, we obtained 100 sets of 6,989 “genes” and 100 sets of 1,005 “genes” that mimicked, respectively, the real Drosophila and Saccharomycetales gene families in terms of the number and lengths of genes but with each set populated by alignment columns derived from one gene only. Each of these artificial sets remains subject to sampling variation and to errors of edge length computation, but any potential biological source of variation between the genes is eliminated. For all “genes” in each of these sets, edge lengths were estimated for the tree with the respective species tree topology; trees with short (<0.0005) or long (>3) edges were discarded; the remaining trees were used to estimate the edge length variance. Average per-edge variance was computed for both groups.

Resampling of both Drosophila-derived and Saccharomycetales-derived genes produced similar results (table 1). The mean per-edge variance in these artificial gene sets was 0.10 and 0.14 which represents, respectively, 44% and 55% of the variance observed in the real data. Thus, approximately half of the apparent variation of evolutionary rates of individual genes in each lineage can be accounted for by sampling variation and errors in edge length estimates whereas the other half is likely to arise from biological sources. In other words, this observation suggests that the UPM is overdispersed by a factor of approximately 2 relative to what one would expect from technical reasons alone.

Genome-Wide Universality of the Pacemakers

We have shown previously that despite substantial variation, genes in prokaryotes generally evolve at relative rates that are characteristic for the respective gene families; in other words, a particular gene retains approximately the same position in the distribution of evolution rates in many evolving lineages (Wolf et al. 2013). Here, we show that genes in two distant groups of eukaryotes display similar magnitudes of relative rate variation, so the concept of family-specific relative evolution rates appears to hold across the entire spectrum of cellular life. The existence of stable, family-specific relative evolution rates is the simplest explanation of the striking conservation of the distributions of evolution rates in widely different lineages (Grishin et al. 2000; Wolf et al. 2009). As expected, the evolution rates of Drosophila and Saccharomycetales families form approximately symmetrical bell-shaped distributions in the log scale (fig. 3), similar to the rate distributions in other lineages (Grishin et al. 2000; Wolf et al. 2009).

Fig. 3.—

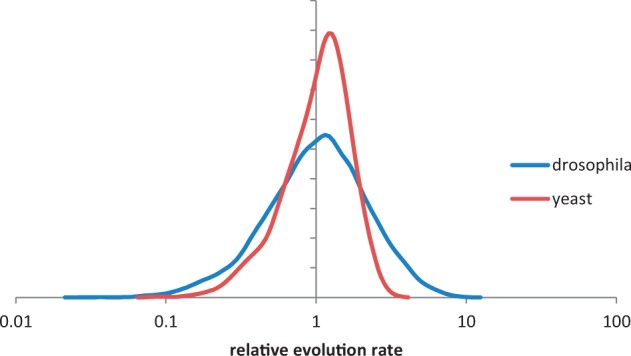
Distribution of relative evolution rates of Drosophila and Saccharomycetales gene families.

Similar to the MC, the UPM is overdispersed (Snir et al. 2012), and in the preceding section, we quantify this overdispersion to show that it exceeds the dispersion predicted from sampling error approximately by a factor of 2. Potentially, the overdispersion of the UPM could be caused by the action of multiple pacemakers that would differentially affect the acceleration or deceleration of evolution of different groups during the evolution of a given lineage. If such groups exist, the corresponding GTs would be expected to have the same topology but distinct shapes, that is, different patterns of relatively long and short branches. Hence, a simple test for the existence of multiple distinct pacemakers. If the edge lengths of a particular GT are divided by the relative evolution rate of the given gene, the normalized relative edge lengths form a vector that identifies a point in a multidimensional space that describes the tree shape. Trees of similar shapes would form clusters in this space. Edge lengths within a tree are not completely independent of each other because real GTs, although not ultrametric, still retain some correlation between the edge length and time intervals separating the speciation events. Thus, it is appropriate first to transform the original space of relative edge lengths into a tree shape space with uncorrelated dimensions. We performed such a transformation using the unscaled principal component analysis. In the principal component space of Drosophila GTs, the first seven principal dimensions account for more than 90% of the original variance of the nine-dimensional edge length space. With Saccharomycetales GTs, the first nine principal dimensions account more than 90% of the original variance of the 15-dimensional edge length space.

Drosophila and Saccharomycetales GTs were placed in the seven- and nine-dimensional tree shape spaces, respectively, and probed for the existence of clusters using the Gap Function statistics (Tibshirani et al. 2001). Neither set of trees showed any indication of statistically significant clustering when grouping into 2–20 clusters were tested for both sets. The lack of significant clustering and the pattern of distribution of GTs in the tree shape space suggests random isotropic scatter around a single centroid, that is, random uncorrelated deviations from a single, universal, genome-wide pacemaker (fig. 4).

Fig. 4.—

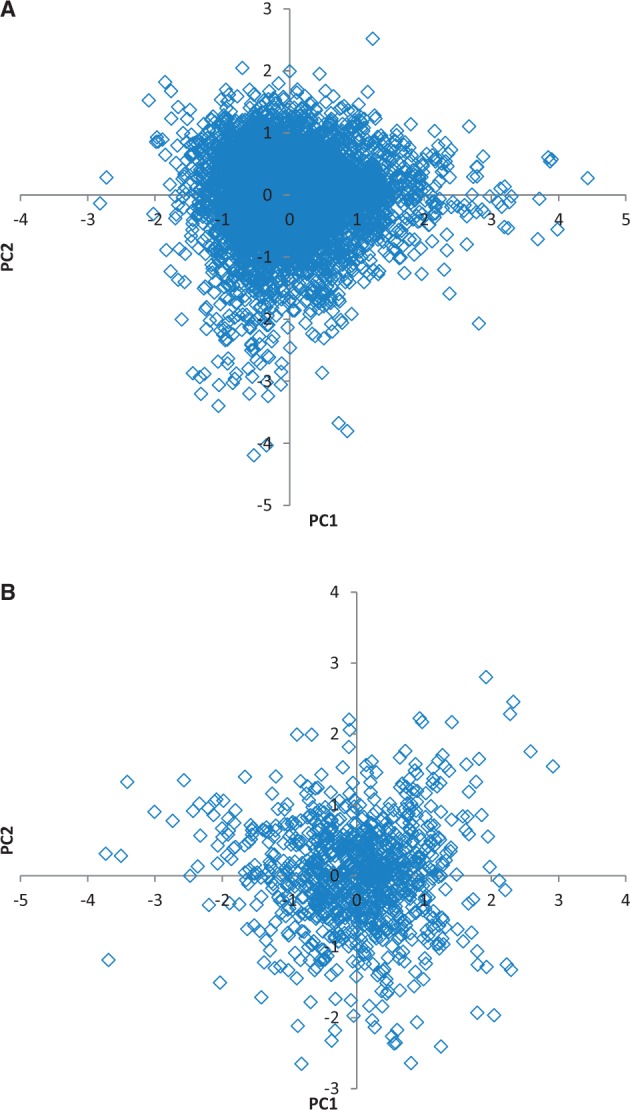
The GTs for Drosophila and Saccharomycetales in the plane of the first two principal components of the tree shape space. (A) 6,989 Drosophila trees; (B) 1,005 Saccharomycetales trees.

Correlates of Evolutionary Rate Variation

There exists a considerable diversity in the magnitude of deviation of individual GTs from the UPM ST, that is, in how strictly the evolution of the given gene follows the UPM. Thus, among the analyzed 6,989 Drosophila genes, the 5th and 95th percentiles correspond to RMSD factors of 1.23× and 2.20×, respectively, with the median of 1.48×. As shown above, sampling variation accounts for approximately half of the variance, so one would expect the deviations in individual genes to correlate with gene features that affect the sampling statistics. Given that the other half of the variance apparently arises from biological sources, it was of interest to explore the properties of genes that might affect how closely they follow the universal genomic pacemaker.

To this end, we calculated the Spearman rank correlation between the deviation of GT edge lengths from UPM-derived expectations and gene length, relative evolution rate, protein abundance, mRNA abundance, and gene “evolutionary age” (table 3; and see Materials and Methods for details). As expected, the magnitude of the deviation from the UPM shows significant negative correlation with both gene length and the relative evolution rate (see supplementary file S1, Supplementary Material online). Indeed, having more actual mutations, either because of a greater gene length or a greater evolution rate or both, increases the accuracy of the distance estimates. Somewhat unexpectedly, a positive correlation was detected between the magnitude of the deviation and gene product abundance, measured either at the protein level or at the mRNA level, that is, genes for abundant proteins tend to deviate from the UPM to a greater extent than genes for low-abundance proteins. A potentially plausible explanation could be that this positive correlation was an indirect effect of the slow evolution that is typical of genes encoding abundant proteins (Duret and Mouchiroud 2000; Pal et al. 2001; Wolf et al. 2006; Drummond and Wilke 2008, 2009). However, multivariate linear regression revealed independent significant contributions of four factors (gene length, relative evolutionary rate, protein abundance, and mRNA abundance) (see supplementary file S1, Supplementary Material online). In particular, perhaps counterintuitively, protein and mRNA abundance make opposite contributions to the deviation of a given GT from the UPM. The “evolutionary age” of a protein, that is, the depth of the last common ancestor for which homologs were detectable (Wolf et al. 2009), did not show any correlation with the evolution rate variability.

Table 3.

Spearman Rank Correlation of the Deviation from the UPM Expectation with Other Gene Characteristics

	Drosophila	Yeast
Alignment length	−0.40*	−0.47*
Relative evolution rate	−0.28*	−0.17*
Protein abundance	0.16*	0.16*
mRNA abundance	0.12*	0.20*
Evolutionary age	0.02	0.06

*Significant at the 0.001 level in a permutation test.

Discussion

In the previous work, we formulated the UPM model and showed that it was a better fit for the evolution of conserved prokaryotic genes than the traditional MC model (Snir et al. 2012). The comparison of the two models of evolution for prokaryotes involved trimming the GTs to the MASTs to fit the edge lengths to those in the ST. The ST itself, in this case, is not a bona fide species tree but rather a consensus of GT topologies that appears to represent a central trend of vertical evolution in the “phylogenetic forest” (Puigbo et al. 2009). Furthermore, the phylogenetic trees for many of the conserved prokaryotic genes involved sequences separated by billions of years of evolution. Taken together, all these confounding factors increase the uncertainty that is associated with the GT to ST fit estimations. In particular, the magnitude of the advantage of the UPM (albeit statistically highly significant) over the MC could have been affected by these uncertainties.

In this study, we chose as the primary data much simpler and “cleaner” sets of eukaryotic genes from two groups of well-characterized model organisms with an unambiguously resolved species trees. From these data sets, it was possible to select large sets of GTs that were topologically identical to the species tree, thus substantially reducing the uncertainty in the comparison of evolutionary models. For both data sets, we obtained results that were readily compatible with those of the previous study, namely that the UPM model gave a better fit to the data than the MC model, with an overwhelming statistical significance. However, this straightforward analysis of relatively recent evolutionary processes again showed that the difference between the two models of evolution accounted for a small part of the variance in the evolutionary rates. We compared the results of this analysis of “perfect” with much larger sets of MASTs for both groups of organisms (following the lines of the previous study [Snir et al. 2012]) and observed full consistency between the two series of analyses, with the advantage of the UPM over the MC being highly significant in all cases but more pronounced for the “perfect” data sets.

Thus, the results of this work, together with the previous findings, indicate that the UPM model most likely describes the course of evolution throughout the entire history of life. Across a broad range of life forms, the UPM model approximates gene evolution better than the MC model albeit by a relatively small margin. Within the framework of the theory developed here, these findings imply that the lineage-specific contribution to the variation of evolutionary rates is consistently and significantly greater than the gene-specific contribution.

MC models spanning the range from strict (equivalent to Var(Ε) = 0 in eq. 5), through various flavors of correlated clock, to totally relaxed (Var(Ε) = ∞) are widely used in molecular phylogenetics (Thorne et al. 1998; Drummond et al. 2006; Drummond and Rambaut 2007; Drummond and Suchard 2010). The key difference between these and the UPM is the level at which the organismal phylogeny affects individual genes and sites. In the context of a single gene, it is practically impossible to distinguish between the UPM and relaxed MC. The major distinction is in the way sets of multiple genes are treated. Under the relaxed MC models, the hypothesis about the ST is applied to individual alignment sites. The likelihood of each site is calculated given the particular ST and combined across the alignment or collection of alignments; in the latter case, all sites across all alignments are assumed to have evolved along precisely the same tree. Under the UPM model, individual gene phylogenies are taken as given and represent the maximum-likelihood hypotheses about the evolution of those genes. Unlike the traditional phylogenetic approach in which the deviations from the global model at individual sites are simply accounted for as a decrease in the total likelihood, within the UPM framework, site histories are assumed to be coherent within genes but not between genes, that is, all GTs are constructed independently. The existence of between-gene correlations is explored a posteriori whereby the ST represents the hypothesis of the common evolutionary history and E² (eq. 1; see Materials and Methods) represents the sum of deviations of GTs from the predictions of this hypothesis. This approach provides for explicit comparison of different global hypotheses in terms of goodness of fit versus free parameters. If, for example, all deviations from the strict MC were uncorrelated between the genes, the UPM model would incur the penalty for extra parameters without decreasing the deviation and would have been rejected.

We developed an approach to disambiguate the overdispersion of the UPM caused by sampling error from the biologically relevant overdispersion. The results indicate that, compared with the expectation from purely technical reasons, the UPM is approximately 2-fold overdispersed. This observation implies that individual genes are subject to selective pressures that cause significant deviations from the UPM. However, these selective factors appear to be highly gene-specific resulting in the observed random distribution of genes in the tree space (fig. 4).

Apparently, even in the optimal situation with respect to the degree of sequence divergence, the tree edge length measurements for a single gene are subject to variation of approximately 0.45 natural log units (table 1; Wolf et al. 2013). This variation imposes an inherent limitation on the precision and accuracy of any quantitative statement based on measurements of evolutionary distances. If the deviations from the “true” edge length are independent, as they appear to be, these limitations can be overcome by employing multiple independent estimates. Because the RMSD of the estimated mean decreases with the square root of the number of measurements, to achieve, for example, a 10% accuracy (RMSD factor of 1.1), (0.45/ln(1.1))² ≈ 22 independent estimates are required. In other words, to obtain an estimate of a relative evolution rate of a gene within a 10% error, it is necessary to analyze distance data from 20 to 25 optimally spaced pairs of genomes or from edges of a tree containing 12–14 leaves. Conversely, pooling data from 20 to 25 genes provides for a 10% accurate estimate of the relative evolution rate of a particular lineage.

We further explored the intriguing possibility of multiple pacemakers specific to different groups of genes but found no evidence of gene clustering in the tree space. These findings suggest that the UPM is a genome-wide phenomenon that affects all the genes in evolving genomes approximately to the same extent or at least that the deviations of the evolution of individual genes from the UPM are largely random (fig. 4). Such a conclusion is compatible with the notion that the UPM is driven by changes in the long-term effective population size of the evolving organisms, whereas the deviations of individual genes from the UPM are, at first approximation, random and uncorrelated. The changes in the population dynamics themselves can be caused by various environmental factors.

The apparent universality of the pacemaker might reflect the limitations of the available data and the approach rather than true lack of groups of genes that might evolve coherently within themselves but discordantly relative to the rest of the genome. Overall, approximately half of the observed variance in the evolution rates seems to result from purely technical factors (sampling deviation and distance calculation errors), limiting our ability to detect deviating groups of genes even when the nontechnical component of the deviation is caused by the same biological factors.

Evolutionary rates of genes show multiple, significant connections to various molecular phenomic characteristics, in particular protein and mRNA abundance (Wolf 2006; Wolf et al. 2006; Drummond and Wilke 2008, 2009). We tested for similar correlations with respect to how closely individual genes follow the UPM and, in addition to the expected dependencies on gene size and relative rate of evolution, identified counterintuitive but significant positive correlation between the magnitude of a gene’s deviation from the UPM and the abundance of its product measured at the level of protein or mRNA. Conceivably, gene-specific selective factors that cause such deviations affect highly expressed genes to a greater extent than lowly expressed genes.

To summarize the results of the present and previous analyses, the pacemaker of genome evolution appears to be universal in two complementary senses. First, the UPM model appears to apply to all evolving lineages although the pace of evolution certainly is lineage specific, and second, the UPM is a genome-wide phenomenon, with the individual gene evolutionary rates apparently deviating randomly from the mean value of acceleration or deceleration set by the pacemaker. Identification of the specific factors that set the pacemaker in various evolutionary lineages seems to be an important task for future investigation.

Supplementary Material

Supplementary file S1 is available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).

Acknowledgments

This work was supported by the Yeshaya Horowitz Association through the Center for Complexity Science to S.S. and by intramural funds of the US Department of Health and Human Services (to National Library of Medicine) to Y.I.W. and E.V.K.