A novel strategy for the estimation of the general height of the visual field in patients with glaucoma

Abstract

Background

More accurate estimation of the general height of the visual field may improve our ability to detect and monitor progression of diseases affecting visual function such as glaucoma. General height (GH) can be affected by factors such as cataracts, pupillary miosis, refractive error, and learning and fatigue effects. The conventional GH index, consisting of subtracting the 85th largest value from the total-deviation map, has been shown to overestimate the height in patients with moderate and advanced glaucoma. We aimed at developing an improved estimator for general height based on ranking of total-deviation values that are within normal limits (GHr).

Methods

Two datasets were used for the comparisons between GH and GHr estimates: one with 369 visual fields for 102 controls and another with 500 visual fields for 124 patients. For controls, we compared the distributions of mean of total deviation (MD) and of mean of pattern deviation (MPD) derived from both the GH and the GHr estimates. For patients, we assessed agreement between both estimates and between pairs of consecutive visits. We also compared linear fits in progression analyses. All data were collected with 24-2 SITA Standard.

Results

For control subjects and patients with MD above −5.5 dB, estimates with the GHr estimator were not significantly different than with the GH estimator. For patients with glaucoma with MD below −5.5 dB, as MD became more negative the GH estimates were increasingly greater than GHr estimates. For patients with glaucoma, test-retest variability was lower with the GHr estimator: between visits agreement was better for GHr estimates than for GH estimates (SD of 0.8 dB versus 1.5 dB; p < 0.0001). Linear progression analysis fitted better the data from the GHr estimator. Root mean square error for GHr was 0.4 dB; lower than the 0.8 dB for GH (p < 0.0001).

Conclusions

The novel GHr estimator is very different from the conventional GH estimator, has more solid foundations and better statistical properties. Nevertheless, it is not always better than the GH estimator, in particular, if no focal loss is present. Pattern-deviation maps obtained with GHr reduce systematic underestimation of glaucomatous damage.

INTRODUCTION

Static automated perimetry is used to assess the severity and progression of visual field losses due to diseases such as glaucoma. In the diagnosis and management of patients with pathological visual field loss, clinicians include assessment of focal patterns of damage in distinguishing between different causes of loss. Factors such as vigilance and fatigue [1-3], and detection criterion [4], will tend to change the height of the measured hill of vision, as will cataractous lens changes, pupillary miosis, or refractive error [5-7]. Reduction in the height may also be due to glaucoma itself [8-10]. In order to assist clinicians in separating global changes and distinguishing focal patterns of loss, conventional perimetric printouts include pattern-deviation maps obtained as an attempt to compensate for differences in the height of the hill of vision.

Many procedures have been proposed for estimating the height of the hill of vision [11-18]. The most common one is to take the, approximately, 85th percentile from the total-deviation (TD) map [11, 12], which corresponds to its 7th largest value in the 24–2 visual field test grid. The estimate of the height of the hill of vision with this procedure is known as the general height (GH). The GH estimator is used in the Humphrey Field Analyzer (Carl Zeiss Meditec, Inc., Dublin, CA) for the derivation of the pattern-deviation (PD) maps [12] and for the glaucoma hemifield test [19]. Yet, this estimator has been shown to overestimate the true height [20]. As a consequence, PD maps can underestimate focal loss of glaucomatous visual field damage [12] and its progression [21]. Furthermore, GH estimates become increasingly unreliable as the disease progresses and damage gets deeper and more extended. Other estimation methods for the height of the hill of vision have been proposed [11-16] that use TD-rank curves (also known as Bebie curves) [22]. Neither they nor the GH estimator take into account that, as the visual field gets worse, the ranking of TD values changes —see e.g. Figure 1 in Asman et al [20]. In Appendix A, we give a brief review of TD-rank curves and illustrate how they might be used to separate differences in the height of the hill of vision from focal losses.

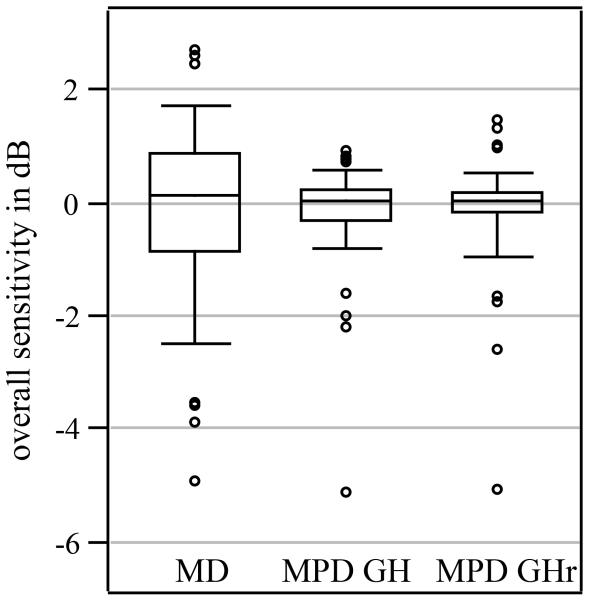
Figure 1. Distribution of MD, MPD from GH, and MPD from GHr for control subjects.

The figure shows boxplots for mean deviation (MD), for mean pattern deviation from general height (MPD from GH) and for mean pattern deviation from general sensitivity (MPD from GHr). The bottom and top of the boxes are the first and third quantile and the bottom and top whiskers are the percentiles 5 and 95, respectively. The open circles are individual values below percentile 1 and above percentile 99.

The aim of this work was to derive an improved estimator for the height of the hill of vision. The novel estimator is based on TD-rank curves. We have called this estimator the GH-rank estimator, or GHr estimator.

METHODS

Subjects and visual field testing

A dataset with 369 visual fields for 102 eyes of 102 healthy control subjects and with 500 visual fields for 124 eyes of 124 patients with glaucoma was used to compare the GHr estimator to the GH estimator. All subjects were enrolled in prospective longitudinal studies at Indiana University School of Optometry and at the State University of New York College of Optometry. The studies were conducted following the tenets of the Declaration of Helsinki. Written informed consent was obtained from each participant before testing and after explaining the procedure and goals of the corresponding studies. The protocols were approved by the Institutional Review Boards of the Indiana University and of the SUNY State College of Optometry.

All visual field tests were performed with the Humphrey Field Analyzer (versions 12.5 through 14.X on the HFA 750 and versions range from 4.X to 5.0 on the 750i) using the 24–2 visual field test grid and SITA Standard algorithm with the Goldman size III stimulus. We set unusually relaxed exclusion criteria, allowing false positives to go as high as 50%. The general height is affected by a subject’s criterion for detection, and these are also reflected in the percentage of false positives. A subject more inclined to “push the button” (a trigger-happy subject) will generally have a higher general height and percentage of false positives. Therefore, a more relaxed exclusion criterion for false positives increases the range of general height in the data. A total of 18 field tests on 15 control subjects and 6 tests on 6 patients with glaucoma were removed that did not pass the reliability criteria.

The GH and GHr estimators

The rationale for the novel GHr estimator is given in Appendix B, including how we account for changes in the ranking of TD values as disease progresses, and the mathematical formalization. Part of the GHr estimation method is the selection of TD values that are within normal limits (above percentile 5 and below percentile 95). We required that at least two TD values were within normal limits; otherwise, the method was regarded as unsuitable and the height of the hill of vision was not estimated. Out of the 500 visual fields for 124 patients with glaucoma available, 11 from 6 patients were regarded as unsuitable. We decided on a cutoff of two TD values within normal limits to reject as few visual fields as possible.

The conventional GH estimator [20] does not have a direct interpretation: a negative GH does not mean below age-corrected mean normal sensitivity. This is because the mean GH for a normal population is 1.8 dB [23], and not zero (see vertical arrow for the 7th position in Figure A1). For this reason, we computed here the GH as 1.8 dB minus the 7th largest TD value from the measured visual field instead of just the 7th largest TD value, and GH is, hence, what needs to be subtracted to a measured visual field so that its height equals that of the age-corrected mean normal. Note that, except for an offset value of 1.8 dB, the GH and PD values calculated here are equivalent to those calculated in conventional perimetric printouts and the probability maps obtained with either are the same. Since GH for mean normal as calculated here is zero, PD values become also directly comparable to TD values, unlike with conventional perimetric printouts.

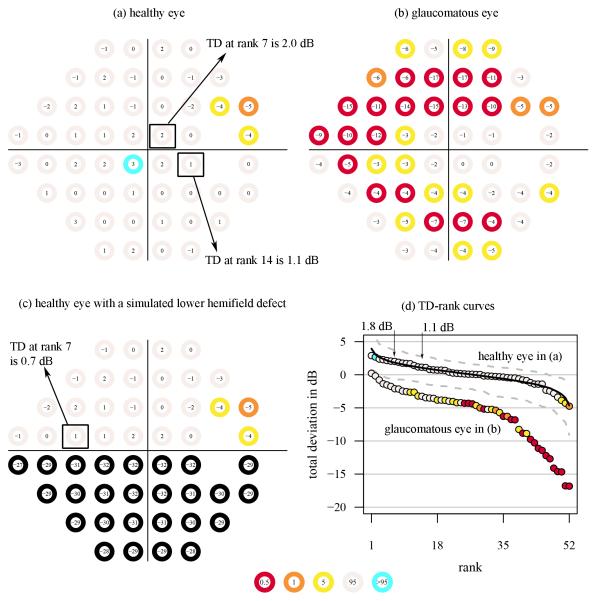
Figure A1. TD maps and TD-rank curves.

Three TD maps (consisting of TD values on top of circles with corresponding color-coded probability categories for (a) a healthy eye and (b) a glaucomatous eye obtained using the 24–2 visual field test grid and SITA standard. The visual field in (c) is the same as for the healthy eye in (a) after artificially adding a lower-field defect (sensitivities equal to zero at all locations). In (d), the TD-rank curves are shown for the visual fields in (a) and (b), but not (c) for clarity. The solid curve shows the mean normal TD-rank curve. The vertical arrows denote the TD at rank positions 7 and 14. The dashed curves in c and d are the 95% confidence limits for the normal TD-rank curve. The color code at each percentile category in the TD probability maps and the empirical TD-rank curves are shown in the bottom middle.

Pattern-deviation values and probability maps were obtained for both the novel GHr estimator and the conventional GH estimator expressed as difference from mean normal. The PD values shown here are therefore about 1.8 dB lower than those shown in conventional perimetric printouts. Mean deviation (MD) was calculated as the weighted mean of the TD values [11], and mean pattern deviation (MPD) as the weighted mean of the PD values. The weights used in both indices were the inverse of the mean normal standard deviation of TD [11] and PD, respectively. The location on top of the blind spot and the location above it were removed from the calculations [11].

Statistical analysis

The R programming environment [24] and its contributed package visualFields [25] were used for all the computations in this paper. The visualFields package contains normative values obtained for static automated perimetry (SAP) with the Goldmann size III stimulus presented with the 24–2 pattern of locations using the SITA-Standard strategy. Details about the control subjects with inclusion and exclusion criteria can be found in Marín-Franch and Swanson [25]. Normative values for PD and corresponding probability maps using the novel GHr estimator were obtained with the same dataset of control subjects.

For controls, we compared MD to MPD from both GH and GHr. For patients with glaucoma, we compared GH estimates to GHr estimates. We also obtained the 95% limits of agreement between two consecutive visits. We then calculated PD from both GH and GHr for two consecutive visits and, for each of the two sets of PD values, we calculated the 95% limits of agreement. For agreement analysis between consecutive visits, a total of 93 patients were selected who had at least two visits for which GHr estimates were regarded as suitable for estimation. The PD values corresponding to the outer ring in the 24–2 visual field test grid were removed to reduce impact of lid and lens artifacts in point-wise comparisons, but not for the estimation of GH, GHr, MD, and MPD.

We also assessed the goodness-of-fit of linear progression analysis over time of GH estimates, GHr estimates, and the MPD from GH and from GHr. Linear-progression analyses were performed on a subsample of 49 eyes of 49 patients with glaucoma that had at least 5 visits for which the GHr estimator was regarded as suitable for estimation. For this subsample of patients, the median follow-up time was 4.5 years, with an inter-quantile interval from 2.6 to 5.1 years and a range from 1.3 to 6.9 years. The root mean square error was used to assess the goodness-of-fit in the linear-progression analyses.

RESULTS

Figure 1 shows a box plot for MD values from all 369 visual fields from 102 control subjects, and two box plots for corresponding MPD values calculated for GH and GHr An outlier is clearly visible in Figure 1 (at −5 dB) that corresponded to a visual field with a lens artifact. The median value for MD was 0.1 dB, whereas the median values for MPD from GH and MPD from GHr were both 0.0 dB, respectively. The amount of variability was significantly reduced: the standard deviation was 1.3 dB for MD and 0.5 dB for both MPD from GH and GHr (F = 6.6, p < 0.0001). There was no difference in means between the GH estimate and the GHr estimate and the 95% limits for agreement between estimates were from −1.0 dB to +1.0 dB.

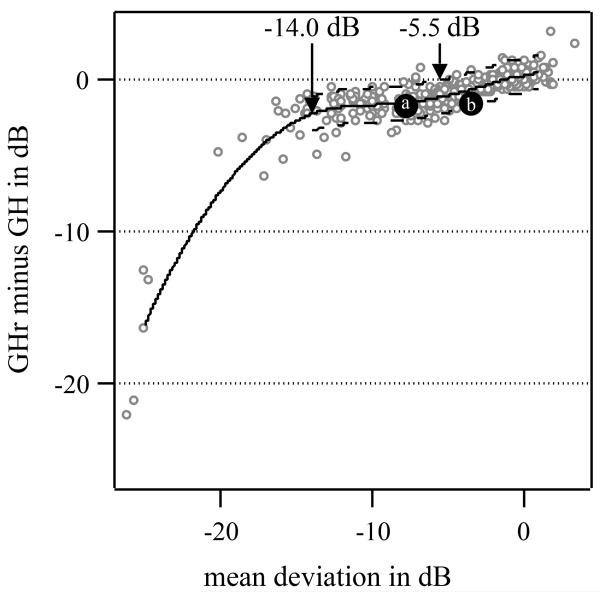
Figure 2 shows the agreement between the GH and GHr estimates as a function of MD for patients with glaucoma. The GH estimates were, on average, increasingly greater than the GHr estimates as visual field damage increased. For MDs below −5.5 dB, the GH estimates were significantly greater than GHr estimates. The 95% limits of agreement for values above −5.5 dB were from −1.5 dB to 1.1 dB. For visual fields with MD values between −5.5 dB and −14.0 dB, the mean difference was almost constant at −1.5 dB. For visual fields with MD values below −14.0 dB, the mean difference was −5.6 dB.

Figure 2. Differences in GH estimates and GHr estimates as a function of mean deviation for patients with glaucoma.

The open circles are individual differences and the solid curve is a loess fit [28] to show central trends in the scatterplot. The loess curve was obtained with the R loess function with parameter values for span and degree equal to 0.4 and 2, respectively. The dashed curves show the loess fit ± 1.96 standard deviation of estimate differences for MD above −14.0 dB, the point from which agreement between GH and GHr is no longer approximately linear. The solid gray circles labeled (a) and (b) are two of the three selected examples commented on in the Discussion section and Figure 4.

There was no mean difference between two consecutive visits for either GH estimates or GHr estimates. The standard deviation was 0.8 dB for GHr estimates, significantly lower than 1.5 dB for GH estimates (F = 3.1, p < 0.0001). For PD values, the mean differences were −0.1 dB for both, and the standard deviations were 4.3 dB for PD from GHr and 4.1 dB for PD from GH. (F = 1.1, p > 0.5).

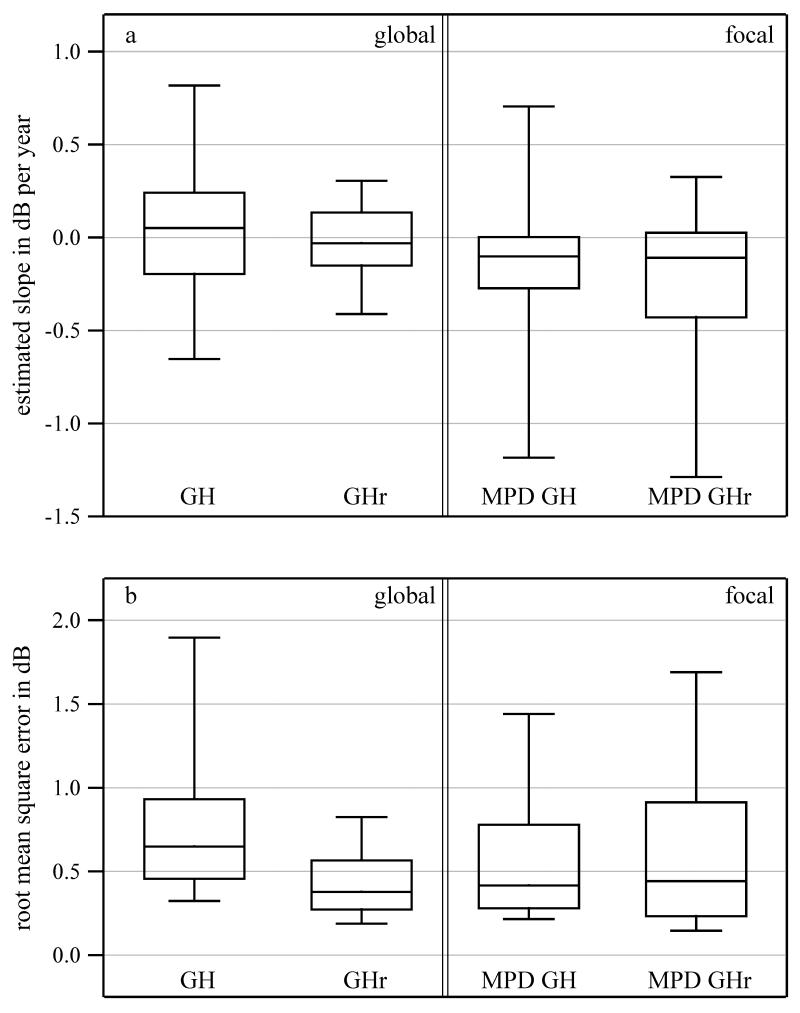
Figure 3 shows boxplots for the estimated slopes and the root-mean-square error of the fits for linear progression of GH, GHr, MPD from GH, and MPD from GHr. The average root mean square error of the simple linear regression for GHr over time was 0.4 dB, and for simple linear regression of GH over time was 0.8 dB (F = 3.5, p < 0.0001). The average root mean square errors for MPD from GH and for MPD from GHr were the same at 0.6 dB.

Figure 3. Assessment of linear-progression analysis for estimates of global damage and focal damage.

Box plots for (a) slopes and (b) root-mean-square errors of fits for the linear progression analyses of GH estimates and GHr estimates, and for MPD from GH and MPD from GHr. The lower and upper ends of the boxes and of whiskers are as in Figure 1. For clarity individual points are not shown.

DISCUSSION

We proposed a novel estimator for the height of the hill of vision, the GH-rank estimator, or GHr estimator, and compared it against the conventional general-height estimator, or GH estimator [11, 12]. The novel GHr estimator is available from the free R package visualFields [25]. Since the GH estimator has been shown to underestimate the height of the hill of vision so that PD maps underestimate the severity of glaucomatous focal loss, improved methods are desirable [20]. The GHr estimator is conceptually similar to the GH estimator and was developed to overcome, or at least reduce, such underestimation problems. Even though underestimation is effectively reduced (see Fig 2), it was at a cost: with the novel GHr estimator, for eyes with very severe cataract (so that there are less than two TD values within normal limits), PD maps cannot be calculated. Moreover, in the case where there is only diffuse loss without focal loss, the GHr estimator will either return very similar values to the GH estimator or be regarded as unsuitable for estimation. In cases where there is only diffuse loss without focal loses the conventional GH estimator is the better estimator to use. For cases when there is great diffuse loss mixed with focal loses, none of the two estimators is reliable: the GHr will be deemed as unsuitable and the GH estimator, whereas it gives an estimate, it is likely an overestimation of the true height [20].

Both estimators were significantly different from each other for visual fields with MD values below −5.5 dB, with GH estimates consistently greater than GHr estimates (see Figure 2). For MD, below approximately −14.0 dB the difference between GH and GHr estimates increased as MD decreased.

The GHr estimator had significantly lower between-visit variability than the GH estimators (p < 0.0001), even though PD from GH and PD from GHr had the same variability (p > 0.5). Linear progression analyses over time described changes for the GHr estimator more accurately than for the GH estimator (p < 0.0001). Yet, there were no significant differences in reliability for global indices based on the corresponding PD maps, the MPD from GH and the MPD from GHr. The statistical differences reported here have very small p-values (below 0.0001). At a significance level of 0.05, even after correcting for multiple comparisons (five tests of hypothesis for the dataset of patients with glaucoma), the Bonferroni-corrected significance value would be 0.01. All significant p-values are well below this significance level.

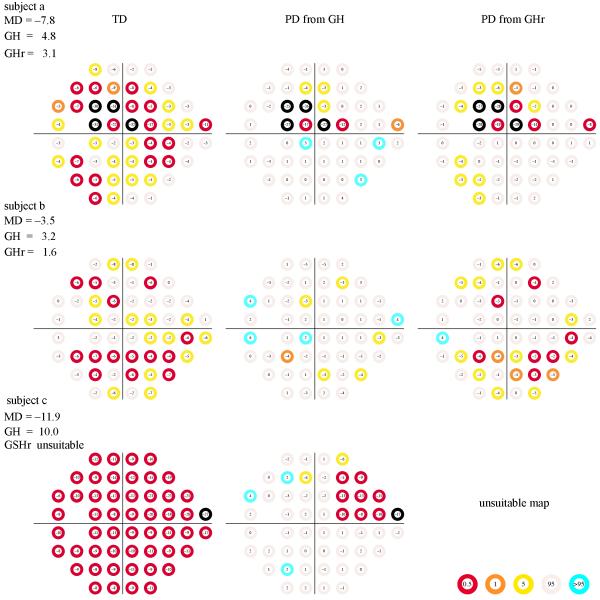
The differences between the GH estimator and the GHr estimator are not subtle and can have a great impact in the appearance of the pattern-deviation map in patients with glaucoma as well as in global indices derived from them, such as the visual field index (VFI). Note that errors in the estimation of the height of the hill of vision will lead to errors in the estimates of PD values, and in turn in the estimation of global indices, such as the VFI, that depend on PD maps. Figure 4 shows TD maps and the corresponding PD maps for three cases. Cases (a) and (b) are marked in Figure 2, whereas case (c) is not as the GHr estimate was regarded as unreliable.

Figure 4. Three visual field examples.

The TD maps (left column), PD from GH (center column), and PD from GHr (right column) for three patients with glaucoma. Patients (a) and (b) are marked in Figure 2. Patient (c) was not present in Figure 2 because the GHr estimate was regarded as unreliable. The PD from GH estimates are slightly different from those observed from the Humphrey Field Analyzer mainly because there is an offset of 1.8 dB (see Methods: The GH and GHr estimators), but also because we used the visualFields package for the generation of the maps, which have different normative values than the Humphrey Field Analyzer. The color code at each percentile category in the TD probability maps and the empirical TD-rank curves are shown in the bottom middle.

In case (a), both PD maps are similar, although PD from GHr shows more locations that are flagged as significantly depressed (below the 5th percentile) than does PD from GH. In case (b), the PD maps are clinically quite different, with PD from GHr showing a pattern of damage that could be due to an incipient arcuate defect in the lower hemifield and PD from GH showing isolated locations with subtle depressions. In case (c), the GHr was regarded as unsuitable for estimation and hence the PD map was not calculated. This was because there were no TD values within normal limits. In all three cases of Figure 4, several locations in the PD maps from GH were flagged as “hypersensitive” (above the 95th percentile), consistent with findings that PD maps tend to underestimate damage [12, 20, 21].

The automatic validation feature of the novel GHr estimator may seem to be a disadvantage with respect to the conventional GH estimator, and it is if only global loss without focal loss is present. Nevertheless, for the GH estimator it is assumed that at least ~ 15% of the TD values are not damaged [12]. When this assumption fails, PD maps can be severely misleading, see Blumenthal and Sapir-Pichhadze [26] for extreme examples. There have been other strategies to select the TD values to be used for the estimation of the height of the hill of vision. For instance, Funkhouser [15] proposed to look at the “plateau” in the TD-rank curve and used these TD values for the calculation of the general height. But this method does not take into account that, as more locations become damaged and their TD values decrease, positions in the TD-rank curves change [20]. In a different approach, Langerhorst and colleagues [13, 14] developed a method based on a pre-selection of “normal points” and an estimation of short-term fluctuation to broaden the selection of such "normal points". This method requires an estimate of short-term fluctuation usually achieved by a repeated visual field measurement.

In the development of the VFI, Bengtsson & Heijl [27] argued that the valid operating range for pattern deviation analysis is for MD above −20 dB and for which the ~85th percentile of TD values is not flagged as significantly depressed. In addition, they argued that the number of significantly depressed locations in PD maps could be underestimated for MD below −20 dB. We argue here that MD is not the most appropriate way to establish the validity of PD maps and that underestimation may occur as early as at MD of −5.5 dB, the point where GH estimates give significantly lower values than the GHr estimates (see Figure 2). Case (b) in Figure 4 is an example where the conventional PD map, PD from GH, shows many fewer significantly depressed locations than PD from GHr (6 versus 21 locations). In total, only 11 visual fields were considered unsuitable for estimation, out of 500 visual fields for 124 eyes of 124 patients with glaucoma, the average MD for these visual fields was −20.5 dB and the average GH estimate was 14.6 dB below mean normal. If we used the VFI unreliability criterion, we would find 49 unreliable PD maps, almost five times as many as with the GHr criterion.

For healthy controls, between-subject variability of the MPD from GH and of the MPD from GHr were not significantly different from each other, but for both variability was significantly lower than for MD (p < 0.0001). That is, PD maps effectively compensate for global changes due to factors such as vigilance and fatigue [1-3], and detection criterion [4], as well as cataractous lens changes, pupillary miosis, or refractive error [5-7].

Since PD maps obtained with the conventional GH estimator tend to underestimate glaucomatous damage, it is advisable not to rely solely on them without taking into consideration the TD maps. The PD maps obtained with the novel GHr estimator reduce systematic underestimation of glaucomatous damage in patients with glaucoma. Nevertheless, if no focal loss is present, the GH estimator is a better estimator for the height of the hill of vision. Although there may still be some systematic bias present in GHr estimates, our pattern deviation maps are arguably more reliable and have a larger valid operating range than the conventional one. "

Appendix A: Review of TD-rank curves

Figure A1 shows three TD maps obtained with visualFields 0.3 [23] for the 24–2 visual field test grid and SITA standard. The TD maps correspond to (a) a healthy eye, (b) a glaucomatous eye, and (c) the healthy eye in (a) with artificial damage added to the lower hemifield. The TD-rank curves for the TD maps in (a) and (b) are shown in panel (d). For its display, the TD values in (a) and (b) were ranked and plotted against their rank position; this is the TD-rank curve —also known as the Bebie cumulative defect curve [22]. The TD-rank curve for the artificial visual field in (c) is not shown to preserve clarity.

The TD-rank curves have been used to derive algorithms for the estimation of the height of the hill of vision [15, 16, 18], some defined from direct visual inspection [15]. From a visual inspection of the TD-rank curve for the glaucomatous visual field in Fig A1b, we see that part of the curve is roughly parallel with the mean normal TD-rank curve (black solid curve). The difference between TD-rank curves in the portion that they go in parallel may be taken as an estimate of the difference in height from mean normal (many times called diffuse loss when height is lower than the age-corrected mean normal height). At around rank position 34, the curve is no longer parallel to the mean normal one and the distance from mean normal of the remaining 18 points is greater. We may then “conclude” that the remaining 18 locations had focal loss.

Appendix B: The general sensitivity estimator

The key to the estimation of the height of the hill of vision is the reconstruction of the “normal part” of the TD-rank curve for patients with a partially damaged visual field. Here, we propose here to select only the TD values that are within normal limits and infer what is the most likely rank position they were in before the visual field was damaged at all. To illustrate why the rank positions need to be recalculated, an artificial visual field was generated (see Figure A1c) from the visual field for a healthy subject (see Figure A1a). The artificial visual field in Figure A1c was obtained by assigning sensitivities of 0 dB to all locations in the lower hemifield of the healthy visual field in Figure A1c. Similar artificial visual fields have been analyzed elsewhere [20].

For the healthy visual field in Figure A1a, the average of the 52 TD values is 0.0 dB, and so is the average of the mean normal TD values (black curve in Figure A1d). That is, the height of the hill of vision for this visual field is the same as that for the age-corrected mean normal hill of vision. If we estimated the height with the GH estimator [11, 20] we would obtain that the height is 0.2 dB above mean normal: 2.0 dB of the seventh largest TD value in the visual field in Figure A1a minus 1.8 dB of the seventh largest TD value from the mean normal visual field (the value of the black curve in Figure A1d marked with a vertical arrow).

Consider the artificial visual field in Figure A1c. The GH estimator for the artificially damaged visual field is 0.7 dB. That is 1.1 dB below mean normal height, an overestimation as the true height of the visual field was equal to mean normal. Since rank positions change as defects appear, it makes sense to assume that the TD value in rank 7 in Figure A1c was actually around rank 14 before half of the visual field in Figure A1c became blind. If we take rank 14 of the mean normal visual field as reference (1.1 dB, marked in an arrow in Figure A1d), then we would estimate the height as 0.3 dB below mean normal, which is a closer estimate to the true height than the GH estimate. The GHr estimator that we introduce here is based on the recalculation of TD rank positions of all within normal limits (above percentile 5 and below percentile 95). To continue with our example in Figure A1c, the number n of TD values within normal limits is 23.

Computationally, a unique solution to the re-calculation of the rank positions can be achieved by meeting two conditions. First, the spacing between recalculated rank positions must be equal and, second, the mid point of the recalculated ranks must equal the mid point of the ranks for the mean normal TD rank. For the 24–2 visual field test grid, for which there are N = 52 TD values (after excluding the blind spot and the location above it), such mid point is 53 / 2 = 26.5. The distance between recalculated ranks must be (N − 1) / (n + 1), so that the recalculated rank positions r, for i = 1, …, n, are

$$r_i=\frac{N-1}{n-1}i+c,$$

where c is a constant obtained from the second condition that the mid point of the recalculated ranks must equal the mid point of the mean normal TD rank curve, thus,

$$c=\frac{N+1}{2}-\frac{N-1}{n(n+1)}\sum _{i=1}^{n}i.$$

Following this approach, for our example with a blind lower hemifield, the recalculated rank positions would be r_i = (17/ 8) i + 1. The value of the mean normal TD-rank curve at those (non-integer) locations can be obtained by linear interpolation. The height estimated with the GHr estimator was 0.1 dB above mean normal; the closest estimate in this example.