Abstract
Transcranial electrical stimulation (TCES) and deep brain stimulation are two different applications of electrical current to the brain used in different areas of medicine. Both have a similar frequency dependence of their efficiency, with the most pronounced effects around 100 Hz. We apply superthreshold electrical stimulation, specifically depolarizing DC current, interrupted at different frequencies, to a simple model of a population of cortical neurons which uses phenomenological descriptions of neurons by Izhikevich and synaptic connections on a similar level of sophistication. With this model, we are able to reproduce the optimal desynchronization around 100 Hz, as well as to predict the full frequency dependence of the efficiency of desynchronization, and thereby to give a possible explanation for the action mechanism of TCES.
Keywords: Transcranial electrical stimulation, Deep brain stimulation, Izhikevich model, Desynchronization, High-frequency stimulation
Introduction
Deep brain stimulation (DBS) has attained much attention during the past fifteen years as a modern treatment of miscellaneous neural and movement disorders, especially in the treatment of the symptoms associated with Parkinson’s disease (PD) (Benabid et al. 1994), namely tremor (Anderson et al. 2006), rigidity and bradykinesia, but also for epilepsy (Velasco et al. 1995), dystonia (Coubes et al. 2000; Kumar et al. 1999; Yianni et al. 2003), and essential tremor (Benabid et al. 1996). DBS also has promising effects in the treatment of obsessive-compulsive disorder (OCD) (Nuttin et al. 2003), Tourette’s syndrom (Houeto et al. 2005; Visser-Vandewall 2007) and depression (Ressler 2007). For the purpose of the treatment, electrodes are chronically implanted in a specific area of the brain. In the majority of cases of movement disorders, the targeted region is the subthalamic nucleus (STN), as the stalling of dopaminergic (inhibitory) neurons in the substantia nigra leads to pathological synchronized oscillations in the STN, which are correlated with the clinical symptoms of PD (Gang et al. 2005). Also other regions of the brain have been targeted for DBS, the globus pallidus internus (GPi) for the treatment of PD (Bellinger et al. 2008; Obesó et al. 2001) as well as treatment of dystonia (Kumar et al. 1999; Yianni et al. 2003), was attempted in the CA1 region of the hippocampus (Jensen 2007; Su et al. 2008), and in the ventral intermediate nucleus of the thalamus (Vim) (Bellinger et al. 2008). Frequencies between 100 and 200 Hz (clinically often 130 Hz are applied) have been proven to give the best results in alleviating the symptoms, whereas low frequencies of roughly 10 Hz can even worsen the symptoms. Understanding the working mechanisms of DBS from computational models is not an easy exercise: recurrent neural networks with inhibitory neurons can exhibit rich behavior including synchronization (Liu et al. 2010; Wang 2011; Zhang et al. 2010); various mechanisms of desynchronization by stimulation (Hauptmann 2010) or nonlinear feedback (Schöll et al. 2009), to mention a few, have been proposed. Although there has been a lot of research, the action mechanism of DBS still remains elusive.
At least in the last years, however, less effort has been made to analyze the action mechanisms of transcranial electrical stimulation, which is used for different purposes and is labelled with different names. Probably the most established one is transcranial electrical stimulation (TCES), a technique which has been used to reduce drug requirements for anaesthesia in surgical operations (Limoge et al. 1999). Although it has been used in over 10,000 operations at least up to 1998 (Limoge et al. 1999), its working mechanism still remains to be explained.
The TCES technique was developed by Limoge in the 1970s (Limoge 1975) and the technical protocol as well as electrode placement is established under the terminus Limoge current (Limoge et al. 1999). Although the way of the Limoge current through the head is still not precisely known, and it is even not known if the current may, at least in parts, act by influencing peripheral nerves outside the cranium (Zaghi et al. 2009), the part of the brain where transcranial electrical stimulation has its greatest effect is presumably the neocortex, because current density decreases with the distance to the electrode. Since the neocortex is the part of the brain closest to the stimulation for all standard electrode positions, it is quite likely the part carrying the greatest fraction of the current. Transcranial direct current stimulation in humans was also shown to enhance excitability (Antal et al. 2004a, b) which on the one hand indicates plasticity effects and on the other hand shows that TCES can have a pronounced effect on neocortical regions and not only on specific subcortical structures as targeted by DBS.
To account for an explanation of the action mechanism of TCES, we have built up a model of a population of neurons from the mammalian cortex, and applied external stimulation with different frequencies. This model is presented in the next section. In the third section we give a short introduction to generalized phase definitions and introduce order parameters which can be used to quantify the phase synchronization of the neurons. Results are presented in the fourth section and discussed in the fifth section. In the final section we give a comprehension and present possible extensions of the model.
The model
As we want to demonstrate the basic effects in a model that is as simple as possible, we do not attempt to account for biological parameter variability, as we expect that the basic mechanism does not rely on detailed properties of a specific cortical region.
Neuron model
Our model cortex consists of Nexc = 1,024 excitatory and Ninh = 256 inhibitory neurons. This reflects the fact that the ratio of excitatory to inhibitory neurons (in the mammalian cortex) is 4:1 (Börgers 2003; Gupta et al. 2000; Izhikevich et al. 2004; Markram et al. 1998). Individual neurons were modelled according to the Izhikevich model of spiking neurons (Izhikevich 2003, 2004), which contains two variables v and u, representing the membrane potential, and a recovery variable, e.g. a slow K+ current, respectively. v and u are governed by the differential equations
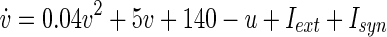 |
1 |
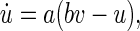 |
2 |
where Iext and Isyn represent the external and the synaptic input current, respectively. If v ≥ 30, a reset is initiated,
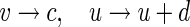 |
3 |
Depending on the four parameters a, b, c, and d, the Izhikevich neuron can map a rich variety of neuronal spiking patterns. We use a = 0.02, b = 0.2, c = −65, d = 8 for the excitatory subpopulation and a = 0.1, b = 0.2, c = −65, d = 2 for the inhibitory subpopulation. These parameter values correspond to ‘regular spiking’ (RS) and the ‘fast spiking’ (FS) pattern, which are exhibited by most of the excitatory and of the inhibitory neurons in the cortex, respectively (Izhikevich et al. 2004; Steriade et al. 2001).
Modeling synapses
Each neuron makes a synaptic connection to any other neuron with probability p = 200/(Nexc + Ninh), so each neuron has 200 synaptic connections on average. In reality, there are thousands of synapses per neuron (Izhikevich et al. 2004), whereof here we model a small subnetwork of a local cortical assembly and therefore cannot explicitely consider long-range connections. Consequently, we also neglect structured connectivity, apart from taking into account a sparse random connectivity. The synaptic input current to a neuron i is given by the sum over the postsynaptic potentials of all neurons j presynaptic to i
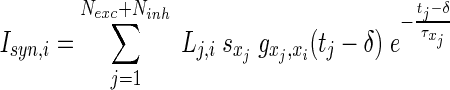 |
4 |
where xj and xi are the types (i.e. excitatory or inhibitory) of the pre- and the postsynaptic neurons, respectively, and can take on the values E and I. Here (Lj,i) is the adjacency matrix describing whether synaptic connections between j and i exist. The sign variables 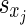 formally account for the excitatory or inhibitory nature of the presynaptic neuron, with sE = +1 and sI = −1. Then, the
formally account for the excitatory or inhibitory nature of the presynaptic neuron, with sE = +1 and sI = −1. Then, the 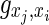 are the synaptic strengths between two types of neurons, with gE,E = 0.6, gE,I = 0.1, gI,E = 0.2 and gI,I = 0.05. We have adapted the ratios of these values according to the reference model (Compte et al. 2003). For the axonal delay we use δ = 0.25 ms;
are the synaptic strengths between two types of neurons, with gE,E = 0.6, gE,I = 0.1, gI,E = 0.2 and gI,I = 0.05. We have adapted the ratios of these values according to the reference model (Compte et al. 2003). For the axonal delay we use δ = 0.25 ms; 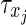 is a time constant depending on the presynaptic neuron, with 0.2 ms for excitatory and 0.4 ms for inhibitory neurons, respectively, and tj denotes the time since the last spike of the presynaptic neuron j (in ms).
is a time constant depending on the presynaptic neuron, with 0.2 ms for excitatory and 0.4 ms for inhibitory neurons, respectively, and tj denotes the time since the last spike of the presynaptic neuron j (in ms).
To consider the dynamics of a local neural assembly under stimulation, it is of low relevance from where incoming projections originate. To ensure non-trivial activity in the network, external input to the neural network is assumed from Next = 128 external excitatory neurons. These neurons are not explicitly modelled, but they make synaptic connections into the network with the same properties as the network synapses, and fire action potentials at random with probability 0.01 during each time step. The model was integrated using a fourth-order explicit Runge–Kutta method with a time step of 0.05 ms.
Phase synchronization
To quantify synchronization of an ensemble of oscillators, more convenient observables than correlation functions can be used. Here we follow an established approach (Acebrón et al. 2005; Lian et al. 2004; Kuramoto 1975) to define a complex-valued order parameter based on a generalized phase in a phase space appropriately chosen for the model at hand.
Generalized phase
There are at least three concepts for a generalized phase definition of chaotic oscillations (Pikovsky et al. 1997). For the sake of numerical simplicity, we use a geometrical phase angle definition. In absence of external stimulation, each neuron has an attracting limit cycle in the 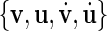 -space; to define a phase, this trajectory has to be suitably projected into a two-dimensional plane, which indeed is possible here. We define the phase of the oscillator i (i.e., the neuron i) as the angle between a given (fixed) direction and the position of the neuron’s state in a chosen plane of the phase space,
-space; to define a phase, this trajectory has to be suitably projected into a two-dimensional plane, which indeed is possible here. We define the phase of the oscillator i (i.e., the neuron i) as the angle between a given (fixed) direction and the position of the neuron’s state in a chosen plane of the phase space,
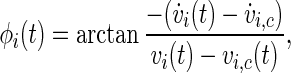 |
5 |
where the point 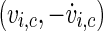 is within the rotation centre of the attractor of the neuron i in the plane of the phase space spanned by vi and
is within the rotation centre of the attractor of the neuron i in the plane of the phase space spanned by vi and 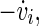 with
with 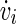 being the time derivative of the membrane potential vi of the neuron i.
being the time derivative of the membrane potential vi of the neuron i.
The first choice for such a plane in the phase space to be used for phase definition would be the  -space, but unfortunately the attractor in this plane has multiple rotation centres and changes its position for different stimulation intensities, so the
-space, but unfortunately the attractor in this plane has multiple rotation centres and changes its position for different stimulation intensities, so the 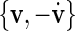 -space is a better choice. To ensure a monotoneous increase of ϕ, one has to choose a coordinate centre within the trajectory loop; here we select the point
-space is a better choice. To ensure a monotoneous increase of ϕ, one has to choose a coordinate centre within the trajectory loop; here we select the point 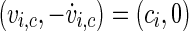 as rotation centre. We further choose
as rotation centre. We further choose 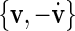 (rather than
(rather than 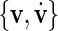 which results in
which results in 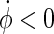 ) to ensure
) to ensure 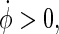 for convenience. Other linear combinations of v, u and their first time derivatives could be used as well as an embedding of the dynamics.
for convenience. Other linear combinations of v, u and their first time derivatives could be used as well as an embedding of the dynamics.
Order parameter
We define the complex-valued order parameter 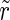 of the phases as
of the phases as
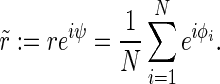 |
6 |
This definition is according to the definition of the order parameter in the Kuramoto model of phase synchronization (Acebrón et al. 2005; Kuramoto 1975). We analyze the synchronization in the whole population (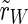 ), the excitatory subpopulation (
), the excitatory subpopulation (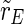 ) and the inhibitory subpopulation (
) and the inhibitory subpopulation (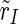 ) as well, so N can be Nexc + Ninh, Nexc and Ninh, respectively. The absolute value r of
) as well, so N can be Nexc + Ninh, Nexc and Ninh, respectively. The absolute value r of 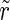 lies in the interval [0,1], where 0 corresponds to a complete unsynchronized state and 1 to complete synchronization.
lies in the interval [0,1], where 0 corresponds to a complete unsynchronized state and 1 to complete synchronization.
As these order parameters oscillate already for the unstimulated system, we are mainly interested in the average of the order parameters, which we denote by a bar, e.g. 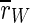 .
.
Results
Behaviour of the unstimulated system
In the unstimulated system, we observe tightly synchronized spike volleys that occur with ∼10 Hz. This is in the alpha-range which is associated with an alert but relaxed state (Geyer et al. 2009). This synchronization phenomenon is widely known for random coupled neural networks (Ananthanarayanan 2007; Börgers 2003; Izhikevich 2003, 2006).
As one can already suspect by looking at the distribution of the spikes over time, all three order parameters have big values close to 1, at least between spike volleys. When such a population spike occurs, the order parameters break down and reach values that can be as small as 0.2 or even smaller for a very short time.
The dynamics of the unstimulated system is shown in Fig. 1 in each of the subfigures (a–h) before the stimulus onset. At 3,000 ms, stimulation impulses were applied according to different protocols as described below. For each stimulation type, Fig. 2 shows the respective network activities (left panels), as well as the time-dependence of the order parameter (right panels).
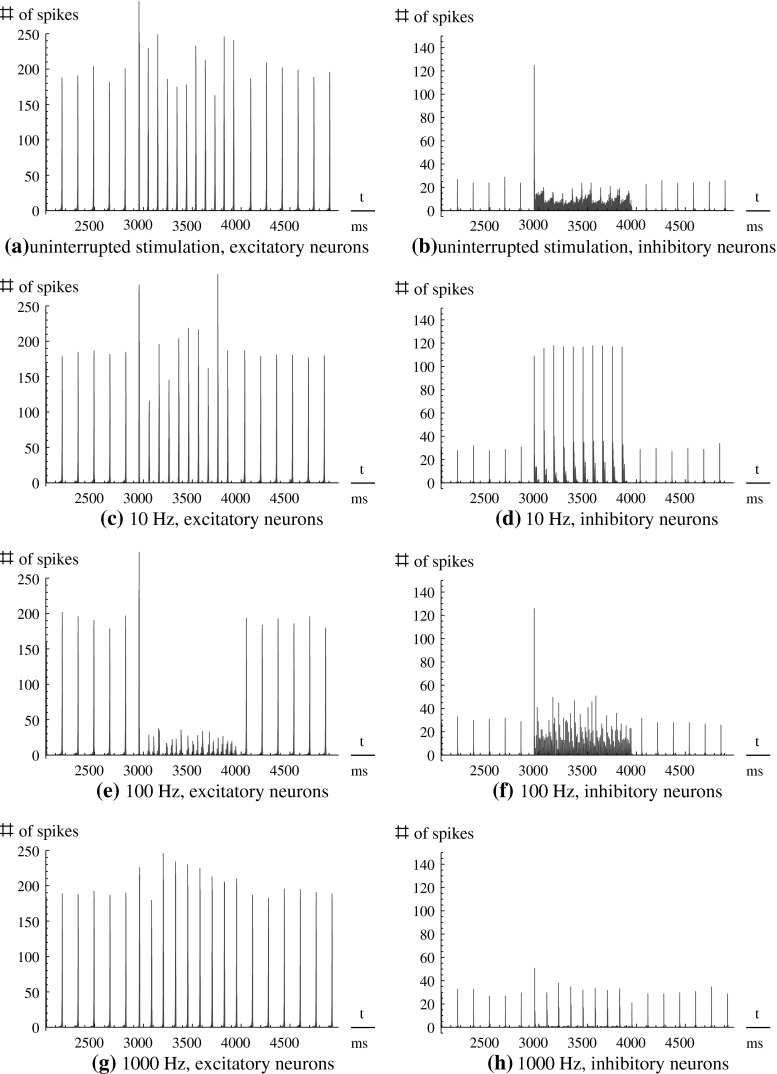
Fig. 1.
Spike histograms of 3,000 ms of four simulations, for the excitatory (left-hand side) and the inhibitory (right-hand side) subpopulation. The stimulation protocol is as follows: Stimulation I ext was switched on 3,000 ms after initialization for 1,000 ms. Each stimulation is monopolar (excitatory DC stimulation) and either uninterupted DC (a, b), or modulated by a rectangular envelope of 10 Hz (c, d), 100 Hz (e, f), or 1,000 Hz (g, h), respectively. Before and after the stimulation, the behavior of the unstimulated system is visible
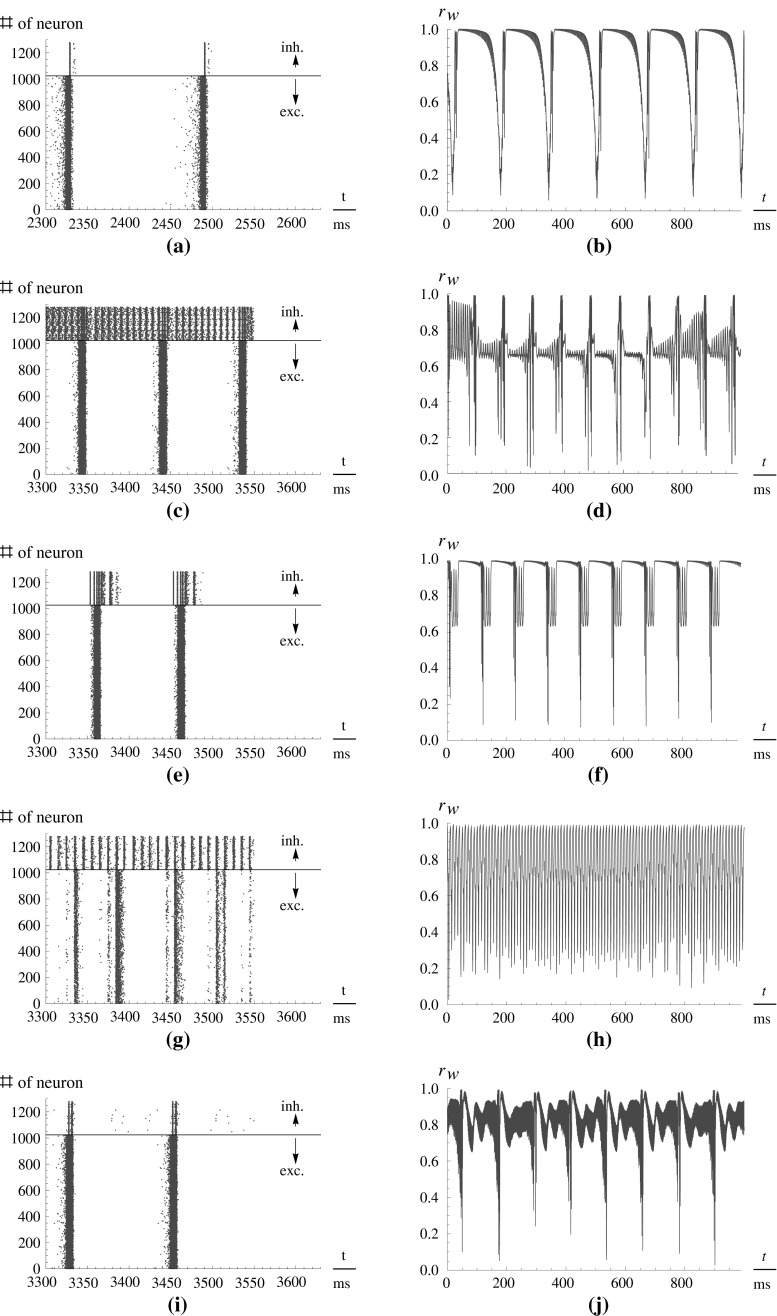
Fig. 2.
Left-hand side Spike times of the neurons in the network. Each point denotes a spike. The ordinate denotes the number of the neuron if numbered serially. Above the black line are the inhibitory neurons, below it the excitatory neurons. Right-hand side The order parameter r W over the time (ordinata: relative to stimulation onset t = 0). Amplitude of stimulation is 10 in both cases. Note the different scaling of the abscissae on the left- and the right-hand side. (a, b) Before stimulation. (c, d) Uninterrupted stimulation. (e, f) 10 Hz rectangular pulses. (g, h) 100 Hz rectangular pulses. (i, j) 1,000 Hz rectangular pulses
Uninterrupted DC stimulation
For (uninterrupted) DC stimulation, the frequency of the spike volleys is increased, but the spike volleys of the excitatory subpopulation still remain discriminable. In contrast to that, the inhibitory subpopulation now fires continuously, as there are only few and relatively weak inhibitory-inhibitory synapses which could affect this subpopulation to cease fire.
For this type of stimulation, 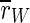 is decreased. In fact, it is the strongest reduction of
is decreased. In fact, it is the strongest reduction of 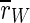 that we observe for all stimulation frequencies. But if one takes a view on the order parameters of the two subpopulations, one gets a different finding.
that we observe for all stimulation frequencies. But if one takes a view on the order parameters of the two subpopulations, one gets a different finding. 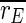 is even increased. In contrast, rI fluctuates strongly and fast almost between 1 and 0. Therefore,
is even increased. In contrast, rI fluctuates strongly and fast almost between 1 and 0. Therefore, 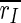 is decreased all in all, but not as strong as
is decreased all in all, but not as strong as 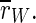 So, the reduction of
So, the reduction of 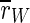 stems in parts from the desynchronization of the inhibitory subpopulation, but also from the desynchronization of both subpopulations from each other.
stems in parts from the desynchronization of the inhibitory subpopulation, but also from the desynchronization of both subpopulations from each other.
Low frequency stimulation (10 Hz)
For low frequency stimulation, the spiking pattern of the excitatory subpopulation remains almost unchanged, but as such frequencies are near the systems eigenfrequency, we have a resonance phenomenon. Therefore, the population spikes are now time-locked to the stimuli, and occur with exactly the frequency of the stimulation. Hence the activity becomes more synchronized, leading to the observable effect that all three order parameters are increased (Fig. 3).
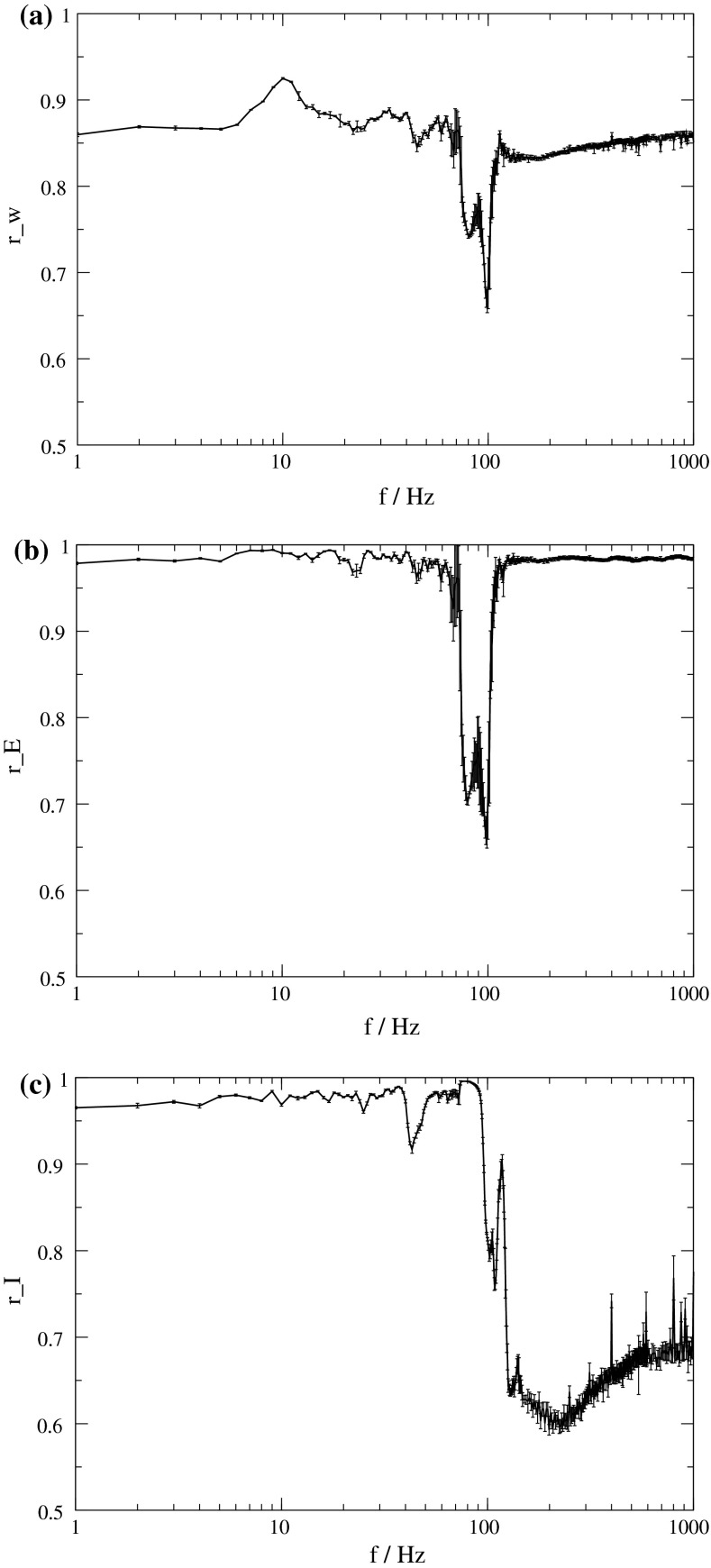
Fig. 3.
Dependence of the order parameter on the frequency of stimulation. Intensity of stimulation is 10. a r W of the whole population. b r E of the excitatory subpopulation. c r I of the inhibitory subpopulation. In all three plots, averages are shown over 15 simulations, and the corresponding standard deviations are indicated by error bars
High frequency stimulation (100 Hz)
If we increase the frequency of the stimulation to high frequencies of ∼100 Hz, the spike volleys still occur during stimulation and synchronize with the stimulation frequency. If the amplitude of the stimulation is not high enough, some stimuli may be missed, so that, for example, three spikes occur locked to the stimuli, and then for another two stimuli, the neural network is silent.
This finding is supported by the order parameter 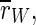 which decreases around 100 Hz. It does not decrease as much as for the uninterrupted stimulation, but in contrast to that kind of stimulation, the order parameter
which decreases around 100 Hz. It does not decrease as much as for the uninterrupted stimulation, but in contrast to that kind of stimulation, the order parameter 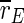 of the excitatory subpopulation decreases as well, and below the baseline value of the unstimulated case. Similarly,
of the excitatory subpopulation decreases as well, and below the baseline value of the unstimulated case. Similarly, 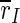 is decreased, but the minimum is not as sharp as for
is decreased, but the minimum is not as sharp as for 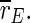
Very high frequency stimulation (1,000 Hz)
If we increase the stimulation frequency further, the individual neurons cannot follow the stimulation frequency, and we observe spike time characteristics that are very similar to the unstimulated case. All three order parameters again increase to higher values. One could think that it is possible to reproduce the desynchronizing effect of the moderate high frequencies by increasing the stimulus amplitude, but unfortunately we could not generate such effect (not shown).
Post-stimulation characteristics
As we did not model aspects like synaptic plasticity, there are no long-term effects of the stimulation. All effects cancel out with cessation of stimulation, except a small reduction in spike rate, which soon returns to baseline values.
Discussion
We applied depolarizing electrical stimulation to a simple cortex model. The stimulating current is interrupted with different frequencies.
If not stimulated, the model exhibits synchronized spike volleys or population spikes at frequencies that lie in the alpha range. This synchronization phenomenon is widely known for randomly coupled neural networks (Ananthanarayanan 2007; Börgers 2003; Izhikevich 2003, 2006). The three order parameters we have defined are close to the maximum value 1 when there are no spike volleys, but break down when population spikes occur. This is not surprising as the movement on the trajectories is very fast during spikes, compared to the time between spikes. Thus, if there is only a little difference between the spike timings of two different neurons, they may be far apart from each other, whereas for the time between population spikes, all neurons have values of v and 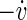 located in a small volume of the phase space. Thus the phases are very similar between population spikes and more different during the population spikes, and the order parameters break down in the latter case.
located in a small volume of the phase space. Thus the phases are very similar between population spikes and more different during the population spikes, and the order parameters break down in the latter case.
For uninterrupted DC stimulation the frequency of the spike volleys increases, and the inhibitory subpopulation begins to fire continously. Although the average order parameter 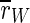 of the whole population decreases strongly, the order parameter
of the whole population decreases strongly, the order parameter 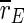 of the excitatory subpopulation is increased by uninterrupted stimulation. Enhanced synchronization in large groups of neurons is also reason for epileptic spasms. As motor neurons (which are—excitatory—pyramidal neurons) can be effected by TCES as well as any other population in the cortex, we think this effect could be a possible explanation of the clonic spasms which are produced by uninterrupted high intensity extracranial DC stimulation (Limoge 1975).
of the excitatory subpopulation is increased by uninterrupted stimulation. Enhanced synchronization in large groups of neurons is also reason for epileptic spasms. As motor neurons (which are—excitatory—pyramidal neurons) can be effected by TCES as well as any other population in the cortex, we think this effect could be a possible explanation of the clonic spasms which are produced by uninterrupted high intensity extracranial DC stimulation (Limoge 1975).
If the stimulation is interrupted at low frequencies, population spikes become time-locked to the stimuli, and the order parameters 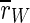 and
and 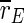 even increase. This is not unexpected as stimulation near the eigenfrequency of a system leads to resonance. If we think about DBS, for which a similar frequency dependence of effectiveness as for TCES is observed (e.g., compare (Limoge 1975; Limoge et al. 1999; Sances 1975) for TCES with (Gang et al. 2005; McIntyre et al. 2004) for DBS), it is known that stimulation with low frequencies can even worsen the symptoms which are associated with too strong pathological synchronization (Garcia et al. 2003). In terms of TCES, such a stimulation would possibly counteract any anaesthetic action, but this cannot be said definitely as there seem to be no experiments on that yet.
even increase. This is not unexpected as stimulation near the eigenfrequency of a system leads to resonance. If we think about DBS, for which a similar frequency dependence of effectiveness as for TCES is observed (e.g., compare (Limoge 1975; Limoge et al. 1999; Sances 1975) for TCES with (Gang et al. 2005; McIntyre et al. 2004) for DBS), it is known that stimulation with low frequencies can even worsen the symptoms which are associated with too strong pathological synchronization (Garcia et al. 2003). In terms of TCES, such a stimulation would possibly counteract any anaesthetic action, but this cannot be said definitely as there seem to be no experiments on that yet.
For stimulation with moderately high frequencies, we found the introduction of a new activity pattern. As the neurons try to follow the stimulation frequency, smaller spike volleys occur which are locked to the stimuli. But due to the short duration of the stimuli, some of them are missed by the population spikes, and only a smaller number of neurons participates in each such spike volley, compared to the intrinsic volleys. Effectively, this is a desynchronizaton of the neural activity. It is well known that Deep Brain Stimulation of the subthalamic nucleus with such moderately high frequencies cancels out the pathological synchronization induced by Parkinson’s disease. We propose that in the cortex this desynchronization phenomenon intercepts neural information processing, as it is known from experiments on electroanaesthesia (EA) (Limoge 1975), which eventually lead to the invention of TCES.
For very high stimulation frequencies, the desynchronizing effect again vanishes. This is in compliance with investigations in DBS (Jensen 2007), reporting stimulation in the kHz range to have no effect, and with old reports on EA showing the current intensity necessary for the loss of consciousness to greatly increase for such high frequencies (Sances 1975). In fact, increasing the stimulation amplitude could not fully compensate the effect of increasing the frequency in our model. Instead, by increasing the amplitude of stimulation, we rather found effects similar to those of uninterrupted current. Perhaps this explains why currents with a frequency of approximately 100 Hz, modulated with ultra high frequency currents (∼100 kHz), are comparatively effective than the unmodulated current (Limoge 1975; Limoge et al. 1999). If the ultra high frequency current acts similar to an uninterrupted current, the effect is expected to be similar to the unmodulated 100 Hz current, but it has lesser secondary effects, as less current is delivered to the brain.
Summary and outlook
Deep brain stimulation and transcranial electrical stimulation are two promising applications of electrical currents in medical practice. Whereas DBS has largely replaced pallidotomy in the treatment of Parkinson’s disease (McIntyre et al. 2004), and is prosperous in the treatment of some other neural diseases (Benabid et al. 1996; Coubes et al. 2000; Nuttin et al. 2003; Velasco et al. 1995; Yianni et al. 2003), TCES yet does not have reached a comparative level of potential applications that it could have in surgical practice.
In summary, we have presented a generic cortex model which reproduces the frequency dependence of the activity of TCES: With uninterrupted stimulation, the overall synchronization is decreased but the synchronization of the excitatory subpopulation is increased. For moderately high frequencies synchronization of the whole population and the excitatory subpopulation is decreased as well. We assume the same mechanism to account for the similar frequency dependence of the efficacy of DBS, resulting in a drastic desynchronization of the spiking activity. Stimulation of our cortex models with unipolar 100 Hz rectangular waveforms leads to distinct changes of the spiking properties of the neural network, and it markedly reduces the synchronization of the network, which is quantified by the order parameters 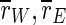 and
and 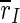 . Whereas slower or higher stimulation frequencies do not lead to such distinct changes, and instead can even tend to enforce the natural behaviour of the model, moderately high frequencies (around 100 Hz) lead to a desynchronization of activity. We therefore suppose that desynchronization of cortical activity and the introduction of cortical noise is at least in parts accountable for the effects of TCES, as it disrupts ongoing signal processing in the cortex.
. Whereas slower or higher stimulation frequencies do not lead to such distinct changes, and instead can even tend to enforce the natural behaviour of the model, moderately high frequencies (around 100 Hz) lead to a desynchronization of activity. We therefore suppose that desynchronization of cortical activity and the introduction of cortical noise is at least in parts accountable for the effects of TCES, as it disrupts ongoing signal processing in the cortex.
This model obviously just gives hints to the the question how TCES actually works. To consolidate our theory that the desynchronization of cortical activity leads to the beneficial effects of TCES we would have to build up a more complex and of course larger model containing more neurons, which should take into account the spatial structure of the brain. If a spatial distribution of the neurons is modeled, one should desist from assuming homogenous electrical fields and model explicitly the electric field distribution. Also, neurons could be modeled in different degree of detail, e.g., according to Izhikevich (2003) taking into account more firing patterns, or as advanced versions of Hodgkin–Huxley neurons with realistic synaptic dynamics, including synaptic plasticity and axonal delays that depend on the spatial distances of the neurons. Similarily, a multi-compartment model—containing at least two or three compartments for axon, soma, and eventually dendrite—could be used. While the quantitative dynamics of such more detailed models might come closer to reality, we expect those models to exhibit a similar desynchronization effect in the 100 Hz regime, as demonstrated in our model.
Acknowledgments
Financial support by the Deutsche Forschungsgemeinschaft (DFG SFB-654 project A8 and Graduate School for Computing in Medicine and Life Science) is gratefully acknowledged.
References
- Acebrón JA, Bonilla LL, Vicente CJP, Ritort F, Spigler R. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev Mod Phys. 2005;77:137–185. doi: 10.1103/RevModPhys.77.137. [DOI] [Google Scholar]
- Ananthanarayanan R, Modha DS (2007) Anatomy of a cortical simulator. In: Supercomputing 07: Proceedings of the ACM/IEEE SC2007 conference on high performance networking and computing. Association for Computing Machinery, New York
- Anderson TR, Hu B, Iremonger K, Kiss ZHT. Selective attenuation of afferent synaptic transmission as a mechanism of thalamic deep brain stimulation-induced tremor arrest. J Neurosci. 2006;26(3):841–850. doi: 10.1523/JNEUROSCI.3523-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antal A, Kincses TZ, Nitsche MA, Bartfai O, Paulus W. Excitability changes induced in the human primary visual cortex by transcranial direct current stimulation: direct electrophysiological evidence. Invest Ophtal Vis Sci. 2004;45:702–707. doi: 10.1167/iovs.03-0688. [DOI] [PubMed] [Google Scholar]
- Antal A, Nitsche MA, Kincses TZ, Kruse W, Hoffmann KP, Paulus W. Facilitation of visuo-motor learning by transcranial direct current stimulation of the motor and extrastriate visual areas in humans. Eur J Neurosci. 2004;19(10):2888–2892. doi: 10.1111/j.1460-9568.2004.03367.x. [DOI] [PubMed] [Google Scholar]
- Bellinger SC, Miyazawa G, Steinmetz PN. Submyelin potassium accumulation may functionally block subsets of local axons during deep brain stimulation: a modeling study. J Neural Eng. 2008;5:263–274. doi: 10.1088/1741-2560/5/3/001. [DOI] [PubMed] [Google Scholar]
- Benabid A, Pollak P, Gross C, Hoffmann D, Benazzouz A, Gao D, Laurent A, Gentil M, Perret J. Acute and long-term effects of subthalamic nucleus stimulation in Parkinson’s disease. Stereotact Funct Neurosurg. 1994;62:76–84. doi: 10.1159/000098600. [DOI] [PubMed] [Google Scholar]
- Benabid AL, Pollak P, Gao D, Hoffmann D, Limousin P, Gay E, Payen I, Benazzouz A (1996) Chronic electrical stimulation of the ventralis intermedius nucleus of the thalamus as a treatment of movement disorders. J Neurosurg 84(2):203–214 [DOI] [PubMed]
- Börgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse. Random Connect Neural Comp. 2003;15:509–538. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- Compte A, Sanchez-Vivez MV, McCormick DA, Wang X-J. Cellular and network mechanisms of slow oscillatory activity (<1Hz) and wave propagations in a cortical network model. J Neurophysiol. 2003;89:2707–2725. doi: 10.1152/jn.00845.2002. [DOI] [PubMed] [Google Scholar]
- Coubes P, Roubertie A, Vayssiere N, Hemm S, Echenne B. Treatment of DYT1-generalised dystonia by stimulation of the internus globus pallidus. Lancet. 2000;355:2220–2221. doi: 10.1016/S0140-6736(00)02410-7. [DOI] [PubMed] [Google Scholar]
- Gang L, Chao Y, Ling L, Lu SC-Y. Uncovering the mechanism(s) of deep brain stimulation. J Phys Conf Ser. 2005;13:336–344. doi: 10.1088/1742-6596/13/1/078. [DOI] [Google Scholar]
- Garcia L, Audin J, D’Alessandro G, Bioulaxc B, Hammond C. Dual effect of high-frequency stimulation on subthalamic neuron activity. J Neurosci. 2003;23(25):8743–8751. doi: 10.1523/JNEUROSCI.23-25-08743.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geyer JD, Talathi S, Carney PR. Introduction to sleep and polysomnography. In: John L, Greenfield JR, Geyer JD, Carney PR, editors. Reading EEGs: a practical approach. Philadelphia: Lippincott Williams & Wilkins; 2009. [Google Scholar]
- Gupta A, Wang Y, Markram H. Organizing principle for a diversity of GABAergic interneurons and synapses in the neocortex. Science. 2000;287:273–278. doi: 10.1126/science.287.5451.273. [DOI] [PubMed] [Google Scholar]
- Hauptmann C, Tass PA (2010) Restoration of segregated, physiological neuronal connectivity by desynchronizing stimulation. J Neural Eng 7:056008 [DOI] [PubMed]
- Houeto JL, Karachi C, Mallet L, Pillon B, Yelnik J, Mesnage V, Welter ML, Navarro S, Pelissolo A, Damier P, Pidoux B, Dormont D, Cornu P., Agid Y. Tourettes syndrome and deep brain stimulation. J Neurol Neurosurg Psychiatry. 2005;76:992–995. doi: 10.1136/jnnp.2004.043273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Simple model of spiking neurons. IEEE Trans Neural Netw. 2003;14(6):1569–1572. doi: 10.1109/TNN.2003.820440. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Which model to use for cortical spiking neurons? IEEE Trans Neural Netw. 2004;15:1063–1070. doi: 10.1109/TNN.2004.832719. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Polychronization: computation with spikes. Neural Comput. 2006;18:245–282. doi: 10.1162/089976606775093882. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM, Gally JA, Edelman GM. Spike-timing dynamics of neuronal groups. Cereb Cortex. 2004;14:933–944. doi: 10.1093/cercor/bhh053. [DOI] [PubMed] [Google Scholar]
- Jensen AL, Durand DM (2007) Suppression of axonal conduction by sinusoidal stimulation in rat hippocampus in vitro. J Neural Eng 4:116 [DOI] [PubMed]
- Kumar R, Dagher A, Hutchison WD, Lang AE, Lozano AM. Globus pallidus deep brain stimulation for generalized dystonia: clinical and PET investigation. Neurology. 1999;53:871. doi: 10.1212/WNL.53.4.871. [DOI] [PubMed] [Google Scholar]
- Kuramoto Y (1975) In: Araki H (ed) International symposium on mathematical problems in theoretical physics. Lecture Notes in Physics, vol 30. Springer, New York, p 420
- Lian J, Shuai J, Durand DM. Control of phase synchronization of neuronal activity in the rat hippocampus. J Neural Eng. 2004;1:46–54. doi: 10.1088/1741-2560/1/1/007. [DOI] [PubMed] [Google Scholar]
- Limoge A. An introduction to electroanaesthesia. Baltimore: University Park Press; 1975. [Google Scholar]
- Limoge A, Robert C, Stanley TH. Transcutaneous cranial electrical stimulation (TCES): a review 1998. Neurosci Biobehav Rev. 1999;23:529–538. doi: 10.1016/S0149-7634(98)00048-7. [DOI] [PubMed] [Google Scholar]
- Liu Y, Wang R, Zhang Z, Jiao X. Analysis on stability of neural network in the presence of inhibitory neurons. Cogn Neurodyn. 2010;4(1):61–68. doi: 10.1007/s11571-009-9100-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Wang Y, Tsodyks M. Differential signaling via the same axon of neocortical pyramidal neurons. Proc Natl Acad Sci. 1998;95:5323–5328. doi: 10.1073/pnas.95.9.5323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC, Savasta M, Kerkerian-Le Groff L, Vitek JL. Uncovering the mechanism(s) of action of deep brain stimulation: activation, inhibition, or both. Clin Neurophys. 2004;115:1239–1248. doi: 10.1016/j.clinph.2003.12.024. [DOI] [PubMed] [Google Scholar]
- Nuttin B, Gabriëls LA, Cosyns PR, Meyerson BA, Andrewitch S, Sunaert S, Maes A, Dupont P, Gybels JM, Gielen F, Demeulemeester HG. Long-term electrical capsular stimulation in patients with obsessive-compulsive disorder. Neurosurgery. 2003;52(6):1263–1272. doi: 10.1227/01.NEU.0000064565.49299.9A. [DOI] [PubMed] [Google Scholar]
- Obesó JA, Olanow CW, Rodriguez-Oroz MC, Krack P, Kumar R, Lang AE. Deep-brain stimulation of the subthalamic nucleus or the pars interna of the globus pallidus in Parkinson’s disease. N Engl J Med. 2001;345:956–963. doi: 10.1056/NEJMoa000827. [DOI] [PubMed] [Google Scholar]
- Pikovsky AS, Rosenblum MG, Osipov GV, Kurths J. Phase synchronization of chaotic oscillators by external driving. Phys D. 1997;104:219–238. doi: 10.1016/S0167-2789(96)00301-6. [DOI] [Google Scholar]
- Ressler KJ, Mayberg HS. Targeting abnormal neural circuits in mood and anxiety disorders: from the laboratory to the clinic. Nat Neurosci. 2007;10(9):1116–1124. doi: 10.1038/nn1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sances A, Jr, Larson SJ. Electroanesthesia—biomedical and biophysical studies. New York: Academic Press; 1975. [Google Scholar]
- Schöll E, Hiller G, Hövel P, Dahlem MA. Time-delayed feedback in neurosystems. Phil Trans R Soc A. 2009;367(1891):1079–1096. doi: 10.1098/rsta.2008.0258. [DOI] [PubMed] [Google Scholar]
- Steriade M, Timofeev I, Grenier F. Natural waking and sleeping states: a view from inside neocortical neurons. J Neurophysiol. 2001;85:1969–1985. doi: 10.1152/jn.2001.85.5.1969. [DOI] [PubMed] [Google Scholar]
- Su Y, Radman T, Vaynsteyn J, Parra LC, Biksom M. Effects of high-freqency stimulation on epileptiform activity in vitro: ON/OFF control paradigm. Epilepsia. 2008;49:1586–1593. doi: 10.1111/j.1528-1167.2008.01592.x. [DOI] [PubMed] [Google Scholar]
- Velasco F, Velasco M, Velasco A, Jimenez F, Marquez I, Rise M. Electrical stimulation of the centralmedian thalamic nucleus in control of seizures: long-term studies. Epilepsia. 1995;36:63–71. doi: 10.1111/j.1528-1157.1995.tb01667.x. [DOI] [PubMed] [Google Scholar]
- Visser-Vandewalle V. DBS in Tourette syndrome: rationale, current status and future prospects. Acta Neurochir Suppl. 2007;97(2):215–222. doi: 10.1007/978-3-211-33081-4_24. [DOI] [PubMed] [Google Scholar]
- Wang R, Zhang Z. Phase synchronization motion and neural coding in dynamic transmission of neural information. IEEE Trans Neural Netw. 2011;22(7):1097–1106. doi: 10.1109/TNN.2011.2119377. [DOI] [PubMed] [Google Scholar]
- Yianni J, Bain P, Giladi N, Auca M, Gregory R, Joint C, Nandi Dm, Stein J, Scott R, Aziz T. Globus pallidus internus deep brain stimulation for dystonic conditions: a prospective audit. Mov Disord. 2003;18:436–442. doi: 10.1002/mds.10380. [DOI] [PubMed] [Google Scholar]
- Zaghi S, Acar M, Hultgren B, Boggio PS, Fregni F (2009) Non-invasive brain stimulation with low intensity electrical currents: putative mechanisms of action of direct and alternating current stimulation. Neuroscientist (in press) [DOI] [PubMed]
- Zhang X, Wang R, Zhang Z. Dynamic phase synchronization characteristics of variable high-order coupled neuronal oscillator population. Neurocomputing. 2010;73:2665–2670. doi: 10.1016/j.neucom.2010.05.001. [DOI] [Google Scholar]