Neuromodulation of STDP through short-term changes in firing causality

Abstract

Spike timing dependent plasticity (STDP) likely plays an important role in forming and changing connectivity patterns between neurons in our brain. In a unidirectional synaptic connection between two neurons, it uses the causal relation between spiking activity of a presynaptic input neuron and a postsynaptic output neuron to change the strength of this connection. While the nature of STDP benefits unsupervised learning of correlated inputs, any incorporation of value into the learning process needs some form of reinforcement. Chemical neuromodulators such as Dopamine or Acetylcholine are thought to signal changes between external reward and internal expectation to many brain regions, including the basal ganglia. This effect is often modelled through a direct inclusion of the level of Dopamine as a third factor into the STDP rule. While this gives the benefit of direct control over synaptic modification, it does not account for observed instantaneous effects in neuronal activity on application of Dopamine agonists. Specifically, an instant facilitation of neuronal excitability in the striatum can not be explained by the only indirect effect that dopamine-modulated STDP has on a neuron’s firing pattern. We therefore propose a model for synaptic transmission where the level of neuromodulator does not directly influence synaptic plasticity, but instead alters the relative firing causality between pre- and postsynaptic neurons. Through the direct effect on postsynaptic activity, our rule allows indirect modulation of the learning outcome even with unmodulated, two-factor STDP. However, it also does not prohibit joint operation together with three-factor STDP rules.

Introduction

Recent experiments have indicated that Dopamine may directly influence the spiking activity of prefrontal neurons by increasing signal-to-noise ratio (Kroener et al. 2009) or gain (Thurley et al. 2008) during synaptic transmission. These studies suggest that an instant effect of Dopamine may only be present during additional synaptic input and that Dopamine may not be capable of eliciting a synaptic response on its own in this case.

While the influence of varying Dopamine on synaptic learning processes has been recognized and modelled in a large number of publications (Farries and Fairhall 2007; Izhikevich 2007; Morrison et al. 2008; Potjans et al. 2009; Reynolds and Wickens 2002), this has usually been done by directly adapting the STDP rule to include an additional third factor signalling dopaminergic reinforcement, beside inclusion of the pre- and postsynaptic activities. The requested synaptic weight change defined by STDP would often be multiplied by a reinforcement factor in the interval [−1,1], yielding no synaptic learning for baseline levels of Dopamine (zero reinforcement) and inverted, or “anti-hebbian”, learning for negative values of reinforcement.

Postsynaptic activity would be only indirectly affected by Dopamine in these models, through the gradual synaptic weight change induced by reinforced STDP.

However, there have been modelling studies incorporating experimental evidence on increased postsynaptic facilitation under Dopamine exposure (Chorley and Seth 2011), albeit by affecting the neuron-wide recovery function of the postsynaptic model neuron. To our knowledge, no previous modelling studies of dopaminergic influence on synaptic transmission with an only indirect effect on the synaptic learning process have been published.

We chose to investigate the possible network level implications of a (Dopamine-like) neuromodulator purely affecting synaptic transmission on a local scale. As any postsynaptic activity is highly dependent on the received synaptic input, changes to this input directly affect the postsynaptic neuron’s spiking activity as the second factor in usual STDP rules (Bi and Poo 2001). Any neuromodulation of synaptic transmission is therefore in principle able to affect the learning outcome of STDP, even when no direct involvement of the modulator in the actual weight adjustment process is present.

There are in theory two ways of affecting the amount of synaptic input a neuron receives. The first would need sufficient control over the spiking activity of presynaptic neurons, which is difficult to provide for inputs arriving from distant brain areas such as the axonal endings arriving in the basal ganglia’s striatum from all parts of the cortex. The second possibility would be to introduce a short-term, reversible effect on the actual process of synaptic transmission, which regulates the amount of input arriving at a postsynaptic neuron through the synaptic connection when a presynaptic neuron fires. If a neuromodulator were to influence the short-term transmission efficacy of synaptic connections, it would temporarily be changing the effective weight of those synaptic connections for all intents and purposes.

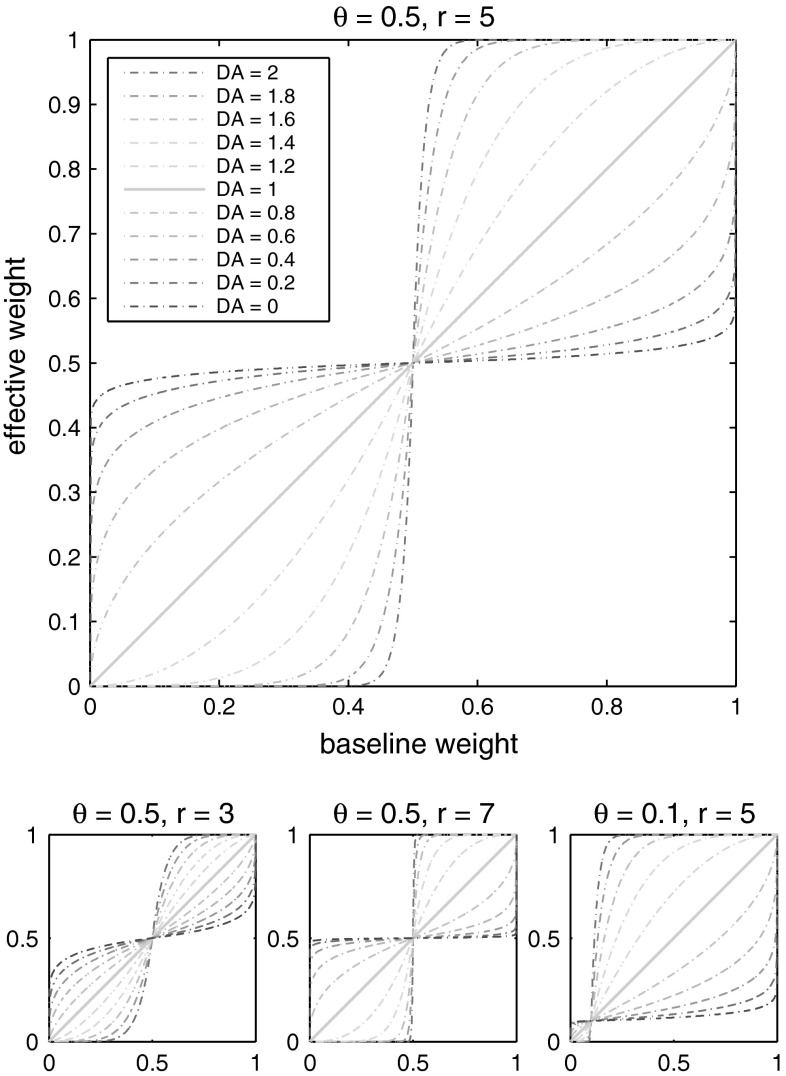
We therefore modulate only synaptic transmission in our model, and show that we can still influence the learning outcome with an unchanged STDP rule. Without any direct reference to existing chemical neuromodulators, we coincidentally call our neuromodulatory reinforcement factor DA. However, simply multiplying the existing baseline weight with the current DA level to form an effective weight would be problematic: Whenever the applied reinforcement would reach a value around zero, all synaptic transmission would stop, which is unwanted behaviour for a neuromodulated synapse. Instead, we use a power law relationship between baseline weights and the current level of DA to form the effective synaptic weights used for transmission. We define a threshold value θ that divides the baseline weights into strong and weak weights and shifts the strong weights above 1 before applying the power law (Eqs. 1, 2). For low DA, all effective weights now become more similar to θ. For high DA, all effective weights move away from θ, towards the extremes of the defined weight range. We call θ the generalisation threshold for low levels of the reinforcement signal and the sparsification threshold for high levels. Due to the shape of our effective weights rule (Fig. 1), no strong baseline weight ever has an effective value below θ, and no weak baseline weight ever has an effective value above θ. Also, as the effective weight curves for low DA mirror those for high DA around the unmodulated weights line (DA = 1, shown in green), the overall postsynaptic firing rate remains unaffected under reinforcement for uniformly distributed baseline weights. For a possible chemical interpretation of θ, see “Conclusion”.

Fig. 1.

Proposed effects of a reinforcement signal DA on synaptic transmission, perceived as a DA-dependent synapse-local change of effective weights. As in biological dopaminergic systems, a tonic base line of the reinforcement signal (DA = 1) exists, which here keeps the effective weights equal to their actual baseline values. The threshold for defining strong and weak weights can be changed by varying θ

Methods

Modulation mechanics

We propose the existence of a neuromodulator which directly affects the process of synaptic transmission. Depending on the ratio of enabling receptors (henceforth called D1-type) to attenuating receptors (henceforth called D2-type) in a neuron’s synapse, an increase of neuromodulator above baseline levels may sparsify synaptic transmission by easing transmission through strong synapses and hindering transmission through weak synapses. Similarly, we suggest that declining amounts of neuromodulator in the surrounding tissue may have a generalising effect on synaptic transmission, where the efficacy of strong and weak synapses becomes more equal around some threshold ratio θ.

We further assume that the threshold θ at which the sparsification bifurcates, and to which the generalisation tends, may slowly be regulated by homeostatic (chemical) gradients within the cell. This will be explored in future work.

Here, we examine the implications of our proposition, and show that synaptic learning can be reliably modulated by only the given mechanisms. No direct influence in the actual spike timing dependent plasticity process is needed for modulation to succeed.

Affecting synaptic excitability

We define a modulatory parameter DA that contains our reinforcement information within the range [0,2], where the value 1 stands for no specific feedback. If it were to be mapped to the activity of dopaminergic cells in the Substantia Nigra pars compacta (SNc), DA = 1 would be equivalent to normal tonic firing and default levels of dopamine released into the striatum.

We simulate DA-dependent changes in perceived synaptic efficacy as changes to effective weightse_ij used for computation of synaptic transmission, in distinction from the default efficacy of synapses at baseline levels of the neuromodulator (DA = 1), which we call baseline weightsw_ij. We set

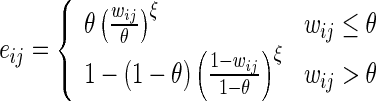1

and

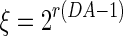2

where 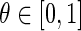is the homeostatic threshold for weight sparsification and generalisation, is the level of Dopamine currently applied to the network, and r is a range parameter for controlling the impact on sparsification or generalisation the neuromodulator can have (see Fig. 1). For simplicity we assume r = 5 and θ = 0.5 within most of this article. Slow homeostatic adaptation of θ and r will be explored in future work. The double power law relationship between the baseline weight and the current DA level (introduced by combining Eqs. 1 and 2) allows a bijectional projection to effective weights and makes the curves for high DA levels mirror those of low DA levels across the DA = 1 line.

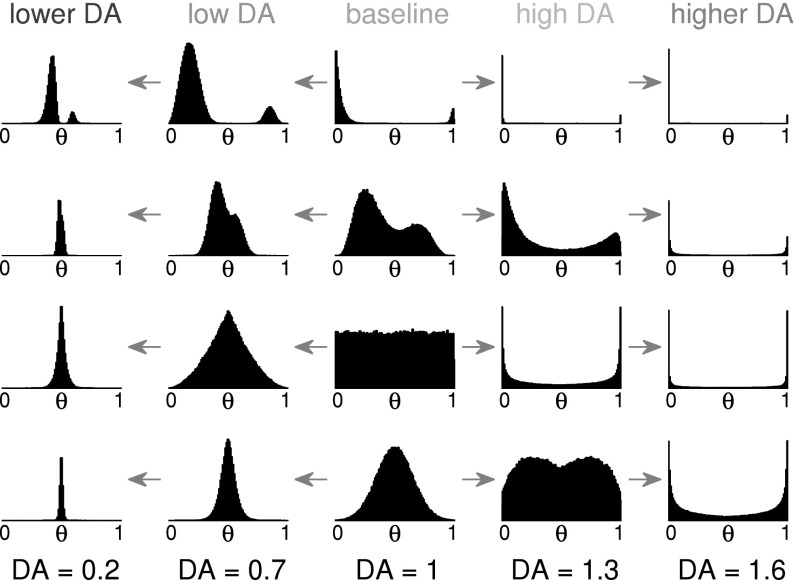
Effective weight distribution

The formulation of effective weights allows us to compare any instant changes in the perceived distribution of weights that are due to changes in neuromodulator level. In Fig. 2 we show a selection of baseline weight distributions in a centre column, and their DA-induced changes as effective weight distributions in the other columns. Synaptic transmission is computed using the current effective weights, while any STDP-induced weight change is applied to the baseline weights. The effective weights are updated on any change of baseline weights or DA level.

Fig. 2.

Effects of the proposed effective weight rule on existing weight distributions. Example weight distributions at DA = 1 are given in the centre column. On the right are the effective weight distributions for high DA, and on the left are the effective weight distributions at low DA levels as defined in Eqs. 1 and 2. Rows 1 and 2 Any double-peak distribution where the two peaks are on opposite sides of θ will remain so for high DA, but with increased sparseness. For low DA levels, the two peaks move closer to θ, and thereby make discrimination of strong versus weak weights increasingly difficult. Rows 3 and 4 A uniform or a normal distribution of weights around θ will act as a true bimodal distribution for high DA levels and become a thin unimodal distribution for low levels of DA. The reduced signal-to-noise ratio for low DA and increased ratio for high DA (assuming the signal is represented by the strong weights) becomes visible

As the neurotransmitter level is increased, any broad distribution of weights becomes more bimodal, away from the sparsification threshold θ. Slightly stronger synapses (weights above the threshold) thereby become dominant in guiding postsynaptic activation, while connections with weights even slightly below the threshold loose influence on postsynaptic activation. A slightly trained network therefore acts as if it has undergone more training and acts more selective to a smaller number of inputs. Any over-representation of strong effective weights that would lead to excessive postsynaptic firing is then gradually reduced by our asymmetric STDP rule towards sparse coincidental firing, given random uncorrelated inputs. This competition reduces the number of strong synapses and readies the neuron for detecting more structured, non-random inputs by adapting it to mostly ignore random background input activity.

As the neurotransmitter level is decreased, any distribution of effective weights becomes more centred around the generalisation threshold θ, leading towards an equalization of effective weights. The effect of each synaptic connection on membrane activity of the postsynaptic neuron becomes less dependent on the actual (baseline) synaptic strength. Instead, all connections start to behave increasingly similar in transmission efficacy, making it harder for the neuron to discriminate strong learnt inputs from ignorable background activity. This amplified noise level leads to frequent random weight adjustments, causing existing baseline weights to perform a semi-random walk. This randomisation process causes the baseline weights to become less sparse, while their mean is also reduced due to the asymmetry of the STDP rule used. Even a strongly trained neuron can thereby be “reset” to a general state with unimodal distribution of weights if the decrease in DA and range parameter r are large enough. As most weights act as being close to θ for very low amounts of neurotransmitter, the definition of θ directly affects the output activity of the postsynaptic neuron: A high value of θ leads to infinite firing of the postsynaptic neuron, while a low value of θ may make the postsynaptic neuron silent as soon as the strongest connections cease to be able to provoke postsynaptic firing. A slow adaptation of θ as a local variable within the postsynaptic neuron may therefore prove useful for continued activity, which may or may not be implemented as a slow chemical gradient for homeostasis.

Network structure

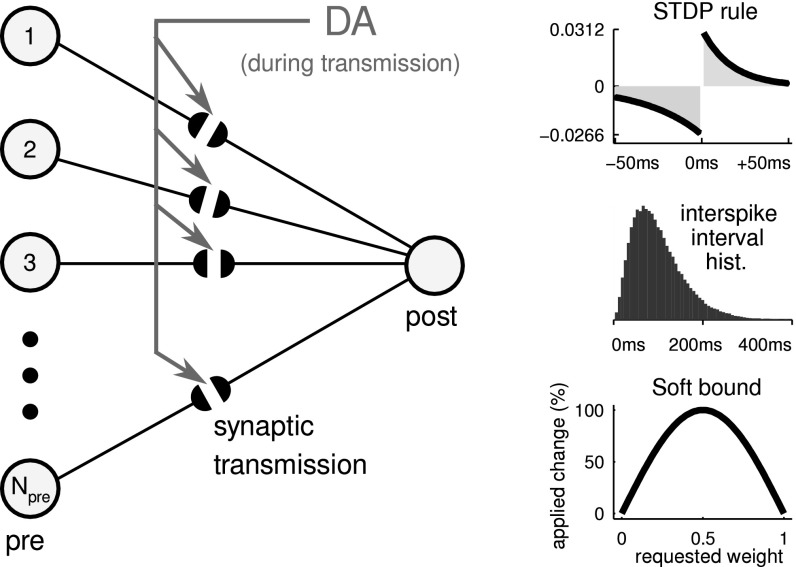
The network structure is shown in Fig. 3a, where the two-layer network consists of N_pre = 1,800 presynaptic units (inputs) that are fully connected to one postsynaptic neuron (output) via DA-modulated synapses. The modulation instantly affects the excitability of each synapse, which can be perceived as a change in effective synaptic weight. The activity-dependent learning process (STDP rule) is not altered.

Fig. 3.

Network structure and dynamics overview. Left Network structure. N _pre = 1,800 presynaptic input units transmit spikes via DA-modulated synapses to one postsynaptic output neuron. The modulation influences the synaptic transmission process, and has no direct involvement in updating long term weights during STDP. Right top Asymmetric STDP rule. The integral over the full range of the curve is negative, so random firing generally leads to a slow decrease of weights. Right middle Interspike interval (ISI) of background noise. The mean ISI is 100 ms in a right-skewed gamma distribution, giving a mean background firing rate of 10 Hz. Right bottom Arbitrary soft bound on weights. The effect of STDP is greatest on medium weight values, and decreases towards the extremes on each side. This also has the effect that synaptic connections are most volatile at medium weight values, while becoming more robust for more extreme weight values

Neuron model

We use the standard Izhikevich model in its one-dimensional form (Izhikevich 2004) as postsynaptic neuron. This gives us the realism of a delayed, self-firing neuron while improving predictability and computational complexity for large-scale simulations. The predictability specifically benefits from the reduction to a one-dimensional model as the neuron’s future activity is fully described by only its current membrane state and the current sum of arriving input currents. The neuron’s membrane potential is controlled by:

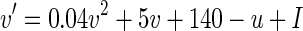3

where u is fixed at its typical starting value of −13, and I is the weighted sum of inputs arriving at the neuron.

The amount of current arriving at the postsynaptic neuron was computed by multiplying each weighted input with 3,000/N_pre to achieve some scalability to the number of input units.

Input statistics

The input layer provides random background inputs with an interspike interval (ISI) distribution that follows the gamma distribution with shape k = 3 and a mean firing rate of 10 Hz.

Additional time-structured patterns are inserted into the input stream, consisting of a chain of serially firing units of fixed length at regular intervals. We set the chain length to 50 ms, with each of three different patterns being presented by 200 units (see Fig. 5a).

Fig. 5.

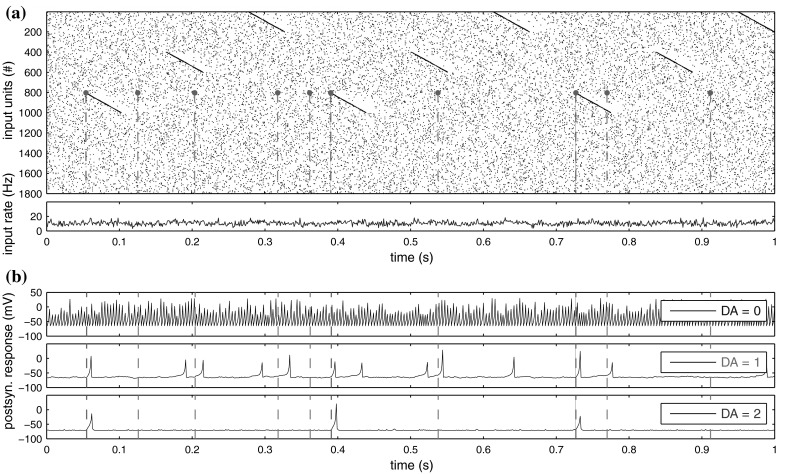
Typical response snapshot for a fixed-weights trial. a Input patterns created by presynaptic input units (see “Methods”). Pattern 1 is repeatedly presented by units 001–200. Pattern 2 by units 401–600. Pattern 3 by units 801–1,000. The first 100 units that present pattern 3 are connected to the postsynaptic neuron through strong weights around 0.7 while all other units are connected through weak weights around 0.1 (compare Fig. 6a). The purple dots represent the firing activity of input unit 804 (used in Fig. 6d as Unit 3), with striped lines representing the times of a spike for comparison with the postsynaptic response. Purple lines signal a spike within pattern presentation, and grey lines signal spiking due to random background activity. The instantaneous firing rate of the input layer is shown below. Only little variation in presynaptic rate is discernable. b The membrane response of the postsynaptic neuron for different levels of DA with θ = 0.5. The full data from which this image is a snapshot was used for the results shown in Fig. 6

As the subsequent background activity of an input unit is affected by any pattern it presents, the overall firing rate of the input layer is only slightly affected during pattern presentation, and remains in the range of random background variation (see Fig. 5a, input rate).

STDP rule

Our weight update rule is based on that of spike-timing dependent plasticity (STDP) used in Masquelier et al. (2008). It is from the class of anti-symmetric rules where the sign of weight modification depends on the pairwise sequence in which the pre- and postsynaptic units fire. It is also an asymmetric rule in that the area-under-curve of the negative side (long term depression, LTD) is greater than that of the positive side (long term potentiation, LTP) for the full defined range. This property slowly decreases the overall distribution of weights towards zero on low random inputs if the postsynaptic neuron is forced to keep firing. Alternatively, if the postsynaptic neuron is allowed to become quiet as all its input weights decline, this asymmetric rule leads to a habituation to the input background activity, making the neuron highly reactive to any non-random time-structured inputs.

The negative integral of the STDP curve within [−50,50] ms does not prohibit the integral from becoming positive within shorter ranges around ±5 ms, e.g. for very high firing rates or bursting, which could lead to a possibly unintended overall increase of synaptic weights. A possible solution for dealing with higher firing rates is proposed in Pfister and Gerstner (2006). We circumvent the problem by reducing the occurrence of bursts by reducing the standard two-dimensional Izhikevich model (Izhikevich 2003) to a one-dimensional model (Izhikevich 2004). We define the prospective weight change as:

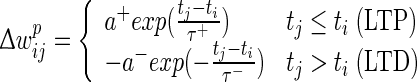4

where a⁺ = 0.03125, a⁻ = 0.85 × a⁺, τ⁺ = 16.8 ms, τ⁻ = 33.7 ms, t_j and t_i are the spike times of the pre- and postsynaptic spikes. Useful features of this STDP rule include:

•  Causal firing (presynaptic, then postsynaptic) leads to fast potentiation.
•  Anti-causal firing (postsynaptic, then presynaptic) leads to fast depression.
•  Acausal (random) firing leads to slow depression because the integral of the STDP curve is negative.

We apply STDP in an all-to-all pairwise matching scheme. To keep all weights within an interval of [0,1], we apply the following soft bound on the weight change.

Weight bounding

We define a soft bound that keeps the actual (baseline) weights from growing to infinity or becoming negative by reducing the amount of weight change as the synaptic weight comes closer to either 0 (lower bound) or 1 (upper bound). We choose to base the mapping function on the sine function within the range [0, π] as it gives us the characteristics of a wide range of applied change around medium weight values and reduced change as weights come closer to their extremes (see Fig. 3b bottom). We define the bounded change of weight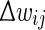s as:

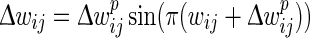5

where w_ij is the synapse’s current weight, 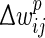is the prospective weight change without bounding, and 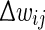is the actual change that will be applied. Different soft bound kernels with steeper slopes may be also used in future work.

Results

We performed two stages of tests with our proposed new method of modulation. During the first stage, we examined the direct effect on postsynaptic activity for a typical distribution of fixed weights, while on-line synaptic modification using spike timing dependent plasticity was incorporated during the second stage of tests.

Instant effects

A central feature of our method is its instant effect on the activity of the postsynaptic cell. All later differences in learning are guided only by this alteration of postsynaptic spiking activity. No modulation whatsoever takes place within the STDP rule itself. The fact that an influence in synaptic learning processes can still be observed in our simulations points to the high importance of how exactly these instant effects in synaptic transmission change the postsynaptic neuron’s instant response.

Firing tendency

In the first test, we examined the amount of input needed to produce a spike response from the one-dimensional Izhikevich neuron. As its recent history can be summed up in the model neuron’s current membrane state, we can ask the question differently: At which preset level of membrane depolarisation does the model neuron still fire, given a specific number of synchronous unit inputs?

The answer is plotted in Fig. 4 for 1, 5 and 10 synchronously arriving inputs, and for range parameters r = 5 and r = 3. At a membrane potential above about −53.5 mV, the model neuron will fire even without inputs. This upper bound is approached when all actual weights are far below θ and the level of neurotransmitter is increased above baseline (DA > 1). Analogously, when all weights are above θ while neurotransmitter level is increased, the neuron’s membrane threshold before inputs can be more negative as any inputs are fully transmitted to the postsynaptic neuron.

Fig. 4.

Effects of various DA levels on firing onset membrane potentials of a 1D-Izhikevich neuron (Izhikevich 2004). At baseline level (DA = 1) the onset potentials seem evenly distributed across a voltage range defined by the amount of neural input (green dots). Lower DA makes the onset potentials become less dependent on the actual weight of the input synapses and instead approach a central mean value dependent on θ as DA goes towards 0 (blue dots). As the activity of the postsynaptic neuron now depends less on the actual weights but mostly on the overall input to the network, we can argue that the firing pattern of the postsynaptic neuron becomes less causal (less dependent on specific inputs) compared to baseline DA levels. In the opposite case of high DA (), the effect of the weights also changes. Increasing levels of DA make inputs arriving through weak connections have an even smaller effect on the postsynaptic neuron’s activity (the upper membrane boundary seen in the figures near −53.5 mV is the neuron’s onset potential in absence of any inputs). The influence of inputs arriving through already stronger connections is increased up to a maximal effect when effective weights are near the maximum value of 1 (the lower membrane boundary seen in the figures is the neuron’s lowest onset potential for the given number of inputs). The effect of partially trained synapses is thereby enhanced, up to a binary effect strongly depending on the synaptic strength

For decreasing levels of neurotransmitter (DA < 1), synaptic transmission always approaches that of weights around the current value of θ. The effect of this may be imagined as a neuron-level reduction in signal to noise ratio, as the effect of strong synapses (possibly having learnt structured patterns) is decreased while that of weak synapses (possibly having learnt to ignore background activity) is increased. This tendency is shown in section “Effects during synaptic learning”.

The amount of synaptic transmission depends less on the actual baseline weight of a synapse as the level of neurotransmitter moves away from baseline. The range of transmission effects is evenly distributed for DA = 1 (green dots in each plot), while decreasing levels of DA make the transmission effect become solely dependent on θ (blue dots) and increasing levels make the effect go towards that of weights in the extremes of 0 and 1 (red dots).

Causal postsynaptic response

Due to its temporary changes in effective weight distribution, our proposed rule for DA-dependent modulation of synaptic efficacy leads to a change in causal relationships between presynaptic and postsynaptic activity.

Figure 5a shows a snapshot of typical input data generated online as described in “Methods”, together with the instantaneous firing rate in 1 ms bins. The purple dots exemplify the spiking behaviour of one input unit that happens to take part in both the random background activity and representing the partially trained time-structured input pattern 3.

The inputs are projected via DA-modulated synapses with fixed, partially trained weights to the postsynaptic model neuron, evoking an output response that strongly depends on the current neuromodulator level (Fig. 5b). For visual clarity, we again used θ = 0.5 during this test, which has the side effect that the postsynaptic firing rate is increased for low values of DA and decreased for high values of DA for any typical (right-skewed) weight distribution. However, apart from the changes in firing rate, the important difference between the three response plots is the increasing selectivity of action potentials on presentation of the partially trained pattern as the neuromodulator level increases. While near-random firing is observed for low values of DA, the output behaviour becomes more sparse at DA = 1, with no misses but some false positives in detecting pattern 3. The detection of the pattern becomes perfect for the highest level of DA = 2 in this case, as the postsynaptic neuron now fires if and only if pattern 3 is presented.

To make a statement on the generality of this observation, we chose a fixed distribution of weights as shown in Fig. 6a and simulated the response of a postsynaptic neuron for 20 s on each of three different levels of DA, repeated 100 times for each DA level. The vast majority of 1,800 synapses had random weights around 0.1, while 100 connections to units coding pattern 3 were given weights around 0.7 (units 801–900). By repeatedly counting the number of occurrences of single events, of causal pairs, and anti-causal pairs, we can examine the relative change in selectivity for the values DA = 0, DA = 1, DA = 2. Events in this context were either a spike of a presynaptic input unit taking part in coding the beginning of a pattern, the presentation of the patterns themselves, or a spike of the postsynaptic neuron. Event pairs were either causal (pre-syn. then post-syn. within 50 ms) or anti-causal (post-syn. then pre-syn. within 50 ms).

Fig. 6.

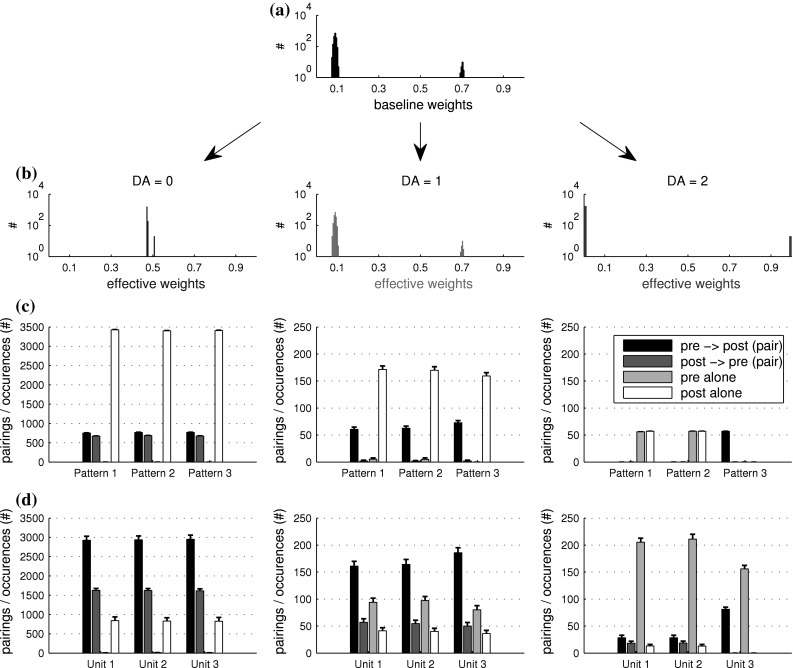
Effective weight distributions and resulting changes in relative spike event pairings. As any deviation of DA from 1 temporarily alters the effective weight of each synapse in our model, we show the effective distribution of weights for three levels of DA above. a Actual (baseline) weight distribution used for this test. b DA-dependent effective weight distributions for DA levels 0, 1, and 2. As all firing of the postsynaptic neuron is caused only by inputs from the input layer, the relative amount of spike pairs gives a hint at the causality relationship between pre- and postsynaptic events. Causal or anti-causal event pairings are counted if a presynaptic and a postsynaptic event occur within 100 ms of each other. If two events occur with longer time difference, both are counted as single presynaptic and single postsynaptic events. c Comparison of event times where the presynaptic event is the presentation time of each pattern, and the postsynaptic event is the time of each spike of the postsynaptic neuron. d Comparison of event times where the presynaptic event is the time of spike of input unit 004 for pattern 1, 404 for pattern 2, and 804 for pattern 3

Each bar plot in Fig. 6c shows groups of causal and anti-causal event pairs and single events where a presynaptic event is the respective onset time of each of the three time-structured input patterns. A postsynaptic event is a spike of the postsynaptic neuron. While the distribution of events is similar for all three patterns on DA = 0, there is a slight increase in causal pairs and a slight decrease in single postsynaptic firing for DA = 1 on presentation of pattern 3 compared to presentation of the other patterns. The difference becomes obvious for DA = 2, as pattern 3 reliably and perfectly provokes a postsynaptic spike on each presentation, with no false positives or misses. The equally high white single event bars for patterns 1 and 2 represent the same postsynaptic activity that was counted as part of the causal pair for pattern 3, except that here it represents a single event, unrelated to neither pattern 1 nor 2.

A more noisy result is seen when comparing not the onset of pattern presentation to postsynaptic firing, but the spiking activity of a presynaptic unit that happens to take part in the pattern. Figure 6d shows the results of this comparison, where the same tendency can be observed: The response to all three patterns seems highly similar for the lowest level of DA, while a slight difference is seen for normal neuromodulator levels. Again, a strong change in response to the unit presenting pattern 3 is observed when the neuromodulator level reaches DA = 2.

The differences in total number of events for different levels of DA are again due to the chosen value of θ = 0.5, which increases the effective weight of the majority of synapses for low levels of neuromodulator. In a (biologically less plausible) left-skewed weight distribution with the majority of weights above θ, the opposite effect on firing rate would be observed. Automatically keeping θ within a homeostatically plausible range is therefore an important topic for widespread applicability in large scale multi-layer networks.

Effects during synaptic learning

After testing our proposed neuromodulation approach on fixed-weight networks, we now examine the modulatory effects of our transmission rule on independent synaptic plasticity. As described in “Methods”, no modulation whatsoever is factored directly into the STDP rule we use. The only adjustment in how STDP-induced synaptic plasticity is converted to actual weight changes is the soft bound to keep all weights within the interval [0,1].

After examining unsupervised learning behaviour at baseline levels of DA, we test reinforced learning with fixed, non-baseline levels of neuromodulator and examine the effects of sudden DA level changes on synaptic learning characteristics.

Fast variation of neuromodulator gradients for large-scale reinforcement learning will need automatic adjustment of θ.

Learning with baseline modulator levels

When the level of neuromodulator remains around the baseline of DA = 1, the network performs unsupervised learning, depending only on the structure of arriving inputs. Figure 7 shows a test where 10 independent postsynaptic neurons were trained in parallel to the same inputs. Each neuron’s weights were initialised randomly around 0.8 within the range [−0.025,0.025] in a uniform distribution. Spike timing dependent plasticity was allowed to change the weights of synaptic connections, but no modulation signal was given (DA = 1). At the start of the simulation, the postsynaptic neurons begin to fire excessively due to the high mean of inputs arriving at each simulation step (thin red vertical line at t = 0 in each plot). This is then reduced by the asymmetric all-to-all STDP rule which adapts the weights to account for the random background activity arriving through the input units (light blue). Without structured patterns occuring within the input stream, all postsynaptic firing would stop at this point (data not shown). However, after about 3 s, the first postsynaptic neurons begin to increase the weights of synaptic connections to pattern presenting input units. After usually no more than 10 s, all postsynaptic neurons have tuned to at least one structured pattern (yellow to orange), and start developing strong connections to the first input units of each pattern (dark red). Shortly after this, synaptic weights to any input units that fire repeatedly at a later stage in pattern presentation are reduced to near zero (dark blue). This fast LTD is due to the repeated (anti-causal) post-pre pairing of spikes in opposition to the slower LTD induced by uncorrelated background activity.

Fig. 7.

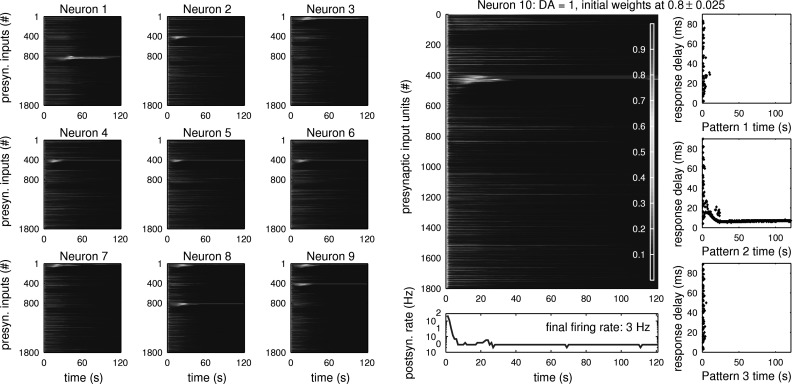
Development of baseline weights: Unsupervised learning of structured input patterns by 10 independent postsynaptic neurons at baseline DA levels (DA = 1). Given equal inputs (see Fig. 5a) and a narrow range of starting weights, the 10 neurons tune to different patterns. The slight preference for choosing pattern 2 here comes from the coincident timing of the equal background inputs, and different random background inputs lead to a different pattern preference. Here, all connections start with strong weights around 0.8, leading to an initial overall decrease due to high postsynaptic activity and the asymmetry of the STDP rule. Then, as only the time-structured inputs repeatedly cause the postsynaptic neuron to fire, the weights of the connections to input units reliably firing just before postsynaptic activation begin to be strengthened. As the now stronger weights (shown in Red) lead to an earlier onset of firing of the postsynaptic neuron relative to pattern presentation times, connections to even earlier firing input units are strengthened. The earliest firing units of a repeating pattern soon form the strongest connection, as seen by the rise of red lines in the weight development plots. Also, connections to input units representing a late part of a pattern are now weakened, because they repeatedly fire after a postsynaptic spike. Far Right Input response delay plots for each of the three patterns show an initially decreasing and then constant delay of the postsynaptic neuron’s response to learnt pattern 2, and an extinction of responses to patterns 1 and 3, to which the neuron did not tune. Bottom Right Instantaneous firing rate of postsynaptic model neuron

The decision on which of the patterns is learnt depends both on the random starting distribution of weights and on coincidental peaks in the background activity (noise). Because of the soft bound on weights we use, narrow initialisation ranges near the extremes can have a similar exploratory effect on tuning preference as a wide initialisation range has around the centre value of 0.5.

In absence of Dopamine or other strong modulatory factors, previous approaches stopped all form of learning (Izhikevich 2007). In our proposed method, learning simply switches from reinforced to unsupervised learning when the modulatory signal remains fixed at baseline levels.

Learning with modulation of causal firing

We now add some permanent reinforcement into the simulation by changing the applied level of neuromodulator. Figures 8 and 9 show the typical development of weights for DA = 1.8, DA = 1.3, DA = 0.7 and DA = 0.2. The strongest change while modulating learning in this way is the increased difficulty of tuning to patterns for low DA levels.

Fig. 8.

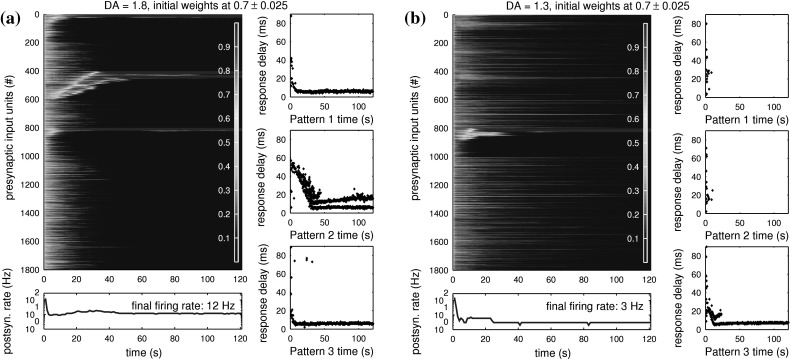
Modulated learning of time-structured input patterns by synaptic weights of two postsynaptic neurons at high levels of DA. Each postsynaptic neuron is more likely to tune to any of the patterns, where just slightly increased baseline weights act as high effective weights, enabling further strengthening of those connections. a For DA = 1.8, this neuron quickly tunes to all three patterns, but initially only with a late response to presentations of pattern 2. Because of natural STDP behaviour, the neuron slowly re-tunes to input units representing the start of pattern 2, while connections to late-firing input units in pattern 2 are weakened. The shortest response delay for pattern 2 is reached after about 30 s of simulation, with a seemingly stable double spike response to pattern 2 presentations. b For DA = 1.3, this neuron happens to only tune to one input pattern, but the effect of high DA levels on weights to background inputs is nicely visible (compare Fig. 7): While the weights to input units taking part in pattern 3 quickly go towards either 0 (blue) or 1 (red), all other weights are only slowly weakened when background activity happens to coincide with postsynaptic firing. Although the baseline weights of connections to background inputs are still between 0.1 and 0.3 and would usually induce postsynaptic firing for normal DA levels, the DA-dependent effective weights to background inputs have become low enough to have no chance in activating the postsynaptic neuron

Fig. 9.

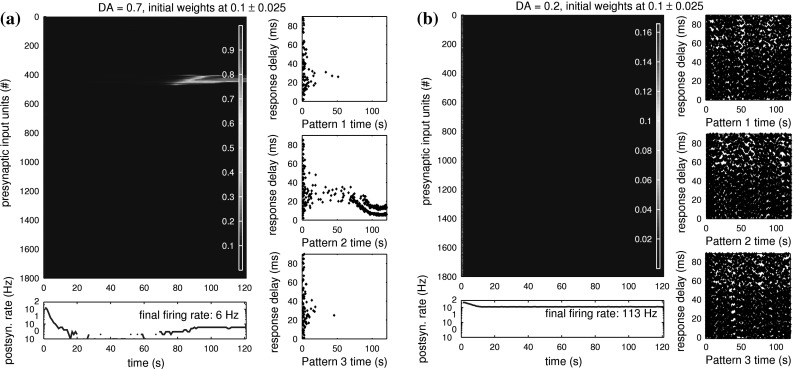
Modulated learning of time-structured input patterns by two postsynaptic neurons at low levels of DA. Each postsynaptic neuron is less likely to tune to patterns, as any initial increase in baseline weights is masked by the high similarity of all effective weights. Any correlated inputs are increasingly difficult to discriminate from background activity as the DA level decreases. a For DA = 0.7, this neuron does finally manage to reliably tune to pattern 2 after about 70 s, and even forms a double spike response shortly before 90 s of simulation have passed. Note that here we were able to start with very low baseline weights around 0.1, because the high value of θ = 0.5 keeps the initial effective weights high enough to produce a postsynaptic response. b For DA = 0.2, no more learning is possible. Most effective weights come very close to θ, completely blocking out any baseline weight variation. In this case, as θ is fixed at the value 0.5, the DA-dependent grouping of effective weights around this value also leads to continuous, pathological firing of the postsynaptic neuron. While this high activity could be reduced by (automatically) lowering θ, the masking of trained versus untrained connections can not

For DA = 1.8 (Fig. 8a), the postsynaptic neuron has the highest tendency to quickly tune to multiple time-structured input patterns. The probability of tuning to new patterns is highest during the first few seconds of simulation and diminishes in absence of any homeostatic weight adjustment due to random background activity while simulation progresses. Here, the postsynaptic neuron starts responding to all three input patterns quickly, but initially has a high response delay (∼50 ms) when detecting pattern 2 because it happens to initially tune to late input units of this pattern. It then slowly re-tunes to the first input units repeatedly firing within pattern 2. As the postsynaptic neuron continues to tune to the first spiking input units of the pattern, connections to units representing late parts of the pattern are again actively decreased, as indicated by the gradual upwards shift of the middle red line.

For DA = 1.3 (Fig. 8b), the postsynaptic neuron tends to tune to less input patterns. Once it has started to fire regularly to one of the patterns, the random background activity continues to diminish all weights to other (randomly active) input units not taking part in the tuned pattern. As the weights to units taking part in other patterns are hereby also slowly reduced, the postsynaptic neuron slowly looses its ability to further tune to more patterns and remains highly specialised. The reduction of weights to background inputs is slower than in Fig. 7 although in both cases the neurons tune to only one pattern, because the increased DA level here decreases transmission by below-θ (weak) weights earlier and the lower resulting firing rate of the postsynaptic neuron produces slower LTD on background activity.

For DA = 0.7 (Fig. 9a), we still see the neuron tune to one of the structured patterns, albeit only after a long time of uncertainty (here ∼70 s). Coincidentally, it also repeatedly fires twice on each pattern presentation for the remaining duration of the test. Note that in this test we were able to start with a very low initial range of baseline weights, because our low DA level lets the effective weights act as closer to our generalisation threshold θ = 0.5.

For DA = 0.2 (Fig. 9b), no more tuning is observed, and the postsynaptic neuron reaches a pathological state of relentless firing. While this high postsynaptic activity could be controlled by lowering θ, the failure in tuning can not be compensated as DA goes towards zero. The structured inputs vanish in the random background activity that is transmitted to the neuron with equal efficacy. From the neuron’s perspective, the signal-to-noise ratio between structured and random inputs is strongly reduced and can no more be used for successful learning.

In the next test we reduce the neuromodulator level suddenly after 60 s of simulation time. Figure 10a shows results of a trial that starts with DA = 1 and drops to DA = 0 after some initial training has occurred. While the neuron now instantly enters the pathological state of excessive firing due to the high θ value, a delayed influence on the learnt weights becomes visible. The response delay plot for pattern 1 shows a repeating two-spike response before the DA level drop. This is due to strong learnt connections to input units ∼1–50 as indicated by the wide red bar at the top of the main plot. About 2–3 s after DA drop, the weights to input units 27–47 are quickly reduced as they move away from the maximum value defined by the soft bound. In a normally firing neuron, this would remove the second response spike to pattern 1, and may be used for pruning a neuron’s response. At about 10–12 s after DA drop, the last existing strong weights (1–23) break down and all weights of the neuron go towards zero. This complete formatting of weights resets the neuron into an unspecialised state. For allowing the neuron to tune to new patterns, some homeostatic form of re-enabling spiking activity would need to be added to the neuron. This may be a combination of either random weight growth or automatic adjustment of θ together with low DA levels. Moderate baseline weight increase can then allow new tuning to correlated inputs as used in Fig. 9a.

Fig. 10.

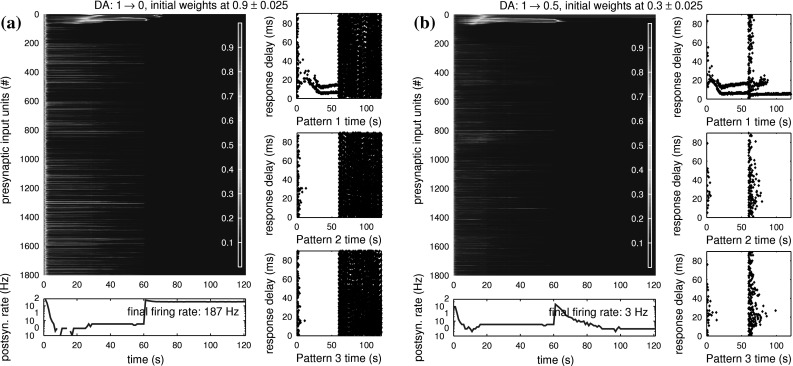
Modulated learning behaviour for baseline levels of DA, dropping to low levels after 60 s. During the first 60 s, the weight development is similar to Fig. 7, and both a and b tune to pattern 1 with a double spike response. a When DA drops to zero, the neuron instantly starts firing quickly as all effective weights move close to θ = 0.5. The effect on trained weights is slower, as it takes about 3 s after DA drop for the first group of weights to be decreased. After about 8 s, all weights have been decreased to values close to zero, as the high spiking activity of the postsynaptic neuron is continued. The drop of DA hereby led to a deletion of trained weights, or unlearning of previously learnt patterns. If weights of this neuron were randomly increased in the future, it would be ready to learn completely new patterns without relation to its previous identity. b When DA only drops to 0.5, the neuron still instantly increases its firing rate, but manages to recover by further reduction of synaptic weights to background inputs. The group of weights causing the second spike response on each presentation of pattern 1 is reduced towards zero during the initial phase of high postsynaptic firing. But the group of weights causing the repeating first spike response to pattern 1 survives here. After the neuron recovers to normal firing, the one-spike response to pattern 1 is still intact. A sudden decrease of DA may therefore be useful as a pruning measure to sparsify trained neural responses

Figure 10b shows a reduction to DA = 0.5 after 60 s, which again initially leads to fast postsynaptic firing. However, in this case the neuron is able to recover normal operation after a few seconds by further reducing weak connections to a level low enough to not be pulled up to high effective weights near θ by the given DA level. This sudden reduction of DA still allows pruning of double spiking to take place, but preserves the single-spike response to trained patterns 1 and 3.

Synaptic competition

With the described effects of our proposed rule for DA-dependent signal transmission, we can affect the network learning process without directly changing the STDP rule. While we can push the network into sparsely fitting an active input signal for high levels of DA, we can induce a randomization process through low levels of DA, thereby resetting the network into a higher-entropy state, or "forgetting" the learnt patterns. Dopamine, or any combination of neurotransmitters signalling reinforcement, can in this way be simulated to either increase the probability of learning a given input pattern or to reduce the probability of learning and even forgetting learnt weights to active inputs. The inputs must be active at least occasionally in order for any change to occur, so completely silent inputs would always remain unchanged.

Apart from fast LTP and LTD through repetitive causal or anti-causal event pairs, we induce slow LTD by taking advantage of the fact that random firing causes weight decrease for asymmetric STDP rules. So by equalising the effective synaptic weights towards θ on low DA, we are allowing the random backgrund activity to induce slow LTD.

If the inputs through strong synapses are strong enough to produce spikes in the postsynaptic neuron and are themselves correlated, the causal relation between the repeated presentation of inputs and postsynaptic firing leads to a further strengthening of these weights (for predictable order of inputs see Masquelier et al. 2008). If, on the other hand, the number of strong weights is high and the presynaptic neurons fire mostly independently, causing the postsynaptic neuron to fire at random, the noisy input leads to an overall decrease of even these strong weights as synapses compete for control over postsynaptic activation. The network behaviour for high levels of DA is therefore the following: If many synapses are strong at the beginning of DA application, an overall reduction of weights takes place, until most synaptic weights have passed the threshold θ and are effectively close to zero. When only a small number of strong weights remain, the competition between synapses for control over postsynaptic firing that caused the overall decrease is weaker, which allows a small number of weights to remain strong and even be reinforced again up to maximal selectivity when some inputs are correlated in time. This allows a sparse distribution of synaptic weights to develop.

Conclusion

In this article, we demonstrated how we can influence the learning outcome of a spiking network simply by applying some global reinforcement during synaptic transmission. All synaptic modification is only dependent on the pre- and postsynaptic spiking activity, and no third (modulatory) factor is used during spike-timing dependent plasticity. Through controlling a global level of neuromodulator concentration, we are able to influence the effective range of synaptic efficacies, and thereby the discriminability of trained vs. untrained inputs arriving at a postsynaptic neuron. This change in synaptic efficacy is computed locally in each synapse, using only the current synaptic strength and the current global neuromodulator concentration.

A variable neuron-wide threshold θ may be used in future work as a homeostatic slow parameter that automatically updates to retain normal excitability on varying neuromodulator levels for non-uniform weight distributions. The size of θ would likely come to be far below 0.5 in an automatically adopting implementation.

Applying modulation by locally affecting synaptic transmission instead of direct manipulation of the STDP rule gives the advantage of direct control over the causal firing relationship between selected presynaptic and postsynaptic neurons, which can instantly be observed as the modulation factor changes. In terms of network learning, the reinforcement signal does not directly increase or decrease active synapses, but instead leads to a temporary sparsification of effective weights for high reinforcement and a generalisation around θ for low reinforcement.

As the modulatory factor needs to be present during the arrival of inputs, we do not approach the distal reward problem (Izhikevich 2007) through our model, but assume for the case of delayed reward an involvement of hippocampus and cortical working memory instead of direct application of delayed reward into an STDP rule. Instead, we hope to provide a possible explanation for experimentally observed (Kroener et al. 2009; Thurley et al. 2008) instantaneous effects during neuromodulator application. Assuming the process of novelty detection by subcortical sensory nuclei performs faster than or equally fast as the semantic processing of some signals in the cortex (Trimmer et al. 2008), our model may also be useful for learning the short-latency novelty portion (Redgrave and Gurney 2006) of the nigral reinforcement signal (Schultz et al. 1997).

Although we have until now only been studying pairwise rules of STDP, there is no reason to assume that the proposed modulation rule should not be combinable with STDP learning based on triplets of spikes (Pfister and Gerstner 2006). Specific examination of this combination is not focus of the current article.

Our model presents some interesting questions for biological validation: It is currently unclear if and how exactly Dopamine affects signal transmission locally at single synapses. Little is known about the exact local concentrations of dopaminergic receptors across a neuron's membrane (Reynolds and Wickens 2002; Shen et al. 2008; Surmeier et al. 2007). Also, it might be useful to look for a biological analogy to our theoretical sparsification/generalisation threshold θ, as this may explain many of the observed instant effects of Dopamine or related substances.

A chemical prediction by our proposed rule may start at the ratio between D1-type and D2-type receptors on a Dopamine-modulated synapse of a D1-dominant postsynaptic neuron. While a neuron-wide baseline ratio of dopaminergic receptors may represent a homeostatic default configuration similar to θ in our model, any strengthening synaptic connection may be found to also increase the local concentration of D1-type receptors towards a higher excitability on raised levels of Dopamine. Similarly, a weakening synaptic connection may reduce the local concentration of D1-type receptors, allowing the existing D2-type receptors to become locally dominant in controlling the synapse's reaction to drops in global Dopamine concentration. Although the actual curve of θ-dependent neuromodulation of synaptic efficacy would be up for experimental refinement, such a weight-dependent dynamic reconfiguration of D1-type/D2-type receptor ratio might allow for fast Dopamine-dependent modulation of synaptic transmission to take place. Similarly, on D2-dominant neurons, the concentration of D2-type dopaminergic receptors may be locally increased with a strengthening of synapses, leading to a supposed opposite behaviour on application of Dopamine.

While both D1-type and D2-type receptors seem to be evenly distributed across the main striatal target areas of dopaminergic projections, it is currently unknown whether local concentrations among and within neurons diverge from this general ratio or if neurons tend towards skewed distribution of receptor ratio depending on synaptic strength and projection target area.

An additional effect of the increased efficacy of weak synapses on D1-type neurons for low DA is that as these synapses tend to be more active, any neurons that have nearly all weights close to zero and may never fire, have a new chance of becoming active to the current inputs. This opens the chance of recovering muted model neurons that would previously never fire, given useful values for θ.

Low DA may inherently support exploration through D1-type neurons in our model, while high DA may inherently support exploitation, with opposite behaviour for D2-type neurons (compare recent work of Humphries et al. 2012).