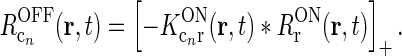Abstract
A striking feature of the organization of the early visual pathway is the significant feedback from primary visual cortex to cells in the dorsal lateral geniculate nucleus (LGN). Despite numerous experimental and modeling studies, the functional role for this feedback remains elusive. We present a new firing-rate-based model for LGN relay cells in cat, explicitly accounting for thalamocortical loop effects. The established DOG model, here assumed to account for the spatial aspects of the feedforward processing of visual stimuli, is extended to incorporate the influence of thalamocortical loops including a full set of orientation-selective cortical cell populations. Assuming a phase-reversed push-pull arrangement of ON and OFF cortical feedback as seen experimentally, this extended DOG (eDOG) model exhibits linear firing properties despite non-linear firing characteristics of the corticothalamic cells. The spatiotemporal receptive field of the eDOG model has a simple algebraic structure in Fourier space, while the real-space receptive field, as well as responses to visual stimuli, are found by evaluation of an integral. As an example application we use the eDOG model to study effects of cortical feedback on responses to flashing circular spots and patch-grating stimuli and find that the eDOG model can qualitatively account for experimental findings.
Keywords: Relay cell, Thalamocortical, Difference-of-Gaussians, Feedback
Introduction
A striking feature of the early visual pathway is the significant feedback from primary visual cortex to cells in the dorsal lateral geniculate nucleus (LGN). This cortical feedback has been shown to switch LGN relay cells from burst to tonic firing modes (McCormick and von Krosigk 1992; Godwin et al. 1996) and to modify the response properties of LGN cells to visual stimuli both in cat (Geisert et al. 1981; Vidyasagar and Urbas 1982; Murphy and Sillito 1987; Sillito et al. 1993, 1994; Cudeiro and Sillito 1996; Wörgötter et al. 1998; Wang et al. 2006; Andolina et al. 2007) and monkey (Marrocco et al. 1982; McClurkin and Marrocco 1984; McClurkin et al. 1994; Marrocco et al. 1996). These studies reported both enhanced and reduced responses of LGN neurons due to cortical feedback, and the identification of a particular functional role of this feedback has been difficult (Briggs and Usrey 2008, 2011). Cortical feedback has been shown to affect the length tuning of relay-cell responses (Murphy and Sillito 1987) and the response to patch-grating stimuli (Sillito et al. 1993; Cudeiro and Sillito 1996; Sillito and Jones 2002).
Relay cells receive synaptic inputs from a variety of sources (Sherman and Guillery 2001): excitatory input from retinal ganglion cells, feedforward inhibition from intrageniculate interneurons, inhibitory feedback from the thalamic reticular nucleus (TRN) and excitatory feedback from the striate cortex. Intrageniculate interneurons and TRN cells also receive feedback from cortex. When trying to decipher the properties of such a complex neural network, mathematical modeling is an essential tool, and a few mathematical models have been constructed to elucidate effects of cortical feedback on LGN neurons. They have focused on the effect of cortical feedback on visual latency (Köhn and Wörgötter 1996), synchronization of thalamocortical oscillations (Destexhe et al. 1998; Destexhe 2000; Mayer et al. 2007), temporal structure of spike trains (Wörgötter et al. 1998), synchronization of LGN-cell firing (Kirkland and Gerstein 1998; Kirkland et al. 2000), object segmentation based on motion cues (Hillenbrand and van Hemmen 2000), LGN responses to bipartite drifting grating stimuli (Hayot and Tranchina 2001), and on LGN impulse responses (Yousif and Denham 2007). These modeling efforts have typically been based on grids of neurons representing the different populations in the early visual pathway (retinal, LGN, TRN, and cortical cells), and results for the question at hand have been found by numerical simulations.
In this article we present a new firing-rate-based model of spatiotemporal LGN relay-cell responses to visual stimuli incorporating cortical feedback. In this extended DOG model (eDOG) the feedforward response is modeled by means of the standard difference-of-Gaussians (DOG) model (Rodieck 1965), and the corticothalamic feedback is assumed to have a phase-reversed push-pull organization (Wang et al. 2006): e.g., inhibitory feedback influence from a cortical ON-cell onto an LGN cell is accompanied by an excitatory feedback influence from a cortical OFF cell. While the resulting model has a more complicated mathematical structure than the DOG model, it is still linear. This means that responses to arbitrary visual stimuli can be calculated by evaluating integrals, though numerical evaluation is generally required. In the eDOG model, characteristics of cortical feedback such as strength, spatial spread and temporal properties are parameterized in a straightforward manner, and possible effects on LGN cells from cortical feedback can be studied more easily—both conceptually and methodologically—than with extensive numerical simulations of networks of neurons.
In section "Impulse response and receptive field" we introduce impulse-response functions and receptive fields. In section "Receptive-field models incorporating phase-reversed push-pull cortical feedback" a general expression for the linear response of relay cells incorporating cortical feedback from a full set of orientation-selective cortical populations is derived, while the eDOG model is presented in section "Extended difference-of-Gaussians model". An example application is given in section "Example application: patch-grating stimuli" where we use the eDOG model to describe the effects of cortical feedback on responses to flashing circular spots and patch-grating stimuli and compare with experimental findings (Sillito et al. 1993; Cudeiro and Sillito 1996; Sillito and Jones 2002). We discuss our findings in the final section.
Preliminary accounts of some of the results presented here have been presented in abstract form previously (Einevoll and Plesser 2003).
Impulse response and receptive field
Impulse-response functions
For a cell in the early visual pathway located at position r in the visual field, the response, i.e., the firing rate, can be written as
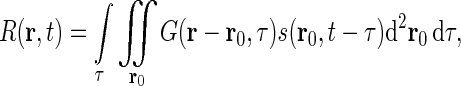 |
1 |
if one assumes (i) linearity, (ii) time invariance, and (iii) local spatial homogeneity. Here G(r, τ) is the spatiotemporal impulse-response function (Heeger 1991). In Eq. 1s(r, t) represents the visual stimulus presented at position r = (x, y) at time t. The spatial integral over r0 goes over all two-dimensional space. For mathematical convenience we have chosen the temporal integration to go from 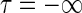 to
to 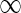 . From causality it follows that G(r, τ < 0) = 0, so the lower integration boundary for τ could also be set to zero.
. From causality it follows that G(r, τ < 0) = 0, so the lower integration boundary for τ could also be set to zero.
The integral in Eq. 1 is a convolution between the stimulus and the impulse-response function, i.e.,
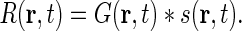 |
2 |
From the theory of Fourier transforms it follows that the integral in Eq. 1 can be reformulated as an integral over temporal and spatial frequencies (Bracewell 1986),
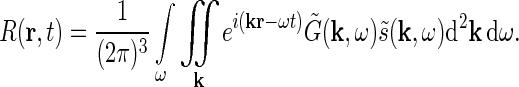 |
3 |
Here 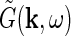 and
and 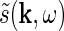 are the complex Fourier transforms of the impulse-response functions G and stimulus s, respectively. The complex Fourier transform we use, and its inverse, are given by
are the complex Fourier transforms of the impulse-response functions G and stimulus s, respectively. The complex Fourier transform we use, and its inverse, are given by
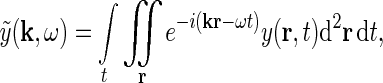 |
4 |
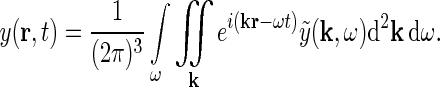 |
5 |
The physiological interpretation of the real-space impulse-response function G(r, t) is that it corresponds to the response to briefly flicking test spots positioned at different positions rtest which are both very small (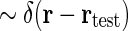 ) and narrow in time (
) and narrow in time (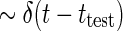 ). Mathematically this corresponds to a stimulus function given by
). Mathematically this corresponds to a stimulus function given by 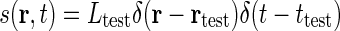 where Ltest is the luminance of the test spot. Inserting into Eq. 1 and using the sifting property of the δ-function (Bracewell 1986), we obtain the response R(r, t) = LtestG(r − rtest, t − ttest). The impulse-response function is thus in principle given by the measured firing rates of neurons at various positions r and times t following a δ-pulse at position rtest at time zero. In practice it is easier to keep the electrode position fixed and measure from a particular cell and instead move the test spot. Therefore the receptive-field function (or point-spread function) is often considered instead. The impulse-response function and the receptive-field function are intimately related: the receptive-field function is the impulse-response function with r replaced with −r and t with −t in the spatial and temporal arguments, respectively (Heeger 1991).
where Ltest is the luminance of the test spot. Inserting into Eq. 1 and using the sifting property of the δ-function (Bracewell 1986), we obtain the response R(r, t) = LtestG(r − rtest, t − ttest). The impulse-response function is thus in principle given by the measured firing rates of neurons at various positions r and times t following a δ-pulse at position rtest at time zero. In practice it is easier to keep the electrode position fixed and measure from a particular cell and instead move the test spot. Therefore the receptive-field function (or point-spread function) is often considered instead. The impulse-response function and the receptive-field function are intimately related: the receptive-field function is the impulse-response function with r replaced with −r and t with −t in the spatial and temporal arguments, respectively (Heeger 1991).
The Fourier-transformed impulse-response 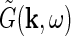 also has a clear physiological interpretation. In Eq. 3, the response to the stimulus s is essentially written as an infinite sum (integral) over contributions from drifting sinusoidal gratings specified by k and ω. Here k is the so called wave vector which is related to the more familiar spatial frequency ν via
also has a clear physiological interpretation. In Eq. 3, the response to the stimulus s is essentially written as an infinite sum (integral) over contributions from drifting sinusoidal gratings specified by k and ω. Here k is the so called wave vector which is related to the more familiar spatial frequency ν via 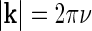 . Correspondingly the angular frequency ω is related to the temporal frequencyf via ω = 2πf. The weight and phase of each different grating required to represent the stimulus s are given by
. Correspondingly the angular frequency ω is related to the temporal frequencyf via ω = 2πf. The weight and phase of each different grating required to represent the stimulus s are given by 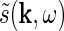 , while
, while 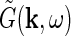 gives the response to a sinusoidal drifting grating specified by k and ω.
gives the response to a sinusoidal drifting grating specified by k and ω.
Example impulse-response function: DOG model
The choice of model for the receptive field can now be incorporated into the expression for the impulse-response function G(r, t). For retinal ganglion cells and relay cells in LGN a simple and common choice is to assume the impulse-response function to be spatiotemporally separable (G(r, t) = f(r)h(t)), and to model the spatial part with the difference-of-Gaussians (DOG) model (Rodieck 1965), i.e.,
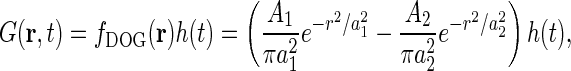 |
6 |
with the accompanying Fourier transform
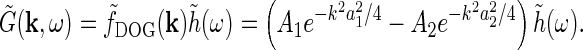 |
7 |
The DOG model is an example of a filter model or descriptive model (Dayan and Abbott 2001) where the main goal is to account mathematically for experimental data (see, e.g., Jing et al. (2010)). Mechanistic models, in contrast, aim to explain experimental data in terms of the underlying neurons and neuronal circuitry (see, e.g., Wang and Zhang 2007; Saglam et al. 2009; Liang et al. 2010).
General mechanistic receptive-field models
In Einevoll and Plesser (2002), we investigated a linear mechanistic model for the impulse-response function for cat relay cells taking both feedforward and feedback aspects of the geniculate circuit into account. Generally, the Fourier-transformed impulse response of geniculate relay cells has the form
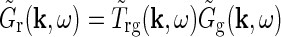 |
8 |
where 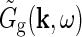 is the Fourier-transformed impulse-response function for retinal ganglion cells providing the feedforward input to the geniculate cells. The geniculate transfer function
is the Fourier-transformed impulse-response function for retinal ganglion cells providing the feedforward input to the geniculate cells. The geniculate transfer function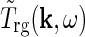 describes the transfer ratio for each sinusoidal grating (specified by k and ω).
describes the transfer ratio for each sinusoidal grating (specified by k and ω).
In Einevoll and Plesser (2002) we further derived a general expression for 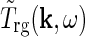 in terms of properties of the neurons and the neuronal connections in the LGN circuit as reviewed in Sherman and Guillery (2001): The relay cells receive excitatory input from retinal ganglion cells as well as feedforward inhibition from intrageniculate interneurons both via dendro-dendritic structures (triads) and presumably axonal output. The interneurons in turn receive excitation from a few retinal ganglion cells. In addition the relay cells receive inhibitory feedback from the thalamic reticular nucleus (TRN) and excitatory feedback from the striate cortex. The intrageniculate interneurons and TRN cells also receive excitatory feedback from cortex. These connections were all incorporated in a general mathematical expression for
in terms of properties of the neurons and the neuronal connections in the LGN circuit as reviewed in Sherman and Guillery (2001): The relay cells receive excitatory input from retinal ganglion cells as well as feedforward inhibition from intrageniculate interneurons both via dendro-dendritic structures (triads) and presumably axonal output. The interneurons in turn receive excitation from a few retinal ganglion cells. In addition the relay cells receive inhibitory feedback from the thalamic reticular nucleus (TRN) and excitatory feedback from the striate cortex. The intrageniculate interneurons and TRN cells also receive excitatory feedback from cortex. These connections were all incorporated in a general mathematical expression for 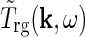 . In combination with a model expression for the (Fourier-transformed) impulse-response function for the retinal ganglion cells
. In combination with a model expression for the (Fourier-transformed) impulse-response function for the retinal ganglion cells 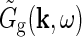 , such expressions for
, such expressions for 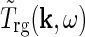 can be used to derive mechanistic expressions for the relay cell impulse response
can be used to derive mechanistic expressions for the relay cell impulse response 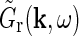 , cf Eq. 8.
, cf Eq. 8.
Receptive-field models incorporating phase-reversed push-pull cortical feedback
General expression with several cortical populations providing feedback
The main focus of this paper is the derivation of receptive-field models for cat relay cells (i.e., impulse-response functions Gr) which explicitly account for feedback effects from a set of orientation-selective cortical populations under the following assumptions: We consider both the four feedforward pathways (X/Y, ON/OFF) and the X and Y cortical feedback pathways to be decoupled (Briggs and Usrey 2009, 2011), while we take the cortical ON and OFF feedback channels to be coupled (Wang et al. 2006).
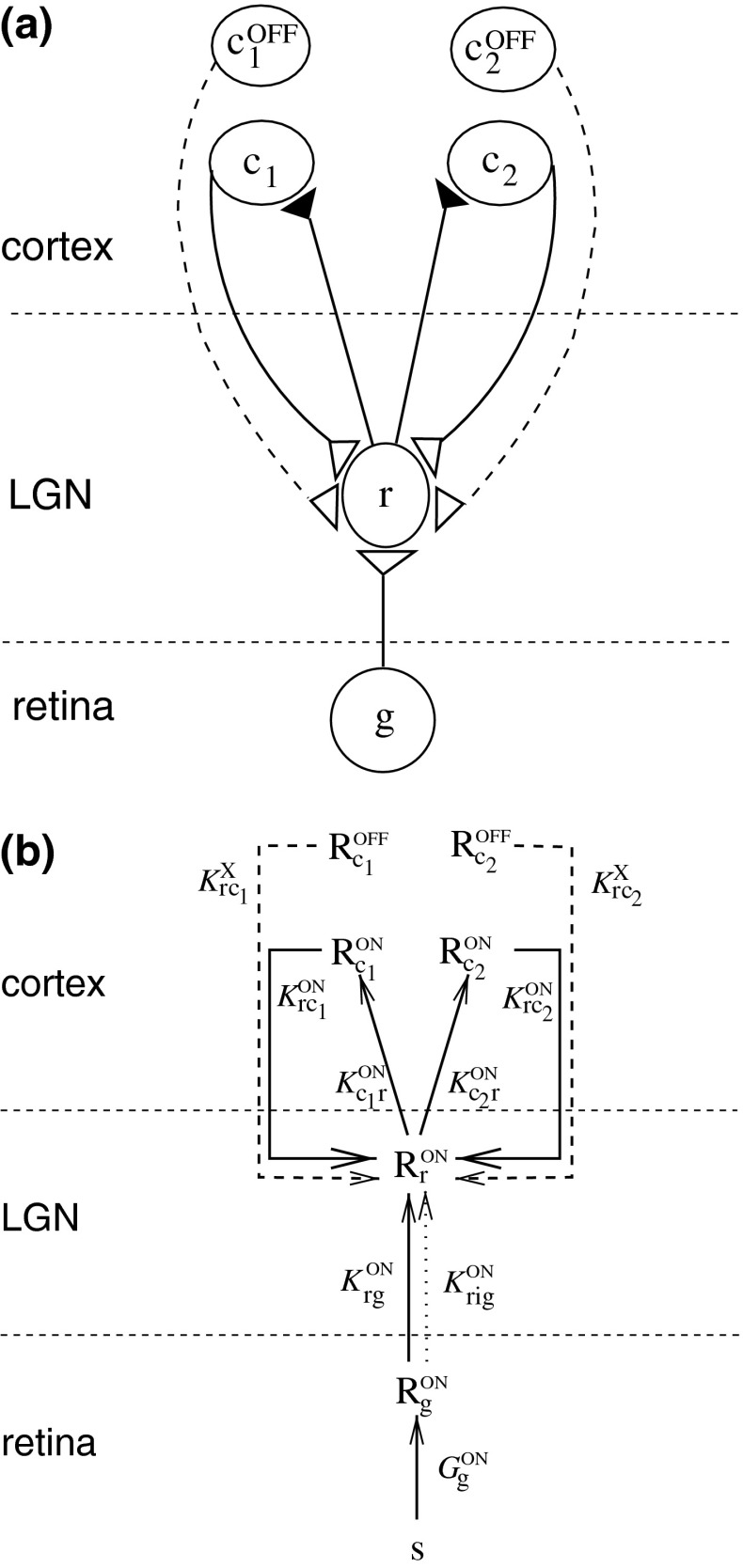
The corticogeniculate feedback comes from orientation-tuned cells in layer 6 in cortex. We thus consider a set of N orientation-selective cortical populations cn, for 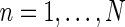 . Each population cn responds preferably to stimuli (bars, gratings) with orientation θn. We assume in our model that (i) all cortical populations receive direct input from relay cells, (ii) provide direct excitatory feedback or indirect inhibitory feedback (via intrageniculate interneurons or TRN neurons) to the relay cells in LGN, and (iii) are mutually uncoupled. The full model circuit is illustrated in Fig. 1; only two cortical populations are drawn even though an arbitrary number of cortical populations is considered in the mathematical analysis.
. Each population cn responds preferably to stimuli (bars, gratings) with orientation θn. We assume in our model that (i) all cortical populations receive direct input from relay cells, (ii) provide direct excitatory feedback or indirect inhibitory feedback (via intrageniculate interneurons or TRN neurons) to the relay cells in LGN, and (iii) are mutually uncoupled. The full model circuit is illustrated in Fig. 1; only two cortical populations are drawn even though an arbitrary number of cortical populations is considered in the mathematical analysis.
Fig. 1.
a Schematic view of present model of the geniculate circuit for the ON X pathway in cat comprising ON retinal ganglion cells (g), ON geniculate relay cells (r), and cells from several cortical cell populations, both ON (cn) and OFF (cOFFn). The feedback cross-connections (from OFF to ON) are shown as dashed lines. For the sake of clarity, only two populations (n = 1, 2) are shown, even though an arbitrary number of populations N are considered in our mathematical analysis, and input to OFF is not shown. The cortical OFF cells are driven by relay OFF cells not depicted in the figure. b Illustration of the mathematical model of the geniculate circuit. 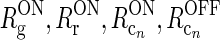 (n = 1, 2) represent the responses of ON retinal ganglion, ON relay, ON cortical, and OFF cortical cells respectively. K
jk (j, k = g, i, r, cn) represents the coupling from ON neurons of type k onto ON neurons of type j.
(n = 1, 2) represent the responses of ON retinal ganglion, ON relay, ON cortical, and OFF cortical cells respectively. K
jk (j, k = g, i, r, cn) represents the coupling from ON neurons of type k onto ON neurons of type j. 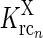 represents the cross-connection in the cortical feedback (dashed arrows), and K
rig represents the indirect feedforward inhibition via intrageniculate interneurons (dotted arrow)
represents the cross-connection in the cortical feedback (dashed arrows), and K
rig represents the indirect feedforward inhibition via intrageniculate interneurons (dotted arrow)
To be specific, we focus on the ON pathway in the derivation below, but a completely analogous derivation can be done for the OFF pathway. The firing-rate responses of the various ON cells in the early visual pathway are assumed to be governed by the following set of equations (Einevoll and Plesser 2002; Norheim et al. 2011):
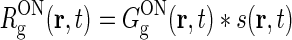 |
9 |
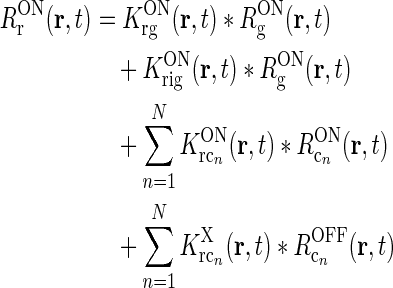 |
10 |
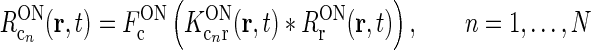 |
11 |
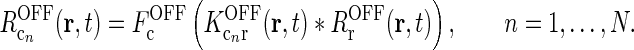 |
12 |
Rg, Rr, and 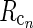 represent the responses of retinal ganglion cells, relay cells, interneurons, and cortical cells, respectively. s(r, t) represents the visual stimulus, i.e., s is zero in the background state. KONjk (j, k:g, r, cn) represents the linear coupling from ON neurons of type k onto ON neurons of type j. The real-space functions KONjk(r, τ) are the spatiotemporal coupling functions which tell how the firing rate of a cell of type k at position r0 and time zero affects the firing of a cell of type j at position r a time τ later. The coupling function KONrg from retinal ganglion cells to relay cells, e.g., will thus depend both on the ganglion-cell synapses on relay cells and how the firing of action potentials in relay cells is governed by synaptic inputs. The coupling function KONrig represents the indirect feedforward inhibition (via intrageniculate interneurons) from ON ganglion cells onto ON relay cells.
represent the responses of retinal ganglion cells, relay cells, interneurons, and cortical cells, respectively. s(r, t) represents the visual stimulus, i.e., s is zero in the background state. KONjk (j, k:g, r, cn) represents the linear coupling from ON neurons of type k onto ON neurons of type j. The real-space functions KONjk(r, τ) are the spatiotemporal coupling functions which tell how the firing rate of a cell of type k at position r0 and time zero affects the firing of a cell of type j at position r a time τ later. The coupling function KONrg from retinal ganglion cells to relay cells, e.g., will thus depend both on the ganglion-cell synapses on relay cells and how the firing of action potentials in relay cells is governed by synaptic inputs. The coupling function KONrig represents the indirect feedforward inhibition (via intrageniculate interneurons) from ON ganglion cells onto ON relay cells.
In the above equation set 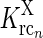 represents the cross-coupling feedback from cortical OFF cells onto relay ON cells. Further,
represents the cross-coupling feedback from cortical OFF cells onto relay ON cells. Further, 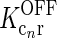 represents the coupling from the relay OFF cells onto these cortical OFF cells. Also, FONc(x) and FOFFc(x) are firing-rate functions converting the input onto the cortical ON and OFF cells, respectively, to firing rates (Norheim et al. 2011).
represents the coupling from the relay OFF cells onto these cortical OFF cells. Also, FONc(x) and FOFFc(x) are firing-rate functions converting the input onto the cortical ON and OFF cells, respectively, to firing rates (Norheim et al. 2011).
In the following we only model the time-dependent part of the relay-cell and cortical responses, i.e., Rr(r, t) and 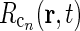 correspond to true firing rates minus the background firing rates. Thus the stimulus function s(r, t) represents the variation of stimulus luminance around the background luminance.
correspond to true firing rates minus the background firing rates. Thus the stimulus function s(r, t) represents the variation of stimulus luminance around the background luminance.
Assumption of phase-reversed push-pull cortical feedback
We now make the following additional assumptions:
- The firing-rate functions of the cortical cells are assumed to be half-wave rectified functions
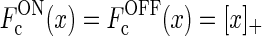 (Troyer et al. 1998; Dayan and Abbott 2001; Norheim et al. 2011), so that Eqs. 11 and 12 become
(Troyer et al. 1998; Dayan and Abbott 2001; Norheim et al. 2011), so that Eqs. 11 and 12 become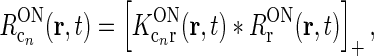
13
with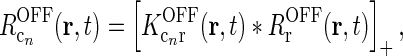
14 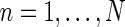 . This assumption can be well fulfilled if the inputs to the cortical cells are close to zero in the background state.
. This assumption can be well fulfilled if the inputs to the cortical cells are close to zero in the background state. - The feedback cross-connection (OFF to ON) is phase-reversed compared to the “same-sign” feedback, i.e.,
The assumption of phase-reversal, i.e., the negative sign, is supported by the experimental study of Wang et al. (2006). As the inhibitory feedback connections will go through one more synapse than the excitatory feedback connections, one may expect that the inhibitory feedback by necessity will be delayed compared to the excitatory feedback, at odds with the assumption inherent in Eq. 16 of identical temporal kernels. However, a study of Ahlsén et al. (1982) found the difference in latency for IPSPs and EPSPs arriving onto relay cells following electrical stimulation of the corticogeniculate feedback pathway, to be lzess than a millisecond. This suggests that the delay due to the extra synapse may be on the order of one millisecond and thus small compared to the overall time it takes the signal to pass around the thalamocortical loop and thus also small compared to the overall time constant in the final temporal loop kernels derived below.
16
With these three assumptions, and use of the mathematical identity [x]+ − [ − x]+ = x, we then find
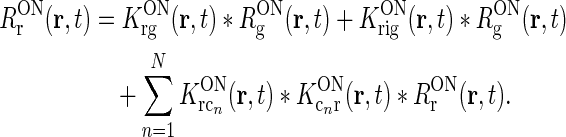 |
17 |
This expression for RONr(r, t) is completely linear, and the Fourier-transformed impulse response of ON relay cells, 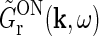 , can now be found using the approach of Einevoll and Plesser (2002):
, can now be found using the approach of Einevoll and Plesser (2002):
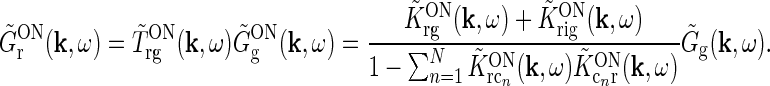 |
18 |
Even though this expression for the geniculate impulse response is quite involved, it has a simple structure. The direct feedforward excitation and the indirect feedforward inhibition via interneurons are represented by the first and second terms in the numerator, respectively. The feedback effects are accounted for in the denominator. Here the sum in the second term represents the effects of the excitatory feedback loop between relay cells and the N cortical populations (relay cell  cortex
cortex  relay cell).
relay cell).
Each of the terms in the denominator (of the type 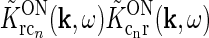 ) will not be circularly symmetric. Rather, their dependence on spatial wave vector k will reflect the orientation-preference of the cortical cells in the particular population n and the synaptic footprint of the corticogeniculate feedback to LGN from this particular population. Equation 12 gives an expression for the response of the cortical orientation-selective cell populations (cn). The coupling kernel
) will not be circularly symmetric. Rather, their dependence on spatial wave vector k will reflect the orientation-preference of the cortical cells in the particular population n and the synaptic footprint of the corticogeniculate feedback to LGN from this particular population. Equation 12 gives an expression for the response of the cortical orientation-selective cell populations (cn). The coupling kernel 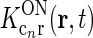 describes the transformation from the (roughly) circular receptive fields of relay cells to the elongated receptive fields of cortical cells (Hubel and Wiesel 1962); it is thus anisotropic. Likewise, there is evidence for an anisotropic organization of the corticothalamic synaptic input to LGN cells (Murphy and Sillito 1996; Murphy et al. 1999) which will be reflected in anisotropic corticogeniculate coupling kernels
describes the transformation from the (roughly) circular receptive fields of relay cells to the elongated receptive fields of cortical cells (Hubel and Wiesel 1962); it is thus anisotropic. Likewise, there is evidence for an anisotropic organization of the corticothalamic synaptic input to LGN cells (Murphy and Sillito 1996; Murphy et al. 1999) which will be reflected in anisotropic corticogeniculate coupling kernels 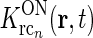 .
.
However, as seen in the denominator of Eq. 18, the total effect of cortical feedback on the response of LGN relay cells is a sum over contributions from allN cortical orientation-selective populations. Since the cortical populations cover all orientation angles, the net feedback effect is expected to be essentially isotropic, i.e., circularly symmetric. This is supported by experimental observations of cortical feedback effects on relay cells using bipartite grating stimuli (Sillito et al. 1993; Cudeiro and Sillito 1996). There, the feedback effects were found to be independent of the absolute orientation of the gratings.
Net effect of feedback from several cortical populations
We now go on to demonstrate that the net feedback effect on relay cells may effectively be circularly symmetric when all cortical populations are included. First, the coupling kernels involved in the thalamocortical loops ( ) are assumed to be spatiotemporally separable, i.e., KON(r, t) = f(r)h(t). Then the terms in the sum in the denominator of Eq. 18 will be of the form
) are assumed to be spatiotemporally separable, i.e., KON(r, t) = f(r)h(t). Then the terms in the sum in the denominator of Eq. 18 will be of the form
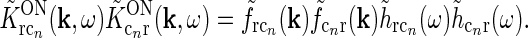 |
The spatial coupling kernel 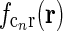 must have an elongated shape in order to assure the orientation-selectivity of the cortical population cn. Likewise, an elongated shape of
must have an elongated shape in order to assure the orientation-selectivity of the cortical population cn. Likewise, an elongated shape of 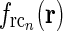 also qualitatively captures experimental findings regarding the anisotropic and topographic organization of the corticothalamic feedback (Murphy and Sillito 1996;Murphy et al. 1999).
also qualitatively captures experimental findings regarding the anisotropic and topographic organization of the corticothalamic feedback (Murphy and Sillito 1996;Murphy et al. 1999).
In our model we assume that the spatial coupling for the loop is elongated and strongest at the the same position in the visual field, i.e., for r = 0. A simple mathematical choice is to model the spatial coupling for the excitatory loop involving cortical population cn (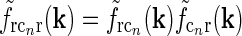 ) as a an elliptic Gaussian, i.e.,
) as a an elliptic Gaussian, i.e.,
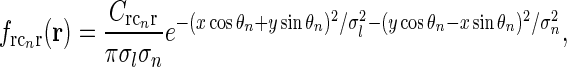 |
19 |
or, equivalently, in Fourier space,
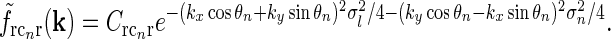 |
20 |
Here σl and σn are the parameters determining the spatial widths of the loop kernel along its long and narrow axes, respectively (σl > σn),  is the loop coupling strength, and θn is the angle the long axis of the ellipse makes with the x-axis. Contour plots of an example spatial-loop kernel are shown in Fig. 2 (left panels). Here the coupling kernel is chosen to be significantly elongated, reflecting both the oriented relay-cell input to orientation-selective cortical cells and a possibly oriented feedback from cortex to LGN.
is the loop coupling strength, and θn is the angle the long axis of the ellipse makes with the x-axis. Contour plots of an example spatial-loop kernel are shown in Fig. 2 (left panels). Here the coupling kernel is chosen to be significantly elongated, reflecting both the oriented relay-cell input to orientation-selective cortical cells and a possibly oriented feedback from cortex to LGN.
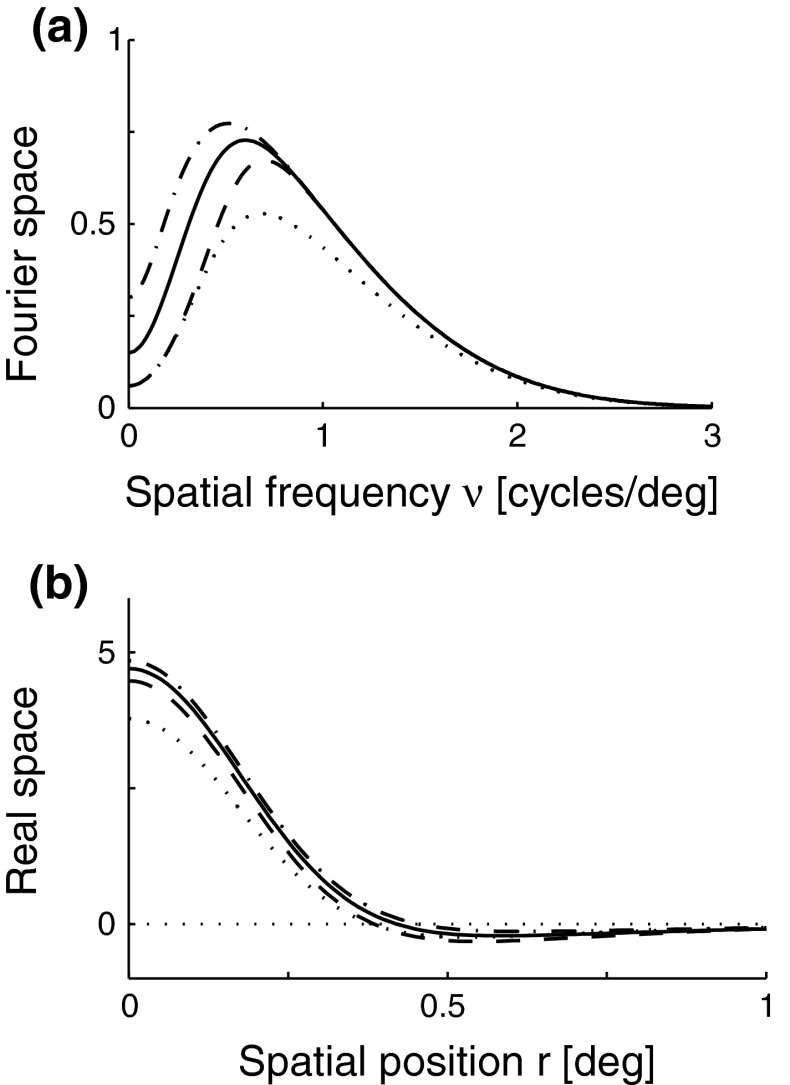
Fig. 2.
Contour plots illustrating spatial part of loop kernel (a, b) and model impulse-response functions (c, d) for relay-cell (DOG model) and impulse-response “input” to cortical cell (e, f). Functions are shown in Fourier-space in the left column (a, c, e) and in real space in the right column (b, d, f). (a) Fourier-space loop kernel for cortical feedback loop modeled as a Gaussian ellipse, 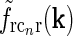 in Eq. 20 (θn = π/4, σn = 0.1 deg, σl = 1.4 deg,
in Eq. 20 (θn = π/4, σn = 0.1 deg, σl = 1.4 deg, 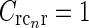 ). (b)
). (b) 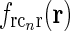 Eq. 19 corresponding to
Eq. 19 corresponding to 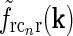 . (c) Fourier-space relay-cell DOG model
. (c) Fourier-space relay-cell DOG model 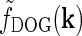 from Eq. 7 (A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg). (d) f
DOG(r) (from Eq. 6) corresponding to
from Eq. 7 (A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg). (d) f
DOG(r) (from Eq. 6) corresponding to 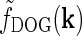 . (e) Fourier-transformed input to cortical cell
. (e) Fourier-transformed input to cortical cell 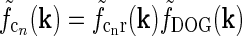 . The spatial parameters for the feedforward coupling kernel
. The spatial parameters for the feedforward coupling kernel 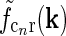 are chosen a factor
are chosen a factor 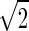 smaller than for the loop kernel
smaller than for the loop kernel 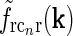 , i.e., σn = 0.07 deg, σl = 0.99 deg, while
, i.e., σn = 0.07 deg, σl = 0.99 deg, while 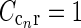 . With the same spatial parameters for a similarly modeled feedback coupling kernel
. With the same spatial parameters for a similarly modeled feedback coupling kernel 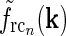 , one would get the loop kernel
, one would get the loop kernel 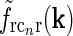 in panel (a). (f)
in panel (a). (f)
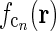 found by an inverse Fourier-transform of
found by an inverse Fourier-transform of 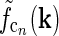 . In panels (a), (b), (c) and (e) white corresponds to the zero level; in panels (d) and (f) white corresponds to a negative value to illustrate the negative lobes of the LGN (DOG) receptive fields and input to cortical cells (subthreshold receptive fields)
. In panels (a), (b), (c) and (e) white corresponds to the zero level; in panels (d) and (f) white corresponds to a negative value to illustrate the negative lobes of the LGN (DOG) receptive fields and input to cortical cells (subthreshold receptive fields)
In Fig. 2 (right panels) we also show an example of a model input to the cortical cell, i.e., its “subthreshold” receptive field, for our simplified thalamocortical projection pattern. In Fourier space this spatial impulse-response function 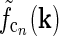 is the product of the relay-cell response (modeled as a DOG, i.e.,
is the product of the relay-cell response (modeled as a DOG, i.e., 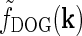 , cf. Fig. 2 (middle panels)) and an elliptical coupling function from relay cells to cortical cells
, cf. Fig. 2 (middle panels)) and an elliptical coupling function from relay cells to cortical cells 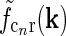 of the form in Eq. 20. As seen in the figure, the real-space cortical receptive field
of the form in Eq. 20. As seen in the figure, the real-space cortical receptive field 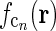 has an elongated shape characteristic for orientation-selective cells. This receptive-field also exhibits both ON and OFF subfields, but a mix of ON and OFF inputs from LGN (not included in our simplified model for
has an elongated shape characteristic for orientation-selective cells. This receptive-field also exhibits both ON and OFF subfields, but a mix of ON and OFF inputs from LGN (not included in our simplified model for 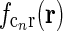 ) would presumably give a more realistic simple-cell receptive field structure (Reid and Alonso 1995). In Fig. 2 the parameters of the DOG model are chosen so that the relay-cell receptive field has a center diameter of 0.8°, and the resulting model cortical receptive-field length is seen in the figure to be about 4°. These numbers are similar to the mean optimal summation sizes (0.9° and 3.6°) observed for LGN cells and visual cortical cells, respectively, in cat (Jones et al. 2000).
) would presumably give a more realistic simple-cell receptive field structure (Reid and Alonso 1995). In Fig. 2 the parameters of the DOG model are chosen so that the relay-cell receptive field has a center diameter of 0.8°, and the resulting model cortical receptive-field length is seen in the figure to be about 4°. These numbers are similar to the mean optimal summation sizes (0.9° and 3.6°) observed for LGN cells and visual cortical cells, respectively, in cat (Jones et al. 2000).
If the relay cell only received feedback from a single cortical population cn, the feedback effect would clearly be orientation selective. However, the relay cell appears to receive inputs from all cortical populations (Sillito et al. 1993; Cudeiro and Sillito 1996). If we assume the temporal coupling kernels to be the same for all thalamocortical loops (i.e., 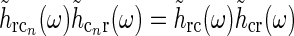 for all cn), the loop term in the denominator of Eq. 18 simplifies as follows:
for all cn), the loop term in the denominator of Eq. 18 simplifies as follows:
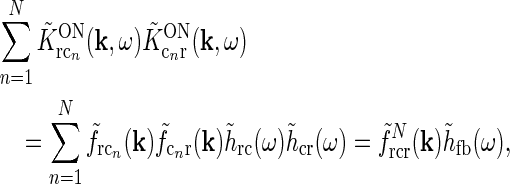 |
21 |
where we have introduced the temporal feedback kernel 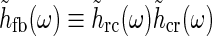 and the summed spatial kernel
and the summed spatial kernel
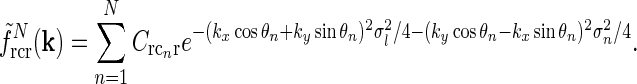 |
22 |
There is no a priori reason why one cortical orientation population should have stronger feedback connections than any other, and we thus assume the loop weight 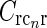 to be the same for all populations cn. If so, the summed spatial kernel
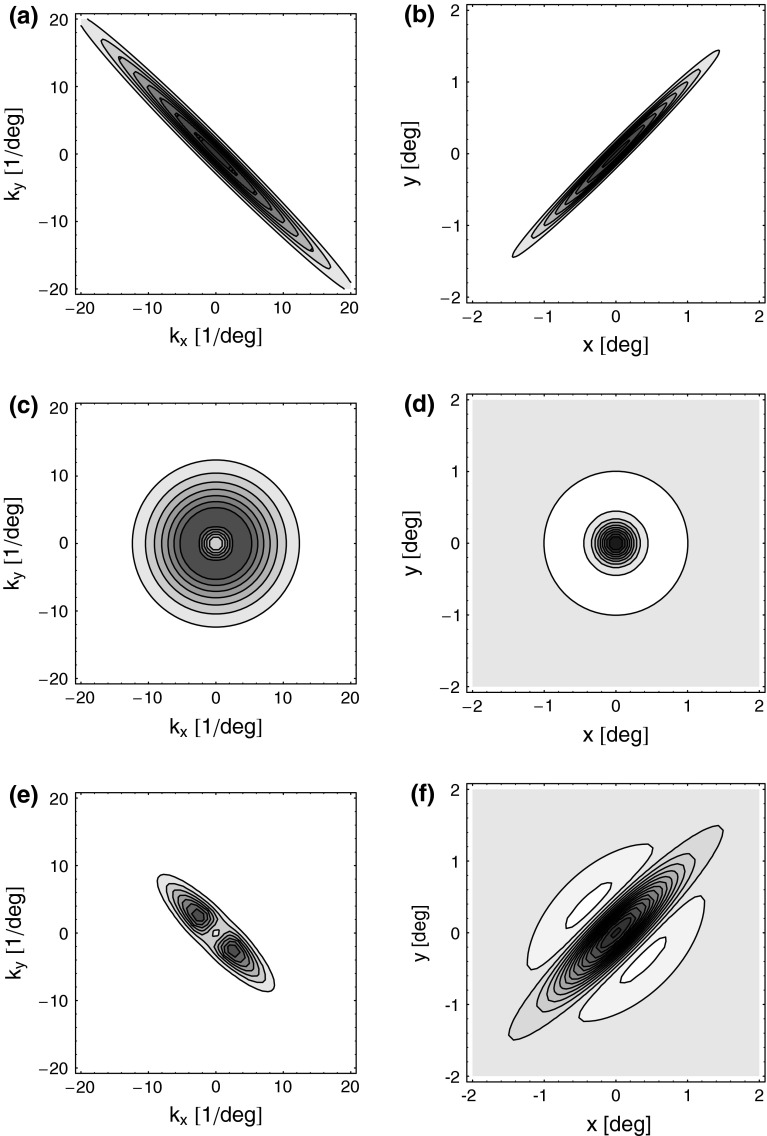
to be the same for all populations cn. If so, the summed spatial kernel 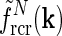 will approach a circularly symmetric form when the number of cortical populations N increases and the preferred angles θn of these orientation-selective cortical populations are assumed to be equidistant in angular space. This is illustrated in Fig. 3 for our model with elliptical Gaussian coupling kernels distinguished only by their orientation θn. As seen in the figure, a sum over eight populations gives essentially a circularly symmetric spatial feedback-loop kernel.
will approach a circularly symmetric form when the number of cortical populations N increases and the preferred angles θn of these orientation-selective cortical populations are assumed to be equidistant in angular space. This is illustrated in Fig. 3 for our model with elliptical Gaussian coupling kernels distinguished only by their orientation θn. As seen in the figure, a sum over eight populations gives essentially a circularly symmetric spatial feedback-loop kernel.
Fig. 3.
Example contour plots of the summed spatial loop kernel including several excitatory cortical feedback loops, Eq. 22, for different numbers of cortical populations N. The Gaussian width parameters are chosen as in Fig. 2, i.e., σn = 0.1 deg, σl = 1.4 deg. Here we use 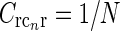 which assures the same overall coupling strength (summed over all k-space) in the set of examples. (a) N = 1, (b) N = 2, (c) N = 3, (d) N = 4, (e) N = 8, (f)
which assures the same overall coupling strength (summed over all k-space) in the set of examples. (a) N = 1, (b) N = 2, (c) N = 3, (d) N = 4, (e) N = 8, (f) 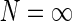 , Eq. 24
, Eq. 24
For our model we can in fact find a closed-form expression for the net summed coupling kernel from N angular equidistant and equally weighted populations in the limit 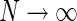 . In this “continuous” limit we have with θn = (n − 1)π/N
. In this “continuous” limit we have with θn = (n − 1)π/N
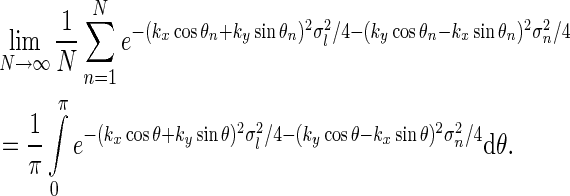 |
23 |
This angular integral can be solved analytically to give the net spatial feedback kernel for this continuous model
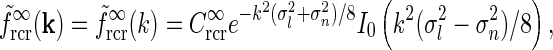 |
24 |
where I0(x) is the zeroth-order modified Bessel function (Abramowitz and Stegun 1965), k2 = k2x + k2y, and we have introduced 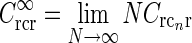 , implicitly assuming that the loop weight
, implicitly assuming that the loop weight 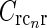 for each cortical population is inversely proportional to N.
for each cortical population is inversely proportional to N.
An example of 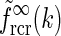 in Eq. 24 and the real-space equivalent
in Eq. 24 and the real-space equivalent 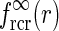 (found by an inverse Fourier transform, cf. Eq. 5) is shown in Fig. 4. For small k, the modified Bessel function I0(k2(σ2l − σ2n)/8) is close to one, and the exponential prefactor
(found by an inverse Fourier transform, cf. Eq. 5) is shown in Fig. 4. For small k, the modified Bessel function I0(k2(σ2l − σ2n)/8) is close to one, and the exponential prefactor 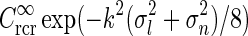 dominates. For large k (and
dominates. For large k (and 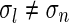 ) we can use the asymptotic expansion
) we can use the asymptotic expansion 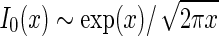 (Abramowitz and Stegun 1965) to obtain
(Abramowitz and Stegun 1965) to obtain
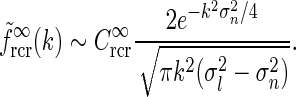 |
25 |
As seen in Fig. 4 the two approximate, but more mathematically transparent, expressions valid in the small-k and large-k regimes, respectively, together describe the function 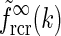 in Eq. 24 quite well.
in Eq. 24 quite well.
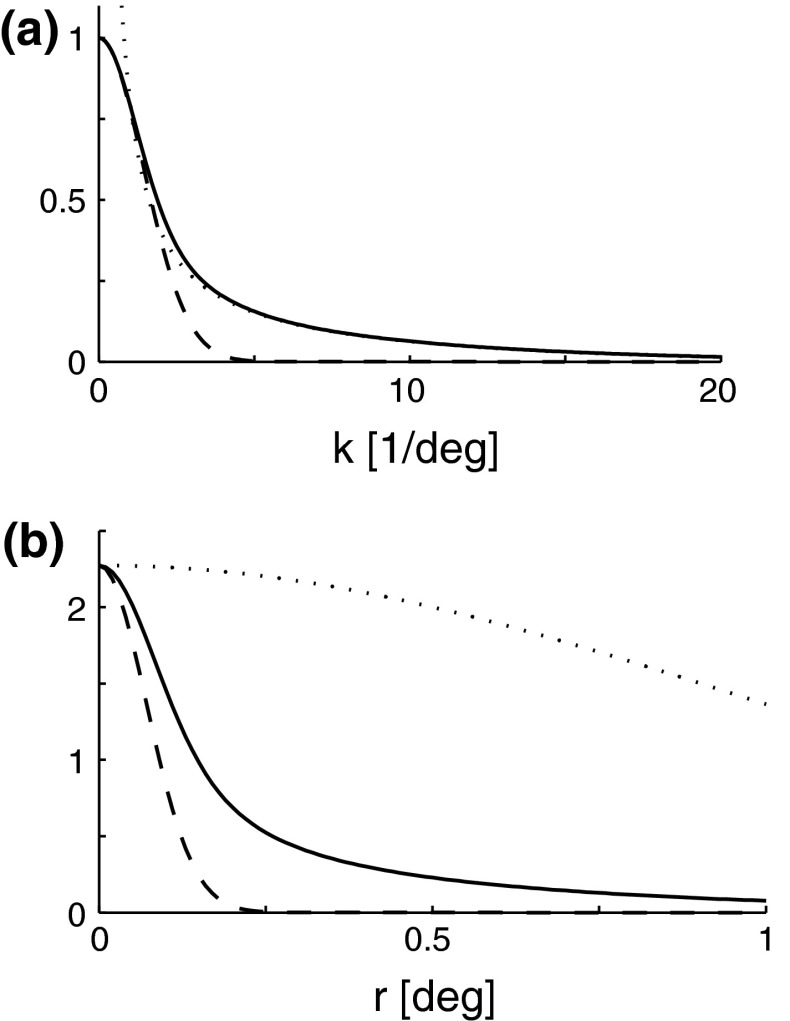
Fig. 4.
a Example plot of net spatial loop kernel in k-space in the limit of infinitely many orientation-selective cortical populations (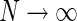 ), i.e.,
), i.e., 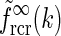 in Eq. 24 (solid line). The dashed line corresponds to the exponential prefactor
in Eq. 24 (solid line). The dashed line corresponds to the exponential prefactor 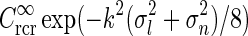 of Eq. 24, while the dotted line shows the asymptotic expansion of Eq. 25, valid for large k. Gaussian width parameters are as in Fig. 2 (σn = 0.1 deg, σl = 1.4 deg,
of Eq. 24, while the dotted line shows the asymptotic expansion of Eq. 25, valid for large k. Gaussian width parameters are as in Fig. 2 (σn = 0.1 deg, σl = 1.4 deg, 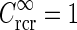 ). b Real-space version of coupling kernel in left panel,
). b Real-space version of coupling kernel in left panel, 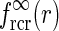 , found by a numerical inverse Fourier transform of
, found by a numerical inverse Fourier transform of 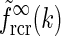 (solid line). The dashed and dotted lines show the coupling kernel
(solid line). The dashed and dotted lines show the coupling kernel 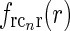 in Eq. 19 along the narrow and long axes, respectively (with
in Eq. 19 along the narrow and long axes, respectively (with 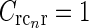 )
)
The main point of the mathematical analysis above is not the particular functional form of the summed “continuous” loop kernel 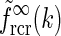 , which is based on modeling the loop kernel for each cortical population as an elliptical Gaussian. Other loop kernels incorporating, for example, mixed ON/OFF input from LGN to cortical cells (Hayot and Tranchina 2001) would have given different summed “continuous” loop kernels. The crucial point—that this summed loop kernel is independent of the direction of k and only depends on the magnitude
, which is based on modeling the loop kernel for each cortical population as an elliptical Gaussian. Other loop kernels incorporating, for example, mixed ON/OFF input from LGN to cortical cells (Hayot and Tranchina 2001) would have given different summed “continuous” loop kernels. The crucial point—that this summed loop kernel is independent of the direction of k and only depends on the magnitude 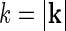 —however, only relies on the summation of identical contributions from sufficiently many angularly equidistant cortical populations covering all orientations. The net effect of the cortical feedback can thus be incorporated in the model via a single (and presently unspecified) term
—however, only relies on the summation of identical contributions from sufficiently many angularly equidistant cortical populations covering all orientations. The net effect of the cortical feedback can thus be incorporated in the model via a single (and presently unspecified) term 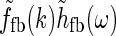 regardless of the detailed form of the loop kernel for individual cortical populations. The Fourier-transformed impulse response of relay cells
regardless of the detailed form of the loop kernel for individual cortical populations. The Fourier-transformed impulse response of relay cells 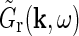 in Eq. 18 can then be rewritten as,
in Eq. 18 can then be rewritten as,
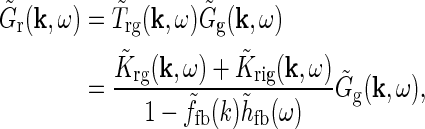 |
26 |
corresponding to the expression assuming a single (hypothetical) cortical population with circularly-symmetric and linear response properties (Einevoll and Plesser 2002).
Note that the assumption of lumping the feedback effect of all orientation-selective cortical populations into a single term without orientation selectivity does not hinge on the assumption of spatiotemporally separable thalamocortical coupling kernels (as long as the coupling kernels are identical except for an angular rotation).
Extended difference-of-Gaussians model
Eq. 26 only determines the overall mathematical structure for the mechanistic model for the relay-cell impulse-response function. To make a model one must make specific choices for the Fourier-transformed retinal ganglion cell impulse-response function 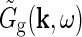 and coupling kernels (
and coupling kernels (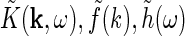 ). These choices will in practice depend on the goal of the modeling. Here we will consider a simple model, which we call the extended difference-of-Gaussians model (eDOG), aimed at elucidating some salient features of effects of cortical feedback.
). These choices will in practice depend on the goal of the modeling. Here we will consider a simple model, which we call the extended difference-of-Gaussians model (eDOG), aimed at elucidating some salient features of effects of cortical feedback.
Spatiotemporal eDOG model
We first replace the numerator of Eq. 26, i.e., the feedforward contribution, with the simple DOG model expression in Eq. 7,
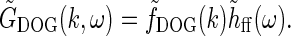 |
27 |
Here we have added the subscript “ff” for “feedforward” to the unspecified temporal function h. We have also removed the bold face on “k” to stress that the spatial DOG function only depends on the magnitude of the wave vector k. Eq. 26 then simplifies to
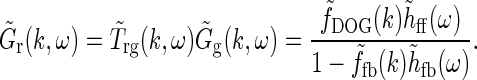 |
28 |
A natural choice for modeling, e.g., the summed spatial loop kernel 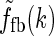 , could be to use the derived loop-kernel function
, could be to use the derived loop-kernel function 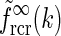 in Eq. 24. However, this loop-kernel function was derived based on the somewhat arbitrary choice of using elliptical Gaussians to model elongated spatial loop kernels involving individual cortical populations. With other choices the result would be different. In lack of physiological observations aiding the specification, we therefore presently use the mathematically simpler circularly symmetric Gaussians (Einevoll and Plesser 2002),
in Eq. 24. However, this loop-kernel function was derived based on the somewhat arbitrary choice of using elliptical Gaussians to model elongated spatial loop kernels involving individual cortical populations. With other choices the result would be different. In lack of physiological observations aiding the specification, we therefore presently use the mathematically simpler circularly symmetric Gaussians (Einevoll and Plesser 2002),
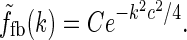 |
29 |
Here the weight parameter C will be negative if the in-phase (i.e., ON to ON) cortical feedback is inhibitory and positive if this in-phase feedback is excitatory. The parameter c parameterize the spatial spread of the thalamocortical feedback loop; a large value of c would indicate that the thalamocortical loop is involved in more global information processing (Murphy and Sillito 1996).
A similarly simple model choice for the temporal coupling functions h(t) could be the delayed exponential coupling kernel (Einevoll and Plesser 2002; Norheim et al. 2011). For the moment, however, we keep the choice of h(t) open; the only constraint we impose is that it should be normalized, i.e., 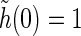 .
.
Then the (Fourier transformed) relay-cell impulse-response function of the extended DOG (eDOG) model, is reduced to
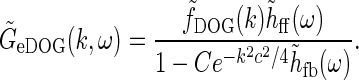 |
30 |
A first observation is that in the general case 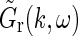 is not spatiotemporally separable, i.e.,
is not spatiotemporally separable, i.e., 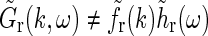 .
.
The space-time impulse-response functionGeDOG(r, t) can be found by taking the inverse Fourier transform of 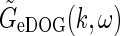 , i.e.,
, i.e.,
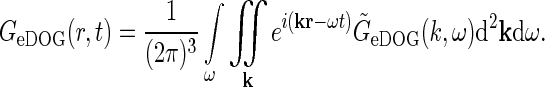 |
31 |
In the general case this integral must be evaluated numerically.
Fast-loop limit
In many experiments with sinusoidally drifting stimuli (full-field grating or bipartite stimuli) the temporal frequencies have been chosen to be in the range 1–3 Hz (Sillito et al. 1993; Cudeiro and Sillito 1996; Cheng et al. 1995). The shortest propagation time around the thalamocortical loop can be less than ten milliseconds (Sillito and Jones 2004; Briggs and Usrey 2007), much shorter than the experimental oscillation period of up to a second (for f = 1 Hz). This suggests that a low-frequency, or “fast-loop”, approximation can be used where 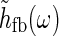 may be approximated as unity, in the modeling of the experiments.
may be approximated as unity, in the modeling of the experiments.
To illustrate the approximation we assume for simplicity that the temporal thalamocortical loop kernel hff(t) is described as a delayed δ-function, i.e., hfb(t) = δ(t − τloop). This corresponds to assuming the signal taking a time τloop to pass around the thalamocortical loop. The Fourier-transformed kernel is then given by
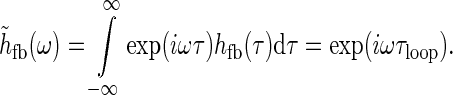 |
32 |
A temporal frequency f = 1 Hz corresponds to an angular frequency of 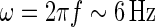 . For τloop = 10 ms we thus have ωτloop = 0.06, so that
. For τloop = 10 ms we thus have ωτloop = 0.06, so that 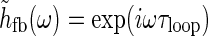 will be close to unity. In this “fast-loop” limit where
will be close to unity. In this “fast-loop” limit where 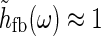 the eDOG relay-cell impulse-response function in Eq. 30 simplifies to
the eDOG relay-cell impulse-response function in Eq. 30 simplifies to
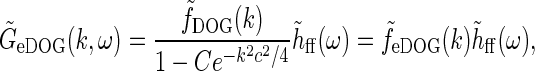 |
33 |
where we have introduced the spatial eDOG function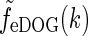 via
via
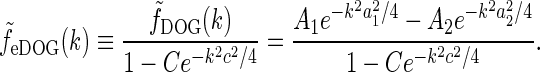 |
34 |
The corresponding real-space impulse-response function describing the spatial receptive field is now given by an inverse Fourier transform of 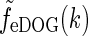 , i.e.,
, i.e.,
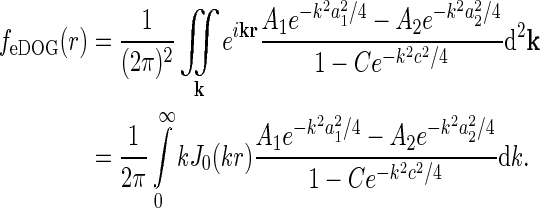 |
35 |
Here we have exploited that 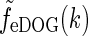 does not depend on orientation and that
does not depend on orientation and that 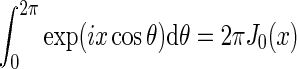 , where J0(x) is the zeroth-order Bessel function (Abramowitz and Stegun 1965).
, where J0(x) is the zeroth-order Bessel function (Abramowitz and Stegun 1965).
In Fig. 5 we show example plots of 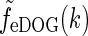 and the corresponding real-space expression feDOG(r). For the case where the in-phase feedback is excitatory, i.e., C > 0, (and the anti-phase feedback thus is inhibitory) we see that the impulse-response function is amplified. We call this situation push-pull excitation. For the opposite case where the in-phase feedback is inhibitory, i.e., C < 0, the impulse-response is correspondingly reduced, and we call this situation push-pull inhibition. In Fig. 5 we also show spatial impulse-response functions for a modified eDOG model where the Gaussian function in the denominator of Eq. 34 is replaced with a function of the type
and the corresponding real-space expression feDOG(r). For the case where the in-phase feedback is excitatory, i.e., C > 0, (and the anti-phase feedback thus is inhibitory) we see that the impulse-response function is amplified. We call this situation push-pull excitation. For the opposite case where the in-phase feedback is inhibitory, i.e., C < 0, the impulse-response is correspondingly reduced, and we call this situation push-pull inhibition. In Fig. 5 we also show spatial impulse-response functions for a modified eDOG model where the Gaussian function in the denominator of Eq. 34 is replaced with a function of the type  (cf. Eq. 24) derived by summing over many elliptical Gaussian loop kernels in section "Net effect of feedback from several cortical populations". In the example plot σn is set to zero, i.e., to the anisotropic limit. To compare with the Gaussian push-pull inhibitory eDOG model, the parameters in the plot are chosen so that the prefactor in Eq. 24 corresponds to the Gaussian eDOG model example. As seen in the left panel, for this example the inhibitory feedback in this modified eDOG model gives, except for the smallest and largest spatial frequencies, a larger reduction of the Fourier-space impulse response compared to the Gaussian push-pull inhibitory eDOG model.
(cf. Eq. 24) derived by summing over many elliptical Gaussian loop kernels in section "Net effect of feedback from several cortical populations". In the example plot σn is set to zero, i.e., to the anisotropic limit. To compare with the Gaussian push-pull inhibitory eDOG model, the parameters in the plot are chosen so that the prefactor in Eq. 24 corresponds to the Gaussian eDOG model example. As seen in the left panel, for this example the inhibitory feedback in this modified eDOG model gives, except for the smallest and largest spatial frequencies, a larger reduction of the Fourier-space impulse response compared to the Gaussian push-pull inhibitory eDOG model.
Fig. 5.
Examples of eDOG spatial receptive fields (spatial impulse-response function) in the “fast-loop” limit. a eDOG function in Fourier space, 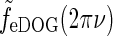 , in Eq. 34 plotted as a function of spatial frequency ν (k = 2π ν). Solid line: C = 0, i.e., standard DOG. Dash-dotted line: Push-pull excitatory feedback for C = 0.5, c = 0.83 deg. Dashed line: Push-pull inhibitory feedback for C = −1.5, c = 0.83 deg. Dotted line: Modified push-pull inhibitory-feedback eDOG model with the Gaussian loop-function replaced with a function of the type in Eq. 24 with the constant
, in Eq. 34 plotted as a function of spatial frequency ν (k = 2π ν). Solid line: C = 0, i.e., standard DOG. Dash-dotted line: Push-pull excitatory feedback for C = 0.5, c = 0.83 deg. Dashed line: Push-pull inhibitory feedback for C = −1.5, c = 0.83 deg. Dotted line: Modified push-pull inhibitory-feedback eDOG model with the Gaussian loop-function replaced with a function of the type in Eq. 24 with the constant 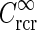 set to −1.5,
set to −1.5, 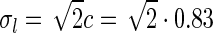 deg
deg 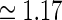 deg and σn = 0. b Real-space eDOG functions, f
eDOG(r), corresponding to the Fourier-space functions in left panel. The DOG parameters used are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg
deg and σn = 0. b Real-space eDOG functions, f
eDOG(r), corresponding to the Fourier-space functions in left panel. The DOG parameters used are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg
When the cortical feedback is small or moderate, i.e., 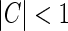 , the integral expression for feDOG(r) in Eq. 35 can be significantly simplified, as shown in Appendix 1.
, the integral expression for feDOG(r) in Eq. 35 can be significantly simplified, as shown in Appendix 1.
Example application: patch-grating stimuli
To clearly elucidate the effects of cortical feedback on response properties of LGN cells, comparison of data from identical experiments done with and without cortical feedback is preferable. This requires removal of cortical feedback to LGN (e.g., by surgical or pharmacological means), and such experiments are scarce in the literature. Sillito and co-workers have, however, measured the effect of cortical feedback on the response properties of LGN relay cells (Murphy and Sillito 1987; Sillito et al. 1993; Cudeiro and Sillito 1996; Andolina et al. 2002; Sillito and Jones 2002).
In one study, they compared responses of flashing circular spots to circular patches of drifting gratings (Andolina et al. 2002; Sillito and Jones 2002). For circular spots the center-surround suppression (i.e., the reduction of the response to large spots compared to the maximum response to a spot covering the receptive-field center) was found to be qualitatively the same with (normal) and without (decorticated) cortical feedback. For circular patches of drifting gratings, a similar center-surround suppression was found in the normal case, while it was significantly reduced in the decorticated case.
In another experiment they compared the spatial frequency tuning of responses to a patch of grating covering the receptive-field center with the responses to a similar full-field grating both for the normal and decorticated cases (Cudeiro and Sillito 1996). They observed lower responses to full-field gratings compared to patch-gratings, and the percentage response reduction was largest for the smallest spatial frequencies. However, the response reduction was generally smaller for the decorticated compared to the normal case, with the difference being more pronounced for the smallest spatial frequencies (particularly for X cells, cf. Figure 8 in Cudeiro and Sillito (1996)).
These studies indicate that cortical feedback provides extra inhibition of LGN relay cells under certain experimental conditions. Corticogeniculate terminals have been found to be preferentially located on LGN interneurons (Weber et al. 1989). A push-pull inhibitory eDOG model is thus a natural choice for a modeling investigation of these experiments. In the experiments a large grating contrast was used (0.36–0.72, cf. Cudeiro and Sillito (1996)). The eDOG model is by construction linear and cannot account for non-linear effects expected to be significantly evoked at such high contrasts. Nevertheless, results from our linear model may give qualitative insights into the observed phenomena.
For circular patches of drifting gratings, the stimulus can mathematically be described as
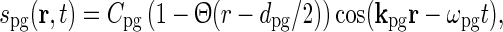 |
36 |
where kpg and ωpg are the wave vector and the angular frequency of the patch-grating, respectively, 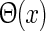 is the Heaviside step function, dpg is the diameter of the patch-grating spot, and Cpg is a measure of the patch-grating contrast; circular patches are obtained for kpg = ωpg = 0. It is mathematically convenient to introduce a complex version of this stimulus function, scpg(r, t), obtained by replacing the cosine-function in Eq. 36 with
is the Heaviside step function, dpg is the diameter of the patch-grating spot, and Cpg is a measure of the patch-grating contrast; circular patches are obtained for kpg = ωpg = 0. It is mathematically convenient to introduce a complex version of this stimulus function, scpg(r, t), obtained by replacing the cosine-function in Eq. 36 with 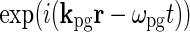 . The Fourier transform of this (complex) patch-grating stimulus is after some mathematical derivation found to be (Einevoll and Plesser 2005)
. The Fourier transform of this (complex) patch-grating stimulus is after some mathematical derivation found to be (Einevoll and Plesser 2005)
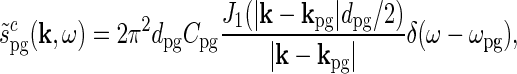 |
37 |
where J1(x) is the first-order Bessel function.
The (complex) response to a patch grating for the eDOG model can now be found by insertion of 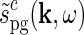 into the general response expression in Eq. 3 together with
into the general response expression in Eq. 3 together with  from Eq. 30. In the above-mentioned experiments by Sillito and co-workers the temporal grating frequency was between 1 and 2 Hz, and in this example application we will consider the “fast-loop” limit and use the simpler expression for
from Eq. 30. In the above-mentioned experiments by Sillito and co-workers the temporal grating frequency was between 1 and 2 Hz, and in this example application we will consider the “fast-loop” limit and use the simpler expression for  in Eq. 33 instead. For a relay-cell with receptive field centered at the center of the patch grating (r = 0), the complex response then becomes
in Eq. 33 instead. For a relay-cell with receptive field centered at the center of the patch grating (r = 0), the complex response then becomes
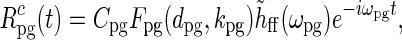 |
38 |
where
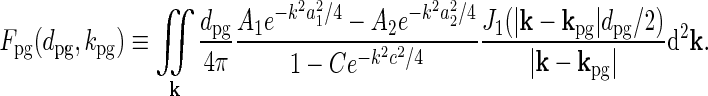 |
39 |
In this model the patch-grating response will thus be harmonically oscillating with the amplitude determined by Fpg(dpg, kpg) and 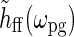 . In the experiments from Sillito’s group firing responses were measured as a function of spot diameter dpg (Sillito and Jones 2002) or spatial frequency of patch grating
. In the experiments from Sillito’s group firing responses were measured as a function of spot diameter dpg (Sillito and Jones 2002) or spatial frequency of patch grating 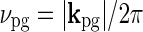 (Cudeiro and Sillito 1996) with a fixed temporal frequency fpg = ωpg/2π. Thus
(Cudeiro and Sillito 1996) with a fixed temporal frequency fpg = ωpg/2π. Thus 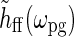 does not change in these experiments, and the relevant quantity to investigate is Fpg(dpg, kpg). Note that Fpg(dpg, kpg) only depends on the magnitude and not the direction of kpg. This is a consequence of the circular spatial symmetry of the eDOG model.
does not change in these experiments, and the relevant quantity to investigate is Fpg(dpg, kpg). Note that Fpg(dpg, kpg) only depends on the magnitude and not the direction of kpg. This is a consequence of the circular spatial symmetry of the eDOG model.
The integral in Eq. 39 must be solved numerically in the general case. However, for the special case where the spatial receptive field is described by a standard DOG (i.e., C = 0), an analytical solution to the integral can be found. The function Fpg(dpg, kpg) can then be written as an infinite series where each term in the series involves the confluent hypergeometric function (Einevoll and Plesser 2005).
To compare with the results of Sillito and Jones (2002) on the difference between patch-grating and flashing-spot responses, we also need a model expression for the response to flashing spots. This we obtain by setting the spatial frequency to zero (i.e., kpg = 0) in Eq. 39. This gives the response to harmonically oscillating spots, but for our spatiotemporally separable version of the eDOG model the flashing-spot response will be directly proportional to the amplitude CpgFpg(dsp,0) of this oscillatory response.
To compare with the results of Cudeiro and Sillito (1996) we further need the response to full-field gratings. The amplitude of this response is simply given by 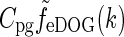 where
where 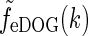 is given by Eq. 34. In Fig. 6 (upper left) we show an example plot of the diameter-dependence of the flashing-spot response of LGN relay cells, i.e., Fpg(dsp,0). The solid line corresponds to the standard DOG model which in our case will correspond to the decorticated case (the DOG model is assumed to account for the feedforward processing). The dashed line corresponds to an eDOG model with the same DOG parameters but including a push-pull inhibitory thalamocortical loop. The eDOG model represents the LGN response when the cortical feedback is intact (normal case). We observe that the eDOG model response overall is reduced compared to the DOG model, but the shape and amount of center-surround suppression are qualitatively similar in the two cases.
is given by Eq. 34. In Fig. 6 (upper left) we show an example plot of the diameter-dependence of the flashing-spot response of LGN relay cells, i.e., Fpg(dsp,0). The solid line corresponds to the standard DOG model which in our case will correspond to the decorticated case (the DOG model is assumed to account for the feedforward processing). The dashed line corresponds to an eDOG model with the same DOG parameters but including a push-pull inhibitory thalamocortical loop. The eDOG model represents the LGN response when the cortical feedback is intact (normal case). We observe that the eDOG model response overall is reduced compared to the DOG model, but the shape and amount of center-surround suppression are qualitatively similar in the two cases.
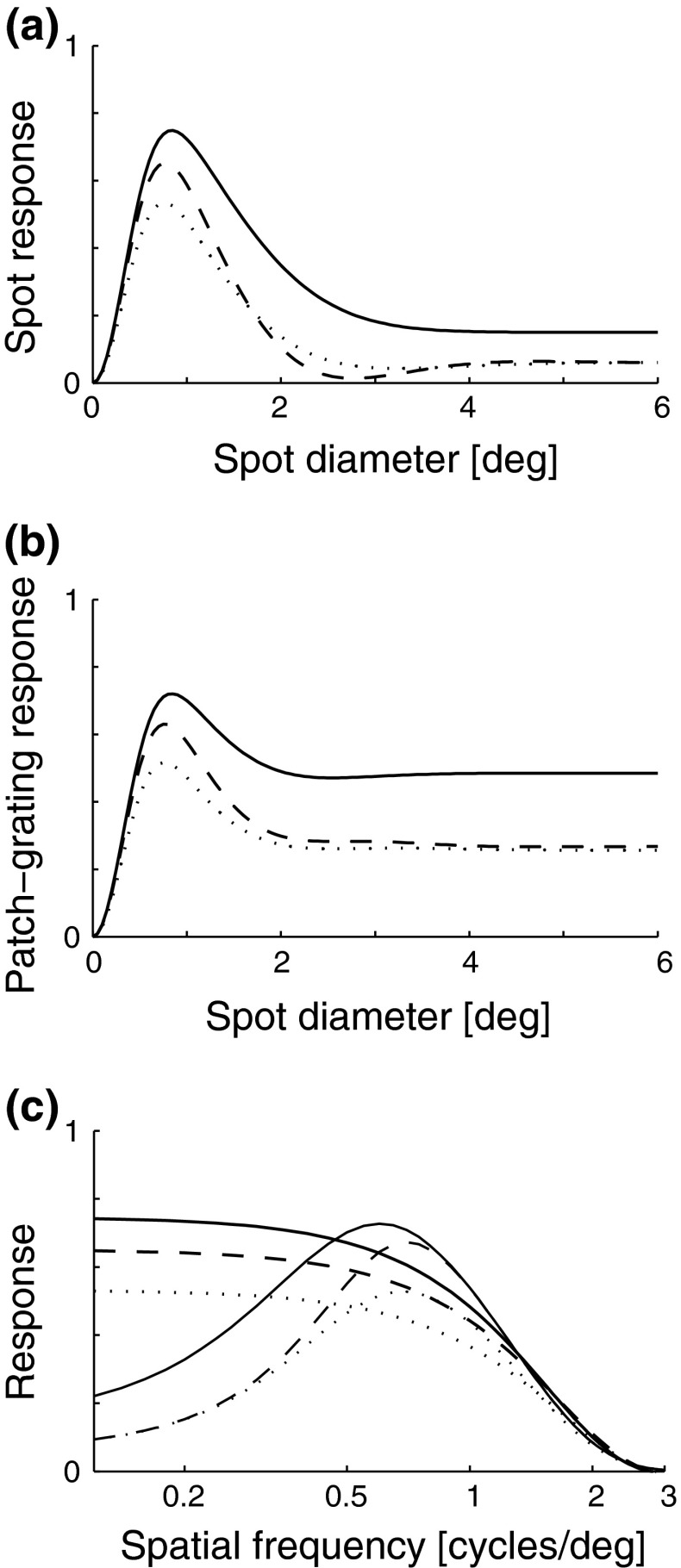
Fig. 6.
Example push-pull inhibitory eDOG model responses for flashing (F
pg(d
pg,0)) and patch-grating (F
pg(d
pg,2πνpg)) spots, cf. Eqs. 38–39. a Flashing-spot response as a function of spot diameter. Solid line: C = 0, i.e., standard DOG. Dashed line: C = −1.5, c = 0.83 deg. Dotted line: Variation of push-pull inhibitory eDOG model with the Gaussian loop-kernel replaced with a function of the type in Eq. 24 with the constant 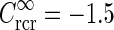 ,
, 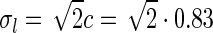 deg
deg 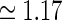 deg and σn = 0; DOG parameters are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg. b Patch-grating response for νpg = 0.3 cycles/deg as a function of spot diameter d
pg for the same models considered in upper left panel. c
Thin lines: Full-field grating response as a function of spatial frequency ν of the grating. Thick lines: Patch-grating response for d
pg = 0.8 deg as a function of spatial frequency νpg of the patch grating. Same models and parameters as in upper panels
deg and σn = 0; DOG parameters are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg. b Patch-grating response for νpg = 0.3 cycles/deg as a function of spot diameter d
pg for the same models considered in upper left panel. c
Thin lines: Full-field grating response as a function of spatial frequency ν of the grating. Thick lines: Patch-grating response for d
pg = 0.8 deg as a function of spatial frequency νpg of the patch grating. Same models and parameters as in upper panels
In Fig. 6 (upper right) we show for the same example models plots of the diameter-dependence of the patch-grating response (i.e., Fpg(dpg,2 π νpg)) with νpg set to 0.3 cycles/deg. Here, the normal case (eDOG model) still has a sizable center-surround suppression, while this suppression is significantly reduced in the decorticated case (DOG model). Hayot and Tranchina (2001, Fig. 7) observed the same effect in network simulations of a similar system (although it was less pronounced in their model than in ours).
We thus find a qualitative similarity between the experimental observations by Andolina et al. (2002) and Sillito and Jones (2002) and the results for these example models with the eDOG model representing the normal case and the DOG model representing the decorticated case.
The qualitative effects of cortical feedback on the center-surround suppression can be elucidated by first considering the plots in Fig. 5 (left). Here the eDOG and DOG impulse-response functions in Fourier space 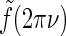 , giving the response to full-field drifting gratings, are shown for the same model parameters used in Fig. 6. The response to full-field “flashing-spot” illumination corresponds to the special case ν = 0, and for the DOG model in Fig. 5 (left) we have
, giving the response to full-field drifting gratings, are shown for the same model parameters used in Fig. 6. The response to full-field “flashing-spot” illumination corresponds to the special case ν = 0, and for the DOG model in Fig. 5 (left) we have 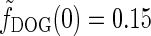 , and for the push-pull inhibitory eDOG models we have
, and for the push-pull inhibitory eDOG models we have 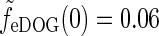 . Since the peak values of the spot response are seen in Fig. 6 (upper left) to be 0.5 or larger, these low full-field responses imply a sizable center-surround suppression for flashing spots for both the DOG and eDOG models, cf. Fig. 6 (upper left).
. Since the peak values of the spot response are seen in Fig. 6 (upper left) to be 0.5 or larger, these low full-field responses imply a sizable center-surround suppression for flashing spots for both the DOG and eDOG models, cf. Fig. 6 (upper left).
In Figure 6 (upper right) we see that the peak response values for the patch-grating case are still quite similar for the DOG and eDOG models. However, the large-patch responses 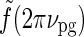 are now quite different for the two models: for ν = νpg = 0.3 cycles/deg we find
are now quite different for the two models: for ν = νpg = 0.3 cycles/deg we find 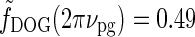 and
and 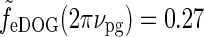 . As seen in Fig. 6 (upper right), the center-surround suppression is reduced for both the DOG and eDOG models compared to the flashing-spot case in Fig. 6 (upper left). However, the reduction is seen to be much larger for the DOG model (decorticated case) than for the “Gaussian” push-pull inhibitory eDOG model (normal case), in qualitative agreement with the findings reported in Sillito and Jones (2002). Note that for larger spatial frequencies νpg the full-field grating response
. As seen in Fig. 6 (upper right), the center-surround suppression is reduced for both the DOG and eDOG models compared to the flashing-spot case in Fig. 6 (upper left). However, the reduction is seen to be much larger for the DOG model (decorticated case) than for the “Gaussian” push-pull inhibitory eDOG model (normal case), in qualitative agreement with the findings reported in Sillito and Jones (2002). Note that for larger spatial frequencies νpg the full-field grating response 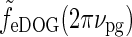 will be larger (cf. Fig. 5 (left)), and the patch-grating center-surround suppression will consequently become small also for the eDOG model (normal case).
will be larger (cf. Fig. 5 (left)), and the patch-grating center-surround suppression will consequently become small also for the eDOG model (normal case).
In Fig. 6 (bottom) we show plots of the spatial-frequency dependence of both the full-field grating response and the patch-grating response for a patch covering the receptive-field center. The same model parameters as in Fig. 6 are used. A first observation is that for low spatial frequencies the full-field grating responses are significantly reduced compared to the corresponding patch-grating responses. For these low frequencies we further see that the percentage reduction is smaller for the decorticated case (DOG model, solid line) compared to the normal case (eDOG model, dashed line). This is in qualitative agreement with the observation for X-cells in Cudeiro and Sillito (1996). Since X-cells exhibit more linear response properties than Y-cells, it is to be expected that our linear models are more suited to account for the response characteristics of these cells.
Hayot and Tranchina (2001) observed a similar effect in network simulations on a similar system. In contrast to our results in Fig. 6 (bottom) and experimental observations of Cudeiro and Sillito (1996), their model predicts no effects of cortical feedback for the lowest spatial frequencies. This difference may be due to the mixed excitatory and inhibitory in-phase cortical feedback assumed in Hayot and Tranchina’s network model, in contrast to the inhibitory in-phase feedback incorporated in the push-pull inhibitory eDOG model.
Overall we conclude that the eDOG model, with the present choice of parameters, accounts qualitatively for the experimental findings by Cudeiro and Sillito (1996) and Sillito and Jones (2002).
Discussion
Scope of eDOG model
The present extended DOG (eDOG) receptive-field model for LGN relay cells predict linear responses, even though the cortical cells providing the thalamocortical feedback themselves have non-linear firing characteristics. This somewhat non-intuitive linearity stems from the assumption in the model of a phase-reversed push-pull arrangement of cortical feedback, supported by recent experimental findings (Wang et al. 2006). The mathematical structure of the spatiotemporal eDOG model is similar to but somewhat more complicated than the purely spatial DOG model. In Fourier space (ω, k-space) the response function 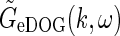 is given by a simple formula, while the real-space response function GeDOG(r, t), as well as responses to particular visual stimuli, in general must be found by numerical evaluation of integrals.
is given by a simple formula, while the real-space response function GeDOG(r, t), as well as responses to particular visual stimuli, in general must be found by numerical evaluation of integrals.
The LGN circuit as illustrated in Fig. 1 exhibits various non-linear effects beyond the non-linearity of the firing response of the cortical cells providing the corticothalamic feedback. Receptive-field models such as eDOG thus cannot be expected to account for all behavior of the circuit. Given that X relay cells in cat under certain conditions have been found to respond approximatively linearly (So and Shapley (1981), Cheng et al. (1995)), our formalism is expected to be particularly suitable for analysis of this pathway.
To model non-linear network effects one is generally forced to do computer simulations of networks of interconnected neurons. The equation set shown in Eq. (12) could be a starting point for such an endeavor. Simulations of sizable networks require significant computer power, however, and extended simulation times often prohibit comprehensive testing of the parameter-dependence of the model results. The use of the linear eDOG model (or variations thereof) to study properties of the thalamocortical circuit is both computationally and conceptually easier. The eDOG model can thus be used as a “linear starting point” for mathematical exploration where the results may function as guidelines for more detailed exploration of non-linear effects with extensive computer simulations.
Linear models cannot account for orientation-discontinuity effect
In experiments the response to a bipartite drifting grating stimulus was found to be independent of the absolute orientation of the grating of the inner and outer stimulus (Sillito et al. 1993; Cudeiro and Sillito 1996). This observation is incorporated in the eDOG model since the impulse-response functions are circularly symmetric, e.g., 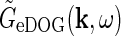 depends only on the magnitude (
depends only on the magnitude (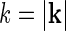 ) and not the orientation of k.
) and not the orientation of k.
The response to a bipartite drifting was, however, also found to depend on the relative orientation of the gratings in the inner and outer stimulus (Sillito et al. 1993; Cudeiro and Sillito 1996). This effect cannot be accounted for by a linear and circularly symmetric model such as the eDOG model: Consider a bipartite stimulus with an inner spot of radius Ri and grating wave vector ki surrounded by an annulus with outer radius Ro and outer grating wave vector ko. We further have 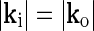 since only the direction of the grating varies between the inner spot and outer annulus. This stimulus can be considered to be the linear sum of two circular grating-spots specified by Ri, ki and Ro, ko, respectively, minus a circular grating-spot specified by Ri, ko. In a linear model the response to the bipartite stimulus will thus be given by the sum of the responses to two circular grating spots specified by Ri, ki and Ro, ko minus the response to a grating spot specified by Ri, ko. Since the response to a grating spot in a circularly symmetric model only depends on the magnitude of k, the responses to the two spots specified by Ri, ki and Ri, ko will cancel since
since only the direction of the grating varies between the inner spot and outer annulus. This stimulus can be considered to be the linear sum of two circular grating-spots specified by Ri, ki and Ro, ko, respectively, minus a circular grating-spot specified by Ri, ko. In a linear model the response to the bipartite stimulus will thus be given by the sum of the responses to two circular grating spots specified by Ri, ki and Ro, ko minus the response to a grating spot specified by Ri, ko. Since the response to a grating spot in a circularly symmetric model only depends on the magnitude of k, the responses to the two spots specified by Ri, ki and Ri, ko will cancel since 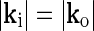 . The total response will thus be given by the response to the grating-spot specified by Ro, ko alone (which will only depend on the magnitude
. The total response will thus be given by the response to the grating-spot specified by Ro, ko alone (which will only depend on the magnitude  ). Consequently, in a linear circularly symmetric model the response will be independent of the relative orientation of the inner and outer gratings. This effect was observed by Hayot and Tranchina (2001) in their neural network simulations of cortical feedback effects on LGN relay cells when the input-output relationships of cortical neurons and LGN neurons were linearized.
). Consequently, in a linear circularly symmetric model the response will be independent of the relative orientation of the inner and outer gratings. This effect was observed by Hayot and Tranchina (2001) in their neural network simulations of cortical feedback effects on LGN relay cells when the input-output relationships of cortical neurons and LGN neurons were linearized.
Note that in the experiments with bipartite drifting gratings, the orientation-alignment effect was found to be only about a quarter (24%) of the observed enhanced inhibition due to cortical feedback (Sillito et al. 1993). The remaining dominant part (76%) was found to be independent of the relative orientation so that the applicability of a linear model (such as eDOG) is not excluded a priori.
Stimulus dependence of cortical feedback effects
Cortical feedback effects also for non-oriented stimuli
It has been argued that since cortical cells predominantly respond to oriented stimuli, only such stimuli will evoke significant cortical feedback effects. As seen in Fig. 6 (upper left) significant cortical feedback effects can also be evoked by circular spot stimuli in our linear eDOG model. Compared to oriented stimuli, circular spot stimuli may not evoke a strong response in any particular cortical population. In our linear model Eq. 12, however, circular spots evoke a small but non-negligible response in all cortical populations cn so that the overall summed cortical feedback effect becomes sizable. In contrast, an oriented stimulus may evoke a strong response in a few cortical populations but little response in the others. The cortical feedback effects from the few activated populations might be substantial, but the overall summed feedback is not necessarily larger than for a non-oriented stimulus.
Clear demonstrations of cortical feedback effects on visually driven relay-cell responses have come from experiments with oriented stimuli such as bipartite drifting gratings and patches of drifting gratings (Sillito et al. 1993; Cudeiro and Sillito 1996; Sillito and Jones 2002). In our model example in Fig. 6 (upper right) we observed a significantly reduced response suppression for large patch-grating diameters when the push-pull inhibitory cortical feedback was removed, in qualitative agreement with experimental observations (Sillito and Jones 2002). Significant inhibitory cortical feedback effects are also present in our eDOG model with circular-spot stimuli (Fig. 6 (upper left)) or full-field grating stimuli (Fig. 5 (left)). However, in these cases the cortical feedback reduces the responses with modest change in the qualitative shape of the response curves, so the effects will be difficult to observe in experiments where the normal and decorticated response curves are measured for different cells.
Model assumptions and variations
Other choices for feedforward model
In the present eDOG model the feedforward aspects of the response of LGN relay cells are represented using the standard difference-of-Gaussians (DOG) model. This mathematically simple choice is motivated by our intention to highlight the effects of corticothalamic feedback.
In Einevoll and Heggelund (2000) and Einevoll and Plesser (2002) we have explored various mechanistic models for the spatial organization of the feedforward LGN circuitry, both with discrete (finite number of retinal inputs to LGN cells) and continuous connection patterns. These models could straightforwardly be implemented in a more comprehensive mechanistic receptive-field model incorporating both feedforward and feedback connections in the LGN circuit. For example, the numerator 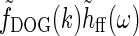 in Eq. 30 could be replaced by two terms, one representing the direct feedforward excitation on relay cells from retinal ganglion cells, and one representing the indirect feedforward inhibition via intrageniculate interneurons (Norheim et al. 2011). Such a comprehensive receptive-field model might be appealing since each term in the formula would be related to a particular synaptic connection between various neuron types. Even though one could explore how the relay cell response depends on the various connections, the large number of model parameters would make it difficult to compare with the limited experimental data available at present.
in Eq. 30 could be replaced by two terms, one representing the direct feedforward excitation on relay cells from retinal ganglion cells, and one representing the indirect feedforward inhibition via intrageniculate interneurons (Norheim et al. 2011). Such a comprehensive receptive-field model might be appealing since each term in the formula would be related to a particular synaptic connection between various neuron types. Even though one could explore how the relay cell response depends on the various connections, the large number of model parameters would make it difficult to compare with the limited experimental data available at present.
Other choices for cortical feedback model
The modeling of corticothalamic effects on LGN cells in terms of simple linear loops, each involving a single population of orientation-selective cells, is clearly a severe simplification. The dominant input from LGN to primary visual cortex appears to arrive in layer 4. However, geniculate inputs also terminate in layer 6, where the neurons providing the corticothalamic feedback are located; cf. Ch. 2 in Sherman and Guillery (2001) and references therein. Simple cells have the most linear response properties of the cells in V1 and are the best candidates for providing corticothalamic feedback resembling the half-wave rectified, linear characteristics assumed in our model. In a study in cat, Grieve and Sillito (1995) found that 71 % of the layer VI cells projecting back to LGN are simple cells.
We derived an analytical expression for a circularly symmetric feedback loop kernel for a specific (and somewhat arbitrary) model for the thalamocortical and corticothalamic connection pattern (cf. Eq. 24), but the important qualitative conclusion regarding the circular loop-kernel symmetry does not depend on this particular model choice. In the absence of contradictory experimental data, we therefore chose to model the spatial part of the feedback loop-kernel as a simple Gaussian function in the present eDOG model. This function parameterizes the connection patterns in two presumably important parameters: coupling strength (C) and spatial spread (c). Other functions such as, e.g., the two-parameter exponential function 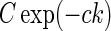 or the three-parameter function
or the three-parameter function 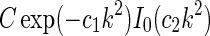 derived in Eq. 24, could equivalently have been chosen; examples of flashing-spot and patch-grating responses for a modified eDOG-model using the latter function are shown in Fig. 6. The advantage of choosing Gaussians is mainly that for moderate cortical feedback strength, the relay-cell receptive field in space-time coordinates can be written as a sum of DOGs (cf. Eq. 40), as shown in the Appendix 1.
derived in Eq. 24, could equivalently have been chosen; examples of flashing-spot and patch-grating responses for a modified eDOG-model using the latter function are shown in Fig. 6. The advantage of choosing Gaussians is mainly that for moderate cortical feedback strength, the relay-cell receptive field in space-time coordinates can be written as a sum of DOGs (cf. Eq. 40), as shown in the Appendix 1.
Significance
The eDOG model has been constructed to elucidate salient features of visually evoked cortical feedback effects on LGN cells. The model has a simple mathematical structure: In Fourier space, the impulse-response function (essentially the receptive field) is given by a simple formula (Eq. 30), while the real-space expression in the general case involves a triple integral (Eq. 31), which must be numerically evaluated. However, for moderate cortical-feedback strengths, a closed-form expression for the spatial receptive field, involving an infinite sum over DOGs, can be found in the “fast-loop” limit (Eq. 40). The eDOG model response to arbitrary visual stimuli can also be found by evaluating a triple integral (Eq. 3).
The main virtue of the eDOG model compared to alternative network models focusing on cortical-feedback effects on LGN cells (Köhn and Wörgötter 1996; Wörgötter et al. 1998; Kirkland and Gerstein 1998; Kirkland et al. 2000; Hillenbrand and van Hemmen 2000; Hayot and Tranchina 2001; Yousif and Denham 2007) is the conceptual and methodological ease in using the model. In the example application to patch-grating stimuli in section "Example application: patch-grating stimuli", the cortical feedback was described by two parameters, the feedback weight C and the spatial spread c. In comprehensive network simulations of the same problem, far more (and often uncertain) model parameters have to be specified, and the parameter-dependence of the results is much harder to assess, cf. Hayot and Tranchina (2001).
Since the eDOG model is much simpler to use and analyze than extended network models, it can be particularly useful as a “linear starting point” for the exploration of various possible scenarios for the organization of the cortical feedback system. One should in particular explore the interplay between the spatial and temporal coupling patterns, parameterized respectively by the push-pull feedback weight C and its spatial spread c and by the temporal kernel  .
.
The eDOG model can also be useful for finding visual stimuli which highlight effects of cortical feedback. In section "Example application: patch-grating stimuli" we found, for example, that for our inhibitory eDOG model the qualitative shape of the response curve for circular spots (cf. Fig. 6, upper left) was little affected by cortical feedback even if it reduced the overall response magnitude. For patch-grating spots the shape and the amount of center-surround antagonism was, however, found to be quite different for the cases with and without cortical feedback (cf. Fig. 6, upper right) making experimental testing for the effect easier (Sillito and Jones 2002).
Acknowledgments
We are grateful to Eivind S. Norheim for carefully reading the manuscript. Partially supported by the eVita program of the Research Council of Norway under grant 178892/V30 and the Honda Research Institute Europe GmbH.
Appendix 1: eDOG model for small cortical feedback strengths
For 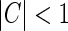 , the denominator term of the integral expression for feDOG(r) in Eq. 35 can be replaced by a series expansion, i.e.,
, the denominator term of the integral expression for feDOG(r) in Eq. 35 can be replaced by a series expansion, i.e.,  . With
. With 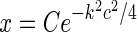 we find by insertion into Eq. 35:
we find by insertion into Eq. 35:
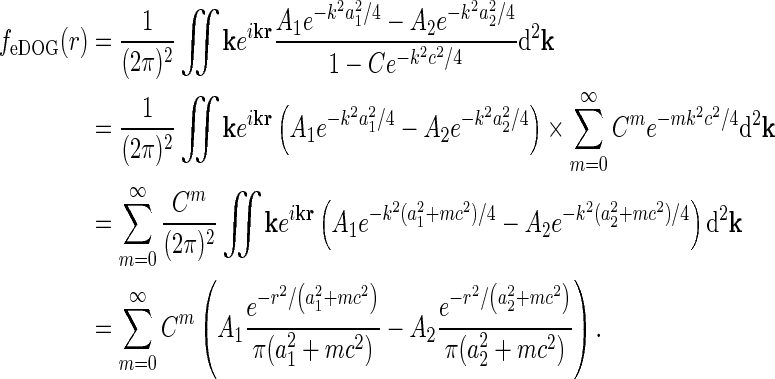 |
40 |
The final expression in Eq. 40 has a relatively simple form: it consists of an infinite sum of DOGs. For small values of C, the higher terms vanish rapidly, so that only a limited number of terms need to be retained. The terms in the sum have increasing spatial extent ( ) and alternating sign when C is negative.
) and alternating sign when C is negative.
The terms in the series have an intuitive interpretation as illustrated by the first three terms:
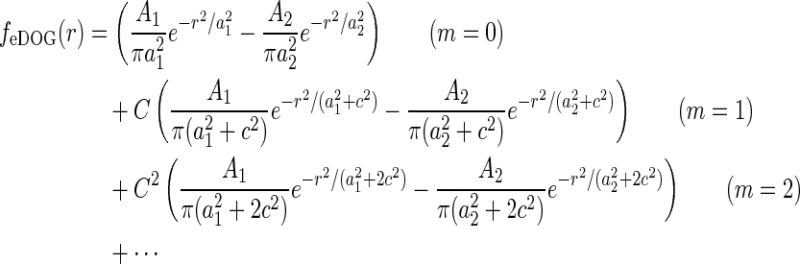 |
The first term corresponds to the “direct” feedforward DOG. The second term corresponds to the correction to this “direct” term due to one round of the feedforward DOG in the cortical feedback loop. The spatial extension of the Gaussians is larger since they have been ”spread out” by the spatial spread of the corticogeniculate loop. Correspondingly, the third term corresponds to a “correction of the correction” after the direct term has gone through the thalamocortical loop twice. This term is spatially even more spread out after two rounds through the loop.
For 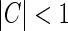 , the series in Eq. 40 can be shown to be uniformly convergent assuring the validity of the mathematical derivation. If the feedback is positive with C = 1, the integrand in Eq. 35 has a singular point corresponding to a resonance in the thalamocortical loop (Einevoll and Plesser 2002).
, the series in Eq. 40 can be shown to be uniformly convergent assuring the validity of the mathematical derivation. If the feedback is positive with C = 1, the integrand in Eq. 35 has a singular point corresponding to a resonance in the thalamocortical loop (Einevoll and Plesser 2002).
Appendix 2: Numerical methods
Figures 2, 3 were created using Mathematica 7 (Wolfram Research), while Figs. 4, 6 were created using Matlab 7.10.0 (MathWorks) on a Lenovo T410i computer running Windows XP.
Contributor Information
Gaute T. Einevoll, Phone: +47-64965433, FAX: +47-64965401, Email: gaute.einevoll@umb.no
Hans E. Plesser, Email: hans.ekkehard.plesser@umb.no
References
- Abramowitz M, Stegun I. Handbook of mathematical functions. New York: Dover; 1965. [Google Scholar]
- Ahlsén G, Grant K, Lindström S. Monosynaptic excitation of principal cells in the lateral geniculate nucleus by corticofugal fibers. Brain Res. 1982;234:454–458. doi: 10.1016/0006-8993(82)90886-1. [DOI] [PubMed] [Google Scholar]
- Andolina I, Wang W, Jones H, Salt T, Sillito A (2002) Effects of feedback on cat lgn cell spatial summation parameters dissected with the difference of gaussian model (DOGM). In: Society for neuroscience abstract, vol 32. Society for Neuroscience, Washington, DC, p 352.17
- Andolina I, Jones H, Wang W, Sillito A. Corticothalamic feedback enhances stimulus response precision in the visual system. Proc Natl Acad Sci. 2007;104:1685–1690. doi: 10.1073/pnas.0609318104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bracewell R. The Fourier transform and its applications. New York: McGraw-Hill; 1986. [Google Scholar]
- Briggs F, Usrey W. A fast, reciprocal pathway between the lateral geniculate nucleus and visual cortex in the macaque monkey. J Neurosci. 2007;27:5431–5436. doi: 10.1523/JNEUROSCI.1035-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey W. Emerging views of corticothalamic functionemerging views of corticothalamic function. Curr Opin Neurobiol. 2008;18:403–407. doi: 10.1016/j.conb.2008.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey W. Parallel processing in the corticogeniculate pathway of the macaque monkey. Neuron. 2009;62:135–146. doi: 10.1016/j.neuron.2009.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey W. Corticogeniculate feedback and visual processing in the primate. J Physiol. 2011;589:33–40. doi: 10.1113/jphysiol.2010.193599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng H, Chino Y, Smith IE, Hamamoto J, Yoshida K. Transfer characteristics of lateral geniculate nucleus X neurons in the cat: effects of spatial frequency and contrast. J Neurophysiol. 1995;74:2548–2557. doi: 10.1152/jn.1995.74.6.2548. [DOI] [PubMed] [Google Scholar]
- Cudeiro J, Sillito A. Spatial frequency tuning of orientation-discontinuity-sensitive corticofugal feedback to the cat lateral geniculate nucleus. J Physiol. 1996;490:481–492. doi: 10.1113/jphysiol.1996.sp021159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Abbott L. Theoretical neuroscience. Cambridge: MIT Press; 2001. [Google Scholar]
- Destexhe A. Modelling corticothalamic feedback and the gating of the thalamus by the cerebral cortex. J Physiol (Paris) 2000;94:391–410. doi: 10.1016/S0928-4257(00)01093-7. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Steriade M. Mechanisms underlying the synchronizing action of corticothalamic feedback through inhibition of thalamic relay cells. J Neurophysiol. 1998;79:999–1016. doi: 10.1152/jn.1998.79.2.999. [DOI] [PubMed] [Google Scholar]
- Einevoll G, Heggelund P. Mathematical models for the spatial receptive-field organization of nonlagged X cells in dorsal lateral geniculate nucleus of cat. Vis Neurosci. 2000;17:871–886. doi: 10.1017/S0952523800176060. [DOI] [PubMed] [Google Scholar]
- Einevoll G, Plesser H. Linear mechanistic models for the dorsal lateral geniculate nucleus of cat probed using drifting-grating stimuli. Netw Comp Neur Syst. 2002;13:503–530. doi: 10.1088/0954-898X/13/4/305. [DOI] [PubMed] [Google Scholar]
- Einevoll G, Plesser H (2003) Extended DOG receptive-field model for LGN relay cells incorporating cortical-feedback effects. In: Society for Neuroscience Abstracts, vol 33. Society for Neuroscience, Washington, DC, p 68.11
- Einevoll G, Plesser H. Response of the difference-of-gaussians model to circular drifting-grating patches. Vis Neurosci. 2005;22:437–446. doi: 10.1017/S0952523805224057. [DOI] [PubMed] [Google Scholar]
- Geisert E, Langsetmo A, Spear P. Influence of the cortico-geniculate pathway on response properties of cat lateral geniculate neurons. Brain Res. 1981;208:409–415. doi: 10.1016/0006-8993(81)90568-0. [DOI] [PubMed] [Google Scholar]
- Godwin D, Vaughan J, Sherman S. Metabotropic glutamate receptors switch visual response mode of lateral geniculate cells from burst to tonic. J Neurophysiol. 1996;76:1800–1816. doi: 10.1152/jn.1996.76.3.1800. [DOI] [PubMed] [Google Scholar]
- Grieve K, Sillito A. Differential properties of cells in the feline primary visual cortex providing the corticofugal feedback to the lateral geniculate nucleus and visual claustrum. J Neurosci. 1995;15:4868–4874. doi: 10.1523/JNEUROSCI.15-07-04868.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayot F, Tranchina D. Modeling corticofugal feedback and the sensitivity of lateral geniculate neurons to orientation discontinuity. Vis Neurosci. 2001;18:865–877. [PubMed] [Google Scholar]
- Heeger D. Nonlinear model of neural responses in cat visual cortex. In: Landy M, Movshon J, editors. Computational models of visual processing. Cambridge: MIT Press; 1991. pp. 119–134. [Google Scholar]
- Hillenbrand U, van Hemmen L. Spatiotemporal adaptation through corticothalamic loops: a hypothesis. Vis Neurosci. 2000;17:107–118. doi: 10.1017/S0952523800171111. [DOI] [PubMed] [Google Scholar]
- Hubel D, Wiesel T. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing W, Liu W-Z, Gong X-W, Gong H-Q, Liang P-J. Visual pattern recognition based on spatio-temporal patterns of retinal ganglion cells’ activities. Cogn Neurodyn. 2010;3:179–188. doi: 10.1007/s11571-010-9119-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones H, Andolina I, Oakely N, Murphy P, Sillito A. Spatial summation in lateral geniculate nucleus and visual cortex. Exp Brain Res. 2000;135:279–284. doi: 10.1007/s002210000574. [DOI] [PubMed] [Google Scholar]
- Kirkland K, Gerstein G. A model of cortically induced synchronization in the lateral geniculate nucleus of the cat: a role for low-threshold calcium channels. Vis Res. 1998;38:2007–2022. doi: 10.1016/S0042-6989(97)00385-4. [DOI] [PubMed] [Google Scholar]
- Kirkland K, Sillito A, Jones H, West D, Gerstein G. Oscillations and long-lasting correlations in a model of the lateral geniculate nucleus and visual cortex. J Neurophysiol. 2000;84:1863–1868. doi: 10.1152/jn.2000.84.4.1863. [DOI] [PubMed] [Google Scholar]
- Köhn J, Wörgötter F. Corticofugal feedback can reduce the visual latency of responses to visual stimuli. Biol Cybern. 1996;75:199–209. doi: 10.1007/s004220050287. [DOI] [PubMed] [Google Scholar]
- Liang L, Wang R, Zhang Z. The modeling and simulation of visuospatial working memory. Cogn Neurodyn. 2010;4:359–366. doi: 10.1007/s11571-010-9129-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrocco R, McClurkin J, Young R. Modulation of lateral geniculate nucleus cell responsiveness by visual activation of the corticogeniculate pathway. J Neurosci. 1982;2:256–263. doi: 10.1523/JNEUROSCI.02-02-00256.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrocco R, McClurkin J, Alkire M. The influence of the visual cortex on the spatiotemporal response properties of lateral geniculate cells. Brain Res. 1996;737:110–118. doi: 10.1016/0006-8993(96)00660-9. [DOI] [PubMed] [Google Scholar]
- Mayer J, Schuster H, Claussen J, Mölle M. Corticothalamic projections control synchronization in locally coupled bistable thalamic oscillators. Phys Rev Lett. 2007;99:68–102. doi: 10.1103/PhysRevLett.99.068102. [DOI] [PubMed] [Google Scholar]
- McClurkin J, Marrocco R. Cortical input to the monkey lateral geniculate nucleus alters visual spatial tuning in monkey lateral geniculate nucleus cells. J Physiol (Lond) 1984;348:135–152. doi: 10.1113/jphysiol.1984.sp015103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClurkin J, Optican L, Richmond B. Cortical feedback increases visual information transmitted by monkey parvocellular lateral geniculate nucleus neurons. Vis Neurosci. 1994;11:601–617. doi: 10.1017/S0952523800002492. [DOI] [PubMed] [Google Scholar]
- McCormick D, von Krosigk M. Corticothalamic activation modulates thalamic firing through glutamate “metabotropic” receptors. Proc Nat Acad Sci. 1992;89:2774–2778. doi: 10.1073/pnas.89.7.2774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy P, Sillito A. Corticofugal feedback influences the generation of length tuning in the visual pathway. Nature. 1987;329:727–729. doi: 10.1038/329727a0. [DOI] [PubMed] [Google Scholar]
- Murphy P, Sillito A. Functional morphology of the feedback pathway from area 17 of the cat visual cortex to the lateral geniculate nucleus. J Neurosci. 1996;16:1180–1192. doi: 10.1523/JNEUROSCI.16-03-01180.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy P, Duckett S, Sillito A. Feedback connections to the lateral geniculate nucleus and cortical response properties. Science. 1999;286:1552–1554. doi: 10.1126/science.286.5444.1552. [DOI] [PubMed] [Google Scholar]
- Norheim E, Wyller J, Nordlie E, Einevoll G (2011) Feedback and feedforward contributions to temporal signal processing in the lateral geniculate nucleus. Cogn Neurodyn (submitted) [DOI] [PMC free article] [PubMed]
- Reid C, Alonso JM. Specificity of monosynaptic connections from thalamus to visual cortex. Nature. 1995;378:281–284. doi: 10.1038/378281a0. [DOI] [PubMed] [Google Scholar]
- Rodieck R. Quantitative analysis of cat retinal ganglion cell response to visual stimuli. Vis Res. 1965;5:583–601. doi: 10.1016/0042-6989(65)90033-7. [DOI] [PubMed] [Google Scholar]
- Saglam M, Hayashida Y, Murayama N. A retinal circuit model accounting for wide-field amacrine cells. Cogn Neurodyn. 2009;1:25–32. doi: 10.1007/s11571-008-9059-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman S, Guillery R. Exploring the thalamus. New York: Academic Press; 2001. [Google Scholar]
- Sillito A, Jones H. Corticothalamic interactions in the transfer of visual information. Phil Trans R Soc Lond B. 2002;357:1739–1752. doi: 10.1098/rstb.2002.1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillito A, Jones H (2004) Feedback systems in visual processing. In: The visual neurosciences, vol 1, MIT Press, Cambridge, pp 609–624
- Sillito A, Cudeiro J, Murphy P. Orientation sensitive elements in the corticofugal influence on centre-surround interactions in the dorsal lateral geniculate nucleus. Exp Brain Res. 1993;93:6–16. doi: 10.1007/BF00227775. [DOI] [PubMed] [Google Scholar]
- Sillito A, Jones H, Gerstein G, West D. Feature-linked synchronization of thalamic relay cell firing induced by feedback from the visual cortex. Nature. 1994;369:479–482. doi: 10.1038/369479a0. [DOI] [PubMed] [Google Scholar]
- So Y, Shapley R. Spatial tuning of cells in and around lateral geniculate nucleus of the cat: X and Y relay cells and perigeniculate interneurons. J Neurophys. 1981;45:107–120. doi: 10.1152/jn.1981.45.1.107. [DOI] [PubMed] [Google Scholar]
- Troyer T, Krukowski A, Priebe N, Miller K. Contrast-invariant orientation tuning in cat visual cortex: thalamocortical input tuning and correlation-based intracortical connectivity. J Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyer T, Krukowski A, Miller K. LGN input to simple cells and contrast-invariant orientation tuning: an analysis. J Neurophysiol. 2002;87:2741–2752. doi: 10.1152/jn.2002.87.6.2741. [DOI] [PubMed] [Google Scholar]
- Vidyasagar T, Urbas J. Orientation sensitivity of cat LGN neurones with and without inputs from visual cortical areas 17 and 18. Exp Brain Res. 1982;46:157–169. doi: 10.1007/BF00237172. [DOI] [PubMed] [Google Scholar]
- Wang R, Zhang Z. Energy coding in biological neural networks. Cogn Neurodyn. 2007;3:203–212. doi: 10.1007/s11571-007-9015-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Jones H, Andolina I, Salt T, Sillito A. Functional alignment of feedback effects from visual cortex to thalamus. Nature Neurosci. 2006;9:1330–1336. doi: 10.1038/nn1768. [DOI] [PubMed] [Google Scholar]
- Weber A, Kalil R, Behan M. Synaptic connections between corticogeniculate axons and interneurons in the dorsal lateral geniculate nucleus of the cat. J Comp Neurol. 1989;289:156–164. doi: 10.1002/cne.902890113. [DOI] [PubMed] [Google Scholar]
- Wörgötter F, Nelle E, Li B, Funke K. The influence of corticofugal feedback on the temporal structure of visual response of cat thalamic relay cells. J Physiol. 1998;509:797–815. doi: 10.1111/j.1469-7793.1998.797bm.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousif N, Denham M. The role of cortical feedback in the generation of the temporal receptive field responses of lateral geniculate nucleus neurons: a computational study. Biol Cybern. 2007;97:269–277. doi: 10.1007/s00422-007-0171-3. [DOI] [PubMed] [Google Scholar]