Abstract
A great number of biological experiments show that gamma oscillation occurs in many brain areas after the presentation of stimulus. The neural systems in these brain areas are highly heterogeneous. Specifically, the neurons and synapses in these neural systems are diversified; the external inputs and parameters of these neurons and synapses are heterogeneous. How the gamma oscillation generated in such highly heterogeneous networks remains a challenging problem. Aiming at this problem, a highly heterogeneous complex network model that takes account of many aspects of real neural circuits was constructed. The network model consists of excitatory neurons and fast spiking interneurons, has three types of synapses (GABAA, AMPA, and NMDA), and has highly heterogeneous external drive currents. We found a new regime for robust gamma oscillation, i.e. the oscillation in inhibitory neurons is rather accurate but the oscillation in excitatory neurons is weak, in such highly heterogeneous neural networks. We also found that the mechanism of the oscillation is a mixture of interneuron gamma (ING) and pyramidal-interneuron gamma (PING). We explained the mixture ING and PING mechanism in a consistent-way by a compound post-synaptic current, which has a slowly rising-excitatory stage and a sharp decreasing-inhibitory stage.
Keywords: Gamma oscillation, Heterogeneity, Synapse, Balanced networks
Introduction
Brain waves consist of a wide range of frequency components. The high frequency components of the brain waves, gamma oscillations, are believed to be relevant to the cognitive functions of neural systems (Buzsaki et al. 2012; Hájos and Paulsen 2009; Li et al. 2011; Nikolic et al. 2013; Womelsdorf et al. 2006). They can be evoked by various kinds of stimuli (Engelhard et al. 2013; Lapray et al. 2009; Bosman et al. 2012; Perry et al. 2013; Schadow et al. 2007a, b) and have been reported in many experimental observations in many brain areas including visual cortex (Hadjipapas et al. 2007; Herrmann and Mecklinger 2000; Laczo et al. 2012; Muthukumaraswamy and Singh 2013; Schwarzkopf et al. 2012), auditory cortex (Schadow et al. 2007a, b), olfactory bulb (Du et al. 2012; Rojas-Libano and Kay 2008), and hippocampal area (Ahmed and Mehta 2012). In these brain areas, neural systems are extremely complex and heterogeneous. The underlying mechanism for the genesis of these highly robust oscillations remains a challenge for the neuroscience society.
Various mechanisms for the robust Gamma oscillations based on simplified neural network models have been proposed. These mechanisms reveal that inhibitory networks play the key role on the gamma oscillation (Bartos et al. 2007; Wang and Buzsáki 1996). Resonance of the gamma frequency component of the population firing rate in recurrent neural circuits is believed to be one possible mechanism for the gamma oscillation (Wang 2010; Brunel and Hakim 1999; Brunel and Wang 2003). As synapses can be treated as filters, the recurrent network can be regarded as a linear system if the responses of neurons approximate linear systems. According to the feedback theory of linear systems, the frequency component of the population firing rate, of which the phase shift happens to be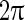 
, will be amplified (resonant). It was found that resonant frequency is located in the gamma band, as the phase shift of the gamma frequency due to the synaptic filtering and the neuronal responses is around 
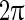. Therefore, the population firing rate is close to sine function with a gamma band frequency. As in many situations, gamma oscillation resides in the population firing rate showing sharp periodic peaks, another mechanism for gamma oscillation in nonlinear regime has been proposed (Bathellier et al. 2008). The mechanism in nonlinear regime believes that oscillation occurs because the firing of a volley of inhibitory neurons produces a surge of inhibitory synaptic currents, which stops the firing of other neurons. The firing of neurons resumes only after this inhibitory synaptic currents decay sufficiently. In addition, some studies believe that there are intrinsic mechanisms in inhibitory network that homogenize the firing rate of each neuron in the network, resulting in the robust synchronized firing of the heterogeneous neurons. Shunting inhibition is believed to confer advantages for the firing rate homogenization (Vida et al. 2006). Inhibitory synapses have three components contributing to the homogenization of the firing rate of the neurons (Wang et al. 2011; Wang and Wong 2013). These mechanisms help to understand the robust gamma oscillation in simplified network model. However, real neural circuits associated with gamma oscillations are extremely complex and highly heterogeneous. They usually consist of multiple types of excitatory and inhibitory neurons with different parameter values and multiple types of synapses with different time constants, forming roughly balanced complex excitatory/inhibitory networks (E/I networks).
The mechanisms of interneuron gamma (ING) and pyramidal-interneuron gamma (PING) are proposed to explain the gamma oscillation in E/I networks (Tiesinga and Sejnowski 2009). In the ING mechanism, the external drive currents are large enough to excite inhibitory neurons. ING mechanism is similar to the mechanism in nonlinear regime discussed in the previous paragraph. Specifically, synchronized firing of a fraction of inhibitory neurons gives a sufficiently strong compound inhibitory current to prevent the firing of other neurons. Only when the inhibitory currents decay sufficiently, does the firing of inhibitory neurons resume. Therefore, the oscillation frequency of ING is determined by the decay time constants of the inhibitory synapses, which controls the decay process of the inhibitory synaptic currents. The inhibitory neurons in turn synchronize the excitatory neurons. In the PING mechanism, synchronized firing of excitatory neurons leads that of inhibitory neurons (BÄorgers and Kopell 2003). It is the synchronous excitatory volley that elicits the synchronous volley of the inhibitory neurons. The resultant inhibition from inhibitory neurons in turn stops the firing of excitatory neurons. Thus, the period of the oscillation is determined by the time for the recovery of the excitatory cells from the inhibition.
ING (or PING) are usually investigated in networks with low or mild level of heterogeneity. However, many real circuits are highly heterogeneous. Furthermore, many gamma oscillations occur after the presentation of the external stimuli. This paper proposes a new regime with mixed ING and PING mechanism for robust gamma oscillation based on highly heterogeneous E/I networks, where the synchronized firing of inhibitory neurons is accurate but that of excitatory neurons is weak. Weak synchronization of excitatory neurons and accurate synchronization of inhibitory neurons produce a compound post-synaptic current (PSC), which is excitatory and rises in the first stage, then decreases sharply and become inhibitory in the second stage. This kind of compound PSC in turn contributes to forge highly robust synchronization of inhibitory neurons, and thus a self-consistent way to generate the robust synchronization is formed. This paper is organized as follows. Models for the neurons and synapses are described in Sect. 2. The highly robust gamma oscillation is reproduced in the E/I network model in Sect. 3. An explanation of the mixed ING and PING mechanism for the robustness of the oscillation is given in Sect. 4. Finally, a summary of the results is presented in Sect. 5.
Models of the neurons and synapses in excitatory–inhibitory networks
Real neural circuits, for example neural circuits in V1 cortex, consist of many types of neurons (Neymotin et al. 2011). These neurons organized into two groups, excitatory neuron group and inhibitory neuron group. Excitatory neurons may have long axons to transmit stimulus signals to other neural circuits, whereas inhibitory neurons are usually fast spiking interneurons that connect locally with other neurons within the circuit. GABAA receptors are common in inhibitory synapses. In excitatory synapses, there are usually two types of receptors, with one having long decay time constant and the other having short decay time constant. Taking account of these physiological observations in neural circuits, we consider a neural network described as follows:
 |
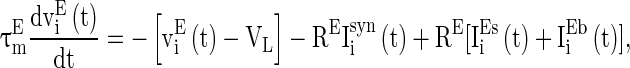1 |
 |
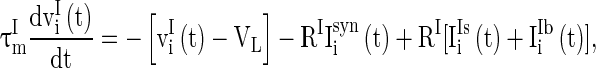2 |
where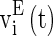 
and 
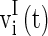are the membrane potentials for the excitatory neurons and inhibitory neurons, respectively. When reaching the threshold potential Vth, the neuron emits a spike and the membrane potential returns to the rest potential Vrest. 
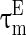and 
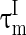are the time constants of the membrane for the excitatory neurons and inhibitory neurons, respectively. RE and RI are the membrane resistances, VL is the balance potential associated with the leak current, 
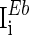and 
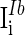are the background input currents to the excitatory neurons and the inhibitory neurons, respectively; 
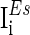and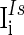 
are the stimuli-associated input currents to the excitatory and the inhibitory neurons, respectively; 
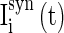is the synaptic current to neuron i:
 |
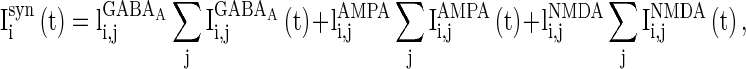3 |
where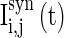 
is the synaptic current from neurons j to i; 
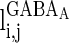describes whether there is a GABAA-synapse connection from neurons j to i: 
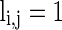if there is a synaptic connection; otherwise 
. 
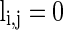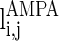and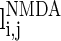 
have a similar definition as 
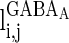, which correspond to the AMPA-synapse and NMDA-synapse, respectively; 
, 
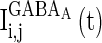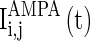, and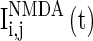 
are the synaptic currents coming from GABAA-synapse, AMPA-synapse, and NMPA-synapse, respectively. The three types of synaptic currents to the excitatory neurons (
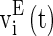in Eqs. (4)–(6) should be replaced by 
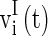for inhibitory neurons) are described as (Dayan and Abbott 2001):
 |
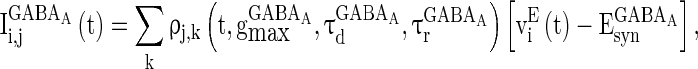4 |
 |
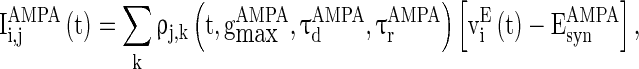5 |
 |
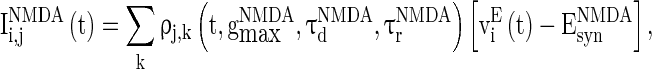6 |
 |
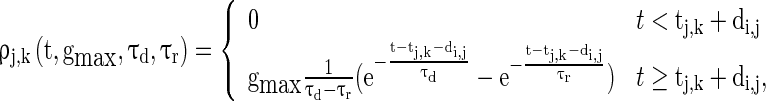7 |
where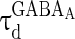 
and 
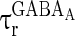are the decay time constant and rise time constant of the GABAA-synapse current, respectively; 
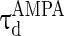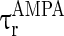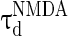and 
(
and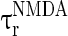 
) are the corresponding time constants for AMPA-synapse (NMDA-synapse); 
, 
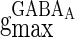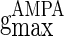, and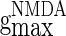 
correspond to the maximum conductance of GABAA-synapse, AMPA-synapse, and NMDA-synapse, respectively, when the ionic channels of the synapses open fully; 
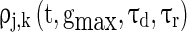takes a form like the α-function; 
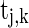is the timing of the k-th spike from neuron j to neuron i; 
, 
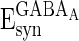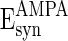, and 
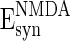are the reversal potentials for GABAA, AMPA, and NMDA synapses, respectively; 
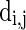is the synaptic delay from neuron j to neuron i.
Highly robust gamma oscillation with co-exist of accurate and weak synchronization
The neural networks described in the previous section have two types of neurons and three types of synapses. Furthermore, the external drives (background input currents and the stimuli-associated input currents) are highly heterogeneous, which we will describe in this section. We will show that gamma oscillation can emerge in such highly heterogeneous neural networks.
According to many physiological observations, the background input current is usually heterogeneous and fluctuating (Bathellier et al. 2008), meaning that the average input current over time is different neuron by neuron and that the input current changes with time. Therefore, we describe the background input current of excitatory neurons in Eq. (1) as:
 |
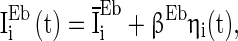8 |
where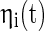 
is the white noise, 
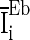is drawn from a normal distribution with mean 
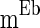and standard deviation 
. 
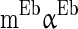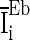is a constant but is different neuron by neuron, i.e.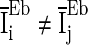 
. 
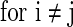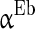is the parameter that describes the level of heterogeneity of the background input current to each neuron. 
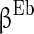is the parameter that characterizes the level of fluctuation of the background current. Similarly, 
, 
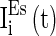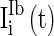, and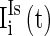 
are heterogeneous and fluctuating as well. The modeling of these three currents are the same as 
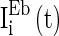. Therefore, we use 
, 
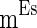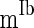, and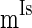 
to denote the mean of the three currents, respectively, and use 
(
), 
(
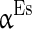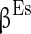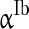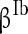), and 
(
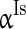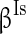) to characterize the level of heterogeneity (fluctuation) of the three currents, respectively.
The inhibitory interneurons have usually higher firing frequency than excitatory neurons. This may be ascribed to the small time constant or the low threshold of the interneurons. Therefore, we let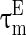 
larger than 
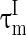in this paper. The strength of the inhibitory synapses is assumed to be stronger than that of the excitatory synapses according to physiological evidences. We set 
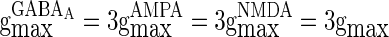in this paper. To make the excitatory and inhibitory synapses approximately balanced, the number of excitatory neurons (NE) outnumber that of inhibitory neurons (NI). Each inhibitory neuron synapses on another neuron (excitatory neuron or inhibitory neuron) by GABAA-synapse with a probability 
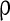. Each excitatory neuron synapses on another neuron by AMPA-synapse with a probability 
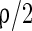and by NMPA-synapse with a probability 
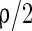. Thereby the total probability that an excitatory neuron has a synapse on another neuron is 
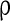. Conventionally, GABAA-synapse and AMPA-synapse have small time constants but NMDA-synapse has large time constant. If not stated otherwise, the parameter values in the network are set as follows (Dayan and Abbott 2001; Wang and Buzsáki 1996). 
, 
, 
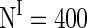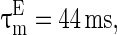
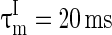, VL = −65 mV, Vth = −45 mV, Vrest = −65 mV,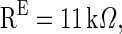 
, 
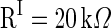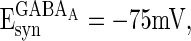
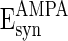= 0 mV, 
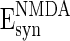= 0 mV, 
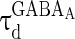= 8 ms, 
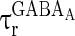= 0.1 ms, 
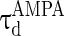= 15 ms, 
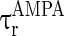= 0.1 ms, 
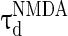= 100 ms, 
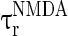= 0.1 ms, gmax = 0.005, di, j is drawn from a normal distribution with mean 4.5 ms and standard deviation 1 ms, mEb = 1.7 μA, mIb = 0.9 μA, 
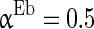, βEb = 0.1, αIb = 0.5, βIb = 0.1, mEs = 4 μA, mIs = 1.2 μA, αEs = 0.3, βEs = 0.3, αIs = 0.3, βIs = 0.3, ρ = 0.4. Considering that the total synaptic current to a neuron has relationship with parameter values of 
, 
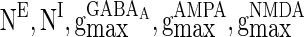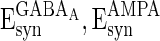, and 
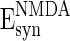, the excitatory and inhibitory feedback of the network are approximately balanced with the parameter values given in this paper.
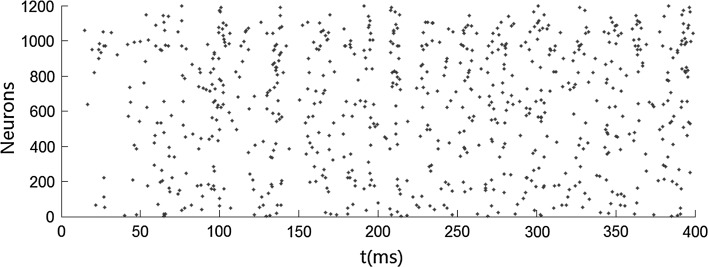
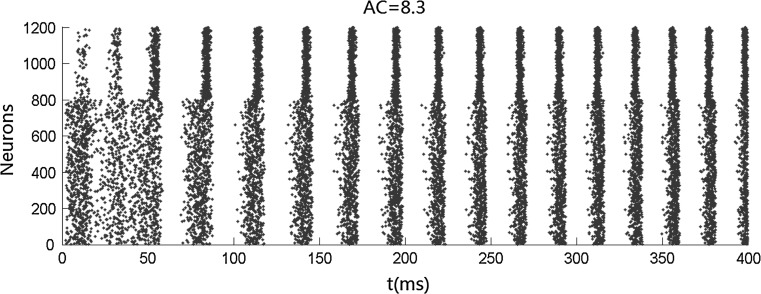
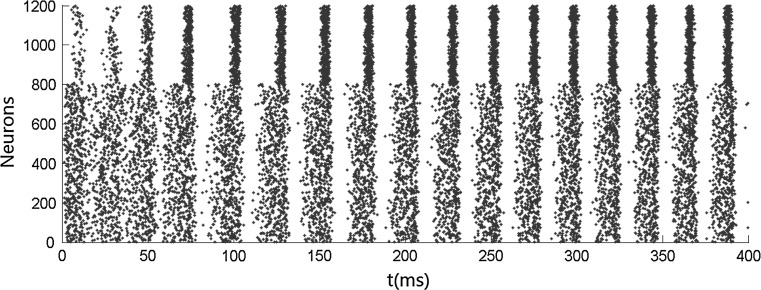
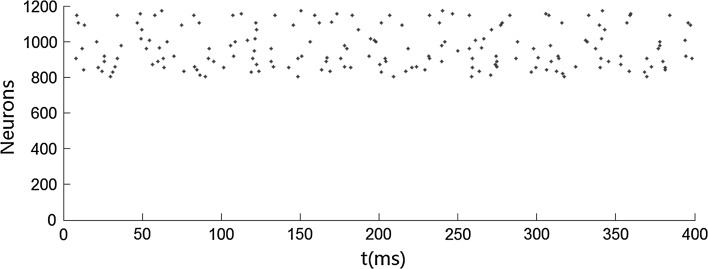
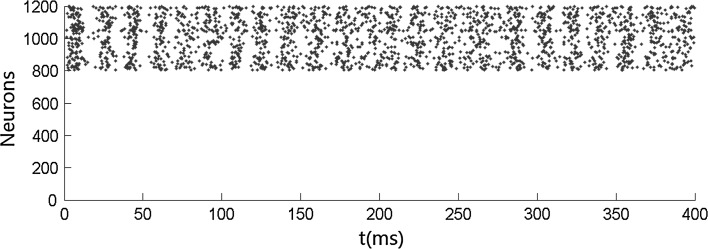
We first carry out simulations when no stimulus is presented. Figure 1 shows that both the inhibitory neurons and the excitatory neurons fire irregularly with low frequency. This ascribes to the fact that the membrane potentials of the neurons cross the threshold randomly due to the fluctuation of the background input current. No oscillation occurs when no stimulus is presented. We then simulate the network when stimulus is presented. Figures 2 and 4 show that the oscillation emerges in the network. The oscillation is strong in the population of inhibitory neurons but is weak (especially in Fig. 4) in the population of excitatory neurons. This is consistent with many previous results that gamma oscillation mainly results from inhibitory interneuron network. Hereinafter, we mainly discuss the oscillation in the population of inhibitory neurons. The frequency of the oscillation is about 41 Hz which is within the band of the gamma oscillation.
Fig. 1.
Irregular firing pattern in excitatory–inhibitory networks driven by background input current which is heterogeneous and fluctuating. Neurons numbered from 1 to 800 are excitatory, while neurons numbered from 801 to 1,200 are inhibitory. mEb = 1.7 μA/cm2, mEs = 0 μA/cm2, αEb = 0.5, βEb = 0.1, mIb = 0.9 μA/cm2, mIs = 0 μA/cm2, αIb = 0.5, βIb = 0.1
Fig. 2.
Gamma oscillation in inhibitory neurons after the presentation of stimulus. The arrangement of the neurons and background currents are the same as those in Fig. 1. mEs = 2 μA/cm2, αEs = 0.3, βEs = 0.3, mIs = 0.2 μA/cm2, αIs = 0.1, and βIs = 0.1
Fig. 4.
Strong gamma oscillation in inhibitory neurons and weak gamma oscillation in excitatory neurons after the presentation of stimulus under high level of heterogeneity. αIs = 0.8, αEs = 0.8
To quantify the accuracy of the oscillation in the population of inhibitory neurons, we use the zero-lag autocorrelation of the global activity (AC).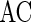 
is calculated for the population of inhibitory neurons as follows (Brunel and Hakim 1999).
 |
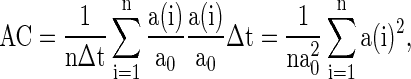9 |
where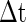 
is the small time bin (0.4 ms in the paper), n is the total time bins (1,000 in the paper), a(i) is the global activity associated with the i-th bin (total number of firing neurons in the i-th bin), and a0 is the average of the global activity over all time bins (
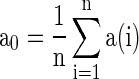). AC of the population of inhibitory neurons in Fig. 2 is 8.3.
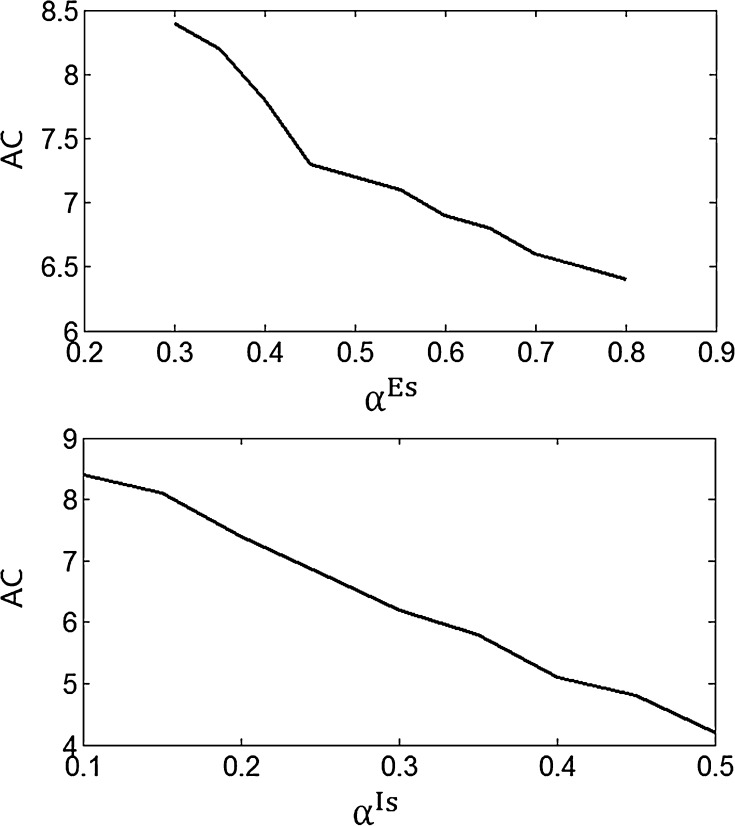
Figure 3 shows the accuracy of the oscillation (quantified by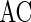 
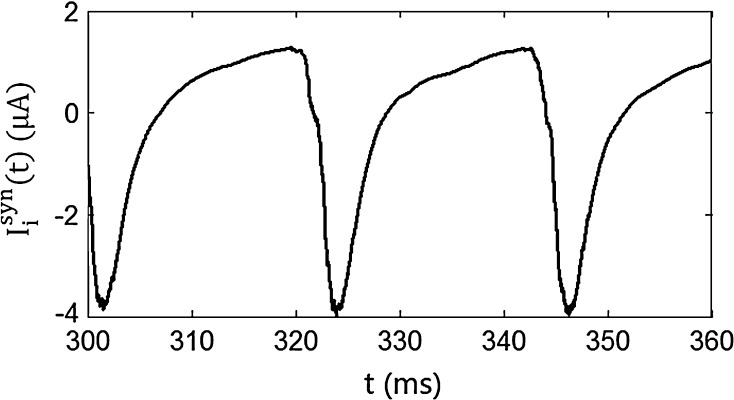
) depends on the level of the heterogeneity of the stimuli. We can see from Fig. 3a that the accuracy of the oscillation in the inhibitory neurons is insensitive to the heterogeneity of the external drives to the excitatory neurons. The accuracy of the oscillation in the inhibitory neurons is also insensitive to the heterogeneity of the external drives to the inhibitory neurons (see Fig. 3b), although it is relatively more sensitive in this case compared with the case described by Fig. 3a. The oscillation preserves even the level heterogeneity is as high as 80 % (see Fig. 4). It is worthy of note that such a high level heterogeneity is as high as that in most of real situations in neural systems. To investigate the dependency of the oscillation on other parameters, we carried out simulations by varying one parameter and fixing other parameter values. Figures 5 and 6 show the dependency of the oscillation on some important parameters such as the synaptic strength, synaptic reversal potential (Jeong and Gutkin 2007), and the synaptic time constant (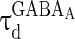
). The results in Figs. 5 and 6 show that the gamma oscillation preserves for a wide range of parameter values. It is worthy of note that too weak synaptic strength may destroy the oscillation according to Fig. 5. This is natural because the oscillation is mainly ascribed to the interaction of neurons via synaptic connection. Besides the parameters discussed aforementioned, our extensive simulations show that the gamma oscillation preserves with variation of other parameters. To show how the synaptic currents contribute to the robust synchronization, the time course of the synaptic current of a silent neuron is plotted in Fig. 7. The time course of the synaptic current of a firing neuron is similar to that in Fig. 7 except that it has a jump at the time when the neuron fires. This is because the neuron resets to the rest potential once it fires, which causes a jump of synaptic current according to Eqs. (4)–(7). Although we cannot exhaust the whole parameter space to explore the robustness of the oscillation, we give a qualitative analysis that the synaptic currents like that in Fig. 7 can produce robust synchronization in highly heterogeneous excitatory–inhibitory networks.
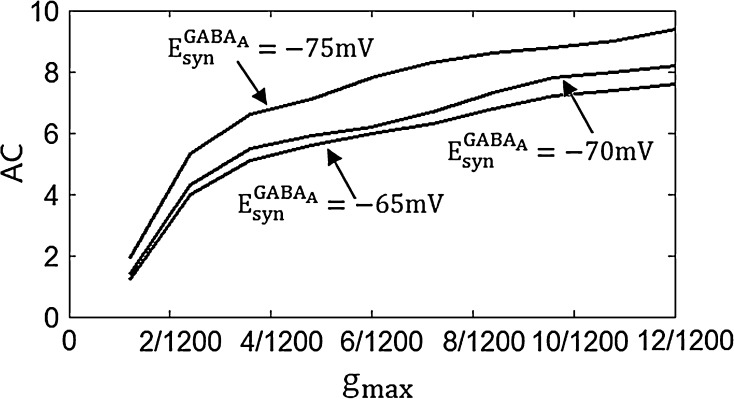
Fig. 3.
The dependency of accuracy of the oscillation in the inhibitory neurons on the level of the heterogeneity of the external currents. αIs is fixed at 0.2 and αEs varies from 0.2 to 0.8 for a; αEs is fixed at 0.4 and αIs varies from 0.1 to 0.5 for b
Fig. 5.
The dependency of accuracy of the oscillation in the inhibitory neurons on the synaptic strength and synaptic reversal potential
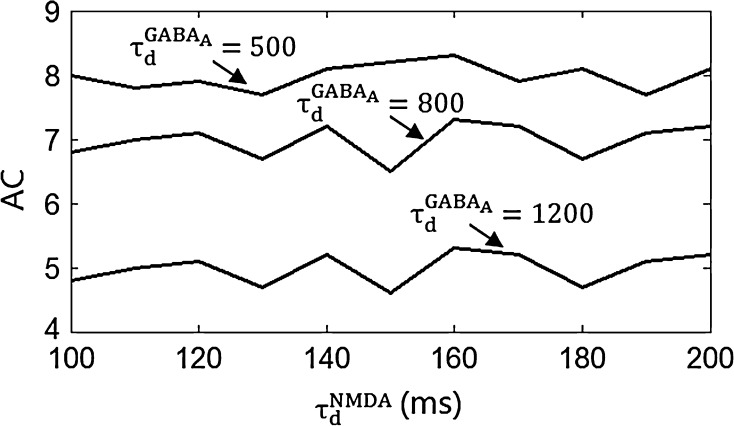
Fig. 6.
The dependency of accuracy of the oscillation in the inhibitory neurons on the decay time constants
Fig. 7.
The time course of the synaptic current of a silent neuron
Analysis of the robust stimuli evoked gamma oscillation
We have shown the stimuli evoked gamma oscillation in a highly heterogeneous network. We next discuss the mechanism of the genesis of this oscillation based on the ING and PING mechanism of the gamma oscillation. We will show in Sect. 4.1 that the mechanism for the gamma oscillation in the highly heterogeneous E/I network is a mixture of ING and PING (We have introduced the ING and PING mechanisms in the introduction section). Then we give a qualitative analysis of this mixed ING–PING mechanism in Sect. 4.2.
Mixed ING–PING mechanism
We can see from Figs. 2 and 4 that the oscillation in the inhibitory neurons is strong but that in the excitatory neurons is weak. These results imply that inhibitory neurons may be the sources of the generation of the gamma oscillation and the oscillation in the excitatory neurons are entrained by that in the inhibitory neurons. Therefore, it seems that mechanism of the gamma oscillation in this paper is ING mechanism.
However, we will next show that excitatory neurons play an important role in generating the gamma oscillation in the network, as well as inhibitory neurons discussed in the previous paragraph, meaning that the gamma oscillation is a mixture of the ING and PING mechanism. Firstly, without excitatory neurons, background currents to the inhibitory neurons are not large enough to drive these neurons to fire in the band of the gamma oscillation. Figure 8 shows such a case where inhibitory neurons fire irregularly with low frequency when no excitatory neurons fire. Secondly, even the background currents are large enough to drive the inhibitory neurons to fire in the band of gamma oscillation, a network with inhibitory neurons alone cannot generate gamma oscillation under the condition of the high level of the heterogeneity. Figure 9 shows that neurons fire approximately at about 45 Hz, but they are not synchronized. This is because neural networks with super-polarized inhibition synchronize only when the level of heterogeneity is medium or low (below 10 %). In the excitatory–inhibitory neural network in this paper, the network synchronizes even when the level of heterogeneity is as high as 80 % (see Fig. 4).
Fig. 8.
Firing patterns of inhibitory neurons with no excitatory synaptic inputs and low background drive currents to the inhibitory neurons. mEb = 0 μA/cm2 and mIb = 0.7 μA/cm2
Fig. 9.
Firing patterns of inhibitory neurons with no excitatory synaptic inputs and large background drive currents to the inhibitory neurons. mEb = 0 μA/cm2 and mIb = 1.5 μA/cm2
Qualitative analysis of the mixed ING–PING mechanism
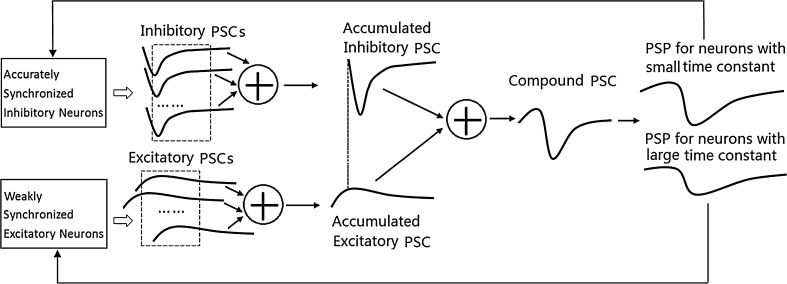
According to the aforementioned analysis, the mechanism of the robust gamma oscillation in this paper is either ING or PING, rather, it is a mixture of ING and PING. The mechanism can be explained by Fig. 10 and acts in a self-consistent way as follows. Firstly, the synchronized firing of the inhibitory neurons produces an accumulated post-synaptic current (PSC). The sharp decrease of the accumulated inhibitory PSC stops the firing of both inhibitory and excitatory neurons. Secondly, the weakly synchronized firing of the excitatory neurons produces an accumulated excitatory PSC, which is ahead of inhibitory PSC and rises slowly. The slowly rising of the excitatory PSC contributes to bring a volley of inhibitory neurons to fire within a short time period. Thirdly, weakly synchronized firing of excitatory neurons and accurately synchronized firing of inhibitory neurons contribute to produce a compound PSC exhibiting a rising-excitatory phase and sharp decreasing-inhibitory phase. This kind of PSC results in weakly synchronized firing of excitatory neurons (which have large membrane time constant or high firing threshold) and accurately synchronized firing of inhibitory neurons (which have small membrane time constant or low firing threshold). We next explain these three points in more details in Sects. 4.2.1, 4.2.2, and 4.2.3, respectively.
Fig. 10.
The mixed ING–PING mechanism acts in a self-consistent way
Properties of accumulated-inhibitory PSC caused by synchronized firing of inhibitory neurons
It is assumed that the rise time constant is extremely small and that the decay time constant is small for inhibitory PSCs, i.e., the PSC induced by the firing of an individual inhibitory neuron take an envelope like that in Fig. 10. If the firing of the inhibitory neurons occurs within a short time period and the variance of the synaptic delay is relatively small compared with the decay time constant (this is actually true for most real neural systems), these individual PSCs can be assumed to arrive almost concurrently at a post-synaptic neuron. The summation of these PSCs produces an accumulated PSC that decreases sharply, reached the negative peak, and then decay rapidly (see Fig. 10). During the short time period when the accumulated PSC drops to the negative peak, the firing of all inhibitory neurons ceases due to this strong inhibition despite of the heterogeneity of these neurons, resulting in the silent phase of the oscillation. The effect of the inhibition decays rapidly, and finally becomes weak enough to allow heterogeneous inhibitory neurons to resume firing, thereby begins the firing phase of the oscillation.
Properties of accumulated-excitatory PSC caused by weakly synchronized firing of excitatory neurons
We have discussed that the firing of all neurons is stopped sharply by the sharp decrease of the accumulated-inhibitory PSC. Synchronized firing of neurons not only needs sharp stopping of the firing of neurons, but also needs a volley of inhibitory neurons resume firing within a short time period once the accumulated-inhibitory PSC decays sufficiently. We next show that the firing of excitatory neurons generates an accumulated-excitatory PSC that contributes to bring a great number of inhibitory neurons to fire within a short time period. Thus, the excitatory and the inhibitory PSCs produce a compound PSC, which first brings a great number of neurons to fire almost concurrently, then sharply stops the further firing of other neurons, forging the phenomenon of synchronized firing of inhibitory neurons. We will discuss the compound PSC in Sect. 4.2.3. In this section, we provide an analysis of the properties of the accumulated-excitatory PSC and corresponding post-synaptic potential (PSP) by the following two steps.
Step (1): As the external drives to the excitatory neurons are larger than that to the inhibitory neurons, excitatory neurons resume to fire ahead of inhibitory neurons, once the inhibitory synaptic currents decay sufficiently. As decay time constant for the excitatory synapses are relatively large, the consecutive firing of these excitatory neurons produces an accumulated-excitatory PSC that rises gradually till the inhibitory neurons are driven to fire by it. The PSP resulting from the accumulated-excitatory PSC also rises till the firing of inhibitory neurons begins.
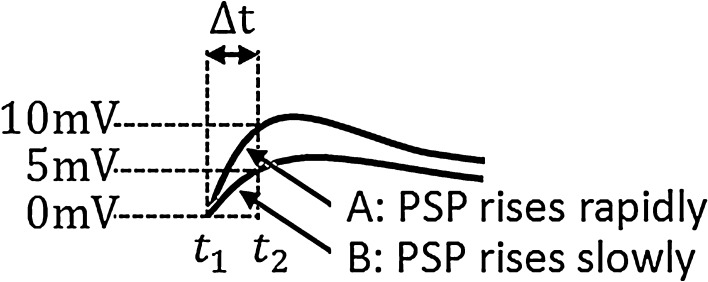
Step (2): More rapidly (see Fig. 11) does the PSP rise at the moment when firing events occur, more neurons will be brought to fire by the PSP within a fixed time slot. For a leaky integrate-and-fire neuron, the sub-threshold membrane potential is the linear summation of the component known as PSP caused by PSC and the components (denoted by Ve in this paper) caused by other currents (external currents, leaky currents, etc.). Suppose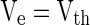 
at t1 for a certain neuron in Fig. 11 and the neuron fires at t1. Then another neuron with 
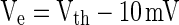will fire at t2 for curve A, as PSP at t2 for curve A is 
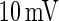. This means that all neurons with Ve between 
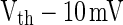and Vth will fire within the time slot 
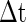for the PSP depicted by curve A. Similarly, all neurons with Ve between 
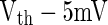and Vth will fire within the time slot 
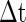for the PSP depicted by curve B. Therefore, for curve A where PSP rises more rapidly, there are more neurons firing within the small time slot 
.
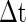Fig. 11.
The effect of the slope at the ascent stage of the PSP on the robust synchronization
Compound PSC and its contribution to the robust oscillation
As the decay time constant of the individual inhibitory PSC is smaller than that of excitatory PSC and the synchronized firing of excitatory neurons is weak, the absolute peak values of the accumulated-inhibitory PSC resulted from the firing of inhibitory neurons are larger than that of the accumulated-excitatory PSC (see Fig. 10), given that the inhibition and excitation are set to be approximately balanced in the E/I networks. Consequently, the summation of the two kinds of synaptic currents results in a compound PSC with an envelope like that in Fig. 10. The compound PSC like that in Fig. 10 produces a PSP for inhibitory neurons with similar envelope as the PSC (see Fig. 10), which may bring a large number of inhibitory neurons fire within a short time slot during the ascent stage of the PSP (refer to the discussion in Sect. 4.2.2) but may stop the firing of the neurons rapidly during the descent stage of the PSP (refer to the discussion in Sect. 4.2.1). Namely, the PSP for inhibitory neurons like that in Fig. 10 contributes to produce a synchronized firing of inhibitory neurons. But the synchronized firing of excitatory neurons is weaker than that of the inhibitory neurons due to any one of the following three factors. (1) If the membrane time constant of the excitatory neurons is larger than that of inhibitory neurons, then the PSP for excitatory neurons will be relatively more flat, given that the compound PSC for both the two kinds of neurons are the same (see PSP for neurons with large time constant and PSP for neurons with small time constant in Fig. 10). Therefore, relatively less excitatory neurons will fire during the ascent stage of the PSP and the firing of excitatory neurons will vanish relatively more slowly during the decreasing stage of the PSP, resulting in a relatively weaker synchronization of excitatory neurons. (2) If the firing threshold for the inhibitory neurons is lower than that of excitatory neurons, then the excitatory neurons are relatively harder to be brought to fire at the ascent stage of the PSP, resulting in a relatively weaker synchronization. (3) It is intuitive that the firing of excitatory neurons may be scattered if the level of the heterogeneity of excitatory neurons is high.
Conclusion and discussion
We showed the stimuli evoked gamma oscillation in a highly heterogeneous complex neural network. In terms of biological evidences, the network is composed of excitatory neurons and inhibitory neurons, where inhibitory neurons are fast spiking neurons with small membrane time constants. Three kinds of synapses are introduced in the network, GABAA inhibitory synapses, AMPA excitatory synapses with relatively short decay time constant, and NMDA excitatory synapses with relatively large decay time constant. Each neuron has a synapse on another neuron with a fixed probability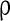 
. The drive currents consist of two parts, the background input drive and the drive current modeling the stimuli. Both the two parts are highly heterogeneous according to their biological nature. Without the input currents coming from stimuli, both the excitatory and inhibitory neurons fire irregularly with low frequency. When stimuli are presented, the new regime of the robust synchronization in E/I networks emerges, i.e. the synchronization of inhibitory neurons is rather accurate but that of excitatory neurons is weak in the case of high level of heterogeneity.
The mechanism underlying the gamma oscillation in this paper is a mixture of ING and PING. Specifically, though the oscillation is originated in the inhibitory neurons, the contributions to the oscillation in inhibitory neurons are ascribed to both excitatory neurons and inhibitory neurons. Either inhibitory neurons or excitatory neurons alone cannot synchronize the firing of inhibitory neurons in the case of high level of heterogeneity. The mechanism of the mixed ING and PING acts in a self-consistent way. After the inhibition decays sufficiently, excitatory neurons begin to fire. The consecutive firing of the excitatory neurons produces a slowly rising accumulated PSC. The rising accumulated-excitatory PSC contributes to bring a volley of inhibitory neurons to fire within a short time period. The spikes from these inhibitory neurons produce a sharp decrease accumulated-inhibitory PSC, which stops the firing of both inhibitory and excitatory neurons. Namely, weakly synchronized firing of excitatory neurons and accurately synchronized firing of inhibitory neurons contribute to produce a PSC (or PSP) exhibiting a rising excitatory phase and sharp decreasing inhibitory phase. In turn, this kind of PSC (or PSP) contributes to generate accurately synchronized firing of inhibitory neurons and weakly synchronized firing of excitatory neurons (the synchronization of excitatory neurons is weak because of its large membrane constant, high firing threshold, or high level of heterogeneity). Thus a self-consistent way is formed, which can explain the new regime of robust synchronization in E/I networks.
Acknowledgments
This research is supported by the NSF of China (Grants No. 70971021, No. 71371046, No. 61075105, and No. 11102038) and Shanghai Education Development Foundation Chenguang Project (No. 10CG33).
References
- Ahmed OJ, Mehta MR. Running speed alters the frequency of hippocampal gamma oscillations. J Neurosci. 2012;32(21):7373–7383. doi: 10.1523/JNEUROSCI.5110-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BÄorgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput. 2003;15:509–538. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bathellier B, Carleton A, Gerstner W. Gamma oscillations in a nonlinear regime: a minimal model approach using heterogeneous integrate-and-fire networks. Neural Comput. 2008;20:2973–3002. doi: 10.1162/neco.2008.11-07-636. [DOI] [PubMed] [Google Scholar]
- Bosman CA, Schoffelen JM, Brunet N, et al. Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron. 2012;75(5):875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 1999;11:1621–1671. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
- Brunel N, Wang XJ. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol. 2003;90:415–430. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Wang XJ, et al. Mechanisms of gamma oscillations. Annu Rev Neurosci. 2012;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- Du Y, Wang RB, Han F, et al. Firing pattern and synchronization property analysis in a network model of the olfactory bulb. Cogn Neurodyn. 2012;6(2):203–209. doi: 10.1007/s11571-011-9189-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelhard B, Ozeri N, Israel Z, et al. Inducing gamma oscillations and precise spike synchrony by operant conditioning via brain-machine interface. Neuron. 2013;77(2):361–375. doi: 10.1016/j.neuron.2012.11.015. [DOI] [PubMed] [Google Scholar]
- Hadjipapas A, Adjamian P, Swettenham JB, et al. Stimuli of varying spatial scale induce gamma activity with distinct temporal characteristics in human visual cortex. Neuroimage. 2007;35(2):518–530. doi: 10.1016/j.neuroimage.2007.01.002. [DOI] [PubMed] [Google Scholar]
- Hájos N, Paulsen O. Network mechanisms of gamma oscillations in the CA3 region of the hippocampus. Neural Networks. 2009;22:1113–1119. doi: 10.1016/j.neunet.2009.07.024. [DOI] [PubMed] [Google Scholar]
- Herrmann CS, Mecklinger A. Magnetoencephalographic responses to illusory figures: early evoked gamma is affected by processing of stimulus features. Int J Psychophysiol. 2000;38(3):265–281. doi: 10.1016/S0167-8760(00)00170-7. [DOI] [PubMed] [Google Scholar]
- Jeong HY, Gutkin B. Synchrony of neuronal oscillations controlled by GABAergic reversal potentials. Neural Comput. 2007;19:706–729. doi: 10.1162/neco.2007.19.3.706. [DOI] [PubMed] [Google Scholar]
- Laczo B, Antal A, Niebergall R, et al. Transcranial alternating stimulation in a high gamma frequency range applied over V1 improves contrast perception but does not modulate spatial attention. Brain Stimul. 2012;5(4):484–491. doi: 10.1016/j.brs.2011.08.008. [DOI] [PubMed] [Google Scholar]
- Lapray D, Bergeler J, Luhmann HJ. Stimulus-induced gamma activity in the electrocorticogram of freely moving rats: the neuronal signature of novelty detection. Behav Brain Res. 2009;199(2):350–354. doi: 10.1016/j.bbr.2008.12.028. [DOI] [PubMed] [Google Scholar]
- Li XM, Morita K, Robinson HPC, et al. Impact of gamma-oscillatory inhibition on the signal transmission of a cortical pyramidal neuron. Cogn Neurodyn. 2011;5(3):241–251. doi: 10.1007/s11571-011-9169-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukumaraswamy SD, Singh KD. Visual gamma oscillations: the effects of stimulus type, visual field coverage and stimulus motion on MEG and EEG recordings. NeuroImage. 2013;69:223–230. doi: 10.1016/j.neuroimage.2012.12.038. [DOI] [PubMed] [Google Scholar]
- Neymotin SA, Lee H, Park E, et al. Emergence of physiological oscillation frequencies in a computer model of neocortex. Front Comput Neurosci. 2011;19:1–17. doi: 10.3389/fncom.2011.00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolic D, Fries P, Singer W. Gamma oscillations: precise temporal coordination without a metronome. Trends cogn Sci. 2013;17(2):54–55. doi: 10.1016/j.tics.2012.12.003. [DOI] [PubMed] [Google Scholar]
- Perry G, Hamandi K, Brindley LM, et al. The properties of induced gamma oscillations in human visual cortex show individual variability in their dependence on stimulus size. NeuroImage. 2013;68:83–92. doi: 10.1016/j.neuroimage.2012.11.043. [DOI] [PubMed] [Google Scholar]
- Rojas-Libano D, Kay LM. Olfactory system gamma oscillations: the physiological dissection of a cognitive neural system. Cogn Neurodyn. 2008;2(3):179–194. doi: 10.1007/s11571-008-9053-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadow J, Lenz D, Thaerig S, et al. Stimulus intensity affects early sensory processing: visual contrast modulates evoked gamma-band activity in human EEG. Int J Psychophysiol. 2007;66(1):28–36. doi: 10.1016/j.ijpsycho.2007.05.010. [DOI] [PubMed] [Google Scholar]
- Schadow J, Lenz D, Thaerig S, et al. Stimulus intensity affects early sensory processing: sound intensity modulates auditory evoked gamma-band activity in human EEG. Int J Psychophysiol. 2007;65(2):152–161. doi: 10.1016/j.ijpsycho.2007.04.006. [DOI] [PubMed] [Google Scholar]
- Schwarzkopf DS, Robertson DJ, Song C, et al. The frequency of visually induced gamma-band oscillations depends on the size of early human visual cortex. J Neurosci. 2012;32(4):1507–1512. doi: 10.1523/JNEUROSCI.4771-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiesinga P, Sejnowski TJ. Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron. 2009;63:727–732. doi: 10.1016/j.neuron.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vida I, Bartos M, Jonas P. Shunting inhibition improves robustness of gamma oscillations in hippocampal interneuron networks by homogenizing firing rates. Neuron. 2006;49:107–117. doi: 10.1016/j.neuron.2005.11.036. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16(20):6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Wong WK. Key role of voltage-dependent properties of synaptic currents in robust network synchronization. Neural Networks. 2013;43:55–62. doi: 10.1016/j.neunet.2013.01.024. [DOI] [PubMed] [Google Scholar]
- Wang Z, Fan H, Aihara K. Three synaptic components contributing to robust network synchronization. Phys Rev E. 2011;83:051905. doi: 10.1103/PhysRevE.83.051905. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Fries P, Mitra PP, Desimone R. Gamma-band synchronization in visual cortex predicts speed of change detection. Nature. 2006;439:733–736. doi: 10.1038/nature04258. [DOI] [PubMed] [Google Scholar]