kmacs: the k-mismatch average common substring approach to alignment-free sequence comparison

Abstract

Motivation: Alignment-based methods for sequence analysis have various limitations if large datasets are to be analysed. Therefore, alignment-free approaches have become popular in recent years. One of the best known alignment-free methods is the average common substring approach that defines a distance measure on sequences based on the average length of longest common words between them. Herein, we generalize this approach by considering longest common substrings with k mismatches. We present a greedy heuristic to approximate the length of such k-mismatch substrings, and we describe kmacs, an efficient implementation of this idea based on generalized enhanced suffix arrays.

Results: To evaluate the performance of our approach, we applied it to phylogeny reconstruction using a large number of DNA and protein sequence sets. In most cases, phylogenetic trees calculated with kmacs were more accurate than trees produced with established alignment-free methods that are based on exact word matches. Especially on protein sequences, our method seems to be superior. On simulated protein families, kmacs even outperformed a classical approach to phylogeny reconstruction using multiple alignment and maximum likelihood.

Availability and implementation: kmacs is implemented in C++, and the source code is freely available at http://kmacs.gobics.de/

Contact: chris.leimeister@stud.uni-goettingen.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Comparative sequence analysis traditionally relies on pairwise or multiple sequence alignment. With the huge datasets that are produced by next-generation sequencing technologies, however, today’s alignment algorithms reach their limits. Thus, with the growing number of completely or partially sequenced genomes, there is an urgent demand for faster sequence-comparison methods. Over the past two decades, a wide variety of alignment-free approaches were proposed (Vinga and Almeida, 2003). Although aligning two sequences takes time proportional to the product of their lengths, most alignment-free methods run in linear time. They are, therefore, increasingly used for genome-based phylogeny reconstruction and for large-scale protein sequence comparison. It is known, however, that alignment-free methods are generally less accurate than alignment-based approaches.

Most alignment-free methods calculate the relative frequencies of words of a fixed length k, also called k-mers, in the input sequences. Other methods are based on variable-length matches; they have the advantage that it is not necessary to specify a fixed word length (Comin and Verzotto, 2012; Didier et al., 2012). These programs achieve usually better results than approaches relying on a fixed word length. However, algorithms using variable word lengths are typically more complex and require more sophisticated data structures than methods relying on fixed word lengths.

A well-known approach that uses word matches of variable length is the average common substring (ACS) method (Ulitsky et al., 2006), which calculates for each position i in one sequence the length of the longest substring starting at i and matching some substring of a second sequence. As a further development of this idea, the shortest unique substring (shustring) approach has been proposed by Haubold et al. (2005). These authors also derived an estimator for the number of substitutions per site between two unaligned sequences based on the average shustring length; they implemented this approach in the program K_r (Haubold et al., 2009). ACS and shustrings can be calculated efficiently using suffix trees (Weiner, 1973).

As the aforementioned methods, most approaches for alignment-free phylogeny reconstruction are based on exact word matches. Recently, we suggested to use spaced-k-mers defined by pre-defined patterns of match and don’t care symbols, instead of contiguous k-mers (Boden et al., 2013; Leimeister et al., 2014). The aim of this study is to apply the idea of inexact matches to word matches of varying lengths. We generalize the ACS approach by considering, for each position i in one sequence, the longest substring starting at i and matching some substring in the second sequence with k mismatches. We propose an efficient heuristic to approximate the lengths of these substrings, and we describe kmacs, an implementation of this approach based on generalized enhanced suffix arrays. A web server for our program is described in Horwege et al. (2014).

2 APPROACH

2.1 The ACS approach and k-mismatch substrings

As usual, for a sequence S over an alphabet Σ, S[i] is the i-th element of S, by $|S|$ we denote the length of S and $S[i\mathrm{..}j]$ is the (contiguous) substring of S from i to j. In particular, $S[i\mathrm{..}|S|]$ is the i-th suffix of S. For two sequences S₁ and S₂, the ACS approach determines for every position i in S₁ the length $s_1(i)$ of the longest substring of S₁ starting at position i and exactly matching some substring in S₂. The lengths $s_1(i)$ are averaged and normalized to define a similarity measure

$$L(S_1,S_2)=\frac{1}{|S_1|}*{\displaystyle \sum _{i=1}^{|S_1|}{s}_1}(i)$$ (1)

which is turned into a (non-symmetric) distance measure by defining

$$d(S_1,S_2)=\frac{log(|S_2|)}{L(S_1,S_2)}-\frac{log(|S_1|)}{L(S_1,S_1)}$$ (2)

To obtain a symmetric distance, the distance between S₁ and S₂ is then defined by Ulitsky et al. (2006) as

$$d_{ACS}(S_1,S_2)=\frac{d(S_1,S_2)+d(S_2,S_1)}{2}$$ (3)

In this article, we generalize this distance measure by using substring matches with k mismatches instead of exact matches. That is, instead of using the maximum substring lengths $s_1(i)$, we define $s_1^k(i)$ as the length of the longest substring of S₁ starting at position i and matching some substring of S₂ with up to k mismatches, minus k. (We subtract k from the length of this string, counting only the matching positions). $s_2^k(i)$ is defined accordingly. We then define a distance measure as above, but with $s_q(i)$ replaced by $s_q^k(i)$. In the special case where k = 0, we have $s_q^0(i)=s_q(i)$, so in this case our distance is exactly the distance d_ACS.

2.2 Approximating the length of k-mismatch substrings

For a pair of sequences, the exact values $s_q^k(i)$ can be calculated in $\mathcal{O}(k*n^2)$ time using suffix trees or similar data structures where n is the maximal length of the sequences. As we want to compare sequences in linear time, however, we propose a heuristic to approximate these values. To do so, we first calculate for each position i in S₁ the length $s_1(i)$ of the longest common substring starting at i matching a substring of S₂, as is done in ACS. Let j be the start of this matching substring in S₂; the character $S_1[i+s(i)]$ must therefore differ from $S_2[j+s(i)]$. We then extend this match without gaps in S₁ from position $i+s(i)+1$ and in S₂ from $j+s(i)+1$, until the next mismatch occurs. This is repeated until the k + 1-th mismatch or the end of one of the two sequences is reached.

In the example below, for position i = 4 in S₁ and with k = 2 mismatches, our approach would return the following k-mismatch common substring, starting at position j = 2 in S₂:

To obtain this k-mismatch common substring, our program would first determine the longest common substring for position i = 4 in S₁ that exactly matches a substring in S₂. We find such a match at position j = 2 in S₂ with the length $s_1(4)=2$. Then this match is extended without gaps until the third mismatch is reached. The length of this 2-mismatch substring is 7, so we have $s_1^2(4)=5$ (in the definition of $s_q^k(i)$, we count only the matching positions).

It should be mentioned that, for a position i in S₁, the corresponding position j in S₂ of the longest exact match to a substring starting at i may not be unique. Consider, e.g. position i = 2 in the first sequence of the above example:

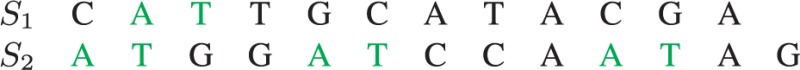
Here, the substring AT starting at position 2 in S₁ is the longest substring starting at this position and matching a substring of S₂—but this substring occurs at positions 1, 5 and 10 in S₂. In such a case, we calculate all k-mismatch extensions of these occurrences as described above, and we define $s_1^k(i)$ as length of the maximal possible extension minus k.

The above heuristic reduces the complexity of finding the k mismatch maximal substring lengths from $\mathcal{O}(k*n^2)$ to $\mathcal{O}(k*n*z)$, where z is the average number of maximal matches to a substring in S₂ starting at a position i in S₁. In principle, this complexity could be achieved by using suffix trees (Weiner, 1973) as the underlying data structure. Here, one would build a generalized suffix tree for the sequences in $\mathcal{O}(|S_1|+|S_2|)$ time, e.g. using Ukkonen’s algorithm (Ukkonen, 1995). To determine the longest substring starting at i in S₁ and also occurring in S₂, one needs to find the lowest node v in the suffix tree that is above leaf i and also above some leaf that belongs to S₂. The length $s_1(i)$ of the longest common substring starting at i is then the string depth of the node v, that is, the length of the edge labels on the path from the root to v. Moreover, the leaves below v appertaining to S₂ exactly correspond to the positions of this longest exact match in S₂.

Next, we want to extend the longest exact matches that we have found by this procedure until the k + 1-th mismatch is found. Thus, we need be able to find the longest exact match between two sequences starting at two given positions i and j (the positions after a mismatch, in our case). In a suffix-tree approach, this could be accomplished by lowest common ancestor (LCA) queries. Similar to the aforementioned approach, we would have to look up the lowest node v that is above both leafs i and j; the string depth of v is then the length of the longest exact match starting at i and j, respectively. LCA queries can be carried out for any i and j in constant time after a linear-time preprocessing step (Harel and Tarjan, 1984), resulting in k constant-time LCA queries for the full k-mismatch extension of an exact longest match.

3 IMPLEMENTATION

Abouelhoda et al. (2004) have shown that every algorithm that uses suffix-trees can be replaced by an algorithm using enhanced suffix arrays that has the same complexity. Here, an enhanced suffix array is defined as a data structure ‘consisting of the suffix array and additional tables’. Both, suffix trees and enhanced suffix arrays, can be calculated in linear time and space, but suffix arrays require substantially less memory per input character than suffix trees do (Manber and Myers, 1990). In our implementation, we therefore used enhanced suffix arrays instead of suffix trees, making use of recent improvements of linear-time suffix array construction algorithms.

A suffix array SA of a string $S=S[1]\dots S[n]$ is a permutation of the indices $\mathrm{1...}n$ according to the lexicographical ordering of the corresponding suffices. That is, we have SA$[i]=j$ if the j-th suffix of S is at the i-th position in the lexicographical ordering of all suffices of S. In addition to the SA, we need the so-called longest common prefix (LCP) array for S. Here, the entry LCP[i] stores the length of the LCP of the SA[i]-th suffix and its predecessor in SA, the SA$[i-1]$-th suffix. The SA of a sequence S together with the corresponding LCP array is called, in this context, the enhanced suffix array of S. To calculate enhanced suffix arrays in linear time, we used a program described by Fischer (2011), which is available at http://algo2.iti.kit.edu/english/1828.php. The underlying algorithm is based on sais-lite by Yuta Mori, a fast implementation of induced sorting (Nong et al., 2009). Suffix arrays provide an efficient solution to our longest k-mismatch substring problem.

For a single sequence S and a position SA[i] in S, the enhanced suffix array of S can be used to find the length of the longest substring in S starting at a different position in S and matching a substring starting at SA[i]. It is easy to see that this substring must be the LCP of the SA[i]-th suffix with one of its neighbours in SA, i.e. either with the SA$[i+1]$-th or the SA$[i-1]$-th suffix, whichever is longer. With an enhanced suffix array, the length of this substring is given as the maximum of the values LCP[i] and $LCP[i+1]$ and can therefore be looked up in constant time. The position where this second substring starts is then either SA$[i-1]$ or SA$[i+1]$—or both of these positions—depending on where the maximum is reached.

If matches between two sequences are to be found, the situation is slightly more complicated. For a position in sequence S₁, we want to find a position in S₂ such that the common substring starting at these two positions is maximal, and vice versa. To solve this problem, we build the generalized enhanced suffix array of our sequences, i.e. the enhanced suffix array of the concatenated sequence $S:=S_1\$S_2$ where $ is a special character not contained the alphabet Σ; see also Babenko and Starikovskaya (2008) for a related approach. Thus, each suffix from S₁ or S₂ is represented in lexicographical order by an entry in SA. Figure 1 shows the enhanced suffix array for two sequences.

Fig. 1.

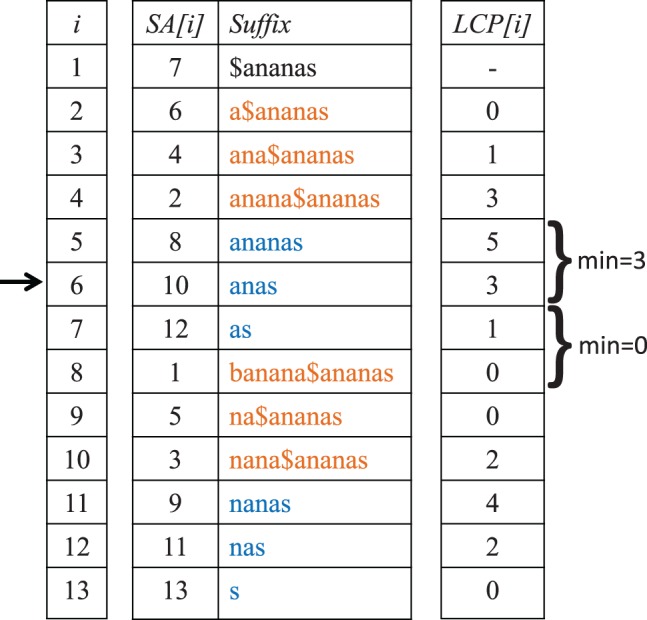
Generalized SA and LCP array for the strings $S_1=banana$ and $S_2=ananas$, concatenated by the symbol $. Suffices of $S_1\$S_2$ starting in S₁ are shown in orange, suffices starting in S₂ are in blue

To find the length of the longest substring starting at SA[i] in one sequence, matching a substring of the other sequence, and its occurrences there, we need to look up the largest integer $p_1(i)$ with $p_1(i)<i$, such that SA$[p_1(i)]$ belongs to the other sequence. Correspondingly, we need the smallest integer $p_2(i)$ with $p_2(i)>i$ with SA$[p_2(i)]$ belonging to the other sequence. The length of this common substring is then given as the minimum of all LCP values between $p_1(i)+1$ and i or the minimum between the LCP values between i + 1 and $p_2(i)$—whichever minimum is larger. Formally, the length of the longest substring starting at a position SA[i] and matching a substring of the respective other sequence is given as follows:

$$s(SA[i])=max(\underset{p_1(i)<x\le i}{\min }LCP[x],\underset{i<y\le p_2(i)}{\min }LCP[y])$$ (4)

with p₁ and p₂ defined as above.

The position of this longest substring in S is then SA$[p_1(i)]$ or SA$[p_2(i)]$ (or both), depending on where the maximum in Equation (4) is reached. All positions in this formula refer to the concatenated sequence S, but it is trivial to retrieve the positions in the original sequences S₁ and S₂ from these values by subtracting $|S_1|+1$ where necessary.

As an example, consider Figure 1. For i = 6, we want to find the longest common substring starting at $SA[6]=10$ (marked by an arrow) that exactly matches a substring starting at some position in the other sequence. Position $SA[6]=10$ in the concatenated sequence S corresponds to a position in sequence S₂, so we have $p_1(6)=4$, as 4 is the largest integer smaller than 6 such that $SA[4]$ belongs to the other sequence, i.e. to S₁. Similarly, we obtain $p_2(6)=8$. According to Equation (4), we get the following:

$$s(SA[6])=\max \left\{\min \{5,3\},\min \{1,0\}\right\}=\max \{3,0\}=3.$$

Position 10 in S corresponds to position 3 in the original sequence S₂, so, as a result, we obtain $s_2(3)=3$, i.e. the longest substring starting at position 3 in S₂ matching a substring from S₁ has length 3 (the substring itself is ‘ana’).

Algorithm 1 Calculation of Equation (4).

Require: SA {generalized suffix array for S₁ and S₂ of length n}

Require: LCP {corresponding longest common prefix array}

Ensure: s {stores the results of Equation (4)}

 $min\leftarrow 0$

 for i = 2 to n – 1 do

  if $SA[i]$ and $SA[i+1]$ belong to the same sequence then

   if $LCP[i+1]<min$ then

    $min\leftarrow LCP[i+1]$

   end if

   $s[i+1]\leftarrow min$

  else

   $min\leftarrow LCP[i+1]$

   $s[i+1]\leftarrow LCP[i+1]$

  end if

 end for

 $min\leftarrow 0$

 for i = n to 2 do

  if $SA[i]$ and $SA[i+1]$ belong to the same sequence then

   if $LCP[i]<min$ then

    $min\leftarrow LCP[i]$

   end if

   $s[i-1]\leftarrow max(min,s[i-1])$

  else

   $min\leftarrow LCP[i]$

   $s[i-1]\leftarrow max(min,s[i-1])$

  end if

 end for

All values s(i) can be calculated for the entire concatenated string S in linear time using Algorithm 1. Here, the first loop computes ${\min }_{p_1<x\le i}LCP[x]$ for all indices i and stores them as s[i]. Then the second loop calculates ${\min }_{i<y\le p_2}LCP[y]$ and updates s[i] if the result is greater than the actual value of s[i]. This way, algorithm 1 applies Equation (4) to all indices i and stores the corresponding values s[i].

Finally, for our heuristic we need to find for an index i all positions belonging to the respective other sequence, where a match of length s(i) occurs. This can be achieved by a simple extension of Algorithm 1. Without loss of generality, we assume that the first minimum in Equation (4) is strictly larger than the second minimum, so $p_1(i)$ is a position where a maximal match to the other sequence occurs (as was the case in our small example above). To find possible additional matching positions, we consider all indices $p\le p_1(i)$ in descending order, as long as one has the following inequality:

$$LCP[p+1]\le \underset{p_1(i)<x\le i}{\min }LCP[x]$$

For all such p that belong to the other sequence, the positions SA[p] are occurrences of longest substrings matching a substring starting at i. In our example, we find one further position p = 3, so SA$[3]=4$ is an additional occurrence. If the maximum in (4) is achieved by the second term, one proceeds accordingly.

Next, the second step in our approach involves finding the length of the longest common substring starting at pre-defined positions in S₁ and S₂, respectively. Using the enhanced suffix array of a sequence S, the length of the longest substring starting at positions SA[i] and SA[j] (with SA$[i]<$ SA[j]) is given as the minimum over the values LCP[p], $i<p\le j$. There is an approach similar to LCA queries to obtain this value known as range minimum queries (RMQ). A RMQ returns the index of an array A that stores the smallest element between two specified indices l and r, denoted as $RM{Q}_A(l,r)$.

Several algorithms are available that can solve RMQ in constant time, after a linear preprocessing step, e.g. Fischer and Heun (2007). According to Fischer and Heun (2006), the longest common substring starting at i and j can be calculated as $LCP[RM{Q}_{LCP}(S{A}^{-1}[i]+1,S{A}^{-1}[j])]$ where $S{A}^{-1}$ is the inverse suffix array. As a result, the same complexity as for suffix trees can be achieved by using enhanced suffix arrays. In our implementation, however, we extend the substrings by matching single characters because in our test runs this ‘naive’ approach was faster than the RMQ implementation that we tested. Nevertheless, our downloadable program has an option for using the RMQ algorithm so the user can compare these two approaches.

4 BENCHMARKING

4.1 Benchmark sequences

To evaluate kmacs and to compare it with other methods of sequence comparison, we applied these methods phylogeny reconstruction. We used a large number of DNA and protein sequence sets for which reliable phylogenetic trees are available, and we measured how similar the constructed trees are to the respective reference trees. The following sequence sets were used in our study:

For eukaryotic DNA comparison, we used a set of 27 primate mitochondrial genomes that were previously used by Haubold et al. (2009) as benchmark for alignment-free methods. These sequences have a total length of 446 kb. A benchmark tree that has been constructed based on a multiple alignment.

As prokaryotic genomes, we used a set of 32 Roseobacter genomes, which were previously analysed by Newton et al. (2010). They constructed a phylogenetic tree for these sequences based on alignments of 70 universal single-copy genes that we used as reference tree in our study. The total size of this sequence set is 135.9 mb.

As benchmark proteins, we used 218 sequence sets contained in the BAliBASE (v3.0) database (Thompson et al., 2005). To obtain reference trees, we applied Maximum Likelihood (Felsenstein, 1981), implemented in the program proml from PHYLIP to the reference multiple alignments in BAliBASE. As these reference alignments are considered to be reliable, the resulting trees should also be reliable.

In addition to these real-world sequences, we used the program Rose (Stoye et al., 1998) to generate simulated DNA and protein families. Rose generates sets of related sequences based on a probabilistic model of substitutions and insertions/deletions for which the parameters can be adjusted by the user. These sequences are created along a randomly generated tree, starting from one common ancestral sequence at the root of the tree. This way, the ‘evolution’ of the generated sequences is logged, so a reference tree is generated alongside the sequences. We used Rose with default parameters, except for the parameter relatedness, which defines the average evolutionary distance between the generated sequences, measured in PAM units. We generated 20 DNA sequence sets, each of which contains 50 sequences with an average length of 16 000 nt using a relatedness value of 70. Furthermore, we generated 20 protein sequence sets, each containing 125 sequences with an average length of 300 amino acids. Here, we set the relatedness to 480.

4.2 Compared methods

We compared our new method with seven state-of-the-art alignment-free methods, namely ACS (Ulitsky et al., 2006), K_r v2.0.2 (Haubold et al., 2009), FFP (Sims et al., 2009), spaced words (Leimeister et al., 2014), CVTree (Qi et al., 2004), the underlying approach (UA) (Comin and Verzotto, 2012) as well as to a generic k-mer-frequency approach. As an eighth method, we ran Clustal W (Thompson et al., 1994) on those sequence sets where this was possible and meaningful. For ACS and the k-mer approach, we used our own implementations, namely kmacs with k = 0 and our spaced-words approach without don’t care positions in the underlying patterns, respectively.

FFP, K_r and CVTree return pairwise distances between the input sequences. For ACS, we calculated distances as defined in (3), and for spaced words and the k-mer approach we used the Jensen–Shannon divergence (Lin, 1991), applied to (spaced)-word frequency vectors as explained in Leimeister et al. (2014). For each of the five groups of benchmark data, we used the word length k for which the k-mer approach produced the best results, i.e. trees with minimal average Robinson–Foulds (RF) distances to the reference trees. For spaced words, we used the same value for k, even though better results might be possible with different values. Accordingly, on every group of benchmark data, we tested FFP, CVTree and UA with different parameter values and used those which produced the best results on this group.

We then constructed phylogenetic trees by applying Neighbor joining (Saitou and Nei, 1987) to the distance matrices obtained with the different alignment-free methods. Finally, we calculated phylogenetic trees for all sequence sets by applying Maximum Likelihood (Felsenstein, 1981) to the Clustal W multiple alignments. All resulting tree topologies were compared with the topologies of the respective reference trees using the RF metric (Robinson and Foulds, 1981). For Neighbor joining and to calculate the RF distances, we used the programs neighbor and treedist contained in the PHYLIP package (Felsenstein, 1989).

5 RESULTS AND DISCUSSION

Figures 2 and 4–7 summarize our test results on the five groups of benchmark sequence sets that we used. The plots show the average RF distances between the produced trees and the corresponding reference trees. For kmacs, results are shown for various values of k. For FFP, CVTree, UA and the k-mer method, we also used a range of parameter values, but for each of these methods, the figures show only the best results on the respective group of benchmark sequences. Thus, for a fair comparison, these methods should be compared with the best results of kmacs in the corresponding figure. On the other hand, K_r, ACS and Clustal could be used with default parameters, which is clearly an advantage of these methods.

Fig. 2.

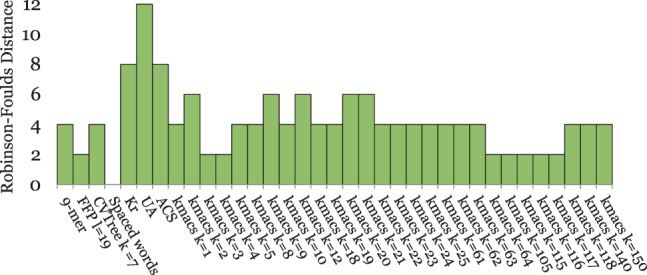
Performance of alignment-free methods on a set of 27 primate mitochondrial genomes. RF distances between constructed trees and a reference tree are shown. The tree calculated by kmacs with k = 70 is shown in Figure 3, together with the reference tree

Fig. 4.

Performance of alignment-free methods on a set of 32 Roseobacter genome sequences. RF distances to the reference tree are shown

Fig. 5.

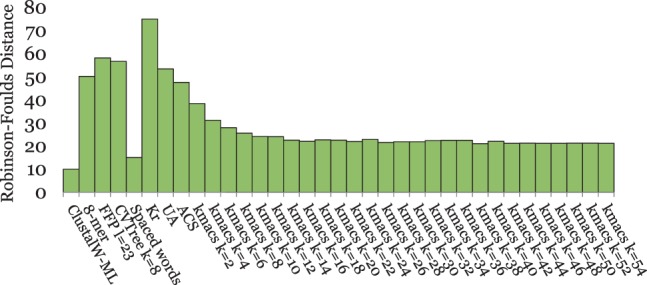
Performance of alignment-based and alignment-free methods on 20 sets of 50 simulated DNA sequences of length 16 000 each. Average RF distances to the respective reference trees are shown

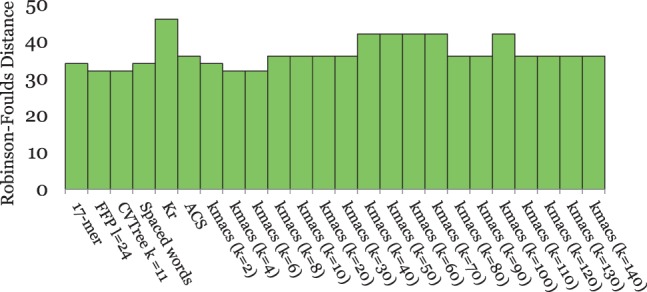
Fig. 6.

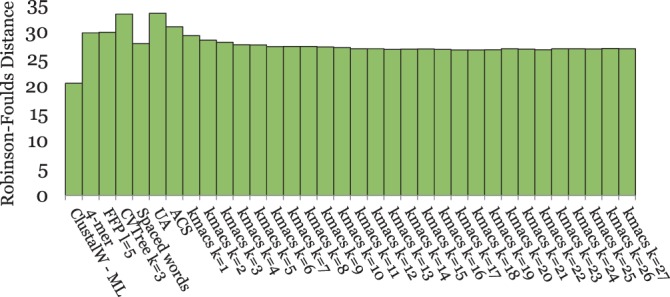
Performance of different methods on 218 protein sequence sets from BAliBASE. Average RF distances to reference trees, calculated based on BAliBASE reference alignments, are shown

Fig. 7.

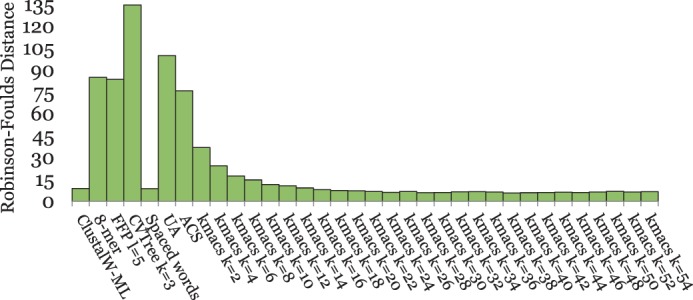
Performance of different methods on 20 sets of 125 simulated protein sequences each

Figure 2 contains the test results on the primate mitochondrial genomes. The best method on this dataset was our previously developed spaced-words approach; the tree topology produced by this method precisely coincides with the topology of the reference tree, i.e. the RF distance is zero. The second best methods were FFP and kmacs with k = 3, 4 and $64\le k\le 117$. ACS, CVTree, UA, kmacs with other values for k and K_r performed worse on these data. As an example, Figure 3 compares the tree calculated with kmacs (k = 70) with the alignment-based reference tree from Haubold et al. (2009). The tree topology calculated by kmacs almost coincides with the topology of the reference tree; the RF distance between these trees is 2.

Fig. 3.

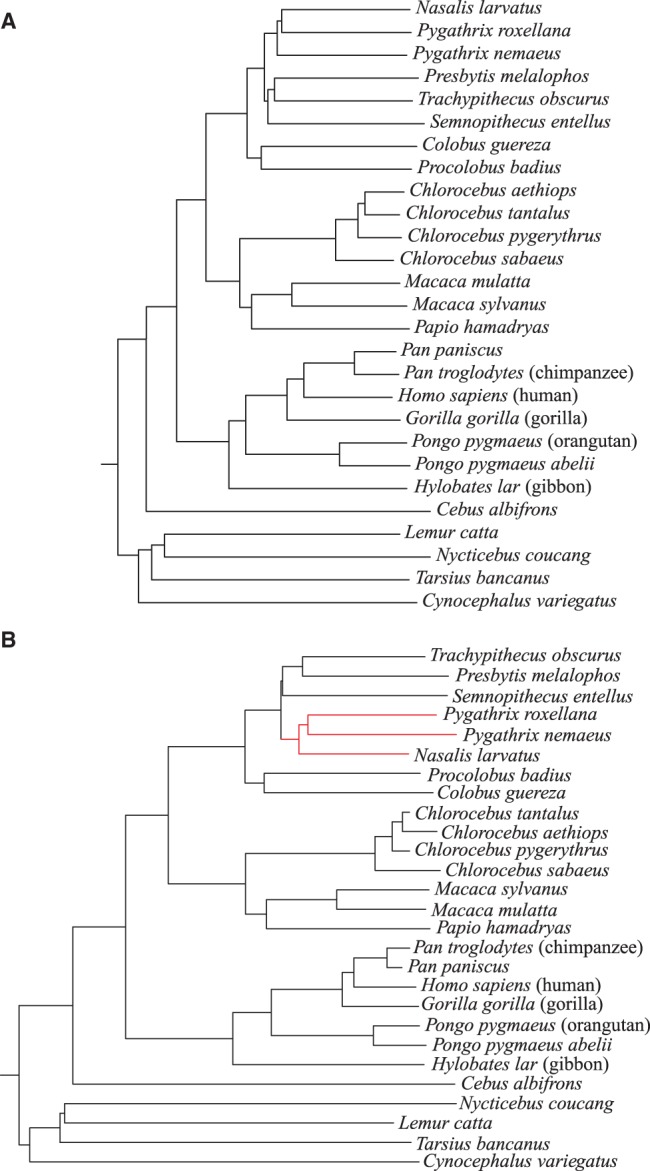
Midpoint-rooted trees of 27 primate mitochondrial genomes. (A) is the alignment-based reference tree obtained from Haubold et al. (2009) and (B) is based on kmacs with k = 70. Red branches represent differences to the reference tree topology. Except for these three species, the topologies of the two trees coincide, resulting in a RF distance of 2 between our tree and the reference tree

On the Roseobacter genomes, the best methods were kmacs with k = 4 and 6, FFP and CVTree as shown in Figure 4. Spaced words and the generic k-mer approach performed slightly worse. None of the tested methods was able to exactly reconstruct the topology of the reference tree. UA is missing in this comparison, as this program is too slow to be run on full bacterial genomes in reasonable time. For our simulated DNA sequence sets, the results were similar as for the primate mitochondrial genomes; see Figure 5. Here too, spaced words was the best alignment-free method, followed by kmacs. This time kmacs outperformed the established alignment-free approaches for all values of k that we tested. On our simulated DNA sequences, we could also run a classical approach to phylogeny reconstruction using Clustal W and Maximum Likelihood. Not surprisingly, this slow and accurate method performed better than all alignment-free approaches.

Figure 6 shows the results for the BAliBASE protein sequences. Spaced words and kmacs again produced better results than the existing alignment-free methods that we evaluated. This time, there was a large range of values for k where kmacs performed similar or even slightly better than spaced words, and both methods outperformed the other alignment-free methods that we tested. As with the previous dataset, the classical approach based on multiple sequence alignment performed best; this time the difference between alignment-based and alignment-free methods was larger. This may be because of the fact that multiple-alignment programs are often tuned to perform well on BAliBASE, the main database to evaluate multiple-alignment methods.

Finally, the results on our simulated protein sequences are shown in Figure 7. As in most previous examples, spaced words and kmacs outperformed other alignment-free approaches and, as on BAliBASE, kmacs was slightly better than spaced words if k was sufficiently large. Surprisingly, on these benchmark sequences spaced words and kmacs even outperformed Clustal W and Maximum Likelihood, although not dramatically.

So far, we evaluated alignment-free and alignment-based methods indirectly, by applying them to phylogeny reconstruction and comparing the resulting trees with trusted reference trees using the RF metric. This is a common procedure to evaluate alignment-free methods. RF distances to reference trees are only a rough measure of accuracy, though, as they are based on tree topologies alone and do not take branch lengths into account. Furthermore, the constructed trees depend not only on the underlying methods for sequence comparison but also on the methods used for tree reconstruction. A more direct and accurate way of comparing alignment-free methods is to directly compare the distance values that they calculate. This can be done, for example, by plotting the distances produced for simulated sequences against their real evolutionary distances (Haubold et al., 2009). Ideally, this should be a linear relation. Figure 8 shows such plots for the algorithms that we compared in our study.

Fig. 8.

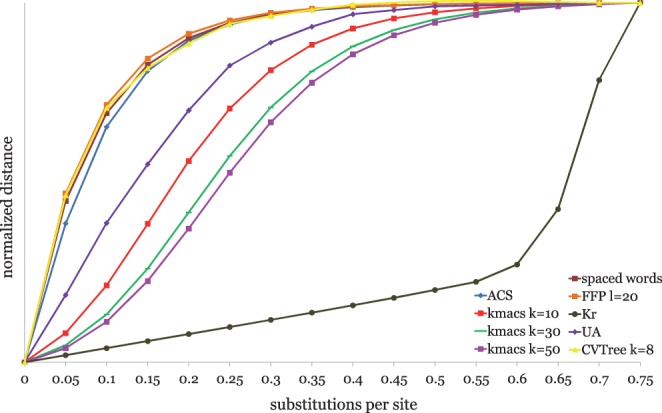
Distances calculated by different alignment-free methods as a function of substitutions per site for pairs of simulated DNA sequences. Distances were normalized such that they are equal for 0.75 substitutions per site

Tables 1 and 2 summarize the run times of the different methods that we tested. When used with moderate values of k, kmacs is faster than spaced words run with a set of 100 different patterns. K_r was more than one order of magnitude faster than kmacs and spaced words, respectively, although UA was the slowest method. The fastest method was our implementation of the generic word-frequency approach, followed by K_r and CVTree. In general, spaced words used with the single-pattern option is only slightly slower than the k-mer approach. As shown in our companion paper, however, spaced words produces considerably better results when used with multiple patterns (Leimeister et al., 2014). We therefore applied only the multiple-pattern version in this study.

Table 1.

Program runtime for different methods on a set of 50 simulated DNA sequences of length 16 000 nt each

Method	Runtime (s)
Clustal W	1817
Clustal Ω	1039
8-mer	0.3
FFP, l = 23	123.3
spaced words, 100 patterns, k = 8	27.6
ACS	2.8
Kr	0.9
CVTree	0.5
UA	572
kmacs, k = 1	4.2
kmacs, k = 10	7.6
kmacs, k = 20	4.2
kmacs, k = 50	21.4

Note: Spaced words was run with 100 random patterns of varying length as described by Leimeister et al. (2014). For Clustal W and Clustal Ω, the time for calculating a multiple alignment is shown; for the six alignment-free methods the time for calculating pairwise distances is shown.

Table 2.

Program run time for different methods on a set of 32 genome sequences of total length 135 mb from various Roseobacter species

Method	Runtime (s)
17-mer	34.9
FFP, l = 24	9022
Spaced words, 100 patterns, k = 17	3617
ACS	531
Kr	206
CVTree	84
kmacs, k = 1	784
kmacs, k = 10	1302
kmacs, k = 50	3158
kmacs, k = 100	5433

Note: Parameters for spaced words as in Table 1.

The relatively long runtime of UA is partially because of the fact that this program is written in Java, while all other programs that we tested are written in C++. As expected, the multiple-alignment approaches Clustal W and Clustal Ω (Sievers et al., 2011) were far slower than the alignment-free methods; the difference in speed between alignment-based and alignment-free methods was between three and four orders of magnitude. All test runs were done on a Intel Core i7 4820k, which we overclocked to 4.5Ghz.

As explained in Section 2.2, kmacs searches for each position i in one sequence the maximum substring starting at i that matches a substring in the second sequence. There can be more than one such maximal match, and all these matches are extended to k-mismatch common substrings. Thus, the runtime of kmacs depends on z, the average number of such maximal substring matches for a given position i. In principle, z can be large and the worst-case time complexity of our algorithm is therefore high. In practice, however, z is small, independent of sequence length and substitution probability. Figure 9 shows values of z for different sequence lengths and mutation frequencies.

Fig. 9.

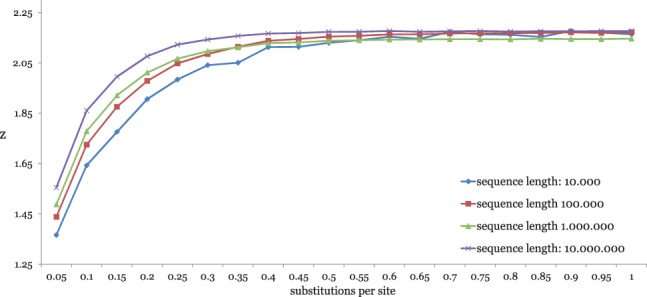
Average number z of maximal exact matches starting at a position i in one sequence to a substring in a second sequence. We used simulated DNA sequences with different lengths and substitution frequencies

Finally, we wanted to know how accurately our greedy heuristic approximates the exact maximal k-mismatch substring length. Figure 10 compares the average maximal k-mismatch substring length for varying substitution probabilities (a) as estimated with our heuristic and (b) calculated with a slow and exact algorithm. The figure shows that our heuristic is clearly suboptimal. But the goal of our project was not so much to precisely estimate the maximal k-mismatch substring lengths, but rather to define a distance measure on sequences that can be efficiently calculated and that can be used to obtain biologically meaningful results. Therefore, we think that the discrepancies between the optimal substring lengths and the values estimated by our heuristic are acceptable. Figure 10 suggests, however, that better estimates of the k-mismatch common substring lengths might improve the sensitivity of kmacs on divergent sequence sets because the curves for the exact solutions converge at higher substitution frequencies. In fact, on the mitochondrial genomes that we used as benchmark data, an exact algorithm led to better phylogenetic trees than our greedy heuristic (Supplementary Material). Therefore, it may be worthwhile to develop heuristics that approximate the maximal k-mismatch substring lengths more accurately.

Fig. 10.

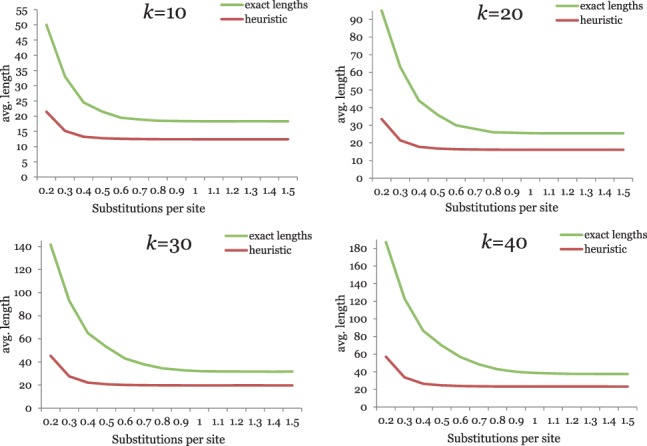
Average common k-mismatch substring lengths depending on the substitution frequency in simulated DNA sequences, estimated with our greedy heuristic (lower curve) and calculated with an exact algorithm (upper curve) for various values of k

6 CONCLUSION

Most alignment-free approaches to sequence analysis are based on exact word matches. In this article, we presented a novel alignment-free algorithm that takes mismatches into account. This is similar in spirit to the spaced-words approach that we previously proposed (Leimeister et al., 2014). But while spaced words uses word pairs of a fixed length with possible mismatches at pre-defined positions, kmacs considers maximal substring matches with k mismatches at arbitrary positions. In the spaced-words approach, the number of match positions in the underlying patterns is a critical parameter for the performance of the method. In contrast, in kmacs, there seems to be a fairly large range of values for k that lead to high-quality results, as shown by our test results. kmacs seems therefore less sensitive to user-defined parameters.

The implementation of our approach using generalized enhanced suffix arrays enables us to analyse large sequence sets efficiently. Still, the program K_r is roughly one order of magnitude faster than kmacs. One reason for this is that K_r uses one single generalized suffix tree representing all input sequences, which can be calculated in time proportional to the number of sequences (Domazet-Lošo and Haubold, 2009). In contrast, kmacs calculates one generalized enhanced suffix array for each pair of sequences, so its run time is quadratic in the number of sequences. On the other hand, calculating suffix arrays for two sequences at a time is less memory consuming, as one does not need to keep the suffix array for all input sequences simultaneously in main memory. Thus, our approach can be applied to larger datasets than K_r.

The two approaches that we developed, kmacs and spaced words, are slower than the corresponding approaches based on exact matches, ACS and the generic k-mer approach. Our new approaches, however, produce significantly better results than those established methods. Our test results suggest that spaced words performs slightly better than kmacs on genomic sequences, whereas on protein sequences, kmacs is superior.

In our program evaluation, we used DNA sequence sets with large evolutionary distances. On these sequences, our new alignment-free methods performed better than established methods that rely on exact word matches. Algorithms using exact matches, on the other hand, seem to work better on smaller evolutionary distances. K_r, for example, performs best on evolutionary distances of up to 0.6 substitutions per site (Haubold et al., 2009). Similarly, we observed that on closely related DNA sequences, kmacs produces sometimes best results with k = 0, i.e. without mismatches (unpublished results). It seems therefore best to apply kmacs to distantly related sequence sets, while methods such as K_r and ACS may be preferred on evolutionarily more closely related sequences.

In biological sequences, substitutions are more frequent than insertions and deletions. Consequently, exact matches between local homologies can usually be extended until the first substitution is reached. The average length of longest common substrings and of shortest unique substrings, respectively, can therefore be used to estimate substitution probabilities (Haubold et al., 2009). This is similar for kmacs as long as k is small enough. In this case, all k mismatches are likely to be used up in a k-mismatch common substring extension before the first indel occurs. Thus, the average length of the longest k-mismatch common substrings depends on the frequency of mismatches and could be used to estimate substitution probabilities, just as in K_r.

In contrast, if k is sufficiently large, substring matches between local homologies are essentially extended until the first indel occurs. From this point on, the mismatch frequency is high and the remaining mismatches will be used up quickly. So in this situation, the average k-mismatch substring length depends on the frequency of indels rather than on the frequency of substitutions. This may explain why ACS and K_r work well on closely related sequences, while kmacs is superior on distantly related sequences where the frequency of indels may be a better measure for evolutionary distances than the frequency of mismatches.

In our study, we used alignment-free methods to reconstruct phylogenetic trees and evaluated the quality of these trees. But phylogeny reconstruction is only one important application of sequence comparison. Clustering, classification and remote-homology detection are other fundamental challenges in DNA and protein sequence analysis. With the rapidly growing size of sequence databases, alignment-free methods have become indispensable for these tasks (Comin and Verzotto, 2012; Hauser et al., 2013; Lingner and Meinicke, 2006). Given the speed of kmacs and the quality of the phylogenetic trees that we could produce with it, our approach should be useful not only for fast phylogeny reconstruction, but also for other tasks in comparative sequence analysis.