Abstract
Recently, we proposed a new algorithm of accelerated barrier optimization compressed sensing (ABOCS) for iterative CT reconstruction. The previous implementation of ABOCS uses gradient projection (GP) with a Barzilai-Borwein (BB) step-size selection scheme (GP-BB) to search for the optimal solution. The algorithm does not converge stably due to its non-monotonic behavior. In this paper, we further improve the convergence of ABOCS using the unknown-parameter Nesterov (UPN) method and investigate the ABOCS reconstruction performance on clinical patient data. Comparison studies are carried out on reconstructions of computer simulation, a physical phantom and a head-and-neck patient. In all of these studies, the ABOCS results using UPN show more stable and faster convergence than those of the GPBB method and a state-of-the-art Bregman-type method. As shown in the simulation study of the Shepp-Logan phantom, UPN achieves the same image quality as those of GPBB and the Bregman-type method, but reduces the iteration numbers by up to 50% and 90%, respectively. In the Catphan©600 phantom study, a high-quality image with relative reconstruction error (RRE) less than 3% compared to the full-view result is obtained using UPN with 17% projections (60 views). In the conventional filtered-backprojection (FBP) reconstruction, the corresponding RRE is more than 15% on the same projection data. The superior performance of ABOCS with the UPN implementation is further demonstrated on the head-and-neck patient. Using 25% projections (91 views), the proposed method reduces the RRE from 21% as in the FBP results to 7.3%. In conclusion, we propose UPN for ABOCS implementation. As compared to GPBB and the Bregman-type methods, the new method significantly improves the convergence with higher stability and less iterations.
Keywords: iterative reconstruction, compressed sensing, total variation, first-order optimization
I. Introduction
Iterative reconstruction algorithms have been increasingly used in different CT imaging applications.(Xia et al., 2011; Han et al., 2011; Nett et al., 2010; Sidky et al., 2011; Ouyang et al., 2011; Choi et al., 2010; Ye et al., 2011) As compared to the conventional filtered-backprojection (FBP) algorithms, iterative reconstruction shows advantages on image artifact reduction when projection data are heavily undersampled or highly noisy (Han et al., 2012; Bian et al., 2010). In this paper, we propose an improved implementation of an iterative CT reconstruction algorithm that was recently developed in our group (Niu and Zhu, 2012).
With a linear model, x-ray projections can be approximated as the production of the object linear attenuation coefficient distribution with the system projection matrix. As the measurement data become fewer, the image solution to the linear equation is underdetermined. Recent studies have shown that artifacts from reduced data measurements (such as view aliasing in few-view reconstruction) are effectively suppressed by searching for the solution that has the minimum total variation (TV) and complies with the data fidelity constraints (Tian et al., 2011; Bian et al., 2010; Sidky and Pan, 2008; Chen et al., 2010). The success of these TV minimization approaches can be justified by the compressed sensing (CS) theory (Candes et al., 2006). CS indicates that sparse signals can be well recovered from reduced data measurements by L-1 norm minimization. As the gradient operation sparsifies CT images (Sidky et al., 2006; Chen et al., 2010), one embodiment of CS in CT reconstruction is to minimize the L-1 norm of the image gradient, i.e. the TV of the image.
Despite the superior reconstruction performance, TV minimization with data fidelity constraints requires intense computation. A more efficient approach is to convert the problem into a TV-regularization based optimization and to solve using a standard non-negative programming method (Park et al., 2012). In TV minimization, the image quality is controlled by the data fidelity tolerance ε, while in TV regularization, the main algorithm parameter is the penalty weight λ on the TV term. With proper settings of ε and λ values, these two approaches are equivalent to each other and obtain the same mathematically optimal solution (Pan et al., 2009). A main disadvantage of TV regularization is that the parameter λ needs to be carefully tuned for different scans, as the optimal λ value is dependent on both the projection noise level and the TV of the true image. On the contrary, the optimal ε value in TV minimization can be accurately estimated directly from the projection data, if noise is dominant in projection errors and the statistics is known (Niu and Zhu, 2012; Lauzier and Chen, 2012).
To achieve a high computational efficiency while retaining the feature of consistent algorithm parameter settings, we recently proposed a new optimization framework of accelerated barrier optimization compressed sensing (ABOCS) reconstruction for cone-beam CT (CBCT) (Niu and Zhu, 2012). In ABOCS, the TV minimization formulation is first converted into a TV regularization based framework with an automatically tuned penalty weight on the data fidelity term. The problem is then efficiently solved using a gradient method. In the published ABOCS implementation, we used gradient projection (GP) with an adaptive Barzilai-Borwein (BB) step-size selection scheme (GP-BB) (Niu and Zhu, 2012). Although a high computational efficiency has been demonstrated on preliminary studies, the GP-BB algorithm is empirical and its convergence is not guaranteed (Barzilai and Borwein, 1988). In this work, we further improve the ABOCS implementation using a modified Nesterov method (Nesterov, 1983). The monotone convergence behavior of Nesterov method, which has been proven in the literature (Jensen et al., 2011), leads to reduced iterative numbers as well as more reliable stopping criteria. A faster computational speed is also achieved due to the more stable convergence. The method is evaluated on both simulation and phantom studies. We finally present the first results of patient studies using ABOCS reconstruction.
II. Method
II.A. The ABOCS framework
The derivation of ABOCS starts from the TV minimization framework with a data fidelity constraint (Sidky and Pan, 2008; Chen et al., 2008), as shown below:
| (1) |
where the vector b⃗ with a length of Nd (i.e., number of detector pixels) represents the line integral measurements (i.e., after the logarithmic operation on the raw projections), M is the system matrix modeling the forward projection, f⃗ is the vectorized patient image to be reconstructed with a length of Ni (i.e., number of image voxels), ||•||2 calculates the L2-norm in the projection space and ||•||TV is the TV term defined as the L1-norm of the spatial gradient image. The user-defined parameter ε is an estimate of total measurement errors.
When statistical noise is dominant in the projection after data correction for deterministic errors, it is possible to estimate ε based on the properties of a known statistical distribution. For example, ε can be accurately estimated from the measured projections, if the measured raw projection obeys Poisson statistics (Zhu et al., 2009a; Choi et al., 2010; Wu et al., 2003; Lauzier and Chen, 2012). Effective scatter correction changes the noise variance of the projections, but a precise estimation of ε is still feasible based on the raw data and the scatter-to-primary ratio (SPR) (Zhu et al., 2009a). As such, the algorithm parameters of Eq. (1) are consistent for different datasets. Nevertheless, the practical use of TV minimization is hindered by its intense computation due to the fidelity constraint. To accelerate the reconstruction, in ABOCS, we convert Eq. (1) into a form similar to that of the conventional TV-regularization based algorithm using a logarithmic barrier method: (Lobo et al., 1998)
| (2) |
Eq. (2) is convex (Boyd and Vandenberghe, 2004) and therefore can be minimized efficiently using gradient-based algorithms. Note that, Eq. (2) is equivalent to an optimization problem with the combined TV and data fidelity objective and an automatically adjusted penalty weight on the data fidelity term. Though requiring a slightly longer reconstruction time than the conventional least-square form with a fixed penalty weight, ABOCS uses consistent algorithm parameter values and is therefore more convenient for practical use. More details of the method derivation and its features can be found in Ref. (Niu and Zhu, 2012).
II.B. The Unknown-parameter Nesterov (UPN) algorithm
In Ref. (Niu and Zhu, 2012), we solve Eq. (2) using the gradient projection (GP) with an adaptive Barzilai-Borwein (BB) step-size selection scheme (Barzilai and Borwein, 1988; Zhou et al., 2006; Park et al., 2012). In spite of the high computational efficiency at each iteration, the empirical GP-BB method has a non-monotone convergence behavior, resulting in a sub-optimal performance on reconstruction time (Jensen et al., 2011). In search of an updating scheme with an improved convergence rate, the Nesterov algorithm becomes a viable option (Nesterov, 1983). Among all the first-order approaches, the Nesterov algorithm has been proven to monotonically converge at the optimal rate if the objective function has an Lipschitz continuous gradient (which implies a continuously differentiable function) and is strongly convex (Nesterov, 1983).
The Nesterov’s method is guaranteed to converge for a continuous and strongly convex objective function (Nesterov, 1983). A direct use of the Nesterov algorithm to solve Eq.(2), however, is hindered by two issues. First, the classic Nesterov algorithm explicitly requires the Lipschitz constant (L) and the strong convex constants (σ), which are used to quantify the continuity and convexity of the objective function, as the input parameters. In iterative CT reconstruction, these two parameter values are difficult to compute due to the large-size and ill-posed system matrix, as well as the singularities in the TV calculation. To circumvent the difficulty in finding the two unknown parameters, we implement the unknown parameter Nesterov (UPN) method as recently proposed by Jensen et al (Jensen et al., 2011). At each Nesterov iteration, we estimate the L value using a backtracking line search scheme and adjust the σ value using a heuristic formula (Jensen et al., 2011). The backtracking strategy approximates the Lipschitz constant by iteratively increasing the estimate until the continuity of the objective function is satisfied. The heuristic formula chooses the decremental σvalue that satisfies the convexity condition of the objective function in each iteration. Details of the UPN algorithm derivation can be found in Ref. (Jensen et al., 2011).
Secondly, the logarithmic term in the objective in Eq.(2), Fdata, is not differentiable at the location where . Therefore, we need to modify the objective function around and outside the singular point of Fdata without affecting the solution of the optimization framework. In this paper, we use a linear function with a large and finite positive slope to replace the segment of the logarithmic function that has infinite values. Figure 1 shows the linear function (dashed line) and the logarithmic function (solid line). To make the objective continuously differentiable, we design the linear function to be tangent to the log-barrier function at the connection (i.e, the same slope and function value at the tangent point). The modified logarithmic term is thus written as:
| (3) |
where and Δ is a user-defined parameter that controls the slope of the linear function.
Fig. 1.
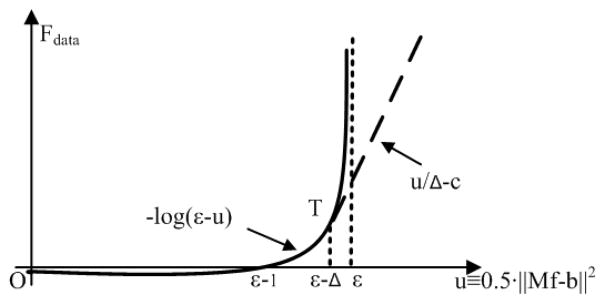
Illustration of the modified logarithmic term (Eq.(3)).
The resultant objective function becomes:
| (4) |
and the optimization problem (Eq.(2)) is re-written as:
| (5) |
Eq.(5) is then solved using the UPN algorithm.
Note that, as seen in Fig. 1, the linear function is used for solutions outside of the solution pool (i.e. when ). The purpose of the modification is to ensure the objective is differentiable such that the algorithm can rapidly converge to the solution pool. Once the estimated solution satisfies the data fidelity condition (i.e. ), the linear function does not affect the value of the objective. The objective function essentially becomes the original log-barrier function. As such, the proposed modification improves the convergence without affecting the result of ABOCS reconstruction using the original log-barrier objective.
II.C. Pseudo code for ABOCS with the UPN implementation
In summary, we present the pseudo-code of the UPN approach for ABOCS as below. The following list summarizes the variables in our code:
Nmax: maximum number of iterations;
L and σ: estimated Lipschitz constant and strong convex constant;
L0 and σ0: initial estimates of the Lipschitz constant and strong convex constant;
sL: magnification factor on L in each step of backtracking;
θ: square root of the ratio between σ and L;
β: intermediate variable in the Nesterov method;
i: index of the detector pixel;
I0(i): intensity of the flat field at pixel i;
stop: stopping criteria, a constant designated by the user;
μ: user-defined parameter to account for the data error other than Poisson noise;
ε: estimated total noise variance of the line integrals;
Δ: user-defined parameter that controls the slope of the linear function (see Fig. 1).
The symbol := means assignment. Both image and data space variables are denoted by a vector sign, e.g., f⃗ and b⃗.
| 1: | ; Nmax: = 1000; L0 = 103, σ0 = 20, stop :=−0.999, , sL:= 1.3, Δ:=0.02ε control parameters |
| 2: | h⃗0 : = f⃗0: = FDK or ART initial image |
| 3: | for k=1, Nmax do main loop |
| 4: | ; |
| 5: | ; (• denotes element-wise multiplication between two vectors) |
| 6: | f⃗old:= f⃗, |
| 7: | if δh >ε − Δ, λ: = 1/Δ; else λ: = 1/(ε − δh); end if; calculate the regularization weight outside and inside the feasible solution set, respectively. |
| 8: | ; gradient of the objective as a function of f⃗ |
| 9: | f⃗ := (h⃗ − L−1∇F)+ ; update image and set non-negativity |
| 10: | while |
| 11: | L = sL · L; |
| 12: | f⃗:= (h⃗ − L−∇F)+ ; |
| 13: | end; backtracking to find the Lipschitz constant L |
| 14: | |
| 15: | |
| 16: | β: = θ(1 − θ)/(θ2 + θnew) |
| 17: | , θ: = θnew, σold: =σ; |
| 18: | if stopping criteria |
| 19: | return f⃗; |
| 20: | break; |
| 21: | end if; |
| 22: | end for; |
The parameters in line 1 control the whole algorithm. Their typical values or ranges are shown in the code, which are used to acquire the results in this paper. The initial guess image is generated using the standard FBP-based Feldkamp-Davis-Kress (FDK) reconstruction (Feldkamp et al., 1984) or the algebraic reconstruction technique (ART), shown in line 2. A zero initial image leads to the same optimal solution but increases the computation time. The main loop, line 3–21, solves the Eq. (2) using the UPN method with an improved convergence rate. Line 4 and 5 calculate the gradients of TV and data fidelity terms as well as the stopping metric (cos(α)). The formulae of numerical calculations of TV and its gradient can be found in Ref. (Niu and Zhu, 2012). To obtain the gradient of the objective function, we first evaluate the automatic regularization weight based on whether the iteration enters the solution pool or not, shown in line 6 and 7. After computing the gradient of the objective function (line 8), line 9 updates the solution (image) using the reciprocal of L as the step size and sets the non-negativity of the solution (denoted as (•)+ ). Line 10–13 is a backtracking scheme to find an appropriate L value for the objective function. Line 14 updates the strong convex parameter (σ). Line 15–17 is the standard Nesterov optimal first order method to update the intermediate variable (f⃗). If the stopping criteria are satisfied, the iteration stops and returns an optimal image h⃗ (line 19).
Different choices of stopping criteria can be used in our algorithm. In our implementation, we find that the cosine of the angle between the gradient vectors of the data fidelity term and the TV term, cos(α), accurately indicates the optimality of the solution. According to the Karush Kuhn-Tuchker (KKT) conditions, at the optimum, the above two vectors must point in exactly opposite directions, i.e., cos(α)= −1 (Sidky and Pan, 2008). Specifically, cos(α) is calculated as:
| (6) |
where is the gradient of TV term and is the gradient of data fidelity. is an indicator function with the same dimension of the reconstructed image h⃗, defined as: (Sidky and Pan, 2008)
| (7) |
In the studies presented in this paper, we used cos(α)< −0.999 as the stopping criterion. Note that, in our previous GP-BB implementation of ABOCS reconstruction, cos(α) is not used as the stopping criterion due to the instability of the convergence (see the result section for detailed comparisons).
II.D. Evaluation
The performance of the proposed algorithm has been evaluated on a digital Shepp-Logan phantom, the physical Catphan©600 phantom and a head-and-neck patient. The physical phantom data were acquired on our tabletop CBCT system at Georgia Institute of Technology. The geometry of this system exactly matches that of a Varian On-Board Imager (OBI) CBCT system on the True-beam radiation therapy machine. The details of system geometry and hardware parameters can be found in Ref. (Niu and Zhu, 2011). In this study, a fan-beam CT scan, with an illumination width of 1 cm in the vertical direction on the detector, was used to inherently suppress scatter signals. The system was operated in the short-scan mode, with 362 projections covering about 200 degrees of rotation. The same fan-beam geometry was also simulated in the digital phantom study. The reconstructed images have a size of 512×512 pixels with 0.5 mm resolution. The projection data on the head-and-neck patient were acquired on the on-board CBCT system installed on the Varian Clinac 23IX radiation therapy machine (Varian Medical System, Palo Alto, CA). The system was operated in the short-scan mode with a bow-tie filter mounted on the outside of the x-ray collimator. 362 projections were acquired in a 195-degree scan. The reconstructed images have a size of 512×512 pixels with 0.684 mm resolution. We limit our investigations on reducing the artifacts from few-view reconstruction. No pre-processing procedures, including scatter and beam-hardening corrections, were applied on the patient projection data. In all the three studies, the detector has 1024 pixels with 0.388 mm resolution and was down-sampled to 512 pixels with 0.776 mm resolution in the reconstruction to avoid large memory consumption.
We compared the performances of UPN, GP-BB and the Bregman Operator Splitting (BOS) methods (Zhang et al., 2010; Zhang et al., 2011) in the reconstruction of the Shepp-Logan phantom with respect to the image quality and the convergence behavior. BOS is a state-of-the-art optimization algorithm that approximates the solution of a least-square problem and hence eliminates inner iterations required in the classical split Bregman method (Zhang et al., 2010; Zhang et al., 2011). Different noise levels were simulated to test the stability of the proposed algorithm. We then evaluated the ABOCS reconstruction using UPN on the physical phantom and the head-and-neck patient by comparing the results with those of the conventional FBP algorithm.
In the image comparisons, the relative reconstruction error (RRE) of the images compared to the reference, similar to that in Ref. (Zhu et al., 2006), was used as the image quality metric:
| (8) |
where xi is i-th pixel the reconstructed image, and xi0 is the corresponding pixel in the reference image. The FBP and the iterative reconstruction have different noise levels and artifact patterns even if the projection data are sufficient. Therefore, in the phantom and patient studies, we used the ABOCS reconstruction with full views as the reference, instead of the full-view FBP reconstruction.
III. Result
III. A. Digital phantom study
Besides those used by the classic Nesterov method, the main user-controlled parameter of our algorithm is the Δ which controls the slope of the linear function. Δ depends on the value of data fidelity tolerance ε. A very small Δ value significantly increases the sharpness of the objective function and therefore the number of iterations since the step size is greatly reduced due to the enlarged Lipschitz constant. On the other hand, a large Δ applies a strong weight on the TV regularization term, which makes the algorithm fail to enter the pre-defined solution set. In this paper, we correlate Δ as the percentage of ε and use Δ=0.02ε in the presented studies. We find that, in general, a Δ value in the range of 0.01ε ~ 0.03ε achieves superior computation performances.
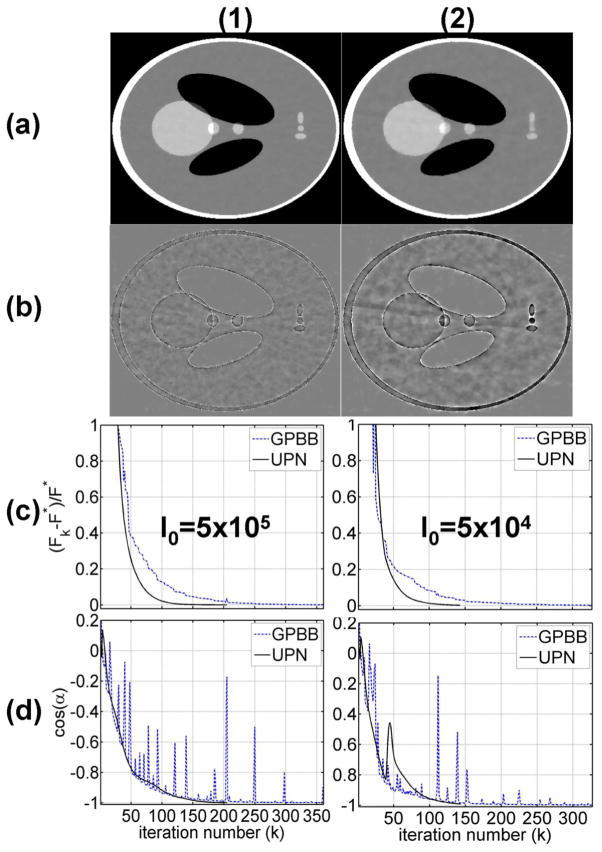
The results on the Shepp-Logan phantom are shown in Fig. 2. Each iteration takes about 0.3 seconds using GPBB and 0.4 seconds using UPN in MATLAB on a Linux workstation with 6 GB memory and a Eight-core Intel Xeon 2.66GHz CPU. Similar computation time is also found in the physical phantom and patient studies. Two different noise levels (i.e. 5×105 and 5×104 photons per ray) are simulated to test the algorithm stability. 5×105 photons per ray is approximately equivalent to a tube current of 80 mA with a 13 ms pulse width, a standard setting of on-board CBCT systems (Niu and Zhu, 2012, 2011). Figs. 2(a) and 2(b) show the ABOCS reconstruction using UPN from 66 projection views and their errors. The algorithm stops at around 200 iterations or less and the RREs for the reconstructed images are 2.0% for Fig. 2(a1) and 2.3% for Fig. 2(a2). Note that, the ABOCS reconstruction using GP-BB has a similar image quality at the same objective function value.
FIG. 2.
Reconstructed images and plots of the objective function and stopping metric values for GPBB and UPN on the digital Shepp-Logan phantom. A total of 66 projections are used in the study. Row (1): using a simulated noise level of I0=5×105 photons per ray; (2): using I0=5×104. Column (a) reconstructed CT image using ABOCS with the UPN implementation, display window: [−500 500] HU; (b) difference image compared with the ground truth, display window: [−100 100] HU; (c) 1d plot of the objective function values versus the iteration number; (d) 1d plot of the stopping metric versus the iteration number.
Figs. 2(c) and 2(d) show the objective function values and the stopping metric (i.e. cos(α)) at different iterations. The results of UPN are compared with those of GP-BB on the same plot. F* denotes the optimal objective value obtained by long iterations (i.e. using a more stringent stopping criterion of cos(α)< −0.999999). It is seen that the UPN algorithm convergences monotonically towards the optimum, a feature missing in the GP-BB implementation. The convergence of UPN is more stable, especially on the stopping metric, which also results in fewer iterations to reach the same objective function value than GP-BB. After about 130 iterations, the relative difference of objective value of UPN drops below 0.4% and the changes in the reconstructed image are no longer visible at a practical gray scale. In both cases, UPN requires about 50% less iterations than GP-BB to obtain the optimal solution.
To further demonstrate the scientific significance, we also compare the proposed algorithm to a recently developed BOS algorithm (Zhang et al., 2010; Zhang et al., 2011). BOS approximates the solution of a least-square problem and hence eliminates inner iterations required in the classical split Bregman method (Goldstein and Osher, 2009). We implement the BOS algorithm for CT reconstruction as a standard least-square problem with a TV regularization term and a carefully-tuned penalty weight. Fig. 3 shows the results obtained by the parameter setting that best compromises efficiency and accuracy of the BOS algorithm. Compared to UPN, BOS requires more iterations to converge (see Fig. 3(c)). On the images reconstructed using the same computation time (Fig. 3), it is seen that UPN achieves smaller reconstruction errors than BOS. Alternatively, BOS takes more iterations to achieve the same optimal solution of UPN. The higher efficiency of UPN compared to BOS is mainly due to the fact that BOS requires restrictive bound on step sizes according to Lipschitz constant of data fidelity term, i.e. the matrix norm of MTM (Zhang et al., 2010). In CT reconstruction, such a step size is too small and causes slow convergence of BOS. On the other hand, UPN adopts Neterov’s optimal gradient technique and uses combination of previous two iterations which yields fast convergence (Nesterov, 1983). As shown in the simulation study of the Shepp-Logan phantom, UPN achieves the same image quality as those of GPBB and the Bregman-type method, but reduces the iteration numbers by up to 50% and 90%, respectively.
FIG. 3.
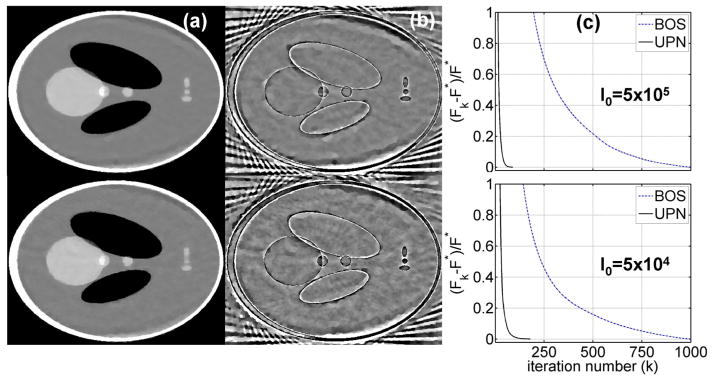
Comparison between BOS and UPN algorithms on the digital Shepp-Logan phantom. A total of 66 projections are used in the study. Row (1): using a simulated noise level of I0=5×105 photons per ray; (2): using I0=5×104. Column (a): reconstructed CT image using BOS with the same computation time as those required to obtain the UPN results shown in Fig. 2(a) (100 seconds for the 1st row and 57 seconds for the 2nd row), display window: [−500 500] HU; (b) difference image compared with the ground truth, display window: [−100 100] HU; (c) 1d plot of the objective function values versus the iteration number.
The reduction of iteration number leads to improvement of computation time. Table 1 compares the computation time for reconstructed images shown in Figs. 2–5 using UPN, BOS and GPBB methods. Note that, we terminate the reconstruction of UPN and GPBB using the same stopping criteria. It is seen that UPN requires less computation time as compared to GPBB. For a better comparison of UPN and BOS on image qualities, we generate the results of BOS reconstruction using the same computation time as that of UPN. As shown in Fig. 3, UPN obtains more accurate reconstruction than BOS with the same computation time. Similar performances of computation time are observed in the following physical phantom and patient studies as well.
Table 1.
Comparison of the computation time (in seconds) for reconstructions shown in Figs. 2–5 using UPN, BOS and GPBB algorithms.
| m Data |
Algorith UPN/BOS | GPBB |
|---|---|---|
| Shepp-Logan I0 = 5 × 105 |
69 | 84 |
| Shepp-Logan I0 = 5 × 104 |
62 | 110 |
| Catphan © 600 | 38 | 47 |
| Head patient | 74 | 125 |
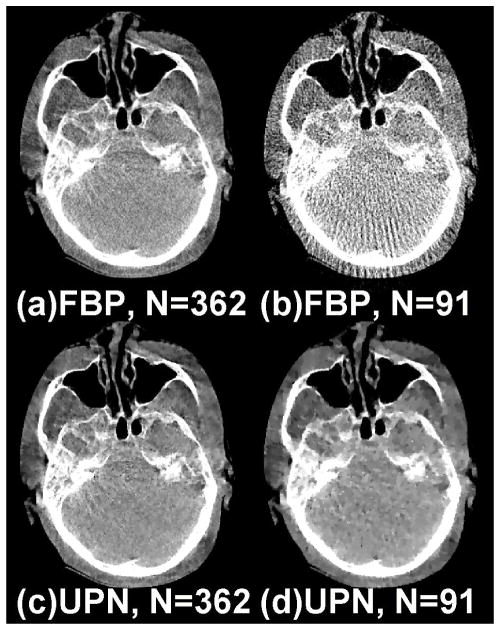
FIG. 5.
Reconstructed head patient images from a 195-deg short-scan mode. (a) FBP: using 362 views; (b)FBP: using 91 views (~25% of the total 362); (c) ABOCS UPN: using 362 views; (d) ABOCS UPN: using 91 views. Window level: [−550 450] HU.
III.B. Catphan © 600 phantom study
We further evaluate the proposed algorithm on the physical phantom. Figure 4 shows the results on the Catphan © 600 phantom. With 60 projection views (about 17% of the total 362 projections from a short scan), the FBP reconstruction has severe view-aliasing artifacts and the RRE compared to the full-view reconstruction is about 15% (see Figs. 4(a) and 4(b)). The ABOCS reconstruction using UPN achieves a comparable full-view image quality (Fig. 4(c)) as that of FBP, and also effectively suppresses the view-aliasing artifacts when the projection views are reduced to 60 (see Fig. 4(d)). The RRE of the few-view reconstruction is 2.4%.
FIG. 4.
Reconstructed Catphan © 600 images from a 200-deg short-scan mode. (a) FBP: using 362 views; (b)FBP: using 60 views (~17% of the total 362); (c) ABOCS UPN: using 362 views; (d) ABOCS UPN: using 60 views. Window level: [−600 400] HU.
III.C. Head-and-neck patient study
This head-and-neck patient study well presents the challenges of iterative CT reconstruction in clinical environments. Besides statistical noise, the projections contain considerable errors from non-ideal effects, including photon scatter, beam hardening and patient motion. Nevertheless, the proposed algorithm still significantly improves the FBP reconstruction. The comparison of reconstructed images is shown in Fig. 5. With 91 views, the FBP reconstruction has an RRE of over 21%. Our algorithm suppresses the streaks from view aliasing and reduces the RRE to 7.3%.
IV. Discussion
In this paper, we propose the UPN algorithm for iterative CT reconstruction using the ABOCS optimization framework. As compared to the previous GP-BB algorithm, the new method significantly improves the convergence stability and reduces the iteration number. The fundamental reason for the improvement is that the GP method converges at a rate inversely proportional to the number of iterations (1/k, where k is iteration number (Jensen et al., 2011)), while the Nesterov approach achieves an optimal convergence rate of (1/k2) (Jensen et al., 2011; Nesterov, 1983).
We modify the objective function to make the UPN algorithm implementable on ABOCS. The main parameter of the modified objective is Δ, which specifies the starting point of the linear function to avoid the singularity of the original logarithmic function. A smallΔresults in a large Lypschitz constant and a small step size (1/L), leading to a slow convergence. On the other hand, a largeΔgives larger step size and but may cause instability during the iteration. In our study, we find that the algorithm is not very sensitive to this parameter in a practical range.
Though demonstrated on 2D reconstructions, the proposed method is readily extendable to 3D cone-beam CT reconstruction. To overcome the impediments of large memory use and intensive computation in 3D reconstruction, we will implement the UPN algorithm based on the hardware acceleration techniques including graphics-processing-unit (GPU) (Jia et al., 2010) or cloud computing (Meng et al., 2011). The feasibility of the GPU implementation of ABOCS reconstruction has been demonstrated in our previous study (Niu and Zhu, 2012). We will further evaluate the performance of the ABOCS reconstruction using UPN on more patient studies. Data correction procedures, such as scatter correction (Niu et al., 2012; Niu et al., 2010; Zhu et al., 2009b) and noise suppression (Zhu et al., 2009a; Wang et al., 2006; Tang and Tang, 2012), will be applied to make our method more valuable in clinical applications. Dose evaluations are important to make studies of iterative reconstruction more complete. We will perform future studies to investigate the relationship between the image quality and imaging dose in a similar way as in Refs. (Yan et al., 2012), (Leipsic et al., 2010) and (Marin et al., 2010).
V. Conclusion
We propose UPN for the ABOCS iterative CT reconstruction. The algorithm has been evaluated on both simulated and physical phantoms. As compared to the previous GPBB and the state-of-the-art BOS algorithm, the new method significantly improves the convergence with higher stability and reduces the total iterations by more than 50% and 90%, respectively. As demonstrated in both phantom and patient studies, the proposed algorithm effectively suppresses view-aliasing artifacts in few-view reconstruction.
Acknowledgments
This work is partially supported by the NIH under the grant number 5R21EB012700-02, and a Varian MRA grant.
References
- Barzilai J, Borwein JM. 2-Point Step Size Gradient Methods. Ima J Numer Anal. 1988;8:141–8. [Google Scholar]
- Bian JG, Siewerdsen JH, Han XA, Sidky EY, Prince JL, Pelizzari CA, Pan XC. Evaluation of sparse-view reconstruction from flat-panel-detector cone-beam CT. Phys Med Biol. 2010;55:6575–99. doi: 10.1088/0031-9155/55/22/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd SP, Vandenberghe L. Convex optimization. Cambridge University Press; 2004. [Google Scholar]
- Candes EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. Ieee T Inform Theory. 2006;52:489–509. [Google Scholar]
- Chen GH, Tang J, Leng SH. Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35:660–3. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GH, Tang J, Nett B, Qi ZH, Leng SA, Szczykutowicz T. Prior Image Constrained Compressed Sensing (PICCS) and Applications in X-ray Computed Tomography. Curr Med Imaging Rev. 2010;6:119–34. [Google Scholar]
- Choi K, Wang J, Zhu L, Suh TS, Boyd S, Xing L. Compressed sensing based cone-beam computed tomography reconstruction with a first-order method. Med Phys. 2010;37:5113–25. doi: 10.1118/1.3481510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC, Kress JW. Practical Cone-Beam Algorithm. J Opt Soc Am A. 1984;1:612–9. [Google Scholar]
- Goldstein T, Osher S. The Split Bregman Method for L1-Regularized Problems. Siam J Imaging Sci. 2009;2:323–43. [Google Scholar]
- Han X, Bian JG, Ritman EL, Sidky EY, Pan XC. Optimization-based reconstruction of sparse images from few-view projections. Phys Med Biol. 2012;57 doi: 10.1088/0031-9155/57/16/5245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han XA, Bian JG, Eaker DR, Kline TL, Sidky EY, Ritman EL, Pan XC. Algorithm-Enabled Low-Dose Micro-CT Imaging. Ieee T Med Imaging. 2011;30:606–20. doi: 10.1109/TMI.2010.2089695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen TL, Jorgensen JH, Hansen PC, Jensen SH. Implementation of an optimal first-order method for strongly convex total variation regularization. BIT Numer Math. 2011;51:1–28. [Google Scholar]
- Jia X, Lou YF, Li RJ, Song WY, Jiang SB. GPU-based fast cone beam CT reconstruction from undersampled and noisy projection data via total variation. Med Phys. 2010;37:1757–60. doi: 10.1118/1.3371691. [DOI] [PubMed] [Google Scholar]
- Lauzier PT, Chen GH. Characterization of statistical prior image constrained compressed sensing. I. Applications to time-resolved contrast-enhanced CT. Med Phys. 2012;39:5930–48. doi: 10.1118/1.4748323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leipsic J, Nguyen G, Brown J, Sin D, Mayo JR. A Prospective Evaluation of Dose Reduction and Image Quality in Chest CT Using Adaptive Statistical Iterative Reconstruction. Am J Roentgenol. 2010;195:1095–9. doi: 10.2214/AJR.09.4050. [DOI] [PubMed] [Google Scholar]
- Lobo MS, Vandenberghe L, Boyd S, Lebret H. Applications of second-order cone programming. Linear Algebra Appl. 1998;284:193–228. [Google Scholar]
- Marin D, Nelson RC, Schindera ST, Richard S, Youngblood RS, Yoshizumi TT, Samei E. Low-tube-voltage, high-tube-current multidetector abdominal CT: improved image quality and decreased radiation dose with adaptive statistical iterative reconstruction algorithm--initial clinical experience. Radiology. 2010;254:145–53. doi: 10.1148/radiol.09090094. [DOI] [PubMed] [Google Scholar]
- Meng B, Pratx G, Xing L. Ultrafast and scalable cone-beam CT reconstruction using MapReduce in a cloud computing environment. Med Phys. 2011;38:6603–9. doi: 10.1118/1.3660200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesterov Y. A method for unconstrained convex minimization problem with the rate of convergence O(1/k2) Doklady AN USSR (translated as Soviet Math Docl) 1983 [Google Scholar]
- Nett BE, Brauweiler R, Kalender W, Rowley H, Chen GH. Perfusion measurements by micro-CT using prior image constrained compressed sensing (PICCS): initial phantom results. Phys Med Biol. 2010;55:2333–50. doi: 10.1088/0031-9155/55/8/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu TY, Al-Basheer A, Zhu L. Quantitative cone-beam CT imaging in radiation therapy using planning CT as a prior: First patient studies. Med Phys. 2012;39:1991–2001. doi: 10.1118/1.3693050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu TY, Sun MS, Star-Lack J, Gao HW, Fan QY, Zhu L. Shading correction for on-board cone-beam CT in radiation therapy using planning MDCT images. Med Phys. 2010;37:5395–406. doi: 10.1118/1.3483260. [DOI] [PubMed] [Google Scholar]
- Niu TY, Zhu L. Scatter correction for full-fan volumetric CT using a stationary beam blocker in a single full scan. Med Phys. 2011;38:6027–38. doi: 10.1118/1.3651619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu TY, Zhu L. Accelerated barrier optimization compressed sensing (ABOCS) reconstruction for cone-beam CT: Phantom studies. Med Phys. 2012;39:4588–98. doi: 10.1118/1.4729837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang L, Solberg T, Wang J. Effects of the penalty on the penalized weighted least-squares image reconstruction for low-dose CBCT. Phys Med Biol. 2011;56:5535–52. doi: 10.1088/0031-9155/56/17/006. [DOI] [PubMed] [Google Scholar]
- Pan XC, Sidky EY, Vannier M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction? Inverse Probl. 2009;25 doi: 10.1088/0266-5611/25/12/123009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park JC, Song BY, Kim JS, Park SH, Kim HK, Liu ZW, Suh TS, Song WY. Fast compressed sensing-based CBCT reconstruction using Barzilai-Borwein formulation for application to on-line IGRT. Med Phys. 2012;39:1207–17. doi: 10.1118/1.3679865. [DOI] [PubMed] [Google Scholar]
- Sidky EY, Duchin Y, Pan XC, Ullberg C. A constrained, total-variation minimization algorithm for low-intensity x-ray CT. Med Phys. 2011;38:S117–S25. doi: 10.1118/1.3560887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky EY, Kao CM, Pan XH. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J X-Ray Sci Technol. 2006;14:119–39. [Google Scholar]
- Sidky EY, Pan XC. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol. 2008;53:4777–807. doi: 10.1088/0031-9155/53/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang SJ, Tang XY. Statistical CT noise reduction with multiscale decomposition and penalized weighted least squares in the projection domain. Med Phys. 2012;39:5498–512. doi: 10.1118/1.4745564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian Z, Jia X, Yuan KH, Pan TS, Jiang SB. Low-dose CT reconstruction via edge-preserving total variation regularization. Phys Med Biol. 2011;56:5949–67. doi: 10.1088/0031-9155/56/18/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Li T, Lu HB, Liang ZR. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography. Ieee T Med Imaging. 2006;25:1272–83. doi: 10.1109/42.896783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T, Stewart A, Stanton M, McCauley T, Phillips W, Kopans DB, Moore RH, Eberhard JW, Opsahl-Ong B, Niklason L, Williams MB. Tomographic mammography using a limited number of low-dose cone-beam projection images. Med Phys. 2003;30:365–80. doi: 10.1118/1.1543934. [DOI] [PubMed] [Google Scholar]
- Xia D, Xiao X, Bian J, Han X, Sidky EY, De Carlo F, Pan X. Image reconstruction from sparse data in synchrotron-radiation-based microtomography. Rev Sci Instrum. 2011;82 doi: 10.1063/1.3572263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan H, Cervino L, Jia X, Jiang SB. A comprehensive study on the relationship between the image quality and imaging dose in low-dose cone beam CT. Phys Med Biol. 2012;57:2063–80. doi: 10.1088/0031-9155/57/7/2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye XJ, Chen YM, Huang F. Computational Acceleration for MR Image Reconstruction in Partially Parallel Imaging. Ieee T Med Imaging. 2011;30:1055–63. doi: 10.1109/TMI.2010.2073717. [DOI] [PubMed] [Google Scholar]
- Zhang XQ, Burger M, Bresson X, Osher S. Bregmanized Nonlocal Regularization for Deconvolution and Sparse Reconstruction. Siam J Imaging Sci. 2010;3:253–76. [Google Scholar]
- Zhang XQ, Burger M, Osher S. A Unified Primal-Dual Algorithm Framework Based on Bregman Iteration. J Sci Comput. 2011;46:20–46. [Google Scholar]
- Zhou B, Gao L, Dai YH. Gradient methods with adaptive step-sizes. Comput Optim Appl. 2006;35:69–86. [Google Scholar]
- Zhu L, Bennett NR, Fahrig R. Scatter correction method for X-ray CT using primary modulation: Theory and preliminary results. IEEE Trans Med Imaging. 2006;25:1573–87. doi: 10.1109/tmi.2006.884636. [DOI] [PubMed] [Google Scholar]
- Zhu L, Wang J, Xing L. Noise suppression in scatter correction for cone-beam CT. Med Phys. 2009a;36:741–52. doi: 10.1118/1.3063001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L, Xie YQ, Wang J, Xing L. Scatter correction for cone-beam CT in radiation therapy. Med Phys. 2009b;36:2258–68. doi: 10.1118/1.3130047. [DOI] [PMC free article] [PubMed] [Google Scholar]