Longitudinal design considerations to optimize power to detect variances and covariances among rates of change: Simulation results based on actual longitudinal studies

Abstract

We investigated the power to detect variances and covariances in rates of change in the context of existing longitudinal studies using linear bivariate growth curve models. Power was estimated by means of Monte Carlo simulations. Our findings show that typical longitudinal study designs have substantial power to detect both variances and covariances among rates of change in a variety of cognitive, physical functioning, and mental health outcomes. We performed simulations to investigate the interplay among number and spacing of occasions, total duration of the study, effect size, and error variance on power and required sample size. The relation between growth rate reliability (GRR) and effect size to the sample size required to detect power ≥ .80 was non-linear, with rapidly decreasing sample sizes needed as GRR increases. The results presented here stand in contrast to previous simulation results and recommendations (Hertzog, Lindenberger, Ghisletta, & von Oertzen, 2006; Hertzog, von Oertzen, Ghisletta, & Lindenberger, 2008; von Oertzen, Ghisletta, & Lindenberger, 2010), which are limited due to confounds between study length and number of waves, error variance with GCR, and parameter values which are largely out of bounds of actual study values. Power to detect change is generally low in the early phases (i.e. first years) of longitudinal studies but can substantially increase if the design is optimized. We recommend additional assessments, including embedded intensive measurement designs, to improve power in the early phases of long-term longitudinal studies.

Most questions in the study of developmental and aging-related processes pertain to “change” in systems of variables and across different time scales. Typical longitudinal studies focus on change processes over months and years while “intensive measurement” studies examine change and variation across much shorter periods of time (e.g. Walls, Barta, Stawski, Collyer, & Hofer, 2011). While the design of particular longitudinal studies relies on both theoretical rationale and previous empirical results, there is general agreement that longitudinal data are necessary in order to approach questions regarding developmental and aging-related change within individuals (e.g. Bauer, 2011; Hofer & Sliwinski, 2006; Schaie & Hofer, 2001). Optimally, the design of the longitudinal study will provide estimates of reliable within-person change and variation in the processes of interest.

In order to model individual differences in change in longitudinal settings, multilevel models are a frequent choice (Laird & Ware, 1982; Raudenbush & Bryk, 2002) because they allow the flexible specification of both fixed (i.e., average) and random effects (i.e., individual departures from the average effect). The degree to which individuals change differently over time is in the variance of a time-based slope, which can be expanded to covariances in the multivariate case involving two or more processes over time (e.g. MacCallum, Kim, Malarkey, & Kiecolt-Glaser, 1997; McArdle, 1988). The covariance among the random slopes provides information whether, and how strongly, these processes are associated. For example, Hofer et al. (2009) report associations among individual differences in level, rate of change, and occasion-specific variation across subscales of the Developmental Behavior Checklist (DBC) in a sample (N = 506) aged 5–19 years and at four occasions over an 11-year period. Correlations among the five DBC subscales ranged from .43 to .66 for level, .43 to .88 for linear rates of change, and .31 to .61 for occasion-specific residuals, with the highest correlations observed consistently between Disruptive, Self-Absorbed, and Communication Disturbance behaviors. In addition to the mean trends (Einfeld et al., 2006), the pattern of these interdependencies among dimensions of emotional and behavioral disturbance provide insight into the developmental dynamics of psychopathology from childhood through young adulthood.

The power to detect the variance and covariance of variables over time is a fundamental issue in associative and predictive models of change. While a number of authors have dealt with questions of sample size planning and power in the context of longitudinal studies (e.g. Hedeker, Gibbons, & Waternaux, 1999; Kelley & Rausch, 2011; Maxwell, 1998; Maxwell, Kelley, & Rausch, 2008; B. O. Muthén & Curran, 1997), relatively few have specifically addressed the power to estimate individual differences in change and associations among rates of change (but see Hertzog, Lindenberger, Ghisletta, & von Oertzen, 2006; Hertzog, von Oertzen, Ghisletta, & Lindenberger, 2008; von Oertzen, Ghisletta, & Lindenberger, 2010).

The estimation of power to detect change and correlated change in longitudinal designs requires consideration of a number of critical parameters, each having potential differential effects on the results. Briey, following early work by Willett (1989), we differentiate between parameters which are not typically under control of the researcher, such as the variability of change over time (i.e., individual differences in slope ${\sigma }_S^2$), the correlation between changes over time (i.e., covariance of slopes σ_SySx), the measurement error variance (${\sigma }_{\epsilon }^2$), and features of the study design that are modifiable such as the sample size (N), the spacing and number of measurement assessments, and the total span or duration of the study. These parameters and design features are directly linked to the reliability to detect individual growth curves (cf. Willett, 1989), which is partly given by the reliability of the measures but can be considerably altered by the study design.

Hence, the purpose of this work is to cast light on the interplay among different factors which contribute to the detection of individual differences in and among rates of change. It is important to know how our decisions regarding longitudinal designs impact power to detect certain effects. In this regard it is of special interest to identify features of the study design that are modifiable and which can be used to optimize power and with it sample size requirements. An important tool to identify the relevant parameters and their interplay is the reliability of the growth rate as proposed by Willett (1989).

Growth Rate Reliability (GRR)

The reliability of the growth rate is central to the analysis of change. In the context of longitudinal multilevel models, the first step usually involves the estimation of an intraclass correlation coefficient (ICC), an index of the ratio of between-subject variance (${\sigma }_{\mathit{\text{class}}}^2$) to total variance. This is done by estimating an unconditional means model whereby the variance due to differences between persons in a repeated-measures setting is expressed as a proportion of the total variance ${\sigma }_{\mathit{\text{class}}}^2/({\sigma }_{\mathit{\text{class}}}^2+{\sigma }_{\epsilon }^2)$ (cf. Raudenbush & Bryk, 2002). If the number of measurement occasions is the same for all participants in a study, the ICC can be expanded to obtain a measure of reliability. Thereby, the residual variance (${\sigma }_{\epsilon }^2$) is divided by the number of measurement occasions to obtain the ICC2 estimate (Bliese, 2000). The ICC2 indicates how much of the between-person variation in observed scores is due to true score variation (see also Kuljanin, Braun, & DeShon, 2011).

In order to obtain an estimate of the reliability of the growth rate, Willett (1989) presented an index which bears some similarity to the reliability estimate ICC2. Willett’s index, however, takes into account the design of the study by dividing the residual variance ${\sigma }_{\epsilon }^2$ by the sum of squared deviations of time points (λ) at measurement occasions (w) in W waves, $\mathit{\text{SST}}={\sum }_{w=1}^W{({\lambda }_w-\overline{{\lambda }_w})}^2$. Hence, Willett (1989) defines growth rate reliability (GRR) as

$$\text{GRR}=\frac{{\sigma }_S^2}{{\sigma }_S^2+\left[\frac{{\sigma }_{\epsilon }^2}{\mathit{\text{SST}}}\right]}.$$ (1)

The GRR estimate provides critical information about the capability to distinguish individual differences in the slope parameters but should not be mistaken for an index of reliability of the measurement instrument as “it confounds the unrelated influences of group heterogeneity in growth-rate and measurement precision” (Willett, 1989, p. 595). For instance, in a situation with no individual differences in slope, GRR will be zero even if the reliability of the measurement is high. At the same time, this feature is desirable for the purpose of understanding and identifying critical design parameters because it takes into account the increasing difficulty to detect slope variances as they approach zero. Hence, GRR is well suited for the identification of critical design parameters which influence the ability to detect individual differences in growth rates. As Willett (1989) showed, the reliability of individual growth is dependent on several factors, including the magnitude of interindividual heterogeneity in growth (${\sigma }_S^2$), the size of the measurement error variance (${\sigma }_{\epsilon }^2$) and SST which is dependent on the number of waves (W), the spacing or interval between these waves, and the total duration of a study. Besides the sample size, these five elements all contribute to the power to detect individual differences in and among rates of change. Of special interest is the SST component because it is typically under the control of the researcher.

The same value of SST can be obtained with different designs varying in study length, number of measurement occasions, and different intervals among the measurement occasions. For example, SST=10 can be obtained with five measurement occasions at the years 0, 1, 2, 3, and 4. The same SST could also be obtained with three measurement occasions at the years 0, 2.2, and 4.5 or with seven occasion at approximately 0, 0.6, 1.2, 1.8, 2.4, 3.0, and 3.6 years. On the other hand, SST can result in different values if the same number of measurement occasions cover different time spans. For example, if five equally spaced waves cover four years SST is 10. If five equally spaced waves cover eight years, SST increases to 40, and if five waves cover two years SST reduces to 2.5. Clearly, decisions regarding the study design can have a strong influence on GRR as SST alters the impact of the error variance. Hence, the reliability of the same slope variance can be quite different depending on the study design and Willett (1989) concluded that “with sufficient waves added, the influence of fallible measurement rapidly dwindles to zero” (p. 598). We would add, that any step taken to increase SST, such as adding years and optimizing design intervals, reduce the impact of “fallible measurement” and increase GRR.

The relation of GRR to power, however, remains an open question. It is reasonable to assume that higher GRR will increase power but it is not well understood how these two quantities are related and how manipulations of GRR elements, such as ${\sigma }_S^2,{\sigma }_{\epsilon }^2$, and especially SST-related design factors will affect power to detect variances and covariances of growth rates. Hence, GRR will be used here to define and examine different longitudinal designs and the impact of these decisions on power to detect individual differences in change.

Growth Curve Reliability (GCR)

It is important to differentiate growth rate reliability GRR (Willett, 1989) from growth curve reliability (GCR) defined by McArdle and Epstein (1987) and applied recently by Hertzog et al. (2006, 2008). GCR is defined as (see also Table 2B in McArdle & Epstein, 1987),

$${\text{GCR}}_w=\frac{{\sigma }_I^2+2{\lambda }_w{\sigma }_{IS}+{\lambda }_w^2{\sigma }_S^2}{{\sigma }_I^2+2{\lambda }_w{\sigma }_{IS}+{\lambda }_w^2{\sigma }_S^2+{\sigma }_{\epsilon }^2},$$ (2)

and describes the relation between the expected variance determined by a growth curve model at a particular measurement occasion (w) and the total variance at that same time point. Besides the slope variance, GCR also accounts for the intercept variance and covariance among the intercept and slope in the computation of predicted total variance of a parameter at a particular occasion. Given that GCR relates model predicted true-score to total variance, the ratio provides different estimates for different occasions if ${\sigma }_S^2>0$ and/or σ_IS ≠ 0.

Table 2.

Total change to error variance ratios

	Hertzog et al. (2006, 2008) with ${\sigma }_S^2=25$
Ratio at year	${\sigma }_{\epsilon }^2=100$	${\sigma }_{\epsilon }^2=90$	${\sigma }_{\epsilon }^2=75$	${\sigma }_{\epsilon }^2=50$	${\sigma }_{\epsilon }^2=25$	${\sigma }_{\epsilon }^2=10$	${\sigma }_{\epsilon }^2=1$
$({\sigma }_6^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.025	0.028	0.033	0.050	0.100	0.249	2.493
$({\sigma }_8^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.044	0.049	0.059	0.089	0.177	0.443	4.432
$({\sigma }_{10}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.069	0.077	0.092	0.139	0.277	0.693	6.925
$({\sigma }_{19}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.250	0.278	0.333	0.500	1	2.5	25
	Hertzog et al. (2006, 2008) with ${\sigma }_S^2=50$
$({\sigma }_6^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.050	0.055	0.066	0.100	0.199	0.499	4.986
$({\sigma }_8^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.089	0.098	0.118	0.177	0.355	0.886	8.864
$({\sigma }_{10}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.139	0.154	0.185	0.277	0.554	1.385	13.850
$({\sigma }_{19}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.500	0.556	0.667	1	2	5	50
	Ratios at percentiles from existing studies
	5th		25th	median	75th		95th
$({\sigma }_6^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0:102		0.274	0:465	0.760		2:248
$({\sigma }_8^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.181		0.487	0.826	1.351		3.997
$({\sigma }_{10}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	0.283		0.761	1.291	2.110		6.246
$({\sigma }_{19}^2-{\sigma }_0^2)/{\sigma }_{\epsilon }^2$	1:022		2.748	4:661	7.618		22:547

While GRR remains unaffected by the intercept variance and the related covariance term, GCR provides an index of reliability of the measurement at a given occasion and may result in high values even if there is no variability in the slope (${\sigma }_S^2=0$). GCR is somewhat complementary to GRR, which can produce high reliability even if GCR approaches zero at one occasion. For example, if the intercept (λ_w = 0) approaches the cross-over point of a growth model, most variance at this occasion will due to residual variance and, accordingly, GCR₀ approaches zero. GRR is unaffected by the location of the intercept and its estimate remains constant across a study design.

The commonality between GRR and GCR is in the error variance. Large error variances decrease both reliability indices whereas small error variances increase their magnitude. The ratios upon which these estimates are based, however, are quite different and have distinct interpretations. Also, with a given residual variance, GCR is defined by the size of the true-score variance. In turn, the detrimental effect of unreliable measurements on power can be attenuated in GRR as longitudinal observations or the duration of the study increase.

As such, GCR provides information about the reliability of static measurements but it does not provide information on how well we can distinguish individual differences in growth processes. Hence, if we are interested in understanding which factors contribute to the power to detect individual differences in rates of change we should rely on the reliability of the growth rate, GRR as it includes the most relevant parameters which impact power.

Critique of Power Analyses by Hertzog et al. (2006,2008) and von Oertzen et al. (2010)

Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) estimated the power to detect correlated change and individual differences in change using latent growth curve models. They tested a number of different models by varying sample size, effect size, number of measurement occasions, and growth curve reliability (GCR₀ at the first measurement occasion w(0)) using a simulation approach. The authors concluded from their results that most existing longitudinal studies do not have sufficient power to detect either individual differences in change or covariances among rates of change. For example, with a sample size of 200 and a correlation among the linear slopes of r = .25 in a bivariate growth curve model power did not exceed .80 for study designs with equal or less than six waves in 10 years unless growth curve reliability (GCR₀) was almost perfect at .98 (Hertzog et al., 2006, Figure 1). The outlook was similar for power to detect slope variances (Hertzog et al., 2008). For example, in the case of a four-wave design over the period of six years, the power to detect a significant slope variance in the best condition (${\sigma }_S^2=50$ and N = 500) is only sufficient if the residual variance is 10 (GCR₀ ≥ .91) or smaller. The closing comments in von Oertzen et al. (2010) “persuade [latent growth curve model] LGCM users not to rest on substantive findings, which might be invalid because of inherent LGCM lack of power under specific conditions” (p. 115). However, the identification of individual differences in change and correlated change does not seem to be particularly difficult or rare in practice and the results from these simulation studies (Hertzog et al., 2006, 2008; von Oertzen et al., 2010) do not appear to correspond to actual results. In the following, we provide a critical evaluation of this set of previous simulation-research on the power to detect individual differences in change.

Figure 1.

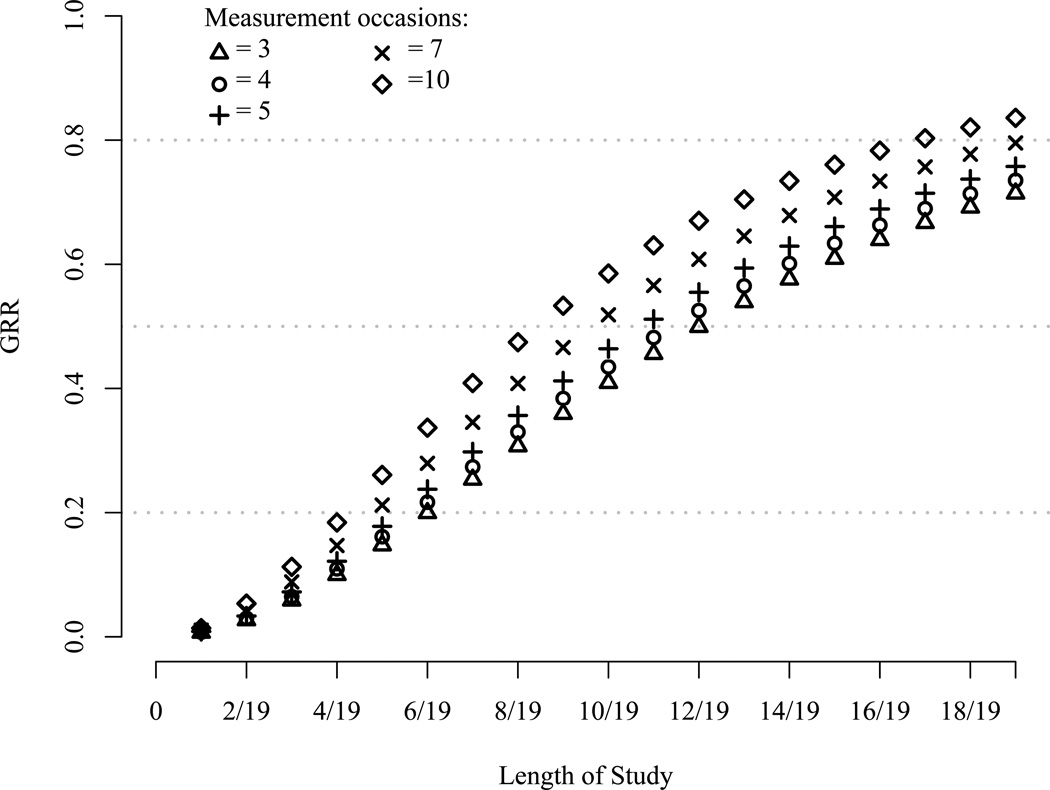
The effect of study length and number of measurement occasions on GRR. The slope variance is ${\sigma }_S^2=50$ and the error variance is ${\sigma }_{\epsilon }^2=10$. Study length is scaled as a one-unit difference comprising 19 years (cf. Hertzog et al. 2006).

Role of GCR on power to detect slope (co-)variances

A key assumption in Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) is that GCR₀ is a primary determinant of power. The authors computed GCR₀ at the first measurement occasion w(0) in order to obtain an estimate of measurement reliability. At the wave where the intercept is defined as λ_w = 0, Equation (2) reduces to the ratio of intercept variance to total variance (${\mathit{\text{GCR}}}_0={\sigma }_I^2/({\sigma }_I^2+{\sigma }_{\epsilon }^2)$). At that specific occasion the ratio bears some similarity to ICC which, however, is based on an unconditional means model and, hence, GCR₀ and ICC usually do not provide the same values.

As discussed earlier, GCR is an index of measurement reliability but does not directly provide information on the ability to detect slope variances. While variations in the intercept and error variance will result in different GCR values, increases or decreases in the slope variance ${\sigma }_S^2$ are not captured by GCR₀ and the index is unaffected by the amount of individual differences in growth rates. GCR₀ does not contain the critical slope-to-error variance ratio and informs only about measurement reliability at the intercept (or at other particular values of time) which can be unrelated to the ability to statistically detect slope variances. GCR can also vary substantially across measurement occasions and is therefore not an invariant index.

Selection of population parameters: Intercept-to-slope variance ratio

Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) framed their simulations using a hypothetical longitudinal study covering 19 years with 20 occasions. The variance of the intercept ${\sigma }_I^2$ defined at the first time point was fixed to 100 and the slope variance ${\sigma }_S^2$ was chosen such that the ratio of total change over true-score variance at the first occasion was either 1:2 or 1:4. Given that the authors used a 0–1 unit scale to cover the full range of 19 years, the slope variance was ${\sigma }_S^2=50$ and ${\sigma }_S^2=25$ accordingly. In the case where the intercept and slope are uncorrelated (σ_IS = 0) their approach yields variance ratios across 20 occasions up to 100:150 $({\sigma }_0^2:{\sigma }_{19}^2\text{for}{\sigma }_S^2=50)\text{and}\mathrm{100:125}({\sigma }_0^2:{\sigma }_{19}^2,\text{for}{\sigma }_S^2=25)$. Table 1 reports ratios of variances $({\sigma }_0^2:{\sigma }_{\mathit{\text{year}}}^2)$ for studies with 6, 8, 10 and the full range of 19 years. These values correspond to the four, five, and six occasion case with a two-year interval and the one case which covered the whole study length of 19 years with one-year intervals (cf. von Oertzen et al., 2010, p.111).

Table 1.

True score variance ratios

	Hertzog et al. (2006, 2008)		Existing studies
Ratio at year	worst (${\sigma }_S^2=25$)	best (${\sigma }_S^2=50$)	5th percentile	median	95th percentile
${\sigma }_0^2:{\sigma }_6^2$	100:102.49	100:104.99	100:103.61	100:119.52	100:222.41
${\sigma }_0^2:{\sigma }_8^2$	100:104.43	100:108.86	100:106.41	100:134.70	100:317.55
${\sigma }_0^2:{\sigma }_{10}^2$	100:106.93	100:113.85	100:110.01	100:154.22	100:439.86
${\sigma }_0^2:{\sigma }_{19}^2$	100:125	100:150	100:136.14	100:295.73	100:1326.42

Note. The ratio of true score variances at different measurement occasions as defined in Hertzog et al. (2006, 2008). The variances are scaled to obtain a total change variance to intercept variance of 1:4 or 1:2.

Hertzog et al. (2006) assumed that they had generated population values which are on the positive side and claimed “…that estimated ratios reported in the literature are generally smaller, in all likelihood making it even more difficult to detect interindividual differences in change” (p. 245). In reality, however, the parameter values selected by Hertzog and colleagues represent, for the most part, unusually small rates of total change to intercept variance. In actual longitudinal studies, ratios of total change to intercept variance seem to be more favorable than the ratios used in these earlier simulations. For example, Lindenberger and Ghisletta (2009, Table 3) report intercept and slope variances for a set of variables from the Berlin Aging Study (BASE; Baltes & Mayer, 1999) which result¹ in variance ratios of ${\sigma }_0^2:{\sigma }_{19}^2=\mathrm{100:221.79}\text{to}{\sigma }_0^2:{\sigma }_{19}^2=\mathrm{100:837.73}$ with a median ratio of ${\sigma }_0^2:{\sigma }_{19}^2=\mathrm{100:397.25}$ indicating that the ratios used in Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) seem to be quite unfavorable.

Table 3.

Description of longitudinal studies and selected variables

Study Title	Start Yr	N (T1)	Age (T1)	Occ Interval	# Occ	Type Sample	Measurements	References
Australian Child to Adult Development Study (ACAD)	1991	578	4–19	4.5, 7.5, 11.3	4	Health, Education, and Family Service agencies that provided services to children with intellectual deficits of all levels	Developmental Behavior Checklist: Disruptive/Antisocial (D); Self-Absorbed (SA); Communication Disturbance (CD); Anxiety (A), Social Relating (SR)	Einfeld & Tonge (1992, 1995, 2002)
English Longitudinal Study of Ageing (ELSA)*	2002	12100	49	2.3, 4.12, 6.19	4	Representative.	Delayed Word Recall (DWR); Prospective Memory (PM); Animal Fluency (AF)	Banks, Breeze, Lessof, & Nazroo (2008); Banks et al. (2010); Huppert, Gardener, & McWilliams (2006); Roth et al. (1986)
Health and Retirement Study (HRS) and AHEAD*	1992	12600	50–60	1.94, 4.10, 6.03, 8.04	5	National sample, minorities oversampled	Immediate (IWRS) and Delayed (DWRS) Word Recall, Subtract 7s (SS); Depressive Symptoms (CESD)	Juster & Suzman (1995); Radloff (1977)
Longitudinal Aging Study Amsterdam (LASA)	1992–1993	3107	55	3.11, 6.08, 9.03, 13.15	5	Stratified random sample of urban and rural municipal registries	Alphabet Coding Task (AlC); Mini-Mental Status Exam (MMSE); Raven Coloured Progressive Matrices (RCPM)	Folstein, Folstein, & McHugh (1975); Huisman et al. (2011); Piccinin & Rabbitt (1999); Raven, Court, & Raven (1995); Savage (1984)
Long Beach Longitudinal Study (LBLS)	1978	509	55–87	3.28, 6.18, 8.41	4	Recruited from Health Maintenance Organization	Letter and Number Series (Reas); STAMAT Recognition Vocabulary (VCB); Composite of Pattern, Number, and Letter Comparison (SPD)	Schaie (1985); Zelinski & Burnright (1997)
Origins of Variance in the Old-Old: Octogenarian Twins (OCTO-Twin)	1990	702	80	2.06, 4.07, 6.04, 8.03	5	Swedish Twin Registry	Memory-in-Reality Free Recall (MiR); Digit Symbol Substitution Test (DST); Koh's Block Design (BlK); Peak Expiratory Volume (PEF)	Cederlöf & Lorich (1978); Cook et al. (1995); Johansson et al. (1999, 2004); McClearn et al. (1997); Wechsler (1991)
Seattle Longitudinal Study (SLS)	1984		55	7.00, 13.63, 21.00	4	Health Maintenance Organization; sequential design	Number Comparison (NC); Word Series Reasoning Test (WST); Word Fluency (WFT); Delayed Word Recall (DWR); Physical Activity from Life Complexity Scale (PHY)	Ekstrom, French, Harman, & Dermen (1976); Schaie (1985); Thurstone & Thurstone (1949)
Victoria Healthy Youth Survey (VHYS)	2003	664	12–18	2.08, 4.05, 6.83	4	Random digit dialing of Greater Victoria area	Brief Child and Family Phone Interview (BCFPI): Anxiety (Anx); Depression (Dep); Oppositional Defiance (OpD); Friends positive and negative activities (FrAc)	Barnes, Mitic, Leadbeater, & Dhami (2009); Cunningham, Boyle, Hong, Pettingill, & Bohaychuk (2009)
Victoria Longitudinal Study (VLS)			55–85	3.06, 6.08, 9.50	4	Community volunteers; sequential design	Simple reaction time (SRT); Word Recall (WRC); Identical Pictures (IPic); Physical Activities (PA); Social Activities (SA)	Dixon & de Frias (2004); Hultsch, Hertzog, Dixon, & Small (1998); Hultsch, Hertzog, Small, & Dixon (1999)

In order to obtain a broader view of change variances in longitudinal studies, we analyzed 35 variables from nine longitudinal studies (cf. Table 4). The lower 5^th and higher 95^th percentile, and median intercept to total change variance ratios for these variables are reported in the right side of Table 1 and yielded, on average, quite large variance ratios. Note that the position of the intercept was shifted to the case where σ_IS = 0 (cf. Stoel & van den Wittenboer, 2003) to obtain ratios that can be compared to those of Hertzog and colleagues.

Table 4.

Descriptive statistics and estimated values from bivariate growth curve models for studies based on three, four, and five waves

Study	y	x	N	${\sigma }_{I_y}^2$	${\sigma }_{S_y}^2$	${\sigma }_{I_x}^2$	${\sigma }_{S_x}^2$	σIySy	σIyIx	σIySx	σSyIx	σSySx	σIxSx	${\sigma }_{\epsilon y}^2$	${\sigma }_{\epsilon x}^2$	σεyεx	Waves	Length
OCTO	BlK	MiR	486	39.630	0.531	4.026	0.138	−0.694	5.817	0.625	0.252	0.162	0.274	9.203	1.894	0.510	3	4.07
OCTO	DST	MiR	433	97.289	1.638	3.533	0.141	−2.317	9.110	1.162	−0.170	0.267	0.306	21.106	1.995	0.512	3	4.07
OCTO	PEF	DST	366	9761.804	49.436	98.967	1.403	−361.767	329.601	3.343	−17.701	3.059	−2.791	2343.186	22.478	0.289	3	4.07
LASA	AlC	MMSE	2571	52.440	0.109	3.325	0.059	0.412	9.900	1.037	0.226	0.036	0.351	5.417	2.795	0.201	3	6.08
LASA	RCPM	AlC	2430	10.983	0.022	50.198	0.101	0.105	16.516	0.131	0.300	0.025	0.115	5.199	5.326	−0.010	3	6.08
ACAD	A	CD	506	6.291	0.039	13.201	0.072	−0.259	4.620	−0.096	−0.175	0.026	0.398	3.867	6.341	1.941	4	11.3
ACAD	A	SR	506	6.270	0.038	7.348	0.035	−0.255	2.949	−0.031	−0.048	0.014	−0.076	3.877	4.660	1.324	4	11.3
ACAD	CD	D	506	13.164	0.070	73.572	0.300	−0.384	18.662	−0.745	−0.577	0.114	−2.438	6.348	21.993	5.957	4	11.3
ACAD	CD	SA	506	13.192	0.071	88.168	0.264	−0.395	15.392	−0.786	−0.393	0.111	−1.849	6.341	21.191	6.030	4	11.3
ACAD	D	SA	506	73.610	0.299	87.869	0.259	−2.454	32.880	−2.020	−0.987	0.248	−1.815	22.034	21.319	13.351	4	11.3
ACAD	D	SR	506	73.366	0.296	7.352	0.034	−2.425	7.747	−0.032	−0.203	0.053	−0.074	22.094	4.663	3.989	4	11.3
ACAD	SA	SR	506	87.962	0.256	7.290	0.035	−1.794	15.919	−0.157	−0.340	0.049	−0.076	21.292	4.676	4.524	4	11.3
ELSA	DWR	AF	11017	261.696	1.410	2463.046	15.530	1.227	549.454	21.609	7.854	2.175	44.304	182.758	1644.878	50.906	4	6.19
ELSA	DWR	PM	10987	259.868	1.475	112.989	1.018	0.900	111.142	0.433	0.675	0.637	−2.749	182.877	230.524	7.914	4	6.19
ELSA	AF	PM	10988	2436.489	15.464	113.482	0.978	40.208	289.294	−1.489	8.825	1.426	−2.820	1648.542	230.514	27.965	4	6.19
LBLS	REAS	SPD	504	122.904	0.358	710.293	1.702	0.034	221.453	2.600	3.145	0.530	5.928	12.886	79.429	2.914	4	8.41
LBLS	REAS	VCB	595	126.211	0.324	103.922	0.394	−0.590	79.494	0.914	−1.359	0.248	−0.272	12.855	12.788	0.314	4	8.41
LBLS	SPD	VCB	508	734.646	1.713	90.687	0.413	9.406	169.857	7.156	1.866	0.486	0.569	80.464	12.884	4.167	4	8.41
SLS	DWR	WFT	765	1400.770	1.539	13192.938	13.953	5.726	2448.552	20.150	−1.563	3.747	−7.692	540.669	3208.648	24.599	4	21
SLS	DWR	NC	766	1395.275	1.480	2105.745	1.691	8.337	752.310	5.176	10.930	0.852	−14.092	541.774	736.465	75.061	4	21
SLS	WFT	NC	783	13132.604	13.000	2103.626	1.598	12.046	2380.849	3.942	32.763	2.940	−13.618	3220.428	743.690	172.179	4	21
SLS	PHY	NC	761	54.125	0.007	2055.156	1.590	−0.444	72.746	1.628	−1.010	−0.045	−14.175	63.798	760.697	2.257	4	21
SLS	PHY	DWR	749	53.352	0.005	1406.833	1.546	−0.400	64.853	1.241	−1.617	0.027	5.016	64.186	546.304	2.153	4	21
VHYS	Anx	Dep	662	3.451	0.044	3.565	0.047	−0.102	1.890	−0.039	0.035	0.022	−0.100	3.220	3.125	0.926	4	6.83
VHYS	Anx	OpD	662	3.441	0.042	3.219	0.029	−0.096	1.240	−0.050	0.045	0.015	−0.103	3.231	2.245	0.609	4	6.83
VHYS	Dep	OpD	662	3.583	0.048	3.220	0.029	−0.102	2.061	−0.066	−0.034	0.023	−0.103	3.115	2.242	0.868	4	6.83
VHYS	Anx	FrAc	662	3.446	0.042	9.600	0.205	−0.098	1.731	−0.343	−0.275	0.055	−0.112	3.233	23.633	0.238	4	6.83
VHYS	Dep	FrAc	662	3.577	0.048	9.636	0.205	−0.105	1.096	−0.301	−0.263	0.036	−0.117	3.120	23.625	0.052	4	6.83
VHYS	OpD	FrAc	662	3.221	0.029	9.602	0.205	−0.104	0.597	−0.024	−0.128	0.023	−0.106	2.246	23.620	−0.069	4	6.83
VLS	RT	WRC	521	2871.932	27.380	14.099	0.056	41.831	−62.296	−3.546	−5.849	−0.591	0.250	2816.220	4.992	−5.299	4	9.5
VLS	RT	IPic	521	2839.340	32.226	28.799	0.838	42.721	−139.087	−2.772	−1.572	−2.940	−0.563	2861.373	17.472	−21.366	4	9.5
VLS	WRC	IPic	522	14.164	0.055	28.989	0.850	0.239	10.101	−0.418	0.301	0.074	−0.656	5.010	17.356	−0.345	4	9.5
VLS	SA	IPic	504	33.556	0.176	28.020	0.898	−0.322	7.423	−0.284	−0.044	0.013	−0.731	12.874	17.494	−0.833	4	9.5
VLS	SA	RT	503	33.611	0.179	2742.526	27.323	−0.327	−17.304	2.364	−2.138	−1.051	23.029	12.843	2769.302	8.736	4	9.5
VLS	PA	RT	503	17.854	0.090	2742.510	27.130	−0.289	−33.759	1.217	−2.792	−0.323	22.341	8.136	2772.468	−7.483	4	9.5
HRS	IWRS	SS	17884	6042.761	19.885	6376.911	13.366	−94.799	3179.747	38.772	−35.270	9.740	4.948	4467.069	3590.358	198.991	5	6.03
HRS	DWRS	SS	17884	6361.483	28.054	6369.391	13.341	−131.150	3035.138	38.917	−39.341	9.911	2.140	4363.758	3591.891	226.381	5	6.03
HRS	CESD	IWRS	18839	2.159	0.014	6200.531	20.298	−0.033	−32.825	0.009	−0.511	−0.024	−103.606	1.632	4489.252	−1.408	5	6.03
HRS	CESD	SS	17819	2.085	0.014	6312.542	12.881	−0.032	−39.164	−0.344	0.256	−0.069	−4.269	1.610	3600.710	−1.607	5	6.03
LASA	RCPM	MMSE	2783	11.845	0.024	3.754	0.054	0.153	4.806	0.282	0.136	0.031	0.229	5.125	2.977	0.212	5	13.15
LASA	RCPM	AlC	2430	11.296	0.024	50.343	0.073	0.062	16.395	0.119	0.359	0.024	0.188	4.885	5.962	0.161	5	13.15
LASA	AlC	MMSE	2571	52.417	0.096	3.579	0.058	0.582	10.204	0.889	0.184	0.056	0.251	5.967	2.996	0.321	5	13.15
OCTO	DST	BlK	429	96.478	0.848	39.210	0.278	−1.517	48.921	−0.207	−0.239	0.375	−0.615	25.984	10.624	3.797	5	8.03
OCTO	DST	MiR	433	95.769	0.801	3.920	0.130	−1.162	9.103	0.919	0.313	0.205	0.143	26.355	2.064	0.846	5	8.03
OCTO	BlK	MiR	486	39.139	0.257	4.320	0.124	−0.457	6.006	0.573	0.219	0.116	0.132	10.659	2.047	0.629	5	8.03
OCTO	PEF	BlK	397	9695.482	39.254	38.904	0.284	−308.506	194.353	−5.023	−3.838	1.063	−0.721	2460.029	10.708	21.892	5	8.03
OCTO	PEF	MiR	568	9748.848	38.954	4.625	0.137	−283.573	40.143	5.377	−3.434	0.764	0.161	2537.874	2.111	0.033	5	8.03
OCTO	PEF	DST	366	9799.248	43.572	98.362	0.795	−331.960	347.794	−3.992	−17.542	3.144	−2.226	2489.178	26.441	6.658	5	8.03

Selection of population parameters: Slope-to-error variance ratio

While in most conditions the magnitude of intercept-to-slope variance ratios were unusually small, the variance ratios in Table 1 are difficult to compare across studies and not interpretable in terms of their impact on power. In reality, the intercept-to-slope variance ratio is not meaningful as it depends on centering and it does not take into consideration the size of the residual variance. The ratio of total change to intercept variance alone, provides little evidence whether the population values are optimistic or pessimistic. It is the size of the residual variance which gauges these values and defines the reliability and ultimately power. Throughout all simulation conditions Hertzog et al. (2006, 2008) used four error variances ${\sigma }_{\epsilon }^2$ (1, 10, 25, and 100) to obtain four prototypical GCR₀ (.99, .91, .80, .50) conditions. However, the simulation results were presented and interpreted using a continuous range of ${\sigma }_{\epsilon }^2=1$ to 100 (cf. Figure 1 in Hertzog et al. 2006, and Figure 2 in Hertzog et al. 2008). There are two relevant issues to consider with the choice of these values.

Figure 2.

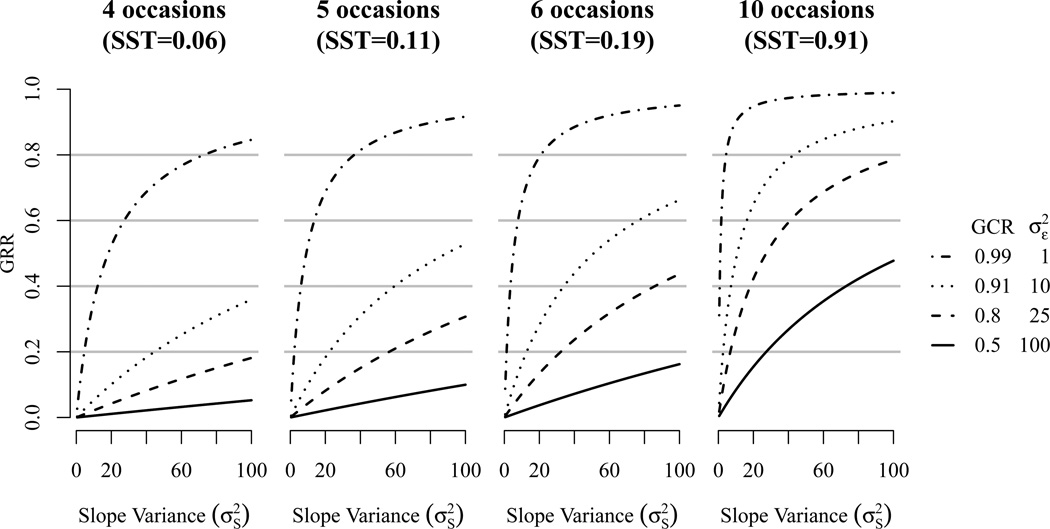
GRR as a function of slope variance (${\sigma }_S^2$) among different numbers of measurement occasions. The four lines are based on four different error variances. The Figure parallels the power plots in Hertzog et al. (2008, Figure 3) and shows how GCR is related to GRR. 4 occasions cover a study duration of 6 years, 5 occasions cover 8 years, 6 occasions cover 10, and 10 occasions cover 18 years.

First, the values in Hertzog et al. (2006, 2008) produce for most simulation conditions slope-to-error variance ratios which are unusually small. Table 2 provides slope-to-error variance ratios for various conditions and study durations in the Hertzog et al. simulations and for a comparable set of ratios obtained from actual studies. In the most favorable case of ${\sigma }_S^2=50$, more than 50% of the slope-to-error variance ratios fall below the range of typically observed ratios. The condition with ${\sigma }_{\epsilon }^2=50$ results in a slope-to-error variance ratio of 1, which is just below the 5^th percentile of ratios observed in existing studies. The condition with ${\sigma }_{\epsilon }^2=10$ results in a ratio of 5, which is close to the median ratio of observed studies and only the best condition with ${\sigma }_{\epsilon }^2=1$ results in a ratio which seems to be more favorable than typically observed. Note also that ${\sigma }_{\epsilon }^2=10$ represents the GCR₀ = .91 condition, indicating that the second best condition in the Hertzog et al. simulation parameters represents an average value within the range of actual studies and variables. For the less optimistic cases where ${\sigma }_S^2=25$, more than 75% of the simulation results are obtained from slope-to-error variance ratios which fall below ratios at the 5^th percentile from actual studies.

Second, the manipulation of error variance was interpreted as a manipulation of GCR₀. In actuality, manipulating slope and residual variance systematically alters GRR as is illustrated in Willett (1989). This is the relevant ratio as it defines the ability to detect individual differences in growth. Note that the same ratio of slope-to-error variance can be obtained within different GCR₀ conditions. For example, if GCR₀ = .91 (${\sigma }_{\epsilon }^2=10$) and σ² = 25 the slope-to-error variance ratio is 25:10. The same ratio can be obtained for the GCR₀ = .80 (${\sigma }_{\epsilon }^2=25$) condition if ${\sigma }_S^2=62.5$. These two different GCR₀ values produce identical ratios and, accordingly GRR remains unaffected by this variation. Hence, GCR₀ is not uniquely related to power and, as such, it is not advisable to follow Hertzog et al.’s (2008) recommendation that

At minimum, researchers should calculate estimates of GCR in their study and evaluate whether it is sufficiently low to raise concerns about power to detect random effects, which could be done to a crude approximation from the simulation results provided in this [Hertzog et al. 2008] study. Generically, our simulation indicates that GCR values under .90 are potentially problematic.” (p.560).

SST: Study-duration, number of occasions, and spacing of occasions

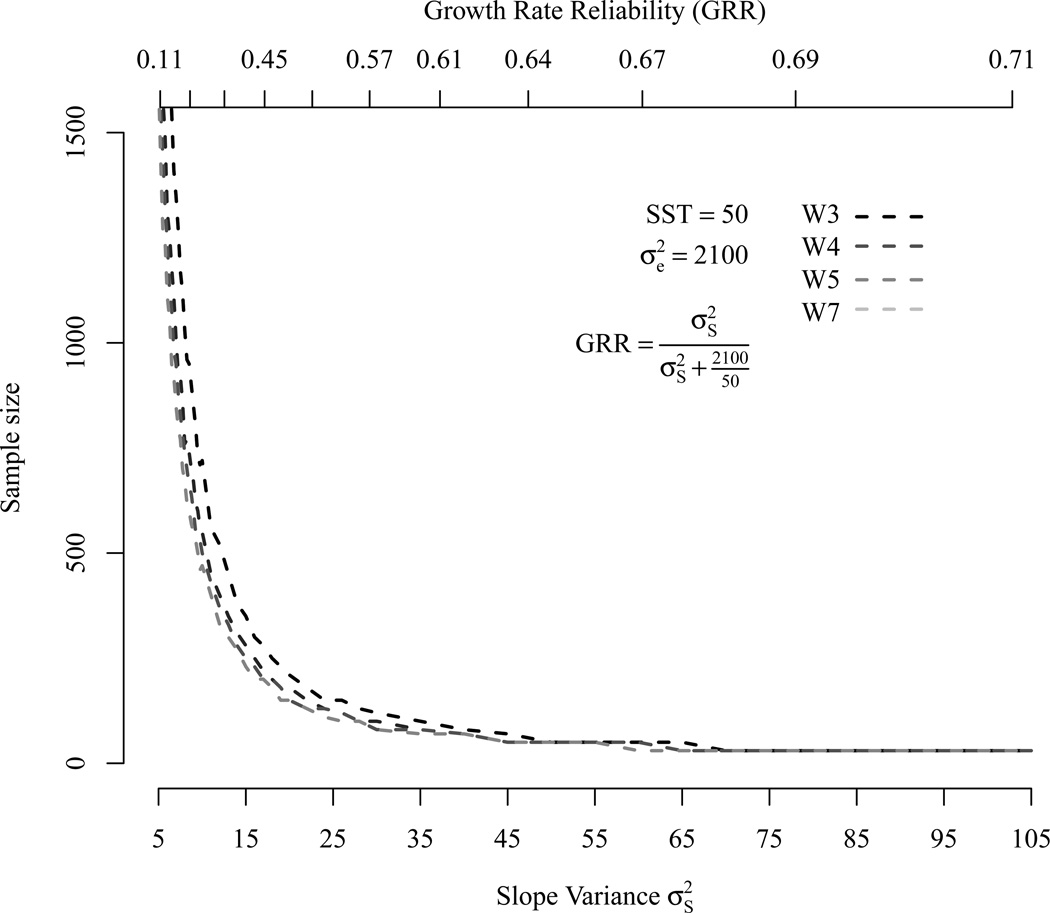
GRR is a function of ${\sigma }_S^2,{\sigma }_{\epsilon }^2$ , and SST whereby the latter is determined by study duration, number of waves, and relative spacing of occasions. In Hertzog et al. (2006, 2008) and von Oertzen et al. (2010), study duration and number of occasions are confounded. The interval between occasions is constant at two years for all conditions (except for the condition where all 20 occasions are presented). As a result, only one of the three facets of SST was systematically manipulated, rendering the results ambiguous with respect to the impact of number of occasions on power. Although the authors concluded from their simulations that number of occasions is a determining factor of power it might as well be argued that it is not the number of measurement occasions but the study length that matters. Given the discussion about the elements of GRR it is clear that study length has an important influence on GRR and on power because it impacts the size of SST. From these previous simulations it remains unknown whether power increased due to more measurement occasions or due to more time covered – or, and probably, both. These factors need to be manipulated independently in order to understand design decisions on power. Unfortunately, however, the Hertzog et al. results convey little information about the interplay of power and design issues such as study length as well as number and spacing of measurement occasions which could have been illustrated even with unusual population parameters. For example, if four waves are administered over six years with ${\sigma }_S^2=50\text{and}{\sigma }_{\epsilon }^2=10$, GRR is .22 (SST=0.05) but increases to .74 (SST=0.56) if the same number of measurement occasions cover the full study length of 19 years. The increase in GRR suggests that covering a longer time period with the same amount of waves has a strong effect on the ability to detect non-zero slope variances. GRR clearly indicates that it is not necessarily the number of waves but also the time covered that can have a beneficial effect on power. Figure 1 illustrates the effect of study duration and number of waves with constant values of ${\sigma }_S^2=50\text{and}{\sigma }_{\epsilon }^2=10$ on GRR. In this example, study length is scaled as a one-unit difference comprising 19 years (cf. Hertzog et al., 2006). Different numbers of measurement occasions are marked with different symbols and range from three to 10 waves within a given amount of time. The effect of increasing study length on GRR under equal numbers of measurement occasions is clearly visible. As more years are covered, GRR increases. At the same time, increasing the number of measurement occasions within the same study length increases GRR as well and both manipulations seem to have a unique effect on GRR.

So far, the above issues treat the impact of various components separately. In reality, a number of interrelating factors that are described in GRR contribute to power. GCR₀, defined by the error variance, is one of them and cannot be considered independently of other values as it reflects only one facet of a number of factors that influence GRR. Figure 2, which mirrors the power plot of Hertzog et al. (2008, Figure 3), illustrates this relation among ${\sigma }_S^2$, GCR₀ (${\sigma }_{\epsilon }^2$), and four different designs. It is clear, that GCR₀ is not uniquely related to power or GRR because altering ${\sigma }_S^2$ also changes the slope-to-error variance ratio and in each of the the four designs SST is different as well. As described previously, the same GRR value is obtained in a number of different GCR₀ conditions and the same GCR₀ condition can result in almost any GRR or power value. For example, a constant value of GCR₀ = .91 yields GRR values that range form 0 to .36 in the four occasions design or from 0 to .90 in the 10 occasions design. Accordingly, power to detect slope variances can take almost any value within a given GCR₀ condition. Figure 2 clearly illustrates that the only value that is uniquely related to power is GRR and it also shows that power is a function of GRR. What remains unknown, however, is the nature of the function that relates power to GRR. Also, the curves illustrate the impact of study-duration with equally-spaced measurement occasions. However, Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) do not indicate the unique impact of study duration, number of measurement occasions, and interval size on GRR.

Figure 3.

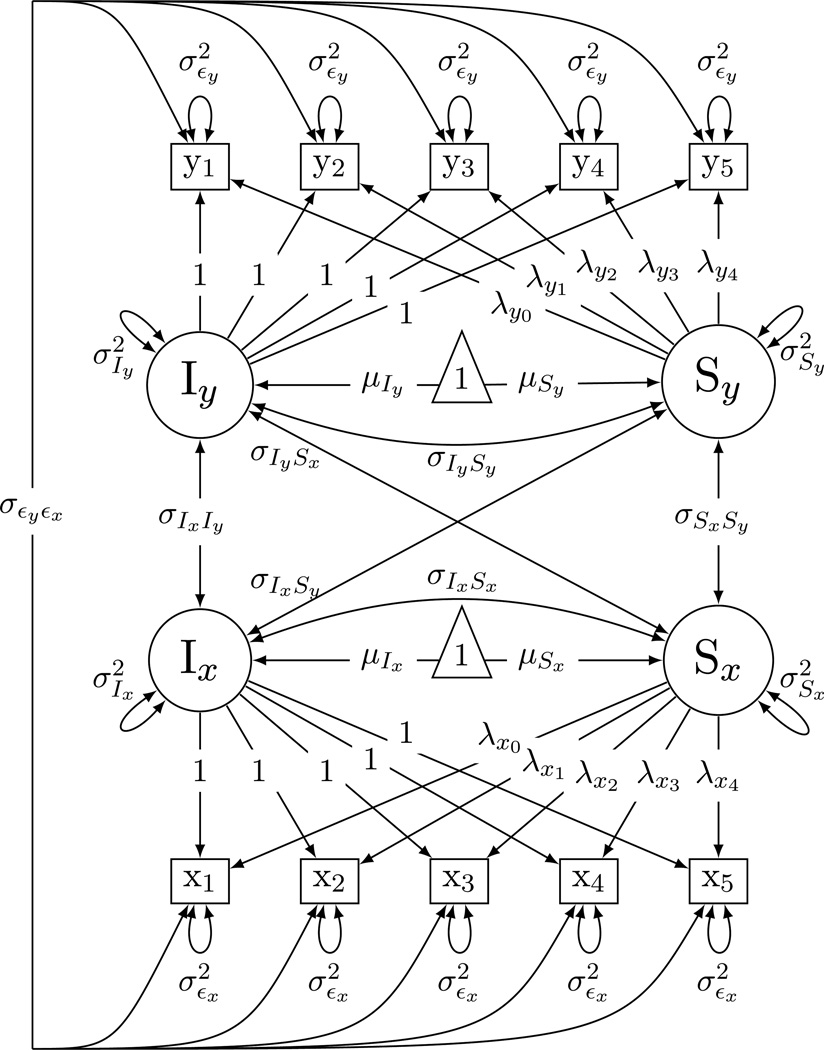
The bivariate latent growth curve model which was used to extract parameter values from existing longitudinal studies. This model was also used to obtain power estimates by means of Monte Carlo simulations.

Aim of the Study

The present study evaluates the power to detect variances and covariances among rates of change in growth curve models using Monte Carlo simulations. We base these simulations on a range of sensible population values from a number of different longitudinal studies comprising early and late life periods and varying in sample size, number of waves, interval lengths, overall study follow-up, variables, heterogeneity of baseline age, and other characteristics of the participants. We examine power across several variable domains that are often the focus within developmental and aging psychology: cognition, affect, physical functioning and dimensions of psychopathology. Together, these studies provide a basis for estimating power as well as a realistic range of population values for further simulation studies.

Our aim is to understand the effect of critical design parameters on power to detect individual differences in growth. GRR, the measure of the reliability of the growth rate proposed by Willett (1989), is used as an index of power to detect individual differences in change but also as a guide to identify the interplay among its elements, slope variance, error variance, number and spacing of waves, and study length. Of special interest are the variables that constitute SST as they are under the control of the researcher conducting a longitudinal study and can be used to optimize power in the early phases of such studies.

Methods

Latent Growth Curve Modeling

Our analyses base on a bivariate linear growth curve (LGC) model where we observe a set of repeated observations on two variables Y and X for individual i in a longitudinal setting with several waves. Let y_i = (y_1i, y_2i, … y_Wi)′ denote the response on Y and x_i = (x_1i, x_2i, …, x_Wi)′ denote the response on X for individual i. The responses are observed according to a set of waves w_i = (1, 2, 3, …, W_i)′, where W_i is the total number of waves for individual i which do not need to be the same for all individuals. A general expression for a time-structured latent curve model for two variables y_i and x_i then is

$${\mathbf{y}}_i={\mathbf{\Lambda }}_{yi}{\mathbf{\eta }}_{yi}={\mathbf{\epsilon }}_{yi}{\mathbf{x}}_i={\mathbf{\Lambda }}_{xi}{\mathbf{\eta }}_{xi}+{\mathbf{\epsilon }}_{xi},$$ (3)

where Λ is the (W_i × p) factor loading matrix with number of rows equal to W_i and where the number of columns is equal to the number of factors or growth parameters (p) estimated in the model (here, p = 2 for each variable). The vector η captures the random effects particular to individual i in the intercept and slope, and ε represents a vector of residuals. We follow standard assumptions where E(ε) = 0 and COV(η, ε) = 0. Further, let E(η) = α, COV(η, η) = Ψ, and COV(ε, ε) = Θ.

In the bivariate LGC model (cf. MacCallum et al., 1997; Tisak & Meredith, 1990, for the general multivariate case) Y and X are modeled simultaneously which is expressed in the means and covariance matrix

$$\mathbf{\mu }=\mathbf{\Lambda }\mathbf{\alpha }$$ (4)

$$\mathbf{\Sigma }=\mathbf{\Lambda }\mathbf{\Psi }\mathbf{\Lambda }\text{'}+\mathbf{\Theta }.$$ (5)

The vector of means α has 2p elements, in the case where we estimate two intercept and two slope parameters the elements in columns 1 and 3 in α pertain to the intercept and the elements in columns 2 and 4 capture the slope of Y and X. Λ defines the loadings (i.e., intercepts and slopes) for both sets of variables with the dimension 2W × 2p and the 2p × 2p covariance matrix Ψ is unstructured leaving the (co-)variances unconstrained

$$\mathbf{\Lambda }=\left[\begin{array}{cccc}1\hfill & {\lambda }_{y_0}\hfill & 0\hfill & 0\hfill \\ 1\hfill & {\lambda }_{y_1}\hfill & 0\hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ 1\hfill & {\lambda }_{y_w}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & {\lambda }_{x_0}\hfill \\ 0\hfill & 0\hfill & 1\hfill & {\lambda }_{x_1}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ 0\hfill & 0\hfill & 1\hfill & {\lambda }_{x_w}\hfill \end{array}\right],\mathbf{\Psi }=\left[\begin{array}{cccc}{\sigma }_{I_y}^2\hfill & \hfill & \hfill & \hfill \\ {\sigma }_{S_y{I}_y}\hfill & {\sigma }_{S_y}^2\hfill & \hfill & \hfill \\ {\sigma }_{I_x{I}_y}\hfill & {\sigma }_{I_x{S}_y}\hfill & {\sigma }_{I_x}^2\hfill & \hfill \\ {\sigma }_{S_x{I}_y}\hfill & {\sigma }_{S_x{S}_y}\hfill & {\sigma }_{S_x{I}_x}\hfill & {\sigma }_{S_x}^2\hfill \end{array}\right].$$

In order to set the intercept at the first wave we assign λ_y0 and λ_x0 the value 0. The loadings λ_W may take different scales, usually they are assigned values which reflect the interval of the measurement occasions but they may be scaled to alternative metrics as well as be individually time-varying. Note that here both variables are measured at the same occasions and, hence, λ_y = λ_x.

In order to account for dependencies across measurements within each wave, we relaxed the condition of uncorrelated residuals and allowed occasion-specific covariances among the residuals across Y and X. The residual covariance matrix with equality constraints across occasion-specific residual covariances is defined as

$$\mathbf{\Theta }=\left[\begin{array}{cccccc}{\sigma }_{{\epsilon }_y}^2\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ 0\hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill \\ ⋮\hfill & ⋮\hfill & {\sigma }_{{\epsilon }_y}^2\hfill & \hfill & \hfill & \hfill \\ {\sigma }_{{\epsilon }_x{\epsilon }_y}\hfill & 0\hfill & \cdots \hfill & {\sigma }_{{\epsilon }_x}^2\hfill & \hfill & \hfill \\ ⋮\hfill & {\sigma }_{{\epsilon }_x{\epsilon }_y}\hfill & 0\hfill & ⋮\hfill & \ddots \hfill & \hfill \\ 0\hfill & \cdots \hfill & {\sigma }_{{\epsilon }_x{\epsilon }_y}\hfill & 0\hfill & \cdots \hfill & {\sigma }_{{\epsilon }_x}^2\hfill \end{array}\right].$$

This bivariate growth model is represented in Figure 3 and it was used to both estimate parameter values from a set of longitudinal studies and served as the basis for all simulations.

Power Estimation

Statistical power is defined as the probability of correctly rejecting the null hypothesis when it is false (Cohen, 1988) which is represented as power (π) = 1 − β where β represents the probability of a Type II error. Statistical power depends on a number of factors such as the Type I error rate, sample and effect size. In the present work we will use the commonly applied values of α ≤ .05 to define statistical significance and values of π ≥ .80 to define sufficient power.

In order to assess the power to detect variance in slopes $({\sigma }_{S_x}^2,{\sigma }_{S_y}^2)$ and covariances among slopes (σ_SxSy) in a first step we estimated the actual power for these parameters in a number of current longitudinal studies. All parameters based on the same bivariate longitudinal growth curve model described in Equation (2) and depicted in Figure 3. The estimates for each combination of variables upon which the simulations were based are reported in Table 4. We used Monte Carlo simulations to estimate the power for each variable combination within the reported longitudinal studies and the sample size needed to obtain power of at least π = .80. For all analyses, the extraction of population values and the estimation of power for different conditions, were based on an annual time scale where one unit represents one year. The choice of an annual time scale is arbitrary and does not change the power estimates but it places the population parameters on a commonly used metric which facilitates their interpretation and comparison to other studies.

In a second step, we systematically varied the number of waves, the interval between waves, the total duration of the study, and the size of the error and slope variance in order to obtain different GRR values. Further we varied the strength of the correlation among the slopes and among the residuals to observe the influence and interplay among these factors on the sample size required to achieve power ≥ .80. The population values for these analyses were derived from the studies reported in Table 4 in order to obtain realistic variance and covariance parameters for the simulation study.

The estimate of power was based on the proportion of statistically significant results relative to the total number of valid replications. For covariances, only covariances with the same sign were counted as hits, that is, if the population covariance was negative and the sample covariance was statistically significant but positive we did not count it as a hit. This decision lead to very slightly lower estimates of power for the covariance term as there were very few cases where population and significant sample covariances differed in sign.

In the estimation of power, the type of statistical test can play an important role. Basically, variances and covariances can be tested via single- or multiparameter tests (cf. Raudenbush & Bryk, 2002). Given that not all tests are equally powerful, the results may change depending on which test one uses to estimate the significance of variances or covariances. Here, we decided to base the majority of our simulation results on the Wald test statistic which is known to typically have lower power primarily because it isolates the effect of the slope variance from related covariances. By relying on the Wald statistic our simulation results may reflect a conservative or worst-case scenario. The Wald test provides the z statistic via the ratio of the parameter estimate divided by its estimated standard error². Hence, the Wald test is based on one parameter no matter whether covariances or variances are tested. In contrast, the likelihood ratio (LR) test, which is typically used in mixed effects modeling (e.g. Pinheiro & Bates, 2000), is based on LR = 2(L₁ − L₀), where L₀ and L₁ are maximized log-likelihood values for an unrestricted and a restricted model. The statistic has an approximate χ² distribution with m degrees of freedom, where m is the difference in the number of parameters between both models (Raudenbush & Bryk, 2002). As long as one covariance is tested, the Wald and LR test both use one parameter and will provide similar results. However, if the significance of variances are tested in models with multiple random effects, the Wald test is based on one parameter whereas the LR test is based on at least two parameters. This is because, in order to define the restricted model, one needs to set the variance and all related covariances to zero. In the present case, where we estimate a bivariate growth curve model, the restricted model uses four df less than the unrestricted model because the test of the variance of S_y requires that we set the following to zero: ${\sigma }_{S_y}^2=0$, σ_SyIy = 0, σ_IxSy = 0, and σ_SxSy = 0.

This important difference between single- and multiparameter tests is the reason why their results can be different if variance components are tested (cf. Berkhof & Snijders, 2001). Accordingly, the Wald test is considered to have less power to detect slope variances compared to the LR test if the relevant covariances are large (e.g. Fears, Benichou, & Gail, 1996; Longford, 1999). As Berkhof and Snijders (2001) have illustrated in the univariate case, the Wald test remains unaffected under different conditions of level/slope correlations whereas the LR test draws much of its power to detect the slope variance via the covariance terms. This result has been replicated by Hertzog et al. (2008) who assumed from their simulation results that the power of the LR test drops to its minimum as the level/slope correlation approaches r = −.10 (p. 551). This only partly reflects the relation among the covariances and power. While it is correct that the lowest power is obtained at a negative correlation, its actual value does not necessarily approach r = −.10 but depends on the growth curve parameters. A LR test will always yield the minimal power at the point where the unrestricted L₀ model and the restricted model L₁ produce the smallest difference. In a univariate LGC model with ${\sigma }_S^2>0$ there is a covariance among σ_IS that nullifies the sum of all growth effects $2\lambda {\sigma }_{IS}+{\lambda }^2{\sigma }_S^2=0$. Resolving for σ_IS results in ${\sigma }_{IS}=-\lambda \frac{{\sigma }_S^2}{2}$. In correlation metric, the correlation among intercept and slope that minimizes power is $r=\frac{-\lambda {\sigma }_S^2/2}{\sqrt{{\sigma }_I^2{\sigma }_S^2}}$ and is always negative (or zero). To illustrate, if the values from Hertzog et al. (2008) are used, the correlations that minimize power in the 4, 5, 6, and 10 occasion study are r₄ = −.11, r₅ = −.15, r₆ = −.19, and r₁₀ = −.35 respectively. Note that these values exactly reflect the findings presented in Figure 1 from Hertzog et al. (2008).

Hence, although the Wald test has known weaknesses and generally results in lower estimates of power (e.g. Fears et al., 1996) we regard it as an informative measure in this present context and we follow Berkhof and Snijders (2001, p. 137) assertion that single parameter tests may be advantageous if the intercept/slope-covariances are of no substantive interest in the study. Given that our primary aim is to obtain distinct power estimates to detect the covariance among rates of change and to detect variances in slopes, we chose to base our simulation studies on the Wald statistic to permit clear conclusions in this regard. Further, the Wald statistic best reflects GRR which only accounts for one parameter, the slope variance, and is independent from covariance effects. In terms of a simulation study, we reiterate that the Wald test may be seen as conservative because it tests variances independently of related covariances and, hence, it does not draw power from this additional source.

To illustrate the differences between the power estimates from the Wald and LR statistic we report both estimates in the Monte Carlo simulations (Table 5). For the estimation of power based on the LR statistic we ran four models for each replication. A baseline model (a) where all parameters were freely estimated and three additional models where (b) the variance term of one slope and its corresponding covariances were fixed to zero (${\sigma }_{S_y}^2=0$, σ_SyIy = 0, σ_IxSy = 0, and σ_SxSy = 0), and (c) the variance term of the other slope with its corresponding covariances fixed to zero (${\sigma }_{S_x}^2=0$, σ_SxIy = 0, σ_SxSy = 0, and σ_SxIx = 0). In the last model (d) the covariance σ_SxSy was fixed to zero. The estimates of power were based on the comparison among models (a) to (b), and (a) to (c) with 4 df and a critical χ² = 9.49 for variances and the model (a) to (d) with 1 df and a critical χ² = 3.84 for covariances.

Table 5.

Power estimates from Monte Carlo simulations based on actual sudy results

					Wald test statistic								LR test statistic
					π with given N for			π = .80, N ≥					π with given N for			π = .80, N ≥
Study	y	x	rSySx	N	rSySx	${\sigma }_{S1}^2$	${\sigma }_{S2}^2$	rSySx	${\sigma }_{S1}^2$	${\sigma }_{S2}^2$	GRRy	GRRx	rSySx	${\sigma }_{S1}^2$	${\sigma }_{S2}^2$	rSySx	${\sigma }_{S1}^2$	${\sigma }_{S2}^2$
OCTO	B1K	MiR	.60	486	.97	.99	1	280	220	150	.32	.38	.97	1	1	275	155	60
OCTO	DST	MiR	.56	433	.97	1	1	250	130	160	.39	.37	.97	1	1	250	155	55
OCTO	PEF	DST	.37	366	.25	.33	.98	1970	1250	200	.15	.34	.26	.81	.95	1850	360	255
LASA	A1C	MMSE	.45	2571	1	1	1	780	330	310	.27	.28	1	1	1	780	190	55
LASA	RCPM	A1C	.53	2430	.78	.44	1	2500	5600	370	.07	.26	.78	1	1	2500	900	360
ACAD	A	CD	.49	506	.99	1	1	240	105	90	.41	.44	.99	1	1	230	130	40
ACAD	A	SR	.38	506	.80	1	1	505	115	160	.40	.34	.81	1	1	500	130	160
ACAD	CD	D	.79	506	1	1	1	90	95	70	.43	.48	1	1	1	80	95	75
ACAD	CD	SA	.81	506	1	1	1	90	90	80	.43	.46	1	1	1	80	90	85
ACAD	D	SA	.89	506	1	1	1	75	70	80	.48	.45	1	1	1	60	65	80
ACAD	D	SR	.53	506	.99	1	1	230	70	165	.48	.33	.99	1	.99	230	80	150
ACAD	SA	SR	.52	506	.97	1	1	280	85	160	.45	.34	.98	1	1	250	100	155
ELSA	DWR	AF	.46	11017	1	1	1	2200	1140	790	.14	.16	1	1	1	2200	640	300
ELSA	DWR	PM	.52	10987	1	1	1	3400	1060	3200	.14	.08	1	1	1	3400	640	2050
ELSA	AF	PM	.37	10988	.95	1	1	6400	790	3400	.16	.08	.96	1	1	5990	300	3400
LBLS	Reas	SPD	.68	504	1	1	1	85	60	80	.53	.46	1	1	1	80	50	55
LBLS	Reas	VCB	.69	595	1	1	1	70	65	50	.50	.55	1	1	1	65	50	35
LBLS	SPD	VCB	.58	508	1	1	1	110	80	50	.46	.56	1	1	1	110	55	35
SLS	DWR	WFT	.81	765	1	1	1	70	110	60	.41	.51	1	1	1	65	55	45
SLS	DWR	NC	.54	766	1	1	1	240	110	145	.40	.36	1	1	1	230	70	130
SLS	WFT	NC	.65	783	1	1	1	130	70	160	.49	.34	1	1	1	135	50	115
SLS	PHY	NC	−.43	761	.17	.05	1	6400	56150	165	.03	.34	.17	.62	1	6300	1050	200
SLS	PHY	DWR	.31	749	.09	.04	1	22000	150000	105	.02	.41	.10	.59	1	22200	1125	80
VHYS	Anx	Dep	.48	662	.81	1	1	660	300	250	.26	.28	.82	1	1	640	260	310
VHYS	Anx	OpD	.43	662	.64	.99	.99	960	330	330	.25	.25	.66	1	.95	950	280	420
VHYS	Dep	OpD	.62	662	.94	1	.99	430	240	325	.28	.25	.94	1	.97	410	275	370
VHYS	Anx	FrAc	.59	662	.81	.98	.83	660	320	635	.25	.18	.81	1	1	660	280	260
VHYS	Dep	FrAc	.36	662	.46	1	.81	1550	245	650	.28	.18	.46	1	1	1550	240	290
VHYS	OpD	FrAc	.30	662	.29	.98	.97	2600	330	620	.25	.18	.29	.97	.97	2600	390	365
VLS	RT	WRC	−.48	521	.91	1	1	370	180	150	.33	.36	.92	1	1	360	90	75
VLS	RT	IPic	−.57	521	1	1	1	110	145	30	.36	.70	1	1	1	105	65	20
VLS	WRC	IPic	.34	522	.96	1	1	300	140	30	.35	.71	.96	1	1	300	75	25
VLS	SA	IPic	.03	504	.06	1	1	35500	105	25	.40	.72	.07	1	1	35200	115	20
VLS	SA	RT	−.48	503	.95	1	1	320	105	170	.41	.33	.95	1	1	320	90	95
VLS	PA	RT	−.21	503	.29	1	1	1950	140	175	.35	.33	.30	1	1	1900	150	110
HRS	IWRS	SS	.60	17884	1	1	1	1450	815	1180	.15	.13	1	1	1	1350	760	540
HRS	DWRS	ss	.51	17884	1	1	1	1380	425	1200	.21	.13	1	1	1	1380	480	530
HRS	CESD	IWRS	−.05	18839	.20	1	1	150000	280	800	.26	.16	.20	1	1	150000	320	1100
HRS	CESD	SS	−.16	17819	.95	1	1	14100	270	1200	.26	.13	.95	1	1	14140	320	1140
LASA	RCPM	MMSE	.86	2783	1	1	1	55	160	30	.33	.65	1	1	1	50	50	15
LASA	RCPM	A1C	.57	2430	1	1	1	140	150	45	.34	.56	1	1	1	140	80	40
LASA	A1C	MMSE	.75	2571	1	1	1	35	35	30	.63	.67	1	1	1	30	25	15
OCTO	DST	B1K	.77	429	1	1	1	55	50	50	.57	.51	1	1	1	50	35	25
OCTO	DST	MiR	.64	433	1	1	1	55	50	25	.55	.72	1	1	1	50	35	15
OCTO	B1K	MiR	.65	486	1	1	1	60	65	25	.49	.71	1	1	1	55	40	15
OCTO	PEF	B1K	.32	397	.76	1	1	440	105	55	.39	.52	.78	1	1	440	100	60
OCTO	PEF	MiR	.33	568	.98	1	1	280	115	25	.38	.72	.98	1	1	275	85	15
OCTO	PEF	DST	.53	366	.99	1	1	140	95	50	.41	.55	1	1	1	130	70	45

Studies and Measures

The simulations reported here are based on parameter estimates drawn from a broad range of longitudinal studies of developmental and aging-related change. Design characteristics of the included longitudinal studies are provided in Table 3 and descriptive statistics are reported in Table 4. Bivariate linear growth models described in Equation (5) were analyzed for each set of outcomes and were used to provide a range of realistic values on which to base an evaluation of power to detect variance in linear slopes and bivariate associations in linear rates of change.

All of the actual longitudinal studies used in this paper had incomplete data due to study attrition. In addition, in longitudinal studies of aging, this attrition is related primarily to dropout due to death. Incomplete data were estimated under the assumption that the data are at least Missing at Random (MAR; where the probability of missing information is related to covariates and previously measured outcomes). Such methods are in regular usage in analysis of longitudinal studies. However, attrition in studies of aging is often non-random, or selective, in that it is likely to result from mortality or declining physical and mental functioning of the participants over the period of observation. In the case of mortality-related dropout, the MAR assumption is likely to be problematic unless age at death is included in the model to account for population selection.

The parameter estimates were obtained using full information maximum likelihood (FIML). We report only linear growth models with fixed time-in-study intervals as the time basis and only models with adequate model fit according to the the comparative fit index (CFI above .95) and the root-mean-square error of approximation (RMSEA below .08; Browne & Cudeck, 1993; MacCallum, Browne, & Sugawara, 1996). Estimates were based on annual rates of change with the intercept specified at baseline. We refrained from using the unit scale transformation applied by Hertzog et al. (2006, and later studies) which covers 19 years because it provides estimates which are uncommon as most researchers scale change in years. The purpose of Table 4 is also to provide an array of actual population values in the most common format. As pointed out earlier, all variance and covariance estimates can be rescaled to be on other time metrics, such as the 0–1 unit scale adopted by these earlier simulation studies, with GRR and power being invariant to such rescaling. Note that our primary aim in the parameter extraction was to obtain a range of realistic values for later use as population values in simulation studies. Hence, we chose to remain with the FIML in order to make full use of the sample sizes and we did not include higher order terms to capture curvilinear changes over time in the few cases where this was indicated.

All of the power estimates in Table 5 were based on 10,000 replications. In order to compute and plot the required N for power of at least π ≥ .80 for given population values we used an iterative approach whereby the final iterations approached π = .80 by steps of N = 10 to ensure sufficient precision. The figures were generated using 5,000 replications in the final iteration steps. All analyses made use of the software package R (Team, 2012) where we relied on the mvrnorm function from the MASS package (Venables & Ripley, 2002) to generate random bivariate samples with the structure given in Equations 4 and 5. The statistical analysis of the LGC models was performed using the freely available structural equation modeling software package OpenMx version 1.2.3 (Boker et al., 2011). In order to check the consistency of the power estimates based on the Wald statistic, we re-ran all models (i.e., data generation and estimation) within the Monte Carlo facility of Mplus (L. K. Muthén & Muthén, 2010). The results from both software packages resulted in close to identical power and sample size estimates. To speed up computing time, all analyses in R were conducted on “Nestor”, a capability cluster geared towards large parallel jobs provided by WestGrid and Compute/Calcul Canada. Sample scripts used in this simulation study are available at the APA website (www.website.com) for download and integration in R or Mplus.

Results

Power Estimates for Actual Study Values

A sample of longitudinal developmental and aging studies was used as a foundation to evaluate power to detect variance in, and associations among, rates of change. Table 4 provides descriptive statistics and estimated values from bivariate growth curve models for a variety of outcomes, including cognitive, physical functioning, and mental health variables. In few cases, particularly in studies with more waves and longer follow-up, quadratic trends were indicated. However, all reported estimates are based on LGC models in order to permit evaluation of linear slope associations and to provide a consistent basis for obtaining LGC parameters for simulation purposes. The values from Table 1 provide the basis for estimating power for particular combinations of variables within actual studies but also for extrapolating to a range of effect sizes, sample sizes, and slope reliabilities. Notably, 95% of the slope-to-error variance in these longitudinal studies ranged from 1:14 to 1:478. The average ratio was 1:335 and the median was 1:81 indicating that the error variance was 81 times larger relative to the slope variance. Accordingly, 95% of GRR ranged from .07 to .71, with a median GRR of .36. For these same variables, 95% of GCR₀ values ranged from 0.33 to 0.90 with a median of .68.

Based on the results of Table 4, Table 5 provides standardized estimates of associations among slopes and power to detect linear slope variances and covariances in bivariate combinations of outcomes. Results from Monte Carlo simulations using both Wald and LR statistics are reported.

Covariance Among Slopes

The correlations among rates of change ranged from −.57 (VLS; RT with IPic) through .03 (VLS; SA with IPic) to .89 (ACAD; D with SA), with an average, absolute correlation of r = |.52|. Power and the sample size needed to obtain power of at least .80 was largely dependent on two factors: The magnitude of the correlation among the slopes (i.e., effect size) and the magnitude of GRR. If any one of these factors was small, sufficient power (π ≥ .80) to detect the covariance was only achieved with large sample sizes. For example, in SLS, the sample size was comparable among the five sets of variable pairs but the power ranged from .09 to 1.0. Power estimates for the covariances appeared to be related to the GRR values of the respective variables. For example, the power to detect the correlation among variables including PHY (GRR ≤ .03) was always very low and there was virtually no chance to detect correlations involving the PHY variable with the available sample size. In turn, the somewhat stronger correlation among DWR and NC in the same study had sufficient power to be detected. Given the simulation results, 240 participants would have been sufficient to detect the statistically significant correlation among the slopes of both variables with π ≥ .80. The main difference in these two examples from Table 5 was in the GRR. Notably, the GRR of the DWR variable was .40 which was considerably larger compared to that of PHY.

Another factor which influenced the power estimate was the number of waves and duration of a study. Note that in Table 5, for the most part, number of measurement occasions and study length was confounded in the sense that more measurement occasions were associated with longer follow-up periods. A clear distinction of the contribution of study length and number of measurement occasions on power is difficult to obtain from Table 5. Nevertheless, analyses of the shorter three-wave designs OCTO and LASA, showed that the number of participants required to obtain sufficient power was much larger compared to the same studies with five waves that covered four to seven more years. The magnitude of this effect was quite remarkable. For example, we estimated the power to detect the significant correlation of .56 among the slopes of DST and MiR in three-waves of OCTO-Twin. The GRR values were at .39 and .37 which is comparably high for a short study with only three waves. Accordingly, power was π = .97 with the actual sample and 250 participants would have been needed to obtain power ≥ .80 to detect the correlation. Four years and two waves later, the same study based on five waves covering eight years had more than sufficient power to detect the correlation among the same two variables (i.e., 55 participants would have been sufficient to detect the correlation of .64 between DST and MiR). The GRR values were now very high with .55 (DST) and .72 (MiR) which, together with the stronger correlation, reduced the required sample size drastically. Similarly, in LASA, the correlation of r = .53 among the slopes of RCPM and AlC was detectable in six years and three waves with an N ≥ 2, 500. In the five-wave design covering the full range of 13.15 years about 140 participants would have sufficed to detect the correlation of r = .57 between RCPM and AlC with π ≥ .80. Note that the associated GRR values increased each by .30 points from .07 (RCPM) and .26 (AlC) to .34 and .56 respectively.

The effect size of the association among the slopes played an important role as well. Small correlations (r = .10) were, if at all, detectable in five-wave studies with more than 7,000 participants such as HRS. Larger effect sizes were associated with higher power. It is important to note that considering one factor alone is not sufficient to obtain an estimate about power. If GRR is small, larger correlations may still not be detectable, such as in the case of VHYS where the correlation of r = .43 among Anx and OpD suffered from low GRR (= .25) values for both variables. Accordingly, the power to detect this specific correlation was moderate and at π = .64 with the available sample size. Note that the power estimates of the covariances were all based on 1 df test and that the results obtained with the Wald and the LR statistic were very close.

Slope Variances

Similar patterns of results were found in the power to detect statistically significant variances although the power to detect variances was in most cases higher compared to the power to detect covariances among linear slopes. Further, a notable difference among the results can be seen for the type of hypothesis test. The power to detect slope variances based on either Wald or LR sometimes resulted in very different results. Note that the Wald statistic for variances is still based on 1 df whereas the LR statistic is now based on 4 df in the bivariate growth model. Notably, the LR-test had more power to detect slope variances if the accompanying covariances were large and positive. The magnitude of this effect was quite remarkable for some situations such as in case of ELSA study. According to the Wald test 790 participants would have been needed to achieve sufficient power to detect the variance of AF. The LR test, in turn, required 300 participants in order to achieve the same power of π = .80 for the same variable. In this case, the LR test drew its power from large associations among the slope of AF and DWR and among its large and positive level and slope covariance which were all medium to large in terms of effect sizes (r_{SAFIDW R} = .34, r_{SAFSDW R} = .46, and r_SAFIAF = .23).

Even though the differences among the Wald and LR statistic were usually not as extreme as in the ELSA data, in most cases the LR test outperformed the Wald statistic in terms of power to detect variances. As described previously, the Wald statistic may be seen as conservative but given that our focus is on slope variances its power estimates can be generalized more easily in the context of this simulation study because the effect of the covariances does not influence, and therefore confound, the power estimate of the variance. Given the Wald statistic, all studies had sufficient power to detect both or at least one of the variances in the given variable combinations.

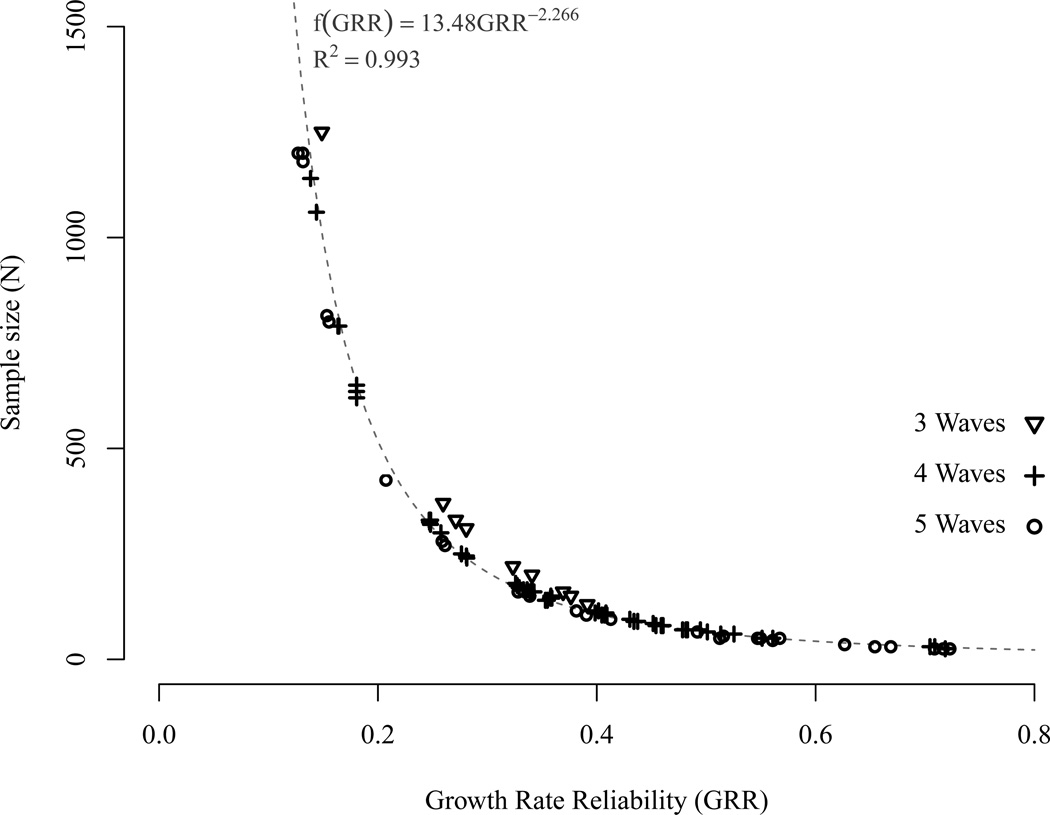
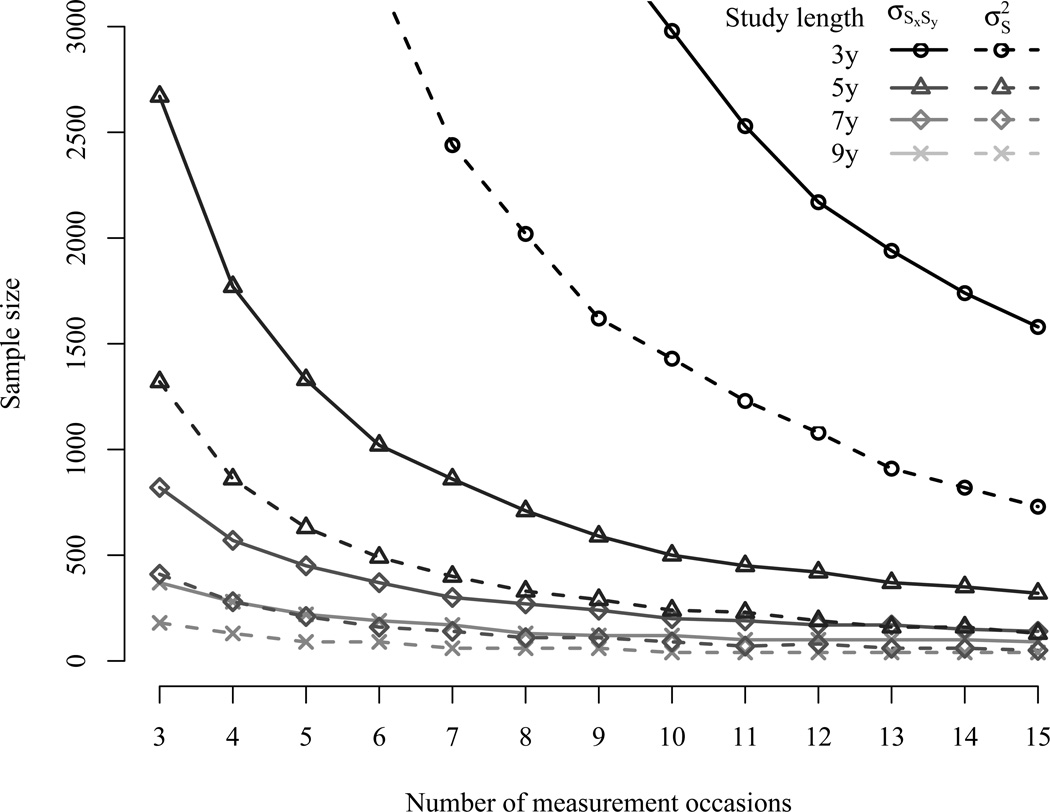
In summary, besides the sample size, design factors such as study length and number of measurement occasions which constitute SST in GRR, influenced the power estimate of the slope variances. To illustrate this relation, in Figure 4, we plotted, for each variable combination reported in Table 5, the sample size needed to obtain power of π ≥ .80 relative to GRR. The number of waves in the studies are represented by the shape of the symbols. Triangles correspond to studies with three waves, squares are for studies with four, and circles correspond to studies with five waves. Each symbol corresponds to an actual estimate within Table 5. Across all studies, the relation among GRR and sample size needed for π ≥ .80 followed a non-linear, asymptotic function with a dramatic decrease in sample size as GRR increased to about .40. For values of GRR above .60 sample size decrements seemed to flatten out and approach an asymptote. A power function (f(GRR) = 13.48GRR^−2.266 with R² = .99) fitted the data points in Figure 4 best and illustrates that GRR is functionally related to the sample size required to obtain a power of π = .80 using a single-parameter test. Even though the non-linear relation seems to hold across all types of studies, three wave designs are discernible from designs with more waves. That is, studies with three waves and short duration seem to require slightly more participants for the same values of GRR compared to four or five wave studies.

Figure 4.

.80 power estimates to detect slope variances given the observed GRR from all variables in the studies reported in Table 5. Each symbol represents the required sample size to achieve a power of .80. Triangles represent studies with three waves, crosses represent studies with four, and circles represent studies with five waves. All values are reported in Table 5. The hatched gray line represents the fitted power function f(GRR) = 13.48GRR^−2.266.

In order to illustrate the effect of GCR on sample size needed to obtain π ≥ .80, we followed Hertzog et al.’s (2006) approach and computed the GCR₀ value at the first measurement occasion where the time scale is defined to be at zero for each variable in Table 5. The relation between GCR and sample size is shown in Figure 5. As in Figure 4 the symbols represent different numbers of waves and each symbol represents one value from Table 5. The visual inspection shows that GCR does not seem to be related to power or sample size estimates, especially for GCR values between .50 and .80. The hatched vertical gray line represents the .90 GCR threshold which, according to Hertzog et al. (2008), should be calculated to identify potentially problematic slope variances. In the present case, practically all variables produce GCR values below the threshold while five variables were at a GCR of .90.

Figure 5.

.80 power estimates to detect slope variances given the observed GCR from all the studies in Table 5. Triangles represent studies with three waves, crosses represent studies with four, and circles represent studies with five waves. The hatched, gray line represents the .90 GCR value. According to Hertzog et al. (2008) values below .90, all values left of the line, are “potentially problematic”.

Simulation Results for Different Cases

Given the observations from Table 5 and Figure 4 as well as the definition of GRR in Equation (1) we systematically varied a number of parameters which are related to the estimation of power to detect change. In the first three cases we manipulated all elements of GRR: SST, ${\sigma }_{\epsilon }^2,\text{and}{\sigma }_S^2$. SST was manipulated via the number of waves, the duration of the study, and the length of the interval among waves. In the last two cases the impact of varying effect sizes of slope covariances and residuals on the power to detect correlated change are investigated. The population values used in the following cases were derived from Table 4 in order to obtain realistic situations and to obtain covariance matrices which were positive definite for all variations of the simulation parameters. These case studies are meant to be instructive as to the potential for altering key elements of the design.

Case 1: The Impact of Design Variations on SST, GRR and Power

The correlation among the slopes in the covariance matrix of the random coefficients was set to r = .50 and the slope variances were both ${\sigma }_{Sy}^2={\sigma }_{Sx}^2=28$. The slope-to-error variance ratio was 1:75 and the intercept to slope variance ratio was 1:180 which is close the median across all reported studies. The effect sizes of the correlations among the intercept and slope were moderate. This covariance matrix reects average values from Table 4 (correlations are in the upper triangle in parentheses):

$$\mathbf{\Phi }=\left[\begin{array}{cccc}\hfill 5040\hfill & \hfill (-0.27)\hfill & \hfill (.48)\hfill & \hfill (.09)\hfill \\ \hfill -100\hfill & \hfill 28\hfill & \hfill (-.08)\hfill & \hfill (.50)\hfill \\ \hfill 2400\hfill & \hfill -29\hfill & \hfill 5040\hfill & \hfill (-.27)\hfill \\ \hfill 32\hfill & \hfill 14\hfill & \hfill -100\hfill & \hfill 28\hfill \end{array}\right].$$

Note that the error variance ${\sigma }_{\epsilon }^2=2100$ and the occasion specific error covariance was set to σ_εyεx = 70 which corresponds to a correlation among the errors of r = .05.

Variable SST and GRR: The Impact of Study Duration and Number of Waves

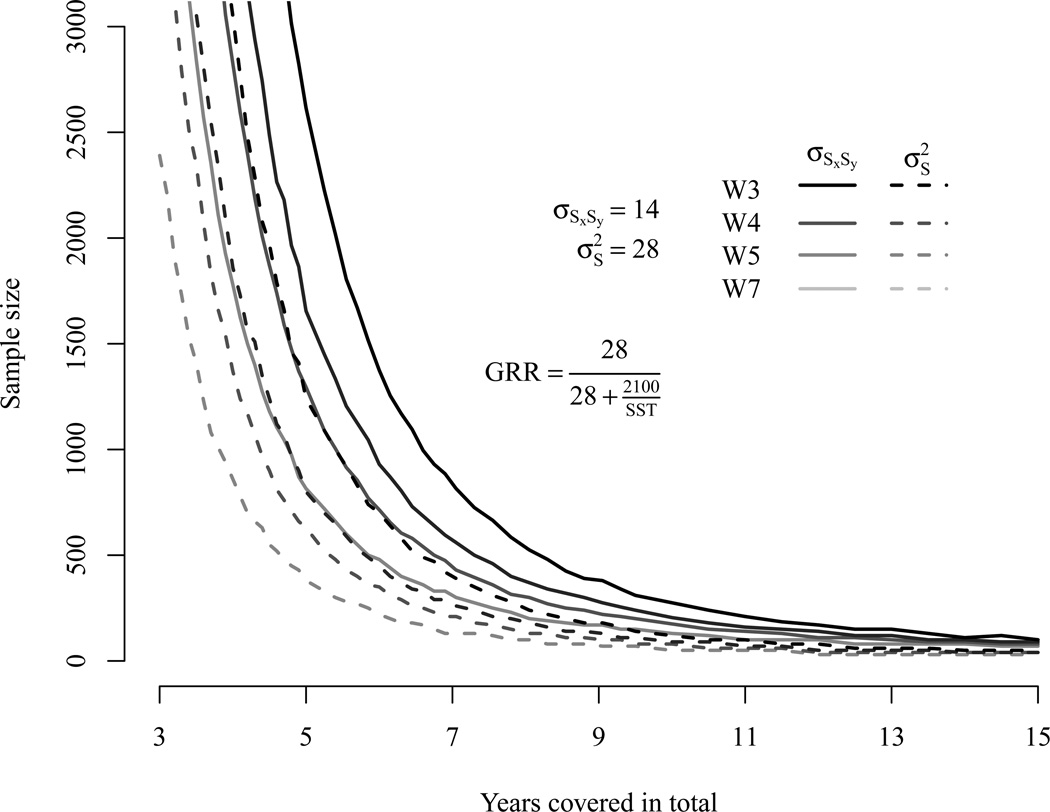
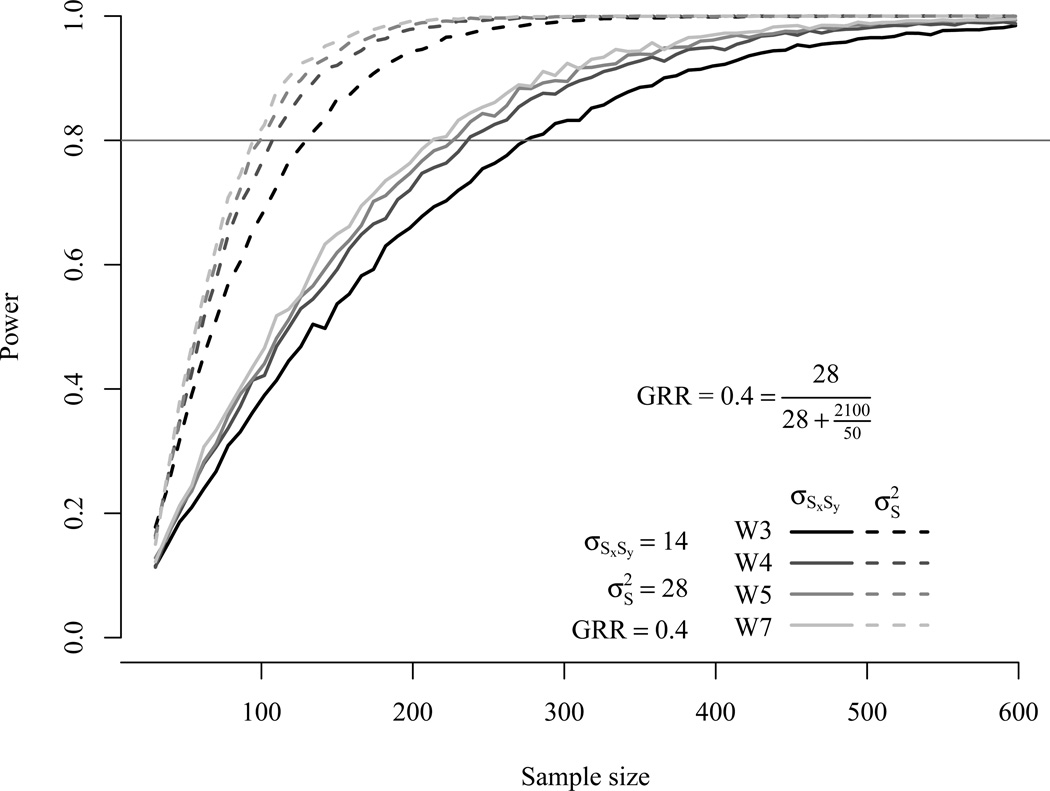
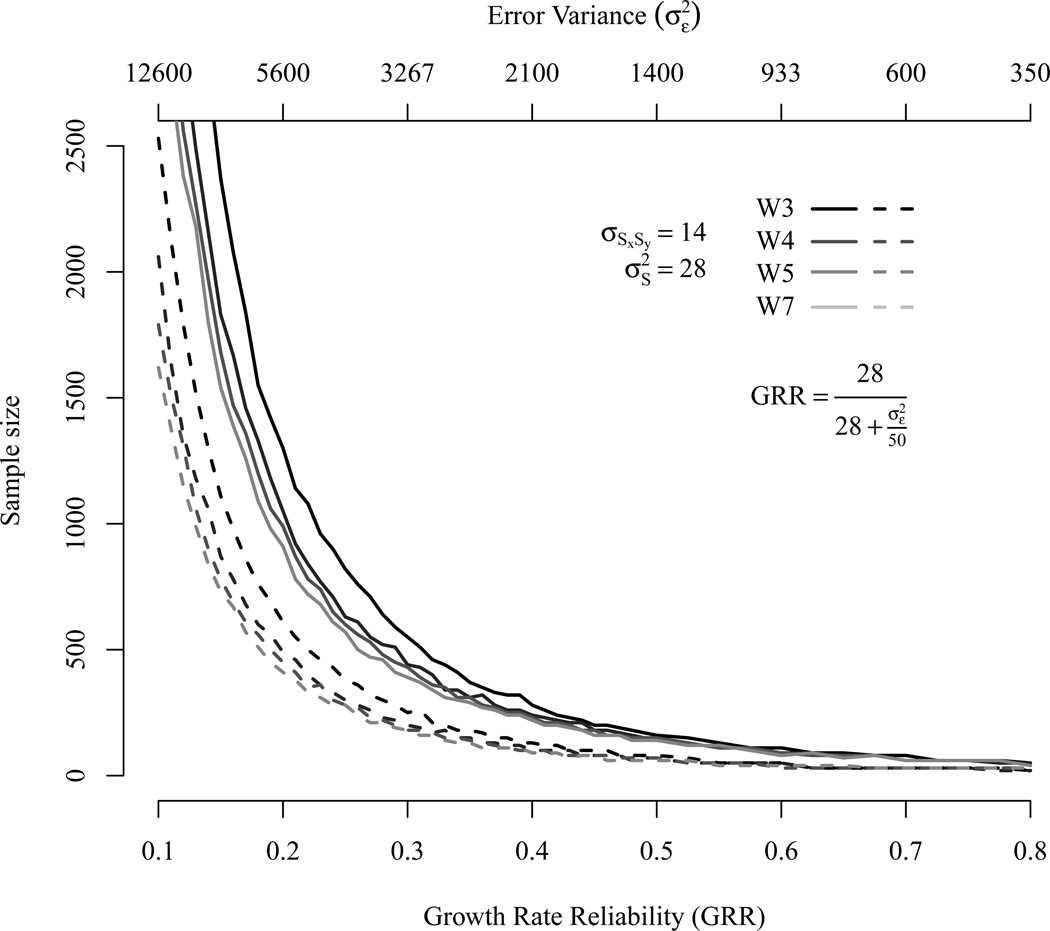
First, we explored the effect of varying study length on power. Therefore we manipulated the duration of the study to range from three to 15 years. We created four different study designs based on three (W3), four (W4), five (W5) and seven (W7) waves. The intervals between measurement occasions within a given study length were equidistant. As shown earlier in Figure 1 different study durations result in different SST values and, hence, in different GRR values. Figure 6 shows the impact of different study durations on the sample size required to obtain at least power of π ≥ .80 to detect significant slope variances and covariances among slopes at p ≤ .05. Solid lines represent .80 power to detect covariances among slopes and hatched lines represent .80 power to detect slope variances.

Figure 6.

Power curves for covariances among slopes (solid lines) and slope variances (dashed lines) given ${\sigma }_S^2=28,{\sigma }_{\epsilon }^2=2100$ and a correlation (r = .50) among the slopes. The figure represents four different design types based on three (W3), four (W4), five (W5), and seven (W7) waves with equidistant intervals. The total study length varied between three and 15 years. Study length and number of waves have interrelated but unique effects on power.

The effect of time was non-linear leading to larger sample size requirements for studies covering few years. At the same time, the requirements on the sample size dropped rapidly as the study duration increased. For example, if the W4 design covers three years, SST is 5 and GRR is 0.06. With this design approximately 5,650 participants are required to obtain power of at least π = .80 to detect a significant slope variance at p ≤ .05. If the W4 design covers four years, SST changes to 8.89, GRR to .11, and the required sample size decreases to 1,860 which is a reduction in N of 67%. The effect of adding one year to the total study length on the critical sample size becomes less pronounced as more years are covered. That is, if the W4 design covers 10 years (STT=55.56, GRR=.42) approximately 90 participants are required to detect a significant slope variance with π ≥ .80. A W4 design that covers 11 years (SST=67.22, GRR=.47) requires 70 participants, 22% less, to detect the same slope variance.

To explore the effect of the number of measurement occasions on power and sample size, we manipulated a larger set of measurement occasions ranging from three to 15 in four study conditions covering in total 3, 5, 7, or 9 years. Figure 7 shows the effect of different numbers of waves that are administered within a given total study duration. Due to the non-linear nature of number of measurement occasions and power, the impact of the number of waves on the sample size was more pronounced for studies with few waves and short durations. For example, if five years (5y) comprise three waves, 1,320 participants are required to detect a significant slope variance at p ≤ .05 with π ≥ .80. If in the same amount of time four waves are administered, sample size reduces by 35% to 860 participants. If seven years are covered with three waves, 410 participants suffice to detect the slope variance and if in the same time span four waves are administered, the required sample size reduces by 32% to approximately 280 participants. Figure 7 also illustrates that short studies that only cover three years would have to operate with very large numbers of measurement occasions in order to reduce the sample size. For example, in a study with a duration of three years, 1,600 participants and nine measurement occasions are needed to detect a significant slope variance at p ≤ .05 with π ≥ .80. To detect the correlation among slopes of r = .50 in the same study, at least 16 measurement occasions would be required.

Figure 7.

Power curves for covariances among slopes (solid lines) and slope variances (dashed lines) given ${\sigma }_S^2=28,{\sigma }_{\epsilon }^2=2100$ and a correlation (r = .50) among the slopes. The lines represents four study durations covering 3, 5, 7, and 9 years in total with equidistant intervals. The number of measurement occasion for each of these four study length varied from 3 to 15.

The relation among power to detect a significant covariance among the slopes was functionally similar but generally resulted in larger samples size requirements compared to slope variances. With, for example, 500 participants and a study length of nine years, correlations among the slopes of r = .50 have more than sufficient power for all studies with three or more waves. That is, 370 participants suffice to detect a significant slope correlation in a study covering nine years with three waves. If five years are covered approximately 10 waves are necessary to detect the same correlation with 500 participants.

As demonstrated above, both the study length and the number of waves have interrelated but unique effects on power in the sense that power can be increased by either including more waves within a given study length or by covering a longer time span with a constant number of waves. Note that SST and GRR are different for all simulation conditions and both, increasing the number of waves and years covered, positively influence SST.

Constant SST and GRR: Different Number of Waves, Different Study Duration

In the previous case we manipulated the number of waves and study duration and with it, SST and GRR. Here, we examined the effect of varying numbers of waves and study duration on power while keeping SST and GRR constant. That is, all parameters in GRR were kept constant while we compared different design types. In order to do so, we kept the reliability constant at GRR = .40 across all conditions. Given that an increase in number of waves also increases the reliability (cf. Equation 1) we chose to adjust the time span covered by different designs in order to keep GRR constant. For instance, the W3 design covered ten years with measurement occasions at time 0, 5, and 10, which amounts to an SST of 50. By holding the error and slope variances constant, we achieved a reliability of $\text{GRR}=\frac{28}{28+[2100/50]}=.40$ which is close to the average GRR in Table 5. In order to achieve the same reliability with the W4 design we needed to reduce the amount of years covered in that design. An SST=50 with four equally spaced waves is obtained in 9.49 years and the measurement occasions were set to 0, 3.16, 6.33, and 9.49 years. The W5 design spanned 8.94 years with measurements at 0, 2.24, 4.47, 6.71, and 8.94 years. The last design W7 spanned 8.02 years and had seven waves at the occasions 0, 1.34, 2.67, 4.01, 5.35, 6.68, and 8.02. Note that with seven waves the total time span of a study reduces by almost 2 years while GRR remains constant.

Figure 8 shows four solid and four hatched lines. The solid lines represent the power curves for the covariances among the slope and the hatched lines represent the power curves for the slope variances which, in the present case, were identical for both sets of variables. The thin horizontal line represents the .80 power threshold indicating that, for example, the sample size needed to detect a correlated slope of r = .50 with three waves and a power of .80 is about N = 275. The slope variance in the same W3 design requires about 130 participants to obtain π ≥ .80. There is a small gap in the sample size needed to uncover significant covariances or variances between the study designs based on three and four waves. In order to uncover the covariance among the slopes in the W4 design about 235 participants are needed – 40 or 15% less than in the W3 design. Similarly, the slope variance may be detected with about 110 participants in the W4 design which are 20 or 15% fewer participants compared to the W3 design. Notably, power to detect slope variances was higher compared to power to detect covariances among slopes. The small but consistent effect of different number of waves on power indicates that SST did not completely absorb all design effects.

Figure 8.

Power curves for covariances among slopes (solid lines) and slope variances (dashed lines) given equal growth curve reliability of GRR= .40, equal slope variances, and equal correlations (r = .50) among the slopes. The figure represents four different design types based on three (W3), four (W4), five (W5), and seven (W7) waves with equidistant intervals. In order to maintain the reliability constant across all four study designs the SST was fixed to 50 and the study designs covered different intervals. The thin gray line represents the .80 power threshold.

Variable SST and GRR: Constant number of Waves, Constant Study Duration, Varying Intervals Among Waves

Following the definition of the growth rate reliability in Equation (1), changes in SST affect the magnitude of the reliability. Hence, the type of the longitudinal study design not only alters the SST by number of waves and overall time span but also via the choice of intervals between waves. By altering the times at which measurements occur, one might maximize SST and, ultimately, reduce the sample size needed to detect a given effect. In order to estimate changes in power due to different interval spacing designs we tested three different designs which involved changes across ten years. All designs involved four waves where Design 1 (D1) had measurement occasions at 0, 1, 9, and 10 years and an SST of 82. The waves in Design 2 (D2) were equally spaced at 0, 3.3, 6.6, and 10 years which equates to an SST of 55.4. Design 3 (D3) had waves at 0, 4.9, 5.1, and 10 years which leads to the smallest SST of 50. Given that we varied the time at which each measurement occurred, we also varied the SST and with it GRR. We chose to set GRR = .35 in D2 which reects the average GRR from studies based on four waves in Table 5. Given the intervals in the other two designs we obtained GRR = .44 for D1 and GRR = .33 for D3. The error variance was set to ${\sigma }_{{\epsilon }_y}^2={\sigma }_{{\epsilon }_x}^2=2883$ in order to obtain a GRR = .35 for D2 with σ² = 28. The occasion specific error covariance was set to be equivalent to a correlation of r = .05 which resulted in ${\sigma }_{{\epsilon }_y{\epsilon }_x}^2=144.2$.

Figure 9 shows the results from the Monte Carlo simulation for three different designs that vary the intervals between waves. Solid lines represent power curves for the slope covariance parameters and the dashed lines represent the power curves for the slope variance parameters. The effect of the design type on the power curves is clearly visible for both the covariances and the variance parameters. For example, in order to detect the covariance among the slopes with π ≥ .80 in the D2 design where the waves are equally spaced a sample of 320 participants or more would be needed. In D3 one would need more than 380 participants to uncover the same correlation but with the D1 design which maximizes the SST, only 190 participants would suffice. As previously observed, the slope variances were detectable with fewer participants compared to the correlation among the slopes.

Figure 9.

Power curves for correlated slopes (solid lines) and slope variances (dashed lines) given three different types of wave intervals which all span 10 years. The correlation between the slopes is r = .50. D1 has measurement occasions at years 0, 1, 9, and 10 (SST=82), D2 at 0, 3.3, 6.6, and 10 (SST=55.4), and D3 at 0, 4.9, 5.1, and 10 (SST=50). The variances and covariances of level, slope and of the errors are held constant across the three interval types. The reliability only changes due to different spacing of the intervals between waves.

Case 2: The Effect of ${\sigma }_{\epsilon }^2$ on the Sample Size

In order to explore the effect of GRR on the power to detect slope variances and covariances we varied the reliability between .10 and .80 via the error variance ${\sigma }_{\epsilon }^2$. We used the same setup as above but now ${\sigma }_{\epsilon }^2$ ranged from 12,600 to 350. To further explore the combination of study type and reliability regarding sample size, we varied GRR in all four previously defined study design types W3 (10y), W4 (9.49y), W5 (8.94y), and W7 (8.02y). To facilitate the interpretation we plotted .80 power curves in Figure 10. Each line represents π = .80 for a given GRR value and a given sample size for four different study designs. SST was again held constant at 50.

Figure 10.

.80 power curves for covariances among slopes (solid lines) and slope variances (dashed lines) given equal slope variances, and equal correlations (r = .50) among the slopes. The figure represents four different design types based on three (W3), four (W4), five (W5), and seven (W7) waves with equidistant intervals. GRR is manipulated via the error term ${\sigma }_{\epsilon }^2$ which ranges from 12,600 to 350.

Figure 10, which shares some similarities with Figure 4, illustrates the non-linear relation between reliability and sample size. As GRR decreases, the number of participants needed to obtain a power of π ≥ .80 increases notably and non-linearly. Further, the absolute sample size and the gradient of change in sample size depends on GRR and on the parameters in question: The sample size to detect covariances among slopes is generally higher compared to the sample size needed to detect slope variances. Also, if GRR is held constant across design types by reducing the total study duration, designs with different numbers of waves produce similar sample size requirements to detect variances or covariances with power of at least π ≥ .80. Note that the required sample sizes are close but not identical across design types and designs with fewer waves, such as W3 need larger samples compared to designs with higher numbers of waves. The size of the gap in the power curve between the three-wave and the four-wave design is accentuated by smaller reliability values.

Case 3: Varying Effect Sizes of the Slope Variance ${\sigma }_S^2$

Up to this point, we varied GRR via the error variance ${\sigma }_{\epsilon }^2$ and SST while keeping the slope variance constant. GRR also depends on the size of the variance in linear change ${\sigma }_S^2$. Here we will manipulate the third, remaining parameter ${\sigma }_S^2$ in GRR. ${\sigma }_S^2$ represents a critical parameter as it will reduce GRR to 0 in the case of ${\sigma }_{\epsilon }^2=0$. In order to evaluate the effect of the slope variance on power we manipulated ${\sigma }_S^2$ to cover a broad range of slope-to-error variance ratios as shown in Table 4. In the present case we estimated power to detect significant slope variances with slope-to-error variance ratios ranging from 1:420 to 1:20. These ratios produced GRR values ranging from .11 to .71. We remained with the population values for the matrix of random coefficients and the error (co)variance from Case 1 but in the present case ${\sigma }_S^2$ ranged from 5 to 105. In order to keep the covariance matrix positive definite we kept the correlations constant at the values given in Case 1. As in the prior cases we evaluated the effect of the manipulations within four different designs, comprising the W3, W4, W5, and W7 designs defined in Case 1 with SST=50.

Figure 11 shows four hatched lines which represent .80 power estimates at a certain sample size for the four design types. Different slope-to-error variance ratios affected the power and the sample size needed to obtain power of π ≥ .80. As seen previously, the curves followed a non-linear pattern indicating that little variance in ${\sigma }_S^2$ needs to be compensated with a large sample size while large ${\sigma }_S^2$ can be detected with much fewer participants. Note that these .80 power estimates of the variance parameters reproduce closely the estimates obtained under the same GRR values in Figure 10.

Figure 11.

.80 power estimates for different slope variances (dashed lines) in four designs based on three (W3), four (W4), five (W5), and seven (W7) waves. The error variance is constant at ${\sigma }_{\epsilon }^2=2100$ and SST is 50. The slope-to-error variance ratio ranges from 1:420 (5:2100) to 1:20 (105:2100). The lower x-axis provides the variances and the top x-axis provides the according GRR values.

Case 4: Varying Effect Sizes of the Slope Covariance

As can be seen from Table 5 the magnitude of the correlation among the slopes largely influenced the power estimate and sample size needed to obtain power of at least .80. In the present case, we investigated the influence of the effect size on the sample size for a given reliability of GRR = .40. The correlations ranged between .10 and .80, covering a realistic range of values from Table 4. Again, we contrasted four conditions based on the W3, W4, W5, and W6 design defined in Case 1 where GRR was held constant across all design conditions. The covariance matrix was derived from the ELSA study using delayed word recall (DWR) and fluency (AF) scores from Table 4 in order to represent findings in cognitive variables and to obtain a covariance matrix which remained positive definite for the entire range of covariance parameters tested here. Note that both slope variances were set to equal values to facilitate the interpretation of the figures. The covariance matrix for this present case was

$$\mathbf{\Phi }=\left[\begin{array}{cccc}\hfill 260\hfill & \hfill (.05)\hfill & \hfill (.62)\hfill & \hfill (.31)\hfill \\ \hfill 1\hfill & \hfill 1.4\hfill & \hfill (.17)\hfill & \hfill [.10;.80]\hfill \\ \hfill 150\hfill & \hfill 3\hfill & \hfill 224\hfill & \hfill (.23)\hfill \\ \hfill 6\hfill & \hfill [0.14;1.12]\hfill & \hfill 4\hfill & \hfill 1.4\hfill \end{array}\right].$$

The values in squared brackets denote the range of the covariances and correlations (above diagonal). Covariances varied between 0.14 and 1.12, accordingly the correlation ranged from .10 to .80. The occasion specific error correlation was set to r = .10.

Figure 12 shows .80 power curves for the four given designs W3, W4, W5, and W7. Generally, the relation among the effect and sample size was negative in the sense that high correlations among the slopes can be detected with fewer participants compared to smaller effect sizes which require more participants. The relationship between the effect size and the sample size was non-linear. As the correlation increased in size the demand on the sample size rapidly decreased until it reached a plateau. For example, in order to detect a correlation of r = .25 between 1070 (W3) and 840 (W7) participants are needed. Correlations of r = .50 are detectable with considerably smaller samples ranging from 280 (W3) to 210 (W7) participants. Similarly, 500 participants suffice to detect correlations ranging from r = .36 in the W3 design to r = .33 in the W7 design.

Figure 12.

.80 power curves for correlated slopes given equal reliability of GRR =.40, and equal slope variances of 1.4. The figure represents four different design types bases on three (W3), four (W4), five (W5), and seven (W7) waves with equidistant intervals.

In order to investigate the relation between effect and sample size with varying GRR, we computed the .80 power curves for GRR values of .20, .40, .60, and .80 in a four-wave design. We used the W4 design defined in Case 1 which covers 9.48 years in total with GRR modified only by changes to the error variance. As can be seen from Figure 13 the power curves are non-linear indicating that smaller effect sizes require increasing sample sizes in order to detect the slope correlations. Notably, the reliability exerts a substantial effect on the sample size. Power curves for higher reliabilities seem to reach an asymptotic level earlier than power curves based on low reliability which yields an increasingly strong but negative dependence between the effect size and the sample size as GRR decreases. For example, a correlation of r = .40 may be detectable with 80 participants if reliability is high (GRR = .80) but more than 1,630 participants are required to detect the same correlation with low reliability of GRR = .20.

Figure 13.

Four .80 power curves for covariances among slopes given different GRR values ranging from .20 to .80 in a four-waves study design with equally spaced intervals.

Case 5: The Effect of Occasion Specific Error Covariances σ_εyεx on the Sample Size to Detect Power ≥ .80

The studies in Table 4 show that the effect size of the time-specific residual covariance was small to moderate with an average correlation of about r = .10. In some studies however, such as in ACAD, the residual covariances were large, up to r = .62. In order to relate the magnitude of the occasion specific error correlation to the sample size we computed .80 power curves across four GRR values (.20, .40, .60, and .80) in a four-waves study spanning six years with equally spaced waves. The covariance matrix used to define the population values was the same as in Case 4 with a slope correlation of r = .50. Apart from the effect of GRR on sample size, Figure 14 shows that the magnitude of the error covariance σ_εyεx exerts a negligible effect on the sample size to detect power ≥ .80. With GRR of .04 and above the effect of the error correlation has little impact on the sample size. For example, if GRR = .60 the increase in sample size associated to an increase in the error correlation from r = .20 (N = 90) to r = .60 (N = 120) is 20 participants. If the reliability is low, at GRR = .20, the sample size increases from 1,110 to 1,350 participants – which corresponds to a difference of 240 participants.

Figure 14.

.80 power curves of correlated slopes for four GRR values ranging from .20 to .80 in a four-waves study design with equally spaced intervals. The occasion specific error correlation spanned from 0.0 to .90.

Discussion

In this study, we investigated the interplay of different factors which contribute to the power to detect variances and covariances in linear rates of change in the context of a broad range of actual longitudinal studies and variables. We emphasized the importance of growth rate reliability (GRR) defined by Willett (1989) which captures relevant parameters associated to power, such as the slope variance, error variance, and design attributes comprising number and spacing of waves, and the total study duration. Power was estimated by means of Monte Carlo simulations using LGC models. Our study was geared mainly towards the understanding of the interplay among the components of GRR and their relation to power and not to report a definitive statement about the range of power to detect individual differences in slope variances and covariances in longitudinal studies. Nonetheless, our results provide a quite positive summary of power in existing studies and demonstrate that most existing longitudinal studies of developmental and aging-related outcomes have more than sufficient power to detect individual differences in change and associations among linear rates of change. This was also the case in many of the studies covering few years with only three measurement occasions. Power to detect covariances among rates of change was generally lower and required larger sample sizes compared to the detection of variances. Also, power can be substantially increased by adding more measurement occasions, particularly when study duration is short (e.g. five years and less) such as in the early phases of every longitudinal study.

The range of GRR and slope-to-error variance ratios is considerable across longitudinal studies (as shown in Tables 2 and 5) and, accordingly, the range of sample size requirements to obtain sufficient power can be very large. While we provide estimates of power for actual values from the studies reported here, we used the model estimates primarily to anchor our power simulations to a range of real parameter estimates for several variable domains. Table 4 provides a range of values for cognitive, physical, and mental health variables that can be used as start values for simulation and power analyses that provide a realistic basis for the design of new longitudinal studies and further extensions of existing studies. Given the large heterogeneity in the relevant parameters ${\sigma }_S^2\text{and}{\sigma }_{\epsilon }^2$ we strongly encourage investigators to run power analyses during the processes of designing longitudinal studies and plan for relatively low power early in the longitudinal follow-up by adding observations, possibly including more intensive measurement designs to capture within-person dynamics and optimize estimates of within-person means.

The selection of realistic simulation parameters is essential, particularly given the discrepancy between results from recent simulations and the increasing number of statistically and substantively significant findings reported from a variety of developmental and aging studies based on longitudinal designs. Crucial to any simulation is its generalizability to the “real world" with the outcome of any simulation being highly dependent on the derivation of population parameters (Paxton, Curran, Bollen, Kirby, & Chen, 2001). Indeed, the large and increasing body of published longitudinal findings and the results of our power analysis are at odds with recent results from a series of simulation studies by Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) who painted a pessimistic picture of current longitudinal studies and related designs. We have critically evaluated these earlier studies of power to detect change in the introduction. We showed that the low power estimates for most conditions reported by these earlier simulation studies was due to their choice of parameter values that were largely out of bounds of actual study values. In particular, their choice of parameter values resulted in low GRR conditions due to little change variability relative to the error variance. Also, Hertzog and colleagues interpreted GCR as an absolute index of power. Their interpretation regarding the pivotal role of GCR in the context of power to detect slope variances and covariances needs to be put into perspective. While measurement reliability is positively related to power, GCR simply reflected variation in error variance within their simulation design. More importantly, the different GCR conditions in their simulations were not static but resulted in different slope-to-error variance ratios and different GRR conditions. We illustrate this effect in Figure 2 across four designs where we show that changes in error variance lead to different GRR values which truly captures the nature of power. For example, the GCR= .91 condition can result in almost any value of GRR in the range between 0 and 1 depending on the size of the slope variance and the number of measurements in the design. Accordingly, almost any value of power between 0 and 1 will be obtained with these variations. Hence, while GCR captures the important aspect of measurement reliability, it is only one element of a very dynamic and complex relation among different facets that are captured in GRR and which constitute power to detect change and covariation in change. Moreover, the simulation work of Hertzog et al. (2006, 2008) and von Oertzen et al. (2010) perfectly confounded study length with number of waves. As a result, a clear distinction of the unique contributions of these study design elements to power to detect variances and covariances among rates of change cannot be made. Any interpretation regarding study design elements in the earlier results reported by Hertzog and colleagues remains ambiguous due to these confounds and contributes little to the understanding of power to identify individual differences in and among growth rates in longitudinal studies.

Growth Rate Reliability (GRR)

The growth rate reliability (Willett, 1989) turned out to be a very useful index which captured the relevant parameters of power to detect growth rates. The relation of GRR and power was first examined using estimates from existing longitudinal studies (Figure 4) and we replicated these findings in several case studies where relevant parameters were systematically varied. It is noteworthy that GCR, the reliability of a growth curve estimate at one point in time, was largely unrelated to power to detect slope variance and covariance in existing studies. Figures 4 and 5 illustrate the explications about GRR and GCR given in the introduction and how these might typically be used in practice.

GRR is a useful index of power, comprised of the most relevant parameters linked to power. Of special interest is the SST component which captures design considerations such as study length, number of waves and spacing of waves. These elements are typically under the control of the investigator and their impact on power and sample size is important to understand and use in practice. Changes in the study design have direct influence on SST which alters GRR. This relation can be easily established (cf. Figure 1 and Willett, 1989) but at the same time the relation among GRR and power was largely unknown. Our results showed that the non-linear relation among GRR and power leads to substantial increases in sample sizes once GRR values are below .20. On the other hand, the sample size requirements become quite stable for values of GRR above .40.

Changes in study designs such as number of measurement occasions, study length, and intervals between observations had the largest effects at the lower end of GRR. For studies which cover fewer than five to seven years, increasing the number of measurement occasions can be beneficial. However, one needs to find a balance among increasing power and other, unwanted effects, such as retest and practice effects. If the total study duration exceeds 10 to 15 years, number of waves hardly influences power to detect variances of and among growth rates. Obviously, power is a major issue in the early stages of longitudinal studies. Given these findings one strategy could be to include more measurement occasions in initial phases of longitudinal studies and then, reduce the amount of measurement occasions once sufficient power is obtained for the analysis of change. However, more frequent assessments and the use of intensive measurement designs can have additional benefits by permitting analysis of within-person dynamics and short-term variation and provide more reliable estimates of within-person level of functioning (e.g. Rast, MacDonald, & Hofer, 2012; Walls et al., 2011).

As can be seen from working through the simulation case studies, GRR provides a standardized estimate which stably predicts power, or required sample size to detect power ≥ .80, given a certain number of measurement waves. That is, the influence of the error and the slope variance follows a non-linear trajectory in each of the simulations. In order to explore this association, we evaluated a number of functions through these trajectories and found that a power function best described the relation among GRR and sample size. This relation among GRR and sample size was close but not perfect indicating that SST did not fully account for the design effects in studies with only three measurement occasions. With four and more waves, this discrepancy becomes negligible and we would second MacCallum et al. (1997, p. 217) suggestion to obtain at least four to five measurement occasions for modeling linear change. The close association of GRR and power to detect longitudinal change in linear slopes encourages the use of GRR as a useful index for the determination of sample size in a linear growth curve model. It is important to note here, that the relation among GRR and power was established in the linear LGC model with constant error variances and based on the more conservative single parameter Wald test. The relation might be different for different variations of LGC models (e.g. with different constraints) and may remain useful for approximating power in non-linear models and for other statistical tests. However, GRR can not fully substitute for the estimation of power using Monte Carlo simulations (or other techniques such as the power estimation introduced by Satorra and Saris (1985) for particular applications). Nonetheless, GRR provides a very effective index to formalize the reliability of growth rates and it illustrates the interplay among a number of study design parameters that have an important role in the power to detect individual change. We expect that these same design factors will be important for more complex and nonlinear models of change.

Keeping these limitations in mind, the implications for the design of longitudinal studies are formalized to some degree in the GRR estimate, providing the impact on power for particular design considerations. Power to detect individual differences in change is directly related to the phenomenon of interest ${\sigma }_S^2$ and to the combined error variance ${\sigma }_{\epsilon }^2$ comprised of time-specific intraindividual variability and measurement reliability. As we demonstrated, the investigator is able to increase GRR by increasing the total duration of the study, optimizing wave intervals or adding in additional waves to increase SST. However, the cautionary notes raised by Willett (1989) apply, suggesting that in most cases it will not be beneficial to focus on one parameter and increase GRR by, for example, maximizing SST. Design considerations should not be reduced to one factor alone and the present results illustrate the complex interplay among effect sizes, type of study design, measurement reliability, and power to detect variance and covariance in rates of change.

Implications for Design of Long-Term Longitudinal Studies

There are a number of implications of this analysis of existing longitudinal studies and related simulations for the design of new longitudinal studies of developmental and aging-related processes. One of the most important aspects is the number and interval between measurement waves and the length of the study. While longitudinal designs are essential for understanding developmental and aging-related change, their value is usually obtained only after many years of effort. In particular, the early phases of longitudinal studies often do not provide a sufficient basis for the analysis and explanation of individual change and variation. Our recommendation is that these early phases of longitudinal studies be enhanced using a variety of potential measurement intensive designs, such as a measurement burst design (e.g. Walls et al., 2011) or by the addition of one or two additional more closely spaced waves. Such study designs would refine detection of individual variation and change and our understanding of intraindividual dynamics over shorter periods of time. Measurement intensive designs and additional waves increase SST and GRR and have a major effect on power to detect change and covariation among rates of change if embedded in more typical longitudinal designs. Such innovations in measurement and intraindividual dynamics would carry forward in important ways to understand change in outcomes and processes that may better capture the complexity of individual development and improve power to detect individual change and variation.