Three-dimensional epithelial morphogenesis in the developing Drosophila egg

Abstract

Morphogenesis of the respiratory appendages on eggshells of Drosophila species provides a powerful experimental system for studying how cell sheets give rise to complex three-dimensional structures. In Drosophila melanogaster, each of the two tubular eggshell appendages is derived from a primordium comprising two distinct cell types. Using live imaging and three-dimensional image reconstruction, we demonstrate that the transformation of this two-dimensional primordium into a tube involves out-of-plane bending followed by a sequence of spatially ordered cell intercalations. These morphological transformations correlate with the appearance of complementary distributions of myosin and Bazooka in the primordium. These distributions suggest that a two-dimensional pattern of line tensions along cell-cell edges on the apical side of the epithelium is sufficient to produce the observed changes in morphology. Computational modeling shows that this mechanism could explain the main features of tissue deformation and cell rearrangements observed during three-dimensional morphogenesis.

Introduction

Regulated deformations of cell sheets, accompanied by cell shape changes, rearrangements and divisions, give rise to three-dimensional structures in development (Davidson, 2012; Keller and Shook, 2011). A canonical example of this type of morphogenesis is provided by early steps of vertebrate neurulation, where bending of the neuroepithelium is followed by delamination and closure of the neural tube, a precursor of the central nervous system (Wallingford, 2005). Morphological transformations of cell sheets are preceded by patterning events, which result in spatially ordered arrangements of cell fates and properties within the sheet. While fate mapping between initial cell positions within the sheet and the final structure has been performed in a number of systems, e.g., (Baker et al., 2008; de Campos-Baptista et al., 2008; England et al., 2006; Kwan et al., 2012; Rohr et al., 2008; Smith et al., 2008), the dynamics of transformation from a flat sheet to a three-dimensional shape are poorly understood. Even less explored are the origins of mechanical forces that can drive these transformations (Keller et al., 2008; Lecuit et al., 2011). Here, we address these issues during the morphogenesis of the Drosophila eggshell, a complex structure derived from the epithelium that envelops the developing egg (Hinton, 1981).

Dorsal appendage formation in the Drosophila egg chamber provides an anatomically simple and genetically tractable model of epithelial morphogenesis (Berg, 2005; Horne-Badovinac and Bilder, 2005). During oogenesis, the epithelium surrounding the egg chamber develops from a simple ovoid surface to a structure with two dorsally projecting tubes. Proteins are secreted from the apical surface of the epithelium, which initially faces the oocyte (Figure 1A); upon cross-linking, these proteins form a solid shell. The proteins secreted into the tubes form two eggshell appendages that are used for gas exchange by the embryo (Hinton, 1981; Wu et al., 2008).

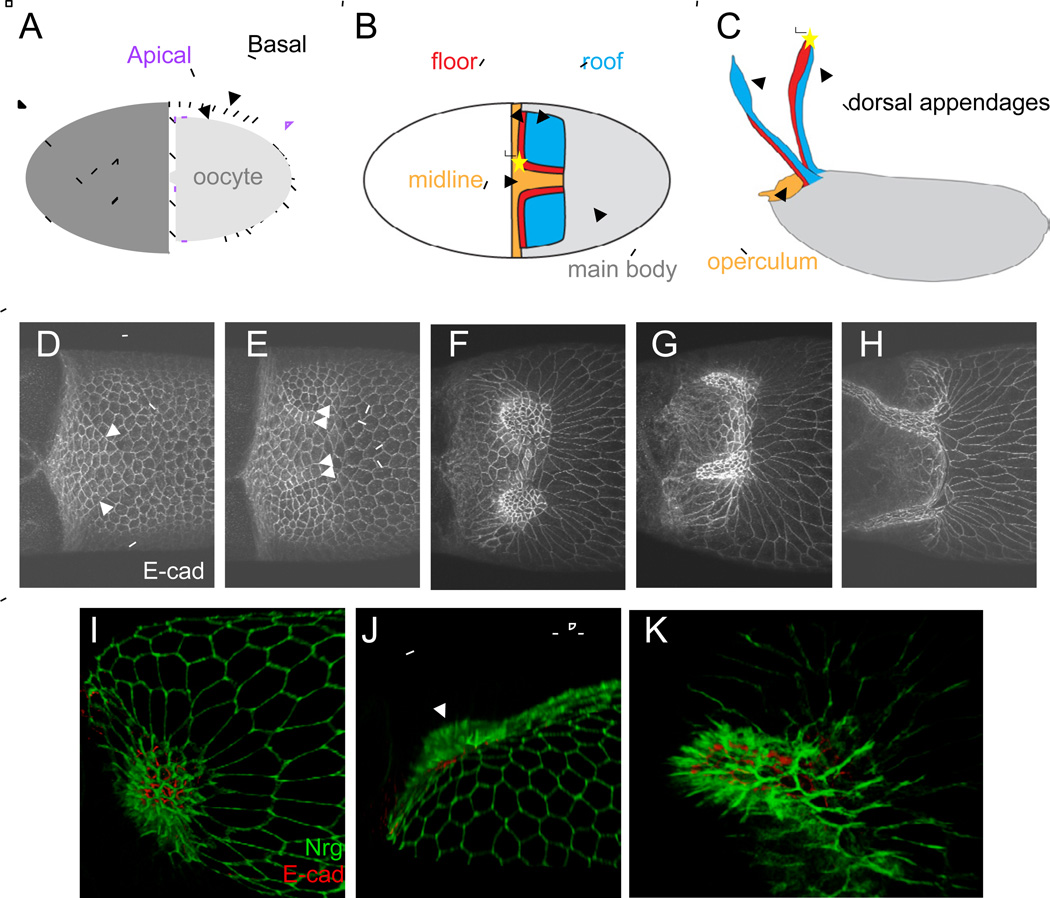
Figure 1. A review of apical cell shape and tissue changes during appendage formation.

(A) Schematized cross-section of stage 10 egg chamber. The oocyte (light gray) is enveloped by the follicular epithelium, with the apical side (purple) of the epithelium facing towards the oocyte.

(B) Schematic of follicle cell types in stage 10 egg chamber. Grey region is occupied by the non-specialized main body cells, blue by the roof cells, red by the floor cells, and orange by the midline cells. The "apex" of the appendage primordium is marked by a yellow star. Anterior is to the left.

(C) Schematic of the eggshell, with regions colored according to the cells from which they are derived.

(D-H) E-cadherin immunostaining of egg chambers at progressive stages of appendage formation. Arrows in D indicate smoothened boundaries between roof and floor cell. Arrows in E indicate smoothened floor-roof and floor-midline boundaries. Scale bar = 50 microns.

(I-K) 3D reconstruction of appendage formation. The dome stage of a single sample is shown viewed from above (I) and the side (J), with direction of rotation indicated by curved arrows. Arrow in (J) points to the dome where the tissue bends out of plane. 3D reconstruction of the nascent appendage stage is shown in (K). Green: Nrg-GFP, red: E-cad.

The dorsal appendage primordium is established in a pattern formation event that is initiated by the localized activation of the EGFR pathway (Deng and Bownes, 1997; Dorman et al., 2004; Peri et al., 1999; Peri and Roth, 2000; Ruohola-Baker et al., 1993; Schupbach, 1987; Ward and Berg, 2005b; Ward et al., 2006). The fate map of this system has been established through the work of Celeste Berg and colleagues (Figure 1B-C). Each primordium comprises an ordered arrangement of two cell types: a patch of "roof" cells, which form the top of the tube, and a single-cell-width arc of "floor" cells, which form the lower side of the tube. The arc of floor cells initially borders the roof domain on both its anterior and dorsal sides. During sealing of the appendage tube, the two sides of floor cell domain extend beneath the roof cells and meet to form a seam. As a result, the dorsal-anterior corner of the primordium (which we will call the "apex") maps to the anterior tip of the tube (Boyle et al., 2010; Dorman et al., 2004).

Appendage morphogenesis proceeds through a sequence of steps involving the formation of a straight border between the floor cells and their neighbors, followed by out-of-plane bending of the primordium, and subsequent sealing and elongation of the tube ((Dorman et al., 2004), also see Figure 1D-H). While the overall sequence of these events is established, the dynamics of cellular processes that seal the tube remained unclear. Below, we demonstrate that these dynamics are based on a combination of sheet bending and an ordered sequence of lateral cell rearrangements. Going beyond this kinematic description, we propose and computationally test a mathematical model of forces that can drive these processes.

Results

The seam is formed by new lateral interfaces between floor cells

A key feature of the dorsal appendage tube is the seam that eventually forms between the two sides of the floor cell domain, but the detailed mechanism by which this seam forms is unknown. The final polarity of the floor cells within the epithelial tube has not been characterized. The seam could be formed by an apical fusion of the floor cells. Alternatively, these cells could fuse at their lateral boundaries with apical surfaces facing the lumen. An additional unknown relates to the polarity of the floor cells during the process of seam formation. The floor cells might temporarily lose their epithelial character, and thus their apical-basal polarity, as they migrate towards each other, as appears to occur in other cell sheet fusion events (Ray and Niswander, 2012). Alternatively, the seam may form by a process of neighbor rearrangements in which the epithelial nature of these cells is continuously maintained.

To examine the polarity of the floor cells during tube formation, we used a floor cell specific driver, rho-GAL4, to drive expression of an apical marker, Bazooka:GFP (Baz:GFP) in the floor cells. The resulting apical outlines show that the floor cells begin as a flat arc of rectangular cells (Figure 2A-A"). The tip of the arc straightens and then bends under, causing what was formerly the apex of the floor domain to be tucked in underneath the neighboring roof cells (Figure 2B-B"). This produces a twist in the arc of floor cells such that what was originally the outside (or floor-midline) boundary of the floor cells at the apex comes to lie deeper and more posterior than the inside (or floor-roof) boundary. At the same time, this causes the floor cells at the apex to face away from the oocyte and towards the inner future luminal side of the epithelium. Further bending of the floor cell arc brings the former outer edges of the dorsal-anterior corner into contact, resulting in the formation of new lateral boundaries between floor cells at the tip of the nascent appendage (Figure 2C-C"). New lateral boundaries continue to form between floor cells adjacent to the tip as the tube extends, such that eventually there are two neighboring rows of floor cells (Figure 2D-D"), corresponding to the two arms of the initial floor cell arc.

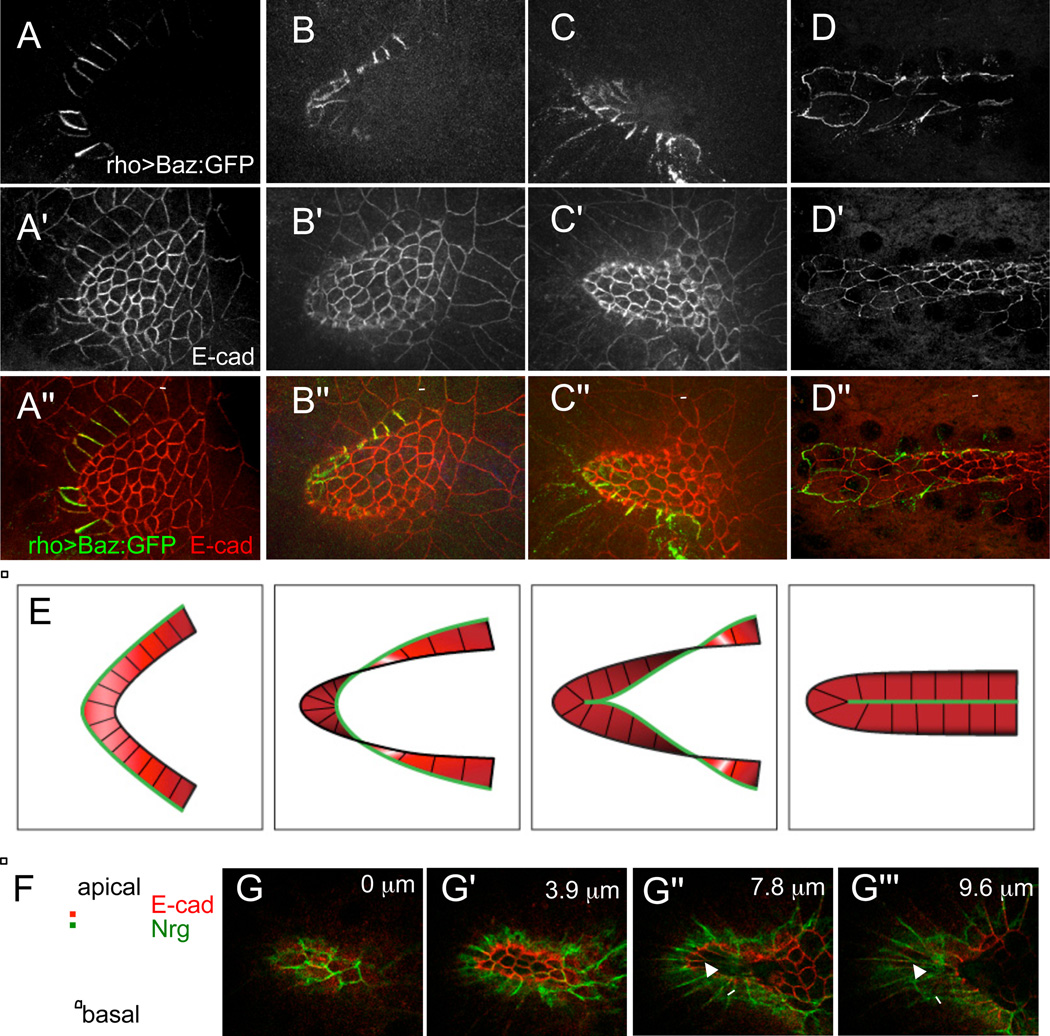
Figure 2. The seam of the tube is formed by lateral interactions between floor cells, with the apical surface of the floor cells facing the lumen of the tube.

(A-D) Floor cells at different stages of appendage formation. (A) The floor domain starts as a flat arc of rectangular cells. (B) The dorsal-anterior corner of the arc starts to bend underneath the roof cells. (C) The outer edges of the dorsal-anterior floor cells, which formerly bordered midline cells, come into contact, forming the new floor-floor boundary. (D) The outer edges along the two halves of the floor arc come into contact, sealing the tube. Apical sides of the floor cells are marked by the apical protein Baz:GFP, driven by a floor-cell specific Gal4 driver (rho-GAL4 BigParent). (A'-D') E-cadherin immunostaining shows apical outlines of all follicle cells. (A"-D") Merged images: Baz:GFP (green), E-cad (red). Scale bars are 20 microns.

(E) Summary of floor cell polarity during tube formation. During appendage formation, the floor cells begin with apical surfaces facing down toward the oocyte, and twist until they end with the apical surfaces facing up towards the lumen of the newly formed tube. The green line marks the outside boundary of the floor cells, which initially contacts midline cells, but then rearranges to form the new floor-floor boundary.

(F) Schematic of the relative locations of markers within an epithelial cell. The adherens junction protein E-cadherin (E-cad) is located more apically, while the septate junction protein, Neuroglian (Nrg) is located more basally.

(G-G"') Z-sections of the nascent appendage shown in Figure 1K, proceeding from the top to the bottom of the tube (with depths from the top indicated). In Drosophila epithelial cells, the adherens junction (marked here by E-cad) is located more apically than the septate junction (marked here by Nrg). Nrg-GFP staining is most prominent above E-cad in the roof cells (G,G'), so the apical sides of the rood cells face downward towards tube lumen. Nrg-GFP staining is most prominent below E-cad in the floor cells (arrows in G",G"'), so the apical sides of the floor cells face upwards towards the lumen.

To summarize, the floor cells maintain apical-basal polarity during tube formation. They begin this process with their apical sides facing the oocyte (down), but end with their apical sides facing towards the lumen of the appendage tube (up), as illustrated in Figure 2E. This conclusion is further supported by the relative locations of the apical marker E-cadherin (E-cad) and a more basally-localized septate junction protein, Neuroglian (Nrg) (Genova and Fehon, 2003; Wu and Beitel, 2004); see Figures 1K, 2F, 2G-G"'.

Live imaging reveals ordered cell intercalation during seam formation

The formation of new lateral interfaces between the floor cells must be accompanied by the loss of interfaces between the floor and midline cells. To follow this process in real time, we turned to live imaging, using previously described protocols for culturing of individual egg chambers (Dorman et al., 2004; Prasad et al., 2007). In these experiments, we used egg chambers dissected from flies expressing the apical marker E-cad:GFP. After establishing that appendage formation occurs normally under these conditions, we focused on events at the interface of the floor cells and their neighbors (Figure 3A-I and Movie S1).

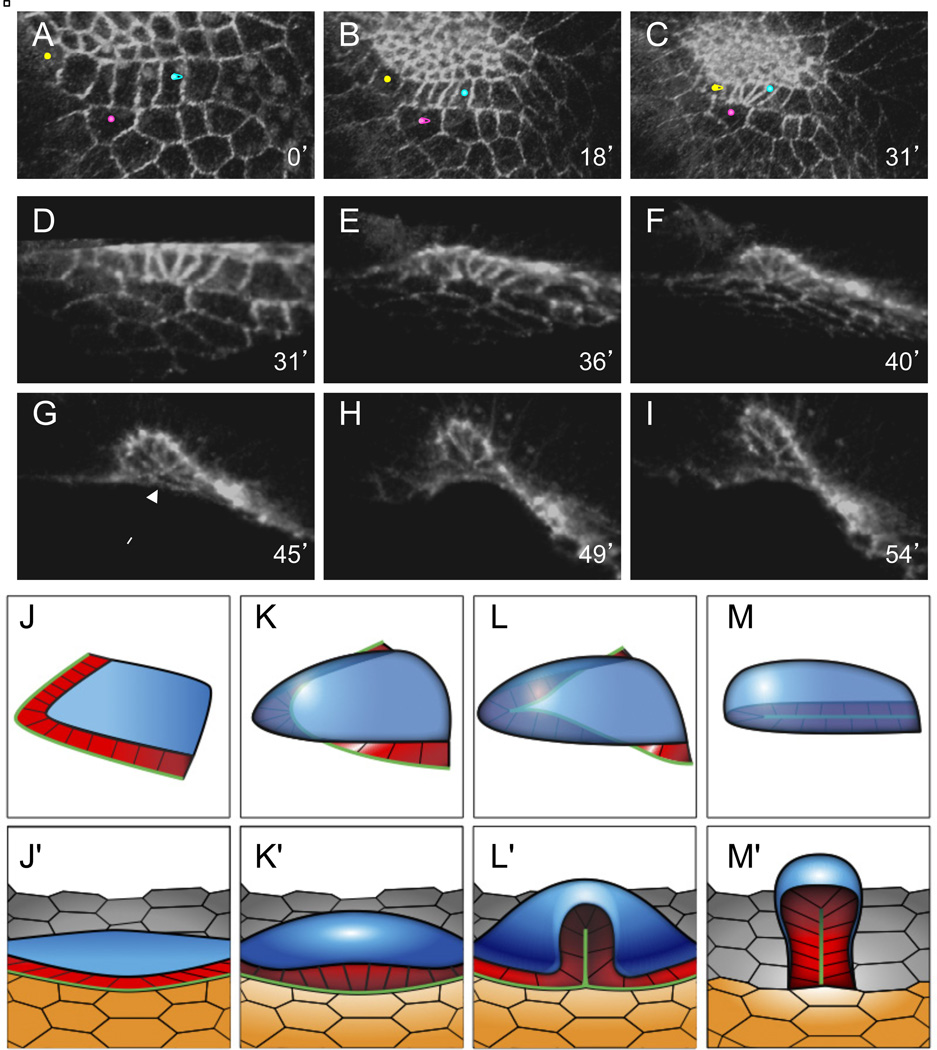
Figure 3. Neighbor exchanges leading to tube seam formation.

(A-I) Rearrangements of the floor cells and their neighbors, visualized in live egg chambers expressing E-cad:GFP; numbers indicate time from the beginning of imaging, rounded to the nearest minute. Orientations in different panels are adjusted to keep the floor cells in the plane of the figure. See also Movie S1.

(A-C) 3D reconstructions of the floor cells and their neighbors, viewed from the oocyte. The floor cells are distinguished by their straight borders (see text); the roof, floor, and midline cells are positioned from top to bottom. As the floor side of the floor-midline border contracts, the marked pair of floor cells (yellow and blue dots) initially borders nonadjacent midline cells, but both eventually contact the same midline cell (pink dot).

(D-I) 3D reconstruction of the floor cells, with the roof cells cropped out. Constriction of floor cell edges bordering the midline continues until several floor cells form a multicellular rosette (G, arrow), which then resolves perpendicularly to its initial configuration (H,I), resulting in new floor-floor borders. See also Movie S2.

(J-M') Summary of dorsal appendage morphogenesis, putting the changes in floor cells geometry (see Figure 2E) into the context of their roof and midline neighbors. Panels J-M show the floor cells (red) with the roof domain (blue). Panels J'-M' add the midline cells (orange). Again, the green line marks the outer border of the floor cells, which initially contacts midline cells, but then rearranges to form the new floor-floor border.

Analyzing our results using 3D image reconstruction software (Movie S2), we found that the early phase of appendage formation involves significant cell rearrangements at the interface of the floor and midline domains. The edges of the floor cells facing the midline cells shrink, resulting in movement of the floor cells relative to the midline cells (Figure 3A-C). As a result of this rearrangement, the number of floor cell neighbors for an individual midline cell at the apex increases from one or two to several. The shortening of these floor cell edges continues while the floor cells bend under the roof domain (Figure 3D-F) until it appears that a multicellular rosette is formed (Figure 3G, see also Movie S2), eliminating several floor-midline edges. In the second phase of rearrangements, the rosette resolves perpendicularly to the floor-midline boundary, creating a new floor-floor boundary and thus initiating the formation of the seam on the lower side of the tube (Figure 3H-I). At the same time as these floor cell rearrangements are occurring, the roof cells constrict apically and form a dome-shaped structure that is eventually pushed up with the movement of the floor cells.

The exchange of floor-midline edges for floor-floor edges clearly proceeds through some process involving spatially ordered cell intercalations, though the detailed cellular events involved remain unclear. It appears that a rosette may be formed and resolved during this process, as is seen in some epithelial tissues undergoing neighbor exchange (Blankenship et al., 2006; Harding and Nechiporuk, 2012; Vichas and Zallen, 2011). However, we cannot exclude the possibility that multiple T1 junctions are formed and resolved in a volume too small to be resolved under our imaging conditions.

The overall kinematics of dorsal appendage formation is summarized in Figure 3J-M'. The early phase of tube formation can be roughly divided into two main stages. First, the floor-midline boundary straightens, then constricts, starting at the apex of the arc. As a result, the epithelial sheet bends so that the apical surface of the floor cells near the apex of the primordium turns from pointing downward toward the oocyte to pointing upwards towards the lumen of the newly created tube (Figure 3J-K). Next, an ordered sequence of cell neighbor exchanges eliminates the floor-midline boundary, creating at the same time a new floor-floor boundary, and thus forming a tube (Figure 3L-M).

Suggested pattern of mechanical forces during appendage morphogenesis

What can be the driving force responsible for formation of the dorsal appendage tube? One hint comes from the first morphological changes that occur prior to any three-dimensional rearrangements, specifically the appearance of smooth floor-roof and floor-midline boundaries (Figure 1D,E).

In other experimental systems, it has been shown that smooth boundaries within epithelial sheets can be caused by the recruitment of myosin II (Dahmann et al., 2011; Landsberg et al., 2009; Lecuit et al., 2011). Therefore, we examined the subcellular localization of myosin in the follicle cells using Sqh-GFP, a fluorescently-tagged fusion of the Drosophila Myosin Regulatory Light Chain. At early stages of appendage formation, Sqh is enriched in two cables along the floor-roof and floor-midline boundaries; additionally, Sqh is enriched on apical outlines of the roof cells (Figure 4A-A'). We also examined the localization of Baz, which has a complementary pattern to myosin in other epithelia undergoing cell rearrangements (Lecuit et al., 2011; Zallen and Wieschaus, 2004). Consistent with these observations, we found that Baz is strongly down-regulated at both the floor-midline and floor-roof boundaries (Figure 4B-B'). Intriguingly, Baz is also strongly down-regulated on a subset of roof cell edges, suggesting some spatial or temporal non-uniformity in roof cell contractility. Taken together, the localization patterns of Sqh and Baz suggest increased tension within the appendage forming domain, and particularly high levels of tension along the floor-midline and floor-roof boundaries.

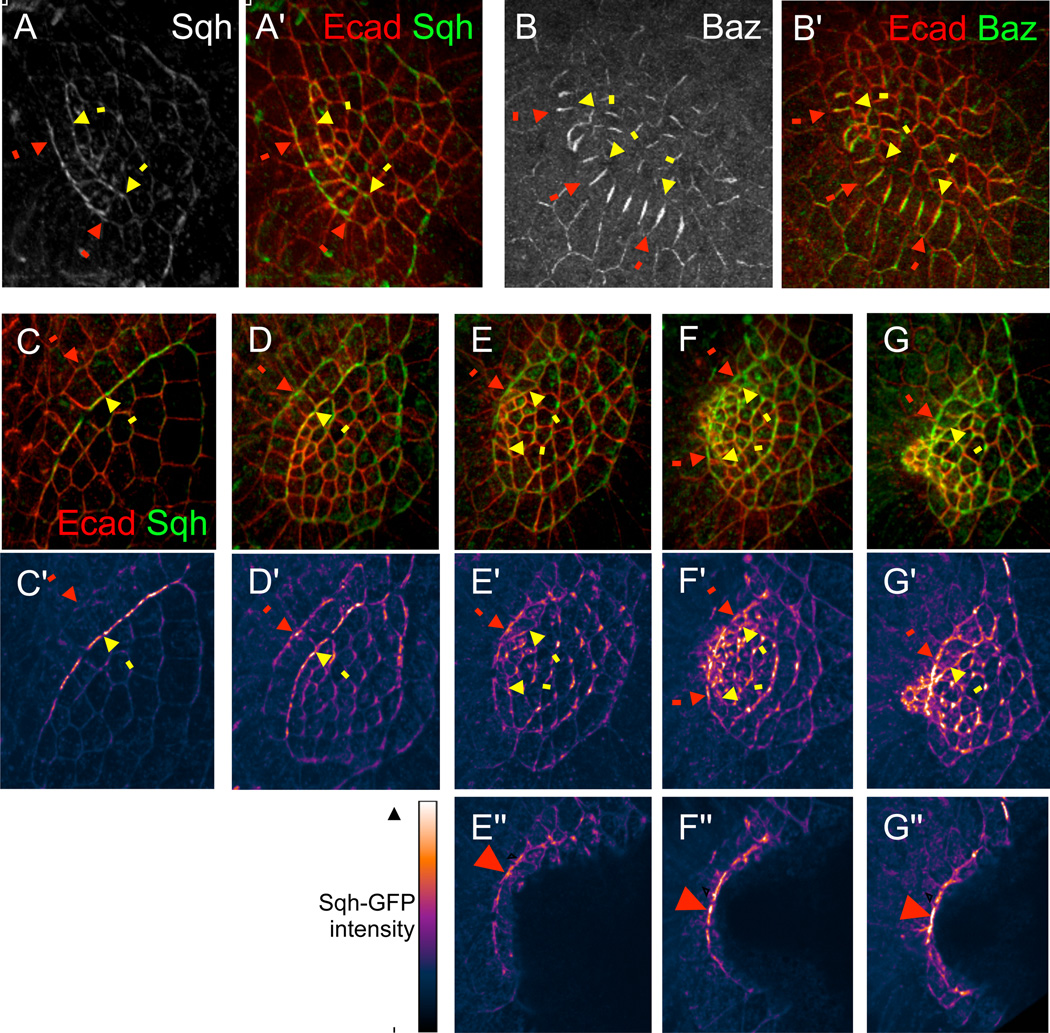
Figure 4. Molecular markers for tension.

(A-B') Immunostaining for Sqh-GFP and Bazooka, two molecular markers for tension, during early stages of appendage morphogenesis. Yellow arrows indicate the floor-roof boundary; red arrows indicate the floor-midline boundary. (A) Sqh-GFP is enriched along the smooth floor-roof and floor-midline boundaries, and is also somewhat enriched on other apical edges within the roof domain. (B) Bazooka is down-regulated along both the floor-roof and floor-midline boundaries, and on a subset of apical edges within the roof domain. Merged images with E-cad counterstainings are also shown (A',B').

(C-G") Sqh-GFP localization at progressive stages of dorsal appendage formation. (C-G) Merged images of Sqh-GFP and E-cad show morphology. Samples are arranged left to right in order of increasing developmental stage. (C'-G') Patterns of Sqh-GFP, with signal intensity shown by color-coding. In early phases of appendage morphogenesis, Sqh localization is largely confined to the floor-roof boundary (yellow arrows, see C'), but as morphogenesis progresses, Sqh levels along the floor-midline boundary (red arrows) surpass Sqh levels along the floor-roof boundary (E'-G'). (E"-G") The same samples as (E'-G'), cropped to remove overlying roof cells, in a similar method to that shown by Movie S2. Intensity distribution of Sqh-GFP along the floor-midline boundary exhibits a peak near the expected location of intercalation (red arrowheads).

We proposed that tube formation may be largely described by considering only the apical surface of the follicle cells. Moreover, the localization patterns of myosin and Baz suggest that the forces driving the formation of the tube may also be apical. Based on these two observations, we hypothesized that the early steps of appendage morphogenesis, from the out-of-plane bending of the primordium to joining of the floor domain, may be explained by a mechanism that accounts only for processes on the apical side of the epithelium. To explore this idea, we turned to computational modeling.

Mathematical model of cell and tissue shapes during appendage formation

To focus on cellular dynamics on the apical side of the epithelium, we used a vertex model, following the approach that has been used to model cell sheets in other contexts (Farhadifar et al., 2007; Honda, 1983; Landsberg et al., 2009; Nagai and Honda, 2001; Nagai et al., 1988). These models represent each cell by a polygon with vertices and edges shared between adjacent cells. The state of this model epithelium is characterized by the coordinates and connectivity of the vertices. Dynamics of this system are predicted based on the following expression for total energy of the system (Farhadifar et al., 2007):

$$E=\sum _{\alpha }(a_{\alpha }{(A_{\alpha }-{A^{(0)}}_{\alpha })}^2+b_{\alpha }{L_{\alpha }}^2)+\sum _{<i,j>}{\sigma }_{\mathit{\text{ij}}}{l}_{\mathit{\text{ij}}}.$$

The first term in this expression corresponds to an area elasticity, where A_α is the actual area of cell α, A⁽⁰⁾_α is the preferred area, and a_α is the elasticity coefficient. Similarly, the second term corresponds to perimeter elasticity, with L_α as the perimeter and b_α as the elasticity coefficient of cell α. In other words, the second term gives rise to a spring force, with "preferred perimeter" set to zero; this is based on the idea that there might be a ring of actomyosin contractility around the apical surface of the cell. The third term describes line tension, where l_ij is the length of the edge connecting vertices i and j , and σ_ij is the tension coefficient. This term corresponds to a constant tension force along membranes, and comes from empirical characterization of many types of interfaces.

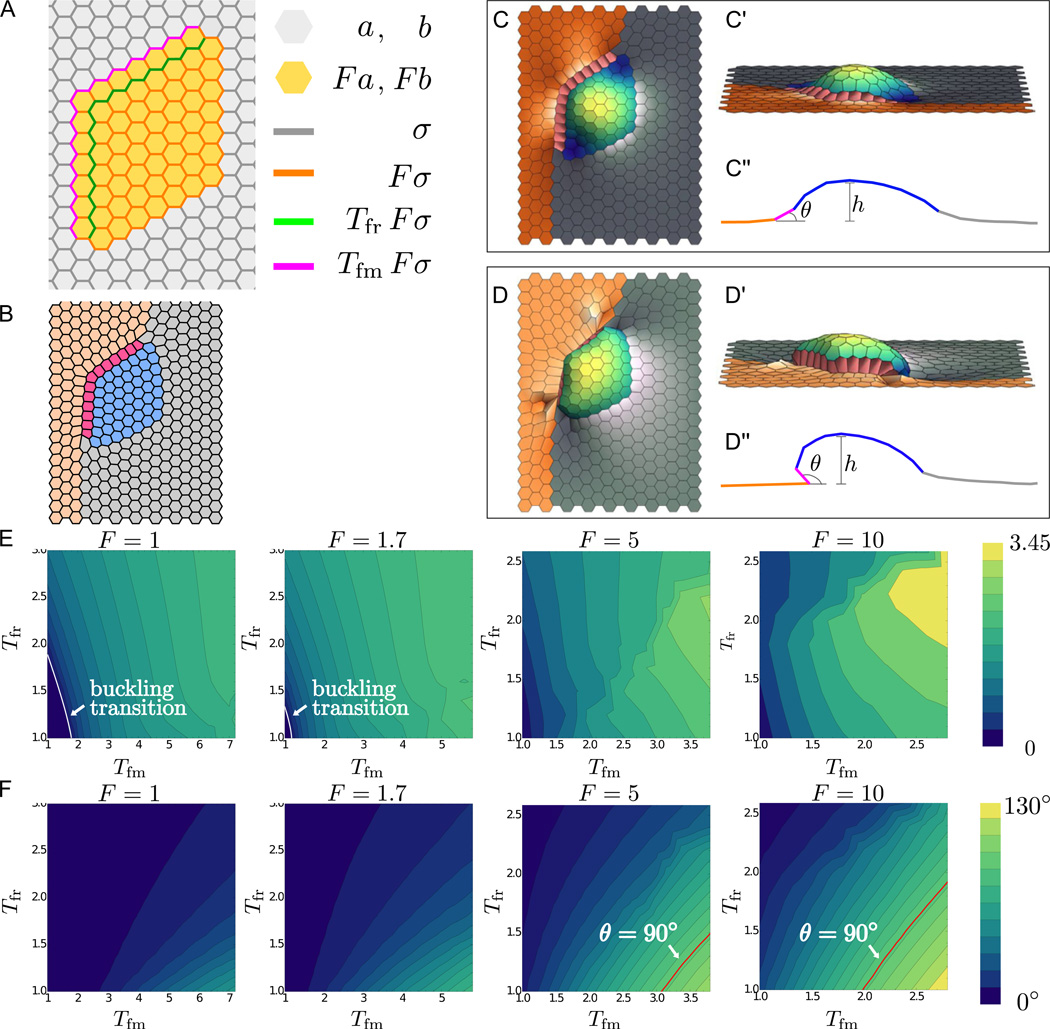
To adapt this model to our system, we need to distinguish cells of four different types (Figure 1B). We start with a hexagonal array, where cells of different types are assigned parameter values that represent hypothesized differences in mechanical properties (Figure 5A).

Figure 5. Computational modeling for out-of-plane bending of the appendage primordium.

(A) Vertex model of a dorsal appendage primordium, showing different cell types, distinguished by different values of parameters in the energy function. Parameter value assignments are indicated by color.

(B) Two-dimensional equilibrium state predicted for the patterned arrangement of cell properties in (A). Gray indicates main body cell assignments, orange indicates midline cells, red indicates floor cells, and blue indicates roof cells. Equilibrium state results from a simulation where vertices are confined to two dimensions; tension multiplicative factors are T_fm = 2, T_fr = 2, and F = 5. Larger cable tensions lead to straight edges; this result is reminiscent of the initial stage of tube formation when straight cell edges appear at roof-midline and roof-floor boundaries.

(C-D") 3D modeling of tissue deformation: The out-of-plane bending of appendage primordium is represented in top (C,D) and side views (C',D'), and as a schematic of a vertical cut through the tissue (C",D"). In panels (C-C"), we use the same parameters as in (B), but allow the vertices to move in all three dimensions; in this case, the tissue buckles out of plane. For panels (D-D"), we put larger T_fm and smaller T_fr values from panel (B-C"), with T_fm = 4, T_fr = 1.4, and F = 5 remaining the same. For these parameters, the floor domain bends under the roof cells.

(E) Heat maps indicating the maximum height h of the appendage cells (schematically represented in C" and D") in the steady state buckled configuration, plotted as functions of T_fm and T_fr for various values of the multiplicative factor F. The buckling transition, where h starts to be different from 0, is indicated on the heat maps by the white line. No such transition exists for F = 5 and F = 10 since h at T_fm = T_fr = 1 is different from zero.

(F) Heat maps indicating the angle θ of the corner floor cell with respect to the plane defined by the neighboring midline cell (schematically represented in C" and D") in the steady state buckled configuration, plotted as functions of T_fm and T_fr for various values of the multiplicative factor F. The θ = 90° line is indicated in red and corresponds to parameter values for which floor cells begin to twist underneath roof cells, such that left of this line, we have θ < 90° and right of this line, we have θ < 90°.

As a first test of this model, we computed equilibrium states corresponding to different parameter values. In particular, we examined the effects of high tension within the appendage-forming domain and along the floor-midline and floor-roof boundaries. We chose our midline and main body cells to have the fixed energy parameter values a, b, and σ used to model Drosophila wing disc epithelium (Farhadifar et al., 2007; Landsberg et al., 2009). We represent higher contractility and stiffness due to myosin accumulation in the appendage primordium by assigning parameters a_α, b_α, and σ_ij for the roof and floor cells to be a factor of F larger than those for midline and main body cells. To model the myosin cables observed in the tissue (Figure 4A), we set the tensions of the floor-midline and floor-roof edges to values larger than those elsewhere in the appendage-forming cells by factors of T_fm and T_fr, respectively. As expected, the equilibrium shape in two dimensions exhibits two key features of the cell outlines in Figure 1E: the rectangular shape of the floor cells and their smooth boundaries (Figure 5B).

Patterned apical forces are sufficient to cause three-dimensional deformation

In addition to influencing cell shapes, the two-dimensional pattern of line tensions along the apical surface may also lead to three-dimensional tissue deformation. To describe such out-of-plane deformations, we extended the traditional vertex model by allowing the vertices to move in three dimensions. Using the same parameter values as Figure 5B, but allowing this additional degree of spatial freedom, we find equilibrium shapes in which the roof and floor cells move out of plane (Figure 5C-C"), in a fashion similar to the early stages of appendage formation (Figure 1F,I-J). With some alterations in parameters, specifically with increasing edge tension for the floor-midline boundary while decreasing edge tension for the floor-roof boundary, the model can reproduce more advanced stages of appendage formation, where the floor cells bend underneath the roof cells (Figure 5D-D" and Figure 2B).

To test the robustness of these results, we explored the effects of varying T_fm, T_fr, and F. For values of these parameters that are low, the equilibrium state of the tissue is flat, but for higher values of any of these parameters, the tissue is no longer flat (Figure 5E). Thus, the three-dimensional deformation of the system can be induced by increased cable tensions, increased roof and floor cell tensions and stiffness, or a combination of these two factors. Although there is a wide range of parameters for which the tissue bends, there is a smaller range of parameters for which the floor cells bend underneath the roof cells (Figure 5F); in particular, tension along the floor-midline boundary must be sufficiently greater than tension along the floor-roof boundary. This agrees well with our observations that, although early myosin localization is restricted to the floor-roof boundary (Figure 4C, C'), myosin levels along the floor-midline boundary increase later as the tissue deforms and eventually surpass the myosin level in the floor-roof boundary (Figure 4D-G, D'-G').

To address how three-dimensional changes arise in this model, we show that the out-of-plane state is a buckled state of the apical surface, resulting from a buckling instability. Specifically, we found that for the same set of parameters beyond some critical values, the model admits multiple steady state solutions. One of these steady states is flat (Figure 5B) but is shown to be unstable (see Methods) with respect to arbitrarily small three-dimensional perturbations. This state, which may be computed by preventing out-of-plane displacements (see Methods), coexists with a steady state that is stable and deformed in three-dimensions (Figure 5C). The stable, bent state is the one observed in simulations.

Dynamics of ordered intercalations

Tissue deformations during the early steps of appendage morphogenesis can be modeled without considering cell neighbor exchanges. However, neighbor exchange is a central feature of later stages of appendage formation. Thus, to test whether patterned tension may be sufficient to explain ordered intercalation, we implemented cell neighbor exchange in the form of T1 transitions (Figure 6B), as has been done by other authors (Farhadifar et al., 2007; Honda, 1983; Landsberg et al., 2009; Nagai and Honda, 2001; Nagai et al., 1988). We examined not only the final equilibrium state, but the time-evolution of the system as well.

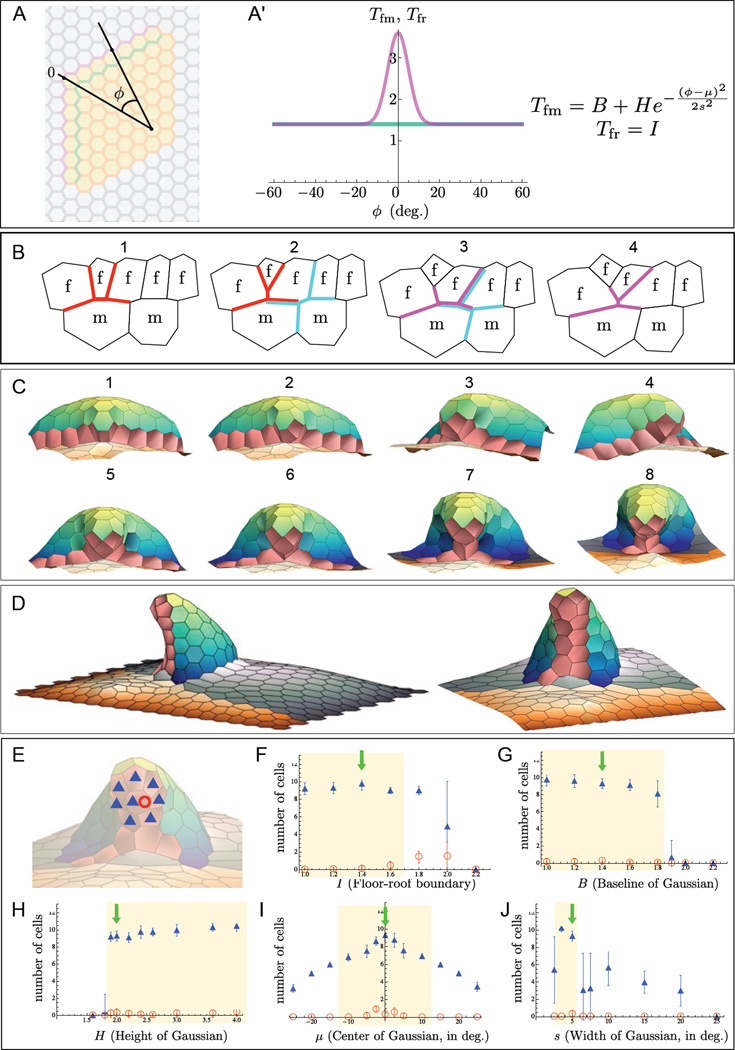
Figure 6. Computational modeling of ordered intercalation during tube formation.

Computational modeling of tension-driven cell intercalations. In these simulations, tensions along the border between the floor and midline cells vary as a function of angle phi along the anterior border of appendage primordium.

(A-A’) The spatial pattern of tensions along the floor-midline border is chosen as a Gaussian function (A', magenta curve) of the angle indicated in (A). As before, the tensions along the floor-roof border are constant (A', green curve). More generally, taking the floor-midline cable to have a Gaussian distribution of tension and the floor-roof cable to have a constant distribution of tension, the most basic form of the tension distributions, described as functions of the angle ϕ illustrated in (A) are: T_fm (ϕ) = B + He^{−(ϕ−µ)2 /(2s2)} and T_fr (ϕ) = I (A'); we test the sensitivities of appendage formation to these distributions in (E-J).

(B) Schematic representation of a sequence of three T1 transitions that result in two floor cells losing their floor-midline edges and gaining floor-floor edges. Similar colors in successive panels indicate the same T1 junction, showing the "before and after" connectivities of the junction.

(C-D) A representative sequence of cell intercalations predicted by the computational model for the following set of parameters: T_fm (ϕ) = 1.4 + 2e^{−ϕ2 / 50}, T_fr (ϕ) = 1.4, and F = 10. The initial condition for this simulation corresponds to the out-of-plane bent state of the primordium, computed for T_fm = 2.8, T_fr = 1.4, and F = 10. Panels in (C) indicate a sequence of eight T1 junctions that result in the loss of a floor-midline edge and a corresponding formation of a floor-floor edge. (D) Appendage formed at the end of the simulation, where the first image indicates a side view of the whole tissue, and the second image indicates a zoomed-in anterior view. See also Movie S3 for additional simulation results.

(E-J) Sensitivity analysis investigating the dependence of appendage formation on the distribution of tension along the floor-roof and floor-midline cables. Taking the parameters used for the simulation in parts (C-D) with B = 1.4, H = 2, µ = 0, s = 5, and I = 1.4 (green arrows in (F-J)) as a point of comparison, we varied each parameter separately, simulating the appendage formation 20 times to account of the role of noise, added to aid the resolution of the T1 cell junctions in simulations. Shown here are the computed average and standard deviation of the two scores defined in (E) that were designed to measure realistic dorsal appendage formation.

(E) Illustration of scoring scheme for plots. We compute two scores for every final equilibrium configuration resulting from the application of tension distributions. Blue triangles indicate the number of floor cells (out of 13) that are not in contact with midline or mainbody cells; red circles indicate the number of floor cells that are completely surrounded by other floor cells. The example here has a scores of 8 (indicated by blue triangles) and 1 (indicated by red circles).

(F-J) Sensitivity analysis. The interpretation of the parameters is indicated on the x-axes of the plots. By rough visual estimation, a large number of blue triangles (approximately less than 6) and a small number of red circles (approximately less than 1) indicate "good-looking" appendages; these regions are highlighted in yellow in (F-J). The simulations are not sensitive to changes in most of the parameter values; there is a range of parameter values for which appendages form successfully.

We began with a pattern of parameters that, when modeled without allowing neighbor exchange, result in floor cells being bent underneath the roof cells, similarly to Figure 5D. When modeled with neighbor exchange allowed, the same parameters lead to insertion of some main body cells between the floor and midline cells due to differential tension at the corners (results not shown). Since this is quite different from the experimentally observed pattern of intercalations, we then explored what patterns of parameters might lead to the experimentally observed rearrangements.

We found that simply changing the floor-midline cable tension from a spatially uniform distribution to a distribution peaked near the apex (Figure 6A-A') was sufficient to induce spatially ordered intercalation of the floor cells and produce an appendage-like structure (Figure 6C-D). To see if this non-uniform tension might be biologically plausible, we looked more closely at the distribution of myosin and found that there is indeed a spatial pattern of myosin concentration along the floor-midline boundary, with a peak near where intercalation occurs (Figure 4E"-G"). We then explored the effect of varying the shape and amplitude of the tension distributions along the floor-midline and floor-roof cables in the simulations. Appendage formation is most sensitive to the width of the peak in the floor-midline tension distribution and is robust within a relatively wide range of values for each of the other parameters we tested (Figure 6E-J).

The origin of ordered intercalation in the model can be rationalized as follows: Due to the hypothesized distribution of tensions, the floor-midline edges near the apex of the primordium pinch to form T1 junctions. These junctions then resolve in favor of new floor-floor boundaries because these boundaries have lower energy than the floor-midline boundaries. This intercalary event then brings new floor-midline interfaces towards to the center where the tensions are again higher, and the process is repeated (Figure 6B).

In the first formulation of the 3D vertex model, we started with a flat sheet and investigated whether 3-dimensional deformations of the tissue could occur due to buckling strictly as a result of patterned tensions, without allowing for cell neighbor rearrangements (Figure 5). In the second formulation of the model, we started with an already buckled sheet, but allowed neighbor exchange, to investigate the effect of different patterns of tension on ordered intercalation; we found that a peaked distribution of tension on the floor-midline boundary is required for proper intercalation and appendage formation (Figure 6). We then tested a model that always allowed neighbor exchange, with the same pattern of tension described in Figure 6, and found that this model could produce a similar tube from a nearly flat sheet (Movie S3).

Discussion

The formation of three-dimensional structures from epithelial sheets is a key feature of embryonic development. The Drosophila egg chamber provides a powerful model for studying these processes (Berg, 2005; Horne-Badovinac and Bilder, 2005). We analyzed how the dorsal appendage tubes emerge from the follicular epithelium. We found that tube formation in this system preserves the integrity of the follicular epithelium and proceeds through a combination of sheet bending and lateral cell rearrangements. Based on the localization patterns of myosin and Baz, we hypothesized that these events are caused by forces within the apical surface of the sheet. The special feature of our model is that it results in tissue transformations similar to those observed experimentally utilizing tensions generated exclusively in the 2D apical surface. Note that previous 3D extensions to the vertex model have modeled cells as three-dimensional prisms (Honda et al., 2004). In contrast, our approach involves allowing an essentially 2D object, the apical surface of the epithelial sheet, to move and deform in 3D space. The morphological changes in our model are driven by apical processes, without consideration of other cellular features such as volume constraints and active processes on the basal surface. At this point, the feasibility of this model is supported mainly by our computational studies that demonstrate how a pattern of tensions within a sheet can first bend the sheet and then initiate ordered intercalations, forming the seam of the tube. The patterns of apical tension predicted by this model agree qualitatively with the localization patterns of myosin in appendage primordial at different stages of tube formation. In the future, however, this model should be tested by direct measurements of tensions, for example by laser ablation, and extended to account for processes on the basolateral cell surfaces as well as the processes associated with tube elongation (Boyle et al., 2010; Dorman et al., 2004).

Several mathematical models have been proposed for bending of cell sheets (Odell et al., 1981; Weliky and Oster, 1990). One mechanism, working in both plants and animals, relies on spatial differences in cell proliferation, which causes tissue deformations (Hannezo et al., 2011; Liang and Mahadevan, 2011). Since the follicle cells do not divide during the stages analyzed in this work, this mechanism does not apply to dorsal appendage morphogenesis. Other mechanisms, such as those put forward for vertebrate neurulation and ventral furrow formation in Drosophila, work through apical constriction, which occurs in our system as well (Brodland et al., 2010; Odell et al., 1981). However, one additional element common to these models is that bending is generated by a difference in apical versus basal properties (Davidson, 2012). This clearly does not drive dynamics in our model, which considers only the apical surfaces. Instead, out-of-plane displacements of the appendage primordium can be understood as a manifestation of buckling, whereby mechanical forces within the sheet give rise to states that can be either flat or bent, with the bent state having a lower energy. It will be interesting to explore whether similar models can predict out-of-plane deformations in other systems, such as those seen during eversion of imaginal discs (Fristrom, 1976; Taylor and Adler, 2008).

In our model, patterned apical tension is sufficient to explain not only buckling but also ordered intercalation. Although cell intercalation in the simulations is spatially ordered in a manner reminiscent to that seen in live imaging, there are some differences that should be interesting to explore in the future. In the imaging data, the floor cells eventually form two rows of floor cells separated by a relatively straight seam, while in the simulations, the seam is more uneven and sometimes disrupted by the presence of one or more floor cells between these rows, as indicated by the red circles in Figure 6E-J. This suggests the possible existence of additional mechanisms for highly ordered intercalation, beyond those included in our model. One potential mechanism to explore further both experimentally and computationally is the possible formation of rosettes, since recent studies in other systems indicate that the use of rosettes in addition to T1 transitions may increase the efficiency of intercalation-mediated processes such as migration and tissue elongation (Tamada et al., 2012; Trichas et al., 2012).

In our model of dorsal appendage formation, patterned line tension plays a key role. Future work will be needed to address the molecular mechanisms by which patterns of tension are established. Included among the genes with patterned expression in the late follicular epithelium are several that encode proteins involved in cytoskeleton regulation or cell-cell adhesion (Dinkins et al., 2008; James et al., 2002; Jordan et al., 2005; Wahlström et al., 2006; Ward and Berg, 2005a; Yakoby et al., 2008; Zartman et al., 2009). Mutations in some of these genes result in dorsal appendage defects (Kleve et al., 2006; Laplante and Nilson, 2006; Zartman et al., 2008), but whether these genes work through regulating tension or through some other process has been largely unexplored.

Tube formation is a common outcome of epithelial morphogenesis (Lubarsky and Krasnow, 2003). Sealing or closure of the tube is one of the least understood aspects in systems where tubes form by wrapping, as in the vertebrate neural tube or the Drosophila ventral furrow (Leptin, 2005; Wallingford, 2005). The dorsal appendage tube appears to be sealed by spatially ordered lateral cell rearrangements. This suggests that lateral rearrangements may play a role in seam sealing in other cases of wrapping as well (Pyrgaki et al., 2010). Lateral rearrangements alone cannot be sufficient to drive morphogenesis in cases where the tube becomes discontinuous from its parental sheet, but future studies may reveal whether lateral rearrangements nevertheless play a key role in such systems.

Experimental Procedures

Fly Stocks and Genetics

The following stocks were used: Oregon R as wild type, rho-LacZ 2.2 (Ip et al., 1992), Nrg-GFP (G305; (Morin et al., 2001)), E-cadherin:GFP (DE-Cad:: GFP; (Huang et al., 2009)), and Sqh-GFP (RLC-GFP; (Royou et al., 2002)). The rho>Baz:GFP flies carried one copy each of rho-GAL4 BigParent (unpublished; a generous gift from Celeste Berg) and UAS-Baz:GFP (Benton and St Johnston, 2003).

Immunohistochemistry

Immunostainings were carried out as described in (Ward and Berg, 2005b), except that PSBTwn with 1% Bovine Serum Albumin (Sigma-Aldrich) was used for blocking and antibody steps. Before imaging, samples were passed through a dilution series of glycerol/PBS, and imaged in 50% glycerol/ 50% PBS in glass bottom dishes (MatTek). Primary antibodies included anti-DE-cadherin (rat, DSHB, 1:50), anti-GFP (GFP-Booster Atto488, Chromotek, 1:200 for Figure 4. Alexa Fluor 488-conjugated rabbit anti-GFP, Invitrogen, 1:500 for Figure 2A-D), anti-Bazooka (rabbit, 1:500, (Blankenship et al., 2006)). Secondary antibodies (Alexa Fluor conjugated, Invitrogen) were used at 1:200.

Live imaging

Individual egg chamber were cultured similarly to published methods (Dorman et al., 2004; Prasad et al., 2007) in a glass bottom dish (MatTek) with Schneider's Medium containing 10% Fetal Bovine Serum and 0.6× Penicillin/Streptomycin. Additionally, CellMask Deep Red (Invitrogen, 1:1000) was added to monitor health of the sample. A stack of 50 microns, taken at 1 micron intervals, was imaged every 2.25 minutes.

Microscopy and image processing

Confocal imaging was done on either a Leica SP5 or a Nikon A1. A 63× (NA 1.4) or 60× (NA 1.4) oil immersion objective was used for imaging of fixed samples, and a 63× (NA 1.3) glycerin immersion objective was used for live imaging. Figures 1D-H, 2A-D" and 4B-B' are maximal projections of z-series produced using ImageJ (Schneider et al., 2012). Figures 1I-K, 3A-I, 4A-A', and 4C-G" and Movie S2 are 3D reconstructions produced using Volocity 3D Image Analysis Software (PerkinElmer). In Figure 3, the images are rotated and in some cases (3D-I) cropped to remove roof cells which would block the view of floor cells. In Figure 4A-A', 4C-G', the images are rotated and cropped to remove signal from the basal surface, which would block the view of the apical surface. Figures 4E"-G" are cropped to remove overlying roof cells as well.

Mathematical modeling

The equilibrium vertex model is described in the Results section. The temporal model is formulated from the energy-based one by assuming the over-damped limit for dynamics, in which forces equivalent to the negative gradient of energy are completely balanced by viscous forces in the ambient fluid in which the vertices move. From this limit, we derive that the velocity of a vertex is proportional to force on the vertex.

For 2D simulations, the initial configuration is a uniform hexagonal array of cells, with the initial area of each cell chosen to be the equilibrium area calculated for a single main body cell in an infinite array, with parameters taken from (Farhadifar et al., 2007) . All 2D simulations were done either by not including a z-component in the calculation or setting the z-component to 0 at all time steps. For out-of-plane 3D simulations, there are multiple equilibrium states for some ranges of parameters. For the 3D simulations described in Figure 5C-D, the initial configuration was the unique equilibrium for F=5, T_fr=T_fm=1. For 3D simulations with intercalation, the initial configuration corresponded to one of the equilibrium states from the analysis without T1 junctions for F=10, T_fr= 1.4, T_fm=2.8. Areas of polygonal cells in 3D were defined as follows: we computed the average position of the vertices, used this centroid to define a triangulation of the polygon, and summed the areas of the triangles. For simplicity, we used fixed boundary conditions at the edges of the simulation domains. Equations were propagated using a second-third order Bogacki-Shampine method implemented in C++.

For the out-of-plane 3D model without cell rearrangements, two vertices participating in a T1 junction were fused into a single vertex with four edges connected to it. This can be generalized to form vertices connected to more than four edges. For the 3D model with neighbor exchanges, the threshold edge length for implementing a T1 transition is twice the tension of the edge multiplied by the mobility constant and by the size of the time step. For a T1 junction that forms repeatedly, we implemented a step in which the tension of the bond that results from the resolution of the junction is either multiplied or divided by a factor p after every additional successive instance in which the junction forms, where multiplication or division by p is chosen at random in each instance. The factor p depends on the number of successive times the junction has already formed. For the 3D model allowing T1 transitions, a small pressure term was added as follows: the normal unit vector for each cell, computed as the weighted average of the normal vectors of the triangles from the triangulation above, was multiplied by cell area and a proportionality constant corresponding to pressure. This value, corresponding to an additional force component, was distributed equally among all vertices of the cell. This pressure term was included to bias the simulation to avoid irregular concavities in the sheet.

To investigate linear stability of computed equilibrium states, a steady state was found from the two-dimensional model, as described above. We then performed linear stability analysis of this state by computing and diagonalizing the corresponding Jacobian, taking into account perturbations in the z direction. For a range of parameter values, this Jacobian is found to have a single positive eigenvalue, indicating that the system is linearly unstable to perturbations in the z direction. In contrast, the 3D steady state configurations shown in Figure 5C,D can be shown to be stable equilibria, both by time integration and linear stability analysis.

Highlights.

Drosophila eggshell appendages form by sheet bending and ordered cell intercalations.

Dynamics of morphogenesis correlates with predicted patterns of line tensions.

Two-dimensional pattern of forces drives three-dimensional morphogenesis in silico.