Likelihood Ratios for Glaucoma Diagnosis Using Spectral Domain Optical Coherence Tomography

Abstract

Purpose

To present a methodology for calculating likelihood ratios for glaucoma diagnosis for continuous retinal nerve fiber layer (RNFL) thickness measurements from spectral domain optical coherence tomography (spectral-domain OCT).

Design

Observational cohort study.

Methods

262 eyes of 187 patients with glaucoma and 190 eyes of 100 control subjects were included in the study. Subjects were recruited from the Diagnostic Innovations Glaucoma Study. Eyes with preperimetric and perimetric glaucomatous damage were included in the glaucoma group. The control group was composed of healthy eyes with normal visual fields from subjects recruited from the general population. All eyes underwent RNFL imaging with Spectralis spectral-domain OCT. Likelihood ratios for glaucoma diagnosis were estimated for specific global RNFL thickness measurements using a methodology based on estimating the tangents to the Receiver Operating Characteristic (ROC) curve.

Results

Likelihood ratios could be determined for continuous values of average RNFL thickness. Average RNFL thickness values lower than 86μm were associated with positive LRs, i.e., LRs greater than 1; whereas RNFL thickness values higher than 86μm were associated with negative LRs, i.e., LRs smaller than 1. A modified Fagan nomogram was provided to assist calculation of post-test probability of disease from the calculated likelihood ratios and pretest probability of disease.

Conclusion

The methodology allowed calculation of likelihood ratios for specific RNFL thickness values. By avoiding arbitrary categorization of test results, it potentially allows for an improved integration of test results into diagnostic clinical decision-making.

INTRODUCTION

Several imaging technologies have been introduced with the purpose of objectively quantifying structural damage to the optic disc and retinal nerve fiber layer (RNFL) in glaucoma. As the number of available technologies increases, difficult decisions arise about which tests should be used and how to incorporate their results in clinical practice. Sensitivity, specificity and the area under the receiver operating characteristic (ROC) curve have traditionally been used as measures of diagnostic accuracy. Although well established, these measures have some limitations in clinical use, which arise mainly from the fact that they are population measures, i.e., they summarize the characteristics of the test over a population. However, in the diagnostic process, clinicians want measures that can be directly incorporated into the decision-making process for individual patients.

During the diagnostic process, a clinician combines medical history and clinical examination to estimate the probability that the disease is present. If there is still uncertainty with regard to the presence of disease, additional diagnostic tests can be performed. The purpose of the diagnostic test will be to modify the pretest probability of disease into a more conclusive post-test probability of disease. Diagnostic likelihood ratios can be directly used to modify the initial suspicion for disease (pretest probability) into a new probability of disease (post-test probability). The use of likelihood ratios has been proposed as the best way of incorporating results of diagnostic tests into clinical decision-making according to the principles of Evidence-Based Medicine.¹ Moreover, like sensitivity and specificity, likelihood ratios have the property of not being affected by the prevalence of the disease.

A few previous studies have reported likelihood ratios for glaucoma diagnosis using optic disc and RNFL analysis from imaging instruments.^2–5 In these studies, results of the diagnostic tests were arbitrarily categorized into normal versus abnormal according to specific cut-offs. The dichotomization of test results with continuous outcomes may result in loss of information, because results that are markedly abnormal are grouped with results that are only mildly abnormal.^6–10 The loss of information is even more important when the patient’s test result is close to the established cut-off.⁶

In the present study, we apply a methodology for estimating likelihood ratios for glaucoma diagnosis that does not require arbitrary categorization of test results. This methodology allows the calculation of likelihood ratios for all values of the test with direct application to the calculation of post-test probability of disease. We demonstrate the methodology using RNFL thickness analysis with spectral domain optical coherence tomography (spectral-domain OCT). Finally, we propose a modified Fagan nomogram that can be used to facilitate the use of likelihood ratios for continuous RNFL thickness measurements into the diagnostic process at the clinical practice.

METHODS

This was an observational cohort study. Patients were recruited from the Diagnostic Innovations in Glaucoma Study conducted at the Hamilton Glaucoma Center (University of California, San Diego). Participants were longitudinally evaluated according to a protocol that included visits with a comprehensive clinical examination and several imaging and functional tests. All participants who met the inclusion criteria described below were enrolled and all data were entered in a computer database. Informed consent was obtained from all participants. The University of California San Diego Human Subjects Committee approved all protocols, and methods adhered to the Declaration of Helsinki.

Each subject underwent a comprehensive ophthalmic examination, including review of medical history, best corrected visual acuity, slit-lamp biomicroscopy, intraocular pressure measurement using Goldmann applanation tonometry, gonioscopy, dilated fundoscopy examination using a 78-diopter lens, stereoscopic optic disc photography, and standard automated perimetry with 24-2 Swedish Interactive Threshold Algorithm (Carl Zeiss Meditec, Inc., Dublin, CA). To be included subjects had to have best corrected visual acuity of 20/40 or better, spherical refraction within ± 5.0 D, cylinder correction less than 3.0 D and open angle with gonioscopy. Subjects with coexisting retinal disease, uveitis or non-glaucomatous optic disc neuropathy were excluded from the study.¹¹

Eyes were classified as glaucomatous if they had repeatable (at least three consecutive) abnormal visual field test results, defined as pattern standard deviation with a P value < 5% and/or a glaucoma hemifield test result outside normal limits, regardless of the appearance of the optic disc. Visual fields with more than 33% fixation losses, more than 33% false negative errors or more than 15% false-positive errors were excluded. The only exception was the inclusion of patients with more than 33% of false negative errors and advanced disease stage (mean deviation lower than – 12dB). In addition all visual fields were reviewed by the Visual Field Assessment Center (University of California at San Diego) and masked to the results of other tests.¹¹ Visual fields were reviewed and excluded in the presence of artifacts such as eyelid or rim artifacts, fatigue effects, inattention or inappropriate fixation. Visual fields were also reviewed for the presence of abnormalities that could indicate diseases other than glaucoma, such as homonymous hemianopia.

We also included in the glaucoma group patients with preperimetric glaucomatous damage. The inclusion of these eyes required longitudinal follow-up to determine their ultimate diagnosis, as described in previous publications.^{3, 12–16} These eyes had normal visual field exams at the time of imaging, but had history of documented evidence of progressive glaucomatous change in the appearance of the optic disc, as assessed by simultaneous stereoscopic photographs (Topcon Instrument Corporation of America, Paramus, NJ). The evidence of progressive glaucomatous damage had to be present before the imaging test date. For evaluation of progressive optic disc damage, stereoscopic sets were examined using a stereoscopic viewer (Asahi, Pentax, Tokyo, Japan). All stereophotographs were evaluated by 2 experienced graders masked to the subject’s identity, chronological sequence of the stereophotographs, and to other tests results. For inclusion, stereophotographs needed to be graded adequate or better. Definition of change was based on focal or diffuse thinning of the neuroretinal rim, increased excavation, or enlargement of the RNFL defects. Changes on rim color, presence of disc hemorrhages, or progressive peripapillary atrophy were not sufficient for characterization of progression. Discrepancies between the 2 graders were resolved by either consensus or adjudication of a third experienced grader. The use of this composite reference standard for glaucoma diagnosis allowed us to evaluate likelihood ratios for continuous RNFL thickness measurements in patients with a broad spectrum of disease severity – as patients with visual field loss and patients with normal visual fields, but confirmed progressive glaucomatous damage, were included.

Healthy eyes had intraocular pressures of 21 mmHg or less with no history of increased intraocular pressure, a normal clinical examination, and at least two reliable baseline normal visual field tests. A normal visual field was defined as a mean deviation and pattern standard deviation within 95% confidence limits and a glaucoma hemifield test result within normal limits. Healthy subjects were recruited from the general population or from spouses and relatives of patients.

Spectralis Spectral-domain OCT

RNFL thickness measurements were obtained using the Spectralis spectral-domain OCT (software version 5.3.3.0, Heidelberg Engineering, Carlsbad, CA). Details of its operation have been published elsewhere.^{15, 17–19} The high-resolution protocol was utilized, obtaining 1536 A-scans from a 3.45mm circle centered at the optic disc, providing an axial resolution of 3.9μm and a lateral resolution of 6.0μm. To increase the image quality, the Spectralis spectral-domain OCT includes an automatic real-time function that gathers multiple frames (B-scans). On average 20.0 B-scans per eye were used to generate the peripapillary RNFL curve. The images were then averaged for noise reduction. The quality score ranges from 0dB (poor) to 40dB (excellent). All images were reviewed by experienced technicians at the Imaging Data Evaluation and Assessment Center.¹¹ To be included, images had to be centered, with accurate segmentation and had to have a signal strength > 15dB. For this study we estimated likelihood ratios for the global RNFL thickness (360° measure). We used this parameter because it represents a global measure of structural damage that has been shown to have good diagnostic performance in previous studies.^{18, 20}

Statistical Analysis

Descriptive statistics included mean and standard deviation for normally distributed variables and mean, median, first quartile and third quartile for non-normally distributed variables (determined by the Kolmogorov-Smirnov normality test). Normally distributed variables were compared between groups using the two-sample t-test, while non-normally distributed variables were compared using the Wilcoxon rank-sum test. Chi-square test was used to test for differences in categorical variables between groups. Generalized estimating equations with robust standard errors were used to adjust for potential correlations between both eyes of the same individual.

The application of likelihood ratios in the interpretation of results of imaging instruments for glaucoma diagnosis has been detailed previously.^{2, 3} Briefly, likelihood ratio is the ratio between two probabilities, the probability of a given test result when the disease is present (true positive ratio), divided by the probability of the same test result when the disease is absent (false positive ratio).^{1, 21} Once determined, a likelihood ratio can be directly incorporated into the calculation of post-test odds of disease by using a formulation of the Bayes’ theorem which uses odds of disease.²²

The first step in the calculation of the post-test probability of disease is to calculate the pretest odds of disease from the pretest probability of the disease using the following equation:

$$\text{odds}=\text{probability}/(1-\text{probability})$$ (1)

Then, the likelihood ratio can be used to modify the pretest odds of disease into a new post-test odds of disease using this equation:

$$\text{post}-\text{test}\text{odds}=(\text{pretest}\text{odds})\times \text{likelihood}\text{ratio}$$ (2)

From the above formula it can be seen that a likelihood ratio of 1 means that the test provides no additional information about the presence of disease as the post-test odds will be equal to the pretest odds. Likelihood ratios higher or lower than 1 will increase or decrease the likelihood of disease, respectively.

Finally, we can calculate the post-test probability of disease from post-test odds of disease using the following equation:

$$\text{probability}=\text{odds}/(1+\text{odds})$$ (3)

Supplemental Figure 1, available at AJO.com, shows the steps necessary for the calculation of the post-test probability of disease and how the modified Fagan’s nomogram²² (described below) simplifies the process.

In the present study, likelihood ratios for continuous RNFL thickness values were estimated using the method described by Gu and Pepe.²³ Formulas used to derive likelihood ratios for continuous RNFL thickness measurements are included in the appendix.^24–31 Adjustments for the presence of both eyes and for differences in confounding variables (age and gender) between cases and controls were performed as described by Alonzo and Pepe.²⁷

All statistical analyses were performed with commercially available software (Stata version 11, StataCorp, College Station, TX). The alpha level (type I error) was set at 0.05.

RESULTS

The study included 262 eyes of 187 patients with glaucoma and 190 eyes of 100 control subjects. Table 1 shows demographic and clinical characteristics of the included subjects. Patients in the glaucoma group were significantly older than the subjects in the control group. In addition, there were more male patients in the glaucoma group. Glaucomatous eyes had, on average, significantly thinner RNFLs when compared to the control group.

Table 1.

Demographic and Clinical Characteristics of the Glaucoma and Control Groups Included in the Study

Characteristic	Glaucoma (n = 262)	Control (n = 190)	P Value
Age, ya	70.5 ± 11.1	53.1 ± 17.2	<.001
Sex, % male	74.6	25.4	<.001
Ancestry, % African-American	67.1	32.9	.143
MD, dBb	−4.3 (−5.6, −2.4, −1.2)	0.4 (−0.4, 0.6, 1.2)	<.001
PSD, dBb	4.8 (2.1, 3.3, 7.5)	1.5 (1.3, 1.5, 1.7)	<.001
Global RNFL thickness, μma	73 ± 15	97 ± 10	<.001

MD = mean deviation; PSD = pattern standard deviation; RNFL = retinal nerve fiber layer.

^aNormally distributed variables; represented by mean (standard deviation).

^bNon-normally distributed variables; represented by mean (first quartile, median, third quartile).

Figure 1 shows the relationship between global RNFL thickness and likelihood ratios greater than 1, i.e., likelihood ratios associated with increase in the probability of disease. As expected, the thinner the RNFL thickness measurement, the greater the associated likelihood ratio. Figure 2 shows the relationship between global RNFL thickness and likelihood ratios smaller than 1, i.e., likelihood ratios associated with decrease in the probability of disease. Thicker RNFL thickness measurements were associated with decreased likelihood ratios.

FIGURE 1.

Relationship between likelihood ratios for glaucoma diagnosis and global retinal nerve fiber layer thickness measurements for likelihood ratios values greater than 1, i.e., associated with increased post-test probability of disease.

FIGURE 2.

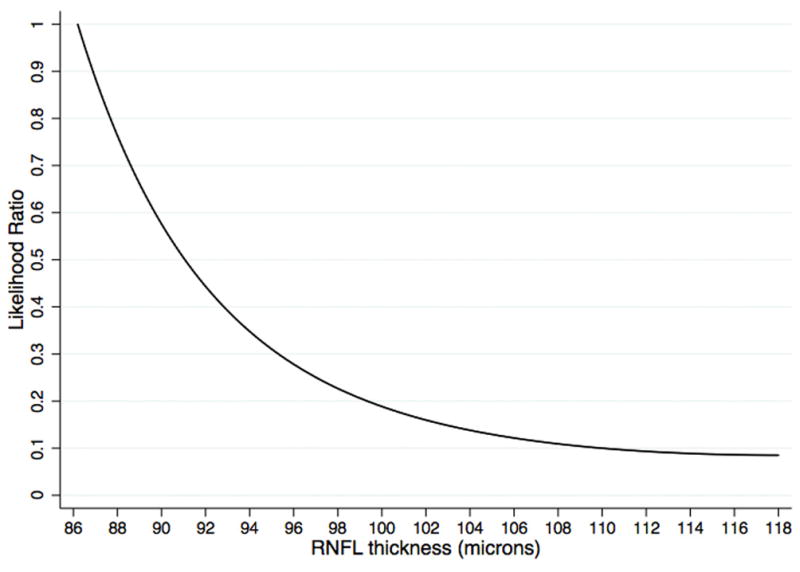
Relationship between likelihood ratios for glaucoma diagnosis and global retinal nerve fiber layer thickness measurements for likelihood ratios values smaller than 1, i.e., associated with decrease in the post-test probability of disease.

Figure 3 illustrates the relationship between post-test probability of disease and global RNFL thickness for arbitrary values of pretest probability of disease. Thinner RNFL values were associated with an increase in the post-test probability of disease. For example, as expected from Figure 3, a global RNFL thickness result of 70μm would have a large effect on the probability of disease modifying a pretest probability of disease from 30% to a new post-test probability of disease of 91%. For the same pretest probability of disease of 30% a global RNFL thickness result of 110μm would result in a post-test probability of 4%, almost excluding the presence of disease. However, an intermediate RNFL thickness result of 85μm would have an insignificant impact on the probability of disease, modifying the pretest probability of 30% to a similar post-test probability of 34%. Figure 4 illustrates the relationship between pretest and post-test probabilities of disease for arbitrary global RNFL thickness results of 70μm, 85μm and 110μm.

FIGURE 3.

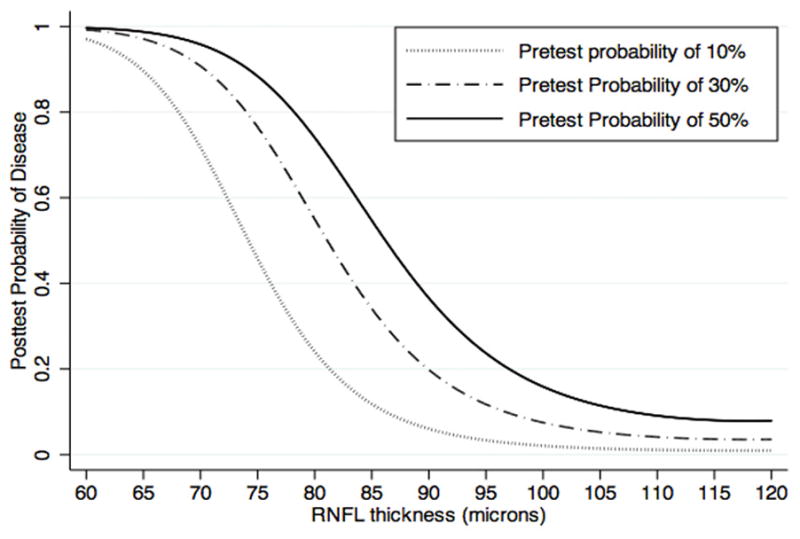
Relationship between post-test probability of disease for glaucoma diagnosis and retinal nerve fiber layer thicknesses.

FIGURE 4.

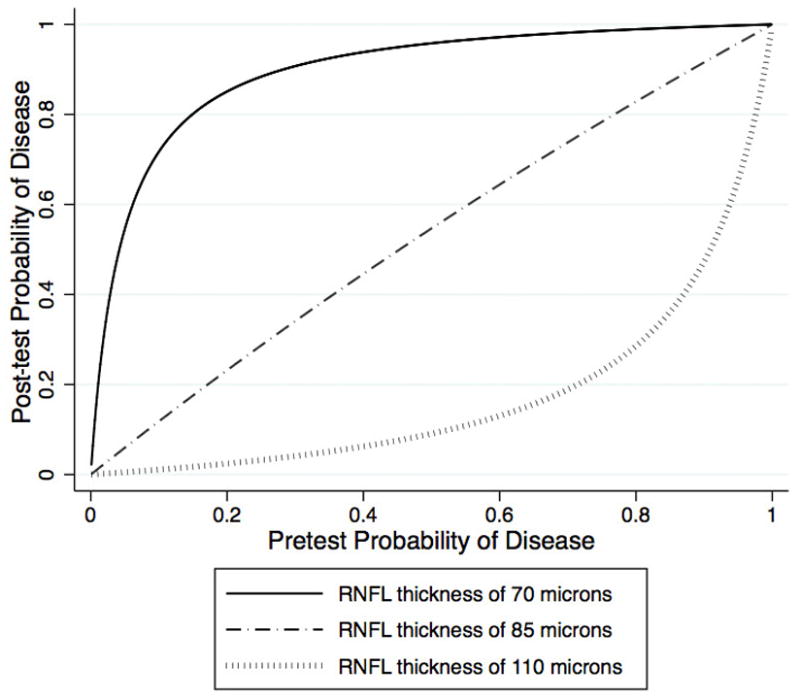
Relationship between post-test probability of disease for glaucoma diagnosis and pretest probability of disease.

Figure 5 shows a modified Fagan’s nomogram²², where the likelihood ratios in the center column were replaced by the corresponding RNFL thickness values. This nomogram can be used for a straightforward estimation of the post-test probability of disease according to the pretest probability of disease and continuous values of global RNFL thickness. A line drawn from the pretest probability of disease in the left column through the RNFL thickness result in the center column gives the post-test probability of disease in the right column.

FIGURE 5.

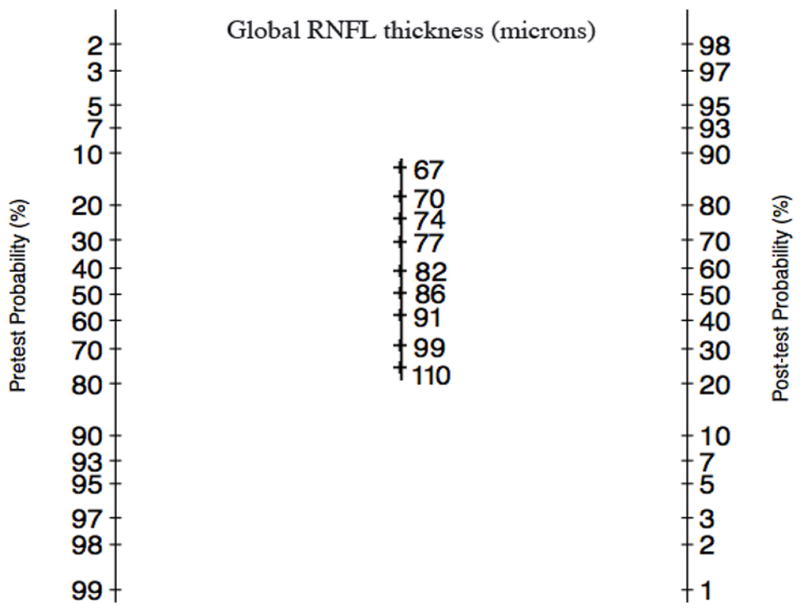
Modified Fagan’s nomogram for calculation of the post-test probability of glaucoma according to the pretest probability of glaucoma and continuous values of global retinal nerve fiber layer thickness.

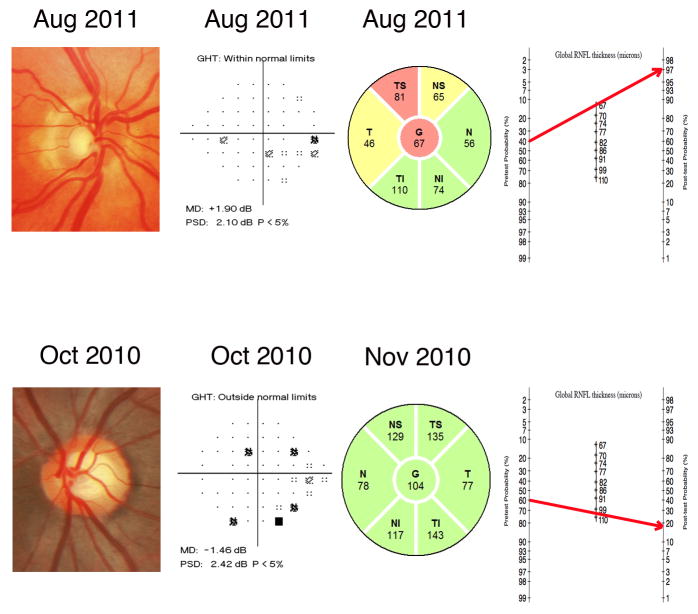
Figure 6 illustrates how likelihood ratios for continuous RNFL thickness measurements can be applied to the clinical practice with the help of the modified Fagan nomogram. After medical history, clinical examination, intraocular pressure and visual field exam the eye at the top was considered to have a pre-test probability of 40%. However, after analyzing the results of the spectral-domain OCT we could see that the RNFL thickness was 67μm. By applying the modified Fagan nomogram we calculated higher post-test probability of 97%. On the other hand, the eye at the bottom was considered to have a pretest probability of 60%. After spectral-domain OCT results showing a RNFL measurement of 104μm and with the help of the Fagan nomogram the post-test probability for glaucoma decreased to 18%.

FIGURE 6.

Examples of eyes included in the study illustrating the benefits of incorporating diagnostic likelihood ratios for continuous test results in the diagnostic process. Based on the medical history, clinical examination, intraocular pressure and visual field exam, the eye at the top was considered to have a pretest probability of 40%. The spectral-domain OCT measured a RNFL thickness of 67μm. By applying the modified Fagan nomogram we can see that the post-test probability increased to 97%. Conversely, the eye at the bottom was considered to have a pretest probability of 60%. The spectral-domain OCT measured a RNFL thickness of 104μm. By applying the modified Fagan nomogram the post-test probability decreased considerably to 18%.

DISCUSSION

In this study, we reported likelihood ratios for continuous values of RNFL thicknesses provided by spectral-domain OCT. To the best of our knowledge, this is the first study to report likelihood ratios for continuous values of a marker in glaucoma. Our results may have significant implications in the diagnostic process of glaucomatous damage, as specific post-test probabilities of disease can be assessed for individual values of RNFL thickness. Further, the methodology used in our study can be easily extended for calculation of likelihood ratios for other parameters and diagnostic tests.

Sensitivity and specificity have previously been used in several studies to report diagnostic accuracies of the spectral-domain OCT technology in glaucoma.^{18, 32–37} Sensitivity and specificity reflect the probability that a particular test result is positive or negative given the presence or the absence of the disease, respectively. However, knowledge of whether or not the disease is present would clearly obviate the need for an auxiliary test. That is, we apply diagnostic tests in clinical practice to patients in which the disease status is unknown. Therefore, sensitivity and specificity offer limited application for direct interpretation of results of diagnostic tests in individual patients. Similarly, the area under the ROC curve is important to compare diagnostic accuracies of ancillary tests, but has little intuitive clinical meaning and offers little help when a clinician wants to evaluate test results for an individual patient. The starting point of the diagnostic process occurs when the clinician combines the medical history with clinical examination in order to estimate the probability of the presence of disease, also known as the pretest probability. Then the results of an ancillary test can be used to modify the pretest probability, yielding a new post-test probability of disease. In other words, the post-test probability is the revised probability of the disease after the knowledge of the diagnostic test result. Likelihood ratios can be used in a practical way to derive the post-test probability of disease by applying the formulas previously provided in the methods section. This allows direct incorporation of diagnostic test results into clinical decision-making. For example, if a pretest probability of glaucoma in a patient suspected of having the disease is 50%, then by applying Equation 1 we can calculate the pretest odds in favor of the disease, which would be 0.5/(1 – 0.5) = 1. Let’s then assume that this same patient has a global RNFL thickness result of 75μm. From Figure 1 we can obtain a likelihood ratio of 8 for this result. By applying Equation 2, the revised post-test odds of glaucoma would be 1 ▢ 8 = 8. This post-test odds, by applying Equation 3, corresponds to a probability of 8/(8 +1) = 88%. Thus, the global RNFL thickness result has been used to revise an initial probability (pretest probability) of disease of 50% into a new probability (post-test probability) of 88%. In order to simplify the calculations exemplified above, the post-test probability of glaucoma for different global RNFL thicknesses can be directly inferred from the modified Fagan’s nomogram illustrated on Figure 5.

The printout of the Spectralis spectral-domain OCT displays classifications of RNFL thickness parameters according to comparisons to a normative database population. Although this categorization has the purpose of simplifying interpretation of results in clinical practice, it can lead to important loss of information and may cause distortions in the interpretation of test results, as widely different RNFL thickness values are potentially given the same diagnostic weight.^7–10 For example, using the conventional diagnostic approach, a clinician would classify an eye as abnormal if the measured RNFL thickness is below the 1% cut-off calculated from the distribution of values in the normative database. Such approach will lead to an “all-or-nothing” decision, which ignores that patients in identical categories may actually have very different probabilities of disease. Two eyes with RNFL thicknesses of 73μm and 65μm would both be categorized as outside normal limits using the conventional approach with no distinction made between them, as both thicknesses would be below the 1% cutoff of the normal population (74μm). However, considering the same pretest probability of 30% for both eyes, for example, the use of likelihood ratios for continuous RNFL thickness values would lead to different post-test probabilities of 83% and 97%. The same reasoning can be applied to eyes classified as within normal limits using the conventional approach. For example, two eyes with RNFL thicknesses of 81μm and 110μm would both be categorized as within normal limits. However, considering the same pretest probability of 30% for both eyes, the use of likelihood ratios for continuous RNFL thickness values would lead to very different post-test probabilities of 51% and 5%. Clearly, these eyes should not be seen as having the same probability for the presence of the disease, as it would be implied by the conventional approach.

In a previous study, Medeiros et al.² reported likelihood ratios for arbitrarily-defined cutoff intervals of RNFL thickness measurements from optical coherence tomography and scanning laser polarimetry. They found that thinner RNFL thickness measurements were associated with larger likelihood ratios. Our results are in agreement with this previous study. However, our investigation provides additional information by calculating likelihood ratios for continuous RNFL thickness measurements, avoiding any arbitrary categorization. Although our method requires some mathematical calculations, it could be easily implemented into standard software of imaging instruments so that clinicians would have direct availability to likelihood ratios and plots of post-test versus pretest probabilities of disease. This approach would provide clinicians with immediate information about the impact of a specific test result in changing the probability of disease.

Currently, there are no formal ways of calculating pretest probabilities in glaucoma diagnosis. An obvious pretest probability to consider would be the prevalence of the disease in the general population but this could not be applicable to clinic-based populations. Therefore, calculations of pretest probabilities are still a subjective component of diagnostic evaluation and can vary substantially among physicians. As clinicians evaluate a patient suspected of having glaucoma, they measure the intraocular pressure, evaluate the optic nerve and obtain visual field tests. If we fully knew the properties of each of these tests, one could move sequentially through them, incorporating each piece of information and continuously recalculating the probability of glaucoma, so that the post-test probability after one test would be the pretest probability before the other. In fact, clinicians do proceed in this way. However, because the formal properties (likelihood ratios) of these items are not available, they must rely on clinical experience and intuition to arrive at the pretest probability that precedes ordering a diagnostic test such as spectral-domain OCT. The correlation among the tests used in the diagnostic process is also an important consideration when using likelihood ratios. If the pretest probability before applying spectral-domain OCT was derived after using a diagnostic test that is highly correlated with spectral-domain OCT, this could affect the calculations of post-test probability using the results presented in our study. As the tests would not be independent, one could not simply multiply the pretest probability (obtained after applying the first test) to the likelihood ratio for the second test without taking into account their correlations. The use of multivariate approaches combining different tests may help overcome these limitations. Further studies should evaluate combined approaches for glaucoma diagnosis that could integrate spectral-domain OCT results with those of other medical tests.

In the present study, we used global RNFL thickness in order to provide a general description of our methodology for calculating likelihood ratios for different RNFL thickness values. Although global RNFL thickness has been described as having good accuracy for glaucoma diagnosis, it is likely that improved accuracy could be obtained by using sectoral RNFL thicknesses or combinations of parameters. Applications of likelihood ratio calculations for RNFL thickness measurements from sectors around the optic disc would have to take into account the inter-dependency among the values. A possible strategy would be to calculate an index combining sectoral measurements, such as in a linear discriminant function³⁸, and then calculate likelihood ratios for this index. The same approach could potentially be used for combining results from multiple instruments. Finally, it should be emphasized that RNFL thickness measurements are not interchangeable between different commercially available spectral-domain OCTs.¹⁷ As a consequence, specific results on likelihood ratios obtained for the Spectralis should not be extrapolated to other spectral-domain OCTs and calculations of likelihood ratios should be done for each instrument.

The cross-sectional design of our study required a control and a case group based on standard definitions about the presence or absence of glaucoma. Although these have been widely accepted and applied to most clinical diagnostic studies in the disease, it is difficult to properly establish an appropriate cut-off to separate healthy from glaucomatous subjects with current available reference standard tests. However, by calculating likelihood ratios for continuous RNFL thicknesses and post-test probabilities, we emphasized the magnitude of abnormality of the diagnostic test result, which helps overcome some limitations of the potentially artificial categorization of subjects into diseased versus non-diseased groups.

In conclusion, the methodology enabled calculation of continuous likelihood ratio values for specific global RNFL thickness measurements provided by the Spectralis. Our results can be used to provide a more accurate estimation of the post-test probability of disease by incorporating likelihood ratios for continuous RNFL thicknesses into the diagnostic process with the help of the modified Fagan nomogram. The methodology can also be easily extended to calculation of continuous likelihood ratio values for other instruments and can potentially facilitate the incorporation of results of diagnostic tests into clinical-decision making in glaucoma.

Supplementary Material

Suppl Figure 1. SUPPLEMENTAL FIGURE 1.

Graphical illustration of the relationship between likelihood ratio and the receiver operating characteristic (ROC) curve. The tangent at a single point c on the ROC curve, i.e., tangent(c), is the likelihood ratio for a single test value corresponding to that point on the ROC curve for a continuous test, i.e., LR(c).

Suppl Figure 2. SUPPLEMENTAL FIGURE 2.

Flowchart demonstrating how to obtain the post-test probability of disease from the pretest probability and likelihood ratio. The Fagan’s nomogram can simplify the calculations necessary to obtain the post-test probability of disease.