A large-scale metabolic model of Arabidopsis with three condition-specific biomass compositions is assembled in a bottom-up fashion to estimate the enzyme costs of Rubisco.
Abstract
Large-scale modeling of plant metabolism provides the possibility to compare and contrast different cellular and environmental scenarios with the ultimate aim of identifying the components underlying the respective plant behavior. The existing models of Arabidopsis (Arabidopsis thaliana) are top-down assembled, whereby the starting point is the annotated genome, in particular, the metabolic genes. Hence, dead-end metabolites and blocked reactions can arise that are subsequently addressed by using gap-filling algorithms in combination with species-unspecific genes. Here, we present a bottom-up-assembled, large-scale model that relies solely on Arabidopsis-specific annotations and results in the inclusion of only manually curated reactions. While the existing models are largely condition unspecific by employing a single biomass reaction, we provide three biomass compositions that pertain to realistic and frequently examined scenarios: carbon-limiting, nitrogen-limiting, and optimal growth conditions. The comparative analysis indicates that the proposed Arabidopsis core model exhibits comparable efficiency in carbon utilization and flexibility to the existing network alternatives. Moreover, the model is utilized to quantify the energy demand of amino acid and enzyme de novo synthesis in photoautotrophic growth conditions. Illustrated by the case of the most abundant protein in the world, Rubisco, we determine its synthesis cost in terms of ATP requirements. This, in turn, allows us to explore the tradeoff between protein synthesis and growth in Arabidopsis. Altogether, the model provides a solid basis for completely species-specific integration of high-throughput data, such as gene expression levels, and for condition-specific investigations of in silico metabolic engineering strategies.
Understanding plant responses to changing environmental conditions provides the opportunity of identifying and modifying the components involved in the underlying cellular mechanisms acting on gene regulation, signaling, and metabolism (Hannah et al., 2010; Caldana et al., 2011). Constraint-based modeling offers the means for predicting the behavior of plants and, thus, their responses in different environments based on the stoichiometry of the considered biochemical reactions (Lewis et al., 2012). Therefore, recent research efforts have been aimed at assembling large-scale models of plant metabolism at different levels of cell type and compartment resolution (de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012). Nevertheless, applications of these models lag behind their equivalents in the microbial kingdom, which have been successfully employed in simulating and predicting the behavior of unicellular organisms under various internal (e.g. genetic modifications) and external (e.g. environmental stimuli) perturbations (Sweetlove and Ratcliffe, 2011; McCloskey et al., 2013).
The existing models have been assembled by following a top-down approach, whereby the list of partial plant-specific, but often not species-specific, annotations is augmented via gap-filling algorithms to achieve a functional network of biochemical reactions (Satish Kumar et al., 2007). For simulating plant responses, an additional assumption is made regarding the optimization of a biomass reaction, reflecting the plant composition arising under a particular condition (de Oliveira Dal’Molin et al., 2010; Williams et al., 2010). Therefore, any predicted solutions, often resulting from the subsequent optimization of secondary objectives, such as photon usage efficiency (de Oliveira Dal’Molin et al., 2010) and total flux minimization (Holzhütter, 2004), pertain to the sole scenario captured in the biomass reaction. Here, we take a bottom-up approach to reconstruct a large-scale metabolic network of Arabidopsis (Arabidopsis thaliana) that relies solely on Arabidopsis-specific annotations and results in the inclusion of only manually curated reactions (and thus avoiding the need of using gap-filling algorithms). In addition, by employing high-throughput data, we have assembled and validated biomass reactions representing carbon-limiting, nitrogen-limiting, and optimal growth conditions for Arabidopsis.
Enzymes are the driving force of biochemical reactions by enhancing the reaction rates and, accordingly, forming the link between proteome and metabolome. Understanding the costs of enzyme production, in terms of energy demand, provides the opportunity to estimate the expenditures for metabolism. In analogy to Craig and Weber (1998), we define metabolic costs as the amount of ATP sacrificed by diverting it to enzyme synthesis instead of utilizing it for ATP production/formation from ADP and inorganic phosphate (Pi). Besides the metabolite interconversion, enzyme synthesis constitutes a large part of the metabolic energy demand. To this end, we investigated and proposed a solution for the problem of quantifying the cost of enzymes partitioned into the costs of amino acid biosynthesis and protein assembly. While the energy demand of protein assembly can be well approximated, as shown in the analysis, the cost of amino acid biosynthesis requires the consideration of the underlying metabolic pathways. A careful curated metabolic model provides the opportunity to determine biochemically meaningful costs by incorporating the complexity of the synthesis pathways (Barton et al., 2010; Sajitz-Hermstein and Nikoloski, 2010; Kaleta et al., 2013; see “Costs of Amino Acids” below). To this end, we make the distinction between physical (e.g. light) energy and metabolic equivalents, including ATP and NAD(P)H. Moreover, as NAD(P)H can be converted into ATP via cellular respiration, metabolic costs can be solely expressed in terms of ATP requirements. Finally, and most importantly, the costs will be biochemically meaningful for photoautotrophic growth conditions if the enzyme synthesis is only based on low-energy inorganic precursors (i.e. water, CO2, Pi, NO3−/NH4+, and SO42−/H2S). Once quantified, the enzyme costs are used to explore the tradeoff between protein synthesis and growth, which is the ultimate application of the assembled model, as illustrated by the case of Rubisco.
Large-scale modeling enables the investigation of specific pathways (e.g. amino acid synthesis) or combinations thereof (e.g. carbon metabolism) within their metabolic context. As metabolic pathways are tightly interconnected, their functionalities, regarded as objectives, usually depend on the remaining network. In the case of Arabidopsis, there already exist a handful of large-scale metabolic models (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012; Cheung et al., 2013) that assemble a wide range of Arabidopsis genome-metabolome associations (Poolman et al., 2009), incorporate compartmentalization (de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012; Cheung et al., 2013), and, in the case of one of the most recent, accounts for pathways of the secondary metabolism (Mintz-Oron et al., 2012). However, these models are unsuitable or incomplete for the purpose of determining condition-specific cellular behavior as well as the metabolic costs of enzyme production. The model of Poolman et al. (2009) reflects heterotrophic environmental conditions, neglects subcellular compartmentalization (and, thus, also transport reactions), and is not mass balanced regarding oxygen and protons. While the updated and improved version of this model, proposed by Cheung et al. (2013), incorporates subcellular compartmentalization, the law of mass conservation is still violated. The subsequent models, including those of de Oliveira Dal’Molin et al. (2010) and Mintz-Oron et al. (2012), also tackle this issue and claim that they are capable additionally of simulating photoautotrophic scenarios. However, the model of de Oliveira Dal’Molin et al. (2010) cannot produce all 20 amino acids providing SO42−, specifically Arg and His. While the latest model of Mintz-Oron et al. (2012) resolves this drawback, other issues arise. On the one hand, the model violates the law of energy conservation in such a way that it can produce, for instance, biomass without any supply of energy, neither in the form of light nor as high-energy precursors. On the other hand, the gene-protein reaction (GPR) associations for enzyme complexes comprising isoforms are inaccurate: for all 19 unique complexes, the logical operators declaring whether genes are encoding different subunits (AND) or isoforms (OR) are given in such a form that the OR operation is of higher precedence than the AND operation. Consequently, for a gene deletion of the large subunit of Rubisco, the model would predict no effect, since the small subunit of Rubisco (RbcS1A, RbcS2B, and RbcS3B) is considered a complete isozyme. Beyond these issues, the model of Mintz-Oron et al. (2012) additionally covers the secondary metabolism, which can be disregarded for our purposes (i.e. examining the central carbon metabolism and estimating enzyme costs). For these reasons, we have assembled a novel metabolic network capable of producing all amino acids by providing only inorganic compounds while benefiting from the inclusion of verified knowledge only.
RESULTS AND DISCUSSION
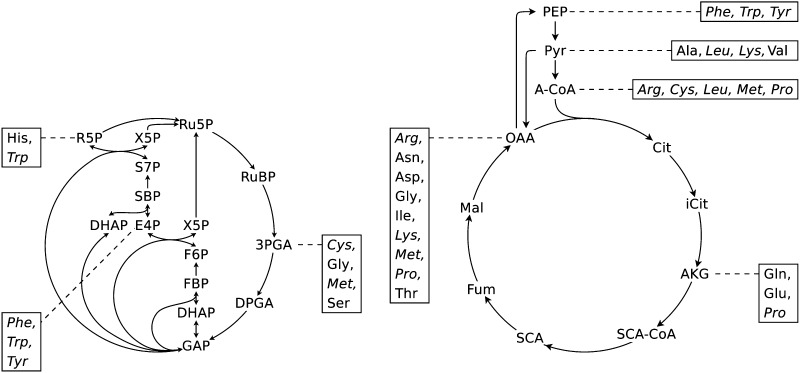
The starting point for the novel metabolic model was the photoautotrophic conditions whereby only the import of light, water, CO2, Pi, NO3− and/or NH4+, and SO42− and/or H2S is allowed. Consequently, pathways enabling the synthesis of all amino acids solely from these inorganic compounds were considered for inclusion. To this end, we first identified the metabolic precursors of the amino acids and their pathways: the Calvin-Benson cycle, glycolysis, and the citric acid cycle (Fig. 1; Supplemental Data S1, Table S11). We then extended the list of required pathways to all associated pathways of the plant central carbon metabolism, such as light reactions and respiration. To assemble a metabolic model that can be employed to simulate various scenarios, we additionally included the synthesis pathways of the remaining known major cell components, or at least their precursors. As a result, the first draft of the model comprised 20 pathways and can produce sink and source sugars (i.e. Fru, Glc, and Suc), a cell wall precursor (i.e. UDP-Glc, a representative of cellulose), a fatty acid precursor (i.e. malonyl-CoA), and a signaling precursor (i.e. trehalose).
Figure 1.
Schematic representation of the most basic biochemical pathways comprising the metabolic precursors for the carbon skeletons of all amino acids. The list of pathways comprising the direct precursors is provided in Supplemental Data S1, Table S11. Amino acids highlighted in italics have more than one precursor. RuBP, Ribulose-1,5-bisphosphate; 3PGA, 3-phosphoglycerate; DPGA, 1,3-diphosphoglycerate; GAP, glyceraldehyde-3-phosphate; DHAP, dihydroxyacetone phosphate; FBP, fructose-1,6-bisphosphate; F6P, fructose-6-phosphate; E4P, erythose-4-phosphate; X5P, xylulose-5-phosphate; SBP, seduheptulose-1,7-bisphosphate; S7P, sedoheptulose-7-phosphate; R5P, ribose-5-phosphate; Ru5P, ribulose-5-phosphate; PEP, phosphoenolpyruvate; Pyr, pyruvate; A-CoA, acetyl-CoA; Cit, citrate; iCit, isocitrate; AKG, α-ketoglutarate; SCA-CoA, succinyl-CoA; SCA, succinate; Fum, fumarate; Mal, malate; OAA, oxalacetate.
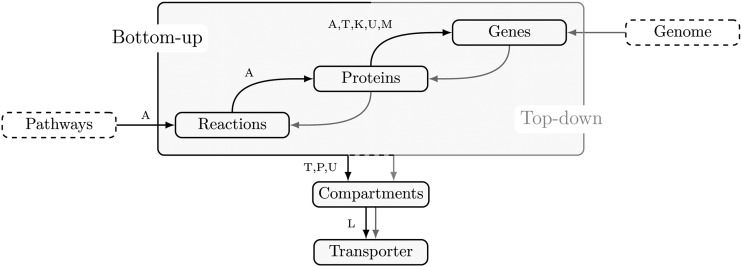
The reconstruction process is almost the same as for a genome-scale metabolic network; therefore, we followed the protocol from Thiele and Palsson (2010) in all steps except the initial step. In contrast to using genome mapping as in previous top-down reconstructions, here we started with the essential pathways of the central carbon metabolism and identified, first, the underlying reactions, their corresponding Enzyme Commission (EC) numbers, and, in the end, the annotated genes (Fig. 2; see “Materials and Methods”). Therefore, we denote our approach as bottom up, resulting in what we term the Arabidopsis core model (Supplemental Data S2).
Figure 2.
Reconstruction workflow for the Arabidopsis core model. The arrow labels represent the databases used: A, AraCyc 11.5 (Mueller et al., 2003); T, The Arabidopsis Information Resource (Lamesch et al., 2012); K, Kyoto Encyclopedia of Genes and Genomes (Kanehisa and Goto, 2000); U, UniProt (UniProt Consortium, 2013); M, MapMan (Thimm et al., 2004); P, Plant Proteome Database (Sun et al., 2009); and L, literature. Black arrows refer to the workflow of the bottom-up approach, while gray arrows denote the steps of the top-down approach.
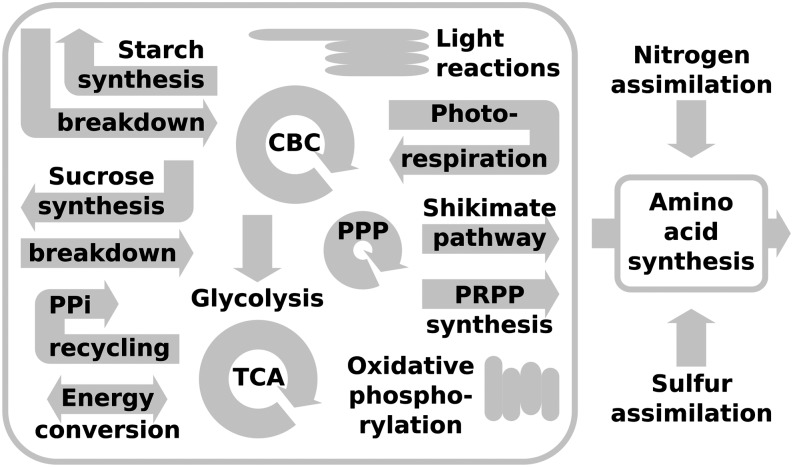
The Arabidopsis core model represents a photoautotrophically growing Arabidopsis leaf cell but is also capable of simulating heterotrophic scenarios by adapting the energy source and disabling the light reactions. Due to three experimentally determined biomass functions (see “Materials and Methods”; Supplemental Data S1, Text S1.4), defined as the fractional contribution of known cell components to the overall biomass, the model can be utilized to simulate three realistic and frequently examined environmental settings, namely, carbon-limiting, nitrogen-limiting, and optimal growth conditions. Altogether, it comprises 236 unique metabolites, 345 unique reactions related to 61 unique subsystems, which comprise 87 unique internal transport reactions (Fig. 3; Supplemental Data S3). The subsystems capture common biochemical pathways and functional groups such as transport. Moreover, the Arabidopsis core model is accurate with respect to mass and energy conservation, a prerequisite to ensure an optimal nutrient utilization and biochemical soundness of the predictions. By means of balancing the atoms of the left-hand and right-hand sides of all internal reactions, the model utilizes exactly the amount of each precursor to produce 1 unit of biomass as the sum of the molecular formula it specifies (Supplemental Data S1, Table S6).
Figure 3.
Schematic overview of the major subsystems of the Arabidopsis core model. CBC, Calvin-Benson cycle; TCA, citric acid cycle, PPP, pentose phosphate pathway; PPi, pyrophosphate; PRPP, phosphoribosyl pyrophosphate.
Model Comparison
The Arabidopsis core model differs in several issues from the existing Arabidopsis models (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012), not only due to the particular reconstruction approach employed. The photoautotrophic scenario permits only the uptake of inorganic compounds, such that nitrogen, sulfur, and phosphorus are taken up as ions, a process mostly associated with proton uptake. In addition, to our knowledge, this is the first model that includes the corresponding additional ATP costs to account for the proton secretion necessary to maintain the intercellular pH value (Supplemental Data S1, Text S1.2). Furthermore, we incorporated the electron transport chains, namely, light reactions and oxidative phosphorylation, as sequences of reactions, with each reaction representing one of the five respective complexes. In doing so, we included the linkage of photosynthesis and nitrate assimilation via the competition for the reduced ferredoxin and facilitated the consideration of the 14-fold symmetry of the ATP synthase subunit C, the proton-powered turbine (Seelert et al., 2000).
Another substantial difference is the consideration of the GPR associations. As mentioned above, we considered only organism-specific annotations such that we accomplished a functional metabolic network without the support of gap-filling algorithms, unlike the existing Arabidopsis models (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012). To this end, for only four biochemical reactions of the Arabidopsis core model are no gene annotations provided, so-called spontaneous reactions (4/[549 − 229] ≈ 1.25%; Table I). In addition, only reactions involved in maintenance, transport, import, and export processes, and reactions related to biomass production, are not annotated (229 inapplicable; Table I). In contrast, for the models of de Oliveira Dal’Molin et al. (2010) and Mintz-Oron et al. (2012), 21% and 37% of these potentially annotated reactions, respectively, have no support for an appearance in Arabidopsis. Importantly, spontaneous reactions are not excluded, as there is not enough information provided for their precise identification. Nevertheless, for the Arabidopsis core model, the four nonannotated reactions are precisely such spontaneous reactions. Moreover, we did not provide only the common GPR associations but also rendered the assignments compartment specific where possible. Additionally, we collected the complete enzyme complex structure with respect to the stoichiometry (Supplemental Data S1, Text S1.5, and Supplemental Data S3). Together with the organism-specific annotations, this enables a reliable incorporation of Arabidopsis high-throughput data, such as gene expression levels, and, accordingly, plausible gene knockout as well as gene expression studies.
Table I. Model comparison regarding network properties pertaining to gene annotation, functionality, biomass production, and flexibility (i.e. flux variability and flux coupling).
*, Reactions that are inapplicable for gene annotations cover reactions involved in maintenance, transport, import, or export processes not related to biomass production. **, The flexibility analysis was performed for the photoautotrophic scenario (Supplemental Data S1, Table S9).
| Property | Arabidopsis Core Model | de Oliveira Dal’Molin et al. (2010) | Mintz-Oron et al. (2012) |
|---|---|---|---|
| Total no. of reactions | 549 | 1,601 | 3,508 |
| Annotated | 316 | 1,177 | 1,696 |
| Inapplicable* | 229 | 111 | 811 |
| Annotation deficient | 4 | 313 | 1,001 |
| Blocked | 0 | 928 | 0 |
| Redundant importer and exporter** | 88 | 9 | 92 |
| Additional blocked** | 35 | 21 | 586 |
| Functional** | 426 | 643 | 2,830 |
| Maximum biomass units per 1,000 units of CO2 | 60.2845 | 55.0119 | 55.0212 |
| Flux variability frequency (greater than 1%) | 0.1423 | 0.2581 | 0.9132 |
| Flux coupling frequency | 0.0919 | 0.0412 | 0.0015 |
| Fully | 0.0047 | 0.0197 | 0.0009 |
| Partially | 0.0145 | 0.0002 | 0.0000 |
| Directionally | 0.0727 | 0.0212 | 0.0006 |
There are some aspects in which the Arabidopsis core model performs differently in comparison with the existing models. First, we tested the biomass simulated by the models through maximizing the production of biomass units under the same photoautotrophic conditions (Supplemental Data S1, Table S9) and by using the biomass reaction of de Oliveira Dal’Molin et al. (2010). Technically, this maximization problem is solved by flux balance analysis (FBA; Supplemental Data S1, Text S3.1). Based on 1,000 units of CO2, the Arabidopsis core model synthesizes 60.2845 units of biomass, while the models of de Oliveira Dal’Molin et al. (2010) and Mintz-Oron et al. (2012) yield 55.0119 and 55.0212 biomass units, respectively (Table I). This shows that the Arabidopsis core model predicts a more efficient conversion of CO2 into biomass. Nevertheless, for this purpose, it assimilates more photons than the model of de Oliveira Dal’Molin et al. (2010). We stress that it is not possible to make such a statement for the model of Mintz-Oron et al. (2012), as, unfortunately, the import of photons is not necessary to produce biomass under photoautotrophic conditions in this model. Since no high-energy, organic compounds are imported in this model, light is the only external energy source. Therefore, the model of Mintz-Oron et al. (2012) violates the law of energy conservation, such that it produces energy out of nothing within the system.
Furthermore, we tested the models for their flexibility by examining flux variability, the reaction-specific range of feasible flux values ensuring optimal biomass production (Supplemental Data S1, Text S3.2), and flux coupling, the pairwise dependencies of feasible reaction fluxes (Supplemental Data S1, Text S3.3). As expected, the Arabidopsis core model has the lowest flux variability frequency and the highest flux coupling frequency (Table I), indicating lower flexibility in comparison with the other models considered. Intuitively, this is caused by the difference in its reconstruction, bottom up instead of top down, and the resulting smaller number of reactions.
Nevertheless, the comparative analyses are based only on the functional fraction of the models to ensure a consistent framework. To this end, we first removed all blocked reactions and, subsequently, all import and export reactions, which were rendered redundant along with the resulting blocked reactions. In this way, we achieved a considerably smaller but completely functional metabolic network specifically for the photoautotrophic conditions. While for the Arabidopsis core model and that of Mintz-Oron et al. (2012), approximately 80% of the original reactions are functional, only 40% of the reactions of the model of de Oliveira Dal’Molin et al. (2010) are operational (i.e. capable of carrying a nonzero flux). The resulting functional network sizes are concordant with the respective flexibility; that is, the large functional model of Mintz-Oron et al. (2012) has a higher flux variability frequency and a lower flux coupling frequency than the others. This might result from the multitude of transport reactions enabling the cell-wide transport of, for instance, ADP, ATP, NAD(P) NAD(P)H, and Pi in this model. Moreover, the flexibilities of the two models capturing only the primary metabolism, namely, the Arabidopsis core model and the model of de Oliveira Dal’Molin et al. (2010), are similar. This demonstrates that, in fact, a bottom-up reconstructed model can achieve a similar functional network size to a genome-scale metabolic network, assembled by a top-down procedure.
Cell Performance with Respect to Different Cellular Scenarios
The performance of a cell is usually described in terms of the properties of a specific biochemical process, regarded as an objective. For instance, energy efficiency, expressed through ATP consumption, is often assumed and used as an objective (Kayser et al., 2005; Kaleta et al., 2013). To this end, one determines the number of required ATPs to produce a metabolite of interest or a set of metabolic precursors representing a biochemical process, such as Suc or biomass. Accordingly, the optimal cell performance can be characterized by the minimum amount of required energy.
The validity of the cell performance depends on a clearly defined cellular state, such as developmental stage, trophic status of the cell, and cell type. Juvenile and mature leaf cells differ in their predominantly active biochemical processes (e.g. photosynthesis to enhance growth and to synthesize Suc, respectively). Therefore, the appropriate choice of the biochemical process of interest is very important. Furthermore, while under heterotrophic conditions, high-energy organic precursors are provided to the cell, these precursors first have to be synthesized from low-energy inorganic substances under autotrophic conditions. Consequently, the energy efficiency would at least differ in the amount of ATP in excess, starting from the high-energy precursors, and the amount of required ATP to synthesize them. For this study, we focused on autotrophic, juvenile leaf cells and assumed that growth enhancement, as well as energy efficiency, are appropriate objectives. As a further objective, we accounted for the optimal resource allocation by determining the minimal precursor requirements for a functional network.
Altogether, we investigated three different environmental conditions (i.e. cellular scenarios), namely, carbon-limiting, nitrogen-limiting, and ambient growth conditions. These scenarios are represented by the three experimentally determined biomass compositions, each reflecting 1 g dry weight of Arabidopsis leaf material (Supplemental Data S1, Text S1.4, and Supplemental Data S4). The ambient, often called optimal, growth conditions are, if at all, limited by the availability of energy, which corresponds to light limitation under autotrophic conditions. The experimental setup for the nitrogen limitation is based on a protocol from Tschoep et al. (2009) that results in a mild but sustained restriction of growth. In accordance with the authors, we stress that this differs from earlier nitrogen deficiency experiments, where strong nitrogen limitations were obtained. In contrast, the carbon limitation is experimentally realized via short-day conditions (8-h-light/16-h-dark cycle; Gibon et al., 2004, 2009; Stitt et al., 2007; Sulpice et al., 2013), which affect the starch accumulation during the day and result in a restriction of carbon availability at night (Gibon et al., 2009; Sulpice et al., 2013).
From the modeling perspective, the limiting environmental settings can be implemented by restricting the import of the respective nutrient source. Thus, carbon limitation is realized via restricted CO2 import and nitrogen limitation by constraining NO3− and/or NH4+ import. For the optimal growth scenario, we acted on the assumption of light limitation, since unlimited resource availability is not applicable. Nonetheless, as the light absorption of a plant is limited by its overall leaf surface, this assumption is biochemically justified. Energy efficiency and minimal precursor requirements are determined by means of FBA (Supplemental Data S1, Text S3.1). Here, the modeling characteristic of the photoautotrophic scenario is the lack of overlap in the supply of nitrogen, carbon, sulfur, and phosphorus (i.e. each imported metabolite comprises only one of these chemical elements). This substantially simplifies the analysis, as the required amount of precursors can be readily determined.
As expected, cell performance varies across the cellular scenarios. The carbon-limiting scenario requires the least amount of each precursor as well as the least amount of energy equivalents to produce 1 unit of biomass, namely, 1 g dry weight (Table II, columns 2–7). This indicates that the biomass contains less organic material in that it comprises more inorganic compounds or water. On the one hand, this is in accordance with the calculated biomass coverage (Supplemental Data S1, Table S7). On the other hand, it points out that the nominal values of the required precursors are inappropriate to compare the different scenarios. Moreover, regarding the ATP requirement of the system, we emphasize that the biomass compositions of the Arabidopsis core model do not include maintenance costs representing the energy demand necessary for cell replication, such as macromolecular synthesis (growth-associated maintenance), and cell maintenance, such as turgor pressure (non-growth-associated maintenance; see “Materials and Methods”). These costs are highly condition specific (Cheung et al., 2013), which would result in distinct, higher overall ATP demands and, accordingly, affected photon requirements. As a consequence, we considered the respective ratios of utilized CO2 and NO3− (Table II, column 8), which are notably smaller for the nitrogen-limiting conditions, implying that the nitrogen incorporation and accumulation are increased. Experimentally, it has been confirmed that Arabidopsis growing under low-NO3− concentrations contains similar levels of proteins and higher levels of free amino acids (Tschoep et al., 2009). In contrast, the cell NO3− content is reduced more than 10-fold, which, nevertheless, results in a small decrease of the total nitrogen concentration. As the biomass reaction does not comprise NO3−, only the increase in the organic nitrogen can be examined. Moreover, it has been experimentally shown that the reduced overall nitrogen availability can almost be compensated by an elevated NO3− assimilation (Sulpice et al., 2013). In support of this claim, the gene expression of the low-affinity NO3− transport system is shown to be induced under low NO3− concentrations (Wang et al., 2000). This demonstrates that the biomass function used in our modeling also reflects cell storage.
Table II. Minimum requirements of precursors and energy equivalents to produce 1 g of dry weight of biomass of the representative cellular scenarios.
The italic entries denote the respective limiting precursor.
| Cellular Scenario | Minimal Precursor Consumption |
Precursor Ratio |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Photon | CO2 | NO3− | Pi | SO42− | ATP | Photon:CO2 | Photon:NO3− | CO2:NO3− | |
| mmol d−1 | |||||||||
| Optimal growth | 196.862 | 20.621 | 2.595 | 0.013 | 0.065 | 186.316 | 9.547 | 75.875 | 7.948 |
| Carbon limitation | 182.639 | 19.192 | 2.350 | 0.013 | 0.058 | 172.854 | 9.517 | 77.714 | 8.166 |
| Nitrogen limitation | 259.648 | 26.737 | 4.104 | 0.014 | 0.099 | 245.738 | 9.711 | 63.260 | 6.514 |
Estimation of Enzyme Costs
Metabolic costs can be considered as the amount of energy, in terms of ATP, sacrificed by diverting it to the synthesis of a building block instead of utilizing it for ATP production/formation from ADP and Pi (Craig and Weber, 1998). The metabolic costs of an enzyme are mainly determined by its de novo synthesis costs related to its turnover and recycling. The half-life, and thus the turnover, of a protein can be approximated by means of the N-terminal amino acid residue, the so-called N-end rule (Varshavsky, 1992). For Escherichia coli, Saccharomyces cerevisiae, and mammalian cells, there exist quite precise protein turnover values for the different N-terminal residues (Bachmair et al., 1986; Gonda et al., 1989). For plants, in contrast, while the stability order of chloroplastic and cytosolic proteins has been resolved (Apel et al., 2010; Graciet et al., 2010), determining the turnover times requires further investigations. Nevertheless, the key aspect of a proper estimation of enzyme costs is the adequate modeling of protein synthesis. This process actually comprises three parts: (1) the biosynthesis of the single amino acids, (2) the composition of the amino acid sequence, and (3) the protein maturation. The costs of each part are separately determined and are then summed.
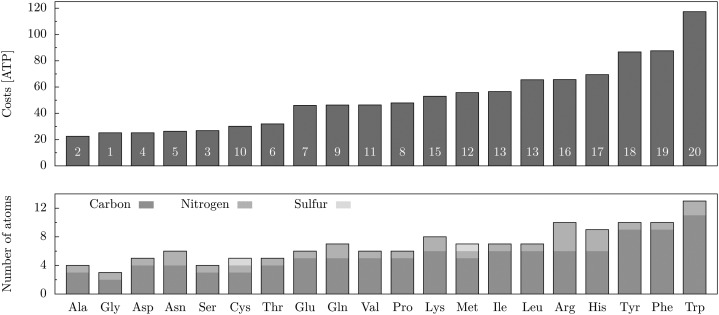
The costs for producing amino acids were approximated based on the assembled model. For this purpose, we relied on the assumption that the plant uses the synthesis pathway requiring the least amount of energy, in terms of ATP. The underlying optimization is solved using FBA (Supplemental Data S1, Text S3.1). Since light energy is provided in the photoautotrophic scenario, we were able to directly restrict the consumption of energy instead of falling back on the utilization of metabolic precursors such as Glc. Subsequently, the minimal amount of required photons was converted into, on the one hand, the amount of ATP required to synthesize the amino acid of interest and, on the other hand, the remaining number of ATPs available for other processes (Supplemental Data S1, Text S3.1). The result of these calculations is the minimal metabolic energy cost in terms of ATP (Fig. 4; Supplemental Data S1, Table S11) and provides one possible steady-state flux distribution (i.e. a possible flux through the system that permits the synthesis of the amino acid without any accumulation or depletion of other metabolites).
Figure 4.
Amino acid costs based on the Arabidopsis core model under optimal growth conditions. The white numbers on the bars denote the average ranking over the amino acid cost estimation of Craig and Weber (1998), Akashi and Gojobori (2002), Seligmann (2003), Wagner (2005), Barton et al. (2010), Sajitz-Hermstein and Nikoloski (2010), and the Arabidopsis core model (Supplemental Data S1, Table S11). For comparison, the amino acid composition with respect to the size of the carbon skeleton and the number of incorporated amine groups and sulfur is given in the bar plot at bottom.
To establish a cost measure for the protein synthesis in terms of assembling the amino acid sequence, a representative amino acid sequence for the respective enzyme has to be determined. This is in almost all cases not unique, as enzymes can be multimers, can have isoforms, and/or different splicing forms can exist. Unfortunately, the complex structure of enzymes is only seldom available, predominantly from the Braunschweig Enzyme Database (Schomburg et al., 2013) and the AraCyc database (Mueller et al., 2003). Moreover, the structure of some enzymes varies across species and/or environmental conditions, such as for ATP synthase (EC 3.6.3.14). Its proton-powered turbine, encoded by subunit III, is predicted to consist of 12 subunits in E. coli, 10 subunits in S. cerevisiae, and 14 subunits for plants (Seelert et al., 2000). Furthermore, there is evidence that the size of this proton-powered turbine changes under stress conditions, indicating a modification in the subunit stoichiometry (Löw et al., 1996). As a consequence, we accounted only for plant data and collected all verified compositions. We followed a similar procedure for the identification of subunit isoforms or whole isozymes as well as for different splicing forms of the encoding genes. Finally, we assembled all different combinations of enzyme compositions and, thereby, yielded for Rubisco 3,003 potential amino acid sequences.
To assign protein assembly costs, the next task consists of identifying the energy-demanding steps, which are 4-fold: (1) the amino acid activation, with an estimated cost of two molecules of ATP per amino acid; and the three stages of the translation process: (2) initiation, (3) elongation, and (4) termination (Supplemental Data S1, Table S8). Thereby, the formation of the initiation complex requires approximately three molecules of ATP per polypeptide, and the elongation of the amino acid sequence consumes two molecules of ATP per cycle and, thus, per amino acid. The final release of the new polypeptide during the termination stage costs another one molecule of ATP per polypeptide.
The third component of the enzyme costs is related to the energy requirements for protein maturation. This comprises costs for error correction and maintenance of the biosynthesis apparatus, the synthesis of signal sequences, and posttranslational processing such as methylation and phosphorylation (Zerihun et al., 1998; Noguchi et al., 2001). Therefore, one can approximate another one molecule of ATP per amino acid for protein maturation (Supplemental Data S1, Table S8). Altogether, the simplified costs of protein synthesis and maturation can be estimated by five molecules of ATP per amino acid residue.
Due to the multitude of previously determined amino acid sequences, the resulting costs of an enzyme may lie in a large range. As the enzyme costs are based on the minimal amino acid costs, they are underestimated. The minimal cost value serves as a lower boundary for the estimation.
The range of costs permits insights into the extent of variation in actual enzyme costs. The comparison of different enzyme costs may be of specific interest to identify enzymes with highly variable costs. These enzymes may serve as a target for improving the systems efficiency, in terms of metabolic engineering.
Costs of Amino Acids
Amino acids are the basic components of all proteins. In metabolic modeling, they are often even used as protein representatives, as the protein synthesis itself is too elaborate to be modeled accurately. The various and intricate synthesis pathways of the different amino acids result in such a highly complex network that even their minimal costs lie in a quite wide range of 22.5 to 117.4 molecules of ATP (Fig. 4; Supplemental Data S1, Table S11). The costs largely comply with the size of the corresponding amino acids. This compliance becomes higher by further considering other chemical features, such as the number of amine groups or the incidence of sulfur. It seems that the incorporation of additional amine groups (e.g. Arg and Lys) as well as the incorporation of sulfur (as for Cys and Met) are expensive. Apparently, also the formation of cyclic, especially aromatic, structures is very expensive. This is the case for Trp, Tyr, and Phe, the aromatic amino acids, as well as for His, which additionally contains three amine groups. Altogether, the calculated minimal costs coincide rather well with the complexity of the corresponding amino acids.
The comparison with existing cost measures facilitates the evaluation of our cost estimation (Supplemental Data S1, Table S11). The existing approaches are 3-fold: (1) based on physiochemical properties of amino acids; (2) relying on selected metabolic pathways; and (3) based on genome-scale models. Seligmann (2003) employed the former approach using the molecular weight of the amino acids as an approximation of their synthesis costs. This enables a valid estimation across all species, as the molecular weight is constant (Supplemental Data S1, Table S11). In contrast, the remaining two approaches incorporate organism-specific information. For instance, Craig and Weber (1998), Akashi and Gojobori (2002), as well as Wagner (2005) followed the second approach, relying on glycolysis, the citric acid cycle, and the pentose phosphate pathway. Intermediates of these pathways are provided as precursors for the amino acid synthesis, and the ATP equivalents directly invested into amino acid synthesis are counted. These studies were conducted for E. coli and S. cerevisiae. With the existing genome-scale metabolic models, the determination of amino acid costs in the metabolic context has been enabled for full genome-sequenced organisms, such that, first, plant-specific costs were calculated. Barton et al. (2010), Sajitz-Hermstein and Nikoloski (2010), and Kaleta et al. (2013) determined the costs for S. cerevisiae, Arabidopsis, and E. coli, respectively, and compared their results with calculations based on central metabolic precursors. Sajitz-Hermstein and Nikoloski (2010) provided an estimation specifically for day and night scenarios, whereby the minimal number of required ATP equivalents is determined with Glc provided to the system.
While all these studies describe heterotrophic scenarios, our estimations are determined for autotrophic conditions. Moreover, as only the approximation of Sajitz-Hermstein and Nikoloski (2010) is plant specific, we only consider the ranking of the amino acids for comparison. By ordering the amino acids regarding their average rank over all measures, they can be divided into four groups coinciding with our cost ranking: the five cheapest amino acids (Ala, Gly, Ser, Asp, and Asn), two groups of six and four moderately costly ones, respectively (Thr, Pro, Cys, Glu, Gln, and Val as well as Met, Ile, Lys, and Leu), and the five most expensive ones (Arg, His, Phe, Tyr, and Trp; Fig. 4; Supplemental Data S1, Table S11). Particularly for the last group, the ranking is fully consistent, as even the order within the group is the same.
Costs of Rubisco
Rubisco is the most abundant protein in plant cells and, moreover, the most abundant protein in the world (Ellis, 1979). It is one of the key enzymes of photosynthesis; more precisely, it is the initial enzyme of the Calvin-Benson cycle. This attributed key position can be explained, on the one hand, by its very low catalytic rate of 3.4 to 3.7 fixed molecules of CO2 per second (Tcherkez et al., 2006); on the other hand, it is justified by the substrate competition. Approximately each fourth reaction proceeds with oxygen instead of CO2 (Peterhansel and Maurino, 2011), whereby the respective catalytic rate is even lower, 0.42 fixed molecules of oxygen per second (Whitney et al., 2009).
A single Rubisco complex comprises 16 subunits, eight large and eight small ones. The large subunits are encoded by a single gene in Arabidopsis, namely, ATCG00490. In contrast, the small subunits can be derived from four different genes, AT1G67090, AT5G38430, AT5G38420, and AT5G38410, which, furthermore, occur in two, one, one, and three splicing forms, respectively. In order to determine the costs for Rubisco, all possible 3,003 amino acid compositions have to be analyzed. The resulting range of costs accounts for 243,287.9 to 269,133.9 molecules of ATP per complex (Supplemental Data S1, Table S12). For the same amount of ATP, between 2,508.1 and 2,774.6 molecules of Suc can be synthesized. To obtain a better impression of this huge amount of ATP, we converted the number of ATP molecules in the standard unit of physical energy. Using the Gibbs free energy of ATP synthase, one can easily establish that 36 kJ mol−1 ATP (Turina et al., 2003) results in 1.454 to 1.609 × 10−14 J per complex or 8.758 to 9.689 J nmol−1 Rubisco. In comparison, 1 nmol of Rubisco has a mass of 0.55 mg, and the human heart and brain consume roughly 2 and 20 J s−1 (Rigden, 1996; Drubach, 2000; Williams et al., 2001), respectively.
Probably of greatest interest is the amortization of the production costs of Rubisco. To this end, one can consider the resource allocation tradeoff between growth and protein synthesis as two contending tasks: increasing the leaf area allows a higher light absorption, while enhancing protein synthesis stimulates and accelerates the metabolism. By means of the biomass composition representing optimal growth conditions, we were able to determine the potential growth enhancement, in terms of produced biomass, if resources are not utilized toward synthesizing Rubisco. Based on the assumption that 1 unit of biomass represents 1 g dry weight of an Arabidopsis rosette, instead of synthesizing 1 nmol of Rubisco, the plant could gain 1.3058 to 1.4445 mg dry weight. The plants that were used to assemble the optimal growth biomass composition had an average mass of 124.36 mg fresh weight (Sulpice et al., 2013), approximately 10.94 mg dry weight, which indicates an increase of 12% to 13% dry weight. Certainly, this is only an approximation, as, on the one hand, de novo synthesis of Rubisco is considered and, on the other hand, cell maintenance costs are not incorporated (see “Materials and Methods”). However, these values seem to be in a physiologically plausible range, considering a half-life of Rubisco of approximately 7 d in mature leaves (Piques et al., 2009) and an absolute growth rate of 0.9 mg dry weight d−1 (Meyer et al., 2004). According to this, Arabidopsis gains approximately 6.3 mg dry weight while one complex of Rubisco has to be resynthesized.
Perspectives of Estimating Enzyme Costs
The presented enzyme cost estimation takes into account only the required energy for de novo synthesizing a complex of Rubisco. However, in homeostasis, synthesis costs are relevant only if the degradation process is also considered. Accordingly, only the amount of degraded enzyme has to be synthesized, whereby the breakdown process itself can involve additional energy requirements. Overall, the actual enzyme costs are highly affected by the protein degradation (rate), which varies with the environmental scenarios.
A possible approach to assess protein degradation is the examination of the relative costs per reaction. One complex of Rubisco can catalyze in parallel eight carboxylation or oxygenation reactions. Moreover, as mentioned above, Rubisco has a half-life of approximately 7 d (Piques et al., 2009), which results in a total number of approximately 1.6 to 1.74 million reactions per complex. Relative to each ongoing reaction, the costs for a complex of Rubisco are between 0.14 and 0.17 parts of a molecule of ATP per Rubisco reaction. These additional costs represent an essential part of the overall metabolic costs that should be incorporated for the involved enzymes. Consequently, the cost estimations for all soluble metabolites, amino acids as well as enzymes, have to be updated. This will improve the current estimations and lead to new insights regarding the metabolic relevance of the enzymes, as the enzymatic influences can be taken into account.
CONCLUSION
In this study, we presented a bottom-up reconstruction of the extended central carbon metabolism of a young Arabidopsis leaf cell and demonstrated that the resulting metabolic network model can be used to effectively simulate photoautotrophic conditions. Due to the bottom-up reconstruction and careful manual curation, we resolved the shortcomings of the existing genome-scale models of Arabidopsis, such as (1) the demand for using gap-filling algorithms and, accordingly, a low gene annotation coverage of the reactions (de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012); (2) the occurrence of dead-end metabolites and blocked reactions (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010); (3) potential violations of mass and energy conservation (Poolman et al., 2009; Mintz-Oron et al., 2012); and/or (4) incorrect GPR associations (Mintz-Oron et al., 2012). Combined with the extended GPR associations presented here (i.e. the incorporation of the complex stoichiometry), the Arabidopsis core model can be readily employed for the integration of high-throughput data (e.g. gene expression studies) and for investigations of other in silico metabolic engineering scenarios (e.g. codon usage optimization).
In comparison with the existing compartmentalized Arabidopsis models (de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012), the Arabidopsis core model presented here shows slightly higher efficiency in carbon utilization and flexibility similar to that of de Oliveira Dal’Molin et al. (2010). In contrast to these models, the Arabidopsis core model comprises three biomass reactions that pertain to frequently examined scenarios: carbon-limiting, nitrogen-limiting, and optimal growth conditions. The underlying compositions are determined experimentally and enable biologically reliable condition-specific analyses of young leaf metabolism and the plant response.
Moreover, we demonstrated the application of the Arabidopsis core model to estimate the energy demand of amino acid and enzyme synthesis in photoautotrophic conditions. Using the example of Rubisco, the predominant protein in the world, we specify the costs of protein de novo synthesis, in terms of ATP requirements, and provide an approximation of the costs per catalyzed reaction. Finally, we used the Arabidopsis core model to explore the tradeoff between protein synthesis and growth to quantify how much energy resources, in terms of ATP, are sacrificed on synthesizing proteins instead of dedicating them to biomass production and vice versa.
MATERIALS AND METHODS
The reconstruction of the Arabidopsis (Arabidopsis thaliana) core model is in accordance with the protocol from Thiele and Palsson (2010), except for the initial step. We started from well-documented and essential biochemical pathways and identified the underlying reactions and their corresponding EC numbers and, in the end, assigned the annotated genes (Fig. 2). This first, automated draft was assembled by means of the AraCyc 11.5 (Mueller et al., 2003), The Arabidopsis Information Resource (Lamesch et al., 2012), Kyoto Encyclopedia of Genes and Genomes (Kanehisa and Goto, 2000), UniProt (UniProt Consortium, 2013), and MapMan (Thimm et al., 2004) databases. Thereby, we only considered organism-specific data, particularly for the gene identification.
In the next manual curation stage, every entry of the draft was examined critically and the information was corrected, improved, or completed. This comprised the assignment of the correct metabolite formulas depending on the occurring pH value. As the model should be adaptable for different cell scenarios and the pH value of the cell varies with the environmental conditions, we enabled the assignment of pH-dependent charged formulas. Thereby, given the pH value of a compartment, the charge and, consequently, the metabolite formula were determined by employing the International Chemical Identifier keys and the resulting pKa values.
Moreover, we assigned information about the subcellular localization of a reaction extracted from The Arabidopsis Information Resource (Lamesch et al., 2012), Plant Proteome Database (Sun et al., 2009), and UniProt (UniProt Consortium, 2013) databases (Fig. 2). We took into account four subcellular compartments: the chloroplast, the mitochondrion, the peroxisome, and the cytosol, which represents all remaining cell compartments. If contradictory or no information was available, we followed these three rules of thumb: (1) assign the compartment of the reactions in the vicinity of the pathway; (2) allow spontaneous reactions to be assigned in all compartments; and otherwise (3) restrict the reaction to take place only in the cytosol.
The compartmentalization not only requires but permits the incorporation of subcellular transport reactions, representing active and passive transport processes across compartment boundaries (also termed transporters). To avoid futile cycles and to achieve a biologically reliable network, we attempted to minimize the number of internal transporters and included primarily verified transport reactions. A thorough literature scan resulted in 87 different suitable transport reactions, including diffusion processes of small, hydrophilic components as well as reactions realized by uniporters, symporters, and antiporters. Transport reactions affecting the peroxisome were modeled as diffusion, since the case is still not fully resolved whether active transporters are needed. Notably, experimentally verified transporters exist only for a small portion of metabolites. To render the model functional, in terms of ensuring that all reactions are functional (i.e. can carry flux), we had to consider incorporating unconfirmed or even unreported transport reactions whose existence is speculated by experimentalists (Pick et al., 2013).
Biologically, probably the most important step is the specification of a biomass function, defined as the fractional contribution of known cell components to the overall biomass. As the biomass varies with the cellular scenario, we have to account for the developmental stage of the cell and the cell type as well as the environmental conditions. While growing cells produce the required components for cell division and expansion, mature leaf cells mainly synthesize the transport sugar, Suc (Williams et al., 2000; Geiger, 2011). In contrast, mature stem cells predominantly serve as a mechanical support and transport system and, usually, convert the transport sugars into cell wall components. In addition, the overall biomass composition under ambient conditions greatly differs from the composition under stress conditions (Obata and Fernie, 2012). For these purposes, we assembled three different biomass functions for the model, focusing on growing leaf cells and, therefore, comprising sugars, amino acids, nucleotides, and precursors for cell wall, fatty acids, and signaling pathways (Table III; Supplemental Data S1, Text S1.4; Supplemental Data S4; Supplemental Data S5). The proposed biomass compositions used in the presented model refer to rosette fresh weight measurements of autotrophically grown plants, which are converted into dry weight for modeling consistency (Supplemental Data S1, Text S1.4). In contrast, the biomass compositions of the existing genome-scale Arabidopsis models were either experimentally determined heterotrophic cell culture compositions (Williams et al., 2008, 2010; Poolman et al., 2009) or estimated leaf cell compositions (de Oliveira Dal’Molin et al., 2010).
Table III. Major biomass components of a photoautotrophic Arabidopsis leaf cell and their approximated composition with respect to dry weight.
The detailed composite is given in Supplemental Data S1, Text S1.4.
| Component | Composition | References |
|---|---|---|
| µmol g−1 dry wt | ||
| Cell wall | 363.88a | DeBolt et al. (2009) |
| Protein | 2,911.09b | Mooney et al. (2006); Sulpice et al. (2013) |
| Soluble metabolites | 214.66b | Sulpice et al. (2013) |
| Lipid | 779.97b | Dörmann et al. (1995) |
| Starch | 294.86a,b | Sulpice et al. (2013) |
| DNA and RNA | 4.25b | Sharrock and Clack (2002) |
Values for Glc dimer. bValues of optimal growth conditions.
It is noteworthy that the biomass compositions of the Arabidopsis core model do not cover the maintenance costs of a cell representing the energy demand necessary for cell replication, such as macromolecular synthesis (growth-associated maintenance), and cell maintenance, such as turgor pressure (non-growth-associated maintenance). The reasons for this are 2-fold: (1) the established underlying experimental determination (Cheung et al., 2013), unfortunately, is not applicable for photoautotrophic scenarios; and (2) a general approximation is biologically implausible, as the maintenance energy demand is highly condition specific. Cheung et al. (2013) could approximate the difference between the energy expenditure of the cell, measured in terms of Glc uptake, and the requirement for synthesizing biomass in silico for heterotrophic Arabidopsis cell cultures. An analogous measurement for the photoautotrophic scenario would require the determination of the respective energy source (e.g. photons). Furthermore, in the study of Cheung et al. (2013), it was shown that the maintenance costs are highly condition specific, between 13% and 79% of total ATP produced. Consequently, the approximation of a general cost value for the three different growth conditions in the photoautotrophic scenario based on the heterotrophic cell culture data would be biologically unacceptable.
After collecting and reviewing, the resulting reconstruction was converted into a mathematical model using the COBRA toolbox. Thereby, we emphasize that this single model can account for all three cellular scenarios by adjusting the model parameters. To facilitate easy access and wide usability, we provide these models in Systems Biology MarkUp Language format (Supplemental Data S2).
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Data S1. Supplemental text, including Tables S1 to S12.
Supplemental Data S2. Arabidopsis core model in Systems Biology MarkUp Language.
Supplemental Data S3. Reaction list.
Supplemental Data S4. Gas chromatography-mass spectrometry data.
Supplemental Data S5. Two-dimensional gel data.
Supplementary Material
Acknowledgments
We thank Alisdair Fernie and Mark Stitt for helpful discussions regarding the biological details of the reconstruction, Saleh Alseekh for measuring additional gas chromatography-mass spectrometry standards, and Max Sajitz-Hermstein and Sergio Grimbs for critically reviewing drafts of the article.
Glossary
- Pi
inorganic phosphate
- GPR
gene-protein reaction
- EC
Enzyme Commission
- FBA
flux balance analysis
Footnotes
The online version of this article contains Web-only data.
References
- Akashi H, Gojobori T. (2002) Metabolic efficiency and amino acid composition in the proteomes of Escherichia coli and Bacillus subtilis. Proc Natl Acad Sci USA 99: 3695–3700 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apel W, Schulze WX, Bock R. (2010) Identification of protein stability determinants in chloroplasts. Plant J 63: 636–650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachmair A, Finley D, Varshavsky A. (1986) In vivo half-life of a protein is a function of its amino-terminal residue. Science 234: 179–186 [DOI] [PubMed] [Google Scholar]
- Barton MD, Delneri D, Oliver SG, Rattray M, Bergman CM. (2010) Evolutionary systems biology of amino acid biosynthetic cost in yeast. PLoS ONE 5: e11935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caldana C, Degenkolbe T, Cuadros-Inostroza A, Klie S, Sulpice R, Leisse A, Steinhauser D, Fernie AR, Willmitzer L, Hannah MA. (2011) High-density kinetic analysis of the metabolomic and transcriptomic response of Arabidopsis to eight environmental conditions. Plant J 67: 869–884 [DOI] [PubMed] [Google Scholar]
- Cheung CYM, Williams TCR, Poolman MG, Fell DA, Ratcliffe RG, Sweetlove LJ. (2013) A method for accounting for maintenance costs in flux balance analysis improves the prediction of plant cell metabolic phenotypes under stress conditions. Plant J 75: 1050–1061 [DOI] [PubMed] [Google Scholar]
- Craig CL, Weber RS. (1998) Selection costs of amino acid substitutions in ColE1 and ColIa gene clusters harbored by Escherichia coli. Mol Biol Evol 15: 774–776 [DOI] [PubMed] [Google Scholar]
- DeBolt S, Scheible WR, Schrick K, Auer M, Beisson F, Bischoff V, Bouvier-Navé P, Carroll A, Hematy K, Li Y, et al. (2009) Mutations in UDP-glucose:sterol glucosyltransferase in Arabidopsis cause transparent testa phenotype and suberization defect in seeds. Plant Physiol 151: 78–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Oliveira Dal’Molin CG, Quek LE, Palfreyman RW, Brumbley SM, Nielsen LK. (2010) AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol 152: 579–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dörmann P, Hoffmann-Benning S, Balbo I, Benning C. (1995) Isolation and characterization of an Arabidopsis mutant deficient in the thylakoid lipid digalactosyl diacylglycerol. Plant Cell 7: 1801–1810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drubach D (2000) Structure of the brain. In The Brain Explained. Prentice Hall, Upper Saddle River, NJ, pp 6–49 [Google Scholar]
- Ellis R. (1979) The most abundant protein in the world. Trends Biochem Sci 4: 241–244 [Google Scholar]
- Geiger D. (2011) Plant sucrose transporters from a biophysical point of view. Mol Plant 4: 395–406 [DOI] [PubMed] [Google Scholar]
- Gibon Y, Bläsing OE, Palacios-Rojas N, Pankovic D, Hendriks JHM, Fisahn J, Höhne M, Günther M, Stitt M. (2004) Adjustment of diurnal starch turnover to short days: Depletion of sugar during the night leads to a temporary inhibition of carbohydrate utilization, accumulation of sugars and post-translational activation of ADP-glucose pyrophosphorylase in the following light period. Plant J 39: 847–862 [DOI] [PubMed] [Google Scholar]
- Gibon Y, Pyl ET, Sulpice R, Lunn JE, Höhne M, Günther M, Stitt M. (2009) Adjustment of growth, starch turnover, protein content and central metabolism to a decrease of the carbon supply when Arabidopsis is grown in very short photoperiods. Plant Cell Environ 32: 859–874 [DOI] [PubMed] [Google Scholar]
- Gonda DK, Bachmair A, Wünning I, Tobias JW, Lane WS, Varshavsky A. (1989) Universality and structure of the N-end rule. J Biol Chem 264: 16700–16712 [PubMed] [Google Scholar]
- Graciet E, Mesiti F, Wellmer F. (2010) Structure and evolutionary conservation of the plant N-end rule pathway. Plant J 61: 741–751 [DOI] [PubMed] [Google Scholar]
- Hannah MA, Caldana C, Steinhauser D, Balbo I, Fernie AR, Willmitzer L. (2010) Combined transcript and metabolite profiling of Arabidopsis grown under widely variant growth conditions facilitates the identification of novel metabolite-mediated regulation of gene expression. Plant Physiol 152: 2120–2129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzhütter HG. (2004) The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur J Biochem 271: 2905–2922 [DOI] [PubMed] [Google Scholar]
- Kaleta C, Schäuble S, Rinas U, Schuster S. (2013) Metabolic costs of amino acid and protein production in Escherichia coli. Biotechnol J 8: 1105–1114 [DOI] [PubMed] [Google Scholar]
- Kanehisa M, Goto S (2000) KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res 28: 27–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser A, Weber J, Hecht V, Rinas U. (2005) Metabolic flux analysis of Escherichia coli in glucose-limited continuous culture. I. Growth-rate-dependent metabolic efficiency at steady state. Microbiology 151: 693–706 [DOI] [PubMed] [Google Scholar]
- Lamesch P, Berardini TZ, Li D, Swarbreck D, Wilks C, Sasidharan R, Muller R, Dreher K, Alexander DL, Garcia-Hernandez M, et al. (2012) The Arabidopsis Information Resource (TAIR): improved gene annotation and new tools. Nucleic Acids Res 40: D1202–D1210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis NE, Nagarajan H, Palsson BO. (2012) Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat Rev Microbiol 10: 291–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löw R, Rockel B, Kirsch M, Ratajczak R, Hörtensteiner S, Martinoia E, Lüttge U, Rausch T. (1996) Early salt stress effects on the differential expression of vacuolar H+-ATPase genes in roots and leaves of Mesembryanthemum crystallinum. Plant Physiol 110: 259–265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCloskey D, Palsson BO, Feist AM. (2013) Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol Syst Biol 9: 661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer RC, Törjék O, Becher M, Altmann T. (2004) Heterosis of biomass production in Arabidopsis: establishment during early development. Plant Physiol 134: 1813–1823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mintz-Oron S, Meir S, Malitsky S, Ruppin E, Aharoni A, Shlomi T. (2012) Reconstruction of Arabidopsis metabolic network models accounting for subcellular compartmentalization and tissue-specificity. Proc Natl Acad Sci USA 109: 339–344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooney BP, Miernyk JA, Greenlief CM, Thelen JJ. (2006) Using quantitative proteomics of Arabidopsis roots and leaves to predict metabolic activity. Physiol Plant 128: 237–250 [Google Scholar]
- Mueller LA, Zhang P, Rhee SY. (2003) AraCyc: a biochemical pathway database for Arabidopsis. Plant Physiol 132: 453–460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noguchi K, Go CS, Miyazawa SI, Terashima I, Ueda S, Yoshinari T. (2001) Costs of protein turnover and carbohydrate export in leaves of sun and shade species. Funct Plant Biol 28: 37–47 [Google Scholar]
- Obata T, Fernie AR. (2012) The use of metabolomics to dissect plant responses to abiotic stresses. Cell Mol Life Sci 69: 3225–3243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterhansel C, Maurino VG. (2011) Photorespiration redesigned. Plant Physiol 155: 49–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pick TR, Bräutigam A, Schulz MA, Obata T, Fernie AR, Weber APM. (2013) PLGG1, a plastidic glycolate glycerate transporter, is required for photorespiration and defines a unique class of metabolite transporters. Proc Natl Acad Sci USA 110: 3185–3190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piques M, Schulze WX, Höhne M, Usadel B, Gibon Y, Rohwer J, Stitt M. (2009) Ribosome and transcript copy numbers, polysome occupancy and enzyme dynamics in Arabidopsis. Mol Syst Biol 5: 314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poolman MG, Miguet L, Sweetlove LJ, Fell DA. (2009) A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol 151: 1570–1581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigden J (1996) Body, physics of. In Macmillan Encyclopedia of Physics: A–D, Vol 1. Simon & Schuster Macmillan, New York [Google Scholar]
- Sajitz-Hermstein M, Nikoloski Z. (2010) A novel approach for determining environment-specific protein costs: the case of Arabidopsis thaliana. Bioinformatics 26: i582–i588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satish Kumar V, Dasika MS, Maranas CD. (2007) Optimization based automated curation of metabolic reconstructions. BMC Bioinformatics 8: 212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schomburg I, Chang A, Placzek S, Söhngen C, Rother M, Lang M, Munaretto C, Ulas S, Stelzer M, Grote A, et al. (2013) BRENDA in 2013: integrated reactions, kinetic data, enzyme function data, improved disease classification: new options and contents in BRENDA. Nucleic Acids Res 41: D764–D772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seelert H, Poetsch A, Dencher NA, Engel A, Stahlberg H, Müller DJ. (2000) Proton-powered turbine of a plant motor. Nature 405: 418–419 [DOI] [PubMed] [Google Scholar]
- Seligmann H. (2003) Cost-minimization of amino acid usage. J Mol Evol 56: 151–161 [DOI] [PubMed] [Google Scholar]
- Sharrock RA, Clack T. (2002) Patterns of expression and normalized levels of the five Arabidopsis phytochromes. Plant Physiol 130: 442–456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stitt M, Gibon Y, Lunn JE, Piques M. (2007) Multilevel genomics analysis of carbon signalling during low carbon availability: coordinating the supply and utilisation of carbon in a fluctuating environment. Funct Plant Biol 34: 526. [DOI] [PubMed] [Google Scholar]
- Sulpice R, Nikoloski Z, Tschoep H, Antonio C, Kleessen S, Larhlimi A, Selbig J, Ishihara H, Gibon Y, Fernie AR, et al. (2013) Impact of the carbon and nitrogen supply on relationships and connectivity between metabolism and biomass in a broad panel of Arabidopsis accessions. Plant Physiol 162: 347–363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Q, Zybailov B, Majeran W, Friso G, Olinares PDB, van Wijk KJ. (2009) PPDB, the Plant Proteomics Database at Cornell. Nucleic Acids Res 37: D969–D974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweetlove LJ, Ratcliffe RG. (2011) Flux-balance modeling of plant metabolism. Front Plant Sci 2: 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tcherkez GGB, Farquhar GD, Andrews TJ. (2006) Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proc Natl Acad Sci USA 103: 7246–7251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiele I, Palsson BO. (2010) A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat Protoc 5: 93–121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thimm O, Bläsing O, Gibon Y, Nagel A, Meyer S, Krüger P, Selbig J, Müller LA, Rhee SY, Stitt M. (2004) MAPMAN: a user-driven tool to display genomics data sets onto diagrams of metabolic pathways and other biological processes. Plant J 37: 914–939 [DOI] [PubMed] [Google Scholar]
- Tschoep H, Gibon Y, Carillo P, Armengaud P, Szecowka M, Nunes-Nesi A, Fernie AR, Koehl K, Stitt M. (2009) Adjustment of growth and central metabolism to a mild but sustained nitrogen-limitation in Arabidopsis. Plant Cell Environ 32: 300–318 [DOI] [PubMed] [Google Scholar]
- Turina P, Samoray D, Gräber P. (2003) H+/ATP ratio of proton transport-coupled ATP synthesis and hydrolysis catalysed by CF0F1-liposomes. EMBO J 22: 418–426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- UniProt Consortium (2013) Update on activities at the Universal Protein Resource (UniProt) in 2013. Nucleic Acids Res 41: D43–D47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varshavsky A. (1992) The N-end rule. Cell 69: 725–735 [DOI] [PubMed] [Google Scholar]
- Wagner A. (2005) Energy constraints on the evolution of gene expression. Mol Biol Evol 22: 1365–1374 [DOI] [PubMed] [Google Scholar]
- Wang R, Guegler K, LaBrie ST, Crawford NM. (2000) Genomic analysis of a nutrient response in Arabidopsis reveals diverse expression patterns and novel metabolic and potential regulatory genes induced by nitrate. Plant Cell 12: 1491–1509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney SM, Kane HJ, Houtz RL, Sharwood RE. (2009) Rubisco oligomers composed of linked small and large subunits assemble in tobacco plastids and have higher affinities for CO2 and O2. Plant Physiol 149: 1887–1895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams LE, Lemoine R, Sauer N. (2000) Sugar transporters in higher plants: a diversity of roles and complex regulation. Trends Plant Sci 5: 283–290 [DOI] [PubMed] [Google Scholar]
- Williams SG, Cooke GA, Wright DJ, Parsons WJ, Riley RL, Marshall P, Tan LB. (2001) Peak exercise cardiac power output: a direct indicator of cardiac function strongly predictive of prognosis in chronic heart failure. Eur Heart J 22: 1496–1503 [DOI] [PubMed] [Google Scholar]
- Williams TCR, Miguet L, Masakapalli SK, Kruger NJ, Sweetlove LJ, Ratcliffe RG. (2008) Metabolic network fluxes in heterotrophic Arabidopsis cells: stability of the flux distribution under different oxygenation conditions. Plant Physiol 148: 704–718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams TCR, Poolman MG, Howden AJM, Schwarzlander M, Fell DA, Ratcliffe RG, Sweetlove LJ. (2010) A genome-scale metabolic model accurately predicts fluxes in central carbon metabolism under stress conditions. Plant Physiol 154: 311–323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerihun A, McKenzie BA, Morton JD. (1998) Photosynthate costs associated with the utilization of different nitrogen-forms: influence on the carbon balance of plants and shoot-root biomass partitioning. New Phytol 138: 1–11 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.