Abstract
Electrical source imaging (ESI) aims at reconstructing the electrical brain activity from scalp EEG. When applied to interictal epileptiform discharges (IEDs), this technique is of great use for identifying the irritative zone in focal epilepsies. Inaccuracies in the modeling of electro-magnetic field propagation in the head (forward model) may strongly influence ESI and lead to mislocalization of IED generators. However, a systematic study on the influence of the selected head model on the localization precision of IED in a large number of patients with known focus localization has not yet been performed.
We here present such a performance evaluation of different head models in a dataset of 38 epileptic patients who have undergone high-density scalp EEG, intracranial EEG and, for the majority, subsequent surgery. We compared ESI accuracy resulting from three head models: a Locally Spherical Model with Anatomical Constraints (LSMAC), a Boundary Element Model (BEM) and a Finite Element Model (FEM). All of them were computed from the individual MRI of the patient and ESI was performed on averaged IED.
We found that all head models provided very similar source locations. In patients having a positive post-operative outcome, at least 74% of the source maxima were within the resection. The median distance from the source maximum to the nearest intracranial electrode showing IED was 13.2, 15.6 and 15.6 mm for LSMAC, BEM and FEM, respectively. The study demonstrates that in clinical applications, the use of highly sophisticated and difficult to implement head models is not a crucial factor for an accurate ESI.
Keywords: Electrical source imaging, Head model, BEM, FEM, High-density EEG, Epilepsy
Highlights
-
•
Electrical source imaging was performed on 38 patients with refractory epilepsy.
-
•
Three different realistic head models were used: LSMAC, BEM and FEM.
-
•
We found accurate and generally similar source localization for all head models.
-
•
FEM is less robust to MRI segmentation inaccuracies.
-
•
There is no need for highly sophisticated head models in clinical applications.
1. Introduction
In pharmacoresistant focal epilepsy the surgical resection of the epileptogenic area is a therapy of choice for reducing the frequency of seizures. During the presurgical evaluation, the precise identification of the epileptogenic zone is crucial in order to guide the removal of the epileptic foci and spare as much as possible the functionally relevant areas of the cortex. Several techniques are considered together to get a trustworthy estimation of the epileptogenic areas. Among them, electrophysiological investigations are particularly suited as they directly measure the neuroelectrical alterations that are the hallmark of epileptic activity. Compared to intracranial recordings, scalp electrical potentials are easy to acquire but they measure remote effects of electrical currents generated within the brain. As such, they do not allow a precise localization of the origin of electrophysiological abnormalities. The electrical source imaging (ESI) attempts to overcome this drawback by reconstructing the activity in the brain from a map of scalp potentials. Reviews (Kaiboriboon et al., 2012; Plummer et al., 2008) recently confirmed that ESI is a valuable tool for estimating the source of interictal epileptic discharges (IEDs) and clinical validation studies showed that these generators are reliable estimates of the seizure onset zone (Coutin-Churchman et al., 2012; Megevand et al., 2014) and the epileptogenic zone (Brodbeck et al., 2011).
ESI involves two steps. The first one, called resolution of the forward problem, consists in modeling how electrical currents generated in the brain propagate to the scalp electrodes, where their consequences are actually recorded. The second step, called resolution of the inverse problem, consists in inverting the forward model in order to get brain activity from scalp potential. The resolution of the forward problem highly depends on the head model (head geometry and tissue conductivity) and is eventually achieved by solving the Maxwell's equations accordingly, producing the forward operator called the leadfield matrix. Regardless of the ability of a method to invert the leadfield matrix, an inaccurate leadfield model will produce a bad inverse solution, and consequently will lead to an inaccurate ESI. More than thirty years ago, when the EEG inverse problem was first considered, the head model was a single semi-sphere with homogenous and isotropic electrical conductivity. Since then, head models have been greatly improved (Grech et al., 2008) and they can now account for multiple types of tissue and anisotropic conductivities. Most important in the context of presurgical evaluation is the use of realistic head models based on the individual MRI of the patient. The most commonly used realistic models are the Boundary Element Models (BEM) and the Finite Element Models (FEM). The superiority of BEM and FEM over 3-shell spherical head models has been proved using simulated data (Akalin Acar and Makeig, 2013; Fuchs et al., 2007) as well as small group of patients (Guggisberg et al., 2011; Wang et al., 2011). The downside of these sophisticated head models is an increased computational load. The Locally Spherical Model with Anatomical Constraints (LSMAC) (Brunet et al., 2011) tries to compensate this computational cost by using analytical equations while keeping the realistic aspect of the head geometry. In this model the leadfield is calculated iteratively using a spherical model with a different radius for each electrode. It is an improved version of the SMAC model (Spinelli et al., 2000) and has been successfully applied in recent experimental studies (Avanzini et al., 2013; Becker et al., 2013; Berchio et al., 2014) but, to our knowledge, has not been validated in patients with known focus localization and has not been compared to the well-established BEM and FEM. Besides, BEM and FEM themselves have not been evaluated on a large set of real data. We here present such a validation and comparison study on data of 38 epileptic patients in whom the irritative zone was known from intracranial recordings and in the majority of whom the epileptogenic area was surgically removed, allowing comparison of the ESI source maximum with the intracranial electrode positions and the resected zone.
2. Material and methods
2.1. Patients
The patient dataset (Megevand et al., 2014) included n = 38 patients (age at evaluation 24 ± 12 years, range 3–51 years, 21 male, 17 female) matching following inclusion criteria: i) they suffered from drug resistant partial epilepsy, ii) they had high-density scalp EEG (128 or 256 channels) showing interictal spikes, iii) they underwent intracranial EEG showing interictal spikes. 32 of them also had a surgical resection of supposed epileptic areas of the brain. The retrospective study presented here is part of a larger neuroimaging program in epilepsy approved by the local ethics committee.
2.2. Scalp EEG
Fourteen patients were recorded using the 128-electrode Geodesic Sensor Net and 24 using the 256 electrode Geodesic Sensor Net. Electrode impedances were kept below 20 kΩ (Ferree et al., 2001) and signal was 0.1–100 Hz band-pass filtered. We recorded at least 30 minutes of continuous EEG at 256–1000 Hz sampling frequency. Peaks of 20–50 interictal spikes with similar scalp distribution were marked by expert neurologists (SV, MS) and averaged within a window of 1s centered on the marked peaks. For further analysis, electrodes on the cheek and the neck were systematically removed from the EEG because they were too noisy and artifact-laden. If other channels exhibited strong and repetitive artifacts, they were also removed and the corresponding signal rebuilt by interpolating neighboring electrodes using a spherical spline. Hence, 204 electrodes from the 256-electrode recordings were used for the analysis, and 125 were kept from the 128-electrode cap.
2.3. Irritative zone
The estimation of the irritative zone (IZ) was based on intracranial EEG recordings. Thirteen patients were implanted with only subdural grids and strips, 12 patients had only depth electrodes, and 13 had both subdural and depth electrodes. Positions of intracranial electrodes were calculated using the post-implantation imaging (CT for 36 patients and MRI for 2 patients) and coregistered with solution points of ESI. Interictal recordings were reviewed by board certified EEG experts (MS, SV). Contacts showing interictal spikes formed the irritative zone. Contacts involved only in the propagation of interictal spikes were not included in the IZ. In IZ the electrode showing in average the highest peak amplitude was considered as the centroid of IZ. The location of this electrode will be denoted by max-IZ in the following.
2.4. Surgery
Surgical resection of the supposed epileptogenic area of the brain was performed on 32 patients. Post-operative follow-up of at least one year allowed neurologists to determine outcome of surgery. 15 patients had an Engel class I outcome (seizure free), 8 had Engel class II (decrease of seizure frequency of more than 80%), 7 had Engel class III (decrease of seizure frequency 50–80%) and 2 had Engel class IV (no change). Engel class I and II were considered as positive outcome while Engel class III and IV were considered as negative outcome. All operated patients had post-operative MRI acquired at 1.5 or 3 Tesla with T1 weighting. We used these images to precisely determine the resected areas and coregistered them with the solution points used in the ESI.
2.5. Inverse solution
We used the inverse method LORETA (Pascual-Marqui et al., 1994) implemented in Cartool (Brunet et al., 2011). This method basically provides a pseudo-inverse matrix of the leadfield matrix using a least square Tikhonov-regularized solution under a smoothness constraint. The pseudo-inverse applied on the peak of averaged spikes gave us an estimation of the underlying brain activity. More precisely, strength of dipoles associated with each solution point was obtained. While several studies suggested that source localization at the peak of the spikes may be contaminated by spike propagations (Alarcon et al., 1994; Lantz et al., 2003a; Ray et al., 2007), we wanted to ensure that the SNR was sufficiently high for all patients, which was not the case when performing the ESI at the half of the rising-phase. The source of surface spikes is known to be spatially extended (Tao et al., 2005). As LORETA is not able to determine the extension, we took into account only the solution point with maximal source strength. This point will be denoted ESI-max in the following.
2.6. Leadfield matrix and head models
The leadfield matrix is a linear operator that transforms current generated at solution points in the brain into scalp potentials. It depends on i) the position of the solution points, ii) the position of the scalp electrodes, and iii) the volume conductor model.
We constrained the solution points in the gray matter using the individual pre-implantation T1 MRI and placed them on a regular grid of 6 mm resolution (yielding 3000 to 5000 solution points). Scalp electrodes were coregistered with the individual T1 pre-implantation MRI performing a 9-parameter transformation of a template cap1 such that T9, T10 and Cz were placed according to the 10–20 system. Electrodes of the transformed template cap were then projected onto the head surface. Solution point generation and electrode coregistration were performed in Cartool (D. Brunet, Geneva University Hospital and Medical School, Center for Biomedical Imaging (CIBM), Geneva, Switzerland http://sites.google.com/site/fbmlab/cartool).
The volume conductor model describes the head geometry (head model) and assigns an electrical conductivity to each type of tissue of the head. We used conductivities of 0.33 S/m for the scalp and the brain. The brain to scalp conductivity ratio was constrained by BESA and therefore set to 1/80. When the cerebrospinal fluid (CSF) was taken into account in the model, its conductivity was 1.79 S/m. For our study we considered three different head models: the Locally Spherical Model with Anatomical Constraints (LSMAC), the Boundary Element Model (BEM), and the Finite Element Model (FEM). Main features of these head models are recalled in Table 1.
Table 1.
Main characteristics of the LSMAC, BEM and FEM head models as used in the study.
| Head model | Type of geometry | Modeled tissues | Skull anisotropy | Solver |
|---|---|---|---|---|
| LSMAC | Surface | Brain/skull/scalp | No | Analytical |
| BEM | Surface | Brain/skull/scalp | No | Numerical |
| FEM | Volume | Brain/CSF/skull/scalp | No | Numerical |
In the LSMAC (Brunet et al., 2011), the thicknesses of the scalp, skull and brain are estimated sequentially at each electrode location. These thicknesses are then used in a 3-shell spherical model with the local radiuses, providing a realistic geometry between solution points and electrodes to be accounted for. The electrical conductivity of each tissue was homogenous and isotropic. The LSMAC could be classified between the 3-shell spherical head model and the BEM, because the head geometry is realistic but the forward solution remains analytical. Also, contrary to the BEM, it does not need an explicit global segmentation of the brain tissues, skipping an otherwise delicate step when the available MRIs are not of good quality.
The BEM defines only interfaces between each tissue of the head. Here we used a three layer model accounting for air/scalp, scalp/skull, and skull/brain interfaces. They were modeled by triangular meshes made of 1800, 1000 and 800 triangles respectively using the pre-implantation T1 MRI and the Fieldtrip toolbox (Oostenveld et al., 2011). Each type of tissue was considered electrically homogenous and isotropic. Adding solution points and electrodes to the head model, the leadfield matrix was finally computed with the boundary element numerical solver implemented in the OpenMEEG library (Gramfort et al., 2010).
In the FEM, the head is separated into a large amount of elementary volume elements. Each element is labeled as a certain type of tissue with isotropic and homogeneous conductivity. The segmentation algorithm as implemented in BESA MRI 2.0 (BESA GmbH, Gräfelfing, Germany) yielded the classification into four different types of tissue on a 1 mm cubic voxel grid: scalp, skull, CSF and brain. Next, a 2 mm geometry-adapted, cubic mesh is constructed for the FEM computation by integrating over the 1 mm voxels (Wolters et al., 2007). Finally, by adding the gray matter solution points and electrodes we computed the FEM leadfield matrix in BESA MRI.
We emphasize that for each head model we used the exact same solution points, electrode position and head conductivities.
2.7. Outcome measure of ESI
As a first measure we investigated how ESI varies with respect to the considered head model without using any ground truth. Thus we calculated the mutual Cartesian distances between ESI-max resulting from LSMAC, BEM and FEM. Eventually we got three measures: LSMAC to BEM, LSMAC to FEM, and BEM to FEM distances. We also calculated the percentage of ESI-max that was at the exact same solution points for two or all head models. This value is denoted by the rate of superimposed ESI-max in the following.
In order to validate ESI accuracy with respect to the choice of head model, we considered two gold standards: the resected area and the irritative zone based on intracranial recordings. First, we estimated the sensitivity, the specificity, the false negative distance and the positive predictive value (PPV) of the ESI with respect to the resected area. The sensitivity is the ability of ESI to detect the region responsible of the epileptic seizures. It is the rate of ESI-max in the resected area when surgery outcome was positive. The specificity is the ability of ESI to reject non-epileptic regions. This is the rate of ESI-max outside the resected area when surgery outcome was negative. Due to lack of information, the term “upper bound of the specificity” is more accurate, because for negative post-operative outcome we did not know the actual epileptic region and consequently, in this situation, and when ESI-max did not coincide with the resected area, we had no way to know whether or not the ESI-max was inside the true epileptic focus. When ESI-max was outside the resected area and surgery outcome was positive (i.e. a false negative occurred), we calculated the so-called “false negative distance” defined as the minimal Cartesian distance between ESI-max and the resected zone. The PPV is the probability of having a positive post-operative outcome when the ESI-max was in the resection. It is a measure of confidence of the ESI.
Concerning the IZ defined by intracranial recordings, we defined two distances (Fig. 1). Firstly, dmin is the minimal distance between estimated source and IZ. It is formally defined as the Cartesian distance from ESI-max to the nearest electrode in IZ. Secondly, dcenter is the distance between the estimated source and the centroid of IZ. It is formally defined as the Cartesian distance from ESI-max to max-IZ. For both distributions of distance, we calculated the median value, the mean value, the standard deviation with respect to the mean (denoted by std), the 1st quartile (Q1) and 3rd quartile (Q3). All these values will be represented in the results as box-and-whisker plots. We also calculated the interquartile range (defined by IQR = Q3 − Q1) which reflects the spread of the distribution.
Fig. 1.
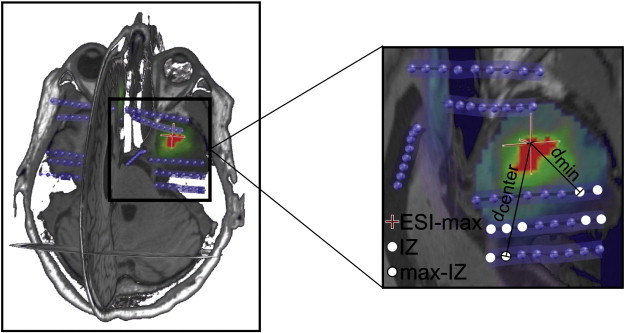
Distance from ESI-max to irritative zone (IZ). White dots represent intracranial electrodes showing interictal spikes, thus they define IZ. The white dot delimited by a black line represents the electrode showing interictal spikes with the maximum amplitude, it defines max-IZ. The distance from ESI-max (cross) to max-IZ is denoted by dcenter and the distance from ESI-max to the nearest electrode belonging to IZ is denoted by dmin. IZ: irritative zone, ESI-max: maximum activation of electrical source imaging.
3. Results
3.1. Distance between head models
Table 2 and Fig. 2 show how ESI differ from each other with respect to the head model. Table 2 reveals that ESI-max was in general very close from each other (median distance is at most 13.4 mm) but can be large in some rare cases (up to 85.9 mm). Similarity was most pronounced for BEM and FEM (median distance is 8.4 mm and rate of superimposed ESI-max is 32%). In 4 cases out of 38 (10%) the ESI-max was at the exact same solution point for all head models.
Table 2.
Distances between ESI-max produced by LSMAC, BEM and FEM, in millimeters.
| LSMAC/BEM | LSMAC/FEM | BEM/FEM | |
|---|---|---|---|
| Median distance | 12.0 | 13.4 | 8.4 |
| Max distance | 46.0 | 85.9 | 77.1 |
Fig. 2.
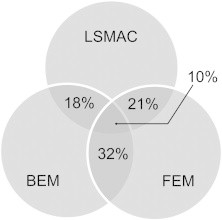
Percentage rate of superimposed ESI-max with respect to the head model.
3.2. ESI and resection
Sensitivity, specificity, PPV and median false negative distance are given in Table 3. Generally speaking LSMAC and BEM had slightly better performance than FEM. All sensitivities were similar ranging from 0.74 (17/23) to 0.78 (18/23). Differences in specificity were more pronounced but were based on very few patients (5 or 6): the LSMAC specificity and FEM specificity are 0.44 (4/9) while that of the BEM was 0.67 (6/9). The PPV ranged from 0.77 (17/22) for the FEM to 0.85 for BEM (17/20). When false negatives occurred, ESI-max of the LSMAC was the closest from the resection with a median distance of 13.7 mm (5 patients). Those of BEM and FEM were 16.1 mm and 23.2 mm respectively (6 patients for both).
Table 3.
Results of ESI with respect to the head model using resection as ground truth. The LSMAC has the best sensitivity and median false negative distance while the BEM has the best specificity and PPV. Overall, the FEM is slightly less than or as efficient as the LSMAC and the BEM. Distances are in millimeters.
| LSMAC | BEM | FEM | |
|---|---|---|---|
| Sensitivity (n = 23) | 0.78 | 0.74 | 0.74 |
| Specificity (n = 9) | 0.44 | 0.67 | 0.44 |
| Positive predictive value (PPV) | 0.78 | 0.85 | 0.77 |
| Median false negative distance | 13.7 | 16.1 | 23.2 |
3.3. ESI and irritative zone
Fig. 3A shows the distribution of the minimum distances from ESI-max to IZ (dmin) and Fig. 3B shows the distance from ESI-max to the centroid of IZ (dcenter). As defined in Subsection 2.7, dmin is the minimal ESI-max/IZ distance and dcenter is the ESI-max/max-IZ distance. Overall, the LSMAC had slightly better performance than BEM and FEM. Its resulting median minimal distance to IZ (13.2 mm) is 18% shorter than that of the FEM and 17% than that of the BEM. These values drop respectively to 6% and 2% for the distance to the centroid of IZ. FEMs dmax values are more spread (std = 19.8 mm, IQR = 23.9 mm) than LSMAC and BEM (std = 15.7 mm, IQR = 18.8 mm and std = 14.4 mm, IQR = 18.7 mm, respectively). The same assessment is true for dmin and particularly pronounced for the standard deviation.
Fig. 3.
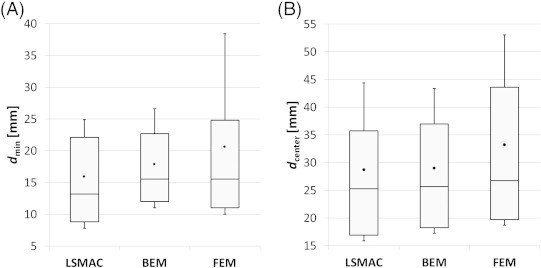
Distance from ESI-max to IZ. The black dots represent the mean distance, and the whiskers the standard deviation with respect to the mean. The horizontal line within the box is the median value, the top line of the box is the 3rd quartile while the bottom line is the 1st quartile. In panel A the minimum distance from ESI-max to IZ (dmin) is represented. In panel B distance from ESI-max to the centroid of IZ (dcenter) is represented.
We also performed a t-test in order to test whether the distributions of distance were statistically different across head models. No p-value was less than 0.05. Distributions are therefore not statistically different.
3.4. Influence of MRI segmentation on ESI
In the FEM pipeline the segmentation was sometimes inaccurate due to large lesions in the brain or to the difficulty of differentiating brain tissues in children. Fig. 4 shows an example of this situation for a patient with successfully operated right mesial temporal lobe epilepsy. The MRI reveals a large lesion in the left frontal lobe. The brain defect is filled by CSF but the segmentation algorithm classified it as bone tissue (yellow outlines), which has a much lower conductivity than that of the CSF. As a consequence, the FEM ESI-max was located in the medial frontal lobe while it should be in the right temporal mesial region. LSMAC and BEM seemed to ignore the lesion and included it within the brain. As brain and CSF have similar conductivities, LSMAC and BEM ESI were more accurate showing a maximum activation in the resected area. Table 4 and Fig. 5 show the same type of results as in Subsections 3.2 and 3.3 but excluding the six patients for whom the segmentation was obviously inaccurate. Performance of the FEM improved significantly without these patients, and was now better or closer to those of LSMAC and BEM.
Fig. 4.
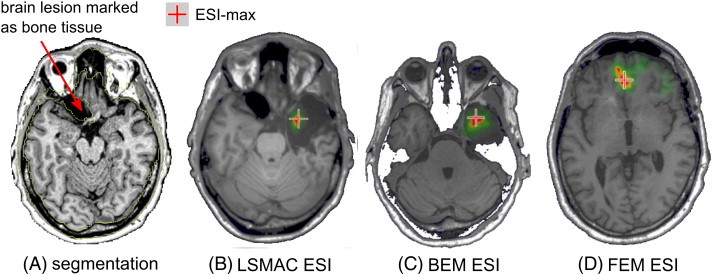
Example of ESI when the segmentation was inaccurate. The patient was operated in the right temporal lobe and was seizure-free after the resection. In panel A, the pre-resection MRI shows a large lesion in the left frontal region containing CSF. The segmentation algorithm marked this part as bone (outlined by yellow lines). Thus these voxels are labeled as skull tissue in the FEM and the resulting ESI (D) shows a maximum in the mesial frontal region. In contrast, LSMAC and BEM ESI (B and C) show accurate localization of the ESI-max in the right mesial temporal lobe.
Table 4.
ESI with respect to resection for different head models and after removing patients with inaccurate segmentation. All values have improved compared to those including inaccurate segmentation. FEM values are now very similar to those of the LSMAC.
| LSMAC | BEM | FEM | |
|---|---|---|---|
| Sensitivity (n = 20) | 0.80 | 0.75 | 0.80 |
| Specificity (n = 6) | 0.5 | 0.67 | 0.5 |
| Positive predictive value (PPV) | 0.84 | 0.88 | 0.84 |
| Median false negative distance | 11.1 | 13.2 | 14.7 |
Fig. 5.
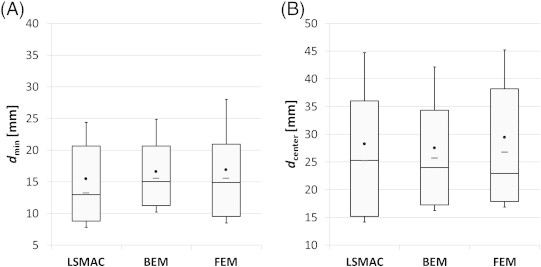
Distance from ESI-max to IZ without patients with inaccurate segmentations (32 patients remaining). The black dots represent the mean distance, and the whiskers the standard deviation with respect to the mean. The horizontal line within the box is the median value, the top line of the box is the 3rd quartile while the bottom line is the 1st quartile. Median distances without removing inaccurate segmentations (see Section 3.3) are recalled by the gray dashes. Minimum distance from ESI-max to IZ (dmin) is displayed in panel A, distance from ESI-max to the center of IZ is displayed in panel B (dcenter). All values but dcenter of LSMAC have improved compared to those including inaccurate segmentation (Fig. 3). This behavior is more pronounced for the FEM.
For each head model, we also performed a t-test between distributions of distances including accurate segmentation only and inaccurate segmentation only. Segmentation inaccuracies have a significant influence on the FEM as the p-value is lower than 0.05 for both dmin (p = 0.002) and dcenter (p = 0.003) distances. It has a limited influence on the BEM, the p-value is slightly lower than 0.05 for dmin (p = 0.041) but greater than 0.05 for dcenter. The LSMAC is not statistically influenced by segmentation inaccuracies.
4. Discussion
Our study investigated the influence of the head model on the ESI in epilepsy. Three widely used head models were compared: the LSMAC, the BEM and the FEM. Localization errors were calculated with respect to the intracranial recordings of 38 epileptic patients and with respect to the resected area of 32 patients.
Our results showed that the ESI was influenced by the head model to a moderate and non-significant degree. The median distance between the maximum ESI obtained by LSMAC and FEM was at most 14 mm. In 4 cases out of 38, ESI-max was at the exact same location for all head models and in 50% of cases at least two head models gave the same ESI-max. This small distance between ESI results (few millimeters) will not significantly influence clinical decision making after the presurgical evaluation. This was confirmed by the fact that there was no significant difference between head models with respect to validation with intracranial recordings. The median minimal distance from ESI to IZ was between 13 and 16 mm while that of ESI to max-IZ was 25–27 mm. Although we noted a slightly reduced overall accuracy for the FEM pipeline, this was not significant. Indeed, when patients with poor segmentation or lesions were removed from the dataset, FEM performance reached or overtook that of LSMAC and BEM, though again the difference to the other pipelines is not statistically significant. This discrepancy is due to the high sensitivity of the segmentation algorithm of the FEM pipeline to MRI quality when trying to separate CSF and skull tissues (Lanfer et al., 2012). Since complementary T2 data were lacking, CSF could not be identified adequately and, thus, lesion tissue could be mislabeled as bone by the automated FEM segmentation algorithm of BESA MRI. The option to manually correct the segmentation results was not used because it was still in development and consequently a cumbersome process impracticable in a clinical context. Thus, the limited performance of FEM in these cases with problematic segmentation was not due to the method as such but to limitations in input.
The relative insensitivity of ESI to the head model in a clinical context probably occurs because the potential benefit of a given head model is too small compared to the confounding effect of other factors such as inaccurate conductivities, segmentation inaccuracies, low resolution of the grid of solution points, noisy data (EEG and MRI), approximate ground truth and inverse method blurring. The most recent head models now take into account white matter anisotropy, and divide the skull in several layers. This fine degree of modeling is of course outstanding and the effort for improving head models must keep going, but, for really impacting ESI in clinical context, this effort has to be done together with enhancing inputs to the model, especially by improving acquisition protocols and the segmentation of MRI. For now, our results suggest that it is not necessary to use these elaborate and time-consuming head models in epilepsy due to the aforementioned issues.
The best gold standard for validating ESI would be the simultaneous recording of both intracranial and scalp EEG. Ideally, controlled events-of-interest should be emitted from a contact itself in order to know exactly the origin of the events observed on scalp EEG. Getting this kind of data for a number of patients sufficient to allow statistical estimation is a real challenge. Thus, in this study, we used intracranial EEG recorded non-simultaneously with scalp EEG. We assumed that IED visible on scalp EEG at the time of its recording originated from the same location as IED marked on intracranial EEG. This assumption may not hold in all cases, since not all intracranial spikes are seen on the surface (Yamazaki et al., 2013). Another limitation is the limited spatial sampling of the brain by intracranial electrodes resulting in the possibility to miss part or all of IZ by intracranial recordings, especially when depth electrodes were used. In addition, even if the IZ was well-covered, the distance between contacts was about 10 mm, thus we do not have a very precise spatial resolution of max-IZ. Concerning subdural recordings with grids or strips placed on the brain surface, the true focus might lay deeper inside the brain, requiring source localization algorithms to properly localize it (Acar et al., 2011). All this brings some uncertainty to our results, but we believe that intracranial EEG remains an excellent gold standard to estimate the yield of ESI because it measures directly the phenomena we want to localize. On the contrary, other commonly used comparisons such as resected area or brain lesion visible on MRI are indirect measures that add even larger uncertainty than the intracranial recordings. The finding of a brain lesion is not a sufficient formal proof of the localization of epileptic activity as the epileptic activity usually arises at the neighborhood or margins of the lesion rather than in the lesion itself and some lesion could be incidental findings unrelated to the epileptic activity (e.g. as in some MRI findings of cavernoma). Regarding the validation using resection areas, the hole left by a successful surgical resection does not directly reflect the origin of IED but a region embracing the seizure onset zone (SOZ). In epilepsy, ESI is applied almost exclusively on IED because this type of event occurs more frequently and with a better signal-to-noise ratio than seizures. Therefore, the origin of our events-of-interest is the IZ, not the SOZ. Nevertheless, these two regions usually overlap as shown in a recent intracranial EEG study (Megevand et al., 2014). Taking the resected area as a gold standard is thus a valuable clinically motivated gold standard allowing the study of the relationship between ESI and post-operative outcome, and more generally of the benefit of ESI in the pre-surgical process of epilepsy.
An important factor influencing the forward modeling is the electrical conductivity of the different layers of the head. The ratio between skull and brain conductivity was constrained to a default value of 1/80 in the BESA MRI version we used for FEM. This ratio is one of those used in the literature (Geddes and Baker, 1967; Goncalves et al., 2003; Gutierrez et al., 2004; Lai et al., 2005; Oostendorp et al., 2000) but it does not correspond to current recommendations that tend to rather be between 1/15 and 1/40 (Ryynanen et al., 2006). However, its influence on ESI seems limited (Stenroos and Hauk, 2013) and we used the same for all head models to ensure a fair comparison.
We did not test the influence of the head models for low-density EEG usually used at the first examination in clinical routine. Numerous studies have shown that high-density EEG greatly improves ESI (Holmes et al., 2010; Lantz et al., 2003b; Yamazaki et al., 2012), and that consequently EEG source analysis should be performed only with high-density recordings.
In summary, we showed that the choice between LSMAC, BEM and FEM head models had no significant influence on ESI outcome. Although LSMAC showed slightly better accuracy than BEM and FEM (few millimeters at best), this non-significant advantage was not present when removing the cases with problematic segmentation. The influence of segmentation inaccuracies affected all models. However, our results showed that the segmentation used in FEM was significantly more sensitive to the quality of the MRI input data. For more accurate head modeling, clinical MRI protocols will need to be improved to acquire T1-weighted images without fat shift artifacts as well as T2-weighted images to improve skull and CSF rendering. Based on current MRI protocols and segmentation, however, the choice between the presented head models does not significantly influence clinical decision making following pre-surgical evaluation in epilepsy. Our study suggests that sophisticated and time-consuming head models have currently no clear benefit in a clinical context as long as other sources of error influencing ESI persist: spatial resolution of the grid of solution points, blurring of the inverse solution, noise in data and limitations in MRI segmentation.
Acknowledgment
This study was supported by the Swiss National Science Foundation (Grant No. 33CM30-140332 to MS and CMM, No. 320020-122073 to SV and P3SMP3_148388 to PM). The development of the software Cartool used in this study was supported by the Lemanic Center of Biomedical Imaging (CIBM). The authors wish to thank Dr. Andre Waelkens from BESA GmbH, Gräfelfing/Germany for his valuable help in building interfaces between the BESA MRI software and Cartool.
Footnotes
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike License, which permits non-commercial use, distribution, and reproduction in any medium, provided the original author and source are credited.
Available at https://sites.google.com/site/cartoolcommunity/files.
Contributor Information
Gwénael Birot, Email: gwenael.birot@unige.ch.
Laurent Spinelli, Email: laurent.spinelli@hcuge.ch.
Pierre Mégevand, Email: pierre.megevand@gmail.com.
Denis Brunet, Email: denis.brunet@unige.ch.
Margitta Seeck, Email: margitta.seeck@hcuge.ch.
Christoph M. Michel, Email: christoph.michel@unige.ch.
References
- Acar Z.A., Palmer J., Worrell G., Makeig S. Electrocortical source imaging of intracranial EEG data in epilepsy. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011;2011:3909–3912. doi: 10.1109/IEMBS.2011.6090971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akalin Acar Z., Makeig S. Effects of forward model errors on EEG source localization. Brain Topogr. 2013;26(3):378–396. doi: 10.1007/s10548-012-0274-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alarcon G., Guy C.N., Binnie C.D., Walker S.R., Elwes R.D., Polkey C.E. Intracerebral propagation of interictal activity in partial epilepsy: implications for source localisation. J. Neurol. Neurosurg. Psychiatry. 1994;57(4):435–449. doi: 10.1136/jnnp.57.4.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avanzini P., Fabbri-Destro M., Campi C., Pascarella A., Barchiesi G., Cattaneo L., Rizzolatti G. Spatiotemporal dynamics in understanding hand–object interactions. Proc. Natl. Acad. Sci. U. S. A. 2013;110(40):15878–15885. doi: 10.1073/pnas.1314420110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker R., Pefkou M., Michel C.M., Hervais-Adelman A.G. Left temporal alpha-band activity reflects single word intelligibility. Front. Syst. Neurosci. 2013;7:121. doi: 10.3389/fnsys.2013.00121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berchio C., Rihs T.A., Michel C.M., Brunet D., Apicella F., Muratori F., Gallese V., Umilta M.A. Parieto-frontal circuits during observation of hidden and visible motor acts in children. A high-density EEG source imaging study. Brain Topogr. 2014;27(2):258–270. doi: 10.1007/s10548-013-0314-x. [DOI] [PubMed] [Google Scholar]
- Brodbeck V., Spinelli L., Lascano A.M., Wissmeier M., Vargas M.I., Vulliemoz S., Pollo C., Schaller K., Michel C.M., Seeck M. Electroencephalographic source imaging: a prospective study of 152 operated epileptic patients. Brain. 2011;134(Pt 10):2887–2897. doi: 10.1093/brain/awr243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunet D., Murray M.M., Michel C.M. Spatiotemporal analysis of multichannel EEG: CARTOOL. Comput. Intell. Neurosci. 2011;2011:813870. doi: 10.1155/2011/813870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutin-Churchman P.E., Wu J.Y., Chen L.L., Shattuck K., Dewar S., Nuwer M.R. Quantification and localization of EEG interictal spike activity in patients with surgically removed epileptogenic foci. Clin. Neurophysiol. 2012;123(3):471–485. doi: 10.1016/j.clinph.2011.08.007. [DOI] [PubMed] [Google Scholar]
- Ferree T.C., Luu P., Russell G.S., Tucker D.M. Scalp electrode impedance, infection risk, and EEG data quality. Clin. Neurophysiol. 2001;112(3):536–544. doi: 10.1016/s1388-2457(00)00533-2. [DOI] [PubMed] [Google Scholar]
- Fuchs M., Wagner M., Kastner J. Development of volume conductor and source models to localize epileptic foci. J. Clin. Neurophysiol. 2007;24(2):101–119. doi: 10.1097/WNP.0b013e318038fb3e. [DOI] [PubMed] [Google Scholar]
- Geddes L.A., Baker L.E. The specific resistance of biological material—a compendium of data for the biomedical engineer and physiologist. Med. Biol. Eng. 1967;5(3):271–293. doi: 10.1007/BF02474537. [DOI] [PubMed] [Google Scholar]
- Goncalves S., de Munck J.C., Verbunt J.P., Heethaar R.M., da Silva F.H. In vivo measurement of the brain and skull resistivities using an EIT-based method and the combined analysis of SEF/SEP data. IEEE Trans. Biomed. Eng. 2003;50(9):1124–1128. doi: 10.1109/TBME.2003.816072. [DOI] [PubMed] [Google Scholar]
- Gramfort A., Papadopoulo T., Olivi E., Clerc M. OpenMEEG: opensource software for quasistatic bioelectromagnetics. Biomed. Eng. Online. 2010;9:45. doi: 10.1186/1475-925X-9-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grech R., Cassar T., Muscat J., Camilleri K.P., Fabri S.G., Zervakis M., Xanthopoulos P., Sakkalis V., Vanrumste B. Review on solving the inverse problem in EEG source analysis. J. Neuroeng. Rehabil. 2008;5:25. doi: 10.1186/1743-0003-5-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guggisberg A.G., Dalal S.S., Zumer J.M., Wong D.D., Dubovik S., Michel C.M., Schnider A. Localization of cortico-peripheral coherence with electroencephalography. Neuroimage. 2011;57(4):1348–1357. doi: 10.1016/j.neuroimage.2011.05.076. [DOI] [PubMed] [Google Scholar]
- Gutierrez D., Nehorai A., Muravchik C.H. Estimating brain conductivities and dipole source signals with EEG arrays. IEEE Trans. Biomed. Eng. 2004;51(12):2113–2122. doi: 10.1109/TBME.2004.836507. [DOI] [PubMed] [Google Scholar]
- Holmes M.D., Tucker D.M., Quiring J.M., Hakimian S., Miller J.W., Ojemann J.G. Comparing noninvasive dense array and intracranial electroencephalography for localization of seizures. Neurosurgery. 2010;66(2):354–362. doi: 10.1227/01.NEU.0000363721.06177.07. [DOI] [PubMed] [Google Scholar]
- Kaiboriboon K., Luders H.O., Hamaneh M., Turnbull J., Lhatoo S.D. EEG source imaging in epilepsy—practicalities and pitfalls. Nat. Rev. Neurol. 2012;8(9):498–507. doi: 10.1038/nrneurol.2012.150. [DOI] [PubMed] [Google Scholar]
- Lai Y., van Drongelen W., Ding L., Hecox K.E., Towle V.L., Frim D.M., He B. Estimation of in vivo human brain-to-skull conductivity ratio from simultaneous extra- and intra-cranial electrical potential recordings. Clin. Neurophysiol. 2005;116(2):456–465. doi: 10.1016/j.clinph.2004.08.017. [DOI] [PubMed] [Google Scholar]
- Lanfer B., Scherg M., Dannhauer M., Knosche T.R., Burger M., Wolters C.H. Influences of skull segmentation inaccuracies on EEG source analysis. Neuroimage. 2012;62(1):418–431. doi: 10.1016/j.neuroimage.2012.05.006. [DOI] [PubMed] [Google Scholar]
- Lantz G., Spinelli L., Seeck M., de Peralta Menendez R.G., Sottas C.C., Michel C.M. Propagation of interictal epileptiform activity can lead to erroneous source localizations: a 128-channel EEG mapping study. J. Clin. Neurophysiol. 2003;20(5):311–319. doi: 10.1097/00004691-200309000-00003. [DOI] [PubMed] [Google Scholar]
- Lantz G., Grave de Peralta R., Spinelli L., Seeck M., Michel C.M. Epileptic source localization with high density EEG: how many electrodes are needed? Clin. Neurophysiol. 2003;114(1):63–69. doi: 10.1016/s1388-2457(02)00337-1. [DOI] [PubMed] [Google Scholar]
- Megevand P., Spinelli L., Genetti M., Brodbeck V., Momjian S., Schaller K., Michel C.M., Vulliemoz S., Seeck M. Electric source imaging of interictal activity accurately localises the seizure onset zone. J. Neurol. Neurosurg. Psychiatry. 2014;85(1):38–43. doi: 10.1136/jnnp-2013-305515. [DOI] [PubMed] [Google Scholar]
- Oostendorp T.F., Delbeke J., Stegeman D.F. The conductivity of the human skull: results of in vivo and in vitro measurements. IEEE Trans. Biomed. Eng. 2000;47(11):1487–1492. doi: 10.1109/TBME.2000.880100. [DOI] [PubMed] [Google Scholar]
- Oostenveld R., Fries P., Maris E., Schoffelen J.M. FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011;2011:156869. doi: 10.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual-Marqui R.D., Michel C.M., Lehmann D. Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain. Int. J. Psychophysiol. 1994;18(1):49–65. doi: 10.1016/0167-8760(84)90014-x. [DOI] [PubMed] [Google Scholar]
- Plummer C., Harvey A.S., Cook M. EEG source localization in focal epilepsy: where are we now? Epilepsia. 2008;49(2):201–218. doi: 10.1111/j.1528-1167.2007.01381.x. [DOI] [PubMed] [Google Scholar]
- Ray A., Tao J.X., Hawes-Ebersole S.M., Ebersole J.S. Localizing value of scalp EEG spikes: a simultaneous scalp and intracranial study. Clin. Neurophysiol. 2007;118(1):69–79. doi: 10.1016/j.clinph.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Ryynanen O.R., Hyttinen J.A., Malmivuo J.A. Effect of measurement noise and electrode density on the spatial resolution of cortical potential distribution with different resistivity values for the skull. IEEE Trans. Biomed. Eng. 2006;53(9):1851–1858. doi: 10.1109/TBME.2006.873744. [DOI] [PubMed] [Google Scholar]
- Spinelli L., Andino S.G., Lantz G., Seeck M., Michel C.M. Electromagnetic inverse solutions in anatomically constrained spherical head models. Brain Topogr. 2000;13(2):115–125. doi: 10.1023/a:1026607118642. [DOI] [PubMed] [Google Scholar]
- Stenroos M., Hauk O. Minimum-norm cortical source estimation in layered head models is robust against skull conductivity error. Neuroimage. 2013;81C:265–272. doi: 10.1016/j.neuroimage.2013.04.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao J.X., Ray A., Hawes-Ebersole S., Ebersole J.S. Intracranial EEG substrates of scalp EEG interictal spikes. Epilepsia. 2005;46(5):669–676. doi: 10.1111/j.1528-1167.2005.11404.x. [DOI] [PubMed] [Google Scholar]
- Wang G., Worrell G., Yang L., Wilke C., He B. Interictal spike analysis of high-density EEG in patients with partial epilepsy. Clin. Neurophysiol. 2011;122(6):1098–1105. doi: 10.1016/j.clinph.2010.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolters C.H., Anwander A., Berti G., Hartmann U. Geometry-adapted hexahedral meshes improve accuracy of finite-element-method-based EEG source analysis. IEEE Trans. Biomed. Eng. 2007;54(8):1446–1453. doi: 10.1109/TBME.2007.890736. [DOI] [PubMed] [Google Scholar]
- Yamazaki M., Tucker D.M., Fujimoto A., Yamazoe T., Okanishi T., Yokota T., Enoki H., Yamamoto T. Comparison of dense array EEG with simultaneous intracranial EEG for interictal spike detection and localization. Epilepsy Res. 2012;98(2–3):166–173. doi: 10.1016/j.eplepsyres.2011.09.007. [DOI] [PubMed] [Google Scholar]
- Yamazaki M., Tucker D.M., Terrill M., Fujimoto A., Yamamoto T. Dense array EEG source estimation in neocortical epilepsy. Front. Neurol. 2013;4:42. doi: 10.3389/fneur.2013.00042. [DOI] [PMC free article] [PubMed] [Google Scholar]


