Effects of compression force on elasticity index and elasticity ratio in ultrasound elastography

Abstract

Objectives:

The purpose of this study was to investigate the relationship between compression force and hardness values in ultrasound elastography.

Methods:

Ultrasound elastography was performed using an elastography phantom, comprising inclusions with different elasticities and echogenicities. The compression force was set to approximately 100 gw (light force) and approximately 500 gw (heavy force). The elasticity index (EI) of the inclusion was measured. The EI was a relative hardness value of a structure within an elastographic image. Similarly, the EI of the background was measured as a reference. The elasticity ratio (ER) was calculated as the EI of the inclusion divided by the EI of the reference.

Results:

The hardness of the phantom could be discerned with both the EI and ER, regardless of the compression force. The EI and ER with heavy force tended to be higher than those with light force, but the difference was not significant. A strong correlation was observed between the EI and ER of soft structures, whereas the correlation between the EI and ER of hard structures was weak, and the ER values varied widely.

Conclusions:

The EI offers potential as a good indicator for assessing the hardness.

Introduction

Ultrasound elastography is an imaging technique that allows non-invasive assessment of tissue hardness. The technique has been used to assess the hardness of various normal and abnormal tissues,^1–6 and to differentiate malignant from benign lesions in the breast, prostate, thyroid, lymph nodes and salivary glands.^7–24

Ultrasound elastography uses either strain or shear wave velocity.^25,26 In strain elastography, tissue strain induced by compression with the probe is used as an indicator of hardness. Strain is smaller in a hard than in a soft tissue and is calculated by comparing echo signals obtained before and after compression. The hardness of tissues or lesions is visually and qualitatively assessed on the basis of the strain distribution and pattern of elastographic images.^{1,6–10,12,15–17,19–24} Semi-quantitative analysis, in which strain is represented in numerical values, has recently been used as a more objective method.^{1–5,9–11,13,17} However, whether these values can be effectively used for clinical assessment remains unclear because the image quality of strain elastography, which is performed manually, depends strongly on the imaging procedure.^14,18 To the best of our knowledge, the effects of compression force on hardness values have not yet been reported.

The purpose of this study was to investigate the relationship between compression force and hardness values with an elastography phantom. Comparisons were performed using directly measured hardness values and their normalized values. Intra- and interoperator agreements were also evaluated to assess the reproducibility of the measured values.

Methods and Materials

Ultrasound scanner and phantom

Ultrasound elastography was performed using a Logiq S8 (GE Healthcare, Milwaukee, WI) with a 10-MHz linear probe (ML6-15-D; GE Healthcare). An elastography phantom (ELPT-002; OST, Chiba, Japan) was used, comprising five inclusions with different elasticities and echogenicities, mounted in a background material of lower elasticity. The five inclusions simulated the Tsukuba elasticity score⁷ (Figure 1a). Three of the inclusions consisting of homogeneous materials and corresponding to Tsukuba elasticity score of 1, 2 and 4 were selected for elastography. We selected inclusions with homogeneous elasticities and echogenicities for concise analysis. The Score 1 inclusion (S1) was as soft as the background, the Score 2 inclusion (S2) was slightly harder than the background, and the Score 4 inclusion (S4) was harder than the background.

Figure 1.

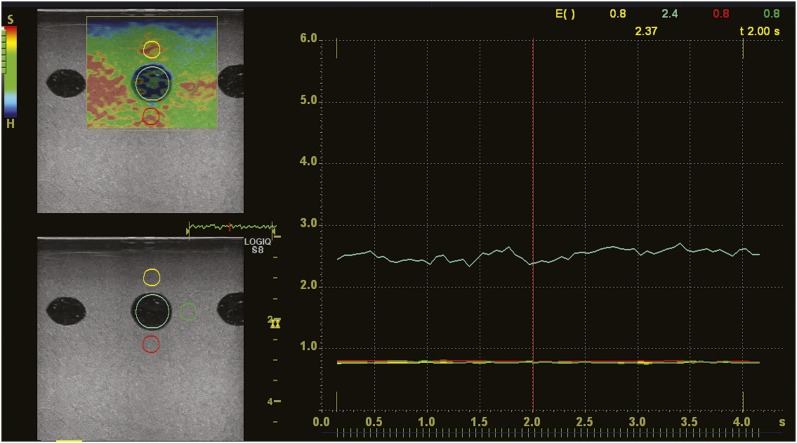
The phantom and an elastographic image. (a) Elastography phantom. The phantom simulates the Tsukuba elasticity score. The five inclusions correspond to Scores 1–5, from left to right. (b) Elastographic image. Red represents soft and blue represents hard. A B-mode image is displayed to the left of the elastographic image. The quality bar is displayed between B-mode and elastographic images, and the quality graph is displayed on the lower right of an elastographic image. These indicators show the appropriateness of the compression force. A hard (blue) band approximately 4–5 mm thick is seen on the surface of the phantom.

Scanning protocol

Elastographic images were obtained by repetitive compression with the probe. We set the compression force to approximately 100 gw (light force) and approximately 500 gw (heavy force). To keep the force constant, operators trained before the examination with the phantom placed on a scale. The examination was performed three times with each force by three operators.

Elastographic images were displayed in real time as colour-coded images within a region of interest (ROI) placed on B-mode images (Figure 1b). The colour indicated the relative hardness of structures within the ROI, red, yellow/green and blue represented soft, moderately hard and hard, respectively. We placed the 30 × 28 mm ROI on the B-mode image with a field of view of 50 × 50 mm. The centre of the ROI was placed on the inclusion. The surface of the phantom was not included in the ROI, and a space of 2 mm was left because it is known that a band of overestimation of hardness on the surface of the phantom when in contact with the probe is seen on elastographic images.²⁷ In this study, a hard (blue) band approximately 4–5 mm thick was seen on the surface of the phantom. B-mode images were displayed beside elastographic images, and the quality bar and quality graph were also displayed on the screen. These indicators showed the appropriateness of the compression force, as evaluated on the basis of echo signal similarity obtained before and after compression. During the examination, we monitored the indicators to keep the compression force as constant as possible.

Image measurement

Elastographic images were stored as motion images. From these, we selected high-quality images that lasted for 3 s. On replayed motion images, the elasticity index (EI) of the inclusion was measured at 0.1-s intervals, and the mean was calculated (Figure 2). The EI was a relative hardness value of a structure within an elastographic image. A mean EI of all structures within an elastographic image was defined as 1. A value of 0–0.09 was assigned to soft structures and 1–6 to hard structures. The EI was measured with a circular ROI of 8 mm in diameter placed on the inclusion. Similarly, the EI of the background was measured as a reference at areas above, below and lateral to the inclusion for normalization of the EI of the inclusion. Because the EI is a simple relative value obtained directly with ultrasound systems, normalization using the EI of a reference is considered effective for obtaining stable and constant results. A circular ROI of 4 mm in diameter was placed 2 mm away from the inclusion. The ROI lateral to the inclusion was placed on the side close to the centre of the phantom. For example, the ROI lateral to the S1 was placed on the side close to the S2. The elasticity ratio (ER) was calculated as the EI of the inclusion divided by the EI of the reference, and the same comparisons were performed as follows.

Figure 2.

Measurement of the elasticity index (EI). A region of interest (ROI) is placed on the inclusion (light blue circle) and the background above (yellow circle), below (red circle) and lateral to the inclusion (green circle). The EI of the background is measured as a reference for calculation of the elasticity ratio. The change in the EI with time is then displayed on a graph. The colour of the graph corresponds to that of the ROI. The EI at a point of time is displayed on the upper right of the graph.

Data analysis

The Kruskal–Wallis and Steel–Dwass tests were used to compare three inclusions for the EI and ER with each force. The (Wilcoxon) signed-ranks test was used to compare the EI and ER of the light force to those of the heavy force. The Friedman and Steel–Dwass tests were used to compare the ER calculated with the three references. Spearman's rank correlation was calculated between the EI and ER of each force.

Intraclass correlation coefficient was calculated for intra- and interoperator agreement. An intraclass correlation coefficient of 0–0.20 indicates poor agreement, 0.21–0.40 indicates fair agreement, 0.41–0.60 indicates moderate agreement, 0.61–0.80 indicates good agreement and 0.81–1.00 indicates excellent agreement. Values of p < 0.05 were considered significant.

Results

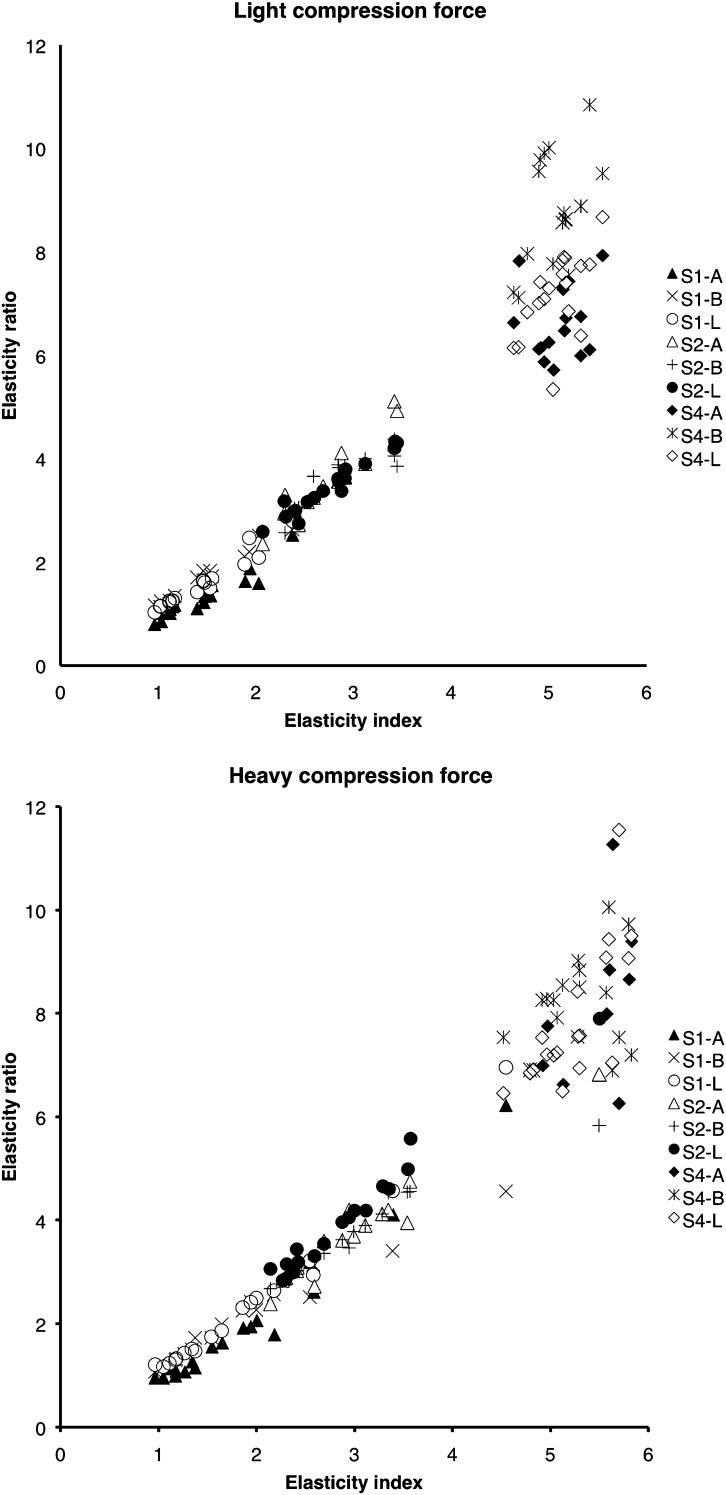
EIs are summarized in Table 1. With both compression forces, EIs showed significant differences among the three inclusions (Kruskal–Wallis test, p < 0.001; Steel–Dwass test, p < 0.001). ERs calculated with the three references were brought together because the differences among them were not significant. The details are described below. ERs are also summarized in Table 1. With both forces, ERs showed significant differences among the three inclusions (Kruskal–Wallis test, p < 0.001; Steel–Dwass test, p < 0.001). EIs and ERs tended to be higher with heavy force than with light force, but the difference was significant only in ERs of S1 [(Wilcoxon) signed-ranks test, p < 0.01; Table 1]. ERs calculated with the three references above, below and lateral to the inclusion are summarized in Table 2. ERs calculated with different reference areas and different forces were different. ERs calculated with references below the inclusion showed the highest values, except for the ER of S2 with heavy force. The Friedman test revealed significant differences among ERs, except for the ERs of S2 with light force (p < 0.02). However, the Steel–Dwass test revealed a significant difference only in the ERs of S4 with light force between the references above and below the inclusion and between the references below and lateral to the inclusion (p < 0.001). Strong correlations were seen between the EI and ER of S1 and S2, regardless of the compression force (Figure 3 and Table 3). S4 showed a weak correlation and ER values varied widely.

Table 1.

Median and interquartile range of the elasticity index and elasticity ratio

Compression force	Elasticity index			Elasticity ratio
	S1	S2	S4	S1	S2	S4
Light	1.44 (1.13–1.55)	2.77 (2.41–2.91)	5.14 (4.93–5.20)	1.35 (1.16–1.69)	3.51 (3.01–3.85)	7.41 (6.73–8.42)
Heavy	1.60 (1.21–2.14)	2.79 (2.39–3.25)	5.28 (4.98–5.59)	1.73 (1.27–2.51)	3.57 (3.02–4.19)	7.55 (7.01–8.53)

S1, score 1 inclusion; S2, score 2 inclusion; S4, score 4 inclusion.

Table 2.

Median and interquartile range of the elasticity ratio calculated with references above, below and lateral to the inclusion

Compression force	S1			S2			S4
	Above	Below	Lateral	Above	Below	Lateral	Above	Below	Lateral
Light	1.20 (1.10–1.53)	1.64 (1.19–1.82)	1.45 (1.24–1.67)	3.51 (3.04–3.84)	3.63 (3.04–3.85)	3.37 (3.04–3.76)	6.67 (6.13–7.30)	8.69 (8.12–9.54)	7.34 (6.83–7.74)
Heavy	1.59 (1.09–2.03)	1.85 (1.34–2.49)	1.81 (1.35–2.60)	3.60 (2.92–4.07)	3.42 (2.98–4.07)	3.75 (3.17–4.51)	7.55 (6.94–7.94)	8.25 (7.53–8.53)	7.38 (6.97–8.90)

S1, score 1 inclusion; S2, score 2 inclusion; S4, score 4 inclusion.

Figure 3.

Correlation between the elasticity index (EI) and elasticity ratio (ER). Strong correlations exist between the EI and ER for the Score 1 inclusion (S1) and Score 2 inclusion (S2), regardless of the compression force. The Score 4 inclusion (S4) shows a weak correlation, and the ER values vary widely. “A” represents the ER calculated with the reference above the inclusion, “B” represents the ER calculated with the reference below the inclusion and “L” represents the ER calculated with the reference lateral to the inclusion.

Table 3.

Spearman's rank correlation coefficient between the elasticity index and elasticity ratio

Compression force	S1	S2	S4
Light	0.90 (p < 0.001)	0.93 (p < 0.001)	0.27 (p = 0.049)
Heavy	0.95 (p < 0.001)	0.94 (p < 0.001)	0.57 (p < 0.001)

S1, score 1 inclusion; S2, score 2 inclusion; S4, score 4 inclusion.

Intra- and interoperator agreement was good or excellent for both the EI and ER and for both compression forces (Table 4).

Table 4.

Intra- and interoperator agreement

ICC	Compression force	Elasticity index			Elasticity ratio
		Operator 1	Operator 2	Operator 3	Operator 1	Operator 2	Operator 3
Intra-operator	Light	0.99	0.95	0.97	0.95	0.96	0.95
	Heavy	0.98	0.93	0.74	0.94	0.93	0.77
Interoperator	Light		0.98			0.98
	Heavy		0.89			0.89

ICC, intraclass correlation coefficient.

Discussion

A light compression force is recommended to obtain appropriate elastographic images because a high pressure force makes the association between pressure and strain become non-proportional.^7,28 We performed elastography with not only light but also heavy forces. With both forces we were able to discern the hardness of the phantom using the hardness values. Hardness values tended to be higher with heavy than with light force. Krouskop et al²⁹ performed elastography with breast tissue samples and also observed an increase in the elastic modulus with strain. Hardness can, therefore, be discerned with heavy force but may be overestimated. Generally, malignant lesions are harder than benign lesions.^{9–11,13,14,17,18,29} Heavy compression forces may lead to false-positive results. The frequency of probe movement also influences image quality. Havre et al³⁰ reported that the best quality was achieved in the range of 80–120 cycles min⁻¹.

In the assessment of hardness on elastographic images, visual evaluation of the hardness pattern and semi-quantitative analysis with numerical hardness values, for which the hardness ratio between the lesion and surrounding tissue is generally calculated, are used. Some studies have compared the diagnostic accuracy of these two methods and reported that the semi-quantitative analysis was equal or superior to visual evaluation.^9,10,17 Franchi-Abella et al²⁷ stated on semi-quantitative analysis that the type of system, position of the ROI in the surrounding tissue and hardness of the lesion change the hardness ratio, which is not proportional to the theoretical ratio in most cases. We used both EI and ER as hardness values and were able to discern hardness of the phantom with both. In the calculation of hardness ratio, it is reasonable that the ROI of the reference is placed at a depth similar to that of the target to avoid stress decay;^{1,11,14,18,27} however, this is not always possible for anatomical reasons.¹ In this study, the ERs were calculated with the three references, above, below and lateral to the inclusion, and little difference was seen among them. The ERs calculated with reference below the inclusion tended to show the highest values.

Regardless of the compression force, strong correlations were seen between the EIs and ERs of the soft inclusions. However, the correlation between the EIs and ERs of the hard inclusions was weak, and the ER values varied widely. This might be because the hard inclusion changed the strain of the background. Strain varies not only with the elasticity of the structure but also with the hardness and position of the surrounding structures and measured EIs are affected by these complex factors. Moreover, although the ER is a normalized value, which is calculated as the EI of the inclusion divided by the EI of the reference, ER showed a correlation with EI. This means that normalization with the surrounding structure is ineffective for obtaining a stable measurement value for the hardness of lesions or tissues. Special attention is necessary for determining diagnostic criteria with the ER.

Intra- and interoperator agreement was good for both the EI and the ER and for both compression forces. These results must be owing to careful monitoring of the compression force to keep it as constant as possible during examinations.

Some limitations of the present study need to be addressed. The first limitation was that we did not know the true elasticity of the phantom. We therefore were unable to verify how well the EI and the ER corresponded to theoretical values. Furthermore, the phantom used in this study simulated the Tsukuba elasticity score, which was proposed for breast disease.⁷ The elasticity and configuration may differ markedly from other lesions and tissues. Second, hardness values vary between systems, and the Tsukuba elasticity score had been determined with a different system. Further studies with other systems should therefore be undertaken. Third, the compression force was applied manually, therefore it was not constant. Finally, our results are preliminary and need to be confirmed in clinical studies. To date, many clinical studies have used ERs as diagnostic criteria.^{1–5,9–11,13,14,17,18} Based on our results, the EI is also worth studying.

In conclusion, the hardness of the phantom could be discerned with both the EI and the ER, regardless of the compression force. EIs and ERs with heavy force tended to be higher than those with light force. The difference, however, was not significant. A strong correlation was observed between the EI and ER of soft structures, whereas the correlation between the EI and ER of hard structures was weak, and ER values varied widely. According to these results, the EI offers potential as a good indicator for assessing the hardness of lesions or tissues. It is expected that the EI may be used solely in the evaluation of the soft tissues. Additional studies including clinical studies are needed to improve the stability and quantitative ability of the value.