Marginal Structural Cox Models for Estimating the Association Between β-Interferon Exposure and Disease Progression in a Multiple Sclerosis Cohort

Abstract

Longitudinal observational data are required to assess the association between exposure to β-interferon medications and disease progression among relapsing-remitting multiple sclerosis (MS) patients in the “real-world” clinical practice setting. Marginal structural Cox models (MSCMs) can provide distinct advantages over traditional approaches by allowing adjustment for time-varying confounders such as MS relapses, as well as baseline characteristics, through the use of inverse probability weighting. We assessed the suitability of MSCMs to analyze data from a large cohort of 1,697 relapsing-remitting MS patients in British Columbia, Canada (1995–2008). In the context of this observational study, which spanned more than a decade and involved patients with a chronic yet fluctuating disease, the recently proposed “normalized stabilized” weights were found to be the most appropriate choice of weights. Using this model, no association between β-interferon exposure and the hazard of disability progression was found (hazard ratio = 1.36, 95% confidence interval: 0.95, 1.94). For sensitivity analyses, truncated normalized unstabilized weights were used in additional MSCMs and to construct inverse probability weight-adjusted survival curves; the findings did not change. Additionally, qualitatively similar conclusions from approximation approaches to the weighted Cox model (i.e., MSCM) extend confidence in the findings.

Multiple sclerosis (MS) is a disease associated with damage to the myelin and nerve fibers in the brain and spinal cord. It is a lifelong disease, typically manifesting in early adulthood, affecting an estimated 2.0–2.5 million people worldwide (1). A relapsing-remitting course is the most common presenting MS phenotype; these patients can experience periods of acute worsening, known as an attack or relapse, followed by relapse-free periods with partial or full recovery. Disability may gradually worsen over time, ultimately becoming irreversible. As evident from various clinical trials, immunomodulatory drugs such as β-interferon (β-IFN) may reduce the risk of an MS relapse and increase the duration of relapse-free periods over the short term (2–6). However, their impact on longer-term outcomes such as irreversible disability is unclear.

There is a real need to determine whether β-IFNs positively influence the course of MS disease over the long term, particularly in the “real-world” clinical practice setting. Observational studies are the most pragmatic means of addressing this need. However, findings from recent observational studies have been contradictory with respect to the impact of β-IFN (7–9). Possible explanations for these inconsistencies include selection bias, immortal time bias, and inappropriate use of analytical tools (10, 11). Hence, the association between β-IFN and the progression of disability in clinical practice remains undetermined.

Recently, researchers assessed the association of β-IFN with time to irreversible disability outcomes among relapsing-remitting MS patients treated in the real-world clinical practice setting of British Columbia, Canada, using a Cox model with time-dependent treatment exposure (9). They compared β-IFN-treated patients with 2 separate control cohorts—a “historical” cohort (patients who first became β-IFN-eligible prior to the approval of β-IFN in Canada in 1995) and a “contemporary” cohort (patients who first became β-IFN-eligible after the approval of β-IFN but remained unexposed to β-IFN). While this approach represented a considerable improvement over previous studies (12), concern remained about the potential for indication bias when the contemporary control cohort was considered (9). Despite adjustment for a number of baseline characteristics, there were also concerns raised about the inability to adjust for subsequent (postbaseline) treatment decisions (9, 13–16). Furthermore, since disease activity, such as relapses, can drive decision-making with respect to starting or stopping β-IFN treatment (17) and might also be associated with the outcome (18), relapses could be considered a potential time-dependent confounder. Simply incorporating such confounders into a time-dependent Cox model as covariates may be inadequate to adjust for selection bias and confounding (19).

Marginal structural Cox models (MSCMs) allow estimation of the causal associations between treatment exposure and survival responses (e.g., time to disability) in the presence of time-dependent confounding and selection bias (19, 20). These models depend on model-based estimates of the inverse probability of the observed treatment and censoring status of each patient to achieve causal interpretation of the findings. Simulation studies with short-term follow-up have repeatedly shown that MSCMs are advantageous in terms of obtaining consistent estimates of associations with time-varying treatment exposures (21–24). When studying MS, a chronic disease, extended observation periods are needed, which may contribute to the construction of highly variable weights (25) and subsequently may lead to an inefficient estimate of the causal association. Furthermore, how robust these models are when follow-up lengths differ for individual patients, as is the case in clinical practice, is largely unknown. To assess and address these practical challenges, we explored the use of different weighting approaches in MSCMs to estimate the causal association between β-IFN and time to irreversible MS disability in a cohort of relapsing-remitting MS patients from British Columbia, Canada.

METHODS

Study population and measurements

This cohort study included data that were collected prospectively from MS patients who were registered at a British Columbia MS clinic and were eligible to receive β-IFN (all preparations of β-IFN were considered as 1 therapeutic class). In Canada, the first β-IFN was licensed for clinical use in July 1995. Therefore, patients who became eligible for β-IFN treatment for the first time between July 1, 1995, and December 31, 2004, were included (only the contemporary control cohort was considered). Broad eligibility criteria for receiving β-IFN treatment were adapted from the British Columbia government's reimbursement scheme—that is, adults (aged ≥18 years) who had a diagnosis of definite MS with a relapsing-onset course and were able to walk (Expanded Disability Status Scale (EDSS) score ≤6.5). The first MS clinic visit at which a patient met the β-IFN eligibility criteria was considered the patient's baseline date (time = 0). The end of follow-up was December 31, 2008. The study was approved by the University of British Columbia's Clinical Research Ethics Board.

The study outcome (irreversible progression of disability) was based on the EDSS (26), a widely used standardized rating system with scores ranging from 0 (no disability) to 10 (death from MS). Our outcome was time to reaching a sustained EDSS score of 6 (“sustained EDSS 6”). An EDSS score of 6 indicates that the patient requires intermittent or unilateral constant assistance (cane, crutch, or brace) to walk about 100 meters with or without resting. Since it is possible to move back and forth along the EDSS, sustained EDSS 6 (i.e., confirmed after at least 150 days, with all subsequent EDSS scores being 6 or greater) was adopted in this study as an indicator of irreversible disability progression (9, 27, 28).

Since a patient's β-IFN exposure status might change during follow-up, this was considered as a time-dependent variable. β-IFN exposure was defined as “any versus none” on a monthly basis. This could be considered an improvement on the previous study design (9), in which only 1 treatment initiation and 1 termination date were considered for each treated patient. Potential confounders included age at baseline, sex, disease duration at baseline, EDSS score at baseline, and relapses.

The relapse variable was selected to be included in the model as a time-varying factor for the following reasons. Firstly, relapses may be associated with the outcome (disability progression). Studies have shown that early relapses may have a significant impact on later disability progression, even though the strength of this association may diminish with time (28). Secondly, β-IFNs have been shown to reduce relapse rates (2–6); therefore, a patient's relapse status may be affected by prior β-IFN treatment. Thirdly, the presence (or absence) of relapses might influence treatment decisions, that is, the determination of whether to start or stop using a β-IFN. Finally, the risk of a relapse is not constant over time; it typically decreases as the patient's disease duration and age increase (29). Therefore, considering only those relapses that occurred prior to a patient's baseline date may be insufficient. Instead, we considered the cumulative number of relapses in the last 2 years (hereafter called “cumulative relapses”) as a time-dependent confounder.

Cumulative relapses could be an intermediate variable between treatment exposure and disability progression; a simplified version of this hypothesized causal relationship is outlined in Figure 1 (also see Web Appendix 1, available at http://aje.oxfordjournals.org/). We also examined whether cumulative relapses were an important predictor of subsequent treatment choices.

Figure 1.

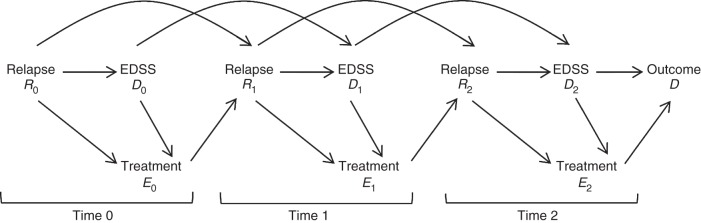
The hypothesized causal relationships in the treatment of multiple sclerosis, with 3 time points: j = 0, 1, 2. Here E_j denotes the binary β-interferon exposure variable that is measured immediately after the time-dependent confounders R_j (cumulative relapses) and D_j (disability progression index—that is, Expanded Disability Status Scale (EDSS) score) for the jth time period. The time-dependent confounder R_j at time j is affected by prior treatment E_j−1. According to the causal diagram, R₀ imposes confounding on the E₀-D relationship (since relapse frequency may dictate the subsequent treatment choice and residual disability left by frequent relapses may accumulate over time, leading to irreversible disability), but R₁ is an intermediate variable for the same relationship (51, 52) (since the prior β-interferon treatment may reduce relapse frequency, which may allow the patient more time to recover from residual disability left by past relapses and may contribute to slower progression of disability over time).

Statistical methods

Conventional Cox model

We defined the model notation as follows. If patient i was followed from the month of β-IFN eligibility (t = 0) to T_i months with treatment exposure in month t represented by A_it (1 = under treatment, 0 = not under treatment), then a_it was the realization of A_it. The patient's baseline covariates were recorded in the vector L_i0, consisting of baseline EDSS score, disease duration, age, and sex. If λ_i(t | L_i0) was the hazard of reaching sustained EDSS 6 at month t for patient i with baseline covariates L_i0, one way to model such data was with the time-dependent Cox proportional hazards model:

$${\lambda }_i(t|L_{i0})={\lambda }_0(t)\exp ({\beta }_1{A}_{it}+{\beta }_{\mathbf{2}}{L}_{i0}),$$ (1)

where λ₀(t) is the unspecified baseline hazard, β₂ is the vector of log hazard ratios for the baseline covariates, and β₁ is the log hazard ratio of the patient's current β-IFN status (A_it). The addition of cumulative relapses (L_it) as a covariate in this model may have failed to adjust for this time-dependent confounder (see Web Appendix 2). Hence, the MSCM approach (19, 30) was applied instead.

Marginal structural Cox model

Within a counterfactual framework, in the pseudopopulation, MSCMs enabled the conceptual comparison of the hazard functions for patients who never received β-IFN (complete nonexposure during follow-up) with those who received β-IFN continuously (complete exposure). To accomplish this, the partial likelihood function of the Cox model (or its approximations; see Web Appendix 3) was modified such that the contribution of patient i to the risk set at time t was weighted by the inverse probability of treatment and censoring (IPTC) weight, w_it, to remove the possible confounding effects of both time-varying and baseline confounders (19).

Weighting schemes

The stabilized inverse probability of treatment (IPT) weight (sw) for patient i at month t was given by

$$s{w}_{it}^T=\prod _{j=0}^t\frac{pr(A_{ij}=a_{ij}|{\overline{A}}_{i(j-1)}={\overline{a}}_{i(j-1)},L_{i0}=l_{i0})}{pr(A_{ij}=a_{ij}|{\overline{A}}_{i(j-1)}={\overline{a}}_{i(j-1)},L_{i0}=l_{i0},{\overline{L}}_{ij}={\overline{l}}_{ij})},$$ (2)

where $\overline{A_{ij}}=\overline{a_{ij}}$ and $\overline{L_{ij}}=\overline{l_{ij}}$ are the observed treatment history and time-varying confounder history, respectively, from baseline to time j. The stabilized IPT weights were inversely related to a function of the time-varying confounder cumulative relapses, since this variable appeared only in the denominator of the weights, whereas the baseline covariates were included in both the numerator and the denominator (see equation 2). The weights $s{w}_{it}^T$ down-weighted the person-time contributions when cumulative relapses were a strong predictor of treatment status in the subsequent time periods, after controlling for the baseline covariates. Assuming that the denominators of the weight models were correctly specified, these weights created a pseudopopulation in which cumulative relapses no longer predicted subsequent β-IFN treatment status (31). The estimates of the β-IFN treatment association in this pseudopopulation would be the same as those in the original target population (32).

Generally, when the numerator in equation 2 is replaced by 1, these weights become the unstabilized IPT weights, $w_{it}^T$ (19), which simultaneously control for time-varying covariates and baseline covariates. Unlike MSCMs using stabilized weights, MSCM analyses using unstabilized weights do not need further adjustment for the baseline covariates (32). Such weights also yield consistent causal estimates that are associated with substantial variability (31).

Consistent estimation of β₁ from censored data can be achieved by incorporating inverse probability of censoring (IPC) weights in the analysis (33). Using logic similar to that leading to the IPT weights for uncensored patients, the stabilized IPC weight for patient i at month t is

$$s{w}_{it}^C=\prod _{j=0}^t\frac{pr(C_{ij}=0|{\overline{C}}_{i(j-1)}=0,{\overline{A}}_{i(j-1)}={\overline{a}}_{i(j-1)},L_{i0}=l_{i0})}{\begin{array}{c}pr(C_{ij}=0|{\overline{C}}_{i(j-1)}=0,{\overline{A}}_{i(j-1)}={\overline{a}}_{i(j-1)},L_{i0}=l_{i0},{\overline{L}}_{i(j-1)}={\overline{l}}_{i(j-1)})\end{array}},$$ (3)

where C_ij denotes the binary censoring status (taking the value 1 if the ith patient was censored in the jth month and 0 otherwise) and $\overline{C_{ij}}=\overline{c_{ij}}$ is the observed censoring history up to time j. The overall stabilized IPTC weights, sw_it, are obtained by multiplying $s{w}_{it}^T$ by $s{w}_{it}^C$ (30, 32).

We applied logistic regression models to estimate the unknown conditional probabilities (appearing in equations 2 and 3) from the data (see Web Appendix 4 and Web Table 1).

The normalized IPTC weights were calculated, normalizing each weight by the mean weight of the corresponding risk set (22):

$$w_{it}^{(n)}=\frac{w_{it}{N}_t}{\sum _i{Y}_{it}{w}_{it}},s{w}_{it}^{(n)}=\frac{s{w}_{it}{N}_t}{\sum _i{Y}_{it}s{w}_{it}},$$ (4)

where Y_it indicates whether patient i belonged to the risk set at time t, sw⁽ⁿ⁾ represents the normalized stabilized weight, and $N_t=\sum _i^N{Y}_{it}$ is the total number of patients in the risk set at time t.

In order to take within-subject correlation (34) into account, confidence intervals based on robust standard errors are usually evaluated, which may be asymptotically conservative (30, 35). Therefore, we calculated the 95% confidence intervals for the causal estimate on the basis of 500 nonparametric bootstrap samples (36–38).

IPTC-weighted survival estimates

IPTC weight-adjusted Kaplan-Meier survival curves did not require assumptions related to parametric survival or the Cox model. We used unstabilized IPTC weights (w or w⁽ⁿ⁾) to adjust the survival curves. This had the added advantage of yielding marginal estimates that provided direct causal interpretations without first requiring fitting of the MSCM model (39); hence, constructing such curves served as a sensitivity analysis. However, these weights can be highly variable compared with sw⁽ⁿ⁾, and the adjusted survival curves are prone to distortion in the presence of extreme weights. Truncation of extreme weights was applied as one ad hoc solution to assuage the problem of extreme weights (40).

Sample code and practical guidance on implementing the weights in such direct and approximate MSCM approaches via various R packages (41) (R Foundation for Statistical Computing, Vienna, Austria) are provided in Web Appendix 5.

RESULTS

Of 1,697 patients included in the study, 1,297 were female (76%). The mean age at baseline was 39.7 years (standard deviation, 9.7), the mean disease duration from symptom onset was 7.0 years (standard deviation, 7.7), and the median EDSS score was 2 (interquartile range, 1–3).

The mean follow-up time was 4.0 years (interquartile range, 1.7–6.0 (4.3 years)), the maximum being 12.7 years. In total, there were 6,890 person-years of follow-up and 2,530 person-years of β-IFN exposure. In all, 829 patients remained untreated during follow-up. Patients at risk of reaching the outcome at the beginning of each year are shown in Figure 2. Overall, 138 patients reached the outcome of sustained EDSS 6. Further description of the data is provided in Web Appendix 6 (see Web Table 2).

Figure 2.

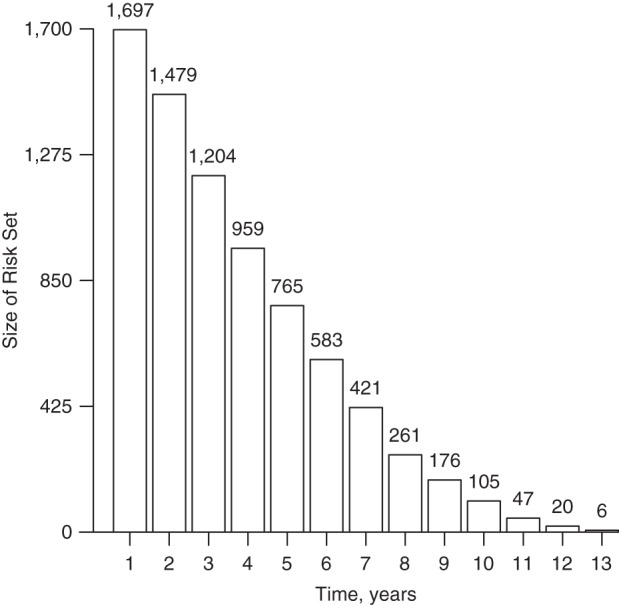
Number of multiple sclerosis patients at risk of reaching a sustained Expanded Disability Status Scale (EDSS) score of 6 during the first month of each follow-up year after baseline, British Columbia, Canada, 1995–2008. Failure to continue to the next risk set results from either censoring or reaching a sustained EDSS score of 6. Analyses were performed by month, but the plot is drawn by year for simplicity.

Time-dependent weights

We found the cumulative relapse variable to be a good predictor of subsequent treatment choices, as evidenced by the significance in the model for the IPT weights (2-sided P < 0.001; see Web Table 1) and also for the IPC weights (2-sided P = 0.03).

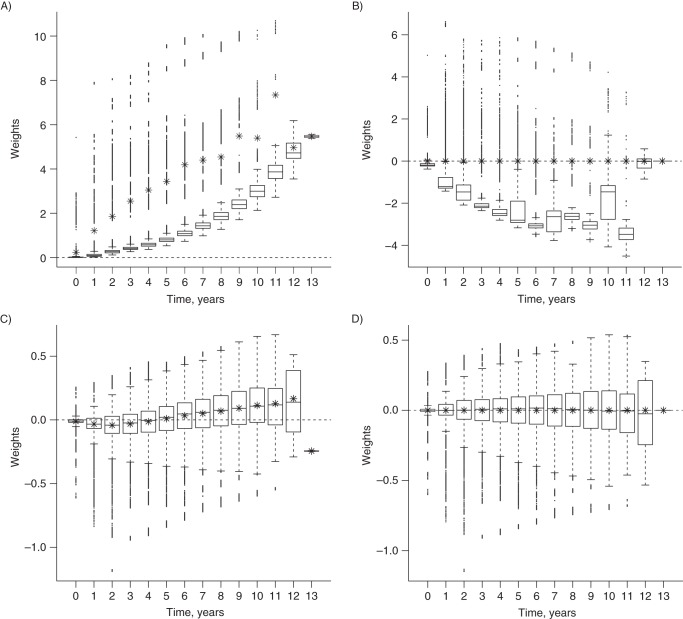
The IPTC weights varied not only from patient to patient but also by time. As the number of patients at risk decreased monotonically over time, the variation in the IPTC weights increased with follow-up time. As shown in Figure 3, parts A–D, in addition to such increasing variability, a clear upward trend over time was evident in the unstabilized weights w. The mean values at successive time points were much closer to 1 after stabilization (sw). However, an upward trend in the mean weights was still apparent as follow-up progressed. As expected, this trend was eliminated when the stabilized weights were normalized (sw⁽ⁿ⁾) (22). When the unstabilized weights were normalized (w⁽ⁿ⁾), even though the mean weight at each time point was 1, the distributions of the weights were highly variable and skewed.

Figure 3.

Distribution of various inverse probability of treatment and censoring weighting schemes for each year of follow-up among multiple sclerosis patients from British Columbia, Canada, 1995–2008. A) unstabilized (w); B) normalized unstabilized (w⁽ⁿ⁾); C) stabilized (sw); D) normalized stabilized (sw⁽ⁿ⁾). The mean value in each boxplot is indicated by an asterisk (*). Weights are shown on a logarithmic scale. Years were used on the horizontal axes instead of months for better visual display. Note that the plots do not have identical scales on the vertical axes.

The mean value and standard deviation of the unstabilized, unnormalized weights (w) were much larger than those of the other weights (Table 1), and the resulting causal association estimate was further removed from the null, with a much wider confidence interval. Normalization resulted in a mean weight of 1 and a markedly reduced standard deviation. Stabilization of the weights had an even greater impact on reducing the standard error of the causal estimate.

Table 1.

Different Versions of IPTC Weights and Corresponding Causal Estimates of the Association Between β-Interferon Treatment and the Hazard of Reaching a Sustained EDSS Score of 6 Among Multiple Sclerosis Patients From British Columbia, Canada, 1995–2008

Schemea	Stabilized	Normalized	Estimated Weight		Causal Estimate
			Mean (Log SD)	Range	HR	95% Bootstrap CIb
w	No	No	28.17 (6.44)	1–43,985.38	1.54	0.09, 26.38
w(n)	No	Yes	1 (2.45)	0.01–753.47	1.36	0.18, 10.40
sw	Yes	No	0.99 (−2.12)	0.30–1.95	1.36	0.95, 1.94
sw(n)	Yes	Yes	1 (−2.18)	0.32–1.71	1.36	0.95, 1.94c

Abbreviations: CI, confidence interval; EDSS, Expanded Disability Status Scale; HR, hazard ratio; IPTC, inverse probability of treatment and censoring; SD, standard deviation.

^a The inverse probability of treatment numerator model included the baseline covariates EDSS score, age, disease duration, sex, treatment status in the previous time interval, and restricted cubic spline (48) of the follow-up month number. The denominator model included the covariates considered in the numerator model and the time-dependent covariate “cumulative number of relapses for last 2 years,” as well as its interaction with treatment status in the previous time interval. The same model specifications were used to generate the inverse probability of censoring weights. With the stabilized versions of the weights, the hazard ratio model of the marginal structural Cox model must include adjustment for the baseline covariates, but this is not necessary with the unstabilized versions of the weights.

^b Based on 500 nonparametric bootstrap samples with patients as sampling units.

^c The 95% CI of the causal association estimate obtained using sw⁽ⁿ⁾ was the smallest, although it was equal to that obtained using sw when results were calculated to 2 decimal places.

A necessary condition for correct model specification is that the mean weight is 1 (42), ideally in each time period rather than just overall. Additionally, a smaller range is an indication of well-behaved weights (40), which generally leads to a smaller confidence interval for the association estimate. In terms of these desirable properties, sw⁽ⁿ⁾ behaved better than the other schemes: These weights had a smaller range, and there was no tendency for the mean to deviate from 1 even after a long period of follow-up (see Figure 3D). This supported the use of sw⁽ⁿ⁾ in this application.

Causal association of β-IFN with sustained EDSS score of 6

Since the normalized stabilized weights (sw⁽ⁿ⁾) had better properties, we relied on the corresponding MSCM estimates (see Table 2). The evidence of an association between current β-IFN exposure status and the hazard of reaching a sustained EDSS score of 6 was inconclusive.

Table 2.

Fit of the Marginal Structural Cox Model With the Normalized Stabilized IPTC Weights (sw⁽ⁿ⁾) for Time to a Sustained EDSS Score of 6 (Sustained EDSS 6) in Estimating the Causal Association Between β-Interferon Treatment and the Hazard of Reaching Sustained EDSS 6 Among Multiple Sclerosis Patients From British Columbia, Canada, 1995–2008

Covariate	Estimated Log HRa	HRb	95% Bootstrap CIc
β-Interferon use	0.31	1.36	0.95, 1.94
EDSS score	0.54	1.72	1.54, 1.92
Disease duration, decades	−0.19	0.83	0.66, 1.05
Age, decades	0.28	1.32	1.08, 1.62
Sexd	−0.22	0.80	0.55, 1.17

Abbreviations: CI, confidence interval; EDSS, Expanded Disability Status Scale; HR, hazard ratio; IPTC, inverse probability of treatment and censoring.

^a Estimated log HR from a marginal structural Cox model. The model also adjusted for the baseline covariates EDSS score, age, disease duration, and sex.

^b Instantaneous risk of reaching a confirmed sustained EDSS score of 6.

^c Based on 500 nonparametric bootstrap samples.

^d Referent: male.

To verify the results, we also obtained the estimates from several approaches that approximate the MSCM (see Table 3). All of the estimates from the models based on sw⁽ⁿ⁾ were consistent. The conclusion concerning the causal association between β-IFN status and time to sustained EDSS score of 6 did not change with the modeling choices.

Table 3.

Estimates of Association Between β-Interferon Treatment and Time to a Sustained EDSS Score of 6, Obtained Using Different Analytical Approaches, Among Multiple Sclerosis Patients From British Columbia, Canada, 1995–2008

Type of Adjustment, by Model Type	Measure of Association	95% CI
Cox
Unweighteda	1.29b	0.91, 1.82c
Weighted by sw(n)	1.36b	0.95, 1.94d
Pooled logistic
Unweighteda	1.29e	0.91, 1.82c
Weighted by sw(n)	1.36e	0.96, 1.95d
Poisson
Weighted by sw(n)	1.36e	0.96, 1.95d
Complementary log-log
Weighted by sw(n)	1.37e	0.96, 1.95d

Abbreviations: CI, confidence interval; EDSS, Expanded Disability Status Scale.

^a Based on time-dependent β-interferon treatment exposure status and covariates measured at baseline: EDSS score, age, disease duration, and sex. This estimate does not have a causal interpretation and is shown for comparison purposes.

^b The hazard ratio is the measure of association obtained from a Cox model.

^c 95% CIs were calculated based on robust standard errors.

^d 95% CIs were obtained from 500 nonparametric bootstrap samples.

^e The hazard ratio from the Cox model was approximated by the odds ratio from the pooled logistic model (49, 50) (see Web Appendix 3) or, under the infrequent event assumption, by the standardized mortality ratio from Poisson regression or by the odds ratio from complementary log-log regression, respectively. The weighted Cox model (19, 22) was approximated using weighted versions of these models. Software specifications for these analyses are provided in Web Appendix 5.

In a complementary analysis, we considered longitudinal EDSS values as an additional time-varying confounder, instead of treating EDSS score as a baseline covariate (see Table 4). Additionally, we evaluated the impact of weight trimming (43) to assess the sensitivity of the findings to the positivity assumption (see Web Appendix 7). We also repeated the analysis after selecting patients via more restricted eligibility criteria (see Web Appendix 8 and Web Table 3). Further analyses were conducted to check the impact of cumulative exposure to β-IFN over the last 2 years on the same outcome (see Web Appendix 9 and Web Table 4). We also assessed the impact of including cumulative relapses in the last year (see Web Appendix 10 and Web Table 5). None of these sensitivity analyses resulted in statistical evidence for an association with treatment.

Table 4.

Fit of the Marginal Structural Cox Model With the Normalized Stabilized IPTC Weights (sw⁽ⁿ⁾) for Time to a Sustained EDSS Score of 6 (Sustained EDSS 6) in Estimating the Causal Association Between β-Interferon Treatment and Sustained EDSS 6 Among Relapsing-Onset Multiple Sclerosis Patients (Sensitivity Analysis Assessing the Impact of EDSS Score as an Additional Time-Varying Confounder), British Columbia, Canada, 1995–2008

Covariate	Estimated Log HRa	HR	95% Bootstrap CIb
β-Interferon use	0.12	1.13	0.76, 1.68
Disease duration, decades	−0.02	0.98	0.82, 1.22
Age, decades	0.32	1.37	1.10, 1.63
Sexc	−0.36	0.70	0.47, 1.02

Abbreviations: CI, confidence interval; EDSS, Expanded Disability Status Scale; HR, hazard ratio; IPTC, inverse probability of treatment and censoring.

^a The model adjusted for cumulative relapses and EDSS as time-varying confounders and the baseline covariates age, disease duration, and sex. Considering EDSS score as a time-varying confounder rather than a baseline covariate in the analysis does not contradict the causal diagram (Figure 1). All missing EDSS values were imputed via the last-value-carried-forward approach.

^b Based on 500 nonparametric bootstrap sample estimates.

^c Referent: male.

IPTC weighting for estimation of survival curves

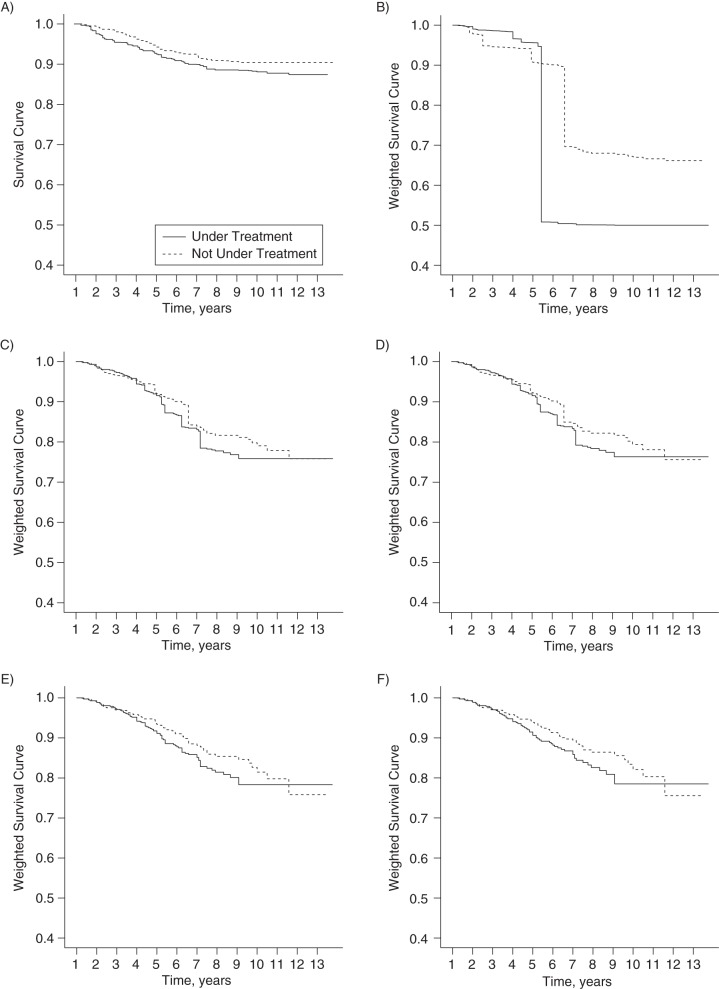
We plotted IPTC weight (w⁽ⁿ⁾)-adjusted Kaplan-Meier survival curves (see Figure 4, parts A–F). However, the large drops in the survival plot in Figure 4B were driven by only a few large weights. Therefore, we investigated the sensitivity of these adjusted Kaplan-Meier curves after progressively truncating w⁽ⁿ⁾.

Figure 4.

Inverse probability of treatment and censoring weight-adjusted Kaplan-Meier-type survival curves for the association between β-interferon treatment and time to a sustained Expanded Disability Status Scale score of 6 among multiple sclerosis patients from British Columbia, Canada, 1995–2008. A) Unweighted; B) adjusted by w⁽ⁿ⁾ (untruncated); C) adjusted by 5% truncated w⁽ⁿ⁾; D) adjusted by 10% truncated w⁽ⁿ⁾; E) adjusted by 25% truncated w⁽ⁿ⁾; F) adjusted by 50% truncated w⁽ⁿ⁾. The truncated weights are derived from the normalized unstabilized weights (w⁽ⁿ⁾) so that the survival probabilities and hazard ratios are marginal estimates with a causal interpretation.

As can be seen from Figure 4C, truncation of the 5% smallest and largest of the w⁽ⁿ⁾ freed the curves from the excess influence of a few extreme weights. In this application, the adjusted survival curves did not change dramatically with greater truncation (see Figure 4, parts D–F).

The magnitude of variability in the weights w⁽ⁿ⁾ affected not only the adjusted survival curve but also the 95% confidence interval for the causal association estimate obtained from the w⁽ⁿ⁾-weighted MSCM. The confidence interval (95% bootstrap confidence interval: 0.18, 10.4; see Table 1) was wider than that obtained with sw⁽ⁿ⁾, even though the two causal association estimates were the same (hazard ratio (HR) = 1.36). As before, truncation of the extreme weights was examined as another sensitivity analysis to increase the precision of the causal estimate (40). Truncating the 5% smallest and largest of the w⁽ⁿ⁾ had a substantial impact in this application: The 95% bootstrap confidence interval shrank to (0.64, 1.95) (see Table 5). Table 5 shows that despite improving the precision of the estimate of the β-IFN treatment association, this ad-hoc truncation approach did not alter the conclusion concerning the causal association between β-IFN and time to sustained EDSS score of 6.

Table 5.

Impact of Truncation of the Normalized Unstabilized IPTC Weights (w⁽ⁿ⁾) on the Estimated Causal Association Between β-Interferon Treatment and Time to a Sustained EDSS Score of 6 Among Multiple Sclerosis Patients From British Columbia, Canada, 1995–2008

Truncation Percentilesa	Estimated Weight		Treatment Association Estimate
	Mean (Log SD)	Range	HR	SEb	95% Bootstrap CIb
None	1 (2.45)	0.01–753.47	1.36	1.41	0.18, 10.40
5 and 95	0.31 (−1.24)	0.04–0.93	1.11	0.32	0.64, 1.95
10 and 90	0.3 (−1.29)	0.05–0.83	1.13	0.31	0.66, 1.95
25 and 75	0.21 (−2.2)	0.09–0.35	1.17	0.25	0.77, 1.76
Medianc	0.19 (−∞)	0.19–0.19	1.29	0.23	0.91, 1.82

Abbreviations: CI, confidence interval; EDSS, Expanded Disability Status Scale; HR, hazard ratio; IPTC, inverse probability of treatment and censoring; SD, standard deviation; SE, standard error.

^a Truncation means that the extreme weights (determined by the selected percentile range) are replaced by the nearest percentile weight value.

^b Based on 500 nonparametric bootstrap samples.

^c Weighting by the median of the weights produces the same treatment association estimate and 95% CI as those obtained from the simple baseline covariate-adjusted Cox model (see Table 3).

DISCUSSION

When adapting an IPTC weight-based MSCM approach to explore the impact of β-IFN on progression of MS disability in the “real-world” clinical practice setting, we did not find a significant association between β-IFN exposure and MS disability progression.

The possibility that cumulative number of (prior) relapses may represent a time-dependent confounder lying on the causal pathway between β-IFN and disability progression led us to propose this MSCM approach (44). From the analysis, it was evident that the cumulative number of relapses in the previous 2 years was an important factor in the weight models. This highlights the importance of controlling for this type of time-dependent confounder and justifies the additional complexity of the MSCM approach. Further advantages of using such models include the ability to adjust for potential informative censoring.

Even though an extended follow-up period is essential to adequately capture the potential association between treatment and disease progression for chronic diseases such as MS, the duration of follow-up may vary considerably from patient to patient in observational settings. This feature of the data poses considerable challenges while applying the MSCM approach, especially when trying to obtain suitable weights. Over time, treatment exposure and other patient characteristics (e.g., age, disease duration, occurrence of relapses) change, further contributing to the complexity of the study design. To account for these changes, the weights at a given time point need to be obtained by combining weights for each previous time period in a multiplicative manner. For patients with an extended duration of follow-up, this may cause estimated weights for later periods to increase dramatically and the overall mean weights for these periods to deviate far from 1. In addition, as follow-up progresses, the decreasing number of patients “at risk” may further contribute to high variability in the weights. Deviation from a mean of 1 at any time point is an indication of possible weight model misspecification, whereas highly variable weights may decrease the precision of the causal association estimate (40). Furthermore, in the presence of very large weights, near nonpositivity may result in a biased and imprecise estimate of the treatment association (33, 45). The large variability in the follow-up periods of the MS patients prompted us to investigate the choice of appropriate weighting schemes for MSCMs.

Stabilization of the weights is generally advocated to decrease weight variation and hence increase the precision of MSCM estimates (19). However, the performance of these weights in the chronic disease context has not been well-studied. Here we noted that as the observation period increased, so did the upward trend of the weights. Even though the normalized weights (sw⁽ⁿ⁾) generally possess desirable properties irrespective of the length of the follow-up period (22), we could find no application of these newly proposed weights to the chronic disease context in the published literature. Application of sw⁽ⁿ⁾ completely eradicated the upward trends, in turn producing an association estimate with slightly higher precision compared with the other weighting schemes, suggesting the potential utility of such weights in studies with longer follow-up.

Adjusting for the time-dependent confounder “cumulative relapses” via IPTC weighting (sw⁽ⁿ⁾) moved the estimated association for β-IFN treatment (HR = 1.36) away from the null in comparison with the unweighted Cox model (HR = 1.29). The corresponding 95% bootstrap confidence intervals from the MSCM analyses were wider than the 95% robust confidence intervals from the unweighted Cox model, appropriately reflecting more uncertainty as a consequence of using estimated weights. The association estimates were consistent for the various approximations of MSCM models that we considered; none provided evidence of a significant benefit of β-IFN exposure in disease progression.

We also explored the application of other weighting schemes, such as normalized unstabilized weights (w⁽ⁿ⁾). Using these weights, we constructed IPTC-weighted adjusted survival curves. These curves serve as sensitivity analyses, since their results are independent of fitting any MSCM. However, unstable survival estimates were produced as a result of a few very large weights. Moreover, as expected, use of the unstabilized weights resulted in larger standard errors of the MSCM estimators than those obtained from the stabilized versions. The ad-hoc strategy of truncating extreme weights produced more stable survival curves and increased the precision of the MSCM estimate based on w⁽ⁿ⁾. Truncation at the 5% level was enough to produce quite stable and smooth survival curves, as well as w⁽ⁿ⁾-based MSCM-estimated standard errors comparable to those based on sw⁽ⁿ⁾.

This study had limitations. In order to make a causal interpretation from the MSCM results, investigators require identifiability conditions such as positivity, consistency, conditional exchangeability, and correct MSCM model specification (40)—most of which are untestable assumptions. In addition, assuming that the IPTC weight models were correctly specified, truncation of the most extreme weights might have introduced bias into the β-IFN association estimates, reflecting the fundamental “bias-variance tradeoff” (40). Our assessment of disease progression was based on the EDSS, which has recognized limitations (46) and may not be able to distinguish differences due to natural aging from those due to MS disability. Additionally, one could consider EDSS score another time-dependent confounder. Our sensitivity analysis implementing this (based on imputed missing EDSS values) substantially moved the estimated hazard ratio towards the null (HR = 1.13, 95% confidence interval: 0.76, 1.68), considerably weakening the suggestion from the main analysis of a stronger association for treatment in the harmful direction. Therefore, the near-significant point estimate (HR = 1.36, 95% confidence interval: 0.95, 1.94) from the main results may have been due to residual confounding. Although we considered important confounders, residual confounding due to unmeasured covariates (both baseline and time-dependent) is still possible. Potential limitations of the observational study design in assessing the association between β-IFN and MS disease progression are similar to those described elsewhere (9).

In summary, use of the Cox model alone may be inadequate to handle the challenges of analyzing longitudinal observational data. The use of such tools may partly explain the seemingly inconsistent findings regarding the association between β-IFN and disability progression in the “real-world” MS clinical practice setting (8, 9). Here, we carefully implemented the MSCM analysis to adjust for potential indication bias and related changes in patient characteristics which might influence the subsequent treatment decisions. Our analyses did not find any association between β-IFN exposure and time to development of a sustained EDSS score of 6 over the course of follow-up. Even though different approaches were used here, our conclusions are consistent with those of other studies (9, 47). Furthermore, none of the sensitivity analyses in the current study changed our conclusion regarding the causal association between β-IFN and MS disease progression. The consistency of the results from all of our MSCM analyses strengthens our confidence in the findings. The methods implemented here are adaptable to chronic disease settings beyond MS.