Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2014 Jul 1;21(7):548–567. doi: 10.1089/cmb.2014.0022

Stochastic Simulation of Notch Signaling Reveals Novel Factors That Mediate the Differentiation of Neural Stem Cells

Wen-Shyong Tzou 1,✉, Ying-Tsang Lo 2, Tun-Wen Pai 2, Chin-Hwa Hu 3, Chung-Hao Li 3
PMCID: PMC4082354  PMID: 24798230

Abstract

Notch signaling controls cell fate decisions and regulates multiple biological processes, such as cell proliferation, differentiation, and apoptosis. Computational modeling of the deterministic simulation of Notch signaling has provided important insight into the possible molecular mechanisms that underlie the switch from the undifferentiated stem cell to the differentiated cell. Here, we constructed a stochastic model of a Notch signaling model containing Hes1, Notch1, RBP-Jk, Mash1, Hes6, and Delta. mRNA and protein were represented as a discrete state, and 334 reactions were employed for each biochemical reaction using a graphics processing unit–accelerated Gillespie scheme. We employed the tuning of 40 molecular mechanisms and revealed several potential mediators capable of enabling the switch from cell stemness to differentiation. These effective mediators encompass different aspects of cellular regulations, including the nuclear transport of Hes1, the degradation of mRNA (Hes1 and Notch1) and protein (Notch1), the association between RBP-Jk and Notch intracellular domain (NICD), and the cleavage efficiency of the NICD. These mechanisms overlap with many modifiers that have only recently been discovered to modulate the Notch signaling output, including microRNA action, ubiquitin-mediated proteolysis, and the competitive binding of the RBP-Jk-DNA complex. Moreover, we identified the degradation of Hes1 mRNA and nuclear transport of Hes1 as the dominant mechanisms that were capable of abolishing the cell state transition induced by other molecular mechanisms.

Key words: : biochemical networks, computational molecular biology, gene networks, stochastic processes.

1. Introduction

Notch signaling is responsible for cell fate determinations that enable biological processes, such as cell differentiation, proliferation, and apoptosis. Notch signaling functions in virtually all developing organs in the embryo and the adult (Artavanis-Tsakonas et al., 1999; Artavanis-Tsakonas and Muskavitch, 2010; Koch et al., 2013; Perdigoto and Bardin, 2013). Notch signaling is both simple in design and complex in function. Upon Delta activation from the neighboring cell and proteolysis, the Notch intracellular domain (NICD) is released into the nucleus. A complex consisting of NICD and RBP-Jk binds the promoter region of target genes, which activates the gene expression of multiple genes, such as Hes1, Notch, and RBP-Jk. The cells with high Hes1 levels inhibit the expression of Hes1, Notch, RBP-Jk, and Ngn2, which maintains the stem cell state (Kageyama et al., 2007; Kovall, 2007; Kovall and Blacklow, 2010). The signal transfer of Notch signaling is linear, and no enzymatic amplification is involved. One NICD molecule released into the cytoplasm indicates that one NICD molecule directly transferred into the nucleus. However, Notch signaling is pleiotropic and confers “context specificity” in different cell types and tissues. Recently, several pathways (e.g., Wnt, TGF-beta, hypoxia, and RTK) crucial to development have been confirmed to cross talk with Notch signaling, creating “context specificity” (Andersson et al., 2011; Borggrefe and Liefke, 2012; Guruharsha et al., 2012).

The computational modeling of Notch signaling is an active field of research and aims to understand the circuit design principle of Notch signaling. Briefly, Julian Lewis and associates demonstrated that Hes1 feedback inhibition, transcription delay, and translation delay enable the oscillation of her genes (Lewis, 2003; Lewis et al., 2009). Barrio et al. (2006) also introduced the transcription and translation delays in hes1 gene and showed that the delays are essential to the sustained oscillation. Monk (2003) showed that, in the autoinhibition feedback network of Hes1, p53, and NF-kappaB, the oscillation period is largely determined by the decay rate of mRNA and protein but not by the transcription and translation rate. In somite development, Cinquin (2007) used a mathematical model to first suggest the role of positional information of repressor dimerization (her1/her7 and her13.2) in the generation of the spatiotemporal pattern of gene expression. Campanelli and Gedeon (2010) suggested that the protein degradation rate of the her7 homodimer must be different from the her7-her13.2 heterodimer to initiate a somitogenesis clock-wave. Collier et al. (1996) built a simplified multiple cell mathematical model to simulate contact-mediated lateral inhibition, demonstrating that the feedback loop is sufficient to generate fine-grained patterns observed in living systems. Sprinzak and colleagues (Shaya and Sprinzak, 2011; Sprinzak et al., 2010, 2011) found that the cis-inhibition of Notch by Delta generates an ultrasensitive switch between two cell states (high or low Notch). Moreover, by using the multiple cell model, cis-inhibition was demonstrated to accelerate the patterning dynamics without transcription-mediated feedback (Sprinzak et al., 2011). More specifically, computer modeling of the differentiation of neural stem cells has recently received attention (Shimojo et al., 2008, 2011; Kageyama et al., 2009, 2010; Kobayashi et al., 2009). Agrawal et al. (2009) constructed a complicated gene regulatory network (GRN) containing Notch, Hes1, and RBP-Jk and found that the transcriptional repression constant of Hes1 switches the model system from a bistable state to an oscillation state. Furthermore, the stochastic model of GRN was established and proved to be able to recapitulate the bistability caused by changes in the Delta signal. Kiparissides et al. (2011) included Hes6 and Mash1 based on the Agrawal et al. (2009) model and used deterministic equations to conclude that the degradation of Hes1 and Mash1 mRNA as well as the dissociation constant of Mash1-E47 heterodimers mediate the transition from stem cell to differentiated cell.

The stochastic model of GRN has long been believed to capture the reality of the dynamics of a biological system (Wilkinson, 2009, 2012). Inference based on a deterministic model of the Notch signaling, GRN can be tested in a stochastic model of the GRN. Here, by extending the work by Agrawal et al. (2009), we demonstrated that the graphics processing unit (GPU)-accelerated simulation of a Notch signaling GRN stochastic model in the neural stem cell recapitulates the stem cell state and its transition to the differentiated state by varying Delta signals. By employing both a constant and pulsating Delta, we discovered that several previously unknown molecular mechanisms contribute to the transition from the stem cell to the differentiated cell. We related this finding to the current understanding of the molecular modifiers capable of modulating the Notch signaling output based on the experimental data. Moreover, we also identified the dominant mechanism that, when changed counterproductively, potentially abolishes the differentiation process despite the productive change of other mechanisms.

2. Methods

2.1. Description of the Notch signaling GRN

The Notch signaling gene regulatory model (Fig. 1) is adapted from Agrawal et al. (2009) with the addition of the Mash1 and Hes6 genes. The reaction network is shown in Supplementary Table S1 (Supplementary Data are available online at www.liebertpub.com/cmb). In a cell without input Delta activation, the important features of the Notch GRN are as follows:

  • 1. The gene expression of Hes1 is repressed by Hes1 itself and RBP-Jk.

  • 2. The gene expression of RBP-Jk is inhibited by itself and Hes1.

  • 3. The gene expression of Notch is also inhibited by Hes1 and RBP-Jk.

FIG. 1.

FIG. 1.

Open in a new tab

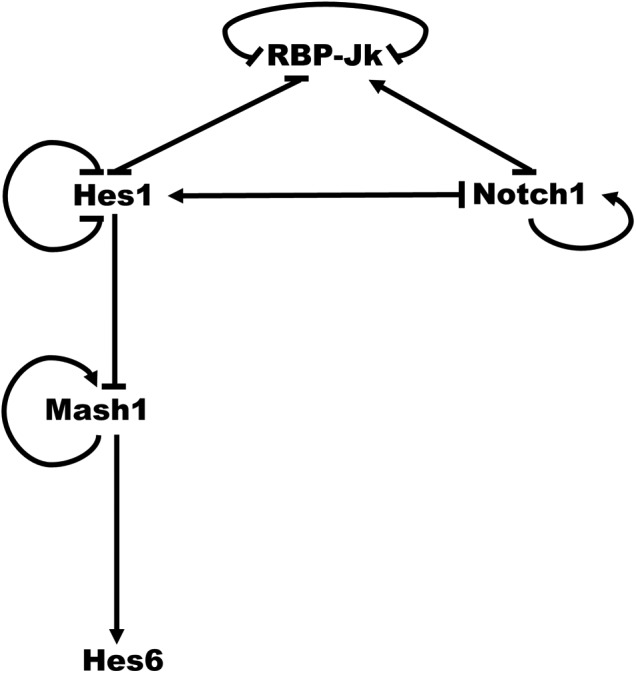
Notch signaling gene regulatory network. Notch1-RBP-Jk-Hes1-Mash1-Hes6 network model. → indicates activation. —| indicates repression.

Upon an input Delta signal, the important features of the Notch GRN include the following:

  • 1. Notch binding with Delta leads to the release of NICD.

  • 2. The nuclear NICD and RBP-Jk protein complex activates the gene expression of Hes1, RBP-Jk, and Notch.

  • 3. The gene expression of Mash1 is inhibited by Hes1 but is activated by Mash1 itself.

  • 4. The gene expression of Hes6 is activated by Mash1.

2.2. The promoter structure

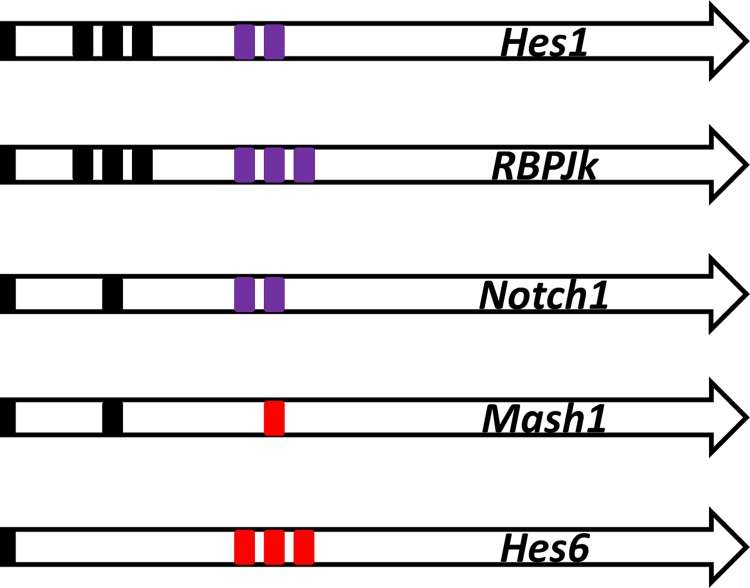
The control of the gene transcription of the Notch signaling GRN occurs via the binding sites in the promoter of these genes (Fig. 2). Three Hes1 binding sites (Nbox) (Takebayashi et al., 1994) and two RBP-Jk binding sites (Brou et al., 1994; Jarriault et al., 1995) were found in the promoter of the Hes1 gene (Takebayashi et al., 1994; Jarriault et al., 1995; Giot et al., 2003). According to a previous study (Agrawal et al., 2009), promoter analysis and experiments suggested that one Hes1 binding site (Nbox) and two RBP-Jk binding sites were present in the Notch gene promoter. Promoter sequence analysis also suggested three Hes1 binding sites (Nbox), and three RBP-Jk binding sites were present in the RBP-Jk gene promoter (Amakawa et al., 1993). Promoter sequence analysis (Transfac) (Wingender, 2008) and experiments suggested that one Hes1 binding site (Nbox) (Chen et al., 1997) and one Mash1 binding site (Ebox) were present in the Mash1 gene promoter. Promoter sequence analysis suggested that three Mash1 binding sites (Ebox) (Scheffer et al., 2007) were present in the Hes6 gene promoter.

FIG. 2.

FIG. 2.

Open in a new tab

Promoter structure. The promoter structure for the transcription factor binding sites. The black box indicates the binding site of the Hes1 dimer. The purple box indicates the binding site of RBP-Jk(-NICD) binding. The red box indicates the binding site for Mash1.

2.3. Transcription activation

The promoter activation magnitude (i.e., the rate of mRNA synthesis) was modeled by BEWARE (Gilman and Arkin, 2002; Lai et al., 2004) by following the protocol in Agrawal et al. (2009).

2.4. Delay of RNA transcription and protein translation

The introduction of the transcription and translation delays in the stochastic simulation were implemented before (Barrio et al., 2006). Both transcription and translation reactions have a delay period before the start of the reaction, and the calculation of the delay time followed the protocol in Agrawal et al. (2009).

2.5. Dimerization description

In the “dimer-cloud” theory, the stability of the Hes proteins was controlled by all dimer combinations (Fig. 3) (Schroter et al., 2012). Dimeric Hes1 bound to the Nbox to inhibit gene expression (Kageyama et al., 2007). We postulated that Hes6 forms a dimer and could alleviate the inhibition of Hes1 by forming a Hes1-Hes6 heterodimer (Bae et al., 2000; Koyano-Nakagawa et al., 2000; Kageyama et al., 2009). We also postulated that Hes1 forms a Hes1-Mash1 heterodimer to inhibit the transactivation ability of Mash1.

FIG. 3.

FIG. 3.

Open in a new tab

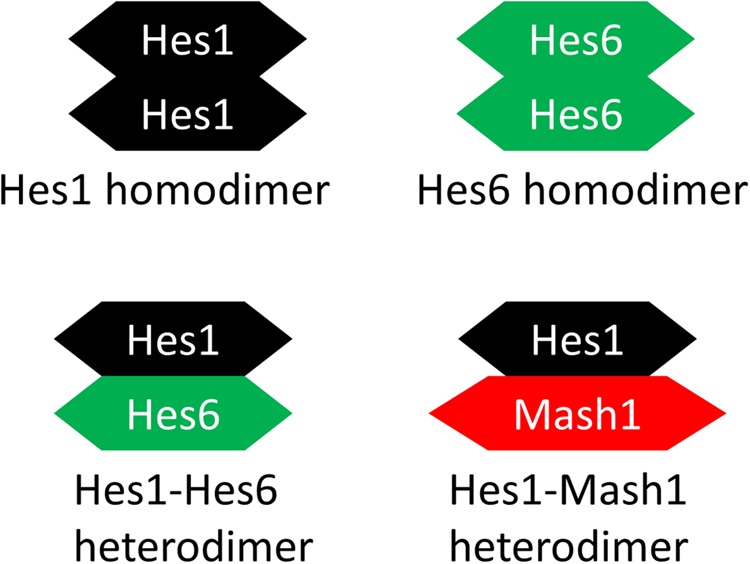
Dimerization description. The proposed dimer cloud: the Hes1 dimer, the Hes6 dimer, the Hes1-Hes6 dimer, and the Hes1-Mash1 dimer.

2.6. The stochastic simulation algorithm scheme for the Notch signaling network

We employed the Gillespie scheme for stochastic simulation and implemented the scheme in the C language (Agrawal et al., 2009). Gene transcription and translation delays were implemented in a map structure. Each biological entity was individually represented as an integer. The directed method of stochastic simulation on GRN has been previously described (Gillespie, 2001, 2007; Agrawal et al., 2009). Briefly, in step 1, the propensity of the occurrence of each biochemical reaction was defined as the product of the number of the reactants and the reaction rate. In step 2, a random number was generated to determine the time step for the next reaction. In addition, another random number was also generated to determine which reaction was going to occur. In step 3, a chosen reaction occurred, and the number of reactants and products was updated. In step 4, the propensity of the occurrence of each biochemical reaction was updated. Finally, the entire pathway was repeated beginning at step 2. The code was an extension of the code generated in (Agrawal et al., 2009). Ten runs of the stochastic simulation of each reaction scheme are executed.

2.7. Species definition for the Notch signaling network

The stochastic simulation algorithm (SSA) reaction schemes were adapted from Agrawal et al. (2009), but several more gene regulation links were added to the current model, including the Mash1 and Hes6 genes (Supplementary Table S2). The initial condition for the species was adapted from Agrawal et al. (2009), and its variation does not alter the main simulation results.

2.8. Model parameters

The parameters for the half-lives of the proteins and mRNA, the association and the dissociation constants of the proteins to their respective DNA binding sites, the dimerization constants, the protein translation and transcription rates, and the mRNA and the protein transfer constants were directly adapted from Agrawal et al. (2009) (Supplementary Table S3). The Mash1 and Hes6 gene protein translation and transcription rates were estimated following the same methods applied in Agrawal et al. (2009).

2.9. Parallel computing using the GPU to generate a random number seed

SSA requires large random numbers to conduct the simulation. Although different programming languages possess various choices of built-in random number generation tools, we preferred to apply the Mersenne Twister random algorithm to simulate random numbers to comply with the average entropies. The Mersenne Twister algorithm (Matsumoto and Nishimura, 1998) was developed by Makoto Matsumoto and Takuji Nishimura in 1997, which quickly produced pseudorandom numbers with high-quality and uniform distributions. The algorithm required longer computational time than normal built-in random number generators to produce a random number, especially when abundant random numbers were required. To increase the speed of the random number generation processes, the Compute Unified Device Architecture (CUDA) parallel processing technology was employed during the cell simulation analysis.

CUDA is an integrated technology developed by the NVIDIA Company for graphic processing. The exploitation of GPU multicore parallel computing architecture involved executing designed programs with repetitive procedures. The accelerated performance significantly improved through multithread parallel processing and high-speed floatingpoint arithmetic. CUDA has been widely applied in various applications in biology. For example, AMBER for molecular dynamics software (Gotz et al., 2012), BLASTp for protein sequence database searches (Liu et al., 2011), and the docking program for protein–DNA interaction analysis (Wu et al., 2012) are well-known programs with a CUDA-enabled version.

2.10. Parameter change, criteria setting, and input Delta

In the Notch signaling network, quite a few molecular mechanisms that potentially change the behavior of the system exist. The parameters built in the stochastic simulation represent various molecular mechanisms. Our objective involved searching for the parameter or for the combinations of parameters (one, two, three, and four) that led to a cell state upon changing the parameter values, for example, from the stem cell state to the differentiated state. On the basis of previous studies (Kiparissides et al., 2011), we defined the stem cell state as the state with oscillating cellular Hes1 and Mcm1 protein (Hcp and Mcp, respectively) levels; we also defined the differentiated state as the state with low Hcp and high Mcp levels. We defined “our criteria” as, when parameters were upon a change, SSA simulation will lead to a simulation result of the alteration of Hcp and Mcp values: average Hcp for the last 2000 min (virtual simulation time) fell down to less than a fourth of the oscillating one; average Mcp for the last 2000 min increased to more than one-third of the differentiated one.

We selected 40 parameters as the candidate parameters that can potentially enable the switch of cell state by varying the parameter values. We do not include the parameters for the translation rate, transcription rates, and the delays time since they can be estimated from the experiments. In the tables and figures that follow, the number of increases and decreases corresponds to the fold changes. For example, a three-fold increase denotes the parameter value that was multiplied by a factor of 3 of its original value. A three-fold decrease denotes the parameter value that was 70% of its original value (a decrease of 30%). During all SSA simulations except as otherwise noted, the parameter changed from 4500 to 6500 min in a linear fashion. Assumingly, any change of parameter values of more than 10-fold will be impractical in biology.

We employed two types of Delta input. One type was a step function with the number of Delta protein being 10. The other Delta input type was a pulsating function with a periodic presence of Delta (the period is 124 min; the number of Delta is one) for 1 minute. All stochastic simulations were conducted as mentioned above while Delta was constant or pulsating.

2.11. The identification of the molecular mechanisms enabling the transition from an oscillatory state to a differentiated state using the heuristic method

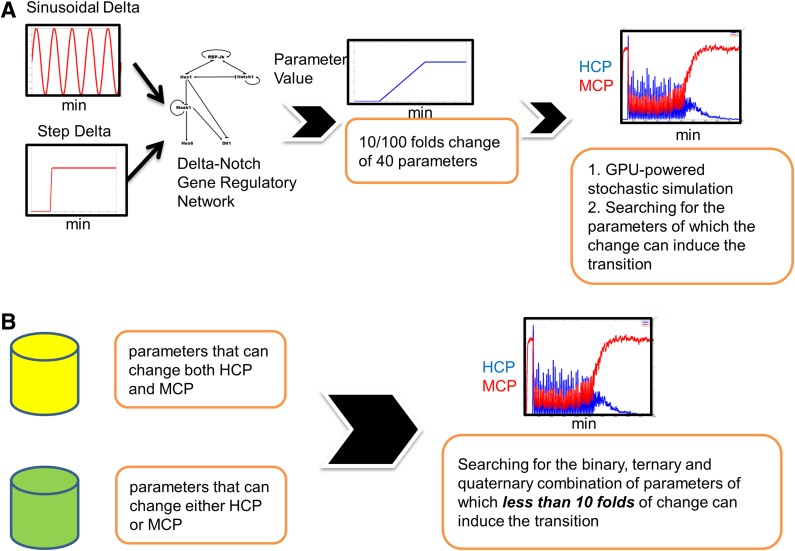
We changed the parameters 10-fold and checked if the simulation led to results that fit our criteria. Unexpectedly, we found no simulation that fit our criteria.

Since the change of any one of the parameters alone cannot lead to a simulation that fit our criteria, we expected that the change of more than one parameter at the same time will fit our criteria. It is difficult to exhaustively search all of the possible combinations of parameters; therefore, we developed a heuristic approach (Fig. 4). In essence, we increased or decreased the parameter 100-fold. We expected that a 100-fold change of a portion of 40 parameter values alone would lead to an SSA simulation result that fit our criteria (in this stage, we designated them as selected parameters). We then moved forward to determine if less than or equal to a 10-fold change of the combination of these selected parameters also fit our criteria.

FIG. 4.

FIG. 4.

Open in a new tab

Heuristic methods of identifying the molecular mechanisms enabling the transition from an oscillatory state to a differentiated state. (A) In our Notch signaling network model, either constant or pulsating input Delta signal was employed. We changed the values of the each of the 40 parameters and confirmed if the GPU-powered SSA simulation fits our criteria. (B) Selected parameters that had the potential to induce the cell state transition were combined to investigate the binary, ternary, and quaternary combination to induce the cell state transition, but the fold change of each parameter must be less than or equal to 10. GPU, graphics processing unit; SSA, stochastic simulation algorithm.

When the input Delta was constant, we found that the simulation of a 100-fold increase of only one parameter (KdHcm) fit our criteria. We abandoned this parameter as the candidate. When the input Delta was pulsating, we can find only five parameters, and a 100-fold increase or decrease of each alone led to a simulation result that fit our criteria. We then searched for the binary or ternary combination of these five parameters, but we only allowed for a fold change of less than or equal to 10-fold for each parameter. For simplicity, the fold change (increase or decrease) was the same for each parameter in combination (Supplementary Table S4).

On the other hand, when we scrutinized the simulation results, we found that a 10-fold change of several parameters was capable of causing either a significant increase of Mash1 protein or a decrease of Hes1 protein but not both (Supplementary Table S4). More specifically, when the input Delta was constant, we found only one parameter (KniHcp) for which a 10-fold increase led to a Hcp decrease, and only one parameter (KdHcm) for which a 10-fold increase led to an Mcp decrease. The simultaneous increase of these two parameters was then investigated in the simulation. When the input Delta was pulsating, we also found only one parameter (KniHcp) for which a 10-fold change led to a Hcp decrease; however, we found six parameters for which a 10-fold change led to an Mcp increase. We then searched for the binary or ternary combination of these six parameters with KniHcp that fit our criteria, but we only allowed for less than or equal to 10-fold changes for each parameter.

2.12. Dominance detection

The increase or decrease of several parameters and their combinations induced the transition from stem cell to differentiation. We also investigated if the reverse change of parameter A (if there was an increase, then there was a decrease; if there was a decrease, then there was an increase) had an antagonistic effect on the change of parameter B in the simulations but not vice versa. In this type of case, parameter A dominated parameter B. Parameter A was denoted as the “dominator,” and parameter B was denoted as the “submitter.”

3. Results

3.1. A GPU accelerated the stochastic simulation

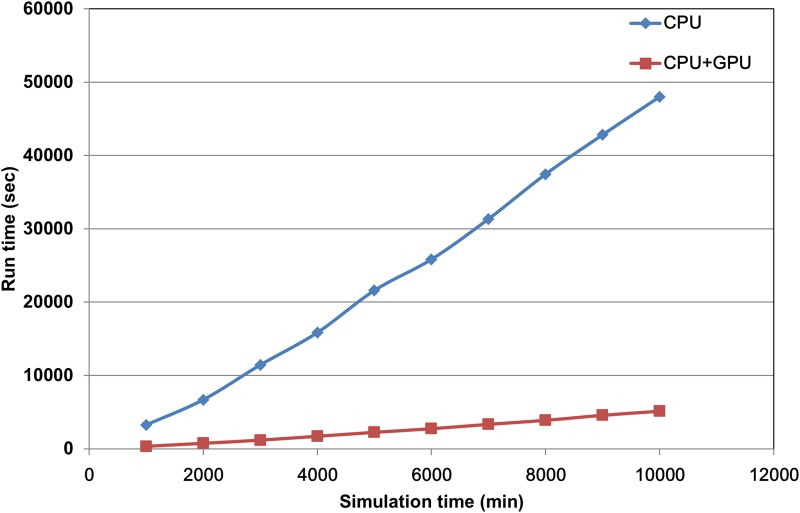
CUDA technology was employed to accelerate the simulation program in this study. The original time requirement for random number generation without CUDA technology was one-third of the total time, which was not acceptable for a cell simulation program. After integration with CUDA computing architecture, with respect to the computational time requirement for random number generation, the proposed system was improved by 6.72-fold when a total of 300 virtual unit time was performed. To compare the saved time against the total account of random numbers, we conducted a simulation and calculated the time requirement for both the CPU architecture alone and the CPU combined with the CUDA computing architecture. The experiments were performed with an Intel Core i7-2600 3.4 GHz and a Geforce GTX580 graphics card within the Windows 7 operating system. As shown in Figure 5, the required computational time for the CPU alone was approximately 10-fold greater than the time required by employing both the CPU and the CUDA architecture simultaneously. Therefore, we employed GPU and CPU together to accelerate our simulation.

FIG. 5.

FIG. 5.

Open in a new tab

The comparison of run time requirement for CPU and GPU. Run time requirement for both CPU architecture alone (blue diamond) and CPU combining the CUDA computing architecture (red square). The x-axis indicates the virtual unit time of simulation, and the y-axis represents the total run time cost for the simulation program. CUDA, Compute Unified Device Architecture.

3.2. The oscillation state and the differentiated state of the Delta-Notch network

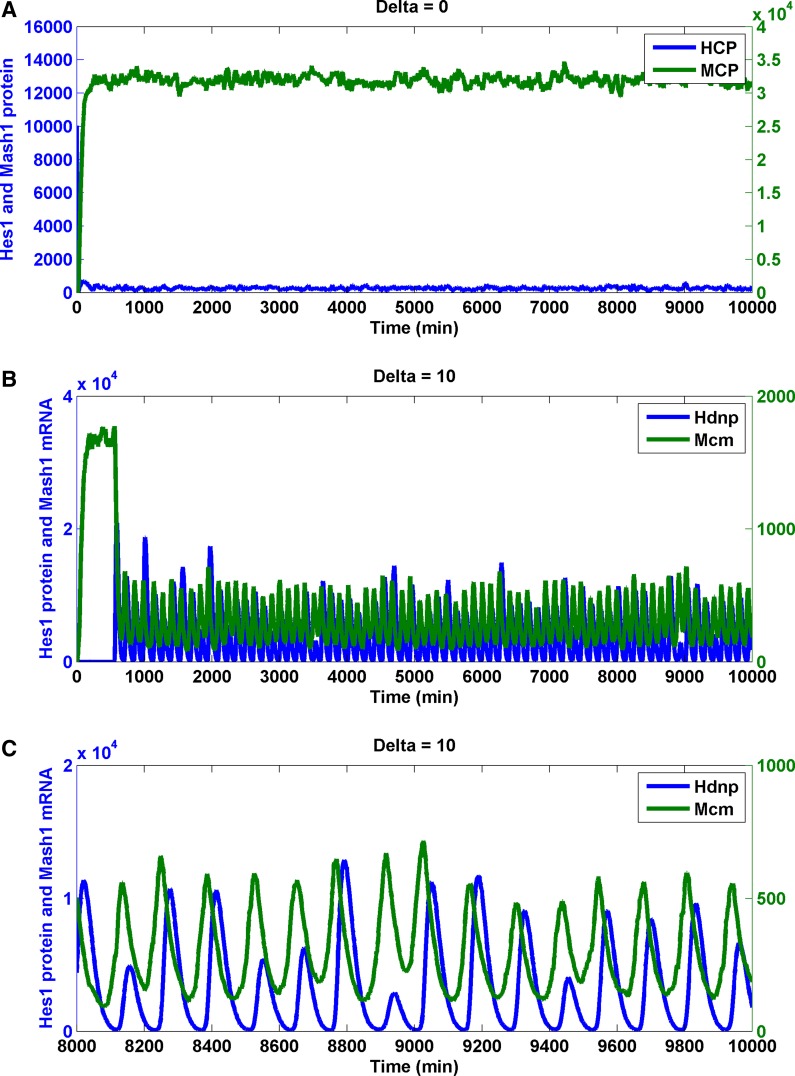
A previous study established that by tuning the transcription repression (rNbox) of Hes1 (Agrawal et al., 2009), the GRN transferred from a bistable switch to an oscillatory state. In the Notch network, with no input Delta signal, Hes1 remained low and Mash1 remained high (Fig. 6A). When the input Delta signal from a neighboring cell existed, an oscillation state for Hes1 and Mash1 persisted (Fig. 6B, C) (the period of nuclear Hes1 dimer is 130.9 ± 9.0 min; the period of cytoplasmic Mash1 mRNA is 130.9 ± 10.8 min). This finding is reminiscent of an experimental observation and a deterministic model (Hirata et al., 2002). The phase difference between the nuclear Hes1 dimer and the Mash1 mRNA was 37.1 ± 3.3 min, which was 28.3% of an oscillation period.

FIG. 6.

FIG. 6.

Open in a new tab

Stochastic simulations of Notch signaling in the neural stem cell and the differentiated cell. Trajectory of the Hes1 protein, the Mash1 protein, and the Mash1 mRNA in the neural differentiated cell (input Delta is absent) (A) and the stem cell (input Delta is present) (B, C). In the differentiated cell, the cellular Hes1 protein (Hcp) was kept low and the cellular Mash1 protein (Mcp) was high. In the stem cell, the nuclear Hes1 protein dimer (Hdnp) and the cellular Mash1 mRNA (Mcm) remained oscillatory. The phase difference between Hdnp and Mcm is evident. (C) is a zoomed version of (B).

In essence, the presence of input Delta induced an oscillation of the Notch-signaling network. The existence and stability of input Delta protein influenced the transition from an oscillatory state to a differentiated state. However, are there other molecular mechanisms involved enabling the transition? We systematically varied the parameters representing a repertoire of molecular mechanisms, including protein–DNA promoter association/dissociation, RNA transcription, protein translation, protein and RNA degradation, dimer association/dissociation, and nuclear transport of protein from cytoplasm.

3.3. The identification of the molecular mechanisms enabling the transition from an oscillatory state to a differentiated state-heuristic approach I

One of the hallmarks of the switch from stem cell state to differentiated state is the abundance of the Mash1 protein and the minute amount of the Hes1 protein (Kageyama et al., 2005). We then varied 40 parameters to investigate the effects of changing each parameter on cytoplasmic Hes1 and Mash1 proteins. The input Delta signal was either a constant value or a pulsating value. Our criteria included that after changing the parameter, it will lead to a significant increase in the Mash1 protein and a decrease in the Hes1 protein (see Methods section).

To our surprise, we did not identify a 10-fold change of any parameter alone that led to the simulation results that fit our criteria regardless if the input Delta signal was constant or pulsating (Supplementary Table S4). We expected that, when the 10-fold change of a single molecular mechanism was not sufficient to stimulate the cell state transition, different molecular mechanisms would cooperatively interact with each other to enable the cell state transition. We then searched for the combination of two or three parameters (responsible for the two or three molecular mechanisms) that were sufficient for such a transition; however, it was computationally prohibited to perform an exhaustive search for these combinations. Therefore, we designed a heuristic method to determine the effective combination of parameters.

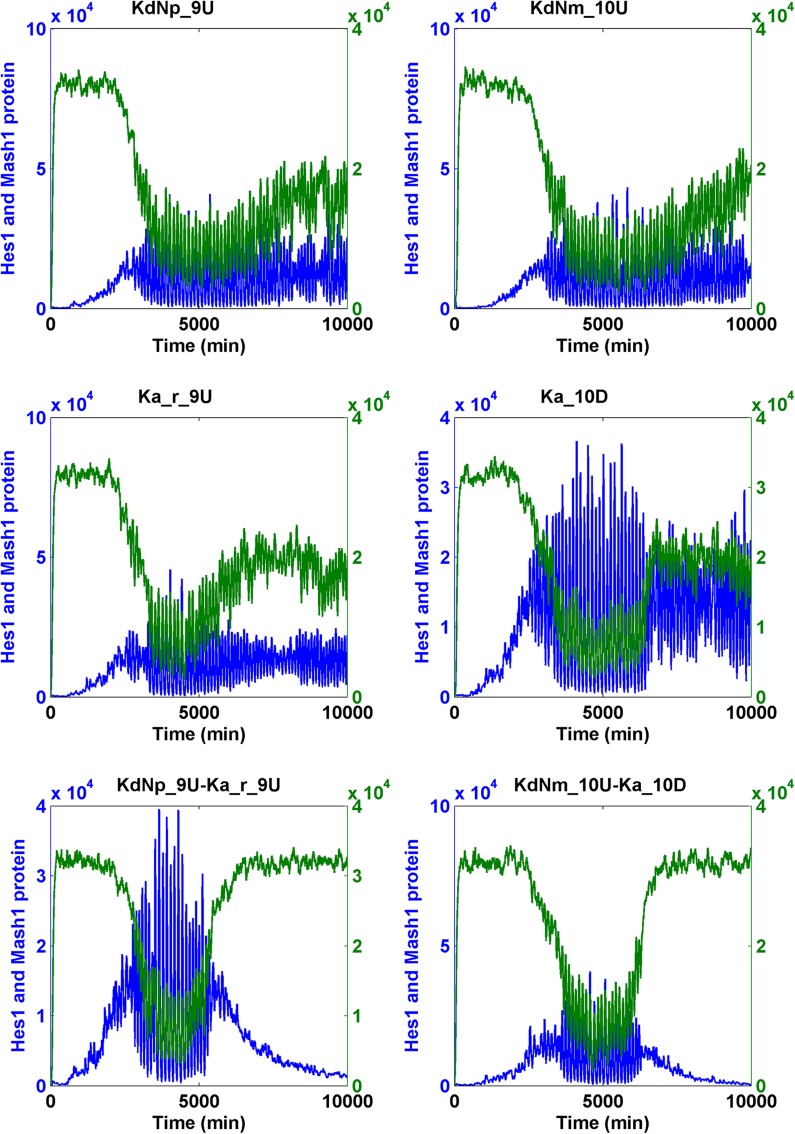
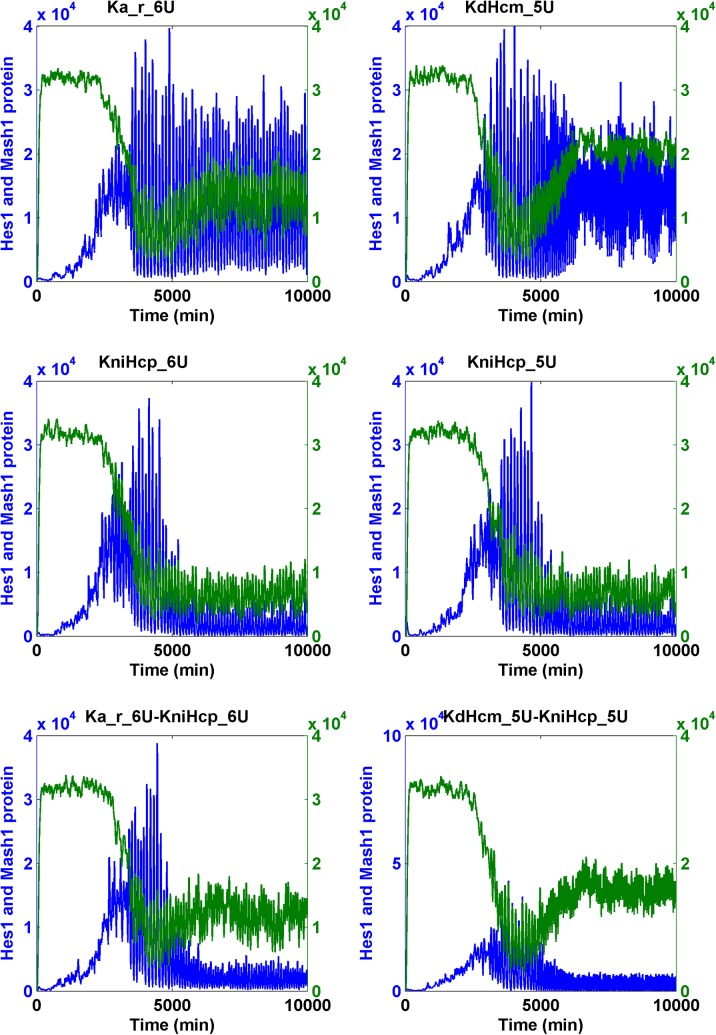
We increased or decreased the magnitude of the parameters by 100-fold and conducted SSA simulations on the Notch signaling model. We found that changing five parameters led to the simulation results that fit our criteria. These changes included an increase of KdNm (degradation rate of Nm), KdNp (degradation rate of Np), and Ka_r (RBP-Jk NICD dissociation constant), and the decrease of Ka (RBP-Jk NICD association constant) when input Delta was pulsating and a decrease of KdHcm (degradation constant of Hes1 messenger RNA) when the Delta was either pulsating or constant (Table 1). Subsequently, we intend to find if the combination of less than 10-fold of change of these five parameters was sufficient for the cell state transition. When a pulsating Delta was employed, we identified numerous effective cooperative interactions between and among the following parameters: the increase of KdNm (degradation rate of Nm), KdNp (degradation rate of Np), and Ka_r (RBP-Jk NICD dissociation constant), and the decrease of Ka (RBP-Jk NICD association constant) (Table 2) (Fig. 7 for binary combination; Fig. 8 for ternary combination).

Table 1.

Sensitivity Analysis of Parameters That Mediate Neural Differentiation

Parametera Definition Fold changeb Hcp responsec Mcp responsec Input Deltad
KdHcm (I) Degradation rate of Hes1 mRNA 100 up Down Up C + P
KdNm (I) Degradation rate of Notch mRNA 100 up Down Up P
KdNp (I) Degradation rate of cytoplasmic Notch protein 100 up Down Up P
Ka_r (I) RBP-Jk NICD dissociation constant 100 up Down Up P
Ka (I) RBP-Jk NICD association constant 100 down Down Up P
KdHcm (II) Degradation rate of Hes1 mRNA 10 up   Up C + P
KdNm (II) Degradation rate of Notch mRNA 10 up   Up P
KdNp (II) Degradation rate of cytoplasmic Notch protein 10 up   Up P
Ka_r (II) RBP-Jk NICD dissociation constant 10 up   Up P
Ka (II) RBP-Jk NICD association constant 10 down   Up P
KniHcp (II) Nuclear transport rate of cytoplasmic Hes1 protein 10 up Down   C + P
KfNcp (II) Forward rate of generation of NICD (Ncp) upon binding of Np to input Delta 10 down   Up P
Open in a new tab
a

Parameter that can induce the change of Hcp and Mcp (I, heuristic approach I; II, heuristic approach II; see text).

b

Fold change of the parameters. Change of all parameters but two parameters (Ka, KfNcp) are increase.

c

Hcp fell down to less than a fourth of the oscillating one; Mcp increased to more than one-third of the differentiated one.

d

Input Delta is constant (“C”) or pulsating (“P,” period is 124 min).

Table 2.

Binary and Ternary Combination for Parameters Able to Mediate Neural Differentiation

Parametera Parametera Parametera Fold changeb Input Deltac Hcp foldd Mcp folde
  KdNp Ka_r 9 P 0.20 (0.02) 0.99 (0.01)
  KdNm Ka_r 8 P 0.25 (0.03) 0.99 (0.00)
  KdNp Ka 10 P 0.22 (0.01) 1.00 (0.00)
  KdNm Ka 10 P 0.14 (0.01) 1.00 (0.00)
  KdNm KdNp 10 P    
Ka_r KdNm KdNp 5 P 0.13 (0.02) 1.00 (0.00)
Ka KdNm KdNp 7 P 0.12 (0.02) 1.00 (0.00)
Open in a new tab
a

Parameters can be combined to induce the cell state transition from stem cell to differentiation (heuristic approach I).

b

Fold change of the parameters. Change of all parameters but three parameters (Ka) are increase.

c

Input Delta is constant (“C”) or pulsating (“P,” period is 124 min).

d

The average ratio of change of Hcp relative to the oscillating Hcp in the stem cell (10 simulations).

e

The average ratio of change of Mcp relative to the differentiated Mcp in the differentiated cell (10 simulations).

FIG. 7.

FIG. 7.

Open in a new tab

The transition of the Notch signaling pathway from the oscillatory stem cell state to the differentiated cell state—heuristic approach I. For each binary combination of parameters, the simulation trajectory for HCP and MCP after the change of each parameter alone is also shown. “U” indicates that the change was the increase; “D” indicates that the change was the decrease. The fold of change is the numerals that prefixed “U” or “D.” Hcp and Mcp are colored in blue and green, respectively.

FIG. 8.

FIG. 8.

Open in a new tab

The transition of the Notch signaling pathway from the oscillatory stem cell state to the differentiated cell state—heuristic approach I and II. (A–D) For each ternary combination of parameters, the simulation trajectory for HCP and MCP after the change of each parameter alone is also shown. “U” indicates an increase; “D” indicates a “decrease.” The fold of change is the numerals that prefixed “U” or “D.” Hcp and Mcp are colored in blue and green, respectively.

3.4. The identification of the molecular mechanisms enabling the transition from an oscillatory state to a differentiated state heuristic approach II

Interestingly, we identified 10-fold changes of several molecular mechanisms capable of causing either the significant increase of the Mash1 protein or the decrease of the Hes1 protein but not both (Table 1 and Supplementary Table S4).

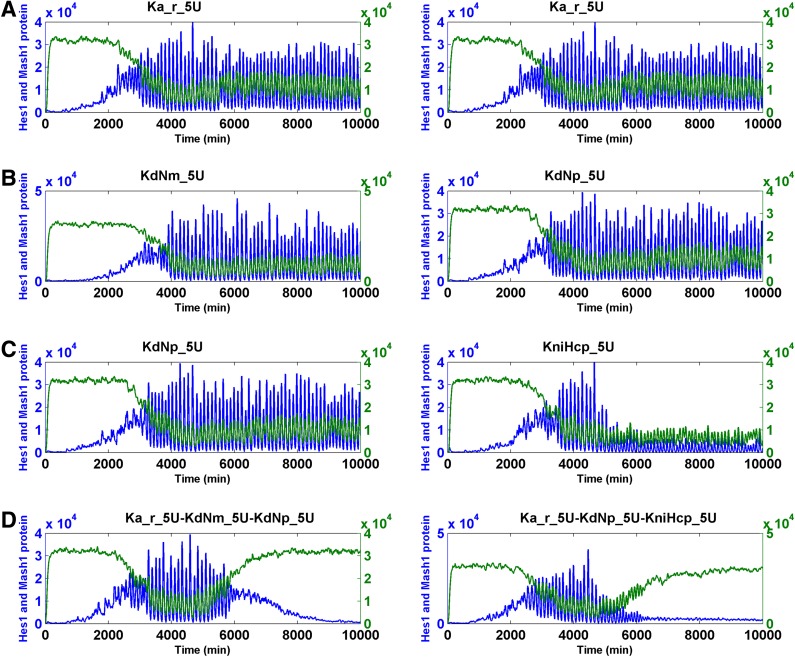
It is possible that the cooperation of two parameters responsible for two different mechanisms led to both the significant increase of Mash1 protein and the decrease of Hes1 protein. By conducting simulations on the pulsating Notch signaling model, we found many additional cooperative interactions among several parameters, including the increase of KdHcm (degradation constant of Hes1 messenger RNA), KdNm (degradation rate of Nm), KdNp (degradation rate of Np), and Ka_r (RBP-Jk NICD dissociation constant) and the decrease of Ka (RBP-Jk NICD association constant) and KfNcp (forward rate of generation of NICD upon binding of Np to Delta). However, all effective combinations must additionally include the parameter KniHcp (nuclear import rate of Hcp). This condition resulted from the fact that KniHcp was the only parameter for which a 10-fold change significantly reduced the Hcp level (Table 3) (Fig. 8 for ternary combination; Fig. 9 for binary combination).

Table 3.

Binary, Ternary, and Quaternary Combination for Parameters Able to Mediate Neural Differentiation

Parametera Parametera Parametera Parametera Foldb Deltac Hcp foldd Mcp folde
    Ka_r KniHcp 6 P 0.18 (0.00) 0.37 (0.02)
    KdHcm KniHcp 5 P 0.24 (0.00) 0.50 (0.01)
    KdNp KniHcp 7 P 0.15 (0.00) 0.38 (0.02)
    Ka KniHcp 10 P 0.12 (0.00) 0.54 (0.02)
    KfNcp KniHcp 10 P 0.11 (0.00) 0.46 (0.02)
    KdHcm KniHcp 5 C 0.23 (0.00) 0.45 (0.01)
    KdMcm KniHcp 4, 10f P 0.15 (0.00) 0.36 (0.02)
  Ka_r KdNm KniHcp 5 P 0.25 (0.01) 0.85 (0.02)
  Ka_r KdNp KniHcp 5 P 0.23 (0.01) 0.91 (0.02)
  KdHcm KdNp KniHcp 6 P 0.23 (0.00) 0.77 (0.01)
  KdHcm Ka_r KniHcp 6 P 0.23 (0.00) 0.79 (0.01)
  KdHcm KdNm KniHcp 6 P 0.23 (0.00) 0.71 (0.00)
  KdNp KdNm KniHcp 6 P 0.18 (0.01) 0.89 (0.02)
  KdHcm Ka KniHcp 6 P 0.22 (0.00) 0.67 (0.01)
  KdHcm KfNcp KniHcp 6 P 0.22 (0.00) 0.67 (0.01)
  KdNp Ka KniHcp 6 P 0.22 (0.00) 0.70 (0.03)
  KdNp KfNcp KniHcp 5 P 0.24 (0.01) 0.51 (0.03)
  Ka_r KfNcp KniHcp 6 P 0.23 (0.00) 0.72 (0.01)
  KdNm Ka KniHcp 5 P 0.22 (0.00) 0.41 (0.02)
  KdNm KfNcp KniHcp 5 P 0.22 (0.00) 0.41 (0.02)
  Ka KfNcp KniHcp 6 P 0.18 (0.00) 0.35 (0.02)
KdHcm KdNm Ka_r KniHcp 5 P 0.17 (0.01) 0.96 (0.00)
KdHcm KdNp Ka KniHcp 6 P 0.17 (0.00) 0.94 (0.01)
KdHcm KdNm Ka KniHcp 6 P 0.22 (0.00) 0.86 (0.01)
Open in a new tab
a

Parameters can be combined to induce the cell state transition from stem cell to differentiation (heuristic approach II).

b

Fold change of the parameters. Change of all parameters but three parameters (Ka, KfNcp, and KdMcm) are increase.

c

Input Delta is constant (“C”) or pulsating (“P,” period is 124 min).

d

The average ratio of change of Hcp relative to the oscillating Hcp in the stem cell (10 simulations).

e

The average ratio of change of Mcp relative to the differentiated Mcp in the differentiated cell (10 simulations).

f

KdMcm: 40% decrease; KniHcp: 10-fold increase.

FIG. 9.

FIG. 9.

Open in a new tab

The transition of the Notch signaling pathway from the oscillatory stem cell state to the differentiated cell state—heuristic approach II. For each binary combination of parameters, the simulation trajectory for HCP and MCP after the change of each parameter alone is also shown. “U” indicates an increase; “D” indicates a “decrease.” The fold of change is the numerals that prefixed “U” or “D.” Hcp and Mcp are colored in blue and green, respectively.

3.5. Dominance

We identified the increase or decrease of several parameters and their combinations that induced the transition from stem cell to differentiation; however, it remained interesting to investigate the effect of the reverse change of this parameter on the induction of the cell state transition caused by other parameters. The result may be a good indicator of the “strength of influence” of the parameter. By employing a “dominance” analysis (Methods section), we found that KdHcm (degradation constant of Hes1 messenger RNA) and KniHcp (nuclear import rate of Hcp) dominated the other parameters (Table 4 and Supplementary Table S5).

Table 4.

Dominance Analysis of the Parameters

Dominator parametera Fold changeb Submitter parametera Submitter parametera Submitter parametera Submitter parametera Submitter parametera
KdHcm down Ka Ka_r KdNp KdNm  
KniHcp down Ka Ka_r KdNp KdNm KdHcm
Open in a new tab
a

The reverse change of the dominator can abolish the cell state transition from stem cell to differentiation caused by other parameters (the submitter) when input Delta is pulsating.

b

Reverse fold change of the dominator parameter (compared with Table 1).

4. Discussion

To further our understanding of Notch signaling, we established the Notch signaling network comprised of the Notch1, RBP-Jk, Hes1, Mash1, and Hes6 genes. We employed detailed molecular models involving transcription, translation, dimer formation, degradation, and nuclear transport. An SSA with time delay for both reactions of transcription and translation was used to simulate the biochemical reaction in real time. To determine the molecular mechanisms triggering the transformation from the neural progenitor cells to the differentiated neuron cell, we employed a heuristic approach in the stochastic simulation of the Notch signaling network model. We found that the changes of a combination of seven parameters representing various molecular mechanisms drove the transition from the stem cell state to the differentiated state. The level of parameter change was as low as a fivefold change.

The Notch signaling pathway does not have a second messenger and does not have an enzymatic amplification step for the pathway to relay its signal either. Therefore, Notch signaling is very sensitive to gene dosage (Artavanis-Tsakonas and Muskavitch, 2010; Mazzone et al., 2010), and the molecular mechanisms that will alter the quantity of the pathway elements potentially affect the pathway output (Guruharsha et al., 2012). Our predicted potential mechanisms for the cell state transition received experimental support or were consistent with several important experimental observations.

4.1. KdNp (degradation rate of Np)

The asymmetric distribution of the Numb protein during asymmetric cell division in embryo was shown to antagonize Notch signaling (Cayouette and Raff, 2002; Shen et al., 2002; Huttner and Kosodo, 2005; Zhong and Chia, 2008). The proposed mechanism suggested that the presence of Numb promoted ubiquitination-mediated Notch1 degradation (McGill and McGlade, 2003; McGill et al., 2009). Our finding that KdNp was involved in the cell state transition is consistent with this finding. The degradation mechanism may occur through microRNAs or ubiquitination. Interestingly, a theoretical study also suggested that the uneven distribution of Numb triggered the cell state transition (Barton and Fendrik, 2013).

4.2. KdNm (degradation rate of Nm)

In addition to Numb, Numb-like protein (Numbl), also a negative regulator of Notch signaling, was demonstrated to be the target of miR-34a in the mouse brain. Interestingly, Notch1 and RBP-Jk transcripts were increased by miR-34a overexpression; furthermore, knockdown of miR-34a diminished the Notch1 transcripts but enhanced the expression of Mash1 (Fineberg et al., 2012). These results are consistent with our simulation results that the increase of the degradation of Notch1 mRNA could induce the cell state transition.

4.3. KfNcp (forward rate of generation of NICD [Ncp] upon binding of Np to input Delta)

Pin1 is a target gene of Notch signaling. Pin1 has been demonstrated to enhance the cleavage of Notch1 acted by gamma-secretase, forming a positive feedback mechanism (Rustighi et al., 2009). Intriguingly, Pin1 regulates the differentiation of the neural progenitor cells by modifying beta-catenin of the Wnt/beta-catenin pathway (Nakamura et al., 2012). Pin1 has also been shown to be required for the maintenance of pluripotency of mouse embryonic stem cells (Nishi et al., 2011). These results are consistent with our simulation results that the increase of KfNcp induced the cell state transition.

4.4. Ka (RBP-Jk NICD association constant) and Ka_r (RBP-Jk NICD dissociation constant)

The transcriptional activation of the Notch signaling pathway relies on the formation of an activator complex composed of RBP-Jk, NICD, Mastermind-like-1 (MAML), and other protein factors. The activator protein is a “central regulatory hub” in Notch signaling (Borggrefe and Liefke, 2012). While RBP-Jk globally represses gene expression by binding to target sequences and recruiting many corepressors, NICD competes for the binding with RBP-Jk and MAML, subsequently leading to the formation of an activating complex that promotes transcriptional activation. In the repressor complex, RBP-Jk associates with SKIP and SMRT. Upon the Delta–Notch interaction, NICD displaces SMRT from interacting with RBP-Jk and SKIP (Kao et al., 1998; Zhou et al., 2000). In the ternary structure, a concave groove formed by both NICD and RBP-Jk contact the long extended alpha helix of MAML (Nam et al., 2006; Wilson and Kovall, 2006). Here, we found that Ka and Ka_r are involved in the potential mechanisms that trigger the cell state transition. A protein factor or posttranslational modification of NICD may potentially exert such an effect (Foltz and Nye, 2001). The possibility that the association and the dissociation between RBP-Jk and NICD as the mechanism for triggering the cell state transition is significant in that Notch signaling cross talks with several other signaling pathways (which were recently discovered) (Kankel et al., 2007; Mummery-Widmer et al., 2009; Shalaby et al., 2009; Saj et al., 2010) to confer cellular context specificity (Guruharsha et al., 2012). In the same vein, in human T-lymphoblastic leukemia cells, combined ChIP-seq and transcriptome experiments have indicated that 33% of RBP-Jk binding sites are not in the promoters. Specifically, three-fourths of NICD target genes are regulated by enhancers but not promoters, and approximately one-third of RBP-Jk binding sites are not co-occupied by NICD when NICD is present (Wang et al., 2011). Similarly, in Drosophila myogenic progenitor-related cells, an enhancer of over 170 genes required the binding of Twist before Notch activation (Bernard et al., 2010). These lines of evidence suggest that the regulation of Notch signaling may be controlled by the competitive binding of NICD on RBP-Jk with other factors, providing a platform in enhancer regions for the integration of cross talk between Notch and other pathways (Guruharsha et al., 2012).

4.5. KniHcp (nuclear transport rate of cytoplasmic Hes1 protein)

By employing genome-wide RNA interference (RNAi) screens, nuclear import pathways of inhibitor molecules have been suggested as the regulators of the Notch signaling pathway in Drosophila (Mummery-Widmer et al., 2009). Interestingly, in the human glioma cell line, TGF-alpha was capable of inducing the upregulation and nuclear translocation of Hes1 (Zheng et al., 2008). Here, we find the movement of the Hes1 molecule (KniHcp) into the nucleus contributes to the cell state transition. Interestingly, a recent similar finding in mouse ESCs shows that the export of the transcription factor TFE3 out of nucleus is demonstrated to be the key mechanism for the exit of pluripotency (Betschinger et al., 2013).

4.6. KdHcm (degradation rate of Hcm)

In addition to the movement of Hcp into the nucleus, the degradation of Hcm is also a potential mechanism involved in the regulation of the cell state transition. microRNAs were suggested to affect the stability of the delayed negative feedback GRN (Xie et al., 2007). In the mouse embryo, microRNA miR-9 was shown to control the stability of Hes1 at the mRNA level. Both the overexpression and the lack of miR-9 dampen the oscillation of Hes1. miR-9 was expressed at E12.5 in the differentiating neurons in the mouse ventricular zone. Interestingly, Hes1 also directly inhibits the transcription of miR-9, forming a double-negative feedback loop (Bonev et al., 2012; Tan et al., 2012). Although we have not included microRNAs in our current model, our simulation results are consistent with the experimental results but includes more details.

4.7. The dominant role of KdHcm

In the developing central nervous system, Hes1 remains sustained in the cells located in the roof plate, floor plate, and boundary regions. However, the proliferation and differentiation can be resumed (Mash1 upregulated) in the boundary regions when sustained Hes1 is demolished (Baek et al., 2006). Moreover, the neural progenitor cells from the compartment region stop neurogenesis upon ectopic expression of Hes1. Here, using dominance analysis, we find that reversing the direction of change of KdHcm potentially prevents the cell from undergoing differentiation via other molecular mechanisms. Our simulation result is reminiscent of the ectopic expression of Hes1 stated above.

4.8. The unexpected behavior of KdMcm (degradation rate of Mcm)

KdHcm and KdMcm were suggested to be the parameters that enable the cell state transition (Kiparissides et al., 2011). miR-181a was recently suggested to downregulate Mash1 (Guibinga et al., 2012). In SSA, a KdHcm increase resulted in a 10-fold increase in both Mcp and Hcp levels. After a 100-fold increase in KdHcm, the Hcp value drops significantly. On the other hand, the decrease in KdMcm increases the Mcp level and simultaneously increases the Hcp level. Our SSA data suggest that the simultaneous change in both KdHcm and KdMcm does not induce the cell state change (data not shown). Instead, we suggest a possible combination of KdMcm and KniHcp.

The potential molecular mechanism predicted by simulation studies is summarized in Table 5. The potential molecular mechanisms identified in this study may serve as a proxy for intrinsic or extrinsic cues (Artavanis-Tsakonas et al., 1999; Poellinger and Lendahl, 2008) to engender the determination of cell fate. The list will be updated after further computational and experimental validations are performed in single or multiple cell models to improve our understanding of Notch signaling. Potential molecular mechanisms can be validated by siRNA or morpholino targeting, for example, the protein degradation machinery or nuclear transport apparatus.

Table 5.

Potential Molecular Mechanisms That Enable the Cell State Transition

Parametera Definition Mediatorb Involved mechanismc Sourced
KdHcm Degradation rate of Hes1 mRNA miR-9 mRNA stability Kiparissides et al. (2011) and this study
KdNm Degradation rate of Notch mRNA miR-34a mRNA stability This study
KdNp Degradation rate of cytoplasmic Notch protein Numb Ubiquitination-mediated proteolysis Barton and Fendrik (2013) and this study
Ka RBP-Jk NICD association constant   Competition This study
Ka_r RBP-Jk NICD dissociation constant   Competition This study
KniHcp Nuclear transport rate of cytoplasmic Hes1 protein   Nuclear transport This study
KfNcp Forward rate of generation of NICD (Ncp) upon binding of Np to Delta Pin1 Gamma-secretase activity This study
KdMcm Degradation rate of Mash1 mRNA miR-181a mRNA stablility Kiparissides et al. (2011) and this study
  Mash1 cellular protein-E47 dissociation constant     Kiparissides et al. (2011)
  Delta-Notch cis-interaction     Sprinzak et al. (2011), Sprinzak et al. (2010), Shaya and Sprinzak (2011)
Open in a new tab
a

Parameters that have the potential to induce the cell state transition from stem cell to differentiation.

b

Possible mediator causing the regulation.

c

The mechanism through which mediator acts.

d

Reference ID.

Supplementary Material

Supplemental data
Supp_TableS1.zip (15.6KB, zip)
Supplemental data
Supp_TableS2.zip (10.1KB, zip)
Supplemental data
Supp_TableS3.zip (10.7KB, zip)
Supplemental data
Supp_TableS4.zip (15.3KB, zip)
Supplemental data
Supp_TableS5.zip (9.1KB, zip)

Acknowledgments

The authors thank Dr. Smita Agrawal and Dr. David Schaffer for the sharing of the computer codes and discussion. This work was supported by the National Science Council, Taiwan, R.O.C. (Grant Nos. NSC 95-2113-M-019-003, NSC 96-2627-B-019-002, NSC 97-2627-B-019-002, NSC 98-2627-B-019-002, NSC 98-2313-B-019-004-MY3, NSC 101-2311-B-019-001, NSC 102-2627-B-019-002-, NSC 102-2633-B-019-001), and the Center of Excellence for the Oceans, National Taiwan Ocean University.

Author Disclosure Statement

No competing financial interests exist.

References

  1. Agrawal S., Archer C., and Schaffer D.V.2009. Computational models of the Notch network elucidate mechanisms of context-dependent signaling. PLoS Comput. Biol. 5, e100039019468305 [Google Scholar]
  2. Amakawa R., Jing W., Ozawa K., et al. 1993. Human Jk recombination signal binding protein gene (IGKJRB): comparison with its mouse homologue. Genomics 17, 306–3158406481 [Google Scholar]
  3. Andersson E.R., Sandberg R., and Lendahl U.2011. Notch signaling: simplicity in design, versatility in function. Development 138, 3593–361221828089 [Google Scholar]
  4. Artavanis-Tsakonas S., and Muskavitch M.A.2010. Notch: the past, the present, and the future. Curr. Top. Dev. Biol. 92, 1–2920816391 [Google Scholar]
  5. Artavanis-Tsakonas S., Rand M.D., and Lake R.J.1999. Notch signaling: Cell fate control and signal integration in development. Science 284, 770–77610221902 [Google Scholar]
  6. Bae S., Bessho Y., Hojo M., and Kageyama R.2000. The bHLH gene Hes6, an inhibitor of Hes1, promotes neuronal differentiation. Development 127, 2933–294310851137 [Google Scholar]
  7. Baek J.H., Hatakeyama J., Sakamoto S., et al. 2006. Persistent and high levels of Hes1 expression regulate boundary formation in the developing central nervous system. Development 133, 2467–247616728479 [Google Scholar]
  8. Barrio M., Burrage K., Leier A., and Tian T.2006. Oscillatory regulation of Hes1: discrete stochastic delay modelling and simulation. PLoS Comput. Biol. 2, e11716965175 [Google Scholar]
  9. Barton A., and Fendrik A.J.2013. Sustained vs. oscillating expressions of Ngn2, Dll1 and Hes1: a model of neural differentiation of embryonic telencephalon. J. Theor. Biol. 328, 1–823499991 [Google Scholar]
  10. Bernard F., Krejci A., Housden B., et al. 2010. Specificity of Notch pathway activation: twist controls the transcriptional output in adult muscle progenitors. Development 137, 2633–264220610485 [Google Scholar]
  11. Betschinger J., Nichols J., Dietmann S., et al. 2013. Exit from pluripotency is gated by intracellular redistribution of the bHLH transcription factor Tfe3. Cell 153, 335–34723582324 [Google Scholar]
  12. Bonev B., Stanley P., and Papalopulu N.2012. MicroRNA-9 modulates Hes1 ultradian oscillations by forming a double-negative feedback loop. Cell Rep. 2, 10–1822840391 [Google Scholar]
  13. Borggrefe T., and Liefke R.2012. Fine-tuning of the intracellular canonical Notch signaling pathway. Cell Cycle 11, 264–27622223095 [Google Scholar]
  14. Brou C., Logeat F., Lecourtois M., et al. 1994. Inhibition of the DNA-binding activity of Drosophila suppressor of hairless and of its human homolog, KBF2/RBP-J kappa, by direct protein-protein interaction with Drosophila hairless. Genes Dev. 8, 2491–25037958912 [Google Scholar]
  15. Campanelli M., and Gedeon T.2010. Somitogenesis clock-wave initiation requires differential decay and multiple binding sites for clock protein. PLoS Comput. Biol. 6, e100072820369016 [Google Scholar]
  16. Cayouette M., and Raff M.2002. Asymmetric segregation of Numb: a mechanism for neural specification from Drosophila to mammals. Nat. Neurosci. 5, 1265–126912447381 [Google Scholar]
  17. Chen H., Thiagalingam A., Chopra H., et al. 1997. Conservation of the Drosophila lateral inhibition pathway in human lung cancer: a hairy-related protein (HES-1) directly represses achaete-scute homolog-1 expression. Proc. Natl. Acad. Sci. USA 94, 5355–53609144241 [Google Scholar]
  18. Cinquin O.2007. Repressor dimerization in the zebrafish somitogenesis clock. PLoS Comput. Biol. 3, e3217305423 [Google Scholar]
  19. Collier J.R., Monk N.A., Maini P.K., and Lewis J.H.1996. Pattern formation by lateral inhibition with feedback: a mathematical model of delta-notch intercellular signalling. J. Theor. Biol. 183, 429–4469015458 [Google Scholar]
  20. Fineberg S.K., Datta P., Stein C.S., and Davidson B.L.2012. MiR-34a represses Numbl in murine neural progenitor cells and antagonizes neuronal differentiation. PLoS One 7, e3856222701667 [Google Scholar]
  21. Foltz D.R., and Nye J.S.2001. Hyperphosphorylation and association with RBP of the intracellular domain of Notch1. Biochem. Biophys. Res. Commun. 286, 484–49211511084 [Google Scholar]
  22. Gillespie D.T.2001. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115, 1716–1733 [Google Scholar]
  23. Gillespie D.T.2007. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–5517037977 [Google Scholar]
  24. Gilman A., and Arkin A.P.2002. Genetic “code”: representations and dynamical models of genetic components and networks. Annu. Rev. Genomics Hum. Genet. 3, 341–36912142360 [Google Scholar]
  25. Giot L., Bader J.S., Brouwer C., et al. 2003. A protein interaction map of Drosophila melanogaster. Science 302, 1727–173614605208 [Google Scholar]
  26. Gotz A.W., Williamson M.J., Xu D., et al. 2012. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 8, 1542–155522582031 [Google Scholar]
  27. Guibinga G.H., Hrustanovic G., Bouic K., et al. 2012. MicroRNA-mediated dysregulation of neural developmental genes in HPRT deficiency: clues for Lesch-Nyhan disease? Hum. Mol. Genet. 21, 609–62222042773 [Google Scholar]
  28. Guruharsha K.G., Kankel M.W., and Artavanis-Tsakonas S.2012. The Notch signalling system: recent insights into the complexity of a conserved pathway. Nat. Rev. Genet. 13, 654–66622868267 [Google Scholar]
  29. Hirata H., Yoshiura S., Ohtsuka T., et al. 2002. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop. Science 298, 840–84312399594 [Google Scholar]
  30. Huttner W.B., and Kosodo Y.2005. Symmetric versus asymmetric cell division during neurogenesis in the developing vertebrate central nervous system. Curr. Opin. Cell Biol. 17, 648–65716243506 [Google Scholar]
  31. Jarriault S., Brou C., Logeat F., et al. 1995. Signalling downstream of activated mammalian Notch. Nature 377, 355–3587566092 [Google Scholar]
  32. Kageyama R., Niwa Y., Shimojo H., et al. 2010. Ultradian oscillations in Notch signaling regulate dynamic biological events. Curr. Top. Dev. Biol. 92, 311–33120816400 [Google Scholar]
  33. Kageyama R., Ohtsuka T., Hatakeyama J., and Ohsawa R.2005. Roles of bHLH genes in neural stem cell differentiation. Exp. Cell Res. 306, 343–34815925590 [Google Scholar]
  34. Kageyama R., Ohtsuka T., and Kobayashi T.2007. The Hes gene family: repressors and oscillators that orchestrate embryogenesis. Development 134, 1243–125117329370 [Google Scholar]
  35. Kageyama R., Ohtsuka T., Shimojo H., and Imayoshi I.2009. Dynamic regulation of Notch signaling in neural progenitor cells. Curr. Opin. Cell Biol. 21, 733–74019783418 [Google Scholar]
  36. Kankel M.W., Hurlbut G.D., Upadhyay G., et al. 2007. Investigating the genetic circuitry of mastermind in Drosophila, a notch signal effector. Genetics 177, 2493–250518073442 [Google Scholar]
  37. Kao H.Y., Ordentlich P., Koyano-Nakagawa N., et al. 1998. A histone deacetylase corepressor complex regulates the Notch signal transduction pathway. Genes Dev. 12, 2269–22779694793 [Google Scholar]
  38. Kiparissides A., Koutinas M., Moss T., et al. 2011. Modelling the Delta1/Notch1 pathway: in search of the mediator(s) of neural stem cell differentiation. PLoS One 6, e1466821346804 [Google Scholar]
  39. Kobayashi T., Mizuno H., Imayoshi I., et al. 2009. The cyclic gene Hes1 contributes to diverse differentiation responses of embryonic stem cells. Genes Dev. 23, 1870–187519684110 [Google Scholar]
  40. Koch U., Lehal R., and Radtke F.2013. Stem cells living with a Notch. Development 140, 689–70423362343 [Google Scholar]
  41. Kovall R.A.2007. Structures of CSL, Notch and Mastermind proteins: piecing together an active transcription complex. Curr. Opin. Struct. Biol. 17, 117–12717157496 [Google Scholar]
  42. Kovall R.A., and Blacklow S.C.2010. Mechanistic insights into Notch receptor signaling from structural and biochemical studies. Curr. Top. Dev. Biol. 92, 31–7120816392 [Google Scholar]
  43. Koyano-Nakagawa N., Kim J., Anderson D., and Kintner C.2000. Hes6 acts in a positive feedback loop with the neurogenins to promote neuronal differentiation. Development 127, 4203–421610976052 [Google Scholar]
  44. Lai K., Robertson M.J., and Schaffer D.V.2004. The sonic hedgehog signaling system as a bistable genetic switch. Biophys. J. 86, 2748–275715111393 [Google Scholar]
  45. Lewis J.2003. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol. 13, 1398–140812932323 [Google Scholar]
  46. Lewis J., Hanisch A., and Holder M.2009. Notch signaling, the segmentation clock, and the patterning of vertebrate somites. J. Biol. 8, 4419486506 [Google Scholar]
  47. Liu W.G., Schmidt B., and Muller-Wittig W.2011. CUDA-BLASTP: accelerating BLASTP on CUDA-enabled graphics hardware. IEEE-ACM Trans. Comput. Biol. Bioinform. 8, 1678–1684 [Google Scholar]
  48. Matsumoto M., and Nishimura T.1998. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 8, 3–30 [Google Scholar]
  49. Mazzone M., Selfors L.M., Albeck J., et al. 2010. Dose-dependent induction of distinct phenotypic responses to Notch pathway activation in mammary epithelial cells. Proc. Natl. Acad. Sci. USA 107, 5012–501720194747 [Google Scholar]
  50. McGill M.A., Dho S.E., Weinmaster G., and McGlade C.J.2009. Numb regulates post-endocytic trafficking and degradation of Notch1. J. Biol. Chem. 284, 26427–2643819567869 [Google Scholar]
  51. McGill M.A., and McGlade C.J.2003. Mammalian numb proteins promote notch1 receptor ubiquitination and degradation of the notch1 intracellular domain. J. Biol. Chem. 278, 23196–2320312682059 [Google Scholar]
  52. Monk N.A.2003. Oscillatory expression of Hes1, p53, and NF-kappaB driven by transcriptional time delays. Curr. Biol. 13, 1409–141312932324 [Google Scholar]
  53. Mummery-Widmer J.L., Yamazaki M., Stoeger T., et al. 2009. Genome-wide analysis of Notch signalling in Drosophila by transgenic RNAi. Nature 458, 987–99219363474 [Google Scholar]
  54. Nakamura K., Kosugi I., Lee D.Y., et al. 2012. Prolyl isomerase Pin1 regulates neuronal differentiation via beta-catenin. Mol. Cell Biol. 32, 2966–297822645310 [Google Scholar]
  55. Nam Y., Sliz P., Song L.Y., et al. 2006. Structural basis for cooperativity in recruitment of MAML coactivators to Notch transcription complexes. Cell 124, 973–98316530044 [Google Scholar]
  56. Nishi M., Akutsu H., Masui S., et al. 2011. A distinct role for Pin1 in the induction and maintenance of pluripotency. J. Biol. Chem. 286, 11593–1160321296877 [Google Scholar]
  57. Perdigoto C.N., and Bardin A.J.2013. Sending the right signal: Notch and stem cells. Biochim. Biophys. Acta 1830, 2307–232222917651 [Google Scholar]
  58. Poellinger L., and Lendahl U.2008. Modulating Notch signaling by pathway-intrinsic and pathway-extrinsic mechanisms. Curr. Opin. Genet. Dev. 18, 449–45418722525 [Google Scholar]
  59. Rustighi A., Tiberi L., Soldano A., et al. 2009. The prolyl-isomerase Pin1 is a Notch1 target that enhances Notch1 activation in cancer. Nat. Cell Biol. 11, 133–14219151708 [Google Scholar]
  60. Saj A., Arziman Z., Stempfle D., et al. 2010. A combined ex vivo and in vivo RNAi screen for notch regulators in Drosophila reveals an extensive notch interaction network. Dev. Cell 18, 862–87620493818 [Google Scholar]
  61. Scheffer D., Sage C., Corey D.P., and Pingault V.2007. Gene expression profiling identifies Hes6 as a transcriptional target of ATOH1 in cochlear hair cells. FEBS Lett. 581, 4651–465617826772 [Google Scholar]
  62. Schroter C., Ares S., Morelli L.G., et al. 2012. Topology and dynamics of the zebrafish segmentation clock core circuit. PLoS Biol. 10, e100136422911291 [Google Scholar]
  63. Shalaby N.A., Parks A.L., Morreale E.J., et al. 2009. A screen for modifiers of notch signaling uncovers Amun, a protein with a critical role in sensory organ development. Genetics 182, 1061–107619448274 [Google Scholar]
  64. Shaya O., and Sprinzak D.2011. From Notch signaling to fine-grained patterning: modeling meets experiments. Curr. Opin. Genet. Dev. 21, 732–73921862316 [Google Scholar]
  65. Shen Q., Zhong W., Jan Y.N., and Temple S.2002. Asymmetric Numb distribution is critical for asymmetric cell division of mouse cerebral cortical stem cells and neuroblasts. Development 129, 4843–485312361975 [Google Scholar]
  66. Shimojo H., Ohtsuka T., and Kageyama R.2008. Oscillations in notch signaling regulate maintenance of neural progenitors. Neuron 58, 52–6418400163 [Google Scholar]
  67. Shimojo H., Ohtsuka T., and Kageyama R.2011. Dynamic expression of notch signaling genes in neural stem/progenitor cells. Front. Neurosci. 5, 7821716644 [Google Scholar]
  68. Sprinzak D., Lakhanpal A., Lebon L., et al. 2010. Cis-interactions between Notch and Delta generate mutually exclusive signalling states. Nature 465, 86–9020418862 [Google Scholar]
  69. Sprinzak D., Lakhanpal A., Lebon L., et al. 2011. Mutual inactivation of notch receptors and ligands facilitates developmental patterning. PLoS Comput. Biol. 7, e100206921695234 [Google Scholar]
  70. Takebayashi K., Sasai Y., Sakai Y., et al. 1994. Structure, chromosomal locus, and promoter analysis of the gene encoding the mouse helix-loop-helix factor HES-1. Negative autoregulation through the multiple N box elements. J. Biol. Chem. 269, 5150–51567906273 [Google Scholar]
  71. Tan S.L., Ohtsuka T., Gonzalez A., and Kageyama R.2012. MicroRNA9 regulates neural stem cell differentiation by controlling Hes1 expression dynamics in the developing brain. Genes Cells 17, 952–96123134481 [Google Scholar]
  72. Wang H., Zou J., Zhao B., et al. 2011. Genome-wide analysis reveals conserved and divergent features of Notch1/RBPJ binding in human and murine T-lymphoblastic leukemia cells. Proc. Natl. Acad. Sci. USA 108, 14908–1491321737748 [Google Scholar]
  73. Wilkinson D.J.2009. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 10, 122–13319139763 [Google Scholar]
  74. Wilkinson D.J.2012. Stochastic Modelling for Systems Biology. CRC Press/Taylor & Francis, Boca Raton, FL [Google Scholar]
  75. Wilson J.J., and Kovall R.A.2006. Crystal structure of the CSL-Notch-Mastermind ternary complex bound to DNA. Cell 124, 985–99616530045 [Google Scholar]
  76. Wingender E.2008. The TRANSFAC project as an example of framework technology that supports the analysis of genomic regulation. Brief Bioinform. 9, 326–33218436575 [Google Scholar]
  77. Wu J., Hong B., Takeda T., and Guo J.T.2012. High performance transcription factor-DNA docking with GPU computing. Proteome Sci. 10 Suppl1, S1722759575 [Google Scholar]
  78. Xie Z.R., Yang H.T., Liu W.C., and Hwang M.J.2007. The role of microRNA in the delayed negative feedback regulation of gene expression. Biochem. Biophys. Res. Commun. 358, 722–72617509530 [Google Scholar]
  79. Zheng Y., Lin L., and Zheng Z.2008. TGF-alpha induces upregulation and nuclear translocation of Hes1 in glioma cell. Cell Biochem. Funct. 26, 692–70018636433 [Google Scholar]
  80. Zhong W., and Chia W.2008. Neurogenesis and asymmetric cell division. Curr. Opin. Neurobiol. 18, 4–1118513950 [Google Scholar]
  81. Zhou S., Fujimuro M., Hsieh J.J., et al. 2000. SKIP, a CBF1-associated protein, interacts with the ankyrin repeat domain of NotchIC To facilitate NotchIC function. Mol. Cell Biol. 20, 2400–241010713164 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_TableS1.zip (15.6KB, zip)
Supplemental data
Supp_TableS2.zip (10.1KB, zip)
Supplemental data
Supp_TableS3.zip (10.7KB, zip)
Supplemental data
Supp_TableS4.zip (15.3KB, zip)
Supplemental data
Supp_TableS5.zip (9.1KB, zip)

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES