Temporal and Spatial Temperature Measurement in Insulator-Based Dielectrophoretic Devices

Abstract

Insulator-based dielectrophoresis is a relatively new analytical technique with a large potential for a number of applications, such as sorting, separation, purification, fractionation, and preconcentration. The application of insulator-based dielectrophoresis (iDEP) for biological samples, however, requires the precise control of the microenvironment with temporal and spatial resolution. Temperature variations during an iDEP experiment are a critical aspect in iDEP since Joule heating could lead to various detrimental effects hampering reproducibility. Additionally, Joule heating can potentially induce thermal flow and more importantly can degrade biomolecules and other biological species. Here, we investigate temperature variations in iDEP devices experimentally employing the thermosensitive dye Rhodamin B (RhB) and compare the measured results with numerical simulations. We performed the temperature measurement experiments at a relevant buffer conductivity range commonly used for iDEP applications under applied electric potentials. To this aim, we employed an in-channel measurement method and an alternative method employing a thin film located slightly below the iDEP channel. We found that the temperature does not deviate significantly from room temperature at 100 μS/cm up to 3000 V applied such as in protein iDEP experiments. At a conductivity of 300 μS/cm, such as previously used for mitochondria iDEP experiments at 3000 V, the temperature never exceeds 34 °C. This observation suggests that temperature effects for iDEP of proteins and mitochondria under these conditions are marginal. However, at larger conductivities (1 mS/cm) and only at 3000 V applied, temperature increases were significant, reaching a regime in which degradation is likely to occur. Moreover, the thin layer method resulted in lower temperature enhancement which was also confirmed with numerical simulations. We thus conclude that the thin film method is preferable providing closer agreement with numerical simulations and further since it does not depend on the iDEP channel material. Overall, our study provides a thorough comparison of two experimental techniques for direct temperature measurement, which can be adapted to a variety of iDEP applications in the future. The good agreement between simulation and experiment will also allow one to assess temperature variations for iDEP devices prior to experiments.

Dielectrophoresis (DEP) is a powerful technique often implemented in microfluidic platforms and has shown to serve as a versatile tool in many bioanalytical applications for cells, organelles, crystals, and biomolecules.¹⁻⁴ The analytical applications span a number of methods such as separation, fractionation, purification, preconcentration, and sorting. DEP is referred to as translational motion of a particle or biomolecule under the influence of an inhomogeneous electric field. The electric field gradients necessary for the occurrence of DEP can be created mainly by integrating microelectrodes on a substrate⁵ or insulating topological structures integrated within a microfluidic channel, named insulator-based dielectrophoresis (iDEP).^6,7

The application of iDEP has been demonstrated with a variety of designs including constrictions with various shapes,⁸⁻¹⁰ oil droplets,¹¹ insulating post arrays with various geometries,¹²⁻²¹ sawtooth devices,^22,23 and serpentine channels.²⁴ With iDEP devices, problems prevalent to electrode based DEP, such as electrode fouling and electrode reactions interfering with DEP, can be eliminated in the regions where DEP occurs.

Despite the aforementioned advantages over the electrode-based applications, iDEP requires relatively high applied potentials to create significant electric field gradients necessary to manipulate sub-μm particles or even biomolecules. The application of high electric fields leads to Joule heating which may result in temperature elevation within the device. Elevated temperatures can have detrimental influence on biological analytes of interest by affecting their viability, biological functionality, and/or stability. Moreover, one would expect a higher temperature rise at the regions of the localized electric field (e.g., constrictions) in iDEP devices due to the large applied electric fields in the order of several hundred up to a few thousand volts necessary to manipulate sub-μm biological objects such as organelles or biomolecules. For example, numerical simulations performed previously by our group showed that the magnitude of the electric field within iDEP devices can reach up to 10⁶ V/m and corresponding electric field gradients amount in as high as 10¹⁷ V²/m³.²⁵ Arising temperature gradients may create an additional electrothermal flow interfering with DEP. For the aforementioned reasons, most experimental iDEP studies have been performed with low conductivity buffers. Although some work has been reported with high conductivity buffers or even physiological buffers,²⁶⁻²⁹ the direct influence of Joule heating on samples has to be alleviated in some ways. Nevertheless, the degree of Joule heating mostly depends on the buffer conductivity, applied potential, device dimension, and insulating structure geometries. Therefore, for realization of iDEP as a reliable analytical tool, it is of extreme importance to monitor and control temperature within the device.

A variety of methods has been employed to measure temperature in microfluidic devices, such as integrated thermocouples,³⁰⁻³³ resistive sensors,³⁴ NMR thermometry,³⁵ or IR thermography.³⁴ These methods are either hampered by low spatial resolution or as in the case of IR thermography can only assess the temperature on the outer surface of the device. Assessing temperature with high spatial resolution can be achieved by addition of thermosensitive substances to the working solutions such as liquid crystalline probes,³⁶⁻³⁸ semiconductor nanocrystals,^39,40 and dyes with temperature dependent optical properties.⁴¹⁻⁴³ Rhodamine B (RhB) is the most commonly used temperature sensitive dye which exhibits strong temperature dependent fluorescence in the range of 0–100 °C.⁴⁴ However, a serious issue arises when RhB is used for polymer-based devices such as poly(dimethylsiloxane) (PDMS), commonly used for microfluidic applications. Small hydrophobic analytes such as RhB are known to strongly adsorb on the PDMS surface and diffuse into the PDMS due to its hydrophobic nature.⁴⁵ Such dye adsorption leads to the fluctuation of the baseline fluorescence intensity, resulting in false temperature reading.

In the past, RhB incompatibility with PDMS was overcome by dynamic coating of PDMS with chemical agents, such as a nonionic surfactant Triton X-100 at high concentrations,⁴⁶ sodium dodecyl sulfate,⁴⁷ Polybrene solution,⁴⁸ a combination of ionic liquid and nonionic surfactant,⁴⁹ and the immobilization of ∼10 nm SiO₂ particles onto the PDMS surface.⁵⁰ The undesirable fluorescence signal derived from the adsorbed dye can also be distinguished from the dye in free solution and eliminated by using fluorescence lifetime imaging.⁵¹ Moreover, Samy et al.⁵² employed an assembly where thin PDMS saturated with RhB is sandwiched in between two glass slides. By introducing such assembly, RhB can be physically separated from the PDMS surface, therefore completely eliminating the adsorption problem.

Temperature changes for DEP applications have been investigated previously. While experimental measurements were reported for eDEP,^34,53 Joule heating effects have not yet been assessed experimentally in iDEP to the best of our knowledge. In iDEP, several studies assessed temperature in iDEP devices with theoretical models. For example, Hawkins et al. investigated Joule heating and the effect of the resultant electrothermal flow in iDEP.⁵⁴ The influence of Joule heating on electroosmotic flow was discussed by Sridharan et al. where the temperature field was solved using numerical simulations.⁵⁵ Another example was performed by Chaurey et al. where temperature rise in a nanoconstriction device was numerically simulated.⁵⁶ Recently, Gallo-Villanueva et al. reported a temperature increase obtained from numerical simulations in PDMS iDEP devices.⁵⁷ Additionally, Zhu et al. demonstrated that the Joule heating effect reduces the particle focusing and trapping due to DEP. However, the extent of temperature rise due to Joule heating was not reported in their work.⁵⁸

In this work, we experimentally investigate fluorescence thermometry using RhB dye for iDEP applications in PDMS/glass hybrid devices with two methods. The first method enables in-channel temperature measurement by introducing a zwitterionic additive to the buffer in order to prevent RhB adsorption onto the PDMS microchannel surface. For the second method, we adapted the sandwich approach by Samy et al.,⁵² where temperature was measured on a thin film of PDMS located about 150 μm below the iDEP channel. Results from both methods show similar temporal temperature variation trends; however, the sandwich method provides ∼20 °C smaller temperature change than the in-channel measurement method. In addition, we present a numerical model, which is in excellent agreement with the experimental results. Furthermore, we applied this temperature measurement technique to the same conditions as previously employed to study iDEP behavior of mitochondria. Our study revealed that the temperature changes are marginal for low conductivity buffers, and therefore, the viability of mitochondria and other biological species is not significantly influenced through temperature variations in iDEP.

Experimental Section

Chemicals and Materials

Si wafers (5 in.) were obtained from University Wafer. The negative photoresist SU-8 2007 and developer were purchased from Microchem (Newton, MA, USA). (Tridecafluoro-1,1,2,2-tetrahydrooctyl)dimethylchlorosilane (TDTS) was purchased from Gelest (Morrisville, PA, USA). Sylgard184, composed of the silicon elastomer base and the curing agent for poly(dimethylsiloxane) (PDMS) was obtained from Dow Corning Corporation (Midland, MI, USA). Rhodamine B, 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES), poly(ethylene glycol)-block-poly(propylene glycol)-block-poly(ethylene glycol) (F108), potassium hydroxide, sucrose, potassium phosphate monobasic, sodium phosphate dibasic, and 3-[(3-Cholamidopropyl)dimethylammonio]-1-propanesulfonate (CHAPS) were purchased from Sigma-Aldrich (St. Louis, MO, USA). Deionized water was supplied from a Synergy purification system (Millipore, USA).

Microchip Fabrication

As shown schematically in Figure 1, the microfluidic device has dimensions of 100 μm width and 10 μm height with triangular insulating post arrays integrated in the 1 cm long channel. The device was fabricated with standard photo and soft lithographic techniques as described previously.¹² For in-channel temperature measurement experiments (method A), the resultant PDMS piece as well as a precleaned 150 μm thick glass slide was treated with oxygen plasma (PDC-001 Harrick Plasma, Harrick, USA) for 60 s at the highest RF setting to obtain a tight seal. For temperature measurement experiments using a thin film of PDMS doped in RhB (method B), we followed the experimental procedures previously reported.⁵²

Figure 1.

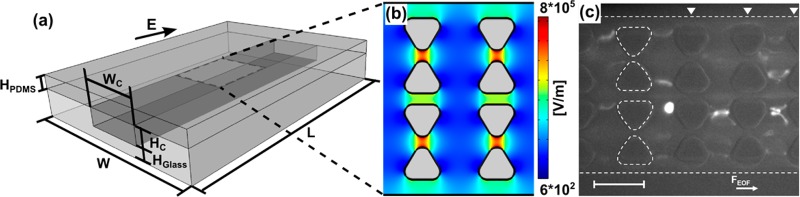
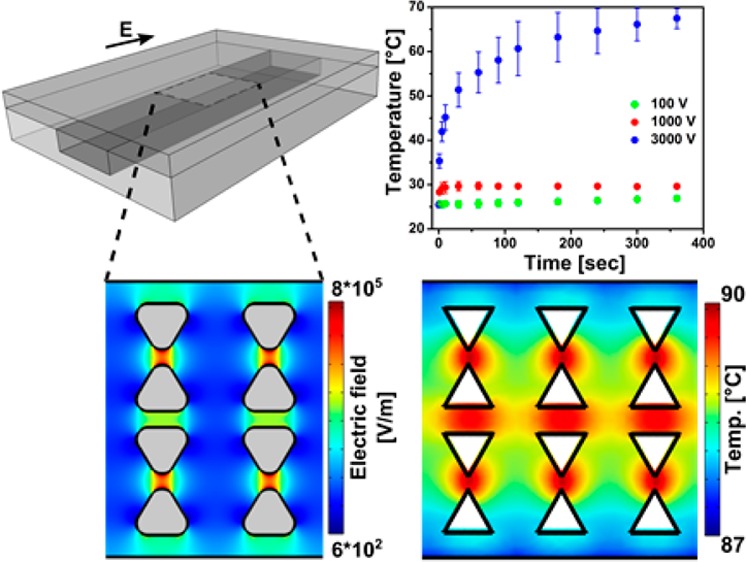
(a) Schematic of the iDEP microfluidic device (not to scale). The arrow represents the direction of applied electric field (E). Sizes shown are the actual device dimensions (without reservoirs for simplification) used for the experiments and applied to the numerical modeling. The dimensions are the following: L (device length) = 1 cm, W (device width) = 2 cm, W_c (channel width) = 100 μm, H_c (channel depth) = 10 μm, H_glass (thickness of the bottom glass slide) = 150 μm for method A and 1.15 mm for method B, and H_PDMS (thickness of the top PDMS wall) = 0.5 mm. (b) Numerically simulated electric field distribution at 3000 V/cm inside of the channel where the insulating triangular posts are integrated to create an inhomogeneous electric field necessary for DEP.(c) The result of mitochondria DEP experiment, providing a fluorescence microscopy image of mitochondria obtained under DC conditions at 3000 V/cm. White dash lines indicate the edges of the channel and that of a row of posts, and the other rows of posts are indicated by triangles. Scale bar is 30 μm.

Temperature Measurement Experiments with iDEP Devices

For method A, the assembled iDEP channel was filled with the desired buffers. Three different buffers were tested: pH 8 phosphate buffer at conductivity of 100 μS/cm, pH 8 phosphate buffer at 1 mS/cm conductivity, and Buffer B (see Supporting Information for the buffer composition) at 300 μS/cm to examine the temperature rise under the same conditions used in mitochondria iDEP experiments. To each buffer, 10 μg/mL RhB and 25 mg/mL CHAPS were added for method A. For method B, the iDEP channel was filled with the buffer after assembly. To compare with the result from method A, the phosphate buffers at the same conductivities (100 μS/cm and 1 mS/cm) were used. For both methods A and B, fluorescence intensities were recorded upon the application of potentials between the inlet and outlet. For each applied potential, experiments were repeated three times to test reproducibility. For each trial, a single nominal temperature value was calculated by averaging the temperature from the entire channel within the image. The average temperature values from three trials were plotted as a function of duration of potential application.

Temperature Calibration

To determine the correlation between the fluorescence intensities of RhB and the corresponding temperature change, two sets of experiments were performed for each temperature measurement methodology. The detailed experimental protocol is found in the Supporting Information. For both methods, images were acquired at various temperatures from room temperature up to ∼90 °C. For the calibration curve, the fluorescent intensity measured at each temperature was normalized with the intensity measured at room temperature. The resultant data sets (normalized intensity vs temperature) were fitted with a third order polynomial, as was previously performed for temperature measurement with RhB.⁴¹

Detection and Data Analysis

RhB fluorescence intensity was recorded either in the microchannel (method A) or in a sandwiched thin PDMS layer underneath the microchannel (method B). For fluorescence microscopy imaging, an inverted microscope (IX 71, Olympus, USA) with a 40× objective (Olympus, USA), a mercury burner (U-RFL-T, Olympus, USA), and an appropriate fluorescent filter set (Olympus, USA) containing a 531/40 nm exciter, 562 nm dichroic, and 593/40 nm emitter was used. Throughout the experiments, two neutral density filters of 12% and 25% were used in order to reduce the excitation light from the source. In addition, sample exposure to the incoming light was controlled by using an automatic shutter (Prior scientific, MA, USA) in order to minimize photobleaching of the dye. Images were acquired at 10 ms/frame for the calibration experiments and 100 ms/frame for the measurement in the microfluidic devices using a CCD camera (Quantum 512 SC, Photometrics, USA) and Micro-Manager software (University of California, USA). Resultant images were analyzed with ImageJ software (version 1.43).

Results and Discussion

A typical iDEP structure is schematically shown in Figure 1. We have performed iDEP experiments with biomolecules such as DNA⁵⁹ and proteins^12,13 previously with similar structures and more recently studied the iDEP behavior of cell organelles such as mitochondria in similar devices. Figure 1b provides a top view of the iDEP devices and the corresponding electric field strength simulated numerically. A DEP force acts on particles in the presence of inhomogeneous electric fields. Figure 1c shows a snapshot of the iDEP trapping of semimembranosus muscle mitochondria labeled with MitoTracker Green under DC conditions in a triangular post device. These experiments were carried out as described in a previous work⁶⁰ as well as in the Supporting Information at a medium pH of ∼7.4 and 300 μS/cm conductivity.⁶⁰ As shown in Figure 1c, we observed negative DEP of mitochondria under DC conditions with the application of 3000 V for a 1 cm channel. The mitochondria showed three different modes of iDEP, related to wiggling in-between posts, trap hopping, or iDEP trapping. Such effects could arise due to aggregates of mitochondria exhibiting different DEP properties than the single mitochondrion. The formation of aggregates might be triggered by temperature increases under iDEP operation. In the following, we thus assess temperature changes related to DC iDEP applications. We compare experimental observations with numerical simulations and test two different methods to measure temperature.

Calibration of the Temperature Dependent Dye

We utilized the temperature dependent fluorescence of RhB dye to probe temperature within the iDEP device. We chose RhB due to its temperature dependent quantum yield in a wide temperature range (0–100 °C), and it is insensitive to pH changes over a solution pH above 6.⁴⁴ The latter point is important especially when using low ionic strength buffers commonly used in iDEP applications since the buffers are susceptible to the pH change within the order of ∼10 min under the application of large electric fields.⁶¹

First, a calibration curve was constructed to determine the dependency of fluorescence intensity on temperature. As described in the Experimental Section, we examined two methods: method A and method B (see Figure 2). Therefore, each method required a separate temperature calibration. For method A, RhB was directly added to the working solution and its temperature dependent fluorescence intensity was measured in a large chamber (1 mL in volume) where the solution temperature was carefully controlled. For method B, a thin layer of PDMS was first spin coated on a glass slide and cured to form a thin film. Subsequently, the PDMS film was saturated with RhB dye by immersing it in 1 mM RhB dye solution. The calibration experiment for method B was performed by directly heating the thin PDMS film and measuring the fluorescence intensities at various temperatures. For both methods, the resulting fluorescence intensities measured at each temperature were normalized to 25 °C and plotted as a function of temperature. The obtained data sets were fit with a third order polynomial for method A (eq 1) and method B (eq 2); see Figure S1, Supporting Information:

1

2

where T is temperature (in °C) and x is the normalized intensity.

Figure 2.

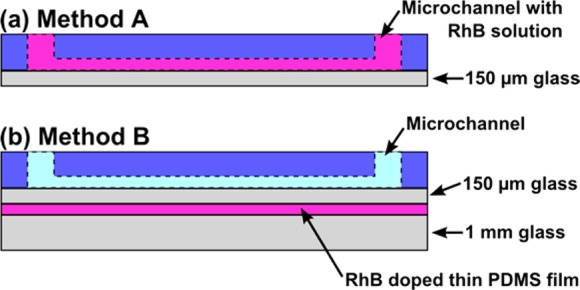
Schematic representation of two methodologies employed to measure temperature in iDEP microfluidic devices. The 2D schematics correspond to the cross-section view of the iDEP device shown in Figure 1 (not to scale). (a) In method A, the channel (dotted line) is filled with the RhB containing buffer (pink). (b) In method B, a thick and thin glass slide sandwich the RhB doped thin PDMS film located 150 μm below the channel. Channel is filled with the desired working buffer which does not contain RhB (light blue).

We confirmed that the temperature dependent fluorescence occurs reversibly by performing the calibration experiment with increasing as well as decreasing temperature. Both calibration curves (see Supporting Information) were similar to the previously reported results by Ross et al.⁴¹ for the in-channel calibration curve and Samy et al.⁵² for the thin-film calibration.

The Choice of Buffer Additive for In-Channel Temperature Measurements

Using the aforementioned calibration curves, we measured temperature changes within our iDEP device by monitoring the fluctuation of the fluorescence intensity. First, the in-channel temperature measurement was performed by adding RhB dye to the working buffer. Note that RhB is known to be incompatible with the hydrophobic PDMS surfaces on which RhB tends to adsorb strongly.⁴⁵ Indeed, when using unmodified PDMS, we observed an increase of the baseline fluorescence intensity even without applying potential, which translates to a temperature decline below room temperature. Since this is physically highly unlikely, we assumed it to be caused by RhB adsorption onto the PDMS surface. The amount of adsorbed dye increases over time, and the adsorption kinetics can vary depending on the conditions in the channel (e.g., temperature).⁶² Therefore, the dye adsorption onto the PDMS surface can lead to a false temperature reading.

However, when we added the zwitterionic surfactant CHAPS, the RhB adsorption was greatly suppressed. For further testing, a series of dye adsorption experiments was performed using various CHAPS concentrations within a large PDMS chamber similar to the ones used for the calibration experiment. These experiments showed that the chemical modification of the PDMS surface via CHAPS dynamic coating above its critical micelle concentration (CMC) significantly suppresses the dye adsorption onto the PDMS (data not shown). Although it has been previously demonstrated that the chemical modification of PDMS reduces RhB adsorption,^46,47 the use of CHAPS as a surface modification agent has not been reported to the best of our knowledge. Using CHAPS as a surface modification agent has several advantages for iDEP applications. First, CHAPS is known to improve protein solubility in bioanalytical applications⁶³ and has already been used for iDEP applications as an additive to reduce protein aggregation.¹² Moreover, since the sulfobetaine-type detergent CHAPS is zwitterionic and has no net charge at the pH range used in our experiments, its addition does not significantly change the overall buffer conductivity.⁶⁴ The latter point is important since relatively low conductivity buffers are commonly used for iDEP experiments and thus increasing buffer conductivity would lead to larger Joule heating effects (see below).

In-Channel Temperature Measurements (Method A)

First, in-channel temperature measurements were performed by monitoring the fluorescence intensity fluctuation with an addition of 25 mg/mL CHAPS and 10 μg/mL RhB in the same working buffer used for the mitochondria DEP experiment. Note that the severe photobleaching of the dye can lead to large intensity variations; thus, sample exposure to the incoming light was minimized by using an automated shutter. Additionally, the extent of photobeaching was assessed prior to the temperature measurement experiments by acquiring an image sequence without applying potential. Since the intensity fluctuations fall within the error obtained from the calibration measurements, we concluded that the contribution of photobleaching to the overall fluorescence intensity is negligible with this approach.

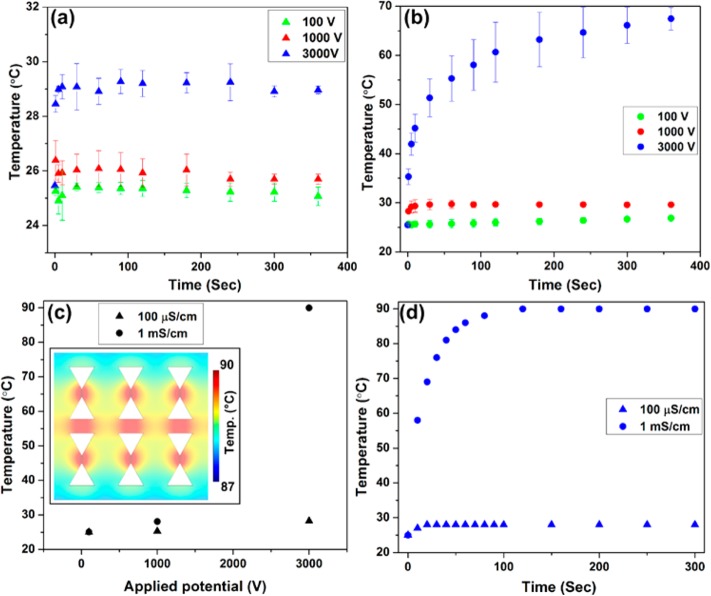
Subsequently, the maximum potential used for the mitochondria DEP experiments (3000 V for a 1 cm channel) was applied to study the maximum temperature rise within the channel using the same buffer (buffer B, 300 μS/cm conductivity) used for mitochondria DEP experiments. Figure 3 shows the temperature surface plot at time t after the initiation of the potential application. These four images at t = 22, 102, 222, and 322 s reveal that the in-channel temperature reaches the steady temperature of ∼34 °C in ∼3 min.

Figure 3.

Temperature surface plot at various times after applying a DC potential of 3000 V for a 1 cm channel using the same buffer as previously used for mitochondria DEP experiments. Temperature evolution within the iDEP channel reveals that the temperature does not exceed 34 °C. White lines indicate the edges of the channel and that of triangular insulating posts. The scale bar is 20 μm.

Next, we performed the temperature measurement within the channel at a conductivity of 100 μS/cm and 1 mS/cm prepared with phosphate buffer. Since these two conductivities are in the range of commonly used iDEP buffers, it is worthwhile to exploit the temperature change with these conditions. Our iDEP device was filled with each buffer containing 25 mg/mL CHAPS and 10 μg/mL RhB, and three different potentials (100, 1000, and 3000 V) were tested for a 1 cm channel. Figure 4a,b shows the in-channel temperature plotted as a function of duration of potential application. In theory, larger Joule heating is expected due to the localized high electric fields between the tips of the triangular posts. However, we observed that the spatial temperature variation in the vicinity of the insulating post regions is less than the temperature resolution of 1 °C estimated from the standard deviation of residuals from the polynomial fit. Furthermore, as shown in Figure 4a, the temperature increases less than 5 °C when using the 100 μS/cm conductivity buffer even with the application of the highest potential (3000 V). A significant temperature increase of up to ∼70 °C (Figure 4b) was observed only when using 1 mS/cm buffer with the highest potential of 3000 V. Figure 4a,b also shows the temporal temperature transition, demonstrating that it takes longer to reach a steady state temperature for larger applied potentials. For example, in the case of 3000 V with 1 mS/cm conductivity buffer, the temperature equilibrates at ∼70 °C after 150 s of potential application, while it takes only 5 s in the case of 1000 V with 1 mS/cm buffer. The small absolute temperature changes of ∼2 °C in the case of 100 μS/cm conditions are within the range of the experimental error (Figure 4a). The experimental method thus does not allow one to resolve the temporal temperature changes in this case.

Figure 4.

(a,b) Experimentally and (c) numerically obtained temperature resulted from Joule heating inside of the iDEP channel, tested with various conductivities and applied potentials. (a,b) Experimentally measured temporal temperature variations using a phosphate buffer with conductivity of (a) 100 μS/cm (∼0.6 mM) and (b) 1 mS/cm (∼5 mM). Three different potentials were tested for each conductivity of 100 μS/cm (triangles) and 1 mS/cm (dots): 100 V (green), 1000 V (red), and 3000 V (blue) for a 1 cm long channel. (c) Numerical simulation results showing the steady state temperatures as a function of applied potential for the buffer conductivity of 100 μS/cm (tringles) and 1 mS/cm (dots). Inset shows the spatial temperature variations, revealing that the temperature variation is ∼1.5 °C within the channel. (d) Temporal temperature variations obtained numerically for 100 μS/cm (triangles) and 1 mS/cm (dots) when 3000 V is applied.

To support the experimental results presented above, numerical simulations were performed to model the Joule heating inside of the channel as described in the Supporting Information in detail. First, steady-state simulations were performed to study the temperature reached with each set of conductivities and applied potentials. As shown in Figure 4c, the temperature rise is less than 5 °C for all cases except when 3000 V is applied with 1 mS/cm conductivity where the temperature increases significantly up to ∼90 °C. The absolute temperature increase was in excellent agreement with the experimental results at 100 and 1000 V; however, it deviated by about 20 °C for 3000 V applied at 1 mS/cm buffer conductivity. We attribute this discrepancy to the increase in RhB adsorption onto the PDMS at exceptionally high temperatures since adsorption kinetics is enhanced with increasing temperature. We also investigated the spatial temperature changes in the iDEP post regions. The temperature variation was negligible for the low conductivity and low applied potentials. The numerical simulation result with 1 mS/cm at 3000 V however shows that the highest temperature was obtained between the tips of the posts and the overall temperature varies spatially by ∼1.5 °C (see inset of Figure 4c). This variation could not be detected in experiments, since the numerically obtained temperature variations fall within the experimental error. A comprehensive table comparing experimentally measured temperature and numerical simulations is provided in the Supporting Information.

Subsequently, the temperature transitions during the potential application were investigated by performing time dependent simulations. Figure 4d provides the resultant temporal variations in temperature with the highest applied potential (3000 V) for 100 μS/cm and 1 mS/cm conductivity. The saturation temperature of ∼90 °C is higher than the experimentally obtained temperature of ∼70 °C (see Figure 4b) but similar to the steady state case (Figure 4c). Again, this discrepancy with measured temperatures can be attributed to the enhanced RhB adsorption at elevated temperatures. Moreover, we found that the numerical simulation also depends strongly on the chosen heat transfer coefficient value (h), which in turn greatly depends on the surrounding environment (i.e., air flow rate). Especially for larger temperatures, this factor can affect absolute temperature changes in the order of 10 °C. Nonetheless, we found that the time scales at which the temperature saturation occurs are similar for both experimental and simulation results. In the case of the low conductivity buffer, temperature equilibrates within a short period of time (<20 s), while it takes much longer (∼150 s) with the high conductivity buffer.

Thin-PDMS Film Temperature Measurement (Method B)

Next, we performed the temperature measurement in the iDEP device by using the thin-PDMS film methodology exploited previously.⁵² The experiment was performed using the 100 μS/cm and 1 mS/cm buffer. However, no RhB or CHAPS were added to these buffers. The change in fluorescence intensity was recorded for each applied potential (100, 1000, and 3000 V) and analyzed similarly to the previous in-channel experiment. The resulting temperature variations experimentally measured in the film located 150 μm below the channel reveal a large temperature rise up to ∼49 °C only when using 1 mS/cm conductivity at 3000 V (see in Figure 5a,b). In contrast, the temperature increase is less than 2 °C for the lower potentials (100 and 1000 V) with 1 mS/cm as well as all potentials tested with 100 μS/cm.

Figure 5.

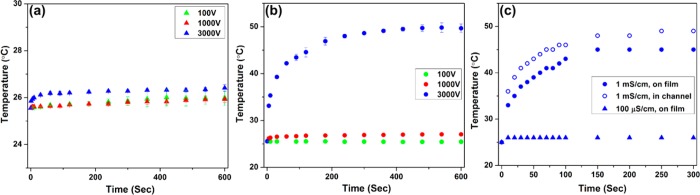
(a, b) Experimentally and (c) numerically obtained temperature resulted from Joule heating with various conductivities and applied potentials. Temperature was measured on thin PDMS film located ∼150 μm below the iDEP channel. (a, b) Experimentally measured temporal temperature variations using a phosphate buffer with conductivity of (a) 100 μS/cm (∼0.6 mM) and (b) 1 mS/cm (∼5 mM). Three different potentials were tested for each conductivity: 100 V (green), 1000 V (red), and 3000 V (blue) for a 1 cm long channel. (c) Temporal temperature variations obtained numerically for 100 μS/cm (triangles) and 1 mS/cm on the film (filled circles) and in the channel (nonfilled circles) when 3000 V is applied.

Next, the numerically obtained temperature transitions were also compared to the experimental results for method B. The temperature values were obtained 150 μm below the channel from the same numerical model as the in-channel cases however with a geometry adapted to the sandwich method employing the thin-PDMS film. For simplicity, a 1.15 mm thick glass composite at the bottom of the channel was employed in the simulation domain instead of the sandwiched assembly. Figure 5c demonstrates the temporal temperature variation with 100 μS/cm and 1 mS/cm conductivity at 3000 V, revealing that the numerical model resulted in slightly lower values than the experiments. The largest discrepancy between the experimentally measured and numerically obtained temperatures on the film was found with 1 mS/cm conductivity at 3000 V with the steady temperature of ∼45 °C obtained numerically and ∼49 °C obtained experimentally. This small inconsistency between the experiment and simulation can be explained with deviations in the actual heat transfer coefficient value (see above) or from the simplified geometry used in the numerical simulation assuming a single thick glass layer (and not the glass/thin-PDMS sandwich) without any restriction of heat transfer between the layers. Despite the discrepancy, the numerical simulation generally captures the trend presented by experiments such as the time frame to reach the steady state temperature (∼150 s). Moreover, the same numerical model allows the estimation of in-channel temperatures which resulted in 3–4 °C higher than the temperature in the film (see Figure 5c). Supporting Information shows a table summarizing experimentally measured saturation temperature and simulation results.

Comparison of the Two Approaches for Temperature Measurements

The two temperature measurement methods (method A and B) can be used complementarily depending on the circumstances. Method A enables the direct temperature measurement within the iDEP channel. Moreover, the measurement of temporal and spatial variations is possible with this method. However, when employing the in-channel method, to circumvent the issue of RhB dye adsorption onto the PDMS surface, it is necessary to use an additional surfactant such as CHAPS. As seen in Figures 4a,b and 5a,b, larger errors are found using method A, which we could attribute to fluorescence intensity fluctuations due to largely reduced but still not entirely suppressed dye adsorption onto the PDMS even with the addition of CHAPS. Adsorption of RhB onto the PDMS surface increases the baseline fluorescence intensity, leading to underestimated temperature values as indicated by a comparison to the numerical simulations especially at exceptionally elevated temperatures. On the other hand, for method B the incompatibility issue of RhB and PDMS is overcome by physically separating RhB from the channel walls with a 150 μm thick glass slide. Moreover, the thin film method could be used in parallel with the iDEP experiment when the set up allows one to detect dual fluorescence from sample analytes and RhB dye.

As a result of the numerical simulations, we found that the temperature increase is marginal for all the conductivity and potential cases using both method A and B except when the highest potential of 3000 V was applied at 1 mS/cm conductivity. In this case, the temperature increased up to ∼90 °C with method A and ∼45 °C in the film located 150 μm below the channel with which the in-channel temperature can be estimated to be ∼49 °C by numerical simulation. Experimentally, the results from both methods are in excellent agreement with the numerical simulation for potentials <1000 V and low conductivity, showing marginal temperature increases. Only in the case of 3000 V at 1 mS/cm conductivity, the temperature changed significantly. In this case, method A resulted in the saturation temperature of ∼70 °C as obtained from experiments, whereas ∼49 °C was measured using method B experimentally. We generally noted that, both experimentally and numerically, temperatures obtained by method A are higher than the temperature measured using method B. This might be caused by the difference in thickness of the bottom glass slides employed in the two methods (i.e., 150 μm in method A and 1 mm for method B). We assume that the heat dissipation is enhanced with the thicker glass slide (method B) with the conditions employed in our study, leading to the lower saturation temperature. Furthermore, the time to reach the steady state is similar for both methods. For example, the system takes ∼150 s to reach the saturation temperature in the case of 1 mS/cm at 3000 V using both methods (see Figures 4b and 5b).

Additionally, we assessed the temperature change under the same conditions where mitochondria iDEP was performed. Our results demonstrated that the in-channel temperature does not exceed 34 °C in iDEP experiments considering the application of an extreme potential as high as 3000 V. Thus, it is expected that the mitochondria viability is not significantly affected by Joule heating during iDEP experiments and thus viable mitochondria can be subsequently used for further analysis in other assays.

Apart from biomolecules and bioparticle degradation, Joule heating can also create electrothermal flow interfering with DEP. In the past, numerical simulations were performed to assess the temperature change due to Joule heating in iDEP devices as well as to evaluate the effect of electrothermal flow on DEP.⁵⁴ Chaurey et al. numerically simulated the temperature change within a nanoconstriction iDEP device and found that the temperature increased up to 43.4 °C with an application of 350 V/cm field at the 100 nm constrictions using 1 S/m conductivity buffer.⁵⁶ In another example, Sridharan et al. reported 52 °C temperature enhancements with 470 μS/cm conductivity buffer with 600 V/cm.⁵⁵ A larger temperature increase of 71 °C was reported by Gallo-Villanueva et al. at a conductivity of 100 μS/cm under an application of 750 V/cm in an iDEP device.⁵⁷ As demonstrated in these examples, the degree of Joule heating mainly depends on the buffer conductivity, applied potential, device dimension, insulating structure geometries, and the microchannel material. Our experimental temperature measurements fall in the range of these previously reported theoretical studies. The direct comparison of temperature measurements with the numerical simulations as presented in our study shows excellent agreement for all cases and is still reasonable for 1 mS/cm and the largest applied potential. We thus postulate that the presented approach is robust and can be used for a variety of iDEP applications in the future.

Conclusions

In this study, we experimentally quantified the temperature change in iDEP devices, which occurs due to Joule heating upon application of high electrical potentials. For an assessment of the arising temperature variations, the thermosensitive optical property of RhB was utilized by monitoring its temperature dependent fluorescence intensities. We applied and evaluated two measurement methods experimentally: directly in the microfluidic channel and slightly below in a thin film. With the former method, in-channel temperature measurement becomes possible in iDEP devices with temporal and spatial resolution with the addition of the surfactant CHAPS to prevent RhB adsorption onto the PDMS surface. However, in the presented study, the temperature variations were marginal and below the error of calibration in the iDEP device and the investigated conditions. Excellent spatial resolution was however provided by the numerical simulation performed in parallel to the experimental study.

With the in-channel method, the incompatibility issue of RhB and PDMS is greatly reduced and the experimental results showed excellent agreement with the numerical simulations. Only at larger conductivity (1 mS/cm) and large applied potential (3000 V), the experimental results start deviating from the numerical models. The second method employing a thin RhB saturated PDMS film underneath the microchannel showed similar temporal trends than the in-channel method; however, absolute temperature changes were smaller both experimentally and numerically. The thicker glass layer is thus advantageous to reduce temperature increases due to Joule heating in iDEP devices under the conditions employed in our previous protein and mitochondria iDEP studies. Moreover, the thin layer method will allow for elegant iDEP studies with fluorescent analytes, while observing temperature changes with adequate fluorescence optics simultaneously.

The two temperature measurement methods investigated in this work are easy to implement in iDEP microfluidic devices and complementary. In summary, our study provides useful guidelines for experimental temperature determination in iDEP devices, which allows one to assess Joule heating effects in future iDEP applications but also provide suitable numerical methods to estimate these changes prior to iDEP experiments with precious biological samples.

Supporting Information Available

Information related to detailed experimental procedures for mitochondria iDEP, dye calibration experiments and resultant calibration curves, and numerical simulation methodology. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States