Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Jun 9;86(13):6454–6460. doi: 10.1021/ac501031y

Determination of Rate Constants and Equilibrium Constants for Solution-Phase Drug–Protein Interactions by Ultrafast Affinity Extraction

Xiwei Zheng 1, Zhao Li 1, Maria I Podariu 1, David S Hage 1,*
PMCID: PMC4082384  PMID: 24911267

Abstract

graphic file with name ac-2014-01031y_0005.jpg

A method was created on the basis of ultrafast affinity extraction to determine both the dissociation rate constants and equilibrium constants for drug–protein interactions in solution. Human serum albumin (HSA), an important binding agent for many drugs in blood, was used as both a model soluble protein and as an immobilized binding agent in affinity microcolumns for the analysis of free drug fractions. Several drugs were examined that are known to bind to HSA. Various conditions to optimize in the use of ultrafast affinity extraction for equilibrium and kinetic studies were considered, and several approaches for these measurements were examined. The dissociation rate constants obtained for soluble HSA with each drug gave good agreement with previous rate constants reported for the same drugs or other solutes with comparable affinities for HSA. The equilibrium constants that were determined also showed good agreement with the literature. The results demonstrated that ultrafast affinity extraction could be used as a rapid approach to provide information on both the kinetics and thermodynamics of a drug–protein interaction in solution. This approach could be extended to other systems and should be valuable for high-throughput drug screening or biointeraction studies.

Studies of the interactions between drugs and serum proteins are important in providing information regarding the absorption, distribution, metabolism, and excretion (ADME) of pharmaceutical agents within the body.1 Human serum albumin (HSA) is the most abundant transport protein in blood (concentration of 30–50 g/L) and is of interest in many drug–protein binding studies.2 This protein can interact with a large variety of drugs, most of which bind to one or two major sites on HSA: Sudlow sites I and II.3−8 Examples of drugs and small solutes that can bind to this protein include warfarin, azapropazone, benzodiazepines, indoles (e.g., l-tryptophan), sulfonylureas, and long-chain fatty acids.3−8

Many techniques have been used to examine the interactions of drugs and solutes with HSA. These techniques have included ultrafiltration, equilibrium dialysis, fluorescence spectroscopy, capillary electrophoresis, UV–vis spectroscopy, solid-phase microextraction, circular dichroism, surface plasmon resonance, nuclear magnetic resonance spectroscopy, and X-ray crystallography.9−15 High-performance affinity chromatography (HPAC) is another technique that has been used to characterize these interactions. In HPAC, one of the components of the interaction (e.g., HSA) is typically immobilized to an HPLC support and used as the stationary phase within a column. The other component (e.g., the drug or solute of interest) is then injected onto the column or applied in the mobile phase while its retention time, peak area or elution profile is monitored to obtain information on this component’s interaction with the immobilized binding agent.1,8,14

Several HPAC methods have previously been developed to measure the equilibrium constants or rate constants for solute–protein interactions. These approaches have included zonal elution and frontal analysis for the determination of equilibrium constants and plate height measurements, peak profiling, or peak decay analysis for kinetic studies.14−17 One limitation of these past HPAC methods is that they require the use of separate experiments or conditions for determining equilibrium constants and rate constants.14,18−23 Also, these methods generally use an immobilized protein or binding agent as one of the components of the interaction that is being examined. This feature means proper validation with model systems and reference methods are ideally required to ensure these HPAC approaches are providing a satisfactory model of how the same protein or binding agent will behave in its soluble or native state.18−23

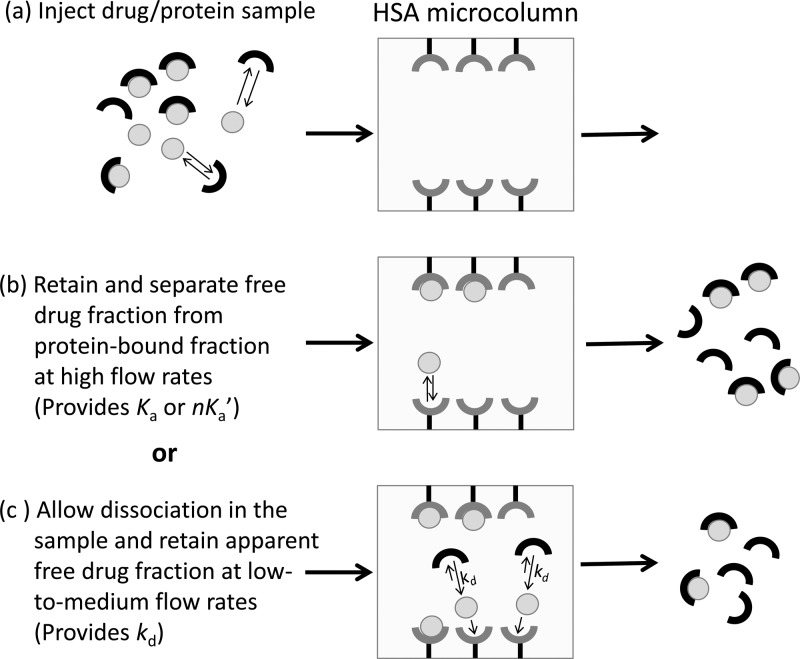
An alternative HPAC method based on ultrafast affinity extraction has recently been described for estimating the equilibrium constants of drugs with HSA, or similar biological interactions, in solution.14,25,26 As illustrated in Figure 1, this method uses an affinity microcolumn that contains an immobilized binding agent, such as an antibody or serum protein, for extraction of the free (or nonprotein bound) fraction of a drug or solute in a sample. If the sample residence time in the column is sufficiently small to avoid appreciable release of the drug/solute from proteins in the sample, the amount of extracted drug/solute can then be used to measure the free fraction of this compound or the equilibrium constant for binding by this drug or solute to a soluble protein in the sample.25,26 This approach has been shown to give equilibrium constants that are in good agreement with those estimated for solution-phase systems when using ultrafiltration as a reference method. In addition, this method requires only microliter-size samples and provides binding data within a few minutes of injection.25,26

Figure 1.

Figure 1

Open in a new tab

General scheme for measuring a free drug fraction by ultrafast affinity extraction. (a) A sample containing a drug/protein mixture is injected onto an affinity microcolumn that contains an immobilized binding agent for the drug, such as HSA. (b) As the sample passes through the microcolumn at a suitably high flow rate, only the free drug fraction will be extracted; this creates a separation of the free and protein-bound forms of the drug in the sample and provides data that can be used to estimate the association equilibrium constant (Ka) or global affinity constant (nKa′) for the interaction. (c) If a slower flow rate is used for sample injection, part of the protein-bound fraction of the drug in the sample may dissociate as it passes through the microcolumn, increasing the apparent free drug fraction; these conditions provide data that can be used to estimate the dissociation rate constant (kd) for the system.

In this study, a new method based on ultrafast affinity extraction is described in which both the rate constants and equilibrium constants can be quickly determined for a drug–protein interaction in solution. This work will use HSA as a model protein and will examine several drugs that are known to bind to this protein.18−23 The theory of this approach will be described, and various experimental parameters will be considered in the optimization of this technique. This method will then be used to examine the interactions of each tested drug with HSA, and the resulting rate constants and equilibrium constants will be compared with those reported for other techniques. The advantages and requirements of this method will be discussed, as well as the possible extension of this approach to other systems and applications.8,27

Experimental Section

Materials and Reagents

The HSA (Cohn fraction V, essentially fatty acid free, ≥96% pure), acetohexamide, chlorpromazine, gliclazide, tolbutamide, racemic verapamil, and racemic warfarin were obtained from Sigma (St. Louis, MO, U.S.A.). The reagents for the bicinchoninic acid (BCA) protein assay were from Pierce (Rockford, IL, U.S.A.). The Nucleosil Si-300 silica (7 μm particle diameter, 300 Å pore size) was purchased from Macherey Nagel (Dűren, Germany). All buffers and aqueous solutions were prepared using water from a Nanopure system (Barnstead, Dubuque, IA, U.S.A.) and were passed through Osmonics 0.22 μm nylon filters from Fisher (Pittsburgh, PA, U.S.A.)

Apparatus

The columns were packed using a Prep 24 pump from ChromTech (Apple Valley, MN, U.S.A.). The chromatographic system consisted of a PU-2080 Plus pump, an AS-2057 autosampler, and a UV-2075 absorbance detector from Jasco (Easton, MD, U.S.A.). An Alltech water jacket (Deerfield, IL, U.S.A.) and a Fisher Isotemp 3013D circulating water bath were used to maintain a column temperature of 37.0 (±0.1) °C during all experiments. ChromNAV v1.18.04 software and LCNet from Jasco were used to control the system. Chromatograms were analyzed through the use of PeakFit v4.12 software (Jandel Scientific, San Rafael, CA, U.S.A.).

Column Preparation

The stationary phase used in these studies consisted of HSA immobilized onto Nucleosil Si-300 silica by the Schiff base method.18 A control support was prepared in the same manner but with no HSA being added during the immobilization step. The protein content of the final HSA support was determined in triplicate by a BCA assay using HSA as the standard and the control support as the blank, giving a value of 65 (±2) mg HSA/g silica or an effective concentration of ∼440 μM HSA in the affinity microcolumns. The supports were placed into stainless steel columns with an inner diameter of 2.1 mm and lengths of 1 mm (using a frit-in-column design)28 or 5 to 10 mm (using traditional stainless steel HPLC housings and end fittings). The packing solution was pH 7.4, 0.067 M potassium phosphate buffer, and the packing pressure was 3000–4000 psi (20–28 MPa). The columns were stored in pH 7.4, 0.067 M phosphate buffer and at 4 °C when not in use.

Chromatographic Studies

The mobile phase used for sample application, elution and sample preparation was pH 7.4, 0.067 M phosphate buffer. All mobile phases were degassed for 30 min prior to use. Each affinity microcolumn was used for approximately 200 sample injections to provide optimum retention and peak resolution; however, these columns were found to be stable for at least 300–400 injections and over 6 months of use. The free fraction measurements were typically made by injecting 1 μL of samples that contained 10 μM of the desired drug or a mixture of 10 μM drug and 20 μM soluble HSA, although other drug and protein concentrations were also considered (see Supporting Information). These mixtures were incubated for at least 30 min prior to injection, with both the sample and mobile phase being preheated to 37 °C before passage through the affinity microcolumn. Other conditions are provided in the Supporting Information.

The dissociation rate constants and equilibrium constants for each drug with soluble HSA were measured by using the general scheme in Figure 1. For the direct measurement of equilibrium constants, an injection flow rate was used that was sufficiently high to minimize dissociation of drug–protein complexes in the sample during their passage through the column. By using lower flow rates, and longer residence times for the sample in the column, the conditions were adjusted so that some of the drug–protein complex could dissociate during passage through the column, thus increasing the apparent free drug fraction and making it possible to determine the dissociation rate constant for the drug with the soluble protein. In both types of studies, the free drug fractions were measured by dividing the drug’s baseline-corrected retained peak area by the total peak area for the same drug in the absence of any soluble protein. The baseline of each chromatogram was normalized using the autofit and subtract baseline method of PeakFit 4.12 prior to data analysis. No significant nonspecific binding with the control support was seen for most drugs examined in this study.18−22 Some nonspecific binding was seen for verapamil, as reported previously;21 however, this nonspecific binding did not have any notable effect on the free fractions that were measured for this drug with soluble HSA.

Results and Discussion

Optimization of Free Drug Fraction Measurements

Several model drugs were examined in this study. Warfarin is an anticoagulant known to have single-site binding to HSA at Sudlow site I on this protein.15,18,29,30 Verapamil is a calcium channel blocking agent, and chlorpromazine is an antipsychotic drug that each have a primary binding site at or near Sudlow site I.21,31 Tolbutamide, acetohexamide, and gliclazide are sulfonylurea drugs used to treat type 2 diabetes and have two major binding regions on HSA, which occur at Sudlow sites I and II.19,20,22 The association equilibrium constants (Ka, in the case of single-site binding) or global affinity constants (nKa′, in the case of multisite binding) for these drugs with HSA at 37 °C and pH 7.4 are in the general range of 104–106 M–1, as is typical for the binding of many drugs with this protein.1,18−24 Dissociation rates from HSA have been examined previously by other methods for four of these drugs (i.e., warfarin, verapamil, acetohexamide, and tolbutamide),15,17 whereas the other two drugs (i.e., gliclazide and chlorpromazine) have not been the subject of prior kinetic studies.

In this study, a drug was injected in either the presence or absence of excess soluble HSA onto an HSA microcolumn according to the scheme given in Figure 1. As the sample passed through the microcolumn at a moderate-to-high flow rate, the protein-bound fraction of the drug and the excess soluble protein eluted as a nonretained peak, while the free fraction of the drug was extracted, retained, and later eluted from the column. Some typical chromatograms that were obtained with this method are provided in the Supporting Information. Results were obtained within 2–10 min for all of the tested drugs (depending on the column size, degree of retention, and the flow rate) and within 2–6 min for drugs with low-to-moderate affinities for HSA.

The injected samples that were typically used in this study contained a 2-fold mole excess of HSA versus each drug (i.e., 20 μM HSA and 10 μM drug). These concentrations avoided the use of an excess of drug versus protein in the samples and provided free drug fractions that could be readily detected. It has been shown in prior work with ultrafast affinity extraction that therapeutic levels of similar drugs26,32,38 and larger concentrations of soluble HSA,26 including physiological levels, could be used in this type of experiment. However, these latter conditions were not required for the purpose of this current study. Samples containing other drug and/or protein concentrations were also examined (see Supporting Information), with no significant changes being noted in either the rate constants or equilibrium constants that were measured under these alternative conditions.

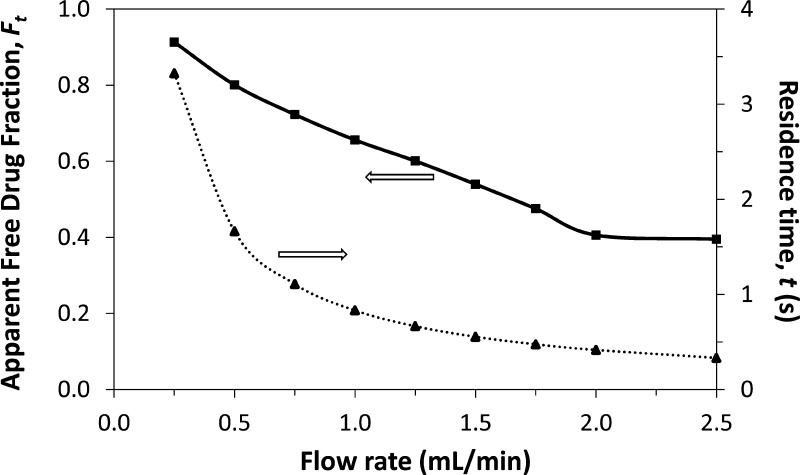
As shown in Figure 2, the relative size of the free drug fraction was affected by the flow rate used for sample injection. This effect has been noted for other applications of ultrafast affinity extraction and was due to the change the flow rate created in the time allowed for dissociation of the protein-bound form of the drug as the sample passed through the column.25,26,32,38 The extraction efficiency for the drug can also vary with the flow rate for some types of affinity microcolumns, but this parameter was 95% or higher for the HSA microcolumns and experimental conditions used in this study25,26 and did not lead to any significant changes in the relative size of the retained peaks as a function of flow rate.

Figure 2.

Figure 2

Open in a new tab

Effect of injection flow rate on the column residence time (dashed line) and apparent free drug fractions (solid line) for 1 μL samples of 10 μM tolbutamide and 20 μM soluble HSA injected onto a 5 mm × 2.1 mm inner diameter (i.d.) HSA microcolumn at pH 7.4 and 37 °C.

The overall effect of changing the flow rate and drug–protein dissociation in the sample is also illustrated in Figure 2. At low-to-moderate flow rates (i.e., < 2.0 mL/min, in this example for a tolbutamide/HSA mixture), the apparent free drug fraction increased with a decrease in the flow rate, due to increased dissociation of the drug from soluble HSA as the sample passed through the column. However, the measured free drug fraction approached a constant value when the flow rate reached a certain critical value (e.g., ≥ 2.0 mL/min, or a column residence time of ∼420 ms or less for the tolbutamide/HSA mixture). This effect was employed by using the latter conditions and high flow rates to estimate the original free drug fraction that was present at equilibrium in the sample and lower flow rates to provide data on the rate of a drug’s dissociation from a soluble protein in the sample.

Column size is another factor to consider when performing a free fraction analysis by ultrafast affinity extraction. Like flow rate, this factor will affect the time allowed for drugs to dissociate from proteins during passage of a sample through the column, following the same trend as illustrated in Figure 2. In addition, both the column size and flow rate will affect the backpressure of the system (e.g., typical column pressures of 1.9–3.2 MPa for 5–10 mm × 2.1 mm i.d. columns at 3.5 mL/min). However, the column size will also affect the elution time of the retained free drug fraction and the resolution of this peak from the nonretained peak due to the protein-bound drug and excess protein in the sample.25

It was found that drugs with relatively strong binding to HSA (e.g., warfarin, tolbutamide, and acetohexamide; affinities, ∼105–106 M–1)18−22,29,30 provided measurable free fractions when using relatively short 5 mm × 2.1 mm i.d. HSA microcolumns. Such columns not only gave good retention for these drugs, but they made it easy to obtain short column residence times for measurement of the small free drug fractions that could occur in such systems. Most drugs with weaker binding to HSA (e.g., gliclazide and verapamil; affinities, ∼104–105 M–1)21,22 were examined by using longer 10 mm × 2.1 mm HSA microcolumns. These longer microcolumns provided higher drug retention while still providing column residence times sufficient to examine the larger free fractions that were present in such systems. An exception to this trend was chlorpromazine, which had fast dissociation kinetics and moderate binding to HSA.23 In this specific case, a 1 mm × 2.1 mm i.d. HSA microcolumn was used.

Determination of Dissociation Rate Constants

Measurements of the apparent free drug fractions at low-to-moderate flow rates were used in this study to estimate the dissociation rate constant for a drug with a soluble protein in the same sample. This experiment was described by the reactions shown in eqs 1 and 2, which occurred simultaneously as a mixture of the drug/analyte and soluble protein (as represented by A and P, respectively) was applied to an affinity microcolumn that contained an immobilized binding agent for the drug, P(s).

graphic file with name ac-2014-01031y_m001.jpg 1
graphic file with name ac-2014-01031y_m002.jpg 2

The reaction in eq 1 describes the binding and equilibrium that has taken place between A and P in the sample prior to entering the column, whereas eq 2 describes the binding and extraction of the free form of A by the immobilized agent P(s) in the microcolumn. The terms ka and kd in eq 1 represent the second-order association rate constant and first-order dissociation rate constant of A with P in solution. The term ka(s) in eq 2 is the second-order association rate constant for A as it interacts with the immobilized binding agent.

The system in eqs 1 and 2 was simplified in this study by using a large excess of the immobilized binding agent versus the soluble protein. For instance, the 1–10 mm × 2.1 mm i.d. microcolumns contained a 76- to 760-fold larger HSA content than a 1 μL solution of 20 μM HSA. In addition, each of these columns had at least a 22-fold larger molar concentration of HSA than was present in even the initial, undiluted samples and mixtures that contained soluble HSA. These conditions meant that P(s) was present in a large excess versus soluble P when using the model described by using eqs 1 and 2. This also meant that the pseudo-first order rate constant ka [P] for the binding of A with P was much less than the pseudo-first-order rate constant ka(s) [P(s)] for the extraction of A (i.e., assuming ka and ka(s) had comparable values, as has been noted to be the case for soluble HSA and the type of immobilized HSA used in this study).1,29,39

The result of these experimental conditions is that the extraction of A by the immobilized binding agent was much faster than the association of A with P. This, in turn, made it possible to ignore this latter process and simplify the reaction in eq 1 to that shown in eq 3.

graphic file with name ac-2014-01031y_m003.jpg 3

It was then possible with this revised model to obtain the integrated rate expressions given in eqs 4 and 5 (see Supporting Information for derivations).

graphic file with name ac-2014-01031y_m004.jpg 4
graphic file with name ac-2014-01031y_m005.jpg 5

In these equations, F0 is the original free fraction of A in the sample, and Ft is the apparent free fraction after AP has been allowed to dissociate for time t. The value of t is equal to the column void time and can be calculated by employing the flow rate and the column void volume (e.g., as found by using the known support porosity, packing density, and column size). Equations 4 and 5 indicate that a plot of either ln[(1 – F0)/(1 – Ft)] or ln[1/(1 – Ft)] versus t should provide, under the appropriate experimental conditions, a linear relationship in which the slope is directly related to the dissociation rate constant kd as A is released from its complex with soluble agent P in the sample.

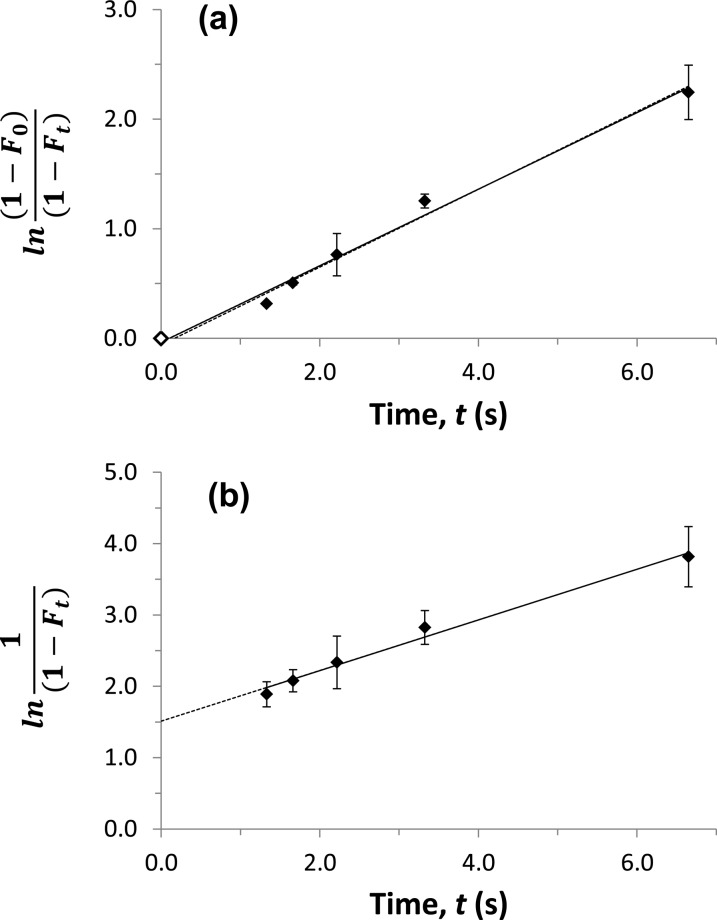
Some typical plots that were obtained when using eqs 4 and 5 are provided in Figure 3. Both types of plots gave a linear response for all of the tested drugs, with correlation coefficients ranging from 0.988 to 0.998 (n = 5 to 8) over dissociation times that allowed measurable changes to be made in the apparent free fractions. The plots that were prepared according eq 4 gave intercepts that were essentially equal to zero, regardless of whether an experimental point at t = 0 and Ft = F0 for the original sample was included in the data set. For plots made according to eq 5, a positive nonzero intercept was obtained that was related to the value of F0.

Figure 3.

Figure 3

Open in a new tab

Measurement of the dissociation rate constant for verapamil and soluble HSA at pH 7.4 and 37 °C, as determined by measuring apparent free drug fractions using ultrafast affinity extraction. The samples contained 10 μM verapamil and 20 μM soluble HSA. The results were analyzed by using (a) eq 4 or (b) eq 5. The solid line in (a) shows the result that was obtained when a point at the origin was included (◊), and the dashed line shows the result obtained when this point was not included; the equations for these two best-fit lines were y = 0.35 (±0.02) x – 0.04 (±0.06) and y = 0.36 (±0.02) x – 0.06 (±0.09), respectively. In (b), the best-fit equation was y = 0.36 (±0.02) x + 1.51 (±0.09). The correlation coefficients for these plots ranged from 0.993 to 0.995 (n = 5−6). The error bars represent a range of ±1 SD and, in some cases, were comparable in size to the data symbols.

The usable time range for these dissociation studies was dependent on the affinity of each drug for soluble HSA (which affected the value of F0) and the dissociation rate for the soluble drug–protein complex. The lower end of this usable time range occurred when the free fraction grew close to its equilibrium value (i.e., conditions under which little dissociation occurred). These times were as low as 100–277 ms for chlorpromazine or warfarin and as high as 950 ms for verapamil. The ranking of these drugs with respect to this time was correlated with a decreasing order in the overall affinities of the drugs for HSA, with the sole exception of chlorpromazine due to its relatively high dissociation rate. The upper end of the usable time range occurred when the drug had sufficient time to reach essentially complete dissociation. For most of the tested drugs, this upper limit occurred over the range of 1.7–6.7 s and, again with the exception of chlorpromazine, followed approximately the same order as seen with the lower time limits for these drugs and the affinities of these drugs for soluble HSA.

Table 1 summarizes the kd values that were obtained in this study. The relative precision of these dissociation rate constants ranged from ±3–9%. The measured kd values differed by only 7–20% from the literature values that have been reported for acetohexamide, tolbutamide, and racemic verapamil.15,17 In the case of warfarin, for which several literature values were available,9,15,40 the results of this study fell within the overall range of all previously reported values for racemic warfarin or its enantiomers. Although gliclazide and chlorpromazine did not have prior kd values that have been reported, the dissociation rate constants measured for these drugs did fit within the range that would be expected for drugs with similar affinities to HSA.15,17,41,42 The same trends were seen for kd values that were measured by ultrafast affinity extraction (1) when a point at the intercept, and representing the original sample, was included during analysis of the data by using eq 4; (2) when eq 4 was used with no such point being included in the data set; or (3) when the data were examined by using eq 5.

Table 1. Dissociation Rate Constants Measured for Various Drugs with Soluble HSA by Using Ultrafast Affinity Extraction on HSA Microcolumnsa.

dissociation rate constant (kd (s–1))
drug estimate (eq 4b) estimate (eq 5) literature [ref]
warfarin 0.80 (±0.05) 0.72 (±0.05) 0.41–2 [9, 15, 40]
tolbutamide 0.59 (±0.03) 0.58 (±0.04) 0.49 (±0.15) [15]
acetohexamide 0.67 (±0.03) 0.63 (±0.03) 0.58 (±0.02) [15]
verapamil 0.35 (±0.02) 0.36 (±0.02) 0.38 (±0.05) [17]
gliclazide 0.61 (±0.02) 0.59 (±0.04) not reported
chlorpromazine 3.96 (±0.13) 3.35 (±0.30) not reported
Open in a new tab
a

The kd values were measured at pH 7.4 and at 37 °C. Each of the injected samples contained 10 μM of the drug and 20 μM of HSA. The values in the parentheses represent a range of ±1 SD, as determined from the slopes of the best-fit lines constructed according to eqs 4 and 5.

b

These values were found by using eq 4 when a point at the origin was included in the data set.

Measurement of Association Equilibrium Constants

It was also possible to use ultrafast affinity extraction to obtain the association equilibrium constant (Ka), or the global affinity constant (nKa′) in the case of a system with multisite binding,1,24 for each drug with soluble HSA. For instance, eq 6 can be used for this purpose by employing the free drug fraction that is measured for a drug/protein mixture at equilibrium (F0) and under injection conditions that minimize release of the drug from soluble proteins as the sample passes through the column.25

graphic file with name ac-2014-01031y_m006.jpg 6

In eq 6, [A]tot and [P]tot are the total concentrations of the drug and soluble protein in the original sample, respectively. This equation was derived for a drug and protein interaction that involves 1:1 binding, but the same expression can be used to estimate the global affinity constant for a multisite drug–protein interaction under a given set of concentration conditions.25,32,35,37

The Ka (or nKa′) values that were obtained by using direct measurements of F0 are provided in Table 2. These values had precisions of ±7–36% and differed by less than 7% for the drugs with single reference values obtained under similar temperature conditions. In the case of warfarin, the measured Ka fell within the range of previously reported values. A second method for estimating Ka was carried out that utilized the value of F0 that was obtained from the intercept of a plot made according eq 5 during the determination of dissociation rate constants. This second set of values, which are also given in Table 2, had precisions of ±8–22% and differed from the literature results by less than 23% or, in the case of warfarin, were similar to the range of previously reported values.

Table 2. Equilibrium Constants Measured for Various Drugs with Soluble HSA by Using Ultrafast Affinity Extraction on HSA Microcolumnsa.

association equilibrium constant, Ka, or global affinity constant, nKa′ (M–1)
drug estimate (eq 6) estimate (eqs 5 and 6) literature [ref]
warfarin 2.4 (±0.4) × 105 1.6 (±0.2) × 105 2.0–5.7 × 105 [18, 29, 30]
tolbutamide 1.1 (±0.4) × 105 0.9 (±0.2) × 105 1.1 (±0.1) × 105 [19]b
acetohexamide 1.8 (±0.5) × 105 1.3 (±0.1) × 105 1.7(±0.1) × 105 [20]b
verapamil 1.5 (±0.4) × 104 1.6 (±0.2) × 104 1.4 (±0.1) × 104 [21]c
gliclazide 8.0 (±0.6) × 104 6.9 (±1.0) × 104 7.9 (±0.1) × 104 [22]b
chlorpromazine 6.2 (±0.5) × 104 4.9 (±0.5) × 104 6.4 × 104 [23]
Open in a new tab
a

These results were measured at pH 7.4 and at 37 °C. The values in parentheses represent a range of ±1 S.D., as determined by error propagation.

b

The global affinity constants for these drugs were calculated from data in the given references.

c

This value represents the average association equilibrium constant for R- and S-verapamil at their high affinity site on HSA.

A comparison of these two approaches indicates that there are distinct advantages to each method for measuring the equilibrium constant for a drug–protein interaction. As the data in Table 2 suggest, the approach that uses fast flow rates and ultrafast affinity extraction to directly measure F0 can provide the more precise estimate of Ka or nKa′. However, this method does require obtaining appropriate flow rate conditions for such a measurement and is carried out at separate flow rates from those that would be used to measure a dissociation rate constant. The second approach, in which the value of F0 is obtained from the intercept of a plot made according to eq 5, provides a slightly less precise estimate of the equilibrium constant but can be carried out with the same experiments and conditions as those used to find kd. This makes the latter method attractive for the simultaneous and rapid determination of both kd and Ka. This approach would also be useful for the estimation of equilibrium constants at column pressures or peak resolutions that may prevent the use of sufficiently high flow rates for the direct determination of F0 and Ka.

Estimation of Association Rate Constants

It was possible from the measured Ka and kd values to also estimate the second-order association rate constant (ka) for each drug with soluble HSA, as found by using the relationship ka = kdKa (see Supporting Information). This method provided the actual ka value for a drug–protein system with 1:1 interactions or the net, apparent value of ka for a system with multisite interactions. The average ka for racemic warfarin that was determined by this approach was 1.7 (±0.3) × 105 M–1 s–1 at pH 7.4 and 37 °C, which gave good agreement with prior values reported for this drug with HSA.9,15,40,43 The association rate constants for tolbutamide, acetohexamide, and racemic verapamil gave ka values of 6.4 (±2.4) × 104 M–1 s–1, 1.1 (±0.3) × 105 M–1 s–1, and 5.4 (±1.5) × 103 M–1 s–1, respectively, which were comparable to the results calculated from previously reported kd and Ka or nKa′ values for these systems.15,17,19−21 Gliclazide and chlorpromazine gave ka values of 4.7 (±0.5) × 104 M–1 s–1 and 2.1 (±0.3) × 105 M–1 s–1, which agreed with the range of values that have been reported for drugs with comparable affinities and dissociation rates for HSA.15,17,41,42

Conclusion

In this report, a new method based on ultrafast affinity extraction and affinity microcolumns containing immobilized HSA was developed and used to measure both the rate constants and equilibrium constants for drug–protein interactions involving soluble HSA. The effects of column size and flow rate were considered in these experiments, and several approaches for these measurements were examined and compared. The dissociation rate constants obtained by this approach gave good agreement with previous rate constants that have been reported for the same drugs or for other solutes with comparable affinities for HSA. The equilibrium constants determined by this method also showed good agreement with the literature.

The results indicated that ultrafast affinity extraction can be an effective method for studying both the kinetics and thermodynamics of a drug–protein interaction in solution. An important advantage of this method is it can directly examine both the equilibrium processes and interaction rates that occur between a drug and the soluble form of a protein, thus avoiding any effects immobilization may have on such interactions.18−23 The moderate-to-high flow rates and small columns used in this method make this technique fast, with analysis times on the order of minutes per sample being possible.25,26 In addition, this approach is not limited to HSA or the drugs examined in this study but could be applied to other systems (e.g., the interactions of drugs or small biomolecules with other soluble proteins or to surface receptors on injected particles). Possible applications for this method include the high-throughput screening of drug candidates and the rapid characterization of solute–protein interactions.1,9,14,17,24

Acknowledgments

This work was supported by the National Institutes of Health under grants R01 GM044931 and R01 DK069629. The authors also thank Lei Li for assisting with the kinetic studies and Ryan Matsuda for his help in work with the sulfonylurea drugs.

Supporting Information Available

Additional Supporting Information is available on the chromatographic conditions that were used in this study, the derivation of key equations that were used in this report, and data that were acquired at various sample concentrations or that made use of the measured dissociation rate constants and association equilibrium constants to estimate association rate constants. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ac501031y_si_001.pdf (598.2KB, pdf)

References

  1. Hage D. S.; Jackson A.; Sobansky M. R.; Schiel J. E.; Yoo M. J.; Joseph K. S. J. Sep. Sci. 2009, 32, 835–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Peters T., Jr.All About Albumin: Biochemistry, Genetics, and Medical Applications; Academic Press: San Diego, CA, 1996. [Google Scholar]
  3. Sudlow G.; Birkett D. J.; Wade D. N. Mol. Pharmacol. 1976, 12, 1052–1061. [PubMed] [Google Scholar]
  4. Kragh-Hansen U. Pharmacol. Rev. 1981, 33, 17–53. [PubMed] [Google Scholar]
  5. Kragh-Hansen U.; Chuang V. T.; Otagiri M. Biol. Pharm. Bull. 2002, 25, 695–704. [DOI] [PubMed] [Google Scholar]
  6. Carter D. C.; He X. M.; Munson S. H.; Twigg P. D.; Gernert K. M.; Broom M. B.; Miller T. Y. Science 1989, 244, 1195–1198. [DOI] [PubMed] [Google Scholar]
  7. Brodersen R. J. Biol. Chem. 1979, 254, 2364–2369. [PubMed] [Google Scholar]
  8. Hage D. S.; Anguizola J.; Barnaby O.; Jackson A.; Yoo M. J.; Papastavros E.; Pfaunmiller E.; Sobansky M.; Tong Z. Curr. Drug. Metab. 2011, 12, 313–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Rich R. L.; Day Y. S.; Morton T. A.; Myszka D. G. Anal. Biochem. 2001, 296, 197–207. [DOI] [PubMed] [Google Scholar]
  10. Matsuda R.; Bi C.; Anguizola J.; Sobansky M.; Rodriguez E.; Badilla J. V.; Zheng X.; Hage B.; Hage D. S.. J. Chromatogr. B, in press. DOI: 10.1016/ j.jchromb.2013.11.043. [DOI] [PMC free article] [PubMed]
  11. Ding F.; Zhao G.; Chen S.; Liu F.; Sun Y.; Zhang L. J. Mol. Struct. 2009, 929, 159–166. [Google Scholar]
  12. Leis D.; Barbosa S.; Attwood D.; Taboada P.; Mosquera V. Langmuir 2002, 18, 8178–8185. [Google Scholar]
  13. Yuan H.; Pawliszyn J. Anal. Chem. 2001, 73, 4410–4416. [DOI] [PubMed] [Google Scholar]
  14. Schiel J. E.; Hage D. S. J. Sep. Sci. 2009, 32, 1507–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yoo M. J.; Hage D. S. J. Chromatogr. A 2011, 1218, 2072–2078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tong Z.; Schiel J. E.; Papastavros E.; Ohnmacht C. M.; Smith Q. R.; Hage D. S. J. Chromatogr. A 2011, 1218, 2065–2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Yoo M. J.; Hage D. S. J. Sep. Sci. 2011, 34, 2255–2263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Chen J.; Hage D. S. Anal. Chem. 2006, 78, 2672–2683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Joseph K. S.; Anguizola J.; Hage D. S. J. Pharm. Biomed. Anal. 2011, 54, 426–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Joseph K. S.; Anguizola J.; Jackson A. J.; Hage D. S. J. Chromatogr. B 2010, 878, 2775–2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mallik R.; Yoo M. J.; Chen S.; Hage D. S. J. Chromatogr. B 2008, 876, 69–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Matsuda R.; Anguizola J.; Joseph K. S.; Hage D. S. Anal. Bioanal. Chem. 2011, 401, 2811–2819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kim H. S.; Wainer I. W. J. Chromatogr. B 2008, 870, 22–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hage D. S.; Anguizola J. A.; Jackson A. J.; Matsuda R.; Papastavros E.; Pfaunmiller E.; Tong Z.; Vargas-Badilla J.; Yoo M. J.; Zheng X. Anal. Methods 2011, 3, 1449–1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mallik R.; Yoo M. J.; Briscoe C. J.; Hage D. S. J. Chromatogr. A 2010, 1217, 2796–2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Zheng X.; Yoo M. J.; Hage D. S. Analyst 2013, 138, 6262–6265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Yoo M. J.; Hage D. S. J. Sep. Sci. 2009, 32, 2776–2785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Schiel J. E.; Ph.D. Thesis, University of Nebraska-Lincoln, Lincoln, NE, 2009. [Google Scholar]
  29. Loun B.; Hage D. S. Anal. Chem. 1994, 66, 3814–3822. [DOI] [PubMed] [Google Scholar]
  30. Yoo M. J.; Schiel J. E.; Hage D. S. J. Chromatogr. B 2010, 878, 1707–1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Silva D.; Cortez C. M.; Louro S. R.W. Spectrochim. Acta, Part A 2004, 60, 1215–1223. [DOI] [PubMed] [Google Scholar]
  32. Ohnmacht C. M.; Schiel J. E.; Hage D. S. Anal. Chem. 2006, 78, 7547–7556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Jiang T.; Mallik R.; Hage D. S. Anal. Chem. 2005, 77, 2362–2372. [DOI] [PubMed] [Google Scholar]
  34. Clarke W.; Hage D. S. Anal. Chem. 2001, 73, 1366–1373. [DOI] [PubMed] [Google Scholar]
  35. Clarke W.; Schiel J. E.; Moser A.; Hage D. S. Anal. Chem. 2005, 77, 1859–1866. [DOI] [PubMed] [Google Scholar]
  36. Clarke W.; Chowdhuri A. R.; Hage D. S. Anal. Chem. 2001, 73, 2157–2164. [DOI] [PubMed] [Google Scholar]
  37. Schiel J. E.; Tong Z.; Sakulthaew C.; Hage D. S. Anal. Chem. 2011, 83, 9384–9390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Burtis C. A.; Ashwood E. R.; Bruns D. E.. Tietz Textbook of Clinical Chemistry and Molecular Diagnostics, 4th ed.; Saunders: St. Louis, MO, 2006. [Google Scholar]
  39. Yang J.; Hage D. S. J. Chromatogr. A 1997, 766, 15–25. [DOI] [PubMed] [Google Scholar]
  40. Chen J.; Schiel J. E.; Hage D. S. J. Sep. Sci. 2009, 32, 1632–1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Yang J.; Hage D. S. J. Chromatogr. A 1996, 725, 273–285. [DOI] [PubMed] [Google Scholar]
  42. Schiel J. E.; Ohnmacht C. M.; Hage D. S. Anal. Chem. 2009, 81, 4320–4333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Loun B.; Hage D. S. Anal. Chem. 1996, 68, 1218–1225. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac501031y_si_001.pdf (598.2KB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES