Binary variable multiple-model multiple imputation to address missing data mechanism uncertainty: Application to a smoking cessation trial

Abstract

The true missing data mechanism is never known in practice. We present a method for generating multiple imputations for binary variables that formally incorporates missing data mechanism uncertainty. Imputations are generated from a distribution of imputation models rather than a single model, with the distribution reflecting subjective notions of missing data mechanism uncertainty. Parameter estimates and standard errors are obtained using rules for nested multiple imputation. Using simulation, we investigate the impact of missing data mechanism uncertainty on post-imputation inferences and show that incorporating this uncertainty can increase the coverage of parameter estimates. We apply our method to a longitudinal smoking cessation trial where nonignorably missing data were a concern. Our method provides a simple approach for formalizing subjective notions regarding nonresponse and can be implemented using existing imputation software.

1 Introduction

Many intervention trials have binary outcome variables that are subject to missingness. For example, in many smoking cessation trials, the primary outcome is a binary variable indicating whether or not the participant is still smoking at some follow-up time point. In cancer screening promotion trials, the outcome is often receipt of a cancer screening procedure such as a mammogram during follow-up among participants non-adherent to screening guidelines at baseline. A widely used strategy for handling missing values in such studies is single imputation: in smoking cessation studies, it is assumed that all non-respondents are smoking [1]; similarly, in cancer screening promotion trials, it is assumed that all non-respondents failed to obtain screening [2]. After singly imputing the missing outcomes, analyses proceed as if all data were observed.

Many authors have discussed the drawbacks to the missing = smoking and other single imputation assumptions [1, 3]. In addition to being a very strong assumption regarding the nature of the missing data, this approach treats missing values as if they were observed and thus fails to account for uncertainty due to missingness. When one treatment group has more missing values than another, missing = smoking can severely bias the treatment effect estimate. Despite these limitations, the approach remains in use. One reason for its continued use is the belief among researchers that participants in smoking cessation trials whose values are missing are more likely to be smokers than participants who are observed. In the missing data literature, this phenomenon—when the probability of missingness depends on unobserved information like the missing value itself—is referred to as nonignorably missing data. Ignorably missing data occur when the probability that a value is missing does not depend on unobserved information [4].

In order to produce valid estimates in the presence of nonignorably missing data, analyses must take into account the process that gave rise to the missing data, commonly referred to as the missing data mechanism. In the context of a clinical trial, failure to take into account the missing data mechanism may result in inferences that make a treatment appear more or less effective. Failure to incorporate uncertainty regarding the missing data mechanism may result in inferences that are overly precise given the amount of available information [5, 6].

Since a nonignorable missing data mechanism is involved with unobserved data, there is little information available to correctly model this process. One approach is to perform a sensitivity analysis, drawing inferences based on a variety of assumptions regarding the missing data mechanism [7]. A full-data distribution is specified, then followed by an examination of inferences across a range of values for one or more unidentified parameters [7, 8]. When the missingness occurs on binary variables, these unidentified parameters can take the form of odds ratios, expressing the odds of a nonrespondent experiencing the event versus a respondent [3, 9, 10].

When a decision is required, a drawback of sensitivity analysis is that it produces a range of answers rather than a single answer [8]. Several authors have proposed model-based methods for obtaining a single inference which involve placing an informative prior distribution on the unidentified parameters that characterize assumptions about the missing data mechanism. Inferences are then drawn that combine a range of assumptions regarding the missing data mechanism [7, 11].

An alternative approach to model-based methods for handling data with nonignorable missingness is multiple imputation, where missing values are replaced with two or more plausible values. Multiple imputation methods have several advantages over model-based methods for analyzing data with missing values. These advantages include: (1) they allow standard complete-data methods of analysis to be performed once the data have been imputed; and (2) auxiliary variables that are not part of the analysis procedure can be included in the imputation procedure to increase efficiency and reduce bias [4, 12, 13].

Most methods for generating multiple imputations assume the missing data mechanism is ignorable. Methods for multiple imputation with nonignorably missing data include those of Carpenter et al. [14] who use a reweighting approach to investigate the influence of departures from the ignorability assumption on parameter estimates. van Buuren et al. [15] perform a sensitivity analysis with multiply imputed data using offsets to explore how robust their inferences are to violations of the assumption of ignorability. Hedeker et al. [3] describe a multiple imputation approach for nonignorably missing binary data from a smoking cessation study. Imputations are generated by positing an odds ratio reflecting the odds of smoking for nonrespondents versus respondents. A limitation of these approaches is that they do not take into account uncertainty regarding the missing data mechanism. Instead, they provide a range of inferences for various ignorability assumptions.

Recently, Siddique et al. [16] developed a multiple imputation approach for handling continuous nonignorably missing data in which multiple imputations are generated from many imputation models where each imputation model represents a different assumption regarding the missing data mechanism. By using more than one imputation model, missing data mechanism uncertainty is incorporated into final parameter estimates.

In this paper, we extend the approach of Siddique et al. [16] to the case of nonignorably missing binary data. We generate our imputations using multiple models and then use specialized combining rules that account for between-model variability to generate inferences that take into account missing data mechanism uncertainty. Our goal is to develop a multiple imputation framework analogous to model-based methods such as those of Daniels and Hogan [7], Kaciroti et al. [10], and Rubin [17] that incorporate a range of ignorability assumptions into one inference. Implementation of our methods is straightforward using standard imputation software.

The outline for the rest of this paper is as follows. In Section 2 we describe a smoking cessation trial that motivated this work. In Section 3 we describe methods for generating multiple imputations for binary data from multiple models that take into account missing data mechanism uncertainty. We also describe diagnostics that measure the amount of missing data mechanism uncertainty that has been incorporated into the standard error of a post-imputation parameter estimate. Section 4 presents the results of a simulation study. In Section 5 we implement our approach using data from the smoking cessation trial. Section 6 provides implementation guidelines and a discussion.

Closely related to the concept of ignorability are the missing data mechanism taxonomies “missing at random” (MAR) and “not missing at random” (NMAR). MAR requires that the probability of missingness depends on observed values only, while ignorability includes the additional assumption that the parameters that generate the data and the parameters governing the missing data mechanism are distinct [4]. While distinctness of these two sets of parameters cannot always be assumed, for the purposes of this paper we will use the terms MAR and ignorable interchangeably and the terms NMAR and nonignorable interchangeably.

2 Motivation: A smoking cessation study

Our data come from a smoking cessation study described in Gruder et al. [18]. This three-arm study evaluated the effectiveness of adding group-based treatment to an existing smoking cessation intervention comprised of a television program and self-help manual. Two types of group-based treatments were evaluated: one that included social support (buddy training) and relapse prevention training, and one that was a general group discussion of stopping smoking. The control condition used only the television and self-help materials. Participants were smokers who had registered for the existing television-based program (to receive the self-help materials) and who indicated an interest in attending group-based meetings. Although participants were randomized to condition, only 50% of the participants scheduled to attend a group session came to at least one meeting. Thus, for analysis, the original report considered four ‘conditions’: the two group treatments, a ‘no show’ group consisting of individuals who were randomized to a group treatment but never showed up for any group meetings, and the no-contact control condition. Here, for simplicity and exposition, we combine the controls and no-shows into one group and the two active treatments into a second group. Hereafter, we refer to this first group as control and the second as treatment.

Smoking outcomes were collected at four postintervention telephone interviews, the first of which was conducted immediately postintervention and then 6, 12, and 24 months later. The first postintervention interview assessed demographic characteristics, television viewing, and manual use. Subjects were dichotomized as either daily users or less-than-daily users for each of these two program media. Abstinence at the first assessment was defined as self-report of no smoking for 3 days prior to the interview, as some subjects were called as soon as 3 days after the quit day specified in the program. At six, 12, and 24 months, abstinence was defined as self-report of no smoking for 7 days prior to the interview.

Table 1 lists the percent smoking and percentage of missing values by measurement wave and treatment group. While there were apparent differences in rates of smoking between groups at the end of the program, rates are very similar from 6 months onward. Postintervention rates of missingness range from 4% to 28% and are higher in the control group at every postintervention time point. Missing data were monotonically missing. Data on race, television viewing, and manual use were complete. In the treatment group, 11% of participants were black and television and manual use were 36% and 56%, respectively. In the control group, 33% of participants were black and television and manual use were 19% and 22%, respectively.

Table 1.

Number (percent) smoking and number (percent) of missing values by measurement wave and treatment group

Measurement Wave	Treatment (n=190)		Control (n=299)
	Smoking No. (%)	Missing No. (%)	Smoking No. (%)	Missing No. (%)
End of program	110/190 (57.9)	0 (0.0)	229/299 (76.6)	0 (0.0)
6 months	150/182 (82.4)	8 (4.2)	232/272 (85.3)	27 (9.0)
12 months	140/176 (79.6)	14 (7.4)	206/253 (81.4)	46 (15.4)
24 months	118/156 (75.6)	34 (17.9)	176/216 (81.5)	83 (27.8)

We focus our attention on the treatment differences in smoking at 24 months. Based on the raw observed status data in Table 1, the odds of smoking in the treatment group at month 24 were lower than those in the control group: odds ratio=0.71; SE=0.18; 95% CI: (0.43, 1.17). This result excludes over a quarter of the sample. Assuming that missing=smoking results in an odds ratio=0.62; SE=0.15; 95% CI: (0.38, 1.01).

The complete-case analysis assumes missing smoking values are ignorably missing. An underlying concern was whether missing values were nonginorably missing. Specifically, investigators believed that participants with missing values were more likely to be smokers than participants with observed values, especially in the control group. The motivation for the work described here was to develop imputation methods for handling missing binary data that use all available information and take into account uncertainty in the ignorability assumption in order to estimate the effect of treatment on smoking outcomes.

3 Methods

Our approach proceeds as follows. First, a distribution of imputation models is specified where each model makes a different assumption regarding the missing data mechanism. Then, nested multiple imputation is conducted by drawing M models from this distribution of models and generating N multiple imputations from each of the M models resulting in M × N complete data sets. The complete-data analysis method is applied to each of the M × N complete data sets, and special nested imputation combining rules are used to obtain point estimates and standard errors for parameters of interest. We also provide formulas for quantifying rates of missing information.

3.1 Specification of the imputation model distribution

The first step in the process is to identify a distribution of models from which to sample. Model choice will depend on subjective notions regarding the dissimilarity of observed and missing values that the imputer wishes to formalize. Ideally, this external information is elicited from experts or those who collected the data.

Rubin [19] notes the importance of using easily communicated models to generate multiple imputations assuming nonignorability so that users of the completed data can make judgments regarding the relative merits of the various inferences reached under different nonresponse models. A simple transformation, due to Rubin [19, p. 203] for generating nonignorable imputed values from ignorable imputed values for a continuous variable Y_i is

$$(\text{nonignorable}\text{imputed}{Y}_i)=k\times (\text{ignorable}\text{imputed}{Y}_i).$$ (1)

For example, if k = 1.2 then the assumption is that, conditioning on other observed information, missing values are 20% larger than observed values. In order to create a distribution of nonignorable (and ignorable) models, Siddique et al. [16] replace the constant multiplier k in Equation 1 with multiple draws from some distribution. When the imputer believes that missing values tend to be larger than observed values then potential distributions for k might be a Uniform (1, 3) or Normal (1.5, 1) distribution. By centering the distribution of k around values equal to 1.0, one can generate imputations that are centered around a missing at random mechanism but with additional uncertainty.

If Y_i is binary, Equation 1 will generate implausible values. We instead propose the following approach. Let π̂_nonignr and π̂_ignr represent the probability of the event under nonignorability and ignorability, respectively, and consider the odds ratio

$$\frac{{\widehat{\pi }}_{\mathit{nonignr}}/(1-{\widehat{\pi }}_{\mathit{nonignr}})}{{\widehat{\pi }}_{\mathit{ignr}}/(1-{\widehat{\pi }}_{\mathit{ignr}})}=k.$$ (2)

Thus k is the odds of the event for subjects with nonignorable missing data as compared to the odds for subjects with ignorable missing data. Taking the logarithm of both sides and rearranging, we obtain

$$\mathit{logit}({\widehat{\pi }}_{\mathit{nonignr}})=log(k)+\mathit{logit}({\widehat{\pi }}_{\mathit{ignr}}).$$ (3)

Using this equation, we can calculate logit(π̂_ignr) under an MAR assumption from, for example, a logistic regression model, then apply the multiplier k to obtain probabilities (after applying the inverse logit transformation) assuming nonignorability. The probability π̂_nonignr is then used to generate binary imputed values assuming nonignorability. The multiplier k encodes beliefs about the nonignorable missing data mechanism on an odds ratio scale. For example, if k = 2, then the assumption is that, conditioning on other observed information, the odds of the event are double for subjects with missing values as compared to subjects with non-missing values. This approach, of expressing the difference between nonrespondents and respondents in terms of an odds ratio is similar to that used by Hedeker et al. [3], White et al. [9], and Kaciroti et al. [10]. A novel aspect of our method is that we take into account both uncertainty in the missing values (via multiple imputation) and uncertainty in the missing data mechanism (by drawing multiple values of k).

As with the multiplier described in Equation 1 above, multiple models can be generated by drawing the multiplier in Equation 3 from some distribution; for example, a Normal or Uniform distribution. If the imputer wants to generate imputations that are centered around a missing at random mechanism but with additional uncertainty, they could specify a distribution centered around log(1) for the multiplier. Note that as k → ∞, we obtain the missing = smoking result. The multiplier k and its distribution are not estimable from the observed data and must be specified by the imputer.

Daniels and Hogan [7] categorize the priors used in a sensitivity analysis as departures from a MAR mechanism. They use the categories: MAR with no uncertainty, MAR with uncertainty, NMAR with no uncertainty, and NMAR with uncertainty. Viewed in this framework, the standard MAR assumption (MAR with no uncertainty) is simply one mechanism across a continuum of mechanism specifications and is equivalent to using a distribution with point mass at log(1) for the multiplier in Equation 3. Note that when we use the term “imputation model uncertainty” we are referring to uncertainty in the missing data mechanism as governed by uncertainty in the multiplier k.

3.2 Nested multiple imputation

Once the distribution of models has been specified, imputation proceeds in two stages. First M models are drawn from the distribution of models. Then N multiple imputations for each missing value are generated for each of the M models, resulting in M × N complete data sets.

More specifically, let the complete data be denoted by Y = (Y_obs, Y_mis). For the first stage, the imputation model ψ is drawn from its predictive distribution ψ^m ~ p(ψ) where m = 1, 2, …, M. The second stage starts with each model ψ^m and draws N independent imputations conditional on ψ^m, $Y_{\text{mis}}^{(m,n)}~p(Y_{\text{mis}}\mid Y_{\text{obs}},{\psi }^m)$ where n = 1, 2, …, N.

Because the M × N nested multiple imputations are not independent draws from the same posterior predictive distribution of Y_mis, it is necessary to use nested multiple imputation combining rules [20, 21] in order to take into account variability due to the multiple models (for justification, see [16]). Nested multiple imputation combining rules are presented in the Appendix.

3.3 Rates of missing information

Harel [21] derived rates of missing information for nested multiple imputation based on the amount of missing information due to model uncertainty and missingness. These rates include an overall rate of missing information γ, which can be partitioned into a between-model rate of missing information γ^b, and a within-model rate of missing information γ^w. Using quantities described in the Appendix, let Q̄ be the overall average of all M × N point estimates, Ū, the overall average of the associated variance estimates, B, the between-model variance, and W, the within-model variance. With no missing information (either due to nonresponse or imputation model uncertainty), the variance of (Q − Q̄) reduces to Ū so that the estimated overall rate of missing information is [21]

$$\widehat{\gamma }=\frac{B+(1-\frac{1}{N})W}{\overline{U}+B+(1-\frac{1}{N})W}.$$ (4)

If the correct imputation model is known, then B, the between-model variance, is 0 and the estimated rate of missing information due to nonresponse is

$${\widehat{\gamma }}^w=\frac{W}{\overline{U}+W}.$$ (5)

Roughly speaking, Equation 4 measures the fraction of total variance accounted for by nonresponse and model uncertainty and Equation 5 measures the fraction of total variance accounted for by nonresponse when the correct imputation model is known. See Harel [21] for details. The estimated rate of missing information due to model uncertainty is then γ̂^b = γ̂ − γ̂^w.

In a multiple-model multiple imputation framework, Siddique et al. [16] use the ratio $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ to measure the contribution of missing data mechanism uncertainty to the overall rate of missing information. For example, a value of $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ equal to 0.5 would suggest that half of the overall rate of missing information is due to mechanism uncertainty, the other half due to missing values. We anticipate that most researchers would not want to exceed this value unless they have very little confidence in their imputation model. Note that most imputation procedures use one model and implicitly assume that $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ is equal to 0.

In the next section we present simulations showing that including more than one imputation model in an imputation procedure increases both γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ and increases the coverage of parameter estimates versus procedures that use only one imputation model.

4 Simulation study

The goal of the simulation study was to better understand how different assumptions regarding ignorability and mechanism uncertainty influence point estimates, their standard errors, and the coverage and width of their nominal 95% confidence intervals. We examined a scenario in which the treatment group data were MAR while the control group data were NMAR. Such settings, in which the missing data mechanism differs across treatment arms, can occur in practice, especially when contact time differs across arms, and represents a situation in which severe bias in the treatment effect estimate could occur when assuming MAR in both conditions. Longitudinal binary data with missing values were simulated according to the following data generating model:

$$y_{ij}={\beta }_0+{\beta }_1{\mathit{Time}}_j+{\beta }_2({\mathit{Drop}}_i\times {\mathit{Time}}_j)+{\beta }_3({\mathit{Drop}}_i\times {\mathit{Time}}_j\times {\text{Trt}}_i)+v_{0i}+{\epsilon }_{ij}$$ (6)

where y_ij is a continuous latent variable to be dichotomized, Time_j is coded 0, 1, 2, 3 for four timepoints, Trt_i is dummy-coded as 1 for treatment and 0 for control, and Drop_i is dummy-coded as 1 for subjects who dropped out of the study at any point and 0 for completers. The regression coefficients were defined to be: β₀ = log(0.3), β₁ = log(1.5), β₂ = log(2), β₃ = log(0.5) = −β₂. Using this setup, the slopes of the treatment group dropouts and nondropouts and the non-dropout control groups are equal (and take the value β₁) while the dropout control group has a steeper slope (equal to β₁ + β₂). Thus, while there is a difference in slopes between the treatment and control groups, failing to take into account the missing data mechanism will result in a treatment effect estimate biased towards zero due to the fact that control subjects with higher values are more likely to be missing.

The random subject effect v_0i was assumed normal with mean zero and variance π²/3 so that the intra-class correlation was 0.5. The errors ε_ij were assumed to follow a standard logistic distribution. Binary data were generated by making simulated values equal to 1 when y_ij ≥ 0 and 0 otherwise. Thus, the expected percent experiencing the event in the treatment group and the non-dropout controls at the four timepoints are 29.3, 34.8, 40.7, and 46.7. For the control group dropouts, the expected percent are 29.3, 44.9, 60.9, and 74.2.

We used a sample size of 150 subjects in each group with 100 dropouts per group. We generated nonignorable missing values on y_ij using the following rule: at time points 1, 2, and 3, subjects in the dropout group dropped out with probabilities (1/3, 2/3, 1) so that the overall proportions of missing values were 0.22, 0.52, and 0.67 for the three final timepoints. Each treatment group was imputed separately so that imputed values depended only on information from other cases in the same treatment arm.

Imputation of the simulated binary data using the multiplier approach of Section 3 proceeded as follows. We first generated 2 imputations for each missing value at time points 1, 2, and 3 using MICE [22] with a logistic regression imputation model [19, pp. 169–170] which assumes the missing data are MAR. The imputation model for each time point conditioned on values from all other time points. Thus, for subject i at time j, our ignorable imputation model is

$$\text{logit}\{Pr(y_{ij}=1)\}={\alpha }_0+{\alpha }^T{y}_{i,-j}$$

where the notation y_i,−j represents values of y_i at all times other than time j.

Imputations were generated after 20 iterations through the Gibbs sampler as suggested by van Buuren and Groothuis-Oudshoorn [22]. The fully conditional specifications method of MICE has been shown to work well in many settings when data are nonignorably missing [23]. To generate nonignorable imputations, we then re-imputed missing values again, this time using Equation 3 with a multiplier drawn from one of the ignorablity/uncertainty distributions described in Sections 4.1 and 4.2. We repeated this procedure 100 times to generate 200 imputations from 100 imputation models. As in Siddique et al. [16], M = 100 imputation models and N = 2 imputations within each model were chosen so that the degrees of freedom for the between-model variance M − 1 and the within-model variance M(N − 1) were approximately equal. This allowed us to estimate between- and within-model variance with equal precision which is necessary for stable measurements of the rates of missing information [21].

We then analyzed the 200 imputed data sets using a logistic regression model to estimate the log odds ratio of the treatment group experiencing the event versus controls at Time_j = 3. We focus our attention on this endpoint as it is the simplest analysis that still allows us to examine how assumptions regarding ignorability and mechanism uncertainty influence our inferences. Results across the 200 imputed data sets were combined using the nested imputation combining rules described in the Appendix. One thousand replications for the above scenario were simulated.

A MICE function for generating nonignorable imputed values using logistic regression imputation is available from the first author. R code for combining nested multiple imputation inferences and calculating rates of missing information is available online [24].

4.1 Ignorability assumptions

We explored the effect of imputing under four different ignorability assumptions which we refer to as MAR, Weak NMAR, Strong NMAR, and Misspecified NMAR. We now discuss each of these assumptions in turn:

1. Missing at Random (MAR): Under this assumption, we generate multiple imputations assuming the data are missing at random. Specifically, we generate imputations where the multiplier in Equation 3 is drawn from a Normal distribution with a mean of log(1) (nonrespondents have the same odds of experiencing the event as respondents).

2. Weak Not Missing at Random (Weak NMAR): Under this assumption, we generate multiple imputations assuming the data are NMAR with nonrespondents somewhat different from respondents. Specifically, the multiplier in Equation 3 is drawn from a Normal distribution with a mean of log(2) (nonrespondents have twice the odds of experiencing the event as respondents).

3. Strong NMAR: Here we generate multiple imputations assuming that nonrespondents are quite a bit different than respondents. Imputations are generated using a multiplier distribution mean of log(3).

4. Misspecified NMAR: Here we generate multiple imputations assuming the data are NMAR but that nonrespondents are less likely to experience the event than respondents even though in truth the reverse is true. Imputations assuming misspecified NMAR are generated using a multiplier drawn from a Normal distribution with a mean of log(0.5) (nonrespondents have half the odds of experiencing the event). We chose this assumption to evaluate whether incorporating model uncertainty can increase coverage even when the imputer is wrong about the nature of nonignorability.

4.2 Missing data mechanism uncertainty assumptions

In addition to generating imputations using the above ignorability assumptions, we also generated imputations based on four different assumptions regarding how certain we were about the missing data mechanism. When there is no mechanism uncertainty, all imputations are generated from the same model. When there is mechanism uncertainty, then multiple models are used. All models are centered around one of the ignorability assumptions in Section 4.1. Uncertainty is then characterized by departures from the central model. The four different uncertainty assumptions used to generate multiple models were no, mild, moderate, and ample uncertainty. These assumptions are described below.

To determine the standard deviation of the multiplier distribution, we used the following approach. Let k_upper and k_lower be the range for the multiplier k in Equation 3 and assume these values correspond to the endpoints of a 95% confidence interval of a normal distribution. The equation for the standard deviation is then

$$sd(\mathit{log}(k))=\frac{\mathit{log}(k_{\mathit{upper}})-\mathit{log}(k_{\mathit{lower}})}{2\times 1.96}=\frac{\mathit{log}(\mathit{ratio})}{3.92}.$$ (7)

Thus we specify the standard deviation of the multiplier distribution in terms of the ratio in Equation 7.

1. No uncertainty: This is the assumption of most imputation schemes. One imputation model is chosen and all imputations are generated from that one model. In particular, the most common imputation approach is to assume the data are MAR with no uncertainty. For the imputation approach described in Equation 3, imputations with no mechanism uncertainty were generated by using the same multiplier for all 100 imputation models.

2. Mild uncertainty: Here we assume that there is a small degree of uncertainty regarding what is the right mechanism. By incorporating uncertainty, imputations are generated using multiple models. Specifically, values for the multiplier log(k) in Equation 3 were drawn from a Normal distribution with a standard deviation based on the ratio in Equation 7 being equal to 2.

3. Moderate uncertainty: Multiple models with moderate uncertainty were generated by setting the ratio in Equation 7 equal to 3.

4. Ample uncertainty: The multiplier was drawn from a Normal distribution with a standard deviation based on the ratio in Equation 7 being equal to 4.

With four ignorability and four uncertainty assumptions, we imputed data under a total of 16 scenarios. For each scenario, we evaluated the bias and RMSE of the post-multiple-imputation treatment log odds at time 3 as well as the coverage rate and width of the nominal 95% confidence interval. In addition, we calculated measures of missing information: the overall estimated rate of missing information (γ̂ in Equation 4), the estimated rate of missing information due to nonresponse (γ̂^w in Equation 5), the estimated rate of missing information due to mechanism uncertainty, γ̂^b = γ̂ − γ̂^w, and the estimated contribution of mechanism uncertainty to the overall rate of missing information as measured by the ratio $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$.

Under the data simulation set up described by Equation 6, the treatment group data are MAR while the control data are NMAR. We performed two sets of imputations for the missing data. In the first set, we imputed the treatment group data assuming MAR with no uncertainty for every scenario and only imputed the control data using the 16 different scenarios (Table 2). The second set of simulations used the same ignorability and uncertainty scenarios for both intervention groups (Table 3).

Table 2.

Treatment effect (log odds ratio) estimates from a simulation study of multiple imputation of binary data using multiple models. One hundred models, 2 imputations within each model. Each row represents a different assumption regarding the control group missing data mechanism. Treatment group missing data are assumed to be MAR with no uncertainty throughout.

Ignore Assump.	Uncertainty	Mult.* Mean	Mult.* Ratio**	Bias	RMSE	Cvg.	Width of CI	γ̂	γ̂w	γ̂b	$\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$
MAR	None	log(1)	log(1)	0.66	0.75	59.1	1.47	0.60	0.60	0.00	0.00
	Mild	log(1)	log(2)	0.66	0.75	62.8	1.55	0.64	0.60	0.03	0.06
	Moderate	log(1)	log(3)	0.66	0.75	67.9	1.65	0.68	0.60	0.08	0.12
	Ample	log(1)	log(4)	0.66	0.75	72.6	1.74	0.71	0.60	0.11	0.16
Weak NMAR	None	log(2)	log(1)	0.22	0.42	90.6	1.47	0.58	0.59	0.00	0.00
	Mild	log(2)	log(2)	0.22	0.42	91.9	1.53	0.62	0.59	0.03	0.05
	Moderate	log(2)	log(3)	0.23	0.43	93.2	1.62	0.66	0.59	0.07	0.11
	Ample	log(2)	log(4)	0.23	0.43	94.9	1.70	0.69	0.59	0.10	0.15
Strong NMAR	None	log(3)	log(1)	−0.01	0.36	94.9	1.46	0.56	0.57	0.00	0.00
	Mild	log(3)	log(2)	−0.01	0.36	95.5	1.51	0.59	0.57	0.03	0.05
	Moderate	log(3)	log(3)	0.00	0.36	97.0	1.58	0.63	0.56	0.06	0.10
	Ample	log(3)	log(4)	0.00	0.36	97.7	1.65	0.65	0.56	0.09	0.14
Misspec. NMAR	None	log(.5)	log(1)	1.10	1.16	14.0	1.48	0.60	0.60	0.00	0.00
	Mild	log(.5)	log(2)	1.10	1.16	16.2	1.55	0.63	0.60	0.03	0.05
	Moderate	log(.5)	log(3)	1.10	1.16	20.7	1.64	0.67	0.60	0.07	0.11
	Ample	log(.5)	log(4)	1.10	1.16	24.2	1.72	0.70	0.60	0.10	0.15

Mult: multiplier; RMSE: root mean squared error; Cvg: coverage

^*Multipliers drawn from a Normal distribution;

^**Multiplier SD= mult. ratio/3.92

Table 3.

Treatment effect (log odds ratio) estimates from a simulation study of multiple imputation of binary data using multiple models. One hundred models, 2 imputations within each model. Each row represents a different assumption regarding the missing data mechanism which is assumed to be the same in both intervention groups.

Ignore Assump.	Uncertainty	Mult.* Mean	Mult.* Ratio**	Bias	RMSE	Cvg.	Width of CI	γ̂	γ̂w	γ̂b	$\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$
MAR	None	log(1)	log(1)	0.66	0.75	59.1	1.47	0.60	0.60	0.00	0.00
	Mild	log(1)	log(2)	0.66	0.76	66.5	1.62	0.66	0.60	0.06	0.09
	Moderate	log(1)	log(3)	0.66	0.76	75.2	1.80	0.72	0.60	0.12	0.16
	Ample	log(1)	log(4)	0.66	0.76	80.2	1.95	0.76	0.60	0.15	0.20
Weak NMAR	None	log(2)	log(1)	0.67	0.76	57.0	1.47	0.58	0.58	0.00	0.00
	Mild	log(2)	log(2)	0.67	0.76	64.2	1.60	0.63	0.58	0.06	0.09
	Moderate	log(2)	log(3)	0.67	0.76	72.4	1.76	0.69	0.57	0.12	0.16
	Ample	log(2)	log(4)	0.68	0.77	77.9	1.89	0.73	0.57	0.16	0.21
Strong NMAR	None	log(3)	log(1)	0.68	0.77	55.5	1.45	0.54	0.54	0.00	0.00
	Mild	log(3)	log(2)	0.69	0.77	61.1	1.56	0.59	0.54	0.05	0.09
	Moderate	log(3)	log(3)	0.69	0.77	68.7	1.69	0.65	0.53	0.11	0.17
	Ample	log(3)	log(4)	0.69	0.77	73.5	1.81	0.69	0.53	0.15	0.22
Misspec. NMAR	None	log(.5)	log(1)	0.66	0.76	58.6	1.47	0.59	0.59	0.00	0.00
	Mild	log(.5)	log(2)	0.66	0.76	65.2	1.60	0.64	0.59	0.06	0.08
	Moderate	log(.5)	log(3)	0.66	0.76	73.8	1.76	0.70	0.59	0.11	0.16
	Ample	log(.5)	log(4)	0.67	0.76	78.9	1.90	0.74	0.58	0.15	0.20

Mult: multiplier; RMSE: root mean squared error; Cvg: coverage

^*Multipliers drawn from a Normal distribution;

^**Multiplier SD= mult. ratio/3.92

4.3 Simulation results

Focusing on MI inference for the log odds ratio, Table 2 provides the results of our imputations under the 16 different ignorability/uncertainty scenarios for the control group and a MAR with no uncertainty assumption for the treatment group using logistic regression imputation and the transformation described in Equation 3. Beginning with the first row, we see that assuming MAR with no mechanism uncertainty for the control group results in estimates that are highly biased with a coverage rate of 59%. This result is not surprising as the control data are nonignorably missing. Since we are assuming no mechanism uncertainty, γ̂^b, the estimated fraction of missing information due to mechanism uncertainty is equal to 0 as is $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$, the estimated contribution of mechanism uncertainty to the overall rate of missing information.

Moving to the subsequent rows in Table 2 still assuming MAR, we see the effect of increasing mechanism uncertainty on post-imputation parameter estimates. Both bias and RMSE are the same as with no uncertainty, but now coverage increases as we increase the amount of mechanism uncertainty in our imputation models. The mechanism here is clear—by increasing the amount of uncertainty in our imputation models, we are now generating imputations under a range of ignorability assumptions. This additional variability in the imputed values translates to wider confidence intervals and hence greater coverage. Both γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ increase as the amount of mechanism uncertainty increases. As mechanism uncertainty increases, it becomes a larger proportion of the overall rate of missing information.

Since control group missing values in our simulation study were more likely to be events than observed control group values, the weak and strong NMAR conditions result in smaller bias than the imputations assuming the control data are MAR. As before, increasing the amount of mechanism uncertainty does not change bias but increases coverage (by increasing the width of the 95% confidence intervals) to the point that weak NMAR with ample uncertainty achieves the nominal level. Under the strong NMAR assumption, bias is small enough that there is no benefit to additional mechanism uncertainty in terms of better coverage. As before, additional mechanism uncertainty is reflected in increasing values of γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$.

Finally, the last four rows of Table 2 present results when the missing data mechanism is misspecified. Here, the missing data are imputed assuming that control group missing values are less likely to be events than observed values (even after conditioning on observed information) when the reverse is true. Not surprisingly, bias and RMSE are poor in this situation, but by incorporating mechanism uncertainly into our imputations we are able to build some robustness into our imputation model. With ample uncertainly, coverage is 24%, an increase over the coverage rate of 14% which is the result of using the same (misspecified) model for all imputations.

Table 3 presents simulation results when the assumption regarding the missing data mechanism is the same for both the treatment and control groups despite the fact that the treatment group missing data mechanism is MAR. As a result, the proportion experiencing the event in both groups changes by the same amount and the resulting log odds ratio remains the same across all 16 scenarios. A similar result was seen in Siddique et al. [16] with continuous data. As in Table 2, increasing the amount of mechanism uncertainty has no effect on bias or RMSE of the log odds ratio but widens the width of the 95% confidence interval, increasing coverage and increasing the contribution of mechanism uncertainty (γ̂^b) to the overall rate of missing information. As before, increasing mechanism uncertainty also provides a hedge against misspecification of the missing data mechanism.

In the scenarios in Tables 2 and 3 where there was no mechanism uncertainty, the rate of missing information due to mechanism uncertainty was negative. As noted by Harel and Stratton [25], this is possible due to the use of the method of moments for calculating the rates of missing information. Following their recommendation, we set γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ equal to 0 when γ̂^b was negative.

5 Application to a Smoking Cessation Study

We applied our methods to the smoking cessation data described in Section 2 by imputing the missing smoking outcomes at each time point using the same approach and imputation model distribution parameters as described in the simulation study. The focus of our inference was the log odds of the treatment effect at 24 months. We chose an endpoint analysis as it is the simplest model which still allows us to focus on how assumptions regarding the missing data mechanism affect inferences. Table 4 lists variables that were used in imputation and analysis models and also indicates the percentage of missing values. Each imputation model conditioned on all the variables listed in Table 4 and smoking outcomes were imputed using a model that conditioned on smoking status at other time points in order to make use of all available information. Let y_ij be the smoking status for participant i at time j, j = 0, 1, 2, 3. Our ignorable imputation model for smoking status at a given time point is

Table 4.

Smoking study variables used for imputation and analysis.

Variable Name	Imputation or Analysis?	Percent Missing	Variable Type
End of Study Smoking Status	Imputation	0.0%	Binary
Month 6 Smoking Status	Imputation	7.2%	Binary
Month 12 Smoking Status	Imputation	12.3%	Binary
Month 24 Smoking Status	Both	23.9%	Binary
Race (white/nonwhite)	Imputation	0.0%	Binary
Daily TV viewer (yes/no)	Imputation	0.0%	Binary
Daily Manual User (yes/no)	Imputation	0.0%	Binary
Treatment Group	Both	0.0%	Binary

$$\mathit{logit}\{Pr(y_{ij}=1)\}={\alpha }_0+{\alpha }_1{\text{TV}}_i+{\alpha }_2{\text{Manual}}_i+{\alpha }_3{\text{Race}}_i+{\alpha }^T{y}_{i,-j}$$

where y_i,−j is the smoking status for participant i at all times other than time j. We analyzed the 200 imputed data sets using a logistic regression model estimating month 24 smoking status as a function of treatment group.

As with the simulation, each treatment group was imputed separately. We first assumed the treatment data were MAR with no uncertainty and only the control group data were imputed under different assumptions. We then performed another set of imputations where the imputation model distribution parameters were the same in both intervention groups.

The Weak NMAR and Strong NMAR assumptions assume that participants with missing values have greater odds of being smokers than respondents with the same covariates. The term “Misspecified NMAR” is a misnomer in this setting because we do not actually know the correct specification. We use the term only to be consistent with the simulation study. For Misspecified NMAR, the assumption is that nonrespondents have lower odds of being smokers than respondents.

Table 5 provides estimates, standard errors, confidence intervals, p-values, and rates of missing information for the log odds ratio between the treatment and control groups at month 24 by the 16 different ignorability/uncertainty scenarios assuming the treatment group missing data are MAR with no uncertainty. Table 6 provides the same information when making the same ignorability and uncertainty assumptions in both intervention groups.

Table 5.

Post-imputation intervention log odds ratio (treatment versus control) by ignorability/uncertainty scenario. One-hundred models with 2 imputations per model were used to generate 200 imputations. Multipliers were generated by drawing from a Normal distribution. MAR, Weak NMAR, Strong NMAR, and Misspecified NMAR correspond to Normal distributions with means of log(1), log(2), log(3), and log(.5), respectively. Amounts of uncertainty None, Mild, Moderate, and Ample correspond to Normal distributions with standard deviations of log(1)/4, log(2)/4, log(3)/4, and log(4)/4, respectively. Missing treatment group data were assumed to be MAR with no uncertainty in all scenarios.

Ignore Assump.	Uncertainty	Est.	SE	LCI	UCI	p-val	γ̂	γ̂w	γ̂b	$\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$
MAR	None	−0.28	0.24	−0.75	0.20	0.252	0.18	0.18	0.00	0.00
	Mild	−0.28	0.25	−0.76	0.21	0.265	0.22	0.16	0.06	0.27
	Moderate	−0.27	0.26	−0.78	0.23	0.283	0.26	0.15	0.11	0.41
	Ample	−0.27	0.26	−0.79	0.24	0.294	0.29	0.15	0.14	0.49
Weak NMAR	None	−0.43	0.25	−0.91	0.05	0.081	0.18	0.18	0.00	0.00
	Mild	−0.43	0.25	−0.92	0.06	0.087	0.21	0.15	0.06	0.29
	Moderate	−0.43	0.26	−0.93	0.07	0.095	0.23	0.14	0.09	0.39
	Ample	−0.43	0.26	−0.94	0.09	0.103	0.26	0.15	0.12	0.44
Strong NMAR	None	−0.51	0.25	−0.99	−0.02	0.041	0.17	0.17	0.00	0.00
	Mild	−0.51	0.25	−1.00	−0.01	0.046	0.20	0.15	0.04	0.22
	Moderate	−0.50	0.26	−1.00	−0.00	0.049	0.22	0.15	0.07	0.31
	Ample	−0.50	0.26	−1.01	0.01	0.053	0.23	0.15	0.09	0.37
Misspec. NMAR	None	−0.10	0.24	−0.57	0.38	0.687	0.21	0.21	0.00	0.00
	Mild	−0.09	0.25	−0.58	0.40	0.709	0.26	0.20	0.05	0.21
	Moderate	−0.09	0.26	−0.60	0.41	0.715	0.30	0.20	0.10	0.32
	Ample	−0.09	0.26	−0.61	0.43	0.725	0.34	0.20	0.13	0.40

SE: standard error; LCI: lower 95% confidence interval; UCI: upper 95% confidence interval

Table 6.

Post-imputation intervention log odds ratio (treatment versus control) by ignorability/uncertainty scenario. One-hundred models with 2 imputations per model were used to generate 200 imputations. Multipliers were generated by drawing from a Normal distribution. MAR, Weak NMAR, Strong NMAR, and Misspecified NMAR correspond to Normal distributions with means of log(1), log(2), log(3), and log(.5), respectively. Amounts of uncertainty None, Mild, Moderate, and Ample correspond to Normal distributions with standard deviations of log(1)/4, log(2)/4, log(3)/4, and log(4)/4, respectively. The same assumptions were used in both intervention groups.

Ignore Assump.	Uncertainty	Est.	SE	LCI	UCI	p-val	γ̂	γ̂w	γ̂b	$\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$
MAR	None	−0.28	0.24	−0.75	0.20	0.252	0.18	0.18	0.00	0.00
	Mild	−0.28	0.25	−0.77	0.21	0.264	0.23	0.18	0.04	0.19
	Moderate	−0.28	0.26	−0.78	0.22	0.277	0.27	0.18	0.09	0.33
	Ample	−0.28	0.27	−0.80	0.24	0.289	0.32	0.18	0.14	0.43
Weak NMAR	None	−0.32	0.25	−0.81	0.17	0.196	0.17	0.17	0.00	0.00
	Mild	−0.32	0.25	−0.82	0.18	0.203	0.20	0.14	0.07	0.32
	Moderate	−0.32	0.26	−0.84	0.19	0.213	0.24	0.13	0.11	0.47
	Ample	−0.32	0.27	−0.85	0.20	0.228	0.28	0.14	0.14	0.51
Strong NMAR	None	−0.35	0.25	−0.84	0.14	0.165	0.15	0.15	0.00	0.00
	Mild	−0.35	0.26	−0.85	0.15	0.174	0.18	0.14	0.05	0.25
	Moderate	−0.35	0.26	−0.86	0.16	0.180	0.21	0.15	0.07	0.32
	Ample	−0.35	0.26	−0.87	0.17	0.185	0.23	0.14	0.09	0.40
Misspec. NMAR	None	−0.22	0.24	−0.69	0.25	0.356	0.23	0.23	0.00	0.00
	Mild	−0.22	0.25	−0.71	0.27	0.371	0.28	0.23	0.05	0.16
	Moderate	−0.22	0.26	−0.73	0.29	0.391	0.34	0.24	0.10	0.30
	Ample	−0.22	0.27	−0.75	0.31	0.408	0.39	0.24	0.15	0.38

SE: standard error; LCI: lower 95% confidence interval; UCI: upper 95% confidence interval

Looking first at Table 5, we see that assumptions regarding ignorability and uncertainty have an impact on parameter estimates and their associated standard errors. Starting with those rows assuming MAR in the control group, the point estimate for the treatment log odds changes very little for all four uncertainty assumptions. However, as we assume more uncertainty, the standard errors increase. This same phenomenon was seen in the simulation study. The additional mechanism uncertainty is also reflected in increasing values of γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$. These values are large under ample uncertainty, reflecting the fact that the ample uncertainty assumption is relatively diffuse (i.e. the 95% confidence interval for the odds of smoking for nonrespondents versus respondents ranges from 0.5 to 2) for these data.

As mentioned above, the Weak NMAR and Strong NMAR assumptions in Table 5 assume that control nonrespondents have greater odds of being smokers than respondents even after conditioning on observed information. These assumptions have the effect of increasing the rates of smoking in the control group as compared to the treatment group. Under an assumption of “Strong NMAR” this difference is large enough (OR=0.6) to achieve statistical significance. Under Strong NMAR with Ample uncertainty, the treatment effect is no longer significant at the 0.05 level as a result of the increased standard error due to the large amount of uncertainty incorporated into the imputations. This result underscores the importance of making reasonable assumptions. As mentioned above, the Ample uncertainty assumption is quite diffuse in this setting. As before, the values of γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ appear to capture missing data mechanism uncertainty.

The “Misspecified NMAR” assumption assumes that control nonrespondents have lower odds of being smokers than respondents and as a result, the log odds ratio is smaller here than in any of the other scenarios.

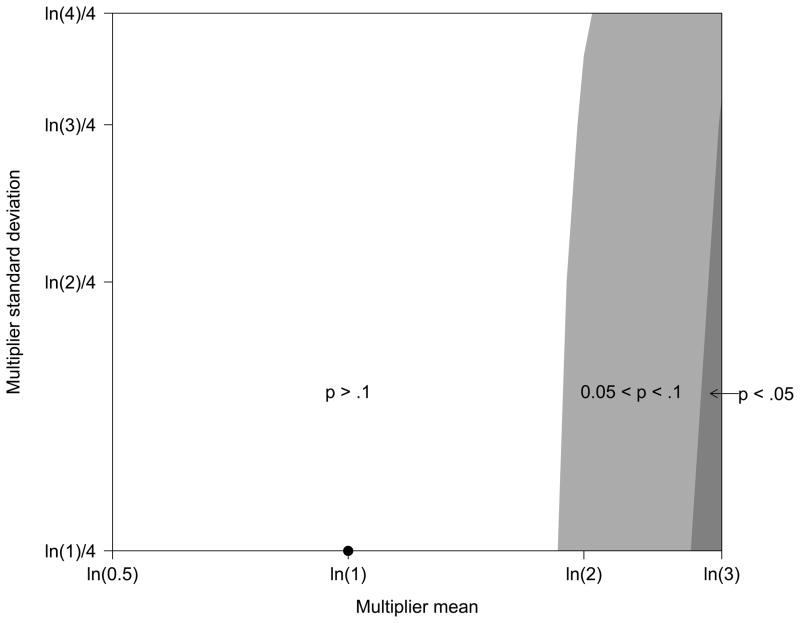
Figure 1 is a contour plot displaying the p-values of the treatment effects in Table 5 [26]. Figure 1 shows the regions where the treatment effect was significant (dark gray), marginally significant (light gray), or non-significant (white) according to a given pair of multiplier means and standard deviations. The point plotted at (ln(1), ln(1)/4) corresponds to a MAR with no uncertainty assumption. Figure 1 makes clear that the effect of the intervention is only significant under the most extreme nonignorability scenarios—Strong NMAR with moderate to no uncertainty.

Figure 1.

Contour plot for the p-values of the treatment effects in Table 5 showing the regions where the treatment was significant (dark gray), marginally significant (light gray), or non-significant (white) according to a given pair of multiplier means and standard deviations. The point plotted at (ln(1), ln(1)/4) corresponds to a MAR with no uncertainty assumption.

Table 6 displays results for the log odds ratio between the treatment and control groups, this time using the same ignorability and uncertainty assumptions in both intervention groups. As in the simulation (Table 3) the point estimate is similar in every ignorability/uncertainty scenario. For each ignorability assumption, the log odds of the control group changed by the same magnitude as the log odds of the treatment group. As a result, their difference remains somewhat constant at each assumption. However, incorporating mechanism uncertainty into the imputations increases the standard error of these parameter estimates.

6 Discussion

We have described a novel method for generating multiple imputations for binary variables in the presence of nonignorable nonresponse. By generating multiple imputations from multiple models, our method allows the user to incorporate missing data mechanism uncertainty into their parameter estimates. This is a useful approach when the missing data mechanism is unknown, which is almost always the case.

As seen in both the simulation studies and the application to the smoking cessation data, post-imputation inferences can be highly sensitive to the choice of the imputation model. With the smoking data, imputation using our methods had a strong effect on the log odds ratio when the treatment group missing data were assumed to be MAR but less of an effect on the odds ratio when the same assumptions were made in both intervention groups. When making the same assumptions in both intervention groups, differences in the odds ratio across assumptions were due to the control group having more missing values so that the odds of smoking in this group was more sensitive to nonignorability assumptions.

A special case of our method is the missing = smoking assumption which is the result when the multiplier k in Equation 3 approaches infinity. Practically speaking, for the smoking cessation data, we obtained results similar to imputing missing = smoking when the multiplier k was approximately equal to 1000 with no uncertainty. This highlights the strong assumption of assuming missing = smoking (nonrespondents have 1000 times the odds of being smokers as respondents) and suggests the use of less extreme assumptions.

The assumption that the treatment group missing data are MAR with no uncertainty while the control group missing data are NMAR (Table 5) is perhaps unreasonable and was chosen to demonstrate that our method allows for different assumptions to be made for each treatment group and to highlight the potential for biased treatment effect estimates when the missing data mechanism differs across conditions. A more realistic assumption might be that the treatment group missing data are “Weak NMAR” while the control group missing data are “Strong NMAR.” At the very least, if the treatment group data are assumed to be MAR, some uncertainty should be attached to this ignorability assumption. The fact that the treatment effect was significant only when making the perhaps unreasonable assumption of MAR in the treatment group and Strong NMAR in the control group (and not significant in all other scenarios) suggests that there is little evidence that the smoking cessation intervention produced a significant treatment effect.

Equation 7 suggests an approach for eliciting expert opinion when choosing a distribution for the multiplier k in Equation 3. First, ask the subject-matter expert to provide an upper and lower bound for the multiplier. Then, assuming the multiplier is normally distributed, set the multiplier distribution mean equal to the average of the lower and upper bounds, and the standard deviation equal to the difference in bounds divided by 3.92. This assumes that the range defined by the upper and lower bounds is a 95% confidence interval which may be appropriate given the tendency of people to specify overly narrow confidence intervals [27]. A similar calculation can be used if assuming a uniform prior.

If the expert is more comfortable working with probabilities, success probabilities under ignorability can be provided and then the probability of success or a risk ratio or risk difference for nonrespondents could be elicited. These values could then be used to calculate an odds ratio for use in Equation 3. See Paddock and Ebener [28] and White et al. [29] for useful references on eliciting expert opinions regarding nonresponse.

We draw our multipliers from normal distributions but this is not required and an analyst may choose any distribution which they think is appropriate. In particular, one may want to draw from a distribution truncated above or below by log(1) if one thinks that nonignorability lies in only one direction. A triangular distribution may be used if the analyst wishes to include lower and upper limits for the distribution of k. Another approach is to draw from a bimodal distribution [30] where the modes represent very different yet equally plausible nonignorability assumptions with little support for an ignorability assumption.

The choice of multiplier distribution and its parameters will have very different effects on inferences and once the data have been imputed, it is important to examine rates of missing information, in particular γ̂^b and $\frac{{\widehat{\gamma }}^b}{\widehat{\gamma }}$ , to confirm that appropriate uncertainty is being incorporated into parameter estimates. For example, if too large a multiplier is used, all imputed values would be imputed as events, resulting in too little variability and decreased coverage.

In line with more of a sensitivity analysis rather than a final analysis, when it is hard to pin down a single range for the multiplier, one may consider a growing set of ranges and observe how subsequent inferences evolve accordingly. This approach will allow the user to make more precise statements regarding the exact conditions under which the obtained results apply [15] and what missing data assumptions result in a change in study conclusions [31]. Contour plots, like those in Figure 1 are useful for interpreting the results obtained from a sensitivity analysis [26] and can help determine whether the significance of a point estimate is robust to different assumptions regarding the missing data mechanism.

Of course, in any applied setting it is impossible to know exactly how strong a nonignorable assumption one should make and how much missing data mechanism uncertainty one should include in their models. We see the second of these dilemmas—incorporating appropriate mechanism uncertainty—as deserving more attention. Attempting to correctly specify the missing data mechanism is difficult in most settings. Still, we see our method as an improvement over methods that assume the missing data mechanism is known. In addition, our method provides easily stated subjective notions regarding nonresponse so that they can be easily stated, communicated, and compared, and can be implemented in a straightforward manner using existing imputation software.

A Appendix: Nested multiple imputation combining rules

In describing nested multiple imputation below, we use notation that follows closely to that of Shen [20].

Let Q be the quantity of interest. Assume with complete data, inference about Q would be based on the large sample statement that

$$(Q-\widehat{Q})~N(0,U)$$

where Q̂ is a complete-data statistic estimating Q and U is a complete-data statistic providing the variance of Q − Q̂. The M × N imputations are used to construct M × N completed data sets, where the estimate and variance of Q from the single imputed data set is denoted by (Q̂ ^(m,n), U^(m,n)) where m = 1, 2, …, M and n = 1, 2, …, N. The superscript (m, n) represents the nth imputed data set under model m. Let Q̄ be the overall average of all M × N point estimates

$$\overline{Q}=\frac{1}{MN}\sum _{m=1}^M\sum _{n=1}^N{\widehat{Q}}^{(m,n)},$$

and let Q̄_m be the average of the mth model,

$${\overline{Q}}_m=\frac{1}{N}\sum _{n=1}^N{\widehat{Q}}^{(m,n)}.$$

Three sources of variability contribute to the uncertainty in Q. These three sources of variability are: Ū, the overall average of the associated variance estimates

$$\overline{U}=\frac{1}{MN}\sum _{m=1}^M\sum _{n=1}^N{U}^{(m,n)},$$

B, the between-model variance

$$B=\frac{1}{M-1}\sum _{m=1}^M{({\overline{Q}}_m-\overline{Q})}^2,$$ (A.1)

and W, the within-model variance

$$W=\frac{1}{M(N-1)}\sum _{m=1}^M\sum _{n=1}^N{({\widehat{Q}}^{(m,n)}-{\overline{Q}}_m)}^2.$$

The quantity

$$T=\overline{U}+(1+\frac{1}{M})B+(1-\frac{1}{N})W$$

estimates the total variance of (Q − Q̄). Interval estimates and significance levels for scalar Q are based on a Student-t reference distribution

$$T^{-\frac{1}{2}}(Q-\overline{Q})~t_v,$$

where v, the degrees of freedom, follows from

$$v^{-1}={\left[\frac{(1+\frac{1}{M})B}{T}\right]}^2\frac{1}{M-1}+{\left[\frac{(1-\frac{1}{N})W}{T}\right]}^2\frac{1}{M(N-1)}.$$

In standard multiple imputation, only one model is used to generate imputations so that the between-model variance B (Equation A.1) is equal to 0 and it is not necessary to account for the extra source of variability due to model uncertainty.