Sample size determination in group-sequential clinical trials with two co-primary endpoints

Abstract

We discuss sample size determination in group-sequential designs with two endpoints as co-primary. We derive the power and sample size within two decision-making frameworks. One is to claim the test intervention’s benefit relative to control when superiority is achieved for the two endpoints at the same interim timepoint of the trial. The other is when the superiority is achieved for the two endpoints at any interim timepoint, not necessarily simultaneously. We evaluate the behaviors of sample size and power with varying design elements and provide a real example to illustrate the proposed sample size methods. In addition, we discuss sample size recalculation based on observed data and evaluate the impact on the power and Type I error rate.

1 Introduction

Traditionally, in clinical trials, a single outcome is selected as a primary endpoint. This endpoint is then used as the basis for the trial design including sample size determination, interim monitoring, and final analyses. However, many recent clinical trials, especially in medical product development, have utilized more than one endpoint as co-primary. “Co-primary” in this setting means that the trial is designed to evaluate if the new intervention is superior to the control on all endpoints, thus evaluating the intervention’s multidimensional effects. Regulators have issued guidelines recommending co-primary endpoints in some disease areas. For example, the Committee for Medicinal Products for Human Use (CHMP) issued a guideline [1] recommending the use of cognitive, functional, and global endpoints to evaluate symptomatic improvement of dementia associated with in Alzheimer’s disease, indicating that primary endpoints should be stipulated reflecting the cognitive and functional disease aspects. Offen et al. [2] provides other examples with co-primary endpoints for regulatory purposes.

The resulting need for new approaches to the design and analysis of clinical trials with co-primary endpoints has been noted [2–4]. Utilizing multiple endpoints may provide the opportunity for characterizing intervention’s multidimensional effects, but also creates challenges. Specifically controlling the Type I and Type II error rates when the multiple co-primary endpoints are potentially correlated is non-trivial. When designing the trial to evaluate the joint effects on ALL of the endpoints, no adjustment is needed to control the Type I error rate. However, the Type II error rate increases as the number of endpoints to be evaluated increases. Thus adjustments in design (i.e., sample size) are needed to maintain the overall power. Methods for clinical trials with co-primary endpoints have been discussed in fixed sample size designs by many authors [5–16]. Even if the correlation among the endpoints is incorporated into the sample size calculation, existing methods often result in large and impractical sample sizes as the testing procedure for co-primary endpoints is conservative. Chuang-Stein et al. [7] and Kordzakhia et al [10] discuss the methods to adjust the significance levels that depend on the correlation among the endpoints in the fixed sample size designs. The methods may provide relatively smaller sample sizes, but also introduce the other challenges. For example, the sample size calculated to detect the joint effect may be smaller than the sample size calculated for each individual endpoint. The prespecified correlation incorporated into the significance level adjustment is usually unknown and may be incorrect. This calls into question whether or not the significance level should be updated based on the observed correlation.

In this paper, we extend previous work for the fixed sample size designs, considering sample size evaluation in the group-sequential setting with co-primary endpoints. As suggested in Hung and Wang [3], a group-sequential design may be a remedial, but practical approach because it offers the possibility to stop a trial early when evidence is overwhelming and thus offers efficiency (i.e., potentially fewer patients than the fixed sample size designs). We discuss the case of two positively correlated continuous outcomes. We consider a two-arm parallel-group trial designed to evaluate if an experimental intervention is superior to a control. The paper is structured as follows: in Section 2 we describe the statistical setting, decision-making frameworks for rejecting the null hypothesis, and definitions of power. In Section 3, we evaluate the behaviors of sample size and power with varying design elements and then provide a real example to illustrate the methods. In Section 4, we describe sample size recalculation and the resulting effect on power and Type I error rate. In Section 5 we summarize the findings and discuss the further developments.

2 Group-sequential designs with two co-primary endpoints

2.1 Statistical setting

Consider a randomized, group-sequential clinical trial of comparing the test intervention (T) with the control intervention (C). Two continuous outcomes are to be evaluated as co-primary endpoints. Suppose that a maximum of L analyses are planned, where the same number of analyses with the same information space are selected for both endpoints. Let n_l and r_ln_l be the cumulative number of participants on the test and the control intervention groups at the l th analysis (l=1,…, L), respectively, where r_l is the sampling ratio. Hence, up to n_L and r_Ln_L participants are recruited and randomly assigned to the test and the control intervention groups, respectively. Then there are n_L paired outcomes (Y_T1i,Y_T2i) (i = 1,…, n_L) for the test intervention group and r_Ln_L paired outcomes (Y_C1j,Y_C2j) (j=1,…, r_Ln_L) for the control intervention group. Assume that (Y_T1i,Y_T2i) and (Y_C1j,Y_C2j) are independently bivariate-normally distributed as $(Y_{\mathrm{T}1i},Y_{\mathrm{T}2i})~{\mathrm{N}}_2({\mu }_{\mathrm{T}1},{\mu }_{\mathrm{T}2},{\sigma }_{\mathrm{T}1}^2,{\sigma }_{\mathrm{T}2}^2,{\rho }_{\mathrm{T}})$ and $(Y_{\mathrm{C}1j},Y_{\mathrm{C}2j})~{\mathrm{N}}_2({\mu }_{\mathrm{C}1},{\mu }_{\mathrm{C}2},{\sigma }_{\mathrm{C}1}^2,{\sigma }_{\mathrm{C}2}^2,{\rho }_{\mathrm{C}})$, respectively. For simplicity, the variances are assumed to be known and common, i.e., ${\sigma }_{\mathrm{T}1}^2={\sigma }_{\mathrm{C}1}^2={\sigma }_1^2$ and ${\sigma }_{\mathrm{T}2}^2={\sigma }_{\mathrm{C}2}^2={\sigma }_2^2$. Note that the method can be applied to the case of unknown variances. For the fixed sample size designs, Sozu et al. (2011) discuss a method for the unknown variance case and show that the calculated sample size is nearly equivalent to that for the known variance in the setting of a one-sided significance level α = 0.025 and power 1−β = 0.8 or 0.9. By analogy from the fixed sample designs, there is no practical difference in the group-sequential setting and the methodology for a known variance provides a reasonable approximation for the unknown variances case.

Let (δ₁, δ₂) denote the differences in the means for the test and the control intervention groups respectively, where δ_k = μ_Tk − μ_Ck (k = 1, 2). Suppose that positive values of (δ₁, δ₂) represent the test intervention’s benefit. We are interested in conducting a hypothesis test to evaluate if the intervention is superior to the control intervention, i.e., the null hypothesis H₀ : δ₁≤ 0 or δ₂ ≤ 0 versus the alternative hypothesis H₁ : δ₁ > 0 and δ₂> 0. Let (Z_1l, Z_2l) be the statistics for testing the hypotheses at the l th analysis, given by $Z_{kl}=({\overline{Y}}_{\mathrm{T}kl}-{\overline{Y}}_{\mathrm{C}kl})/({\sigma }_k\sqrt{{\kappa }_l/n_l})$, where κ_l = (1+r_l)/r_l, and Ȳ_Tkl and Ȳ_Ckl are the sample means given by ${\overline{Y}}_{\mathrm{T}kl}=n_l^{-1}{\sum }_{i=1}^{n_l}{Y}_{\mathrm{T}ki}$ and ${\overline{Y}}_{\mathrm{C}kl}={(r_l{n}_l)}^{-1}{\sum }_{j=1}^{r_l{n}_l}{Y}_{\mathrm{C}kj}$. Z_1l and Z_2l are normally distributed as $\mathrm{N}(\sqrt{n_l/{\kappa }_l}{\delta }_1/{\sigma }_1,1^2)$ and $\mathrm{N}(\sqrt{n_l/{\kappa }_l}{\delta }_2/{\sigma }_2,1^2)$, respectively. Thus (Z_1l, Z_2l) is bivariate-normally distributed with the correlation (r_lρ_T + ρ_C)/(1 + r_l). Furthermore, the joint distribution of (Z₁₁, Z₂₁,…, Z_1L, Z_2L) is 2L multivariate normal with their correlations given by $\text{corr}[Z_{kl},Z_{k^{\prime }{l}^{\prime }}]=\sqrt{{\kappa }_l{n}_{l^{\prime }}/{\kappa }_{l^{\prime }}{n}_l}$ if k = k′; $\sqrt{{\kappa }_l{n}_{l^{\prime }}}(r_l{\rho }_{\mathrm{T}}+{\rho }_{\mathrm{C}})/\{\sqrt{{\kappa }_{l^{\prime }}{n}_l}(1+r_l)\}$if k ≠ k′.

2.2 Decision-making framework, stopping rules, and power

When evaluating the joint effects on both of the endpoints within the context of group-sequential designs, there are the two decision-making frameworks associated with hypothesis testing. One is to reject H₀ if and only if superiority is achieved for the two endpoints simultaneously (i.e., at the same interim timepoint of the trial) (DF-1). The other is to reject H₀ if superiority is achieved for the two endpoints at any interim timepoint (i.e., not necessarily simultaneously) (DF-2). We will discuss the two decision-making frameworks separately as the corresponding stopping rules and power definitions are unique.

DF-1

The DF-1 is relatively simple: if superiority is demonstrated on only one endpoint at an interim, then the trial continues and the hypothesis testing is repeated for both endpoints until the joint significance for the two endpoints is established simultaneously. The stopping rule for DF-1 is formally given as follows:

• At the l th analysis (l=1,…, L−1)

  $$\begin{array}{ll}\text{If}{Z}_{1l}>c_{1l}\text{and}{Z}_{2l}>c_{2l},\hfill & \text{then}\text{reject}{\mathrm{H}}_0\text{and}\text{stop}\text{the}\text{trial},\hfill \\ \text{otherwise},\hfill & \text{continue}\text{to}\text{the}(l+1)\text{th}\text{analysis},\hfill \end{array}$$
  at the Lth analysis

  $$\begin{array}{ll}\text{if}{Z}_{1L}>c_{1L}\text{and}{Z}_{2L}>c_{2L},\hfill & \text{then}\text{reject}{\mathrm{H}}_0,\hfill \\ \text{otherwise},\hfill & \text{do}\text{not}\text{reject}{\mathrm{H}}_0,\hfill \end{array}$$

  where c_1l and c_2l are the critical values, which are constant and selected separately, using any group-sequential method such as the Lan-DeMets (LD) alpha-spending method [17] to control the overall Type I error rate of α, as if they were a single primary endpoint, ignoring the other co-primary endpoint. The testing procedure for co-primary endpoints is conservative. For example, if a zero correlation between the two endpoints is assumed and each endpoint is tested at the one-sided significance level of 2.5%, then the Type I error rate is 0.0625 %. As shown in Section 4, the maximum Type I error rate associated with the rejection region of the null hypothesis increases as the correlation goes toward one, but it is not greater than the targeted significance level.

The power corresponding to DF-1 is

$$1-\beta =Pr\left[{\cup }_{l=1}^L\{A_{1l}\cap A_{2l}\}|{\mathrm{H}}_1\right],$$ (1)

where A_kl = {Z_kl > c_kl }(k= 1,2; l = 1,…, L). The power (1) can be numerically assessed by using multivariate normal integrals. A detailed calculation is provided in Appendix A.1.

DF-2

DF-2 is more flexible than DF-1. If superiority is demonstrated on one endpoint at the interim, then the trial will continue but subsequent hypothesis testing is repeatedly conducted only for the previously non-significant endpoint until superiority is demonstrated. The stopping rule for DF-2 is formally given as follows:

• At the l th analysis (l=1,…, L−1)

  $$\begin{array}{ll}\text{If}{Z}_{1l}>c_{1l}\text{and}{Z}_{2l^{\prime }}>c_{2l^{\prime }}\text{for}\text{some}1\le l^{\prime }\le l,\hfill & \text{then}\text{reject}{\mathrm{H}}_0\text{and}\text{stop}\text{the}\text{trial},\hfill \\ \text{if}{Z}_{2l}>c_{2l}\text{and}{Z}_{1l^{\prime }}>c_{1l^{\prime }}\text{for}\text{some}1\le l^{\prime }\le l,\hfill & \text{then}\text{reject}{\mathrm{H}}_0\text{and}\text{stop}\text{the}\text{trial},\hfill \\ \text{otherwise},\hfill & \text{continue}\text{to}\text{the}(l+1)\text{th}\text{analysis},\hfill \end{array}$$
• at the Lth analysis

  $$\begin{array}{ll}\text{if}{Z}_{1L}>c_{1L}\text{and}{Z}_{2l^{\prime }}>c_{2l^{\prime }}\text{for}\text{some}1\le l^{\prime }\le L,\hfill & \text{then}\text{reject}{\mathrm{H}}_0,\hfill \\ \text{if}{Z}_{2L}>c_{2L}\text{and}{Z}_{1l^{\prime }}>c_{1l^{\prime }}\text{for}\text{some}1\le l^{\prime }\le L,\hfill & \text{then}\text{reject}{\mathrm{H}}_0,\hfill \\ \text{otherwise},\hfill & \text{do}\text{not}\text{reject}{\mathrm{H}}_0.\hfill \end{array}$$

Therefore, following DF-2, the power is

$$1-\beta =Pr\left[\left\{{\cup }_{l=1}^L{A}_{1l}\right\}\cap \left\{{\cup }_{l=1}^L{A}_{2l}\right\}|{\mathrm{H}}_1\right].$$ (2)

Similarly as in the power (1), the power (2) can be calculated by using multivariate normal integrals. For the details, please refer to Appendix A.1.

For simplicity, consider a two-stage group-sequential design with one interim and one final analysis. The probability of rejecting the null hypothesis at the interim analysis is same for DF-1 and DF-2. The difference in power between DF-1 and DF-2 is due to whether or not the null hypothesis is rejected at the final analysis. The difference in decision-making for DF-1 and DF-2 comes from the following two situations where the interim analysis result is inconsistent with the final analysis result even the alternative hypothesis is true, i.e., (i) Endpoint 1 is statistically significant at the interim, but not at the final analysis and similarly and (ii) Endpoint 2 is statistically significant at the interim, but not at the final analysis. Thus DF-1 fails to reject the null hypothesis in both situations even if the alternative hypothesis is true, but DF-2 is able to reject the null hypothesis in both situations. However the likelihood of this scenario occurring is quite low. Thus there is little practical difference in the power and sample size determinations for DF-1 and DF-2. However, DF-2 offers the option of stopping measurement of an endpoint for which superiority has been demonstrated. Stopping measurement may be desirable if the endpoint is very invasive or expensive although stopping measurement may also introduce an operational difficulty into the trial. This will be illustrated in Section 3.

2.3 Maximum sample size and average sample number

We discuss two sample size concepts, i.e., the maximum sample size (MSS) and the average sample number (ASN) based on DF-1 and DF-2, and the corresponding powers (1) and (2) discussed in the previous section.

The MSS is the sample size required for the final analysis to achieve the desired power 1−β. The MSS is given by the smallest integer not less than n_L satisfying the power (1) or (2) for a group-sequential design at the pre-specified δ₁, δ₂, ρ_T and ρ_C, with Fisher’s information time for the interim analyses, n_l/n_L, l = 1,…, L. To find a value of n_L, an iterative procedure is required to numerically solve for the power (1) or (2). This can be accomplished by using a grid search to gradually increase n_L until the power under n_L exceeds the desired power, although this often requires considerable computing resources. To reduce the computational resources, the Newton–Raphson algorithm in Sugimoto et al. [14] or the basic linear interpolation algorithm in Hamasaki et al. [15] may be utilized.

The ASN is the expected sample size under a specific hypothetical reference. Given these pre-specifications, the ASN per intervention group for DF-1 is given by

$$\text{ASN}=n_L\left(1+{\sum }_{l=1}^{L-1}Pr\left[\left\{{\overline{A}}_{11}\cup {\overline{A}}_{21}\right\}\cap \cdots \cap \left\{{\overline{A}}_{1l}\cup {\overline{A}}_{2l}\right\}\right]\right)/L,$$ (3)

and for DF-2,

$$\text{ASN}=n_L\left(1+{\sum }_{l=1}^{L-1}Pr\left[\left\{{\overline{A}}_{11}\cap \cdots \cap {\overline{A}}_{1l}\right\}\cup \left\{{\overline{A}}_{21}\cap \cdots \cap {\overline{A}}_{2l}\right\}\right]\right)/L,$$ (4)

where r_l = 1 and n_l = ln₁, l = 1,…,L. The representations for calculating ASN (3) and (4) are described in Appendix A.2.

The powers, MSS and ASN will depend on the design parameters including differences between means, the correlation structure between the endpoints, the testing procedure (e.g., O’Brien-Fleming (OF) boundary [20], Pocock (PC) boundary [21]), the number of analyses, and the information time.

3. Evaluation of the sample size

3.1 Behavior of the sample size

In this section, we evaluate the behavior of the power, MSS, and ASN as the design parameters vary. Here, without loss of generality, ${\sigma }_1^2={\sigma }_2^2=1^2$ is chosen for simplicity, so that δ₁ and δ₂ are interpret as (standardized) effect sizes.

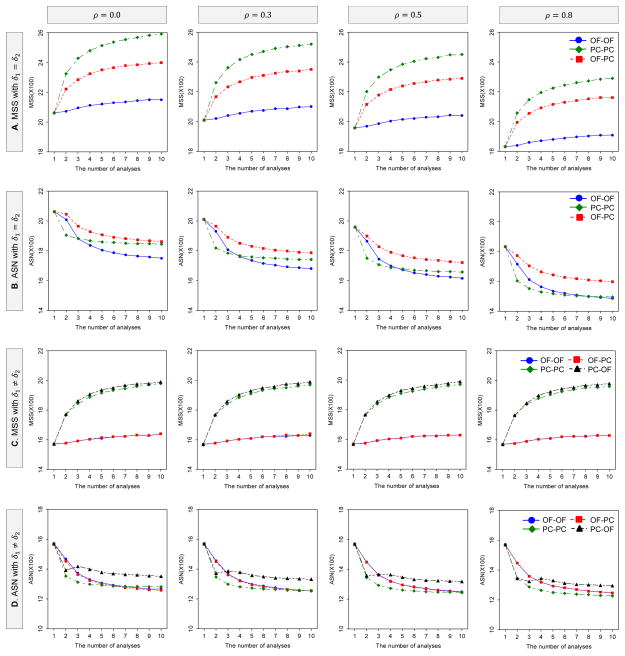
Figures 1 illustrates how the MSS and ASN per intervention group for DF-1 behave as a function of the number of analyses and the boundaries when effect sizes are equal and unequal, i.e., δ₁ = δ₂ and δ₁ ≠ δ₂ between the two endpoints. The MSS and ASN for DF-1 and DF-2 (equally-sized groups: r_l = 1) were calculated to detect the joint difference in the two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where δ₁ = δ₂ = 0.1 for equal effect sizes and δ₁ = 0.1 and δ₂ = 0.2 for unequal effect sizes; ${\sigma }_1^2={\sigma }_2^2=1^2$; ρ_T = ρ_C = ρ = 0.0, 0.3, 0.5 and 0.8. The critical values are determined by the three boundary combinations, i.e., (i) the OF for both endpoints (OF-OF), (ii) the PC for both endpoints (PC-PC) and (iii) the OF for δ₁ and the PC for δ₂ (OF-PC), with the LD alpha-spending method with equal information space.

Figure 1.

Behavior of MSS and ASN for DF-1 as the number of analyses and boundaries vary. The MSS and ASN per intervention group (equally-sized groups: r_l=1) were calculated to detect the joint difference in the two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where δ₁ = δ₂ = 0.1 for A and B, and δ₁ = 0.1 and δ₂ = 0.2 for C and D; ${\sigma }_1^2={\sigma }_2^2=1^2$. When differences between means are equal, the and critical values are determined by the three boundary combinations, i.e, (i) the OF for both endpoints, (ii) the PC for both endpoints and (iii) the OF for δ₁ and the PC for δ₂, with the LD alpha-spending method with equal information space. When differences between means are unequal, in addtion to the three combinations, (iv) the PC for δ₁ and the OF for δ₂ is considered.

When effect sizes are equal, the MSS for the three boundary combinations increases as the number of analyses increases and the correlation is smaller. In all of ρ = 0, 0.3, 0.5 and 0.8, the largest MSS is given by PC-PC, and the smallest MSS by OF-OF. On the other hand, the ASN for the three boundary combinations decreases as the number of analyses increases and the correlation is larger. In all of ρ = 0, 0.3, 0.5 and 0.8, the largest ASN is given by OF-PC.

When effect sizes are unequal δ₁ < δ₂, in addition to the three boundary combinations, one more combination of (iv) the PC for δ₁ and the OF for δ₂ (PC-OF) is considered, δ₁ = 0.1 and δ₂ = 0.2. Similarly as seen with equal effect sizes, the MSS for the four boundary combinations increases as the number of analyses increases, but it does not change as with the correlation varies. The largest MSS is given by PC-PC and PC-OF, and the smallest MSS by OF-OF and OF-PC. On the other hand, the ASN for the four boundary combinations decreases as the number of analyses increases independently of the correlation. The largest ASN is given by OF-OF and OF-PC, and the smallest ASN by PC-PC and PC-OF. When one effect size is relatively smaller (or larger) than the other, the MSS and ASN will be driven by the smaller effect size. In this illustration, as the OF is selected for the smaller effect size and the PC for the larger, the MSS and ASN by OF-PC are approximately equal to those by OF-OF.

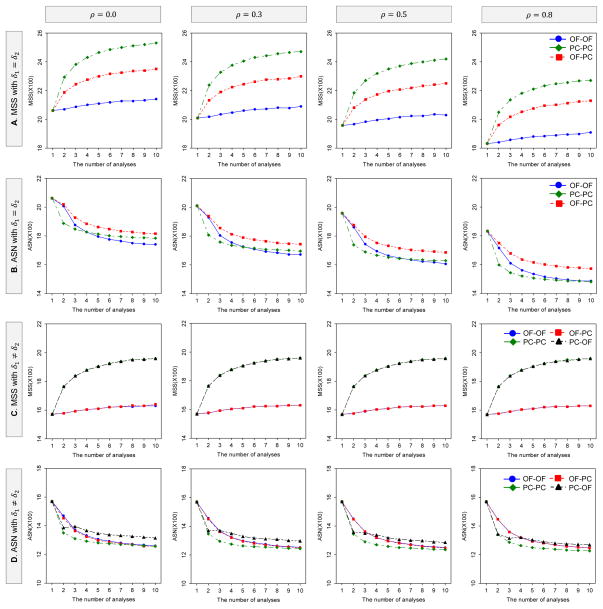
Figures 2 illustrates how the MSS and ASN per intervention group for DF-2 behave as a function of the number of analyses and the boundaries when effect sizes are equal δ₁ = δ₂ and unequal δ₁ ≠ δ₂ between the two endpoints with the same parameter settings as in Figure 1. The MSS and ASN behaviors are similar to those observed for DF-1. The major difference between DF-1 and DF-2 is that the MSS and ASN for DF-2 are smaller than those for DF-1. They are notably smaller as the number of analyses increases, especially when the correlation is low.

Figure 2.

Behavior of MSS and ASN for DF-2 as the number of analyses and boundaries vary. The MSS and ASN per intervention group (equally-sized groups: r_l=1) were calculated to detect the joint difference in the two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where δ₁ = δ₂ = 0.1 for A and B, and δ₁ = 0.1 and δ₂ = 0.2 for C and D; ${\sigma }_1^2={\sigma }_2^2=1^2$. When differences between means are equal, the critical values are determined by the three boundary combinations, i.e, (i) the OF for both endpoints, (ii) the PC for both endpoints and (iii) the OF for δ₁ and the PC for δ₂, with the LD alpha-spending method with equal information space. When differences between means are unequal, in addtion to the three combinations, (iv) the PC for δ₁ and the OF for δ₂ is considered.

If the trial was designed to detect effects on at least one endpoint with a prespecified ordering of endpoints, a choice of different boundaries for each endpoint (i.e., the OF for the primary endpoint and the PC for the secondary endpoint) can provide a higher power than using the same boundary for both endpoints [18, 19]. However, as shown in Figures 1 and 2, the selection of a different boundary has a minimal effect on the power.

3.2 Example

We provide an example to illustrate the sample size methods discussed in the previous sections. Consider the clinical trial, “Effect of Tarenflurbil on Cognitive Decline and Activities of Daily Living in Patients With Mild Alzheimer Disease”, a multicenter, randomized, double-blind, placebo-controlled trial in patients with mild Alzheimer disease (AD) [22]. Co-primary endpoints were cognition as assessed by the Alzheimer Disease Assessment Scale Cognitive Subscale (ADAS-Cog; 80-point scale) and functional ability as assessed by the Alzheimer Disease Cooperative Study activities of daily living (ADCS-ADL; 78-point scale). A negative change score from baseline on the ADAS-cog indicates improvement while a positive change score on the ADCS-ADL indicates improvement. The original sample size per intervention group of 800 patients provided an overall power of 96% to detect the joint difference in the two primary endpoints between the tarenflurbil and placebo groups, by using a one-sided test at 2.5% significance level, with the standardized effect size of 0.2 for both endpoints. In addition, the correlation between the two endpoints was assumed to be zero in the calculation of the sample size although the two endpoints were expected to be correlated (for example, see Doraiswamy [23]).

Table 1 displays the MSS and ASN per intervention group (equally-sized groups: r_l = 1) for the DF-1 and DF-2. The sample size was with an alternative hypothesis of a difference for both ADAS-Cog (δ₁ = 0.2) and ADCS-ADL (δ₂ = 0.2), with the overall power of 96% at the one-sided significance level of 2.5%, where ρ = ρ_T = ρ_C = 0.0, 0.3, 0.5, and 0.8; L = 1, 2, 3, 5, 8 and 10. The critical values are determined by the three boundary combinations, i.e., the OF for both endpoints (OF-OF), the PC for both endpoints (PC-PC), and OF for ADAS-Cog and the PC for ADCS-ADL (OF-PC).

Table 1.

MSS and ASN per intervention group (equally-sized groups) for detecting the joint difference for ADAS-Cog (0.2) and ADCS-ADL (0.2), with DF-1 and DF-2 and the overall power of 96% at the one-sided significance level of 2.5%

Decision-making framework	Correlation	Number of analyses	(i) OF-OF		(ii) PC-PC		(iii) OF-PC
			MSS	ASN	MSS	ASN	MSS	ASN
DF-1	0.0	1	804	804	804	804	804	804
		2	808	725	886	607	854	693
		3	816	647	918	572	876	652
		5	825	604	945	548	895	608
		8	832	579	968	535	912	587
		10	840	573	970	530	920	581
	0.3	1	799	799	799	799	799	799
		2	802	702	880	593	850	676
		3	810	633	912	552	870	638
		5	820	589	940	525	890	593
		8	824	563	960	511	904	571
		10	830	556	970	507	910	564
	0.5	1	791	791	791	791	791	791
		2	794	684	872	580	842	662
		3	801	620	903	536	864	627
		5	810	574	930	506	885	582
		8	816	549	952	492	896	558
		10	820	542	960	488	900	551
	0.8	1	764	764	764	764	764	764
		2	768	644	842	549	818	635
		3	774	588	873	501	840	603
		5	785	543	900	469	860	556
		8	792	520	920	453	872	533
		10	800	514	920	447	880	527
DF-2	0.0	1	804	804	804	804	804	804
		2	808	725	882	605	848	690
		3	813	645	912	569	867	646
		5	825	603	940	540	890	602
		8	832	578	960	524	904	579
		10	830	568	960	518	910	572
	0.3	1	799	799	799	799	799	799
		2	802	702	876	591	842	672
		3	807	632	906	549	861	632
		5	815	586	935	520	880	586
		8	824	562	952	503	896	564
		10	830	555	960	498	900	556
	0.5	1	791	791	791	791	791	791
		2	794	684	868	579	834	658
		3	801	620	897	533	855	621
		5	810	574	925	502	875	575
		8	816	549	944	486	888	552
		10	820	541	950	481	890	544
	0.8	1	764	764	764	764	764	764
		2	768	644	840	549	810	631
		3	774	588	870	499	831	597
		5	785	543	895	467	850	550
		8	792	520	912	450	864	528
		10	790	510	920	445	870	521

Based on the selected parameters described in Green et al. [22], i.e., L = 1 and ρ = 0.0, the sample size per intervention group is calculated as 804. If four interims and one final analysis are planned (i.e., L = 5) with DF-1, and conservatively assuming a zero correlation between the endpoints, then the MSS is 825 for OF-OF, 945 for PC-PC and 895 for OF-PC, and the ASN is 604 for OF-OF, 548 for PC-PC and 608 for OF-PC. If the correlation is incorporated into the calculation when ρ = 0.3, 0.5 and 0.8, then the MSS are 820, 810 and 785 for OF-OF; 940, 930 and 900 for PC-PC; 890, 885 and 860 for OF-PC. The ASN are 589, 574 and 543 for OF-OF; 525, 506 and 469 for PC-PC and 593, 582, and 556 for OF-PC. When comparing DF-2 to DF-1, there are no major differences in MSS and ASN for all of the boundary combinations, although DF-2 provides a slightly smaller MSS and ASN than DF-1, for PC-PC and OF-PC. However, if the endpoint is very invasive and thus stopping measurement may be ethically desirable, there is a benefit of using DF-2 as DF-2 offers the option of stopping measurement of an endpoint for which superiority has been demonstrated. For example, when four interims and one final analysis with DF-2 are planned (i.e., L = 5), the average total number of measurements for each intervention group are 1052, 1045, 1041 and 1021 for OF-OF; 846, 845, 841 and 831 for PC-PC; 966, 961, 958 and 944 for OF-PC, corresponding to ρ = 0.0, 0.3, 0.5, and 0.8. They are relatively smaller than those for DF-1 as the average total number of measurements for DF-1 are 1208, 1178, 1148 and 1086 for OF-OF; 1096, 1050, 1012 and 938 for PC-PC; 1216, 1186, 1164 and 1112 for OF-PC.

4. Sample size recalculation

Clinical trials are designed based on assumptions often constructed based on prior data. However prior data may be limited or an inaccurate indication of future data, resulting in trials that are over/under-powered. Interim analyses provides an opportunity to evaluate the accuracy of the design assumptions and potentially make design adjustments (i.e., to the sample size) if the assumptions were markedly inaccurate. The tarenflurbil trial mentioned in the previous section, failed to demonstrate a beneficial effect of tarenflurbil on both ADAS-Cog and ADCS-ADL. The observed treatment effects were smaller than the assumed effects. Group-sequential designs allow for early stopping when there is sufficient statistical evidence that the two treatments are different. However more modern adaptive designs may also allow for increases in the sample size if effects are smaller than assumed. Such adjustments must be conducted carefully for several reasons. Challenges include: (a) maintaining control of statistical error rates, (b) developing a plan to make sure that treatment effects cannot be inferred via back-calculation of a resulting change in the sample size, (c) consideration of the clinical relevance of the treatment effects, and (d) practical concerns such as an increase in cost and the challenge of accruing more trial participants. In this section, we discuss sample size recalculation based on the observed intervention’s effects at an interim analysis with a focus on control of statistical error rates.

4.1 Test statistics and conditional power

Consider that the maximum sample size is recalculated to $n_L^{\prime }$ based on the interim data at the R th analysis. Suppose that $n_L^{\prime }$ is subject to $n_R<n_L^{\prime }\le \lambda n_L$, where λ is a pre-specified constant for the maximum allowable sample size. For simplicity, assume a common correlation between the treatment groups, i.e., ρ_T = ρ_C = ρ. Let (δ̃₁, δ̃₂) and let ( ${\delta }_1^{\ast },{\delta }_2^{\ast }$) be the mean differences used for planned sample size and for recalculated sample size, respectively.

Here we consider the Cui-Hung-Wang (CHW) statistics [24] for sample size recalculation in group-sequential designs with two co-primary endpoints to preserve the overall Type I error rate at a pre-specified alpha level even when the sample size is increased and conventional test statistics are used. The CHW statistics are,

$$Z_{km}^{\prime }=\sqrt{\frac{n_R}{n_m}}{Z}_{kR}+\sqrt{\frac{n_m-n_R}{n_m}}\frac{{\sum }_{i=n_R+1}^{n_m^{\prime }}{Y}_{\mathrm{T}ki}-{\sum }_{j=n_R+1}^{n_m^{\prime }}{Y}_{\mathit{Ckj}}}{\sqrt{2(n_m^{\prime }-n_R)}},$$

where $n_m^{\prime }=(n_m-n_R)(n_L^{\prime }-n_R)/(n_L-n_R)+n_R$ and r_R = r_m = 1 (k=1,2; R=1,…, L−1; m=R+1,…, L). The same critical values utilized for the case without sample size recalculation are used.

The sample size is increased or decreased when the conditional power evaluated at the R th analysis is lower or higher than the desired power 1−β. Under the planned maximum sample size and a given observed value of (Z_1R, Z_2R), for DF-1, the conditional power is defined by

$$CP=Pr\left[{\cup }_{m=R+1}^L\left\{A_{1m}\cap A_{2m}\right\}\mid a_{1R},a_{2R}\right]$$ (5)

if Z_1l ≤ c_1l or Z_2l ≤ c_2l for all l = 1,…, R, where (a_1R, a_2R) is a given observed value of (Z_1R, Z_2R). On the other hand, the conditional power for DF-2 is given by

$$CP=\{\begin{array}{l}\begin{array}{l}Pr\left[{\cup }_{m=R+1}^L{A}_{1m}\mid a_{1R},a_{2l^{\prime }}\right]\\ \text{if}{Z}_{1l}\le c_{1l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{2l^{\prime }}>c_{2l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[{\cup }_{m=R+1}^L{A}_{2m}\mid a_{2R},a_{1l^{\prime }}\right]\\ \text{if}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{2l^{\prime }}>c_{1l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[\left\{{\cup }_{m=R+1}^L{A}_{1m}\right\}\cap \left\{{\cup }_{m=R+1}^L{A}_{2,m}\right\}\mid a_{1R},a_{2R}\right]\\ \text{if}{Z}_{1l}\le c_{1l}\text{and}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R.\end{array}\hfill \end{array}$$ (6)

The detailed calculation of the conditional powers for DF-1 and DF-2 are provided in the Appendix A.3. Since (δ₁, δ₂) is unknown, it is customary to substitute ( ${\delta }_1^{\ast },{\delta }_2^{\ast }$), the estimated mean differences at the R th analysis (δ̂_1R, δ̂_2R) or the assumed mean differences during trial planning (δ̃₁, δ̃₂). We consider the conditional power based on $({\delta }_1^{\ast },{\delta }_2^{\ast })=({\widehat{\delta }}_{1R},{\widehat{\delta }}_{2R})$, which allows evaluation of behavior of power independent of (δ₁, δ₂).

When recalculating the sample size, three options are possible: (i) only allowing an increase in the sample size, (ii) only allowing a decrease in the sample size, and (iii) allowing an increase or decrease in sample size. For all the cases, we assign $Z_{km}^{\prime }$ and $n_m^{\prime }$ instead of Z_km and n_m in the conditional powers (5) and (6) for the conditional power with sample size recalculation. Consider the rule for determining the recalculated sample size $n_L^{\prime }$, when the sample size may be increased only, which is:

$$n_L^{\prime }=\{\begin{array}{ll}{n}_L,\hfill & \text{if}CP\ge 1-\beta \text{or}min({\widehat{\delta }}_{1R},{\widehat{\delta }}_{2R})\le 0,\hfill \\ min\left(n_L^{″},\lambda n_L\right),\hfill & \text{otherwise},\hfill \end{array}$$

where $n_L^{″}$ is the smallest integer $n_L^{\prime }(>n_R)$, where the conditional power achieves the desired power 1−β. When the sample size may be decreased only, the recalculated sample size $n_L^{\prime }$ is:

$$n_L^{\prime }=\{\begin{array}{ll}{n}_L^{″},\hfill & \text{if}CP>1-\beta ,\hfill \\ n_L,\hfill & \text{otherwise}.\hfill \end{array}$$

When the sample size may be increased or decreased, then the recalculated sample size $n_L^{\prime }$ is:

$$n_L^{\prime }=\{\begin{array}{ll}{n}_L^{″},\hfill & \text{if}CP>1-\beta ,\hfill \\ n_L,\hfill & \text{if}CP=1-\beta \text{or}min({\widehat{\delta }}_{1R},{\widehat{\delta }}_{2R})\le 0,\hfill \\ min\left(n_L^{″},\lambda n_L\right),\hfill & \text{otherwise}.\hfill \end{array}$$

4.2 Simulation study

A simulation study was performed to evaluate the impact of sample size recalculation based on DF-1 and DF-2 on the power and Type I error rate. We consider group-sequential designs with a single interim, i.e., one interim and one final analyses, and with multiple interims, i.e., three interims and one final analyses. In addition, we discuss the three options of: (i) only decreasing the sample size, (ii) only increasing the sample size, and (iii) increasing or decreasing the sample size, based upon the observed intervention’s effect. The planned MSS per intervention group is calculated to detect the joint difference for two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where (δ̃₁, δ̃₂) = (0.2, 0.2), ${\sigma }_1^2={\sigma }_2^2=1^2$ and the correlation is assumed to be known correlation at the design stage, i.e., ρ = 0.0, 0.3, 0.5, and 0.8. For the evaluation of the Type I error rate, the two pairs of the mean differences (δ₁, δ₂) = (0.0, 0.0) and (0.0, 0.2) are considered under H₀. For the designs with a single interim, the timing of the interim analysis for sample size recalculation is evaluated at 0.25, 0.50 and 0.75 of information time. For designs with multiple interims, one sample size recalculation is considered and the timing is evaluated at the 1st, 2nd and 3rd of interim analysis. The critical values are determined by the OF boundary for both endpoints with the LD alpha-spending method, with equal information space. The upper limit of the recalculated sample size is set to $n_2^{\prime }=\lambda n_2$ with λ = 1.5. The number of replications for the simulation is set to 1,000,000 for the evaluation of the Type I error rate and 100,000 replications for the power. These number of replications for the simulation was determined based on the precision, where a sample size of 1,000,000 provides a two-sided 95% confidence interval with a width equal to 0.001 when the proportion is 0.025, and a total number of replications of 100,000 provides a two-sided 95% confidence interval with a width equal to 0.005 when the proportion is 0.80.

Suppose that the sample size recalculation is based on the interim estimates of (δ₁, δ₂). Note that the value of correlation assumed at the design stage is retained for the sample size recalculation, i.e., without updating based on observed correlation at the interim as the correlation is a nuisance parameter in hypothesis testing. All results are summarized in Tables S1 to S4 in the Supplemental Data. As there are no significant differences between DF-1 and DF-2 with respect to the Type I error rates and empirical powers, we limit discussion to the behavior of the Type I error rates and power for DF-1.

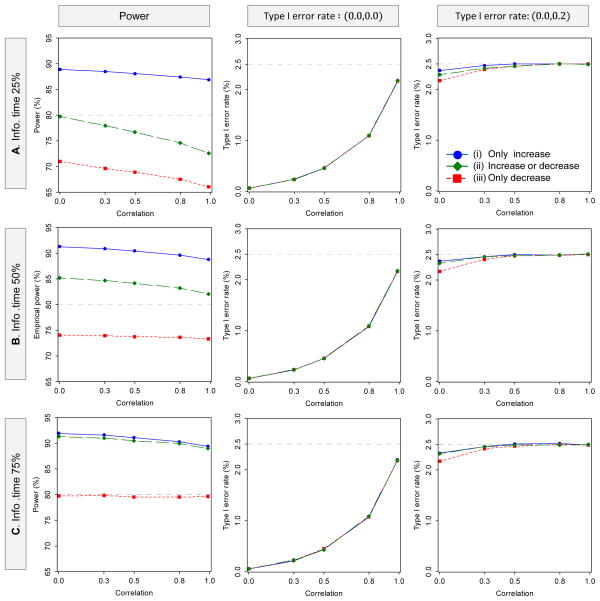
Figure 3 illustrates how the Type I error rates and powers behave as a function of the correlation, the timing of the interim analysis for sample size recalculation, and the sample size recalculation options for DF-1 in the single-interim case. In all three recalculation options, the Type I error rates increase as the correlation increases, but they are not exceed the targeted 2.5%. There is no practical difference in the behavior of the Type I error rates depending on the timing of the interim analysis for sample size recalculation. On the other hand, for the behavior of the power, when only allowing an increase in the sample size, the empirical powers are higher than the desired power of 80% in all of the three timings of sample size recalculation, although the power is slightly decreased with higher correlation. When allowing an increase or a decrease in the sample size, if the timing for sample size recalculation is at 25% information time, then the empirical power is lower than the desired power of 80%, especially with higher correlation. However, if the timing for sample size recalculation is 50% or 75%, then the empirical powers are higher than in all three timings of sample size recalculation. When only allowing a decrease in the sample size, if the timing for the sample size recalculation is at 25% or 50% information time, then the empirical powers are always lower than the desired power, especially with higher correlation. If the timing for sample size recalculation is at 75% information time, then the empirical power is almost achieved at the desired power of 80%.

Figure 3.

Behavior of the power and Type I error rate as a function of the correlation with sample size recalculation in two-stage group-sequential designs, where the information times of 0.25, 0.50 and 0.75 were selected as the timing of the sample size recalculation. The planned MSS per intervention group is calculated to detect the joint difference for two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where one interim and one final analysis are to be performed. The critical values are determined by the OF boundary for both endpoints, with the LD alpha-spending method. The upper limit of recalculation sample size is $n_2^{\prime }=\lambda n_2$ with λ = 1.5. The number of replications for simulation is set to 1,000,000 for evaluation of the Type I error rate and 100,000 replications for the power (DF-1)

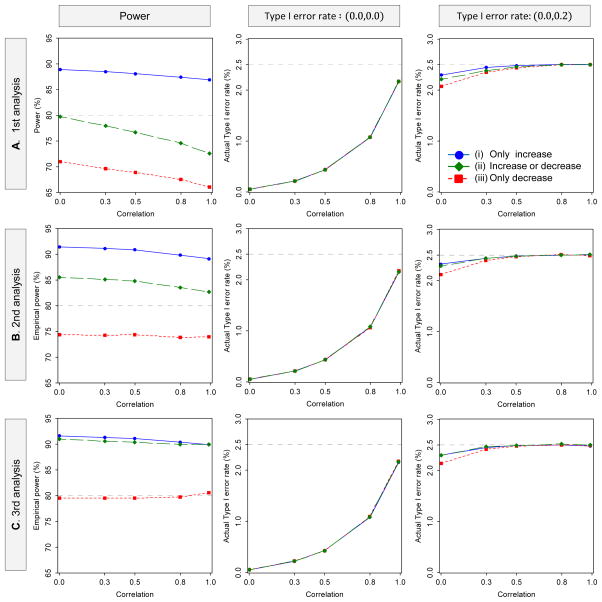
Figure 4 illustrates how the Type I error rates and powers behave as a function of the correlation, the timing of the interim analysis for sample size recalculation, and the sample size recalculation options for DF-1, in the multiple-interim case. The results are similar to those in the single-interim case; when only allowing an increase in the sample size, compared with the desired power of 80%, the empirical powers are improved in all of the three timings for the sample size recalculation, but the empirical power is much lower than the desired power if the sample size recalculation is conducted early in the study, especially when allowing a decrease in the sample size.

Figure 4.

Behavior of the power and Type I error rate as a function of the correlation with sample size recalculation in four-stage group-sequential designs, where the 1st, 2nd and 3rd interim point were selected as the timing of the sample size recalculation. The planned MSS per intervention group is calculated to detect the joint difference for two endpoints with the overall power of 80% at the one-sided significance level of 2.5%, where three interims and one final analysis are to be performed. The critical values are determined by the OF boundary for both endpoints, with the LD alpha-spending method. The upper limit of recalculation sample size is $n_2^{\prime }=\lambda n_2$ with λ = 1.5. The number of replications for simulation is set to 1,000,000 for evaluation of the Type I error rate and 100,000 replications for the power (DF-1)

These results suggest incorporating the uncertainty of the estimates at the interim into the sample size recalculation is important. The power is much lower than desired power if the sample size recalculation is conducted early in the study, especially when allowing for a decrease in the sample size.

5. Summary and discussion

The determination of sample size and the evaluation of power are fundamental and critical elements in the design of a clinical trial. If a sample size is too small then important effects may not be detected, while a sample size that is too large is wasteful of resources and unethically puts more participants at risk than necessary. Recently many clinical trials are designed with more than one endpoint considered as co-primary. As with trials involving a single primary endpoint, designing such trials to include interim analyses (i.e., with repeated testing) may provide efficiencies by detecting trends prior to planned completion of the trial. It may also be prudent to evaluate design assumptions at the interim and potentially make design adjustments (i.e., sample size recalculation) if design assumptions were dramatically inaccurate. However such design complexities create challenges in the evaluation of power and the calculation of sample size during trial design.

We discuss group-sequential designs with co-primary endpoints. We derive the power and sample size methods under two decision-making frameworks: (1) designing the trial to detect the test intervention’s superiority for the two endpoints simultaneously (i.e., at the same interim timepoint of the trial) (DF-1), and (2) designing the trial to detect superiority for the two endpoints at any interim timepoint (i.e., not necessarily simultaneously) (DF-2). The former is simpler while the latter is more flexible and may be useful when the endpoint is very invasive or expensive, as it allows for stopping the measurement of any endpoint upon which superiority has been demonstrated. We evaluate the behavior of sample size with varying design elements and provide an example to illustrate the methods. We also discuss sample size recalculation using CHW statistics and evaluate the impact on the power and Type I error rate. Although DF-2 will provide a slightly smaller sample size than DF-1, there is modest difference between two. However, if the endpoint is very invasive and thus stopping measurement may be ethically desirable, there is a benefit of using DF-2 as DF-2 offers the option of stopping measurement of an endpoint for which superiority has been demonstrated. However stopping measurement on one endpoint could also create operational challenges in study conduct and patient monitoring. The timing of the sample size recalculation should also be carefully considered as the power does not reach desired levels if the sample size recalculation is done early in the study when considering a decrease in the sample size.

There are other practical issues and extensions to consider when designing a group-sequential clinical trial with co-primary endpoints. They include: how the value of correlation should be selected at the planning and interim, evaluating futility or efficacy and futility simultaneously, other endpoint scales, and other inferential goals. We discuss each of these issues.

There are two important questions regarding the choice of the correlation in sample size calculations. One is whether the observed correlation from external or pilot data should be utilized or whether correlation is assumed to be zero. The other is whether the sample size should be recalculated based on the observed correlation at the interim. Incorporating the observed correlation at the planning or interim may affect the Type I error rate and power. Our experience suggests that when standardized effect sizes are unequal between the endpoints, the power is not improved with higher correlation. With unequal standardized effect sizes, incorporating the correlation into the sample size calculation at planning or interim may have no advantage [25, 26]. Further investigation will be required to assess how the choice of the correlation impacts the operation characteristics of the design.

Since the main objective of the paper is to provide the fundamental foundation in group-sequential designs for co-primary endpoints, our discussion is restricted to a superiority clinical trial comparing two interventions based on two continuous endpoints. The study design allows for early stopping when larger intervention differences are observed, i.e., rejecting a null hypothesis only. However, this work provides a foundation for designing clinical trials with other design features. In addition to this fundamental situation, the method discussed here can be straightforwardly extended to other situations such as evaluating futility (rejecting the alternative hypothesis) or evaluating both efficacy and futility.

Time-to-event outcomes are common in oncology, cardiovascular and infectious disease clinical trials. The method for continuous endpoints described in the paper may not be directly extended to time-to-event endpoints. When considering a trial with two time-to-event outcomes as co-primary with a plan for using the logrank test to compare two interventions in a group-sequential design, information for the two endpoints may accumulate at different rates. This creates challenges when designing trials, i.e., the amount of information for the endpoints may be different at any particular interim timepoint of the trial. Further investigation is required to assess this issue.

Although our primary interest is co-primary endpoints, these results provide a fundamental foundation to other inferential goals, e.g., designing a trial to detect an effect on at least one endpoint. Many authors have proposed methods for the at least one endpoint goal in fixed sample size designs, e.g., a weighted Bonferroni procedure, the prospective alpha allocation scheme method, the adaptive alpha allocation approach, the Bonferroni-type parametric procedure, and the fallback-type parametric procedure (e.g., see Dmitrienko et al. [4], Moyé [27] and Moyé and Baranuik [28]). In addition, several authors have discussed an extension of methods to the group-sequential designs with an inferential goal of at least one endpoint [29–32]. For example, Tang and Geller [30] discuss a method based on closed testing procedures and Tamhane et al. [31, 32] discuss sample size methods in two-stage group-sequential designs based on the gatekeeping procedures with hierarchically ordered multiple endpoints.

Appendix

A.1 Power calculation

The power (1) for DF-1 can be calculated by partitioning the set in (1) into mutually exclusive subsets and taking the sum of their probabilities as follows:

$$\begin{array}{l}1-\beta =Pr\left[{\cup }_{l=1}^L\left\{A_{1l}\cap A_{2l}\right\}\mid {\mathrm{H}}_1\right]\\ =Pr\left[A_{11}\cap A_{21}\mid {\mathrm{H}}_1\right]+\sum _{l=2}^{L}Pr\left[{\cap }_{l^{\prime }=1}^{l-1}\left\{{\overline{A}}_{1l^{\prime }}\cup {\overline{A}}_{2l^{\prime }}\right\}\cap \left\{A_{1l}\cap A_{2l}\right\}|{\mathrm{H}}_1\right],\end{array}$$ (A1)

where A_kl = {Z_kl > c_kl} and Ā_kl ={Z_kl ≤ c_kl} (k = 1,2; l = 1,…, L). The probability of {Ā_1l′ ∪ Ā_2l′} can be written as $Pr[{\overline{A}}_{1l^{\prime }}\cup {\overline{A}}_{2l^{\prime }}]=Pr[{\stackrel{\sim }{A}}_{l^{\prime }}^1]+Pr[{\stackrel{\sim }{A}}_{l^{\prime }}^2]+Pr[{\stackrel{\sim }{A}}_{l^{\prime }}^3]$, where $A_{l^{\prime }}^1=\{{\overline{A}}_{1l^{\prime }}\cap A_{2l^{\prime }}\},{\stackrel{\sim }{A}}_{l^{\prime }}^2=\{A_{1l^{\prime }}\cap {\overline{A}}_{2l^{\prime }}\}$ and ${\stackrel{\sim }{A}}_{l^{\prime }}^3=\{{\overline{A}}_{1l^{\prime }}\cap {\overline{A}}_{2l^{\prime }}\}(l^{\prime }=1,\dots ,L-1)$. Similarly, the probability of the union of {Ā_1l′ ∪ Ā_2l′} can be written by the sum of the probabilities of the unions composed of ${\stackrel{\sim }{A}}_{l^{\prime }}^1,{\stackrel{\sim }{A}}_{l^{\prime }}^2$ and ${\stackrel{\sim }{A}}_{l^{\prime }}^3$. Then, the second term of the right-hand side in (A1) can be rewritten as

$$\sum _{l=2}^{L}Pr\left[{\cap }_{l^{\prime }=1}^{l-1}\left\{{\overline{A}}_{1l^{\prime }}\cup {\overline{A}}_{2l^{\prime }}\right\}\cap \left\{A_{1l}\cap A_{2l}\right\}|{\mathrm{H}}_1\right]={\sum }_{l=2}^L\left({\sum }_{h_1=1}^3\cdots {\sum }_{h_{l-1}=1}^{3}Pr\left[\left\{{\cap }_{l^{\prime }=1}^{l-1}{\stackrel{\sim }{A}}_{l^{\prime }}^{h_{l^{\prime }}}\right\}\cap \left\{A_{1l}\cap A_{2l}\right\}|{\mathrm{H}}_1\right]\right).$$

The probability of ${\stackrel{\sim }{A}}_{l^{\prime }}^1$ is calculated by a bivariate normal integral as follows:

$$Pr\left[{\stackrel{\sim }{A}}_{l^{\prime }}^1\right]={\int }_{-\infty }^{c_{1l^{\prime }}}{\int }_{c_{2l^{\prime }}}^{\infty }{f}_2\left(z_{1l^{\prime }},z_{2l^{\prime }}\right){dz}_{2l^{\prime }}{dz}_{1l^{\prime }},$$

where f₂(z_1l′, z_2l′) is the density function of the joint distribution of (Z_1l′, Z_2l′) with the means and the covariance matrix given in Section 2.1. The probabilities of ${\stackrel{\sim }{A}}_{l^{\prime }}^2,{\stackrel{\sim }{A}}_{l^{\prime }}^3$ and {A_1l′ ∩ A_2l′} are calculated similarly. Then the probability of the union composed of ${\stackrel{\sim }{A}}_{l^{\prime }}^1,{\stackrel{\sim }{A}}_{l^{\prime }}^2,{\stackrel{\sim }{A}}_{l^{\prime }}^3$ and {A_1l′ ∩ A_2l′} is calculated by a multivariate normal integral and the power is the sum of (3^L−1)/2 multivariate normal integrals. For details of the computation related to multivariate normal, please see Genz and Bretz [24].

For illustration, we provide the case of L = 2 and r = r₁ = r₂. In this case, the power can be rewritten as

$$\begin{array}{l}1-\beta =Pr\left[A_{11}\cap A_{21}\mid {\mathrm{H}}_1\right]+{\sum }_{h_1=1}^{3}Pr\left[{\stackrel{\sim }{A}}_1^{h_1}\cap \left\{A_{12}\cap A_{22}\right\}\mid {\mathrm{H}}_1\right]\\ ={\int }_{c_{11}}^{\infty }{\int }_{c_{21}}^{\infty }{f}_2\left(z_{11},z_{21}\right){dz}_{21}{dz}_{11}+{\int }_{-\infty }^{c_{11}}{\int }_{c_{21}}^{\infty }{\int }_{c_{12}}^{\infty }{\int }_{c_{22}}^{\infty }{f}_4\left(z_{11},z_{21},z_{12},z_{22}\right){dz}_{22}{dz}_{12}{dz}_{21}{dz}_{11}\\ +{\int }_{c_{11}}^{\infty }{\int }_{-\infty }^{c_{21}}{\int }_{c_{12}}^{\infty }{\int }_{c_{22}}^{\infty }{f}_4\left(z_{11},z_{21},z_{12},z_{22}\right){dz}_{22}{dz}_{12}{dz}_{21}{dz}_{11}\\ +{\int }_{-\infty }^{c_{11}}{\int }_{-\infty }^{c_{21}}{\int }_{c_{12}}^{\infty }{\int }_{c_{22}}^{\infty }{f}_4\left(z_{11},z_{21},z_{12},z_{22}\right){dz}_{22}{dz}_{12}{dz}_{21}{dz}_{11},\end{array}$$

where f₂(z₁₁, z₂₁) is the density function of the bivariate normal distribution of Z₂ = (Z₁₁, Z₂₁)^T, which is given by

$$f_2({\mathit{Z}}_2)=\frac{1}{2\pi |{\mathbf{\sum }}_2{|}^{1/2}}exp\left[-\frac{1}{2}{({\mathit{Z}}_2-{\mathit{\mu }}_2)}^{\mathrm{T}}{{\mathbf{\sum }}_2}^{-1}({\mathit{Z}}_2-{\mathit{\mu }}_2)\right],-\infty <z_{11},z_{21}<\infty$$

with mean vector ${\mathit{\mu }}_2=\sqrt{{rn}_1/(1+r)}{({\delta }_1/{\sigma }_1,{\delta }_2/{\sigma }_2)}^{\mathrm{T}}$ and correlation matrix

$${\mathbf{\sum }}_2=\left(\begin{array}{cc}{1}^2& (r{\rho }_{\mathrm{T}}+{\rho }_{\mathrm{C}})/(1+r)\\ (r{\rho }_{\mathrm{T}}+{\rho }_{\mathrm{C}})/(1+r)& 1^2\end{array}\right).$$

and f₄ (z₁₁, z₂₁, z₁₂, z₂₂) is the density function of the tetra-variate normal distribution of Z₄ = (Z₁₁, Z₂₁, Z₁₂, Z₂₂)^T given by

$$f_4({\mathit{Z}}_4)=\frac{1}{{(2\pi )}^2|{\mathbf{\sum }}_4{|}^{1/2}}exp\left[-\frac{1}{2}{({\mathit{Z}}_4-{\mathit{\mu }}_4)}^{\mathrm{T}}{{\mathbf{\sum }}_4}^{-1}({\mathit{Z}}_4-{\mathit{\mu }}_4)\right],-\infty <z_{11},z_{21},z_{12},z_{22}<\infty$$

with mean vector ${\mathit{\mu }}_4=\sqrt{(1+r)/r}{(\sqrt{n_1}{\delta }_1/{\sigma }_1,\sqrt{n_1}{\delta }_2/{\sigma }_2,\sqrt{n_2}{\delta }_1/{\sigma }_1,\sqrt{n_2}{\delta }_2/{\sigma }_2)}^{\mathrm{T}}$ and correlation matrix

$${\mathbf{\sum }}_4=\left(\begin{array}{cc}{\mathbf{\sum }}_2& \sqrt{n_1/n_2}{\mathbf{\sum }}_2\\ \sqrt{n_1/n_2}{\mathbf{\sum }}_2& {\mathbf{\sum }}_2\end{array}\right),$$

where Σ₄ is positive definite matrix under |ρ_T|, |ρ_C| < 1 and n₁ ≠ n₂ as |Σ₄|=|Σ₂|² (1−n₁/n₂)².

The power (2) for DF-2 can be calculated from two L–variate normal integrals and a 2L–variate normal integral.

$$\begin{array}{l}1-\beta =Pr\left[\left\{{\cup }_{l=1}^L{A}_{1l}\right\}\cap \left\{{\cup }_{l=1}^L{A}_{2l}\right\}|{\mathrm{H}}_1\right]\\ =1-\left(Pr\left[{\cap }_{l=1}^L{\overline{A}}_{1l}|{\mathrm{H}}_1\right]+Pr\left[{\cap }_{l=1}^L{\overline{A}}_{2l}|{\mathrm{H}}_1\right]-Pr\left[{\cap }_{l=1}^L\left\{{\overline{A}}_{1l}\cap {\overline{A}}_{2l}\right\}|{\mathrm{H}}_1\right]\right).\end{array}$$

The power can be calculated similarly as discussed in the power (1) for DF-1.

A.2 ASN calculation

The ASN (3) for DF-1 can be calculated by the sum of multivariate normal integrals

$$\begin{array}{l}\text{ASN}=n_L\left(1+{\sum }_{l=1}^{L-1}Pr\left[\left\{{\overline{A}}_{11}\cup {\overline{A}}_{21}\right\}\cap \cdots \cap \left\{{\overline{A}}_{1l}\cup {\overline{A}}_{2l}\right\}\right]\right)/L\\ =n_L\left\{1+{\sum }_{l=1}^{L-1}\left({\sum }_{h_1=1}^3\cdots {\sum }_{h_l=1}^{3}Pr\left[{\cap }_{l^{\prime }=1}^l{\stackrel{\sim }{A}}_{l^{\prime }}^{h_{l^{\prime }}}\right]\right)\right\}/L.\end{array}$$

Similarly, the ASN (4) for DF-2 can be calculated by

$$\begin{array}{l}\text{ASN}=n_L\left(1+{\sum }_{l=1}^{L-1}Pr\left[\left\{{\overline{A}}_{11}\cap \cdots \cap {\overline{A}}_{1l}\right\}\cup \left\{{\overline{A}}_{21}\cap \cdots \cap {\overline{A}}_{2l}\right\}\right]\right)/L\\ =n_L\left\{1+{\sum }_{l=1}^{L-1}\left(Pr\left[{\cap }_{l^{\prime }=1}^l{\overline{A}}_{1l^{\prime }}\right]+Pr\left[{\cap }_{l^{\prime }=1}^l{\overline{A}}_{2l^{\prime }}\right]-Pr\left[{\cap }_{l^{\prime }=1}^l\left\{{\overline{A}}_{1l^{\prime }}\cap {\overline{A}}_{2l^{\prime }}\right\}\right]\right)\right\}/L.\end{array}$$

A.3 Conditional Power

The conditional power (5) for DF-1 is described by

$$\begin{array}{l}CP=Pr\left[{\cup }_{m=R+1}^L\left\{A_{1m}\cap A_{2m}\right\}\mid a_{1R},a_{2R}\right]\\ =Pr\left[A_{1,R+1}\cap A_{2,R+1}\mid a_{1R},a_{2R}\right]+{\sum }_{m=R+2}^{L}Pr\left[{\cap }_{m^{\prime }=R+1}^{m-1}\left\{{\overline{A}}_{1m^{\prime }}\cup {\overline{A}}_{2m^{\prime }}\right\}\cap \left\{A_{1m}\cap A_{2m}\right\}\mid a_{1R},a_{2R}\right],\end{array}$$ (A2)

if Z_1l ≤ c_1l or Z_2l ≤ c_2l for all l = 1,…, R, where A_km ={Z_km > c_km}, Ā_km = {Z_km ≤ c_km} (k = 1,2; m = R +1,…, L) and (a_1R, a_2R) is a given observed value of (Z_1R, Z_2R). The second term of the right-hand side in (A2) can be calculated in a similar way to that for the power calculation (Appendix A.1.). The conditional distribution of (Z_1,R+1, Z_2,R+1,…, Z_1L, Z_2L|a_1R, a_2R) is a multivariate normal with their means $\mathrm{E}[Z_{km}\mid a_{1R},a_{2R}]=\sqrt{n_m/2}{\delta }_k+\sqrt{n_R/n_m}(a_{kR}-\sqrt{n_R/2}{\delta }_k)$ and covariance given by $cov[Z_{km},Z_{k^{\prime }{m}^{\prime }}\mid a_{1R},a_{2R}]=(n_{m^{\prime }}-n_R)/\sqrt{n_m{n}_{m^{\prime }}}$ if k = k′; $(n_{m^{\prime }}-n_R)\rho /\sqrt{n_m{n}_{m^{\prime }}}$if k ≠ k′, where m′ ≤ m = R +1,…, L. For DF-2, the conditional power (6) can be described as

$$CP=\{\begin{array}{l}\begin{array}{l}Pr\left[{\cup }_{m=R+1}^L{A}_{1m}\mid a_{1R},a_{2l^{\prime }}\right]=1-Pr\left[{\cap }_{m=R+1}^L{\overline{A}}_{1m}\mid a_{1R},a_{2l^{\prime }}\right]\\ \text{if}{Z}_{1l}\le c_{1l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{2l^{\prime }}>c_{2l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[{\cup }_{m=R+1}^L{A}_{2m}\mid a_{2R},a_{1l^{\prime }}\right]=1-Pr\left[{\cap }_{m=R+1}^L{\overline{A}}_{2m}\mid a_{2R},a_{1l^{\prime }}\right]\\ \text{if}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{1l^{\prime }}>c_{1l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[\left\{{\cup }_{m=R+1}^L{A}_{1m}\right\}\cap \left\{{\cup }_{m=R+1}^L{A}_{2m}\right\}\mid a_{1R},a_{2R}\right]\\ =1-Pr\left[{\cap }_{m=R+1}^L{\overline{A}}_{1m}\mid a_{1R},a_{2R}\right]-Pr\left[{\cap }_{m=R+1}^L{\overline{A}}_{2m}\mid a_{1R},a_{2R}\right]\\ +Pr\left[{\cap }_{m=R+1}^L\left\{{\overline{A}}_{1m}\cap {\overline{A}}_{2m}\right\}\mid a_{1R},a_{2R}\right]\\ \text{if}{Z}_{1l}\le c_{1l}\text{and}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R,\end{array}\hfill \end{array}$$

and calculated similarly as discussed in the power for DF-2 (Appendix A.1.).

When R = L−1, the conditional power for DF-1 can be rewritten as

$$CP=Pr\left[A_{1L}\cap A_{2L}\mid a_{1R},a_{2R}\right]={\mathrm{\Phi }}_2(-c_1^{\ast },-c_2^{\ast }\mid \rho ),$$

where Φ₂ (·, ·, | ρ) is the cumulative distribution function of the standard bivariate normal distribution with the correlation ρ, and $c_1^{\ast }=(c_{1L}-a_{1R}\sqrt{t})/\sqrt{1-t}-{\delta }_1\sqrt{n_L-n_R}/\sqrt{2}$ and $c_2^{\ast }=(c_{2L}-a_{2R}\sqrt{t})/\sqrt{1-t}-{\delta }_2\sqrt{n_L-n_R}/\sqrt{2}$ with t = n_R/n_L. For DF-2, the conditional power can be rewritten as

$$CP=\{\begin{array}{l}\begin{array}{l}Pr\left[A_{1L}\mid a_{1R},a_{2l^{\prime }}\right]=1-\mathrm{\Phi }(c_1^{\ast })\\ \text{if}{Z}_{1l}\le c_{1l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{2l^{\prime }}>c_{2l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[A_{2L}\mid a_{2R},a_{1l^{\prime }}\right]=1-\mathrm{\Phi }(c_2^{\ast })\\ \text{if}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R\text{and}{Z}_{1l^{\prime }}>c_{1l^{\prime }}\text{for}\text{some}{l}^{\prime }=1,\dots ,R,\end{array}\hfill \\ \begin{array}{l}Pr\left[A_{1L}\cap A_{2L}\mid a_{1R},a_{2R}\right]={\mathrm{\Phi }}_2(-c_1^{\ast },-c_2^{\ast }\mid \rho )\\ \text{if}{Z}_{1l}\le c_{1l}\text{and}{Z}_{2l}\le c_{2l}\text{for}\text{all}l=1,\dots ,R,\end{array}\hfill \end{array}$$

where Φ(·) is the cumulative distribution function of the standardized normal distribution.