Simulations of Remote Mutants of Dihydrofolate Reductase Reveal the Nature of a Network of Residues Coupled to Hydride Transfer

Abstract

Recent experimental and theoretical studies have proposed that enzymes involve networks of coupled residues throughout the protein that participate in motions accompanying chemical barrier crossing. Here we have examined portions of a proposed network in dihydrofolate reductase (DHFR) using quantum mechanics/molecular mechanics simulations. The simulations employ a hybrid quantum mechanics-molecular mechanics approach with a recently developed semi-empirical AM1-SRP Hamiltonian that provides accurate results for this reaction. The simulations reproduce experimentally determined catalytic rates for the wild type and distant mutants of E. coli DHFR, underscoring the accuracy of the simulation protocol. Additionally the simulations provide detailed insight into how residues remote from the active site affect the catalyzed chemistry, through changes in the thermally averaged properties along the reaction coordinate. The mutations do not greatly affect the structure of the transition state near the bond activation, but we observe differences somewhat removed from the point of C-H cleavage that affect the rate. The mutations have global effects on the thermally averaged structure that propagate throughout the enzyme and the current simulations highlight several interactions that appear to be particularly important.

Introduction

One of the most important unresolved questions towards a comprehensive understanding of enzyme catalysis is why enzymes are so large. Given that active sites can often be defined by just a few residues, one may ask why enzymes often contain hundreds or thousands of residues. It is well established that enzymes provide preorganized active sites that are conducive to catalysis.¹ A hotly debated hypothesis is whether enzymes achieve their enormous rate enhancements partly by taking advantage of dynamic motions throughout the enzyme that are coupled to the reaction coordinate.^2-9 Deciphering any such motions could have important implications for rational drug design, as well as biomimetic catalysis, which could take advantage of specific motions that contribute to catalyzed reactions. We note that we use the term “dynamics” to indicate any motions involved in the reaction, not just non-equilibrium effects.

A commonly used model enzyme for studying dynamic effects is dihydrofolate reductase (DHFR). E. coli DHFR (ecDHFR) is a small (159-residue monomer), flexible enzyme that catalyzes a very simple hydride transfer (Scheme 1). In addition to serving as a model for understanding the basic features of enzymatic hydride transfers, the product of the DHFR reaction, tetrahydrofolate, is necessary for DNA synthesis, making DHFR a vulnerable target for chemotherapy and antibiotic agents. Experimental work on a series of mutants remote from the active site proposed that a number of residues may be involved in a network of coupled motions that aid the hydride transfer at the active site. In particular, the increase in free energy of activation (ΔG^‡, calculated with the Eyring equation from experimental rates) for the hydride transfer caused by certain double mutants (although not the particular one studied here) was non-additive: ΔΔG^‡ for the double mutants vs. wild-type (wt) was greater than the sum of ΔΔG^‡ for the respective single mutants.¹⁰ Furthermore, measurements of the temperature dependence of kinetic isotope effects (KIEs) indicated that the differences indeed reflect changes in the physical mechanism of H-transfer.¹¹ Genomic analysis also suggested an evolutionary significance to the relationship between the residues of the network.¹²

Scheme 1.

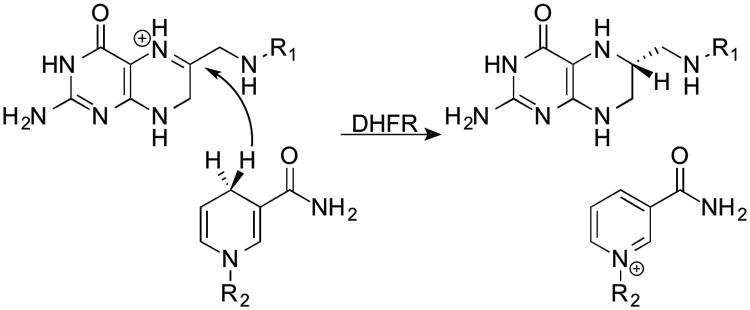
The hydride transfer catalyzed by DHFR.

Several theoretical works have examined the nature of this coupled network through molecular dynamics simulations at various levels,^13-22 and some recent studies have begun to examine how perturbations in the mass of the enzyme affect the dynamics of the reaction.^23,24 Here we build upon these earlier studies by examining the nature of a series of mutants using a recently developed semi-empirical^25-27 potential surface. We begin by demonstrating the accuracy of the new method in hybrid QM/MM²⁸ simulations by reproducing experimentally determined rates and then attempt to understand how mutations distant from the active site can affect the reaction at the active site. We explore possible roles for thermally averaged structural changes throughout the enzyme that may contribute to the reaction coordinate.

Methods

The simulations followed the general procedures described in ref. 25 The starting structure for the simulations came from the crystal structure of the wt ecDHFR ternary complex with folate and NADP⁺ (PDB: 1RX2).²⁹ This structure represents an active form of the Michaelis complex with the M20 loop in the closed conformation. The structure includes all 159 residues, 153 crystallographic waters, and the complete ligands. The crystallographic ligands were replaced in silico with the substrates, dihydrofolate and NADPH. Hydrogens were added to the protein and substrates using the HBUILD module in CHARMM.^30,31 We generally set the protonation state of ionizable residues to pH=7.0, with the following caveats. Histidine protonation states were set based on the most likely hydrogen bonding networks apparent in the crystal structure (surface histidines were generally assumed to be positively charged), and Asp27 was deprotonated in accordance with the results of ref. 32. The 2′-phosphate of NADP⁺ was treated as a dianion, based on a pKa of 5.9 for NADP⁺ in cytochrome P-450 oxidoreductase.³³ As in previous studies, the coordinates of OE1 and NE2 of the carboxamide of Gln102 were swapped to form more reasonable hydrogen bonding contacts. The resulting enzyme had a charge of -14 and dimensions of ca. 34 × 42 × 50 ų. The protein, ligands, and crystallographic waters were dissolved in a 65 × 65 × 65 ų box of 9461 water molecules, which was neutralized by the addition of 14 Na⁺ ions in random locations around the protein. Water molecules within 2.5 Å of any other atom (e.g. protein or Na⁺) were removed. In the mutant enzymes (M42W, G121V, and M42W-G121V) the mutations were built in silico from the wt structure, using Discovery Studio 3.0 (Accelrys, Inc.) to determine the most reasonable conformation for the additional bulk of the side-chains. Subsequent processing and simulations followed the same procedure as for the wt.

Simulations on these systems were conducted with CHARMM³⁰ using a hybrid QM/MM potential surface²⁸ described by the Hamiltonian³⁴

$$\widehat{H}={\widehat{H}}_{\mathit{\text{QM}}}+{\widehat{H}}_{\mathit{\text{MM}}}+{\widehat{H}}_{\mathit{\text{QM}}/\mathit{\text{MM}}}$$ [1]

where Ĥ_QM is the Hamiltonian for the QM region, Ĥ_MM is the Hamiltonian for the MM region, and Ĥ_QM/MM is the Hamiltonian for the interactions between the two regions. The QM region consisted of 69 atoms, including 38 atoms of the H₃folate⁺ (the pterin ring, the N-methylene-substituted p-aminobenzoyl moiety, and the NH atoms of the glutamate moiety) and 29 atoms from the NADPH (the nicotinamide and ribose rings). The remainder of the system was included in the MM region. Additionally, in order to satisfy the valence of the atoms at the boundaries between the QM and MM regions, two hydrogen link atoms were included along the covalent bonds transcending the boundaries. The partitioning between QM and MM regions, along with the link atoms, is shown in figure 1.

Figure 1.

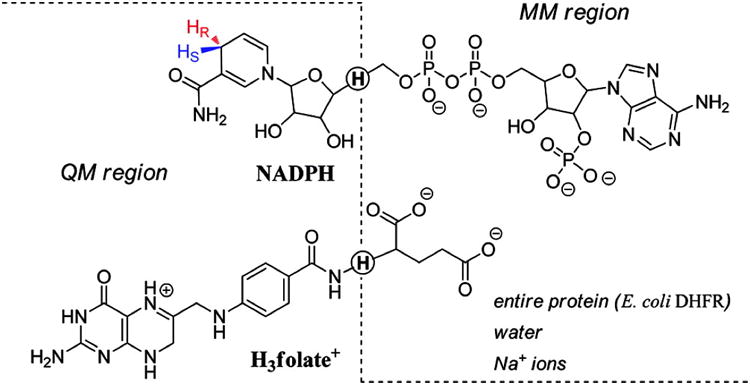
QM/MM partitioning scheme. The dashed line divides the QM and MM regions, and the quantum hydrogen link atoms are circled. Reproduced from ref. 25 with permission from ACS.

The QM region was treated with the AM1-SRP Hamiltonian described in ref. 25 and the CHARMM36 force field was used to treat the MM region.³⁵ Atom types and force field parameters for the MM atoms of the substrate were chosen based on analogy with similar functional groups, according to ref. 17. Water molecules were represented by the TIP3P model.³⁶ The simulations were conducted under periodic boundary conditions with the Ewald summation method for electrostatic interactions on a 64 × 64 × 64 FFT grid.³⁷ The real-space summation used a 13.0 Å group-based cutoff for electrostatic and van der Waals interactions and a κ value of 0.340 Å^-1.

Prior to conducting simulations, we partially optimized the systems at the MM level as follows, using adopted-basis set Newton-Raphson (ABNR) optimization. Initially, the ligands were optimized while holding all other atoms in fixed positions. Harmonic restraints were placed on the positions of the heavy atoms of the ligands during 30-step optimizations, where after each optimization, the force constant of the restraint was decreased and the optimization continued for another 30 steps. This included six 30-step optimizations with force constants decreasing from 100 kcal/mol·Å² to 0. At this point, the protein and solvent were optimized while holding the atoms of the ligands at fixed positions. Similarly to the ligands, the heavy atoms of the protein and solvent were restrained harmonically with force constants ranging from 10 kcal/mol·Å² to 0 during four 10-step optimizations. Finally, all restraints were removed while the system underwent an additional 30-step optimization.

The optimized system was then gradually heated to 298 K and 1 atm during MD simulations with NOE restraints on the hydride donor-acceptor distance (DAD, C4 of NADPH to C6 of H₃folate⁺) while the SHAKE algorithm³⁸ constrained bonds involving hydrogen atoms. The system heating was initiated at 48 K and 1 atm and was heated 10 K/ps using 1 fs time steps until reaching the target temperature of 298 K. The simulations employed the extended system pressure/temperature (CPT) algorithm of Andersen³⁹ with an effective mass of 500 amu and a Hoover thermostat⁴⁰ with an effective mass of 1000 kcal/mol·ps². Once at the target temperature, the system was further equilibrated for 1 ns at the MM level, followed by an additional 200 ps equilibration at the QM/MM level. During the MM equilibration, NOE restraints were added to the following distances (in addition to the DAD): N7 of NADPH to A7 O, N7 of NADPH to I14 O, and O7 of NADPH to A7 N. All restraints except for the DAD restraint were removed for the QM/MM equilibration. The systems were equilibrated for at least an additional 100 ps after removing the DAD restraint before data collection.

Classical potentials of mean force (PMFs) were calculated using umbrella sampling to sample the high-energy regions along the reaction coordinate. The reaction coordinate (ζ) was defined as the difference in distances from C4 of NADPH to hydride and C6 of H₃folate⁺ to hydride. This reaction coordinate was divided into 13-15 discrete regions (“windows”) at every 0.25 Å. Simulations were conducted with a biasing potential along ζ (roughly equal to the negative of the PMF) and a harmonic restraint centered at each window, with force constants (f) ranging from 20 to 60 kcal/mol·Å². To construct the PMF, systems were equilibrated in each window for 15 ps and the final coordinates and velocities in one window were used to generate the starting state for the next neighboring window. Systems were further equilibrated within each window for at least 100 ps prior to data collection. Each window was sampled for 200 ps and the probability density at each value of ζ was collected and sorted into 0.01 Å bins. The PMF was obtained by the weighted histogram analysis method (WHAM).⁴¹ The simulations were continued until the difference in free energy barrier between sequential PMFs was less than ± 1 kcal/mol.

Quantum corrections to the free energy barrier in the classical PMF were obtained by path-integral (PI) simulations⁴² in the ground state and transition state windows. The PI method treats quantized nuclei by replacing the classical particle with a string of quasi-particle beads connected by harmonic potentials. In the present case, the transferred hydride was treated as a ring of 32 beads and the PI simulations were conducted for 100 ps in each window. This method accounts for both zero point energy and tunneling effects.

Prior to trajectory analyses, the frames in each trajectory were reoriented to remove net translations and rotations during the course of the simulations. Covariance matrices were calculated based on 200 ps of sampling in the ground state and transition state, where the covariance (C_ij) between two atoms i and j is given by

$$C_{ij}=\langle ({\mathit{x}}_{\mathit{i}}-\langle {\mathit{x}}_{\mathit{i}}\rangle )\cdot ({\mathit{x}}_{\mathit{j}}-\langle {\mathit{x}}_{\mathit{j}}\rangle )\rangle$$ [2]

where x_i is the position of atom i. The normalized covariance (c_ij) is obtained by

$$c_{ij}=C_{ij}/{(C_{ii}{C}_{jj})}^2$$ [3]

Results and Discussion

We calculated classical PMFs for wt E. coli DHFR (ecDHFR), as well as three mutants (G121V, M42W, and G121V-M42W) that reproduce the experimentally determined trends in rates for the hydride transfer (k_H). The PMFs are displayed in Figure 2 and the experimental and calculated activation parameters are listed in Table 1. One can see in Table 1 that both the classical and the quantum-corrected free energy barriers follow the trend of the experimentally determined free energy barriers (ΔG^‡). The fact that the simulations reproduce the trend of the experimental rates for the series of mutants gives us some confidence in the accuracy of the QM/MM method, and particularly, the recently developed AM1-SRP Hamiltonian for the QM region.²⁵ The accuracy of this Hamiltonian has been shown in the work of Luk et al.²³ and Ruiz-Pernia et al.²⁴ We stress that no mutant specific information is assumed in the calculation other than the point-mutations themselves. From the PMFs (Figure 2), it is clear that the mutations increase the activation energy (ΔG^‡) for the hydride transfer and also make the reactions less exothermic. Consistent with Hammond's postulate, as the mutations make the reactions less and less exothermic, the position of the transition state (TS) moves closer and closer to being symmetric (i.e., reaction coordinate at the transition state=0.0 Å).

Figure 2.

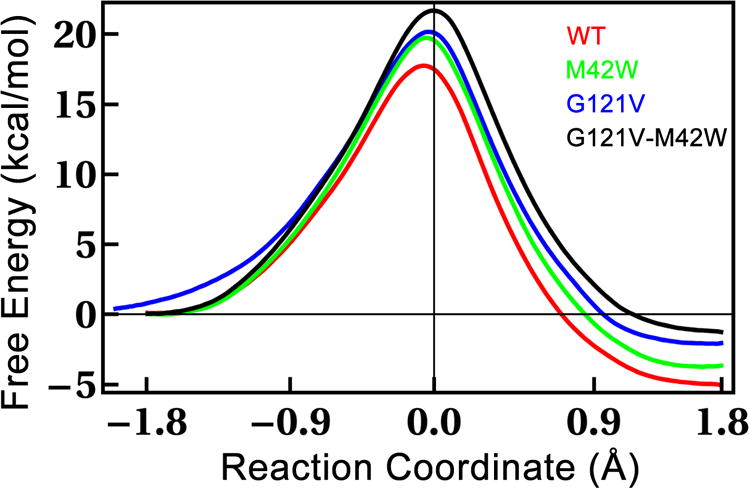
Classical mechanical PMFs for ecDHFR and a series of mutants. Each PMF represents 200 ps of sampling in each of 13-15 windows along the reaction coordinate. Thermodynamic parameters from these PMFs are listed in Table 1.

Table 1.

Experimental and Computed activation parameters for the systems studied here.

	Experimental Valuesa			Calculated Values
				Classical		Quantum-Corrected
Enzyme	kH (s-1)	ΔG‡	ΔΔG‡b	ΔG‡	ΔΔG‡	ΔG‡	ΔΔG‡
Wt	220	14.2	0.0	17.8	0	15.5	0.0
G121V	1.4	17.2	3.0	20.2	2.4	18.1	2.6
M42W	5.6	16.4	2.2	19.8	2.0	17.8	2.3
G121V-M42W	0.030	19.5	5.3	21.7	3.9	19.4	3.9

^aExperimental rates are from ref. 10 and corresponding activation energies were calculated with the Eyring equation. We note that ref. 43 demonstrated that the pH-independent rate for the wt is 950 s^-1, which may be more relevant to our calculations. Unfortunately, pH independent rates are not available for the mutants, but the effect of the mutations on the rates from ref. 10 is expected to be pH-independent, even if the absolute rates are not pH-independent. All free energies are in kcal/mol.

^bΔΔG^‡ is the difference in free energy barrier vs. the wild-type.

Some previous computational studies have explored how these mutations, which are quite distant from the active site, affect the rate at the active site.^{15,20-22,44,45}Most studies have focused on possible disruptions to correlated motions that may be coupled to the reaction coordinate. We have examined possible correlated motions through calculations of the covariance between α-carbons in the reactant state and transition state (Figure S1). Previous studies found that correlated motions such as those displayed in figure S1 were severely disrupted in various mutants.^20,44,45 Our simulations show some subtle changes in the mutants, but seemingly smaller than what was observed previously. This disparity could be due to the different simulation protocols employed, which can influence the extent of equilibrium solvation.

While the covariance matrices do not show substantial changes in the mutants, analogous distance matrices (Figure 3) do show significant differences among the mutants. The matrices in Figure 3 indicate the global structural changes that occur along the reaction path from reactant to transition state. One can see from these matrices that certain motions along the reaction coordinate are severely disrupted in the mutants, while other motions—that may be anti-catalytic in nature—become quite pronounced. Other mutations in DHFR appear to have similar effects on these types of global motions.⁴⁶ We note that one recent study²² of DHFR suggested that a possible source of rate enhancement in the wt is that the M20 loop shows a great deal of flexibility at the TS, which decreases the entropic barrier to reaction. The G121V-M42W mutant, however, was far more rigid, hindering catalysis. In our simulations of the wt, we do not observe substantial changes in the M20 loop between reactant and TS. Considering the good agreement between the computed barriers and the experimental rates, this might suggest that the M20 loop is at least partially closed during catalysis in native, single- and double mutant variants of DHFR.

Figure 3.

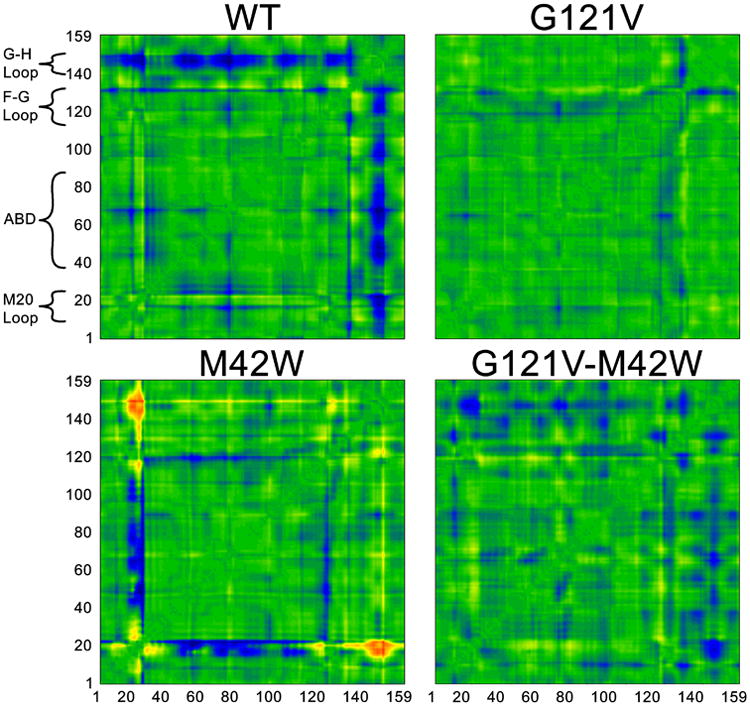
Distance matrices showing changes in distance between α-carbons of each enzyme in going from the reactant to the transition states. The axes are residue numbers and the color at each point indicates the change in distance between each pair of residues in going from the reactant to the TS. The color scale follows the visible spectrum with blue corresponding to -3 Å (residues are closer at TS than reactant) and red corresponding to +3 Å (residues are farther apart at TS than reactant). ABD=Adenosine Binding Domain. We note that these matrices are symmetric across the diagonal (y=x).

Analysis of Figure 3 offers a global perspective on how the mutations affect the catalyzed hydride transfer, highlighting the far-reaching consequences of rather subtle mutations. These pictures hint at a connection between structure/dynamics and the changes in free energy barriers for the mutants. Seemingly, each system – wt and mutants – has a distinct fingerprint of structural changes in moving from the reactant to the TS. Based on these plots we can conclude that the wt enzyme is more flexible and residues approach one another as the system is reaching the TS. In particular the G-H loop, which interacts directly with the M20 loop changes significantly in going from the RS to TS, approaching most other residues in the enzyme. The M20 loop in the vicinity of Met20 also changes during the course of the reaction. These changes permeate to the parallel β-sheets, which interact directly with the co-factor. The binding region of the pterin ring of dihydrofolate seems to change significantly less. This suggests that during the chemical step, structural changes are largely confined to the vicinity of the nicotinamide ring of NADPH, i.e. the nicotinamide ring approaches the pterin ring during the course of the reaction. The G121V single mutant shows significant loss of flexibility as the changes are considerably smaller in moving from the reactants to the TS. Residue 121 is part of the F-G loop, which interacts directly with the M20 loop, and is therefore likely to be important in allowing the nicotinamide ring approach the pterin ring during the reaction. Therefore, rigidifying this loop by introducing a Val in place of Gly is likely to increase the reorganization cost of moving from the reactant to the TS. These findings are in agreement with those of Watney et al.¹⁵ The other single mutant, M42W, appears to impair some of the required flexibility for catalysis, such as the flexibility in the G-H loop. This is seemingly an indirect effect, as there is no direct contact between residue 42 and the G-H loop. Thus, G121V rigidifies the F-G loop, while M42W influences the G-H loop, resulting in an additive effect. Interestingly, the double mutant seems to recover some of the wt flexibility, although the flexibility is more delocalized throughout the protein than in the wt enzyme, which has distinct rigid regions. This could be indicative of a loss of important interactions throughout the protein, which impairs motions required for reaction. That is to say, the motions leading to reaction are very specific, so the overall flexibility may not correlate strongly with the free energy barrier. We note that an important component is missing from these pictures, namely, the enzyme side chains. A deeper analysis is necessary to understand how specific interactions contribute to lowering the free energy barrier in the wt, and how those interactions are perturbed in the mutants.

One hypothesis is that the hydrogen donor-acceptor distance (DAD) coordinate is perturbed in the mutants, affecting the shape of the barrier near the transition state. On the basis of the temperature dependence of KIEs, we have proposed that the mutants have a longer DAD with a broader distribution.^11,47 The present simulations, though, suggest that the DAD at the TS is unperturbed in the mutants. The DAD we find is 2.63-2.64 ± 0.06 Å for the wt and mutants. We note that the DAD calculated here is for the classical TS, whereas the analysis of KIEs assumes that the reaction goes through a tunneling ready state, which is not a saddle point on the potential surface, but a point from which H can tunnel.⁴⁷ One computational study that used an EVB potential for the DHFR reaction also showed that a longer and broader distribution of DADs can account for the observed KIEs in these mutants.²¹ Specifically, ref. 21 found that the single mutants have longer and broader DAD distributions than the wt, and that the double mutant has a longer and broader DAD distribution than the single mutants, which led to reproduction of the temperature dependence of the experimental KIEs. Another theoretical study replicated the temperature dependence of KIEs for the wt and double mutant studied here, but it was not clear from that study if the DAD was substantially different in the mutant or if some other mechanism changed the temperature dependence of the KIEs.²² We note that the DADs calculated here are obtained using umbrella sampling techniques, which might perturb the true DAD distribution due to unphysical dynamics along the reaction coordinate. Interestingly, the method obtains reasonably accurate barrier heights in spite of a possible erroneous description of the fine details of the TS. More work will be necessary to determine the connection between the DAD and KIEs.

We did observe some interactions that may play a more significant role in determining changes to the free energy barrier in these mutants. The nicotinamide ring of the cofactor is bound to the enzyme by important H-bonds to the backbone amides of residues A7 and I14, and the mutations appear to substantially alter these H-bonds. For example the distance from A7 N to the amide O of the nicotinamide increases somewhat in the mutants (see Table 2). The distance from A7 O to the amide N of nicotinamide also increases in the mutants, but this increase appears to be confined to the reactants, not the TS. Conversely, the distance from I14 O to amide N of NADPH decreases in the mutants, and increases in going from reactants to TS. These various changes contribute to an overall weakening of the H-bonding to the cofactor in the mutants, which was particularly apparent as the weakened H-bonding necessitated additional restraints during heating and equilibration (see methods). Without those restraints, in the G121V and the double mutant the nicotinamide ring began to dissociate from the active site fairly easily. Disruptions in these H-bonds were also noted in a study that used MD simulations to examine the effects of active site mutations.⁴⁸ The active site mutants display similar changes in experimental rates and KIEs, so these H-bonds may be a key determining factor in the physical mechanism of the catalyzed H-transfer. Another interaction that may help to stabilize the TS is the H-bond between the S atom of M20 and the proton on N5 of DHF. This bond becomes much tighter at the TS of the wt and all mutants, but the effect is much more pronounced in the wt than any of the mutants. Furthermore, the length of this bond at the TS follows the same trend as the experimental rates (i.e., length in wt < single mutants < double mutant). The M20 loop has been proposed to play an important role in many aspects of the DHFR-catalyzed reaction and this further highlights the central role of this residue in the reaction.

Table 2.

Distances in the active site that change along the reaction coordinate and/or among the mutants.

	Wt		G121V		M42W		G121V-M42W
	Reactant	TS	Reactant	TS	Reactant	TS	Reactant	TS
DAD	3.65 ± 0.16	2.64 ± 0.06	3.66 ± 0.15	2.63 ± 0.06	3.63 ± 0.17	2.64 ± 0.06	3.62 ± 0.16	2.64 ± 0.06
A7 N-NADP O7	3.23 ± 0.24	2.99 ± 0.14	3.75 ± 0.50	3.08 ± 0.23	3.30 ± 0.27	2.95 ± 0.12	3.57 ± 0.43	3.14 ± 0.20
A7 O-NADP N7	3.02 ± 0.19	3.00 ± 0.19	3.40 ± 0.41	3.12 ± 0.28	3.06 ± 0.23	2.94 ± 0.16	3.24 ± 0.38	3.02 ± 0.22
I14 O-NADP N7	3.30 ± 0.29	3.66 ± 0.33	3.14 ± 0.26	3.43 ± 0.32	3.04 ± 0.21	3.08 ± 0.22	3.08 ± 0.22	3.14 ± 0.25
M20 S-DHF N5H	3.54 ± 0.46	2.81 ± 0.28	3.57 ± 0.47	3.05 ± 0.41	3.68 ± 0.40	3.12 ± 0.36	3.85 ± 0.55	3.32 ± 0.39

These changes at the active site are likely important in determining the reaction rates of the mutants. Something that is less clear, however, is how mutations so far from the active site cause structural changes that propagate all the way to the active site. We can tell from the distance matrices of figure 3 that there are many structural changes induced by the mutants that propagate throughout the enzyme, but we can only begin to understand the details of how such subtle mutations can lead to such long-range structural perturbations. In the future we hope to elucidate additional details of these effects.

Concluding Remarks

We have examined the mechanism of hydride transfer in DHFR and a series of mutants using a recently developed, highly accurate QM/MM Hamiltonian. Our PMF calculations produced free energy barriers of the wt and mutants at pH 7, which reproduced the trend of the experimentally determined rates. This finding provides additional evidence of the usefulness of the AM1-SRP Hamiltonian and ought to encourage other investigators of the benefits of this kind of method for studying DHFR, as well as other enzyme systems. Additionally, we have provided structural and dynamic analyses that begin to explain how subtle mutations that are quite distant from the active site can drastically affect the kinetics of an enzymatic reaction. Previous studies have pointed to networks of coupled residues as potentially important in the catalytic mechanism of DHFR,¹³ and we have highlighted aspects of how changes to these residues propagate through the enzyme, causing structural and dynamic perturbations that affect catalysis. Additional work will be necessary to develop a comprehensive picture of how motions of residues throughout the protein are coupled to the reaction coordinate and how distal mutations can affect the physical nature of C-H activation.