INFERRING FUNCTIONAL NETWORK-BASED SIGNATURES VIA STRUCTURALLY-WEIGHTED LASSO MODEL

Abstract

Most current research approaches for functional/effective connectivity analysis focus on pair-wise connectivity and cannot deal with network-scale functional interactions. In this paper, we propose a structurally-weighted LASSO (SW-LASSO) regression model to represent the functional interaction among multiple regions of interests (ROIs) based on resting state fMRI (R-fMRI) data. The structural connectivity constraints derived from diffusion tenor imaging (DTI) data will guide the selection of the weights which adjust the penalty levels of different coefficients corresponding to different ROIs. Using the Default Mode Network (DMN) as a test-bed, our results indicate that the learned SW-LASSO has good capability of differentiating Mild Cognitive Impairment (MCI) subjects from their normal controls and has promising potential to characterize the brain functions among different condition, thus serving as the functional network-based signature.

1. INTRODUCTION

A major research objective of neuroscience is to model and quantify the functional interaction patterns among neural networks at different spatial and temporal scales, in that meaningful interaction patterns reflect the working mechanisms of neural systems and represent their relationships related to the external world. However, inferring robust and meaningful interaction patterns from high-dimensional neural datasets impose significant challenges from computational perspectives. For instance, so far many efforts have been focused on the pairwise connectivity analyses of networks of brain regions based on resting state fMRI (R-fMRI) data. Though these pairwise functional connectivity analyses may provide useful information regarding neural systems, their descriptive power is limited. The major reason is that higher-order functional interactions among neural nodes cannot be captured in pair-wise connectivity analysis.

There are two major advantages for studying higher-order interactions using our method instead of pair-wise connectivities. The first is that the latter only focuses on the relation between two regions. By using linear regression model, though, our proposed method could simultaneously characterize the interaction of one ROI with all other ROIs and has the capability of quantitatively measuring the percentage of contributions among different ROIs. The other advantage of our method is that it makes it possible to consider “directionality” when studying functional interaction. In this paper, given structural connectivity constraint, we propose a novel structurally-weighted LASSO (SW-LASSO) regression model and use it to represent the functional interactions within the DMN based on R-fMRI data. The neuroscience basis behind using structural connectivity information as the weight to constrain the regression process is that if two regions have strong structural connections, they tend to have strong functional dependence between each other.

2. METHODS

2.1. Overview and data preprocessing

The main steps in our proposed framework are outlined in Fig.1. First, by using group-wise independent component analysis (gICA) [1] and a DMN template, we identified eight DMN ROIs on both MCI patients and normal controls. The structural connectivity patterns among these eight ROIs were derived from DTI data and entered as prior knowledge into our SW-LASSO regression model, along with the eight ROIs’ R-fMRI BOLD signals. The learned coefficients matrix will be treated as the functional network-based signatures and applied in the classification of MCI and controls via the SVM classifier [2].

Fig. 1.

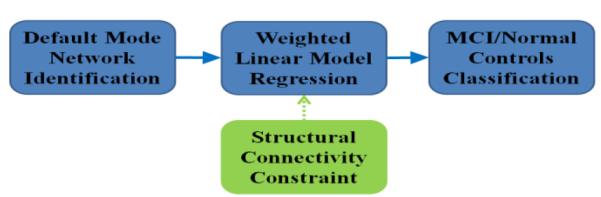
The flowchart of our proposed framework.

The dataset include twenty-eight participants (10 MCI patients and 18 socio-demographically matched normal controls (NC)). The detailed information can be found in [3]. For all the NC and MCI subjects, we constructed their DMN by using the group independent component analysis (gICA) [1] implemented in the GIFT toolbox [4]. Eight DMN ROIs were determined using a t-test (P<0.05) based on the group mean independent components and their anatomical labels are listed in table 1.

Table 1.

The atlas labels of eight DMN ROIs. The atlases used here are the Harvard-Oxford cortical and subcortical structural atlases and Talairach Daemon Labels.

DMN-ID	Atlas Labe
DMN-1	Angular Gyrus (Right)
DMN-2	Angular Gyrus (Left)
DMN-3	Posterior Cingulate (Right)
DMN-4	Posterior Cingulate (Left)
DMN-5	Middle Temporal Gyrus (Right)
DMN-6	Middle Temporal Gyrus (Left)
DMN-7	Medial Frontal Gyrus (Left)
DMN-8	Medial Frontal Gyrus (Right)

2.2. Structurally-Weighted LASSO (SW-LASSO) regression model

2.2.1. LASSO and weighted LASSO

The LASSO [5] is one of the most commonly used high-dimensional regression models for variable selection, feature prediction, and sparsity learning. The LASSO estimates are defined as:

$${\widehat{\beta }}_{\mathit{LASSO}}=\arg \min {\Vert \mathrm{y}-\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}{\beta }_{\mathrm{i}}\Vert }^2+\lambda \sum _{\mathrm{i}=1}^{\mathrm{n}}\mid {\beta }_{\mathrm{i}}\mid$$ (1)

The second term in Eq.(1) is known as the “ℓ₁ penalty” which makes the LASSO continuously shrink the coefficients toward zero as λ increases. If λ is large enough, some coefficients will be exactly zero and thus feature selection is achieved automatically. But the LASSO shrinkage produces biased estimates for those large coefficients, and hence it could be suboptimal considering the estimation risk [6]. Many improved LASSO methods have been proposed including the Adaptive LASSO [6], which tends to assign each covariate different penalty parameters to avoid having larger coefficients penalized more heavily than small coefficients. However, we still face two problems in practice: variable selection is highly unstable and some preferred features are not selected. To alleviate this, we want to adjust the regression procedure using external or domain knowledge.

In this paper, we introduce a novel weighted LASSO model which will use structural connectivity information derived from DTI tractography data as the constraint to construct the weight. The difference between our method and the adaptive LASSO is that the latter uses ℓ₂ initial estimation to adjust and reweighted ℓ₁ penalty in an iterative algorithm, while our method will decide the weight directly according to the structural brain connectivity analysis. The neuroscience basis of our method is that axonal fiber connections are the structural substrates of functional interactions, and a variety of neuroscience research studies have reported this strong correlation [7]. That is, stronger structural connections among ROIs indicate higher functional interactions, and this principle can be used as the biologically meaningful guidance in the search of functional interaction patterns during LASSO regression. Another advantage of introducing the structural connectivity constraint is the consideration of computational complexity: the regression space grows exponentially as the number of ROIs increases. By using structural information one can efficiently and effectively reduce the search space and which is grounded on sound neuroscience principle.

2.2.2. Construction of weights using structural connectivity constraint

After identified the DMN ROIs, we constructed the structural connectivity matrix based on the number of fibers connecting one ROI to the others [8]. As shown in Fig.2a, the line colors encode the number of fibers between any pair of ROIs (colored bubbles). Fig. 2b shows the structural connectivity matrix constructed based on Fig.2a. Then, for each ROI, we calculated the percentages of the fibers connecting to the other ROIs: f_i,j represents the ratio of the number of fibers linking the i-th and j-th ROI to the total number of fibers connecting to the i-th ROI. Thus, we have ${\sum }_{j=1}^n{f}_{i,j}=1,\mathrm{i}\ne \mathrm{j}$ and here n=8. In our weighted LASSO regression model, a lower weight value represents a smaller penalty to the corresponding variable, making it more likely to be included in the selected regression model. We define the weight as:

$$w_{i,j}=1-f_{i,j}∕\mathrm{p},\mathrm{p}>1$$ (2)

Fig. 2 (c) shows the corresponding weight matrix (p=2), and we can see that stronger structural connectivity will have a lower weight value. Another point to be noted is that the weight matrix is not symmetric, since f_i,j and f_j,i are not necessarily equal.

Fig. 2.

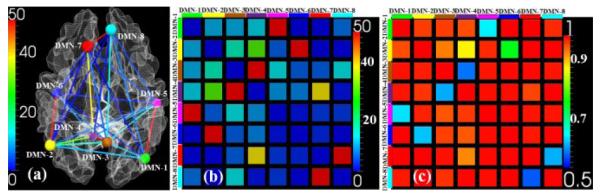
Illustration of constructing weight constraint. (a) Structural connectivity patterns within eight DMN ROIs. The color of lines encodes the number of fibers between any pair of ROIs. (b) The corresponding structural connectivity matrix of (a). (c) The generated weight matrix based on Eq. (2) when p equals 2.

2.3. SW-LASSO regression

In this section we will formally define the structural weighted LASSO (SW-LASSO) regression model used in this paper. Suppose we have response y_r and k regressors X_r:{x₁, x₂, …, x_k}. For both response and regressors, we have N sample values (the number of MCI subjects or controls). y_r(j) and x_i(j) represent the j-th sample value of response and the i-th regressor x_i respectively, i=1, 2, …, k and j=1,2, …, N. Then, we perform weighted ℓ₁ constrained regression of y_r on X_r:

$$\begin{array}{cc}\hfill {\widehat{\beta }}_{\text{Lasso}}=& \arg \min \left\{\sum _{\mathrm{j}=1}^{\mathrm{N}}{\left({\mathrm{y}}_{\mathrm{r}}\right(\mathrm{j})-\sum _{\mathrm{i}=1}^{\mathrm{k}}{\beta }_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}(\mathrm{j}\left)\right)}^2\right\}\hfill \\ \hfill & +\lambda \sum _{\mathrm{i}=1}^{\mathrm{k}}(1-{\mathrm{f}}_{\mathrm{r},\mathrm{i}}∕\mathrm{p})\mid {\beta }_{\mathrm{i}}\mid \hfill \end{array}$$ (3)

Eq. (3) is similar in concept to the adaptive LASSO, but the major difference is that the weight term comes from the structural connectivity, instead of learning from the dataset. In this paper, we extract the BOLD signals of eight DMN ROIs for both MCI patients (10) and NC (18). For each ROI, we use its R-fMRI signal as the response (y(j) in Eq. (3)), and the R-fMRI signals of the other seven ROIs as the regressors (x(j) in Eq. (3)), with the corresponding structural weight vector as the constraint (1 – f_r,i/p in Eq. (3)). In comparison with the traditional pair-wise functional connectivity analysis that only considers the temporal correlation of two ROIs, here, we considered that one ROI is interacting with multiple ROIs in the network and thus its time series can be regressed by other fMRI time series via the optimally weighted linear regression model in Eq. (3). Since the structural connectivity mapping among the DMN ROIs already demonstrated that one ROI could be structurally connected to multiple ROIs (Fig. 2b), it makes sense to assume that one ROI functionally interacts with multiple ROIs. During the regression, we fixed p=2 and λ is determined by fivefold cross-validation. It is obvious that Eq.(3) is essentially a ℓ₁ penalization problem which can be solved very efficiently [6]. We adopted the LARS algorithm [9] to solve Eq. (3) based on the widely used SPAMS sparse learning package [10].

3. RESULTS

3.1. Accuracy of the SW-LASSO

To measure how well our proposed weighted LASSO regression model fits the DMN’s R-fMRI signals, we employed the coefficient of determination (COD) [11] as the measurement. From the table 2, we can see that compared to the traditional regression algorithm (OLS), our method did not sacrifice much regression accuracy when introducing the external prior knowledge of structural connection pattern as the weight constraint. It should be noted that the average COD values of both regression methods are 46%, which means that for each DMN ROI, around half of its R-fMRI BOLD signals can be explained by other ROIs in the same functional network. One possible reason might lead to around half of the signals are unpredictable is that we only consider DMN in this paper. The DMN ROIs we focused on may functionally interact with other ROIs outside the DMN. Under such a situation, only the contribution within the DMN ROIs can be covered in our COD estimation in the current stage.

Table 2.

The comparison of COD of ordinary least squares and our method.

COD	OLS	SW-LASSO	Difference
DMN-1	0.466	0.461	1.2%
DMN-2	0.457	0.450	1.7%
DMN-3	0.573	0.561	2.1%
DMN-4	0.575	0.562	2.2%
DMN-5	0.342	0.344	0.6%
DMN-6	0.404	0.386	4.2%
DMN-7	0.436	0.428	1.9%
DMN-8	0.492	0.480	2.4%

3.2. Functional network-based signatures of MCI/Normal controls

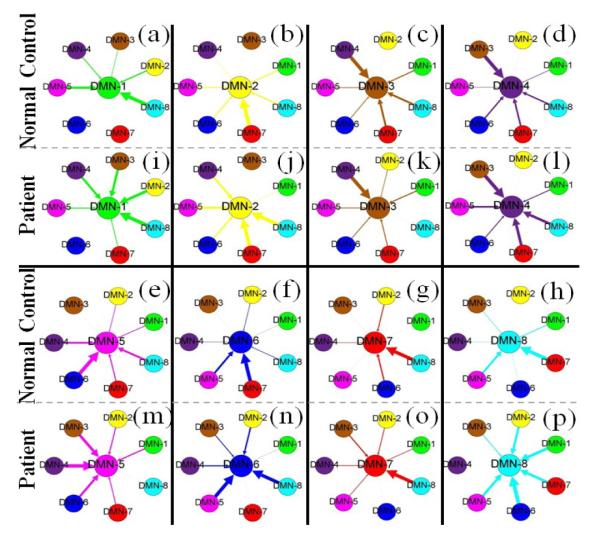
We averaged the SW-LASSO coefficient patterns of all DMN ROIs for both MCI patients and NC, as shown in Fig. 3. Different DMN ROIs are encoded with different colors and the thickness of the arrows reflects the contribution in the SW-LASSO regression model. One important observation is that for the same DMN ROI, MCI patients tend to have more ROIs with relatively larger weights in the regression model than the NC. Moreover, different from the NC which are likely to have one or two dominant regressors, MCI patients tend to have multiple equal contributors. For example, for the first ROI (DMN-1), the ROI DMN-8 shows dominant interaction in NC; in MCI patients, however, the DMN-2, DMN-3, DMN-4 and DMN-8 have relatively equal contributions to the regression of DMN-1. Another obvious example is DMN-8: in NC, DMN-5 and DMN-7 are the two dominant regressors; but for MCI patients, all DMN ROIs have strong interactions with it except the DMN-4. To quantitatively measure this difference, we sorted the coefficients with descending order and computed the ratio of the first coefficient (the largest) to the second, third and fourth, respectively. For the normal controls, these ratios are 1.71, 2.28 and 2.68, respectively. But for MCI patients, the ratios are 1.45, 1.77 and 1.94. It is evident that normal controls exhibit significantly larger ratios than MCI patients (p-value=0.002), which suggests that the latter has much flatter distribution of SW-LASSO coefficients and more regressors tend to have equal contributions.

Fig. 3.

The coefficient patterns of eight DMN ROIs for both normal controls and MCI patients. Different color encodes different DMN ROIs. The arrow represents the direction of regression and the thickness reflects the contribution of the corresponding ROI during the regression procedure.

The above observation might be explained by the recent neuroscience findings regarding the origin of Alzheimer’s disease (AD) [12]: AD might initially involve DMN regions, which results in AD patients demonstrating higher-functional activity in the DMN than NC. That is, the DMN ROIs tend to functionally interact with more other DMN ROIs than healthy controls, as suggested by our results in Fig. 3.

3.3. Classification of MCI and normal controls based on functional network-based signatures

After we performed the regression using the SW-LASSO model, for each DMN ROI we achieved 7 coefficients corresponding to other ROIs within the DMN. Thus, each subject has 56 learned coefficients and we name them as “functional network-based signatures”. We calculated these signatures for all the subjects including 10 MCI patients and 18 normal controls, and used the widely used SVM classifier [2] to conduct the classification. As a comparison, we also computed the pair-wise functional connectivity between DMN ROIs as another feature set, which was fitted into the SVM classifier using the same dataset as well.

In the experiment, because of the limited number of subjects we adopted a leave-one-out strategy and the average accuracy of classification using our “functional network-based signatures” and pair-wise functional connectivity are 86% and 64%, respectively. It is evident that under the same conditions, including the same classifier and dataset, our “functional network-based signatures” have much better classification performance than the pair-wise functional connectivity. Considering we only used the information of one functional network (DMN) in the experiment, we believe our method will achieve better classification accuracy when we add additional functional networks to our regression model in the future.

4. CONLUSION

In this paper, we proposed a novel SW-LASSO regression model to represent the higher-order interactions among multiple ROIs in brain networks. Our major contribution is that through introducing structural connectivity constraint, we can better examine the functional dependences of ROIs within the brain network. By using the DMN as a test bed, the “functional network-based signatures” showed better differentiability than the traditional pair-wise functional connectivity in groups of MCI and normal controls. Finally, we envision that the “functional network-based signatures” have great potential in revealing and quantitatively measuring the complex functional interactions within and across other brain networks in the future.