Large Deformation Diffeomorphic Registration of Diffusion-Weighted Images with Explicit Orientation Optimization

Abstract

We seek to compute a diffeomorphic map between a pair of diffusion-weighted images under large deformation. Unlike existing techniques, our method allows any diffusion model to be fitted after registration for subsequent multifaceted analysis. This is achieved by directly aligning the diffusion-weighted images using a large deformation diffeomorphic registration framework formulated from an optimal control perspective. Our algorithm seeks the optimal coordinate mapping by simultaneously considering structural alignment, local fiber reorientation, and deformation regularization. Our algorithm also incorporates a multi-kernel strategy to concurrently register anatomical structures of different scales. We demonstrate the efficacy of our approach using in vivo data and report on detailed qualitative and quantitative results in comparison with several different registration strategies.

1 Introduction

Diffusion-weighted imaging (DWI) is widely used to noninvasively study tissue micro-structures in the human brain. To compare DWI data across subjects or groups we have to handle the alignment of macro-structures and the reorientation of micro-structures simultaneously. Concurrent optimization of these two components is very challenging but is required for accurate registration.

For registration of DWI data, a commonly used approach is to fit some diffusion model to the DWI data to estimate relevant information such as orientation distribution functions (ODFs), and then incorporate such information into a registration algorithm for structural alignment. Early work uses the relatively simple diffusion tensor model [3,14]. Recent studies [6,5,8,9,12,4,16] have moved forward by using more complicated models that take into account complex fiber configurations such as crossings.

Geng et al. [6] aligned ODFs represented by spherical harmonics (SHs) using an elastic registration algorithm. Du et al. [5] integrated a similarity metric for the ODFs, which is defined in a Riemannian manifold, into a large deformation diffeomorphic metric mapping (LDDMM) algorithm [7]. Yap et al. [12] extracted coarse-to-fine features from the ODFs for hierarchically refined alignment. Instead of using ODFs, Hong et al. [8] performed registration with the help of T₂-weighted images and then subsequently reoriented the fiber orientation distribution (FOD). Raffelt et al. [9] registered DWI data by mapping the FODs via a subject-template-symmetric diffeomorphic framework.

However, the aligned data generated by the above approaches are not in the form of diffusion-weighted images. The ability to produce diffusion-weighted images as the final registration outcome is important for common-space analysis using diffusion models that do not have warping and reorientation algorithms.

To overcome this problem recent studies propose to register DWI data directly in the Q-space [4,16]. Dhollander et al. [4] tackled the problem by utilizing an SH-based reorientation algorithm together with a diffeomorphic demons algorithm [11]. In [16] we achieved a similar goal by using a set of fiber basis functions (FBFs) [13] and a simplified shooting algorithm [1]. Both methods regard spatial alignment and local fiber reorientation as two separate components, and perform optimization by repeating the following two steps: (1) compute the map between the DWI data without considering reorientation, and (2) reorient the data using the resulting map. Although this strategy is simple, it ignores the crucial role reorientation plays in correspondence establishment.

In this paper we describe a method that is able to register diffusion-weighted images in the Q-space. Our work distinguishes itself from [16] by concurrently achieving image matching, data reorientation, and deformation regularization in a single framework. To the best of our knowledge, this is the first work that integrates spatial alignment and local reorientation into a single cost function to address the direct registration of DWI data. In addition, our mathematical formulation reveals how reorientation affects registration, and such insight cannot be gained from [16]. Our work is also different from [3] and [14], where reorientation is incorporated into the cost function to address the registration of diffusion tensor models.

Below we first introduce the shooting algorithm used in this work. We then describe the integration of diffusion data reorientation into the shooting algorithm in Sect. 3. We demonstrate the efficacy of our algorithm in Sect. 4, and conclude our work in Sect. 5.

2 Geodesic Shooting

Let I₀ be the source image and I₁ be the target image. We would like to minimize

$$\begin{array}{cc}\hfill E\left({\mathit{v}}_t\right)=& \frac{1}{2}{\int }_0^1{\Vert {\mathit{v}}_t\Vert }_V^2\mathrm{d}t+\frac{1}{{\sigma }^2}{\Vert I_0\circ {\varphi }_{1,0}-I_1\Vert }_{{\ell }^2}^2,\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\stackrel{.}{\varphi }}_{t,0}+\left(D{\varphi }_{t,0}\right){\mathit{v}}_t=0,{\varphi }_{0,0}=\text{id},\hfill \end{array}$$ (1)

where v_t is a time-dependent velocity field to be solved, σ > 0 is a regularization constant, ϕ_s,t is a map induced by v_t, mapping a voxel from its position at time s to its position at time t, and id is an identity map. ${\Vert {\mathit{v}}_t\Vert }_V^2={\langle L^{†}L{\mathit{v}}_t,{\mathit{v}}_t\rangle }_{{\ell }^2}$, where L is a proper differential operator controlling the smoothness of v_t, which, in turn, guarantees a diffeomorphic solution [2]. Usually smoothing is achieved by convolving momentum L^†Lv_t with a kernel K = (L^†L)⁻¹. Here we use a multi-Gaussian kernel scheme [10] to introduce a natural multi-resolution property to the solution. ${\stackrel{.}{\varphi }}_{t,0}=\partial {\varphi }_{t,0}∕\partial t$ and D· is the Jacobian operator. Note that ${\stackrel{.}{\varphi }}_{t,0}+\left(D{\varphi }_{t,0}\right){\mathit{v}}_t=0$ simply amounts to transport equations for the individual coordinates of the map, which can be understood as a natural consequence of diffeomorphism (see [2] for details). This is different from [16], where transport equations for image intensity are used.

The minimization of (1) leads to the following optimality conditions:

$$\begin{array}{c}\hfill {\stackrel{.}{\varphi }}_{t,0}+\left(D{\varphi }_{t,0}\right){\mathit{v}}_t=0,\hfill \\ \hfill L^{†}L{\mathit{v}}_t+{\left(D{\varphi }_{t,0}\right)}^T{\lambda }_t=0,\hfill \\ \hfill -\mathrm{d}{\lambda }_t∕\mathrm{d}t-{\left[\mathrm{div}\right({\lambda }_t^1{\mathit{v}}_t),\mathrm{div}({\lambda }_t^2{\mathit{v}}_t),\mathrm{div}({\lambda }_t^3{\mathit{v}}_t\left)\right]}^T=0,\hfill \end{array}$$ (2)

$$\begin{array}{c}\hfill {\lambda }_1=\frac{2}{{\sigma }^2}{({\mathit{DI}}_0\circ {\varphi }_{1,0})}^T(I_1-I_0\circ {\varphi }_{1,0}),\hfill \\ \hfill {\varphi }_{0,0}=\text{id},\hfill \end{array}$$ (3)

where ${\lambda }_t^k$ is the k-th element of λ_t. The minimization of (1) involves (i) converting it to an unconstrained energy functional via Lagrange multipliers (e.g., introducing multiplier λ_t for the constraint ${\stackrel{.}{\varphi }}_{t,0}+\left(D{\varphi }_{t,0}\right){\mathit{v}}_t=0)$; (ii) computing functional variation w.r.t v_t, ϕ_t,0 and the Lagrange multipliers; and (iii) obtaining the optimality conditions by setting the variation to zero.

The gradient of (1) w.r.t v_t is given by ▽_vtE = L^†L_vt + (Dϕ_t,0)^Tλ_t. As geodesic shooting allows us to perform gradient descent only for t = 0 by leveraging conservation of momentum [1], we can write an equivalent gradient as ▽_v0E = L^†L_v0 + ∣Dϕ_0,1∣λ₁○ϕ_0,1. As (2) should hold at all times at convergence, we have λ = –L^†L_v0 at t = 0. Hence, the final gradient used is given by

$${\nabla }_{{\lambda }_0}E={\lambda }_0-\mid D{\varphi }_{0,1}\mid {\lambda }_1\circ {\varphi }_{0,1}.$$ (4)

Note that we perform gradient descent directly on λ₀ by pulling the final adjoint λ₁ back to t = 0. The pullback can be achieved by computing a forward map (from t = 0 to t = 1) on the fly during a backward integration. In this work we use line search for gradient descent. Note that this is a simplification (inspired by Ashburner and Friston [1]) to the actual gradient descent w.r.t. the initial condition which would require the computation of a second-order adjoint system (see [1] for details).

3 Geodesic Shooting with Reorientation

We now briefly review the major concepts involved in reorientation using the FBFs [13] and then describe how this can be integrated into the above shooting algorithm.

3.1 Reorientation of Diffusion-Weighted Data

Reorientation in Q-space can be achieved in three steps: (1) decompose the diffusion signal profile into a set of weighted FBFs; (2) reorient each FBF independently using a local transformation; (3) recompose the reoriented FBFs to obtain the desired profile.

Let S(q_i) be the diffusion signal measured in direction q_i (i = 1, … , M). It can be represented by a set of N FBFs, each of which being realized by a Waston distribution function with mean direction ${\mu }_j:S\left({\mathit{q}}_i\right)=w^0{f}_0+{\sum }_{j=1}^N{w}^{j}f({\mathit{q}}_i\mid {\mu }_j,\kappa )$, where $f({\mathit{q}}_i\mid {\mu }_j,\kappa )=C\left(\kappa \right)\exp \left(\kappa {\left({\mu }_j^T{\mathit{q}}_i\right)}^2\right)$ is a probability density function of the Watson distribution, κ is a constant and is the concentration parameter, and C(κ) is a normalization factor; w^j is the weight associated with the j-th FBF; f₀ ≡ C(0) is a constant representing the isotropic diffusion component. Let S be the signal vector, then we have S = Fw, where S = [S(q₁), S(q₂), … , S(q_M)]^T, w = [w⁰, w¹, … , w^N]^T and

$$\mathit{F}=\left[\begin{array}{cccc}\hfill f_0\hfill & \hfill f({\mathit{q}}_1\mid {\mu }_1,\kappa )\hfill & \hfill \cdots \hfill & \hfill f({\mathit{q}}_1\mid {\mu }_N,\kappa )\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill f_0\hfill & \hfill f({\mathit{q}}_M\mid {\mu }_1,\kappa )\hfill & \hfill \cdots \hfill & \hfill f({\mathit{q}}_M\mid {\mu }_N,\kappa )\hfill \end{array}\right].$$

Since typically, M < N + 1, this is a set of under-determined linear equations, which can be solved by a L₁ regularized least-squares solver with a non-negative constraint (see [13] for details).

A local affine transformation A is used to reorient the directions of the FBFs, i.e. ${\mu }_j^{\prime }=\mathit{A}{\mu }_j∕\Vert \mathit{A}{\mu }_j\Vert$. Usually A is estimated from the map resulting from registration. A matrix of reoriented FBFs, F’, is calculated based on ${\mu }_j^{\prime }$ and then used to obtain the orientation-rectified profile S’ by S’ = F’ w. Note that the isotropic component is not reoriented.

3.2 Integration with the Shooting Algorithm

Let I be a vector-valued image representing diffusion signal vector S at each position x. We define the action of a map ϕ on I as I ○ ϕ = F_ϕW ○ ϕ, where W is a weight image associated with I and contains a sparse weight vector w at each x, and F_ϕ is a reoriented FBF image, whose voxel at x is a matrix and is given by

$$F_{\varphi \left(\mathit{x}\right)}=\left[\begin{array}{cccc}\hfill f_0\hfill & \hfill f\left({\mathit{q}}_1\mid \frac{{\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_1}{\Vert {\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_1\Vert },\kappa \phantom{\mid }\right)\hfill & \hfill \cdots \hfill & \hfill f\left({\mathit{q}}_1\mid \frac{{\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_N}{\Vert {\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_N\Vert },\kappa \phantom{\mid }\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill f_0\hfill & \hfill f\left({\mathit{q}}_M\mid \frac{{\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_1}{\Vert {\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_1\Vert },\kappa \phantom{\mid }\right)\hfill & \hfill \cdots \hfill & \hfill f\left({\mathit{q}}_M\mid \frac{{\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_N}{\Vert {\left(D\varphi \right(\mathit{x}\left)\right)}^{-1}{\mu }_N\Vert },\kappa \phantom{\mid }\right)\hfill \end{array}\right].$$

To reflect reorientation we can now rewrite the cost function (1) as

$$\begin{array}{cc}\hfill E\left({\mathit{v}}_t\right)=& \frac{1}{2}{\int }_0^1{\Vert {\mathit{v}}_t\Vert }_V^2\mathrm{d}t+\frac{1}{{\sigma }^2}{\Vert F_{{\varphi }_{1,0}}{W}_0\circ {\varphi }_{1,0}-I_1\Vert }_{{\ell }^2}^2,\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\stackrel{.}{\varphi }}_{t,0}+\left(D{\varphi }_{t,0}\right){\mathit{v}}_t=0,{\varphi }_{0,0}=\text{id},\hfill \end{array}$$ (5)

where W₀ is the weight image associated with I₀. Similarly, we can obtain a set of optimality conditions (deviation details omitted due to space limit). All conditions are the same as given in Sect. 2 except for condition (3), which is now given by

$${\lambda }_1=\frac{2}{{\sigma }^2}\left[\begin{array}{c}\hfill \langle I_1-I_0\circ {\varphi }_{1,0},B_1\rangle \hfill \\ \hfill \langle I_1-I_0\circ {\varphi }_{1,0},B_2\rangle \hfill \\ \hfill \langle I_1-I_0\circ {\varphi }_{1,0},B_3\rangle \hfill \end{array}\right],$$ (6)

where B₁, B₂ and B₃ are vector-valued images of the same size as I₀ and I₁. Let b_k be the voxel of B_k at position x. b_k is a M × 1 vector and its i-th element is computed as follows

$$\begin{array}{cc}\hfill & b_k^i=f_0\frac{\partial w_0^0}{\partial x^k}\circ {\varphi }_{1,0}\left(\mathit{x}\right)+\hfill \\ \hfill & \sum _{j=1}^{N}f\left({\mathit{q}}_i\mid \frac{{\tilde{\mu }}_j}{\Vert {\tilde{\mu }}_j\Vert },\kappa \phantom{\mid }\right)\left(2\kappa \langle \frac{{\tilde{\mu }}_j}{\Vert {\tilde{\mu }}_j\Vert },{\mathit{q}}_i\rangle \mathrm{div}\left({\tilde{q}}_{\mathit{ij}}^k{\tilde{\mu }}_j\right)w_0^j\circ {\varphi }_{1,0}\left(\mathit{x}\right)+\frac{\partial w_0^j}{\partial x^k}\circ {\varphi }_{1,0}\left(\mathit{x}\right)\right),\hfill \end{array}$$

where x^k is the k-th element of x, $w_0^j$ is the j-th element of the voxel of W₀ at x, ${\tilde{\mu }}_j={\left(D{\varphi }_{1,0}\right(\mathit{x}\left)\right)}^{-1}{\mu }_j$ and ${\tilde{q}}_{\mathit{ij}}^k$ is the k-th element of ${\tilde{\mathit{q}}}_{\mathit{ij}}={\left({\nabla }_{{\tilde{\mu }}_j}\left[\frac{{\tilde{\mu }}_j}{\Vert {\tilde{\mu }}_j\Vert }\right]{\left(D{\varphi }_{1,0}\right(\mathit{x}\left)\right)}^{-1}\right)}^{\mathrm{T}}{\mathit{q}}_i$.

Note that (6) reveals how spatial alignment and reorientation interact with each other. The shooting process is used to obtain an initial map, which, together with data reorientation, is used to compute λ₁ using (6). The new λ₁ is then pulled back to t = 0 as described in Sect. 2 to compute the gradient (4) for updating the map via shooting. The whole process is repeated until convergence. Our work considers spatial alignment and reorientation in a single cost function (5). Reorientation plays an active role in the whole registration process. In contrast, spatial alignment and reorientation are regarded as two separate components in [16], and their relationship is unclear.

4 Experiments

DWI data were acquired from 11 adults using a Siemens 3T TIM Trio MR Scanner with an EPI sequence. Diffusion gradients were applied in 120 non-collinear directions with diffusion weighting b = 2000 s/mm². The imaging matrix was 128×128 with a field of view of 256×256mm². 80 contiguous slices with thickness of 2 mm covered the whole brain.

We randomly chose an image as the target image and used the rest as source images. For each image, we fit the FBFs, with 321 directions uniformly distributed on a unit sphere, to estimate the associated weight image, which was then used to obtain a reconstructed version of the image. A set of affine transformations was estimated between the target image and each source image using their anisotropy images computed from the reconstructed data.

We used our method (Sect. 3.2) to register each source to the target using the estimated affine transformations. To show the advantage of our method, we compared it with the following DWI registration strategies:

1. Scalar Registration: For each reconstructed source, we warped its anisotropy image using an affine transformation, and then aligned the warped image with the anisotropy of the reconstructed target;

2. Vector Registration: We reconstructed each source using an affine transformation. Note that this is different from the above case where the source images were reconstructed without any transformation. We registered each reconstructed source to the same reconstructed target as used in the above case;

3. Our early work [16]: This is an iterative registration scheme. Each stage consists of three steps: (1) reconstructing the source and target images; (2) aligning the two via a shooting algorithm; (3) concatenating the resulting map with the previous one. The source is reconstructed using the composite map together with an affine transformation, while the target is always reconstructed without any transformation. At each stage the reconstruction is done by using an increasing number of diffusion directions and a decreasing concentration κ.

In all three cases, the previously estimated affine transformations were used for warping or reconstruction, and the image alignment was done as described in Sect. 2. We ran line search of 30 iterations for the proposed method, scalar registration and vector registration. For our early work [16] we used 5 stages and 30 iterations for the registration in the first two stages, 20 for the middle stages and 10 for the final stage. The number of diffusion directions was set to 1, 6, 21, 81 and 120 for each stage and κ gradually decreased from 0. The spatial regularization was set to be the same for the proposed work and [16].

To quantify the comparison we reconstructed each source using the associated affine transformation and the resulting map. We used the same metric, root mean square (RMS) error as in [16], to compute registration error. Averaging the resulting RMS error images across subjects for each method leads to the mean images shown in Fig. 1. We also show the mean RMS error image of the source warped and reoriented using affine transformation alone. For each mean RMS error image we computed its statistics (e.g., mean, s.d.) over all voxels and report the results in Table 1a. We also computed the mean intensity value for each RMS error image, and used the means across subjects to perform a student’s t-test (two-tailed) between the proposed method and the other methods. The results are given in Table 1b.

Fig. 1.

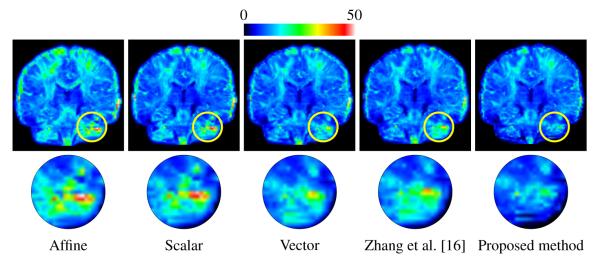
From top to bottom: the mean RMS error images and the close-ups of the regions marked by yellow circles. Note that the images were not sliced to show left-right symmetry.

Table 1.

A detailed quantitative comparison of different DWI registration strategies

(a)				(b)
Method	Mean±s.d.	Median	90%-ile	Method	p-value
Affine	12.6±5.9	11.3	18.9	Affine	p < 10−5
Scalar	11.5±5.7	10.4	17.2	Scalar	p < 10−4
Vector	10.7±4.7	9.9	15.4	Vector	p < 10−4
Zhang et al. [16]	10.6±4.7	9.8	15.3	Zhang et al. [16]	p < 10−3
Proposed method	9.8±4.1	9.4	14.1	Proposed method	–

Table 1 clearly shows that affine transformation is insufficient for DWI registration. The registration accuracy can be greatly improved with the help of non-rigid registration as indicated by the results from scalar and vector registration. Despite the improvements, both strategies, as well as our early work [16], do not take into account reorientation in registration. In contrast, our method yields significantly better registration accuracy due to explicit reorientation in registration.

Figure 2 shows the anisotropy images of the target and averaged reconstructed source. It shows that our method registers all main structures well and results in a crisp mean anisotropy image. Results from other methods are not shown due to space limit. The anisotropy image produced by affine registration is quite blurred due to structural misalignment. Results from the other three non-rigid registration methods are visually similar to the result shown for our method. Figure 2 also shows exemplar ODFs, which indicate that the result produced by our method is in close agreement at voxel level with the target image. This is important for applications such as white matter tractography, which is sensitive to error in local fiber orientations.

Fig. 2.

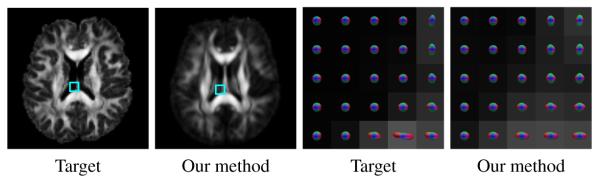
Left two columns: anisotropy images. Right two columns: exemplar ODFs generated from the region (marked by cyan rectangles) in the original target and averaged reconstructed source.

We implemented our algorithm in C++ using the Insight Segmentation and Registration Toolkit¹ (ITK). The typical running time²/memory consumption (for 30 iterations) is 4.3 minutes/1GB for scalar registration and 4.2 hours/5GB for the proposed method.

5 Conclusion and Future Work

We have described a method for directly registering the DWI data under large deformation. This is achieved by incorporating a DWI data reorientation technique into a variant of geodesic shooting algorithm. Unlike most of existing methods, our approach produces diffusion-weighted images as output, thus allowing the fitting of any diffusion model for subsequent analysis. Experimental results indicate that our method significantly outperforms several other DWI registration strategies. Future work includes validation and comparison with other methods like DTI-TK [15] using a large dataset.