Analysis of osmotic stress-induced Ca²⁺ spark termination in mammalian skeletal muscle

Abstract

Ca²⁺ sparks represent synchronous opening of the ryanodine receptor (RyR) Ca²⁺ release channels located at the sarcoplasmic reticulum (SR) membrane. Whereas a quantal nature of Ca²⁺ sparks has been defined in cardiac muscle, the regulation of Ca²⁺ sparks in skeletal muscle has not been well studied. Osmotic-stress applied to an intact skeletal muscle fiber can produce brief Ca²⁺ sparks and prolonged Ca²⁺ burst events. Here, we show that termination of Ca²⁺ bursts occurs in a step wise and quantal manner. Ca²⁺ burst events display kinetic features that are consistent with the involvement of both stochastic attrition and coordinated closure of RyR channels in the termination of SR Ca²⁺ release. Elemental unitary transition steps could be defined with a mean ΔF/F₀ of ~0.28, corresponding to the gating of 1–2 RyR channels. Moreover, the amplitude of the elemental transition steps declines at the later stage of the burst event. In tandem Ca²⁺ burst events where two Ca²⁺ bursts occur at the same position within a fiber in rapid succession, the trailing event is consistently of lower amplitude than the initial event. These two complementary results suggest that SR Ca²⁺ release may be associated with local depletion of SR Ca²⁺ stores in mammalian skeletal muscle.

Introduction

The calcium ion (Ca²⁺) acts as a vital second messenger in many cell types influencing myriad cellular processes, including contraction of muscle fibers. Release of sequestered Ca²⁺ from the sarcoplasmic reticulum (SR) through ryanodine receptor (RyR) channels constitutes the major signal driving excitation-contraction (E-C) coupling in muscle cells. In skeletal, cardiac and smooth muscle the elemental components of SR Ca²⁺ release are discrete, localized units known as Ca²⁺ sparks^1–5. These Ca²⁺ release events originate from highly structured paracrystalline arrays of RyR channels in the SR^6–8.

While spontaneous Ca²⁺ sparks ensure rhythmic contractile activity of the cardiac muscle, in skeletal muscle, SR Ca²⁺ release must be tightly repressed during the resting state, capable of rapid activation upon arrival of action potential stimulation and promptly terminate to end contraction. Initial studies detecting Ca²⁺ sparks in skeletal muscle have been performed with amphibian muscle². Ca²⁺ sparks are also detected in embryonic mammalian skeletal muscle⁹, where they are attributed to the presence of the type 3 RyR (RyR3), the dominant RyR isoform at this stage of development^10,11. While rare observations of Ca²⁺ sparks have been made in resting intact mammalian fibers^9,11, until recently biophysical studies of Ca²⁺ sparks in mammalian skeletal muscle were generally performed with fibers where the sarcolemma is disrupted through various physical or chemical skinning methods^12–14.

Our laboratory has determined that stress generated by membrane deformation induces a fluttered SR Ca²⁺ release response that is confined to the periphery of the intact mammalian muscle fibers^15–17. These events originate from RyR1 using pharmacological inhibition and experiments in knockout mouse models for RyR3. These events are also dependent on activation of the Type 1 inositol (1,4,5)-trisphosphate receptor for activation of this response¹⁸. In addition to the short Ca²⁺ release events that resemble Ca²⁺ sparks observed in cardiac and permeabilized skeletal muscles, a distinct population of prolonged Ca²⁺ burst events is generated in intact skeletal muscle fibers following osmotic shock.

The slow, asynchronous termination of Ca²⁺ bursts provide a unique case to investigate the coordination of RyR closure and the mechanisms that influence SR Ca²⁺ release termination. Through kinetic analysis of these Ca²⁺ burst events, we now present evidence to support a quantal nature of SR Ca²⁺ release termination in intact mammalian skeletal muscle. As quantal SR Ca²⁺ release has been observed in cardiomyocytes¹⁹, characterization of the elemental units of SR Ca²⁺ release in both skeletal and cardiac muscles should provide insight into the regulatory processes of Ca²⁺ signaling in muscle and cardiovascular physiology.

Methods

Induction of Ca²⁺ sparks and Ca²⁺ bursts

Ca²⁺ sparks were induced using previously established techniques²⁰. Male C57Bl6/J mice, aged 8–12 weeks, were maintained under conditions in agreement with local regulation with regulated light cycles and standard rodent diet. Mice were sacrificed by cervical dislocation and flexor digitorum brevis (FDB) muscles were surgically removed in an isotonic balanced salt solution (Tyrode) consisting of the following 140 mM NaCl, 5 mM KCl, 2.5 mM CaCl₂, 2 mM MgCl₂, 10 mM HEPES (pH 7.2), with a measured osmolarity of 290 mOsm. Muscles were digested in the same solution supplemented with 2 mg/ml type I collagenase (Sigma C-0130, St. Louis, MO) for 55 min at 37°C.

Following collagenase treatment, FDB muscles were washed twice by immersion in Tyrode buffer and then gently dissociated by several passages through a series of pipettes with decreasing diameter. Fibers were plated on ΔTC3 glass-bottomed dishes (Bioptechs, Butler, PA) in Tyrode and immediately loaded with 10 µM Fluo-4-AM Ca²⁺ indicator (Molecular Probes, Eugene, OR) for 60 min at room temperature. Excess Fluo-4-AM was removed by washing four-times by replacing half the volume of the dish with fresh Tyrode. All muscle fibers used in analysis were confirmed to have intact sarcolemmal membranes and regular striation patterns by phase-contrast microscopy and were used within 6 h after Fluo-4 loading. Selected fibers were perfused with Tyrode buffer from a fast flow perfusion system until measurements began. Cell swelling was induced by perfusion with a hypotonic solution containing 50 mM NaCl, 5 mM KCl, 2.5 mM CaCl₂, 2 mM MgCl₂, 10 mM HEPES (pH 7.2), with a measured osmolarity of 170 mOsm. After 60–180 s exposure to hypotonic solution, cells were perfused with isotonic Tyrode to allow a return to normal cell volume. Measurements of Fluo-4 fluorescence on a 512 × 512 pixel panel were performed on a Radiance-2100 confocal microscope (BioRad, Hercules, CA) with an argon laser (488 nm) and a 40×, 1.3NA oil immersion objective (Nikon, Melville, NY). Line-scan images were acquired at a sampling rate of 2 ms per line and serial X-Y images of muscle fibers were acquired at 3.08 s per frame. Data analysis was performed using IDL software with custom routines^16,17.

Kinetic analysis of the termination of Ca²⁺ sparks and Ca²⁺ bursts

Because of the heterogeneity of Ca²⁺ spark responses that followed an osmotic shock in intact muscle fibers, traditional methods of Ca²⁺ spark image analysis were modified to accommodate the kinetic analysis of the Ca²⁺ spark and Ca²⁺ burst populations. Three major modalities of analysis were employed in this study.

First, a semi-automatic user-directed imaging program was used to identify localized Ca²⁺ release events in line-scan measurements. Due to the semi-automatic nature of the analysis event frequencies were not determined. To define a Ca²⁺ burst event, Ca²⁺ transients with durations longer than 400 ms that were spatially confined to 5 µm width and a peak amplitude value of at least 0.5 ΔF/F₀ were considered. These criteria essentially distinguish Ca²⁺ bursts from the ember events found in previous studies with permeabilized mammalian muscle^12–14. Second, whenever possible, exponential functions were used to derive the time constant for termination of Ca²⁺ spark events that exhibit apparent monophasic decay. This analysis was mainly used to compare the kinetics of brief Ca²⁺ sparks and prolonged Ca²⁺ bursts. Third, for events with stepwise transitions amplitude histograms were used to resolve the distinct transition steps within a Ca²⁺ burst event. For this analysis, the mean ΔF/F₀ for each point (2 ms) of an event was calculated and imported into Origin software (OriginLab) for graphic analysis. Raw ΔF/F₀ values were smoothed by Fast Fourier-Transformation using a value of 20 points as a smoothing criterion. All smoothed ΔF/F₀ values from the Ca²⁺ burst peak to the return to baseline were ordered into 0.025 bins and the resulting histogram was fit with the sum of multiple Gaussian functions:

$$f(x)=\sum _{i=0}^{N_{\mathit{\text{step}}}}{A}_i•e^{\frac{-{(x-x_i)}^2}{{\sigma }_i^2}}$$ (1)

where A_i, x_i and σ_i are the magnitude, position and spread of the ith Gaussian. From this analysis, the number of steps within a discrete Ca²⁺ release event (N_step) and the magnitude of the unitary transition step (UTS = x_i+1 − x_i) can be derived. Events were considered not to display stepwise closure when distinct peaks, periodic no-zero and zero values were not found in the histograms. This analysis was expanded to tandem Ca²⁺ burst events that occurred in rapid succession at the same position, where fitting with Gaussian distributions allowed the comparison of changes in N_step and UTS between the initial and trailing events.

Results

Ca²⁺ sparks and Ca²⁺ bursts in intact mammalian skeletal muscle fibers

While Ca²⁺ sparks are rarely observed in intact mammalian skeletal muscle fibers, such events can be induced in normal quiescent fibers by stress generated by varying the osmolarity of the extracellular solution¹⁶. These SR Ca²⁺ release events were generally localized to the periphery of the muscle fiber (Fig. 1a).

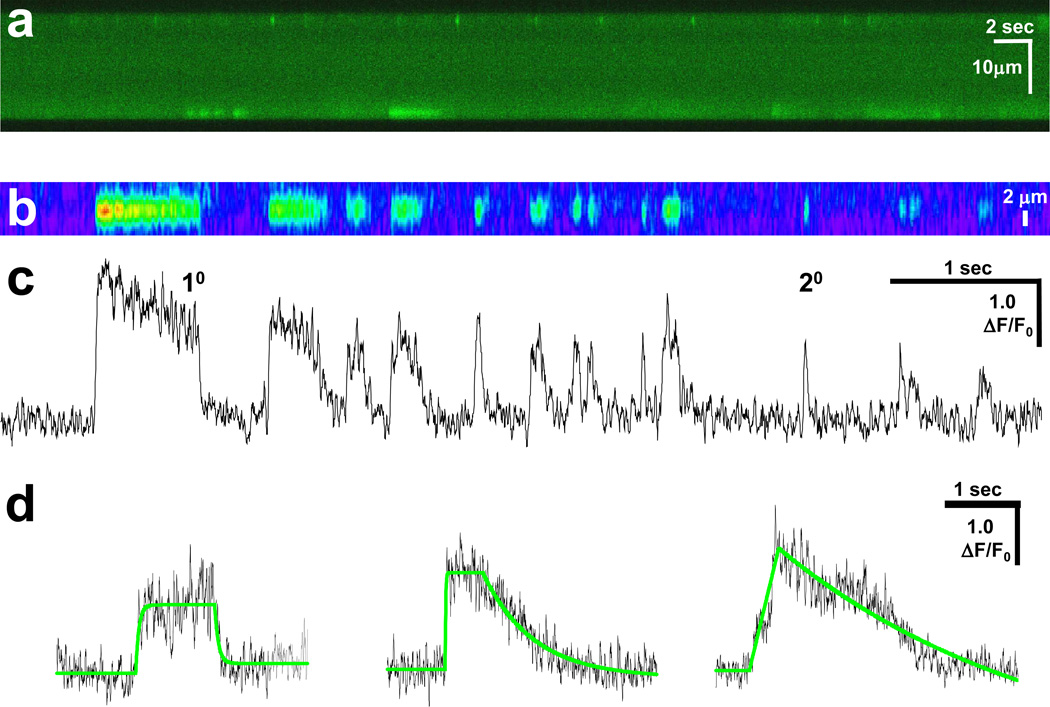
Fig 1. Osmotic shock induces Ca²⁺ sparks and Ca²⁺ bursts of varying duration.

(a) Transverse line-scan of Fluo-4 loaded FDB fibers after osmotic shock revealed a robust response at the periphery of the fiber that included brief Ca²⁺ sparks and prolonged Ca²⁺ bursts; (b) Pseudo-colored magnified line-scan images from another fiber; (c) Unfiltered amplitude (ΔF/F₀) trace of matching line-scan in panel b. Tracings reveal that the termination phase of Ca²⁺ bursts can occur in a rapid manner similar to Ca²⁺ sparks (2⁰) and in a prolonged fashion (1⁰). Both Ca²⁺ bursts and Ca²⁺ sparks can originate from the same location in a fiber; and (d) Representative unfiltered traces (black) of Ca²⁺ bursts displaying various termination kinetics. Single exponential curve fitting results are shown (green line).

Three populations of Ca²⁺ release events were observed in this response. The first group includes short duration Ca²⁺ sparks that displayed rapid initiation and rapid termination of Ca²⁺ release with a mean τ = 62.8 ± 9.0 ms. The second group showed rapid initiation and termination kinetics very similar to those seen in the first group, but the duration of Ca²⁺ release was much greater (τ = 429 ± 10.0 ms) (Fig. 1b). In addition to the above groups, a distinct population of events displayed prolonged Ca²⁺ transients that showed similar activation kinetics, but terminated in a stepwise fashion, rather than terminating rapidly. Some Ca²⁺ sparks and Ca²⁺ bursts could originate from the same location (Fig. 1), suggesting that the differential kinetics of these two populations reflected either varying gating of SR Ca²⁺ release channels or alteration of SR Ca²⁺ uptake and intracellular Ca²⁺ buffering capacity within the muscle fiber.

The width of Ca²⁺ bursts remained spatially restricted during prolonged Ca²⁺ release. In addition, the time constant of decay in Ca²⁺ bursts could be as rapid as in Ca²⁺ sparks (Fig. 1c and d), suggesting that prolonged Ca²⁺ bursts did not result from alterations in intracellular Ca²⁺ buffering or Ca²⁺ clearance machinery, rather they reflected a different gating property of RyR-mediated SR Ca²⁺ release.

Quantal nature for termination of Ca²⁺ bursts in skeletal muscle

While some Ca²⁺ bursts displayed rapid termination kinetics, the majority of Ca²⁺ bursts terminated in an apparent stepwise fashion (Fig. 1d, right panel). Individual Ca²⁺ burst events were thus analyzed to determine if discrete steps could be resolved during the termination of Ca²⁺ release (Fig. 1d and 2a). Histograms of hundreds of amplitude data points were generated for multiple individual Ca²⁺ burst events were fitted with Gaussian functions allowing the program to determine the position (x_i) and width (σ_i) of each peak (Eqn. 1). Clearly, distinct transition steps could be resolved within the majority (~60%) of Ca²⁺ burst events, as shown in Fig. 2b.

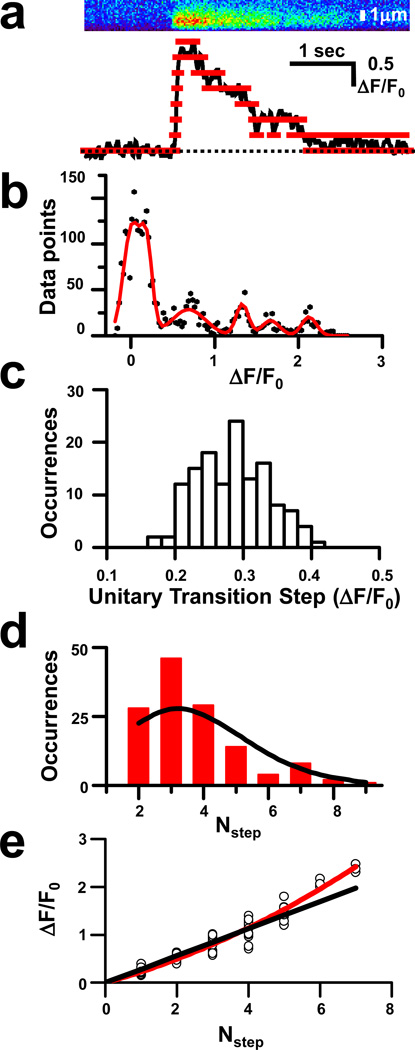
Fig 2. Decreased magnitude of quantal elements in termination of prolonged Ca²⁺ bursts.

(a) Tracings (bottom panel) of smoothed data from line-scan data (top panel) reveal several steps (red lines); (b) Histogram of bin data for smoothed ΔF/F₀ values fitted by multiple Gaussian functions (red line). Mean distance between the peaks determines the UTS amplitude. All peak distances in an event do not always match the standard UTS, as broader peaks likely contain contributions from adjacent transitions; (c) Distribution of the occurrence of given UTS values in the data set (n = 133), with a mean UTS of 0.283 ± 0.004 (mean ± SE). Such a range of UTS likely reflects slight deviation in data obtained from confocal line scans, where the local plane of focus may slightly influence the signal recorded. The Gaussian distribution of this relationship suggests our data set is not biased towards events of high or low amplitude; (d) Distribution of the occurrence of events with a particular N_step value (red bars), with the predicted distribution indicated (black line). Predicted values are based on a Poisson distribution using the formula P(n)=(λⁿ*e^−λ)/n!, where λ is the mean value for the data set (λ=3.67); and (e) Plot of the amplitude (ΔF/F₀) for each N_step value (circle) for multiple events (n=20) with a fit curve (red line) and line following the predicted value (black line) based on a regression line with a slope = 0.283 that passes through the origin.

Analysis of the distances between neighboring peaks (x_i+1 − x_i) allowed the resolution of the unitary transition steps (UTS) for the event. Furthermore, both UTS and σ_i were found to be close to independent of i, indicating that indeed elementary steps of channel closure were resolved. However, two deviations from this equally spaced pattern of x_i were found. First, UTS seemed to be slightly larger at greater i. This finding will be examined in more detail later. Second, in a subset of Ca²⁺ burst events, large UTS were observed that sometimes coincided with an increased σ_i, suggesting a contribution from adjacent transitions. Careful examination of these large UTS revealed that they were multiples of other UTS determined from the same histogram, indicating a co-operative gating behavior of RyR Ca²⁺ release channels. In these events, N_step was calculated with the notion that in Eqn. 1 A_i could be zero for a certain i.

Since the UTS amplitude did vary with the number of transitions, an average unitary transition step was obtained by dividing the peak ΔF/F₀ of the event with N_step for each individual burst. Plotting the frequency of average UTS values in the data set revealed an approximate Gaussian distribution with a mean value of ΔF/F₀ = 0.283 ± 0.004 (Fig. 2c). Additional analysis revealed that the occurrence for the N_step values for individual events followed a Poisson distribution, as would be expected considering a stochastic nature of RyR opening (Fig. 2d). The close match of our data with the predicted Poisson distribution helps to validate our selection criteria and analysis as unbiased.

If a continuous supply of Ca²⁺ was maintained during the course of Ca²⁺ bursts, one expected a linear relationship between UTS amplitude at corresponding N_step values. It is well-known that local SR Ca²⁺ concentration plays an important role in maintaining Ca²⁺ release, as previous studies have hypothesized^21–23 or directly shown that local Ca²⁺ depletion influences SR Ca²⁺ release during Ca²⁺ sparks in cardiomyocytes²⁴ and permeabilized amphibian skeletal muscle fibers²⁵. Since this local depletion of SR Ca²⁺ stores has not been previously observed in intact mammalian skeletal muscle, we examined if the local SR Ca²⁺ load modulated the activation or termination of Ca²⁺ release from the SR during extended Ca²⁺ bursts^26,27. By plotting all UTS values with the corresponding N_step value for multiple events, we found that UTS did not vary in a linear fashion with N_step (Fig. 2e). A linear relationship would be expected since Ca²⁺ bursts having a constant plateau, indicating that equilibrium was reached. In this case, deviation from a linear relationship could only result from reducing the current through individual RyR channels and forcing the curve downwards. Our observation of a significant upward deflection indicated that the amplitude of UTS during initial closing steps (higher N_step) was elevated above the expected values based on the UTS amplitude of the later closing steps. This non-linear relationship suggested that the amplitude of the each UTS decreased during the prolonged closing phase of a Ca²⁺ burst.

Multiple processes contribute to termination of Ca²⁺ bursts

The stepwise closing phase of Ca²⁺ bursts also displayed increases in Ca²⁺ that likely result from reopening of RyR channels that had closed or the initial opening of additional RyR channels (Fig. 3a). Both opening and closing events during the decay phase could pass through multiple step levels (as mentioned earlier and see also Fig. 3a), suggesting that coupled gating of RyR channels could occur during the decay phase.

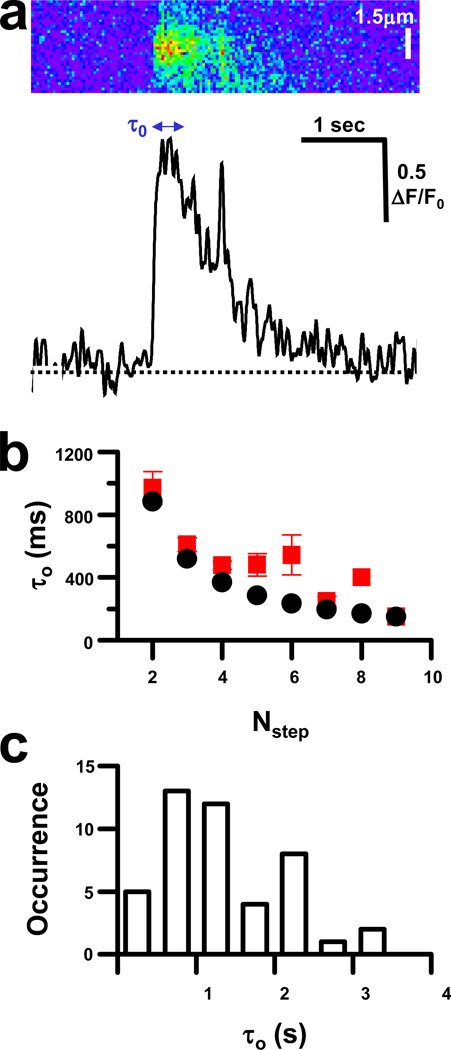
Fig 3. Coupling of RyR closure in Ca²⁺ burst termination.

(a) Tracings (bottom panel) of line-scan images (top panel) reveal that Ca²⁺ release can briefly return to a previous step during the otherwise decreasing decay phase of Ca²⁺ bursts, sometimes returning to the same level as the initial opening; (b) Distribution of the mean duration of first opening (τ₀) for events with different number of steps (red squares). Stochastic closure of RyR channels would result in a decay curve displayed (Eqn. 2; black circles); and (c) Occurrence of different τ₀ in the complete data set.

In addition to SR Ca²⁺ load, two other factors are thought to contribute to the rapid termination of Ca²⁺ sparks in muscle cells²¹; stochastic attrition and Ca²⁺-dependent inactivation of RyR channel release. The distribution of the dwell time of first opening (τ₀) for each N_step is expected to follow a logarithmic decay curve

$${\tau }_0=\tau •\text{ln}\left(\frac{N}{N-1}\right)$$ (2)

where τ is the time constant of overall decay (1.28 ± 0.27 s), if only stochastic attrition controls the transition from the first to second level of Ca²⁺ release during a Ca²⁺ burst. In events with fewer steps (lower N_step values), measured τ₀ values closely matched values predicted to reflect stochastic RyR closing (Fig. 3b) in the data set that represented a variety of different τ₀ values (Fig. 3c). Interestingly, the only events that varied significantly from predicted stochastic values involved those with intermediate N_step. This could result from simultaneous RyR channel closings, either as a result of direct coupling of RyR closing, or by inactivation of adjacent RyR by local Ca²⁺ concentrations.

Local depletion of SR Ca²⁺ stores during prolonged Ca²⁺ release

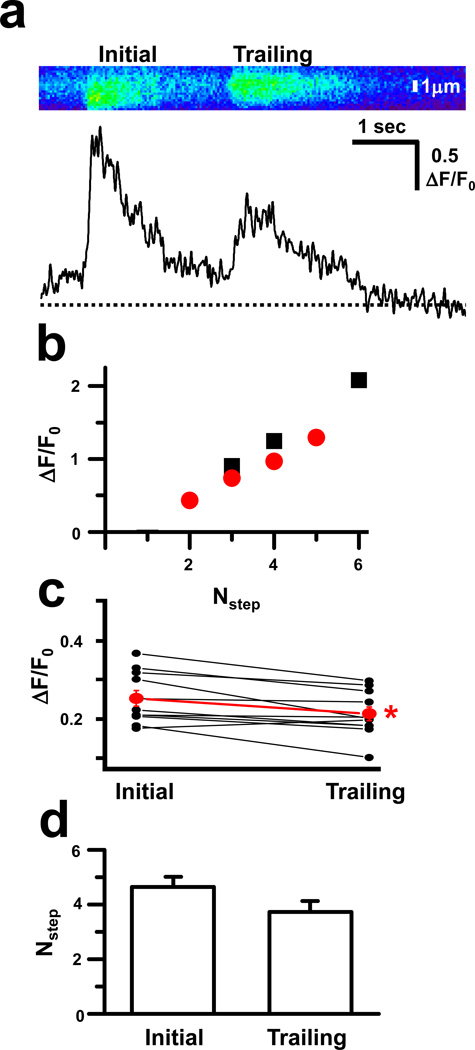
Additional insight into the role of local SR Ca²⁺ store depletion came from analysis of Ca²⁺ burst events that originated from the same location in rapid succession. In such tandem events, the trailing burst was consistently reduced in amplitude compared to the initial burst (Fig. 4a). Resolution of individual steps within the decay phase of tandem events revealed that even at the same N_step values, the trailing burst displayed reduced step amplitude compared to the initiating burst (Fig. 4b). Examination of multiple tandem events established that the mean UTS in trailing bursts was significantly diminished when compared to initiating bursts (Fig. 4c), while the mean number of steps remained essentially the same (Fig. 4d). The maintenance of the number of discrete steps coupled with diminished amplitude of these steps suggested a reduction in the quantity of Ca²⁺ released by the same number of RyR channels. In this case, a local reduction of SR Ca²⁺ store would occur during the initial burst, resulting in less Ca²⁺ available for release during the trailing burst until the local Ca²⁺ store could be replenished.

Fig 4. Tandem Ca²⁺ bursts reveal local depletion of SR Ca²⁺ stores.

(a) Line-scan analysis (top panel) suggests that when Ca²⁺ bursts occur in rapid succession at the same location, the peak amplitude (bottom panel) is decreased in the trailing event; (b) Individual steps within the decay phase of a single tandem event with the amplitude for the initial (black squares) and trailing (red circles) bursts at matching N_step values; (c) Amplitude for initial step for both the initial and trailing Ca²⁺ bursts for several (n = 16) tandem events. Mean ± SE presented in red. * p<0.05; and (d) Mean±SE for the number of steps per Ca²⁺ burst for the initial and trailing Ca²⁺ bursts in tandem events. There is no statistically significance difference between these two values.

Discussion

Since Ca²⁺ sparks and bursts constitute the elemental units of SR Ca²⁺ release in skeletal muscle cells, a precise understanding of the nature of these individual Ca²⁺ release events will greatly contribute to determining fundamental mechanisms that maintain Ca²⁺ homeostasis in skeletal muscle health and disease. This study establishes that the prolonged termination phase of Ca²⁺ bursts display a quantal nature. Characterization of these transition steps suggests that mostly stochastic attrition as well as coordinated gating underlie the closing of RyR channels. The rapid decline observed in Ca²⁺ sparks and some Ca²⁺ bursts likely results from Ca²⁺-dependent inactivation of RyR channels and is thus distinct from the prolonged, step-wise decline present in other Ca²⁺ bursts. Our findings suggest that local depletion of the Ca²⁺ store during prolonged Ca²⁺ bursts results in decreased amplitude, particularly during tandem Ca²⁺ bursts that originate from the same spatial position.

During the decay of Ca²⁺ bursts, the amplitude occasionally returns to a higher step (Fig. 3a), which likely results either from re-opening of RyR channels previously closed or the opening of additional RyR channels. The opening of additional RyR channels would likely result from propagating Ca²⁺-induced Ca²⁺ release (CICR) within a cluster, however, stochastic or coordinated channel openings could also contribute. If CICR propagation contributes to RyR re-opening, this would suggest that RyR inactivation due to local elevated cytosolic Ca²⁺ levels could be overcome, perhaps by a combination of diminished SR Ca²⁺ release and clearance of Ca²⁺ from the cytosol. Furthermore, if this is the case, one would expect to see a prolonged restoration of Ca²⁺ release. As the duration of additional Ca²⁺ release tends to be brief, this suggests that both direct coupling and CICR are at work in skeletal muscle RyR arrays. It is possible that they are complementary in amplification of Ca²⁺ release in mammalian skeletal muscle.

A role for direct coupling of RyR channels within SR RyR arrays during termination of Ca²⁺ release is also supported by the finding that the τ_o value for events with an intermediate N_step is elevated above values projected for simple stochastic decay of RyR opening (Fig. 3b). It is interesting that it is the intermediate N_step events that do not meet this stochastic prediction. If it were short events with presumably less Ca²⁺ released that did not meet the stochastic prediction, then one might expect that the differences seen between a stochastic response and the observed values were due to insufficient Ca²⁺ present to produce Ca²⁺ inactivation. Or, if the events with high N_step resulted in non-stochastic closing one would assume that this was the result of spatial effects, where some RyR channels are exposed to higher levels of Ca²⁺ than other channels due to the large quantity of Ca²⁺ released. However, since it is the intermediate values that display non-stochastic closing, this suggests that other factors such as direct coupling or inherent differential gating properties of RyR channels must contribute to their closing in Ca²⁺ bursts.

The appearance of Ca²⁺ blinks or skraps, nanoscale depletions of the SR Ca²⁺ store associated with Ca²⁺ sparks, have been observed in mammalian cardiomyocytes²⁴ and permeabilized amphibian skeletal muscle fibers²⁵. Our study presents two findings that suggest this is also the case in mammalian skeletal muscle. First, our observation of decreased amplitude in late stage UTS of prolonged Ca²⁺ burst argues that local depletion of the SR Ca²⁺ store can occur in skeletal muscle fibers. As the prolonged Ca²⁺ burst continues, Ca²⁺ release continues to terminate in a step wise pattern, however, the UTS amplitude appears to decrease slightly during the later steps (Fig. 2e). This slight decrease in UTS is unlikely to result from the closure of RyR channels, since closure of RyR would probably result in a much larger drop than the observed change in subsequent UTS. With the number of active RyR channels remaining the same, this decrease would depend on a diminished supply of Ca²⁺ to be released, as one would expect to see as a result of a locally diminished SR Ca²⁺ store. While our analysis cannot precisely establish the number of RyR channels that contribute to Ca²⁺ bursts, certain predictions can be made. Previous studies from other laboratories allow us to establish that the mean UTS value obtained here, ΔF/F₀ ~0.28, likely results from the opening of 1–2 RyR channels^13,19,28.

Second, we find that in Ca²⁺ busts that occur in tandem the trailing events are generally of lower peak amplitude than the initial burst, suggesting that during Ca²⁺ bursts the quantity of Ca²⁺ released not only decreases in quantal units, but also that a supplemental decay mechanism contributes. In this situation, the most likely mechanism at work is local decreases in the Ca²⁺ store available for release from SR. It is important to note, however, that additional factors such as altered sarcolemmal Ca²⁺ uptake or changes in intracellular Ca²⁺ buffering capacity could also contribute to the observations in this study. Further experimentation may reveal that this depletion could be linked to the activation of store-operated Ca²⁺ entry to replenish the SR Ca²⁺ store. It is interesting to note that dystrophic muscle displays both accelerated store-operated Ca²⁺ entry^29–32 and elevated Ca²⁺ spark activity^16,33.

A matter of central importance in muscle physiology and E-C coupling research is the mechanism involved in activation and termination of RyR channels. By resolving the step wise closure of Ca²⁺ bursts into discrete units, we provide evidence that the quantal nature of Ca²⁺ bursts is similar to that seen in Ca²⁺ sparks from cardiomyocytes¹⁹. Variation in the amplitude of UTS, and decreased UTS values in trailing tandem Ca²⁺ bursts suggest that local SR Ca²⁺ depletion occurs during the termination of these prolonged Ca²⁺ release events. Furthermore, we find evidence that direct coupling between RyR channels may supplement CICR in regulation of Ca²⁺ release from paracrystalline arrays of RyR channels in skeletal muscle. Determining the extent that these two mechanisms contribute to regulation of internal Ca²⁺ homeostasis would provide valuable insight into E-C coupling and provide guidance for developing treatments to affect numerous disorders involving Ca²⁺ dysregulation.

Abbreviations

ΔF/F₀

amplitude

CICR

calcium-induced calcium release

E-C

excitation-contraction

FDB

flexor digitorum brevis

N_step

number of steps

x_i

position

RyR

ryanodine receptor

RyR1

ryanodine receptor type 1 RyR

RyR3

ryanodine receptor type 3 RyR

SR

sarcoplasmic reticulum

UTS

unitary transition step

σ_i

width