Abstract
Optimization models explain many aspects of biological goal-directed movements. However, most such models use a finite-horizon formulation which requires a pre-fixed movement duration to define a cost function and solve the optimization problem. To predict movement duration, these models have to be run multiple times with different pre-fixed durations until an appropriate duration is found via trial and error. The constrained minimum time model directly predicts movement duration; however, it does not consider sensory feedback and is thus only applicable to open-loop movements. To address these problems, we analyzed and simulated an infinite-horizon optimal feedback control model, with linear plants, that contains both control dependent and independent noise and optimizes steady-state accuracy and energetic costs per unit time. The model applies the steady-state estimator and controller continuously to guide an effector to, and keep it at, target position. As such, it integrates movement control and posture maintenance, without artificially dividing them with a precise, pre-fixed time boundary. Movement pace is determined by the model parameters and the duration is an emergent property with trial-to-trial variability. By considering the mean duration, we derived both the log and power forms of Fitts’s law as different approximations of the model. Moreover, the model reproduces typically observed velocity profiles and occasional transient overshoots. For unbiased sensory feedback, the effector reaches the target without bias, in contrast to finite-horizon models that systematically undershoot target when energetic cost is considered. Finally, the model does not involve backward and forward sweeps in time, its stability is easily checked, and the same solution applies to movements of different initial conditions and distances. We argue that biological systems could use steady-state solutions as default control mechanisms and might seek additional optimization of transient costs when justified or demanded by task or context.
Keywords: stationary, time invariant, speed-accuracy tradeoff, stochastic, coordination, variability
1. Introduction
Many optimization models for goal-directed movement control have been proposed (Flash and Hogan, 1985; Uno et al., 1989; Harris and Wolpert, 1998; Todorov and Jordan, 2002; Scott, 2004; Todorov, 2004; Diedrichsen et al., 2010). Despite their enormous success in explaining motor behaviors, these models adopt a finite-horizon formulation by optimizing a cost function whose definition requires specifying the movement duration in advance. Consequently, they pre-fix duration instead of predicting it (Tanaka et al., 2006). Some models have been extended to predict duration and simulate Fitts’s law (Harris and Wolpert, 1998; Guigon et al., 2008), the empirical characterization of speed-accuracy trade-off in goal directed movements (Fitts, 1954). However, they have to be run many times with different pre-fixed durations until an appropriate duration, according to some criteria, is found. This procedure assumes that motor systems run trial-and-error internal simulations using complete knowledge of the control problem. For feedback models, this knowledge includes both actual and estimated system states, which is unrealistic and defeats the purpose of estimating states in the first place. Alternatively, motor systems would need to store or approximate all durations for all possible movements, sensory feedback conditions, system initial conditions (position, velocity, acceleration, etc.), target distances and widths, and update this information whenever plant or noise parameters change (e.g., change of clothes or fatigue). As these possibilities appear implausible or inefficient, Tanaka et al. (2006) proposed a constrained minimum time model, which directly predicts movement duration [see also related work by Harris (1998) and Harris and Wolpert (2006)]. However, that model does not consider sensory feedback and is thus only applicable to fast or open-loop movements.
To address these fundamental limitations, we propose an alternative framework based on Phillis’s (1985) infinite-horizon optimal feedback control model that includes both control-dependent and independent noise. Unlike finite-horizon formulations, this model considers steady-state costs per unit time, rather than transient costs integrated over a pre-fixed period, thus eliminating the need to know movement duration in advance. To relate this model to biological motor control, we hypothesized that motor systems apply steady-state solutions continuously to estimate system state, execute movements, and maintain posture. Movement duration is an emergent property of the model. Huh et al. first discussed infinite-horizon optimal control for goal-directed movements in an abstract (Huh et al., 2010a) and a conference paper (Huh et al., 2010b). Independently, we reported some preliminary results in a conference paper (Jiang et al., 2011). These studies share infinite-horizon framework but differ considerably in formulation, solution, and analysis. For example, Huh et al. assumed that system state is known exactly whereas we estimated the state by combining internal prediction and partial observations and thus solved for coupled optimal estimator and controller. Huh et al. investigated relationships among different models and simulated Fitts’s law and motor motivation (Mazzoni et al., 2007) whereas we analyzed Phillis’s (1985) solution to examine its stability and to derive, as well as simulate, both the log and power forms of Fitts’s law (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006).
2. Theory
We applied Phillis’s (1985) infinite-horizon, optimal feedback control model to goal-directed movements. Similar to other linear models of stochastic optimal feedback control [e.g., Todorov (2005)], we consider a system governed by stochastic differential equations (Phillis, 1985):
| (1) |
| (2) |
where x is the state n-vector, u is the control m-vector, and y is the sensory-feedback k-vector (observations). The first component of x is the position of the end effector (e.g., hand) being controlled. For one-dimensional movements that follow second-order Newtonian dynamics and a second-order equation relating neural control signal u to muscle force (Winters and Stark, 1985), x has a dimension of n=4 (Todorov and Jordan, 2002; Tanaka et al., 2006). β and γ are scalar Wiener processes, and ω and ζ are n- and k-vector Wiener processes; they model noise in control and sensory feedback. All the Wiener processes and their components are independent of each other. They are standardized so that over a time step dt, the corresponding Gaussian white-noise processes have a variance dt. A, B, C, D, F, G, and Y are constant matrices of proper sizes. A and B define the motor plant according to Newtonian mechanics and the muscle-force equation; an example is Eq. 23 below. C is the observation matrix whose rank can be less than n to include partial observation cases and D determines observation noise. The F and Y terms are, respectively, the state- and control-dependent noise, also known as multiplicative noise or signal-dependent noise, and the G term represents control-independent noise. (We modified Phillis’s notations slightly here and below to avoid notational conflicts.)
The actual state x is not directly available for control but has to be estimated according to the linear equation:
| (3) |
where the first term on the right is the prediction based on an internal model of the system dynamics and an efference copy of the control signal, and the second term is the correction according to the difference between the received and expected sensory feedback. is an unbiased estimator of x if the sensory feedback is unbiased. The control signal is assumed to be a linear function of :
| (4) |
The goal is to determine the Kalman gain matrix K and the control law matrix L by optimizing certain costs (see below).
Phillis (1985) studied both a finite- and an infinite-horizon formulation. Since the former has the same problem of pre-fixing movement duration as discussed in Introduction, we focused on the latter. As no terminal time is pre-specified, Phillis defined the estimator cost as the steady-state variance of the estimation error :
| (5) |
and the controller cost as the steady-state cost per unit time according to:
| (6) |
where matrices U,Q,and R are constant and symmetric; they are assumed to be positive definite (Phillis, 1985) presumably for stability considerations although our simulations show that some of them can be positive semi-definite. In the Results section, we will discuss a criterion for checking control-system stability. The target state is always defined to be x = 0 so that x really represents the difference between the current and the target state. This relative representation agrees with the fact that biological systems are more sensitive to relative than absolute quantities. The first term in Eq. 6 measures the accuracy of reaching the target. The second term is the energetic cost that measures effort.
To solve the problem, Phillis (1985) first defined:
| (7) |
where X is an extended state vector, and transformed the system equations to:
| (8) |
With the further definitions:
| (9) |
| (10) |
where P is the covariance matrix of X (with respect to target X=0, not the mean of X), the system equations and the total cost are transformed to:
| (11) |
| (12) |
where tr represents matrix trace. Because of the signal-dependent noise, the estimator and controller cannot be solved separately, so their costs are combined. The problem becomes optimizing Eq. 12 under the constraint of Eq. 11. Importantly, the original stochastic system equations have been converted to a deterministic equation of covariance P, and the optimization problem can be solved with Lagrange multiplier method. For steady states, , J = tr(VP), and the solution is (Phillis, 1985):
| (13) |
| (14) |
| (15) |
| (16) |
where
| (17) |
contains Lagrange multipliers. Note that unlike typical algebraic Riccati equations, Eqs. 15 and 16 only contain linear terms of S and P, and can be written in the standard form of a matrix multiplying a vectorized S or P by using Kronecker products. Also note that in addition to the steady-state cost and solution considered above, one could use other costs, such as an integration of temporally discounted cost terms, in an infinite-horizon framework.
We simulated and analyzed the steady-state solution to explore its implications for biological motor control. The steady-state L, K, P, and S are constant matrices and their computation from Eqs. 13-16 does not involve backward or forward sweeps in time. Although steady state P is constant, P evolves in time according to Eq. 11 in the process of reaching its steady-state value.
Our key assumption is that biological systems apply the steady-state estimator (K) and controller (L) continuously for both transient movements and steady-state posture maintenance without pre-specifying an artificial time boundary between these two processes. Therefore, steady-state K and L are used in , and matrices of Eq. 11 to determine the time course of P.
For simulations, we used the following numerical procedure (Jiang et al., 2011):
Initialize L and K
Go to step 2 till convergence
We simulated single-joint movements of the forearm at the elbow with plant dynamics and parameters as in Tanaka et al. (2006) and different from Jiang et al. (2011). The elbow angle θ satisfies the Newtonian equation:
| (18) |
where I is the moment of inertia and b the intrinsic viscosity (damping). The net muscle torque τ is related to a scalar control signal u according to:
| (19) |
where ta and te are muscle activation and excitation time constants (Winters and Stark, 1985). We combine Eqs. 18 and 19 to obtain:
| (20) |
where:
| (21) |
Defining the state vector with angular position, velocity, acceleration, and jerk as components:
| (22) |
we thus obtain linear system dynamics in the form of Eq. 1 with:
| (23) |
As in Tanaka (2006), we let I=0.25 kg m2, b=0.2 kg m2/s, ta=0.03 s, and te=0.04 s. The noise parameters in Eq. 1 were F=0, Y=0.02B, G=0.03I4, where I4 is the four-dimensional identity matrix. The parameters for sensory feedback Eq. 2 were:
| (24) |
This C matrix assumes that the fourth component of the state vector is unobservable (Todorov, 2004). The parameters for the cost functions were Q = diag(1, 0.01, 0, 0), R = 0.0001, and U = diag(1, 0.1, 0.01, 0).
For the ease of the following presentation, we always convert the elbow angle θ to the end effector (“hand”) position s along the movement path by multiplying θ with the forearm length (L0=0.35 m). This is equivalent to using a state vector and multiplying the D and G matrices by L0.
We have obtained similar results with other parameter sets. The Matlab code is available from NQ upon request. The convergence of the numerical procedure depends on the parameters but is generally fast. For our standard parameter set, the convergence typically occurred within 20 iterations when L and K were initialized to random numbers. The convergence was even faster (within 10 iterations) if L and K were initialized to a previous solution for a different parameter set.
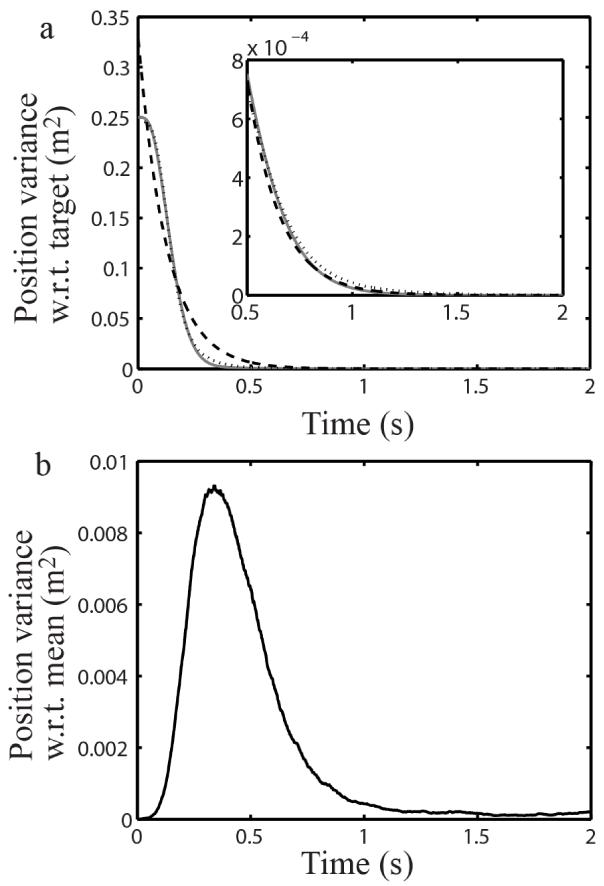
We finally note that the estimator matrix K and the controller matrix L can be computed before a movement starts whereas the control signal u(t) can only be determined during a movement because it depends on the estimated state vector, which in turn depends on sensory feedback. In this sense, the model involves both pre-planning and online processing. However, in the special case where K is set to zero so as to ignore sensory feedback, the state estimation (Eq. 3) relies on efference-copy-based internal prediction alone, and the entire control-signal sequence can be pre-computed before movement onset. Under this open-loop condition, because accumulation of noise over time is not corrected by sensory feedback, the variance of the state with respect to the mean grows monotonically with time. For typical reaching movements, however, the variance of the hand position with respect to the mean is smaller at the end of a movement than during the movement (cf. Fig. 5b), suggesting that the motor system uses feedback when it is available (Woodworth, 1899; Meyer et al., 1988; Todorov and Jordan, 2002).
Fig. 5.
Hand position variance defined in two ways. (a) The hand position variance with respect to the target position was calculated from Eq. 26 (solid gray curve), and fitted with the exponential (dashed curve) and modified power (dotted curve) functions. The tail of the solid gray curve was magnified in the inset, and re-fitted with these two functions. (b) The hand position variance with respect to the mean trajectory was calculated with 50 sample trials. We also used the same sample trials to calculate the variance with respect to the target and the result (not shown) is virtually indistinguishable from the solid gray curve in (a).
3. Results
We considered Phillis’s exact steady-state solution to an infinite-horizon optimal feedback control model, which includes both signal dependent and independent noise (see Methods). We first applied the model to arm movements directed to a target and demonstrate that the model captures key characteristics of biological reaching movements without pre-specifying movement duration. Some of these characteristics are not shared by finite-horizon control models. We then analyzed system stability and derived both the log and power forms of Fitts’s law (MacKenzie, 1992; Tanaka et al., 2006) as different approximations of the model. Finally, we validated our analysis numerically.
3.1 Movement profiles
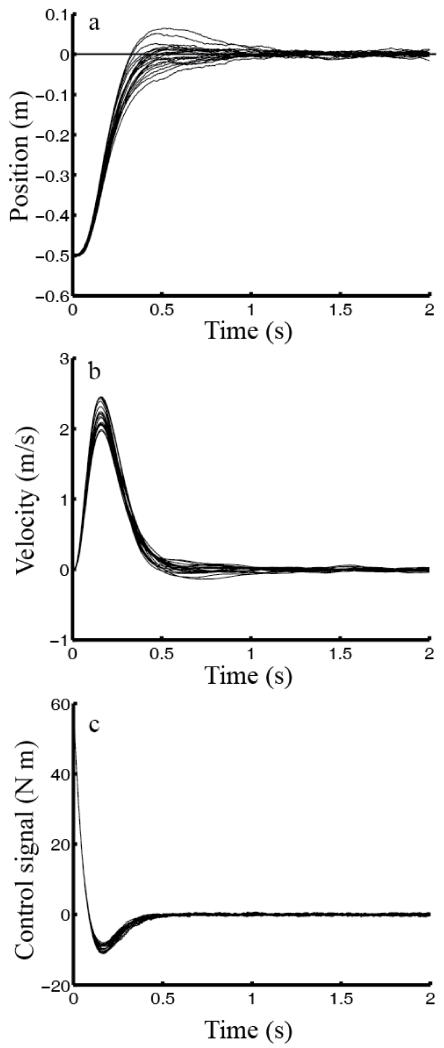
We considered single-joint reaching movements. We numerically obtained optimal steady-state estimator (K) and controller (L) and then applied the results to move the hand toward a target (whose position is defined as 0) according to system dynamics. The hand position and speed as a function of time are shown in panels a and b of Fig. 1, respectively. In each panel, the curves represent results from 20 sample trials. The model correctly moved the hand to the target and produced velocity profiles similar to those observed experimentally (Morasso, 1981; Cooke et al., 1989). Importantly, movement duration was not pre-fixed. Instead, the steady-state estimator and controller act continuously to move the hand toward, and keep the hand on, the target, without specifying when the transient movement ends and the posture maintenance begins. Fig. 1c shows the control signal u (Eq. 4) as a function of time, with a biphasic profile; the net torque τ (not shown) is a double low-pass filtered version of u (Eq. 19).
Fig.1.
Simulations of reaching movements of 50 cm. (a) position, (b) speed, and (c) control signal (before adding noise) as a function of time. In each panel, the curves represent 20 individual sample trials.
We have run additional simulations to examine how control-dependent noise (Y), control-independent noise (G), and the relative importance of the accuracy and energetic costs (R) affect movement. We scaled each of these qualities by five folds while keeping all other parameters constant. Increasing the control-dependent noise decreased the peak speed, increased the movement duration and variability, but had little effect on the final, steady-state variability. This is because the control signal, and thus the control-dependent noise, were large only during the movement. In contrast, increasing the control-independent noise increased the final, steady-state variability, as expected. Surprisingly, this change also increased the peak speed and reduced the movement duration a little; the reason is that a larger steady-state variability called for a larger control signal u (via a larger L) to improve accuracy. Increasing the importance of the energetic cost (larger R) relative to the accuracy cost reduced the peak speed and increased movement duration. Interestingly, none of these manipulations had significant impact on the skewness of the speed profile.
3.2 Transient energetic cost and the steady-state-control hypothesis
Fig. 1 reveals that during transient movements, the hand either gradually approaches the target (from the negative starting position to 0 target position in Fig. 1a) or slightly overshoots (above 0 in Fig. 1a) and then returns to the target. These features match experimental data well (Morasso, 1981; Cooke et al., 1989). Since the system operates continuously, the hand always reaches, or fluctuates slightly around, the target, provided that the sensory feedback is unbiased. Interestingly, these features are not shared by finite-horizon feedback control models that also include accuracy and energetic costs; rather, those models systematically under-shoot the target at the end of movements despite unbiased sensory feedback (Todorov and Jordan, 2002; Todorov, 2005; Liu and Todorov, 2007). The reason is simple: the optimization is a compromise between accuracy and energetic costs over a fixed time period, and this compromise produces an accuracy bias at the end of the fixed time. Other things being equal, an under-shoot bias requires less energy than an over-shoot bias of the same magnitude, and is thus optimal according to finite-horizon models.
The infinite-horizon model does not have this undershoot bias mainly because transient energetic cost does not affect steady-state solution, which drives the hand toward target constantly. This can be seen by re-writing Eq. 6 as:
| (25) |
Thus, transient behavior within any finite time t0 does not affect steady-state cost or solution. To uniquely specify transient behavior, we hypothesize that biological control systems parsimoniously apply the same steady-state solution to both transient movements and steady-state posture maintenance. Fig. 1 shows that this steady-state-control hypothesis reproduces typical movement profiles without pre-fixing movement duration or systematically under-shooting the target.
3.3 Broad applicability of the steady-state solution
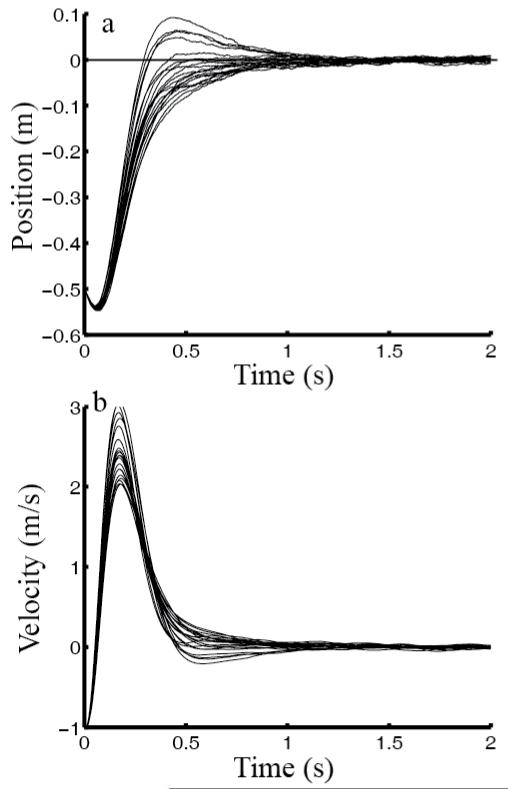
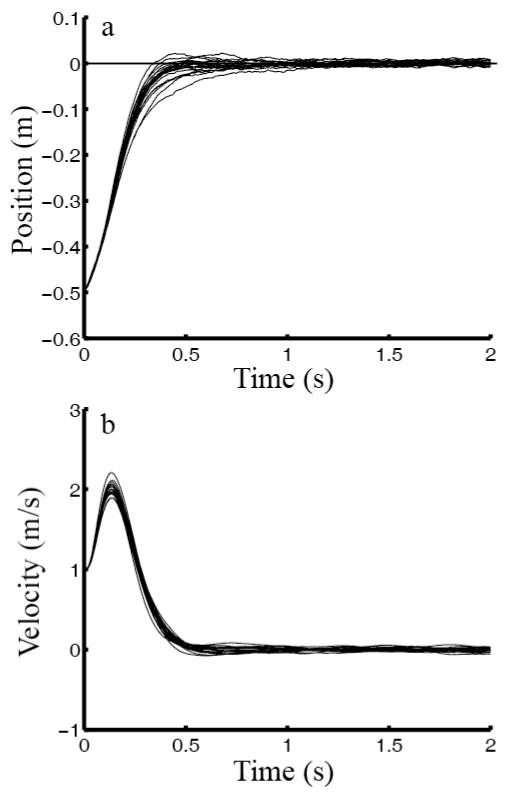
Another advantage of our steady-state-control hypothesis is that once the optimal estimator and controller are obtained, they are applicable to movements of any distances, target widths, initial conditions or perturbations of the state, and durations because the steady-state solution does not depend on those parameters but only on the plant and cost parameters. To illustrate, we repeated Fig. 1 simulations with one change: the hand was no longer stationary at the starting point but had an initial velocity either away from (−1 m/s) or toward (+1 m/s) the target. The results shown in Figs. 2 and 3 were obtained with exactly the same estimator and controller as for Fig. 1. When the initial velocity was away from the target (Fig. 2), the system used a larger control signal to turn the hand around, producing a larger control-dependent noise, larger variation among individual trials, and a longer time to converge on the target. The opposite was true when the initial hand velocity was toward the target (Fig. 3). A finite-horizon model would have to know different movement durations for different initial conditions first and then perform different optimization to produce different time-dependent solutions. None of these is necessary for steady-state solutions of infinite-horizon models as long as the motor plant and cost function do not change. Even when these latter parameters do change, it is much easier to re-compute the new steady-state estimator and controller than the transient ones (see Methods).
Fig. 2.
Simulations of reaching movements with an initial hand velocity away from the target (−1 m/s). All other parameters were identical to those for Fig. 1. (a) position, and (b) speed as a function of time. In each panel, the curves represent 20 individual sample trials.
Fig. 3.
Simulations of reaching movements with an initial hand velocity toward the target (+1 m/s). All other parameters were identical to those for Fig. 1. (a) position, and (b) speed as a function of time. In each panel, the curves represent 20 individual sample trials.
3.4 Fitts’s law and system stability
Since no termination time is specified in infinite-horizon formulations, we assume that when the hand-position variation with respect to target is comparable to the target width (specified by Eq. 30 below) for the first time, the target is reached, as suggested by experimental data (Meyer et al., 1988). We used this assumption to derive Fitts’s law. Using the first (i.e., shortest) time is consistent with the constrained minimum time model (Tanaka et al., 2006). Note that unlike finite-horizon models, this assumption does not affect the control process in any way and is used to read off, instead of pre-specifying, mean movement duration. (One could also use a single-trial-based assumption to read off movement duration in each trial.)
Eq. 11 governs how the covariance matrix (P) of the extended state vector X evolves in time. Since the steady-state estimator (K) and controller (L) are applied at all time, they are used in , , and matrices of Eq. 11 to determine the time course of P. Consequently, Eq. 11 is linear in P with all the other quantities constant. We can vectorize P by stacking its columns (with the first column on top for convenience) to form vector p, and re-write Eq. 11 as:
| (26) |
where (I2n is the 2n-dimensional identity matrix and ⊗ represents Kronecker product) and g is the vectorized form of GGT. (If x is n dimensional, then X is 2n dimensional, p is 4n2 dimensional, and M is 4n2 × 4n2.)
By definition, the first component of p [i.e., the (1, 1) element of P] is the variance of the hand position with respect to the target position at zero. Its solution from Eq. 26 can be written as:
| (27) |
where μi’s are the eigenvalues of M. (For degenerate cases of repeated eigenvalues, there will be terms of the form th eμt; this will not affect the approximations below because exponentials dominate.)
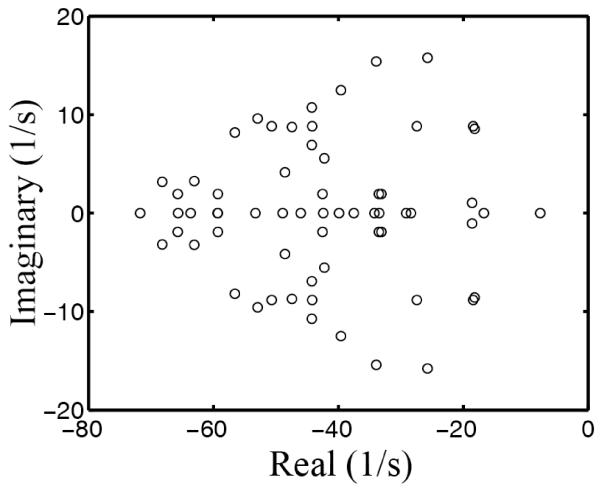
Obviously, p1(t) converges to p1(∞) (i.e., the hand moves to the target) if and only if Re μi < 0 for all i (where Re indicates the real part of a complex number). This provides a simple stability condition for the control system. Using the parameters for simulations in Fig. 1, we computed the eigenvalues of M and the results are shown in Fig. 4. Since M is real, the eigenvalues are either real or form conjugate pairs. The negative real parts of all the eigenvalues guarantee that this particular control system is stable for movements of any size and duration. The imaginary parts are much smaller than the real parts in magnitude (notice the different scales for the real and imaginary axes in Fig. 4). Therefore, oscillations are much slower than exponential decays, and the variance must decrease with time nearly monotonically. The black curve in Fig. 5a shows p1(t) calculated according to Eq. 26 with the same model parameters as for Fig.1. We also calculated p1(t) using trajectories of 50 sample trials and the result (not shown) is virtually indistinguishable from the black curve in Fig. 5a. These and other simulations confirm that the position variance with respect to the target indeed decreases nearly monotonically, and oscillations are usually small. [When the hand has an initial velocity opposite to the target location (Fig. 2), the hand position variance with respect to the target briefly increases and then decreases; this is not the condition for typical Fitts’s experiments.] Note that p1(t) is the position variance with respect to the target; the position variance with respect to the mean path is far from monotonic but peaks during the movment (Fig. 5b, also see the sample trajectories in Fig. 1a), consistent with the minimum intervention principle (Todorov and Jordan, 2002).
Fig. 4.
Eigenvalues of M with the same parameters as used in Fig. 1 simulations.
For stable systems, Eq. 26 (or Eq. 16) indicates:
| (28) |
The stability condition above guarantees that M is invertible because negative real parts for all eigenvalues ensure no zero eigenvalue. The steady-state position variance p1(∞) equals the first component of (−M−1g). Therefore, p1(∞) depends on GGT, the covariance matrix of the signal-independent noise over unit time. This noise keeps the hand jitter a little around the target state, and the system maintains the posture via continuous sensory feedback and small corrective control. Since the hand does not jitter much when it is not moving, p1(∞) must be very small.
Suppose that the hand starts at a certain position with a steady-state variance p1(∞) from a previous movement. The system then plans to move a distance d to reach a new target of width w. The initial condition for p1(t) of the pending movement is thus:
| (29) |
As noted above, we assume that the target is reached at time tf when:
| (30) |
where k specifies how reliably the system wants to hit the target (smaller k for greater reliability). The product kw can also be viewed as the effective target width that a subject is aiming at. Obviously, (kw)2 has to be larger than p1(∞) or the target is never considered as reached.
To derive the log and power forms of Fitts’s law (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006), we consider two different approximations of Eq. 27. First, let us assume that one of the eigenvalues μj dominates the decay. This can happen if the corresponding coefficient bj is very large, or if (−Re μj) is the smallest among all eigenvalues (the rightmost point in Fig. 4). Then, Eq. 27 can be approximated as:
| (31) |
Using Eqs. 29 and 30 and assuming p1(∞) is very small, we obtain the log form of Fitts’s law:
| (32) |
An alternative approximation of Eq. 27 is inspired by the mathematical result that sum of a large number of decaying exponentials can approximate a decaying power function for t larger than a small t0 (Beylkin and Monzón, 2010). Thus, we may approximate Eq. 27 as:
| (33) |
where a and μ are positive. By using t0 as the initial time, we obtain the power form of Fitts’s law:
| (34) |
Since the power function Eq.33 diverges at t=0, a better approximation is the modified power function:
| (35) |
This also leads to the power form of Fitts’s law:
| (36) |
where we assume that the distance is usually much larger than the effective width.
We checked how well the exponential function (Eq. 31) and the modified power function (Eq. 35) fit the position variance with respect to the target and the results are shown in Fig. 5a. The modified power function (dotted curve) fits the variance curve (solid gray) better than the exponential function (dashed curve) does; both functions fit the variance well when the first 0.5 s is excluded (inset of Fig. 5). The modified power function has one more free parameter than the exponential function. To match the number of free parameters, we also used a modified exponential function of the form:
| (37) |
as suggested by degenerate eigenvalues. It is better than the exponential but still not as good as the modified power function (results not shown). More importantly, our focus here is not on curve fitting per se but on approximating Eq. 27 to derive Fitts’s law. Eq. 37 and many other functions (e.g., sum of two exponentials) may fit the variance data fine but do not allow derivations of either form of Fitts’s law. Also note that both the log and power forms of Fitts’s law have two free parameters.
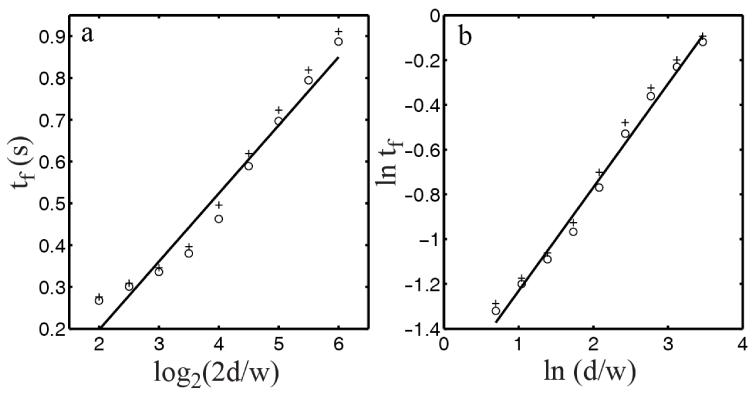
Finally, we numerically simulated movement duration (tf) for various d and w, using a k=0.5 in Eq. 30. Fig. 6 shows the results from simulations where we let w=0.04 m (circles) or 0.02 m (crosses), and for each w, we varied d from 2w to 32w. In Fig. 6a, we plotted tf as a function of log2(2d/w) so that the log Fitts law predicts a straight line. In Fig. 6b, we plotted ln(tf) as a function of ln(d/w) so that the power Fitts law predicts a straight line. We fitted the w=0.04 m results (circles) with a straight line in each panel. As expected from the above analysis, the power form is a little more accurate, in agreement with curve fitting of experimental data (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006).
Fig. 6.
Log and power forms of Fitts’s law. Circles and crosses represent movement times (tf) calculated from the model with target widths of 0.04 and 0.02 m, respectively, and various distances (see text). (a) tf is plotted as a function of log2(2d/w). The log Fitts law predicts a straight line. (b) ln tf is plotted as a function of ln(d/w). The power Fitts law predicts a straight line. In each panel, linear fit of the circles, not crosses, is shown. The power index, given by the slope of the line in panel b, is 0.46.
In particular, Tanaka et al. (2006) fitted both the log (Eq. 32) and power (Eq. 36) forms to Fitts’s original data (Fitts, 1954) and found residual errors of 0.012 and 0.005, respectively. Incidentally, the power index given by the slope of the fitted line in Fig. 6b is 0.46, close to 0.5 of the square-root power law (Meyer et al., 1988). Schmidt and Lee (1998) found a power index of 1 but they trained subjects to use a fixed movement duration.
Experimental data (Fitts, 1954; Welford et al., 1969) also indicate that for a same d/w ratio, movements with small w (and d) take longer time than those with large w (and d). Our simulations show the same w-dependence (cf. circles and cross in Fig. 6). The reason is that when w is very small, p1(∞) in the above analysis cannot be neglected, and according to Eqs. 34 and 36, this term increases movement duration. Therefore, the model predicts stronger w-dependence when (kw)2 gets closer to p1(∞), which, as noted above, depends on the covariance of the signal-independent noise (the G term in Eq. 1). By varying k, w, and G, the model can produce various degrees of w-dependence.
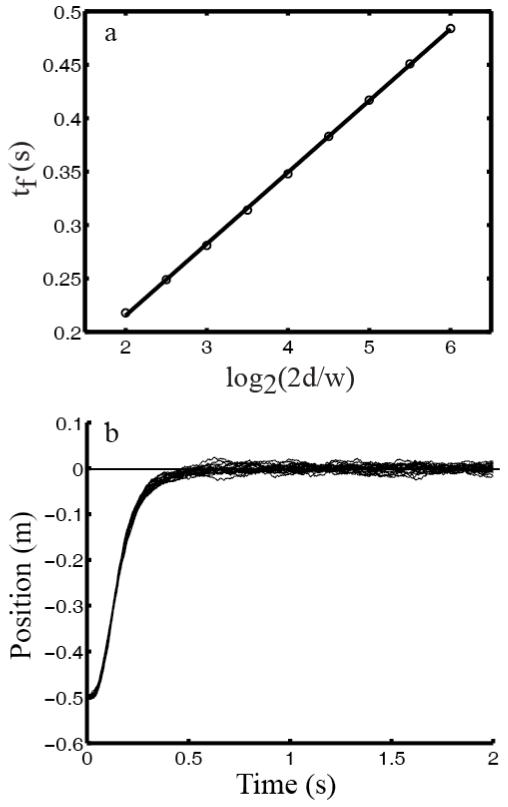
The Fitts law analysis above does not depend on whether or not there is signal-dependent noise in the control system (the Y term in Eq. 1). We confirmed this assertion numerically in Fig. 7a by setting Y=0 and doubling the signal-independent noise (G=0.06I4) while keeping all the other parameters the same as in Fig. 6. Interestingly, the result follows the log Fitts law better than that in Fig. 6a. This is likely because the signal dependent and independent noise terms affect movement duration differently, producing a convex-shaped curve when tf is plotted against log2(2d/w). Consequently, when Y=0 this curve becomes straighter and better agrees with the log Fitts law. However, the actual data (Fitts, 1954) plotted in the same way do produce a convex curve as predicted by the simulations with signal dependent noise included (Fig. 6a). Additionally, movement trajectories without signal-dependent noise, shown in Fig. 7b, do not show the typically observed variability during movements (Todorov and Jordan, 2002). These results suggest that signal-dependent noise contribute to real movements (Meyer et al., 1988; Harris and Wolpert, 1998; Todorov and Jordan, 2002).
Fig. 7.
Simulations without signal-dependent noise and with doubling of signal-independent noise. (a) Circles represent movement time (tf) calculated from the model with a target width of 0.04 m and various distances. A straight line well fits tf plotted against log2(2d/w). (b) Hand position as a function of time for 20 individual sample trials.
The simplicity of the above Fitts-law derivations is consistent with the universality of Fitts’s law. The derivations only assume that the control system is stable so that the hand position variance with respect to target decays with time, but are largely independent of other details. In fact, the derivation holds for any constant estimator (K) and controller (L) matrices (not just the optimal ones) provided that all eigenvalues of the resulting M matrix have negative real parts (to ensure stability). Even for non-linear models not studied in this paper, the position variance relative to the target still has to decay in order for the hand to reach the target. If this decay could be reasonably approximated by an exponential or power function (see Discussion), then the log or power form of Fitts’s law would result. The derivations also explain why the power form is more accurate than the log form (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006) because the latter focuses on only one exponential in Eq. 27. Moreover, the derivations explain why the log form becomes accurate for large values of movement duration (Fitts, 1954) because that is when the slowest component in Eq. 27 dominates. Additionally, the derivations suggest that there is no special meaning for the log or power form in Fitts’s law because the exponential and modified power functions are just two of many possible ways of fitting the variance data. Finally, the derivations suggest that by examining how a parameter influences the eigenvalues of the M matrix, we can predict its effect on movement duration. For example, other things being equal, a parameter change that makes the eigenvalues more negative (larger magnitudes), and thus the system more stable, will speed up movements.
4. Discussion
4.1 Summary of main results
We investigated biological implications of Phillis’s (1985) time-invariant solution for an infinite-horizon optimal feedback control model that contains both signal dependent and independent noise and minimizes steady-state accuracy and energetic costs per unit time. To relate this model to biological motor control, we hypothesize that the optimal steady-state estimator and controller from this model act continuously to estimate system state, execute movements, and maintain posture (the steady-state-control hypothesis). Consequently, it is unnecessary to artificially pre-specify when movements end and posture maintenance begins. The model reproduces typically observed position and velocity profiles, including occasional transient overshoots of targets. The profiles are relative smooth probably because jerky corrections of deviations from the target increase the steady-state accuracy and energetic costs. Additionally, the model correctly predicts that the hand eventually reaches, or fluctuates around, the target if sensory feedback is unbiased. Finally, we semi-analytically derived both the log and power forms of Fitts’s law (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006) as different approximations of how the hand-position variance with respect to the target position decays with time. This analysis and the related simulations clarify the relationship between the two forms of Fitts’s law, explain why the power form is usually more accurate (Meyer et al., 1988; MacKenzie, 1992; Tanaka et al., 2006) and why the log form is also accurate for large values of movement time (Fitts, 1954). The derivation holds for any constant estimator and controller (not just the optimal ones) provided that they ensure system stability and no large oscillations, which can be checked by examining the eigenvalues of the M matrix. Our work predicts that Fitts’s law per se does not require signal-dependent noise. However, the discrepancy between the log Fitts law and experimental data and the variability in movement trajectories are better explained with the inclusion of signal-dependent noise.
4.2 Other Fitts’s-law derivations and sub-movements
To our knowledge, this is the first derivation of movement duration and Fitts’s law in an optimal feedback control model. The constrained minimum time model (Tanaka et al., 2006) shows analytically that movement duration depends on target distance-to-width ratio, but still resorts to simulations to demonstrate the power function [see also Harris and Wolpert (1998)]. In addition, that model does not consider sensory feedback, which is important for typical reaching movements (Woodworth, 1899; Meyer et al., 1988; Todorov and Jordan, 2002). Many models use kinematic properties to predict movement duration. Some of these (Crossman and Goodeve, 1983) make assumptions that aim specifically at producing Fitt’s law. Others (Polyakov et al., 2009) are based on general principles that explain a large number of motor behaviors. Unlike dynamic models such as ours presented here, kinematic models do not consider how a control system determines appropriate forces, via control signals, to drive movements according to Newtonian mechanics. On the other hand, kinematic models provide useful insights when system dynamics is too complex to analyze. In this sense, dynamic and kinematic approaches are complementary.
Some models rely on sub-movements to derive Fitts’s law. An early model produces the log Fitts law by assuming that a movement consists of a geometrically decreasing sequence of sub-movements, and that each sub-movement takes the same time (Crossman and Goodeve, 1983). A later model derives the square-root form of the power Fitts law by assuming exactly two sub-movements that minimize movement duration (Meyer et al., 1988). Although real movements often contain irregularities that can be interpreted as corrective sub-movements (Carlton, 1980; Meyer et al., 1988; Milner, 1992; Novak et al., 2000), such interpretations require assumptions that are difficult to confirm independently. The issue is further complicated by the lack of a principled definition or a unique extraction of sub-movements (Milner, 1992; Novak et al., 2000; Rohrer and Hogan, 2003). Although there is no explicit sub-movement planning in our model, the transient overshoots and subsequent corrections shown in our simulations would be classified as sub-movements (Milner, 1992; Novak et al., 2000). By increasing the noise in our model, we can produce trajectories with multiple corrections, and thus multiple sub-movements. Sub-movements can also be explicitly introduced into optimal feedback control models by assuming that the system aims at a sequence of positions leading to the target, or on different parts of a target, either because of sensory errors (e.g., caused by poor peripheral vision) or as a strategy.
4.3 Advantages of the present model
Our infinite-horizon, steady-state model has several advantages. First, it is unnecessary for a control system to pre-fix movement duration. The model does not need duration information although the duration can be read off from the model. Second, unlike finite-horizon models that minimizes transient accuracy and energetic costs, the steady-state model does not predict an undershoot bias. Indeed, the model matches the intuitive notion that the system simply keeps moving the effector toward the target until it is reached. This seems more natural than the implicit assumption of finite-horizon models that the effector should stop at a pre-specified time even though the target has not been reached. Third, the model integrates movement control and posture maintenance and may thus help unify these two motor functions. Fourth, the movement characteristics (including duration) are determined by the system and task parameters. This is consistent with the notion that biological systems appear to move at an intrinsic pace (Mazzoni et al., 2007). The fact that we are able to move at different paces when demanded by tasks or context suggests that the brain could switch among different steady-state solutions obtained with different cost parameters or even different cost functions. For example, a reduced energetic cost (smaller R) speeds up movements. Fifth, Phillis’s (1985) steady-state solution for linear systems is easy to compute, applicable to different effector states and movement parameters, and amenable to analysis. Finally, system stability is guaranteed for all movements if all eigenvalues of the M matrix have negative real parts.
4.4 Extension to nonlinear case
Although Phillis’s (1985) solution and our analysis are for linear plants, the infinite-horizon approach should be, in principle, applicable to nonlinear cases, such as multi-joint movements, via numerical simulations. In practice, however, finding a globally optimal time-invariant solution for nonlinear systems is computationally intractable. The reason is that one has to search for the optimal solution numerically by discretizing the entire state space and will run into the curse-of-dimensionality problem for realistic biomechanical motor plants (Liu and Todorov, 2007). An alternative would be to approximate a nonlinear plant with a set of piecewise linear plants via Taylor expansion around the current state as it evolves, and then apply the infinite-horizon solution for linear systems to each linear approximation locally. This would yield a locally optimal solution that varies with time as the state evolves through different linear approximations. This time-dependence makes the solution more similar to those for finite-horizon models (Todorov, 2005) but the method would still have the advantage of not requiring pre-specification of movement duration or involving backward and forward sweeps in time to compute a solution. Furthermore, when a nonlinear plant gets close to a target, its linear approximation will not change much for the rest of the control process, and our analysis of the position variance in this paper might still apply. Whether and how well this method works is an open question for future research.
4.5 Movement and posture control
Whether the motor system applies common principles to the control of movement and posture remains unclear (Bullock et al., 1998; Mussa-Ivaldi and Bizzi, 2000; Graziano et al., 2002; Kurtzer et al., 2005; Feldman and Levin, 2009). Physiologically, partially overlapping populations of posture- and movement-related cells have been found in primary motor cortex (Kurtzer et al., 2005), suggesting both separate and shared processing of posture and movements. On the other hand, microstimulation of primary motor and premotor cortex can drive the limb to specific postures via apparently natural movements (Graziano et al., 2002), indicating that a common neuronal network controls both movements and posture. Our model assumes that the same principle governs movement and posture control. However, the model is at the computational level and may be compatible with multiple neural implementations. The integration of movement and posture control in our model is also reminiscent of the equilibrium point hypothesis (Polit and Bizzi, 1978; Feldman and Levin, 2009). However, in our model the effector’s state is actively estimated and controlled all the time, and is not the passive consequence of a change in set postures. Our model produces the movement trajectory at run time rather than explicitly plans the trajectory in advance.
4.6 Extension to multiple targets/movements and first-exit criteria
One might argue that without specifying a movement end time, our infinite-horizon model would keep the effector at a fixed target position indefinitely. However, like other motor-control models, our model can be readily extended to multiple target/movement cases. It is reasonable to assume that a motor system’s desired target is not fixed but changes with time. While finite-horizon models have to know a new movement duration and compute a new solution for each target, our infinite-horizon model can be run continuously to reach successive targets. Specifically, the estimator and controller of the model will always guide the effector toward the current target which may change with time. If the current target is reached, the effector will stay there until the system decides to reach a new target. (For example, a Ping-Pong player may move her hand/racket to a desired position and hold it there until she decides to serve the ball.) Similarly, a system may want to reach a target position only briefly and then return to a default state or be within a relatively broad range of default states. (For example, a Ping-Pong player may reach his hand laterally to hit a ball and then quickly return the hand to a more central position.) In this case, the default state may be viewed as the new target right after the first movement. More generally, a system may terminate the current movement according to a proper criterion (e.g., the current target is reached or a new target is selected). Liu and Todorov (2007) introduced a first-exit criterion: a movement terminates when the hand exceeds the horizontal distance of the target or when the duration exceeds a pre-set maximum value. Similar termination criteria can be introduced into our infinite-horizon model. In fact, our Fitts’s law derivation and simulations relied on a first-exit criterion: the mean movement duration is the shortest time at which the hand variance with respect to the target is reduced to a target-size-related value. As mentioned before, we could also define a first-exit criterion for individual trials, e.g., when the hand first touches any part of the target or is within a certain distance of the target center.
4.7 Limitations of the present model
Obviously, any model is only an approximation of reality and has a limited scope. We discuss some of the many limitations of our model. First, our model only concerns movement duration but not reaction time. It would be interesting to add a reaction-time component to optimal feedback control models. Second, we recognize that other factors, such as reward or value (Xu-Wilson et al., 2009), influences movement duration and should be incorporated into our framework in future research.
Third, without additional considerations, our model predicts that movements to targets of different sizes at the same distance have the same trajectory except different degrees of final convergence (because of the dependence of termination criterion on target size). Although this prediction agrees with Soechting’s (1984) data (see his Fig. 2 to compare full trajectories for a large and a small target), it appears problematic in light of other data. For example, Milner and Ijaz (1990) found lower peak speeds for smaller targets at a fixed distance. While this problem requires future investigation, we discuss a possible solution. Miler and Ijaz’s subjects were instructed not to touch a board when inserting pegs into target holes on the board. Since smaller holes made it more likely for subjects to hit the surrounding board, the subjects may have aimed at a shorter, initial distance, producing a smaller peak speed. The same strategy might be used by subjects in Fitts’s tapping paradigm: because subjects were not allowed to correct their movements after touching the surface containing the targets, they may have aimed at a shorter initial distance for smaller targets to avoid touching extra-target areas. We can thus make a specific prediction: if subjects are free to touch extra-target areas before converging on the target, then movement trajectories to targets of different sizes at the same distance will be the same except different degrees of final convergence. To test this prediction, it would be best to use a planar movement task in which subjects always touch the surface containing the target and thus are unlikely to make an implicit assumption that they should avoid extra-target areas. A related prediction is that even for a fixed target size (and distance), the peak speed should decrease with increased avoidance of extra-target areas.
A final limitation of our model concerns possible integration of transient and steady-state costs in some situations, as explained below.
4.8 Optimization of transient and steady-state costs
One may argue that control systems can do better by performing a finite-horizon optimization instead of applying a steady-state solution to execute movements. This issue depends on what one means by “better”. In terms of the total cost summed over a fixed movement duration, a finite-horizon solution that optimizes this transient cost is obviously better than an infinite-horizon solution that optimizes steady-state cost per unit time. However, the former approach requires knowing movement durations in advance. As discussed in the Introduction, in finite-horizon feedback control formulations, this entails either multiple, trial-and-error internal simulations using complete knowledge of everything (including actual as well as estimated state vectors), or storage/approximation of movement durations for all possible movements under all possible situations. In addition to plausibility and efficiency problems, these options incur additional neural costs not included in the optimization process. Moreover, for a given, pre-fixed duration, optimization in finite-horizon feedback models involves multiple backward and forward sweeps in time (Todorov, 2005) while optimization in infinite-horizon models does not. When these extra costs of the finite-horizon approach are considered, it is no longer obvious whether it is still “better” than the infinite-horizon approach. Finally, the occurrence of transient overshoot, the lack of final undershoot under veridical sensory feedback, and a recent study of Kistemaker et al. (2010) all suggest that the motor system does not always minimize transient energetic cost.
On the other hand, there are situations where a finite-horizon approach that minimizes transient costs does seem to be better. One example is periodic movements set by a metronome. Another example is movements repeated frequently and exactly (e.g., typing on the same keyboard). In these cases, movement duration is known (from repetition) and the solution from a single finite-horizon optimization process can be used many times. The total savings in transient costs over many trials can be substantial enough to justify computing the finite-horizon solution, which may be learned from movement repetition. Note that even for these cases, the finite-horizon solution needs to be adjusted to avoid undershooting the target.
We therefore suggest that biological systems might use steady-state solutions as default mechanisms both to control movements and to maintain posture, might apply different steady-state solutions (K’s and L’s corresponding to different cost parameters or cost functions) to produce different paces for different situations, and might seek additional optimization of transient costs for movements when time boundaries are known and frequent use of the solution leads to substantial cost savings.
Acknowledgements
Supported by AFOSR grant FA9550-10-1-0370, NEI grant EY016270, Weinstein Foundation, NINDS grant NS050824, and the Parkinson’s Disease Foundation. We thank Ben Huh, Terry Sejnowski, and Emo Todorov for sharing unpublished results on infinite-horizon optimal control and for helpful comments.
References
- Beylkin G, Monzón L. Approximation by exponential sums revisited. Applied and Computational Harmonic Analysis. 2010;28:131–149. [Google Scholar]
- Bullock D, Cisek P, Grossberg S. Cortical networks for control of voluntary arm movements under variable force conditions. Cerebral Cortex. 1998;8:48–62. doi: 10.1093/cercor/8.1.48. [DOI] [PubMed] [Google Scholar]
- Carlton LG. Movement control characteristics of aiming responses*. Ergonomics. 1980;23:1019–1032. doi: 10.1080/00140138008924811. [DOI] [PubMed] [Google Scholar]
- Cooke JD, Brown SH, Cunningham DA. Kinematics of arm movements in elderly humans. Neurobiol Aging. 1989;10:159–165. doi: 10.1016/0197-4580(89)90025-0. [DOI] [PubMed] [Google Scholar]
- Crossman ERFW, Goodeve PJ. Feedback-control of hand-movement and Fitts’ law. Q J Exp Psychol Sect A-Hum Exp Psychol. 1983;35:251–278. doi: 10.1080/14640748308402133. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Shadmehr R, Ivry RB. The coordination of movement: optimal feedback control and beyond. Trends in Cognitive Sciences. 2010;14:31–39. doi: 10.1016/j.tics.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. The equilibrium-point hypothesis--past, present and future. Adv Exp Med Biol. 2009;629:699–726. doi: 10.1007/978-0-387-77064-2_38. [DOI] [PubMed] [Google Scholar]
- Fitts PM. The Information Capacity of the Human Motor System in Controlling the Amplitude of Movement. J Exp Psychol. 1954;47:381–391. [PubMed] [Google Scholar]
- Flash T, Hogan N. The coordination of arm movements - an experimentally confirmed mathematical-model. J Neurosci. 1985;5:1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graziano MSA, Taylor CSR, Moore T. Complex movements evoked by microstimulation of precentral cortex. Neuron. 2002;34:841–851. doi: 10.1016/s0896-6273(02)00698-0. [DOI] [PubMed] [Google Scholar]
- Guigon E, Baraduc P, Desmurget M. Computational motor control: feedback and accuracy. European Journal of Neuroscience. 2008;27:1003–1016. doi: 10.1111/j.1460-9568.2008.06028.x. [DOI] [PubMed] [Google Scholar]
- Harris C, Wolpert D. The Main Sequence of Saccades Optimizes Speed-accuracy Trade-off. Biological Cybernetics. 2006;95:21–29. doi: 10.1007/s00422-006-0064-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris CM. On the optimal control of behaviour: a stochastic perspective. Journal of Neuroscience Methods. 1998;83:73–88. doi: 10.1016/s0165-0270(98)00063-6. [DOI] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Huh D, Todorov E, Sejnowski TJ. Infinite horizon optimal control framework for goal directed movements Society for Neuroscience Annual Meeting; 2010a; Online:Program No. 492.411. [Google Scholar]
- Huh D, Todorov E, Sejnowski TJ. Infinite Horizon Optimal Control Framework for Goal Directed Movements. Advances in Computational Motor Control. 2010b;9:1–2. [Google Scholar]
- Jiang Y, Jiang ZP, Qian N. Optimal control mechanisms in human arm reaching movements; Proceedings for 30th Chinese Control Conference; 2011.pp. 1377–1382. [Google Scholar]
- Kistemaker DA, Wong JD, Gribble PL. The Central Nervous System Does Not Minimize Energy Cost in Arm Movements. J Neurophysiol. 2010;104:2985–2994. doi: 10.1152/jn.00483.2010. [DOI] [PubMed] [Google Scholar]
- Kurtzer I, Herter TM, Scott SH. Random change in cortical load representation suggests distinct control of posture and movement. Nat Neurosci. 2005;8:498–504. doi: 10.1038/nn1420. [DOI] [PubMed] [Google Scholar]
- Liu D, Todorov E. Evidence for the Flexible Sensorimotor Strategies Predicted by Optimal Feedback Control. The Journal of Neuroscience. 2007;27:9354–9368. doi: 10.1523/JNEUROSCI.1110-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKenzie IS. Fitts’ law as a research and design tool in human-computer interaction. Human-Computer Interaction. 1992;7:91–139. [Google Scholar]
- Mazzoni P, Hristova A, Krakauer JW. Why don’t we move faster? Parkinson’s disease, movement vigor, and implicit motivation. J Neurosci. 2007;27:7105–7116. doi: 10.1523/JNEUROSCI.0264-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer DE, Kornblum S, Abrams RA, Wright CE, Smith JEK. Optimality in human motor-performance: Ideal control of rapid aimed movements. Psychol Rev. 1988;95:340–370. doi: 10.1037/0033-295x.95.3.340. [DOI] [PubMed] [Google Scholar]
- Milner TE. A model for the generation of movements requiring endpoint precision. Neuroscience. 1992;49:487–496. doi: 10.1016/0306-4522(92)90113-g. [DOI] [PubMed] [Google Scholar]
- Milner TE, Ijaz MM. THE EFFECT OF ACCURACY CONSTRAINTS ON 3-DIMENSIONAL MOVEMENT KINEMATICS. Neuroscience. 1990;35:365–374. doi: 10.1016/0306-4522(90)90090-q. [DOI] [PubMed] [Google Scholar]
- Morasso P. Spatial control of arm movements. Exp Brain Res. 1981;42:223–227. doi: 10.1007/BF00236911. [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA, Bizzi E. Motor learning through the combination of primitives. Philos Trans R Soc Lond B Biol Sci. 2000;355:1755–1769. doi: 10.1098/rstb.2000.0733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak KE, Miller LE, Houk JC. Kinematic properties of rapid hand movements in a knob turning task. Exp Brain Res. 2000;132:419–433. doi: 10.1007/s002210000366. [DOI] [PubMed] [Google Scholar]
- Phillis YA. Controller-design of systems with multiplicative noise. IEEE Transactions on Automatic Control. 1985;30:1017–1019. [Google Scholar]
- Polit A, Bizzi E. Processes controlling arm movements in monkeys. Science. 1978;201:1235–1237. doi: 10.1126/science.99813. [DOI] [PubMed] [Google Scholar]
- Polyakov F, Stark E, Drori R, Abeles M, Flash T. Parabolic movement primitives and cortical states: merging optimality with geometric invariance. Biological Cybernetics. 2009;100:159–184. doi: 10.1007/s00422-008-0287-0. [DOI] [PubMed] [Google Scholar]
- Rohrer B, Hogan N. Avoiding spurious submovement decompositions: a globally optimal algorithm. Biological Cybernetics. 2003;89:190–199. doi: 10.1007/s00422-003-0428-4. [DOI] [PubMed] [Google Scholar]
- Schmidt RA, Lee TD. Motor Control and Learning: A Behavioral Emphasis. Human Kinetics Publishers; Champaign, IL: 1998. [Google Scholar]
- Scott SH. Optimal feedback control and the neural basis of volitional motor control. Nat Rev Neurosci. 2004;5:532–546. doi: 10.1038/nrn1427. [DOI] [PubMed] [Google Scholar]
- Soechting JF. EFFECT OF TARGET SIZE ON SPATIAL AND TEMPORAL CHARACTERISTICS OF A POINTING MOVEMENT IN MAN. Exp Brain Res. 1984;54:121–132. doi: 10.1007/BF00235824. [DOI] [PubMed] [Google Scholar]
- Tanaka H, Krakauer JW, Qian N. An optimization principle for determining movement duration. J Neurophysiol. 2006;95:3875–3886. doi: 10.1152/jn.00751.2005. [DOI] [PubMed] [Google Scholar]
- Todorov E. Optimality principles in sensorimotor control. Nat Neurosci. 2004;7:907–915. doi: 10.1038/nn1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Stochastic optimal control and estimation methods adapted to the noise characteristics of the sensorimotor system. Neural Computation. 2005;17:1084–1108. doi: 10.1162/0899766053491887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Uno Y, Kawato M, Suzuki R. Formation and control of optimal trajectory in human multijoint arm movement - minimum torque-change model. Biological Cybernetics. 1989;61:89–101. doi: 10.1007/BF00204593. [DOI] [PubMed] [Google Scholar]
- Welford AT, Norris AH, Shock NW. Speed and accuracy of movement and their changes with age. Acta Psychologica. 1969;30:3–15. doi: 10.1016/0001-6918(69)90034-1. [DOI] [PubMed] [Google Scholar]
- Winters JM, Stark L. Analysis of fundamental human movement patterns through the use of in-depth antagonistic muscle models. IEEE Trans Biomed Eng. 1985;32:826–839. doi: 10.1109/TBME.1985.325498. [DOI] [PubMed] [Google Scholar]
- Woodworth RS. The accuracy of voluntary movement. Psychol Rev. 1899;3(3, Suppl 13):1–119. [Google Scholar]
- Xu-Wilson M, Zee DS, Shadmehr R. The intrinsic value of visual information affects saccade velocities. Exp Brain Res. 2009;196:475–481. doi: 10.1007/s00221-009-1879-1. [DOI] [PMC free article] [PubMed] [Google Scholar]