Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2014 Jun 18;5:4149. doi: 10.1038/ncomms5149

Petawatt laser absorption bounded

Matthew C Levy 1,2,a, Scott C Wilks 2, Max Tabak 2, Stephen B Libby 2, Matthew G Baring 1
PMCID: PMC4083416  PMID: 24938656

Abstract

The interaction of petawatt (1015 W) lasers with solid matter forms the basis for advanced scientific applications such as table-top particle accelerators, ultrafast imaging systems and laser fusion. Key metrics for these applications relate to absorption, yet conditions in this regime are so nonlinear that it is often impossible to know the fraction of absorbed light f, and even the range of f is unknown. Here using a relativistic Rankine-Hugoniot-like analysis, we show for the first time that f exhibits a theoretical maximum and minimum. These bounds constrain nonlinear absorption mechanisms across the petawatt regime, forbidding high absorption values at low laser power and low absorption values at high laser power. For applications needing to circumvent the absorption bounds, these results will accelerate a shift from solid targets, towards structured and multilayer targets, and lead the development of new materials.

Inline graphicPetawatt laser-matter interactions could open the way to fusion energy or compact particular accelerators, but predicting the amount of light absorbed in these interactions is challenging. New analysis by Levy et al. reveals the theoretical upper and lower limits of this absorption.

Irradiation of solids by petawatt laser light (Il λl2>1018 W μm2 cm−2, where I1 is intensity and λ1 is wavelength) creates extreme states of matter with temperatures exceeding 10 million degrees Celsius and pressures exceeding one billion earth atmospheres. These high energy density conditions are driven at the microscopic scale by dense currents of relativistic electrons (~1011 A cm−2), oscillating violently in the intense laser fields (>1010 V cm−1), as well as the plasma processes arising when these particles are dephased and injected into the high density target1. Suitably harnessed, this set-up opens the way to table-top relativistic particle accelerators1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, laser fusion16,17,18,19,20,21,22,23, laboratory astrophysics24,25,26, ultrafast imaging systems27,28,29, high-energy radiation sources30 and intense high harmonic generation31,32,33,34. Over the past two decades, the promise of these applications has driven considerable theoretical and experimental study of the crucial problem of how the laser energy is converted to target particle energy. Dozens of energy transfer mechanisms have been identified1,2,3, and most treatments to date have focused on examining individual mechanisms in isolation to help guide interpretation of results. In realistic situations, however, these absorption mechanisms can be strongly nonlinear and several often act concurrently.

In this article we report the theoretical maximum and minimum absorption for each laser-solid configuration across the petawatt regime. We find that these extrema constrain nonlinear absorption mechanisms3,35,36,37,38,39, bounding the laser energy transfer in a more general manner. The present analysis overcomes difficulties of particle nonlinearity by creating a kinematic basis on which to formulate the interaction. We use a geometry centred at the laser-matter interface, taking advantage of the laser decay into an evanescent wave over a relativistic collisionless skin depth in the optically thick target. Here Rankine-Hugoniot-like conservation laws40,41 must be satisfied by the forward-going evanescent light wave, the backward-going reflected wave, forward-drifting highly relativistic electrons and moderately relativistic ions accelerated by the laser. By representing the complex motion of individual particles with ensemble properties such as density and momentum, accounting for the relativistically correct laser-solid physics42,43,44,45,46,47,48, we realize an essentially four body kinematics situation. We show that these kinematics restrict values the ensemble properties of electrons and ions can take on. Since acceleration of electrons and acceleration of ions are modes of absorption of laser light, we demonstrate that these kinematic restrictions can be transformed into useful upper and lower bounds on absorption. Excellent agreement with a broad range of published experimental and simulation data37,44,48,49 confirms that the absorption bounds are distilling a fundamental aspect of the nonlinear dynamical physics. For applications using solid targets, our results show a new general metric for measuring efficiency. Since the design space to be explored is contracted, these findings will enable research efforts to focus on useful regions of parameter space thus accelerating the development of future laser-solid applications. We also identify applications requiring efficiency exceeding that permitted by the absorption bounds. Our results indicate that these applications would benefit by shifting towards structured50,51,52 or multilayer53,54 target designs.

Results

Relativistic interaction model

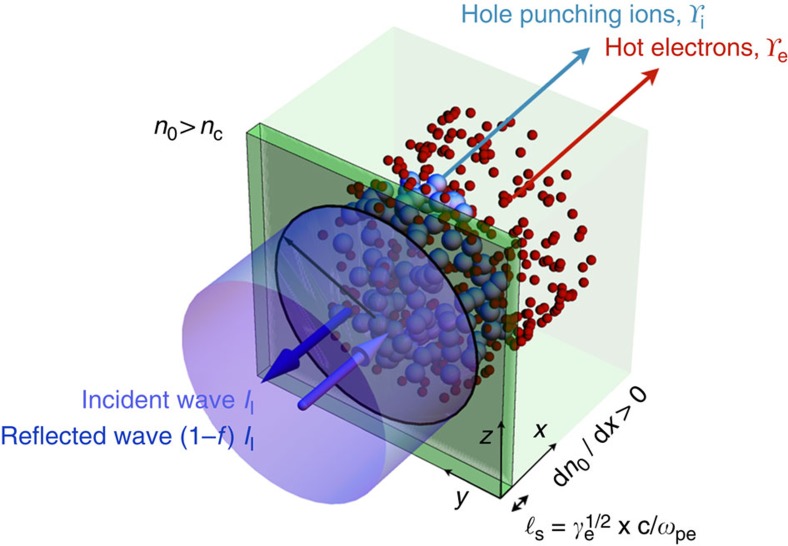
Essential features of petawatt laser-solid interactions are shown in Fig. 1. Here an ultraintense a0>1 light pulse (where a0=eEl/(me c ωl) is the laser strength parameter, c is the speed of light, e is the fundamental charge, me is the electron mass, E1 is the laser electric field and ωl is the laser angular frequency) is seen to irradiate a thick target of electron density n0(x)>nc, for realistic spatial profile n0(x) and critical density nc=meωl2/(4πe2) (see Methods for additional details). Electrons oscillate relativistically in the intense laser fields allowing the light wave to penetrate into the field-ionized overdense (optically thick) plasma55, an axial distance equal to the Lorentz-transformed collisionless skin depth, 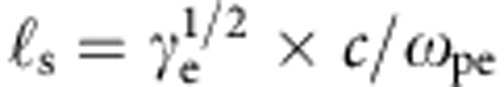Inline graphic (where γe=(1−βe2)−1/2 is the electron Lorentz factor, βec is the electron speed and ωpe=(4πe2n0/me)1/2 is the plasma frequency). This forms the scale size for the interaction. Within 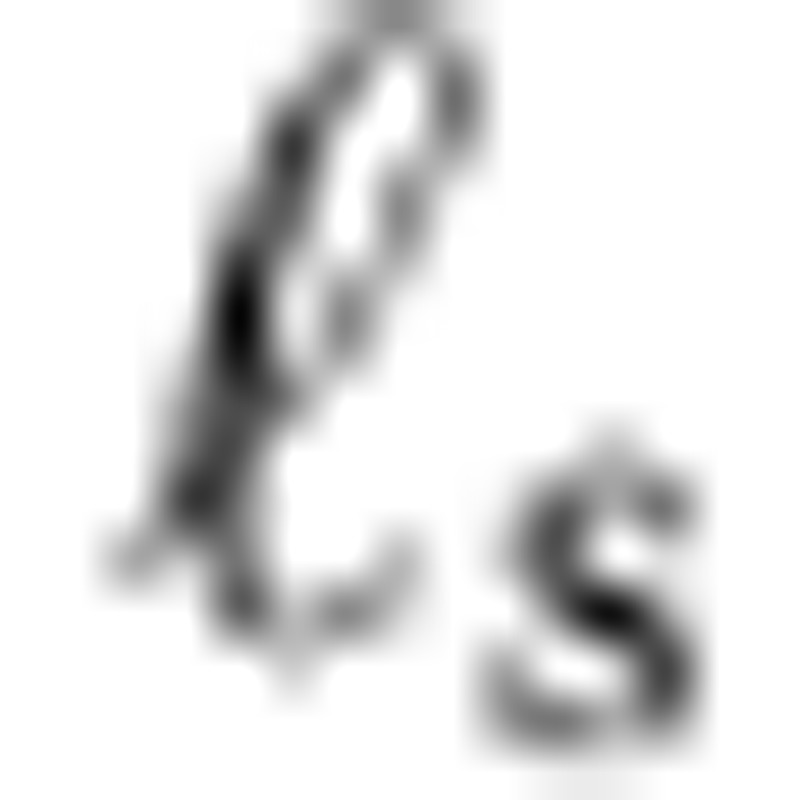Inline graphic, radiation reaction effects are small due to Debye shielding and electron and ion collisional mean-free paths satisfy 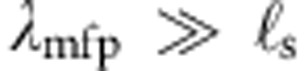Inline graphic. Therefore, as shown in Fig. 1, electrons and ions are the only particle populations entering into the petawatt-scale kinematic interaction. Irrespective of the specific mechanism of energy transfer, these particles absorb energy from the laser collisionlessly42,56, and their ensemble properties enter into formulae describing the total absorption f=fi+fe , where fi is the absorption into ions and fe is the absorption into electrons.

Figure 1. Schematic showing key features of the petawatt laser-solid interaction.

Figure 1

Open in a new tab

A high-power laser with strength parameter a0>1 is shown striking an overdense target, interacting over the Lorentz-transformed collisionless skin depth 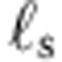Inline graphic (dark green region), and exciting a highly relativistic electron flux (red spheres) and moderately relativistic ion flux (blue spheres). Laser and excited particle properties are connected across 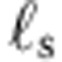Inline graphic by applying relativistic Rankine-Hugoniot-like relations at the laser-matter interface, allowing abstraction of downstream effects, for example, scattering in the 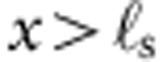Inline graphic target (light green region). Depiction uses a frame of reference co-moving with the interface.

Unbounded fe and fi solutions are obtained by applying a relativistic kinematic model at the laser-matter interface, establishing a connection between the laser pulse and the particles it excites across the density discontinuity48 (realizing an essential similarity to the Rankine-Hugoniot relations in magnetohydrodynamic shocks41). Ion dynamics are constrained by a snow plow-like process called ‘hole punching’ driven by the laser ponderomotive pressure, which can exceed >109 atmospheres42. In contrast, electron dynamics can be governed by a number of different collisionless mechanisms depending on parameters such as laser polarization and angle of incidence3,35,36,37,38,39. To calculate results independent of the specific mechanism, ensemble electron properties are determined based on a general Lorentz-invariant ansatz distribution function57. Solutions accounting for these realistic dynamical conditions are computed numerically; however, an analytic form exists for the representative case 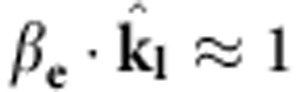Inline graphic for laser propagation in 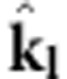Inline graphic (see Methods). Here ion absorption is 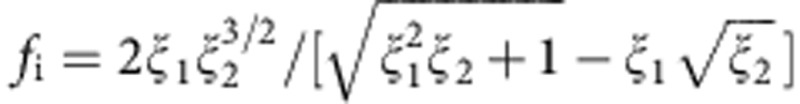Inline graphic and electron absorption is Inline graphic, using the convenient control parameters ξ1, ξ2 and ξ3. Intensity and density conditions are controlled by ξ1=[Zmenc/(2Min0)]1/2a0 for uniform interface charge state Z and ion mass M1.ξ2=Il,reflected/Il,incident corresponds to net photon flux deposited in the laser-matter interface, and 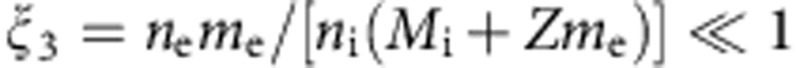Inline graphic is a small parameter exhibiting the disparate mass scales that characterize the petawatt laser-solid absorption modes.

Absorption bounds

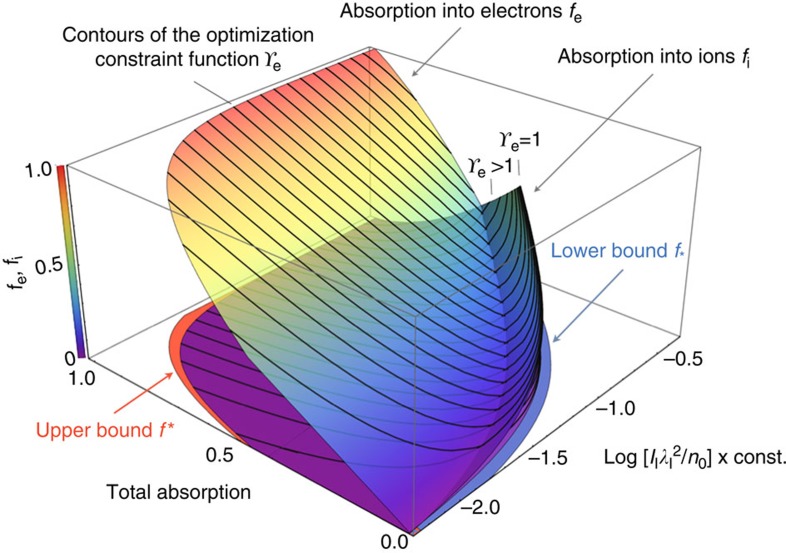
Absorption bounds reflect the fact that solutions to the kinematic equations for fe and fi can become unphysical for values of f between zero and one. These bounds are derived using constrained optimization techniques58 with f=fi+fe as the objective function. We optimize f over ξ2 imposing the simple constraint that the electron energy is real, and the minimization equation is written as f*=Min(fe + fi), s.t. γe≥1. Because the utility function is nonlinear in the control variables, minimization is performed numerically by means of cylindrical algebraic decomposition59, and the resulting points are fit to a polynomial using interval Δξ1≈10−3 over the physically relevant range in ξ1 between [0.01, 0.5]. For the fully ionized laser-plasma interface, we calculate that f*≈1.9ξ1−2.75ξ12+1.91ξ13, indicating that the lower limit on laser absorption is closely related to the process of ion acceleration by an intense circularly polarized radiation pressure source3,37,60. Deviations from the absorption associated with this process occur at small ξ1 as energy is reapportioned into relativistic electrons, highlighting that the kinematic coupling between ions and electrons represents an important feature of the interaction. When the electronic coupling is removed, we confirmed that f* converges to the well-established ion acceleration result f*→2ξ1/(1+2ξ1) (ref. 37) Maximizing the absorption through f*=Max(fe + fi), again subject to the constraint that γe≥1, yields the upper limit to be f*=1−ξ3/(2ξ12). In contrast to the lower limit, there is no well-established analytic result that describes absorption along the f* curve based on a simple physical mechanism. Here we proceed allowing that ne ≈ nc, implying that absorption along f=f* corresponds to electrons excited with γe≈a02/2, within a factor of order unity of the full laser ponderomotive potential. Figure 2 presents a comprehensive description of the absorption, showing surfaces corresponding to fe and fi, as well as bounding regions corresponding to f* and f*. Ions are seen to dominate the absorption along f=f*, the region corresponding to γe=1. As the target absorbs more of the laser energy, Fig. 2 shows that this energy is predominantly coupled into relativistic electrons. Electrons dominate the absorption along f=f*, with f>f* causing fe to be complex.

Figure 2. Bounds on absorption and subpartitioning of absorbed light.

Figure 2

Open in a new tab

The lower-right axis corresponds to ξ1 describing the initial laser and target conditions, and the total absorption f=1−ξ2. Two surfaces corresponding to the absorption into electrons fe and into ions fi are shown (the former having slight transparency for visualization purposes). Contours of the optimization function γe are superimposed on these surfaces using dark grey. The lower limit f* (blue) and upper limit f* (red) on absorption are shown bounding fe and fi.

Comparison between absorption bounds and published data

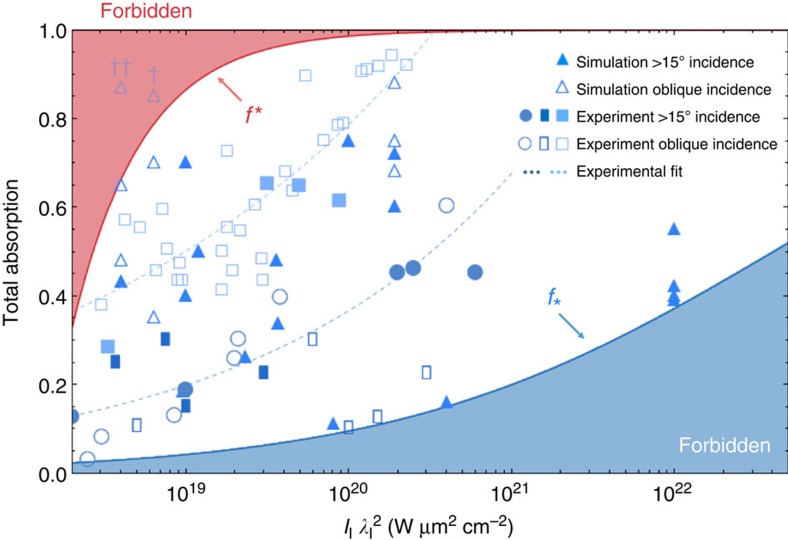
Comparison with published data is facilitated by specifying an interaction-averaged density, which is well-represented by a corrected relativistic critical density55 given by a02≈(27/64)(n0/nc)4 for 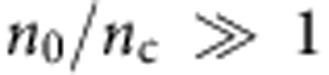Inline graphic. Figure 3 shows these limits applied to experimental data and simulation results published over two decades, spanning a broad range of laser and plasma parameters, obtained at several laser facilities. From this figure, it is clear that experimental data and kinetic particle-in-cell simulations at a variety of realistic conditions37,44,48,49 show excellent agreement with the absorption bound predictions.

Figure 3. Comparison between absorption bounds and published data.

Figure 3

Open in a new tab

The complete data set compiled in Davies49 is reproduced here, spanning experimental and simulation data published over the past two decades, across a variety of laser and plasma conditions. Dashed lines corresponding to fits of selected experimental data are shown to guide the eye. Additional high-intensity simulation data are reproduced from Levy et al.48 The upper limit on absorption f* is depicted in red and the lower limit f* in blue, with forbidden regions indicated using shading. The two outlying data points correspond to simulations of (†) a very thin 0.2 μm pre-deformed target, and (††) an essentially underdense nc > n0 interaction, both violating assumptions underpinning the laser-solid model (see Methods).

Absorption bounds in terms of laser and plasma parameters

Transforming from the control coordinates, the condition f*≤f≤f* can be written simply in terms of the laser power and unperturbed plasma density as,

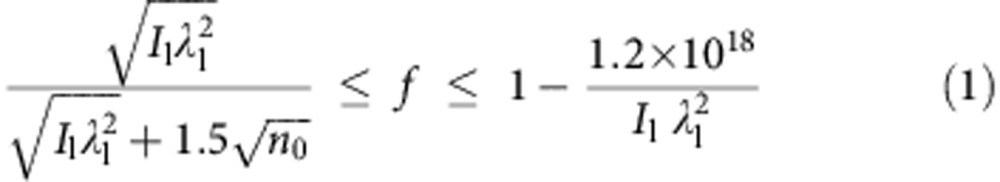graphic file with name ncomms5149-m10.jpg

where [Il λl2]=W μm2 cm−2, [n0]=cm−3, and Ilλl2>1.3 × 1018. Equation (1) bounds the laser-solid interaction through its dynamical history for a realistic time-dependent laser envelope and plasma profile37,48.

Discussion

Figures 2 and 3 highlight that f* becomes increasingly strict with laser power, forbidding 35% of possible absorption values at 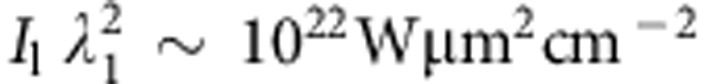Inline graphic, a regime accessible at laser facilities such as ELI61 scheduled to come online in the next few years. These results will therefore play a central role in guiding the next generation of multi-petawatt experiments.

By shrinking the design space to be explored, these results will enable research efforts to focus on useful regions of parameter space thus accelerating the development of laser-solid applications. For these applications, the metric f/f* using equation (1) provides a theoretical baseline enabling efficiency to be measured and ultimately improved62.

For applications needing to circumvent the absorption bounds in equation (1), these results will drive a shift towards new interaction paradigms. To see that assumptions underpinning the laser-solid interaction model must be violated to exceed these limits, it is instructive to examine the two outlying points shown in Fig. 3. The data point labelled (†) corresponds to one simulation of a pre-deformed, very thin target of λl > d where d is the target thickness, realizing a strongly refluxing configuration (see Methods). The point labelled (††) corresponds to one simulation of a laser interacting with 20 μm of nc > n0 plasma in front of a thin n0=20nc target, realizing an essentially underdense situation. We thus confirm that very thin and underdense targets allow absorption in excess of f* at low laser power, as they should. However, several important applications that have conventionally used solid targets also depend on high absorption at relatively low laser power. These applications include laser-based anti-matter generation for scaled astrophysical studies63,64, ultrafast charged-particle imaging systems27, where increasing absorption reduces noise and improves imaging resolution, and certain approaches to electron-driven fast ignition laser fusion16. Recently works that have shifted from solid targets have started to report enhanced results in these areas52,53,54. The results presented here will accelerate this shift across the petawatt field, and lead the development of novel low density, structured and multilayer targets.

Methods

The essential kinematic relations forming the basis of the optimization analysis reported in this article were published in ref. 48. The general consideration of optimal couplings under the constraint of phase space conservation motivates the present studies65. Radiation-hydrodynamic simulations show that particle density in interactions can often be approximated by an exponential distribution 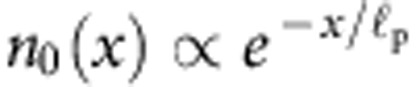Inline graphic for scalelength 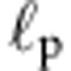Inline graphic, due to amplified spontaneous emission (ASE) associated with laser pulse compression generating a ‘pre-plasma’1. Petawatt laser-solids satisfy 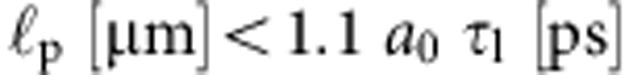Inline graphic for pulse duration τl such that the primary interaction occurs in the classically overdense n0/nc>1 region, while small-scale underdense regions are swept away by the strong laser ponderomotive force, as indicated by energy balance between electron acceleration in the underdense and overdense regions. 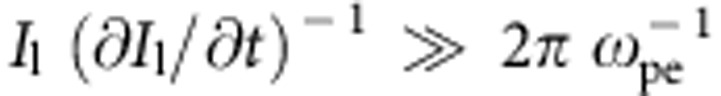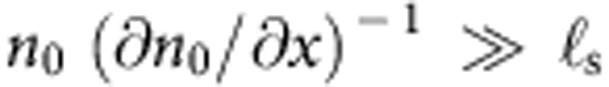The laser temporal envelope Inline graphic and the plasma density profile are subject to Inline graphic, both readily satisfied under realistic conditions. 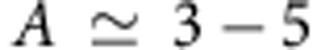Damping of transient momentum effects requires that τl ωpi > 2πA where ωpi=(4πe2Zn0/Mi)1/2 and Inline graphic, and the target thickness d should exceed the hole punching depth and the effective refluxing hot electron range, 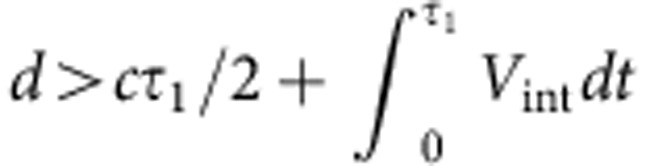Inline graphic for motion of the laser-matter interface at velocity Vint. Deviations from 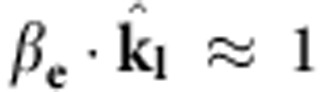Inline graphic are second order in the angle 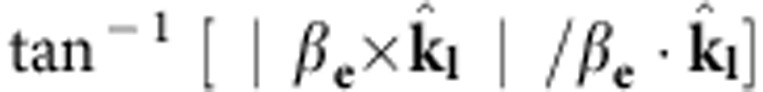Inline graphic and therefore do not substantively affect the absorption bound results for realistic scenarios. Energy apportionment into ions increases with this angle but qualitative trends in fe and fi are maintained66. For electrons following the ponderomotive energy scaling42, the cooling length 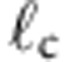Inline graphic associated with the radiation reaction force within 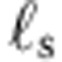Inline graphic can be estimated67 as 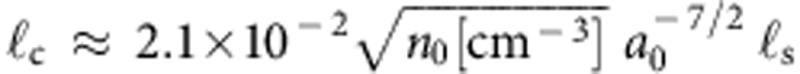Inline graphic due to Debye shielding. Thus, 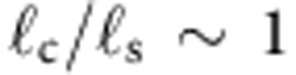Inline graphic only at the 10-petawatt level 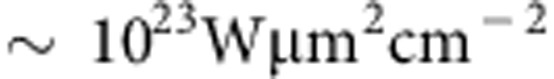Inline graphic, confirming the selection of absorption modes characterizing the petawatt-scale interaction.

Author contributions

M.C.L. developed the analytical theory with support from S.C.W. and M.T. Assistance with conceptualizing the physical arguments and preparing the manuscript was provided by S.B.L. Theoretical support was provided by M.G.B.

Additional information

How to cite this article: Levy, M. C. et al. Petawatt laser absorption bounded. Nat. Commun. 5:4149 doi: 10.1038/ncomms5149 (2014).

Acknowledgments

M.C.L. is grateful to B. Breizman and A. Link for discussions. M.C.L. acknowledges the LLNL Lawrence Scholarship for support and the Institutional Computing Grand Challenge for computational resources. S.C.W. acknowledges support from Fusion Energy Sciences in the DOE Office of Science. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344.

References

  1. Macchi A. A Superintense Laser-Plasma Interaction Theory Primer SpringerBriefs in Physics (2013). [Google Scholar]
  2. Pukhov A. Strong field interaction of laser radiation. Rep. Prog. Phys. 66, 47–101 (2003). [Google Scholar]
  3. Wilks S. C. & Kruer W. L. Absorption of ultrashort, ultra-intense laser light by solids and overdense plasmas. IEEE J. Quantum Electron. 33, 1954–1968 (1997). [Google Scholar]
  4. Daido H., Nishiuchi M. & Pirozhkov A. S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 75, 056401 (2012). [DOI] [PubMed] [Google Scholar]
  5. Robinson A. P. L., Arefiev A. V. & Neely D. Generating superponderomotive electrons due to a Non-wake-field interaction between a laser pulse and a longitudinal electric field. Phys. Rev. Lett. 111, 065002 (2013). [DOI] [PubMed] [Google Scholar]
  6. Hegelich B. M. et al. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 439, 441–444 (2006). [DOI] [PubMed] [Google Scholar]
  7. Fuchs J. et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2, 48–54 (2005). [Google Scholar]
  8. Toncian T. et al. Ultrafast laser-driven microlens to focus and energy-select mega-electron volt protons. Science 312, 410–413 (2006). [DOI] [PubMed] [Google Scholar]
  9. Esirkepov T., Borghesi M., Bulanov S., Mourou G. & Tajima T. Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 92, 2–5 (2004). [DOI] [PubMed] [Google Scholar]
  10. Bulanov S. V. et al. Unlimited ion acceleration by radiation pressure. Phys. Rev. Lett. 135003, 1–4 (2010). [DOI] [PubMed] [Google Scholar]
  11. Roth M. et al. Energetic ions generated by laser pulses: a detailed study on target properties. Phys. Rev. Special Topics 5, 061301 (2002). [Google Scholar]
  12. Sentoku Y., Cowan T. E., Kemp A. & Ruhl H. High energy proton acceleration in interaction of short laser pulse with dense plasma target. Phys. Plasmas 10, 2009 (2003). [Google Scholar]
  13. Flippo K. A. et al. Increased efficiency of short-pulse laser-generated proton beams from novel flat-top cone targets. Phys. Plasmas 15, 056709 (2008). [Google Scholar]
  14. Petrov G. M. & Davis J. Laser acceleration of light ions from high-intensity laser-target interactions. Appl. Phys. B 96, 773–779 (2009). [Google Scholar]
  15. Kar S. et al. Ion acceleration in multispecies targets driven by intense laser radiation pressure. Phys. Rev. Lett. 109, 185006 (2012). [DOI] [PubMed] [Google Scholar]
  16. Tabak M. et al. Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634 (1994). [Google Scholar]
  17. Kodama R. et al. Plasma devices to guide and collimate a high density of MeV electrons. Nature 432, 1005–1008 (2004). [DOI] [PubMed] [Google Scholar]
  18. Theobald W. et al. Hot surface ionic line emission and cold K-inner shell emission from petawatt-laser-irradiated Cu foil targets. Phys. Plasmas. 13, 043102 (2006). [Google Scholar]
  19. Johzaki T. et al. Pre-plasma effects on core heating and enhancing heating efficiency by extended double cone for FIREX. Nucl. Fusion 51, 073022 (2011). [Google Scholar]
  20. Bartal T. et al. Focusing of short-pulse high-intensity laser-accelerated proton beams. Nat. Phys. 8, 139–142 (2011). [Google Scholar]
  21. Robinson A. et al. Theory of fast electron transport for fast ignition. Nucl. Fusion 54, 054003 (2014). [Google Scholar]
  22. Norreys P. et al. Fast electron energy transport in solid density and compressed plasma. Nucl. Fusion 54, 054004 (2014). [Google Scholar]
  23. Kemp A. et al. Laserplasma interactions for fast ignition. Nucl. Fusion 54, 054002 (2014). [Google Scholar]
  24. Ryutov D. et al. Similarity criteria for the laboratory simulation of supernova hydrodynamics. Astrophys. J. 518, 821–832 (1999). [Google Scholar]
  25. Remington B., Drake R. & Ryutov D. Experimental astrophysics with high power lasers and Z pinches. Rev. Mod. Phys. 78, 755–807 (2006). [Google Scholar]
  26. Kugland N. L. et al. Self-organized electromagnetic field structures in laser-produced counter-streaming plasmas. Nat. Phys. 8, 809–812 (2012). [Google Scholar]
  27. Wilks S. C. et al. Energetic proton generation in ultra-intense lasersolid interactions. Phys. Plasmas 8, 542 (2001). [Google Scholar]
  28. Barty C. et al. An overview of LLNL high-energy short-pulse technology for advanced radiography of laser fusion experiments. Nucl. Fusion 44, S266–S275 (2004). [Google Scholar]
  29. Zylstra A. B. et al. Using high-intensity laser-generated energetic protons to radiograph directly driven implosions. Rev. Sci. Instrum. 83, 013511 (2012). [DOI] [PubMed] [Google Scholar]
  30. Nakamura T. et al. High-power γ-ray flash generation in ultraintense laser-plasma interactions. Phys. Rev. Lett. 108, 195001 (2012). [DOI] [PubMed] [Google Scholar]
  31. Norreys P. A. et al. Efficient extreme UV harmonics generated from picosecond laser pulse interactions with solid targets. Phys. Rev. Lett. 76, 1832–1835 (1996). [DOI] [PubMed] [Google Scholar]
  32. Gibbon P. Short Pulse Laser Interactions with Matter Imperial College Press (2005). [Google Scholar]
  33. Gordienko S., Pukhov A., Shorokhov O. & Baeva T. Coherent focusing of high harmonics: a new way towards the extreme intensities. Phys. Rev. Lett. 94, 103903 (2005). [DOI] [PubMed] [Google Scholar]
  34. Dollar F. et al. Scaling high-order harmonic generation from laser-solid interactions to ultrahigh intensity. Phys. Rev. Lett. 110, 175002 (2013). [DOI] [PubMed] [Google Scholar]
  35. Brunel F. Not-so-resonant, resonant absorption. Phys. Rev. Lett. 59, (1987). [DOI] [PubMed] [Google Scholar]
  36. Kruer W. L. & Estabrook K. JB heating by very intense laser light. Phys. Fluids 28, 430 (1985). [Google Scholar]
  37. Naumova N. et al. Hole boring in a DT pellet and fast-ion ignition with ultraintense laser pulses. Phys. Rev. Lett. 102, 1–4 (2009). [DOI] [PubMed] [Google Scholar]
  38. Kemp A., Sentoku Y. & Tabak M. Hot-electron energy coupling in ultraintense laser-matter interaction. Phys. Rev. Lett. 101, 8–11 (2008). [DOI] [PubMed] [Google Scholar]
  39. May J. et al. Mechanism of generating fast electrons by an intense laser at a steep overdense interface. Phys. Rev. E. 84, 025401 (2011). [DOI] [PubMed] [Google Scholar]
  40. Taub A. H. Relativistic Rankine-Hugoniot equations. Phys. Rev. 74, 1–7 (1948). [Google Scholar]
  41. de Hoffmann F. & Teller E. Magneto-hydrodynamic shocks. Phys. Rev. 80, 692–703 (1950). [Google Scholar]
  42. Wilks S. C., Kruer W. L., Tabak M. & Langdon A. B. Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1386 (1992). [DOI] [PubMed] [Google Scholar]
  43. Haines M., Wei M., Beg F. & Stephens R. Hot-electron temperature and laser-light absorption in fast ignition. Phys. Rev. Lett. 102, 1–4 (2009). [DOI] [PubMed] [Google Scholar]
  44. Ping Y. et al. Absorption of short laser pulses on solid targets in the ultrarelativistic regime. Phys. Rev. Lett. 100, 6–9 (2008). [DOI] [PubMed] [Google Scholar]
  45. Robinson A. P. L. et al. Relativistically correct hole-boring and ion acceleration by circularly polarized laser pulses. Plasma Phys. Controlled Fusion 51, 024004 (2009). [Google Scholar]
  46. Gibbon P., Andreev A. A. & Platonov K. Y. A kinematic model of relativistic laser absorption in an overdense plasma. Plasma Phys. Controlled Fusion 54, 045001 (2012). [Google Scholar]
  47. Kemp A. & Divol L. Interaction physics of multipicosecond petawatt laser pulses with overdense plasma. Phys. Rev. Lett. 109, 195005 (2012). [DOI] [PubMed] [Google Scholar]
  48. Levy M. C., Wilks S. C., Tabak M. & Baring M. G. Conservation laws and conversion efficiency in ultraintense laser-overdense plasma interactions. Phys. Plasmas 20, 103101 (2013). [Google Scholar]
  49. Davies J. R. Laser absorption by overdense plasmas in the relativistic regime. Plasma Phys. Controlled Fusion 51, 014006 (2009). [Google Scholar]
  50. Zhao Z. et al. Acceleration and guiding of fast electrons by a nanobrush target. Phys. Plasmas 17, 123108 (2010). [Google Scholar]
  51. Jiang S., Krygier A. G., Schumacher D. W., Akli K. U. & Freeman R. R. Effects of front-surface target structures on properties of relativistic laser-plasma electrons. Phys. Rev. E 89, 013106 (2014). [DOI] [PubMed] [Google Scholar]
  52. Purvis M. A. et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nat. Photonics 7, 796–800 (2013). [Google Scholar]
  53. Sgattoni A., Londrillo P., Macchi A. & Passoni M. Laser ion acceleration using a solid target coupled with a low-density layer. Phys. Rev. E 85, 1–9 (2012). [DOI] [PubMed] [Google Scholar]
  54. Sarri G. et al. Table-Top laser-based source of femtosecond, collimated, ultrarelativistic positron beams. Phys. Rev. Lett. 110, 255002 (2013). [DOI] [PubMed] [Google Scholar]
  55. Cattani F., Kim A., Anderson D. & Lisak M. Threshold of induced transparency in the relativistic interaction of an electromagnetic wave with overdense plasmas. Phys. Rev. E. Stat. Phys. Plasmas. Fluids. Relat. Interdiscip. Topics. 62, 1234–1237 (2000). [DOI] [PubMed] [Google Scholar]
  56. Denavit J. Absorption of high-intensity subpicosecond lasers on solid density targets. Phys. Rev. Lett. 69, (1992). [DOI] [PubMed] [Google Scholar]
  57. Kluge T. et al. Electron temperature scaling in laser interaction with solids. Phys. Rev. Lett. 107, 205003 (2011). [DOI] [PubMed] [Google Scholar]
  58. Mehrotra S. On the implementation of a primal-dual interior point method. SIAM J. Optimization 2, 575–601 (1992). [Google Scholar]
  59. Collins G. E. Quantifier elimination for Real Closed Fields by Cylindrical Algebraic Decomposition Vol. 33. Lecture Notes in Computer ScienceSpringer (1975). [Google Scholar]
  60. Schlegel T. et al. Relativistic laser piston model: Ponderomotive ion acceleration in dense plasmas using ultraintense laser pulses. Phys. Plasmas 16, 083103 (2009). [Google Scholar]
  61. ELI - extreme light infrastructure, http://www.eli-beams.eu/ (2014).
  62. Gates B. & Gates M. Annual Letter http://www.gatesfoundation.org/Who-We-Are/Resources-and-Media/Annual-Letters-List/Annual-Letter-2013 (2013). [Google Scholar]
  63. Liang E., Wilks S. C. & Tabak M. Pair production by ultraintense lasers. Phys. Rev. Lett. 81, 4887–4890 (1998). [Google Scholar]
  64. Chen H. et al. Relativistic positron creation using ultraintense short pulse lasers. Phys. Rev. Lett. 102, 1–4 (2009). [DOI] [PubMed] [Google Scholar]
  65. Fisch N. J. & Rax J. Free energy in plasmas under wave-induced diffusion. Phys. Fluids B 5, 1754–1759 (1993). [Google Scholar]
  66. Levy M. C., Wilks S. C., Tabak M. & Baring M. G. Hot electron divergence in the kinematic analysis of relativistic light on solids. J. Phys.: Conf. Series (2014). [Google Scholar]
  67. Esarey E., Ride S. & Sprangle P. Nonlinear Thomson scattering of intense laser pulses from beams and plasmas. Phys. Rev. E 48, 3003–3021 (1993). [DOI] [PubMed] [Google Scholar]

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES