Abstract
Purpose.
This study investigates the relationship between intraocular pressure (IOP) and retinal hemodynamics and predicts how arterial blood pressure (BP) and blood flow autoregulation (AR) influence this relationship.
Methods.
A mathematical model is developed to simulate blood flow in the central retinal vessels and retinal microvasculature as current flowing through a network of resistances and capacitances. Variable resistances describe active and passive diameter changes due to AR and IOP. The model is validated by using clinically measured values of retinal blood flow and velocity. The model simulations for six theoretical patients with high, normal, and low BP (HBP-, NBP-, LBP-) and functional or absent AR (-wAR, -woAR) are compared with clinical data.
Results.
The model predicts that NBPwAR and HBPwAR patients can regulate retinal blood flow (RBF) as IOP varies between 15 and 23 mm Hg and between 23 and 29 mm Hg, respectively, whereas LBPwAR patients do not adequately regulate blood flow if IOP is 15 mm Hg or higher. Hemodynamic alterations would be noticeable only if IOP changes occur outside of the regulating range, which, most importantly, depend on BP. The model predictions are consistent with clinical data for IOP reduction via surgery and medications and for cases of induced IOP elevation.
Conclusions.
The theoretical model results suggest that the ability of IOP to induce noticeable changes in retinal hemodynamics depends on the levels of BP and AR of the individual. These predictions might help to explain the inconsistencies found in the clinical literature concerning the relationship between IOP and retinal hemodynamics.
Keywords: intraocular pressure, retina, blood flow, mathematical model, autoregulation
A mathematical model is introduced to describe and quantify the effects of intraocular pressure (IOP), blood pressure (BP), and blood flow autoregulation (AR) on retinal hemodynamics. IOP alterations are predicted to induce noticeable hemodynamic changes only for certain levels of BP and AR.
Introduction
Alterations in retinal and retrobulbar hemodynamics are associated with many ocular and systemic diseases, including glaucoma,1–3 age-related macular degeneration (AMD),4,5 and diabetes.5,6 Because the retinal vasculature is in direct contact with the intraocular pressure (IOP), it seems very likely that IOP has an impact on retinal blood flow and velocity. However, clinical evidence of such an impact is not unanimous. Several clinical studies showed a decrease in retinal and retrobulbar blood flow and velocity when IOP was increased,7–14 whereas other studies did not find any significant changes in retinal and retrobulbar hemodynamics with changes in IOP.15–27
Most of the hemodynamic measurements obtained after trabeculectomy provide evidence of increased blood velocity as a result of lowering IOP.9,13,14 Galassi et al.9 found that, following trabeculectomy, end-diastolic velocity (EDV) was increased and resistive index (RI) was decreased in the ophthalmic artery (OA), central retinal artery (CRA), and short posterior ciliary arteries (SPCAs). Similarly, Trible et al.14 found sustained increases in mean flow velocity (MFV) and EDV and decreases in RI in the CRA and SPCAs after trabeculectomy. Synder et al.13 demonstrated an increase in blood velocity in the posterior ciliary arteries in the 18 trabeculectomy cases they investigated. However, Cantor17 found that despite a mean IOP reduction of 17.1 mm Hg, 15.5 mm Hg, and 15.1 mm Hg at 3, 6, and 12 months after trabeculectomy, respectively, the 17 glaucoma patients evaluated in the study did not show any significant change in ocular hemodynamic parameters.
The effects of IOP-lowering topical medications (such as prostaglandin analogues, carbonic anhydrase inhibitors, and beta blockers) on retrobulbar hemodynamics also have been assessed. Some studies found slightly increased retrobulbar circulation in patients on these medications,7,11,12 whereas most of the studies found that treatment with topical medications did not have a significant effect on retrobulbar hemodynamics.15,16,19–23,25–27
Only a few studies have been conducted to evaluate the effect of IOP elevations on ocular hemodynamics, and these also have provided variable results. Harris et al.10 used suction ophthalmodynamometry to increase IOP from a baseline average value of 14 mm Hg to 45 mm Hg in 11 healthy subjects. In the CRA, peak systolic velocity (PSV) and EDV decreased and the RI increased in steady progression as IOP was acutely elevated, while no changes occurred in the OA. Findl et al.8 found that increased IOP (+10, +20 mm Hg via suction cup) led to decreased blood velocities (as measured by Doppler sonography) in the CRA in 10 healthy volunteers, but no changes in the OA. However, Conway et al.18 used suction with laser in situ keratomileusis (IOP was elevated above 85 mm Hg for 90 seconds) in 10 healthy subjects and no hemodynamic changes were found after releasing the suction (as measured by Color Doppler Imaging [CDI], Heidelberg Retinal Flowmeter, and ocular blood-flow analyzer).
In summary, clinical evidence for the relationship between changes in IOP and consequent changes in retinal and retrobulbar hemodynamics is inconsistent and therefore difficult to interpret. However, the inconsistent results are likely due to the numerous factors, including arterial blood pressure (BP)2,28–32 and blood flow autoregulation (AR),2,33–35 that influence the relationship between IOP and ocular hemodynamics, and the intrinsic difficulty of evaluating the individual contribution of these factors in a clinical setting.
Mathematical modeling can be used to investigate the complex relationship between IOP and retinal and retrobulbar hemodynamics by assessing the mechanical action of IOP on clinically measurable hemodynamic quantities, such as total retinal blood flow and CRA blood velocity.36,37 Over the past 2 decades, theoretical models have been used to study stress and strain distributions induced by IOP elevation in ocular tissues,38–56 most importantly in the lamina cribrosa, although these models did not consider blood supply to the tissue. Theoretical models also have been used to assess the arteriovenous distribution of hemodynamic parameters in the retinal microvasculature,57–60 but they did not consider the biomechanical response of the retinal vasculature to IOP. Recently, Arciero et al.61 used a theoretical model to study the retinal microcirculation and predict the relative importance of regulatory mechanisms in achieving blood flow autoregulation, but the model did not incorporate the effects of the hemodynamics in the central retinal vessels. Guidoboni et al.62 used a theoretical model to study the effects of IOP elevation on CRA hemodynamics, but the model was not linked to the blood circulation in the retinal microvasculature.
The current study introduces the first mathematical model that simultaneously accounts for blood flow in the central retinal vessels, blood flow in the retinal microvasculature, retinal blood flow autoregulation, biomechanical action of IOP on the retinal vasculature, and time-dependent arterial BP . The model uses a hydraulic analogy to Ohm's law in which blood flow in the central retinal vessels and retinal microvasculature is analogous to the current flowing through a network of resistances and capacitances. Variable resistances describe active and passive diameter changes due to blood flow AR and IOP, and systemic arterial BP is an input to the model. Model outputs include total retinal blood flow and blood velocity in the CRA, central retinal vein (CRV), and microvasculature, thereby allowing for direct comparison between model predictions and clinically measurable quantities. The main goal of the present study is to use this mathematical model to interpret the inconsistent clinical observations concerning the relationship between IOP and retinal and retrobulbar hemodynamics.
Methods
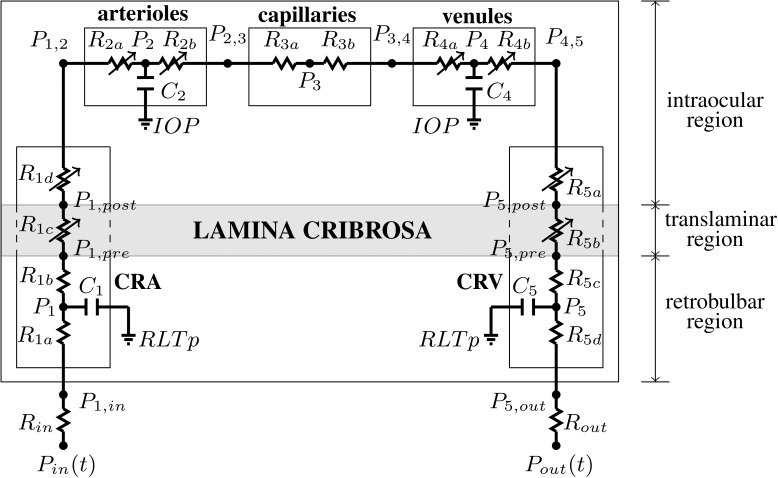
The retinal vasculature is represented by the model depicted in Figure 1. The vasculature is divided into five main compartments: the CRA, arterioles, capillaries, venules, and the CRV. Using the analogy between hydraulic and electrical circuits, blood flow is modeled as current flowing through a network of resistors (R), representing the resistance to flow offered by blood vessels, and capacitors (C), representing the ability of blood vessels to deform and store blood volume. Resistors and capacitors have been labeled with numbers from 1 to 5 to distinguish between compartments, and additional alphabetic labels are used to distinguish between segments within the same compartment. For example, the CRA compartment is referenced by the label 1 and it includes a retrobulbar segment with resistances R1a and R1b, a translaminar segment with resistance R1c, and an intraocular segment with resistance R1d. We remark that the resistance of the retrobulbar segment has been split into R1a and R1b so that the capacitance C1 acts on the mean retrobulbar pressure, P1. The blood flow through the retinal vascular network is driven by Pin and Pout, which represent the BPs upstream of the CRA and downstream of the CRV, respectively.
Figure 1.
Network model for the retinal vasculature. The vasculature is divided into five main compartments: the CRA, arterioles, capillaries, venules, and the CRV. Each compartment includes resistances (R) and capacitances (C). The intraocular segments are exposed to the IOP, the retrobulbar segments are exposed to the RLTp, and the translaminar segments are exposed to an external pressure that depends on the internal state of stress within the lamina cribrosa (gray shaded area). Diameters of venules and intraocular and translaminar segments of the CRA and CRV are assumed to vary passively with IOP, whereas arterioles are assumed to be vasoactive.
The vascular segments are exposed to various external pressures depending on their position in the network. The intraocular segments are exposed to the IOP, the retrobulbar segments are exposed to the retrolaminar tissue pressure (RLTp), and the translaminar segments are exposed to an external pressure that depends on the internal state of stress within the lamina cribrosa. The IOP-induced stress within the lamina cribrosa is computed by using a nonlinear elastic model described in the Appendix.
The resistances of the venules and intraocular and translaminar segments of the CRA and CRV are assumed to vary passively with IOP, as detailed in the Appendix. The resistance of arterioles is assumed to vary actively to achieve a relatively constant blood flow despite changes in the ocular perfusion pressure (OPP), defined as OPP = 2/3 MAP – IOP, where MAP is the mean arterial pressure at the level of the brachial artery (MAP = 2/3 DP + 1/3 SP), and DP and SP are diastolic and systolic arterial BPs, respectively. Arrows have been used in Figure 1 to indicate all resistances that can vary, either passively or actively.
Governing Equations
Ohm's law states that the flow Q through a resistor is directly proportional to the pressure drop ΔP across the resistor, with a proportionality constant equal to the reciprocal of the resistance, namely Q = ΔP/R. The flow Q through a capacitor is directly proportional to the time derivative of the pressure drop across the capacitor, with a proportionality constant equal to the capacitance, namely Q = C d(ΔP)/dt. Kirchoff's law guarantees the conservation of mass in the system, which means that at every network node the following relationship must hold: volume change = flow in – flow out. The application of Kirchoff's law to the retinal vascular network shown in Figure 1 leads to the following system of ordinary differential equations for the pressures (P):
 |
The inlet and outlet pressures Pin and Pout vary with time along a cardiac cycle and, consequently, the pressures calculated via Equation 1 are time dependent.
Control Values of Flow Rate, Resistances, Pressures, and Capacitances
A control state for the system is defined to represent typical conditions of a healthy eye. Control values of any given quantity will be indicated with an overline bar.
External and Systemic Pressures.
We assume that, for a healthy individual,
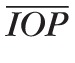 = 15 mm Hg,63–65
= 15 mm Hg,63–65
 p = 7 mm Hg,66,67
p = 7 mm Hg,66,67
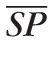 = 120 mm Hg, and
= 120 mm Hg, and
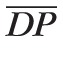 = 80 mm Hg.
= 80 mm Hg.
Retinal Blood Flow.
The control value Q̄ of the retinal blood flow can be estimated by applying Poiseuille's law to the CRA, since the CRA is the only vessel supplying blood to the retinal vascular network. In the hypotheses of laminar flow and cylindrical geometry, Poiseuille's law yields Q̄ = πV̄cra,max
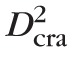 /8, where
/8, where
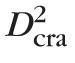 is the CRA diameter, and V̄cra,max is the average value of the CRA centerline velocity over a cardiac cycle. Measurements from human patients are used to define the control state values for
is the CRA diameter, and V̄cra,max is the average value of the CRA centerline velocity over a cardiac cycle. Measurements from human patients are used to define the control state values for
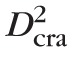 = 175 μm,68 and = 5.67 cm/s,10,68 which yield a physiological value of Q̄ = 6.8178 10−4 mL/s.68–72
= 175 μm,68 and = 5.67 cm/s,10,68 which yield a physiological value of Q̄ = 6.8178 10−4 mL/s.68–72
Resistances.
According to Poiseuille's law, the resistance of a vessel is R = 128 μL/πD4, where D and L are vessel diameter and length and μ is the blood viscosity. Using this law and the data reported in Table 1, the control values of the CRA and CRV resistances are computed and summarized in Table 2. Determining the control values of arteriolar, capillary, and venular resistances is more complex, because these compartments include a hierarchy of numerous vessels of various diameter. We adopt the dichotomous network (DN) model for the retinal microcirculation proposed by Takahashi et al.60 to describe the hierarchical architecture of arterioles, capillaries, and venules and compute their resistances. The DN model includes 14 levels of arterioles, 1 level of capillaries, and 14 levels of venules; each level includes a specific number of parallel vessels. In our model framework, we divided these 29 vascular levels into the corresponding model compartments according to vessel size. All the vessels with diameter less than 6.5 μm were defined as capillaries, as shown in Figure 2. Vessel number, diameter, length, and blood viscosity for the 29 levels in the DN model are reported in Takahashi et al.,60 and the corresponding values of the lumped resistances used in the current model are summarized in Table 2. It is important to note that the viscosity values used in the model are effective viscosity values that are based on an empirical relationship and depend on vessel diameter. In this way, the model takes into account the corpuscular nature of blood. Rin and Rout incorporate the vasculature upstream of the CRA and downstream of the CRV. Their control values are determined by the control value Q̄ of the total retinal blood flow and the control values of pressures P̄in, P̄1,in, and P̄out, P̄5,out (defined below).
Table 1.
Geometric and Physical Parameters for the CRA and CRV
|
Parameters |
CRA |
CRV |
||
|
Value |
Source |
Value |
Source |
|
| Diameter D, μm | 175 | Dorner et al.68 | 238 | Takahashi et al.60* |
| Length L, mm, total | 10 | Harris et al.92 | 10 | Harris et al.92 |
| Segment a | 4.4 | Harris et al.92 | 1 | Lee et al.93 |
| Segment b | 4.4 | Harris et al.92 | 0.2 | Jonas et al.94 |
| Ren et al.95 | ||||
| Segment c | 0.2 | Jonas and Holbach94 | 4.4 | Harris et al.92 |
| Ren et al.95 | ||||
| Segment d | 1 | Lee et al.93 | 4.4 | Harris et al.92 |
| Blood viscosity μ, cP | 3.0 | Fung96 | 3.24 | Takahashi et al.60† |
| Quarteroni et al.97 | ||||
| Wall Young's Modulus E, MPa | 0.3 | Armentano et al.98 | 0.6 | Deng and Guidoin100 |
| Fung99 | ||||
| Quarteroni et al.97 | ||||
| Wall Poission's ratio ν, 1 | 0.49 | Armentano et al.98 | 0.49 | ‡ |
| Fung99 | ||||
| Quarteroni et al.97 | ||||
| Wall thickness h, μm | 39.7 | Baleanu et al.101 | 10.7 | Wetterer et al.102 |
CRA/CRV diameter ratio is assumed to be the same as that for the first generation arteries/veins in the model by Takahashi et al.60
Blood viscosity in the CRV is assumed to be 8% larger than that in the CRA as in the model by Takahashi et al.60
Poisson's ratio of the CRV wall is assumed to be the same as that for the CRA wall.
Table 2.
Computed Values of the Vascular Resistances at the Control State
|
Resistance |
Value, mm Hg s/mL |
Resistance |
Value, mm Hg s/mL |
| R̄in | 2.25 · 104 | R̄3b | 5.68 · 103 |
| R̄1a | 4.30 · 103 | R̄4a | 3.11 · 103 |
| R̄1b | 4.30 · 103 | R̄4b | 3.11 · 103 |
| R̄1c | 1.96 · 102 | R̄5a | 3.08 · 103 |
| R̄1d | 9.78 · 102 | R̄5b | 6.15 · 103 |
| R̄2a | 6.00 · 103 | R̄5c | 1.35 · 103 |
| R̄2b | 6.00 · 103 | R̄5d | 1.35 · 103 |
| R̄3a | 5.68 · 103 | R̄out | 5.74 · 103 |
Figure 2.

Relationship between the DN model by Takahashi et al.60 and the chosen geometry of our model. The 29 vascular levels of the DN model have been divided into three model compartments for arterioles, capillaries, and venules according to vessel size.
Pressures.
The control value of the input pressure is chosen to be two-thirds of the MAP measured at the level of the brachial artery, where the factor two-thirds accounts for the distance from the brachial artery to the eye.73 Because
 = 120 mm Hg and
= 120 mm Hg and
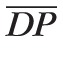 = 80 mm Hg, it follows that P̄in = 62.2 mm Hg, as reported in Table 3. The control pressure between arterioles and capillaries, P̄2,3, is set at 32 mm Hg.61,74 The control pressures at all the other nodes of the network are computed using Ohm's law and the previously computed control values of the resistances, namely P̄i = P̄j − R̄i,j
Q̄, where the subscripts i and j indicate any two consecutive nodes and R̄i,j indicates the resistance between them. The control value of the outlet pressure is chosen to be P̄out = 14 mm Hg, so that it is less than P̄5,out and higher than the jugular venous pressure (normally between 4 and 6 mm Hg75). All control pressures are summarized in Table 3.
= 80 mm Hg, it follows that P̄in = 62.2 mm Hg, as reported in Table 3. The control pressure between arterioles and capillaries, P̄2,3, is set at 32 mm Hg.61,74 The control pressures at all the other nodes of the network are computed using Ohm's law and the previously computed control values of the resistances, namely P̄i = P̄j − R̄i,j
Q̄, where the subscripts i and j indicate any two consecutive nodes and R̄i,j indicates the resistance between them. The control value of the outlet pressure is chosen to be P̄out = 14 mm Hg, so that it is less than P̄5,out and higher than the jugular venous pressure (normally between 4 and 6 mm Hg75). All control pressures are summarized in Table 3.
Table 3.
Computed Values of Intraluminal BPs at the Control State
|
Pressure |
Value, mm Hg |
Pressure |
Value, mm Hg |
| P̄in | 62.22 | P̄3,4 | 24.25 |
| P̄1,in | 46.85 | P̄4 | 22.13 |
| P̄1 | 43.92 | P̄4,5 | 20.01 |
| P̄1,pre | 40.99 | P̄5,post | 19.80 |
| P̄1,post | 40.85 | P̄5,pre | 19.76 |
| P̄1,2 | 40.19 | P̄5 | 18.84 |
| P̄2 | 36.09 | P̄5,out | 17.92 |
| P̄2,3 | 32.00* | P̄out | 14.00 |
| P̄3 | 28.13 |
Capacitances.
The capacitance of a fluid compartment represents its ability to store fluid volume for a given difference between the pressure inside and outside the compartment. The capacitance of vascular compartments can be computed as the product of vascular volume (Vol) and distensibility (Dist).76 The control values of the CRA and CRV volumes are computed as
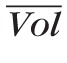 cra = π
cra = π
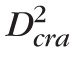 Lcra/4 and
Lcra/4 and
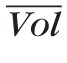 crv = π
crv = π
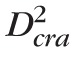 Lcrv/4. Analogously, the control values of the volumes of arterioles, capillaries, and venules are computed by using the level architecture and data reported by Takahashi et al.60 The distensibilities of the CRA and the retinal arterioles are assumed to be equal to those of the cerebral arteries,76 namely Distcra = Dist2 = 34.12 · 10−4 mm Hg−1. Following the work by Lakin et al.,76 the distensibilities of retinal venules and the CRV are assumed to be eight times larger than those of the arteries, namely Distcrv = Dist4 = 27.30 · 10−3 mm Hg−1. The control volumes and capacitances are reported in Table 4.
Lcrv/4. Analogously, the control values of the volumes of arterioles, capillaries, and venules are computed by using the level architecture and data reported by Takahashi et al.60 The distensibilities of the CRA and the retinal arterioles are assumed to be equal to those of the cerebral arteries,76 namely Distcra = Dist2 = 34.12 · 10−4 mm Hg−1. Following the work by Lakin et al.,76 the distensibilities of retinal venules and the CRV are assumed to be eight times larger than those of the arteries, namely Distcrv = Dist4 = 27.30 · 10−3 mm Hg−1. The control volumes and capacitances are reported in Table 4.
Table 4.
Computed Values of Volumes and Capacitances at the Control State
|
Segment |
Volume, mL |
CapacitanceC, mL/mm Hg |
| CRA | 2.12 · 10−4 | 7.22 · 10−7 |
| Arterioles | 2.20 · 10−4 | 7.53 · 10−7 |
| Venules | 6.12 · 10−4 | 1.67 · 10−5 |
| CRV | 3.92 · 10−4 | 1.07 · 10−5 |
Time-Profiles of the Input and Output Pressure Waves
The time profile of Pin and Pout at the control state are determined through an inverse problem based on CDI measurements of blood velocity in the CRA and CRV, as shown in Figure 3a. The centerline blood velocity V(t) in the CRA and CRV is given by V(t) = 8Q(t)/πD2, where Q(t) = ΔP(t)/R(t) and ΔP(t) is the pressure drop across the resistor. Thus, Equation 1 can be used to determine the time profiles Pin(t) and Pout(t) that give the CRA blood velocity profiles shown in Figure 3b when the system is at its control state. The control profiles of P̄in(t) and P̄out(t) are shown in Figure 3c, and their mean values are P̄in = 62.2 mm Hg and P̄out = 14 mm Hg. At the control state, the maximum and minimum values of P̄in(t) are P̄in,max = 92.2 mm Hg and P̄in,min = 39.6 mm Hg, and their ratios with respect to
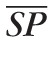 and
and
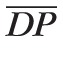 are P̄in,max/
are P̄in,max/
 = 0.7683 and P̄in,min /
= 0.7683 and P̄in,min /
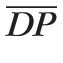 = 0.4945. These ratios are used to scale the Pin(t) profile in the simulations of clinical conditions where SP and DP are different from their control state values.
= 0.4945. These ratios are used to scale the Pin(t) profile in the simulations of clinical conditions where SP and DP are different from their control state values.
Figure 3.
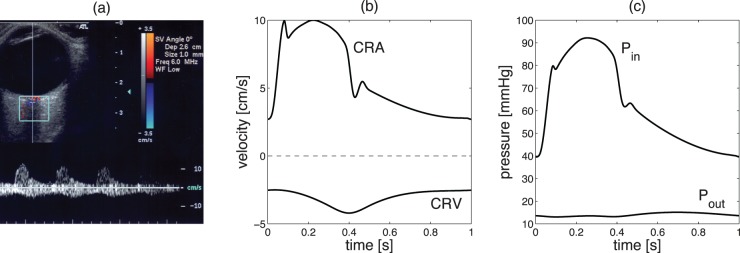
(a) Typical CDI measurement of the blood velocity in the CRA and CRV. (b) Time profiles of the blood velocity in the CRA and CRV at the control state. (c) Time profile of the inlet and outlet pressures P̄in(t) and P̄out(t) at the control state.
Results
In this study, Matlab (MathWorks, Natick, MA, USA) is used to solve Equation 1 for six different cases corresponding to different clinical conditions. Specifically, the six cases represent patients with high, normal, and low arterial BP (HBP-, NBP-, LBP-), with functional or absent blood flow autoregulation (-wAR, -woAR), as summarized in Table 5. Systolic/diastolic arterial BPs for cases HBP-, NBP-, and LBP- are assumed to be 140/90 mm Hg, 120/80 mm Hg, and 100/70 mm Hg, respectively. Functional AR is simulated by allowing arteriolar resistances R2a and R2b to vary according to Equation 4 in the Appendix. To simulate the absence of autoregulation, arteriolar resistances R2a and R2b do not change and are set equal to their control values R̄2a and R̄2b.
Table 5.
Representative Cases for Model Simulations
|
Case |
Description |
| HBP- | Systolic/diastolic blood pressure = 140/90 mm Hg |
| NBP- | Systolic/diastolic blood pressure = 120/80 mm Hg |
| LBP- | Systolic/diastolic blood pressure = 100/70 mm Hg |
| -wAR | Variable arteriolar resistances, see Equation 4 in Appendix |
| -woAR | Fixed arteriolar resistances, kept at control values |
The cases represent individuals with NBP-, HBP-, or LBP-, and with -wAR or -woAR.
Model Validation
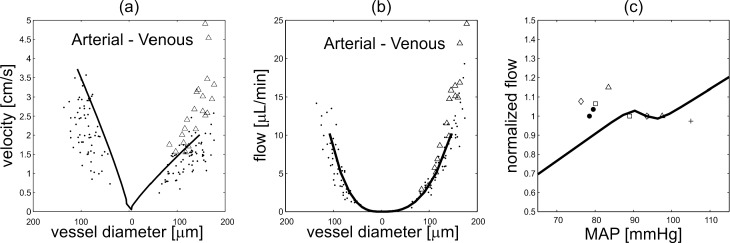
The model-predicted mean values of blood velocity and flow along the retinal vascular network obtained for the NBPwAR case, representing a normal clinical condition, are compared in Figures 4a and 4b with measurements obtained by Garcia et al.77 and Riva et al.78 using bidirectional laser Doppler velocimetry in healthy individuals. The pressures at each node of the network are computed from Equation 1 and then velocity and flow in arterioles, capillaries, and venules are determined assuming the network architecture proposed by Takahashi et al.60 The model-predicted values of total retinal blood flow for IOP = 15 mm Hg and MAP between 65 and 115 mm Hg are compared with data measured by Dumskyj et al.,69 Feke and Pasquale,70 Feke et al.,71 and Harris et al.63 in Figure 4c. The model-predicted values are normalized with respect to the control state, and the measured data are normalized with respect to their reported baseline value.
Figure 4.
(a) Comparison of model predicted values (solid line) of blood velocity with measured data (open triangles,77 black dots78) for vessels of various diameter. (b) Comparison of model predicted values (solid line) of volumetric blood flow with measured data (open triangles,77 black dots78) for vessels of various diameter. (c) Comparison of model values (solid line) of normalized total retinal blood flow with measured data (black dots,69 open triangles,70 open squares,70 open diamonds,71 plusses63) for various MAPs. In all model simulations, IOP = 15 mm Hg.
Theoretical Investigations
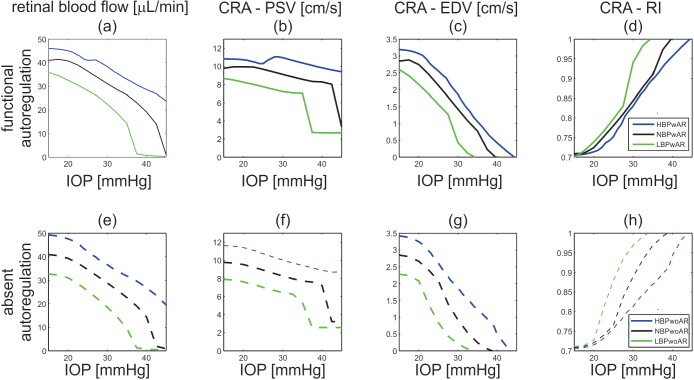
The mathematical model is used to investigate the effects of BP and blood flow AR on the IOP-induced hemodynamic changes in total retinal blood flow, CRA blood velocity, and intraluminal BP along the retinal vasculature. The model predictions for total retinal blood flow, computed as the time-average of Q(t) over a cardiac cycle, PSV, EDV, and RI in the CRA are compared for cases NBPwAR, NBPwoAR, HBPwAR, HBPwoAR, LBPwAR, and LBPwoAR in Figure 5.
Figure 5.
Model predicted values of total retinal blood flow; peak systolic velocity in the central retinal artery (CRA − PSV); end diastolic velocity in the CRA (CRA − EDV); and resistivity index in the CRA (CRA − RI) as IOP varies between 15 and 40 mm Hg for theoretical patients with LBP-, NBP-, or HBP-, and -wAR or -woAR.
Figure 6 reports the IOP ranges for which the values of total retinal blood flow (Q), and PSV, EDV, and RI in the CRA are within ±5% of their control values, as predicted by the mathematical model for six theoretical patients. In the low BP cases (LBPwAR and LBwoAR), the values of Q, PSV, and EDV are never within 5% of their control values. The small (5%) change in blood flow is chosen as a rough threshold for quantifying the regime when AR is successful.
Figure 6.
Model-predicted ranges of IOP for which the values of total retinal blood flow (Q, black), PSV (blue), EDV (red), and RI (green) are within ±5% of their control state values for six theoretical patients with LBP-, NBP-, or HBP-, and –wAR or -woAR.
Total Retinal Blood Flow.
As shown in Figures 5 and 6, the model-predicted average blood flow over a cardiac cycle remains relatively constant for IOP between 15 and 23 mm Hg for NBPwAR individuals. In the HBPwAR case, relatively constant flow is predicted for IOP between 23 and 29 mm Hg. In the remaining cases, the model predicts a slight or nonexistent AR plateau for IOP between 15 and 45 mm Hg.
CRA Blood Velocity.
Although a monotone decrease in PSV and EDV with IOP elevation is predicted in most of the theoretical patients, Figures 5b and 5c show that the NBPwAR and HBPwAR cases exhibit a slight PSV increase for IOP within the regulating range, namely between 15 and 23 mm Hg for NBPwAR and between 23 and 29 mm Hg for HBPwAR. For all six cases, the model predicts an increase of the CRA resistivity index RI = (PSV − EDV)/PSV with IOP, as shown in Figures 5d and 5h. As shown in Figure 6, the range of IOP for which PSV is within 5% of its control values is significantly larger than the range for EDV, and the ranges do not overlap in the HBPwAR and HBPwoAR cases.
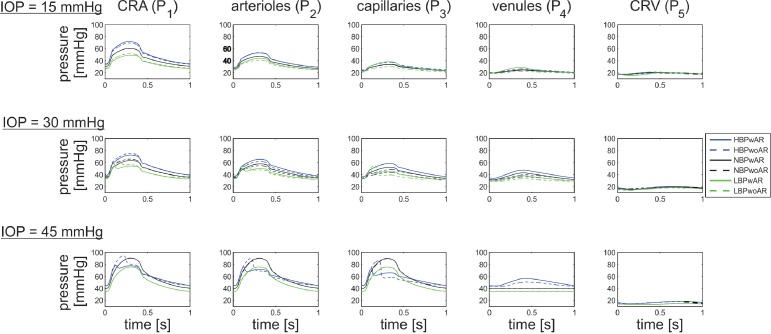
Intraluminal Blood Pressure.
The model-predicted values of BP in the five model compartments of the retinal vasculature for IOP equal to 15, 30, and 45 mm Hg are compared in Figure 7 for the six representative clinical cases described in Table 5. Pronounced changes in pressure are visible in the CRA, arterioles, capillaries, and venules with IOP elevation, while the pressure in the CRV remains relatively constant. As expected, when IOP is sufficiently high, the venules collapse. The degree to which the vessels collapse depends on the MAP of the individual. In particular, the model predicts that for an IOP = 45 mm Hg, the venules are collapsed to a lesser extent in HBP patients than in NBP and LBP patients.
Figure 7.
Model-predicted values of BP in CRA (P1), arterioles (P2), capillaries (P3), venules (P4), and CRV (P5) for IOP = 15, 30, and 45 mm Hg for six theoretical patients with HBP- (blue), NBP- (black), and LBP- (green), and -wAR (solid) or -woAR (dashed).
Clinical Data and Theoretical Predictions
The mathematical model is used to aid the interpretation of clinically measured hemodynamic responses to surgical IOP reduction in glaucoma patients and induced IOP elevation in healthy individuals.
Surgical IOP Reduction on Glaucoma Patients.
Galassi et al.9 and Trible et al.14 report an increase in CRA blood velocity and a decrease in RI following trabeculectomy (group [a] in Galassi et al.9 and Trible et al.14) and deep sclerectomy (group [b] in Galassi et al.9), as indicated by the changes (Δ) in MFV, PSV, EDV, and RI summarized in Table 6. Because the study by Trible et al.14 reports MAP values of 107 ± 14.7 mm Hg, we use HBP-model predictions that correspond to MAP = 106.7 mm Hg as a comparison with clinical data. Also, to be consistent with the data, model simulations assume that IOP = 30 mm Hg before surgery and IOP = 15 mm Hg after surgery. The model assumptions have been indicated with shaded boxes in Table 6. Model-predicted values of ΔMFV, ΔPSV, ΔEDV, and ΔRI for the HBPwoAR case and the trabeculectomy data reported by Trible et al.14 differ by only 0.3 cm/s, 0.38 cm/s, 0.58 cm/s, and 0.01 cm/s, respectively. The model predicted values of ΔEDV and ΔRI for the HBPwAR and HBPwoAR cases and the deep sclerectomy data reported by Galassi et al.9 (group [b]) also show the same qualitative trends.
Table 6.
Changes in PSV, EDV, RI, and MFV in the CRA as IOP Is Reduced by Trabeculectomy (Group [a] in Galassi et al.9 and Trible et al.14), Deep Sclerectomy (Group [b]) in Galassi et al.9) and Model Simulations
| Parameter |
Clinical Studies |
Mathematical Model |
|||
|
Study |
Galassi et al.9 Group (a) |
Galassi et al.9 Group (b) |
Trible et al.14 |
HBPwAR |
HBPwoAR |
| Preoperative IOP, mm Hg | 25.27 ± 6.24 | 24.05 ± 4.27 | 27.5 ± 8.8 | 30 | 30 |
| Postoperative IOP, mm Hg | 9.86 ± 2.10 | 10.79 ± 2.27 | 12.5 ± 10.5 | 15 | 15 |
| Preoperative MAP, mm Hg | — | — | 107 ± 14.7 | 106.7 | 106.7 |
| Postoperative MAP, mm Hg | — | — | 102.2 ± 11.5 | 106.7 | 106.7 |
| ΔMFV, cm/s | — | — | 1.4 | 1.0 | 1.7 |
| ΔPSV, cm/s | — | — | 1.2 | −0.13 | 1.58 |
| ΔEDV, cm/s | 0.40 | 0.47 | 0.96 | 1.33 | 1.54 |
| ΔRI, 1 | −0.06 | −0.05 | −0.12 | −0.13 | −0.11 |
Model assumptions are reported in boldface. Dashes indicate that the quantity was not reported in the article.
Induced IOP Elevation on Healthy Individuals.
The model-predicted values of PSV and EDV in the CRA for IOP between 15 and 45 mm Hg are compared with the clinical data by Harris et al.10 in Figure 8a. In the study by Harris et al., PSV and EDV measurements were performed at an intermediate location between the lamina cribrosa and the eye globe, corresponding to the intraocular CRA segment of our model. Because the study involved healthy individuals, the clinical data are compared with the NBP-model predictions. Figure 8A shows that the PSV values measured by Harris et al.10 and predicted by our model in the NBP- case fall precisely in the same range.
Figure 8.
(a) Comparison between PSV and EDV measured by Harris et al.10 in the CRA and the model-predicted values in the NBPwAR and NBPwoAR cases. (b) Comparison between the percent change in CRA mean flow velocity measured by Findl et al.8 and the model-predicted values in the NBPwAR and NBPwoAR cases.
The model-predicted values of percent change in the CRA mean flow velocity with IOP elevation are compared with the clinical data by Findl et al.8 in Figure 8b. In the study by Findl et al.,8 IOP was raised 20 mm Hg above baseline in two steps and then was reduced by 10 mm Hg before releasing the suction cup. Measurements were performed at approximately 3 mm behind the optic disc surface, corresponding to the retrobulbar CRA segment in our model. Findl et al.8 considered healthy individuals and therefore the clinical data are compared with the NBP- model predictions.
Discussion
The combination of multiple factors, including IOP, BP, and AR, plays a primary role in determining retinal and retrobulbar hemodynamics. It is widely recognized that IOP elevation poses a serious challenge to tissue perfusion, and several animal and human studies, in addition to the results of the theoretical model presented here, have suggested that arterial BP2,28–32 and blood flow AR2,33–35 are also important factors influencing blood flow. However, the difficulty of isolating and assessing the contributions of arterial BP and blood flow AR in vivo limits the current understanding of their effects on tissue perfusion as IOP varies.28 The current study introduces a mathematical model that can serve as a virtual laboratory where the contributions of arterial BP and blood flow AR can be isolated and their influence on the tissue susceptibility to IOP challenge can be predicted and assessed independently.
Model Validation
Every mathematical model is based on simplifying assumptions whose validity needs to be verified by comparing model predictions with data from independent experimental and clinical studies. Figure 4 shows that the model-predicted values of velocity and flow are consistent with clinical measurements.63,69–71,77,78 These measurements were used for comparison purposes only and were not used to estimate any of the model parameters listed in Tables 1, 4, 7, 8, and 9. It is important to note that many of the model parameters vary among individuals. In particular, many studies have shown that the geometric and mechanical properties of the lamina cribrosa and sclera undergo change with age,41,42 ethnicity,36,79 and disease,47,48 and these changes strongly affect the biomechanical response of the optic nerve head tissues to IOP alterations.50–56 The clinical studies63,69–71,77,78 used for model comparison did not report the parameter values for the geometric and mechanical properties of the lamina cribrosa and sclera, and therefore the model simulations were performed using the literature-based parameter choice reported in Tables 7 and 8. Future data on the geometric and structural properties of the retinal vessels collected from populations of a wide age range will help to improve on the current model predictions.
Table 7.
Radius and Thickness Values Used in the Mathematical Model for the Lamina Cribrosa and Sclera
Table 8.
Model Values of Young's Modulus Elc and Shear Modulus μlc for the Lamina Cribrosa as a Function of the Effective Stress σe, as in Newson and El-Sheikh105 and Woo et al.106
|
Elc, MPa |
μlc, MPa |
Range of σe, MPa |
| 0.358 | 0.12 | 0.008 > σe ≥ 0.000 |
| 0.656 | 0.22 | 0.015 > σe ≥ 0.008 |
| 1.818 | 0.61 | σe ≥ 0.015 |
Table 9.
Physical Parameters for the Arterioles and Venules
|
Parameter |
Arterioles |
Venules |
| Wall Young's Modulus E, MPa | 0.022 | 0.066 |
| Wall Poission's ratio ν, 1 | 0.49 | 0.49 |
| Wall-to-Lumen ratio | 0.23 | 0.05 |
Despite the simplified vascular architecture and the literature-based parameter choice, the model predictions of velocity and flow reported in Figure 4 are consistent with six independent clinical studies, providing evidence that our modeling choices are appropriate and physiologically reasonable.
Theoretical Investigations
The model simulations suggest that the hemodynamic response of the retinal vasculature to IOP variations noticeably differ among individuals with different BP and functionality of AR.
Total Retinal Blood Flow.
The model predicts that the AR plateau would shift toward higher IOP values as MAP increases, as shown in Figure 6. This is in agreement with the study by He et al.,30 who induced IOP elevations on Long-Evans rats with low, moderate, and high MAP levels and found that a higher IOP was needed to attenuate ocular blood flow in animals with higher MAP. The shift in the AR plateau also was predicted by the theoretical work of Arciero et al.,61 whose microcirculation model suggested that AR fails to operate over its expected range of arterial pressure if IOP is increased.
CRA Blood Velocity.
The model predicts that the blood flow velocity in the CRA does not always decrease with IOP elevation. Figures 5b and 5c show a slight increase in PSV in the range of IOP values for which AR is achieved, namely between 15 and 23 mm Hg for NBPwAR and between 23 and 29 mm Hg for HBPwAR.
These findings have important clinical implications. For example, the model suggests that a 10-mm Hg IOP reduction in an individual with normal BP and functional AR (NBPwAR) would result in a noticeable increase in PSV and EDV in the CRA blood velocity and a noticeable increase in total retinal blood flow if IOP is reduced from 40 to 30 mm Hg. However, only minimal hemodynamic changes are predicted if IOP is reduced from 25 to 15 mm Hg. These findings could help to explain why some studies9,13,14 report significant hemodynamic changes following trabeculectomy, whereas others do not.17,24 The model also suggests that IOP reductions of approximately 5 mm Hg would result in minor hemodynamic changes in all the cases considered here, which is consistent with clinical data related to topical medications.7,11,12,15,16,19–23,25–27 However, reductions in IOP greater than 5 mm Hg may have a more significant effect on retinal hemodynamics. The hypotensive effects of prostaglandin analogues, combination therapies, and surgical interventions may far exceed this threshold depending on the patient's IOP level before medical intervention.
Intraluminal Blood Pressure.
Intraluminal BP is the main driving force of local tissue perfusion and can be measured in retinal vessels by artificially increasing IOP using ophthalmodynamometry.80–83 However, the level of IOP may have an important impact on the intraluminal pressure in retinal vessels, which is uncovered by the mathematical model. The model predicts that increased IOP induces a significant increase in the intraluminal BP in all vascular compartments upstream of the CRV. This finding is consistent with the experimental observations by Glucksberg and Dunn84 and Attariwala et al.85 on live anesthetized cats. A hydraulic feedback mechanism could explain this phenomenon.84,85 Veins are more susceptible than arteries to IOP elevation, because veins have thinner walls and lower intraluminal pressure than arteries and, under extreme conditions, act like a Starling resistor and collapse. Thus, as IOP increases, resistance to flow increases in veins more than in arteries, leading to an overall increase in intraluminal pressure upstream of the veins.86,87 In addition, the model predicts that IOP elevation would affect intraluminal arterial pressure differently depending on whether blood flow AR is functional or absent. The study by Jonas83 supports this finding, as correlation coefficients between intraluminal BP measured via ophthalmodynamometry and systemic BP were found lower in eyes with retinal or orbital diseases than in the control group.
Clinical Data and Theoretical Predictions
A good qualitative and quantitative agreement in the hemodynamic response to IOP changes was found between clinical data and model predictions. This suggests that the mathematical model could be used to anticipate the hemodynamic outcome of clinical IOP modulation on specific patients.
Surgical IOP Reduction on Glaucoma Patients.
The clinical studies by Galassi et al.9 and Trible et al.14 suggest that clinically measurable changes in the retinal hemodynamic parameters occur in patients with elevated BP as IOP is reduced from 30 to 15 mm Hg. The theoretical analysis in the current study suggests that these changes are less pronounced in HBPwAR patients than in HBPwoAR patients, likely due to the compensatory mechanisms of autoregulation.88 However, the model also suggests that if a 15 mm Hg IOP reduction falls within the regulating range predicted for HBP patients, the consequent hemodynamic changes would be negligible. This might explain why the trabeculectomy study by Cantor17 did not observe any significant change in ocular blood flow parameters despite significant IOP reduction.
Induced IOP Elevation on Healthy Individuals.
The ability to autoregulate blood flow has a noticeable effect in individuals with normal BP experiencing induced IOP elevation. Figure 8a shows good agreement between clinical data and model predictions in the NBPwoAR case when IOP is increased. Blood velocity measurements were performed immediately after IOP elevation (ie, before AR took effect), explaining why the NBPwoAR model predictions match the data more closely than the NBPwAR predictions. Consistent with this interpretation, there is better agreement between the data and the NBPwAR case in Figure 8b, as the blood velocity measurements were performed at least 5 minutes after IOP elevation, leaving time for AR to exert its influence.
Limitations of the Present Model
In the model, the geometrical architecture of the retinal vasculature is reduced to five main compartments, which do not account for the three-dimensional spatial arrangements of the vessels. An extension of the model to more realistic geometries could help to uncover hemodynamic differences observed among nasal, temporal, superior, and inferior retinal quadrants.89 Currently, blood flow AR is modeled only phenomenologically as the ability of retinal arterioles to alter their resistance to maintain relatively constant blood flow over a certain pressure range. Expanding the model to incorporate a mechanistic AR description, such as the one developed by Arciero et al.,61 could help to investigate the hemodynamic consequences of IOP alterations in subjects who suffer from metabolic1 or endothelial90 dysfunction. Using the mechanistic AR description also will very likely increase the current pressure range for which AR is predicted to function. The current AR range of approximately 8 to 10 mm Hg is not consistent with the larger AR plateaus observed clinically. Implementing the model for a more realistic network geometry instead of lumping all arterioles into a single compartment also will help to yield a larger AR plateau. Finally, the lamina cribrosa is assumed to be circular, isotropic, and homogeneous, whereas its geometrical and mechanical properties are much more complex45,49 and vary with age,41,42 ethnicity,36,79 and disease.47,48 The model could be extended to include a more realistic description of the lamina cribrosa to allow for a more accurate evaluation of the effects of aging, racial differences, and diseases on the relationship between IOP and blood flow.
Concluding Remarks
Despite its several underlying assumptions, the mathematical model developed in this study offers the first theoretical framework capable of linking the mechanical action of IOP to clinically measurable hemodynamic quantities, such as total retinal blood flow and CRA blood velocity. Model simulations are used to assess the independent effects of varying arterial BP and blood flow AR on the relationship between IOP and blood flow.
Studies have generally not examined the respective roles of BP and AR on flow due to the difficulty in isolating and evaluating these two factors clinically. Our mathematical model, which is validated with clinically attained values of retinal blood flow and velocity, is used to predict how BP levels (high, normal, or low) and AR ability (functional or absent) affect retinal blood flow in response to changes in IOP. Because our model predictions are consistent with clinical data for IOP reduction via surgery and medications, as well as for induced IOP elevation, this investigation represents a first attempt to use a patient's BP and AR to more accurately predict how a patient's retinal blood flow may or may not be influenced by clinically altered IOP levels. A better understanding of this relationship could have important implications for improving the way that we therapeutically address diseases associated with retinal blood flow, including glaucoma,1–3 AMD,4,5 and diabetes.5,6
Acknowledgments
Supported in part by National Science Foundation Grant DMS-1224195, National Institutes of Health Grant 1R21EY022101-01A1, and the Indiana University Collaborative Research Grant of the Office of the Vice President for Research.
Disclosure: G. Guidoboni, None; A. Harris, None; S. Cassani, None; J. Arciero, None; B. Siesky, None; A. Amireskandari, None; L. Tobe, None; P. Egan, None; I. Januleviciene, None; J. Park, None
Appendix
IOP-Induced Stress in the Lamina Cribrosa
The lamina cribrosa is modeled as a nonlinear, homogeneous, isotropic, elastic circular plate of radius Rlc and finite thickness hlc, satisfying the equilibrium equation ∇ · S = 0, where S = λlc(σe)tr(E)I + 2 μlc(σe)E is the stress tensor, E = [∇u + (∇u)T + (∇u)T∇u]/2 is the Green-Saint Venant strain tensor, u is the displacement vector, μlc is the shear modulus, λlc = μlc(Elc − 2μlc)/(3μlc − Elc) is the Lame's parameter, and Elc is the Young's modulus. The elastic parameters λlc and μlc vary with the effective stress σe, as described by Guidoboni et al.36,62 The problem is solved in cylindrical coordinates, as shown in Figure A1, with the boundary conditions Sn = − IOPn at ζ = h/2, Sn = −RLTpn at ζ = −h/2, nSn = T and uζ = 0 at s = Rlc, where T is the scleral tension computed via Laplace's law T = IOP Rs/ 2hs, where Rs and hs are the radius and thickness of the sclera, respectively. Geometrical and mechanical properties of the lamina and sclera are summarized in Tables 7 and 8; the numerical solution of the elastic problem via finite elements is described in Guidoboni et al.62 The radial component of the normal stress Sss at s = 0 resulting from the solution of this elastic problem is assumed to be the external pressure acting on the intralaminar segments of the CRA and CRV, which are assumed to pierce the lamina in its center.62
Figure A1.
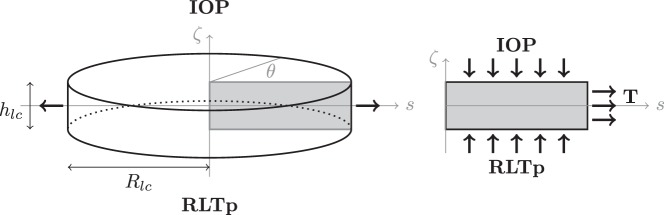
Schematic representation of geometry and boundary conditions of the elasticity problem for the lamina cribrosa. The anterior surface (ζ = hlc/2) is subject to the IOP, whereas the posterior surface (ζ = −hlc/2) is subject to the RLTp. The lateral surface (s = Rlc ) is connected to the sclera and experiences the scleral tension T.
Passive Variable Resistances
The vascular resistance of a blood vessel can be obtained by combining a tube law, describing the mechanical response of the vessel wall to changes in transmural pressure ΔP, and a hydrodynamic law, describing the fluid flow through the tube.
In the case of arteries, the Law of Laplace is used to describe a pressurized cylindrical shell and Poiseuille's law is used to describe fluid flow through the vessel. As a result, CRA resistance varies according to
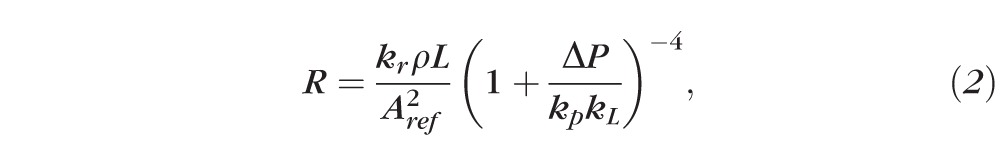 |
with kr = 8 πμ/ρ, where μ and ρ are the fluid viscosity and density, respectively; kp = (Eh3/
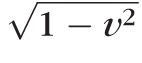 )(π/Aref)3/2, where E, ν, and h are the Young's modulus, the Poisson's ratio, and the thickness of the vessel wall, respectively; Aref is the vessel cross-sectional area when ΔP = 0 (assumed to be circular); and kL = 12 Aref/πh2.
)(π/Aref)3/2, where E, ν, and h are the Young's modulus, the Poisson's ratio, and the thickness of the vessel wall, respectively; Aref is the vessel cross-sectional area when ΔP = 0 (assumed to be circular); and kL = 12 Aref/πh2.
In venules and veins, the transmural pressure difference may become negative, causing the vessel to collapse. This phenomenon, known as a Starling resistor, is modeled here by replacing the Law of Laplace with a more realistic tube law91 that allows for drastic changes in the cross-sectional area when ΔP < 0. Resistance is thus calculated as
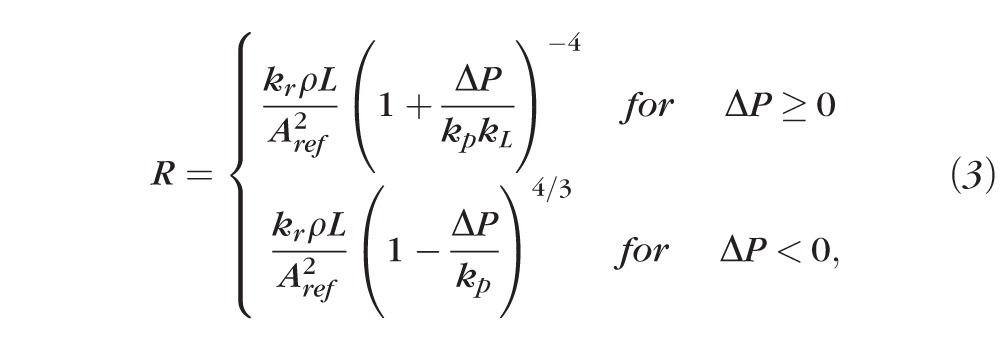 |
where the values for Young's modulus, Poisson's ratio, and the wall-to-lumen ratio are provided in Table 9. It is worth noticing that changes in ΔP can be due to variations in the external pressure and/or intraluminal BP. Equation 2 is used for the segment 1d, with external pressure equal to IOP, and the segment 1c with an external pressure that depends on the IOP-induced stress in the lamina cribrosa.62 Equation 3 is used for segments 4a, 4b, and 5a with external pressure equal to IOP, and for the segment 5b with an external pressure that depends on the IOP-induced stress in the lamina cribrosa.
Active Variable Resistances
Blood flow AR relies on the adaptation of the vascular tone of resistance vessels to changes in the perfusion pressure or metabolic needs of the tissue. Recently, Arciero et al.61 developed a mathematical model that describes the response of resistance vessels to local changes in pressure, shear stress, carbon dioxide, and to the downstream metabolic state communicated via conducted responses. The model is based on a mechanical representation of resistance vessel walls where the total circumferential wall tension is generated by a passive component (representing the wall tension generated by the structural components of the vessel wall) and an active component (representing the wall tension generated in response to changes in smooth muscle tone). A stimulus function is defined to describe changes in smooth muscle tone according to a linear combination of various regulatory mechanisms.
The model proposed by Arciero et al.61 cannot be directly coupled with the model for retinal blood flow developed in the present article, because the first model is stationary whereas the second model is time-dependent. The extension of the model by Arciero et al.61 to the time-dependent case would require the description of the mechanisms regulating retinal blood flow in response to time variations of intravascular pressures, blood velocity, and shear stress, which, although beyond the scope of this article, we acknowledge as a limitation in the current article.
Thus, here we adopt a simpler phenomenological description of blood flow AR, following the method used by Lakin et al.76 in the context of cerebral blood flow. The absence of AR is modeled by keeping the arteriolar resistance R2a constantly equal to its control value R̄2a despite changes in OPP, whereas functional AR is modeled by letting arteriolar resistance vary according to the formula:
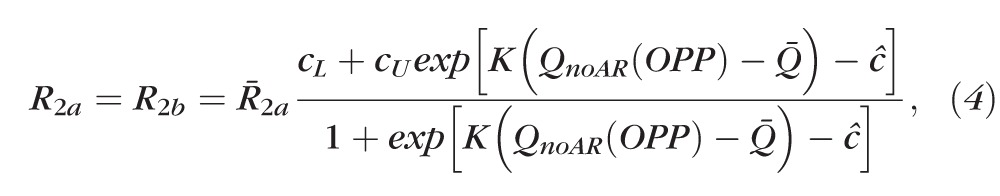 |
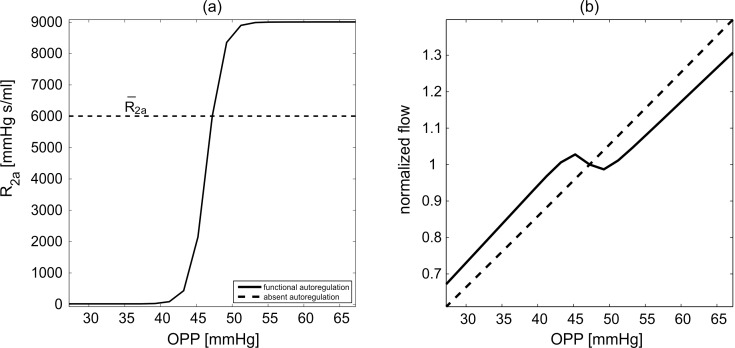
where cL = 2.50 · 10−3 and cU = 1.5 determine the lower and upper bounds for the variation in resistance, K = 6.91 · 104 s/mL determines the resistance sensitivity to changes in OPP ( = 2/3 MAP − IOP), QnoAR(OPP) is the total retinal blood flow predicted by the model in the absence of AR for a given OPP and c̄ = ln(CU – 1) – ln(1 – cL) ensures that R2a = R̄2a and R2b = R̄2b at the control state. The numerical values of cL, cU and K have been chosen to yield an increase in resistance over the range of OPP depicted in Figure A2. Model simulations of normalized flow in the case of functional and absent AR are reported in Figure A2B for various OPP values (attained by setting IOP = 15 mm Hg and varying MAP between 63 and 123 mm Hg).
Figure A2.
Arteriolar resistance (a) and normalized flow (b) for model simulations with functional (solid line) or absent (dashed line) AR for various OPPs attained by setting IOP = 15 mm Hg and varying MAP.
Figure 4C shows that the model predicted values of retinal blood flow in the case of functional AR are consistent with clinical measurements for various MAP levels, and this suggests that formula (3) and its related assumptions are appropriate modeling choices for retinal blood flow autoregulation.
References
- 1. Harris A, Kagemann L, Ehrlich R, Rospigliosi C, Moore D, Siesky B. Measuring and interpreting ocular blood flow and metabolism in glaucoma. Can J Ophthalmol. 2008; 43: 328–336 [DOI] [PubMed] [Google Scholar]
- 2. Leske MC. Open-angle glaucoma—an epidemiologic overview. Ophthalmic Epidemiol. 2007; 14: 166–172 [DOI] [PubMed] [Google Scholar]
- 3. Leske MC, Heijl A, Hyman L, Bengtsson B, Dong L, Yang Z. Predictors of long-term progression in the early manifest glaucoma trial. Ophthalmology. 2007; 114: 1965–1972 [DOI] [PubMed] [Google Scholar]
- 4. Ehrlich R, Harris A, Kheradiya NS, Winston DM, Ciulla TA, Wirostko B. Age-related macular degeneration and the aging eye. Clin Interven Aging. 2008; 3: 473–482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pemp B, Schmetterer L. Ocular blood flow in diabetes and age-related macular degeneration. Can J Ophthalmol. 2008; 43: 295–301 [DOI] [PubMed] [Google Scholar]
- 6. Rassam SM, Patel V, Kohner EM. The effect of experimental hypertension on retinal vascular autoregulation in humans: a mechanism for the progression of diabetic retinopathy. Exp Physiol. 1995; 80: 53–68 [DOI] [PubMed] [Google Scholar]
- 7. Alagoz G, Gurel K, Bayer A, Serin D, Celebi S, Kukner S. A comparative study of bimatoprost and travoprost: effect on intraocular pressure and ocular circulation in newly diagnosed glaucoma patients. Ophthalmologica. 2008; 222: 88–95 [DOI] [PubMed] [Google Scholar]
- 8. Findl O, Strenn K, Wolzt M, et al. Effects of changes in intraocular pressure on human ocular haemodynamics. Curr Eye Res. 1997; 16: 1024–1029 [DOI] [PubMed] [Google Scholar]
- 9. Galassi F, Giambene B, Corvi A, Falaschi G, Menchini U. Retrobulbar hemodynamics and corneal surface temperature in glaucoma surgery. Int Ophthalmol. 2008; 28: 399–405 [DOI] [PubMed] [Google Scholar]
- 10. Harris A, Joos K, Kay M, et al. Acute IOP elevation with scleral suction: effects on retrobulbar haemodynamics. Br J Ophthalmol. 1996; 80: 1055–1059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Huber-van der Velden KK, Lux A, Severing K, Klamann MK, Winterhalter S, Remky A. Retrobulbar hemodynamics before and after oculopression with and without dorzolamide. Curr Eye Res. 2012; 37: 719–725 [DOI] [PubMed] [Google Scholar]
- 12. Koz OG, Ozsoy A, Yarangumeli A, Kose SK, Kural G. Comparison of the effects of travoprost, latanoprost and bimatoprost on ocular circulation: a 6-month clinical trial. Acta Ophthalmol Scand. 2007; 85: 838–843 [DOI] [PubMed] [Google Scholar]
- 13. Synder A, Augustyniak E, Laudanska-Olszewska I, Wesolek-Czernik A. [Evaluation of blood-flow parameters in extraocular arteries in patients with primary open-angle glaucoma before and after surgical treatment]. Klin Oczna. 2004; 106: 206–208 [PubMed] [Google Scholar]
- 14. Trible JR, Sergott RC, Spaeth GL, et al. Trabeculectomy is associated with retrobulbar hemodynamic changes. A color Doppler analysis. Ophthalmology. 1994; 101: 340–351 [DOI] [PubMed] [Google Scholar]
- 15. Akarsu C, Yilmaz S, Taner P, Ergin A. Effect of bimatoprost on ocular circulation in patients with open-angle glaucoma or ocular hypertension. Graefes Arch Clin Exp Ophthalmol. 2004; 242: 814–818 [DOI] [PubMed] [Google Scholar]
- 16. Arikan OK, Akarsu C, Unal B, Ergin A, Koc C. Effect of oxymetazoline nasal spray on intraocular pressure and retrobulbar hemodynamics. J Otolaryngol. 2006; 35: 30–35 [DOI] [PubMed] [Google Scholar]
- 17. Cantor LB. The effect of trabeculectomy on ocular hemodynamics. Trans Am Ophthalmol Soc. 2001; 99: 241–252 [PMC free article] [PubMed] [Google Scholar]
- 18. Conway ML, Wevill M, Benavente-Perez A, Hosking SL. Ocular blood-flow hemodynamics before and after application of a laser in situ keratomileusis ring. J Cataract Refract Surg. 2010; 36: 268–272 [DOI] [PubMed] [Google Scholar]
- 19. Erkin EF, Tarhan S, Kayikcioglu OR, Deveci H, Guler C, Goktan C. Effects of betaxolol and latanoprost on ocular blood flow and visual fields in patients with primary open-angle glaucoma. Eur J Ophthalmol. 2004; 14: 211–219 [DOI] [PubMed] [Google Scholar]
- 20. Fuchsjager-Mayrl G, Georgopoulos M, Hommer A, et al. Effect of dorzolamide and timolol on ocular pressure: blood flow relationship in patients with primary open-angle glaucoma and ocular hypertension. Invest Ophthalmol Vis Sci. 2010; 51: 1289–1296 [DOI] [PubMed] [Google Scholar]
- 21. Harris A, Garzozi HJ, McCranor L, Rechtman E, Yung CW, Siesky B. The effect of latanoprost on ocular blood flow. Int Ophthalmol. 2009; 29: 19–26 [DOI] [PubMed] [Google Scholar]
- 22. Hommer A, Sperl P, Resch H, et al. A double-masked randomized crossover study comparing the effect of latanoprost/timolol and brimonidine/timolol fixed combination on intraocular pressure and ocular blood flow in patients with primary open-angle glaucoma or ocular hypertension. J Ocul Pharmacol Ther. 2012; 28: 569–575 [DOI] [PubMed] [Google Scholar]
- 23. Inan UU, Ermis SS, Yucel A, Ozturk F. The effects of latanoprost and brimonidine on blood flow velocity of the retrobulbar vessels: a 3-month clinical trial. Acta Ophthalmol Scand. 2003; 81: 155–160 [DOI] [PubMed] [Google Scholar]
- 24. James CB. Effect of trabeculectomy on pulsatile ocular blood flow. Br J Ophthalmol. 1994; 78: 818–822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kaup M, Plange N, Niegel M, Remky A, Arend O. Effects of brinzolamide on ocular haemodynamics in healthy volunteers. Br J Ophthalmol. 2004; 88: 257–262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Poinoosawmy D, Indar A, Bunce C, Garway-Heath DF, Hitchings RA. Effect of treatment by medicine or surgery on intraocular pressure and pulsatile ocular blood flow in normal-pressure glaucoma. Graefes Arch Clin Exp Ophthalmol. 2002; 240: 721–726 [DOI] [PubMed] [Google Scholar]
- 27. Stankiewicz A, Misiuk-Hojlo M, Grabska-Liberek I, et al. Intraocular pressure and ocular hemodynamics in patients with primary open-angle glaucoma treated with the combination of morning dosing of bimatoprost and dorzolamide hydrochloride. Acta Ophthalmol. 2011; 89: e57–63 [DOI] [PubMed] [Google Scholar]
- 28. Caprioli J, Coleman AL. Blood pressure, perfusion pressure, and glaucoma. Am J Ophthalmol. 2010; 149: 704–712 [DOI] [PubMed] [Google Scholar]
- 29. Hayreh SS, Zimmerman MB, Podhajsky P, Alward WL. Nocturnal arterial hypotension and its role in optic nerve head and ocular ischemic disorders. Am J Ophthalmol. 1994; 117: 603–624 [DOI] [PubMed] [Google Scholar]
- 30. He Z, Nguyen CT, Armitage JA, Vingrys AJ, Bui BV. Blood pressure modifies retinal susceptibility to intraocular pressure elevation. PloS One. 2012; 7: e31104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Leighton DA, Phillips CI. Systemic blood pressure in open-angle glaucoma, low tension glaucoma, and the normal eye. Br J Ophthalmol. 1972; 56: 447–453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Memarzadeh F, Ying-Lai M, Chung J, Azen SP, Varma R. Blood pressure, perfusion pressure, and open-angle glaucoma: the Los Angeles Latino Eye Study. Invest Ophthalmol Vis Sci. 2010; 51: 2872–2877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Galassi F, Giambene B, Varriale R. Systemic vascular dysregulation and retrobulbar hemodynamics in normal-tension glaucoma. Invest Ophthalmol Vis Sci. 2011; 52: 4467–4471 [DOI] [PubMed] [Google Scholar]
- 34. Moore D, Harris A, Wudunn D, Kheradiya N, Siesky B. Dysfunctional regulation of ocular blood flow: a risk factor for glaucoma? Clin Ophthalmol. 2008; 2: 849–861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Sines D, Harris A, Siesky B, et al. The response of retrobulbar vasculature to hypercapnia in primary open-angle glaucoma and ocular hypertension. Ophthalmic Res. 2007; 39: 76–80 [DOI] [PubMed] [Google Scholar]
- 36. Guidoboni G, Harris A, Arciero J, et al. Mathematical modeling approaches in the study of glaucoma disparities among people of African and European descents. J Coupled Syst Multiscale Dyn. 2013; 1: 21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Harris A, Guidoboni G, Arciero JC, Amireskandari A, Tobe LA, Siesky BA. Ocular hemodynamics and glaucoma: the role of mathematical modeling. Eur J Ophthalmol. 2013; 23: 139–146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Burgoyne CF, Downs JC, Bellezza AJ, Suh JK, Hart RT. The optic nerve head as a biomechanical structure: a new paradigm for understanding the role of IOP-related stress and strain in the pathophysiology of glaucomatous optic nerve head damage. Prog Retin Eye Res. 2005; 24: 39–73 [DOI] [PubMed] [Google Scholar]
- 39. Burgoyne CF. A biomechanical paradigm for axonal insult within the optic nerve head in aging and glaucoma. Exp Eye Res. 2011; 93: 120–132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Fazio MA, Grytz R, Bruno L, et al. Regional variations in mechanical strain in the posterior human sclera. Invest Ophthalmol Vis Sci. 2012; 53: 5326–5333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Fazio MA, Grytz R, Morris JS, et al. Age-related changes in human peripapillary scleral strain. Biomech Model Mechanobiol. 2014; 13: 551–563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Girard MJ, Suh JK, Bottlang M, Burgoyne CF, Downs JC. Scleral biomechanics in the aging monkey eye. Invest Ophthalmol Vis Sci. 2009; 50: 5226–5237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Grytz R, Meschke G. Constitutive modeling of crimped collagen fibrils in soft tissues. J Mech Behav Biomed Mater. 2009; 2: 522–533 [DOI] [PubMed] [Google Scholar]
- 44. Grytz R, Meschke G. A computational remodeling approach to predict the physiological architecture of the collagen fibril network in corneo-scleral shells. Biomech Model Mechanobiol. 2010; 9: 225–235 [DOI] [PubMed] [Google Scholar]
- 45. Grytz R, Meschke G, Jonas JB. The collagen fibril architecture in the lamina cribrosa and peripapillary sclera predicted by a computational remodeling approach. Biomech Model Mechanobiol. 2011; 10: 371–382 [DOI] [PubMed] [Google Scholar]
- 46. Grytz R, Downs JC. A forward incremental prestressing method with application to inverse parameter estimations and eye-specific simulations of posterior scleral shells [published online ahead of print January 6, 2012]. Comput Methods Biomech Biomed Eng. doi:10.1080/10255842.2011.64119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Grytz R, Sigal IA, Ruberti JW, Meschke G, Downs JC. Lamina cribrosa thickening in early glaucoma predicted by a microstructure motivated growth and remodeling approach. Mech Mater. 2012; 44: 99–109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Grytz R, Girkin CA, Libertiaux V, Downs JC. Perspectives on biomechanical growth and remodeling mechanisms in glaucoma(). Mech Res Commun. 2012; 42: 92–106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Grytz R, Fazio MA, Girard MJ, et al. Material properties of the posterior human sclera. J Mech Behav Biomed Mater. 2014; 29: 602–617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Norman RE, Flanagan JG, Sigal IA, Rausch SM, Tertinegg I, Ethier CR. Finite element modeling of the human sclera: influence on optic nerve head biomechanics and connections with glaucoma. Exp Eye Res. 2011; 93: 4–12 [DOI] [PubMed] [Google Scholar]
- 51. Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Finite element modeling of optic nerve head biomechanics. Invest Ophthalmol Vis Sci. 2004; 45: 4378–4387 [DOI] [PubMed] [Google Scholar]
- 52. Sigal IA, Flanagan JG, Ethier CR. Factors influencing optic nerve head biomechanics. Invest Ophthalmol Vis Sci. 2005; 46: 4189–4199 [DOI] [PubMed] [Google Scholar]
- 53. Sigal IA, Ethier CR. Biomechanics of the optic nerve head. Exp Eye Res. 2009; 88: 799–807 [DOI] [PubMed] [Google Scholar]
- 54. Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Modeling individual-specific human optic nerve head biomechanics. Part I: IOP-induced deformations and influence of geometry. Biomech Model Mechanobiol. 2009; 8: 85–98 [DOI] [PubMed] [Google Scholar]
- 55. Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Modeling individual-specific human optic nerve head biomechanics. Part II: influence of material properties. Biomech Model Mechanobiol. 2009; 8: 99–109 [DOI] [PubMed] [Google Scholar]
- 56. Sigal IA. An applet to estimate the IOP-induced stress and strain within the optic nerve head. Invest Ophthalmol Vis Sci. 2011; 52: 5497–5506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Ganesan P, He S, Xu H. Development of an image-based network model of retinal vasculature. Ann Biomed Eng. 2010; 38: 1566–1585 [DOI] [PubMed] [Google Scholar]
- 58. Ganesan P, He S, Xu H. Modelling of pulsatile blood flow in arterial trees of retinal vasculature. Med Eng Phys. 2011; 33: 810–823 [DOI] [PubMed] [Google Scholar]
- 59. Ganesan P, He S, Xu H. Development of an image-based model for capillary vasculature of retina. Comput Methods Programs Biomed. 2011; 102: 35–46 [DOI] [PubMed] [Google Scholar]
- 60. Takahashi T, Nagaoka T, Yanagida H, et al. A mathematical model for the distribution of hemodynamic parameters in the human retinal microvascular network. J Biorheol. 2009; 23: 77–86 [Google Scholar]
- 61. Arciero J, Harris A, Siesky B, et al. Theoretical analysis of vascular regulatory mechanisms contributing to retinal blood flow autoregulation. Invest Ophthalmol Vis Sci. 2013; 54: 5584–5593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Guidoboni G, Harris A, Carichino L, Arieli Y, Siesky B. Effect of intraocular pressure on the hemodynamics of the central retinal artery: a mathematical model. Math Biosci Eng. 2014; 11: 523–546 [DOI] [PubMed] [Google Scholar]
- 63. Harris A, Arend O, Bohnke K, Kroepfl E, Danis R, Martin B. Retinal blood flow during dynamic exercise. Graefes Arch Clin Exp Ophthalmol. 1996; 234: 440–444 [DOI] [PubMed] [Google Scholar]
- 64. Iester M, Torre PG, Bricola G, Bagnis A, Calabria G. Retinal blood flow autoregulation after dynamic exercise in healthy young subjects. Ophthalmologica. 2007; 221: 180–185 [DOI] [PubMed] [Google Scholar]
- 65. Nemeth J, Knezy K, Tapaszto B, Kovacs R, Harkanyi Z. Different autoregulation response to dynamic exercise in ophthalmic and central retinal arteries: a color Doppler study in healthy subjects. Graefes Arch Clin Exp Ophthalmol. 2002; 240: 835–840 [DOI] [PubMed] [Google Scholar]
- 66. Morgan WH, Yu DY, Alder VA, et al. The correlation between cerebrospinal fluid pressure and retrolaminar tissue pressure. Invest Ophthalmol Vis Sci. 1998; 39: 1419–1428 [PubMed] [Google Scholar]
- 67. Ren R, Jonas JB, Tian G, et al. Cerebrospinal fluid pressure in glaucoma: a prospective study. Ophthalmology. 2010; 117: 259–266 [DOI] [PubMed] [Google Scholar]
- 68. Dorner GT, Polska E, Garhofer G, Zawinka C, Frank B, Schmetterer L. Calculation of the diameter of the central retinal artery from noninvasive measurements in humans. Curr Eye Res. 2002; 25: 341–345 [DOI] [PubMed] [Google Scholar]
- 69. Dumskyj MJ, Eriksen JE, Dore CJ, Kohner EM. Autoregulation in the human retinal circulation: assessment using isometric exercise, laser Doppler velocimetry, and computer-assisted image analysis. Microvasc Res. 1996; 51: 378–392 [DOI] [PubMed] [Google Scholar]
- 70. Feke GT, Pasquale LR. Retinal blood flow response to posture change in glaucoma patients compared with healthy subjects. Ophthalmology. 2008; 115: 246–252 [DOI] [PubMed] [Google Scholar]
- 71. Feke GT, Hazin R, Grosskreutz CL, Pasquale LR. Effect of brimonidine on retinal blood flow autoregulation in primary open-angle glaucoma. J Ocul Pharmacol Ther. 2011; 27: 347–352 [DOI] [PubMed] [Google Scholar]
- 72. Grunwald JE, DuPont J, Riva CE. Retinal haemodynamics in patients with early diabetes mellitus. Br J Ophthalmol. 1996; 80: 327–331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Strauss AL, Kedra AW. Experiences with a new procedure for the measurement of the ophthalmic artery pressure: ophthalmomanometry-Doppler. Med Instrum. 1987; 21: 255–261 [PubMed] [Google Scholar]
- 74. Friedland AB. A mathematical model of transmural transport of oxygen to the retina. Bull Math Biol. 1978; 40: 823–837 [DOI] [PubMed] [Google Scholar]
- 75. Walker HK, Hall WD, Hurst JW. Clinical Methods: The History, Physical, and Laboratory Examinations. 3rd ed. Boston: Butterworths; 1990. [PubMed] [Google Scholar]
- 76. Lakin WD, Stevens SA, Tranmer BI, Penar PL. A whole-body mathematical model for intracranial pressure dynamics. J Math Biol. 2003; 46: 347–383 [DOI] [PubMed] [Google Scholar]
- 77. Garcia JP Jr, Garcia PT, Rosen RB. Retinal blood flow in the normal human eye using the canon laser blood flowmeter. Ophthalmic Res. 2002; 34: 295–299 [DOI] [PubMed] [Google Scholar]
- 78. Riva CE, Grunwald JE, Sinclair SH, Petrig BL. Blood velocity and volumetric flow rate in human retinal vessels. Invest Ophthalmol Vis Sci. 1985; 26: 1124–1132 [PubMed] [Google Scholar]
- 79. Yan D, McPheeters S, Johnson G, Utzinger U, Vande Geest JP. Microstructural differences in the human posterior sclera as a function of age and race. Invest Ophthalmol Vis Sci. 2011; 52: 821–829 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Jonas JB. Ophthalmodynamometric assessment of the central retinal vein collapse pressure in eyes with retinal vein stasis or occlusion. Graefes Arch Clin Exp Ophthalmol. 2003; 241: 367–370 [DOI] [PubMed] [Google Scholar]
- 81. Jonas JB. Ophthalmodynamometric measurement of orbital tissue pressure in thyroid-associated orbitopathy. Acta Ophthalmol Scand. 2004; 82: 239 [DOI] [PubMed] [Google Scholar]
- 82. Sugiura Y, Okamoto F, Okamoto Y, Hasegawa Y, Hiraoka T, Oshika T. Ophthalmodynamometric pressure in eyes with proliferative diabetic retinopathy measured during pars plana vitrectomy. Am J Ophthalmol. 2011; 151: 624–629.e1 [DOI] [PubMed] [Google Scholar]
- 83. Jonas JB. Ophthalmodynamometric determination of the central retinal vessel collapse pressure correlated with systemic blood pressure. Br J Ophthalmol. 2004; 88: 501–504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Glucksberg MR, Dunn R. Direct measurement of retinal microvascular pressures in the live, anesthetized cat. Microvasc Res. 1993; 45: 158–165 [DOI] [PubMed] [Google Scholar]
- 85. Attariwala R, Giebs CP, Glucksberg MR. The influence of elevated intraocular pressure on vascular pressures in the cat retina. Invest Ophthalmol Vis Sci. 1994; 35: 1019–1025 [PubMed] [Google Scholar]
- 86. Denardo SJ, Yamada EG, Hargrave VK, Yock PG. Effect of stenosis inlet geometry on shear rates of blood flow in the upstream region. Am Heart J. 1993; 125: 350–356 [DOI] [PubMed] [Google Scholar]
- 87. Woodman CR, Trott DW, Laughlin MH. Short-term increases in intraluminal pressure reverse age-related decrements in endothelium-dependent dilation in soleus muscle feed arteries. J Appl Physiol (1985). 2007; 103: 1172–1179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Boltz A, Schmidl D, Werkmeister RM, et al. Regulation of optic nerve head blood flow during combined changes in intraocular pressure and arterial blood pressure. J Cereb Blood Flow Metab. 2013; 33: 1850–1856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Chung HS, Harris A, Halter PJ, et al. Regional differences in retinal vascular reactivity. Invest Ophthalmol Vis Sci. 1999; 40: 2448–2453 [PubMed] [Google Scholar]
- 90. Verma S, Buchanan MR, Anderson TJ. Endothelial function testing as a biomarker of vascular disease. Circulation. 2003; 108: 2054–2059 [DOI] [PubMed] [Google Scholar]
- 91. Pedley TJ, Brook BS, Seymour RS. Blood pressure and flow rate in the giraffe jugular vein. Philos Trans R Soc Lond B Biol Sci. 1996; 351: 855–866 [DOI] [PubMed] [Google Scholar]
- 92. Harris A, Jonescu-Cuypers CP, Kagemann L, Ciulla TA, Krieglstein GK. Atlas of Ocular Blood Flow. Vascular Anatomy, Pathophysiology, and Metabolism. Philadelphia, PA: Elsevier; 2010. [Google Scholar]
- 93. Lee EJ, Kim TW, Weinreb RN. Variation of lamina cribrosa depth following trabeculectomy. Invest Ophthalmol Vis Sci. 2013; 54: 5392–5399 [DOI] [PubMed] [Google Scholar]
- 94. Jonas JB, Holbach L. Central corneal thickness and thickness of the lamina cribrosa in human eyes. Invest Ophthalmol Vis Sci. 2005; 46: 1275–1279 [DOI] [PubMed] [Google Scholar]
- 95. Ren R, Wang N, Li B, et al. Lamina cribrosa and peripapillary sclera histomorphometry in normal and advanced glaucomatous Chinese eyes with various axial length. Invest Ophthalmol Vis Sci. 2009; 50: 2175–2184 [DOI] [PubMed] [Google Scholar]
- 96. Fung YC. Biomechanics: Circulation. New York: Springer-Verlag; 1997. [Google Scholar]
- 97. Quarteroni A, Tuveri M, Veneziani A. Computational vascular fluid dynamics: problems, models and methods. Comput Visual Sci. 2000; 2: 163–197 [Google Scholar]
- 98. Armentano RL, Barra JG, Levenson J, Simon A, Pichel RH. Arterial wall mechanics in conscious dogs. Assessment of viscous, inertial, and elastic moduli to characterize aortic wall behavior. Circ Res. 1995; 76: 468–478 [DOI] [PubMed] [Google Scholar]
- 99. Fung YC. Biomechanics: Mechanical Properties of Living Tissues. 2nd ed. New York: Springer-Verlag; 1993. [Google Scholar]
- 100. Handbook of biomaterial properties. Deng X, Guidoin R. Arteries, veins and lymphatic vessels. Handbook of Biomaterial Properties. London: Chapman & Hall; 1998; 81–105 [Google Scholar]
- 101. Baleanu D, Ritt M, Harazny J, Heckmann J, Schmieder RE, Michelson G. Wall-to-lumen ratio of retinal arterioles and arteriole-to-venule ratio of retinal vessels in patients with cerebrovascular damage. Invest Ophthalmol Vis Sci. 2009; 50: 4351–4359 [DOI] [PubMed] [Google Scholar]
- 102. Wetterer E, Bauer RD, Pasch T. Arteriensystem. In: Bauereisen E, Bartels H, Trendelenburg W, et al. Physiologie des Kreislaufs. Berlin: Springer-Verlag; 1971; 1–66 [Google Scholar]
- 103. Jonas JB, Mardin CY, Schlotzer-Schrehardt U, Naumann GO. Morphometry of the human lamina cribrosa surface. Invest Ophthalmol Vis Sci. 1991; 32: 401–405 [PubMed] [Google Scholar]
- 104. Norman RE, Flanagan JG, Rausch SM, et al. Dimensions of the human sclera: thickness measurement and regional changes with axial length. Exp Eye Res. 2010; 90: 277–284 [DOI] [PubMed] [Google Scholar]
- 105. Newson T, El-Sheikh A. Mathematical modeling of the biomechanics of the lamina cribrosa under elevated intraocular pressures. J Biomech Eng. 2006; 128: 496–504 [DOI] [PubMed] [Google Scholar]
- 106. Woo SL, Kobayashi AS, Schlegel WA, Lawrence C. Nonlinear material properties of intact cornea and sclera. Exp Eye Res. 1972; 14: 29–39 [DOI] [PubMed] [Google Scholar]