The genetic covariance between life cycle stages separated by metamorphosis

Abstract

Metamorphosis is common in animals, yet the genetic associations between life cycle stages are poorly understood. Given the radical changes that occur at metamorphosis, selection may differ before and after metamorphosis, and the extent that genetic associations between pre- and post-metamorphic traits constrain evolutionary change is a subject of considerable interest. In some instances, metamorphosis may allow the genetic decoupling of life cycle stages, whereas in others, metamorphosis could allow complementary responses to selection across the life cycle. Using a diallel breeding design, we measured viability at four ontogenetic stages (embryo, larval, juvenile and adult viability), in the ascidian Ciona intestinalis and examined the orientation of additive genetic variation with respect to the metamorphic boundary. We found support for one eigenvector of G (g_obsmax), which contrasted larval viability against embryo viability and juvenile viability. Target matrix rotation confirmed that while g_obsmax shows genetic associations can extend beyond metamorphosis, there is still considerable scope for decoupled phenotypic evolution. Therefore, although genetic associations across metamorphosis could limit that range of phenotypes that are attainable, traits on either side of the metamorphic boundary are capable of some independent evolutionary change in response to the divergent conditions encountered during each life cycle stage.

1. Introduction

Metamorphosis marks dramatic physiological, morphological and ecological changes in the life cycles of animals [1]. Consequently, metamorphosis can coincide with a sudden shift in selection. Partitioning of the life cycle into separate stages therefore raises some unique evolutionary problems, as the same genome must perform well in two or more discrete stages with distinct body plans and different ecological contexts [2–4]. Despite these complications, metamorphosis is common in animals, and there are many examples of closely related species that show remarkable phenotypic divergence in one life cycle stage but phenotypic convergence in another [1,4]. While these patters suggest that pre- and post-metamorphic phenotypes are uncoupled to a large extent, the underlying genetic associations for traits separated by metamorphosis are generally unknown.

For genetically correlated traits separated by metamorphosis, selection acting on one trait will result in indirect selection on correlated traits [5–7]. If this indirect selection causes maladaptive changes in traits across stages, evolutionary change in the direction of selection can be constrained by traits expressed in a different stage of the life cycle [8]. For traits with distinct functions and possibly under opposing selection, reconciling the costs and benefits of traits expressed in different stages of a complex life cycle is unlikely to be straightforward. Accordingly, the adaptive decoupling hypothesis for the benefits of metamorphosis [4] predicts that traits separated by metamorphosis should be genetically uncorrelated, thereby allowing evolutionary change to occur within each stage, without corresponding effects on phenotypes expressed in other stages. Studies that have tested this prediction by examining genetic associations across metamorphosis have found contradictory results [9–12], and so the relevance of the adaptive decoupling hypothesis for organisms with complex life cycles remains unclear.

The adaptive decoupling hypothesis predicts that traits separated by metamorphosis should be genetically uncorrelated; however, genetic correlations need not be zero for some genetic decoupling to exist. For example, Watkins [10] and Phillips [9] tested the prediction that larval and juvenile body size should be genetically uncorrelated in two separate experiments in two frog species. Phillips [9] showed that genetic correlations across metamorphosis were not significantly different from zero, thereby providing support for the adaptive decoupling hypothesis. By contrast, Watkins [10] found significant genetic correlations across metamorphosis. Nevertheless, in both cases genetic correlations between larval and juvenile body size traits were positive and of a moderate to large magnitude [9,10]. Importantly, because the genetic correlations are less than one, there is still some genetic variation available for independent evolution across metamorphosis. For instance, the mean across metamorphosis genetic correlation presented in Watkins [10] was r = 0.845, even for such a high genetic correlation we would still expect 29% of the genetic variation (one minus the square of the genetic correlation multiplied by 100) in larval and juvenile frog size could respond to selection independently.

A more useful null hypothesis for testing evolutionary constraints in studies where traits are measured in different contexts (e.g. different sexes or different environments) is a genetic correlation of one [13,14]. Genetic correlations less than one will allow some degree of independent evolution, and even small deviations from a correlation of one can allow evolutionary change towards multiple optima [13,14]. The same logic can be applied to quantitative genetic studies of associations across metamorphosis—for traits measured pre- and post-metamorphosis, a genetic correlation across metamorphosis significantly less than one would suggest that independent evolution across metamorphosis is possible. In addition, this framework for examining constraints across metamorphosis can be extended beyond a simple examination of the bivariate genetic correlation between two traits, to any number of traits separated by metamorphosis.

Although genetic correlations are intuitive descriptors of genetic associations between traits, eigenanalysis of the genetic variance–covariance matrix, G, demonstrates how genetic correlations affect the distribution of genetic variation, and thereby the mechanism underlying evolutionary constraints [15]. For example, in the eigenanalysis of G for two traits with a genetic correlation equal to one, there will be one eigenvector with an eigenvalue equal to the sum of the genetic variances of the two traits and one eigenvector with an eigenvalue of zero. Because eigenvalues quantify genetic variation in the trait combinations described by the eigenvectors, the distribution of eigenvalues will determine the bias in a response to selection [15,16], and eigenvalues of zero represent trait combinations with zero genetic variation and thereby absolute evolutionary constraints. Moreover, when considering more than two traits, the eigenanalysis of G avoids simultaneously interpreting multiple bivariate genetic correlations, and instead directly quantifies genetic variance across all trait combinations. In the context of the current experiment, focusing on the magnitude of the genetic variance associated with the eigenvectors of G facilitates hypothesis tests examining genetic associations across metamorphosis. By rotating G to a region of the genetic space where genetic associations across metamorphosis are equal to one, it is possible to examine the genetic variance underlying the trait combinations that would prevent independent evolution across metamorphosis. To the best of our knowledge, such an approach has not been employed in an analysis of genetic constraint. Here, we show how target matrix rotation applied within a Bayesian mixed model framework allows explicit tests of multivariate associations across metamorphosis in a sessile marine invertebrate with a complex life cycle.

In marine systems, many studies have examined phenotypic associations among traits separated by metamorphosis [17–19], yet few have examined the genetics underlying these quantitative traits [20–23], or how additive genetic variation is partitioned across the metamorphic boundary [24–28], particularly in a multivariate context. Here, we measured viability during four ontogenetic stages (embryo, larval, juvenile and adult viability) of the ascidian Ciona intestinalis and examined the distribution of additive genetic variation across the metamorphic boundary. Metamorphosis in C. intestinalis marks the transition from between the dispersive pre-metamorphic stages (embryos and larvae) and the sessile post-metamorphic stages (juveniles and adults). The pre-metamorphic stages are pelagic and individuals have no feeding organs, hence individuals rely on maternal provisioning for nutrition. Conversely, the juvenile and adult stages remain attached to hard substrates and are the life cycle stages responsible for feeding, growth and reproduction. Despite the substantial differences in the form, function and environment experienced during the pre- and post-metamorphic stages in C. intestinalis, because of the close association between viability and fitness we expect positive selection for increased viability in each life cycle stage. Consequently, the most appropriate null hypothesis for fitness components separated by metamorphosis is genetic correlations across metamorphosis equal to positive one.

2. Material and methods

(a). Study site and species

All experiments and collections were carried out at the Lincoln Cove Marina, Port Lincoln, South Australia (34°44′28.76″ S, 135°52′02.88″ E). The field site was a sheltered marina connected to a large bay via a canal with regular tidal exchange. Ambient water temperature during the experiment was 14°C, and culture rooms maintained an average temperature of 14°C (±2°C). Our study species, C. intestinalis, is a hermaphroditic, solitary ascidian. In C. intestinalis, sperm and eggs are broadcast into the surrounding environment, and as a result, fertilization and embryo development are external. Embryos are negatively buoyant and develop within the chorion before larvae emerge as tadpoles. The larvae of C. intestinalis are non-feeding and are competent to begin metamorphosis within 2 h of hatching.

(b). General laboratory and field methods

Reproductive adults were collected approximately 1 m below the water surface from the floating docks at the field site. Adults were maintained in flow-through aquaria for 48 h, in complete darkness, before gametes were extracted. To extract gametes, we made a slit along the length of the tunic to expose the sperm duct and the oviduct, then a small incision was made in either the sperm duct (sires) or oviduct (dams), and gametes were extracted with a syringe. For each dam, a control clutch of eggs (100–200 eggs) was not exposed to sperm. Cell division in the control clutch of eggs (i.e. successful fertilization) indicated contamination by self-sperm and resulted in the termination of the entire block. Extracted sperm was filtered through 25 μm Nytex mesh to prevent accidental transfer of eggs among crosses. We calculated the concentration of sperm in each extraction with a Neubauer haemocytometer, then standardized the sperm concentration (2 × 10⁶ sperm ml⁻¹) for all sires by adding the corresponding volume of fresh seawater to each sperm extraction. To fertilize eggs, a well-mixed 0.1 ml egg solution and 0.25 ml sperm solution were mixed in each Petri dish. After 30 min, eggs were rinsed in fresh seawater and placed in new dishes. Two hours after the initial exposure to sperm, the eggs were between the 2- and 8-cell stage, thus allowing us to differentiate fertilized from unfertilized eggs. For each cross, we sampled 70–100 fertilized eggs, and then transferred them to hatching dishes that were filled with 2.5 ml of seawater. We used a dissecting microscope for all post-fertilization assays.

Larvae hatched between 20 and 23 h post-fertilization at ambient seawater temperature. Thirty minutes after the first larvae began to hatch, 45 apparently healthy, swimming larvae were selected at random and transferred to settlement dishes that were filled with 2.5 ml of fresh seawater. Settlement dishes were roughened with sandpaper and conditioned in flow-through aquaria for 2 days. The embryos that remained in hatching dishes were allowed an extra 3 h to complete development. Pilot data revealed that fertilized eggs which appeared to develop normally to the 2- to 8-cell stage, but did not hatch within 3 h of the first successful hatchlings in their dish, failed to hatch 68 h post-fertilization and were considered unviable. To estimate embryo viability, we counted the number of larvae in hatching dishes plus the 45 larvae transferred to settlement dishes.

The larvae in settlement dishes were allowed 24 h (44–47 h post-fertilization) in constant darkness, at ambient seawater temperature to settle. We estimated larval viability as the number of larvae that had attached and begun metamorphosis plus the number of larvae that were still swimming in each dish 24 h post-hatching. Although C. intestinals larvae can settle and survive for up to 9 days post-fertilization in the laboratory [29], field experiments suggest, larvae that settle more than 48 h post-fertilization are unviable (see paragraph below). Accordingly, we only used larvae that had settled within 48 h of fertilization in our experiments. Settled larvae were then circled with a graphite pencil and the settlement dishes placed in a flow-through aquarium for 24 h to allow recruits to acclimate to flowing seawater conditions.

Pilot experiments indicated that juveniles derived from larvae that delayed metamorphosis for more than 24 h (i.e. more than 48 h post-fertilization) did not survive more than 7 days in the field: juvenile viability in 24 h delay treatment = 0%; juvenile viability in natural settlement treatment = 93% (±4.98). In these pilot experiments, larvae were forced to delay settlement by placing vials filled with filtered seawater and larvae on a mechanical roller. The constantly moving vial prevents successful attachment of larvae and enforces continued swimming and delay of metamorphosis [30]. At the end of the experimental delay period (i.e. 24 h), larvae were placed in settlement dishes and allowed to settle naturally.

Three days after the initial exposure of eggs and sperm in laboratory, we randomly selected 10 recruits in each dish and transferred them to the field. All other individuals were removed with forceps. In the field, dishes were attached to four large PVC panels (550 × 550 × 6 mm) suspended 1 m below the water surface to imitate the orientation of wild individuals at the field site. After 14 days in the field, we returned dishes to the laboratory and counted the number of recruits remaining in each dish to estimate juvenile viability. We returned dishes with surviving juveniles to the field within 2 h. After 70 days in the field our focal individuals had reached maturity, so we returned dishes to the laboratory and counted the number of individuals remaining in each dish to estimate adult viability.

(c). Breeding design and variance components analysis

Although C. intestinalis is hermaphroditic, individuals were haphazardly assigned as either sires or dams. We then crossed the sperm of three sires and with the eggs of three dams, in all combinations to produce nine families for each block. For each sire × dam combination, there were two replicate dishes. There were 19 blocks in total. At each major life cycle transition (i.e. fertilization, hatching, settlement and recruitment), the dishes for each block were processed in a random order and the location of dishes (location on the bench for pre-metamorphic viability and location on the panel for post-metamorphic viability) was randomized. The final diallel design consisted of 57 sires and 57 dams and a total of 171 full-sib families. We then estimated variance components by fitting the multivariate generalized linear mixed effects model

where sire (S_j), dam (D_k), sire × dam interaction (S_j × D_k) and Petri dish nested within sire × dam interaction (PD_l(jk)) were fitted as random effects. Fixed effects were the intercept (μ) and block (B_i). The response vector (y_ijklm) contained the binary viability scores: 0 = unviable, 1 = viable for the four fitness components (embryo viability, larval viability, juvenile viability and adult viability). e_m(jkl) was the residual error. Additive genetic sources of phenotypic variation were summarized by the G_obs (co)variance matrix which was equal to four times the sire (co)variance matrix [31].

We used the MCMCglmm package [32] to fit our model. MCMCglmm fits generalized linear mixed models in Bayesian framework using Marcov chain Monte Carlo sampling to produce estimates of the location effects and variance components. For the location parameters, priors were normally distributed and diffuse about a mean of zero and a variance of π²/3. For the variance components, we used priors conforming to a scaled non-central F-distribution [33] with the location parameter equal to zero and scale parameter equal to diag(p(1 − p)), where p is mean probability of viability for each trait. The MCMC chain had a total of 1 050 000 iterations, with a burn-in period of 50 000 iterations and a thinning interval of 1000 iterations. Model fit was confirmed by showing that mean probability of viability for each fitness component (p) was within the 95% highest posterior density (HPD) intervals of the posterior predictive distribution of the corresponding fitness component (embryo viability: p = 0.735, posterior predictive HPD = 0.732–0.745; larval viability: p = 0.499, posterior predictive HPD = 0.488–0.510; juvenile viability: p = 0.735, posterior predictive HPD = 0716–0.757; and adult viability: p = 0.167, posterior predictive HPD = 0.145–0.187).

We constructed posterior mean G_obs from the means of the marginal posterior distributions for each variance component. The posterior distributions of the genetic correlations were calculated by dividing the covariance between two traits by the geometric mean of the variances (i.e. 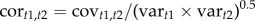, where t₁ and t₂ are the two fitness components).

(d). Testing the significance of the variance components

A condition of implementing MCMC approaches to sample the posterior distributions of parameters in complex models, where full Bayesian posterior distributions cannot be derived analytically, is that the G-matrices are constrained to be positive definite. This analytical constraint causes hypothesis tests based on examining whether posterior density intervals of variance components overlap zero to be uninformative. Thus, to provide a measure of significance for our genetic variances, we generated a null distribution that captured the genetic variance we would expect by chance, given our data and our statistical model. The procedure we used to generate our null distribution is similar to conventional randomization methods used in restricted maximum-likelihood analyses. Specifically, we randomized individuals among families and then fitted the statistical model described above to the randomized data, thereby producing estimates of G_null where there is no underlying biological structure. This procedure was repeated 100 times to capture any uncertainty introduced by the randomization procedure. For each randomization, we stored the last 10 samples of an MCMC chain with 1 050 000 iterations, a burn-in of 50 000 iterations and a thinning interval of 1000 iterations. This procedure resulted in 1000 samples (i.e. 10 samples from 100 randomizations) of the posterior distribution of G_null.

The approach we then used to evaluate the significance of the variances is based on the range of equivalence method described in Spiegelhalter et al. [34] (see [35]). Briefly, we used the upper 90% HPD interval of the genetic variance estimates of G_null as the upper bound for our range of equivalence. Because variances must be non-negative, the upper 90% HPD interval of the variance estimates of G_null reflects a one-tailed test. The probability of equivalence was evaluated by calculating the probability that the observed genetic variances are less than the upper 90% HPD interval of the corresponding null genetic variances. Probabilities of equivalence less than 0.05 were considered to support a significant difference between the observed posterior distribution and the null posterior distribution.

(e). Eigenstructure of G and matrix dimensionality

To estimate the number eigenvectors of G_obs with significant additive genetic variance, we first calculated the eigenvectors of posterior mean G_obs. Then, we projected these eigenvectors through the MCMC samples of G_obs to generate a posterior distribution of the genetic variance for the eigenvectors of posterior mean G_obs [36]. Similarly, we generated a posterior distribution of null genetic variance by projecting the eigenvectors of posterior mean G_obs through the MCMC samples of G_null. Last, we calculated the probability of equivalence between the upper 90% HPD interval of the posterior distribution of the null genetic variance and the posterior distribution of the observed genetic variance. Throughout our analysis, the same eigenvectors, the eigenvectors of posterior mean G_obs, were projected through G_obs, G_null, G_rot1 and G_rot2 (see below).

(f). An explicit test of multivariate genetic associations across metamorphosis

Although bivariate genetic correlations suggested that genetic associations exist between pre- and post-metamorphic viability (see Results), a multivariate assessment of associations across metamorphosis may be more biologically meaningful. Therefore, to provide an explicit multivariate test of genetic constraints across metamorphosis, we used rotation to a specified target matrix. The target matrix of primary interest in our study was one where the genetic correlations across the metamorphic boundary are set equal to positive one; cor(hatch, juvenile) = 1, cor(hatch, adult) = 1, cor(larval, juvenile) = 1, cor(hatch, adult) = 1. Given the genetic variances of the corresponding fitness components, the covariances required to satisfy the condition that cor_t1,t2 = 1 are found by rearrangement of 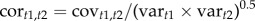. Replacing the observed genetic covariances with these calculated genetic covariances, gives the rotated target G-matrix (G_rot1) that satisfies the null hypothesis of genetic correlations across the metamorphic boundary being equal to positive one.

To construct a hypothesis test using the null hypothesis target matrix G_rot1, we adapted the approach outlined by Agrawal & Stinchcombe [37] for determining how a G-matrix with genetic correlations equal to zero would influence the predicted response to selection. Here, we compared the observed genetic variance in g_obsmax with the genetic variance of the same eigenvectors projected through G_rot1. Specifically, we projected g_obsmax of posterior mean G_obs through each of the MCMC samples of G_obs and G_rot1, resulting in a posterior distribution of the observed genetic variance (Va_obs(g_obsmax)) and the genetic variance in the same eigenvector when aligned with the hypothesis that independent evolution across metamorphosis cannot occur (Va_rot1(g_obsmax)). As each MCMC sample of G_obs has a corresponding MCMC sample of G_rot1, the estimated genetic variances could be compared in a pairwise manner by calculating the difference in the genetic variance between paired samples of G_obs and G_rot1. This difference had an unbounded distribution with a null expectation of zero. Therefore, if the probability of including zero in the posterior distribution of Va_obs(g_obsmax) – Va_rot1(g_obsmax) was less than 0.05, we interpreted this as evidence that the observed distribution of genetic variance does not support genetic correlations equal to positive one.

Although positive genetic correlations of one are the most informative null hypothesis for our four fitness components, given the substantial changes in phenotype that occur during metamorphosis, it is reasonable to test whether across metamorphosis genetic correlations in multiple fitness components also differ from zero. Therefore, we used target matrix rotation to test the null hypothesis of genetic correlation across metamorphosis equal to zero. The second target matrix was the covariance matrix where the elements in the lower left and upper right quadrants of posterior mean G_obs result in genetic correlations of zero. The same procedure as we describe above for G_rot1 was conducted for G_rot2 to test the hypothesis that there are no genetic associations across metamorphosis.

3. Results

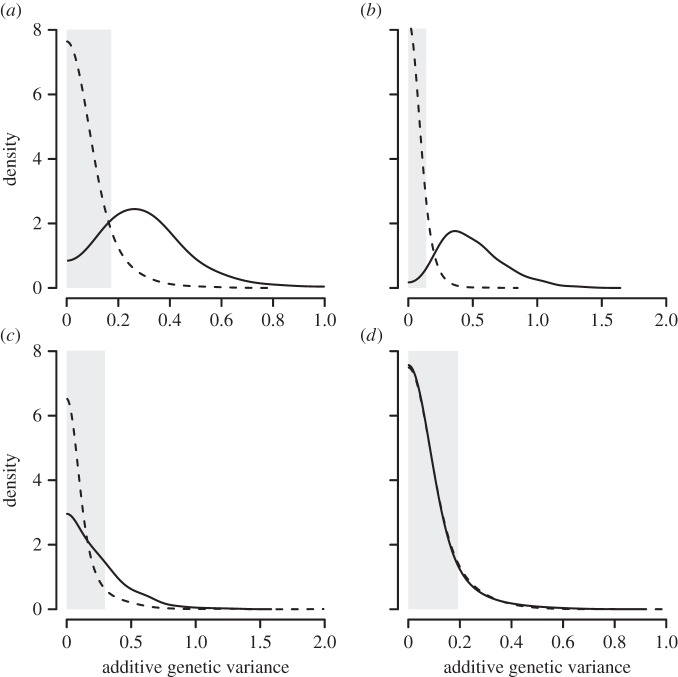
The mean proportional viability of C. intestinalis differed for each developmental stage (table 1). Mean viability was high for embryos and juveniles but lower for larvae and declined considerably for adults (p(hatch) = 0.774, p(larval) = 0.526, p(juvenile) = 0.774, p(adult) = 0.172). Additive genetic variance (Va) showed similar trends throughout development (table 1); however, Va was only significant for larval viability (probability of equivalence between Va_null(larval) and Va_obs(larval) = 0.023; figure 1b). As expected for fitness components, the heritabilities for the four fitness components were of low to moderate magnitude (h²(hatch) = 0.125, h²(larval) = 0.204, h²(juvenile) = 0.127, h²(adult) = 0.060). We found evidence for two negative bivariate genetic correlations: one between embryo and larval viability, and one between larval and juvenile viability (table 1). Furthermore, although not statistically significant, we found a positive genetic correlation between embryo and juvenile viability. These genetic correlations indicate associations between genes underlying embryo, larval and juvenile viability.

Table 1.

Mean viability and posterior mean additive genetic variance–covariance matrix (G_obs) calculated from the multivariate mixed effects model. Variances are displayed on the diagonal in bold, covariances are below the diagonal and correlations (±95% HPD intervals) are above the diagonal. Note that the coefficients are on the logit scale.

	embryo viability	larval viability	juvenile viability	adult viability
trait means
	1.427	0.122	1.429	−1.822
G
	0.302	−0.792 (−1.000 – −0.385)	0.542 (−0.312 – 1.000)	0.033 (−0.965 – 1.000)
	−0.290	0.494*	−0.721 (−1.000 – −0.090)	−0.090 (−1.000 – 0.967)
	0.131	−0.243	0.249	0.100 (−0.948 – 0.999)
	0.003	−0.014	0.012	0.070

*p < 0.05.

Figure 1.

Posterior density distributions for the observed genetic variance (solid line) and the null genetic variance (dashed lines) of the four fitness components considered in our study: (a) embryo viability, (b) larval viability, (c) juvenile viability and (d) adult viability. Grey areas denote the regions of equivalence for the observed and null distributions.

We found support for only one significant eigenvector of G_obs (probability of equivalence between Va_null(g_obsmax) and Va_obs(g_obsmax) = 0.006; figure 2a). The effective number of dimensions [38] also suggested there are less than two dimensions in posterior mean G_obs (n_D = 1.3). The dominant eigenvector of posterior mean G_obs (g_obsmax) describes 75% of the additive genetic variation in offspring viability. g_obsmax has a strong contribution from larval viability that was in the opposite direction to embryo and juvenile viability (table 2).

Figure 2.

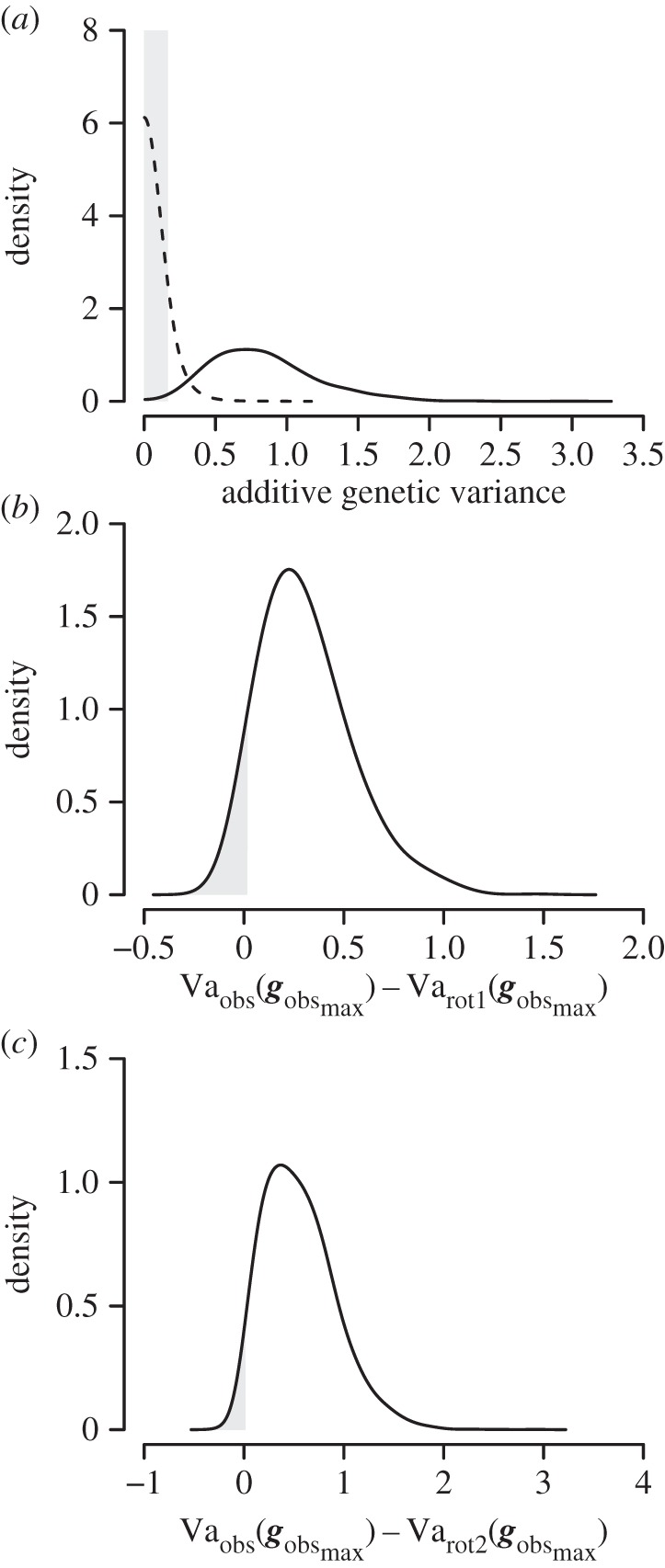
(a) Posterior density distribution for the observed genetic variance (solid line) and the null genetic variance (dashed lines) of g_obsmax. Grey area denotes the region of equivalence between the observed and null distribution. (b,c) Posterior density distribution for the difference in genetic variance between Va_obs(g_obsmax) and Va_rot1(g_obsmax) as well as the difference in genetic variance between Va_obs(g_obsmax) and Va_rot2(g_obsmax), (b) and (c), respectively. Grey areas denote the 5% lower posterior density interval.

Table 2.

Eigenvectors of G_obs. λ and % denote the eigenvalues and percentage of the variance contributed by each eigenvector of G_obs, respectively.

	gobsmax	gobs2	gobs3	gobs4
λi	0.833*	0.143	0.072	0.068
%	75	13	6	6
embryo viability	0.513	0.661	−0.445	0.320
larval viability	−0.745	0.026	−0.567	0.351
juvenile viability	0.426	−0.743	−0.482	0.182
adult viability	0.023	−0.099	0.499	0.861

*p < 0.05.

We used a target matrix rotation to test the hypothesis that genetic correlations between pre- and post-metamorphic viability are equal to positive one. Rotation of G_obs to a part of the space which supported the null hypothesis that independent evolution cannot occur (G_rot1) resulted in a 37% decrease in genetic variance (posterior mean Va_obs(g_obsmax) = 0.833 posterior mean Va_rot1(g_obsmax) = 0.522) and a 0.030 probability that Va_rot1(g_obsmax) was greater than Va_obs(g_obsmax). Rotation of G to a part of the space which supported the null hypothesis that genetic correlations are equal to zero (G_rot2) resulted in a 26% decrease in genetic variance (posterior mean Va_obs(g_obsmax) = 0.833 posterior mean Va_rot2(g_obsmax) = 0.620) and a 0.048 probability that Va_rot2(g_obsmax) was greater than Va_obs(g_obsmax). These analyses indicated support for genetic correlations across metamorphosis correlations that are significantly less one and not to equal zero (figure 2b,c).

4. Discussion

The larvae and adults of the same species often differ substantially in form and function, and maintaining a common body plan throughout ontogeny could compromise performance in one stage. Partitioning the life cycle into distinct stages may carry benefits, because by allowing larvae and adults to respond independently to the unique selection pressures of each stage, organisms with complex life cycles are able to use resources or perform specialized functions (e.g. dispersal, growth or reproduction) more effectively [3,4,39]. The genetic decoupling of pre- and post-metamorphic events as a consequence of metamorphosis is hypothesized to be a major evolutionary benefit of complex life cycles [4], but few studies have demonstrated the genetic independence of pre- and post-metamorphic phenotypes [9,25]. Part of the problem in finding consistent support for adaptive decoupling may be that if the same traits are measured pre- and post-metamorphosis, a more useful null hypothesis for examining genetic independence is a genetic correlation of one [13,14]. Our target matrix rotation analyses show that a genetic architecture representing positive genetic correlations of one is not supported by our data. Instead, our data are best described by a mixture of positive and negative genetic associations between pre- and post-metamorphic viability in C. intestinalis.

The dramatic changes that accompany metamorphosis in marine invertebrates are expected to exert profound changes in selection [40], and differential gene expression across metamorphosis seems common in marine invertebrates with complex cycles [41–43]. However, evidence for complete independence is equivocal, and our quantitative genetic assessment of developmental associations across metamorphosis is supported by molecular studies of C. intestinalis. For instance, using microarray techniques, Azumi et al. [42] showed that approximately 20% of genes are expressed at similar levels in life cycle stages separated by metamorphosis. Our results indicate that there is genetic variation segregating among loci with additive effects on pre- and post-metamorphic traits.

The additive genetic associations we found between embryo, larval and juvenile viability in g_obsmax may reveal important limits on evolution in C. intestinalis. We found that offspring from sires with genes that conferred higher levels of viability during the larval stage had increased mortality during embryogenesis and after metamorphosis. As such, despite selection for higher viability in each life cycle stage, all three stages are bound to suffer some mortality because of the genetic associations among fitness components. While the genetic basis (pleiotropy or linkage disequilibrium) of the negative genetic associations among fitness components we found in our study remains unknown, in many studies of marine larvae, hatching and metamorphic success are rarely 100% [44–46]. For example, Evans et al. [28] found a negative phenotypic correlation for hatching viability and metamorphic success in the sea urchin Heliocidaris erythrogramma. Post-metamorphic mortality rates of marine invertebrates are notoriously high and can sometimes limit population growth rates [47]. Traditionally, the high mortality rates of larvae and recruits has been attributed to external environmental factors or more recently, the physiological condition of settling larvae [47,48]. If genetic associations such as those observed here are common in marine invertebrates [24,28], these correlations may play a larger role in limiting marine populations than is appreciated currently [18].

Genetic variation for fitness components is the product of many genes underlying the combined effects of multiple traits. Therefore, although we have shown that independent evolution across metamorphosis is possible, by investigating genetic decoupling for viability we have estimated the average effects of many genes. It is unlikely that genetic variation is distributed similarly across metamorphosis for all traits contributing to viability. For instance, the strength of developmental independence across metamorphosis may differ for homologous (e.g. larval and juvenile size) and analogous traits (e.g. acquiring a settlement site as a larva and acquiring planktonic food as a juvenile). Unfortunately, studies to date have predominantly examined morphological decoupling across metamorphosis [9,25], and so it is difficult to compare the relative strength of adaptive decoupling among trait types (i.e. physiological, behavioural, morphological and life-history traits). Furthermore, in the few studies where associations across metamorphosis have included different trait types [10,24], traits appear to have been chosen based on experimental convenience, rather than to allow balanced comparisons of the strength of adaptive decoupling among trait types. Detailed studies that systematically estimate the strength of genetic associations across metamorphosis within and among different trait types would significantly advance our understanding of the evolutionary benefits of metamorphosis.

By systematically removing some individuals from the population, viability selection in earlier life cycle stages can bias the distribution of traits measured in later life cycle stages, and thereby influence estimates of evolutionary parameters [49–51]. For example, Mojica & Kelly [52] found that estimates of selection on flower size in Mimulus guttatus changed sign when the negative association between flower size and survival to maturity was included in their analyses. Similarly, Hadfield [50] and Steinsland et al. [51] show that ignoring missing data when data are not missing at random can bias estimates of predicted breeding values and additive genetic variation. In our study, viability was the missing data process, as well as the focus of our investigations, hence viability selection was explicitly considered in our genetic analyses. For traits with low heritability, such as in our study (heritability < 0.25 for all traits), the bias in univaritate estimates of genetic variation caused by ignoring the missing data process can be relatively small [51]. However, our data and the field data of Steinsland et al. [51] demonstrate that the genetic covariance associated with viability can be large. Genetic associations involving viability may significantly alter predictions of evolutionary change, because given that viability is a fitness component indirect selection on traits associated with viability is likely to be common.

Our results should be interpreted with the important caveat that pre-metamorphic viability was estimated in the laboratory, whereas post-metamorphic viability was estimated in the field. Ideally, viability during both phases would have been estimated under natural conditions. Unfortunately, tracking individual embryos and larvae of known pedigree in the water column is impossible for our study species. Nevertheless, we suspect that the estimated genetic associations across metamorphosis are representative of the likely associations in natural populations. The main sources of mortality during the pelagic, early life cycle stages of many marine organisms are predation and advection away from suitable habitat [53]. To the best of our knowledge, there is no evidence to suggest that larval predation or advection are genotype-specific and as such, insulating embryos and larvae from these sources of mortality may inflate overall viability, but is unlikely to generate spurious genetic associations between pre- and post-metamorphic viability.

Since the early development of the adaptive decoupling hypothesis, empirical studies have been designed to prove or disprove adaptive decoupling by examining genetic correlations for traits on the same side of metamorphosis and traits separated by metamorphosis [9,10,54], or by examining the stage, or stages in which genes with specific functions are expressed [11,12,55]. Although these studies show that adaptive decoupling and developmental constraints across the metamorphic boundary exist, the evolutionary consequences of genetic associations across metamorphosis still remain uncertain. We suggest that studies examining associations across metamorphosis must carefully consider the appropriate null hypothesis for the test of interest, and we provide a new framework that allows an explicit test of genetic associations across metamorphosis in multiple traits. Such approaches should allow us to quantify the relative contribution of coupled versus decoupled traits to fitness, and thus the overall constraints on phenotypic evolution in organisms with complex life cycles.

Data accessibility

Dryad data reference: doi:10.5061/dryad.n5rj9.

Funding statement

This work was funded by an Australian Research Council grant to D.J.M. J.D.A. was supported in part by a University of Queensland Research Scholarship, Te Kotahitanga o Te Arawa Fisheries and the Ngati Whakawe Education Trust.