Significance
Alzheimer's disease and several related disorders are associated with the assembly of specific proteins into ordered fibrillar aggregates. In Alzheimer's disease, the key component of pathological aggregates, the Aβ peptide, is produced from a precursor protein in variable lengths: Aβ40 is more abundant and Aβ42 more aggregation-prone. To shed light on the molecular basis of disease progression, the aggregation process has been studied in vitro. New theoretical models allow us to relate kinetic measurements to the rates of the individual processes underlying the aggregation reaction. We find that the loss of two residues in Aβ40 relative to Aβ42 significantly slows nucleation of aggregates in solution, thereby shifting the mechanism yet more strongly towards nucleation on the surface of fibrils.
Keywords: protein aggregation, rate law, neurodegeneration, aggregation mechanism
Abstract
The two major forms of the amyloid-beta (Aβ) peptide found in plaques in patients suffering from Alzheimer’s disease, Aβ40 and Aβ42, only differ by two amino acids in the C-terminal region, yet they display markedly different aggregation behavior. The origins of these differences have remained challenging to connect to specific molecular-level processes underlying the aggregation reaction. In this paper we use a general strategy to apply the conventional workflow of chemical kinetics to the aggregation of the Aβ40 peptide to identify the differences between Aβ40 and Aβ42 in terms of the microscopic determinants of the aggregation reaction. Our results reveal that the major source of aggregates in the case of Aβ40 is a fibril-catalyzed nucleation process, the multistep nature of which is evident through its saturation behavior. Moreover, our results show that the significant differences in the observed behavior of the two proteins originate not simply from a uniform increase in all microscopic rates for Aβ42 compared with Aβ40, but rather are due to a shift of more than one order of magnitude in the relative importance of primary nucleation versus fibril-catalyzed secondary nucleation processes. This analysis sheds light on the microscopic determinants of the aggregation behavior of the principal forms of Aβ and outlines a general approach toward achieving an understanding at the molecular level of the aberrant deposition of insoluble peptides in neurodegenerative disorders.
Alzheimer’s disease is the most prevalent of several increasingly common neurodegenerative diseases, all fundamentally related to the self-assembly of a specific, often misfolded, protein (1–8). The two major components of protein deposits in Alzheimer’s disease are two fragments of the amyloid beta peptide, Aβ42 and Aβ40, where Aβ42 has two additional amino acids at the C terminus. These two forms of Aβ are known to display significantly different aggregation propensities at the same pH values and concentrations (9–11), but the underlying origin of these differences has not yet been firmly established.
Commonly, biomolecular assembly pathways, such as the aggregation of proteins, take the form of complex networks whose analysis in terms of elementary reaction steps presents a significant challenge, yet is the key to a molecular-level understanding of these processes. For simple chemical transformations, this challenge can be addressed through the use of the established framework of chemical kinetics to test for specific types of reaction mechanisms, an approach that represents a powerful tool to elucidate the various microscopic processes of which all chemical reactions are composed. A central requirement for the successful application of this approach is the ability to summarize the net reactive fluxes in the system through an integrated rate law. Such rate laws have until recently only been available for transformations between a finite and typically small number of distinct classes of chemical species (12). In this paper we show how the framework of chemical kinetics can be extended to account for transformations within a complex chemical network characteristic of biomolecular assembly pathways underlying the differences in the aggregation behavior of the Aβ peptides.
We apply the rate laws derived in this work to elucidate the aggregation mechanism of the most abundant form of the Aβ peptide (13), Aβ40. By comparison with the previously defined aggregation mechanism of Aβ42 (9), this allows us to determine which differences in the microscopic processes are responsible for the differing aggregation behaviors of the two forms of Aβ. We find that the nucleation step in the aggregation of Aβ40, like that of Aβ42, is strongly catalyzed by existing aggregates, but that the reaction follows a Michaelis–Menten-type dependence known from other forms of biocatalytic reactions, notably of enzymes (14), thereby revealing its multistep nature. Furthermore, a shift in the relative rates of the individual microscopic reaction steps, with primary nucleation being most affected, is found to contribute to the differing aggregation kinetics of the two peptides.
Results and Discussion
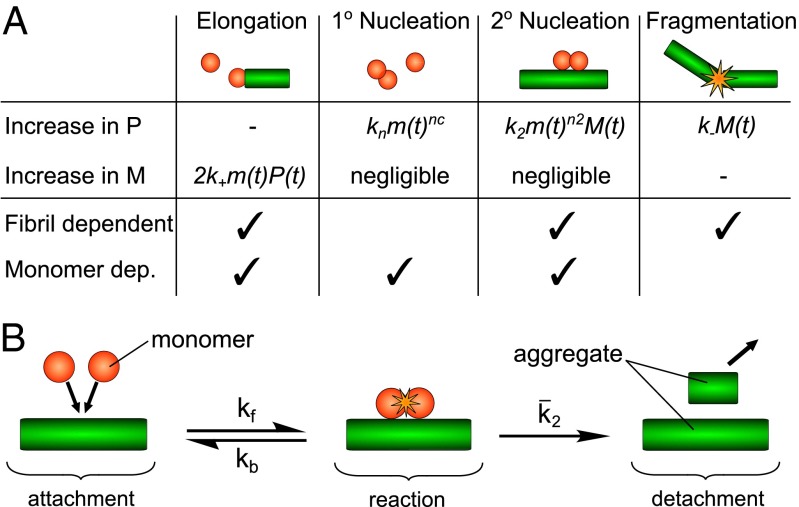
Because protein aggregation pathways are more complex than those of the types of chemical transformations that are routinely analyzed through the use of the framework of chemical kinetics, it is crucial to carry out and analyze the results from a significant number of individual experiments performed under distinct but carefully controlled conditions. It is essential to consider only mechanisms that account quantitatively for the entire body of experimental data by means of global analysis to obtain sufficient constraints for fitting the data to complex rate laws. In the most general case, microscopic steps that make up linear growth reactions consist of nucleation processes, which create new aggregates, and growth processes, which contribute to the elongation of existing aggregates as shown in Fig. 1A. To have a mechanistic understanding of an aggregation reaction, therefore, it is crucial to define the manner in which the microscopic processes contribute to the overall reaction, and to establish whether or not the basic classes of nucleation and growth processes consist of a single elementary step or are multistep in nature.
Fig. 1.
A schematic depiction of the microscopic steps involved in fibrillar aggregation. (A) The principal processes relevant for filamentous aggregation, their dependence on the concentrations of monomers (m) and fibrils, and how they contribute to the changes in the number (P) and mass concentrations (M) of fibrils. The rate constants are k+ (elongation at fibril ends), kn (primary nucleation in solution of order nc), k2 (secondary nucleation on the fibril surface of order n2), and k− (fibril fragmentation). (B) A graphical depiction of the proposed reaction scheme for secondary nucleation (Supporting Information, section 1.1) wherein monomers first come together in the presence of an aggregate, then monomer-independent reaction and detachment steps take place to yield the product.
To achieve sufficient reproducibility in the aggregation behavior of the Aβ40 peptide to allow for quantitative analysis of the microscopic steps defining its overall reaction mechanism, we used recombinant peptide to ensure a fully homogeneous sequence. The presence of multiple similar sequences in synthetic peptides of this length has been shown to lead to an overall retardation of aggregation and changes the shape of individual curves (15). Moreover, we minimized extrinsic, potentially bioactive surfaces from the system by using degassed buffer and half-area low-binding plates and subjected the peptide to several rounds of size-exclusion chromatography to eliminate the presence of a small number of preformed aggregates at uncontrolled concentrations, which can lead to highly variable behavior of the system. We monitored the reaction by using a fluorescent reporter dye, thioflavin T (ThT); we performed extensive controls (Supporting Information, section 2.3 and Fig. S1) to ensure that ThT reports accurately on the progress of the reaction within the given concentration range.
A comprehensive body of data was obtained by performing controlled aggregation experiments at a series of initial monomer concentrations [m]0 ranging from 3.5–70 μM. We initially focus on and analyze a global measure of the progress of the reaction, the characteristic half-time, t1/2, which is the time at which 50% of the protein is found in aggregated form. The monomer dependence of t1/2 is commonly observed to take the form of a power law, , where γ is a characteristic exponent that yields information about the dominant nucleation mechanism present (16–20). We find, however, from our experiments that for Aβ40 this scaling exponent is highly dependent on the concentration regime under which the reaction is performed: Indeed, γ varies from −1.2 ± 0.2 at low protein concentrations (ca. 5 μM) to −0.2 ± 0.05 at higher protein concentrations (ca. 60 μM).
The observation of the concentration dependence of the exponent γ strongly suggests that one or more of the microscopic processes contributing to the aggregation reaction changes its monomer dependence and hence becomes saturated at higher monomer concentrations. Several other possible origins of a concentration dependence of γ and why they fail to describe the present system are discussed in detail in Supporting Information, section 1.3 and Fig. S2. A saturation process has previously been found for the elongation step of amyloid growth from a range of proteins and revealed the elongation reaction to be a multistep process (21, 22). However, owing to its weak first-order dependence on monomer concentration (23), the resulting change in exponent from a saturation of elongation (<0.5) can contribute to but is not sufficient to explain the increase of 1.0 ± 0.2 observed in the data in Fig. 2B. Moreover, we performed a number of strongly seeded aggregation experiments that allowed us to extract separately the elongation rate and show that a saturation of elongation is insignificant below monomer concentrations of 30 μM (Supporting Information, section 1.7 and Fig. S3). Hence, the observed variation in γ strongly suggests that the secondary nucleation steps in protein aggregation are also capable of undergoing saturation and therefore must be multistep in nature. Thus, we set out to use chemical kinetic measurements to dissect the nucleation pathways of Aβ40 aggregation.
Fig. 2.
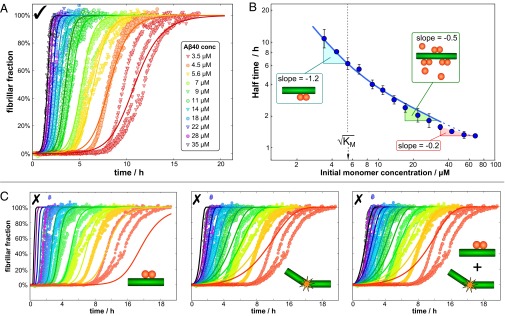
Global fit to experimental data. (A) The global fit of Eq. 4 to the unseeded aggregation data with three free parameters: KM and the combinations k+kn and k+k2 for the entire dataset (n2 and nc were set to 2). The three independent experiments for each monomer concentration are in the same color, with the fit to those three runs being a solid curve in the same color. A zoomed-in version of the high concentration curves and the residuals are shown in Supporting Information, section 1.8 and Figs. S5 and S6. The values of the fitted parameters are given in Fig. 3B. (B) A plot of the average half-time versus the initial monomer concentration. The solid blue line is the theoretical prediction, not a fit, of the half-time, using Eq. 11 and the parameters determined in A. The regions of unsaturated and fully saturated secondary nucleation are marked on the graph, gives the concentration of half-saturation of secondary nucleation, and the dashed blue line denotes the region where elongation may begin to saturate. (C) Fits to the three possible models with simple secondary pathways (single-step secondary nucleation, fragmentation without secondary nucleation, and a competition of fragmentation and single-step secondary nucleation) were performed to show that neither can achieve a good global fit (see also Fig. S6).
Theoretical Model of Filamentous Growth with Multistep Nucleation.
To derive the integrated rate laws required for a kinetic analysis, we use the framework of filamentous aggregation models (16, 18, 19, 24– 26), which allows us to connect macroscopic measurements of Aβ40 aggregation to the underlying microscopic mechanisms. We generalize the filamentous aggregation framework to account for saturation of secondary nucleation. The proposed general scheme is shown in Fig. 1B (Fig. S4) and results in a kinetic description of the aggregation process that is formally analogous to the Michaelis–Menten kinetics of two-step enzyme activity. We note that an equivalent expression can be derived by considering a Langmuir-like adsorption onto the fibril surface, as done by Ferrone et al. (16) (Supporting Information, section 1.1).
The saturation effects are found to be determined by a single constant, KM, which plays a role analogous to the Michaelis constant in enzymology and represents a threshold concentration above which the monomer dependence of the secondary nucleation process becomes saturated. Although the physical basis of amyloid growth and enzymatic action is different, the formal analogy to Michaelis–Menten kinetics that emerges from Eq. 3 can be understood in general by considering that the monomers take the role of the substrate, nuclei take the role of the product, and fibrils take the role of the enzyme as they facilitate the conversion of the monomeric peptide into its amyloid form. The monomer concentration enters the kinetic equations as a power n2, the number of monomers that take part in the reaction, whereas in the common Michaelis–Menten scheme the substrate concentration enters simply to the first power, because only one substrate molecule is converted to product at a time. The constant KM determines when the surface-catalyzed secondary nucleation step is saturated: At low monomer concentrations, , the secondary nucleation rate is limited by the attachment of the free monomer present, and the form for a single-step nucleation process (9, 16) is recovered. At high monomer concentrations, , the second, and monomer-independent, step in Fig. 1B becomes rate-limiting because the sites for secondary nucleation are fully saturated and the overall rate is determined by the conversion to and detachment of new nuclei. Note that in the case of an unseeded aggregation reaction the time evolution of the system depends only on combinations of the rate constants k2k+ and k+kn, not the individual rate constants.
Analysis of the Experimental Kinetic Data.
The analysis of the measurements of the kinetic profiles for Aβ40 aggregation as a function of its concentration reveal, remarkably, that the entire set of kinetic data at multiple concentrations can be described by the single rate law Eq. 4 that emerges from a multistep secondary nucleation process (Fig. 2 and Fig. S5). We stress that the fits describe the data in a fully global manner; the aggregation profiles at different concentrations are not fitted individually, but rather a single rate law applies to the complete dataset where the microscopic rate constants are fixed, and only the independently measured initial concentrations are entered as initial conditions for the individual experiments. Furthermore, the analysis in Fig. 2 demonstrates that rate laws with either an elementary single-step secondary pathway with a fixed reaction order, or two such pathways competing in parallel, are not able to describe the data even qualitatively when considering the entire dataset (Fig. S6). Any given curve at a single concentration can, however, be fitted even with an incorrect rate law, highlighting the fundamental importance of global analysis of concentration-dependent data when probing mechanisms of complex biomolecular assembly pathways such as that studied here. The demonstration that all of the curves can be fitted to a single function simply by varying the known amounts of peptide is a very powerful validation of the proposed mechanism.
The Michaelis constant for saturation of secondary nucleation, KM, was determined to be 31 μM2, a value that predicts that secondary nucleation becomes half-saturated at monomer concentrations of 5–6 μM. The values of the rate constants determined from the global fitting procedure were then used to predict the values of the reaction half-time t1/2 at the different initial monomer concentrations, Eq. 11, and then plotted against the experimental values of t1/2 in Fig. 2B. The agreement is very good for monomer concentrations below 30 μM. At low monomer concentrations, the secondary nucleation rate is limited by the monomer-dependent step, whereas at high monomer concentrations it is limited by the monomer-independent step. At even higher monomer concentrations exceeding 30 μM the observed γ is −0.2, which is above the maximum possible γ of −0.5 predicted in Eq. 11. This effect may be partly attributed to the possibility of the saturation of the elongation step at high monomer concentrations. To investigate the saturation of elongation, a number of strongly seeded aggregation experiments were performed. In such experiments, sufficient preformed fibrils are added to the reaction mixture that the role of the intrinsic nucleation processes becomes negligible, and hence the evolution of the reaction under this type of strongly seeded conditions is only dependent on the elongation of the aggregates (23). This analysis reveals that the slopes of the kinetic profiles increase less strongly when the monomer concentration exceeds 30 μM than at lower concentrations, a possible indication that saturation of elongation, as observed for other systems (21), may occur for Aβ40 when the monomer concentration exceeds 30 μM (Supporting Information, section 1.7 and Fig. S3). To determine the fundamental rate constants pertaining to secondary nucleation, we therefore focused on the data in the range where no saturation of elongation occurs, [m]0 < 30 μM (Supporting Information, section 1.8 and Fig. S7).
Comparison with Aβ42.
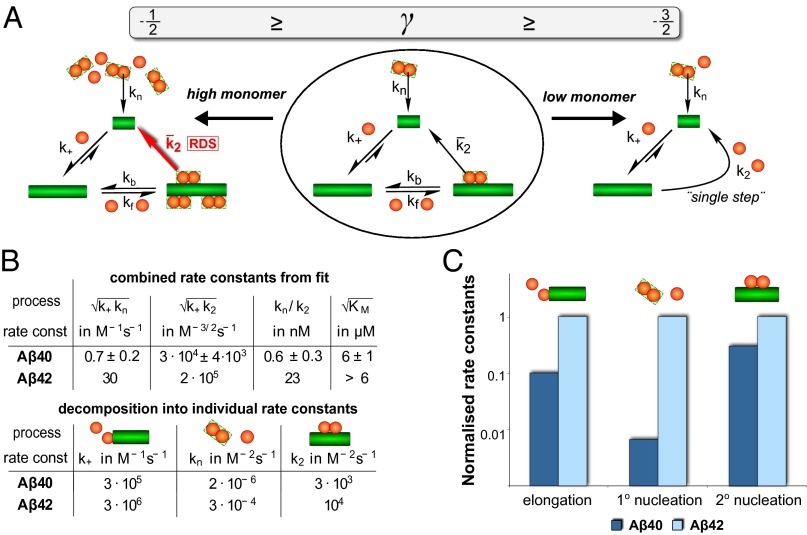
The determination of the aggregation pathway and of the microscopic rate constants of Aβ40 aggregation in the present work provides us with the opportunity to understand the nature of the differences in the molecular-level determinants of the behavior of Aβ40, the most abundant form of the Aβ peptide in vivo, from that of Aβ42, the form of the peptide that dominates the deposition in Alzheimer’s disease and has emerged as the primary risk factor for this condition. We find that the combined rate constants obtained from the fit in Fig. 2A are both an order of magnitude smaller than the rate constants determined for Aβ42 (Fig. 3C), a finding that is reflected in the substantially larger values of t1/2 for Aβ40 than for Aβ42. These data explain the requirement for significantly higher concentrations of Aβ40 to observe and measure aggregation on timescales comparable to those for Aβ42. Even more interestingly, however, for Aβ42 no saturation is observed at concentrations up to 6 μM (9).
Fig. 3.
Rates and mechanistic differences between Aβ40 and Aβ42 aggregation. (A) Summary of the full reaction scheme. On the left and right, the limiting cases of high and low monomer concentration are shown. In low monomer conditions secondary nucleation is effectively single-step and in the high monomer limit the second step of the secondary nucleation process becomes rate-determining (RDS). Whereas both are relevant for Aβ40, only the low monomer behavior is observed for Aβ42. (B) Table of the combined rate constants obtained from the global fit and the individual microscopic rate constants of aggregation (in both cases n2 = nc = 2). The ratio kn/k2 describes the aggregate concentration above which secondary nucleation will be producing more nuclei than primary nucleation and shows that secondary nucleation is significantly more important than primary nucleation for Aβ40. The errors in the upper table were estimated by fitting different subsets of the replicates at each concentration; for details see Supporting Information, section 1.6. The elongation rate and hence all parameters in the lower table are only accurate to within a factor of 3 (Supporting Information, section 2.1). (C) Comparison of the individual rate constants of Aβ40 and Aβ42, normalized to the rate in Aβ42 and shown on a logarithmic scale. Note that the relative difference in rate constant is significantly larger for primary nucleation than for the other two processes.
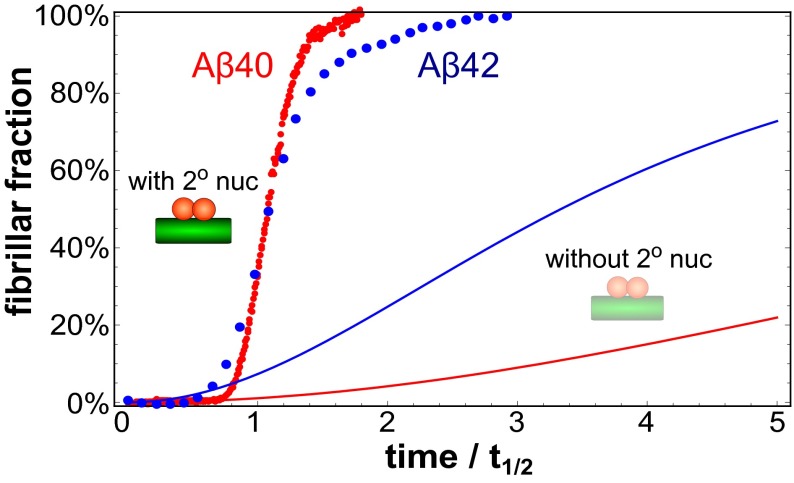
To decompose the combined rate constants, and , obtained from the global fitting procedure into individual values for kn and k2, an estimate of the elongation rate constant k+ is required. To obtain such estimates, we used cryogenic transmission electron microscopy (cryo-TEM) (Fig. S8) to define the average fibril length, L, and thereby the fibril number, [P]t=0 = [M]t=0/L, in the seeded experiments (Supporting Information, sections 2.1 and 2.2). Unlike the combined rate constants, which can be determined accurately from the global fits, the individual rate constants obtained in this manner contain a source of uncertainty owing to the error in the initial gradient of the seeded data and the estimate of the fibril length. We note, however, that both the saturation effect and the relative increase in importance of secondary nucleation for Aβ40 are both independent of this estimation of k+. An examination of the data shows that the rate constants for all of the microscopic processes are decreased for Aβ40, relative to Aβ42, indicating higher energy barriers for all microscopic processes, rather than simply increased dissociation rates or retardation of one specific microscopic step, as could well have been concluded from the simple increase in half-times. In particular, the relative contribution from primary nucleation is decreased by over an order of magnitude in Aβ40 relative to Aβ42 (as evident in Fig. 3). This result is also reflected in the curve shapes in Fig. 4, where the relative increase in aggregate mass for Aβ40 can be seen to occur considerably more suddenly as a result of the more pronounced autocatalytic nature of the reaction owing to a larger relative contribution from secondary nucleation.
Fig. 4.
Comparison of Aβ40 and Aβ42 aggregation data. Comparison of the experimental kinetic datapoints of Aβ40 (red) and Aβ42 (blue) at a monomer concentration of 3.5 μM. The times for each dataset are rescaled by the corresponding half-times and the steeper increase of the Aβ40 curve is indicative of its stronger autocatalytic behavior, on a relative scale. The solid lines (Aβ40 in red and Aβ42 in blue) are a prediction for the same system in the absence of secondary nucleation but with all of the other rate constants at the values determined from the experiment. The significant difference in these predictions highlights the larger relative contribution of secondary nucleation for Aβ40 relative to Aβ42.
It is interesting to speculate that the increased hydrophobicity imposed by residues Ile41 and Ala42 plays an important role in all of the microscopic aggregation processes by decreasing all barriers of aggregation for Aβ42, suggesting that common features in the transition states controlling the different microscopic processes may exist. Moreover, the weaker effect on elongation and secondary nucleation, compared with primary nucleation, suggests that interactions with the fibrils decrease the importance of residues 41 and 42 in the assembly reaction, compared with assembly of free monomers in solution characteristic of primary nucleation processes.
Conclusions
We have used chemical kinetics to dissect the aggregation behavior of the Aβ40 peptide into its component microscopic steps. We have shown that a dominant contribution to the formation of new aggregates under the quiescent conditions used is a fibril-catalyzed secondary pathway, a mechanistic feature that is shared between both the major variants of the Aβ peptide, Aβ40 and Aβ42. In contrast to the aggregation process of the Aβ42 peptide, however, the reaction order of the secondary pathway in Aβ40 aggregation is highly dependent on the concentration of monomeric peptide in solution. We show that this fact originates from the multistep nature of secondary nucleation; below a characteristic monomer concentration, the generation of secondary nuclei depends on the concentration of free monomers and their attachment to the fibril surface, whereas at high monomer concentrations the reaction becomes dominated by the conversion and detachment of bound peptide molecules, a process that is independent of the surrounding free monomer concentration. Moreover, we find that all microscopic rate constants of aggregation are smaller for Aβ40 relative to those of Aβ42, which indicates that the presence of residues 41 and 42 in Aβ42 plays an important role in lowering the energy barrier for all of the steps in the conversion process of monomer to fibrils. One of the major consequences of fibril-catalyzed nucleation, identified here for the Aβ40 peptide, is the emergence of positive feedback, which increasingly favors the formation of new aggregates once even a small concentration of such species is formed. In the context of the development of neurodegenerative disease, such a situation is likely to contribute to the difficulty in controlling and curtailing the extent of aggregation once it has been initiated.
Materials and Methods
Materials.
The Aβ(M1-40) peptide (here called Aβ40) with amino acid sequence MDAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGG was expressed in Escherichia coli from a synthetic gene and purified from inclusion bodies as described elsewhere (27). Purified monomer was lyophilized by freezing the monomeric protein in 20 mM sodium phosphate buffer, 0.2 mM EDTA, 0.02% sodium azide, pH 7.4 at −80 °C and then drying under vacuum. It was then dissolved in 1 mL 6 M GuHCl and subjected to size-exclusion chromatography in degassed buffer (20 mM sodium phosphate, 200 μM EDTA, 0.02% sodium azide, pH 7.4) on a Superdex75 column (GE Healthcare). The fraction corresponding to the center of the monomer peak was again lyophilized and the gel filtration procedure repeated to ensure pure monomer at time 0. The monomer was collected on ice and a dilution series was prepared in the same buffer on ice in low-bind tubes (Axygen). All chemicals were of analytical grade.
Kinetic Assays.
Forty-two unseeded aggregation experiments of Aβ40 were performed, at 14 different monomer concentrations between 3.5 μM and 70 μM, as triplicate repeats at 37 °C in quiescent conditions, in half-area low-binding plates (Corning 3881). The whole procedure was repeated three times with similar results. The differences between repeats of the same experiment at low monomer concentrations are due to experimental error and provide a limit on the possible accuracy of the fits. The data were collected by fluorescence spectroscopy, using 100 μM of the dye ThT as a reporter molecule (Supporting Information, section 2.3). At this concentration the dye gives a linear relationship between fluorescence intensity and aggregate concentration as evaluated using a strategy similar to that in ref. 28. Note that the rate constants for Aβ42 given in Fig. 3B were obtained at a slightly higher pH (8.0 for Aβ42 versus 7.4 for Aβ40). This was owing to the fact that the aggregation of Aβ40 proceeds too slowly at pH 8.0 to produce reliable data, hence the differences in rate constants for the two peptides are expected to be even larger at pH 8.0 than apparent in the tables.
A sample was taken when the sigmoidal curve reached the plateau and formation of fibrils was confirmed by cryo-TEM (Fig. S8); all experimental details can be found in Supporting Information, section 2.2.
Each set of experimental data was baseline-corrected and normalized such that the relative mass concentration of aggregates is 0 at time 0 and 1 at completion of the aggregation. The seeded experiments were performed in the same monomer concentration range as in the unseeded case, but starting with an initial seed concentration of [M]0 = 21 μM or 10 μM. For the unseeded experiments the individual half-times for each run were extracted by fitting a straight line to the normalized trajectory between [M]norm = 0.4 and [M]norm = 0.6 and then using the value of t at the point where this line crosses [M]norm = 0.5. To obtain global fits, a basin-hopping algorithm was used as described in Supporting Information, section 1.5 and Fig. S9. To fit the full time course of the aggregation, Eq. 4 was used in this fitting algorithm, with three free parameters only: KM and the combinations k+kn and k+k2. We set nc = n2 = 2, as was found for Aβ42 (9), to allow direct comparison of the rate constants of the two proteins. To check the validity of setting nc = n2 = 2 a number of fits starting at different initial guesses and fitting all five parameters were performed. The fits obtained all converged to the same values and were only a slight improvement with n2 and nc close to 2, justifying our choice of n2 and nc. The fits in Fig. 2C were obtained in the same manner, for the fit of single-step secondary nucleation, the secondary nucleation rate was constraint to values where it dominates over primary nucleation.
Integrated Rate Law.
The general kinetic model of aggregation treats fibrils as linear aggregates of monomers, whereby the monomers can attach to the ends of such fibrils with an elongation rate constant k+. Nuclei can, in general, form either homogeneously (29) in solution with rate constant kn or heterogeneously (16), on the surface of existing aggregates with rate constant k2; the former process represents primary nucleation, the latter secondary nucleation. The reaction orders of primary and secondary nucleation with respect to monomer concentration are given by nc and n2, respectively (19). New fibril ends, to which monomers can attach, can also be created by fragmentation of fibrils (26), a secondary process that does not possess a dependence on the concentration of monomers (Fig. 1A). Explicit consideration of how these molecular processes contribute to the changes in aggregate concentrations results in a series of differential rate equations, through the use of the master equation formalism that describes rate laws for the mass [M] and number [P] concentrations of aggregates as a function of time t (18, 19):
| [1] |
| [2] |
where [m] is the monomer concentration. Note that filament fragmentation is included within this description through setting n2 = 0 and identifying k2 with a fragmentation rate constant k−. To include saturation of secondary nucleation, the change in number concentration of aggregates is generalized from Eq. 1 to
| [3] |
In the low monomer limit from Fig. 1 can be related to the single-step k2 as and the Michaelis constant is given by (see Supporting Information, section 1.1 for detailed derivation).
We integrate Eqs. 2 and 3 through the use of self-consistent arguments as detailed in refs. 18–20 and Supporting Information, section 1.2 and find the integrated rate law for the normalized aggregate mass concentration as
| [4] |
where the definitions of the parameters are
| [5] |
| [6] |
| [7] |
| [8] |
| [9] |
| [10] |
[m]0 is the initial monomer concentration and [P]0, [M]0 and [P]∞, [M]∞ are the aggregate number and mass concentration at the start of the reaction and in equilibrium, that is, after completion of the aggregation. [P]∞, the long time limit of the aggregate number, is derived in Supporting Information, section 1.2. For a comparison with the numerical result see Supporting Information, section 1.4 and Fig. S10.
Of particular interest is the behavior of the half-time and hence the scaling exponent, γ, which is found from Eq. 4 to within logarithmic corrections as
| [11] |
Thus, without any further free parameters, this kinetic pathway predicts at low monomer concentration and at high monomer concentrations .
Supplementary Material
Acknowledgments
We thank Thomas Mueller and Patrick Varilly for discussion of the paper. We acknowledge financial support from Cambridge Home and EU Scholarship Scheme (G.M.), Newman Foundation (T.P.J.K.), Biotechnology and Biological Sciences Research Council (T.P.J.K. and C.M.D.), Schiff Foundation (S.I.A.C.), Swedish Research Council and its Linneaus center Organizing Molecular Matter (S.L.), European Research Council (S.L. and T.P.J.K.), The Swedish Alzheimer Foundation (S.L.), Crafoord Foundation (S.L.), Royal Physiographic Society (E.H.), and China Scholarship Council (X.Y.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1401564111/-/DCSupplemental.
References
- 1.Dobson CM. Protein folding and misfolding. Nature. 2003;426(6968):884–890. doi: 10.1038/nature02261. [DOI] [PubMed] [Google Scholar]
- 2.Aguzzi A, Haass C. Games played by rogue proteins in prion disorders and Alzheimer’s disease. Science. 2003;302(5646):814–818. doi: 10.1126/science.1087348. [DOI] [PubMed] [Google Scholar]
- 3.Aguzzi A, O’Connor T. Protein aggregation diseases: Pathogenicity and therapeutic perspectives. Nat Rev Drug Discov. 2010;9(3):237–248. doi: 10.1038/nrd3050. [DOI] [PubMed] [Google Scholar]
- 4.Hardy J, Selkoe DJ. The amyloid hypothesis of Alzheimer’s disease: Progress and problems on the road to therapeutics. Science. 2002;297(5580):353–356. doi: 10.1126/science.1072994. [DOI] [PubMed] [Google Scholar]
- 5.Hu X, et al. Amyloid seeds formed by cellular uptake, concentration, and aggregation of the amyloid-beta peptide. Proc Natl Acad Sci USA. 2009;106(48):20324–20329. doi: 10.1073/pnas.0911281106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Barral JM, Broadley SA, Schaffar G, Hartl FU. Roles of molecular chaperones in protein misfolding diseases. Semin Cell Dev Biol. 2004;15(1):17–29. doi: 10.1016/j.semcdb.2003.12.010. [DOI] [PubMed] [Google Scholar]
- 7.Ruschak AM, Miranker AD. Fiber-dependent amyloid formation as catalysis of an existing reaction pathway. Proc Natl Acad Sci USA. 2007;104(30):12341–12346. doi: 10.1073/pnas.0703306104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sawaya MR, et al. Atomic structures of amyloid cross-beta spines reveal varied steric zippers. Nature. 2007;447(7143):453–457. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 9.Cohen SIA, et al. Proliferation of amyloid-beta 42 aggregates occurs through a secondary nucleation mechanism. Proc Natl Acad Sci USA. 2013;110:9758–9763. doi: 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Barrow CJ, Yasuda A, Kenny PT, Zagorski MG. Solution conformations and aggregational properties of synthetic amyloid beta-peptides of Alzheimer’s disease. Analysis of circular dichroism spectra. J Mol Biol. 1992;225(4):1075–1093. doi: 10.1016/0022-2836(92)90106-t. [DOI] [PubMed] [Google Scholar]
- 11.Sánchez L, et al. Aβ40 and Aβ42 amyloid fibrils exhibit distinct molecular recycling properties. J Am Chem Soc. 2011;133(17):6505–6508. doi: 10.1021/ja1117123. [DOI] [PubMed] [Google Scholar]
- 12.Connors K. Chemical Kinetics: Study of Reaction Rates in Solution. New York: Wiley; 1990. [Google Scholar]
- 13.Seubert P, et al. Isolation and quantification of soluble Alzheimer’s β-peptide from biological fluids. Nature. 1992;359(6393):325–327. doi: 10.1038/359325a0. [DOI] [PubMed] [Google Scholar]
- 14.Fersht A. Structure and Mechanism in Protein Science. New York: Freeman; 1999. [Google Scholar]
- 15.Finder VH, Vodopivec I, Nitsch RM, Glockshuber R. The recombinant amyloid-beta peptide Abeta1-42 aggregates faster and is more neurotoxic than synthetic Abeta1-42. J Mol Biol. 2010;396(1):9–18. doi: 10.1016/j.jmb.2009.12.016. [DOI] [PubMed] [Google Scholar]
- 16.Ferrone FA, Hofrichter J, Eaton WA. Kinetics of sickle hemoglobin polymerization. II. A double nucleation mechanism. J Mol Biol. 1985;183(4):611–631. doi: 10.1016/0022-2836(85)90175-5. [DOI] [PubMed] [Google Scholar]
- 17.Ferrone F. Analysis of protein aggregation kinetics. Methods Enzymol. 1999;309:256–274. doi: 10.1016/s0076-6879(99)09019-9. [DOI] [PubMed] [Google Scholar]
- 18.Knowles TPJ, et al. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326(5959):1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 19.Cohen SIA, et al. Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J Chem Phys. 2011;135(6):065105. doi: 10.1063/1.3608916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cohen SIA, Vendruscolo M, Dobson CM, Knowles TPJ. Nucleated polymerization with secondary pathways. II. Determination of self-consistent solutions to growth processes described by non-linear master equations. J Chem Phys. 2011;135(6):065106. doi: 10.1063/1.3608917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Knowles TP, et al. Role of intermolecular forces in defining material properties of protein nanofibrils. Science. 2007;318(5858):1900–1903. doi: 10.1126/science.1150057. [DOI] [PubMed] [Google Scholar]
- 22.Esler WP, et al. Alzheimer’s disease amyloid propagation by a template-dependent dock-lock mechanism. Biochemistry. 2000;39(21):6288–6295. doi: 10.1021/bi992933h. [DOI] [PubMed] [Google Scholar]
- 23.Cohen SI, Vendruscolo M, Dobson CM, Knowles TP. From macroscopic measurements to microscopic mechanisms of protein aggregation. J Mol Biol. 2012;421(2-3):160–171. doi: 10.1016/j.jmb.2012.02.031. [DOI] [PubMed] [Google Scholar]
- 24.Oosawa F, Asakura S. Thermodynamics of the Polymerization of Protein. New York: Academic; 1975. [Google Scholar]
- 25.Oosawa F, Kasai M. A theory of linear and helical aggregations of macromolecules. J Mol Biol. 1962;4:10–21. doi: 10.1016/s0022-2836(62)80112-0. [DOI] [PubMed] [Google Scholar]
- 26.Collins SR, Douglass A, Vale RD, Weissman JS. Mechanism of prion propagation: Amyloid growth occurs by monomer addition. PLoS Biol. 2004;2(10):e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Walsh DM, et al. A facile method for expression and purification of the Alzheimer’s disease-associated amyloid beta-peptide. FEBS J. 2009;276(5):1266–1281. doi: 10.1111/j.1742-4658.2008.06862.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hellstrand E, Boland B, Walsh DM, Linse S. Amyloid β-protein aggregation produces highly reproducible kinetic data and occurs by a two-phase process. ACS Chem Neurosci. 2010;1(1):13–18. doi: 10.1021/cn900015v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jarrett JT, Lansbury PT., Jr Seeding “one-dimensional crystallization” of amyloid: A pathogenic mechanism in Alzheimer’s disease and scrapie? Cell. 1993;73(6):1055–1058. doi: 10.1016/0092-8674(93)90635-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.