Significance
Using mathematical models to extend knowledge of pathogen transmission and recommend optimized control efforts is dependent on the accuracy of model parameters. The rate at which susceptible individuals become infected [the force of infection (FoI)] is one of the most important parameters, but due to data constraints it is often incorrectly assumed to be constant over time. Using a bespoke method for a 12-y longitudinal dataset of serotype-specific dengue virus (DENV) infections, we estimated time-varying, serotype-specific FoIs for all four DENV serotypes. The FoI varied markedly in time, which implies that DENV transmission dynamics are complex and are best summarized using time-dependent transmission parameters. Our results provide more accurate measures of virus transmission dynamics and a basis for improving selection of control and disease prevention strategies.
Keywords: disease ecology, emerging infections, arthropod-borne virus
Abstract
Infectious disease models play a key role in public health planning. These models rely on accurate estimates of key transmission parameters such as the force of infection (FoI), which is the per-capita risk of a susceptible person being infected. The FoI captures the fundamental dynamics of transmission and is crucial for gauging control efforts, such as identifying vaccination targets. Dengue virus (DENV) is a mosquito-borne, multiserotype pathogen that currently infects ∼390 million people a year. Existing estimates of the DENV FoI are inaccurate because they rely on the unrealistic assumption that risk is constant over time. Dengue models are thus unreliable for designing vaccine deployment strategies. Here, we present to our knowledge the first time-varying (daily), serotype-specific estimates of DENV FoIs using a spline-based fitting procedure designed to examine a 12-y, longitudinal DENV serological dataset from Iquitos, Peru (11,703 individuals, 38,416 samples, and 22,301 serotype-specific DENV infections from 1999 to 2010). The yearly DENV FoI varied markedly across time and serotypes (0–0.33), as did daily basic reproductive numbers (0.49–4.72). During specific time periods, the FoI fluctuations correlated across serotypes, indicating that different DENV serotypes shared common transmission drivers. The marked variation in transmission intensity that we detected indicates that intervention targets based on one-time estimates of the FoI could underestimate the level of effort needed to prevent disease. Our description of dengue virus transmission dynamics is unprecedented in detail, providing a basis for understanding the persistence of this rapidly emerging pathogen and improving disease prevention programs.
The force of infection (FoI) describes the per-capita rate at which susceptible individuals become infected with a pathogen (1, 2). An accurate estimate of the FoI is essential for parameterizing disease models (3). It can be used to calculate key quantities such as the basic reproductive number () (2, 4) and the critical vaccination coverage threshold () of a pathogen (5), which are frequently used to guide disease control programs and for determining the control effort required to eliminate a disease (6).
Dengue, a mosquito-borne disease whose incidence and geographic range have increased considerably in the past 50 y (7, 8), is caused by any of four related but antigenically distinct virus serotypes (DENV-1, DENV-2, DENV-3, and DENV-4). Previous estimates of the FoI for DENV are few and uncertain owing to limitations inherent to most available DENV datasets, including difficulty in specifying when an individual DENV infection occurred. Given the growing public health need for optimal vector management strategies and the growing potential for deployment of a dengue vaccine in the near future (9), there is a pressing need for accurate, serotype-specific estimates of the FoI and for DENV. Here, we use a unique, long-term serological dataset from Iquitos, Peru to provide to our knowledge the first such estimates.
Basic mathematical models of pathogen transmission, such as the catalytic model where the FoI was initially introduced (1), make simplifying assumptions about the parameters governing transmission, including the frequent assumption that parameters do not vary through time in epidemiologically important ways (10). The assumption that the FoI is constant in time is, however, inconsistent with current understanding of DENV epidemiology because transmission clearly varies seasonally and year to year (8, 11–14). Resolving the magnitude of temporal variations in the quantities that govern or summarize transmission requires (i) adequate, temporally resolved incidence data and (ii) development of an estimation approach specifically designed to use such a dataset to compute time-varying quantities.
Review of approaches for estimating the FoI of dengue (3) shows that, mostly owing to data limitations, two approaches have predominated over the last 30 y (2): (i) methods intended for use with data collected passively from clinics and hospitals (clinical cases) and (ii) methods for use with data actively collected from age-stratified serologic surveys. Data that are collected from verified clinical cases are temporally resolved but only capture clinically apparent infections. Not accounting for the potentially large proportion of undetected, inapparent infections can greatly diminish the accuracy of FoI estimates (15). Indeed, the ratio of DENV infections that are subclinical (i.e., inapparent*) to those that are clinically apparent can be variable and often quite large, ranging from 0.9:1–40:1 and higher (11, 16–18).
Thus, estimates of the DENV FoI based on verified clinical cases (e.g., refs. 19–21) are uncertain. In contrast, serological surveys theoretically capture all (or most) infections in a study population. The tradeoff is that the actual time of the infection cannot be defined from a single blood sample, and so the individual’s age is used instead. An important complication for multistrain pathogens, like DENV, is that the infecting strain is often not determined in serological surveys. Investigators in several studies estimated the FoI of DENV using single serological surveys (e.g., refs. 4, 13, and 22), but cross-reactive antibodies obscure identification of the infecting serotype. Thus, in most dengue endemic settings one cannot resolve potentially important relationships among serotypes such as antigenic-dependent enhancement (23) using single blood specimens from cross-sectional surveys. Owing to limitations of both serology and reported clinical case data, current estimates of the FoI for DENV are uncertain and potentially inaccurate.
Prospective, longitudinal studies generate serial samples from the same individuals over several years that can be used to validate serological results and derive serotype-specific infection information (11). A longitudinal study design, therefore, provides data that are amenable to estimating the FoI, particularly if the FoI changes from year to year and is serotype-specific (24). Because existing FoI estimation approaches were not designed to use longitudinal data, we developed a spline-based modeling approach to analyze a 12-y longitudinal serology dataset (11,703 participants and 38,416 blood samples) from the city of Iquitos, Peru and produced the first, to our knowledge, time-varying, serotype-specific FoI estimates for DENV.
Methods
Approval of Experiments Involving Human Subjects.
This study used information from participants in five overlapping cohorts. Each had separate human subjects protocols (see SI Appendix, Table S1 for protocol numbers) that were in compliance with US federal regulations governing the protections of human subjects. All protocols received approval from the institutional review boards (IRBs) of all participating institutions and from a Peruvian Ethics Committee that ensured that all Peruvian regulations governing the protection of human subjects were followed. Starting in 2007, the Naval Medical Research Center Detachment (now NAMRU-6) formed an IRB that is registered with the Department of Defense, the Office Human Research Protection, and the Peruvian Ethics Committee. In addition, all protocols were reviewed and approved by the Loreto Regional Health Department, which oversees health-related research in Iquitos. In all instances, written consent was provided by study participants.
Data and Seroconversion Identification.
Iquitos is an isolated city of ∼370,000 inhabitants located in the Amazon basin of northeastern Peru. It has been well described elsewhere (11). All four DENV serotypes have been introduced into Iquitos and subsequently circulated endemically: DENV-1 in 1990 (25), DENV-2 in 1995 (26), DENV-3 in 2001 (11), and DENV-4 in 2008 (27, 28). Our analysis includes 12 y (1999–2010) of data from five longitudinal dengue cohorts involving Iquitos residents >5 y of age (see SI Appendix, section S1 and Table S1 for details; Fig. 1). In each cohort, participants provided blood samples for testing by plaque reduction neutralization tests (PRNTs) at 6–9 mo intervals. In some circumstances, studies overlapped in time and space (SI Appendix, section S1). For our analysis, we combined all cohorts into a single subsample of the Iquitos population with extensive turnover of individuals throughout the study period. Some of the later cohort studies recruited individuals that were either not yet born or too young to qualify for inclusion in the first cohort (i.e., aged less than 5 y in 1999). As such, to maintain a comparable subpopulation (and avoid confounding effects of birth and a changing population size in Iquitos), we removed individuals from consideration who were born after 1995. This resulted in the removal of 1,465 children from consideration. Thus, our analyses were based on the subpopulation of individuals born before 1995, which henceforth we will refer to as the sample population.
Fig. 1.
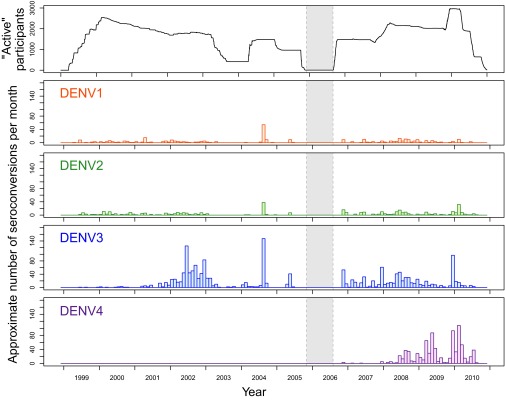
Summary of participants and interval-censored infections. The top panel shows the total number of active participants across cohort studies from 1999 to 2010. The absence of a cohort study from late 2005 to mid-2006 is indicated by the gray shaded region. Remaining panels: After applying the seroconversion identification algorithm to the raw data the number of interval censored infections are plotted against time. For all, the midpoint of the interval over which the infection was censored is used to time infections.
All blood samples from 1999 through 2010 were analyzed for the presence of DENV neutralizing antibodies by serotype-specific PRNT (11) in baby hamster kidney BHK21 cells using a carboxymethyl cellulose overlay. Samples were considered positive when plaques were reduced 70% or more (PRNT70) using dilutions of 1:60, 1:80, 1:60, and 1:40 for DENV-1, DENV-2, DENV-3, and DENV-4, respectively (11) (SI Appendix, section S2). Chronological sets of PRNT70 results, coupled with knowledge of the timing of DENV serotype introductions into Iquitos, provided confidence in our interpretation of serologic results (29). On this basis, we designed an algorithm to identify infections that minimized the probability of false-positive results by (i) using serotype-specific thresholds, (ii) ignoring all transient positive results (e.g., negative–postive–negative), and (iii) eliminating all participants who had any instance of seroconversion to more than one serotype in the same blood sampling interval (see SI Appendix, section S2 for details). Completely eliminating such participants from all analyses is quite conservative, but our method of identifying seroconversions relies on investigating the entire serohistory of an individual. As such, any possibly erroneous PRNT casts doubt on results for all serotypes. This conservative approach means our estimates of FoIs are biased low. Our approach allowed us to identify tertiary and quaternary DENV infections (29) in part because of sequential introductions of two novel serotypes. Simultaneous virus isolation and identification from dengue cases (i.e., case data) (30) provided independent validation of the patterns we describe (Discussion and SI Appendix, section S2).
Model Description.
For likelihood-based inference, we estimated the proportion of the study population that had already been infected by time t [denoted ], rather than estimating the FoI directly. Defining as the FoI at time t, we have (SI Appendix, section S3)
| [1] |
This equation implicitly assumes that the population is homogeneous and well mixed (i.e., every individual is equally at risk to be infected by of any infectious individual). This assumption is imperfect and some of its consequences are discussed below. The data were left-censored (SI Appendix, Fig. S1A), interval-censored (Fig. 1), and right-censored (SI Appendix, Fig. S1B), corresponding to individuals who entered the study already seroconverted, seroconverted between two blood draws, and left the study having never seroconverted, respectively. Using the probability density function of the infection times of infected people, , the likelihood for the three types of censored data are given in SI Appendix, Table S3 (where I denotes the time of infection) (31). We considered each individual’s infection status to be independent of others, which permitted us to take the likelihood of the data as the product of each individual’s likelihood (SI Appendix, section S3).
To estimate the FoI through time, we used a nonparametric spline-based approach (32). Specifically, we defined a set of B-splines (33) as basis functions for f. The advantages of B-splines over other bases, such as monomials and trigonometric functions, are that they are flexible and do not a priori assume periodicity. Based on deviation information criterion (DIC; for details see SI Appendix, section S5 and Table S2), we identified six B-splines per year (72 total) as the optimal basis for f for the four serotypes and present these results in the main text. A model using four B-splines per year (48 total) also worked well (SI Appendix, Table S2, section S6, and Figs. S2–S11). There were no qualitative differences between results obtained when using a model with four B-splines per year compared with a model with six B-splines per year.
We could not estimate the function f before 1999 because we did not have data before that date. Seroconversions that occurred before 1999 were left-censored, allowing estimation of the proportion of the population that was exposed before the beginning of the study. We defined κ as the proportion of the population that had seroconverted before 1999:
| [2] |
with representing the beginning of the study. Using Eq. 2, the likelihood of both right-censored and left-censored observations was rewritten using κ.
Model-Fitting Procedure.
To estimate the pdf f, we used a Markov chain Monte Carlo (MCMC) approach, specifically an adaptive, Metropolis-within-Gibbs algorithm (34, 35) (for complete details on the fitting procedure, see SI Appendix, section S4 and Figs. S12–S15). We ran 10 chains, each of length 100,000, and evaluated convergence primarily by monitoring scale reduction factors (SI Appendix, Fig. S13) (36, 37), trace plots (SI Appendix, Fig. S14), and acceptance probability plots (SI Appendix, Fig. S15). For our analysis, we combined the last 15,000 steps of each chain and randomly sampled 1,000 steps to remove autocorrelation. The parameters were not independent of each other, so to create credible regions for f (and later the FoI and ) we used the 1,000 sampled steps of the chain to create 1,000 estimates of f. This formed an empirical estimate of the posterior distribution of f. For each day, we then selected the middle 90% of the estimates to form our Bayesian credible interval (BCI) at that point. Throughout, in addition to BCIs, we present the posterior medians. There were two parameters that a priori we knew would have identifiability and convergence issues: the parameters corresponding to the very beginning and very end of the study. We, therefore, truncated our estimates to the region where our chains converged (SI Appendix, section S4 and Figs. S16 and S17). All analyses were done with R (38) and the R package fda (39). We evaluated convergence with the R package CODA (40).
Parameter and Quantity Estimation.
With our estimates of f we computed the proportion of our study population (those born before 1995) still susceptible at time t, denoted , as
| [3] |
The FoI, , was then (SI Appendix, section S3)
| [4] |
The number of secondary infections caused by a single infectious person at any time t was the effective reproductive number, denoted . To estimate for the entire population of Iquitos, we used our FoI estimates to calculate the fraction of the entire population susceptible at any time t, denoted (SI Appendix, section S3). Using the estimated mean time between successive DENV infections (i.e., serial interval) of 15–17 d (41), we approximated on day d as the ratio of the number of infections that occurred between day d and day and the average number of infections 15–18 d in the future as follows (SI Appendix, section S3):
| [5] |
We assessed the sensitivity of to this interval in SI Appendix, section S5. We then used this approximation of the effective reproductive number to calculate an estimate of the basic reproductive number, , on day d by scaling our approximation by the fraction of the entire population that is susceptible, :
| [6] |
was used to calculate the critical vaccination coverage required to eliminate a pathogen. Specifically, the critical vaccination coverage level, , satisfies the following relationship (5):
| [7] |
Results
Serotype-Specific Infections.
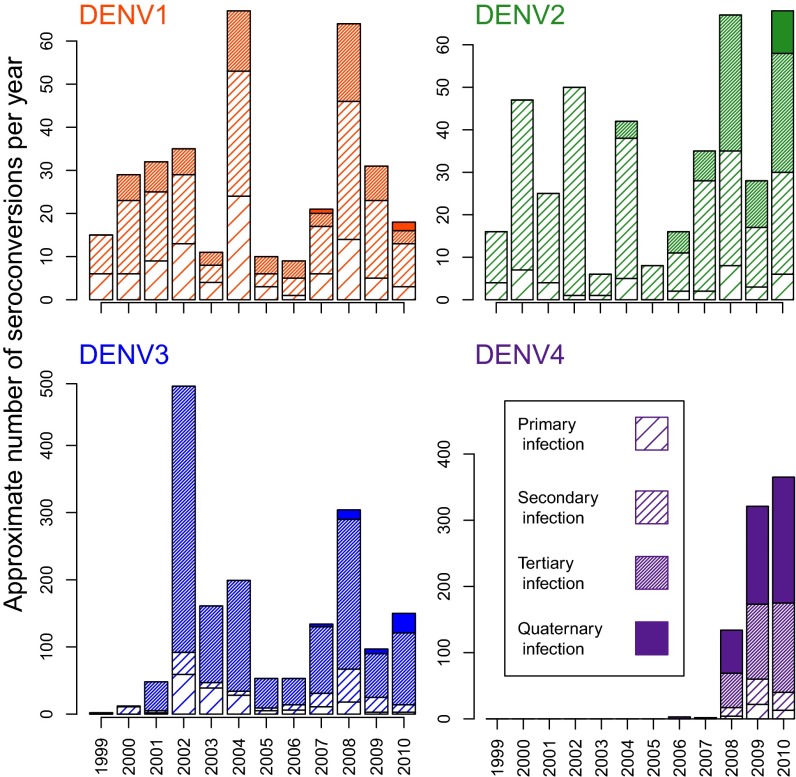
The final dataset included 38,416 blood samples that provided serotype-specific infection information for 11,703 individuals. Participants provided 1 to 13 (mean = 3.3) sequential samples an average of 249.5 d apart. We identified 22,301 serotype-specific DENV infections, 3,276 of which were interval-censored (Table 1). Because DENV-1 and DENV-2 had already circulated in Iquitos for several years before the study began, the number of left-censored infections for those serotypes was higher than for DENV-3 and DENV-4. Conversely, the number of interval-censored infections for DENV-3 and DENV-4 was higher, with DENV-3 accounting for more than half of all interval-censored infections. Even though DENV-4 was not detected in clinics until 2008, there was still enough transmission for more than 800 individuals that joined the study after 2008 to seem to have already had neutralizing antibody against DENV-4 (Table 1). Using the mid date between sample pairs to time when seroconversions occurred, we found the number of observed infections per month varied markedly through time (Fig. 1). Testing conducted in 2004 was not spread out throughout the year and instead occurred at two times. As such, the mid date of many individuals occurred within same month (July 2004) which does not necessarily mean that all of these individuals were actually infected in July. Owing to the gap between cohort studies from late 2005 to mid-2006 (indicated by the shaded region in Fig. 1), we have no information on infections that occurred during that period (SI Appendix, section S1). In total, 84.0% of the 11,703 study participants seroconverted to at least one DENV serotype by the time they left the study. Transmission varied year to year and across serotypes, with a steady increase in the number of postsecondary infections (tertiary and quaternary) later in the study (Fig. 2). Overall, the majority of DENV-3 and DENV-4 infections were tertiary or quaternary (65.2% and 77.4%, respectively). For 36.2% of all individuals who seroconverted to DENV-4, it was their fourth infection with a DENV.
Table 1.
Summary of censored data type by serotype
| Data type | DENV-1 | DENV-2 | DENV-3 | DENV-4 |
| Left-censored | 7,714 | 7,464 | 2,980 | 867 |
| Interval-censored | 342 | 408 | 1,701 | 825 |
| Right-censored | 2,527 | 2,724 | 5,800 | 4,658 |
For each serotype, the number of individuals that were either left-, interval-, or right-censored. Left-censored individuals entered the study already seroconverted to the specific serotype. Interval-censored individuals became infected to the specific serotype during their time in the study period. Right-censored individuals left the study having never been infected to the specific serotype. Note that none of the above columns adds up to 11,703 (the total number of participants). For some individuals, no PRNT test was conclusive for certain serotypes, and as such they were removed from consideration toward the calculations concerning that serotype. Additionally, DENV-4 was not tested for until 2006, and the smaller number of censored individuals for DENV-4 reflects this.
Fig. 2.
Number and order of interval censored infections by serotype. For each serotype the number of interval-censored infections are plotted against year. Note that for comparison purposes the scale of the y axis is not the same in each panel. Per individual, these infections are broken down by which infection they constitute (primary, secondary, tertiary, or quaternary). Because both DENV-1 and DENV-2 cocirculated before the beginning of the study period, the majority of individuals were already exposed to at least one of these serotypes and thus most interval-censored infections were not primary infections. For this same reason (the cocirculation of DENV-1 and DENV-2 before 1999), there are considerably fewer DENV-1 and DENV-2 interval-censored infections than DENV-3 and DENV-4 interval-censored infections.
Model Parameter Estimates.
The proportion of the population infected before 1999, κ (SI Appendix, Fig. S18), was 55.4% (90% BCI: 53.8–57%) for DENV-1 (SI Appendix, Fig. S18A) and 52.7% (90% BCI: 51.5–54%) for DENV-2 (SI Appendix, Fig. S18B). Conversely, κ was essentially 0 for DENV-3 and DENV-4 [0.004% (SI Appendix, Fig. S18C) and 0.004% (SI Appendix, Fig. S18D), respectively], which were introduced later. It is important to note, however, that DENV-4 was not included in our PRNT assays until 2006. The fact that these estimates were not exactly 0 was likely an artifact of the fitting procedure because no individuals were identified with a left- or interval-censored DENV-3 or DENV-4 infection until after the respective introductions of those viruses. Our estimates of the daily probability of infection, f, showed rough seasonal fluctuations in magnitude across serotypes (SI Appendix, Fig. S19). These estimates were greatest for DENV-3, particularly in 2002–2003. Over the period of study, the susceptible proportion of the study subpopulation, (Methods), decreased for all serotypes (SI Appendix, Fig. S20). At the end of the study, was reflective of the order of serotype introductions into Iquitos: DENV-1 (first reported in 1990) = 22.9% (90% BCI: 21.9–23.9%), DENV-2 (first reported in 1995) = 26.8% (90% BCI: 26.8–28.7%), DENV-3 (first reported in 2001) = 32.0% (90% BCI: 30.9–33.2%), and DENV-4 (first reported in 2008) = 56.7% (90% BCI: 54.4–58.6%). Unlike estimates for the sample population, the susceptible proportion of the entire population of Iquitos, , was relatively stable for DENV-1 and DENV-2 (SI Appendix, Fig. S21). However, susceptible estimates within Iquitos for the invading serotypes (DENV-3 and DENV-4) decreased at rates similar to those within the sample population (SI Appendix, Fig. S21). The estimated age distribution of infections skewed toward younger individuals the longer the serotype circulated within Iquitos (SI Appendix, Figs. S22 and S23 and section S5).
FoI.
Depending on year and serotype, daily FoI estimates ranged from 0 to 0.002 (Fig. 3), with the highest estimates being for DENV-3 and DENV-4. Although there was a gap between cohorts from late 2005 to mid-2006, we did identify nonzero point estimates of the FoI owing to the slight systematic increase in the proportion of left-censored individuals that occurred after that period compared with before. After analyzing the consistency of estimates across this gap (SI Appendix, section S5 and Fig. S24), we found that the loss of data increased median values and credible intervals of estimates around the gap. Away from the gap, estimated FoI values were consistent with those in Fig. 3. Further, the large credible intervals and timing of the estimated peak FoI for 2004 (July 2004) may be an artifact of the synchronized timing of blood draws in 2004.
Fig. 3.
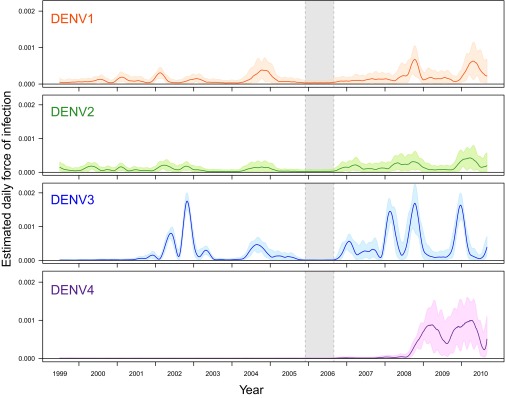
Daily estimates of FoI. For each serotype, daily estimates of FoI as well as the 90% BCI are plotted against time. The absence of a cohort study from late 2005 to mid-2006 is indicated by the gray shaded region.
Our longitudinal studies captured the introduction of a novel DENV serotype twice. In late 2001/early 2002, the FoI of the recently introduced DENV-3 was estimated to be significantly nonzero, indicating circulation (11). Owing to the regular testing of the longitudinal cohort participants, the timing of this increase was distinguishable from that of DENV-1 and DENV-2 (Fig. 3). This pattern was repeated at the time of the introduction of DENV-4 in late 2008/early 2009. In both instances, the novel serotype replaced the existing serotype(s). Weekly and monthly estimates of the FoI (SI Appendix, Fig. S25 A and B) displayed similar patterns.
There were periods when transmission of multiple serotypes seemed to synchronize. We computed Spearman rank correlations on daily estimates of the FoI between serotypes and found that DENV-1, DENV-2, and DENV-3 were all highly correlated (DENV-1/DENV-2: , DENV-1/DENV-3: , and DENV-2/DENV-3: ). DENV-4, having been introduced in late 2008, does not display high, if any, correlation with the other serotypes (, , and ). FoIs for all serotypes were elevated, however, in late 2009/early 2010, with DENV-1, DENV-2, and DENV-4 reaching their local maxima at almost the same time in early 2010.
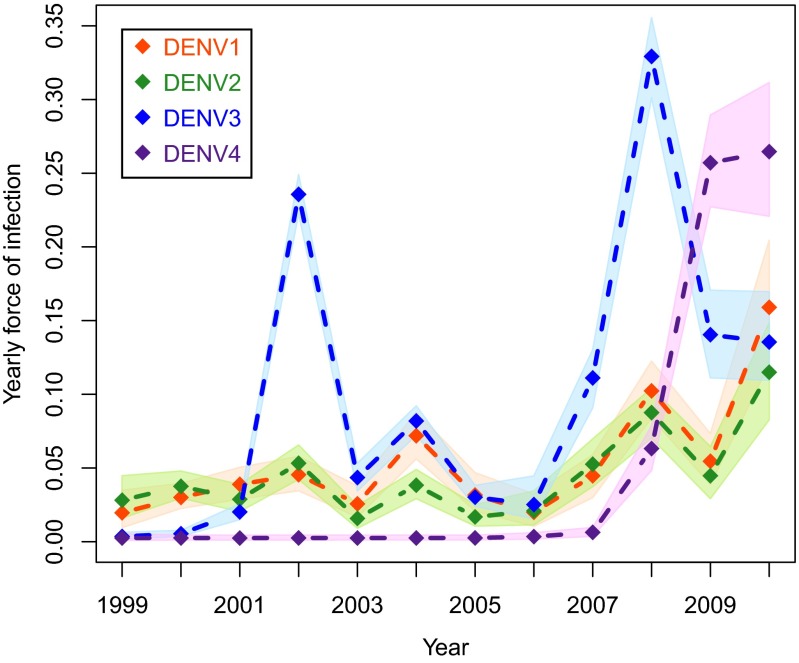
Aggregating our estimates by year indicated that the FoIs for DENV-3 and DENV-4 were highest (Fig. 4). For both, there were two years where the yearly FoI exceeded 0.2. The largest yearly FoI for any serotype was the 2008 estimate for DENV-3 [0.33 (90% BCI: 0.3–0.36)]. Every serotype had at least one year with a yearly FoI that exceeded 0.1, corresponding to seroconversion in 10% of members of the study population that were still susceptible to that serotype in that year. The FoIs for multiple serotypes were relatively high in 2002, 2004, 2008, and 2010. Conversely, the FoIs of multiple serotypes were simultaneously relatively low during 2001, 2003, 2005, and 2006 (relative to serotype-specific values for the surrounding years). The yearly FoIs of DENV-1, DENV-2, and DENV-3 were all correlated (Spearman rank correlations: DENV-1/DENV-2, ; DENV-1/DENV-3, ; and DENV-2/DENV-3, ). Spearman rank correlations with DENV-4 were not informative because there were only three estimated yearly FoIs for DENV-4. As noted above with the daily FoI estimates, the yearly estimates for all four serotypes were high in 2010, each exceeding 0.1.
Fig. 4.
Yearly estimates of FoI. For each serotype yearly estimates of FoI as well as the 90% BCI are plotted against time. The absence of a cohort study from late 2005 to mid-2006 does not preclude the estimation of yearly FoI estimates for either 2005 or 2006, as evidenced by nonzero FoI estimates for the circulating serotypes for both of those years.
Serotype-Specific and Vaccination Thresholds.
Our estimates of and for each serotype fluctuated temporally (SI Appendix, Figs. S26 and S27, respectively). Small variations in the daily estimates of resulted in large variations in because appeared in the denominator of Eq. 6. This resulted in wide BCIs; the posterior distributions had long upper tails (SI Appendix, Fig. S27). Thus, for the purposes of comparison, we plotted estimates of with the corresponding 50% BCI (Fig. 5) to truncate extreme values on the upper end of the posterior distribution. We investigated the sensitivity of these results to our definition of the serial interval and found that the estimated values were robust to changes in this interval (SI Appendix, section S5 and Figs. S28 and S29).
Fig. 5.
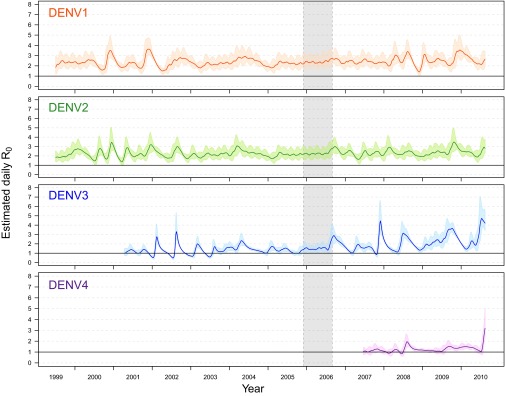
Daily estimates of . For each serotype daily estimates of as well as the 50% BCI are plotted against time. The absence of a cohort study from late 2005 to mid-2006 is indicated by the gray shaded region. The estimates for both DENV-3 and DENV-4 are truncated, excluding estimation before their respective introductions.
We did not estimate a value of under 1 for DENV-1 or DENV-2, except for a small portion of the credible interval in a few instances. The median values of for DENV-1 ranged from 1.40 to 3.64. The median values for DENV-2 were lower (1.36–3.49). Our estimates of DENV-3 ranged from below 1 to 4.72 by 2010. For DENV-4, stayed below 2 until 2010, when it increased to 3.19 (Fig. 5). Weekly and monthly estimates of (SI Appendix, Fig. S25 C and D) resulted in similar, slightly lower values. There was a considerable amount of fine-scale temporal variation in all four estimates. Computing the cross-correlation between the FoI and revealed a systematic lag of ∼60–80 d (Pearson correlation, SI Appendix, Fig. S30A and Spearman correlation, SI Appendix, Fig. S30B). Plotting against the FoI (SI Appendix, Fig. S31) illustrates that sharp increases in the FoI were preceded by sharp spikes in .
Analogous to the computation of yearly FoI estimates, we computed yearly average values (SI Appendix, Fig. S32) by taking the weighted average of the daily estimates (weighted by relative number of infections). As with the daily estimates, the yearly estimates for DENV-1 and DENV-2 were relatively similar, with DENV-1 estimates slightly higher. The yearly estimate of DENV-3 experienced the largest jumps from one year to the next (2005–2006: 1.38–1.97 and 2008–2009: 1.82–2.61). Averaging over an entire year ignores seasonality, and the highest yearly estimates were lower than the highest daily estimates for all serotypes. For DENV-2 and DENV-3, the highest yearly estimates occurred in 2010 [DENV-2: 2.54 (50% BCI: 2.45–2.63) and DENV-3: 2.61 (50% BCI: 2.55–2.69)], and the highest yearly estimate for DENV-1 and DENV-4 occurred in 2010 [DENV-1: 2.62 (50% BCI: 2.56–2.68) and DENV-4: 1.43 (50% BCI: 1.39–1.47)].
From serotype to serotype and across years, values of and, in turn, , varied. When DENV-3 or DENV-4 were first introduced (when the entire study population was susceptible), the estimated was effectively 1 [DENV-3: 50% BCI: (0.80–1.45); DENV-4: 50% BCI: (0.76, 1.44)], giving . Using the upper bound on the 90% credible interval for DENV-4 at the time of its introduction (2.18), we found . In the first 4 y of the study, the largest median calculated was 3.64 for DENV-1 in 2001. In the next 4 y, the largest identified was 3.07 for DENV-2 in 2004. In the last 4 y, the largest identified was 4.72 for DENV-3 in 2010. These values result in recommendations of vaccination coverage of 73, 67, and 79% of the population, respectively. Using the largest yearly estimate (2.61 for DENV-3 in 2009), 62% of the population would need to react to vaccination with a protective immune response. Conservatively, following the highest estimated overall (4.72 for DENV-3 in 2010), our results indicate a vaccine should be distributed to 79% of the population.
Discussion
Our results quantify temporal variation in the FoI for each DENV serotype over a 12-y period, highlighting marked differences in transmission intensity both intra- and interannually. We found that FoI estimates for the recently introduced serotypes DENV-3 and DENV-4 were higher than those of DENV-1 and DENV-2, which caused outbreaks before but not during the period investigated (1990 and 1995, respectively). Overall, there was high correlation between FoIs across serotypes. There were years of relatively high (e.g., 2002, 2004, 2008, and 2010) and relatively low (e.g., 2001, 2003, 2005, and 2006) transmission, pointing to common drivers of DENV transmission dynamics. Our estimates for varied from ∼1 to over 5, depending on year and serotype. During the years following its invasion, DEN-4 estimates were less than those for other serotypes. This is consistent with the notion that DENV-4 is less transmissible than the other three serotypes (42, 43). It should be noted, however, that for DENV-4 appeared to be increasing as our study period ended. was variable across seasons, warning against quick estimates for critical vaccination coverage. Using the highest estimated values (for DENV-3 from 2010), we conservatively calculated to be 79%.
Our yearly DENV FoI estimates mostly fell within the wide range of previously calculated estimates conducted in a variety of locations using an array of methods and datasets that often aggregated across DENV serotypes. Yearly FoI estimates ranged from 0.07– 0.14 (19) to 0.2–0.25 (4, 22) in Thailand to 0–0.3 (13) in Brazil. Similar to the FoI, our estimates of the of DENV fell within the wide range of previously published values (1.3–6.3) (44). As detailed in a review of previous estimation efforts (44), only three estimation methods used serotype-specific data (4, 19, 45), and only one of those was based on serological surveys (a study using single blood samples from 1,009 children all collected in early 1980) (4). Our estimates indicate dengue is slightly more transmissible than directly transmitted diseases such as severe acute respiratory syndrome () (46) and influenza () (47) and less transmissible than fast-spreading diseases such as measles and pertussis ( and ∼12–18, respectively) (48). Although our estimated critical vaccination percentage of 79% was high, it was considerably lower (and thus vaccination would be a more reasonable control option) than that for measles and pertussis (∼92–94%).
Our serotype-specific approach revealed synchronous dynamics among DENV serotypes. There were high correlations in both the daily and yearly estimates of FoI between DENV-1, DENV-2, and DENV-3. DENV-1, DENV-2, and DENV-4 all achieved their local maxima at essentially the same time in 2010. There were several transmission seasons when, independent of the size of the serotype-specific susceptible pool, there seemed to be more than 40 seroconversions to at least three different serotypes (Fig. 2), specifically in 2004, 2008, and 2010, even though for at least 2004 surveillance data suggested a single serotype dominated (30). Even under stricter schemes for identification of seroconversions (SI Appendix, section S2 and Fig. S33), there remained periods where multiple serotypes seemed to circulate concurrently. This emphasizes the potential for differences between patterns of disease (i.e., clinically apparent infections) and patterns of infection. A study identifying the timing of serotype-specific outbreaks of dengue in Thailand (49) similarly identified seasonal synchronization across serotypes, specifically between DENV-1, DENV-2, and DENV-3. DENV-4, however, was reported to be out-of-phase. Our estimated FoIs for DENV-1, DENV-2, and DENV-4 were at or close to their highest values at almost the exact same time in 2010, indicating that the interserotypic immune reactions that drive patterns of transmission among serotypes may vary in their influence in different contexts. We also noted that invading serotypes replaced the existing serotype(s) that had been previously circulating at relatively high levels. Novel serotype invasions are rare events, in our case two over 12 y, which prevented us from performing statistical tests on serotype replacement patterns.
The synchrony between serotypes indicates there are common drivers. DENV is dependent on a mosquito population to complete its transmission cycle. Interannual variation in climate drivers can thus impose variation on transmission dynamics through their influence on mosquito biology and ecology. As in many cities with endemic dengue, Iquitos employs various mosquito control strategies in response to increases in dengue cases. We are currently investigating relationships between interannual variation in potential climate drivers, vector control efforts, and FoI estimates.
Although we computed daily estimates of , there was no inherent reason why these estimates should not all be equal. By investigating which assumptions were violated to produce such temporally fluctuating estimates and, in particular, produce the lagged patterns observed between our estimates of and the FoI, it was possible to indirectly deduce characteristics of transmission dynamics. For instance, the repeating pattern of a sharp spike in followed by a relatively slower increase and then decrease of the FoI was consistent with violation of the assumption of a well-mixed, spatially homogeneous population. We considered the Iquitos cohort to be one subpopulation, but in reality people (and their exposure to Aedes aegypti bites in locations other than their home) were nonhomogeneously distributed across the city (28, 50). These heterogeneities can have important implications for epidemiological prediction and inference (51). Localized outbreaks occur in Iquitos (52), and thus focal outbreaks would best be scaled by focal levels of human immunity. Perhaps if we incorporated the relatively rapid depletion of locally susceptible individuals there would be a more gradual change in the estimated values of . Another spatial heterogeneity that could contribute to the patterns we observed was the variation in individual movements. Some people may have contributed more to transmission than others by moving about more, being bitten by more mosquitoes, being more infectious, or some combination of these factors (53). Perhaps once an outbreak was initiated the pathogen spread to less-transmissible individuals, decreasing the aggregated estimates.
Certain caveats exist with our approach. First, cross-reacting anti-DENV antibodies can result in false-positive PRNT results (54, 55). We compensated for this by excluding individuals who seemed to seroconvert to multiple serotypes in the same time period and by using an individual’s entire serohistory to guard against transient false positives. This does not guarantee that we completely controlled for incorrectly serotyping an infection owing to a cross-reaction. Although there were periods of synchrony between the serotypes, increases, for example, in the number of DENV-3 seroconversions were not systematically accompanied by an increase in DENV-1 seroconversions. As such, we concluded that it is unlikely that cross-reacting antibodies, rather than cocirculation of multiple serotypes of DENV, were responsible for our results. Second, although the virus isolation and PCR data confirm certain patterns (e.g., the timing of the DENV-3 and DENV-4 invasions), virus detection was not always concordant with the longitudinal serological data. Virus detection in cell culture and PCR indicated that one or at most two predominant serotypes at a time produced clinically apparent infections. The patterns of inapparent infections do not by definition exactly match those of apparent infections (15). Considering the complex interplay between order of infection and severity of disease, especially for tertiary and quaternary infections (29, 56), it was not surprising that virus isolation/PCR data and the longitudinal serologic data did not always perfectly agree. Third, we modeled each serotype independently, ignoring the potential effects of temporary cross-protection. Following a DENV infection, an individual has temporary immunity to heterologous DENV infection (57), which may have affected our estimates (44). Correcting for cross-protection would result in a systematic increase in our FoI estimates because temporarily immune individuals would be removed from the heterologous susceptible pool in the denominator of Eq. 4. Likewise, incorporating death would increase our estimates.
Although they require considerable effort, time, and resources, longitudinal studies provide valuable detailed information on pathogen transmission, especially when rates of asymptomatic infection are high, like they are for DENV (16). Because most estimation attempts are not based on longitudinal data, the methods to use such detail are not well developed. As noted earlier, the use of likelihood-based fitting of smooth functions for the FoI has been developed for data from a single serological survey of individuals within the study population (2). By combining a spline-based approach with equations previously derived in the field of reliability (31) we developed an estimation method that incorporates the detailed information provided by a longitudinal study and allows for temporal flexibility in FoI estimates. Our method was designed to work with a particular dataset but could be adapted to other longitudinal studies for dengue and other infectious diseases.
Our analysis and the interpretation of serological data were facilitated by the two novel DENV introductions that took place during the period of study. In both cases, the novel serotype initially displaced the preexisting serotypes. After this initial phase, however, neither of the novel serotypes seemed to interfere with the others. If Iquitos begins to sustain simultaneous transmission of all four serotypes, the maintenance of longitudinal cohort studies will provide valuable data for confirming the patterns we identified and/or reveal further complexity in the interplay among serotypes.
Conclusions
Beyond clear intra-annual, seasonal variation, the observed temporal variation in epidemiological parameters (especially from year to year) implies that the transmission dynamics of DENV in Iquitos are complex and cannot be summarized with synoptic data or assumptions of time-independent transmission parameters. In addition to informing dengue prevention strategies, connecting the variation of these estimates to other processes, such as measures of entomological risk (i.e., mosquito abundance) and climatic variation, will inform local control strategies. The minimal vaccine coverage required to effectively control dengue varies by serotype. Given a potentially limited number of doses, efficiently distributing a vaccine within and between communities can only be optimized when these variations are understood and taken into account. Because vaccines may not have perfect efficacy (9), the incorporation of accurate, serotype-specific estimates of critical transmission parameters will be crucial for selecting delivery strategies and determining the optimal mix of vaccination and vector control for sustainable prevention of dengue.
Supplementary Material
Acknowledgments
We thank Neil Ferguson and an anonymous reviewer for comments that improved this manuscript. In particular, we acknowledge Dr. Ferguson's helpful suggestions regarding our calculations of R0. We thank Tom Lindström for insightful comments on our Bayesian approach. This work was supported by the Research and Policy for Infectious Disease Dynamics program of the Science and Technology Directory, Department of Homeland Security, and Fogarty International Center, National Institutes of Health (NIH); NIH Grants RO1 AI-42332 and RO1 AI069341; Innovative Vector Control Consortium; US Department of Defense Global Emerging Infections Systems Research Program Work Unit 847705.82000.25GB.B0016; Military Infectious Disease Research Program Work Units 6000 RAD1.S.B0302, S0002 04 LI, DOD S0017 03LI, DOD 32519, and S0088 06 NM; Deployed Warfighter Protection Program DOD S0002 04; and Wellcome Trust Grant 08571. A.L.L. acknowledges support from NIH Grant R01AI091980 and National Science Foundation Grant DMS 1246991. E.S.H. and T.J.K. are military service members and B.M.F., S.V., H.A., I.B., A.L., and A.C.M. are employees of the US Government. This work was prepared as part of their official duties. Title 17 U.S.C. §105 provides that “Copyright protection under this title is not available for any work of the United States Government.” Title 17 U.S.C. §101 defines a US Government work as a work prepared by a military service members or employees of the US Government as part of those persons’ official duties.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1314933111/-/DCSupplemental.
See Commentary on page 9370.
*Throughout the manuscript, the terms “inapparent” and “clinically apparent” are used to differentiate between asymptomatic infections or infections with mild symptoms that do not result in detection through passive case detection (inapparent) and infections severe enough that the individual seeks medical attention (clinically apparent).
References
- 1.Muench H. Derivation of rates from summation data by the catalytic curve. J Am Stat Assoc. 1934;29(185):25–38. [Google Scholar]
- 2.Grenfell BT, Anderson RM. The estimation of age-related rates of infection from case notifications and serological data. J Hyg (Lond) 1985;95(2):419–436. doi: 10.1017/s0022172400062859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hens N, et al. Seventy-five years of estimating the force of infection from current status data. Epidemiol Infect. 2010;138(6):802–812. doi: 10.1017/S0950268809990781. [DOI] [PubMed] [Google Scholar]
- 4.Ferguson NM, Donnelly CA, Anderson RM. Transmission dynamics and epidemiology of dengue: Insights from age-stratified sero-prevalence surveys. Philos Trans R Soc Lond B Biol Sci. 1999;354(1384):757–768. doi: 10.1098/rstb.1999.0428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Anderson R, May R. Infectious Diseases of Humans: Dynamics and Control. Oxford Univ Press, Oxford; 1992. [Google Scholar]
- 6.Fraser C, Riley S, Anderson RM, Ferguson NM. Factors that make an infectious disease outbreak controllable. Proc Natl Acad Sci USA. 2004;101(16):6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brady OJ, et al. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl Trop Dis. 2012;6(8):e1760. doi: 10.1371/journal.pntd.0001760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Simmons CP, Farrar JJ, Nguyen W, Wills B. Dengue. N Engl J Med. 2012;366(15):1423–1432. doi: 10.1056/NEJMra1110265. [DOI] [PubMed] [Google Scholar]
- 9.Sabchareon A, et al. Protective efficacy of the recombinant, live-attenuated, CYD tetravalent dengue vaccine in Thai schoolchildren: A randomised, controlled phase 2b trial. Lancet. 2012;380(9853):1559–1567. doi: 10.1016/S0140-6736(12)61428-7. [DOI] [PubMed] [Google Scholar]
- 10.Reiner RC, Jr, et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970-2010. J R Soc Interface. 2013;10(81):20120921. doi: 10.1098/rsif.2012.0921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Morrison AC, et al. Epidemiology of dengue virus in Iquitos, Peru 1999 to 2005: Interepidemic and epidemic patterns of transmission. PLoS Negl Trop Dis. 2010;4(5):e670. doi: 10.1371/journal.pntd.0000670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nisalak A, et al. Serotype-specific dengue virus circulation and dengue disease in Bangkok, Thailand from 1973 to 1999. Am J Trop Med Hyg. 2003;68(2):191–202. [PubMed] [Google Scholar]
- 13.Rodriguez-Barraquer I, et al. From re-emergence to hyperendemicity: The natural history of the dengue epidemic in Brazil. PLoS Negl Trop Dis. 2011;5(1):e935. doi: 10.1371/journal.pntd.0000935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Balmaseda A, et al. Trends in patterns of dengue transmission over 4 years in a pediatric cohort study in Nicaragua. J Infect Dis. 2010;201(1):5–14. doi: 10.1086/648592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.King AA, Ionides EL, Pascual M, Bouma MJ. Inapparent infections and cholera dynamics. Nature. 2008;454(7206):877–880. doi: 10.1038/nature07084. [DOI] [PubMed] [Google Scholar]
- 16.Endy TP, et al. Epidemiology of inapparent and symptomatic acute dengue virus infection: A prospective study of primary school children in Kamphaeng Phet, Thailand. Am J Epidemiol. 2002;156(1):40–51. doi: 10.1093/aje/kwf005. [DOI] [PubMed] [Google Scholar]
- 17.Burke DS, Nisalak A, Johnson DE, Scott RM. A prospective study of dengue infections in Bangkok. Am J Trop Med Hyg. 1988;38(1):172–180. doi: 10.4269/ajtmh.1988.38.172. [DOI] [PubMed] [Google Scholar]
- 18.Eamchan P, Nisalak A, Foy HM, Chareonsook OA. Epidemiology and control of dengue virus infections in Thai villages in 1987. Am J Trop Med Hyg. 1989;41(1):95–101. [PubMed] [Google Scholar]
- 19.Cummings DA, et al. The impact of the demographic transition on dengue in Thailand: Insights from a statistical analysis and mathematical modeling. PLoS Med. 2009;6(9):e1000139. doi: 10.1371/journal.pmed.1000139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thai KT, et al. Age-specificity of clinical dengue during primary and secondary infections. PLoS Negl Trop Dis. 2011;5(6):e1180. doi: 10.1371/journal.pntd.0001180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cuong HQ, et al. Quantifying the emergence of dengue in Hanoi, Vietnam: 1998-2009. PLoS Negl Trop Dis. 2011;5(9):e1322. doi: 10.1371/journal.pntd.0001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Egger JR, et al. Reconstructing historical changes in the force of infection of dengue fever in Singapore: Implications for surveillance and control. Bull World Health Organ. 2008;86(3):187–196. doi: 10.2471/BLT.07.040170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rothman A. Dengue Virus. Springer, Berlin; 2010. [Google Scholar]
- 24.Scott T, Morrison A. Longitudinal field studies will guide a paradigm shift in dengue prevention. In: Atkinson PW, editor. Vector Biology, Ecology and Control. Berlin: Springer; 2010. pp. 139–161. [Google Scholar]
- 25.Phillips I, Need J, Escamilla J, Colán E, Sánchez S, Rodríguez M, Vásquez L, Seminario J, Betz T, da Rosa AT. First documented outbreak of dengue in the Peruvian amazon region. Bull Pan Am Health Organ. 1992;26(3):201–207. [PubMed] [Google Scholar]
- 26.Watts DM, et al. Failure of secondary infection with American genotype dengue 2 to cause dengue haemorrhagic fever. Lancet. 1999;354(9188):1431–1434. doi: 10.1016/S0140-6736(99)04015-5. [DOI] [PubMed] [Google Scholar]
- 27.Forshey BM, et al. Dengue virus serotype 4, northeastern Peru, 2008. Emerg Infect Dis. 2009;15(11):1815–1818. doi: 10.3201/eid1511.090663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stoddard ST, et al. House-to-house human movement drives dengue virus transmission. Proc Natl Acad Sci USA. 2013;110(3):994–999. doi: 10.1073/pnas.1213349110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Olkowski S, et al. Reduced risk of disease during postsecondary dengue virus infections. J Infect Dis. 2013;208(6):1026–1033. doi: 10.1093/infdis/jit273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Forshey BM, et al. NMRCD Febrile Surveillance Working Group Arboviral etiologies of acute febrile illnesses in Western South America, 2000-2007. PLoS Negl Trop Dis. 2010;4(8):e787. doi: 10.1371/journal.pntd.0000787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Meeker WQ, Escobar LA. Statistical Methods for Reliability Data. Wiley, New York; 1998. [Google Scholar]
- 32.Ziv S, Marc A, Geert M, Philippe B, Pierre Van D. Modelling forces of infection by using monotone local polynomials. J R Stat Soc Ser C Appl Stat. 2003;52(4):469–485. [Google Scholar]
- 33.Ramsay J. Functional Data Analysis, Springer Series in Statistics. Springer, New York; 2005. [Google Scholar]
- 34.Tierney L. Markov chains for exploring posterior distributions. Ann Stat. 1994;22(4):1701–1728. [Google Scholar]
- 35.Roberts GO, Rosenthal JS. Examples of adaptive MCMC. J Comput Graph Statist. 2009;18(2):349–367. [Google Scholar]
- 36.Gelman A, Rubin D. Inference from iterative simulation using multiple sequences. Stat Sci. 1992;7(4):457–472. [Google Scholar]
- 37.Brooks SP, Gelman A. General methods for monitoring convergence of iterative simulations. J Comput Graph Statist. 1998;7(4):434–455. [Google Scholar]
- 38. R Development Core Team (2012) R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna). Available at www.R-project.org. Accessed May 16, 2013.
- 39. Ramsay, JO, Wickham H, Graves S, Hooker G. (2012) fda: Functional data analysis. R package version 2.2.8. Available at http://CRAN.R-project.org/package=fda. Accessed May 16, 2013.
- 40.Plummer M. Best N, Cowles K, Vines K (2006) CODA: Convergence diagnosis and output analysis for MCMC. R package version 2.2.8. Available at http://CRAN.R-project.org/doc/Rnews. Accessed May 16, 2013.
- 41.Aldstadt J, et al. Space-time analysis of hospitalised dengue patients in rural Thailand reveals important temporal intervals in the pattern of dengue virus transmission. Trop Med Int Health. 2012;17(9):1076–1085. doi: 10.1111/j.1365-3156.2012.03040.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nisalak A, et al. Serotype-specific dengue virus circulation and dengue disease in Bangkok, Thailand from 1973 to 1999. Am J Trop Med Hyg. 2003;68(2):191. [PubMed] [Google Scholar]
- 43.Nguyen MN, et al. Host and viral features of human dengue cases shape the population of infected and infectious Aedes aegypti mosquitoes. Proc Natl Acad Sci USA. 2013;110(22):9072–9077. doi: 10.1073/pnas.1303395110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Johansson MA, Hombach J, Cummings DA. Models of the impact of dengue vaccines: A review of current research and potential approaches. Vaccine. 2011;29(35):5860–5868. doi: 10.1016/j.vaccine.2011.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nagao Y, Koelle K. Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever. Proc Natl Acad Sci USA. 2008;105(6):2238–2243. doi: 10.1073/pnas.0709029105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. 2004;160(6):509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mills CE, Robins JM, Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature. 2004;432(7019):904–906. doi: 10.1038/nature03063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fine PE. Herd immunity: History, theory, practice. Epidemiol Rev. 1993;15(2):265–302. doi: 10.1093/oxfordjournals.epirev.a036121. [DOI] [PubMed] [Google Scholar]
- 49.Adams B, et al. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc Natl Acad Sci USA. 2006;103(38):14234–14239. doi: 10.1073/pnas.0602768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vazquez-Prokopec GM, et al. Using GPS technology to quantify human mobility, dynamic contacts and infectious disease dynamics in a resource-poor urban environment. PLoS ONE. 2013;8(4):e58802. doi: 10.1371/journal.pone.0058802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Perkins TA, Scott TW, Le Menach A, Smith DL. Heterogeneity, mixing, and the spatial scales of mosquito-borne pathogen transmission. PLOS Comput Biol. 2013;9(12):e1003327. doi: 10.1371/journal.pcbi.1003327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Liebman KA, et al. Spatial dimensions of dengue virus transmission across interepidemic and epidemic periods in Iquitos, Peru (1999-2003) PLoS Negl Trop Dis. 2012;6(2):e1472. doi: 10.1371/journal.pntd.0001472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438(7066):355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Thomas SJ, et al. Dengue plaque reduction neutralization test (PRNT) in primary and secondary dengue virus infections: How alterations in assay conditions impact performance. Am J Trop Med Hyg. 2009;81(5):825–833. doi: 10.4269/ajtmh.2009.08-0625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Rainwater-Lovett K, Rodriguez-Barraquer I, Cummings DA, Lessler J. Variation in dengue virus plaque reduction neutralization testing: Systematic review and pooled analysis. BMC Infect Dis. 2012;12:233. doi: 10.1186/1471-2334-12-233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.OhAinle M, et al. Dynamics of dengue disease severity determined by the interplay between viral genetics and serotype-specific immunity. Sci Transl Med. 2011;3:114ra128. doi: 10.1126/scitranslmed.3003084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sabin AB. Research on dengue during World War II. Am J Trop Med Hyg. 1952;1(1):30–50. doi: 10.4269/ajtmh.1952.1.30. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.