Probing red blood cell mechanics, rheology and dynamics with a two-component multi-scale model

Abstract

This study is partially motivated by the validation of a new two-component multi-scale cell model we developed recently that treats the lipid bilayer and the cytoskeleton as two distinct components. Here, the whole cell model is validated and compared against several available experiments that examine red blood cell (RBC) mechanics, rheology and dynamics. First, we investigated RBC deformability in a microfluidic channel with a very small cross-sectional area and quantified the mechanical properties of the RBC membrane. Second, we simulated twisting torque cytometry and compared predicted rheological properties of the RBC membrane with experimental measurements. Finally, we modelled the tank-treading (TT) motion of a RBC in a shear flow and explored the effect of channel width variation on the TT frequency. We also investigated the effects of bilayer–cytoskeletal interactions on these experiments and our simulations clearly indicated that they play key roles in the determination of cell membrane mechanical, rheological and dynamical properties. These simulations serve as validation tests and moreover reveal the capabilities and limitations of the new whole cell model.

1. Introduction

Blood is composed primarily of microscopic cellular particles like red blood cells (RBCs), white blood cells (WBCs) and platelets. The blood cells are suspended in a blood's liquid medium called blood plasma, which consists of water and other submicrometre elements such as proteins, glucose, mineral ions and carbon dioxide. The most abundant cells in vertebrate blood are RBCs. A human RBC is a nucleus-free cell; it is essentially a membrane encapsulating haemoglobin solution. Owing to the elastic nature of the RBC membrane and the fluidic nature of the haemoglobin, the RBC is capable of dramatic deformations and rich dynamics, while the membrane surface area and volume remain constant [1,2].

The deformability of a RBC is determined by the geometry, elasticity and viscosity of its membrane. A healthy RBC has a biconcave shape when not subject to any external stress and is approximately 8.0 μm in diameter and 2.0 μm in thickness [3,4]. The RBC membrane consists of a lipid bilayer supported by an attached spectrin-based cytoskeleton. The resistance of the lipid bilayer to bending elasticity is controlled by the bending rigidity, k_c, while the spectrin network's resistance to shear strain is characterized by the in-plane shear modulus, μ_s. Various RBC properties have been measured in a number of experiments, including micropipette aspiration [5], optical tweezers [6], optical magnetic twisting cytometry (OMTC) [7], membrane thermal fluctuations [8], atomic force microscopy [9], shear flow [10,11] and optical stretcher [12]. The micropipette aspiration and optical tweezers techniques subject the RBC directly to mechanical deformation and predict the macroscopic interfacial shear modulus of healthy RBCs in the range of 2–12 μN m⁻¹. Optical magnetic twisting cytometry and membrane thermal fluctuations provide measurements of membrane rheological properties and characterize the viscoelastic response of the RBC membrane.

Experimental observations of RBC behaviours in flow mimicking the microcirculation reveal dramatic deformations and rich dynamics. The extreme deformability allows the RBC to squeeze without any damage when passing through narrow capillaries in the microcirculation. In a steady shear flow, an individual RBC exhibits complex dynamic behaviours [2,13–15]. Specifically, a RBC in shear flow exhibits two types of dynamical motion [10,16,17]: a tumbling (TB) motion that is characterized by the flipping of the cell resembling a rigid-body motion, and a tank-treading (TT) motion in which the cell membrane and the interior liquid follow a rotational motion, while the cell aligning at an angle with respect to the flow direction remains nearly steady.

Dynamic simulation and multi-scale modelling help in predicting how RBCs behave in shear flow and provide insights into how viscous flow transforms the shapes of RBCs and how the deformable RBC distorts the surrounding flow. Several computational models, including spectrin-level and MS-RBC models [18–20], have been recently developed and applied to RBC simulations at different length scales. In these models, the membrane is usually considered as a single-component shell with effective properties that seek to estimate the combined effects of the lipid bilayer and the cytoskeleton. Under normal conditions, the cytoskeleton is attached to the lipid bilayer from the cytoplasmic side. However, under certain conditions, such as RBCs which assume a crescent shape in sickle cell disease, the cytoskeleton may become dissociated from the lipid bilayer [21]. The mechanical properties associated with the bilayer–cytoskeletal interactions strongly influence biorheology, erythrocyte function and the onset and progression of RBC diseases. Thus, it is desirable to develop a new two-component, particle-based, whole-cell model to study the biophysics of RBCs arising from the interactions between the lipid bilayer and the cytoskeleton.

Recently, we developed a new two-component MS-RBC model based on the dissipative particle dynamics (DPD) simulation technique [22]. The two-component RBC model has been shown to accurately reproduce realistic biophysical and rheological properties of RBCs arising from the interaction between the lipid bilayer and the cytoskeleton. In this study, we perform more simulations and compare the predictions of the whole cell model with several available experiments to confirm that the new RBC model is able to probe the RBC mechanics, rheology and dynamics. The rest of this paper is organized as follows: in §2, we describe the simulation method and employed DPD model. We present and discuss the simulation results in §3. Finally, in §4, we summarize the findings and present the conclusions. In the video clips, we present the dynamic processes of RBCs flowing in a microfluidic channel and the microbead responses to applied oscillating torque in simulations.

2. Simulation model and method

We study the mechanics, rheology and dynamics of RBCs with the help of the two-component RBC model. For completeness, the method and the multi-scale model are briefly reviewed below, whereas details on the DPD method and the two-component RBC model are available elsewhere [22].

(a). Two-component red blood cell model

In the two-component RBC model, the membrane is modelled by two distinct components, i.e. the lipid bilayer and the cytoskeleton. Specifically, through the DPD approach, each component is constructed by a two-dimensional triangulated network with N_v vertices, where each vertex is represented by a DPD particle. Different from the one-component RBC model, where we refer to the MS-RBC model [19,20], the lipid bilayer of the two-component RBC model has no shear stiffness but only bending stiffness and a very large local area stiffness, whereas the cytoskeleton has no bending stiffness but possesses a finite shear stiffness. Also, we include both the elastic and friction interactions between the lipid bilayer and the cytoskeleton. The potential energy of the RBC membrane including these two different components is defined as

2.1

where U_s is the elastic energy that mimics the elastic spectrin network, given by

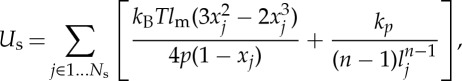2.2

where l_j is the length of the spring j, l_m is the maximum spring extension, x_j=l_j/l_m, p is the persistence length, k_BT is the energy unit, k_p is the spring constant and n is a specified exponent. The shear modulus of the RBC membrane, independent of the coarse-grained (CG) level of the triangulated network, is determined by

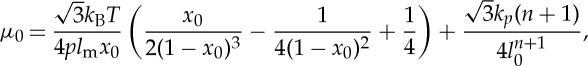2.3

where l₀ is the equilibrium spring length and x₀=l₀/l_m.

The membrane viscosity is imposed by introducing a viscous force on each spring, which has the form

2.4

and

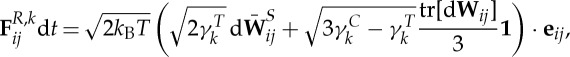2.5

where 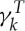and 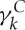are dissipative parameters, and k=b, s stands for the lipid bilayer or the cytoskeleton, respectively. v_ij is the relative velocity of spring ends, and 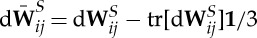is the traceless symmetric part of a random matrix representing the Wiener increment. The viscosity of the RBC membrane is then calculated as

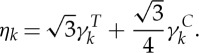2.6

Following Fedosov et al. [20], 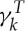is set to 3 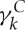in all simulations as 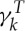accounts for a large portion of the viscous contribution.

The bending resistance of the RBC membrane is modelled by

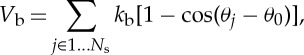2.7

where k_b is the bending constant, θ_j is the instantaneous angle between two adjacent triangles having the common edge j and θ₀ is the spontaneous angle. In addition, the RBC model includes the area and volume conservation constraints, which mimic the area incompressibility of the lipid bilayer and the volume incompressibility of the internal fluid, respectively. The corresponding energy is given by

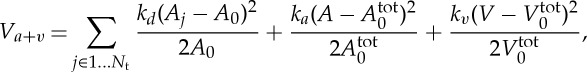2.8

where N_t is the number of triangles in the membrane network, A₀ is the triangle area, and k_d, k_a and k_v are the local area, global area and volume constraint coefficients, respectively. The terms 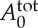and 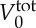are the specified total area and volume, respectively.

The last term in equation (2.1), U_int, is the potential defining the contribution for capturing the interaction between the lipid bilayer and the cytoskeleton, which has the form

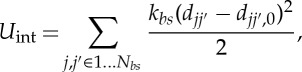2.9

where k_bs and N_bs are the spring constant and the number of bond connections between the lipid bilayer and the cytoskeleton, respectively. d_jj′ is the distance between the vertex j of the cytoskeleton and the corresponding projection point j′ on the lipid bilayer, with the corresponding unit vector n_jj′; d_jj′,0 is the initial distance between the vertex j and the point j′, which is set to zero in our simulations. The corresponding elastic force on the vertex j of the cytoskeleton is given by

2.10

and the tangential friction force between the lipid bilayer and the cytoskeleton is represented by

2.11

where f_bs is the tangential friction coefficient, and v_jj′ is the difference between the two velocities.

The RBC membrane interacts with the fluid particles through DPD forces, and the temperature of the system is controlled through the DPD thermostat [23,24]. The internal and external fluids are modelled by collections of free DPD particles and their separation is enforced by bounce-back reflections of these particles at the RBC membrane surface. Similar to the MS-RBC model, the two-component RBC model is multi-scale, as the RBC can be represented on the spectrin level, where each spring in the network corresponds to a single spectrin tetramer with the equilibrium distance between two neighbouring actin connections of approximately 75 nm. On the other hand, for more efficient computation, the RBC network can also be highly CG with equilibrium spring lengths of up to 500–600 nm. As suggested by Pivkin & Karniadakis [19], the equilibrium length of the springs depends on the CG level through an approximate formula, which is given by

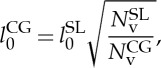2.12

where 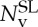and N^CG_v are the number of vertices in the spectrin-level and CG models. Using a similar geometric argument, we adjust the spontaneous angle as

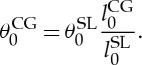2.13

On the other hand, the mechanical properties of the RBC membrane, such as the shear and elastic area compression moduli, are independent of the CG level of the triangulated network. Therefore, we will use the same physical values of k_b and μ₀ for different CG levels.

(b). Model and physical units scaling

In a DPD approach, it is convenient to use reduced units [23]. The unit of length is defined by the cut-off radius r_c; the unit of the mass is defined by the mass of a particle; and the unit of energy is defined by k_BT. It is difficult to have a precise idea of the scales involved in DPD simulations. The real size of a DPD particle may vary from one to several dozens of atoms, depending on the interaction potential and the time scale. Several recent papers have dealt with this issue and have attempted to map the computed results into dimensional units [20,25–28]. A mapping strategy developed by Fedosov et al. [20] is adopted to provide an estimate of the physical length and time scales in the DPD simulations of RBC flow. Following their mapping strategy, we obtain the DPD length and time scale,

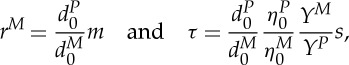2.14

where the superscript M denotes a quantity in reduced DPD units, while P identifies physical units. d₀ is the cell diameter, η₀ is a characteristic viscosity of fluid or RBC membrane and Y ₀ is the membrane Young's modulus. In the current simulations, the RBC diameter, the membrane Young's modulus and the interior fluid viscosity are 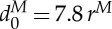, 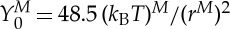and 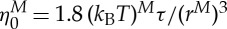, respectively, corresponding to 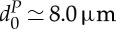, 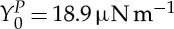and η_i≃0.006 pN μm⁻² s (6 cP) in physical units; thus, the DPD length scale is r^M≃1.0 μm and the time scale is τ≃8.7 ms.

We model the RBC using the stress-free membrane model with the following properties: N_v=500, RBC area 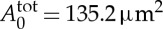and volume 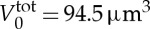, RBC membrane bending and shear stiffness are kept at k_c=2.4×10⁻¹⁹ J and μ₀=6.3 pN μm⁻¹, respectively. The simulations are performed using a modified version of the atomistic code LAMMPS [29]. The time integration of the motion equations is computed through a modified velocity Verlet algorithm [23] with λ_vv=0.50 and time step Δt=(0.0005–0.002)τ≈(4.3–17.4) μs. It takes 5.0×10⁵ time steps for a typical simulation performed in this study.

3. Results and discussion

In this section, the two-component RBC model is compared against several available experiments that investigate RBC mechanics, rheology and dynamics. First, we probe the mechanical properties of a RBC traversing a microfluidic channel with very small cross-sectional area and quantify the cell deformation. Second, we study the rheological properties of the modelled membrane and validate them against OMTC experiments. Finally, we simulate the RBC dynamics in shear flow and investigate the effect of channel width variations on the TT frequency.

(a). Measurement of red blood cell large deformation in a microfluidic system

A RBC is highly deformable, allowing it to travel through in vivo capillaries with diameter smaller than the RBC's size [30]. When RBCs flow through capillaries, they undergo severe deformation by shear stress. Accordingly, microfluidic channels are used to mimic human capillaries and study RBC deformability.

The microfluidic channel, as illustrated in figure 1a, is filled with fluid particles containing RBCs. A narrow cuboid channel with length l=30.0 μm, width w=4.0 μm and height h=2.7 μm is created in the middle of the microfluidic channel, and two symmetrical wide channels with width W=23.4 μm and height H=2.7 μm are then created on the left and right domains of the narrow channel. The wide and narrow channels are connected by inclined walls. The solid walls of the microfluidic channel are formed by stationary DPD particles, and an adaptive boundary condition is adopted for fluid DPD particles to control their density fluctuations [31,32].

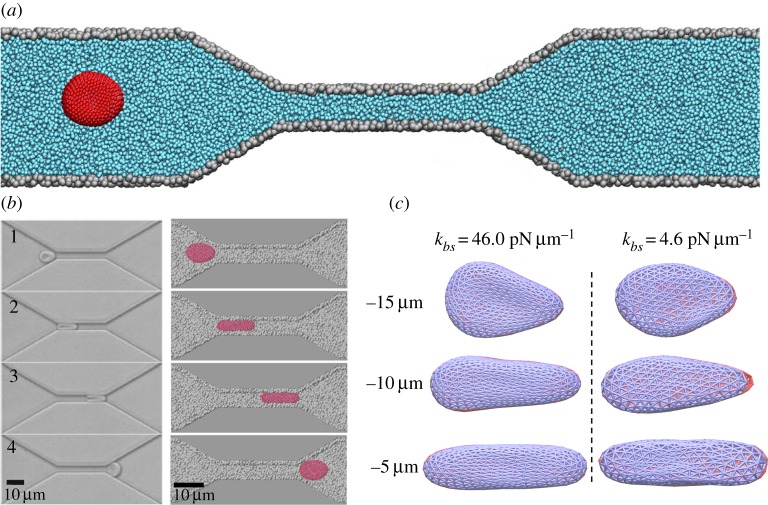
Figure 1.

(a) Schematic representation of a RBC traversing across a microfluidic channel, with a constriction 30 μm long, 4 μm wide and 2.7 μm high. The cell, fluid and wall particles are rendered in dark grey, light grey, and grey, respectively (in red, cyan, and grey, respectively, in the online version). (b) Shape characteristics of a RBC traversing across microfluidic channels from the experimental (left) and simulation (right) data. (c) Bilayer–cytoskeletal detachment for a RBC traversing the microfluidic channel at different bilayer–cytoskeletal elastic interactions. The lipid bilayer and the cytoskeleton are shown as dark and light grey (red and blue in the online version) triangular networks, respectively, and only half of the triangular network of the lipid bilayer is shown for clarity. (Online version in colour.)

Figure 1b and the electronic supplementary material, video clip S1, show a typical dynamic process of a pressure-driven RBC flowing through the microfluidic channel. They can help in clearly understanding the process of RBC traversal across a microfluidic channel and reveal that the RBC initially drifts along the flow direction due to collisions with the fluid particles. The RBC is also disturbed by the fluid particles near the narrow channel because of the mismatch between the RBC size and the pore size of the narrow channel. That is, the RBC undergoes a continuous and severe transition from its normal biconcave shape to an ellipsoidal shape by the elongation of its size in the flow direction (longitudinal axis) and shortening of its size in the cross-flow direction (transverse axis). The RBC enters into the entrance of the narrow channel by undergoing these deformations. Once the entire RBC enters the constriction, it deforms further to pass through the microfluidic channel. Figure 1b shows a qualitative comparison of the simulation observations with experimental results by Quinn et al. [30]. The dynamic observations of the shape deformation of RBC traversal across the microfluidic channel are in accordance with the experimental phenomena.

Next, we study the effect of the bilayer–cytoskeletal elastic interaction coefficient k_bs and monitor the instantaneous position of the RBC during the transit processes as shown in figure 1c. We find that when using the default value of k_bs=46.0 pN μm⁻¹, which is estimated on the basis of simulating a channel flow stretching experiment [22], the target particles on the lipid bilayer and the cytoskeleton move together. This is indicated by the simulation data in figure 2a. A small difference in the detachment length, which is defined as the distance along the longitudinal axis from the rightmost part of the lipid bilayer to that of the cytoskeleton, is present. The deviations are sufficiently small or purely due to statistical fluctuations; hence, there is no significant bilayer–cytoskeletal detachment in this case. However, assuming a pathological RBC state where k_bs is significantly lower, an apparent bilayer–cytoskeletal detachment occurs when the RBC traverses the microfluidic channel (see figure 1c and the electronic supplementary material, video clip S2). Specifically, the detachment length between the lipid bilayer and the cytoskeleton is less than 30 nm in the case with k_bs=46.0 pN μm⁻¹; however, it is up to 600 nm in the case with k_bs=4.6 pN μm⁻¹.

Figure 2.

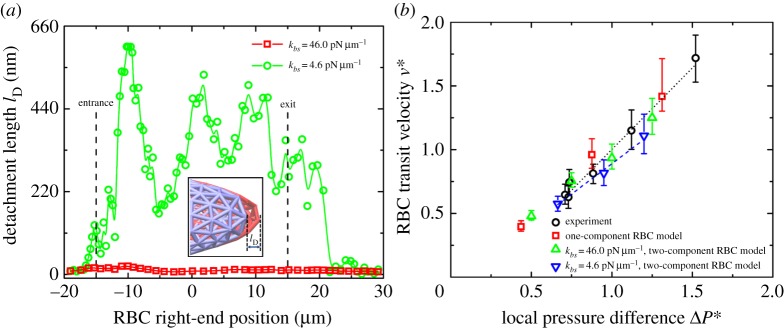
(a) Measured detachment length, l_D, between the lipid bilayer and the cytoskeleton at different locations of the right-end of the RBC when it passes through the microfluidic channel. In the figure, l_D represents the distance from the far rightmost edge of the lipid bilayer to that of the cytoskeleton. Vertical dashed lines indicate the locations of the narrow channel entrance and exit. Inset shows a sketch of the bilayer–cytoskeletal detachment. (b) Dependence of the cell transit velocity on the local pressure difference for the microfluidic channel with w=4.0 μm. Experimental data (black circles) from [30] are shown. v* is a reduced velocity that is obtained through the physical velocity divided by a certain value at ΔP=0.1 kPa, and ΔP* is a reduced pressure difference that is obtained through the physical pressure difference divided by the value of 0.1 kPa. (Online version in colour.)

We then calculate the cell transit velocity, which is defined as the average transit distance divided by the transit time. The transit time is the time it takes from when a RBC enters the narrow channel to when it exits from the rightmost part of the narrow channel. Figure 2b shows the dependence of the cell transit velocity on the local pressure difference for the RBC traversal across the microfluidic channel. The simulation results of the two-component RBC model at k_bs=46.0 pN μm⁻¹ are consistent with the experimental measurements and the prediction of the one-component RBC model by Quinn et al. [30]; however, the cell velocity is decreased in the case of k_bs=4.6 pN μm⁻¹, which indicates that the bilayer–cytoskeletal elastic interaction coefficient k_bs plays a key role in the RBC traversing narrow microfluidic channels. When k_bs is large, there is a strong coupling between the lipid bilayer and the cytoskeleton, i.e. they behave as if they were one effective membrane. If k_bs is small, the bilayer–cytoskeletal coupling is weak, and the detachment of the lipid bilayer from the cytoskeleton is much more likely to occur.

(b). Membrane rheology from twisting torque cytometry

Blood cells are subjected to intense mechanical stimulation from both blood flow and vessel walls, and their rheological properties are important to their effectiveness in performing their biological functions in the microcirculation. The latest experimental techniques have explored the mechanical properties of RBCs and can shed light on their deformation in terms of the shear, bending, area expansion moduli and relaxation times. Recently, dynamical experiments on RBC rheology using OMTC have allowed researchers to explore the time-dependent responses of RBCs. The rheological measurements of RBC membrane properties provide a detailed description of the complex time-dependent membrane response and may reveal complex behaviour, i.e. yield stress, shear thinning and viscoelasticity. Here, we simulate the membrane rheology from twisting torque cytometry (TTC). TTC is a numerical analogue of the OMTC used in experiments [7], where the magnetic twisting cytometry applies both a static and oscillating magnetic field to a microbead bonded to the surface of a cell membrane. In analogy with the experimental set-up, in simulations a microbead is attached to the top of a RBC membrane and is also subjected to an oscillating magnetic field, as shown in figure 3a. The RBC–wall adhesion is simulated by keeping 15% of vertices stationary on the bottom of the lipid bilayer component of the RBC membrane, while the RBC–microbead adhesion is simulated by including several RBC vertices in the lipid bilayer component near the bottom of the microbead in its rigid motion.

Figure 3.

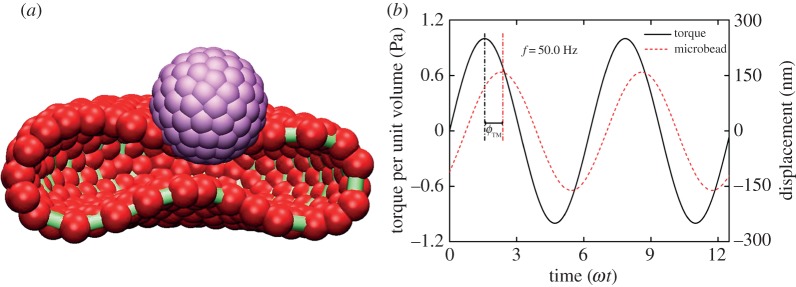
(a) Schematic representation of the set-up of the twisting torque cytometry. The microbead, lipid bilayer and cytoskeleton are shown in light grey, dark grey, and silver, respectively (purple, red, and green, respectively, in the online version). An oscillating torque is applied to the microbead and deforms the RBC, which causes the microbead to rotate and translate. (b) Characteristic response of an attached microbead (dashed line) subjected to oscillating torque. ϕ_TM represents the phase shift angle between the applied oscillating torque and the displacements of microbead. (Online version in colour.)

Figure 3b shows a typical microbead response to an oscillating torque measured in simulations. The microbead presents a periodic displacement of the same oscillating frequency as the applied torque, but with a shifted phase angle ϕ with respect to the latter. The complex elastic moduli are computed from ϕ as

3.1

where g′ and g′′ are the two-dimensional storage and loss moduli, and ΔT and Δd are the torque and microbead displacement amplitudes. The values of ΔT and Δd can be directly determined from the limits of the displacement–torque loop (figure 4a) and the area, A, bounded by the loop, and are related to ϕ by

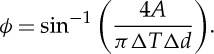3.2

For a single RBC with an applied oscillating field, the phase shift ϕ between the applied torque and the resulting displacement increases with increasing frequency. The increasing phase shift is reflected by the larger area A enclosed by the displacement–torque loop at a higher frequency (figure 4a).

Figure 4.

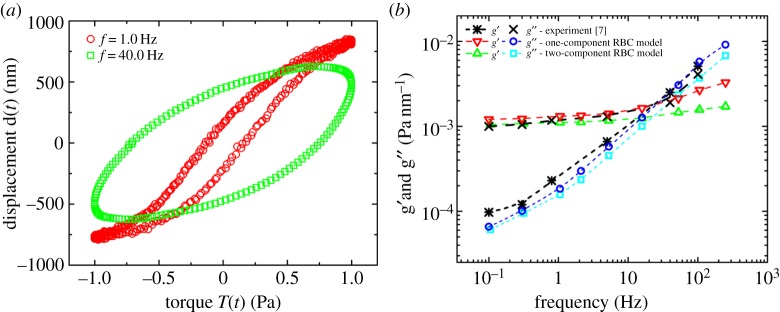
(a) Displacement–torque loops for a representative microbead at different frequencies. (b) Two-dimensional storage and loss moduli, g′ and g′′, of the RBC membrane obtained by calculating the limits and enclosed area of the displacement–torque loops and using equations (3.1) and (3.2). (Online version in colour.)

The values of ΔT, Δd and ϕ can also be obtained by fitting the simulation data with sinusoidal functions, which are given as

3.3

After these values are obtained using these two different approaches, the apparent storage g′ and loss g′′ moduli can be calculated using equation (3.1) and compared with the experimental data (figures 4b and 5a). Similar to the experimental measurements, the values of g′ and g′′ obtained from these two different approaches are almost the same. The only discrepancy between the approaches occurred at the very highest frequency, that is, g′ firstly increases then decreases with the increase in the applied oscillating frequency when we use the second method shown in equations (3.1) and (3.3) (figure 5a), while it continues to increase when we use the first one shown in equations (3.1) and (3.2) (figure 4b), in which case the displacement–torque loop does not approximate an ellipse, and a rather large error would occur. Thus, the second method using equations (3.1) and (3.3) is thought to be preferable at very high frequencies.

Figure 5.

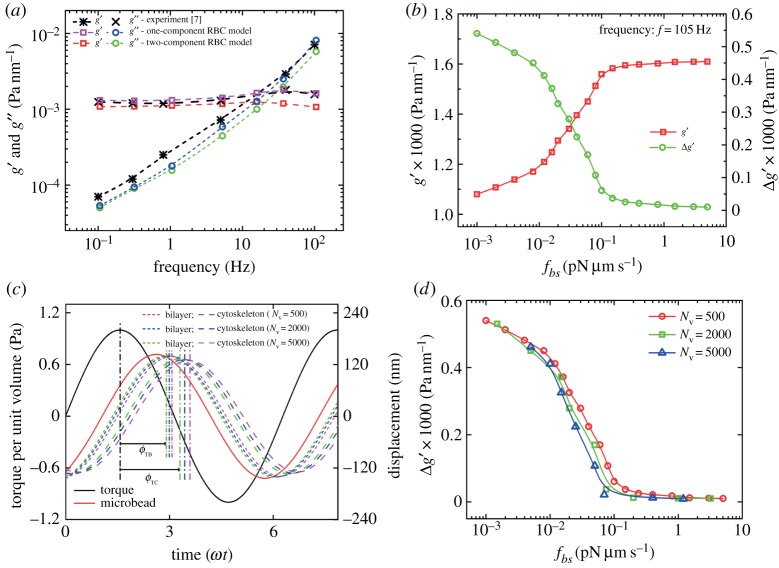
(a) Two-dimensional storage and loss moduli, g′ and g′′, of the RBC membrane obtained by fitting a sinusoidal function to the displacement response and using equations (3.1) and (3.3). (b) Effect of the bilayer–cytoskeletal friction coefficient f_bs on the g′ of the RBC membrane. (c) Characteristic response of the attached RBC vertices in the lipid bilayer and the cytoskeleton near the oscillating microbead using two-component models with N_v=500, 2000 and 5000. ϕ_TB and ϕ_TC represent the phase-shift angle between the applied oscillating torque and the displacements of the marked particles in the lipid bilayer and cytoskeleton, respectively. (d) Comparison of Δg′ of the RBC membrane between the one-component RBC model and the two-component RBC model with N_v=500, 2000 and 5000. (Online version in colour.)

Compared with the values obtained from the one-component RBC model, a decrease in the storage modulus g′ at high frequency with the two-component RBC model appears; however, the difference, 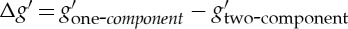, is reduced when we increase the friction between the lipid bilayer and the cytoskeleton (figure 5b). This is because there is no bilayer–cytoskeletal slip with large f_bs and the local area deformation of the cytoskeleton is the same as that of the lipid bilayer; hence, we have local conservation of the surface area of the cytoskeleton. However, if f_bs is small, we do not have local conservation of the surface area of the cytoskeleton, and an apparant bilayer–cytoskeletal slip occurs during the oscillation. In addition, the responses of the attached particles in the lipid bilayer and cytoskeleton of RBCs at different CG levels are obtained (figure 5c). We can see that there is a small phase shift in the displacement between the lipid bilayer and the cytoskeleton. The difference in phase shift, Δϕ_BC=ϕ_TC−ϕ_TB, becomes smaller with increasing N_v. For example, at f=105 Hz, the values of Δϕ_BC are 26.9°, 25.8° and 22.4° at N_v=500, 2000 and 5000, respectively. The electronic supplementary material, video clips S3 and S4, shows the microbead responses to the same oscillating torque frequency measured in simulations with the one-component and the two-component RBC models. We can find that the apparent bilayer–cytoskeleton slip occurs after a few oscillating cycles for the latter case. Figure 5d shows Δg′ for different f_bs and different CG levels for an individual RBC with N_v=500, 2000 and 5000. We find that Δg′ rapidly decreases with f_bs, whereas it smoothly approaches saturation at high f_bs in these three different cases. The critical value of f_bs is smaller for the RBC model with N_v=5000 due to the finer resolution, in which the effective tangential friction coefficient of a single junctional complex connection is larger, so that it reaches saturation faster. Hence, by explicitly incorporating the bilayer–cytoskeletal friction in the two-component RBC model, we successfully test that the whole cell model can be used to quantify the bilayer–cytoskeletal slip and probe its role in cell rheology.

(c). Single-cell dynamics and deformation

Using the two-component RBC model, we have also simulated the motion of a RBC in shear flow. An important characteristic of the dynamics of an individual RBC in shear flow is the TT frequency. Although many experimental studies have been devoted to the measurement of TT frequency, considerable uncertainty exists with respect to the dependence of the TT frequency f of a RBC on the shear rate 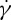and viscosity ratio λ of the internal to suspending fluid viscosities. For example, Fischer et al. [10] and Tran-Son-Tay et al. [11] found that f increases linearly with 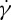. By contrast, Fischer found that f increases with 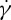in a nonlinear fashion satisfying a scaling law 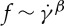with scaling exponents ranging between 0.85 and 0.95 [33]. With regards to the dependence of f on λ, Fischer et al. [10] found no dependence of 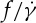on λ, whereas Tran-Son-Tay et al. [11] found that 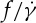increases with decreasing λ. Fischer [33] also found a similar dependence of 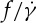on λ, but with a reduced slope that was less than half of that reported by Tran-Son-Tay et al. [11]. Here, we simulate the TT motion of a RBC in shear flow to investigate the correct functional relationship between f and 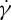(or λ). Specifically, by placing a single RBC in shear flow between two planar solid walls, we simulate the TT motions of a RBC over a wide range of three relevant parameters: the suspending fluid viscosity η₀ ranging from 0.0 to 109.3 cP, the shear rate 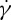varying from 0.0 to 285.0 s⁻¹, and the degree of confinement given by the ratio of the diameter of the RBC to the channel width, 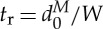, which varies between 0.22 and 0.67.

The fluidic channel is filled with fluid particles containing a RBC. Periodic boundary conditions are used in the y and z directions, whereas the flow is bounded by solid walls in the x direction. The domain dimensions are set to 45.0 μm×15.0 μm×W, where W is the channel width between the two planar solid walls. An extra bounce-back rule, i.e. the velocity of a DPD particle that collides with the solid wall is reflected back into the fluidic channel, is applied to the RBC and fluid particles to prevent them entering the solid wall domain. To produce a shear flow in the fluidic channel, a Couette flow driven by the two solid walls at the top and the bottom having same speed but moving in opposite directions is applied to the suspending fluid. Different shear rates can be obtained by changing the speed of the solid walls.

First, we consider η₀=28.9 cP and 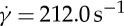for which the RBC can tank-tread in a steady shear flow according to the Keller–Skalak model [34] and the experiment [33]. The RBC is released in the shear flow at time t=0.0 s. It gradually deforms its shape and eventually obtains an oblate or a convex ellipsoid shape. The RBC membrane and the internal fluid are observed to make a TT motion, while the RBC aligns at an inclination angle with the flow direction. To gain insight into RBC dynamics in the TT motion, we investigate the TT frequency of the RBC by tracking a marker particle in the RBC membrane. The instantaneous position of the marker particle is monitored in time (figure 6a). We find that the marker particle moves back and forth in the RBC membrane. At the end of one cycle, the marker particle comes back to its starting point. The simulation data are fitted with a sinusoidal function 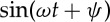, where ω=2πf, in order to extract the frequency f in s⁻¹. The time-dependent angular trajectories of the marker particle in figure 6b provide a more direct way to calculate the TT period P_tt, and, thus, to obtain f through f=1/P_tt. By decreasing the degree of confinement from t_r=0.67 to t_r=0.22, a similar dynamics is observed during which the RBC orientation remains nearly the same while the marker particle moves slower, and the P_tt becomes larger compared with its motion at t_r=0.67 as shown in figure 6, which means that there is a decrease in f when increasing the channel width.

Figure 6.

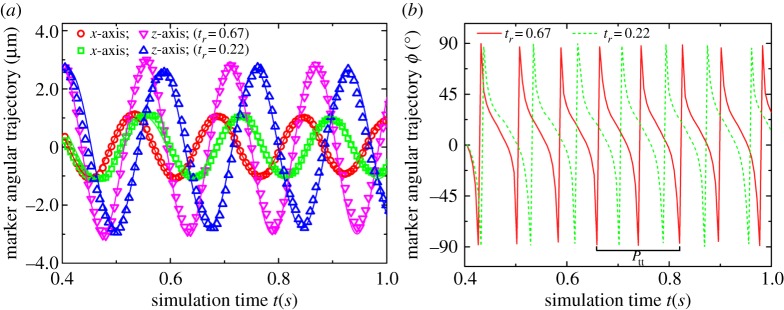
Numerical results of time-dependent axial (a) and angular (b) trajectories of a marker particle in the RBC membrane during the TT motion for different t_r at η₀=28.9 cP and 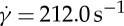. In the figure, ϕ is the angle between the vector from the centre of the RBC to the position of the marked particle and z-axis direction. (Online version in colour.)

It has been assumed that changing the channel width of the solid walls can affect the TT frequency, and the relationship between f and 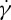is channel width dependent [33], i.e. it is linear in a narrow channel flow while it is nonlinear with increasing the channel width. We demonstrate here the plausibility of the effect of channel width variations on the RBC dynamics. Figure 7a shows the TT frequency f as a function of shear rate 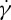at suspending fluid viscosity η₀=28.9 cP. The simulation results show that f increases linearly with 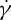at t_r=0.67, which is consistent with the experimental findings by Fischer et al. [10] and Tran-Son-Tay et al. [11]. One interesting observation is that, when we decrease the degree of confinement to a small value such as t_r=0.22, a nonlinear dependence of f on 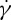is obtained (figure 7a). For this case, there is a decrease in f for large 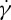. The f– 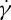relationship is nonlinear and satisfies a scaling law 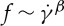with scaling exponent β≃ 0.91. The simulation results agree with the results by Fischer [33] in his experiment with a wide channel.

Figure 7.

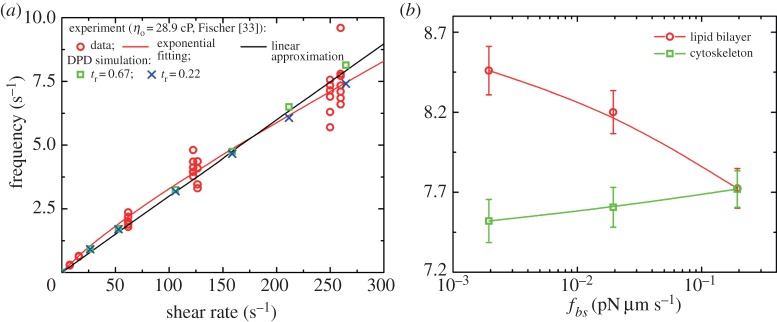
(a) TT frequency f of a RBC as a function of shear rate at the degrees of confinement t_r=0.67 (squares) and 0.22 (crosses). Numerical results are compared with experimental data (circles) by Fischer [33]. (b) Effect of the bilayer–cytoskeletal friction coefficient f_bs on TT frequency f of a RBC at . (Online version in colour.)

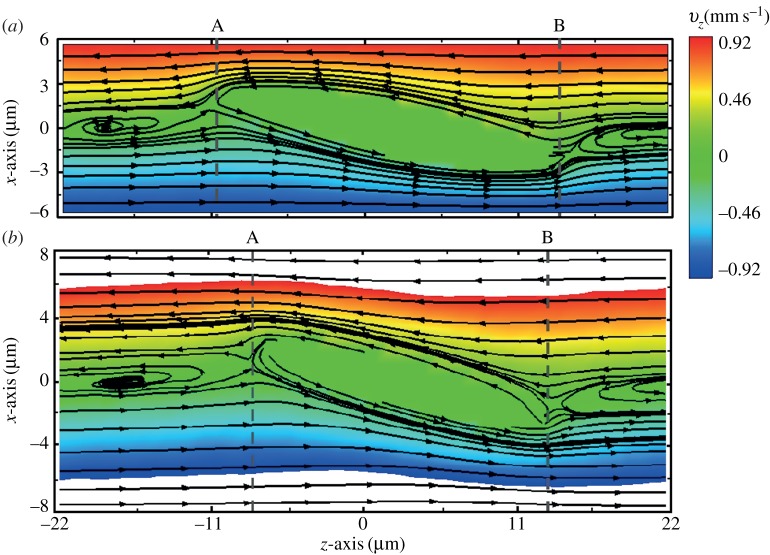
When the RBC rotates in shear flow, the velocity field of fluid flow around the RBC changes significantly [35]. In figure 8, we present the flow streamlines and the two-dimensional velocity contours within the x−z cross-section for two different degrees of confinement. In a narrow channel, the strong confinement enforces fluid particles and induces a flow parallel to the channel walls, resulting in enhanced local shear stress around the RBC. In a wide channel, the influence of solid walls on the local flow field around the RBC is very small or even negligible. Thus, there is a slight decrease in f compared with that for the RBC in a narrow channel. The functional relationship between f and is similar for both the one-component and the two-component RBC models, although the values of f for the latter are somewhat lower.

Figure 8.

Flow streamlines and flow contours within an x−z cross-section of the suspending fluid flowing around the RBC for η₀=28.9 cP and 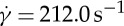at t_r=0.67 (a) and 0.22 (b). In the figure, each arrow represents the direction of the fluid flow velocity, and the flow contour of the velocity field is shown with the velocity in the range between −0.92 and 0.92 mm s⁻¹. The middle regions without streamlines indicate the presence of the RBC. The colour contour takes positive and negative values depending on the direction of the velocity of fluid flow. (Online version in colour.) 

Next, we study the effect of the bilayer–cytoskeletal friction coefficient f_bs on the RBC TT frequency as shown in figure 7b. We find that when using the value of f_bs=0.194 pN (μm⋅s)⁻¹, which is derived on the basis of experimentally measured diffusivities of transmembrane proteins and the fluctuation dissipation theorem [36,37], two marked particles on the lipid bilayer and the cytoskeleton move together, and there is no significant bilayer–cytoskeletal slip, thus the TT frequency of the lipid bilayer and the cytoskeleton is almost the same. However, assuming a pathological RBC state where f_bs is decreased by one or two orders of magnitude, an apparent bilayer–cytoskeletal slip occurs after a few TT cycles, and the marked particle on the lipid bilayer moves faster than the marked particle on the cytoskeleton, resulting in a difference between the two TT frequencies. Specifically, the TT frequency of the lipid bilayer increases as f_bs is decreased, while the TT frequency of the cytoskeleton shows an opposite trend (figure 7b). From the figure, we find that the TT frequency of the lipid bilayer and the cytoskeleton with f_bs=0.194 pN (μm⋅s)⁻¹ is lower than the frequency of the lipid bilayer but greater than the frequency of the cytoskeleton in the case with f_bs=0.0194 or 0.00194 pN (μm⋅s)⁻¹. Hence, our two-component RBC model can be used to quantify the existence of the bilayer–cytoskeletal slip and probe its role in the TT frequency.

Using the two-component RBC model, we also investigate the dependence of the TT frequency on the suspending fluid viscosity η₀ in shear flow with different degrees of confinement. The measurement of the f–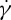 relationship of the RBC is performed at several η₀ and two t_r. We find that the ratio of f to 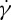always satisfies a linear dependence at t_r=0.67, while f increases with 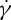in an exponential fashion that satisfies a scaling law 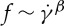with the scaling exponent β varying in the range from 0.85 to 0.96 when the degree of confinement decreases to t_r=0.22 (figure 9a). These results agree with the experimental results by Fischer [33].

Figure 9.

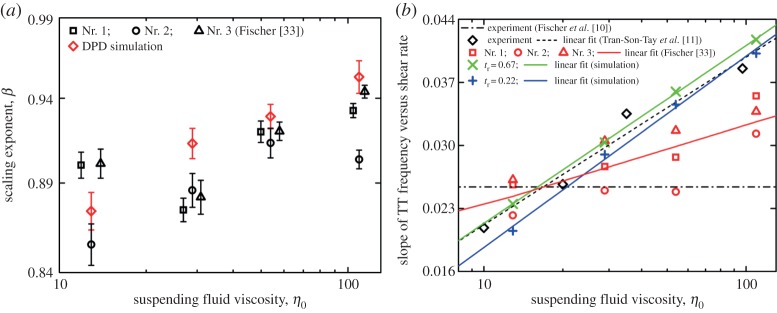
(a) Semilogarithmic plot of the scaling exponent of the fit function versus η₀. (b) Semilogarithmic plot of 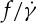of previous experiments and present data at different η₀. Experimental results are obtained from [10,11,33]. For clarity, the data of donor Nr. 1 and 3 (open symbols) in [33] are shifted horizontally. (Online version in colour.)

Considering the uncertainty between 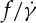and η_o in experiments [10,11,33], here, we want to investigate whether the 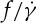ratio depends on η_o or not in the DPD simulations. Because the dependence of f on 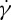is nonlinear in a smaller t_r, the definition of the slope of 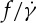requires an approximation. Following Fischer [33], values of 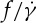of the fitted curves at 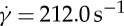are used to estimate the slopes. In figure 9b, the semilogarithmic plot of the ratio of f to 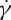on η_o is shown. It can be seen that a linear dependence of 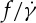versus η_o exists, and the slope of this dependence obtained at t_r=0.67 is close to the one in previous experimental data by Tran-Son-Tay et al. [11]; however, compared with this slope, the one obtained at t_r=0.22 has a slight increase, which is different from Fischer [33], who found that the slope is much lower than that by Tran-Son-Tay et al. [11]. Actually, the value of scaling exponent β increases with increasing η_o (figure 9a); thus, at the same 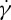the difference in f between the two different degrees of confinement, Δf=f_tr=0.67−f_tr=0.22, becomes smaller with increasing η_o. For example, at 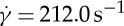, the values of Δf are 0.71, 0.47, 0.44 and 0.40 s⁻¹ at η_o=12.9, 28.9, 53.9 and 109.3 cP, respectively. Thus, the values of 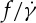at t_r=0.22 are gradually closer to the ones at t_r=0.67 with increasing η_o from 12.9 to 109.3 cP, resulting in a slight increase in the slope of the dependence between 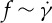and η_o.

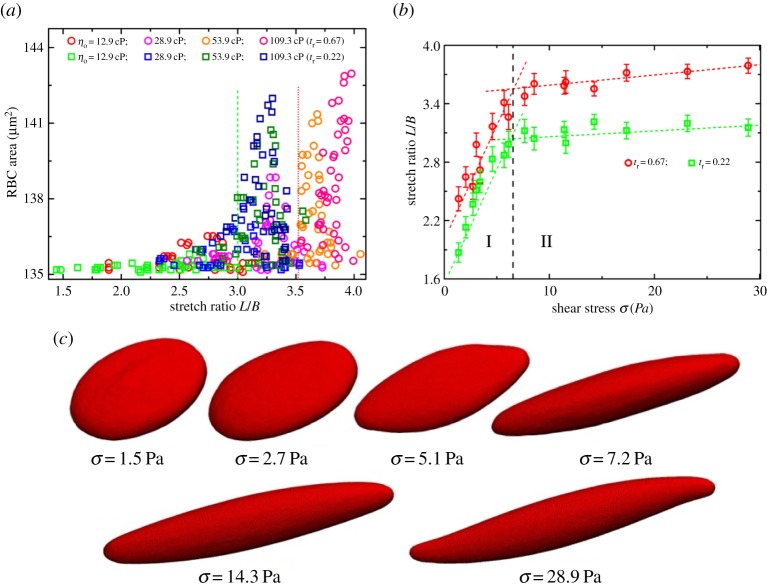
A RBC in shear flow can undergo dramatic changes in shape from an oblate to a prolate ellipsoid where a constant surface area of RBC membrane is maintained. A direct means of characterizing the RBC deformation is given by measuring the stretching of the RBC [11,17,33]. To do this, we first calculate the surface area of the RBC to verify whether the RBC membrane conserves its surface area during the TT motion at different shear stresses. As evident in figure 10a, the maximum deviation from the given value 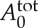is less than ≃8 μm², corresponding to a 5.7% increase in the maximum percentage deviation. Even though there is a small deviation between the measured data and the given value of 135.2 μm², the surface area of the RBC is considered to be always maintained during the simulations as the deviation is within the statistical uncertainty. We then calculate the stretch ratio L/B of the elongated RBC and determine its variation with the increase of shear stress, 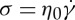(figure 10b). There are two regimes for L/B dependence on σ, that is, L/B increases rapidly with σ at low shear stress (regime I), while it increases slightly or approaches smoothly a saturation value for larger σ (regime II). In the latter regime, an increase of σ does not significantly affect the stretch ratio, which means the inclination angle between the RBC and the flow direction is almost the same.

Figure 10.

(a) Surface area of a RBC versus the stretching ratio L/B. The dashed and dotted lines show the boundary between regimes I and II at t_r=0.67 and 0.22, respectively. (b) Stretch ratio L/B versus shear stress σ. The dashed line divides the system into two regimes. (c) Shape deformation of a RBC at different shear stresses σ. (Online version in colour.)

In regime I, clearly, there is a shape transformation of the RBC from its biconcave shape to an oblate then to a convex ellipsoid with increasing σ (figure 10c). Thus, the deformation of the RBC increases continuously in the regime. Interestingly, we find that there is only a slight increase in the surface area of the RBC membrane in regime I from figure 10a, which means that the RBC responds to the variation of the shear stress by deforming its shape in order to control the membrane tension. In regime II, we see that the biconcave shape is completely absent, and the RBC always has a convex elongated shape (see the last three shapes of the RBC in figure 10c, in which the RBC is behaving as strain hardening as the surface area and the volume of RBC are preserved). The RBC already has an elongated shape, thus its shape remains basically the same. Instead, the elongated RBC increases its major axial length by the imposed fluid flow but the average inclination angle is kept almost constant when increasing the shear stress σ.

4. Summary

RBCs exhibit complex rheological response and rich dynamic behaviour governed by their membrane mechanical properties and the external/internal fluid viscosities. In this paper, we have studied the RBC mechanics, rheology and dynamics by applying the two-component RBC model to simulate three independent experiments on RBCs. First, we simulated the flow dynamics of human RBCs in a microfluidic system and quantified cell deformation and pressure–velocity relationships. The results show that the bilayer–cytoskeletal elastic interaction coefficient, k_bs, plays a key role in the RBC traversing small microfluidic channels. Second, the RBC membrane rheology was probed by TTC, showing good agreement with the experiment measurements. Compared with the one-component RBC model, a decrease in the storage modulus at very high frequency with the two-component RBC model appears; however, the difference is reduced when we increase the friction coefficient between the lipid bilayer and cytoskeleton. Finally, the RBC dynamics was studied in a simple shear flow. The effect of channel width variations between the two planar solid walls on the TT dynamics of the RBC was investigated. The simulation results with the two-component RBC model are demonstrated to capture the dependency between the TT frequency f and the shear rate 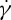for RBCs with different degrees of confinement, i.e. it follows a linear relationship for a narrow channel but a nonlinear one for a wide channel. In addition, we probed the effect of the bilayer–cytoskeletal friction efficient f_bs on RBC TT dynamics; our results demonstrate that the TT motion is too fast for the bilayer–cytoskeletal slip to occur for healthy RBCs. However, if f_bs is significantly reduced for certain diseases, the apparent bilayer–cytoskeletal slip occurs, which results in a difference in the TT frequency between the lipid bilayer and the cytoskeleton. We also presented some simulation results of the influence of suspending fluid viscosity on TT frequency. The results show that linear dependencies of the ratio of f to 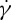exist, and the slope of the dependence obtained in wide channel flow has a slight increase compared with that in a narrow one.

These findings demonstrate that the two-component RBC model based on the particle-based DPD method can be used for qualitative and quantitative interpretation and predictions of mechanical, rheological properties and dynamic behaviour of RBCs in health or in haematological diseases. Assuming healthy RBC properties and under normal physiological conditions, in most cases the one-component and two-component RBC models do not differ too much; however, we want to emphasize that, under extreme mechanical conditions or disease states, the two-component RBC model is needed.

Funding statement

This work is supported by the National Institutes of Health (NIH) grant no. U01HL114476 and the new DOE Collaboratory on Mathematics for Mesoscopic Modeling of Materials (CM4).