Quantitative genetic variance and multivariate clines in the Ivyleaf morning glory, Ipomoea hederacea

Abstract

Clinal variation is commonly interpreted as evidence of adaptive differentiation, although clines can also be produced by stochastic forces. Understanding whether clines are adaptive therefore requires comparing clinal variation to background patterns of genetic differentiation at presumably neutral markers. Although this approach has frequently been applied to single traits at a time, we have comparatively fewer examples of how multiple correlated traits vary clinally. Here, we characterize multivariate clines in the Ivyleaf morning glory, examining how suites of traits vary with latitude, with the goal of testing for divergence in trait means that would indicate past evolutionary responses. We couple this with analysis of genetic variance in clinally varying traits in 20 populations to test whether past evolutionary responses have depleted genetic variance, or whether genetic variance declines approaching the range margin. We find evidence of clinal differentiation in five quantitative traits, with little evidence of isolation by distance at neutral loci that would suggest non-adaptive or stochastic mechanisms. Within and across populations, the traits that contribute most to population differentiation and clinal trends in the multivariate phenotype are genetically variable as well, suggesting that a lack of genetic variance will not cause absolute evolutionary constraints. Our data are broadly consistent theoretical predictions of polygenic clines in response to shallow environmental gradients. Ecologically, our results are consistent with past findings of natural selection on flowering phenology, presumably due to season-length variation across the range.

1. Introduction

Adaptation to environmental gradients plays a major role in several areas of evolutionary biology, including the evolution and maintenance of clines (e.g. [1–4]), how sexual isolation along a cline can lead to speciation [5], the evolution of geographical range limits (e.g. [6–8]), studies of parallel adaptation [9–12], and attempts to detect evolutionary responses to global climate change (e.g. [13–14]). While there are numerous examples of clinal variation in individual traits, we have a comparatively weaker understanding of how suites of correlated traits change along environmental gradients. Understanding how suites of traits have evolved in concert to environmental gradients—and whether their future evolution is constrained—is necessary to understand the evolution of complex, integrated phenotypes. For climatic gradients in particular, understanding how suites of correlated traits have evolved in concert, and can evolve in the future, will be necessary to predict the likely multivariate evolutionary responses to global climate change [15]. Fully evaluating the evolution of multiple, correlated phenotypes to climatic variation can be approached by testing for divergence and evolution in trait means to examine past evolutionary responses, and testing for changes in the genetic architecture itself (genetic variances and covariances) which might limit or influence future evolutionary responses. Here, we test for latitudinal clines in a suite of quantitative traits in the Ivyleaf morning glory (Ipomoea hederacea) with the goal of evaluating whether adaptive differentiation has occurred in a suite of traits, and whether there are any concomitant trends in the quantitative genetic variance in those traits that might reflect past selection or limit future responses.

Clines in individual quantitative traits have frequently been interpreted as evidence of adaptive evolution, although there are several neutral or demographic processes that could also produce them [1,16]. Consequently, several lines of evidence are often used to conclude that a cline has arisen for adaptive reasons. Studies of parallel clines—particularly following introductions or biological invasions—strongly suggest the action of natural selection and adaptive clines (e.g. [9–10,12,17]). An alternative approach is to compare clinal patterns in either quantitative traits or focal loci to background patterns of differentiation at presumably neutral markers, which should serve as a benchmark for patterns created by stochastic forces. Patterns of differentiation in putatively neutral markers should primarily reflect non-adaptive divergence, and several studies have detected evidence consistent with adaptive clines by showing greater differentiation or stronger gradients in focal traits or loci than in neutral markers (e.g. [11–12,18]). The approach of comparing trends in phenotypes to trends in neutral markers has rarely been implemented in a multivariate framework, limiting our understanding of the clinal evolution of suites of potentially correlated traits.

While extant patterns in trait means (or allele frequencies) can give clues as to past evolutionary responses, predicting future changes and evolutionary responses—or the lack thereof, due to constraints—requires an understanding of the distribution of genetic variance along a cline. We have a comparatively weaker understanding of how genetic variances change along clines. Our lack of knowledge is unfortunate because it precludes investigations of whether, for example, adaptation to climatic gradients is thwarted by a lack of genetic variation [19–22], the prevalence and magnitude of genetic constraints in peripheral populations [23], or whether directional selection and adaptation in peripheral populations has eroded genetic variance [24]. Theoretical predictions on how quantitative genetic variances change along clines remain challenging. The outcome depends on numerous factors, almost all of which are very difficult to determine: the genetic architecture of quantitative traits, the steepness of environmental gradients relative to gene flow or dispersal, and whether the genetic variance itself can evolve [2–4]. A general theoretical result is that with relatively steep gradients, genetic variance should peak in intermediate areas of the cline, while for gentle gradients, genetic variance should be approximately equal across the cline [2–4].

Empirical evidence on how genetic variance changes along clines is relatively limited and shows a range of outcomes. For example, Sgrò & Blows [25] found that non-additive, rather than additive, genetic variance showed the greatest change in a region of the cline with the greatest change in the mean of life-history and developmental traits in Drosophila serrata, a pattern broadly similar to predictions from Barton's [3] models. By contrast, other studies show directional changes in genetic variances along gradients. Colautti et al. [23] found latitudinal clines in size and flowering time, a decrease in the total genetic variance in these traits and in increase in skew among breeding values along a latitudinal cline in purple loosestrife (Lythrum salicaria). In Drosophila birchii, a lack of genetic variation in desiccation resistance and chill coma recovery may also play a role in establishing limits to latitudinal [20–22] and altitudinal gradients [26], respectively. In Drosophila melanogaster, van't Land et al. [27] detected latitudinal clines in wing length and area, along with positive associations between latitude and the heritability of these traits (cf. their fig. 1 and table 2); these associations, however, are reduced when considering the coefficient of genetic variation [28], suggesting that the trends may be due to changes in environmental variance rather than genetic variance. Studies comparing within-population genetic variation in quantitative traits to between-population divergence in trait means (e.g. [29]), and F_ST−Q_ST comparisons (i.e. comparisons of neutral and quantitative genetic differentiation; reviewed by [30–32]) contain the necessary data, although clines in quantitative genetic variance are rarely evaluated. Collectively, these studies suggest few generalizations about clinal trends in genetic variance.

The annual vine, Ivyleaf morning glory, I. hederacea, is a promising species to test for latitudinal clines in both the mean and variance of quantitative traits. Ipomoea hederacea inhabits a broad distribution, and in eastern North America can be readily found from Florida to southern Pennsylvania. The species exhibits a latitudinal cline in leaf shape: northern populations are composed primarily of lobed genotypes, while southern populations are polymorphic [18]. Although the molecular basis of the leaf shape polymorphism and the ecological mechanisms behind the cline remain ambiguous, the leaf shape cline appears to be adaptive [33], suggesting the potential for adaptive differentiation across the range in quantitative traits as well. The extent of quantitative genetic differentiation across the eastern North America range, and the potential contribution of the leaf shape locus to it, remains unknown. Season length varies dramatically in eastern North America, suggesting latitudinally varying selection on growth- and phenology-related traits is likely.

In this study, we ask the following questions: (i) Is there population differentiation of quantitative traits? (ii) Is there clinal variation in quantitative traits, when individuals are grown in a common environment, consistent with adaptation? (iii) Do the traits that show the greatest population differentiation and clinal trends in the mean also show clines in their genetic variances?

2. Material and methods

(a). Study species

Ivyleaf morning glory, I. hederacea (L.) Jacquin (Convolvulaceae) is a weedy, annual vine species commonly found in disturbed areas such as roadsides and agricultural field edges across eastern USA, extending northward to Pennsylvania, USA. Plants germinate in early to mid-summer and die at first frost in the autumn [34]. The species frequently self-fertilizes, with selfing rates ranging from approximately 65% [35], 73% (reanalysis of amplified fragment length polymorphism (AFLP) data in [18]), and some estimates more than 90% [33,36]. While it is uncertain whether it is native to North America, early flora records indicate that it has been in the present range for approximately 150 years [37], and in addition to the latitudinal cline in leaf shape [18], entire-leaved genotypes show a latitudinal cline in flowering time across the southwestern portion of its range [38]. Leaf shape in I. hederacea is determined by a single Mendelian locus [18,34,39]. Homozygous individuals either have heart-shaped leaves (ll) or three-lobed leaves (LL); heterozygotes (Ll), which are rare in natural populations, show intermediate lobing.

(b). Common garden experiment

To test for clinal variation in ecologically important quantitative traits, we grew offspring of maternal seed-families that had been previously collected from 20 populations in the eastern USA range of I. hederacea (see [18]). Ten populations were north of the clinal boundary between polymorphic and lobed populations described by Campitelli & Stinchcombe [18], and 10 were south of it. We scored phenotypes on F₁ offspring that were the product of one generation of selfing in the greenhouse under common environmental conditions, thus equalizing maternal environmental effects. Population genetic analysis of 173 AFLP from populations in the eastern USA suggests no pattern of isolation by distance or spatial autocorrelation of AFLP allele frequencies, in either a larger sample of 77 populations [18], or in the subset of 20 populations used here (electronic supplementary material, figure S1). Accordingly, we treat and analyse our entire sample as a single group, rather two sub-populations. These molecular data also suggest that clines in quantitative traits are unlikely to be generated by neutral or demographic processes, and likely represent adaptation.

From each population, we randomly selected 10 maternal lines, and then up to eight seeds per line, for a total of 1537 plants (some lines did not have eight seeds available). Seeds were weighed prior to planting, scarified with a razor blade and planted in Ray Leach ‘Cone-tainers’ (Stuewe & Sons, Tangent, OR, USA). We set initial photoperiod and temperature cycles to 14 h of light (at 24–26°C) and 10 h of dark (at 22–24°C). To promote flowering and simulate natural changes in photoperiod and temperature, we decreased day lengths and lowered temperatures on two occasions, such that final conditions were 8 h days (at 20–22°C) and 16 h nights at (18–20°C). Individuals were arranged in a randomized, spatially blocked design in the greenhouse, with two individuals per line planted into four spatial blocks, in random order/location.

We visually scored the leaf shape genotype of all germinants and measured five quantitative traits on all individuals: initial seed mass (grams), growth rate (leaf production per day, over 9 days), days to flowering (days), and on the first flower produced, anther–stigma distance and corolla width (both in millimetres).

(c). Data analysis

(i). Quantitative genetic variation

We first tested for quantitative genetic variation in the phenotypic traits using a hierarchical mixed model (Proc Mixed, SAS). Briefly, for each trait as a response variable, we included block and leaf shape genotype as fixed effects, and population and lines nested within populations as random effects. We included block as a fixed effect because our greenhouse blocks were not random samples of spatial variation about which we wished to generalize. To test the statistical significance of random effects, we compared the −2 log likelihoods of models with and without the random effect of interest. The difference between −2 log likelihoods is χ² distributed with 1 d.f. and because variances cannot be less than zero, we halved the p-values of these tests to perform a one-tailed test [40]. We tested for population variation and genetic variation within populations using traits in their original units. Because we used inbred lines, our estimates of genetic variance are estimates of the total genetic variance, rather than the additive genetic variance. However, given the high selfing rate of I. hederacea, it is likely that the total genetic variance is more relevant for responses to selection in this species [41]. In addition, the crosses necessary to estimate additive genetic variances would create individuals and families of unusually high heterozygosity that would be of questionable relevance to natural populations [41].

(ii). Characterizing population divergence and clinal variation

Prior to characterizing population divergence and clinal variation, we transformed all individual trait values by dividing them by their experiment-wide means [42]. For size and growth traits, this transformation is informative because these traits have a natural zero, and the mean-standardized values are comparable [42]. For flowering time, which is on an interval scale [42], this transformation does not alter conclusions about the relative timing differences between genotypes or individuals, although the exact values obtained depend on the inferred origin of the trait (e.g. days since germination versus days since snow-melt; [41,42]).

To characterize population divergence in quantitative traits, we estimated the matrix D, the variance–covariance matrix of population means for the five traits. (Note that while the experiment-wide mean of each trait will be 1, individual populations will have mean values above or below the experiment-wide average.) We then estimated the first principal component of D, d_max, which is the linear combination of phenotypic traits that shows the greatest variance among populations. We used the trait loadings, or elements of d_max, to calculate d_max scores for each individual in the experiment. For example, for individual i in the experiment, its d_max score was estimated as

2.1

where x₁–x₅ are the elements or trait loadings of PC1; and ASD_i, CW_i, FT_i, Growth_i and Mass_i indicate the anther–stigma distance, corolla width, flowering time, growth rate and seed mass of individual i, respectively. Because all of the traits contribute to d_max, it explicitly accounts for the correlations and covariances among traits.

As a point of comparison for d_max, we also estimated d_min—the linear combination of traits showing the least variance among populations—from the trait loadings from the fifth principal component of D. Our hypothesis was that d_min, because it reflects the combination of traits showing the least divergence in among populations, would show different patterns of clinal variation and genetic variance than d_max. Because d_max and d_min are linear combinations of quantitative traits, they are themselves also quantitative traits and describe the phenotypes that show the greatest and least variance among populations, respectively.

To characterize clinal variation in the suite of phenotypes, we used both regression of phenotypes on latitude and redundancy analysis. For the former, we regressed line means of each trait on latitude of origin. For the latter, we regressed line means of all five traits simultaneously against latitude (Proc Cancorr, SAS) and saved the raw canonical coefficients that described the contribution of the phenotypic traits. The redundancy variate is the linear combination of quantitative traits that shows the greatest correlation with latitude; the coefficients of the redundancy variate indicate the contribution of each of the original traits to the composite quantitative trait that shows the strongest latitudinal cline. We used the raw canonical coefficients to estimate individual phenotypic scores for the trait showing the maximal clinal pattern, which we refer to as cline_max. To estimate cline_max scores for individual i, we used a similar procedure as described above

2.2

where r₁–r₅ are the raw canonical coefficients of the redundancy variate; and ASD_i, CW_i, FT_i, Growth_i and Mass_i indicate the anther–stigma distance, corolla width, flowering time, growth rate and seed mass of individual i, respectively. Similar to d_max, cline_max accounts for the multivariate structure of the data, as it represents the combination of traits showing the strongest cline.

(iii). Trends in quantitative genetic variance

Our final goal was to test for latitudinal trends in quantitative genetic variance in d_max, d_min and cline_max. In other words, how does genetic variance in the traits associated with maximal and minimal population divergence, and clinal variation change across the latitudinal gradient? To answer this question, we used a combination of mixed models and Bayesian modelling. First, we fit hierarchical mixed models as described above, using block and leaf shape as fixed effects, and population and line within population as random effects, with individual phenotypic d_max, d_min and cline_max scores as the response variable. To complement these analyses of the entire dataset, we also estimated genetic variance components for each population separately using mixed models with block and leaf shape genotype as fixed effects; the only random effect was line. For both sets of mixed models, we tested the statistical significance of random effects with likelihood ratio tests.

The limited within-population and within-line sampling (10 lines, eight replicates per line) has two implications for our analyses of genetic variation in d_max, d_min and cline_max. First, we should have limited power, and second, we expect large sampling variability in our estimates of quantitative genetic variance. We expect the power of our hierarchical analyses of populations and lines within populations, even if it is limited, to be similar for the composite traits (d_max, d_min and cline_max) and the original component traits underlying them. To address the latter issue, we fit separate Bayesian models in Proc Mixed for each population, to sample the posterior distribution of possible values for the line variance component in each population [40]. We specified 1000 samples from the posterior distribution, using a non-informative prior, and the ‘nobound’ option in the model statement to allow variance components to be negative.

3. Results

(a). Quantitative genetic variation

All five quantitative traits showed significant quantitative genetic variance in the form of significant line (population) terms from mixed models (χ² > 12.4, p < 0.0002). Statistical support for significant among-population genetic variation was more variable, with anther–stigma distance, corolla width and days to flowering showing highly significant differences (χ² > 27, p < 0.0001), while growth rate and seed mass showed non-significant among-population variation (χ² = 0.5, p = 0.24 and χ² = 1.3, p = 0.125, respectively). Collectively, these data suggest that the lines used showed genetic differences in quantitative traits, with three of the traits exhibiting significant among-population variation.

(b). Population divergence and clinal variation

The variance–covariance matrix of population means, after mean-standardization, is shown in table 1. At the level of population means, anther–stigma distance and flowering time covary positively, and both load heavily on d_max; d_max explains 72.6% of the variance in population means. Corolla width and growth rate had slight positive loadings on d_max, and both exhibit negative covariances with anther–stigma distance as expected from the elements of PC1. We tested for latitudinal variation in d_max scores by regressing line means for d_max on latitude and found a significant latitudinal cline (r = 0.402, p < 0.0001; figure 1). As expected, the fifth principal component of D, d_min, explained 1.4% of the variation in population means and failed to show any latitudinal trends (r = −0.01, p = 0.84).

Table 1.

Covariance matrix for population means of the quantitative traits, along with loadings on PC1 (d_max). PC1 explained 72.7% of the variance in population means. Prior to analysis, all traits were divided by their experiment-wide means.

	anther–stigma distance	corolla width	days to flower	growth rate	seed mass	PC1 loading
anther–stigma distance	0.05674					−0.9644
corolla width	−0.00219	0.00166				0.0315
days to flower	0.01292	0.00119	0.01282			−0.2586
growth rate	−0.00098	−0.00049	−0.00242	0.00342		0.0269
seed mass	0.00322	−0.00164	−0.00535	0.00649	0.00850	−0.0339

Figure 1.

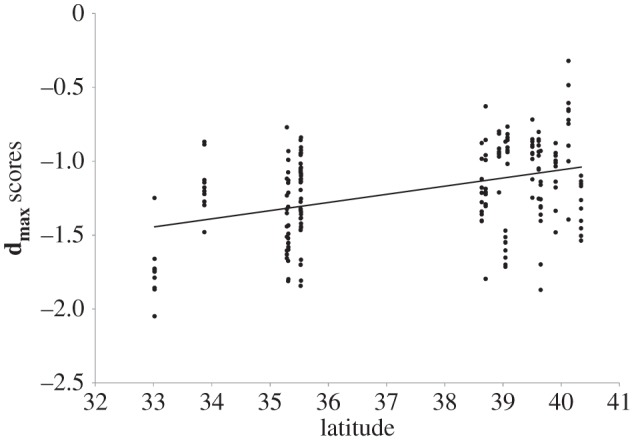
Significant latitudinal cline in d_max scores, the composite trait that shows the greatest population divergence, estimated from inbred line means.

All five of the quantitative traits showed significant or marginally significant latitudinal clines when we analysed line means. We analysed line means because all traits were genetically variable at the level of lines, indicating that lines were significantly different from each other for all phenotypes; for traits where we also detected an effect of population, this indicates that the line means for an individual population will be more similar to each other than to other populations. The traits showing the strongest latitudinal clines were anther–stigma distance (r = −0.39, p < 0.0001) and days to flowering (r = −0.22, p = 0.0018), where lines from Northern sites had smaller anther–stigma distances and flowered earlier. Growth rate exhibited a marginally significant negative relationship with latitude (r = −0.13, p = 0.067), with lines from northern latitudes growing more slowly. Lines from northern latitudes had significantly larger corolla widths (r = 0.15, p = 0.039) and marginally heavier seeds (0.127, p = 0.07). Scatter plots showing the relationship between line means for all five quantitative traits and latitude are presented in the electronic supplementary material, figure S2a–e. The composite quantitative trait that exhibited the maximum clinal pattern with latitude, cline_max, showed a highly significant relationship with latitude that was stronger than any of the individual component traits themselves (canonical correlation, r = 0.53, F_5,194 = 15.13, p < 0.0001; figure 2). The three traits showing negative latitudinal clines (anther–stigma distance, flowering time and growth rate) had negative loadings on cline_max, whereas corolla width and seed mass had positive loadings.

Figure 2.

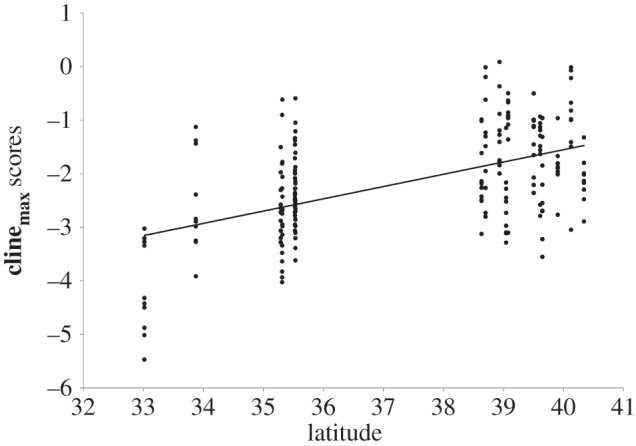
Significant latitudinal cline in cline_max scores, estimated from inbred line means.

(c). Genetic variance in composite traits

Similar to the individual quantitative traits used to create them, we observed significant among population and among line, within-population genetic variance in d_max, d_min and cline_max. Likelihood ratio tests revealed highly significant among-population variance for d_max and cline_max (χ² = 64.4 and 57.7, p < 0.0001) and significant among-population variance for d_min, the composite trait associated with the least amount of variation in population means (χ² = 2.9, p = 0.044). All composite traits showed highly significant among-line within-population variance (χ² = 302.4, 87 and 83.2, respectively, for d_max, d_min and cline_max). We also performed traditional likelihood ratio tests for each population separately to determine whether individual genetic variances within populations were significantly different from zero. When we examined each population individually, we found that 12, 7 and 10 populations showed significant among-line variance in d_max, d_min and cline_max at p < 0.05 (14, 12 and 14 at p < 0.1, respectively). The limited sample size within each population obviously limits the power of these analyses. Nonetheless, they suggest significant genetic variance in d_max and cline_max exists in at least some populations, and that the trait showing the least population differentiation (d_min) shows appreciable genetic variance within populations.

(d). Latitudinal clines in the genetic variance

We observed no significant latitudinal trends in quantitative genetic variance in either d_max or cline_max (figure 3), or d_min (results not shown). Northern populations, despite having significantly different mean phenotypes, did not have appreciably more or less genetic variance in either the trait showing maximal clinal divergence, or maximal population divergence. Bayesian posterior intervals, constructed from the 95% intervals of the posterior samples of the variance components, were generally asymmetric for both d_max and cline_max (figure 3), and rarely overlapped zero. Although these posterior intervals are wide, they do not suggest that sampling variance obscured any latitudinal trends: uncertainty in genetic variance components is broad across the range. The asymmetrical posterior intervals are not unexpected, as estimated variance components are usually greater than zero, and genetic variances in particular can be small and close to zero; these considerations potentially pose a problem for using posterior intervals of variance components for hypothesis testing, particularly for cases showing skewed posterior intervals with estimates near zero. Although we specified the ‘nobound’ option of Proc Mixed to allow negative variance components, negative variance components in hierarchical designs are usually limited to cases in which the intra-class correlation (in this case, the correlation among individuals of the same inbred line) is negative [40, pp. 150–154].

Figure 3.

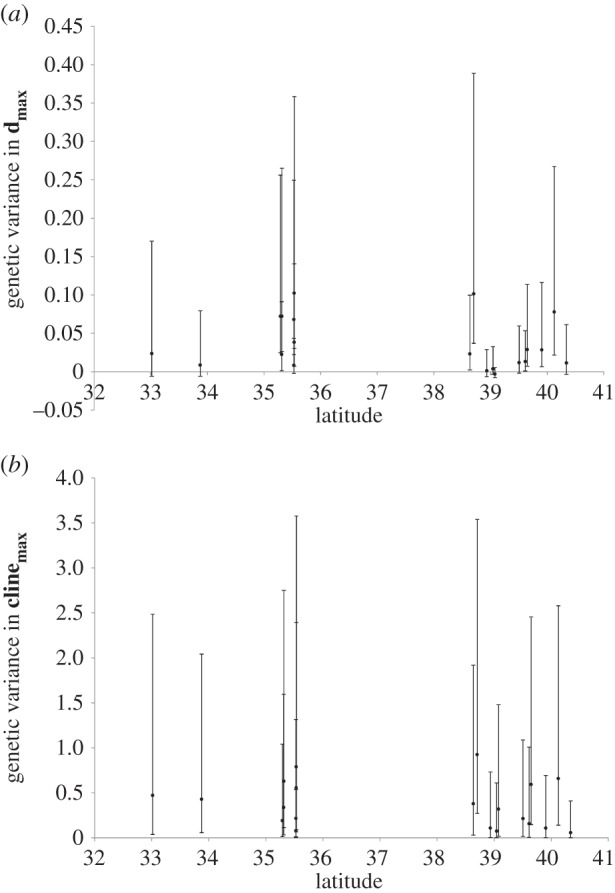
Latitudinal trends in quantitative genetic variance. (a) Genetic variance in d_max, the composite trait that shows the greatest population divergence. (b) Genetic variance in cline_max scores, the composite trait that shows the strongest latitudinal cline. Error bars depict 95% confidence intervals, calculated from 1000 samples from the posterior distribution.

4. Discussion

The dominant trend that emerges from our analysis of quantitative traits in I. hederacea is the absence of absolute constraints on adaptation: we observe significant latitudinal clines in a suite of quantitative traits, despite an absence of genetic structure at AFLPs (electronic supplemental material) or single nuclear polymorphisms [33], significant quantitative genetic variance in individual and composite traits within populations and across the range as a whole, and little evidence that selection has eroded quantitative genetic variance in the traits that show the greatest clinal variation or most population differentiation. Below, we first discuss the implications of our approach of analysing d_max, d_min and cline_max, and then we evaluate the potential ecological mechanisms underlying the clinal variation, population differentiation and quantitative genetic variance we detected.

(a). Analysis of composite traits and alternatives

Our analysis of composite traits, rather than the individual traits we measured, entailed both benefits and costs. On the practical side, estimating single composite traits such as d_max, d_min and cline_max is much simpler, less computationally demanding and less prone to estimation error than attempting to estimate, analyse and interpret clinal trends in 20 G matrices. For example, d_max and d_min are reliant on the variances and covariances of population means, which are estimated with more precision than within-population genetic covariances, or the variances and covariances of within-population genetic variances and covariances. Similarly, estimating genetic variances in univariate traits will have more power for a given sample size, simply because fewer parameters need to be estimated—1, rather than n(n + 1)/2 covariance parameters for n traits. In addition, because it is often unclear a priori whether selection is acting on individual traits or their combinations [43], metrics such as d_max and cline_max capture information about the entire phenotype accounting for the covariances among traits. Biologically, we expect that the traits most likely to show eroded quantitative genetic variance due to strong selection would be those showing the greatest population differentiation and clinal variation—i.e. d_max and cline_max. In this manner, these two traits are best-case scenarios when strong selection, such as that producing population differentiation or latitudinal clines, will reduce within-population genetic variances.

The potential cost of composite traits comes in interpretability. Conner [44] has strongly criticized multivariate metrics such as d_max, d_min and cline_max, arguing that they are too far removed from the traits to which ecological function and mechanism can be ascribed. For the present data, this challenge is somewhat mitigated by the relatively simple nature of d_max—it appears to be strongly driven by anther–stigma distance and flowering time, with lesser contributions from the other traits. For cline_max, the interpretational challenge is also somewhat reduced, because rather than a direction in multivariate space determined by the magnitude of variances (like a PC), the trait loadings are specifically in reference to a common scale, latitude. Consequently, individuals with large cline_max scores are those that flower early, have small anther–stigma distances, grow slowly, have large corollas and heavy seeds, and are mainly found in northern latitudes. Another potential downside is that both d_max and cline_max are not measured on a scale transferable to other systems—they are necessarily reflective of the patterns of variation and covariation, and latitudinal range of sampling contained in the experiment. These drawbacks can also be reduced by selecting traits for study where natural history, field observations or other pieces of evidence such as the pattern of natural selection suggest that the traits are important and worthy of study.

We considered, but did not implement, two alternative approaches. The first was to use F_ST–Q_ST comparisons (e.g. [45]), including recent extensions that allow for multivariate information to be included in the calculation of Q_ST (e.g. [46,47]) rather than typical one trait at a time approaches. Apart from the numerous statistical challenges inherent in implementing this approach [32], we elected not to pursue it because simple examination of the data revealed it to be unnecessary: there is no detectable isolation by distance between our sampled populations using AFLPs, and F_ST was effectively zero. These data suggest that the clinal patterns we have documented do not represent the neutral or stochastic effects of gene flow or dispersal, but rather are likely indicative of responses to divergent natural selection. The second alternative, which we were prevented from implementing due to sample size limitations, is the covariance tensor approach as advocated by Hine, Blows and co-workers [48,49]. In this approach, one would estimate G in each population, and then construct a matrix describing the variances and covariances of the genetic variances and covariances, followed by eigen-analysis. The eigentensors obtained from such an analysis describe independent axes of variation, but of the genetic variances and covariances of traits rather than the traits themselves. Similar to traditional principal components analysis, the eigenvectors of the eigentensors can be used to describe the contribution of individual traits to the axes showing the greatest genetic variance among populations [48,49]. We elected not to implement this approach because our design focused on broader sampling of populations (N = 20) at the expense of within-population sampling of inbred lines (N = 10 max), precluding the estimation of separate G matrices within each population.

(b). Ecological mechanisms

The simplest clinal pattern to interpret in our data is the flowering time cline, which is consistent with previous studies in I. hederacea: northern populations tend to flower earlier [38]. The likely explanation for this trend is that northern populations experience shorter growing seasons, producing an advantage for lines that are capable of growing, reproducing and maturing fruit before a killing frost ends the season. In previous experiments—one well north of the current range (44.03° N; [41]) and one towards the centre of the latitudinal range sampled here (39.064° N; [50])—we have documented strong natural selection favouring earlier flowering individuals and genotypes, and that frost damage to maturing fruits significantly decreases seed viability [41].

The clinal patterns in other traits are more difficult to ascribe ecological mechanisms to, especially the floral traits. Reduced anther–stigma distance is commonly associated with increased self-fertilization in morning glories [36,51]. Smith & Rausher [52], in a series of experiments, showed that decreased anther–stigma distance in I. hederacea reduces the negative effects of con-generic pollen flow from I. purpurea and that the presence of I. purpurea leads to natural selection favouring increased clustering of the anthers around the stigma in I. hederacea (i.e. reduced anther–stigma distance; [53]). Interpreting the cline in anther–stigma distance as an adaptation to I. purpurea's presence, or a lack of pollinators in northern populations (as would be predicted by a reproductive assurance argument) is difficult because I. hederacea and I. purpurea have largely sympatric, overlapping ranges, and estimated selfing rates in I. hederacea are usually quite high (74–93%; [33,36]). Anther–stigma distance is positively correlated with flowering time at the level inbred line means (r = 0.22, p = 0.002, N = 200), suggesting that it could evolve as a correlated response to selection on flowering phenology, and population means of the two traits are also strongly correlated (r = 0.48, p = 0.03, N = 20), suggesting that the two traits have diverged in concert. Nonetheless, the anther–stigma distance cline is unlikely to be solely a correlated response to latitudinally varying selection on flowering time, as it shows a stronger latitudinal cline than flowering time does.

Increased corolla width is often associated with higher male fitness [54], presumably due to its role in attracting pollinators [55]. Greater information on pollinator visitation rates and species composition, in situ, would aid in interpreting these clines. For example, Maad et al. [55] detected altitudinal clines in flower size in Campanula rotundifolia, with larger flowers found in sites with increased pollinator body size and reduced visitation rates, suggesting that pollinators were the selective mechanism behind the pattern. Both our data and Smith & Rausher's [53] results show opposing trends for corolla width and anther–stigma distance. We found that northern populations had wider corollas and smaller anther–stigma distances, while they found that the presence of I. purpurea led to natural selection favouring increased corolla diameters and greater anther clustering—in both cases, the trend was for traits with generally opposing effects on outcrossing to change in concert. One possibility is that corolla width is genetically correlated with anther traits: Smith & Rausher [56] also found that corolla width showed a significant positive genetic correlation with the height of the tallest and shortest anthers, while we failed to detect genetic correlations between corolla width and anther–stigma distance.

(c). Quantitative genetic variance and constraint

Taken at face value, our data suggest that I. hederacea likely inhabits a range with gradual environmental gradients: we observed gradual gradients in trait means (individually and as composite traits) and relatively constant genetic variances underlying these traits. Both of these patterns are consistent with theoretical models of clinal evolution [3] and environmental data across I. hederacea's range on temperature, precipitation and growing season length (BE Campitelli and JR Stinchcombe 2013, unpublished data). The ubiquitous presence of significant genetic variation for clinally varying traits, the most differentiated traits and the least differentiated traits do not suggest any absolute genetic constraints to latitudinal adaptation and population divergence, or that the least differentiated traits have failed to diverge because of a lack of genetic variance. Our results stand in contrast to past findings of genetic constraints to clinal adaptation in Drosophila [20–22,26] and Lythrum [23]. Unfortunately, generalizations about how genetic variances change along a cline are likely to remain scarce until we have greater sampling of species and life histories—comparisons are difficult between two fruit fly species, a tetraploid perennial plant (L. salicaria) and a diploid annual plant (I. hederacea).

The two traits most likely to show an erosion of genetic variance due to directional selection and/or genetic drift—d_max and cline_max—show significant genetic variation when we analyzed the entirety of our data in a single analysis, and frequently did as well when we restricted our analysis to individual populations (max N = 80). Likewise, our prediction was that d_min should also be lacking genetic variance within populations—either because the trait combination was never variable enough in the first place to lead to a response to selection and divergence between populations, or because stabilizing selection favoured the same trait combination in each population. Collectively, our data suggest that the traits showing the greatest divergence between populations, the least divergence between populations and the greatest latitudinal differentiation all still have abundant potential to evolve within and between populations. For example, the second northernmost population in our study is near the northern limit of where we have observed and collected I. hederacea in the eastern USA (BE Campitelli and JR Stinchcombe 2013, unpublished data). Despite sampling only 10 inbred lines from this population, we still detected significant genetic variance in d_max, cline_max and d_min scores. It is hard from these data to support the hypothesis that further evolution of these trait combinations will be limited by a lack of genetic variation.

Our interpretation that the future evolution of population differentiation and clinal phenotypes will not be constrained by a lack of genetic variation rests on two assumptions. First, we assume that the evolutionary dynamics that have produced the clines and observed population differentiation form a reasonable prediction of current and future dynamics. If dramatic changes in climate or the ecological environment lead to a pattern of natural selection that favours different combinations of traits, our sampled populations may be lacking the appropriate genetic variance to respond. As Chenoweth et al. [29] point out, as soon as G matrices are different from spherical, any natural selection favouring combinations of traits other than g_max (PC1 of G) will lead to correlated responses to selection dominated by the trait combinations with the most variance, even if they differ dramatically from those actually favoured by selection. Second, we assume that the existing quantitative genetic variance is capable of producing a response to selection, rather than representing deleterious variation at mutation-selection balance or alleles with deleterious pleiotropic effects on fitness [57].

(d). Future directions

Our results suggest two promising future directions that would confirm our inferences of the absence of evolutionary constraint in I. hederacea. First, artificial selection and experimental evolution [57–59] would be ideal to confirm our hypothesis that the genetic variance in d_max, d_min and cline_max is capable of producing a response to selection. Second, creating experimental populations of genetically variable material in the northern end of the range would allow a measurement of natural selection on d_max, d_min and cline_max and the component traits that make them up. In this manner, one could evaluate directly the role of selection on traits producing population differentiation and clinal evolution. These experiments, while ambitious and challenging, will help directly assess the role of genetic constraints (or the lack thereof) in multivariate clinal evolution.

Data accessibility

Data from this experiment will be available in Dryad (http://dx.doi.org/10.5061/dryad.k4p48).

Funding statement

We thank NSERC Canada, CFI and the Department of Ecology and Evolutionary Biology for financial support.