HOW POPULATION STRUCTURE SHAPES NEIGHBORHOOD SEGREGATION

Abstract

This study investigates how choices about social affiliation based on one attribute can exacerbate or attenuate segregation on another correlated attribute. The specific application is the role of racial and economic factors in generating patterns of racial residential segregation. I identify three population parameters—between-group inequality, within-group inequality, and relative group size—that determine how income inequality between race groups affects racial segregation. I use data from the Panel Study of Income Dynamics to estimate models of individual-level residential mobility, and incorporate these estimates into agent-based models. I then simulate segregation dynamics under alternative assumptions about: (1) the relative size of minority groups; and (2) the degree of correlation between race and income among individuals. I find that income inequality can have offsetting effects at the high and low ends of the income distribution. I demonstrate the empirical relevance of the simulation results using fixed-effects, metro-level regressions applied to 1980-2000 U.S. Census data.

1. INTRODUCTION

Sociologists have a longstanding interest in how population composition constrains patterns of inequality and social separation. The idea originated in Simmel’s texts on intersecting social affiliations (Simmel 1906, 1955), and was later elaborated in Blau’s theory of social structure (Blau 1974, 1977; Blau and Schwartz 1984). This body of work is motivated by the observation that people occupy multiple social positions simultaneously; for example, each person has an age, sex, income, nationality, occupation, and race. These attributes are often correlated, and the degree of correlation has implications for how individuals’ in-group tendencies aggregate into patterns of social separation or integration.

Blau’s central theorem is that a weaker correlation in social differences promotes intergroup contact (Blau 1984: 586). At one extreme, we can imagine a world in which social characteristics of individuals are orthogonal, for example there is no correlation between race and income, or education and sex. Blau’s theory implies that social affinities that lead to segregation along one dimension will tend to reduce social separation along other dimensions because a person’s in-group members for one attribute will contain many out-group members on other attributes. At the other extreme, there is complete consolidation in social attributes; for example, the incomes of whites never overlap with those of blacks, and even the highest educated woman is still less educated than the least educated man. In this case, Blau’s theory suggests that social processes that produce separation along one dimension will reinforce separation on other dimensions.

Blau’s ideas inform a great deal of contemporary work that investigates how population parameters shape marriage patterns, occupational and residential segregation, and network homophily (e.g., Moody 2001; Wimmer and Lewis 2010, Marsden 1987; Kalmijn 1998; Tienda and Lii 1987). However, while Blau’s original framework is compelling, it conflates two dimensions of the correlation between social attributes: within-attribute variation versus between-attribute variation. The extent to which sorting on multiple attributes exacerbates or attenuates social separation depends on the explicit configuration of these two dimensions.

This study extends Blau’s work to investigate how choices about social grouping based on one attribute can exacerbate or attenuate segregation on another correlated attribute. The specific application is the role of racial and economic factors in generating patterns of racial residential segregation. Blau’s theory suggests that if both racial and economic factors matter in residential mobility and race and income are highly correlated (that is, minorities are poorer on average than whites), racial segregation will be higher than if race and income were uncorrelated. Within the segregation literature, this line of reasoning is referred to as the spatial assimilation hypothesis, which argues that racial and ethnic differences in residence reflect status differences among groups (Gordon 1964; Alba and Logan 1993). The spatial assimilation hypothesis is typically contrasted with the place stratification hypothesis, which emphasizes barriers to mobility such as discrimination and racial steering. The place stratification hypothesis posits that racial and ethnic minorities are excluded from white neighborhoods, and this limits the ability of even the socially mobile members of these groups to reside in the same communities as comparable whites (Alba and Logan 1993, p. 1391).

Studies attempting to assess the degree to which status differences between blacks and whites explain high levels of black-white segregation show that racial segregation varies little by the education or income status of blacks (Massey and Fischer 1999) and high income blacks typically live in poorer areas than high income whites (Alba, Logan, and Stults 2000). This is generally taken as evidence in favor of the place stratification hypothesis. My aim is to show that the dynamics of racial residential segregation resulting from sorting across multiple, correlated social attributes are more complicated and nuanced than is captured in either the place stratification or the spatial assimilation hypothesis, as changes in income inequality among race groups can have opposite and offsetting effects at the high and low ends of the income distribution. I propose an analytical framework for understanding how the joint distribution of race and income affects patterns of racial segregation.

The correlation between race and income is comprised of two parts: between-race and within-race income inequality. Between-race income inequality reflects average differences in income between race groups, for example as captured by the ratio of black median income to white median income. Within-race income inequality reflects within-race income heterogeneity. Given some baseline level of racial segregation, any increase in black-white income inequality increases the average income differences between black and white neighborhoods. Under conditions of low within-race income inequality, substantial between-race income inequality reinforces race-based patterns of residential mobility, thus exacerbating segregation. But under moderate to high within-race income inequality, high between-race income inequality has different effects at opposite ends of the income distribution.

Consider the case where blacks are substantially poorer, on average, than other race groups. Poor blacks experience greater racial isolation. But more affluent blacks must choose between higher income, nonblack neighborhoods and poorer, black neighborhoods. Some of them remain in black neighborhoods. But a nontrivial proportion, as I show below, end up in nonblack areas. In the event of elimination or substantial attenuation of between-race income inequality, the decrease in racial isolation that poor blacks experience is partially counterbalanced by an increase in neighborhood proportion black experienced by higher income blacks. These offsetting effects attenuate the total change in racial segregation that occurs due to changes in between-race income inequality.

I begin with a review of classic and contemporary approaches to studying residential segregation with a specific focus on studies examining the role of income in racial residential segregation. I then outline a basic analytical model for understanding the macro-level consequences of micro-level sorting processes involving multiple attributes that considers: (1) the level of correlation between the relevant social attributes (i.e., their joint distribution); (2) the relative size of each social group in the population; and (3) the relative importance of different attributes in individuals’ decisions about unit.¹ The model extends Blau’s original thesis to provide a more nuanced account of how different dimensions of population distributions condition the degree to which a given regime of in-group preferences results in aggregate patterns of segregation. It also provides several predictions concerning how the joint distribution of the population by race and income influences racial segregation.

The balance of the article tests the empirical validity of these predictions. The analysis consists of three parts: (1) simulation experiments that use artificial populations in a highly stylized city; (2) simulation experiments that use real populations and geography; and (3) a metro-area level statistical analysis of how between- and within-race income inequality and the size of the black population correspond to changes in segregation in major American cities between 1980-2000. All simulation experiments assume agents’ mobility behavior follows empirical patterns of residential choice. I use the Panel Study of Income Dynamics (PSID) data to estimate statistical models of residential choice.

Overall, the results suggest that income inequality affects racial segregation, but in ways that are masked when one focuses only on average income disparities among race groups and/or ignores the feedback between racial and economic processes. Under empirically plausible levels of within-race income inequality, higher between-group income inequality increases the salience of economic factors in residential mobility decisions. The end result is that high-income blacks live in whiter neighborhoods than they would otherwise. At the same time, poorer blacks are racially (and economically) isolated. Whether these offsetting processes result in a net increase or decrease in segregation depends on the relative size of the black population, the salience of racial versus economic factors in residential mobility decisions, and the shape of the income distribution.

Although the arguments and analyses presented in this work refer to the case of residential segregation, the results apply more generally to any social context or institution— for example, families, friendship networks—in which individuals make decisions about group affiliation based on multiple social attributes. The article concludes with a discussion of how these results might be extended to other contexts in which people sort themselves into groups based on multiple group attributes.

2. THE ROLE OF INCOME IN RACIAL SORTING

Sociology and demography have a long tradition of empirical studies trying to disentangle the causes of racial segregation between whites and blacks. Explanations for existing patterns of segregation typically focus on three potential mechanisms (Quillian 2002; Charles 2003). The first explanation emphasizes the role that preference for living among one’s own ethnic group (or avoiding other ethnic groups) plays in the formation and maintenance of racially segregated neighborhoods (Farley et al. 1978; Clark 1997; Emerson, Yancey, and Chai 2001; Krysan and Farley 2002). The second explanation emphasizes the importance of institutional barriers that limit blacks’ access to white neighborhoods (Yinger 1995; Galster and Godfrey 2005). The third line of work focuses on racial differences in economic resources (e.g., Clark and Ware 1997; Clark 1986, 2007). The logic is that—given that whites on average have higher incomes than other ethnic groups—white households can live in neighborhoods with higher prices, effectively creating an affordability constraint that limits access to lower income minority groups even in the absence of institutional discrimination.

The most common strategies researchers use to investigate the role of economic factors in race/ethnic segregation are standardization methods applied to aggregate Census data, or regression-based decomposition applied to individual-level data. Aggregate studies typically compute the amount of race segregation that would be expected if race groups sorted only on the basis of economic factors (i.e., indirect standardization), or compare the racial neighborhood composition of white and nonwhite households in the same income or educational bracket to see if higher status minorities experience the same sorts of neighborhoods as their white counterparts (e.g., Taueber and Taueber 1969; Farley 1977; Simkus 1978; Massey and Fischer 1999; Iceland, Sharpe, and Steimetz 2005). The micro-level analyses—often referred to as “locational attainment” models—examine individuals’ residential choices conditional on education, income, and/or wealth (e.g., Alba and Logan 1993; Alba, Logan, and Stults 2000; South and Crowder 1997; Crowder, Chavez, and South 2006). In all cases, the goal is to see whether racial differences in neighborhood composition persist after standardizing/conditioning on economic attributes and segregation by income. This literature demonstrates that socioeconomic status differences explain only a small part of blacks’ segregation from whites (although this portion may be increasing, as evidenced by Fischer 2003).

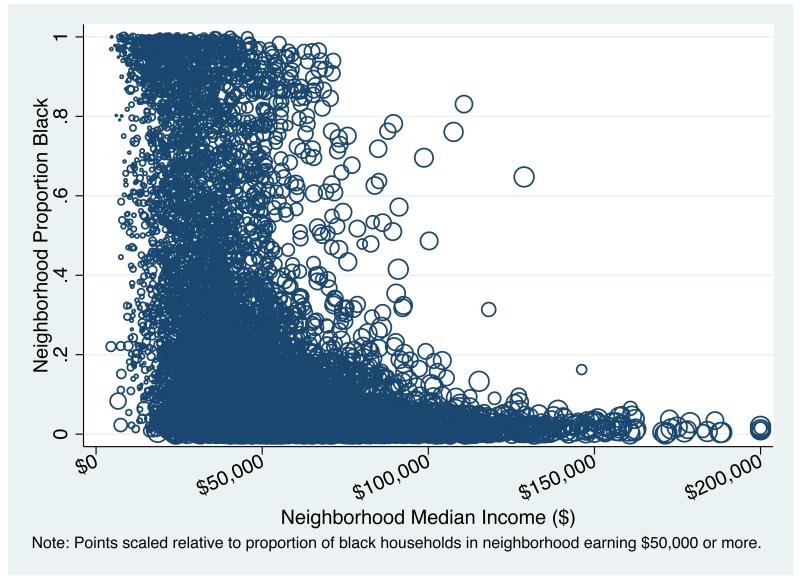
There are two problems with these approaches. First, these methods ignore the underlying structural constraints imposed by the joint distribution of attributes within the population. The reality is that there are very few neighborhoods in American cities that are both affluent and predominantly black. Figure 1 shows the joint distribution of neighborhood proportion black and neighborhood median income across all Metropolitan Statistical Areas in 2000. Each data point represents a Census block group; the points are scaled relative to the proportion of black households in the neighborhood with an annual income of $50,000 or more. Thus larger circles denote a greater number of high-income blacks in the neighborhood. Overall, we see that high-income blacks tend to live in either poorer black neighborhoods or predominantly nonblack areas. Only 38 block groups in the United States at that time had both a median income of at least $75,000 and were at least 30 percent black. Fourteen of these are in the Washington D.C.-Baltimore Metro area, and 7 are in Chicago. A Census block group generally contains between 600 and 3,000 people with an optimum size of 1,500. Given that 32 percent of the total black population in the United States in 2000 earned at least $50,000 and given that black survey respondents consistently express a desire to live in neighborhoods with a significant black presence (c.f. Farley et al. 1978; Farley, Fielding, and Krysan 1997; Krysan and Farley 2002), this suggests a unmet demand for middle-class black neighborhoods. Where those neighborhoods are not available, higher income blacks may be forced to choose between neighborhoods where their racial own group is well represented and neighborhoods where their economic or educational group is well represented.

Figure 1. Joint Distribution of Neighborhood Median Income and Neighborhood Proportion Black, All Metro Area Census block groups in 2000.

The second problem with approaches using both aggregate and individual-level data is that the statistical methods and logic of argument implicitly assume that economic segregation reflects sorting based purely on economic factors, and thus one can partition out economic factors by standardizing on income or comparing the segregation of people with different races but the same income and/or wealth. This would be a reasonable assumption if people actually selected neighborhoods based only on economic factors or if income/wealth and race were independently assigned characteristics. In this case, any changes in racial composition would not affect residential mobility based on income/wealth, and vice-versa. However, when people select neighborhoods based on both racial and economic factors, then the total amount of income segregation reflects not only inequalities in income, but also the correlation between race and income, the relative size of the minority population, and residential mobility by both race and income (see also Sethi and Somonathan 2004). In other words, because both race and income matter in residential mobility decisions and because race and income are correlated attributes of individuals, there is feedback between processes that generate racial segregation and processes that generate economic segregation. Under these circumstances, standard statistical approaches cannot reveal the relative contributions of racial and economic factors to observed neighborhood patterns. An alternative approach is to dynamically simulate neighborhood formation and change under alternative assumptions about residential choice behavior and the joint distribution of race and income within the population.

The most widely cited model of feedback between individuals’ decisions and population dynamics is Schelling’s (1971, 1978) model of residential tipping. Using rudimentary computational models applied to artificial agents, he showed how the preferences of individuals about where to live give rise to (often unanticipated) aggregate patterns of residential segregation. These patterns, moreover, may be at odds with the majority of individuals’ preferences (Panes and Vriend 2003). The Schelling model assumes a highly styled city populated by two race groups: blacks and whites. Both race groups are assumed to be willing to live in any neighborhood so long as its own race group is the local majority. This model has been extended by a number of scholars over the years to incorporate different assumptions about racial preferences (Fossett 2006; Bruch and Mare 2006, 2009), explicit geography (Benenson, Hatna, and Or 2009), and social class (Benard and Willer 2007). But simulation approaches have not been used to explicitly tease apart how racial composition, income inequality, and residential mobility combine to generate racial segregation patterns. More generally, we lack an analytic framework for understanding how sorting along multiple attributes such as race, income, or age affects inequality across social units. In the next section, I describe the key parameters of such a framework and provide a preliminary sketch of how they fit together.

3. A FRAMEWORK FOR UNDERSTANDING SORTING ON MULTIPLE ATTRIBUTES

Blau’s Theory of Social Structure

Blau’s approach is based on Simmel’s (1955) insights about the importance of quantitative dimensions for social life. Blau (1977: 278) defines social structure as the joint distribution social attributes within the population. One key component of social structure is the degree of diversity in the population along a given attribute, for example ethnic diversity. Another key component is the extent to which various social distinctions are related, for example the correlation between ethnicity and income (Blau, Blum, and Schwartz 1982: 46). Blau’s two major theorems relate to these features of social structure. First, Blau postulates that greater diversity on an attribute counteracts in-group tendencies to seek like others based on that attribute. In other words, holding preferences constant, greater diversity is associated with greater social integration. Second, Blau argues that a weaker correlation among socially salient attributes leads to greater social integration. This is because in a world where people hold many weakly correlated, intersecting affiliations, any person who is an in-group member on one dimension is likely to be an out-group member on other dimensions.²

This study extends Blau’s framework in three different ways. First, in both his theoretical and empirical work, Blau conflates two aspects of the association between attributes: between-versus within-attribute variation.³ Blau’s theory only holds up under certain configurations of between- and within-group variance. Second, Blau recognizes that both the size of social groups and the correlation between social attributes matters, but does not consider how these two features of population composition interact. In the case of residential segregation, I show that the extent to which income inequality between race groups contributes to racial segregation depends on the relative size of racial groups. Finally, Blau’s empirical tests focus on marriage, a unit that requires only two people to exist. I articulate how the size of social units (neighborhoods) might condition how the joint distribution of attributes shapes aggregate patterns of social separation or integration, and provide an alternative test of Blau’s argument based on neighborhoods (a social unit that is substantially larger than marriage).

The Role of Between- and Within-Group Heterogeneity in Segregation Dynamics

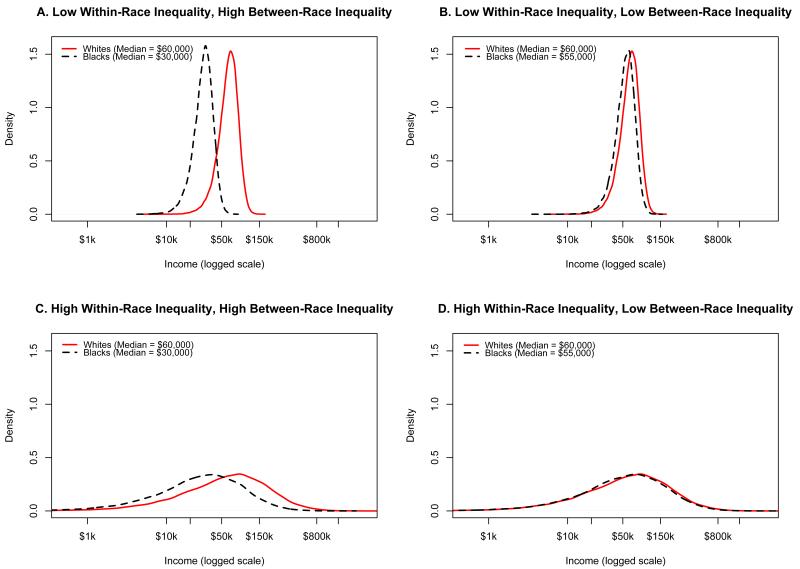
Let’s consider how different dimensions of the joint distribution of attributes condition the relationship between individuals’ preferences for neighbors and aggregate patterns of segregation. Figure 2 shows four black-white income distributions that illustrate variation in within- and between-race income inequality. Panels A and B assume a low level of within-race income inequality whereas Panels C and D assume a high level of within-race income inequality.⁴ Panels A and C show a high level of between-race income inequality, whereas Panels B and D show a low level of between-race income inequality. In all cases, blacks and whites have the same within-race income inequality. But in Panels A and C, blacks have a median income of $30,000 while whites have a median income of $60,000; compare this with a median income of $60,000 for whites and $55,000 for blacks as shown in Panels B and D.

Figure 2. Stylized Patterns of Between- and Within-Race Income Inequality.

We know from studies of revealed and stated preferences that people prefer to live where their own group is the local majority (c.f. Charles 2003, p. 182-5), and it is reasonable to assume that people prefer to live in a neighborhood where their own income is not less than the average income of the neighborhood. For the same preference regime, we would expect racial segregation to be higher under Panel A as compared to Panel C, and Panel B as compared to Panel D. The reason is simple: holding between-race income inequality constant, greater within-race income heterogeneity implies an increased level of within-race variation in residential mobility behavior, which would lead to lower levels of racial segregation. But it is less clear what levels of racial segregation we might expect under Panel A as compared to Panel B, or Panel C as compared to Panel D. In other words, holding within-race income variation constant, how might racial segregation change if we increase between-race income inequality?

When we increase average income differences between blacks and whites, we also increase the average income difference between black and white neighborhoods. When within-race income variation is small, as in Panels A and B, higher income blacks may not feel a strong pull towards higher income white areas. However, under higher within-race income heterogeneity (as shown in Panels C and D), holding preferences constant, higher income blacks will experience greater salience of economic factors in residential mobility decisions.⁵ Thus they are less likely to choose poorer black neighborhoods, and more likely to move into neighborhoods where their own income group has greater representation. More generally, for a sufficiently high level of within-race income heterogeneity, any increase in between-race income inequality will decrease the attractiveness of black neighborhoods for more affluent blacks, and thus increase their willingness to move into white, affluent neighborhoods. This decrease in the average neighborhood percent black experienced by higher income blacks will be “offset” by the increased racial isolation of lower income blacks. Of course, at higher levels of black-white income inequality, high-income blacks make up a smaller part of the total black population. Thus the extent to which these opposing processes result in a net increase, decrease, or no change in segregation depends on the shape of the income distribution and the relative salience of racial versus economic factors in residential mobility decisions.⁶

Critical Numbers, Income Inequality, and the Size of the Metro Black Population

If increased income inequality between blacks and whites leads to a decrease in the average neighborhood proportion black experienced by affluent blacks, then a substantial decrease or elimination in income differences between blacks and whites will result in an increase in the average neighborhood proportion black experienced by affluent blacks. There are two possible reasons why a convergence in income between blacks and whites may lead to an increase in the average proportion black experienced by affluent blacks. First, an elimination or substantial attenuation of black-white income inequality may result in sufficient numbers of middle-class blacks to generate sustainable middle-class black neighborhoods. Neighborhoods require a critical number of households to be sustainable. For example, one thousand households might not be able to maintain their own neighborhood (with clearly defined boundaries that protect property values and the quality of public schools) but ten thousand can. The poorer blacks are relative to whites, the less likely it is that there are sufficient numbers of higher income blacks to support higher income black neighborhoods. In addition, the smaller the size of the black community, the harder it is to form economically distinct black neighborhoods. It is no accident that the two cities with established black, middle class communities—Atlanta and Washington D.C.—are also areas with a sizeable black population. Cities with larger minority populations can sustain more economically diverse minority neighborhoods.⁷

Second, a decrease in black-white income inequality may lead to an increased flow of black households moving into higher income white areas. Because whites are only willing to tolerate a small minority neighborhood black (Farley et al. 1993, Farley et al. 1994; Charles 2000), this may prompt local white residents to move out, resulting in a net increase in the average proportion black experienced by affluent blacks in these areas. Here, again, the size of the black population matters. For a given level of black-white income inequality, a larger black metro population implies a greater the number of nonpoor black households moving into nonpoor white areas. Thus we might expect the threshold level of black-white income inequality that leads to an out-migration of white residents to be lower when the black metro population is larger.

The above argument suggests two testable hypotheses. First, for moderate to high levels of within-race income inequality, I expect a negative relationship between black-white income inequality and the neighborhood proportion black experienced by poor blacks, and a positive relationship between black-white income inequality and the neighborhood proportion black experienced by affluent blacks. Second, because the two mechanisms which might explain an increase in the neighborhood proportion black for affluent blacks (outlined in the previous section) are both predicated on having a “critical mass” of higher income black households, I expect the relationship between between-race income inequality and the average proportion black experienced by affluent blacks to be nonlinear, and depend on the size of the black population. Because previous studies have not explicitly examined the roles of between- and within-race income inequality in racial segregation, there is no prior research regarding these hypotheses. The balance of the article uses simulation and fixed effects models to test these predictions.

4. SIMULATION EXPERIMENTS

I use agent-based models to explore how the joint distribution of income and race shape patterns of racial residential segregation. The overarching strategy is to explore what segregation dynamics occur under alternative assumptions about the relative size of race/ethnic groups and the degree of within- and between-race income inequality, holding mobility behavior constant. The first set of simulation results are based on a theorized set of agents moving within a highly styled city (“stylized model”). This approach allows me to exercise complete control over the three parameters of interest: between-race income inequality, within-race income inequality, and the relative size of the minority population. It provides a highly controlled test of the hypothesis that, when within-group income inequality is high, a convergence in income inequality between blacks and whites results in offsetting effects at the high and low ends of the black income distribution. However, the agent-based model uses a very stylized geography and population. For example, the model assumes a world of only blacks and whites, and sets the initial distribution of the agents to a state of complete integration. To more firmly attach these results to real cities and segregation patterns, I also implement a more realistic agent-based model (“empirically grounded model”) that simulates segregation dynamics using empirical populations and highly realistic geography for three cities: Atlanta GA, Chicago IL, and Los Angeles CA. Table 1 summarizes the two agent-based models used in the analysis.

Table 1.

Agent-Based Models Used in Analysis

	Stylized Model	Empirical Model 1
Population	34,000 households Blacks and whites Metro percent black: 15 or 30	Drawn from 2000 STF 3A Census data 20% sample of all households Blacks, whites, Asians, and Hispanics
Geography	200×200 grid Each cell represents 1 housing unit	GIS map of city blocks Each block can hold multiple households
Initial Distribution	Random	Corresponds to 2000 population at Census tract level
Neighborhoods	5×5 sub-sections of the grid	Census block groups
Agent Behavior	Empirically estimated from PSID	Empirically estimated from PSID
Comparisons	Systematically vary within- and between-race inequality	Empirical population composition Blacks assigned white income distribution

¹Empirical model initialized for three cities: Los Angeles, Atlanta, and Los Angeles

Specifying Agent Behavior

Both simulation models assign agents a model of residential choice behavior based on statistical estimates from the PSID. These models describe the probability that a person with a given race and household income will select a new neighborhood (or stay put), given the racial and economic composition of the current neighborhood, as well as all potential destinations.

Data

The PSID is a nationally representative, longitudinal survey of U.S. residents and their families. The survey began in 1968 with approximately 5,000 families. Panel families were interviewed annually between 1968 and 1997, and every two years thereafter. New families have been added to the panel as children and other members of the original panel families form separate households. I use the PSID’s Geocode Match Files to link the addresses of individual respondents at each interview to their corresponding census tract identifiers. These identifiers make it possible to trace the mobility of PSID respondents across neighborhoods between successive interviews. I merge the geocoded PSID data with decennial Census data.⁸ To maintain consistency across survey years, I analyze two-year mobility windows. Additional moves within years do not enter into the analysis. Because my analysis focuses on urban segregation dynamics, I restrict my sample to person-years where the respondent was living in metropolitan areas in adjacent interview years. Periods when respondents were living in rural areas or moved between rural and urban areas are excluded from the analysis.⁹ Table 2 summarizes the information available in the PSID sample. Each respondent may contribute up to four residential mobility decisions, one for each 2-year time interval. The 12,684 respondents provide information on 28,232 biannual mobility decisions. In most cases, these are decisions to remain in the current unit. However, 10,698 are moves between Census tracts within a given metro area. The remaining cells of the table describe neighborhood attributes of the chosen tract in each time interval.¹⁰ Thus, for the 1991-1993 interval, this refers to the residence in 1993. We see that, on average, PSID respondents tend to live in areas with higher median incomes than their own. We also see a small but steady decrease in the neighborhood proportion black experienced by black respondents. White PSID respondents live in overwhelmingly white neighborhoods. Overall, the neighborhood patterns observed in the data are consistent with the moderate to high levels of racial segregation observed in the United States.

Table 2.

Summary of Observations in PSID Data, 1991-1999

	Total	White	Black	Asian	Hispanic
Residential Mobility Decisions
1991-1993	8,142	3,465	2,493	29	2,155
1993-1995	8,635	3,757	2,642	33	2,203
1995-1997	5,566	3,199	1,940	113	314
1997-1999	5,889	3,295	2,080	125	389
Moves Between Tracts
1991-1993	1,912	763	681	8	460
1993-1995	3,691	1,499	1,220	14	958
1995-1997	2,587	1,268	939	91	283
1997-1999	2,508	1,289	973	66	180
Household Median Income
1991-1993	$22,802	$38,080	$14,280	$58,191	$17,791
1993-1995	$22,939	$36,171	$15,312	$48,392	$17,289
1995-1997	$28,890	$40,660	$19,612	$38,520	$19,284
1997-1999	$31,930	$43,363	$23,690	$43,631	$22,660
Neighborhood Proportion Black
1991-1993	0.242	0.060	0.621	0.126	0.099
1993-1995	0.236	0.061	0.606	0.101	0.092
1995-1997	0.244	0.063	0.581	0.089	0.072
1997-1999	0.246	0.065	0.571	0.065	0.073
Neighborhood Proportion Hispanic
1991-1993	0.121	0.040	0.030	0.101	0.359
1993-1995	0.139	0.050	0.045	0.112	0.406
1995-1997	0.092	0.063	0.071	0.179	0.486
1997-1999	0.106	0.068	0.084	0.173	0.531
Neighborhood Proportion Asian
1991-1993	0.025	0.026	0.016	0.121	0.034
1993-1995	0.026	0.027	0.017	0.090	0.035
1995-1997	0.209	0.030	0.019	0.139	0.053
1997-1999	0.031	0.031	0.020	0.154	0.046
Neighborhood Median Income
1991-1993	$37,661	$53,491	$34,631	$52,437	$36,713
1993-1995	$40,512	$54,824	$36,213	$55,370	$38,714
1995-1997	$48,248	$62,409	$41,265	$61,054	$43,547
1997-1999	$49,645	$64,105	$42,960	$71,201	$45,167

Note: All incomes scaled to 2000 dollars.

Statistical Approach

My analysis of residential mobility is based on discrete choice (conditional logit) models for residential location (McFadden 1973, 1978; Bruch and Mare 2012). The models incorporate the effects of individuals’ personal attributes as well as their opportunities for mobility; that is, characteristics of all neighborhoods to which they might move. To define a meaningful choice set, I limit the analysis to moves that occur within the same metro area.¹¹ I assume the potential destinations considered by PSID respondents consist of all Census tracts within their metro area. The sample includes both owners and renters.¹²

The discrete choice model focuses on the effects of race-ethnic and economic composition of neighborhoods on residential choice. In each 2-year period, individuals face the probability of staying within their neighborhood or moving to another neighborhood within the same metro area. The model assumes that the potential utility that an individual expects from each potential destination (including the decision not to move) is a function of his or her race/ethnicity, household income, the race/ethnic composition of each potential destination, the median income of each potential destination, the 20^th percentile housing price of each potential destination, and whether a given destination requires that the individual move or stay in their current neighborhood. Housing prices are calculated from the distribution of neighborhood residents’ monthly gross rent and monthly mortgage payments. The 20^th percentile price represents a lower bound of affordability. For the ith individual who is considering the jth neighborhood destination in the tth period, the utility can be written as:

$$\begin{array}{cc}\hfill & U_{ijt}=F({\text{Ethnicity}}_i,{\text{Household Income}}_i,{\text{Neighborhood Ethnic Composition}}_{jt},{\text{Neighborhood Median Income}}_{jt},\hfill \\ \hfill & {{\text{Neighorhood 20th Percentile Price}}_{jt},{\text{Neighborhood Median Income}}_{jt},D_{ijt})}^{\prime }\hfill \end{array}$$ (1)

where D_ijt equals 1 if the potential destination j is the origin tract for individual i in year t and 0 otherwise.

I estimate the effect of these factors using a conditional logit model for discrete choice. In particular, if p denotes the probability of choosing the jth neighborhood in the tth period by the ith individual, the model can be written as:

$$p_{ijt}\left(x_{ijt}\right)=\left[\exp \right(\beta x_{ijt}\left)\right]∕\left[\sum _{k\in C\left(i\right)}\exp \right(\beta x_{ikt}\left)\right],$$ (2)

where x_ijt and x_ikt denote vectors of attributes of Census tracts j and k (possibly interacted with traits of individuals), β denotes a vector of parameters to be estimated, and C(i) denotes the set of potential destinations available to individual i. In the present application, this is defined as all Census tracts within the metro area that the person is residing in at the beginning of the mobility interval. Thus the choice set will vary across PSID respondents, depending on their geographic location.¹³ I specify Huber-White robust standard errors to account for the clustering of mobility decisions within individuals across years.¹⁴

The models allow for the following types of effects. First, all else equal, people are more likely to choose to remain in their current place of residence rather than move. As shown in (1), this is represented as a dummy variable that equals 1 if the tract in question is the current tract of residence and 0 for all other potential destinations. I also allow for the possibility that people evaluate the racial and economic composition of their own neighborhood differently from all other potential destinations. For example, people may be less sensitive to changes in neighborhood prices in their current neighborhood due to tenure discounts.

Second, I include information on the race-ethnic composition of each tract, which may affect its attractiveness to potential movers. The model allows for the possibility that this effect is nonlinear. For example, some groups may have a taste for diversity. To incorporate these effects, I include linear and quadratic terms for the proportions in each of the four race-ethnic groups (non-Hispanic whites, Hispanics, non-Hispanic blacks, non-Hispanic Asians) as separate variables in the discrete choice model. Third, I allow members of race/ethnic groups to have different responses to neighborhood racial composition. Individuals are likely to prefer areas where their own group is well represented and may display group-specific tendencies to be drawn to or avoid areas populated predominantly by other groups. In addition, I allow the effects of housing costs to vary by household income by including a variable that is the ratio of housing costs to household income. I also allow for the possibility that people evaluate neighborhood income relative to their own income. I explore a variety of specifications of the discrete choice model that include alternative combinations of these effects.^15,16

Results

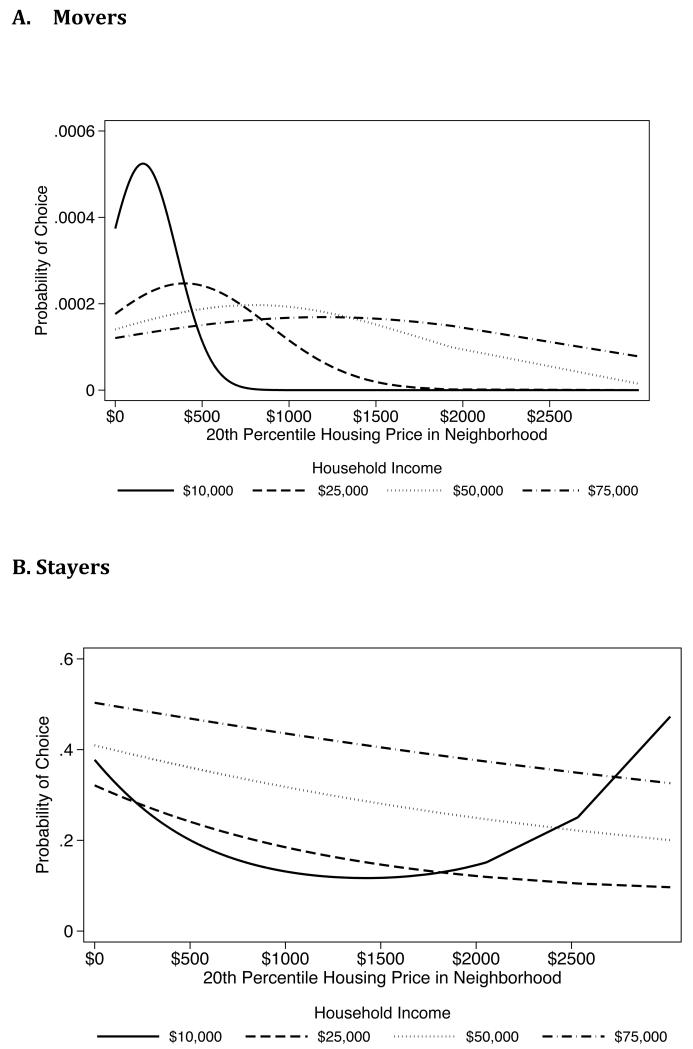
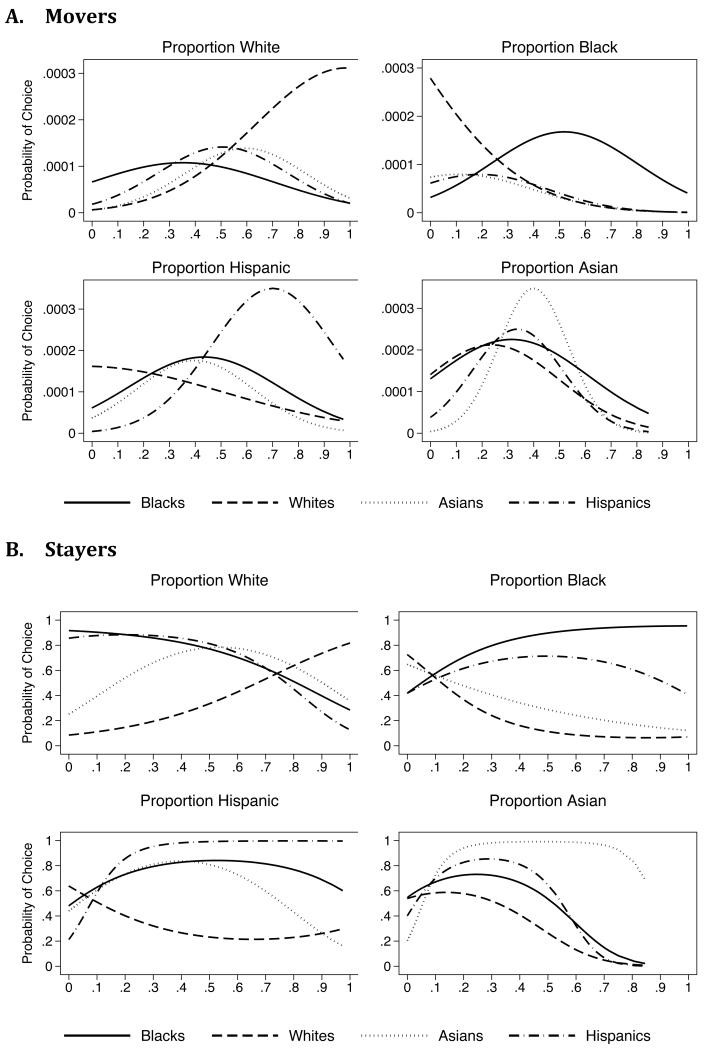
The parameter estimates (reported in Table A1) indicate that, over the course a two-year window, individuals are more likely to remain in their own neighborhoods rather than move. Beyond that, it is difficult to interpret the model from parameters alone especially given the three-way interactions. Further insights can be obtained from the predicted probabilities of neighborhood choice as a function of neighborhood racial and economic composition. Figure 3 shows the probability of choosing a neighborhood based on housing costs. Separate profiles are shown for movers (people who changed Census tracts in the two year interval) and stayers (people who remained in the same Census tract over the two year interval). Looking at Panel A, we see the expected patterns: poorer households are highly constrained with regards to what neighborhoods are available to them. As household income increases, individuals are more likely to move into areas with higher prices. Panel B, which shows the probabilities for stayers, indicates that overall there is a gradually declining probability associated with choosing to remain in the current neighborhood as a function of neighborhood prices. The exception is the poorest households, who (if they are lucky enough to find themselves already living in a very expensive neighborhood) have a high probability of remaining there.

Figure 3. Probability of Choosing a Housing Unit by Monthly Housing Costs.

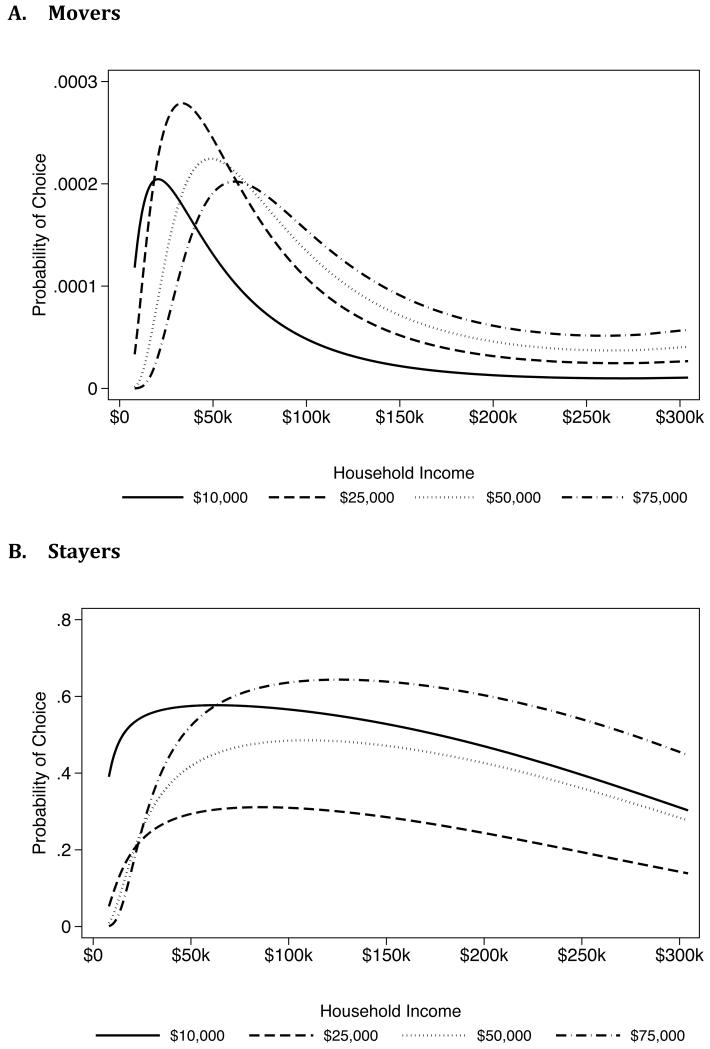
Figure 4 shows the probability of choosing a neighborhood based on neighborhood median income. We see that, conditional on prices and other factors, people tend to choose areas where the median income is similar to their own. The same pattern is observed among stayers although curves are significantly more graduated, consistent with the results observed for neighborhood prices. In practice, neighborhood prices and neighborhood median income are highly correlated, so it is difficult to separate out their effects on mobility. Figure 5 shows the probability of choosing a new neighborhood or remaining in one’s current neighborhood based on neighborhood racial composition. Although the model produces estimates of residential preferences for all four race-ethnic groups, estimates for Asians are not reliable because they are based on a very small number of moves (Table 2). Thus I confine my discussion to the other three race-ethnic groups. Among movers, we see that whites have a strong tendency to move into predominantly white neighborhoods, and avoid black neighborhoods. Blacks tend to choose integrated areas where they are neither the overwhelming majority nor the minority. Hispanics tend to select majority Hispanic areas. Among stayers, we see that whites’ probability of remaining in the current neighborhood sharply decreases with neighborhood proportion black. In contrast, both blacks and Hispanics are willing to remain in their current area with increasing proportions of whites, up until a white majority. Hispanics and blacks are more or less equally willing to remain in their current neighborhood regardless of neighborhood proportion own-group, as long as they have some baseline representation. Note that these are all “net” effects after controlling for economic factors. Overall, we see that all race-ethnic groups display a tendency to live among their own group, although they distinguish among potential out-group neighbors. There is also variation in extent to which different race groups are willing to tolerate out-group neighbors. The parameters from the discrete choice models are assigned to agents in two different simulation models, described in the next sections.

Figure 4. Probability of Choosing a Housing Unit by Neighborhood Median Income.

Figure 5.

Probability of Choosing a Housing Unit by Neighborhood Racial Composition

Agent-Based Models

Stylized Model

The stylized agent-based model consists of a 200×200 grid with 40,000 cells.¹⁷ Each cell corresponds to a housing unit. This lattice is populated with approximately 34,000 agents, each representing one household. To allow agents to move relatively freely on the lattice, 15 percent of the cells on the lattice are vacant. Agents respond only to the ethnic and economic composition in their immediate neighborhood or other potential neighborhood destinations; they have no information about the overall level of segregation in the city. Agents’ neighborhoods are defined as 5x5 cell sub-regions of the city. These neighborhoods are designed to approximate Census tracts or another objectively defined boundary. Housing units are identical, and rents are uniform within each neighborhood.

Agents in this model differ along two dimensions: race and income. For ease in interpreting the results, I assume a world consisting only of two race groups: whites and blacks. I simulate segregation dynamics assuming the city proportion black is either 15 or 30 percent. I assign the agents incomes that follow an empirically plausible parametric distribution, Singh-Maddala, which allows me to systematically manipulate the degree of income inequality between and within ethnic groups.¹⁸ This function has the advantage that I can specify both the median income and the overall level of inequality by changing the values of the distribution parameters. The distribution has the density:

$$f\left(x\right)=\alpha q\frac{x^{\alpha -1}}{{\beta }^{\alpha }{\left(1+{\left[\frac{x}{\beta }\right]}^{\alpha }\right)}^{1+q}},$$ (4)

where α > 0,β > 0,q > 0, and x ≥ 0 . By modifying β (scale parameters), I can manipulate the median income. By modifying α and q (shape parameters), I can manipulate the shape of the distribution and thus the overall level of income inequality. Appendix A provides more details about the specific parameters used to generate each income distribution.

I hold whites’ median incomes constant at approximately $60,000, but specify the black income distribution to have a median income of approximately $25,000, $40,000, or $60,000.¹⁹ These regimes are referred to as high inequality, moderate inequality, and income equality. I also examine segregation dynamics under different levels of within-race income heterogeneity. For any given simulation, I assume that both race groups have the same level of within-group income variation. Within-race income heterogeneity is summarized by the Gini coefficient.²⁰ I specify that levels of within-race income inequality range from a Gini index of 0.15 to a Gini index of 0.75.²¹

At the start of the simulation, the agents are randomly distributed across the city. Then, one agent is randomly sampled and given an opportunity to move. The agent evaluates its current unit and 100 randomly sampled destination units according to the race-appropriate statistical choice function estimated from the PSID data. The agent then decides to move or stay put with probabilities proportional to relative differences in neighborhood desirability. Given the costs of moving, agents often choose to remain in their current place of residence. Each time an agent moves, they change the composition of the neighborhood they left behind and the neighborhood they move into. Over time, the choices available to present agents are a result of previous mobility decisions.

I run the agent-based models to a dynamic equilibrium, where the agents may still be moving but aggregate segregation levels are no longer changing. In practice, this occurs after approximately 3 million time steps. Racial segregation is measured by the Index of Dissimilarity, which captures the evenness of the distribution of people by race across neighborhood units within a city. This classic measure of racial segregation is not without its limitations—most notably, it is insensitive to the macro-level spatial configuration of neighborhoods—but it is widely used in the literature and has a straightforward, intuitive meaning. I supplement this summary statistic with local neighborhood compositional measures, for example the average neighborhood proportion black experienced by blacks in different income strata.²²

As neighborhood composition changes, neighborhood attractiveness (and therefore housing prices) will also change. I update housing prices at regular intervals to reflect changes in neighborhood desirability using hedonic pricing equations that predict logged house prices based on neighborhood ethnic and income composition (see Sheppard 1999 for an overview of the specification and estimation of hedonic pricing models for housing markets). These pricing equations are estimated from 2000 Census block group data for Atlanta, GA.²³ I regress logged median monthly housing costs on block group racial and income composition, to determine the relationship between neighborhood characteristics and expected housing costs. The coefficients and associated standard errors from these models are reported in the first panel of Appendix B1. The prices estimated by the model are plausible, and are well within the range of rents observed for households. Neighborhoods with higher median incomes and/or more white residents tend to have higher rents. Neighborhoods with a substantial number of black residents have lower rents.

Empirically Grounded Model

While the stylized model allows for highly structured experiments that generate easily interpretable results, this approach assumes a world that consists only of two groups—whites and blacks—and starts from a state of complete integration. Thus, it is difficult to extrapolate from these results to real world segregation patterns. Thus, I also explore segregation dynamics using an empirically grounded agent-based model of segregation dynamics that recreates the geographic and population distribution of three U.S. cities: Los Angeles, Atlanta, and Chicago.²⁴ In each case, the model uses Geographic Information Systems (GIS) data at the block, block group, and tract level to create a realistic space in which the agents move about. Agents live in housing units nested within Census blocks, and their neighborhoods are defined relative to real world geographic barriers such as freeways, rivers, and major roads. The population of agents and their initial spatial distribution matches that of Atlanta, Chicago, or Los Angeles in 2000. I simulate segregation dynamics assuming agents’ mobility behavior corresponds to the residential choice models estimated from the PSID, and compare segregation outcomes under empirical income distributions to outcomes assuming income equality between blacks and whites. All moves occur within city boundaries.

Table 4 shows the population density, size, and racial and economic composition of Los Angeles, Atlanta, and Chicago in 2000.²⁵ The first column shows the race/ethnic composition of each city. Atlanta is almost two-thirds black, with Asians and Hispanics making up only 3 percent of the total population. Los Angeles is multi-ethnic; Hispanics represent almost half (47%) of the total population, while blacks are a little over one tenth of the total population. Chicago has roughly equal numbers of blacks and whites, and has a substantial Hispanic population (26%). The second and third columns show the median income and the within-race income inequality (as captured by the Gini Index) for each race group.²⁶ In both Los Angeles and Chicago, the black median income is roughly one half that of whites. Atlanta has the highest black-white income inequality of the three cities, with the black median income a little more than one third that of whites. Los Angeles has higher within-race income inequality, as compared to Atlanta and Chicago. In all three cities, within-race income inequality is higher among blacks than among whites. The final two columns report total population size and land area for each city. Atlanta is much smaller than Los Angeles and Chicago, with a population of less than half a million people compared with well over 2 million for the other two cities. It also covers a smaller area, 132 square miles, compared with 234 for Chicago and 469 for Los Angeles.

Table 4.

Empirical Populations

Area	Race/Ethnic Group	% of Population	Median Income	Income Inequality	Population	Total Area (Square Miles)
Los Angeles	White	33	$44,841	0.45	3,964,820	469
	Black	11	$27,310	0.46
	Asian	10	$37,186	0.42
	Hispanic	47	$28,759	0.43
Atlanta	White	33	$60,936	0.38	416,474	132
	Black	61	$23,128	0.41
	Asian	2	$37,759	0.40
	Hispanic	5	$36,545	0.42
Chicago	White	34	$46,680	0.38	2,896,016	234
	Black	36	$29,086	0.45
	Asian	4	$40,519	0.39
	Hispanic	26	$36,543	0.39

Notes: Within-race income inequality is measured by the Gini index. U.S. Census data for places downloaded from the National Historic Geographic Information System web site (NHGIS).

I initialize the agent-based model using tables from the 2000 Census STF 3A data that describe the joint distribution of race/ethnicity and income for all households in a given Census tract. Each agent is a household, and the population represents a 20 percent sample of all households living in each Census tract.²⁷ Agents are assigned to one of four exclusive race/ethnic groups: blacks, whites, Hispanics, and Asians. Income is categorical and defined as the midpoint of the sixteen 2000 Census income categories: $0-9999, $10000-14999, $15000-19999, $20000-24999, $25000-29999, $30000-34999, $35000-39999, $40000-44999, $45000-49999, $50000-59999, $60000-74999, $75000-99999, $100000-124999, $125000-149999, $150000-199999, and $200000 or more.²⁸ For the open-ended, highest income interval, I assign agents an income of $250,0000.²⁹ Within each neighborhood, I specify that an additional 15 percent of all housing units are vacant.³⁰ Neighborhoods are defined as all housing units situated within the same Census block group.³¹ Agents are initially distributed in space such that at the Census tract level the distribution of households in the model corresponds to the distribution of households in 2000 Chicago, Los Angeles, or Atlanta.³²

In each time step, a 0.01% sample of households is given an opportunity to choose a new neighborhood. Each agent evaluates the neighborhood it is currently living in and a 10 percent sample of all vacant housing units in the metro area.³³ The agent then moves to a new destination or stays put with probabilities proportional to the weights calculated in the utility function. Over time, the neighborhood options confronted by agents change as a function of previous mobility decisions. As neighborhoods change, housing prices change as well. I update housing prices using city-specific hedonic regression models estimated from 2000 data. As discussed in the previous section, the models predict how median housing prices change as a function of changes in neighborhood median income and racial composition. The coefficients from these hedonic regression models are reported in Table A1. Note that the simple pricing models omit many factors relevant to housing valuation (for example: number of rooms; presence of fireplaces, garages, or swimming pools; structure type; age of unit; distance to central businesses). However, the predictive validity of these pricing equations is surprisingly robust to a number of omitted variables and specification errors although the coefficients lose their structural interpretation (Butler 1982). Plots of fitted versus observed prices (available from the author) show that the predicted prices correspond closely to actual values.

I compare results under two scenarios: (1) a world where agents have their empirical income distributions; and (2) a world where blacks’ incomes follow the same distribution as whites.³⁴ The second scenario preserves initial empirical levels of racial segregation. I run the agent-based models until the spatial distribution of agents reaches a dynamic equilibrium where agents may still be moving but the composition of neighborhoods is no longer changing. In practice, this occurs after approximately 50,000 time steps. I then calculate overall measures of segregation as well as the average neighborhood experienced by low-, middle-, and high-income blacks.³⁵

Results

Stylized Model

The simulations using artificial populations and geography produce three key findings. First, the extent to which between-race income inequality affects racial segregation depends on the level of within-race income inequality. When within-group income inequality is low, income differences between blacks and whites significantly increase levels of racial segregation. Table 3 shows the black-white Index of Dissimilarity across various scenarios. We see that when within-group income inequality is low (i.e., Gini = 0.15), an increase from Medium to High black-white income inequality increases racial segregation by roughly 0.09 when city proportion black is 0.15, and roughly 0.07 when the city proportion black is 0.3. In contrast, when within-race income inequality is high, for example with a Gini index of 0.75, an increase in black-white income inequality has a much smaller effect on racial segregation. In between these two extremes, we see that the increase in racial segregation associated with increasing between-race income inequality attenuates at higher levels of within-race inequality.

Table 3.

Segregation Outcomes Under Different Assumptions about Within- and Between-Race Inequality

		Racial Composition
Inequality Regime		15% Black	30% Black
Gini = 0.15
	High	0.88	0.93
	Medium	0.79	0.86
	None	0.74	0.82
Gini = 0.35
	High	0.80	0.85
	Medium	0.73	0.82
	None	0.71	0.79
Gini = 0.55
	High	0.65	0.73
	Medium	0.64	0.72
	None	0.59	0.68
Gini = 0.75
	High	0.47	0.55
	Medium	0.45	0.51
	None	0.44	0.50

Note: “High” refers to a regime where blacks’ median income is $25,000. “Medium” refers to a regime where blacks’ median income is $40,000. “None” refers to a regime where here is no black-white income inequality, and blacks’ median income is $60,000. In all cases, whites’ median income is $60,000.

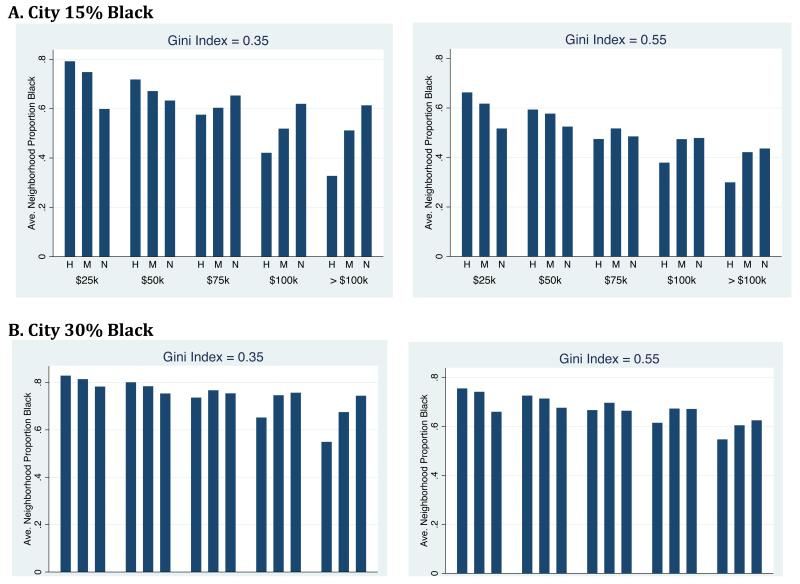
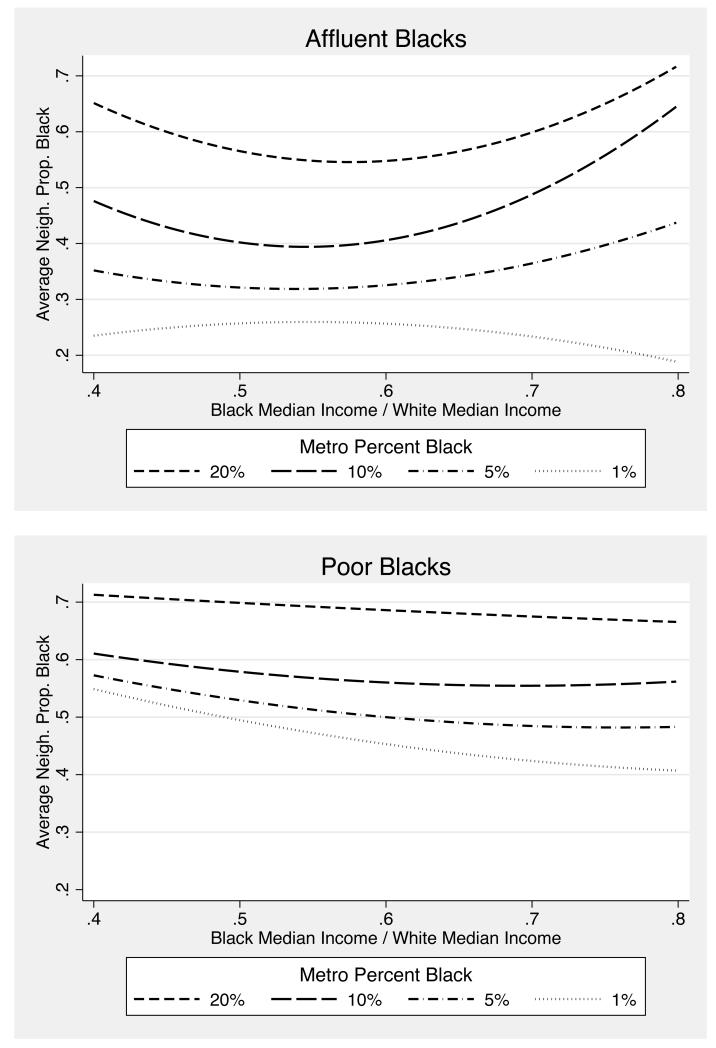
Second, this process results from offsetting effects at the high and low ends of the income distribution. Figure 6 shows the average proportion black experienced under different inequality regimes by blacks at different income strata. The figure reports results under scenarios assuming a within-race Gini Index of 0.35 and 0.55. In both cases, decreasing black-white income inequality results in a steady decline in the average proportion black experienced by poorer blacks. But the opposite relationship holds among the higher income blacks. Here, a convergence in incomes between blacks and whites results in an increase in exposure to black neighborhoods. This offsetting is more pronounced when the black population is 15 percent of the total population than when it is 30 percent of the total population, and also when within-race income inequality is 0.35 compared to 0.55. This is consistent with the argument that the extent to which offsetting occurs depends on the relative size of the black population, and the degree of within-race heterogeneity.

Figure 6. Average Neighborhood Proportion Black Experienced by Blacks Under Alternative Between- and Within-Race Inequality Regimes [H=High between race inequality; M=Moderate between race inequality; N=No between race inequality].

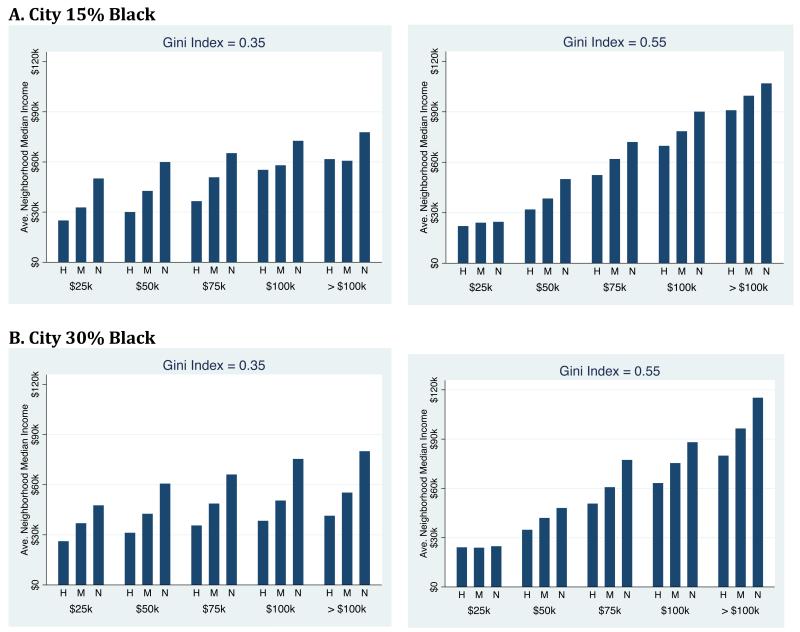
Third, when blacks are poorer on average than whites, high-income blacks will live in poorer neighborhoods on average then their white counterparts. Note that this pattern is also found in U.S. Census data (c.f. Logan 2011). Since the model by design excludes the possibility of institutional racism, this effect may be due to the forced choice these blacks must make between their racial and economic affiliation. Figure 7 shows the average neighborhood income experienced by blacks in different income strata. Here we see blacks at all points in the income distribution experience an increase in neighborhood median income as black incomes reach parity with whites. The figure also shows that the increase in neighborhood median income experienced by blacks across different levels of black-white income inequality is more pronounced when the city is 30 percent black than when the city is 15 percent black. One might be tempted to attribute this to the fact that a city where blacks’ incomes are less than whites’ will be poorer overall when the population proportion black is larger. But there is no change in the average median income experienced by whites across different regimes of between-race income inequality.³⁶

Figure 7. Average Neighborhood Median Income Experienced by Blacks & Whites Under Alternative Between-Race Inequality Regimes, Within Race Gini Index = 0.55 [H=High between race inequality; M=Moderate between race inequality; N=No between race inequality].

Overall, I find that at moderate to high levels of within-race income inequality, the decrease in racial segregation that results from an attenuation or elimination of black-white inequality is a result of offsetting processes at the high and low ends of the income distribution.³⁷ The effect is magnified when the black population is smaller relative to whites. These results are useful insofar as many factors are implicitly “held constant” in the simulation. But it is difficult to know whether the same patterns occur under more realistic circumstances. In the next section, I replicate a subset of these experiments using a more realistic agent-based model.

Empirically Grounded Model

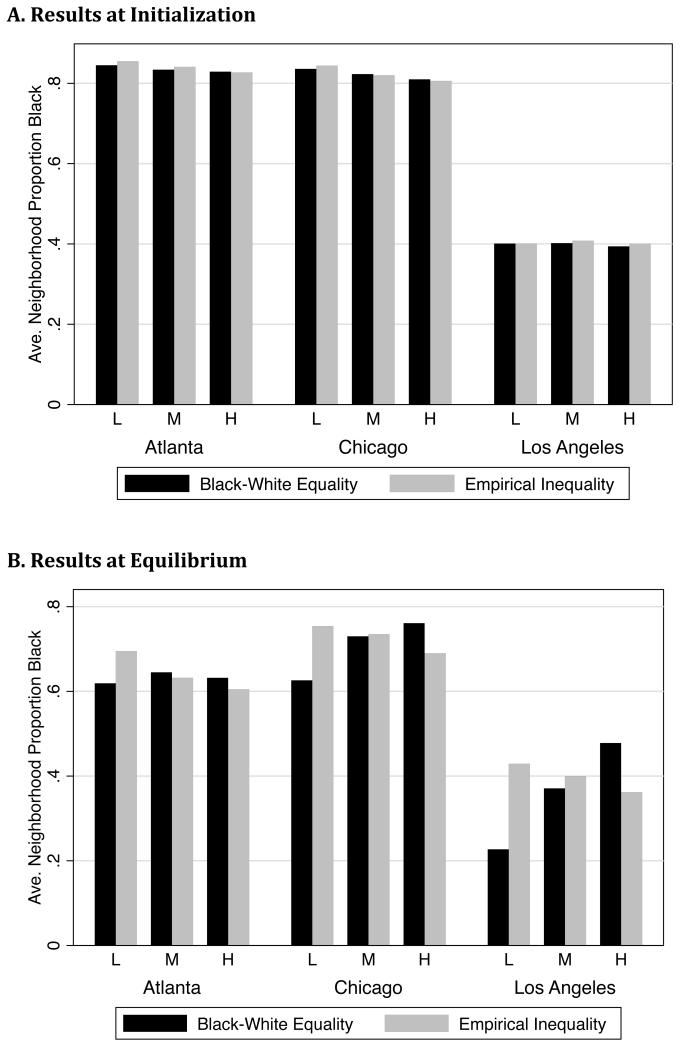
For the most part, the results from the realistic simulation models confirm the findings discussed in the previous section. Figure 8 shows the average neighborhood proportion black experienced by blacks in Chicago, Los Angeles and Atlanta under the two scenarios. The top panel reports the average neighborhood proportion black experienced at model initialization. We see that the neighborhood composition experienced by blacks in each of the three income categories is fairly constant across the two scenarios, and the average proportion black experienced by Los Angeles blacks is far lower than that experienced by blacks in Atlanta and Chicago. There is also slight variation in the average proportion black experienced by blacks across income categories within cities. For example, in Atlanta the average proportion black experienced by high and low income blacks, respectively, is 0.827 and 0.845. The bottom panel of the figure shows the average neighborhood proportion black experienced at model equilibrium. Overall, these results support the offsetting argument and findings laid out in the previous section. A convergence in income between blacks and whites results in opposite effects for high and low income blacks. Moreover, this effect is more pronounced in Los Angeles, where the black population is smaller in relative size than in Atlanta and Chicago.

Figure 8. Neighborhood Outcomes for Low, Middle, and High Income Blacks.

However, across all cases, the model equilibrium suggests a greater level of within-race variation in neighborhood racial experiences than is present at model initialization. In addition, while the simulation results under empirical levels of income inequality preserve key features of black-white segregation under income inequality (e.g., affluent blacks live in areas that have fewer black neighbors than poor blacks), the agent-based model does not preserve initial levels of segregation observed in 2000. Rather, for both the “Empirical Inequality” and “Black-White Income Equality” cases, the model suggests that over time all black households will experience a substantial decline in exposure to black neighbors.

One possible reason for this is that the model is projecting mobility over a very long time frame, absent of any outside systemic shocks. But other factors may also contribute to this predicted decline in segregation. First, the model assigns the same preference parameters to agents in all three cities, but there may be heterogeneity in preferences across areas. Second, the model does not distinguish between owners and renters. Since owned and rented housing is segregated in space, and there are racial disparities in homeownership, this omits a potentially important feature of segregation processes. Third, the model assumes agents have full information about a sample of available housing units from all over the county. In practice, we expect households to only hear about a small subset of available units, and/or to only look for units in a handful of neighborhoods. Finally, the agent-based model assumes no discrimination on the part of real-estate agents, landlords, and lenders. Any of these factors can result in the agent-based model predicting a decline in racial segregation.

On the one hand, there is no reason to expect that an agent-based model—even one that perfectly captures segregation dynamics in a given city—will reproduce or maintain exact patterns of segregation in a specific geographic area. This is because it is unlikely that existing neighborhoods are in equilibrium. So projecting mobility forward in time would be expected to change neighborhood conditions, even in a model that perfectly captures segregation dynamics. On the other hand, I want to ensure that the model is providing inferences that accurately capture mechanisms at work in real cities. Thus, as a final test of the framework, I examine 1980-2000 neighborhood change data from the 100 largest U.S. metro areas to see if, controlling for the relative size of the black population and within-race income inequality, a change in between-race inequality results in the predicted offsetting effects for high and low income blacks.

5. THE RELATIONSHIP BETWEEN INCOME INEQUALITY AND RACIAL SEGREGATION IN UNITED STATES METRO AREAS, 1980-2000

The goal of this analysis is to determine the degree to which offsetting occurs in real cities. I estimate the effect of between- and within-race income inequality on the average neighborhood experiences of low and high income blacks using a set of fixed-effects models that control for time varying and time-invariant metro attributes as well as changes over time common across all metro areas.³⁸

Data and Methods

I use U.S. Census data from the 1980 Summary Tape Files 3A, the 1990 Summary Tape Files 4A, and the 2000 Summary Tape Files 3A (Geolytics 2004). I impose consistent metropolitan area definitions across census years to ensure the comparability of the results over time. I restrict my sample to the 100 metro areas with the largest populations in 2000; these areas account for 62 percent of the total U.S. population. Following past work looking at neighborhood change over time (Jargowsky 1996; Reardon and Bischoff 2011), I further constrain my sample to only include metro areas in which there were at least 10,000 black families in 1980, 1990, and 2000. This results in a final estimation sample of 93 metro areas.

There are two outcome variables: the average neighborhood proportion black experienced by affluent black families and the average neighborhood proportion black experienced by poor black families. Affluence is measured relative to the income distribution of each metro area, and is defined as twice the metro median family income. Neighborhoods are defined as Census tracts. The three predictors of interest are metro between-race income inequality (BRI), which is measured as a ratio of black median family income to white median family income, metro within-race income inequality (WRI), which is captured by the black Gini index, and the relative size of the black population (BP). Recall the two hypotheses laid out at on pp. 17-18: (1) If offsetting occurs in real neighborhoods, we would expect that, under sufficiently high WRI, an increase in BRI results in a decrease in the neighborhood proportion black experienced among affluent blacks and an increase in the neighborhood proportion black experienced by poor blacks; and (2) the effect of BRI is nonlinear and depends on the relative size of the black population. Taken together, these imply an interaction effect between WRI and BRI, an interaction effect between BRI and BP, and potentially higher order effects of BRI, WRI, and BP.

More formally, I estimate the effect of changes in within- and between-race inequality on changes in the average neighborhood proportion black experienced by affluent or poor blacks as:

$$\begin{array}{cc}\hfill B{P}_{my}^{AFFLUNETIPOOR}=& \sum _{i=1,2}\sum _{j=1,2}{\varsigma }_{ij}WR{I}_{my}^{i}BR{I}_{my}^i\hfill \\ \hfill & +\sum _{i=1,2}\sum _{j=1,2}{\gamma }_{ij}BR{I}_{my}^{i}B{P}_{my}^i\hfill \\ \hfill & +\sum _{i=1,2}{\phi }_{i}WR{I}_{my}^i+\sum _{i=1,2}{\delta }_{i}B{P}_{my}^i+\sum _{i=1,2}{\beta }_{i}BR{I}_{my}^i\hfill \\ \hfill & +{\theta }_m+{\Delta }_y+\vartheta X_{my}+{\epsilon }_{my}\hfill \end{array}$$ (5)

where m indexes metropolitan areas, y indexes Census years, and BP and BRI are as defined above, and the superscripts i and j denote linear and squared terms. The first line of Equation 5 captures the hypothesis that, at sufficiently high levels of WRI, the average proportion black experienced by affluent (poor) blacks will be lower (higher) at higher levels of BRI. The second line captures the hypothesis that the effect of BRI varies nonlinearly with the relative size of the black population. The third line of Equation 5 includes all lower order terms, and the fourth line of the model includes metropolitan area (φ_m) and decade (Δ_y) fixed effects.

The metro fixed effects control for all features of metro areas that are constant over decades; the year fixed effects capture all metro-invariant factors that change over time which might be associated with the neighborhood experiences of whites and blacks. To ensure that my results are not confounded by attributes of metro areas that change over time, the model also includes a set of time-varying covariates (X_my). These include logged population size, unemployment rate, the proportion of the population under 18 years of age, the proportion of the population over 65, proportion the proportion if the population 25 years or older with less than a high school education, the proportion foreign born, and per capital income. Because each metro area contributes three data points, I compute bootstrapped standard errors to take into account the clustered nature of the observations.

Table 5 presents summary statistics for both the outcome measures and the focal covariates. We see that, on average, affluent blacks live in areas with lower concentrations of blacks than do poor blacks. However, blacks at all points in the income spectrum live disproportionately with other blacks, given metro population composition. Over time, the average proportion black experienced by both affluent and poor blacks has decreased. The black Gini index has been increasing over time, and the income gap between blacks and whites has increased slightly since 1980. These findings are consistent with other research documenting trends in racial segregation and income inequality (e.g., Reardon and Bischoff 2011; DeNavas-Walt, Proctor, and Smith 2012).

Table 5.

Average Neighborhood Proportion Black and Between- and Within-Race Income Inequality Trends, 1980-2000

	1980	1990	2000	Change
Ave. Neighborhood Proportion Black for Affluent Blacks	0.455 (0.200)	0.376 (0.188)	0.360 (0.198)	−0.10
Ave. Neighborhood Proportion Black for Poor Blacks	0.554 (0.208)	0.498 (0.211)	0.466 (0.215)	−0.09
Metro Proportion Black (BP)	0.121 (0.086)	0.126 (0.087)	0.139 (0.092)	0.02
Between-Race Income Inequality (BRI)	0.625 (0.071)	0.595 (0.091)	0.605 (0.103)	−0.02
Within-Race Income Inequality (WRI)	0.405 (0.021)	0.425 (0.034)	0.432 (0.029)	0.03
Total Metro Areas	93	93	93

Notes: Between-race income inequality is captured by the ratio of black median income to white median income; within-race income inequality is captured by the black Gini index. Sample includes observations from 100 largest metro areas in 2000, excluding observations from the 7 metro areas that had fewer than 10,000 black families in all three decades.

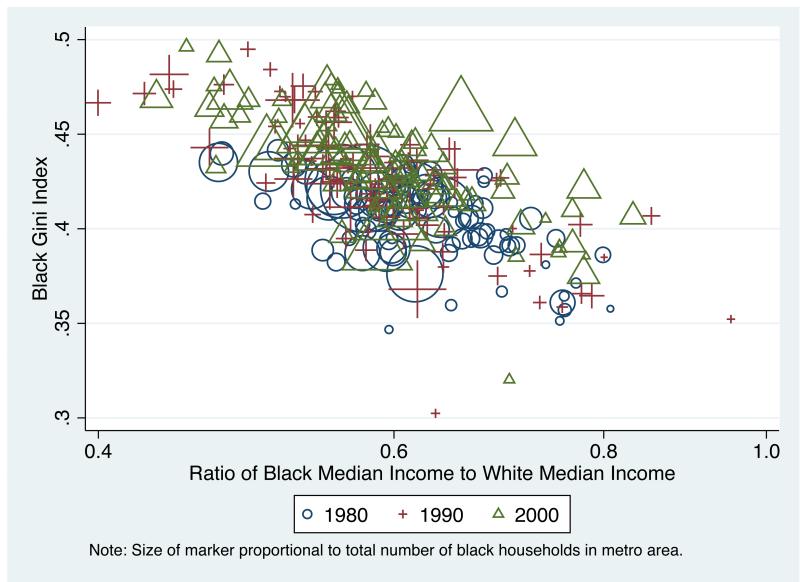
Figure 9 plots the relationship between black-white income inequality, the black Gini index, and the size of the black population for all metro areas across all years. Different markers denote different years, and the size of the marker is proportional to the total number of blacks in the metro area. We see that there is a substantial correlation between black-white income inequality and the black Gini index; areas with high black-white income inequality also have substantial income inequality within the black population. We also see that areas with larger black populations (in absolute value) tend to have greater black-white income inequality. There is only one metro-decade observation where the ratio of black median income to white median income is close to 1.0, El Paso, TX in 1990, which has a very small black population.

Figure 9. Relationship Between Gini Index (WRI) and Ratio of Black Median Income to White Median Income (BRI) [markers scaled to total size of population].

Results

I estimate regression models using mean-deviated transformations of the covariates. Inspection of the data revealed no evidence of higher order effects of within-race income inequality (the black Gini coefficient), so these parameters are omitted from the analysis. Table 6 reports the final model. The first two columns of the table present results where the outcome variable is the average neighborhood experience of affluent blacks, while the second two columns of the table present results where the outcome variable is the average neighborhood experience of poor blacks. Model 1 reports results using only metro and year fixed effects, while Model 2 reports results using both the metro and year fixed effects, and also the time-varying metro variables. Because of the fixed effects, the coefficients capture the average within-metro association over time between the focal attributes and the average neighborhood proportion black experienced by affluent or poor blacks.

Table 6.

Estimated Effect of Between- and Wiithin-Race Income Inequality on Average Neighborhood Proportion Black

	Outcome Variable
	Average Neighborhood Prop. Black Experience by Affluent Blacks		Ave. Neighborhood Prop. Black Experience by Poor Blacks
	Model 1	Model 2	Model 1	Model 2
BRI	0.236 (0.198)	0.435* (0.245)	−0.334** (0.153)	−0.099 (0.158)
BRI2	5.205*** (1.255)	4.458** (1.526)	0.561 (0.823)	0.586 (0.840)
BP	1.201 ( 1.058)	1.482* (0.889)	1.317** (0.572)	1.236** (0.445)
BP2	−3.415* (1.973)	−1.197 (2.123)	0.858 (1.321)	0.359 (1.898)
BRI*BP	−0.394 (1.935)	−0.233 (1.766)	−0.973 (2.297)	0.839 (1.634)
BRI*BP2	−67.591** (21.567)	−44.231* (19.393)	−11.468 (18.462)	−13.465 (18.813)
BRI2*BP	10.227 (11.876)	12.189 (13.953)	−6.535 (12.302)	−3.812 (11.538)
BRI2*BP2	−387.490*** (105.547)	311.780*** (93.497)	−46.249 (69.733)	−32.040 (85.336)
WRI	−.470 (0.522)	0.235 (0.518)	−1.037** (0.401)	−0.863*** (0.253)
Year = 1990	−0.097*** (0.013)	−0.103* (0.043)	−0.053*** (0.006)	−0.085** (0.026)
Year = 2000	−0.115** (0.020)	−0.099 (0.064)	−0.095*** (0.012)	−0.138** (0.041)
Intercept	0.431*** (0.021)	3.171** (1.059)	0.535*** (0.020)	2.095** (0.779)
Model Specification
Metro & Year Fixed Effects	X	X	X	X
Metro-Year Covariates		X		X
Adjusted R2	0.942	0.964	0.968	0.976
N	279	279	279	279

Notes: Variables specificied as deviations from mean values. Bootstrapped standard errors in parentheses.

^*p<.05

^**p<.01

^***p<.001.

Sample includes observations from 100 largest metro areas in 2000, excluding observations from the 7 metro areas that had fewer than 10,000 black families in all three decades. Coefficients on time-varying metro covariates and fixed effects not shown. Metro-year covariates include city proportion black, racial diversity, metro population size, unemployment rate, proportion under age 18, proportion over age 65, proportion with a high school diploma, proportion foreign born, and per capita income.

Looking at the first panel of results, we see that there is strong evidence of a nonlinear, positive association between black-white income inequality and the average proportion black experienced by affluent blacks. The statistically significant coefficients for interactions between black-white income inequality and metro proportion black also support the second hypothesis: that the relationship between black-white income inequality and the average neighborhood proportion black experienced by affluent blacks depends on the relative size of the black population. The quadratic effect of metro proportion black is also statistically significant, implying that all else equal, a larger black metro population is associated with a greater average proportion black experienced by affluent blacks. Note that none of the variables associated with within-race income inequality are statistically significant.

The second panel reports results where the average neighborhood proportion black experienced by poor blacks is the outcome variable. Here we see a weak negative relationship between black-white income inequality and the average neighborhood proportion black experienced by poor blacks; this effect becomes statistically insignificant once I control for the time-varying metro covariates. There is no strong evidence that the effect of income inequality on the average proportion black experienced by poor blacks depends on the relative size of the black population. However, the main effect of metro black proportion black is positive and statistically significant; poor blacks experience a higher number of black neighbors in areas with larger black populations. Unlike the case for affluent blacks, the measure of within-race income inequality is statistically significant. Higher levels of black income inequality are associated with lower average neighborhood proportion black for poor blacks.

Because of the transformations, interactions, and higher order effects, it is difficult to grasp the substantive implications of the numbers reported in Table 6. Figure 10 graphically illustrates the relationship between black-white income inequality and the neighborhood experiences of poor and affluent blacks, assuming the metro percentage black is 1%, 5%, 10%, or 20%. The lines are drawn using coefficients from Model 2 (which controls for time-varying metro characteristics); all other variables are held constant at their mean values. Looking at the top panel, we see clearly the nonlinear and interactive relationship between black-white income inequality, black population size, and the average neighborhood proportion black experienced by affluent blacks. At very high levels of black-white income inequality, a decrease in black-white income inequality results in a decrease in the average proportion black experienced by affluent blacks. However, at lower levels of black-white income inequality, a decline in black-white income inequality results in an increase in the average proportion black experienced by affluent blacks, except in the case where the black population is very small (1 percent of the total population). This increase is more pronounced when blacks are greater than 10 percent of the metro population. In contrast, looking at the bottom panel, we see that a decrease in the level of black-white income inequality results in a corresponding decrease in the average proportion black experienced by poor blacks.

Figure 10. Predicted Relationship between Between-Race Income Inequality and Neighborhood Composition by Metro Percent Black, U.S. Census Data 1980-2000.

Overall, the results suggest that offsetting occurs in real populations when the black population is sufficiently large relative to the rest of the metro population, and when black-white income inequality is not too extreme. Recall that the average metro percentage black in the top 100 metro areas is around 12 percent, sufficiently large to lead to the offsetting effect.

6. CONCLUSION

People are separated in many contexts, and within each context along multiple social attributes. Friendship networks are typically composed of people who share the same aspirations, family backgrounds, race, and education (Marsden 1987; Fischer 1982; Moody 1999, 2001). Within neighborhoods, we observe clustering by age, income, race, ethnicity, political affiliation, and sexual orientation (Massey and Denton 1988; Bishop 2008). Marriages and families bring together individuals with similar religion, education, age, and social class background (Kalmijn 1998; Schwartz and Mare 2005). Sociologists have a longstanding interest in the degree to which status attributes are correlated within individuals and across social contexts. To the extent that the same social dimensions characterize separation across multiple contexts, and to the extent that key social attributes tend to be highly correlated among individuals, their effects will reinforce one another and consolidate group differences (Lenski 1954; Blau 1977; Blau and Schwartz 1997; Simmel 1908).

There are three potential pathways through which social differentiation along multiple attributes can occur. First, people may evaluate others based on only one attribute, but that attribute is correlated with another characteristics that affect group composition. For example, the 1990s ban on affirmative action in college admissions in Texas and California state schools meant an elimination of race-based consideration. But since race and SAT scores are highly correlated, the end result was a significant drop in admission rates for blacks and Hispanics. Second, people may care about multiple, uncorrelated group characteristics. For example, children tend to choose friends who resemble them based on race/ethnicity and sex. The result is that friendship networks are segregated by both race and gender, but these reflect separate sorting processes. Third, people may care about multiple, correlated group characteristics. For example, individuals care about both the racial and economic composition of their neighborhoods and race and income are correlated attributes of individuals. Whites and Asians are, on average, wealthier than blacks and Hispanics. In this case, there is residential segregation by both race and income, and the processes that govern segregation by race and segregation by income are interrelated. The extent to which sorting along one dimension magnifies or attenuates inequalities along other dimensions depends on the joint distribution of relevant traits within a population.

This study focuses on the segregation patterns that result from people sorting on multiple, correlated attributes. I propose an analytical framework that explicates the role of between- and within-race income inequality on racial segregation dynamics. The focal mechanism is offsetting: under sufficiently high levels of within-race income heterogeneity, increasing between-race income inequality can have opposite effects at the high and low ends of the income distribution. The effect is nonlinear and depends on the relative size of the black population, suggesting some kind of critical mass.

My methodological strategy combines agent-based models with statistical models of residential choice estimated from the PSID to generate empirically grounded simulation experiments. I first use a highly stylized agent-based model consisting of only two race/ethnic groups (blacks and whites) to explore how racial and economic sorting jointly produce segregation outcomes under different assumptions about the relative size of the minority population and the level of income inequality between and within race groups. The goal is to develop intuition for why, when, and how between- and within-group income inequality affects racial segregation. I find that when there is sufficient within-race income inequality, an increase in between-race income inequality increases lower income blacks’ explore to black neighbors but decreases higher income blacks’ exposure to black neighbors. Depending on the size of the minority group and the degree of between- and within-race income inequality, the end result may be substantial decrease in racial segregation or virtually no decrease in racial segregation.

Next, I explore segregation dynamics in an empirically grounded agent based model that assumes that the demographic composition, geography, and the initial population distribution approximate Chicago, Los Angeles, or Atlanta in 2000.³⁹ While this model offers less analytical tractability than the highly stylized model discussed above, it offers more empirical plausibility (e.g., a realistic starting level of segregation and a multiethnic racial context). I compare segregation dynamics under empirical income distributions with segregation outcomes assuming income parity between blacks and whites. The results provide support for the offsetting mechanism; the elimination of black-white income inequality increases higher income blacks’ exposure to black neighbors, and decreases poorer blacks’ exposure to black neighbors. In all three cases, the convergence in income results in a small net decrease in segregation.

Finally, I use 1980-2000 United States Census data to test whether the offsetting mechanism can help explain segregation dynamics in the 100 largest American cities. I estimate metropolitan area level statistical models of how the average proportion black experienced by high and low income blacks changes as a function of between-race income inequality, within-race income inequality, and the relative size of the black population. The models include fixed effects for metro areas and decade, and also control for time-varying features of metro areas. The statistical analysis supports the offsetting mechanism but suggests that it only comes into play at moderate or low levels of black-white income inequality and when the black population is relatively at least 5 percent of the total population.

Taken together, the simulation and empirical analyses support the argument that offsetting is a potentially important and unrecognized mechanism that can attenuate the total change in racial segregation occurring with a convergence in income between blacks and whites. Theoretically, the results provide an analytical account of how the correlation among attributes and relative population size interact with in-group preferences to give rise to aggregate patterns of social separation and integration. I also suggest several key parameters— the size of race/ethnic groups and the degree of between- and within-race income variation— that determine how income inequality shapes overall levels of racial segregation. Methodologically, the analysis lays out an alternative to the conventional strategy for assessing the role of differences in income on racial segregation, one that allows income and racial sorting to be dynamically interdependent.

The Role of Offsetting in Segregation Dynamics

A natural question to ask is: how much should we revise our understanding of the role of economic factors in racial segregation processes in light of this study? The dominant finding in the empirical literature is that economic parity between blacks and whites does not result in a substantial net decrease in segregation, which is often taken as evidence that income inequities among racial groups do not play a critical role in driving patterns of racial segregation. This study suggests that the small effect of income is due to opposing processes that occur at the high and low ends of the income distribution. At moderate to high levels of segregation, higher income blacks often must choose between living among economically similar households and living among racially similar households. As the incomes of blacks reach parity with whites, the decrease in racial isolation experienced by poor blacks is offset by the increase in racial isolation experienced by higher income blacks.⁴⁰ Depending on the level of between- and within-race income inequality and the relative size of the black population, the end result may be a net decrease in racial segregation, a net increase in racial segregation, or no change in racial segregation. The findings from this study suggest that we move beyond the distinctions emphasized by “spatial assimilation” and “place stratification”—which focus our attention primarily on between group differences—and rather consider how both between- and within-race inequality shapes neighborhood formation and change.

The extent to which income inequality affects racial segregation depends on the level of income inequality in the population. A key contribution of this work is to draw attention to the distinct roles of between- and within-race heterogeneity in residential mobility decisions. While there is a large body of work exploring the role of between-race inequality in segregation dynamics, within-race heterogeneity has received far less attention. However, it is well established that the last forty years have been characterized by growing income inequality, and inequality among blacks is growing faster than income inequality among whites (Autor, Katz, and Kearney 2006, 208; Piketty and Saez 2003). This increase has been reflected in residential patterns; income segregation is on the rise overall, and since 1980 income segregation has been greater among blacks than among whites (Reardon and Bischoff 2011). At the same time, the black-white gap in median income has stagnated; it is three percentage points smaller today than it was in 1979 (DeNavas-Walt, Cleveland, and Webster 2003). I have shown that, holding between-race income inequality constant, an increase in within-race income inequality will lead to greater divergence in the residential mobility behavior of high and low income blacks. This suggests that the offsetting mechanism may play a greater role today than in the past.⁴¹

One important consideration, however, is the self-limiting aspect of the offsetting mechanism. When between-race income inequality is high, the average proportion black experienced by higher income blacks may be lower, but there are fewer of these households to offset the higher average proportion black experienced by higher income blacks. Also, in the case of very high between-race inequality, a decrease in between-race inequality will likely produce to a reduced racial isolation for both high and low income blacks. Thus, offsetting is most pronounced at moderate to low levels of between-race inequality. This point was illustrated in Figure 10, which showed that in U.S. metro areas an increase in income parity between blacks and whites only results in greater racial isolation for affluent blacks when the ratio of black median income to white median income is 0.6 or more.⁴²

There is also reason to believe that when blacks move to integrated neighborhoods, these neighborhoods are often unstable and thus any decrease in black exposure produced by residential mobility is temporary as the neighborhood changes around local residents (Sharkey 2012; Quillian 1999). This suggests that the integrative effect of income inequality among higher income blacks is attenuated, as these blacks are moving to areas that are or will be becoming increasingly black. In this case, the total integrative effect of income inequality on the neighborhood experiences of higher income blacks is substantially lower than what it might otherwise be.

The Role of Offsetting in other Contexts

The framework developed for this study can be applied to other cases in which individuals sort themselves into units based on multiple correlated attributes. For example, high school students select friends who resemble them based on race, gender, grade in school, and family background. In a school where minority groups are poorer than whites, a black or Hispanic student coming from a more affluent household must choose between peers who resemble her based on family income and peers who resemble her based on race. Were income disparities between whites and minority groups to be eliminated, this choice would not be necessary. Along these lines, Moody (2001) documents a nonlinear relationship between racial heterogeneity within schools and the odds of having a same race friend. He attributes this to a change in preferences, arguing that as racial heterogeneity in schools increases, the preference for a same-race friend also increases. He notes that the nonlinearity suggests a “critical mass” type relationship where preferences only change once racial diversity in the school crosses a given threshold. An alternative explanation is that preferences remain constant, but the increase in racial heterogeneity leads to a critical number of minority group members who meet friendship criteria along multiple dimensions. The larger the size of the minority group, the lower the level of racial heterogeneity necessary to generate this critical number.⁴³

Sociology has a long tradition of formal analysis investigating how structural factors such as the size and composition of populations constrain what social groupings are possible (e.g., Simmel 1908; Blau 1977; Blau and Schwartz 1984; McPherson 1983; Rytina and Morgan 1982; Wimmer and Lewis 2010). However, there is little knowledge of how this process unfolds dynamically, or how the joint distribution of traits in the population interacts with individuals’ multidimensional preferences to generate macro-level patterns of inequality. Blending agent-based models with empirical analyses provides one potentially fruitful strategy for assessing how population composition interacts with individual behavior to generate population patterns of social separation or integration.

APPENDIX A. PARAMETER ESTIMATES FROM DISCRETE CHOICE MODELS, PANEL STUDY OF INCOME DYNAMICS

Table A1. Coefficients from Discrete Choice Models, Panel Study of Income Dynamics.

Variable	Coefficient Estiamates
	Beta	Std. Error	P-Value
Dij	5.983	0.519	0.000
Racial Factors
%black	−0.421	0.641	0.512
%black2	−3.083	0.652	0.000
black*%black	5.146	0.725	0.000
black*%black2	−0.583	0.721	0.419
Hispanic*%black	0.359	0.891	0.687
Hispanic*%black2	0.223	1.157	0.847
%Hispanic	−2.144	0.906	0.018
%Hispanic2	−0.364	1.145	0.750
Hispanic*%Hispanic	8.121	1.078	0.000
Hispanic*%Hispanic2	−3.704	1.299	0.004
Black*%Hispanic	1.386	1.107	0.211
Black*%Hispanic2	−0.765	1.484	0.606
%Asian	−1.611	0.667	0.016
%Asian2	−1.049	1.548	0.498
Asian*%Asian	14.985	2.602	0.000
Asian*%Asian2	−17.687	4.865	0.000
%white2	−2.242	0.258	0.000
white*%white2	2.010	0.313	0.000
Dij*%black	−3.002	1.226	0.014
Dij*%black2	6.126	1.529	0.000
Dij*black*%black	−1.935	1.055	0.067
Dij*black*%black2	−1.940	1.603	0.226
Dij*Hispanic*%black	4.367	2.219	0.049
Dij*Hispanic*%black2	−2.746	4.274	0.521
Dij*%Hispanic	−1.488	1.572	0.344
Dij*%Hispanic2	2.698	2.460	0.273
Dij*Hispanic*%Hispanic	0.102	1.357	0.940
Dij*Hispanic*%Hispanic2	−1.666	2.488	0.503
Dij*black*%Hispanic	3.036	1.712	0.076
Dij*black*%Hispanic2	−3.160	3.369	0.348
Dij*%Asian	5.805	1.587	0.000
Dij*%Asian2	−10.838	3.816	0.005
Dij*Asian*%Asian	−12.251	5.176	0.018
Dij*Asian*%Asian2	22.061	12.896	0.087
Dij*%white2	0.350	0.534	0.512
Dij*white*%white2	−0.989	0.208	0.000
Economic Factors
IncomeRatio	−1.215	0.121	0.000
IncomeRatio2	0.002	0.000	0.000
Dij*IncomeRatio	0.479	0.124	0.000
Dij*IncomeRatio2	−0.016	0.010	0.123
PriceRatio	2.075	0.693	0.003
PriceRatio2	−4.654	1.092	0.000
Dij*PriceRatio	−3.858	1.370	0.005
Dij*PriceRatio2	5.176	2.021	0.010
MedianIncome	−0.031	0.003	0.000
MedianIncome2	0.000	0.000	0.000
Dij*MedianIncome	0.031	0.005	0.000
Dij*MedianIncome2	0.000	0.000	0.055
N		951719
Log Likelihood		−39308

Note: Observation unit is person-years. IncomeRatio is the ratio of household income to neighborhood median income; PriceRatio is the ratio of the 20th percentile monthly rent in the neighborhood to monthly household income (1/12th of annual income). Median income is in $1,000s.

APPENDIX B. PARAMETERS USED FOR SING-MADDALA DISTRIBUTIONS

The theoretical income distributions used in the stylized agent-based model are generated from the Sing-Maddala statistical distribution. The 3-parameter Singh-Maddala distribution is the 4- parameter generalized beta II distribution with shape parameter p=1. It is also known as the Burr distribution, Pareto IV, beta-P, and generalized log-logistic distribution. See Kleiber and Kotz (2003) for more information. Table B1 shows the parameters used to generate each distribution. I use the rsinmad function in the “sinmad” R statistical package to generate random deviates. Files containing simulated income distributions are available from the author by request.

Table Bl. Hedonic Pricing Equations.

	Atlanta			Los Angeles			Chicago
	Beta	Std. Error	P-value	Beta	Std. Error	P-value	Beta	Std. Error	P-value
% black	0.336	0.015	0.000	−0.533	0.002	0.000	−0.437	0.005	0.000
% Asian	−0.005	0.031	0.876	−0.554	0.003	0.000	−0.628	0.007	0.000
% Hispanic	−0.367	0.014	0.000	−0.037	0.003	0.000	−0.223	0.006	0.000
% black2	−0.475	0.008	0.000	0.426	0.002	0.000	0.156	0.003	0.000
% white2	−0.246	0.009	0.000	−0.456	0.002	0.000	−0.127	0.004	0.000
% Hispanic2	0.327	0.020	0.000	−0.238	0.002	0.000	−0.144	0.004	0.000
% Asian2	−1.887	0.192	0.000	0.504	0.003	0.000	0.387	0.010	0.000
Median Income (in 1000s)	0.022	0.000	0.000	0.027	0.021	0.000	0.020	0.000	0.000
Median Income2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Constant	5.815	0.008	0.000	6.128	0.001	0.000	6.028	0.003	0.000
N =		251,445			2,445,250			1,319,150
R2 =		0.914			0.882			0.772

Note: Estimated from 2000 Census STF3A data. Outcome is logged median neighborhood monthly housing costs. Units are neighborhoods ( Census tracts), weighted by the total number of households living in the area.

APPENDIX C. HEDONIC PRICING MODELS

Housing prices in the agent-based model are updated based on estimates from a hedonic pricing model. This model was estimated from Census 2000 Summary Tape Files 3A for Los Angeles, CA and Atlanta, GA. The coefficients are shown in table C1.

Table C1. Parameters used to Gererate Income Distributions for Hypothetical Populations.

Gini Index	Median Income	Parameters
		a	q	scale
0.15	$63,331	1.05	3.51	270000
	$40,855	1.05	3.51	175000
	$26,960	1.05	3.51	117000
0.35	$64,500	1.80	3.51	150000
	$40,854	1.80	3.51	95000
	$27,411	1.80	3.51	64000
0.55	$63,256	4.80	3.51	87000
	$41,321	4.80	3.51	56000
	$27,643	4.80	3.51	37000
0.75	$63,256	4.80	3.51	87000
	$41,321	4.80	3.51	56000
	$27,643	4.80	3.51	37000

Note: These income distributions were generated using the R package VGAM, which contains the function

APPENDIX D. TECHNICAL DETAILS FOR GEOGRAPHICALLY AND DEMOGRAPHICALLY GROUNDED AGENT-BASED MODEL OF SEGREGATION DYNAMICS

This appendix describes some of the technical details of the model implementation for the empirically grounded agent-based model discussed in Section 4. The model is written in Java and uses the REPAST (http://repast.sourceforge.net/) and JUMP (http://www.vividsolutions.com/jump/) libraries. I use Unified Modeling Language (UML) diagrams to graphically representing the object oriented programing code. UML lays out a set of well-defined and standardized schematics—independent of any specific programming language—for representing the underlying logic of a model. This technique has become the gold standard for describing object oriented programming code (Fowler 2003), and there has recently been a call for agent-based modelers to incorporate these diagrams into documentation and publications (Bersini 2012). The two UML diagrams I make use of below are Class diagrams (which describe the variables and methods contained within a given module of the program) and Sequence diagrams (which describe how different aspects of the model interact). More detailed discussion of the basic architecture of agent-based models can be found in Macal and North (2010).

The model consists of 12 main classes. Figure D1 shows the overall class structure of the model. Note that each class denotes a particular type of agent, each with its own attributes (variables) and things that it does (methods). The main class, Mirar (“Model of Income, Race, And Residence”), controls the overall sequence of actions executed by the model. It contains the functions that both set up the initial physical environment and populate it with agents. This class also executes a series of commands to sample and move agents in each time step. The MirarUtils class contains all the small helper functions used within the model. For example, all the random distributions (multinomial, binomial) used within various parts of the model are managed within this class. The Block, BlockGroup, and CensusTract classes generate the different levels of geography. Blocks are nested within block groups, which are nested within tracts. Several classes exist solely to manage different components of the model. For example, the AgentHandler class contains commands that gather, sort, and sample from the population of agents while the CensusUnitHandler class manages interactions among the Census tracts, block groups, and blocks. This class also computes all segregation measures used in the model. The JumpHandler class contains commands to manage the spatial information (GIS) used in the model, and to generate a display of the agents distributed across the urban landscape. The Mediator class manages interactions between Census units, geographic relationship among Census units, and agents. Thus, for example, when agents want to get information about the neighborhood associated with their current housing unit or other potential destinations, these requests are handled through the Mediator. Finally, the AgentDecision class holds the PSID coefficients used to calculate utility. This class also contains all the functions used to compute various dimensions of neighborhood composition (e.g., neighborhood proportions black, white, Asian, and Hispanic).

Figure D2 shows selected variables and methods for the Agent and AgentDecision classes. Each agent has a unique race, income, and place of residence (HousingUnit). Agents are also assigned a memory, which records all housing units that agent has lived in over the course of the simulation. To calculate the desirability of their current unit and all potential destination units, agents are assigned an AgentDecision. The program was designed such that, in theory, each agent could have a unique decision rule. The variables held by the AgentDecision include the agent to which it is associated as well as a matrix of coefficients used in the calculation of utility. For the results reported in this study, these coefficients come from the Panel Study of Income Dynamics. The AgentDecision class uses attributes of its associated agent to plug in the appropriate race and income attributes for calculating utility values.

Figure D3 shows how various pieces of the agent-based model interact for a given mobility decision. The Mediator class samples a subset of agents, and gives each one an opportunity to move. Each agent makes a call to its associated AgentDecision, which in turn asks the HousingUnit and Blocks associated with each potential destination to provide information about their neighborhood racial and economic composition. This information is used to calculate utilities associated with the current housing unit and all potential destinations. The AgentDecision class then passes those utilities to the MirarUtils class, which turns them into probabilities (by dividing by the sum of the utilities) and samples one unit based on those probabilities. The MirarUtils class returns the chosen unit to the AgentDecision class, which in turn passes it back to the Agent.

Figure D1.

Figure D2.

Figure D3.