Effects of environmental levels of cadmium, lead and mercury on human renal function evaluated by structural equation modeling

Abstract

A relationship between exposure to heavy metals, including lead and cadmium, and renal dysfunction has long been suggested. However, modeling of the potential additive, or synergistic, impact of metals on renal dysfunction has proven to be challenging. In these studies, we used structural equation modeling (SEM), to investigate the relationship between heavy metal burden (serum and urine levels of lead, cadmium and mercury) and renal function using data from the NHANES database. We were able to generate a model with goodness of fit indices consistent with a well-fitting model. This model demonstrated that lead and cadmium had a negative relationship with renal function, while mercury did not contribute to renal dysfunction. Interestingly, a linear relationship between lead and loss of renal function was observed, while the maximal impact of cadmium occurred at or above serum cadmium levels of 0.8 µg/L. The interaction of lead and cadmium in loss of renal function was also observed in the model. These data highlight the use of SEM to model interaction between environmental contaminants and pathophysiology, which has important implications in mechanistic and regulatory toxicology.

Introduction

Lead (Pb), cadmium (Cd) and mercury (Hg) are known to be nephrotoxic at high levels (Gonick 2008; Sommar et al. 2013). Additive or synergistic interactions among heavy metals such that toxic effects may result even at low levels following environmental exposure (Fadrowski et al. 2010; Wallin et al. 2013; Weaver et al. 2011a). With few exceptions (Navas-Acien et al. 2009; Sanchez et al. 2001; Shelley et al. 2012), most studies have examined the effects of each metal in isolation. In this study, we have constructed a structural equation model (SEM) to identify and quantify the effects of lead, cadmium and mercury in a random subsample subjects participating in the National Health and Nutrition Examination Survey.

In structural equation modeling (SEM), a hypothesized model of relationships between variables is designed and then evaluated to determine if the experimental data supports that model. SEM has two key features: the measurement model, which defines the relationships between measurable variables and non-measurable latent factors, and the structural model, which delineates the path links and coefficients between and among the latent variables (Collin et al., 2009). As a modeling technique SEM has several advantages in that it allows for the modeling of complex, multivariate processes beyond simple correlations among single sets of variables; it is not limited by measurable variables, but it allows for the inclusion of latent factors, i.e., factors that cannot be measured or observed on their own, but that can be expressed by measurable variables (Kline, 1991). SEM is also able to accurately measure unreliable events because it can quantify an error measurement that is indicative of errors including as biological variance. Most data sets are imperfect and more common modeling techniques, such as multiple regression and observed variable path analyses, cannot account for these flaws; however SEM compensates for these issues (Kline, 1991).

Although SEM has been utilized in the fields of sociology and psychology for many years, it is underutilized in the biological sciences. However, our group (Gardiner et al., 2012) and others (Fisher et al., 2011) have used SEM to model chronic kidney disease (CKD), which has complicated pathophysiology involving a number of factors. Given the complexity of assessing the relationship between environmental exposures and CKD, SEM is a valuable tool to begin to assess the relationship between heavy metals and renal dysfunction.

Methods

Study Population

Demographic, laboratory and examination variables were obtained from 5 consecutive 2-year cycles of the National Health and Nutrition Examination Survey (continuous NHANES), which are made available online for public use by the Centers for Disease Control (Centers for Disease Control and Prevention 1999–2008). Because subjects are identified by sequence number only, no special permissions are required to access the data. Of the 51,653 subjects that were both interviewed and examined from 1999–2008, 30,257 had simultaneous entries for serum lead, serum cadmium and serum (total) mercury; 8,847 had entries for detectable levels of urine lead, urine cadmium and urine mercury. Blood metal measures were available on all but 551 of the subjects with urine metal values. Individuals missing one or more measures of kidney function were excluded from this set, which left n = 7,236 subjects for analysis. Demographic and other relevant characteristics of the study population are listed in Table 1.

Table 1.

Demographics and related characteristics of the subjects

Age
Mean (yrs)		40.99 ± 0.40a
Distribution
0–5 yrs		0%
6–11 yrs		0%
12–19 yrs		12.3%
20–39 yrs		37.0%
40–59 yrs		34.0%
60+		16.6%
Race/Ethnicity
Mexican American		8.6%
Other Hispanic		4.9%
NonHispanic White		70.3%
NonHispanic Black		11.5%
Other Races		4.7%
Sex
Male		41.0%
Female		59.0%
Kidney Status
GFR ≥ 60 ml/min/1.73 m2		94.6%
GFR < 59 ml/min/1.73 m2		5.4%
Macroalbuminuria
Absent (ACR ˂ 300 mg/g)		99.0%
Present (ACR ≥ 300 mg/g)		1.0%
Body Measures
BMI (kg/m2)		27.71 ± 0.14 a
Waist Circumference (cm)		94.60 ± 0.39 a
Weight (kg)		78.36 ± 0.46 a

^a=mean±linearized SEM

Data Preparation

Because of changes in assay methods, serum creatinine values for the 1999–2000 and 2005–2006 data sets had to be adjusted to ensure comparability with standard creatinine (Selvin et al. 2007). Creatinine clearance was calculated from the corrected serum creatinine values using the Cockcroft-Gault formula (Cockcroft and Gault 1976). Albuminuria was calculated as the ratio of urine albumin to urine creatinine (ACR) expressed in units of mg/g. Limits of detection for blood and urine metals varied slightly across the survey cycles. In those subjects where the result was below the limit of detection, a concentration equal to the limit of detection divided by the square root of two was used (Centers for Disease Control and Prevention 2007–2008; Centers for Disease Control and Prevention 2009; Centers for Disease Control and Prevention 2013). Metal concentration data that contain values below a lower detection limit are referred to as left-censored or censored from below. Excluding metal concentrations below the limit of detection (LOD) is not recommended, as it not only reduces the sample size but also yields upwardly biased results (Hornung and Reed 1990). A number of methods have been proposed for handling values falling below the LOD (Helsel, 2010). A fraction of the LOD (e.g. LOD/2 or LOD/√2) is often substituted for the problem values in regression modeling. Metal concentrations falling below the LOD in NHANES surveys are pre-transformed by substitution with LOD/√2 prior to publishing, and have been used in this format by investigators working with NHANES data (Navas-Acien et al. 2009; Shelley et al. 2012). The bias is small if the percentage of data below the LOD is small and the data are not highly skewed (Baccarelli et al., 2005).

Given recent concerns over the use of data substitution, we investigated an alternate method for handling the problem: multiple imputation. Model-based multiple imputation is an alternative to substitution for left-censored data (Baccarelli et al. 2005; He et al., 2010). To examine the effect of multiple imputation in this study, each metal concentration below the LOD was first replaced by a missing value code. Then, for each missing value, 20 new values were generated using Markov Chain Monte Carlo (MCMC) simulations, to create 20 complete data sets containing no missing values (Rubin, 1987; Shafer, 1997). These data sets were then used as the basis for imputation by Bayesian estimation of the SEM model in MPlus. Briefly, the SEM model was run for each of the 20 complete data sets, and combined by the MPlus program into a single set of results that incorporated uncertainty due to the missing data. An assumption of multiple imputation is that the data are missing at random. To the extent that metal values falling below the LOD may not comply with this assumption, some bias is expected. There was no substantial difference in structure, coefficients or fit indices between the model derived from multiple imputation and that derived using LOD/√2 substitution (data not shown). This suggests that for this data set, the SEM model is robust to changes in the method of handling metal concentrations falling below the limit of detection.

All continuous variables were tested for normality prior to analysis. The Jarque-Berra statistic (Jarque and Bera 1980) provides a sensitive index of both skewness and kurtosis and was used to evaluate the need for transformation. Based on this metric, all 10 observed variables used in the model were found to require log-transformation prior to analysis. We tested for possible multicollinearity among the transformed measures by computing variance inflation factors (VIF): these were found to be negligible (VIF range: 1.06 – 2.23, mean = 1.77). When two or more predictor variables in a statistical model are highly correlated, it becomes difficult to statistically determine which variable has the most impact on the predicted result. The variables are collinear, and the results show what is termed multicollinearity. Multicollinearity increases the variance (standard errors) of the model coefficients and can cause what should be significant predictors to be considered non-significant. Variance inflation factors measure how much the variance of the estimated coefficients are increased over what they would be in the absence of correlations among the preditor variables. There is no formal cutoff for the upper limit of acceptable VIF values; however values above 5 are a usually a cause of concern and values of 10 are a definite indicator of extreme multicollinearity (Kutner et al., 2004)

NHANES guidelines recommend using weights corresponding to the smallest subpopulation containing any of the variables of interest. Metals in urine were generally measured in a random 1/3^rd subsample of the participants; therefore these subsample weights were used for constructing combined 10-year sample weights across survey cycles.

Data Analysis

Development and testing of the structural equation model was performed with MPlus software (version 6.11, Muthén and Muthén; www.StatModel.com). Data were imported from an ASCII file in free format, with each row representing a subject and each column a variable. In addition to the 10 observed variables, the data contained stratification, cluster (PSU), and sample weight variables as required for analysis of complex survey designs. Sample correlation and covariance matrices for the data are provided in Table 2. The default estimation method in MPlus for survey data is a maximum likelihood estimator (MLR) that results in parameter estimates and standard errors that are robust to non-normality and non-independence of observations when used with complex data types. Stata for Windows (version 13, StataCorp LP; www.stata.com) was used for constructing the diagram of the model solution. Statistical analysis of path effects and predicted latent factor scores were computed with Stata’s nlcom and predict, latent postestimation commands, respectively.

Table 2.

Sample correlation and covariance matrices for the structural equation model of Figure 1.

Correlations
	ACR	BUN	CrCl	SCd	SCr	SHg	SPb	UCd	UHg	UPb
ACR	1.0000
BUN	0.0572	1.0000
CrCl	−0.1344	−0.3738	1.0000
SCd	0.0833	−0.0175	−0.1929	1.0000
SCr	−0.0178	0.4303	−0.5616	0.0597	1.0000
SHg	−0.0501	0.1348	−0.0796	−0.0023	0.0427	1.0000
SPb	0.0219	0.1915	−0.3219	0.3521	0.2874	0.1413	1.0000
UCd	0.0981	0.1040	−0.1801	0.4332	0.1041	0.0585	0.2938	1.0000
UHg	−0.0714	0.0625	0.0431	−0.0401	−0.0217	0.4625	−0.0157	0.3803	1.0000
UPb	0.0052	0.0849	−0.0318	0.1470	0.0708	0.0523	0.5116	0.5581	0.3675	1.0000
Covariances
	ACR	BUN	CrCl	SCd	SCr	SHg	SPb	UCd	UHg	UPb
ACR	0.9994
BUN	0.0212	0.1370
CrCl	−0.0532	−0.0548	0.1566
SCd	0.0668	−0.0052	−0.0612	0.6433
SCr	−0.0047	0.0421	−0.0587	0.0127	0.0699
SHg	−0.0513	0.0511	−0.0323	−0.0019	0.0116	1.0486
SPb	0.0143	0.0462	−0.0830	0.1840	0.0495	0.0943	0.4246
UCd	0.0654	0.0257	−0.0475	0.2317	0.0183	0.0399	0.1277	0.4447
UHg	−0.0799	0.0259	0.0191	−0.0360	−0.0064	0.5301	−0.0115	0.2838	1.2526
UPb	0.0044	0.0264	−0.0106	0.0992	0.0157	0.0451	0.2803	0.3130	0.3459	0.7072

Results

The Model

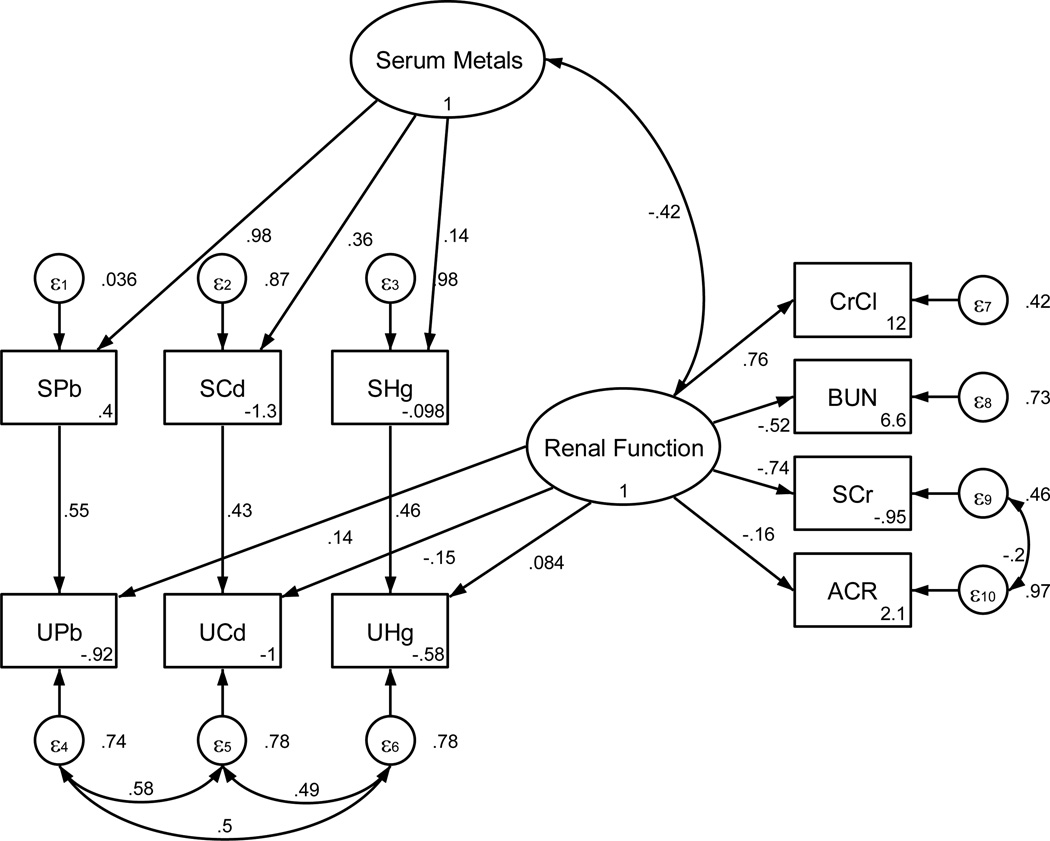
The structural equation model is shown diagrammatically in Figure 1. By convention, latent or unobserved factors are depicted as circles or ovals while the observed or measured variables are shown as rectangles. There are two latent or unobserved factors Renal Function and Serum Metals. Renal Function represents the overall status of kidney function and is measured by four observed variables: creatinine clearance, blood urea nitrogen (BUN), serum creatinine and the ratio of urine albumin to urine creatinine (ACR). Serum Metals is measured by blood levels of Pb, Cd and (total) Hg and, as such, can be considered to represent the combined influence of these metals. The interaction between serum metals and kidney function is depicted by the curved double-headed arrow linking the Serum Metals and Renal Function latent factors. Because the level of kidney function can influence urinary metal excretion, urine levels of Pb, Cd and Hg were allowed to load on (i.e. correlate with) the Renal Function latent factor. This is represented in the model diagram as arrows extending from Renal Function to each urine metal variable. Because the urine concentration of each metal is also dependent upon individual serum concentrations, we added paths between each pair of observed (serum and urine) variables to model the regression of urine concentration upon serum concentration. The overall model therefore contains elements of confirmatory factor analysis (latent factors measured by observed variables) and path analysis (relations among observed variables).

Figure 1.

Structural equation model of the interaction of serum and urine metals on human renal function. Ovals represent unobserved or latent factors. Rectangles represent observed or measured variables. Single arrows represent the direct influence of one variable upon another, while dual-head arrows represent covariance. Standardized path coefficients are indicated by the numbers next to the arrows and represent the correlation or strength of the relationship between factors. Negative coefficients indicate inverse relationships between the variables, while positive coefficients indicate direct positive relationships. Small circles labeled ε₁ – ε₁₀ represent unexplained or residual variance in each observed variable the value of which is listed to their right of each in the diagram. Equation intercepts are listed in the lower right of each rectangle. Correlations between measurement errors of SCr and ACR, as well as among UPb, UCd, and UHg were added during model refinement. Correlations among the measurement errors of all of the urine metal concentrations may indicate that some other common factor, besides serum concentrations or Renal Function, accounts for a portion of their variance. This could occur if another aspect or factor affects their renal elimination but is not adequately measured by the four indices of kidney function included in this model.

All parameter values depicted in Figure 1 correspond to the standardized solution (sem, standardized in Stata; StdYX standardization in MPlus). Standardized path coefficients are similar to beta weights in regression, and are useful for comparing the relative influence or importance among variables, particularly when the scale of measurements varies greatly. For example, an increase of 1 standard deviation (SD) in kidney function would be associated with an increase of 0.76 SD in CrCl, but with decreases in SCr, BUN and ACR of 0.74 SD, 0.52 SD and 0.16 SD, respectively. This suggests that for these data, SCr is a more sensitive indicator of declining renal function than either BUN or ACR.

Small circles labeled ε₁through ε₁₀ represent the residual variance or error associated with the measurement of each observed variable. Values in the lower right corner of each rectangle correspond to intercepts. The general relationship among these parameters may be more clearly understood by inspection of Table 3. Estimation of each observed variable (x_i) in the model follows the general form

• x_i = α_i + Xβ_i + e.x_i

  x_i = α_i + Xβ_i + e.x_i

where α_i is the intercept, X represents the independent or predictor variable, either latent or observed, β_i is the path coefficient or loading, and e.x_i is the residual (error) variance associated with the i^th variable. Except for the urine metals, which are seen to depend on both an observed and latent factor, other observed variables depend only upon a latent factor. The covariances/correlations represented by curved double-headed arrows in the diagram of Figure 1, as well as the other standardized model values and their estimated standard errors are shown in Table 4.

Table 3.

Structural Equations and standardized coefficients corresponding to the path diagram in Figure 1.

Latent Variable	Symbol	Equation
Kidney Function	Renal Function	--
Serum Metals	Serum Metals	--
Observed Variable
Blood Urea Nitrogen	BUN	BUN = 6.6 − Renal Function × 0.52 + 0.73
Creatinine Clearance	CrCl	CrCl = 12 + Renal Function × 0.76 + 0.42
Serum Creatinine	SCr	SCr = −0.95 − Renal Function × 0.74 + 0.46
Serum Cadmium	SCd	SCd = −1.3 + Serum Metals × 0.36 + 0.87
Serum Lead	SPb	SPb = 0.4 + Serum Metals × 0.98 + 0.036
Serum Mercury	SHg	SHg = −0.98 + Serum Metals × 0.14 + 0.98
Urine Albumin / Urine Creatinine	ACR	ACR = 2.1 − Renal Function × 0.16 + 0.97
Urine Cadmium	UCd	UCd = −1.0 + SCd × 0.43 − Renal Function × 0.15 + 0.78
Urine Lead	UPb	UPb = −0.92 + SPb × 0.55 + Renal Function × 0.14 + 0.74
Urine Mercury	UHg	UHg = −0.58 + SHg × 0.46 + Renal Function × 0.084 + 0.78

Table 4.

Parameters and standard errors for the structural equation model of Figure 1

		Std. Estimate	SE	t	P > |t|
Loadings/Effects
SPb ← Serum Metals		0.982	0.047	20.97	< 0.001
SCd ← Serum Metals		0.358	0.019	19.32	< 0.001
SHg ← Serum Metals		0.144	0.017	8.50	< 0.001
CrCl ← Renal Function		0.765	0.012	66.49	< 0.001
BUN ← Renal Function		−0.522	0.017	−30.55	< 0.001
SCr ← Renal Function		−0.737	0.015	−48.29	< 0.001
ACR ← Renal Function		−0.160	0.020	−8.14	< 0.001
UPb ← Renal Function		0.136	0.015	9.10	< 0.001
UCd ← Renal Function		0.146	0.016	−9.10	< 0.001
UHg ← Renal Function		0.084	0.013	6.30	< 0.001
UPb ← SPb		0.551	0.012	44.63	< 0.001
UCd ← SCd		0.426	0.013	32.49	< 0.001
UHg ← SHg		0.462	0.011	43.46	< 0.001
Residual Variances
e.SPb		0.036	0.092
e.SCd		0.872	0.013
e.SHg		0.979	0.005
e.CrCl		0.415	0.018
e.BUN		0.727	0.018
e.SCr		0.458	0.022
e.ACR		0.974	0.006
e.UPb		0.739	0.011
e.UCd		0.779	0.011
e.UHg		0.784	0.010
e.Serum.Metals		1	.
e.Renal.Function		1	.
Covariances
Serum Metals ↔ Renal Function		−0.416	0.025	−16.50	< 0.001
SCr ↔ ACR		−0.203	0.021	−9.90	< 0.001
UPb ↔ UCd		0.579	0.012	48.49	< 0.001
UPb ↔ UHg		0.502	0.011	43.99	< 0.001
UCd ↔ UHg		0.487	0.013	38.24	< 0.001

Available goodness of fit indices (Table 5) are all consistent with a well-fitting model. The CFI or comparative fit index, considered one of the best indices of fit, exceeded the minimum value (0.95) considered acceptable. The SRMR represents the average value across all standardized residuals and can range from 0 to 1; values less than 0.08 characterize well-fitting models. The coefficient of determination, or R², indicates that 99% of the variability in the data is explained by the model. RMSEA values are generally one of the more preferred criteria, and are sensitive to both discrepancy and over-fitting. RMSEA values above 0.10 indicate poor fit, those between 0.08 and 0.10 mediocre fit. Values less than 0.06 are considered to indicate a good fit between the hypothesized model and the observed data (Hu and Bentler, 1999). Other aspects of the RMSEA also point to a highly acceptable fit. The 90% CI is narrow and represents a high degree of precision with an upper bound (0.055) less than 0.06. Finally, P_close, a p value for a one-sided test of the null hypothesis that the RMSEA = 0.05, is non-significant, confirming that this is a well-fitting model.

Table 5.

Model fit indices.

Index	Abbreviation	Value	Criteria for acceptable fit
Comparative Fit Index	CFI	0.951	≥ 0.95
Standardized Root Mean Square Residual	SRMR	0.036	≤ 0.08
Root Mean Square Error of Approximation	RMSEA	0.051	≤ 0.06
90% Confidence Interval around RMSEA	90% CI	0.047–0.055	Upper bound 0.08
P value for H0: RMSEA <= 0.05	PCLOSE	0.328	> 0.05
Coefficient of Determination	CD (R2)	0.990	No set value

Metal effects

The percentile distributions of serum and urine metals, along with the four measures of renal function used in the model are listed in Table 6. As shown, 90% of the 7236 subjects had lead, cadmium and mercury serum levels below 3.2 µg/dL, 1.0 µg/L and 2.8 µg/L; urine concentrations of lead, cadmium and mercury were below 1.8, 0.79, and 2.2 ng/mL in 90% of the subjects. Interactions between variables in the model can be characterized as direct or indirect. Direct effects are quantified by the coefficients associated with the single-headed arrows in the path diagram, such as 0.98 between Serum Metals and SPb, or −0.52 between Renal Function and BUN. Indirect effects represent the influence of a variable mediated by one or more intervening variables. For example, the interaction between SPb and Renal Function is indirect because it is mediated through the Serum Metals factor. The correlation between any two variables in the model diagram can be expressed as the sum of the values (direct plus indirect) of the compound paths linking the two variables. Provided the compound path follows Wright’s rules (Loehlin 2004), the value of the path is the product of the coefficients corresponding to each of the arrows along the path. These correlative effects were computed and are tabulated separately for serum, and urine concentrations, as well as for the net total influence of each metal in Table 7. Lead and cadmium displayed a significant negative relationship with kidney function across the table. Serum mercury had a minor negative influence on Renal Function that was only 1/10^th that of lead and cadmium, while urine mercury exhibited a small positive correlation with kidney function that essentially cancelled any net influence. Comparisons among the average effects in Table 7 indicate that: a) serum lead levels may be 4–5 times more sensitive as indicator of renal toxicity than urine lead levels; b) both serum and urine cadmium appear associated with nephrotoxicity; and c) mercury exhibited no significant adverse effects on the kidney function at the levels of exposure reflected by these serum and urine concentrations.

Table 6.

Percentile distribution of observed variables used in the structural equation model of Figure 1

	Percentile
Measured Variable	10%	25%	50%	75%	90%
Creatinine Clearance (ml/min)	69.8	94.9	125	159	206
Serum Creatinine (mg/dL)	0.52	0.62	0.75	0.92	1.1
BUN (mg/dL)	7.0	9.0	11.0	14.0	18.0
ACR (mg/g)	3.25	4.51	7.07	13.6	37.6
Serum Lead (µg/dL)	0.57	0.80	1.3	2.1	3.2
Serum Cadmium (µg/L)	0.14	0.20	0.30	0.51	1.0
Serum Mercury (µg/L)	0.20	0.40	0.80	1.5	2.8
Urine Lead (ng/mL)	0.23	0.37	0.64	1.1	1.8
Urine Cadmium (ng/mL)	0.06	0.11	0.22	0.45	0.79
Urine Mercury (ng/mL)	0.10	0.21	0.43	0.97	2.2

Table 7.

Standardized effects (± SE) of heavy metals on kidney function for the combined direct plus indirect effect of each metal source. Values and statistical significance were obtained using nonlinear combination of the coefficients along the corresponding path.

Metal			Source
Lead		Serum	Urine	Total
	Std. Effect	−0.408 ± 0.013	−0.089 ± 0.015	−0.498 ± 0.023
	t	−30.32 (P < 0.001)	−6.03 (P < 0.001)	−21.22 (P < 0.001)
Cadmium
	Std. Effect	−0.150 ± 0.015	−0.210 ± 0.016	−0.359 ± 0.024
	t	−10.23 (P < 0.001)	−13.06 (P < 0.001)	−14.70 (P < 0.001)
Mercury
	Std. Effect	−0.0597 ± 0.0088	0.056 ± 0.013	−0.004 ± 0.017
	t	−30.32 (P < 0.001)	4.18 (P < 0.001)	−0.21 (P = 0.836)

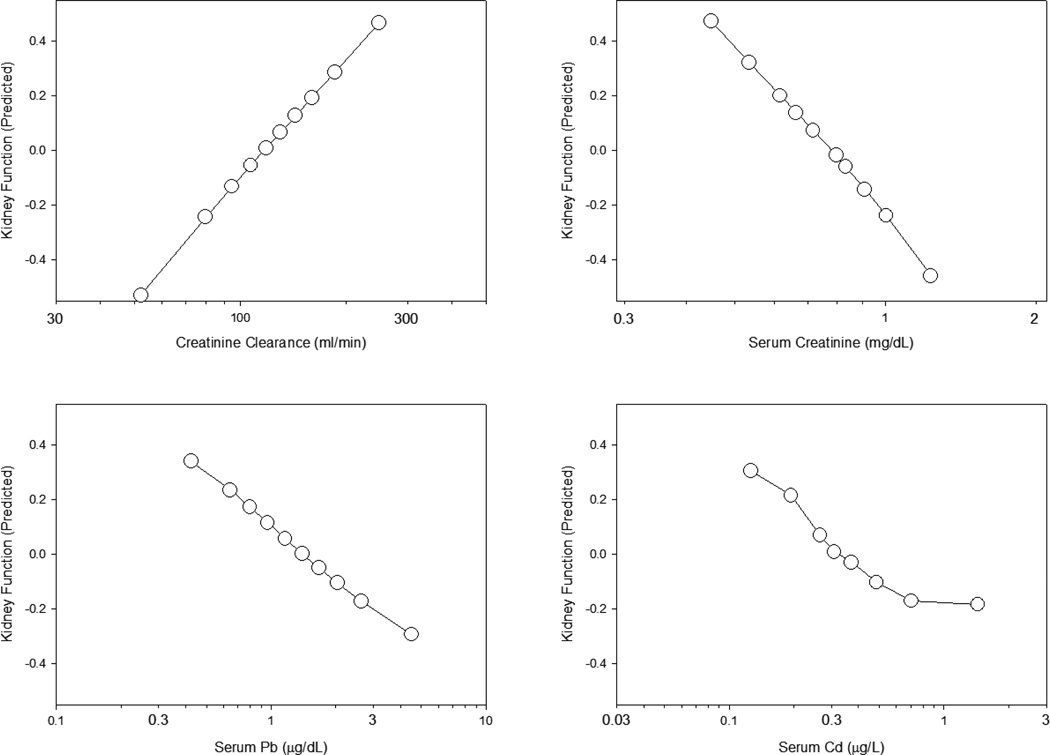
The concentration dependence of these effects is illustrated in Figure 2. For these plots, predicted scores for the Renal Function latent factor were averaged over all subjects at various concentrations of selected observed variables. Latent factors, being unmeasured, have no intrinsic metric scale. Measurement scales may be set during model fitting by fixing the unstandardized loading of one of the observed variables at 1: for the Renal Function latent factor that observed variable was creatinine clearance (CrCl). Values of the latent factor ranged from negative to positive with a mean of 0.

Figure 2.

Concentration-effect relationships for creatinine clearance, serum creatinine, serum lead and serum cadmium on kidney function as predicted from the structural equation model in Figure 1. Each point corresponds the the mean of 678–760 subjects. Vertical and horizontal linearized SE bars are plotted but are masked by the symbols.

Effects of lead and cadmium are depicted in the two lower panels; effects of creatinine clearance and serum creatinine are plotted in the upper panels for comparison. A steady linear decrease in the Renal Function score was observed with increasing log-concentrations of lead, similar to the relationship between Renal Function and log [serum creatinine] seen in the upper right panel. The effect of cadmium, by contrast, appeared sigmoidal in shape, with an apparent maximal decline in Renal Function score occurring at serum cadmium levels above 0.8 µg/L. However, it is difficult to discern the full extent or rate of decline in kidney function, as effects of each metal are averaged across all concentrations of the other.

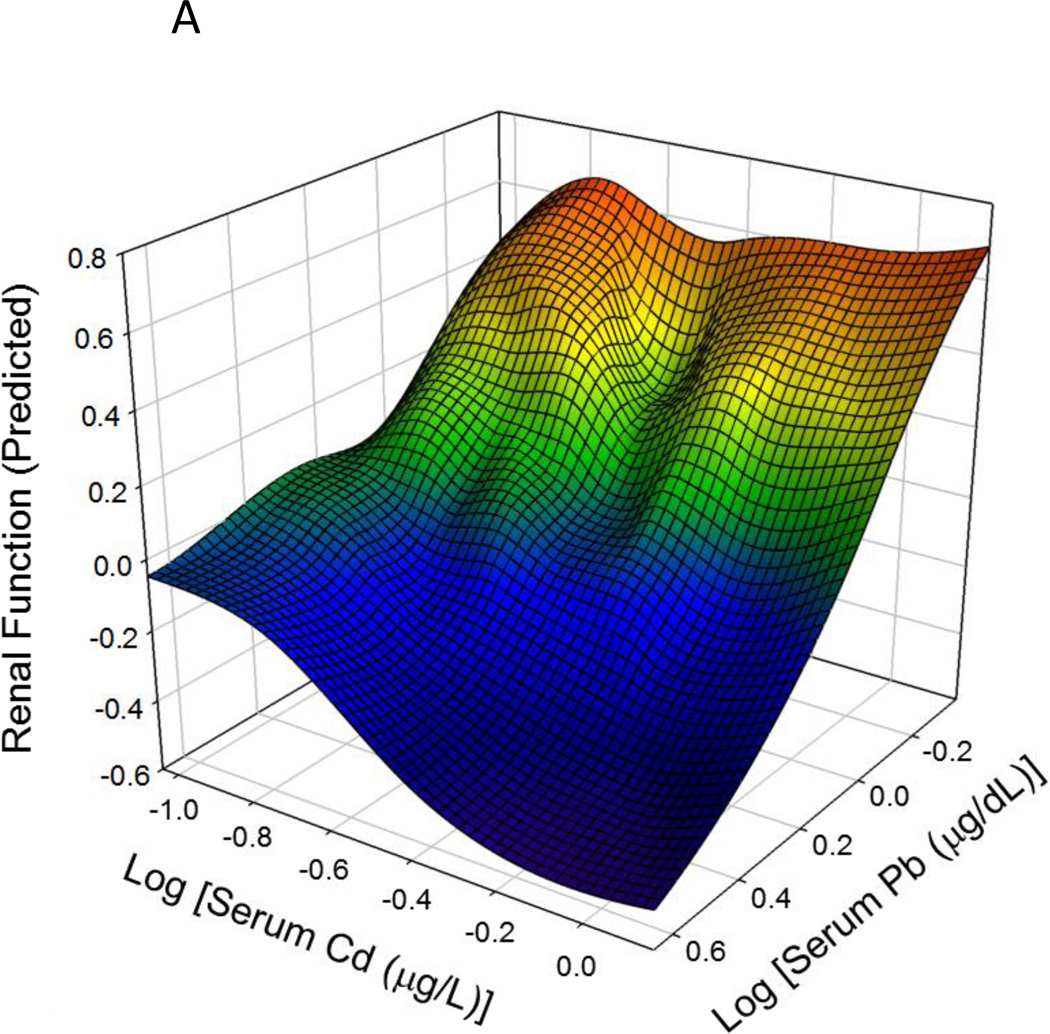
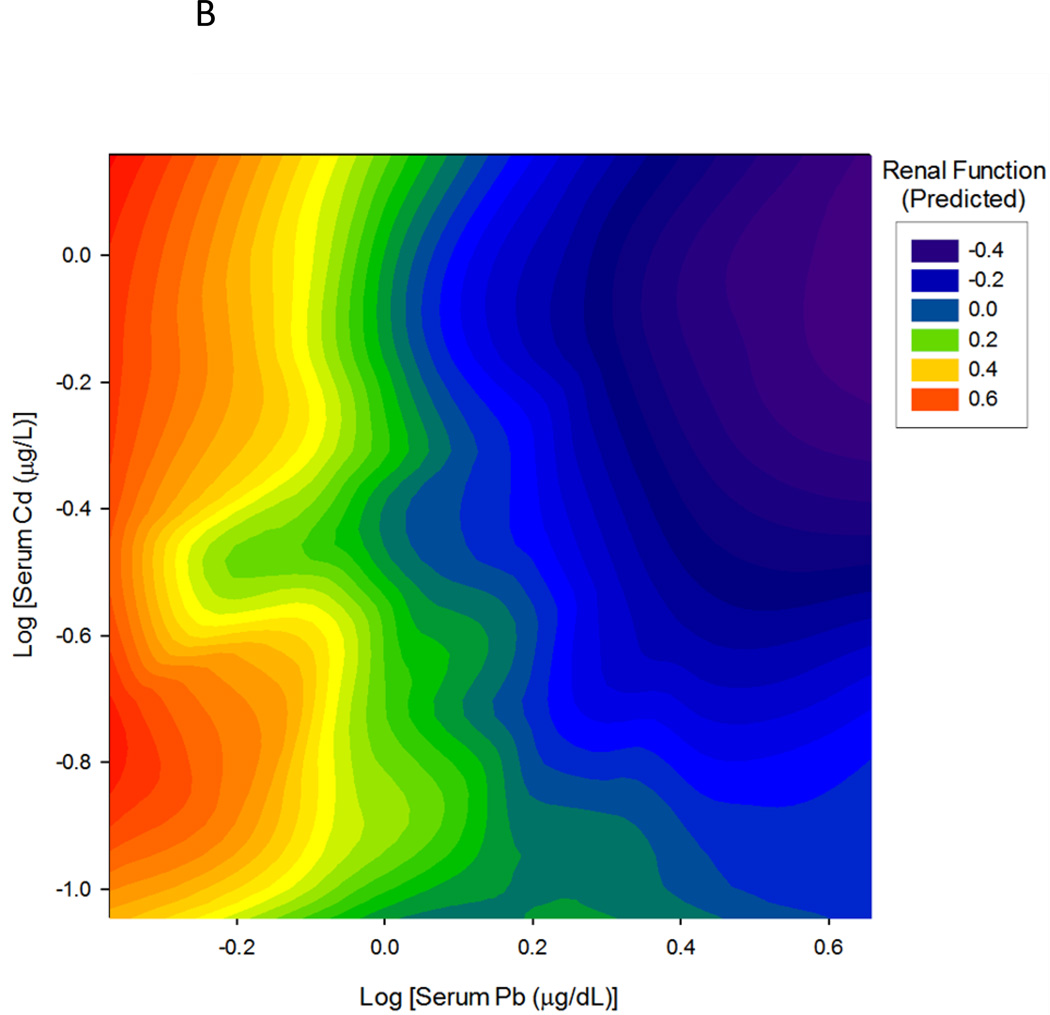
An important property of multivariate statistical models and of structural equation models, in particular, is the ability to quantify the influence of any particular predictor variable independently of the other predictors in the model. This statistical property is often referred to as ceteris paribus, or 'all other things held constant'. In this case, the structural equation model predicts the influence of Pb on renal function at any given concentration of Cd, or the influence of Cd at any concentration of Pb, independently of the effects of each metal, and independently of other influential variables such as CrCl, BUN, ACR etc. We took advantage of the independence of the estimated effects of Pb and Cd to construct the interaction plot shown in Figure 3. The results of the SEM model were used to predict the effect of Pb and Cd on Renal Function over a range of 10 logarithmically-spaced concentrations of each metal, for a total of 100 different combinations of metal serum concentrations (10 Pb × 10 Cd). To avoid extrapolation beyond the observed data, the concentration ranges were chosen to lie entirely within, and span the 10th to 90th percentiles of observed Pb and Cd serum levels. In Figure 3, cadmium concentrations are increasing from left to right while lead concentrations increase from the back toward the front of the page. Values of the Renal Function latent variable increase along the vertical axis and are also indicated by color in the legend box. Comparing the left and right edges of the surface, one may see that the rate and extent of lead effect on Renal Function are greater at high than at low cadmium concentrations; the same is true of cadmium's effect which is greater at high (front) than at low (rear) lead concentrations. Not surprisingly, the lowest values of kidney function are found near the lower right corner of the plot, where both lead and cadmium concentrations are highest. Taken together, the data demonstrate the potential of SEM in assessing the relationship between toxicants and renal function, which is assessed by a battery of variables, rather than a single measure.

Figure 3.

Interaction plot of the effects of lead and cadmium on predicted renal function. Both the rate and extent of decline in estimated renal function score for each metal increase with increasing levels of the other metal. Folds in the surface may be caused by the smoothing algorithm compensating for variations in frequency and sampling of data points across combinations of the metal concentrations.

Discussion

Using data from NHANES 1999–2006, Navas-Acien and colleagues recently demonstrated that low-levels of blood lead and cadmium were independent risk factors for albuminuria and decreased eGFR (Navas-Acien et al. 2009). Through use of structural equation modeling, we were able to both support and extend those findings. Our model overcomes potential limitations imposed by the use of single measures of renal function by employing a latent composite measure of renal function that is derived from measured values of creatinine clearance, BUN, serum creatinine and albuminuria. The structural model was able to not only incorporate the both blood and urine metals, but was able to account for the dependence of urine metal concentrations on both serum metal levels and the degree of renal function. The model was not limited to comparisons between quartiles, but could examine the effect of the metals on renal function across the entire range of measured concentrations. Finally, through use of predicted renal function scores, we were able to illustrate the extent to which combinations of low concentrations of lead and cadmium may interact and augment each other’s nephrotoxic effects.

One of the questions raised in similar studies is whether or not the effects of metals on kidney function are actually reverse causation: that is, changes in kidney function affect serum or urine metal concentrations rather than the opposite. In SEM, as with all statistical measures of association, correlation cannot prove causation. For example, switching the curved double-headed (covariance) arrow between the Serum Metals and Renal Function latent factors to a straight (causal) arrow extending either from Serum Metals to Renal Function or from Renal Function to Serum Metals does not affect the fit indices or the direction or magnitude of any of the path coefficients. Thus, the model itself cannot be used to statistically distinguish cause and effect.

Nevertheless, we do not consider reverse causation a likely explanation. Examination of the direct path coefficients linking Renal Function and urine metal concentrations reveals significant differences in both magnitude and sign that are not explainable by reverse causation. Furthermore, the negative coefficient for the direct path between urine cadmium and Renal Function clearly indicates that increases in kidney function are associated with decreases in urine cadmium concentrations, exactly the opposite of what would occur with reverse causation.

Our finding of a negative association between urine cadmium and kidney function agrees with previous data indicating both blood and urine cadmium were associated with lower creatinine clearance and eGFR in women (Akesson et al. 2005). However a subsequent report found higher urine cadmium levels paradoxically associated with higher creatinine clearance and eGFR values and with lower serum creatinine concentrations (Weaver et al. 2011a). In that study, the ratio of urine cadmium to urine creatinine was used to adjust for urine dilution. Additional investigations using cystatin C based eGFR measures strongly suggested that the positive association of urine cadmium with kidney function may be a statistical effect related to the use of urine creatinine adjustments and serum creatinine based measures of kidney function (Weaver et al. 2011b).

Interestingly, the effect of cadmium on renal function reached a maximal effect at concentrations at or above 0.8 ug/L. Conversely, there was a linear association between lead concentration and decreased renal function. This is consistent with recent studies which have yet to identify a threshold for lead (Bellinger, 2011). The lack of a relationship between mercury and decreased renal function was not surprising, given that this metal is associated with acute, rather than chronic, renal injury (Berlin et al., 2007). An important caveat to this conclusion is that the NHANES study does not differentiate the levels of inorganic mercury, which represents the most nephrotoxic form of the metal (Ratcliffe et al., 1996), but rather measures total mercury. However, other studies have reached similar conclusions (Sommar et al., 2013).

We tested the effect of adjusting urine metal concentrations with urine creatinine in our model and found no change in the direction of correlation between the urine metals and the Renal Function variable. It may be that the composite latent variable is more robust to the effects of the adjustment. Unfortunately these replacements resulted in a negative residual variance between SPb and the Serum Metals factor and a non-positive definite psi matrix, which precluded further model development and testing using these measures. Variations in the urinary excretion of lead, cadmium and other metals in metal workers have been found previously to be statistically similar to the variations in urinary creatinine excretion (Araki and Aono 1989). It may be these similarities in variance that cause problems when modeling the variance-covariance structure of the observed variables.

SEM analysis of the 1999–2008 NHANES data confirms that low-level serum and urine concentrations of lead and cadmium individually are associated with decreases in a composite measure of renal function, and in combination appear to accentuate those functional decreases. In contrast, serum (total mercury) and urine mercury were not associated with significant deficits in kidney function at these levels of exposure.

SEM is a novel method to model multi-variable, biological issues

The impact of cadmium on renal function was sigmoidal

The impact of lead on renal function was linear

List of Abbreviations Used

ACR

urine albumin – urine creatinine ratio

BUN

blood urea nitrogen

CD

coefficient of determination

Cd

cadmium

CFI

comparative fit index

CrCl

creatinine clearance

eGFR

estimated glomerular filtration rate

Hg

mercury

H₀

null hypothesis

NHANES

national health and nutrition examination survey

Pb

lead

P_close

p-value for null hypothesis that RMSEA is ≤ 0.05

PSU

primary sampling unit

SCr

serum creatinine concentration

SD

standard deviation

SE

standard error

SEM

structural equation model

SHg

(total) serum mercury concentration

SPb

serum lead concentration

UCr

urine creatinine concentration

UHg

urine mercury concentration

UPb

urine lead concentration

VIF

variance inflation factor