Homogeneity tests of clustered diagnostic markers with applications to the BioCycle Study

Abstract

Diagnostic trials often require the use of a homogeneity test among several markers. Such a test may be necessary to determine the power both during the design phase and in the initial analysis stage. However, no formal method is available for the power and sample size calculation when the number of markers is greater than two and marker measurements are clustered in subjects. This article presents two procedures for testing the accuracy among clustered diagnostic markers. The first procedure is a test of homogeneity among continuous markers based on a global null hypothesis of the same accuracy. The result under the alternative provides the explicit distribution for the power and sample size calculation. The second procedure is a simultaneous pairwise comparison test based on weighted areas under the receiver operating characteristic curves. This test is particularly useful if a global difference among markers is found by the homogeneity test. We apply our procedures to the BioCycle Study designed to assess and compare the accuracy of hormone and oxidative stress markers in distinguishing women with ovulatory menstrual cycles from those without.

1. Introduction

Diagnostic trials are often carried out to test and compare the diagnostic accuracy of markers. Elegant methods have been proposed to combine markers after the trials are finished (see, for example, [1, 2]). However, these methods may not be applicable when the investigators try to determine the power during the design phase and in the initial analysis stage. A homogeneity test offers a better alternative. When more than two markers are measured on the same set of diseased and non-diseased subjects, how to appropriately obtain the test statistic and its variance becomes challenging.

The BioCycle Study [3, 4] is a longitudinal study conducted at the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the National Institutes of Health. One of the primary objectives of the study is to assess and compare the accuracy of endogenous hormones (i.e., estrogen and progesterone) and oxidative stress markers during the menstrual cycle in distinguishing women with ovulatory menstrual cycles from those without. This helps further the understanding of the implications of oxidative stress in the risk of human infertility and the mechanisms by which oxidative stress may be associated with female infertility. The study enrolled healthy premenopausal women and measured both oxidative stress markers and endogenous hormones in serum on multiple days [3].

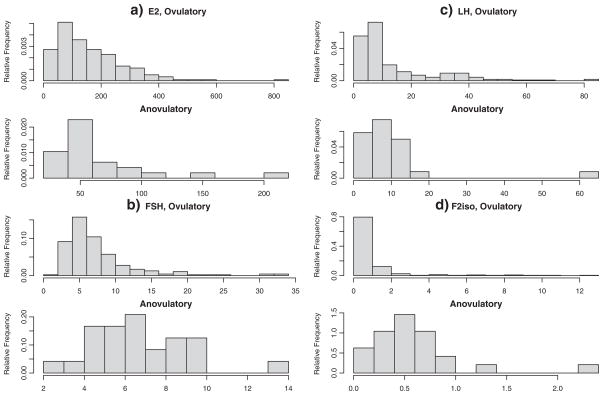
In this study, we initially classified menstrual cycles as anovulatory if the peak progesterone concentration across the cycle was <5 ng/mL. To minimize misclassification, we employed a more conservative definition of anovulation in which cycles with progesterone concentrations ≤5 ng/mL and an observed serum luteinizing hormone (LH) peak in the mid or late luteal phase visit were considered ovulatory. On the basis of this algorithm, 35 out of 259 women had at least one anovulatory cycle, and the rest of the women were ovulatory. The investigators were interested in comparing three hormones [estradiol (E2), follicle stimulating hormone (FSH), and LH and an oxidative stress marker F2isoprostanes (F2iso) on the visits around ovulation (corresponding to the late follicular phase, LH/FSH surge, and predicted ovulation) to see whether these markers have different diagnostic accuracy and, if so, which of these markers are better. Figure 1 shows the histograms of four markers’ levels at the first visit around ovulation. We can see that it is difficult to make a reasonable parametric assumption about the distributions of marker measurements in our study. It is also impossible to transform the marker observations to follow some known distributions because part (a) in Figure 1 clearly indicates that observations from the anovulatory group and the ovulatory group tend to skew differently. Therefore, a nonparametric or semiparametric test that does not require any distribution assumptions would be more appropriate than parametric methods.

Figure 1.

Relative frequency histograms of ovulatory and anovulatory women for the markers estradiol (E2), follicle stimulating hormone (FSH), luteinizing hormone (LH), and F2-isoprostanes (F2iso).

The primary scientific questions to be answered in the BioCycle Study include the following: (1) testing homogeneity among markers and (2) power and sample size calculation for this study. However, to the best of our knowledge, no method is available to address these two questions. Although we may extend semiparametric kernel ROC methods proposed in [5] to compare multiple markers by obtaining test statistics under the null hypothesis using some resampling methods, it is difficult to carry out the resampling under the alternative. It is also infeasible to conduct resampling at the design stage when no data are available. In this paper, we will introduce a formal homogeneity test for testing diagnostic accuracy among markers. The proposed procedure tests a global hypothesis. The χ² distribution derived under the alternative for the test statistic is useful for power analysis based on hypothesized differences among markers. When the number of markers is only two, the proposed global test reduces to the commonly used test by [6]. In addition, we will also propose a simultaneous pairwise comparison procedure based on generalized ROC summary statistics. This procedure is applicable if the test of homogeneity rejects the null hypothesis and a subsequent analysis is needed to search for the set of most accurate markers. The contributions of the proposed tests are not limited to the aforementioned example. The tests are also applicable in comparing multiple medical imaging modalities which are of wide interest in radiological studies (see, for example, [7, 8]).

The rest of the article is organized as follows. In Section 2, we propose a global test based on the hypothesis of homogeneous accuracy and discuss its theoretical properties. In Section 3, we introduce a simultaneous pairwise comparison test if significance is found by the homogeneity test. We also investigate the theoretical property of the procedure. We apply the proposed procedures to the BioCycle Study data in Section 4. Section 5 reports simulation results to illustrate the small sample performance of the proposed method. We defer the proof of the asymptotic distributions to the Appendix.

2. A test of homogeneity

In this section, we introduce a test of homogeneity based on ROC summary statistics for clustered observations. We start with a brief introduction to ROC summary statistics. We then use these summary statistics to construct the test.

Let X_ℓip denote test result of marker ℓ on day p in the diseased subject i, where ℓ = 1,…, L, p = 0, 1, …, m_ℓi, and i = 1,… I. Let Y_ℓjq denote test result of ℓth marker on day q in the non-diseased subject j, where ℓ = 1,…, L, q = 0, 1, …,n_ℓj, and j = 1, …J. Here, the total number of subjects is N = I + J. Define the joint survival function (X_ℓ1ip1, X_ℓ2ip2) ~ S_D,ℓ,1,ℓ2 (x₁, x₂) p₁ =1, …, m_ℓ1i, p₂ = 1, …,m_{ℓ 2i}, for the diseased subjects with marginal survival functions X_ℓip ~ S_D,ℓ(x). Similarly, define (Y_ℓ1jq1, Y_ℓ2jq2) ~ S_{D̄, ℓ1,ℓ2} (y₁, y₂), q₁ = 1, …,n_ℓ1i, q₂ = 1, …, n_ℓ2i for the non-diseased subjects with marginal survival functions Y_ℓjq ~ S_{D̄, ℓ}(y). Without loss of generality, we assume that measurements tend to be larger for the diseased than for the non-diseased. Let u be the false positive rate (FPR), which is also 1-specificity. The ROC curve for the ℓth marker is ${\text{ROC}}_{\ell }(u)=S_{D,\ell }\{S_{\overline{D},\ell }^{-1}(u)\}$, where u ∈ [0, 1]. The resulting ℓth weighted area under curve (wAUC) is

$${\mathrm{\Omega }}_{\ell }={\int }_0^1[S_{D,\ell }\{{S_{\overline{D},\ell }}^{-1}(u)\}]\mathrm{d}W(u),$$ (1)

with a probability measure W(u)defined on u, for u ∈ (0, 1). Included in this class of accuracy measures are AUC (when W(u) = u for 0 < u < 1), partial AUC (pAUC) between FPRs u₁ and u₂ (when W(u) = (u − u₁)/(u₂ − u₁) for 0 < u₁ ≤ u ≤ u₂ ≤ 1), and the sensitivity at a given level of FPR u₀ (when W(u) is a point mass at u₀). The nonparametric wAUC estimator is given by ${\widehat{\mathrm{\Omega }}}_{\ell }={\int }_0^1[{\widehat{S}}_{D,\ell }\{{\widehat{S}}_{\overline{D},\ell }^{-1}(u)\}]\mathrm{d}W(u)$, where Ŝ_D,ℓ and Ŝ_D̄,ℓ are empirical functions of S_D,ℓ and S_D̄,ℓ defined by

$${\widehat{S}}_{D,\ell }(x)=1-\frac{1}{{\sum }_{i=1}^I{m}_{\ell i}}\sum _{i=1}^I\sum _{p=1}^{m_{\ell i}}I(X_{\ell ip}\le x),$$

and

$${\widehat{S}}_{\overline{D},\ell }(x)=1-\frac{1}{{\sum }_{j=1}^J{n}_{\ell j}}\sum _{j=1}^I\sum _{q=1}^{n_{\ell j}}I(Y_{\ell jq}\le x).$$

Denote Ω = (Ω₁, Ω₂,…, Ω_L). By substituting Ŝ_D,ℓ and Ŝ_D̄,ℓ in Equation (1), the nonparametric estimator of Ω is given by Ω̂ = (Ω̂₁, Ω̂₂, …, Ω̂_L).

2.1. Comparing multiple diagnostic tests

We will consider the following null hypothesis of homogeneity among markers:

$$H_0:{\mathrm{\Omega }}_1={\mathrm{\Omega }}_2=\cdots ={\mathrm{\Omega }}_L.$$

This hypothesis is an important initial step in comparing multiple markers [9]. Rejecting this null hypothesis is indicative of significant difference among some markers. Subsequent analysis such as pairwise comparisons can then be conducted to search for the optimal set of markers which have the best diagnostic accuracy. To construct a test statistic for the null hypothesis, we define a new vector as

$${\mathbf{\Omega }}_c=({\mathrm{\Omega }}_{c,1},{\mathrm{\Omega }}_{c,2},\dots ,{\mathrm{\Omega }}_{c,L-1}),$$

where Ω_c,ℓ = Ω_ℓ − Ω_L, for ℓ< L. In fact, any of the markers can serve as marker L to construct the test statistic. This is due to the fact that the hypothesis of homogeneity is equivalent to testing H₀: Ω_c = 0 vs. H_a: Ω_c ≠ 0. A consistent estimator of Ω_c is given by Ω̂_c = (Ω̂₁ − Ω̂_L, Ω̂₂ − Ω̂_L, …, Ω_L−1 − Ω̂_L)′. The relationship between Ω̂ and Ω̂_c can be expressed by Ω̂_c = MΩ̂, where M = (I_L−1, −1_L−1), with an identity matrix I_L−1 and a vector of one’s 1_L−1 =(1, 1,…, 1)′.

Denote $m_{\ell }={\sum }_{i=1}^I{m}_{\ell i}$ and $n_{\ell }={\sum }_{j=1}^J{n}_{\ell j}$. Assume that I/J → λ < ∞, as I, J → ∞. Let

$$r_{\ell }(u)=S_{D,\ell }^{\prime }\{S_{\overline{D},\ell }^{-1}(u)\}/S_{\overline{D},\ell }^{\prime }\{S_{\overline{D},\ell }^{-1}(u)\},\text{for}\ell =1,\dots ,L,$$

where $S_{D,\ell }^{\prime }$ and $S_{\overline{D},\ell }^{\prime }$ are the first derivatives of S_{D, ℓ} and S_D̄,ℓ, respectively.

Define

$$W_{\ell ,i}={m_{\ell }}^{-1/2}\sum _{p=1}^{m_{\ell i}}\int [I\{X_{\ell ip}>{\widehat{G}}_{\ell }^{-1}(u)\}-{\widehat{S}}_{D,\ell }\{{\widehat{G}}_{\ell }^{-1}(u)\}]\mathrm{d}W(u),$$

and

$$V_{\ell ,j}={n_{\ell }}^{-1/2}\sum _{q=1}^{n_{\ell j}}\int {\widehat{r}}_{\ell }(u)[I\{X_{\ell jq}>{\widehat{G}}_{\ell }^{-1}(u)-u\}]\mathrm{d}W(u),$$

and r̂_ℓ(u) is the kernel density estimate of r_ℓ(u). In [10], the authors used the Epanechnikov kernel function $E(x)=\frac{3}{4}(1-x^2)I(\mid x\mid \le 1)$ with the bandwidth of 4/max(min(I, J)^4/5, 50), where I and J are sample sizes for the diseased group and the non-diseased group, respectively. The same setting was used in our simulation studies and the example. Other kernel functions such as the Gaussian kernel may also be used. A detailed discussion on kernel methods can be found in [11]. Denote

$${\stackrel{\sim }{\mathit{W}}}_i=\left(\begin{array}{c}{W}_{1,i}-W_{L,i}\\ W_{2,i}-W_{L,i}\\ ⋮\\ W_{L-1,i}-W_{L,i}\end{array}\right),\text{and}{\stackrel{\sim }{\mathit{V}}}_j^{\prime }=\left(\begin{array}{c}{V}_{1,j}-V_{L,j}\\ V_{2,j}-V_{L,j}\\ ⋮\\ V_{L-1,j}-V_{L,j}\end{array}\right).$$

In the Appendix, we show that Ω̂_c asymptotically follows a multivariate normal distribution given by

$${\mathit{N}}_L({\mathbf{\Omega }}_c,{\mathbf{\sum }}_c=E({\stackrel{\sim }{\mathit{W}}}_i{\stackrel{\sim }{\mathit{W}}}_i^{\prime })/I+E({\stackrel{\sim }{\mathit{V}}}_j{\stackrel{\sim }{\mathit{V}}}_j^{\prime })/J).$$ (2)

A nonnegative definite covariance estimator of Σ_c is

$${\widehat{\mathbf{\sum }}}_c=I^{-2}\sum _{i=1}^I{\stackrel{\sim }{\mathit{W}}}_i{\stackrel{\sim }{\mathit{W}}}_i^{\prime }+J^{-2}\sum _{j=1}^J{\stackrel{\sim }{\mathit{V}}}_j{\stackrel{\sim }{\mathit{V}}}_j^{\prime }.$$ (3)

The asymptotic distribution of the test statistic $T_c:={\widehat{\mathbf{\Omega }}}_c{\widehat{\mathbf{\sum }}}_c^{-1}{\widehat{\mathbf{\sum }}}_c^{\prime }$ is provided in the following theorem and is proved in the Appendix.

Theorem 1

With mild regularity conditions, T_c converges in distribution to a χ² distribution with d.f. L minus; 1 under H₀, and T_c converges in distribution to a noncentral chi-square distribution ${\chi }_{L-1}^2(\varphi )$ distribution with the non-centrality parameter,

$$\varphi ={\mathbf{\Omega }}_c^{\prime }{\mathbf{\sum }}_c^{-1}{\mathbf{\Omega }}_c,$$

under the alternative hypothesis, as I, J → ∞.

For L = 2, Σ_c reduces to one element, var(Ω̂₁ − Ω̂₂). The asymptotic distribution of T_c = (Ω̂₁ − Ω̂₂)²/var(Ω̂₁ − Ω̂₂) reduces to a ${\chi }_1^2(\varphi )$ distribution with the non-centrality ϕ = c²/var(Ω̂₁ − Ω̂₂) under the alternative H_a: Ω₁ − Ω₂ = c. It implies that $({\widehat{\mathrm{\Omega }}}_1-{\widehat{\mathrm{\Omega }}}_2)/\sqrt{var({\widehat{\mathrm{\Omega }}}_1-{\widehat{\mathrm{\Omega }}}_2)}$ has an approximately normal distribution with mean $\sqrt{\varphi }$ and variance 1 under H_a and has approximately a standard normal distribution under H₀. This asymptotic normality has been studied by [12] and [13]. Their expression of var(Ω̂₁ − Ω̂₂) is the same as ours.

When different subjects are measured with different markers, Ω̂_ℓ’s are independent estimators, and we can derive an explicit form for the variance–covariance matrix of Ω̂_c. Assume that I/m_ℓ → α_ℓ, and I/n_ℓ → β_ℓ, as I, J → ∞. Here, α_ℓ and β_ℓ are finite numbers. We also assume that ${\sum }_{i=1}^I{m}_{{\ell }_{1}i}{m}_{{\ell }_{2}i}/I^2\to {\eta }_{{\ell }_1,{\ell }_2}^X$, and ${\sum }_{j=1}^J{n}_{{\ell }_{1}j}{n}_{{\ell }_{2}j}/I^2\to {\eta }_{{\ell }_1,{\ell }_2}^Y$, as I, J → ∞. It follows that

$${\mathbf{\sum }}_c=\left(\begin{array}{cccc}{v}_1& 0& \cdots & 0\\ 0& v_2& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \cdots & v_{L-1}\end{array}\right)+v_L{\mathbf{11}}^{\prime },$$

where 1 = (1, 1, …, 1)′, and v_ℓ = var(Ω̂_ℓ), whose explicit form is given in Theorem 2 by letting h(·) = Ω_ℓ,

$$\begin{array}{l}{v}_{\ell }=I^{-1}\sum _{\ell }{\alpha }_{\ell }^2{\eta }_{\ell ,\ell }^x\left({\int }_0^1{\int }_0^1[S_{D,\ell ,\ell }\{S_{\overline{D},\ell }^{-1}(s),S_{\overline{D},\ell }^{-1}(t)\}-S_{D,\ell }\{S_{\overline{D},{\ell }_1}(s)\}{S}_{D,\ell }\{S_{\overline{D},\ell }^{-1}(t)\}]\mathrm{d}W(s)\mathrm{d}W(t)\right)\\ +I^{-1}\sum _{\ell }{\beta }_{\ell }^2{\eta }_{\ell ,\ell }^y\left({\int }_0^1{\int }_0^1{r}_{\ell }(s)r_{\ell }(t)[S_{\overline{D},\ell ,\ell }\{S_{\overline{D},\ell }^{-1}(s),S_{\overline{D},\ell }^{-1}(t)\}-st]\mathrm{d}W(s)\mathrm{d}W(t)\right).\end{array}$$ (4)

Given the special form of the variance–covariance matrix Σ_c, the inverse matrix ${\mathbf{\sum }}_c^{-1}$ is given by an explicit expression using results in matrix operations. Theorem 1 then gives a simplified distribution result of T_c, which is summarized in the following corollary.

Corollary 1

With mild regularity conditions, as I, J → ∞, T_c converges in distribution to a χ² distribution, with L − 1 degree of freedom under H₀, and converges in distribution to a noncentral chi-square distribution ${\chi }_{L-1}^2(\varphi )$ with

$$\varphi =\sum _{\ell =1}^{L-1}{v}_{\ell }^{-1}{({\mathrm{\Omega }}_{\ell }-{\mathrm{\Omega }}_L)}^2-{\{\sum _{\ell =1}^{L-1}{v}_{\ell }^{-1}({\mathrm{\Omega }}_{\ell }-{\mathrm{\Omega }}_L)\}}^2/\sum _{\ell =1}^L{v}_{\ell }^{-1}$$

under H_a.

2.2. Power and sample size

The explicit forms of χ² distributions under H_a in either Theorem 1 or Corollary 1 are useful for power analysis. The power under H_a is given by

$$P(X^2>{\chi }_{L-1,\alpha }^2),$$

where $X^2~X_{L-1}^2(\varphi )$, and $X_{L-1,\alpha }^2$ is the upper α critical value of a chi-square distribution with L − 1 degrees of freedom. The non-centrality ϕ can be estimated by $\widehat{\varphi }={\mathbf{\Omega }}_c^{\prime }{\widehat{\mathbf{\sum }}}_c^{-1}{\mathbf{\Omega }}_c$, where the hypothesized value of Ω_c is specified under the alternative. Asymptotically, ϕ̂ converges to its true value.

For a given power 1 − β, we have the following relationship

$${\chi }_{L-1,\beta }^2(\varphi )={\chi }_{L-1,\alpha }^2,$$ (5)

where $X_{L-1,\beta }^2(\varphi )$ is the upper β critical value of a noncentral chi-square distribution with L − 1 degrees of freedom. By fixing the power 1 − β and type I error rate α, the non-centrality parameter ϕ can be solved numerically to satisfy the relationship in (5). Let the solution for ϕ be ϕ_α,1−β. By combining the expression of ϕ in Theorem 1 and the expression of Σ_c in (2), it follows that

$${\varphi }_{\alpha ,1-\beta }={\mathbf{\Omega }}_c^{\prime }{[E({\stackrel{\sim }{\mathit{W}}}_i{\stackrel{\sim }{\mathit{W}}}_i^{\prime })/I+E({\stackrel{\sim }{\mathit{V}}}_j{\stackrel{\sim }{\mathit{V}}}_j^{\prime })/J]}^{-1}{\mathbf{\Omega }}_c.$$ (6)

The minimal relevant difference, Ω_c, among ROC summary measures can be specified by investigators. Using either pilot studies or specific distribution assumptions, we can estimate $E({\stackrel{\sim }{\mathit{W}}}_i{\stackrel{\sim }{\mathit{W}}}_i^{\prime })$ and $E({\stackrel{\sim }{\mathit{V}}}_j{\stackrel{\sim }{\mathit{V}}}_j^{\prime })$. By specifying a ratio between I and J, we can then solve (6) for the required sample sizes for the diseased and non-diseased patients.

3. Post hoc pairwise comparisons based on Δ-statistics

After the test finds a significant difference among markers, we can use a post hoc pairwise comparison to identify the most accurate markers by using differences between the weighted AUCs, Δ_ℓk = Ω_ℓ − Ω_k, for ℓ ≠ k. The estimator Δ̂_ℓk = Ω̂_ℓ − Ω̂_k, for ℓ ≠ k can be obtained from the data. A general setting for Ω̂_ℓ − Ω̂_k is when m_ℓi, n_ℓj ≥ 1. In this paper, the multivariate normality of Ω̂_c in (8) of the Appendix allows derivation of the explicit expression of the asymptotic variance of Δ̂_ℓk.

Theorem 2

With mild regularity conditions,

$$\sqrt{I}({\widehat{\mathrm{\Delta }}}_{\ell k}-{\widehat{\mathrm{\Delta }}}_{\ell k})\stackrel{d}{\to }\mathcal{N}(0,v_X+\lambda v_Y),\text{as}I,J\to \infty ,$$

where

$$\begin{array}{l}{v}_X=\sum _{\ell =1}^2{\alpha }_{\ell }^2{\eta }_{\ell ,\ell }^x\left({\int }_0^1{\int }_0^1{S}_{D,\ell }\{S_{\overline{D},\ell }^{-1}(s\wedge t)\}\mathrm{d}W(s)\mathrm{d}W(t)-{\left[{\int }_0^1{S}_{D,\ell }\{S_{\overline{D},\ell }^{-1}(s)\}]\mathrm{d}W(s)\right]}^2\right)\\ -2{\alpha }_1{\alpha }_2{\eta }_{1,2}^x{\int }_0^1{\int }_0^1\left[S_{D,1,2}\{S_{\overline{D},1}^{-1}(s),S_{\overline{D},2}^{-1}(t)\}-S_{D,1}\{S_{\overline{D},1}^{-1}(s),S_{D,2}\{S_{\overline{D},2}^{-1}(t)\}\right]\mathrm{d}W(s)\mathrm{d}W(t),\end{array}$$

and

$$\begin{array}{l}{v}_Y=\sum _{\ell =1}^2{\beta }_{\ell }^2{\eta }_{\ell ,\ell }^y\left[{\int }_0^1{\int }_0^1{r}_{\ell }(s)r_{\ell }(t)(s\wedge t)\mathrm{d}W(s)\mathrm{d}W(t)-{\left\{{\int }_0^1{r}_{\ell }(s)\mathrm{d}W(s)\right\}}^2\right]\\ -2{\beta }_1{\beta }_2{\eta }_{1,2}^y{\int }_0^1{\int }_0^1{r}_1(s)r_2(t)[S_{\overline{D},1,2}\{S_{\overline{D},1}^{-1}(s),S_{\overline{D},2}^{-1}(t)\}-st]\mathrm{d}W(s)\mathrm{d}W(t),\end{array}$$

where

$$r_{\ell }(u)=S_{D,\ell }\{S_{\overline{D},\ell }^{-1}(u)\}/S_{\overline{D},\ell }\{S_{\overline{D},\ell }^{-1}(u)\},\text{for}\ell =1,\dots ,L.$$

Theorem 2 is a direct result obtained by combining the multivariate normal distribution of Ω̂ and the Cramer–Wold device [14, Theorem 1.5.2]. Special details are omitted here.

For the purpose of pairwise comparisons after the simultaneous test, L − 1 Δ-statistics can be defined to be the difference between markers. That is, Δ̂_1L = Ω̂₁ − Ω̂_L, Δ̂_2L = Ω̂₂ − Ω̂_L, …, Δ̂_L−1,L = Ω̂_L−1 − Ω̂_L. By directly using results in Theorem 2, p-values can be obtained for these pairwise comparisons. By comparing these p-values to a certain threshold from multiple comparison procedures such as the Bonferroni test or false discovery rate method, markers which have better accuracy can be identified.

The pairwise comparison after the proposed homogeneity test in diagnostic trials is analogous to post hoc tests after the analysis of variance test in clinical trials. In our setting, we use an overall significance test to monitor the diagnostic trial, for example, to determine early stopping of the trial. After the trial is terminated on the basis of the global test, methods such as a step-down approach are then employed to identify individual biomarkers.

4. The BioCycle Study revisited

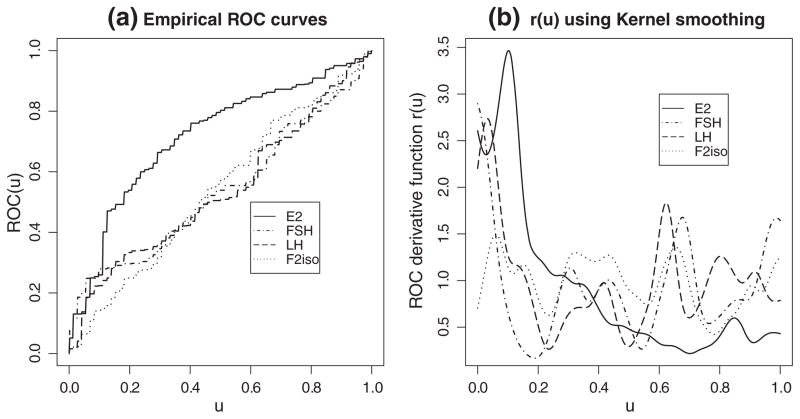
In the aforementioned BioCycle Study, 35 women were anovulatory, and 224 women were ovulatory. The markers were measured at three visits for all patients. The investigators were interested in comparing accuracy between markers of E2, FSH, LH, and F2iso in distinguishing between ovulatory and anovulatory menstrual cycles using ROC summary measures. The empirical ROC curves of these markers are shown in Figure 2(a). The ROC derivative function r(u)using kernel density smoothing estimation for each marker is illustrated in Figure 2(b). We first compared these markers on the basis of their AUCs. We conducted a homogeneity test of all these markers using results from Theorem 1 with α = 0.05. We estimated the AUCs of E2, FSH, LH, and F2iso,

Figure 2.

Empirical ROC curves and their derivative functions of the markers estradiol (E2), follicle stimulating hormone (FSH), luteinizing hormone (LH), and F2-isoprostanes (F2iso).

$$\widehat{\mathbf{\Omega }}=(0.7132,0.5347,0.5318,0.5218).$$

In this example, we chose F2iso as a reference biomarker. Note that the results remain the same when we use either biomarker as the reference. We calculated differences between individual markers and the reference marker of Ω̂_c of (0.1915, 0.0130, 0.0100). The variance–covariance matrix Σ_c of Ω̂_c was further estimated by (3):

$${\widehat{\mathbf{\sum }}}_c=\left(\begin{array}{ccc}0.0080& 0.0033& 0.0028\\ 0.0033& 0.0136& 0.0095\\ 0.0028& 0.0095& 0.0078\end{array}\right).$$

The chi-square statistic was calculated, $T_c={\widehat{\mathbf{\Omega }}}_c{({\widehat{\mathbf{\sum }}}_c)}^{-1}{\widehat{\mathbf{\Omega }}}_c^{\prime }=5.06$, under H₀. The p-value given by $P({\chi }_3^3\ge 10.85)=0.17$ for this test does not show a significant difference among these markers based on their AUCs.

As these markers were developed to screen a large population of women and distinguish between ovulatory and anovulatory menstrual cycles, the accuracy at a FPR less than 0.6 was also determined to be important. In fact, similar decisions to look at small FPRs are often made for cancer screening markers. We conducted a homogeneity test of all these markers on the basis of the pAUCs with α = 0.05. We calculated the partial AUC estimates of the biomarkers, (0.3590, 0.2286, 0.2196, 0.2026). This gave differences between individual markers and the reference marker of (0.1564, 0.0260, 0.0170). The variance–covariance matrix Σ_c of Ω̂_c was further estimated by (3):

$$\left(\begin{array}{ccc}0.0047& 0.0026& 0.0025\\ 0.0026& 0.0043& 0.0030\\ 0.0025& 0.0030& 0.0029\end{array}\right).$$

The chi-square statistic was $T_c={\widehat{\mathbf{\Omega }}}_c{({\widehat{\mathbf{\sum }}}_c)}^{-1}{\widehat{\mathbf{\Omega }}}_c^{\prime }=8.14$ under H₀. The p-value is 0.04 for this test, indicating a significant difference among these markers based on their partial AUCs.

The results we derived in Theorem 1 were used for power analysis. Suppose the variance–covariance matrix of Ω̂ remains the same under H_a. With a hypothesized Ω_c and type I error rate 0.05, the power under H_a is given by

$$P(X^2>{\chi }_{3,0.05}^2),$$

where $X^2~{\chi }_3^2(\widehat{\varphi })$, and ${\chi }_{3,\alpha }^2$ is the upper α critical value of a chi-square distribution with three degrees of freedom. Here, ϕ̂ is the estimate of the non-centrality parameter, $\widehat{\varphi }={\mathbf{\Omega }}_c^{\prime }{\widehat{\mathbf{\sum }}}_c{\mathbf{\Omega }}_c$. Table I gives the powers for various hypothesized differences between partial AUCs of the reference marker and the other markers.

Table I.

Power of the homogeneity test.

(Δ1L, Δ2L, Δ3L)	Power (%)
(0.15, 0.05, 0.05)	44.49
(0.15, 0.10, 0.05)	60.27
(0.15, 0.10, 0.10)	62.49
(0.20, 0.05, 0.05)	41.87
(0.20, 0.10, 0.05)	85.25

We also illustrate the sample size calculation using the method proposed in Section 2.2. Let the hypothesized difference between partial AUCs of the reference marker and the other markers be (0.15, 0.05, 0.05). The power is 44.49% in Table I with 35 anovulatory women and 224 ovulatory women in the original study. We calculated the required sample sizes to obtain 80% power. With type I error rate 0.05, the non-centrality parameter was calculated to be ϕ_0.05,0.80 ≈ 14.64. We then used the function uniroot in R package to solve the equation (6) and obtained the required sample sizes, I = 96 and J = 48, with the ratio of 2:1 between anovulatory and ovulatory women. Comparing with the original sample sizes, we can see that the required sample size for ovulatory women is only one-fourth of the original sample size. But the power of 80% is almost twice as large as the original power. Interestingly, the findings indicate that recruiting less anovulatory women and more ovulatory women may dramatically increase the test power.

Because a significant difference among pAUCs was found, we conducted post hoc pairwise comparisons while using the conservative Bonferroni criteria to adjust for multiple comparisons. The estimated pairwise differences between the reference marker and other markers are given by Δ̂_ℓL for ℓ = 1, …, 3, and the estimated variances of these differences are given by the diagonal elements in Σ̂_c. We may also estimate the variances using results in Theorem 2. In fact, variance estimates given by Theorem 2 are similar to those in Σ̂_c. As we are interested in whether other markers have different accuracy from the reference marker, the z-statistics for pairwise comparisons are (2.2785, 0.3972, 0.3140). The Bonferroni adjusted threshold is given by z_0.05/3 = 2.12. Comparing the z-statistics with this threshold, it can be seen that E2 has different accuracy from F2isoprostane in distinguishing women with and without ovulation, and there is no significant difference between other markers and F2isoprostane.

5. A simulation study

We report simulation studies to evaluate the simulated type I error rates of the proposed test procedure. We simulated 1000 datasets under multivariate normal and multivariate log-normal distributions. We simulated multivariate normal random variables X̃ ~ N(μ_X, Σ_X) and Ỹ ~ N(μ_Y, Σ_Y), where μ_X = (1, 1, 2, 2, 1.5, 1.5), μ_Y = (0, …, 0), and Σ_X = Σ_Y is the variance–covariance matrix with diagonal elements (1, 1, 4, 4, 2.25, 2.25) and correlation coefficient, ρ. Here, ρ gives within-subject correlation. We let L = 3 markers and K = 2 repeated measurements for each subject. We chose the correlation coefficient ρ to be −0.2, −0.1, 0, 0.2, or 0.5. We let I = J = (50, 100, 200). For comparing AUCs, we let W(u)= 1 for 0 < u < 1. For comparing partial AUCs, we let W(u) = 1 for 0 < u < 0.8. To simulate multivariate log-normal random variables, we applied exponential transformation, X = exp (X̃) and Y = exp (Ỹ), to get simulated log-normal data, where X̃ and Ỹ were simulated using the aforementioned settings.

We also simulated multivariate log-normal random variables under unequal sample sizes and unequal covariance matrices with L = 3 markers and K = 2 repeated measurements for each subject. In the simulation, we let I = 80, and J = (100, 200). We let μ_X = (0, …, 0), μ_Y =(0, …, 0), and the covariance matrix for the non-diseased population have diagonal elements (1, 1, 4, 4, 2.25, 2.25) and a correlation coefficient, ρ, and let the covariance matrix for the non-diseased population have the same diagonal elements but with a different correlation coefficient ρ + 0.2. We again let ρ be −0.2, −0.1, 0, 0.2, or 0.5. We first simulated multivariate normal random variables X̃ ~ N(μ_X, Σ_X) and Ỹ ~ N(μ_Y, Σ_Y). The exponential transformation, X = exp (X̃) and Y = exp (Ỹ), was then applied to get simulated log-normal data.

It is clear that the null hypothesis of equal AUCs or equal partial AUCs is true under these simulation settings. We then applied the proposed simultaneous comparison procedure to simulated datasets. For each simulated dataset, we estimated Ω̂_c = (Ω̂₂ − Ω̂₁, Ω̂₃ − Ω̂₁) and its variance–covariance matrix Σ̂_c. We then calculated the χ² statistic, $T_c:={\widehat{\mathbf{\Omega }}}_c{\widehat{\mathbf{\sum }}}_c^{-1}{\widehat{\mathbf{\Omega }}}_c^{\prime }$. The null hypothesis was rejected if $T_c>{\chi }_2^2(0.95)$. We counted the frequency that the null hypothesis of equal AUCs or pAUCs was rejected out of 1000 simulated datasets in each simulation setting. Tables II and III show simulated rejection rates of our test procedure with the nominal level of 0.05. For sample sizes of 100 and 200, most rejection rates are within the 95% prediction interval.

Table II.

Rejection rates of the proposed procedure for equal sample sizes.

Multivariate normal
ρ	AUC			pAUC
	I = J = 50 (%)	100 (%)	200 (%)	I = J = 50 (%)	100 (%)	200 (%)
−0.2	7.90	6.20	5.80	8.20	6.50	6.00
−0.1	6.80	6.20	6.20	6.80	6.80	6.20
0	6.40	5.90	6.20	6.70	5.70	5.90
0.2	8.20	5.80	5.80	8.30	5.70	5.80
0.5	5.60	5.30	5.20	5.90	5.50	5.20
Multivariate log-normal
−0.2	7.10	5.00	5.70	6.90	4.90	6.10
−0.1	6.90	4.70	4.90	7.20	5.10	5.10
0	6.90	6.10	6.00	7.20	5.80	5.80
0.2	7.50	6.10	5.80	7.20	5.60	3.90
0.5	6.00	6.80	5.80	5.90	4.70	5.60

The 95% predictive interval for the error rate is (3.5%, 6.5%).

Table III.

Rejection rates for unequal sample sizes with I = 80.

ρ	AUC		pAUC
	J = 100 (%)	J = 200 (%)	J = 100 (%)	J = 200 (%)
−0.2	5.40	5.60	7.10	5.80
−0.1	5.60	6.30	6.10	5.60
0	5.50	5.40	5.30	4.00
0.2	7.60	5.50	5.70	5.20
0.5	3.70	5.70	3.80	3.80

The 95% predictive interval for the error rate is (3.5%, 6.5%).

6. Discussion

This article provides formal methods for the homogeneity test of several markers. The proposed methods are nonparametric and have important applications in comparing diagnostic markers. The associated theoretical properties are easy to implement in clustered ROC data. They provide new insights for analyzing clustered ROC data. Currently, the existing statistical inferences for evaluating complex ROC markers mainly rely on bootstrap or other resampling methods. The results studied in this paper give the closed-form expression of covariance structure for both within and between empirical ROC curves for clustered data. We provided the formula for power calculation and the numerical method for sample size calculation. The R code for conducting the proposed tests is available from the first author.

Appendix: Proofs

We follow similar lines in the proof of Theorem 1 in [15] and use continuous mapping theorem [16, Theorem 1.3.6,] to show that $\sqrt{I}({\widehat{\mathbf{\Omega }}}_c-{\mathbf{\Omega }}_c)$ is asymptotically equivalent to

$$\sum _{i=1}^I{\stackrel{\sim }{\mathit{W}}}_i/\sqrt{I}-\lambda \sum _{j=1}^J{\stackrel{\sim }{\mathit{V}}}_j^{\prime }/\sqrt{J}.$$ (7)

Note that the two summands of (7) are independent. Also, the first summation of (7) is the sum of independent mean zero random vectors, W̃_i, and the second summation of (7) is the sum of independent mean zero random vectors, Ṽ_j. Thus, it follows from multivariate central limit theorem [14, Theorem 1.9.2B] that

$$\sqrt{I}({\widehat{\mathbf{\Omega }}}_c-{\mathbf{\Omega }}_c)\stackrel{d}{\to }{\mathit{N}}_L(\mathbf{0},{\mathbf{\sum }}_c=E({\stackrel{\sim }{\mathit{W}}}_i{\stackrel{\sim }{\mathit{W}}}_i^{\prime })+\lambda E({\stackrel{\sim }{\mathit{V}}}_j{\stackrel{\sim }{\mathit{V}}}_j^{\prime })).$$ (8)

The eigen-decomposition of Σ_c is given by ${\sum }_{\ell =1}^{L-1}{\lambda }_{(\ell )}{\mathit{Q}}_{\ell }{\mathit{Q}}_{\ell }^{\prime }$, where λ_(ℓ) is the ℓth largest eigenvalue out of L − 1 eigenvalues, and Q_ℓ is the corresponding orthonormal eigenvector. On the basis of (8), we have

$$\left|\right|I{\widehat{\mathbf{\sum }}}_c-I{\widehat{\mathbf{\sum }}}_c\left|\right|\stackrel{p}{\to }0.$$ (9)

where ||·|| is a norm on R^(L−1)2. Denote

$$Z_{\ell }={\lambda }_{(\ell )}^{-1/2}{\widehat{\mathrm{\Omega }}}_{c,\ell }{Q}_{\ell }.$$

ℓ= 1, …, L − 1. Using Cramer–Wold device, we can show that asymptotically, Z_ℓ’s are independent and follow standard normal. We substitute λ̂_(ℓ) for λ_(ℓ) and Q̂_ℓ for Q_ℓ in Z_ℓ. Using the law of large numbers, it follows from (9) that

$$({\widehat{Z}}_1,{\widehat{Z}}_2,\dots ,{\widehat{Z}}_{L-1})\stackrel{d}{\to }N(\mathbf{0},{\mathit{I}}_{L-1}).$$

Because T_c is essentially ${\sum }_{\ell =1}^{L-1}{\widehat{Z}}_{\ell }^2$, the proof of Theorem 1 is completed by applying Theorem 3.5 in [14].