Feature-based Alignment of Volumetric Multi-modal Images

Abstract

This paper proposes a method for aligning image volumes acquired from different imaging modalities (e.g. MR, CT) based on 3D scale-invariant image features. A novel method for encoding invariant feature geometry and appearance is developed, based on the assumption of locally linear intensity relationships, providing a solution to poor repeatability of feature detection in different image modalities. The encoding method is incorporated into a probabilistic feature-based model for multi-modal image alignment. The model parameters are estimated via a group-wise alignment algorithm, that iteratively alternates between estimating a feature-based model from feature data, then realigning feature data to the model, converging to a stable alignment solution with few pre-processing or pre-alignment requirements. The resulting model can be used to align multi-modal image data with the benefits of invariant feature correspondence: globally optimal solutions, high efficiency and low memory usage. The method is tested on the difficult RIRE data set of CT, T1, T2, PD and MP-RAGE brain images of subjects exhibiting significant inter-subject variability due to pathology.

1 Introduction

Multiple medical imaging modalities, e.g. MR and CT images of the brain, are useful in highlighting complementary aspects of anatomy, however, they must first be aligned within a common spatial reference frame or atlas. A straight forward approach is to align all images to a single reference image or template via standard image registration methods, however, alignment and subsequent image analysis may be biased by the choice of template [1]. Group-wise alignment aims to reduce bias by jointly aligning image data. While a significant body of literature has addressed group-wise alignment of mono-modal image data [2–5], the more difficult context of multi-modal data is rarely addressed [6, 7].

Pair-wise image alignment is challenging due to factors such as pathology, resection, variable image cropping, multi-modal appearance changes and inter-subject variability. In the general case, it may be difficult to justify assumptions of smooth, one-to-one correspondence between images adopted by many registration techniques. Practical algorithms must be robust to poor initial misalignment, for example due to DICOM error [8]. Group-wise alignment poses several additional challenges. Typical iterative algorithms compute multiple image-to-image or model-to-image alignment solutions for each image, and thus memory and computational requirements are generally linear and super-linear in the number of images, respectively. In the context of multi-modal data, a mechanism is required in order to address inter-modality intensity differences, e.g. simultaneously learning models of tissue classes [6] or the joint intensity relationship between modalities [7].

We propose a new group-wise alignment method to address these challenges. Rather than attempting to model a potentially complex global intensity relationship, we propose learning a collection of locally linear intensity relationships throughout the image. To do this effectively, we adopt a model based on local scale-invariant image features [9, 10], similar to approaches used with mono-modal 2D images [11, 5] and in full 3D volumes [12]. Local scale-invariant features can be repeatably extracted in the presence of global variations in image geometry and intensity, and encoded for computing global correspondence between images despite a high degree of occluded or missing image content. Recent efficient 3D scale-invariant feature encodings [12] are particularly useful for group-wise alignment, since once extracted, the memory and computational requirements of multiple, iterative alignment phases are significantly reduced in comparison to intensity-based methods.

This paper extends the feature-based alignment technique [12], and makes two primary technical contributions. A novel scale-invariant feature encoding is presented for computing inter-modality image correspondences, based on locally inverted intensity profiles, that significantly increases the number of correspondences possible between different image modalities. Similar ideas have been presented in the context of 2D image data [13], however, these do not generalize to volumetric data due to 3D orientation. A novel probabilistic model is then developed, incorporating this encoding into a feature-based model. A fully automatic algorithm iterates between model learning and model-to-image alignment, converging efficiently to a group-wise alignment solution with no pre-processing or pre-alignment. Previous approaches to multi-modal, group-wise alignment have assumed minor deformations around pre-aligned images of healthy subjects [6] or an individual subject [7].

Experiments demonstrate group-wise alignment on the challenging Retrospective Image Registration Evaluation (RIRE) multi-modal brain image data [14], where all subjects exhibit a high degree abnormal variability due to pathology. The inverted intensity encoding is crucial in achieving fully automatic and efficient group-wise alignment solutions. The model resulting from group-wise alignment can be used subsequently for globally optimal alignment of new multimodal images of the same domain.

2 Invariant Feature Extraction

A scale-invariant feature in 3D is defined geometrically by a scaled local coordinate system S within image I. Let S = {X, σ, Θ}, where X = {x, y, z} is a 3-parameter location specifying the origin, σ is a 1-parameter scale and Θ = {θ̂₁, θ̂_2, θ̂₃} is a set of three orthonormal unit vectors θ̂₁, θ̂_2, θ̂₃ specifying the orientations of the coordinate axes. Invariant feature extraction begins by identifying a set of location/scale pairs {(X_i, σ_i)} in an image. This is done by detecting spherical image regions centered on location X_i with radius proportional to scale σ_i that locally maximize a function f(X, σ) of image saliency. For example, SIFT feature extraction identifies local extrema of the difference-of-Gaussian (DoG) function [9]:

$$\{(X_i,{\sigma }_i)\}=\underset{X,\sigma }{\text{local}\text{argmax}}\mid f(X,\kappa \sigma )-f(X,\sigma )\mid ,$$ (1)

where f(X, σ) is the convolution of the image I with a Gaussian kernel of variance σ² and κ is a multiplicative scale sampling rate. DoG detection generalizes trivially from 2D to higher dimensions and can be efficiently implemented using Gaussian scale-space pyramids [15, 9]. Following detection, each region is assigned an orientation Θ, and an image patch centered on X_i and proportional in size to σ_i is cropped from the image, reoriented and rescaled after which image intensity is encoded. We adopt the 3D orientation assignment and intensity encoding methods described in [12]. Briefly, orientation is assigned based on dominant image gradient orientations ∇I computed within regions {(X_i, σ_i)}. Let H(∇I) be a spherical 3D histogram generated from image gradient samples ∇I within region (X, σ). Orthonormal unit vectors Θ = {θ̂₁, θ̂₂, θ̂₃} are determined as follows:

$$\begin{array}{l}{\widehat{\theta }}_1=\underset{\widehat{\theta }}{\text{argmax}}\{H(\nabla I)\},\\ {\widehat{\theta }}_2=\underset{\widehat{\theta }}{\text{argmax}}\left\{H({\widehat{\theta }}_1\times (\nabla I\times {\widehat{\theta }}_1))\right\},{\widehat{\theta }}_3={\widehat{\theta }}_1\times {\widehat{\theta }}_2.\end{array}$$ (2)

With geometry S_i identified, region (X, σ) is cropped from the image, scaled and reoriented according to σ and Θ to a canonical image patch of fixed size, after which intensity is encoded. An efficient 3D version of the gradient orientation histogram (HoG) descriptor [9] is adopted as in [12], where spatial location and gradient orientation are quantized uniformly into eight spatial locations and eight 3D orientations, resulting in a compact 8 × 8 = 64-element vector.

A challenge in invariant feature matching is to reliably identify and characterize instances of the same anatomical structure in images acquired from different modalities, e.g. CT and MR. Regions identified in Equation (1) are essentially image blobs approximating center-surround patterns reminiscent of mammalian visual receptive fields [16]. Given that relationship between intensities arising from the same tissues in different modalities is generally non-linear and multimodal in nature [17], patterns in different image modalities arising from the same underlying anatomical structure will generally vary to the extent they cannot be extracted.

It has been noted, however, that multi-modal image registration can be achieved by assuming a locally linear intensity relationship, with either positive or negative correlation [18]. Generalizing this observation, we propose that the same holds true for distinctive image patterns localized in scale and space. Our reasoning is as follows: distinctive patterns present in different images arise from the interface between different tissue classes in the image. Although multiple tissue classes may be present within a local window, in many instances the image content may be dominated by a small number of intensity classes, e.g. white and grey matter, in which case the intensity relationship may be approximated as locally linear.

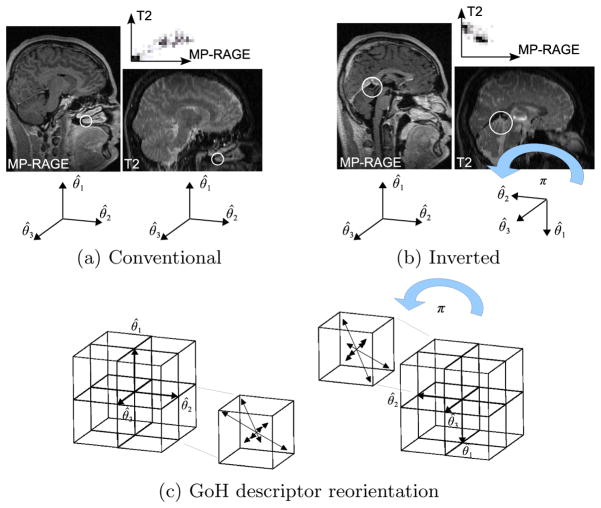
In can be shown that the set of image regions {(X_i, σ_i)} identified via Equation (1) remains constant across linear intensity variations, either positive or negative. Negative linear variations, or intensity inversions, however, cause an inversion of the image gradient, which has a major affect on feature orientation Θ and intensity encoding. Thus in order to correctly normalize and compare features across intensity inversion, primary and secondary coordinate axes must be inverted in order to correctly align spatial locations, which is equivalent to a rotation of π about axis θ̂₃, see Figure 1b). The same inversion must be performed on the spatial locations and orientation bins of the associated orientation GoH encoding, see Figure 1c). Note that the tertiary coordinate axis remains unchanged as the cross product does not change with the negation of vectors θ̂₃.

Fig. 1.

(a) and (b) illustrate scale-invariant feature correspondences automatically computed between MP-RAGE and T2 modalities. White circles illustrate feature locations and scales, graphs above the images illustrate the local joint intensity relationship associated with features. Intensities associated with tissues within the brain (b) generally exhibit an intensity inversion between these modalities, this is not the case for structures external to the brain such as bone and air-filled sinuses (a). (c) illustrates reorientation of the GoH intensity encoding in the case of intensity inversion. From left to right, a rotation of π about θ̂₃ is applied both to the 8 spatial location bins (boxes) and to the 8 orientation bins which they each contain (arrows).

Note that different image modalities may generally exhibit local intensity mappings other than linear relationships. In such cases, features cannot be extracted and matched, and alternative methods are necessary. Considering both positive and negative correlations significantly increases the number of possible correspondences. To illustrate the usefulness of inverted features, for the T2-MP-RAGE pair in Figure 1, only 2 correct correspondences are identified via nearest neighbor descriptor matching of conventional features (a), however, 22 additional correspondences are identified throughout the brain when inverted feature correspondences are considered (b).

3 Feature-based Group-wise Alignment

The feature-based alignment (FBA) method [12] is limited to a single image modality and requires pre-aligned training images. This section extends the FBA model to multiple image modalities, and presents a novel group-wise alignment algorithm that can achieve alignment without assuming pre-alignment.

Let S_ij represent the geometry of the j^th feature extracted in the i^th image, and let I_ij represent its associated intensity encoding. Let $\overline{IS}=\{(I_{ij},S_{ij})\}$ represent a vector of feature appearance/geometry pairs extracted in N images. Let T̄ = {T_i} be a set of unknown coordinate transforms, where T_i maps locations image i to a common reference or atlas space. In the context of this paper, T_i is a global 7-parameter similarity transform, about which further deformations are described independently in the neighborhood of local features. T̄ is modeled here as a random variable characterized by the posterior $p(\overline{T}\mid \overline{IS})$. Group-wise alignment aims to identify the transform set T̄_MAP maximizing the posterior probability, which can be expressed using Bayes’ theorem as follows:

$${\overline{T}}_{\mathit{MAP}}=\underset{\overline{T}}{\text{argmax}}\{p(\overline{T}\mid \overline{IS})\}\propto \underset{\overline{T}}{\text{argmax}}\{p(\overline{IS}\mid \overline{T})p(\overline{T})\}.$$ (3)

In Equation (3), $p(\overline{IS}\mid \overline{T})$ is the probability of image feature set $\overline{IS}$ conditional on transform set T̄, p(T̄) is the prior probability of transform set T̄. The prior probability can be expressed as p(T̄) = Π_i p(T_i), under the assumption that transforms for different images T_i and T_j, i ≠ j are independent. Factor $p(\overline{IS}\mid \overline{T})$ can be expressed as:

$$p(\overline{IS}\mid \overline{T})=\prod _{i,j}p(I_{ij},S_{ij}\mid \overline{T})=\prod _{i,j}p(I_{ij},S_{ij}\mid T_i),$$ (4)

where the two equalities in Equation (4) follow from two modeling assumptions. The first is the assumption of conditionally independent features (I_ij, S_ij) given transform set T̄. Intuitively, this states that the appearance and geometry (I_ij, S_ij) of one image feature provide no information regarding the appearance and geometry of another feature, provided image-wise mappings T̄ are known. The second equality results from the assumption of conditional independence of features I_ij, S_ij and all transforms T_j, i ≠ j given transform T_i.

Alignment is driven by distinctive local image features, for instance scale-invariant features arising from tissue patterns in the brain. In a single image modality, such features can be characterized by their geometry, e.g. location, scale and orientation, and by their appearance, e.g. intensity encoding. In the case of multiple modalities, structures are also characterized by distinct modes of appearance, for example conventional and inverted intensities as in the previous section. Features may be incorporated as a latent random variable and marginalized out in determining T̄_MAP. As in [12], we consider a discrete random variable of feature identity F = {f_k,l}, where f_k,l indicates a specific anatomical structure k ∈ {1, …, K} and binary local appearance mode l ∈ {0, 1} (e.g. conventional or inverted). Marginalization is expressed as a sum over discrete model feature instances f_k,l:

$$p(I_{ij},S_{ij}\mid T_i)=\sum _{k,l}p(S_{ij},I_{ij},f_{k,l}\mid T_i)=\sum _{k,l}p(S_{ij},I_{ij}\mid f_{k,l},T_i)p(f_{k,l}).$$ (5)

The right-hand side of Equation (5) results from Bayes’ theorem and the assumption of independence between F and T_i, i.e. p(f_k,l|T_i) = p(f_k,l). Intuitively, this independence assumption indicates that transform T_i provides no additional information regarding the probability of model feature f_k,l. Factor p(f_k,l) is the discrete probability of model feature f_k,l and p(S_ij, I_ij|f_k,l, T_i) represents the probability of feature geometry and appearance (S_ij, I_ij) conditional on latent model feature f_k,l and transform T_i. This factor can be further expressed as:

$$p(S_{ij},I_{ij}\mid f_{k,l},T_i)=p(I_{ij}\mid S_{ij},f_{k,l},T_i)p(S_{ij}\mid f_{k,l},T_i)=p(I_{ij}\mid f_{k,l})p(S_{ij}\mid f_{k,l},T_i),$$ (6)

assuming conditional independence of feature intensity encoding I_ij and feature geometry and transform (S_ij, T_i) given specific model feature f_k,l. Factor p(I_ij|f_k,l) is a conditional density over feature intensity encoding I_ij given model feature f_k,l, taken to be a Gaussian density over conditionally independent descriptor elements. Factor p(S_ij|f_k,l, T_i) is a conditional density over feature geometry given model feature f_k,l and transform T_i, which can be factored into conditional distributions over feature location, scale and orientation:

$$p(S_{ij}\mid f_{k,l},T_i)=p(X_{ij}\mid f_{k,l},T_i)p({\sigma }_{ij}\mid f_{k,l},T_i)p({\mathrm{\Theta }}_{ij}\mid f_{k,l},T_i).$$ (7)

In Equation (7), factor p(X_ij|σ_ij, f_k,l, T_i) is a density over extracted feature location X_ij, conditioned on model feature f_k,l and transform T_i, here taken to be an isotropic Gaussian density with variance proportional to σ_ij. p(σ_ij|f_k,l, T_i) is a density over extracted feature scale, conditioned on (f_k,l, T_i), here taken to be a Gaussian density in log σ. p(Θ_j|f_k,l, T) is a von Mises density [19] over independent angular deviations of coordinate axes, here approximated as an isotropic Gaussian density over Θ for simplicity under a small angle assumption. The final expression for the posterior probability of T̄ becomes $p(\overline{T}\mid \overline{IS})\propto$

$$\prod _{i}p(T_i)\prod _j\sum _{k,l}p(f_{k,l})p(I_{ij}\mid f_{k,l})p(X_{ij}\mid f_{k,l},T_i)p({\sigma }_{ij}\mid f_{k,l},T_i)p({\mathrm{\Theta }}_{ij}\mid f_{k,l},T_i).$$ (8)

3.1 Group-wise Alignment

The goal of group-wise alignment is to estimate transform vector T̄ from feature data $\overline{IS}$ extracted in a set of images. If the model feature set F and the parameters of its associated probability factors are known, then the posterior in Equation (8) can be maximized directly by independently maximizing transforms T_i associated with individual images. They are unknown, however, and determining T̄ and F is thus a circular problem. We propose an iterative solution which alternates between estimating T̄ and F, in an attempt to converge to reasonable estimates of both. The algorithm consists of 1) initialization, 2) model estimation 3) image alignment and 4) feature updating, where steps 2–4 repeated iteratively until estimates of T̄ converge. Note that alignment is based solely on scale-invariant features extracted once in each image.

1. Initialization involves setting individual transforms T_i to approximately correct alignment solutions according to location, orientation and scale. The primary requirement is that a subset of initializations to be approximately correct, the group-wise alignment is robust to a significant degree of error and a high number of completely incorrect transforms. This is performed here by choosing one image as an initial reference frame, then aligning all images to this model via a 3D Hough transform [20]. Due to inter-subject and inter-modality differences, many images may not initially align correctly, however, only a small subset is required to bootstrap model estimation.

2. Model Estimation aims to identify a set of model feature set F = {f_k,l} and associated factors in Equation (8) from features extracted in training images. Equation (8) takes the form of a mixture model with K components, defined by conditional densities over model feature appearance and geometry p(I_ij|f_k,l)p(S_ij|f_k,l, T_i) and mixing proportions p(f_k,l). The model parameters could thus potentially be estimated via methods such as expectation maximization [21] or Dirichlet process modeling [22], however, there are several challenges that make this difficult. First, the number of mixture components K is unknown and potentially large. Moreover, the current set of transforms T̄^t may be noisy and contain a high number of incorrect, outlier transforms T_i. A robust clustering process similar to the mean shift algorithm [23] is used to identify clusters of features that are similar in terms of their geometry and appearance as in [12]. Each cluster represents a single model feature f_k,l, and feature instances in a cluster are used to estimate parameters for associated probability factors, i.e. Gaussian means, variances and mixing proportions. Note that for the purpose of estimation, all model features are assumed to bear conventional appearance l = 0. Intensity-inversion l = 1 is incorporated later in alignment.

3. Alignment proceeds by maximizing $p(\overline{T}\mid \overline{IS})$ via marginalization, as in Equation (8). With known model feature set F, this proceeds by maximizing each individual transform T_i independently:

   $$T_{\mathit{iMAP}}=\underset{T_i}{\text{argmax}}\{p(T_i\mid \overline{IS})\}.$$ (9)

   Maximization proceeds by determining candidate model-to-image correspondences between features in image i and learned intensity distributions p(I_i,j|f_k,l). A candidate correspondence exists between model feature f_k,l and image feature descriptor I_i,j if I_k,l and I_i,j are nearest neighbors (NN) according to the Euclidean metric, where I_k,l represents the mean of density p(I_i,j|f_k,l). Candidate correspondences are used to identify model-to-image similarity transform candidates T_i for evaluation under p(T_i|I) in manner similar to the Hough transform [20]. Note that T_iMAP is globally optimal in the space of similarity transforms. This procedure can be carried out efficiently via approximate nearest neighbor techniques [24], and by considering only a subset of the most frequently occurring model features, as identified by p(f_k,l) in learning. Although a single image feature can potentially be attributed to multiple model features, appearance descriptors representing distinctive image patterns lie in sparse, high dimensional space, where it can be assumed that there is at most one significantly probable model correspondence.

   Two types of alignment are considered here, conventional and multi-modal. Conventional alignment considers only appearance mode l = 0, whereas multimodal alignment marginalizes over both conventional and inverted features l = 0, 1 under the assumption that p(f_k,l=0) = p(f_k,l=1). Multi-modal alignment has the capacity to identify correspondences despite local intensity inversions, however, it runs a higher probability of identifying incorrect correspondences and requires a higher search time. Experiments contrast conventional vs. multimodal alignment.

4. Feature Update with T̄^t estimated, the geometry of each image feature S_i,j is updated according to $T_{\mathit{iMAP}}^t$ for subsequent iterations. Feature intensity encodings are invariant under similarity transforms and need not be updated.

4 Experiments

Experiments use the high-resolution RIRE data set [14], consisting of brain images of nine subjects and five modalities: CT, T1, T2, PD and MP-RAGE, for a total of 39 images (not all modalities are available for all subjects). Group-wise alignment of this data set is challenging for several reasons: all subjects exhibit significant anatomical abnormalities due to large brain tumors, there are no healthy or normal subjects. Images are acquired with a high degree of anisotropy which varies between modalities and subjects, with (X, Y, Z) voxels sizes of approximately (0.86,0.86,3.00) for T1, T2, PD, (0.98,1.37,0.98) for MP-RAGE and (0.45,0.45,3.00) for CT.

While several authors report multi-modal group-wise registration for recovering small deformations about known ground truth for a single subject [7, 25] or healthy subjects [6], we are not aware of literature addressing the more challenging context of inter-subject, multi-modal alignment involving significant abnormality and no pre-alignment. The only image preprocessing applied here is to resample images as isotropic, with voxels sizes 0.86mm for T1, T2, PD, 0.98mm for MP-RAGE and 0.45mm for CT. Knowledge of the image modality, the voxel size, image orientation or translation is not required or used.

Feature extraction requires approximately 25 seconds per volume of size 256× 256 × 200. Features arising from degenerate structures that cannot be reliably localized in 3D such as surfaces are identified and discarded via an analysis of the local structure tensor as in [26]. Model learning makes use of approximately 83K features, requiring 8.3MB of memory, note original image data in isotropic floating point format require 1700MB. Individual learning and fitting phases require approximately 25 and 10 seconds each on a 2.4GHz processor. The total running time here is ≈ 22 minutes note that mono-modal group-wise registration algorithms require ≈ 19 hours for comparable amounts of data [3, 4].

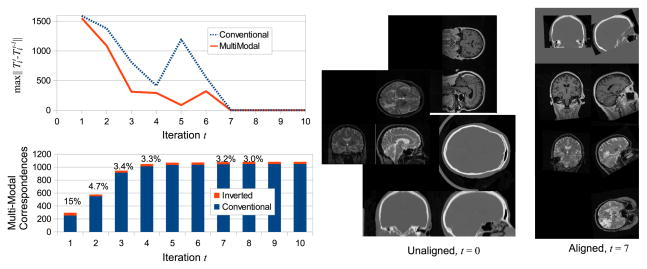
Group-wise alignment converges in 7 iterations for both conventional and multi-modal alignment as shown in the upper left graph of Figure 2, when set T̄ no longer changes with further iterations. The lower left graph of Figure 2 shows the relative numbers of conventional and inverted model-to-subject correspondences as a function of t for multi-modal alignment. In early iterations, a relatively large percentage of correspondences (e.g. 15% at t = 1) result from inverted matches, as relatively few model features exist due to initial misalignment. Inverted matches make up increasingly smaller portions of correspondences (e.g. 3%, t = 7), as improved alignment results in a larger set of model features. After convergence, a model with a stable latent feature set F has been learned, reflecting features present in the alignment/training image. This model can be used with either conventional alignment in order to efficiently align additional images of modalities present in training, or with multi-modal alignment to align images of new modalities unseen in training.

Fig. 2.

The upper left graph illustrates transform set T̄ change vs. iteration t, where change is measured by the maximum Frobenius norm affine transform matrix difference $\mathit{max}\left|\right|T_i^t-T_i^{t-1}\left|\right|$. Learning converges after 7 iterations, after which T̄ does not change. The lower left graph shows the relative numbers of conventional and inverted correspondences over iteration t, where the percentages reflect the proportion of inverted correspondences. Image sets to the right show images before alignment t = 0 and resampled after convergence according to T_i at t = 7. Note the slightly elevated orientation in aligned images; since alignment here is fully automatic, the final geometry of group-wise alignment is determined by the data.

Recall that each mapping T_i represents a coarse global transform between images, about which individual image-to-model feature correspondences reflect refined, localized deformations. While T_i do not represent highly accurate transforms, images resampled according to T_i can be used to visually assess general success/failure of alignment. Multi-modal alignment successfully aligns all subjects, whereas conventional alignment produces three failure cases with clearly incorrect alignment solutions, see Figure 3. All failures arise from CT images, which have low image contrast in the brain and produce fewer features than other modalities. Precise quantification of alignment error could be performed on a feature-by-feature basis by contrasting the discrepancy of image-to-model correspondence with human labelers as in [11], we leave this for future work. The vast majority of correspondences in successful alignment solutions appear qualitatively correct, typical examples are shown in Figure 1.

Fig. 3.

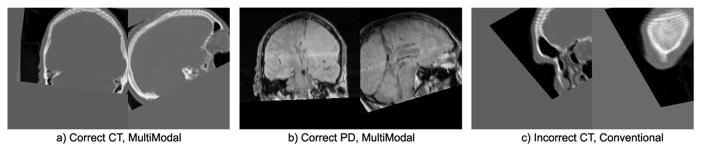
a) and b) show typical instances of correct multi-modal alignment solutions, c) shows one of three clearly incorrect conventional alignment solutions.

5 Discussion

This paper investigates a new method for addressing group-wise alignment of difficult, multi-modal image data. Inverted scale-invariant feature correspondences are proposed, which address multi-modality in the form of locally inverted joint intensity relationships. For several combinations of brain modalities, e.g. MP-RAGE and T2, this results in a significant increase in the number of image correspondences identified in comparison to conventional correspondence which assumes a positive linear joint intensity relationship.

Inverted correspondences form the basis for a novel feature-based model and group-wise alignment algorithm, which is shown to be effective in the case of a difficult, multi-modal brain image data set. Experiments demonstrate that considering multi-modality in the form of locally inverted intensity mappings leads to successful group-wise alignment, where conventional feature-based alignment fails. Although allowing for a wider range of intensity mappings potentially permits a higher number of incorrect correspondences and alignment solutions, these are unlikely to occur in practice due to smoothness of natural images.

Once a feature-based model of multi-modal intensity patterns has been learned for a set of modalities, it serves as prior knowledge for efficient and robust alignment of images of the same modalities considering strictly positive intensity correlations. This is analogous to theoretical findings in dense image registration, where the use of multi-modal vs. mono-modal similarity measures can be explained in terms of the informativness of the Bayesian prior [27].

A significant practical contribution of this paper is a system that is able to achieve group-wise alignment of difficult, multi-modal image data. The code used in this paper for feature extraction and inversion is available to the research community ³, which will facilitate the use of scale-invariant feature technology in medical image analysis. We have evaluated our group-wise alignment method several difficult contexts, including infant brain MR exhibiting intensity contrast changes and multi-subject truncated body CT scans, and results are promising.