Modeling Change in the Presence of Non-Randomly Missing Data: Evaluating A Shared Parameter Mixture Model

Abstract

In longitudinal research, interest often centers on individual trajectories of change over time. When there is missing data, a concern is whether data are systematically missing as a function of the individual trajectories. Such a missing data process, termed random coefficient-dependent missingness, is statistically non-ignorable and can bias parameter estimates obtained from conventional growth models that assume missing data are missing at random. This paper describes a shared-parameter mixture model (SPMM) for testing the sensitivity of growth model parameter estimates to a random coefficient-dependent missingness mechanism. Simulations show that the SPMM recovers trajectory estimates as well as or better than a standard growth model across a range of missing data conditions. The paper concludes with practical advice for longitudinal data analysts.

Missing data can be difficult to avoid in longitudinal research. One type of missing data that is uniquely troubling for longitudinal research is when the probability of a data point being missing at a given occasion of measurement is related to the latent individual trajectory of change on the outcome under study. Commonly used growth modeling approaches, such as multilevel growth models and latent curve models, are vulnerable to bias resulting from this type of missing data. Our goal is to introduce and evaluate a new model, the shared parameter mixture model (SPMM), that avoids many of the drawbacks of existing methods for handling non-ignorable missing data,.

Our paper is organized in the following way. As a point of contrast and to define our notation, we begin with a short description of the conventional latent curve modeling (LCM) framework. After laying the groundwork, we describe the assumption of random missingness that is inherent in traditional growth models, and the implications of this assumption. Second, we introduce the SPMM, evaluating its strengths and weaknesses. Because little is known regarding the performance of the SPMM, we then present results from a simulation study comparing results obtained from this model with a standard growth model, under a variety of real-world data conditions. Finally, we discuss the practical implications of our findings.

The Latent Curve Model

In the LCM, the observed repeated measures for an individual are posited to reflect an underlying (or latent) growth trajectory (see Bollen & Curran, 2006; McArdle & Epstein, 1987; Meredith & Tisak, 1990). Formally, the LCM can be defined as

$${\mathbf{Y}}_i=\mathbf{\Lambda }{\mathbf{\eta }}_i+{\mathbf{\epsilon }}_i{\mathbf{\eta }}_i=\mathbf{\alpha }+\mathbf{\Gamma }{\mathbf{X}}_i+{\mathbf{\zeta }}_i$$ (1)

where Y_i is a T × 1 vector of repeated measures for individual i over T measurement occasions and η_i is a m × 1 vector of latent growth parameters (e.g., intercept, linear slope, quadratic slope) that are linked to the repeated measures via the T × m factor loading matrix Λ. The columns of Λ are often set to predefined functions of time to specify a particular form for the individual trajectories (e.g., linear or quadratic growth). In turn, the growth parameters are regressed on a q × 1 vector of covariates X_i such that α defines a m × 1 vector of intercepts, Γ is a m × q matrix of regression coefficients capturing systematic variability in η_i due to X_i, and ζ_I is a m × 1 vector that captures random (unexplained) variability in η_i. Last, the T × 1 vector ε_i contains the time-specific residuals, or variability in the observed repeated measures not accounted for by the individual’s latent trajectory.

Conventionally, the random components of the model are assumed to be normally distributed and are allowed to covary with one another (i.e., ζ_i ~ N(0,Ψ)). Time-specific residuals are also assumed to be normally distributed and (often) independent (i.e., ε_i ~ N(0, Θ), where Θ is a diagonal matrix), though the assumption of independence can be relaxed. Further, it is assumed that the residuals are uncorrelated with the growth factors.

Ignorable and Non-Ignorable Missing Data Mechanisms

Rubin (1976) showed that one of the most important characteristics of missing data is whether they are ignorably or non-ignorably missing. Missing data are usually ignorable if they are Missing at Random (MAR) or Missing Completely at Random (MCAR). In contrast, missing data that are Missing Not at Random (MNAR) are non-ignorably missing. To help explicate these different missing data processes, we must first define several terms. Let Y_i be a T × 1 vector of potentially observed repeated measures for individual i, including as subsets the observed repeated measures ${\mathbf{Y}}_i^o$ and the missing repeated measures ${\mathbf{Y}}_i^m$. In turn, let R_i be a T × 1 response pattern vector of missing data indicators for individual i, where r_it = 1 if an observation is missing, r_it = 0 if an observation is observed. MAR, MCAR and MNAR processes can then be defined with respect to the distribution of R_i given ${\mathbf{Y}}_i^o,{\mathbf{Y}}_i^m$, the predictors X_i, and the random coefficients η_i. The conditional distribution for R_i can then be expressed as:

$$f({\mathbf{R}}_i|{\mathbf{Y}}_i,{\mathbf{\eta }}_i,{\mathbf{X}}_i)=f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,Y_i^m,{\mathbf{\eta }}_i,{\mathbf{X}}_i).$$ (2)

Ignorable missingness occurs when (Schafer, 1997):

$$f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{Y}}_i^m,{\mathbf{\eta }}_i,{\mathbf{X}}_i)=f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{X}}_i).$$ (3)

What we can see from this expression is that missing data are ignorably missing if the probability of missingness depends only on the observed data ${\mathbf{Y}}_i^o$ and X_i, and not on any unobserved data. Thus the probability of an observation being missing, given the observed data, is the same for all observations. If a study were designed such that participants dropped out of a study after having reached a particular observed value on the dependent variable, then this would be a MAR missingness mechanism in a longitudinal context.

Missing data are MNAR and non-ignorable when the simplification in Equation 3 is not possible; that is, when the conditional probabilities for observations to be missing are not equal even after accounting for observed data (X_i and ${\mathbf{Y}}_i^o$). The probability that a given observation is missing thus depends directly upon ${\mathbf{Y}}_i^m$ (and, by extension, also indirectly on the unobserved random parameters in the model, η_i or ε_i). This type of missingness might occur if participants dropped out of a study due to unobserved scores on the dependent variable. For instance, a participant might drop out of a study immediately prior to reaching a value on the dependent variable, or due to of a slower-than-average rate of change on the dependent variable, in each case contributing to non-ignorable missingness.

When the missing data process is ignorable and the causes of missingness are included within the analysis model of interest, current strategies for analyzing longitudinal data using LCMs or other multilevel, hierarchical or mixed models will result in unbiased inferences. The missingness mechanism can be statistically ignored when the full information maximum likelihood fitting function is used (Arbuckle, 1996; Enders, 2001; Wothke, 2000). If the missing data process is MAR but the observed causes of missingness are not included in the analysis model, pre-processing of the data and post-processing of the results using multiple imputation procedures will also result in unbiased parameter inferences if the reasons for missingness are included in the imputation model (Collins, Schafer, & Kam, 2001; Rubin, 2004; Schafer, 2003).

When missing data are non-ignorable, however, fitting a trajectory model under the assumption that the missing data are ignorable will result in estimates that are biased to an indeterminate degree. This bias arises because the unobserved or unmeasured process responsible for the missing data is related to the longitudinal process underlying change in the repeated measures over time. Excluding information about the missing data from the likelihood function ignores important information about the trajectory process, resulting in incorrect estimates for the trajectory model of interest (Little, 1995; Little & Rubin, 2002). Unfortunately, no test exists to empirically distinguish between ignorable and non-ignorable missingness, so a data analyst who relies on maximum likelihood or multiple imputation to make inferences about a longitudinal process must be confident that the MAR assumption is correct. It is therefore incumbent upon the researcher to consider the possibility that missing data are MNAR as well as potential options for appropriately analyzing change over time in the presence of MNAR missing data.

Random Coefficient-Dependent and Outcome-Dependent MNAR Processes

Little (1995) noted the importance of distinguishing between two types of MNAR mechanisms. The first, Outcome-Dependent MNAR (OD-MNAR), occurs when missingness is caused by the unobserved values of the repeated measures themselves (e.g., a person fails to respond to a wave for any reason that has to do with the outcome of interest). This might occur, for example, if an individual did not respond to a daily diary study of substance use on days when they used a substance. This mechanism can be expressed as:

$$f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{Y}}_i^m,{\mathbf{\eta }}_i,{\mathbf{X}}_i)=f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{Y}}_i^m,{\mathbf{X}}_i).$$ (4)

The second type of MNAR mechanism, Random Coefficient-Dependent MNAR (RC-MNAR), occurs when missing data is related to individuals’ unobserved trajectories (i.e., or an underlying latent trajectory process that is imperfectly measured, as well as potential future observations arising from this process; Demirtas & Schafer, 2003). For example, this type of missingness could occur in a longitudinal assessment of cognitive functioning in older adults in which diseases status is unknown. In this case, individuals with the most dramatic decline might be the most likely to be missing, thereby providing an overly optimistic picture of average cognitive functioning in aging adults. The RC-MNAR mechanism can be expressed as:

$$f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{Y}}_i^m,{\mathbf{\eta }}_i,{\mathbf{X}}_i)=f({\mathbf{R}}_i|{\mathbf{Y}}_i^o,{\mathbf{\eta }}_i,{\mathbf{X}}_i).$$ (5)

RC-MNAR mechanism can be construed as a sub-type of OD-MNAR in the longitudinal setting. Equation 1 shows that Y_i (and ${\mathbf{Y}}_i^m$ by extension) is partially due to η_i; RC-MNAR is therefore a special case of OD-MNAR where the only unobserved component of variation in ${\mathbf{Y}}_i^m$ that influences the probability that observations are missing is η_i (and not also ε_i). Because we regard RC-MNAR as a potentially common missingness mechanism in longitudinal data, the current study focuses primarily on conducting sensitivity analyses to test for bias related to this specific MNAR process.

Modeling Growth in the Presence of Non-Randomly Missing Data: The Shared Parameter Mixture Model

All methods for handling non-randomly missing data must incorporate information about the missing data process into the model for the data. An in-depth review and illustration of several approaches for accomplishing this goal within longitudinal models was recently provided by Enders (2011), Gottfredson (2011), and Muthén, Asparouhov, Hunder, and Leuchter (2011). Readers are encouraged to refer to these papers for an overview of alternative missing data models. There are two general classes of models: selection models and shared parameter models. The Shared Parameter Mixture Model (SPMM) is a flexible hybrid of these approaches.

The SPMM achieves three objectives. First, the model does not require the explicit specification of the missing data mechanism (unlike selection models and traditional shared parameter models). The assumption underlying the first objective is that an analyst may have difficulty forming a correctly specified shared parameter model for the process underlying their missing data. Second, in order for inference to be less contingent on assumptions about the missing data patterns, the SPMM specifies the growth model to be conditionally independent from the missing data indicators after accounting for exogenous variables and shared parameters (the idea behind traditional shared parameter models). This specification contrasts with traditional pattern mixture models that condition parameter estimates directly on the observed patterns of missing data. Third, the SPMM minimizes dependence on the missing data model by utilizing a shared parameter that is distinct from the growth parameters and that has a flexible (i.e., semi-parametric) distribution, as discussed below.

The shared parameter is a central part of the model because of its role in creating conditional independence between the repeated measures and the missing data indicators (Tsonaka et al., 2009). Traditional shared parameter models rely on growth parameters (random effects) as the shared parameters, which are typically specified to be normally distributed. Misspecification of the shared-parameter distribution and its relation to other variables may lead to violation of the conditional independence assumption, leading to bias in trajectory estimates (Tsonaka et al., 2009). The SPMM circumvents this problem by conditioning the growth factors and the missing data patterns on discrete latent classes (the new shared-parameters) in order to approximate the unknown joint distribution between the growth factors and the missing data patterns. Indeed, latent mixture distributions are often used to semi-parametrically approximate unknown continuous densities (Heckman & Singer, 1984; e.g., Nagin, 1999, suggested using discrete ‘points of support’ to recover an unknown random effect distribution, rather than assuming normality of these effects).

Mathematically, the way that the SPMM factors the joint likelihood for the repeated measures and the missing data indicators can be expressed as follows:

$$f({\mathbf{Y}}_i,{\mathbf{R}}_i,{\mathbf{\eta }}_i,{\mathbf{C}}_i|{\mathbf{X}}_i)=f({\mathbf{Y}}_i|{\mathbf{\eta }}_i,{\mathbf{X}}_i)f({\mathbf{\eta }}_i|{\mathbf{C}}_i,{\mathbf{X}}_i)f({\mathbf{R}}_i|{\mathbf{C}}_i,{\mathbf{X}}_i)f({\mathbf{C}}_i)$$ (6)

where R_i is the usual vector of binary missing data indicators and C_i is a set of latent, discrete shared-parameter variables for the non-ignorable missing data mechanism. Note that both the growth parameters and the missing data patterns are conditioned on the latent class variables, C_i, as well as on the covariates X_i.¹ The effects of observed predictors may be included in the conditional distribution for R_i to account for a MAR mechanism, in order to make the model more statistically efficient.

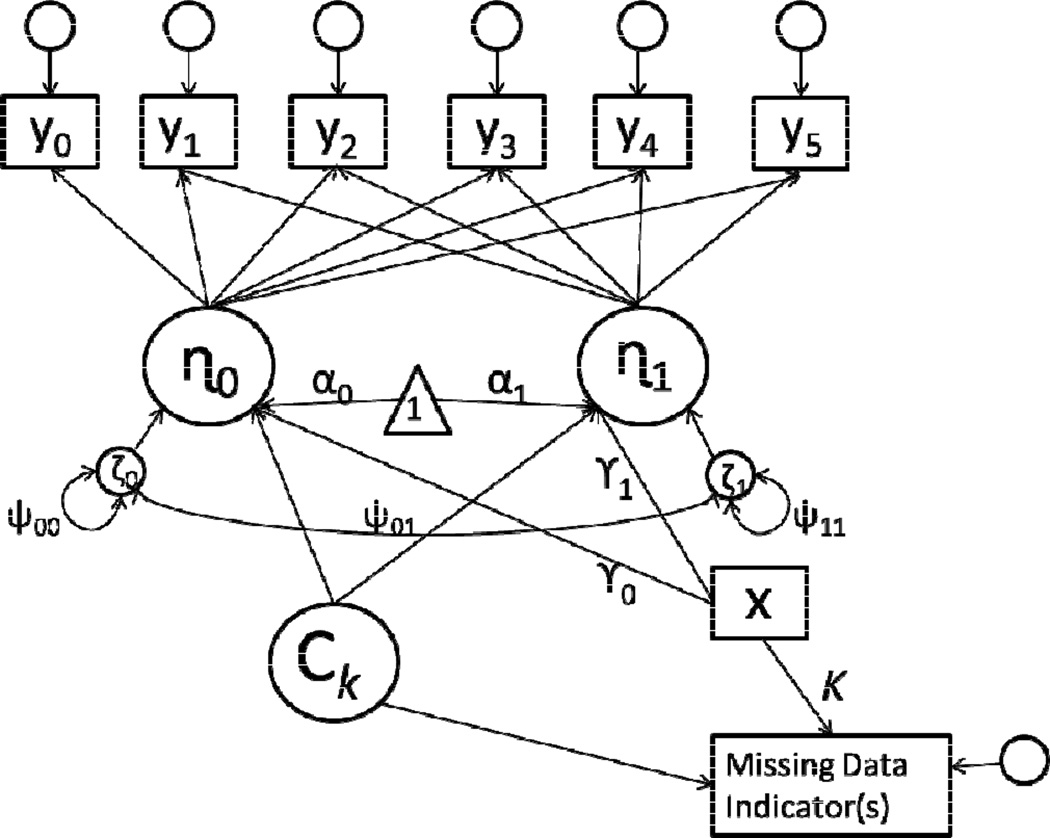
In practice, SPMMs can be specified as Structural Equation Mixture Models (Arminger, Stein, & Wittenberg, 1999; Dolan & van der Maas, 1998; Jedidi, Jagpal, & DeSarbo, 1997; Yung, 1997), and they can be estimated by maximum likelihood with the expectation maximization algorithm using conventional software. A path diagram is shown in Figure 1 and sample Mplus syntax is provided in an online appendix.² With maximum likelihood estimation, the optimal number of classes is determined by fitting a series of Structural Equation Mixture Models, varying the number of latent classes present in each model, and comparing model fit using measures such as Akaike’s Information Criterion (AIC; Akaike, 1974) or Bayesian Information Criterion (BIC; Schwarz, 1978). To estimate a SPMM, one specifies a mixture of latent curve models (i.e., a Growth Mixture Model; Verbeke & LeSaffre, 1996; Muthén & Shedden, 1999) with the form of growth that characterizes the individual trajectories (e.g., linear, quadratic, piecewise), as shown below:

$${\mathbf{Y}}_i=\mathbf{\Lambda }{\mathbf{\eta }}_i+{\mathbf{\epsilon }}_i{\mathbf{\eta }}_i={\mathbf{\alpha }}_k+\mathbf{\Gamma }{\mathbf{X}}_i+{\mathbf{\zeta }}_i$$ (7)

where ζ_i ~ N(0,Φ), ε_i ~ N(0,Θ), and the k subscript indicates a class-varying parameter. Unlike a conventional Growth Mixture Model, the SPMM jointly includes missing data indicators for the shared latent class variables via the equation

$${\mathbf{\nu }}_i={\mathbf{\beta }}_k+\mathbf{K}{\mathbf{X}}_i$$ (8)

where ν_i is a vector of values for the linear predictor of R_i, β_k is a vector of intercepts and Κ is a matrix containing the direct effects of the covariates X_i on the missingness indicators. For instance, if binary missing data indicators are present, then ν_i might be specified as a vector of logits.

Figure 1.

Path diagram of SPMM with six repeated measures; error terms shown with small circles are not labeled.

Note that the class-varying parameters in the SPMM of Equations (7) and (8) are α_k and β_k. Allowing these parameters to vary across classes enables the model to capture the dependence of the individual trajectories and the missing data. That is, joint differences in these parameter vectors allow K average trajectories (represented through α_k) to be associated with K average patterns of missing data (represented through β_k). In principle, other parameters could also be permitted to vary across classes, but limiting the number of class-varying parameters helps to retain parsimony, makes interpretation more straightforward (Dantan et al., 2008), and reduces the likelihood of some estimation problems (Hipp & Bauer, 2006).

When the number of repeated measures becomes large, estimation of SPMMs with binary indicators of missingness may become difficult. For this reason, Roy (2007) suggested replacing binary missing data indicators with summary measures in a related model. Examples of potential summary indicators are the number of total observations for individual i or the occasion of dropout for individual i.³

When fitting a SPMM, one question is how many classes to include in the analysis. Numerous fit indices, including the AIC, the BIC, and many others, have been compared via simulation to determine the index with the optimal performance for Growth Mixture Models (Lubke & Muthén, 2007; Tofighi & Enders, 2007). However, these studies have examined direct applications of mixtures and class recovery when true classes exist, whereas the goal of class enumeration is quite different here. The primary purpose of the latent classes in the SPMM is to explain the dependence between missing data patterns and growth parameters; the aim of class enumeration is to include enough latent classes to achieve this goal, but to also estimate as few as possible to maximize efficiency. The goal is not to determine the “correct” number of latent classes. Simulation work by Morgan-Lopez and Fals-Stewart (2008) and by Gottfredson (2011) has shown that it is preferable to take a conservative approach to class enumeration when relying on SPMM-type models for accommodating missing data; thus, the BIC is a better metric than the AIC because the efficiency lost by over-extracting classes is larger than the marginal reduction in bias that is gained.

Computation of Aggregate Effect Estimates

Although Roy (2003) initially viewed the latent classes as a pattern reduction device, within more recent work on SPMM-type models the latent classes have sometimes been interpreted to represent natural subgroups of individuals who differ qualitatively with respect to both their missing data patterns and their growth trajectories. A more conservative strategy, however, may be to focus interpretation on the across-classes average (similar to conventional pattern mixture models), given mounting evidence that seemingly distinct latent groups can often be estimated even when heterogeneity is strictly continuous in nature (Bauer & Curran, 2003; Sampson, Laub, & Eggleston, 2004; Bauer, 2007). Therefore, once the number of classes has been selected, the next step in an SPMM analysis is to aggregate over class estimates to obtain population level effects (i.e., growth factor means and variances; the parameters that would be obtained in a standard LCM if missing data were missing due to a MAR process). Aggregate values for the growth parameter means or intercepts are calculated by applying the following formula (Vermunt & van Dijk, 2001; Bauer, 2007):

$$\mathbf{\alpha }=\sum _{k=1}^K{\pi }_k{\mathbf{\alpha }}_k$$ (9)

where K is the total number of latent classes and π_k represents the class probability (mixing proportion, or weight) for class k. That is, class-specific means (for unconditional models) or intercepts (for conditional models), α_k, are weighted by their associated class probabilities, π_k, to obtain a population-average vector of growth factor means/intercepts.

Aggregate variance and covariance estimates for the random effects can be calculated by combining the between-class covariance matrix (created by mean differences across classes) with the within-class covariance matrix, as shown below (Vermunt & van Dijk, 2001; Bauer, 2007):

$$\mathbf{\Psi }=\sum _{k=1}^K\sum _{j=k+1}^K{\pi }_k{\pi }_j({\mathbf{\alpha }}_k-{\mathbf{\alpha }}_j)({\mathbf{\alpha }}_k-{\mathbf{\alpha }}_j)\text{'}+\mathbf{\Phi }.$$ (10)

For both Equations (9) and (10), aggregate estimates are obtained by substituting sample estimates for population parameters. Standard errors for the aggregate estimates can be computed via the delta method (e.g., Raykov & Marcoulides, 2004). Because all other parameters of the SPMM (e.g., predictor effects) are assumed to be class-invariant they can be interpreted immediately as across-class averages without further computations.

Modeling Limitations of SPMM

Enders (2011) showed that different approaches for accommodating MNAR data can provide widely varying substantive results. This is true in part because of the different assumptions required by each model, and in part because some models were created to handle slightly different forms of missingness (e.g., traditional selection models were intended for outcome-dependent missingness and shared parameter and pattern mixture models were intended for random coefficient-dependent missingness).

In this vein, it should be emphasized that SPMM is intended to assess or ameliorate parameter bias specifically due to random-coefficient-dependent missing data. Where SPMMs may fail is with the type of outcome-dependent missing data that includes time-varying residuals as a cause of missingness (as opposed to strict random coefficient-dependent missing data; e.g., a participant fails to respond to a daily diary survey of alcohol use only on evenings when they drink). SPMMs cannot be expected to mitigate parameter bias associated with this type of problem entirely because, although the repeated measures are in part due to covariates and random coefficients, they are also a function of residual error that includes omitted, systematically time-varying information. Latent classes only vary between persons, and not within, and hence cannot capture this information. A similar observation may be made concerning more traditional pattern mixture models (with observed patterns) and it is noteworthy that these models have sometimes performed poorly with outcome-dependent missingness (Yang & Maxwell, 2009; Maxwell & Yang, 2010).

Evaluating the Performance of the SPMM

Existing research indicates that SPMMs are a useful tool for modeling MNAR data; however, the sparse prior literature evaluating this model leaves several questions unaddressed regarding its performance. Morgan-Lopez and Fals-Stewart’s (2008) evaluation of SPMM-type models was an important first step for showing that the model could work under ideal conditions, but it was somewhat circular in that data were first generated to be maximally consistent with a SPMM (i.e., discrete missingness groups literally exist in the population) and then the fitted SPMMs were shown to recover the model parameters well. A more challenging and realistic test of the SPMM is to determine how well the model performs when it is not literally true but rather serves as an approximation, for instance, when the MNAR missing data process is characterized by continuous variability rather than discrete missingness groups.

Hypotheses

The SPMM is designed to accommodate random coefficient-dependent missingness. Thus, we hypothesized that SPMMs ought to provide less biased trajectory estimates than LCMs when the true missing data mechanism is a model-consistent mechanism (i.e., varying across latent classes, as in Morgan-Lopez & Fals-Stewart, 2008). Similarly, we expected that the SPMM would also outperform the traditional LCM when a continuous random coefficient mechanism is monotonically linked to the probability of missingness (i.e., the probability of missingness either monotonically increases or monotonically decreases; the traditional conception of random coefficient dependent missingness, e.g., Little, 1995).

The SPMM may have somewhat greater difficulty approximating non-monotonic random-coefficient missing data mechanisms. For instance, it could be the case that both high and low values of the random coefficients are related to an increased probability of missingness, so that there is a U-shaped association between random coefficients and the probability of missingness. Such an association might occur in a treatment study where drop out could be higher among those who fail to improve, on the one hand, and those who improve most rapidly, on the other. We expect that the SPMM might have difficulty approximating this relationship with the available information. Our reasoning is as follows: if a mid-ranged random effect value is related to the lowest probability of missing data, with high probabilities of missingness on either tail of the random effect distribution, then the number of missing observations will be virtually uncorrelated with the growth factors. SPMMs can be expected to perform most poorly with outcome-dependent missingness when the outcome-dependent processes are driven more by the error term(ε_i) rather than by the random coefficients (η_i). The SPMM may, however, still provide superior parameter estimates than the LCM to the extent that the random coefficients (η_i) contribute to the variance in ${\mathbf{Y}}_i^m$. Finally, it is reasonable to expect that the LCM might provide more efficient parameter estimates than the SPMM when the MAR assumption is met because it is a more parsimonious model in this case. However, both the SPMM and the LCM should result in unbiased growth parameter estimates when the missing data process is ignorable.

Data Generation

SPMM performance was evaluated under a variety of missing data mechanisms, including MAR (i.e., ignorable) missingness, latent class-dependent missingness (i.e., SPMM-consistent missingness), random (growth) coefficient-dependent missingness that is either monotonic (RC-MNAR-M) or nonmonotonic (RC-MNAR-NM), and a more general outcome-dependent missingness (OD-MNAR). Five hundred replicated samples of size 300 were generated for each missing data mechanism condition. For most of the conditions, data generation occurred in two steps. First, complete data (Y_i) were generated, and then the observed repeated measures ${\mathbf{Y}}_i^o$ were selected based on the missingness mechanism. To maximize ecological validity, parameter generating values were based on a longitudinal analysis of psychotherapy outcomes that was analyzed in Baldwin, Berkeljon, Atkins, Olsen, and Nielsen (2009). An overall probability of 35% missingness was retained across all study conditions, and missingness was intermittent. To test the robustness of results obtained using an intermittent missingness process, data were also generated under a monotone dropout mechanism (with details on data generation available in an online appendix, address to be determined). Data on ten repeated measures were generated to be consistent with the following conditional LCM with a linear form:

$$y_{ti}={\eta }_{0i}+{\lambda }_t{\eta }_{1i}+{\epsilon }_{ti}{\eta }_{0i}={\alpha }_0+{\gamma }_0{x}_i+{\zeta }_{0i}{\eta }_{1i}={\alpha }_1+{\gamma }_1{x}_i+{\zeta }_{1i}$$ (11)

where y_ti denotes complete data at time t for individual i, η_0i denotes the random intercept, λ_t is time (λ_t = {0,1,…,9}), η_1i is the random slope, and ε_it is the time-varying residual term, ε_ti ~ N(0,180). The baseline intercept was set to α₀ = 69 and random slope intercept was set to α₁ = −2.5. Both were conditioned on the same binary time-invariant covariate, x_i (x_i ~ Bernoulli(.5)), where the effect of the covariate is measured by regression parameters γ₀ = 10 (a moderate Cohen’s d effect size of .52) and γ₀ = −1.13 (a moderate Cohen’s d effect size of .42). Each growth factor was influenced by a randomly distributed disturbance term, ζ_0i and ζ_1i, respectively. The disturbances were distributed as follows:

$$\left[\begin{array}{c}\hfill {\zeta }_{0i}\hfill \\ \hfill {\zeta }_{1i}\hfill \end{array}\right]~N\left(\right[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}],(\begin{array}{cc}\hfill 375\hfill & \hfill -10.38\hfill \\ \hfill -10.38& \hfill 7.18\end{array}\left)\right).$$ (12)

Data for the SPMM-consistent, discrete missing data process were generated somewhat differently. Data in this condition were generated from three groups, each with a different probability of missingness (retaining an overall missingness probability of 35%). Each group also differed with respect to the average slope, but not with respect to the average intercept or covariate effects. Each group comprised 1/3 of the population, and the overall population mean trajectory for this condition matched other conditions. Also, the population-level observed rate of change was −3.58, which is equivalent to the observed rate of change in the RC-MNAR-M condition.

Data deletion to produce intermittent missingness for the four SPMM-inconsistent conditions is as follows: (1) MAR. Within each replication, the probability that a repeated measure was missing depended only on time (where t = 0 to 9), (2) Outcome dependent MNAR (OD-MNAR). The probability of missingness increased as the value of y_ti increased, (3) Random coefficient dependent MNAR - monotonic process (RC-MNAR-M). The odds that a repeated measure was missing increased as a function of the individual slope, and (4) Random coefficient-dependent MNAR - nonmonotonic process (RC-MNAR-NM). Information on both tails of the random effect distribution was more likely to be missing. To achieve this, a piecewise, U-shaped distribution was used to select observations.

Data Analysis

One- through five- class SPMMs were estimated for each replicate dataset. A summary indicator, the number of repeated measures observed for individual i, was used to provide information on the missingness process. The summary indicator was treated as a continuous indicator and was assumed to be normally distributed within class. The assumption of normality is known to be violated because the summary indicator is a count measure, but with ten repeated measures the assumption violation is not egregious, and this assumption assists with computational feasibility (which is the impetus for using a summary indicator in the first place). Modeling the conditional distribution of the summary indicator as Poisson made no meaningful difference in pilot research.

For each replication, a class solution was removed if it was not positive definite, if the solution was a clear outlier upon visual inspection, or if the solution contained a class with probability less than .10.⁴ Aggregate point estimates and delta-method standard error estimates were generated by Mplus (version 6) using Equations 9 and 10. Class enumeration was determined on a replication-by-replication basis; the models with the lowest BIC values were selected for comparison. A standard LCM, which assumes MAR, was also estimated for each replicate dataset for comparative purposes.

For the sake of brevity, we present results exclusively for intermittent missingness, but meaningful differences between dropout and intermittent missingness are indicated in the text at the end of the results section and more detailed results for drop out mechanisms are available in an online appendix (address to be determined). Table 1 reports rates of convergence to a positive definite (proper) solution and frequencies of positive definite solutions removed due to being an outlier or having a low class probability, by missing data mechanism for the SPMM solutions. The frequency with which one-through five-class solutions were selected by the BIC are also reported in Table 1. As shown, estimating up to five classes appears to have been more than sufficient for reaching conditional independence between growth factors and missing data indicators, at least as suggested by the BIC. Many high-class solutions were removed due to low class proportions, particularly when the missing data mechanism was MAR or OD-MNAR. It is encouraging to note that a single class was very rarely selected when the missing data mechanism was SPMM Consistent or RC-MNAR-M.

Table 1.

Rates of Convergence to a Proper Solution, Solution Deletion, and Model Selection

Classes	Converged	Low π̂k	Outlier	Remaining	Lowest BIC
MAR Mechanism
1	499	NA	0	499	305
2	498	121	10	367	74
3	492	236	4	252	78
4	476	342	0	134	38
5	469	445	0	24	4
SPMM Consistent Mechanism
1	500	NA	0	500	0
2	500	0	0	500	1
3	500	0	0	500	195
4	497	31	21	445	227
5	500	279	0	221	77
RC-MNAR-M Mechanism
1	500	NA	0	500	2
2	500	0	0	500	0
3	495	0	2	493	45
4	483	2	9	472	305
5	425	125	3	297	148
RC-MNAR-NM Mechanism
1	500	NA	0	500	112
2	500	136	0	364	251
3	499	259	0	240	117
4	461	407	0	54	13
5	387	103	0	10	7
OD-MNAR Mechanism
1	500	NA	0	500	428
2	500	0	0	500	1
3	411	54	0	357	1
4	496	338	2	156	63
5	177	156	0	21	7

Standardized bias and root mean squared error (RMSE) were used as performance criteria for evaluating bias and precision of the fixed effect and variance component estimates from the LCM and SPMM. Standardized bias was calculated as follows, where θ̂_j is the estimate for θ in the jth repetition, and N is the total number of replications that are properly converged:

$$SB=\frac{100}{SE({\mathrm{\theta ̂}}_j)}*(\frac{\sum _{j=1}^N{\mathrm{\theta ̂}}_j}{N}-\theta )$$ (13)

Standardized bias measures the magnitude of parameter bias as a percentage of the standard error for each parameter. It can be interpreted as the amount (in percentage of standard deviation units) that the average estimate differs from the true parameter value (Collins et al., 2001). According to Collins et al., standardized bias within ± 40%, or ± .4 SD units, are considered ‘acceptable.’

RMSE is a measure of the variation or imprecision of estimation that was calculated as follows:

$$\text{RMSE}=\sqrt{\frac{\sum _{j=1}^N{({\mathrm{\theta ̂}}_j-\theta )}^2}{N}}.$$ (14)

Accuracy of inferences related to predictor effects and growth factor means were further assessed by examining the ratio between the standard error estimates and the true, empirical standard deviations of the sampling distribution for each point estimate.

Results

Trajectory Recovery under MAR

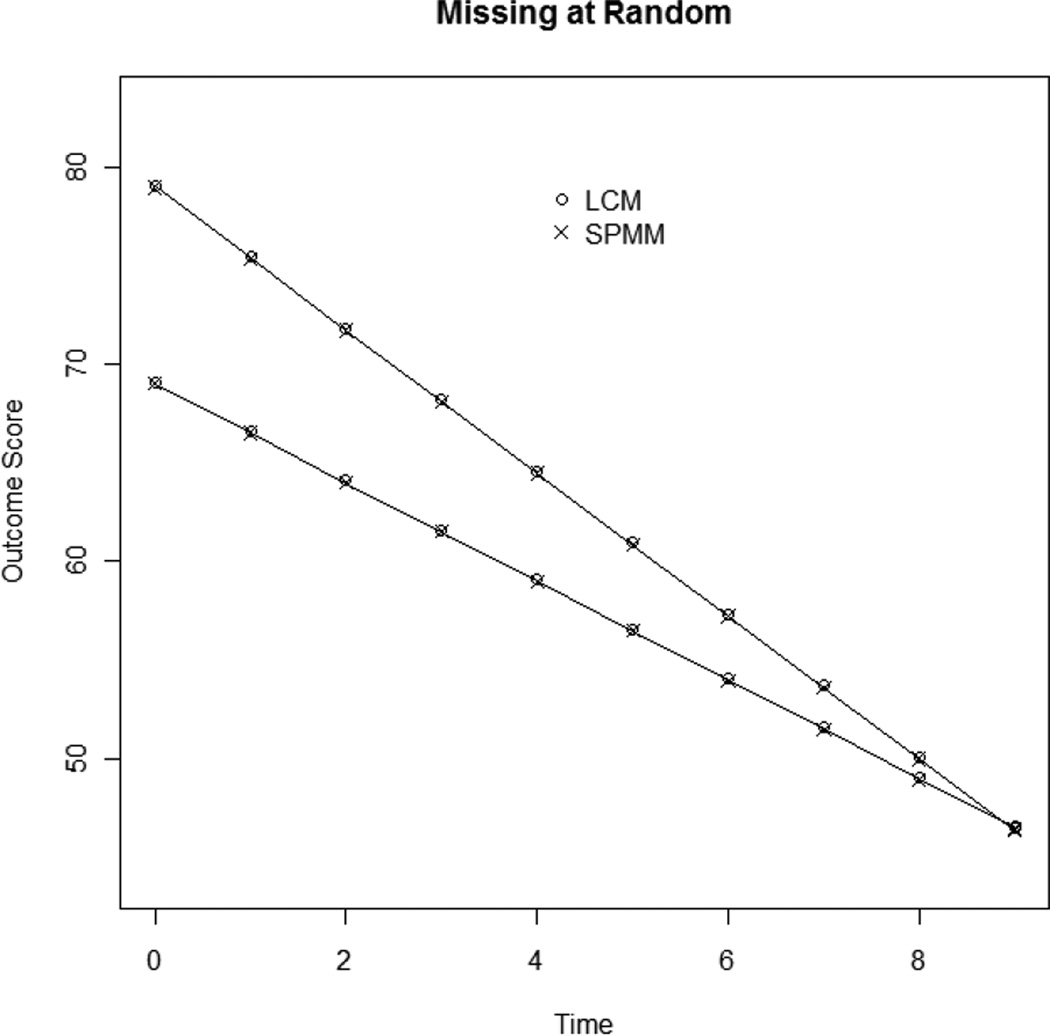
We posited that both LCM- and SPMM-implied trajectories would be equivalently unbiased in the fixed effects under a MAR mechanism, but that the LCM would be more precise than the SPMM. Table 2 compares SB and RMSE of fixed effect trajectory estimates implied by the LCM, and by the SPMM, and Figure 2 shows that the average LCM- and SPMM-implied trajectories are both indistinguishable from the generating model. Table 2 illustrates that both the LCM and the SPMM produce fixed effect and variance component estimates with little bias; the RMSE values presented in Table 2 also indicate that LCM is slightly more efficient in recovering variance components than the SPMM, but that efficiency is about equivalent for fixed effect estimates.

Table 2.

Bias and Efficiency of Trajectory Recovery under a MAR Mechanism

	LCM		SPMM (Best BIC)
	SB (%)	RMSE	SB (%)	RMSE
Fixed Effects
Conditional Intercept (α0)	4.89	1.84	−1.64	1.83
Conditional Slope (α1)	.00	.33	−2.94	.34
Intercept Predictor (γ0)	−1.89	2.65	14.13	2.67
Slope Predictor (γ1)	2.22	.46	.00	.48
Variance Components
Intercept Variance (ψ00)	−10.30	37.43	−18.48	61.44
Slope Variance (ψ11)	−9.82	1.12	−25.69	1.58
Covariance (ψ01)	2.28	4.82	9.90	6.54

Note. SB ± 40% is acceptable.

Figure 2.

Comparison of LCM- and SPMM-Implied Trajectories for x_i = 0 and x_i = 1 when the ‘missing at random’ assumption is met. The population generating model is shown with a solid line.

Trajectory Recovery under MNAR

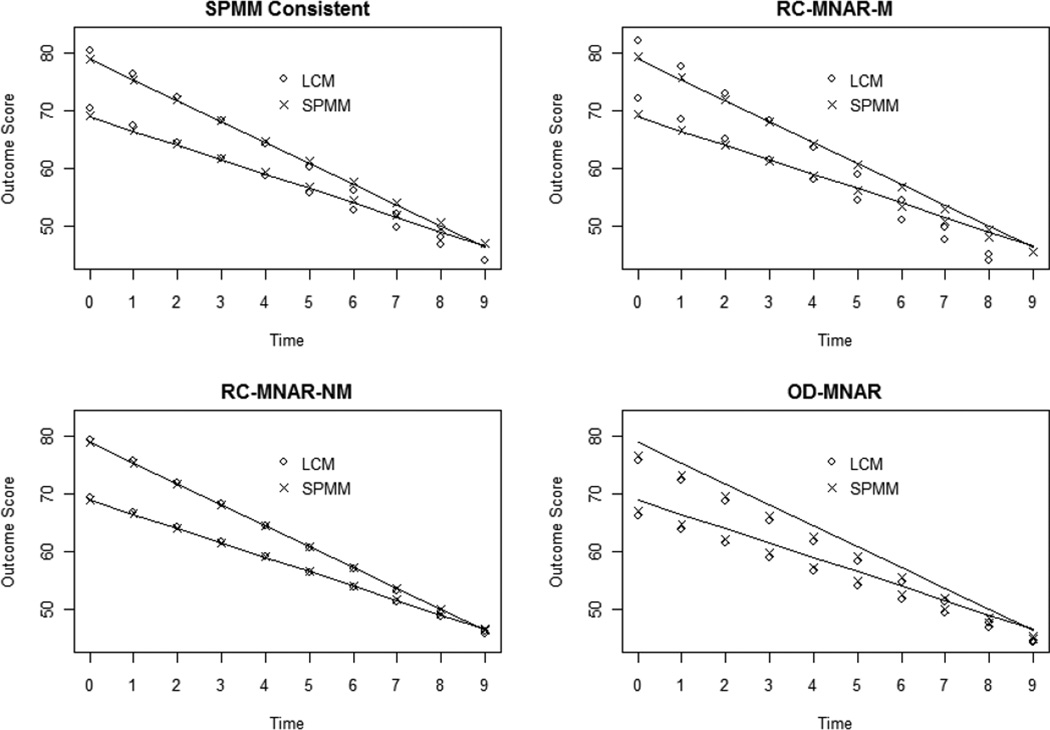
It was expected that the SPMM would recover trajectory estimates better than the LCM when the missing data mechanism was random coefficient-dependent, but that neither model would recover trajectories well under an outcome dependent MNAR process. Table 3 compares standardized bias and RMSE values across MNAR study conditions and models, and Figure 3 shows the average LCM and SPMM performance under the four MNAR conditions. Beginning with the condition most favorable to the SPMM relative to the LCM (SPMM-consistent missingness), Table 3 shows that LCM fixed effect estimates of the intercept and slope are substantially biased, but that predictor effects are relatively unbiased, whereas SPMM fixed effect estimates are all within the acceptable range for standardized bias. RMSE values are also moderately lower for the SPMM fixed effect estimates of the intercept and slope. Except for estimated variation in the random slope, the LCM variance component estimates are within the acceptable bias range. The SPMM variance component estimates are all relatively unbiased and the RMSE is moderately lower for the SPMM estimates than for the LCM estimates.

Table 3.

Bias and Efficiency of Trajectory Recovery under Several MNAR Mechanisms

	LCM		SPMM (Best BIC)
	SB (%)	RMSE	SB (%)	RMSE
SPMM-Consistent
Fixed Effects
Conditional Intercept (α0)	76.84	2.4	7.73	1.95
Conditional Slope (α1)	−128.57	.57	17.65	.34
Intercept Predictor (γ0)	−1.85	2.70	−8.89	2.75
Slope Predictor (γ1)	6.25	.48	7.14	.42
Variance Components
Residual Intercept Variance (ψ00)	−2.87	43.59	−3.97	45.19
Residual Slope Variance (ψ11)	−60.81	5.74	1.85	1.10
Covariance (ψ01)	27.79	6.41	−3.30	5.20
RC-MNAR-M
Fixed Effects
Conditional Intercept (α0)	163.16	3.63	.48	2.09
Conditional Slope (α1)	−404.00	1.05	−18.18	.33
Intercept Predictor (γ0)	6.92	2.61	4.87	2.60
Slope Predictor (γ1)	−2.70	.37	5.26	.35
	LCM		SPMM (Best BIC)
	SB (%)	RMSE	SB (%)	RMSE
Variance Components
Residual Intercept Variance (ψ00)	−21.22	42.26	−21.16	47.78
Residual Slope Variance (ψ11)	−335.80	2.84	−34.50	5.37
Covariance (ψ01)	129.86	6.92	14.75	8.90
RC-MNAR-NM
Fixed Effects
Conditional Intercept (α0)	22.60	1.81	8.84	1.81
Conditional Slope (α1)	−37.50	.26	−7.14	0.28
Intercept Predictor (γ0)	3.28	2.44	9.64	2.44
Slope Predictor (γ1)	−8.82	.34	3.03	.33
Variance Components
Residual Intercept Variance (ψ00)	−29.54	38.41	−26.71	53.33
Residual Slope Variance (ψ11)	−270.51	2.25	−113.82	3.52
Covariance (ψ01)	130.15	6.52	76.43	7.76
OD-MNAR
Fixed Effects
Conditional Intercept (α0)	−152.78	3.29	−117.49	2.87
Conditional Slope (α1)	28.00	.26	26.92	.27
Intercept Predictor (γ0)	−15.66	2.52	−15.56	2.73
Slope Predictor (γ1)	8.33	.36	5.56	.37
	LCM		SPMM (Best BIC)
	SB (%)	RMSE	SB (%)	RMSE
Variance Components
Residual Intercept Variance (ψ00)	−85.80	52.03	−61.34	86.63
Residual Slope Variance (ψ11)	−55.17	.99	−51.72	1.19
Covariance (ψ01)	14.87	4.64	18.62	5.17

Note. Standardized bias (SB) values above 40% or below −40% are bolded to indicate severe bias

Figure 3.

Comparison of LCM- and SPMM-Implied Trajectories for x_i = 0 and x_i = 1 under a variety of non-random missing data mechanisms: SPMM consistent (top left), RC-MNAR-M (top right), RC-MNAR-NM (bottom left), and OD-MNAR (bottom right). The population generating model is shown with a solid line.

Moving to the RC-MNAR-M condition, the next most favorable condition for the SPMM, the same pattern of results is observed for the LCM (i.e., growth factor means and variance component estimates are substantially biased but predictor effects are unbiased). Again, SPMM fixed effect and variance component estimates are substantially less biased than the estimates implied by the LCM. Indeed, the bias of SPMM estimates is within the “acceptable” range for almost all parameters. However, the RMSE of the random slope variance and the covariance between the random intercept and random slope is more efficient under the LCM.

Moving next to the RC-MNAR-NM condition, Table 3 shows that the brunt of the bias induced by this missingness mechanism lies in the variance component estimates, rather than in the fixed effects. This is expected since the RC-MNAR-NM considered here removes cases from either tail of the random slope distribution, leaving the mean relatively unchanged but substantially reducing the observed population variability. In this condition, bias in both the SPMM fixed effect estimates and variance component estimates is lower than the bias of the corresponding LCM estimates, but SPMM variance component estimates never reach an acceptable level of bias.

Finally, with the OD-MNAR missing data process, fixed effect estimates for the intercept are substantially biased, regardless of whether the LCM or SPMM is used. Variance component estimates are also biased under OD-MNAR, and SPMM is not useful for correcting this bias. In this case, RMSE values suggest that LCM performs better than the SPMM because the estimates are less variable, though neither model performs particularly well. Indeed the results in this condition are instructive in showing that a lack of difference between LCM and SPMM estimates does not necessarily entail that the missing data process is MAR.

Considering the possibility that bias in variance components might lead to bias in the standard errors of the fixed effects, we computed the ratio of the mean estimated standard error to the empirical standard deviation of the point estimates (where a ratio of one means that the estimates are unbiased; see Table 4). As a comparison, the ratios for LCM estimates under the five different missing data mechanism are presented first, and can be seen to be close to one under all conditions. The ratios for the SPMM are also generally close to one and standard errors are generally in the same range as those obtained in the LCM.

Table 4.

Comparison of Average Standard Error Estimates and Empirical Standard Deviation of Sampling Distributions for Fixed Effect Parameters by Missingness Condition and Model

	LCM			SPMM
	Average ${\overline{SE}}_j$	Empirical SD	Ratio	Average ${\overline{SE}}_j$	Empirical SD	Ratio
MAR
α0	1.74	1.84	.94	1.74	1.87	.93
α1	.30	.33	.91	.31	.34	.91
γ0	2.46	2.65	.93	2.47	2.66	.93
γ1	.43	.45	.96	.43	.50	.86
SPMM-Consistent
α0	1.85	1.90	.97	2.03	1.90	1.07
α1	.35	.35	1.00	.36	.33	1.09
γ0	2.61	2.71	.96	2.63	2.62	1.00
γ1	.49	.48	1.02	.42	.41	1.02
RC-MNAR-M
α0	1.88	1.90	.99	2.03	2.11	.96
α1	.25	.25	1.00	.30	.32	.94
γ0	2.66	2.60	1.02	2.63	2.67	.99
γ1	.36	.37	.97	.31	.36	.86
RC-MNAR-NM
α0	1.78	1.77	1.01	1.78	1.81	.98
α1	.24	.24	1.00	.25	.28	.89
γ0	2.51	2.44	1.03	2.51	2.46	1.02
γ1	.35	.34	1.03	.33	.33	1.00
OD-MNAR
α0	1.76	1.80	.98	1.84	1.79	1.03
α1	.25	.27	.92	.26	.27	.96
γ0	2.50	2.49	1.00	2.44	2.65	.92
γ1	.38	.36	1.06	.38	.37	1.03

Results from Dropout Conditions

We found that the LCM had more trouble accommodating missingness due to non-ignorable dropout than non-ignorable erratic missingness. This occurred because the observed repeated measures provide less information about the latent trajectories when the range of the observations is restricted. See Gottfredson (2011) for an analytical description of this phenomenon. When the SPMM was applied to the same data, slightly fewer classes were supported with a dropout mechanism than with erratic missingness. However, relatively few classes are needed to estimate unbiased fixed effects. Variance component estimates were more downwardly biased for the dropout conditions compared with erratic missingness conditions.

Summary of Simulation Study

Results from this study replicate previous findings that the LCM, which assumes that missing data are MAR, can produce biased estimates of growth factor fixed effects and variances when the MAR assumption is violated. Our results also replicate prior research by showing that the SPMM performs well with missing data that are generated using latent missingness classes. Extending prior research, we found that the SPMM mitigates bias with random coefficient dependent processes that are not isomorphic with the fitted model. This finding suggests that the SPMM may work well under commonly occurring conditions where the model is not literally correct. Indeed, the only condition for which the SPMM produced badly biased fixed effect estimates was the outcome dependent MNAR condition (i.e., when the missing data is partly due to a stochastic within-time process). It is also noteworthy that the SPMM was not able to recover variance components well when the missing data mechanism was RC-MNAR-NM. Finally, the SPMM outperforms the LCM under random coefficient-dependent missingness processes regardless of whether the missingness process is characterized by intermittent missingness or by dropout.

Under no condition did the SPMM provide more biased parameter estimates than the LCM; however, variance component estimates were less statistically efficient when the SPMM was used with MAR missingness. A researcher who obtains effectively identical point estimates when comparing results obtained using an LCM with results obtained using a SPMM may thus wish to rely on LCM results for the sake of parsimony because inefficiency in parameter estimation results in reduced power to detect effects.

Conclusions

A variety of techniques for handling non-randomly missing data have been presented in the literature (including major developments by Heckman, 1976; Wu & Carroll, 1986; Little, 1993; Diggle & Kenward, 1994; Roy, 2003; Lin et al., 2004, with summaries by Little, 2009, Enders, 2011, and Muthén et al., 2011). Yet, it seems that these techniques are employed only by those who develop the methods and a handful of other applied methodologists in the social sciences (e.g., Morgan-Lopez & Fals-Stewart, 2007). Enders (2011) suggested that the slow uptake of non-ignorable missing data modeling in the social sciences has been in part due to the lack of availability of user-friendly software programs to implement these models. Muthén et al. (2011) demonstrated how to implement a variety of missing data models in available software.

A second reason for the reluctance of applied researchers to implement models for handling non-randomly missing data is skepticism about the validity of results obtained by these models. Indeed, just as there have been numerous papers promoting methodological developments for handling missing data, several papers have pointed out shortcomings of these models (e.g., Winship & Mare, 1992; Kenward, 1998; Demirtas & Schafer, 2003; Molenberghs, Beunckens, & Sotto, 2008), and for good reason. There is no question that every model for handling non-randomly missing data relies on untestable assumptions.

The SPMM, in particular, makes the following assumptions: 1) that non-randomly missing data is exclusively random-coefficient dependent, 2) that the missing data indicators are adequate to summarize the information necessary to account for non-ignorability of the missing data process, 3) that conditional independence exists between the missing data indicators and the repeated measures (conditional on the latent classes), and 4) that it is meaningful to aggregate across missingness patterns to make inferences for the whole population.

What is less obvious, perhaps, is that the LCM (and similar commonly implemented techniques for longitudinal data analysis) also relies on an untestable assumption that missing data are MAR. In many applications, this assumption may be less tenable than those underlying SPMM or other models for MNAR data. The LCM is therefore not a justifiable modeling choice when MNAR missingness is possibly present, particularly when the level of informativeness of the missing data mechanism is potentially high. The problem with non-randomly missing data lies in its own nature, and not in the models used to handle it. As a number of methodologists have highlighted, the best way to handle missing data is through sensitivity analyses with full awareness of the assumptions and limitations inherent in various models (e.g., Little, 1994; Verbeke, Molenberghs, Thijs, Lesaffre, & Kenward, 2001; Enders, 2011). Contrasting the results of LCM and SPMM represents one such sensitivity analysis.

Beyond knowing the theoretical limitations of our models, it is also important to understand their practical limitations under real-world data conditions. This is one of the main contributions of the present manuscript. The simulation study presented here expanded Morgan-Lopez and Fals-Stewart’s (2008) earlier finding that latent mixture models work well with latent class dependent missingness. We demonstrated that SPMMs also work well with random coefficient dependent missingness that depends on latent continua, not just on latent classes. That is, this is the first research conducted that shows that the SPMM can ameliorate bias due to an MNAR process where the model provides an approximation (rather than literal embodiment) of this process. As expected, the approximation is best with random coefficient dependent missingness, but is, in general, insufficient with OD-MNAR. Additionally, the model has some difficulty recovering variance components when non-random selection operates on both ends of the random effect distribution. Encouragingly, this study showed that there is no substantial downside to estimating fixed effects using an SPMM (relative to LCM) even if data are randomly missing.

Practical Advice for Researchers

The SPMM should be used as a tool for carefully and thoughtfully checking of the sensitivity of traditional growth model results to violations of the MAR assumption. As with all statistical tools, the SPMM should not be employed mechanically, without regard to the theoretically plausible mechanisms underlying the missing data. Our primary piece of practical advice for researchers is to consider the plausibility of various missing data assumptions within their own data. In our experience, it is rarely the case that MNAR-type missingness can be safely assumed not to exist. If outcome-dependent missingness is a possibility, analysts should consider using a selection model, unless it can plausibly be assumed that it is the underlying trajectory for the outcome that is driving the missingness. If random coefficient-dependent missingness is possible, then SPMM should be used to check the sensitivity of model parameter estimates. The results presented here suggest that, when LCM-based parameter estimates differ from SPMM-based estimates, there is good evidence for a non-ignorable missing data process. In this case, the SPMM estimates are less biased than LCM estimates.

Our simulation study showed that there are three situations that lead to similar fixed effect estimates in the LCM and SPMM. The first is an MAR process, the second is a non-monotonic random coefficient-dependent process whereby there is selection occurring from both sides of the random effect distribution, and the third is an OD-MNAR process. Bias in variance component estimates is also expected to be similar across all of these conditions. In other words, when SPMM and LCM results are similar, there is no empirical way to test whether missingness is approximately conditionally random, whether it is due to a time-specific, outcome-dependent process, or whether data are missing due to two opposite, but non-random processes.

If it can reasonably be assumed that the missing data are not OD-MNAR, then it is safe to rely on the fixed effect estimates that are obtained in the LCM and SPMM. Reliance on variance component estimates is more uncertain, but the simulation study suggests that it is safe to say that the variance component estimates represent a lower bound of the true population variability. True variance components will be larger than the estimates presented here to the extent that there are non-random forces operating on both sides of the random slope distribution.

Limitations and Future Directions

As a matter of practicality, simulation studies are always limited in scope. We manipulated what we regarded as the most critical factors to evaluate, while limiting or holding constant other factors. One limitation of the simulation studies presented here is that the generating growth model was linear in form. It is possible, and even likely, that the SPMM will experience more difficulty efficiently accounting for random coefficient dependent missingness when the number of growth factors increases. For a related model, the semi-parametric growth model (Nagin, 1999), Sterba, Baldasaro, and Bauer (in press) found that the approximation of variance components declines as the number of latent growth factors increases. Unlike the semi-parametric growth model, however, the SPMM allows for within-class variability. The approximation afforded by the SPMM may thus be more robust to the addition of growth factors. Future research on SPMM performance should emphasize more complex models, both with respect to models of growth and with respect to missing data mechanisms. Another potential complication that might arise with more complex models for growth is the possibility of model under-identification. Future research should examine whether there are circumstances that lead to the need to rely on identification restrictions in these models.

In addition, future work should compare performance of SPMM with other types of models for random coefficient dependent missingness. For instance, it would be valuable to compare performance of the SPMM with traditional pattern mixture models when a small number of repeated measures are present, and to compare the SPMM with a parametric selection / shared parameter model in the presence of dropout. It will also be important to consider potential difficulties that may arise with categorical repeated measures. The most interesting future directions for research will involve thoughtful, real-world applications of SPMM across a range of contexts. It is hoped that the increasing awareness of MNAR and its implications will cause researchers to stop ignoring non-randomly missing data and to make use of the many MNAR modeling approaches that now exist. The practice of regularly conducting sensitivity analyses for missing data assumptions should be encouraged by editors and reviewers.