Structured functional additive regression in reproducing kernel Hilbert spaces

Summary

Functional additive models (FAMs) provide a flexible yet simple framework for regressions involving functional predictors. The utilization of data-driven basis in an additive rather than linear structure naturally extends the classical functional linear model. However, the critical issue of selecting nonlinear additive components has been less studied. In this work, we propose a new regularization framework for the structure estimation in the context of Reproducing Kernel Hilbert Spaces. The proposed approach takes advantage of the functional principal components which greatly facilitates the implementation and the theoretical analysis. The selection and estimation are achieved by penalized least squares using a penalty which encourages the sparse structure of the additive components. Theoretical properties such as the rate of convergence are investigated. The empirical performance is demonstrated through simulation studies and a real data application.

1. Introduction

Large complex data collected in modern science and technology impose tremendous challenges on traditional statistical methods due to their high-dimensionality, massive volume and complicated structures. Emerging as a promising field, functional data analysis (FDA) employs random functions as model units and is designed to model data distributed over continua such as time, space and wavelength; see Ramsay and Silverman (2005) for a comprehensive introduction. Such data may be viewed as realizations of latent or observed stochastic processes and are commonly encountered in many fields, e.g. longitudinal studies, microarray experiments, brain images.

Regression models involving functional objects play a major role in the FDA literature. The most widely used is the functional linear model, in which a scalar response Y is regressed on a functional predictor X through a linear operator

$$E(Y\mid X)={\int }_{\mathcal{T}}X\left(t\right)\beta \left(t\right)\mathit{dt},$$ (1)

where X(t) is often assumed to be a smooth and square-integrable random function defined on a compact domain $\mathcal{T}$, and β(t) is the regression parameter function which is also assumed to be smooth and square-integrable. A commonly adopted approach for fitting model (1) is through basis expansion, i.e. representing the functional predictor as the linear combinations of a set of basis $\left\{{\varphi }_k\right\}:X\left(t\right)=\mu \left(t\right)+{\sum }_{k=1}^{\infty }{\xi }_k{\varphi }_k\left(t\right)$, where μ(t) = EX(t). Model (1) is then transformed to a linear form of the coefficients $\{{\xi }_k,k=1,2,\dots \}:E(Y\mid X)=b_0+{\sum }_{k=1}^{\infty }{\xi }_k{b}_k$, where $b_0={\int }_{\mathcal{T}}\beta \left(t\right)\mu \left(t\right)\mathit{dt}$ and $b_k={\int }_{\mathcal{T}}\beta \left(t\right){\varphi }_k\left(t\right)\mathit{dt}$. More references on functional linear regression can be found in Cardot et al. (1999, 2003), Fan and Zhang (2000), etc. Extensions to generalized functional linear models were proposed by James (2002), Müller and Stadtmüller (2005) and Li et al. (2010). The basis set {ϕ_k} can be either predetermined (e.g. Fourier basis, wavelets, B-splines), or data-driven. One convenient choice for the latter is the eigenbasis of the auto-covariance operator of X, in which case the random coefficients {ξ_k} are called functional principal component (FPC) scores. The FPC scores have mean zero and variances equal to the corresponding eigenvalues {λ_k, k = 1, 2, …}. This isomorphic representation of X is referred to as the Karhunen-Loève expansion, and the related methods are often called functional principal component analysis (FPCA) (Rice and Silverman, 1991; Yao et al., 2005; Hall et al., 2006; Hall and Hosseini-Nasab, 2006; Yao, 2007). Due to the rapid decay of the eigenvalues, the orthogonal eigenbasis provides a more parsimonious and efficient representation compared to other basis. Furthermore, FPC scores are mutually uncorrelated, which can considerably simplify the model fitting and theoretical analysis. We focus on the FPC representation of the functional regression throughout this paper, nevertheless, the proposal is also applicable to other prespecified basis.

Although widely used, the linear relationship can be restrictive for general applications. This linear assumption is then relaxed by Müller and Yao (2008) who proposed the functional additive model (FAM). The FAM provides a flexible yet practical framework that accommodates nonlinear associations and at the same time avoids the curse of dimensionality encountered in high dimensional nonparametric regression problems (Hastie and Tibshirani, 1990). In the case of scalar response, the linear structure was replaced by the sum of nonlinear functional components, i.e.

$$E(Y\mid X)=b_0+\sum _{k=1}^{\infty }{f}_k\left({\xi }_k\right),$$ (2)

where {f_k(·)} are unknown smooth functions. In Müller and Yao (2008), the FAM was fitted by estimating {ξ_k} using FPCA (Yao et al., 2005) and estimating {f_k} using local polynomial smoothing.

Apparently regularizing (2) is necessary. In Müller and Yao (2008) the regularization was achieved by truncating the eigen-sequence to the first K leading components, where K was chosen to explain the majority of the total variation in the predictor X. Despite its simplicity, this naive truncation procedure can be inadequate in many complex problems. First, the impact of FPCs on the response does not necessarily coincide with their magnitudes specified by the auto-covariance operator of the predictor process alone. For instance, some higher order FPCs may contribute to the regression significantly more than the leading FPCs. This phenomenon was discussed by Hadi and Ling (1998) in the principal component regression context, and later was observed in real examples of high-dimensional data (Bair et al., 2006) and functional data (Zhu et al., 2007), respectively. Second, although a small number of leading FPCs might be able to capture the major variability in X due to the rapidly decaying eigenvalues, one often needs to include more components for better regression performance, especially for the prediction purpose as observed in Yao and Müller (2010). On the other hand, retaining more than needed FPCs brings the risk of over-fitting, which is caused by including components that contribute little to the regression but introduce noise. Therefore a desirable strategy is to automatically identify “important” components out of a sufficiently large number of candidates, whereas shrink those “unimportant” ones to zero.

With the above consideration, we seek an entirely new regularization and estimation framework for identifying the sparse structure of the FAM regression. Model selection that encourages sparse structure has received substantial attention in the last decade mostly due to the rapidly emerging high-dimensional data. In the context of linear regression, the seminal works include Lasso (Tibshirani, 1996), adaptive Lasso (Zou, 2006), SCAD (Fan and Li, 2001) and the references therein. Traditional additive models are considered by Lin and Zhang (2006), Meier et al. (2009) and Ravikumar et al. (2009); and the extensions to generalized additive models (GAM) are studied by Wood (2006) and Marra and Wood (2011). In comparison with these works, the sparse estimation in functional regression is much less explored. To our knowledge, most existing works are for functional linear models with sparse penalty(James et al., 2009; Zhu et al., 2010) or L² type penalty (Goldsmith et al., 2011). Relevant research for additive structures is scant in the literature. In this paper, we consider the selection and estimation of the additive components in FAMs that encourage a sparse structure, in the framework of reproducing kernel Hilbert space (RKHS). Unlike in standard additive models, the FPC scores are not directly observed in FAMs. They need to be firstly estimated from the functional covariates and then plugged into the additive model. The estimated scores are random variables, which creates a major challenge to the theoretical exploration. It is necessary to properly take into account the influence of the unobservable FPC scores on the resulting estimator. Furthermore, the functional curve X is not fully observed either. We typically collect repeated and irregularly spaced sample points, which are subject to measurement errors. The presence of measurement error in data adds extra difficulty for model implementation and inference. All of these issues are tackled in this paper. We propose a two-step estimation procedure to achieve the desired sparse structure estimation in FAM. For the regularization, we adopt the COSSO (Lin and Zhang, 2006) penalty due to its direct shrinkage effect on functions in the reproducing kernel Hilbert space. On the practical side, the proposed method is easy to implement, by taking advantage of existing algorithms of FPCA.

The rest of the article is organized as follows. In Section 2, we present the proposed approach and algorithm, as well as the theoretical properties of the resulting estimator. Simulation results with comparison to existing methods are included in Section 3. We apply the proposed method to the Tecator data in Section 4, studying the regression of the protein content on the absorbance spectrum. The concluding remarks are provided in Section 5, while the details of the estimation procedure and technical proofs are deferred to the appendices.

2. Structured functional additive model regression

Let Y be a scalar response associated with a functional predictor $X\left(t\right),t\in \mathcal{T}$, and let ${\{y_i,x_i(\cdot \left)\right\}}_{i=1}^n$, be the i.i.d. realizations of the pair {Y, X(·)}. The trajectories $\left\{x_i\right(t):t\in \mathcal{T}\}$ are often observed intermittently on possibly irregular grids t_i = (t_i1, …, t_iNi)^T Denote the discretized x_i(t) in the vector form as x_i = (x_i1, …, x_iNi)^T. To be realistic, we also assume that the trajectories are subject to i.i.d. measurement error, i.e. x_ij = x_i(t_ij) + e_ij with Ee_ij = 0 and Var(e_ij) = ν². Following the FPCA of Yao et al. (2005) and Yao (2007), denote ξ_i,∞ = (ξ_i1, ξ_i2, …)^T as the sequence of FPC scores of x_i, which is associated with eigenvalues {λ₁, λ₂, …} such that λ₁ ≥ λ₂ ≥ ⋯ ≥ 0.

2.1. Proposed methodology

As discussed in Section 1, the theory of FPCA enables isomorphic transformation of random functions to their FPC scores, which brings tremendous convenience to model fitting and theoretical development in functional linear regression. To establish a framework for the nonlinear and nonparametric regression, we consider regressing the scalar responses {y_i} directly on the sequences of FPC scores {ξ_i,∞} of {x_i}. For the convenience of model regularization, we would like to restrict the predictor variables (i.e. FPC scores) to take values on a closed and bounded subset of the real line, e.g. [0, 1] without loss of generality. This is easy to achieve by taking a transformation of the FPC scores through a monotonic function $\Psi :\Re \to [0,1]$, for all {ξ_ik}. In fact the choice of Ψ is rather flexible. A wide range of CDF functions can be used (see (a.2) in Section 2.2 for the regularity condition). Additionally one may choose Ψ so that the transformed variables have similar/same variations. This can be achieved by allowing Ψ(·) to depend on the eigenvalues {λ_k}, where {λ_k} serve as scaling variables. For simplicity, in the sequel we use a suitable CDF (e.g. normal), denoted by Ψ(·, λ_k), from a location-scale family with mean zero and variance λ_k. It is obvious that, if ξ_ik’s are normally distributed, the normal CDF leads to uniformly distributed transformed variables on [0, 1].

Denoting the transformed variable of ξ_ik by ζ_ik, i.e. ζ_ik = Ψ(ξ_ik, λ_k), and denoting ζ_i,∞ = (ζ_i1, ζ_i2, …)^T, we propose an additive model as follows:

$$y_i=b_0+\sum _{k=1}^{\infty }{f}_{0k}\left({\zeta }_{\mathit{ik}}\right)+{∊}_i,$$ (3)

where {∊_i} are independent errors with zero mean and variance σ², and $f_0\left({\zeta }_{i,\infty }\right)=b_0+{\sum }_{k=1}^{\infty }{f}_{0k}\left({\zeta }_{\mathit{ik}}\right)$ is a smooth function. For each k, let H^k be the lth order Sobolev Hilbert space on [0, 1], defined by H^k([0, 1]) = {g | g^(ν) is absolutely continuous for ν = 0, 1, … , l – 1; g^(l) ∈ L²}. One can show that H^k is an reproducing kernel Hilbert space (RKHS) equipped with the norm

$${\Vert g\Vert }^2=\sum _{\nu =0}^{l-1}{\left\{{\int }_0^1{g}^{\left(\nu \right)}\right(t\left)\mathit{dt}\right\}}^2+{\int }_0^1{\left\{g^{\left(l\right)}\right(t\left)\right\}}^2\mathit{dt}.$$

See Wahba (1990) and Lin and Zhang (2006) for more details. Note that H^k has the orthogonal decomposition $H^k=\left\{1\right\}\oplus {\stackrel{‒}{H}}^k$. Then the additive function f₀ corresponds to $\mathcal{F}$ which is a direct sum of subspaces, i.e. $\mathcal{F}=\left\{1\right\}\oplus {\sum }_{k=1}^{\infty }{\stackrel{‒}{H}}^k$ with $f_{0k}\in {\stackrel{‒}{H}}^k$, for all k. It is easy to check that, for any $f=b+{\sum }_k{f}_k\in \mathcal{F}$, we have ${\Vert f\Vert }^2=b^2+{\sum }_{k=1}^{\infty }{\Vert f_k\Vert }^2$. In this paper, we take l = 2 but the results can be extended to other cases straightforwardly. To distinguish the Sobolev norm from the L² norm, we write ∥ · ∥ for the former and for ∥ · ∥_L² for the latter.

As motivated in Section 1, it is desirable to impose some type of regularization conditions on model (3) to select “important” components. An important assumption commonly made in high-dimensional linear regression is the sparse structure of the underlying true model. This assumption is also critical in the context of functional data analysis, which enables us to develop a systematic strategy than the heuristic truncation that retains the leading FPCs. Although widely adopted, retaining the leading FPCs is a strategy guided solely by the covariance operator of the predictor X, and therefore it fails to take into account the response Y . To be more flexible, we assume that the number of important functional additive components that contribute to the response is finite, but not necessarily restricted to the leading terms. In particular, we denote $\mathcal{I}$ the index set of the important components and assume that $\mid \mathcal{I}\mid <\infty$, where ∣ · ∣ denotes the cardinality of a set. In other words, there exists a sufficiently large s such that $\mathcal{I}\subseteq \{1,\dots ,s\}$, which implies that f_k ≡ 0 as long as k > s. The FAM is thus equivalent to

$$y_i=b_0+\sum _{k=1}^s{f}_{0k}\left({\zeta }_{\mathit{ik}}\right)+{∊}_i.$$ (4)

It is noticed that the initial truncation s merely controls the total number of additive components to be considered, which is different from the heuristic truncation suggested by Yao et al. (2005) and Müller and Yao (2008) based on model selection criteria such as cross validation, AIC, or the fraction of variance explained. In practice we suggest to choose s large so that nearly 100% of the total variation is explained. This often leads to more than 10 FPCs in most empirical cases.

With the above assumption, the regression function $f_0\left(\zeta \right)=b_0+{\sum }_{k=1}^s{f}_{0k}\left({\zeta }_k\right)$ lies in the truncated subspace ${\mathcal{F}}^s=\left\{1\right\}\oplus {\sum }_{k=1}^s{H}^k$ of $\mathcal{F}$, where ζ is the truncated version of ζ_∞, i.e. ζ = (ζ₁, … , ζ_s)^T with the dependence on s suppressed if no confusion arises. To nonparametrically regularize the unknown smooth functions {f_0k}, we employ the COSSO regularization defined for the function estimation in RKHS and estimate f₀ by finding $f\in {\mathcal{F}}^s$ that minimizes

$$Q(f\mid {\zeta }_i)=\frac{1}{n}\sum _{i=1}^n{\{y_i-f({\zeta }_i\left)\right\}}^2+{\tau }_n^{2}J\left(f\right),\text{with}J\left(f\right)=\sum _{k=1}^s\Vert P^{k}f\Vert ,$$ (5)

where P^kf is the orthogonal projection of f onto ${\stackrel{‒}{H}}^k$. Here τ_n is the only smoothing parameter that requires tuning, whereas the common smoothing spline approach involves multiple smoothing parameters. The penalty J(f) is a convex functional and is a pseudonorm in ${\mathcal{F}}^s$. One interesting connection between COSSO and LASSO is that, when f_0k(ζ_k) = ζ_kβ_0k, the penalty in (5) reduces to ${\sum }_{k=1}^s\mid {\zeta }_k{\beta }_{0k}\mid$, which becomes the adaptive Lasso penalty (Zou, 2006).

Different from the standard additive regression models, the transformed FPC scores {ζ_i} serving as predictor variables in (5) cannot be observed. Therefore we need to estimate the FPC scores first before the estimation and structure selection of f. A simple two-step algorithm is given as follows.

Algorithm

Step 1

Implement FPCA to estimate the FPC scores {ξ_i1, … , ξ_is} of x_i, and then the transformed variables ${\widehat{\zeta }}_{\mathit{ik}}=\Psi ({\widehat{\xi }}_{\mathit{ik}},{\widehat{\lambda }}_k)$, where ${\widehat{\lambda }}_k$ is the estimated eigenvalue, and s is chosen to explain 100% of the total variation.

Step 2

Implement the COSSO algorithm of Lin and Zhang (2006) to solve

$$\underset{f\in {\mathcal{F}}^s}{\min }Q(f\mid {\widehat{\zeta }}_i)=\underset{f\in {\mathcal{F}}^s}{\min }\frac{1}{n}\sum _{i=1}^n{\{y_i-f(\widehat{\zeta }\left)\right\}}^2+{\tau }_n^{2}J\left(f\right),\text{with}J\left(f\right)=\sum _{k=1}^s\Vert P^{k}f\Vert .$$ (6)

We would like to refer to Appendix A for the details in case of densely or sparsely observed predictor trajectories. We call the proposed method the component selection and estimation for functional additive model, abbreviated as CSE-FAM.

2.2. Theoretical properties

We focus on the consistency of the resulting estimator of CSE-FAM for the case when {x_i(t)} are densely observed in this subsection, where the rate of convergence is assessed using the empirical norm. In particular, we introduce the empirical norm and the entropy of ${\mathcal{F}}^s$ as follows. Let $g\in {\mathcal{F}}^s$, the empirical norm of g is defined as ${\Vert g\Vert }_n=\sqrt{1∕n{\sum }_{i=1}^{n}g{\left({\zeta }_i\right)}^2}$. The empirical inner product of the error term ∊ and g is defined as ${(∊,g)}_n=1∕n{\sum }_{i=1}^n{∊}_{i}g\left({\zeta }_i\right)$. Similarly, the empirical inner product of f and g in ${\mathcal{F}}^s$ is ${(f,g)}_n=1∕n{\sum }_{i=1}^{n}f\left({\zeta }_i\right)g\left({\zeta }_i\right)$.

The assumptions on the regression function f and the transformation Ψ(·,·) are listed below in (a.1)–(a.2), while the commonly adopted regularity conditions on the functional predictors {x_i(t)}, the dense design, and the smoothing procedures are deferred to (b.1)–(b.3) in Appendix B.

(a.1) For any $f\in {\mathcal{F}}^s$, there exist independent ${\left\{B_i\right\}}_{i=1}^n$ with $E\left(B_i^2\right)<\infty$, such that with probability 1,

$$\mid \frac{\partial f\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}\mid \le B_i{\Vert f\Vert }_{L^2}.$$

(a.2) The transformation function Ψ(ξ, λ) is differentiable at ξ and λ, and satisfies that ∣∂/∂ξΨ(ξ, λ)∣ ≤ Cλ^γ and ∣∂/∂λΨ(ξ, λ)∣ ≤ Cλ^γ∣ξ∣ for some constant C and γ (γ < 0). The assumption (a.1) is a regularization condition that controls the amount of fluctuation in f relative to its L² norm. For (a.2), one can easily verify that, if choosing Ψ(·,·) to be the normal CDF with zero mean and variance λ, then C = 1 and γ = −1/2 (when λ > 1) or γ = −3/2 (when 0 < λ < 1). One can also choose the CDF of student-t distributions with variances λ.

For brevity of the presentation, the technical lemmas and proofs are deferred to Appendix B. It is noticed that the existence of the minimizer for the criterion (5) is guaranteed in analogy to Theorem 1 of Lin and Zhang (2006), by considering a design conditional on the input {y_i, ζ_i1, … , ζ_is}, i = 1, … , n, where s is the initial truncation parameter.

Theorem 1

Consider the regression model (4) with ζ_ik = Ψ(ξ_ik, λ_k), where ${\left\{{\xi }_{\mathit{ik}}\right\}}_{k=1}^s$ are FPC scores of x_i(t) based on densely observed trajectories, and ${\left\{{\lambda }_k\right\}}_{k=1}^s$ are the corresponding eigenvalues. Let $\widehat{f}$ be the minimizer of the target function (6) over $f\in {\mathcal{F}}^s$, and let τ_n be the tuning parameter in (6). Assume that the assumptions (a.1)–(a.2) and (b.1)–(b.3) hold. If J(f₀) > 0 and

$${\tau }_n^{-1}=n^{2∕5}{J}^{3∕10}\left(f_0\right),$$ (7)

then ${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-2∕5}\right)J^{1∕5}\left(f_0\right)$ and $J\left(\widehat{f}\right)=J\left(f_0\right)O_p\left(1\right)$. If J(f₀) = 0 and

$${\tau }_n^{-1}=n^{1∕4},$$ (8)

then ${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-1∕2}\right)$ and $J\left(\widehat{f}\right)=O_p\left(n^{-1∕2}\right)$. It is worth mentioning that the technical difficulty arises from the unobserved variables ζ_i, and major effort has been devoted to tackle the influence of the estimated quantities ${\widehat{\zeta }}_i$ on the resulting estimator by utilizing the analytical tools from the spectral decomposition of the auto-covariance operator of X. Theorem 1 suggests that, if the repeated measures observed for all individuals are sufficiently dense and J(f₀) is bounded, the resulting estimator $\widehat{f}$ obtained from (6) has the rate of convergence n^−2/5, which is the same as the rate when {ζ_i} are directly observed.

3. Simulation studies

To demonstrate the performance of the proposed CSE-FAM approach, we conduct simulation studies under different settings. In Section 3.1 and 3.2, we study the performance of CSE-FAM for dense and sparse functional data, respectively, assuming that the underlying true model contains both “important” and “unimportant” additive components. We compare the CSE-FAM approach with the FAM-type methods and the multivariate adaptive regression splines (MARS). The FAM-type methods are implemented in three different ways, two of which are the “oracle” methods: FAM_O1 and FAM_O2, both assuming full knowledge of the underlying model structure. In particular, the FAM_O1 serves as the gold standard, in which both the true values of {ζ_ik} and the true non-vanishing additive components are used. The FAM_O2 is another type of oracle, in which the values of {ζ_ik} are estimated through FPCA, but the true non-vanishing additive components are used. In Section 3.3, we study the performance of CSE-FAM when the underlying true model is actually non-sparse, and compare the results with the saturated and truncated FAM models. For each setting, we perform 100 Monte Carlo simulations and present the model selection and prediction results for the methods under comparison.

3.1. Dense functional data

We generate 1, 000 i.i.d. trajectories using 20 eigenfunctions, among which n = 200 are randomly allocated to the training set and the rest 800 form the test set. The functional predictors x_i(t), t ∈ [0, 10], are measured over a grid with 100 equally spaced points, with independent measurement error e_ij ~ N(0, v²), v² = 0.2. The eigenvalues of x_i(t) are generated by λ_k = ab^k−1 with a = 45.25, b = 0.64. The true FPC scores {ξ_ik} are generated from N(0, λ_k), and the eigenbasis {ϕ_k(·)} is taken to be the first twenty Fourier basis functions on [0, 10]. The mean curve is set to be μ_x(t) = t + sin(t). We use the normal CDF to obtain the transformed variables: ζ_k = Ψ(ξ_k; 0, λ_k), k = 1, … , 20. The values of y_i are then generated by y_i = f₀(ζ_i) + ∊_i, where ∊i ~ N(0, σ²) and σ² = 1. We assume that the f₀ only depends on three nonzero additive components, the first, the second and the fourth, i.e. f₀(ζ_i) = b₀ + f₀₁(ζ_i1) + f₀₂(ζ_i2) + f₀₄(ζ_i4), $\mathcal{I}=\{1,2,4\}$. Here we take b₀ = 1.4, f₀₁(ζ₁) = 3ζ₁ − 3/2, f₀₂(ζ₂) = sin(2π(ζ₂ − 1/2)), f₀₄(ζ₄) = 8(ζ₄ − 1/3)² − 8/9 and f_0k(ζ_k) ≡ 0 for $k\notin \mathcal{I}$. This gives the signal-to-noise ratio (SNR) 2.2, where the SNR is defined as SNR = Var(f₀(ζ))/Var(∊), where $\mathrm{Var}\left(f_0\right(\zeta \left)\right)={\sum }_{k\in \mathcal{I}}{\int }_0^1{f}_{0k}^2\left({\zeta }_k\right)d{\zeta }_k=2.2$ given that ζ_k ~ U[0, 1].

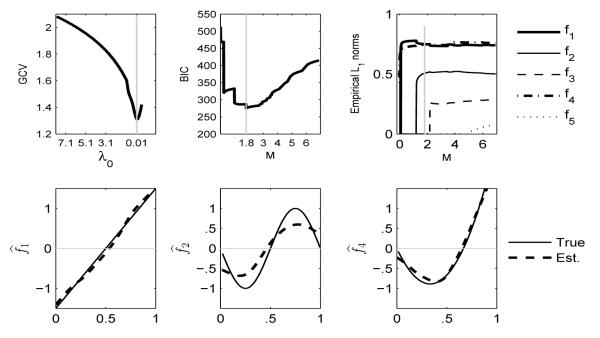
We apply the proposed CSE-FAM algorithm to the training data, following the FPCA and COSSO steps described in Section 2.1 and Appendix A. For illustration, we pick one Monte Carlo simulation and display the component selection and estimation results in Figure 1. In FPCA, the initial truncation is s = 18 accounting for nearly 100% of the total variation, and is passed to the COSSO step. The component selection is then achieved by tuning the regularization parameters λ₀ in (9) with generalized cross validation(GCV) and M in (10) with Bayesian information criterion(BIC), illustrated in the top left and top middle panels of Figure 1, while the empirical L₁ norms of ${\widehat{f}}_k$, (computed by $n^{-1}{\sum }_{i=1}^n\mid {\widehat{f}}_k\left({\widehat{\zeta }}_{\mathit{ik}}\right)\mid$ at different M) are shown in the top right panel. In the bottom panels of Figure 1, the resulting estimates of f_k, k = 1, 2, 4, are displayed, and $\{{\widehat{f}}_k,k\ne 1,2,4\}$ are shrunk to 0 as desired.

Fig. 1.

The plots of component selection and estimation results from one simulation. Top Left: GCV vs. λ₀. Top middle: BIC vs. M. Top right: empirical L₁ norms at different M values. The gray vertical bars in the top panels indicate the tuning parameters chosen. The three bottom panels show the estimated f_k’s (dashed line) vs. the true (solid line), for k = 1, 2, 4.

The model selection and prediction results are presented in the top panel of Table 1. We implement the FAM procedure in a different manner from that in Müller and Yao (2008). Instead of using local polynomial smoothing for estimating each f_k separately, we perform a more general additive fitting, the generalized additive model (GAM), on the transformed FPC scores which allows back-fitting and also provides a p-value for each additive components. The only reason for doing so is that the GAM algorithm shows more numerical stability especially when the number of additive components is large. Due to the use of the true model structure, both oracle methods FAM_O1 and FAM_O2 are expected to outperform the rest. Because of the estimation error induced in the FPCA step, FAM_O2 is expected to sacrifice certain estimation accuracy and prediction power as compared to FAM_O1. The FAM_S is the saturated model based on the estimated FPC scores and the leading s terms used in the CSE-FAM. No model selection is performed in FAM_S. The s values vary from 17 to 19 which take into account nearly 100% of the total variation of {x_i(t)}. The MARS method is based on Hastie et al. (2001).

Table 1.

Summary of the model selection and prediction in 100 Monte Carlo simulations under the dense and sparse design.

Data	Model	Model Size								Selection Frequency								PE
		1	2	3	4	5	6	7	8	${\widehat{\zeta }}_1$	${\widehat{\zeta }}_2$	${\widehat{\zeta }}_3$	${\widehat{\zeta }}_4$	${\widehat{\zeta }}_5$	${\widehat{\zeta }}_6$	${\widehat{\zeta }}_7$	${\widehat{\zeta }}_8$
	CSE-FAM	0	5	61	29	5	0	0	0	100	94	22	100	7	3	0	1	1.30 (.13)
	FAMS	0	0	10	32	21	21	8	4	100	98	51	100	32	14	12	8	1.50 (.17)
Dense	MARS	-	-	-	-	-	-	-	-	100	99	60	100	41	23	25	18	1.46 (.16)
design	FAMO2	0	1	99	-	-	-	-	-	100	99	-	100	-	-	-	-	1.28 (.12)
	FAMO1	0	0	100	-	-	-	-	-	100	100	-	100	-	-	-	-	1.07 (.06)
	CSE-FAM	0	22	61	13	4	0	0	0	100	78	10	82	12	9	7	1	2.07 (.16)
	FAMS	0	0	14	30	25	20	9	2	100	98	41	96	35	17	9	12	2.17 (.16)
Sparse	MARS	-	-	-	-	-	-	-	-	100	98	58	98	56	30	20	23	2.11 (.14)
design	FAMO2	0	4	96	-	-	-	-	-	100	98	-	98	-	-	-	-	2.01 (.14)
	FAMO1	0	0	100	-	-	-	-	-	100	100	-	100	-	-	-	-	1.05 (.05)

It is noticed that the subjective truncation based on the explained variation in X is suboptimal for regression purpose (results not reported for conciseness). Therefore, in Table 1, we report (under the “model size” column) the counts of selected number of nonvanishing additive components in CSE-FAM, and the counts of the number of significantly nonzero additive components in FAM, FAM_O1 and FAM_O2. For display convenience, only the counts for model size up to 8 are reported. The “selection frequency” of Table 1 records the number of times that each additive component is estimated to be nonzero. For MARS, if the jth covariate ${\widehat{\zeta }}_j$ is selected in one or more basis functions, we counted as 1 and 0 otherwise. Regarding the prediction error (PE), we use the population estimate from the training set (e.g. mean, covariance and eigenbasis) to get the FPC scores for both training and test set, then apply the $\left\{{\widehat{f}}_k\right\}$ estimated from the training set to get predictions for {y_i} in the test set. The prediction errors are calculated by $n^{-1}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2$. From the top panel of Table 1, we see that under the dense design, the CSE-FAM chooses the correct models (with model size equals three) 61% of the time whereas the FAM_S always overselects (α = 0.05 is used to retain significant additive components). The PE of CSE-FAM is the smallest among the three non-oracle models. As compared with the oracle methods, the CSE-FAM has less prediction power than FAM_O2 (slightly) and FAM_O1, which can be regarded as the price paid by both estimating the ζ and selecting the additive components.

To assess the estimation accuracy, the averaged integrated squared errors (AISE) for the first eight additive components are presented in the top panel of Table 2, where the ISE is defined by $\mathrm{ISE}\left(f_k\right)=E_{{\zeta }_k}{\left\{{\widehat{f}}_k\right({\zeta }_k)-f_k({\zeta }_k\left)\right\}}^2={\int }_0^1{\left({\widehat{f}}_k\right(t)-f_k(t\left)\right)}^2\mathit{dt}$. From Table 2, we see the CSE-FAM provides smaller ISE for the truly zero components (f_j, j = 1, 3, 6, 7, 8) than the FAM_S. For the nonzero components, the CSE-FAM, FAM_S and FAM_O2 have similar AISE values.

Table 2.

Averaged ISE for 100 Monte Carlo simulations under the dense and sparse design.

	Name	AISE
		f 1	f 2	f 3	f 4	f 5	f 6	f 7	f 8	f
	CSE-FAM	.038	.117	.022	.038	.005	.001	.000	.001	.226
Dense	FAMS	.030	.095	.050	.047	.031	.018	.016	.015	.476
design	FAMO2	.027	.090	-	.042	-	-	-	-	.158
	FAMO1	.007	.028	-	.019	-	-	-	-	.054
	CSE-FAM	.033	.22	.036	.298	.055	.040	.045	.001	.720
Sparse	FAMS	.016	.118	.032	.159	.102	.121	.399	2.64	> 103
design	FAMO2	.026	.129	-	.220	-	-	-	-	.376
	FAMO1	.007	.016	-	.013	-	-	-	-	.036

3.2. Sparse functional data

To compare with the dense case, we also conducted a simulation to examine the performance of CSE-FAM for sparse functional data. We generated 1, 200 i.i.d. trajectories, with 300 in the training set and 900 in the test set. In each trajectory, there are 5 – 10 repeated observations uniformly located on [0, 10], with the number of points chosen from 5 to 10 with equal probabilities. The other settings are the same as in the dense design. The summary of the model selection, prediction and estimation results are presented in the bottom panel of Table 1 and Table 2. We observe the similar pattern as in the dense design case. Moreover, Table 2 suggests that, for the sparse design, the FAM_S estimate of f_k becomes quite unstable for higher order components (e.g. k ≥ 7). The AISE increases rapidly due to the influence of outlying estimates. This is not a surprise, because under the sparse design the high-order eigenfunctions and FPC scores are difficult to be estimated accurately due to the sparseness of the data and the moderate sample size, which leads to inaccurate f_k estimates when the saturated model FAM_S is used. In this situation, we see that the proposed CSE-FAM model still performs quite stable, since the COSSO penalty has the effect of automatically down-weighting the “unimportant” components. This provides further support for the proposed CSE-FAM approach.

3.3. Non-sparse underlying additive components

To show the model performance when the true additive components are actually non-sparse, we conduct an additional simulation with two settings (Study I and Study II) for the dense design, and compare the CSE-FAM with two versions of the FAM model: the saturated model FAM_S as defined in Section 3.1, and the truncated model FAM_T with a truncation chosen to retain 99% of the total variation. In Study I, the true model contains three “larger” additive components {f₀₁, f₀₂, f₀₄}, taking the same form as in Section 3.1 except being rescaled by a constant 1/2. The rest are “smaller” additive components, each randomly selected from {f₀₁, f₀₂, f₀₄} with equal probability and rescaled by a smaller constant uniformly chosen from [1/17, 1/14]. The data generated have a lower (more challenging) signal-to-noise ratio (SNR) around 0.60, among which 8.7% are from the “smaller” components. The results are listed in the top panel of Table 3, which shows that the CSE-FAM tends to favor smaller model size than FAM_S. We also observe that the model size of FAM_T tends to be smaller than CSE-FAM since it adopts more truncation with the 99% threshold. It is important to note that CSE-FAM in fact yields PE and AISE substantially smaller than FAM_S, and the results of CSE-FAM are comparable to that of FAM_T. In Study II, we replace the three “larger” components by the “smaller” ones, therefore all additive components have roughly equal small contributions. We select the scaling constant uniformly from [1/8, 1/6] so that the total SNR is 0.30 on average. The results listed in the bottom panel of Table 3 suggest that the CSE-FAM now tends to select more components (i.e. produce non-sparse fits) and again yields smaller PE and AISE than both FAM_S and FAM_T. Overall, this simulation suggests that, the proposed CSE-FAM is still a reasonable option even if the underlying true model is non-sparse. It is also worth mentioning that the gain of the CSE-FAM is more apparent in the challenging settings with low SNR.

Table 3.

An additional simulation for cases with non-sparse additive components. I: the true model contains both “larger” and “smaller” additive components; II: the true model only contains “small” additive components.

	Model	Model Size								Selection Frequency								PE	AISE of f
		1	2	3	4	5	6	7	8	${\widehat{\zeta }}_1$	${\widehat{\zeta }}_2$	${\widehat{\zeta }}_3$	${\widehat{\zeta }}_4$	${\widehat{\zeta }}_5$	${\widehat{\zeta }}_6$	${\widehat{\zeta }}_7$	${\widehat{\zeta }}_8$
	CSE-FAM	0	3	20	34	26	9	6	2	100	88	12	100	17	12	10	10	1.19 (.08)	.17
I	FAMS	0	4	16	18	29	17	7	8	100	92	16	99	20	17	19	16	1.33 (.12)	.33
	FAMT	0	4	39	35	15	6	0	1	100	91	15	100	19	15	9	9	1.22 (.08)	.18
	CSE-FAM	1	2	4	12	13	20	26	13	46	42	33	42	36	42	38	44	1.25 (.07)	.12
II	FAMS	1	6	8	25	14	13	13	10	42	45	29	37	29	38	36	36	1.38 (.11)	.42
	FAMT	13	30	22	20	6	6	2	0	34	35	20	31	25	38	34	30	1.32 (.08)	.20

4. Real data application

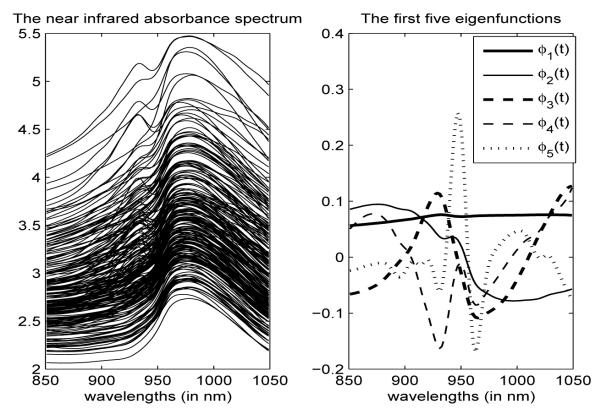
We demonstrate the performance of the proposed method through the regression of protein content on the near infrared absorbance spectral measured over 240 meat samples. The dataset is collected by the Tecator company and is publicly available on the StatLib web-site (http://lib.stat.cmu.edu). The measurements were made through a spectrometer named Tecator Infratec Food and Feed Analyzer. The spectral curves were recorded at wavelengths ranging from 850nm to 1050nm. For each meat sample the data consist of a 100 channel spectrum of absorbances (100 grid points) as well as the contents of moisture (water), fat and protein. The absorbance is −log₁₀ of the transmittance measured by the spectrometer. The three contents, measured in percent, are determined by analytic chemistry. Of primary interest is to predict the protein content using the spectral trajectories. The 240 meat samples were randomly split into a training set (with 185 samples) and a test set (with 55 samples). We aim to predict the content of protein in the test set based on the training data. Figure 2 illustrates the spectral curves and the first five eigenfunctions estimated using FPCA.

Fig. 2.

The near infrared absorbance spectral curves (left) and the first five estimated eigenfunctions(right).

We initially retain the first 20 FPCs which take into account nearly 100% of the total variation. The proposed CSE-FAM is then applied for component selection and estimation. The determination of the tuning parameters in the COSSO step is guided by the GCV criterion for λ₀ which gives λ₀ = 0.0013, and by 10-fold cross-validation for M which gives M = 10.0. The estimated additive components are plotted in Figure 3, from which we see that the CSE-FAM selects 12 out of the 20 components, $\{{\widehat{f}}_1,\dots ,{\widehat{f}}_8,{\widehat{f}}_{10},{\widehat{f}}_{13},{\widehat{f}}_{16},{\widehat{f}}_{17}\}$, and the other components are estimated to be zero. To assess the performance of the proposed method, we report the prediction error (PE) on the test set in Table 4, where the PE is calculated in the same way as in Section 3. We also report the quasi-R² for the test set, which is defined as $R_Q^2=1-{\sum }_i{(y_i-{\widehat{y}}_i)}^2∕{\sum }_i{(y_i-{\stackrel{‒}{y}}_i)}^2$. To show the influence of the initial truncation, we also use a small value of s, s = 10 in CSE-FAM, which gives suboptimal results. This suggests that we shall use a suffciently large s to begin with. The FAM is carried out with the leading 5, 10, 20 FPCs, respectively. An interesting phenomenon is that, though the high-order FPCs (over 10) explain very little variation of the functional predictor (less than 1%), their contribution to the prediction is surprisingly substantial. Such phenomena are also observed for MARS and partial least squares (PLS is a popular approach in chemometrics; see Xu et al. (2007) and the references therein). One more comparison is with the classical functional linear model (FLM) with the estimated leading FPCs served as predictors, where a heuristic AIC is used to choose the first 7 components. From Table 4, we see that, when the initial truncation is set at 10, the proposed CSE-FAM is not obviously advantageous compared to FAM. As the number of FPCs increases to 20, the proposed method provides much smaller PE and higher $R_Q^2$ than all other methods. A sensible explanation is that, for this data, most of the first 10 FPCs (except the 9th) have nonzero contributions to the response (shown in Figure 3), therefore penalizing these components does not help to improve the prediction. However, as the number of FPC scores increases, more redundant terms come into play, so the penalized method (CSE-FAM) gains more prediction power. We have repeated this analysis for different random splits of the training and test sets, and the conclusions stay virtually the same.

Fig. 3.

Plots of the estimated additive components {f_k(·), k = 1, … , 20}.

Table 4.

Prediction results on the test set as compared with several other methods. Note: PC10 indicates that 10 FPC scores are used. PLD20 indicates the number of PLS directions used is 20. AIC7: 7 FPC scores are used based on the regression AIC criterion.

	CSE-FAM		FAM			MARS	PLS	FLM
	s = 10	s = 20	PC5	PC10	PC20	PC20	PLD20	AIC7
PE	2.22	0.72	3.98	2.13	0.84	0.77	1.02	1.50
$R_Q^2$	0.82	0.94	0.68	0.83	0.93	0.93	0.92	0.88

5. Discussion

We proposed a structure estimation method for functional data regression where a scalar response is regressed on a functional predictor. The model is constructed in the framework of FAM, where the additive components are functions of the scaled FPC scores. The selection and estimation of the additive components are performed through penalized least squares using the COSSO penalty in the context of RKHS. The proposed method allows for more general nonparametric relationships between the response and predictors, therefore serves as an important extension of the functional linear regression. Through the adoption of the additive structure, it avoids the curse of dimensionality caused by the infinite-dimensional predictor process. The proposed method provides a way to select the important features of the predictor processes and simultaneously shrink the unimportant ones to zero. This selection scenario takes into account not only the explained variation of the predictor process, but also its contribution to the response. The theoretical result shows that, under the dense design, the nonparametric rate from component selection and estimation will dominate the discrepancy due to the unobservable FPC scores.

A concern raised is whether the sparsity is necessary in the FAM framework. The sparseness assumption in general helps balance the trade-off between variance and bias, which may lead to improved model performance. This can be particularly useful when part of the predictor has negligible contribution to the regression. Even if the underlying model is in fact non-sparse and one only cares about estimation and prediction, the proposed CSE-FAM is still a reasonable option, as illustrated by the simulation in Section 3.3. We also point out that, when all non-zero additive components are linear, the COSSO penalty reduces to the adaptive Lasso penalty. An additional simulation (not reported for conciseness) has shown that the proposed method produces estimation and prediction results comparable with adaptive Lasso. Moreover, the COSSO penalty requires that s < n, which does not conflict with the requirement that the initial truncation s is chosen suffciently large to include all important features. In practice the number of FPCs accounting for nearly 100% predictor variation is often far less than the sample size n due to the fast decay of the eigenvalues. Finally both simulated and real examples indicate that the model performance is not sensitive to s as long as it is chosen large enough.

On the computation side, our algorithm takes advantage of both FPCA and COSSO. On a desktop with Intel(R) Core(TM) i5-2400 CPU with a 3.10 GHZ processor and 8GB RAM, each Monte Carlo sample in Section 3.1 takes 30 seconds; and the real data analysis takes about 10 seconds. As far as the dimensionality is concerned, the capacity and speed depend on the particular FPCA algorithm used. We have used the PACE algorithm which can deal with fairly large data (http://anson.ucdavis.edu/~ntyang/PACE/). For dense functional data with 5000 or more dimensions, pre-binning is suggested to accelerate the computation. FPCA algorithm geared towards extremely large dimension (with identical time grid for all subjects) is also available; for instance, Zipunnikov et al. (2011) considered fMRI data with dimension in the order of O(10⁷) through partitioning the original data matrix to blocks and performing SVD using blockwise operation.

Although we have focused on the FPC-based analysis in this work, the CSE-FAM framework is generally applicable to other basis structure, e.g. splines and wavelets, where the additive components are functions of the corresponding basis coeffcients of the predictor process. It may also work for nonparametric penalties other than COSSO, such as the sparsity-smoothness penalty proposed in Meier et al. (2009). The proposed method may be further extended to accommodate categorical responses, where an appropriate link function can be chosen to associate the the mean response with the additive structure. Another possible extension is the regression with multiple functional predictors, where component selection can be performed for selecting significant functional predictors. In this case the additive components associated with each functional predictor need to be selected in a group manner.

Appendix A. The estimation procedure

To estimate ζ_i, we assume that the functional predictors are observed with measurement error on a grid of $\mathcal{T}$ . We adopt two different procedures for functional data that are either densely or sparsely observed.

• Obtain ${\widehat{\zeta }}_i$ in the dense design. If {x_i(t)} are observed on a suffciently dense grid for each subject, we apply the local linear smoothing to the data {t_ij, x_ij} j=1,…,N_i individually, which gives the smooth approximation ${\widehat{x}}_i\left(t\right)$. The mean and covariance function are obtained by $\widehat{\mu }\left(t\right)=1∕n{\sum }_{i=1}^n\widehat{x}\left(t\right)$, and $\widehat{G}(s,t)=1∕n{\sum }_{i=1}^n\left\{{\widehat{x}}_i\right(s)-\widehat{\mu }(s\left)\right\}\left\{{\widehat{x}}_i\right(t)-\widehat{\mu }(t\left)\right\}$, respectively. The eigenvalues and eigenfunctions are estimated by solving the equation ${\int }_{\mathcal{T}}\widehat{G}(s,t){\varphi }_k\left(s\right)\mathit{ds}={\lambda }_k{\varphi }_k\left(t\right)$ for λ_k and ϕk(·), subject to ${\int }_{\mathcal{T}}{\varphi }_k^2\left(t\right)\mathit{dt}=1$ and ∫τ ϕm(t)ϕk(t)dt = 0 for m ∉ k, k,m = 1, … , s. The FPC scores are obtained by ${\widehat{\xi }}_{\mathit{ik}}={\int }_{\mathcal{T}}\left({\widehat{x}}_i\right(t)-\widehat{\mu }(t\left)\right){\widehat{\varphi }}_k\left(t\right)\mathit{dt}$. Finally CDF transformation yields ${\widehat{\zeta }}_{\mathit{ik}}=\Psi ({\widehat{\xi }}_{\mathit{ik}};0,{\widehat{\lambda }}_k)$.

• Obtain ${\widehat{\zeta }}_i$ in the sparse design. We adopt the principal component analysis through the conditional expectation (PACE) proposed by Yao et al. (2005), where the mean estimate $\widehat{\mu }\left(t\right)$ is obtained using local linear smoothers based on the pooled data of all individuals. In particular, $\widehat{\mu }\left(t\right)={\sum }_{i=1}^n{\sum }_{j=1}^{N_i}K\left\{\right(t_{\mathit{ij}}-t)∕b\}{\{x_{\mathit{ij}}-{\beta }_0-{\beta }_1(t-t_{\mathit{ij}}\left)\right\}}^2$ with K(·) a kernel function and b a bandwidth. For the covariance estimation, denote $G_{\mathit{ijl}}=\{x_{\mathit{ij}}-\widehat{\mu }(t_{\mathit{ij}}\left)\right\}\{x_{\mathit{il}}-\widehat{\mu }(t_{\mathit{il}}\left)\right\}$ and the $K_h^{\ast }(\cdot ,\cdot )$ be a bivariate kernel function with a bandwidth h, one minimizes ${\sum }_{i=1}^n{\sum }_{j\ne l}{K}^{\ast }\left\{\right(t_{\mathit{ij}}-s)∕h,(t_{\mathit{il}}-t)∕h\}{\{G_{\mathit{ijl}}-{\beta }_{00}-{\beta }_{11}(s-t_{\mathit{ij}})-{\beta }_{12}(t-t_{\mathit{il}}\left)\right\}}^2$. One may estimate the noise variance ν² by taking the difference between the diagonal of the surface estimate $\widehat{G}(t,t)$ and the local polynomial estimate obtained from the raw variances {(t_ij, G_ijj) : j = 1, … , N_i; i = 1, … , n}. The eigenvalues/functions are obtained as in the dense case. To estimate the FPC scores, denote x_i = (x_i1, … , x_iNi)^T, the PACE estimate is given by ${\widehat{\xi }}_{\mathit{ik}}={\widehat{\lambda }}_k{\widehat{\varphi }}_{\mathit{ik}}^{⊺}{\widehat{\Sigma }}_{{\mathit{x}}_i}^{-1}(x_i-{\widehat{\mu }}_i)$, which leads to ${\widehat{\zeta }}_{\mathit{ik}}=\Psi ({\widehat{\xi }}_{\mathit{ik}};0,{\widehat{\lambda }}_k),k=1,\dots ,s$. Here ϕik = (ϕk(t_i1), … , ϕk(t_iNi))^T, μ_i = (μ(t_i1), … , μ(t_iNi))^T, and the (j, l)th element (∑_xi)_j,l = G(t_ij, t_il) + ν²δ_jl. with δ_jl = 1 if j = l and 0 otherwise, and “$\widehat{\cdot }$” is the generic notation for their estimates.

We next estimate $f_0\in {\mathcal{F}}^s$ by minimizing (6), following the COSSO procedure conditional on the estimated values ${\widehat{\zeta }}_i$. It is important to note that the target function (6) is equivalent to $1∕n{\sum }_{i=1}^n{\{y_i-f({\widehat{\zeta }}_i\left)\right\}}^2+{\lambda }_0{\sum }_{k=1}^s{\theta }_k^{-1}{\Vert P^{k}f\Vert }^2+\lambda {\sum }_{k=1}^s{\theta }_k$, subject to θ_k ≥ 0 (Lin and Zhang, 2006), which enables a tow-step iterative algorithm. Specifically, one first find $c\in {\Re }^n$ and $b\in \Re$ by minimizing

$${(y-{\mathbf{R}}_{\theta }c-b{1}_n)}^{⊺}(y-{\mathbf{R}}_{\theta }c-b{1}_n)+n{\lambda }_0{c}^T{\mathbf{R}}_{\theta }c,$$ (9)

with fixed θ = (θ₁, … , θ_s)^T, where y = (y₁, … , y_n)^T, λ0 is the smoothing parameter, 1n is the n × 1 vector of 1’s, ${\mathbf{R}}_{\theta }={\sum }_{k=1}^s{\theta }_k{\mathbf{R}}_k$, and Rk is the reproducing kernel of ${\stackrel{‒}{H}}^k$, i.e. ${\mathbf{R}}_k={\left\{R_k\right({\widehat{\zeta }}_{\mathit{ik}},{\widehat{\zeta }}_{\mathit{jk}}\left)\right\}}_{1\le i,j\le n}$. This optimization is exactly a smoothing spline problem. We then fix c and b, and find θ by minimizing

$${(z-Q\theta )}^{⊺}(z-Q\theta )\text{subject to}{\theta }_k\ge 0;\sum _{k=1}^s{\theta }_k\le M,$$ (10)

where z = y – (1/2)nλ₀c – b1n and Q is an n × s matrix with the kth column being R_kc. This step is the same as calculating the non-negative garrote estimate using M as the tuning parameter. Upon convergence, the final estimation of f is then given by $\widehat{f}\left(\zeta \right)={\sum }_{i=1}^n{\widehat{c}}_i{R}_{\widehat{\theta }}({\widehat{\zeta }}_i,\widehat{\zeta })+\widehat{b}$.

Regarding the choice of tuning parameters, besides the sufficiently large initial truncation s, the most relevant are the λ₀ and M in the COSSO step, while the bandwidths in the smoothing step of FPCA are chosen by traditional cross-validation or its generalized approximation. For more details, see Fan and Gijbels (1996) for the dense case and Yao et al. (2005) for the sparse case. We suggest to select λ₀ using the generalized cross validation(GCV), i.e. $\mathrm{GVC}\left({\lambda }_0\right)={(\widehat{\mathit{y}}-\mathit{y})}^{⊺}(\widehat{\mathit{y}}-\mathit{y})∕{\left\{n^{-1}\mathrm{tr}\right(I-A\left)\right\}}^2$ with $\widehat{\mathit{y}}=A\mathit{y}$. For choosing M, we adopt the BIC criterion i.e. $\mathit{BIC}\left(M\right)={(\widehat{\mathit{y}}-\mathit{y})}^{⊺}(\widehat{\mathit{y}}-\mathit{y})∕{\widehat{\sigma }}^2+\log \left(n\right)\cdot \mathit{df}$ where df is the degree of freedom in (10), while an alternative is the cross-validation which requires more computation.

Appendix B. Technical assumptions and proofs

We first lay out the commonly adopted regularity conditions on the functional predictor process X for the dense design. Recall that {t_ij, j = 1, … , N_i; i = 1, … , n} is the grid on the support $\mathcal{T}$ over which the functional predictor x_i(t) is observed. Without loss of generality, let $\mathcal{T}=[0,a]$. Denote t_i0 = 0, t_iNi = a and ${\mathcal{T}}_d=[-d,a+d]$ for some d > 0. Denote the bandwidth used for individually smoothing the ith trajectory as b_i.

(b.1) Assume that the second derivative X⁽²⁾(t) is continuous on ${\mathcal{T}}_d$ with probability 1 (w.p.1.), and ∫E[{X^(k)(t)}⁴]dt < ∞ w.p.1. for k = 0, 2. Also assume $E\left(e_{\mathit{ij}}^4\right)<\infty$, where e_ij is the i.i.d. measurement error of the observed trajectory x_i.

(b.2) Assume that there exists m ≡ m(n) → ∞, such that min_iN_i ≤ m as n → ∞. Denoting Δ_i = max{t_ij – t_i,j–1 : j = 1, … ,N_i + 1}, assume that max_iΔ_i = O(m−1).

(b.3) Assume that there exists a sequence b = b(n), such that cb ≤ min_ib_i max_ib_i ≤ Cb for some C ≥ c > 0. Furthermore, b → 0 and m → ∞ as n → ∞ in rates such that (mb)⁻¹ + b⁴ + m⁻² = O(n⁻¹), e.g. b = O(n^−1/2), m = O(n^3/2). Also assume that the kernel function K(·) is compactly supported and Lipschitz continuous.

Denote the operator associated with the covariance function G(s, t) by G, and define ${\Vert G\Vert }_S^2={\int }_{\mathcal{T}}{\int }_{\mathcal{T}}{G}^2(s,t)\mathit{dsdt}$. Denote the smoothed trajectory of X_i(t) using local linear smoothing with bandwidth b_i by ${\widehat{X}}_i$ and the estimated eigenvalue/function and FPC score in the dense design by ${\widehat{\lambda }}_k,{\widehat{\Phi }}_k,{\widehat{\xi }}_{\mathit{ik}}$, respectively. Since the decay of eigenvalues plays an important role, define δ₁ = λ₁ – λ₂ and δ_k = min_j≤_k(λ_j–1 – λ_j, λ_j – λ_j+1) for k ≥ 2.

Lemma 1

Under the assumptions (b.1)–(b.3), we have

$$E\left({\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}^2\right)=O\left(n^{-1}\right),{\Vert \widehat{\mu }-\mu \Vert }_{L^2}=O_p\left(n^{-\frac{1}{2}}\right),{\Vert \widehat{G}-G\Vert }_S=O_p\left(n^{-\frac{1}{2}}\right),$$ (11)

$$\mid {\widehat{\lambda }}_k-{\lambda }_k\mid \le {\Vert \widehat{G}-G\Vert }_S,{\Vert {\widehat{\varphi }}_k-{\varphi }_k\Vert }_{L^2}\le 2\sqrt{2}{\delta }_k^{-1}{\Vert \widehat{G}-G\Vert }_S,$$ (12)

$$\mid {\widehat{\xi }}_{\mathit{ik}}-{\xi }_{\mathit{ik}}\mid =O_p({\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}+{\delta }_k^{-1}{\Vert X_i\Vert }_{L^2}\cdot {\Vert \widehat{G}-G\Vert }_S),$$ (13)

where O(·) and O_p(·) are uniform over 1 ≤ i ≤ n. Note that the measurement error e_ij is independent of the process X_i, which makes it possible to factor the probability space Ω = Ω_X × Ω_e and characterize the individual smoothing and cross-sectional averaging separately. Then (11) can be shown using standard techniques with local polynomial smoothing (not elaborated for conciseness), see Hall et al. (2006) for more details of this type of arguments. Consequently (12) and (13) follow immediately by the classical perturbation result provided in Lemma 4.3 of Bosq (2000). We see from Lemma 1 that, when the measurements are suffciently dense for each subject satisfying (b.3), the impact due to individual smoothing on the estimated population quantities (e.g. mean, covariance, eigenvalues/functions) are negligible.

The following lemma characterizes the discrepancy between the underlying and estimated transformed variables ζ_ik, as well as the boundedness of the derivative of the resulting estimate $\widehat{f}$.

Lemma 2

Under the assumptions (a.2) and (b.1)–(b.3), we have

$$\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid =O_p\left({\lambda }_k^{\gamma }\{{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}+({\delta }_k^{-1}{\Vert X_i\Vert }_{L^2}+\mid {\xi }_{\mathit{ik}}\mid \left){\Vert \widehat{G}-G\Vert }_S\right\}\right),$$ (14)

$$\frac{1}{n}\sum _{i=1}^n{\left(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)}^2=O_p\left(n^{-1}\right),$$ (15)

Additionally, if the assumption (a.1) holds, let $\widehat{f}$ be the estimate of f₀ obtained by minimizing (6). Then there exists a constant ρ > 0, such that

$$\mid \frac{\partial \widehat{f}\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}\mid \le \rho ,$$ (16)

uniformly over 1 ≤ k ≤ s and 1 ≤ i ≤ n.

Proof of Lemma 2

From Lemma 1 and (a.2), one has in probability,

$$\begin{array}{cc}\hfill \mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid & =\mid ({\widehat{\xi }}_{\mathit{ik}}-{\xi }_{\mathit{ik}})\frac{\partial }{\partial {\xi }_{\mathit{ik}}}\Psi ({\xi }_{\mathit{ik}},{\lambda }_k)+({\widehat{\lambda }}_k-{\lambda }_k)\frac{\partial }{\partial {\lambda }_k}\Psi ({\xi }_{\mathit{ik}},{\lambda }_k)+o_p(\mid {\widehat{\xi }}_{\mathit{ik}}-{\xi }_{\mathit{ik}}\mid +\mid {\widehat{\lambda }}_k-{\lambda }_k\mid )\mid \hfill \\ \hfill & \le \mid {\widehat{\xi }}_{\mathit{ik}}-{\xi }_{\mathit{ik}}\mid \cdot \mid {\frac{\partial }{\partial \xi }}_{\mathit{ik}}\Psi ({\xi }_{\mathit{ik}},{\lambda }_k)\mid +\mid {\widehat{\lambda }}_k-{\lambda }_k\mid \cdot \mid \frac{\partial }{\partial {\lambda }_k}\Psi ({\xi }_{\mathit{ik}},{\lambda }_k)\mid +o_p(\mid {\widehat{\xi }}_{\mathit{ik}}-{\xi }_{\mathit{ik}}\mid +(\mid {\widehat{\lambda }}_k-{\lambda }_k\mid )\hfill \\ \hfill & =O_p\left({\lambda }_k^{\gamma }\{{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}+({\delta }_k^{-1}{\Vert X_i\Vert }_{L^2}+\mid {\xi }_{\mathit{ik}}\mid \left){\Vert \widehat{G}-G\Vert }_S\right\}\right).\hfill \end{array}$$

Abbreviate ${\Sigma }_{i=1}^n$ to ∑_k and O_p(·) to ~. Since $E{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}\le {\left\{E\right({\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}^2\left)\right\}}^{1∕2}=O\left(n^{-1∕2}\right)$, it easy to see that $E\left(n^{-1}{\Sigma }_i{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}\right)=E{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}=O\left(n^{-1∕2}\right)$ To show (15) for any fixed s, note $n^{-1}{\Sigma }_i{\left({\Sigma }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)}^2\le {\mathit{sn}}^{-1}{\Sigma }_i{\Sigma }_{k=1}^s{\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid }^2$. Then

$$\begin{array}{cc}\hfill \frac{1}{n}& \sum _{i=1}^n\sum _{k=1}^s{({\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}})}^2\sim \frac{1}{n}\sum _{i=1}^n\sum _{k=1}^s{\lambda }_k^{2\gamma }{\left\{{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}+({\delta }_k^{-1}{\Vert X_i\Vert }_{L^2}+\mid {\xi }_{\mathit{ik}}\mid ){\Vert \widehat{G}-G\Vert }_S\right\}}^2\hfill \\ \hfill \sim & \frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}^2+\frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\delta }_k^{-2}{\Vert X_i\Vert }_{L^2}^2{\Vert \widehat{G}-G\Vert }_S^2+\frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\mid {\xi }_{\mathit{ik}}\mid }^2{\Vert \widehat{G}-G\Vert }_S^2\hfill \\ \hfill & +\frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}{\delta }_k^{-1}{\Vert X_i\Vert }_{L^2}{\Vert \widehat{G}-G\Vert }_S+\frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}\mid {\xi }_{\mathit{ik}}\mid {\Vert \widehat{G}-G\Vert }_S\hfill \\ \hfill & +\frac{1}{n}\sum _i\sum _k{\lambda }_k^{2\gamma }{\delta }_k^{-1}\mid {\xi }_{\mathit{ik}}\mid {\Vert X_i\Vert }_{L^2}{\Vert \widehat{G}-G\Vert }_S^2,\hfill \end{array}$$

Denoting the additive terms in above formula E₁ through E₆, we have $E_1=\left({\Sigma }_k{\lambda }_k^{2\gamma }\right)\left(n^{-1}{\Sigma }_i{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}^2\right)=O_p\left(n^{-1}\right),E_2={\Vert \widehat{G}-G\Vert }_S^2\left({\Sigma }_k{\lambda }_k^{2\gamma }{\delta }_k^{-2}\right)\left(n^{-1}{\Sigma }_i{\Vert X_i\Vert }_{L^2}^2\right)=O_p\left(n^{-1}\right),E_3={\Vert \widehat{G}-G\Vert }_S^2(1∕n{\Sigma }_i{\Sigma }_k{\lambda }_k^{2\gamma }{\mid {\xi }_{\mathit{ik}}\mid }^2)=O_p\left(n^{-1}\right),\text{as}E\left(n^{-1}{\Sigma }_{i=1}^n{\Sigma }_{k=1}^s{\lambda }_k^{2\gamma }{\mid {\xi }_{\mathit{ik}}\mid }^2\right)={\Sigma }_k{\lambda }_k^{2\gamma +1}=$ O(1). For E₄, applying Cauchy-Schwarz inequality,

$$\begin{array}{cc}\hfill E_4& \sim {\Vert \widehat{G}-G\Vert }_S\left(\sum _{k=1}^s{\lambda }_k^{2\gamma }{\delta }_k^{-1}\right)\left(\frac{1}{n}\sum _{i=1}^n{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}{\Vert X_i\Vert }_{L^2}\right)\hfill \\ \hfill & \le 2C{\Vert \widehat{G}-G\Vert }_S\left(\sum _{k=1}^s{\lambda }_k^{2\gamma }{\delta }_k^{-1}\right)\sqrt{\left(\frac{1}{n}\sum _{i=1}^n{\Vert {\widehat{X}}_i-X_i\Vert }_{L^2}^2\right)\left(\frac{1}{n}\sum _{i=1}^n{\Vert X_i\Vert }_{L^2}^2\right)}\hfill \\ \hfill & =O_p\left(n^{-1∕2}\right)O\left(1\right)O_p\left(n^{-1∕2}\right)O_p\left(1\right)=O_p\left(n^{-1}\right).\hfill \end{array}$$

Similarly, one has E₅ = O_p(n⁻¹), using the facts that $E\left\{{({\Sigma }_{k=1}^s{\lambda }_k^{2\gamma }\mid {\xi }_{\mathit{ik}}\mid )}^2\right\}\le s{\Sigma }_{k=1}^s{\lambda }_k^{4\gamma +1}=O\left(1\right)$ and $E{({\Sigma }_{k=1}^s{\lambda }_k^{2\gamma }{\delta }_k^{-1}\mid {\xi }_{\mathit{ik}}\mid )}^2\le s{\Sigma }_{k=1}^s{\lambda }_k^{4\gamma +1}{\delta }_k^{-2}=O\left(1\right)$. This proves (15).

We now turn to (16). For any $f\in {\mathcal{F}}^s$, one has

$$f\left({\zeta }_i\right)={\langle f(\cdot ),R({\zeta }_i,\cdot )\rangle }_{{\mathcal{F}}^s}\le \Vert f\Vert {\langle R({\zeta }_i,\cdot ),R({\zeta }_i,\cdot )\rangle }_{{\mathcal{F}}^s}^{1∕2}=\Vert f\Vert R^{1∕2}({\zeta }_i,{\zeta }_i),$$

where R(·, ·) is the reproducing kernel of space ${\mathcal{F}}^s$ and $\langle \cdot ,\cdot \rangle$ is the corresponding inner product. Therefore,

$$\frac{\partial f\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}={\langle f(\cdot ),\frac{\partial R({\zeta }_i,\cdot )}{\partial {\zeta }_{\mathit{ik}}}\rangle }_{{\mathcal{F}}^s}\le \Vert f\Vert {\langle \frac{\partial R({\zeta }_i,\cdot )}{\partial {\zeta }_{\mathit{ik}}},\frac{\partial R({\zeta }_i,\cdot )}{\partial {\zeta }_{\mathit{ik}}}\rangle }_{{\mathcal{F}}^s}^{1∕2}.$$

Since J(f) is a convex functional and a pseudonorm, we have

$$\sum _{k=1}^s{\Vert P^{k}f\Vert }^2\le J^2\left(f\right)\le s\sum _{k=1}^s{\Vert P^{k}f\Vert }^2.$$ (17)

We first claim that ∥f∥ ≤ J(f), due to ${\Vert f\Vert }_2=b^2+{\Sigma }_{k=1}^s{\Vert P^{k}f\Vert }^2$. If b = 0, the inequality in (17) implies that ∥f∥ ≤ J(f). If b ≠ 0, one can write $\tilde{J}\left(f\right)=b+J\left(f\right)=b+{\Sigma }_{k=1}^s\Vert P^{k}f\Vert$. For minimizing (5), it is equivalent to substitute J(f) with $\tilde{J}\left(f\right)$, and (17) implies ${\Vert f\Vert }^2=b^2+{\Sigma }_{k=1}^s{\Vert P^{k}f\Vert }^2\le b^2+J^2\left(f\right)\le {\tilde{J}}^2\left(f\right)$. Therefore we have ∥f∥ ≤ J(f) in general. Secondly, due to the orthogonality of $\left\{{\stackrel{‒}{H}}^k\right\}$, we can write R(u, v) = R₁(u₁, v₁)+R₂(u₂, v₂)+ … + R_s(u_s, v_s) by Theorem 5 in Berlinet and Thomas-agnan (2004), where R_k(·, ·) is the reproducing kernel of the subspace $\left\{{\stackrel{‒}{H}}^k\right\}$. For $\left\{{\stackrel{‒}{H}}^k\right\}$ being a second order Sobolev Hilbert space, we have R_k(s, t) = h₁(s)h₁(t) + h₂(s)h₂(t) – h₄(∣s – t∣), with h₁(t) = t – 1/2, $h_2\left(t\right)=\left[h_1^2\right(t)-1∕12]∕2$ and $h_4\left(t\right)=\left[h_1^4\right(t)-h_1^2(t)∕2+7∕240]∕24$. Therefore R_k(s, t) is continuous and differentiable over [0, 1]² and we can find constants a_k and b_k such that

$${\langle R_k(u,\cdot ),R_k(u,\cdot )\rangle }_{{\mathcal{F}}^s}<a_k,{\langle \frac{\partial R_k(u,\cdot )}{\partial u},\frac{\partial R_k(u,\cdot )}{\partial u}\rangle }_{{\mathcal{F}}^s}\le b_k,$$

for k = 1,…, s. One can find a uniform bound c with ${\langle \partial ∕\partial {\zeta }_{\mathit{ik}}R({\zeta }_i,\cdot ),\partial ∕\partial {\zeta }_{\mathit{ik}}R({\zeta }_i,\cdot )\rangle }_{{\mathcal{F}}^s}\le c$. On the other hand, a $\widehat{f}$ minimizing (6) is equivalent to minimizing $n^{-1}{\Sigma }_i{\{y_i-f({\widehat{\zeta }}_i\left)\right\}}^2$ under the constraint that $J\left(f\right)\le \tilde{c}$ for some $\tilde{c}>0$. Therefore let ρ = c^1/2 · $\rho =c^{1∕2}\cdot \tilde{c}$, we have

$$\mid \frac{\partial \widehat{f}\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}\mid \le \Vert \widehat{f}\Vert {\langle \frac{\partial R({\zeta }_i,\cdot )}{\partial {\zeta }_{\mathit{ik}}},\frac{\partial R({\zeta }_i,\cdot )}{\partial {\zeta }_{\mathit{ik}}}\rangle }_{{\mathcal{F}}^s}^{1∕2}\le J\left(\widehat{f}\right)c^{1∕2}\le \tilde{c}{c}^{1∕2}=\rho .$$

Before stating Lemma 3, we define the entropy of ${\mathcal{F}}^s$ with respect to the ∥·∥_n metric. For each ω > 0, one can find a collection of functions {g₁, g₂,…g_N} in ${\mathcal{F}}^s$ such that for each $g\in {\mathcal{F}}^s$, there is a j = j(g) ∈ {1, 2, … N} satisfying ∥g – g_j∥_n ≤ ω. Let $\mathbb{N}(\omega ,{\mathcal{F}}^s,{\Vert \cdot \Vert }_n)$ be the smallest value of N for which such a cover of balls with radius ω and centers g₁, g₂,…, g_N exists. Then $H(\omega ,{\mathcal{F}}^s,{\Vert \cdot \Vert }_n)=\log \mathbb{N}(\omega ,{\mathcal{F}}^s,{\Vert \cdot \Vert }_n)$ is called the ω-entropy of ${\mathcal{F}}^s$.

Lemma 3

Assume that ${\mathcal{F}}^s=\left\{1\right\}\oplus {\Sigma }_{k=1}^s{\stackrel{‒}{H}}^k$, where ${\stackrel{‒}{H}}^k$ is second order Sobolev space. Denote the ω-entropy of $\{f\in {\mathcal{F}}^s:J(f)\le 1\}\text{by}H(\omega ,\{f\in {\mathcal{F}}^s:J\left(f\right)\le 1\},{\Vert \cdot \Vert }_n)$ Then

$$H(\omega ,\{f\in {\mathcal{F}}^s:J\left(f\right)\le 1\},{\Vert \cdot \Vert }_n)\le A{\omega }^{-1∕2},$$ (18)

for all ω > 0, n ≥ 1, and for some constants A > 0. Furthermore, for ${\left\{{∊}_i\right\}}_{i=1}^n$ independent with finite variance and J(f₀) > 0,

$$\underset{f\in {\mathcal{F}}^s}{\sup }\frac{\mid {(∊,f-f_0)}_n\mid }{{\Vert f-f_0\Vert }_n^{3∕4}{\left(J\right(f)+J(f_0\left)\right)}^{1∕4}}=O_p\left(n^{-1∕2}\right).$$ (19)

The inequality (18) is implied by Lemma A.1. of Lin and Zhang (2006). As the {∊_i} satisfy the sub-Gaussian error assumption, the same argument as in Van de Geer (2000) (pg. 168) leads to (19). We are now ready to present the proof of the main theorem.

Proof of Theorem 1

We first center the functions as in the proof of theorem 2 in Lin and Zhang (2006) so that (18) and (19) holds. Write $f\left(\widehat{\zeta }\right)=c+f_1\left({\widehat{\zeta }}_1\right)+\dots +f_s\left({\widehat{\zeta }}_s\right)=c+\tilde{f}\left(\widehat{\zeta }\right)$, such that ${\Sigma }_{i=1}^n{f}_k\left({\widehat{\zeta }}_{i,k}\right)=0$, and write $f_0\left(\zeta \right)=c_0+f_{01}\left({\zeta }_1\right)+\dots +f_{0s}\left({\zeta }_s\right)=c_0+{\tilde{f}}_0\left(\zeta \right)$ such that ${\Sigma }_{i=1}^n{f}_{0k}\left({\zeta }_{i,k}\right)=0$ and $\widehat{f}\left(\zeta \right)=\widehat{c}+{\widehat{f}}_1\left({\zeta }_1\right)+\dots +{\widehat{f}}_s\left({\zeta }_s\right)$. Since the target function can be written as

$$\begin{array}{cc}\hfill Q(f\mid {\widehat{\zeta }}_i)& =\frac{1}{n}\sum _{i=1}^n{\{y_i-f({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(f\right)=\frac{1}{n}\sum _{i=1}^n{\{c_0+{\tilde{f}}_0({\zeta }_i)+{∊}_i-c-\tilde{f}({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(f\right)\hfill \\ \hfill & ={(c_0-c)}^2+\frac{2}{n}(c_0-c)\sum _i{∊}_i+\frac{1}{n}\sum _{i=1}^n{\left\{{\tilde{f}}_0\right({\zeta }_i)+{∊}_i-\tilde{f}({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(f\right),\hfill \end{array}$$

one must have that $\widehat{c}$ minimizes {(c₀ – c)² + 2n⁻¹ (c₀ – c) Σ_i∊_i} and the additive parts of $\widehat{f}$ minimizes the rest. Therefore we have $\widehat{c}-c_0=n^{-1}{\sum }_i{∊}_i$, implying $\mid \widehat{c}-c_0\mid =O_p\left(n^{-1∕2}\right)$. Denote

$$\tilde{Q}(\tilde{f}\mid {\widehat{\zeta }}_i)=1∕n\sum _{i=1}^n{\left\{{\tilde{f}}_0\right({\zeta }_i)+{∊}_i-\tilde{f}({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(f\right).$$ (20)

One can substitute ${\tau }_n^{2}J\left(f\right)$ with ${\tau }_n^{2}J\left(\tilde{f}\right)$ in (20). In the rest of the proof, we suppress the tilde notation of ${\tilde{f}}_0$ and $\tilde{f}$ for convenience. Since $\widehat{f}=\underset{f\in {\mathcal{F}}^s}{\mathrm{argmin}}\tilde{Q}(f\mid \{{\widehat{\zeta }}_i\left\}\right)$, one has $\tilde{Q}(\widehat{f}\mid \{\widehat{\zeta }\left\}\right)\le \tilde{Q}(f_0\mid \{\widehat{\zeta }\left\}\right)$, which implies

$$\frac{1}{n}\sum _{i=1}^n{\left\{f_0\right({\zeta }_i)+{∊}_i-\widehat{f}({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le \frac{1}{n}\sum _{i=1}^n{\left\{f_0\right({\zeta }_i)+{∊}_i-f_0({\widehat{\zeta }}_i\left)\right\}}^2+{\tau }_n^{2}J\left(f_0\right).$$

Simplification of the above inequality gives

$$\begin{array}{cc}\hfill & \frac{1}{n}\sum _{i=1}^n{\left(f_0\left({\zeta }_i\right)-\widehat{f}\left({\widehat{\zeta }}_i\right)\right)}^2+{\tau }_n^{2}J\left(\widehat{f}\right)\hfill \\ \hfill \le & \frac{2}{n}\sum _{i=1}^n{∊}_i\left(\widehat{f}\left({\widehat{\zeta }}_i\right)-f_0\left({\widehat{\zeta }}_i\right)\right)+\frac{1}{n}\sum _{i=1}^n{\left(f_0\left({\zeta }_i\right)-f_0\left({\widehat{\zeta }}_i\right)\right)}^2+{\tau }_n^{2}J\left(f_0\right).\hfill \end{array}$$ (21)

Let $g(\cdot )=\widehat{f}(\cdot )-f_0(\cdot )$. Since both $\widehat{f}$ and $f_0$ are in ${\mathcal{F}}^s$, $g\in {\mathcal{F}}^s$. Taylor expansion of g(·) gives $g\left(\widehat{\zeta }\right)=g\left(\zeta \right)+\mathit{Dg}\left(\zeta \right)(\widehat{\zeta }-\zeta )+o_p\left({\sum }_{k=1}^s\mid {\widehat{\zeta }}_k-{\zeta }_k\mid \right)$, for all ζ ∈ (0, 1)^s, where

$$\frac{2}{n}\sum _{i=1}^n{∊}_{i}g\left({\widehat{\zeta }}_i\right)=\frac{2}{n}\sum _{i=1}^n{∊}_{i}g\left({\zeta }_i\right)+\frac{2}{n}\sum _{i=1}^n{∊}_i\left\{\mathit{Dg}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)+o_p\left(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)\right\},$$

and plug it into the right hand side (r.h.s.) of (21), leading to the following upper bound,

$$\begin{array}{cc}\hfill \frac{2}{n}\sum _{i=1}^n{∊}_i& \left(\widehat{f}\left({\zeta }_i\right)-f_0\left({\zeta }_i\right)\right)+\frac{2}{n}\sum _{i=1}^n{∊}_i\left\{\left(D\widehat{f}\right({\zeta }_i)-{\mathit{Df}}_0({\zeta }_i\left)\right)({\widehat{\zeta }}_i-{\zeta }_i)+o_p\left(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)\right\}\hfill \\ \hfill & +\frac{1}{n}\sum _{i=1}^n{\left(f_0\left({\zeta }_i\right)-f_0\left({\widehat{\zeta }}_i\right)\right)}^2+{\tau }_n^{2}J\left(f_0\right).\hfill \end{array}$$ (22)

Applying Lemma 3, one can bound the first term in (22) as follow,

$$\frac{2}{n}\sum _{i=1}^n{∊}_i\left(\widehat{f}\left({\zeta }_i\right)-f_0\left({\zeta }_i\right)\right)=2{(∊,\widehat{f}-f_0)}_n\le O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\right(\widehat{f})+J(f_0\left)\right)}^{1∕4}.$$

For the left hand side (l.f.s.) of (21), applying the Taylor expansion, $\widehat{f}\left({\widehat{\zeta }}_i\right)=\widehat{f}\left({\zeta }_i\right)+D\widehat{f}\left({\widehat{\zeta }}_i\right)({\widehat{\zeta }}_i-{\zeta }_i)+o_p({\sum }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )$, to the first term

$$\begin{array}{cc}\hfill & \frac{1}{n}\sum _{i=1}^n{\left(f_0\left({\zeta }_i\right)-\widehat{f}\left({\widehat{\zeta }}_i\right)\right)}^2=\frac{1}{n}\sum _{i=1}^n{\left\{f_0\left({\zeta }_i\right)-\widehat{f}\left({\zeta }_i\right)-D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)-o_p(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )\right\}}^2\hfill \\ \hfill =& \frac{1}{n}\sum _{i=1}^n\left\{{\left(f_0\left({\zeta }_i\right)-\widehat{f}\left({\zeta }_i\right)\right)}^2+{\left(D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\right)}^2-2\left(f_0\left({\zeta }_i\right)-\widehat{f}\left({\zeta }_i\right)\right)D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)+R_i\right\},\hfill \end{array}$$

where $R_i={\left\{o_p\right({\sum }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \left)\right\}}^2-o_p({\sum }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )\left\{f_0\right({\zeta }_i)-\widehat{f}({\zeta }_i)-D\widehat{f}({\zeta }_i\left)\right({\widehat{\zeta }}_i-{\zeta }_i\left)\right\}$. Substituting the terms on both sides of (21), we obtain

$$\begin{array}{cc}\hfill & {\Vert \widehat{f}-f_0\Vert }_n^2+\frac{1}{n}\sum _{i=1}^n\left\{{\left(D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\right)}^2+2\left(\widehat{f}\left({\zeta }_i\right)-f_0\left({\zeta }_i\right)\right)D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)+R_i\right\}+{\tau }_n^{2}J\left(\widehat{f}\right)\hfill \\ \hfill & \le O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\right(\widehat{f})+J(f_0\left)\right)}^{1∕4}+\frac{1}{n}\sum _{i=1}^n{\left(f_0\left({\zeta }_i\right)-f_0\left({\widehat{\zeta }}_i\right)\right)}^2+{\tau }_n^{2}J\left(f_0\right)\hfill \\ \hfill & +\frac{2}{n}\sum _{i=1}^n{∊}_i\left\{\left(D\widehat{f}\right({\zeta }_i)-{\mathit{Df}}_0({\zeta }_i\left)\right)({\widehat{\zeta }}_i-{\zeta }_i)+o_p(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )\right\}.\hfill \end{array}$$

Dropping the positive term $n^{-1}{\sum }_i{\left(D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\right)}^2$ on the l.h.s. and rearranging the terms,

$$\begin{array}{cc}\hfill {\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le & O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\right(\widehat{f})+J(f_0\left)\right)}^{1∕4}+{\tau }_n^{2}J\left(f_0\right)\hfill \\ \hfill & +T_1+T_2+T_3+\frac{2}{n}\sum _{i=1}^n{∊}_i{\tilde{R}}_{2i}+\frac{1}{n}\sum _{i=1}^n{\tilde{R}}_{1i}\hfill \end{array}$$ (23)

where $T_1=-2n^{-1}{\sum }_i\left\{\right(\widehat{f}\left({\zeta }_i\right)-f_0\left({\zeta }_i\right)\left\}D\widehat{f}\right({\zeta }_i\left)\right({\widehat{\zeta }}_i-{\zeta }_i),T_2=2n^{-1}{\sum }_i{∊}_i\{\left(D\widehat{f}\right({\zeta }_i)-{\mathit{Df}}_0({\zeta }_i\left)\right)({\widehat{\zeta }}_i-{\zeta }_i)\},T_3=n^{-1}{\sum }_i{\left\{f_0\right({\zeta }_i)-f_0({\widehat{\zeta }}_i\left)\right\}}^2,{\tilde{R}}_{1i}=o_p({\sum }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \left)\right\{f_0\left({\zeta }_i\right)-\widehat{f}\left({\zeta }_i\right)-D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\}$ and ${\tilde{R}}_{2i}=o_p({\sum }_{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )$

For T₁, by Cauchy-Schwarz inequality and Lemma 2, we have $T_i\le 2\sqrt{{\Vert \widehat{f}-f_0\Vert }_n^{2}A}$, where

$$A=\frac{1}{n}\sum _{i=1}^n{\left(\sum _{k=1}^s\frac{\partial \widehat{f}\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}({\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}})\right)}^2\le \frac{{\rho }^2}{n}\sum _{i=1}^n{\left(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)}^2=O_p\left(n^{-1}\right),$$

i.e. $T_1={\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)$. From (a.1) and (16) of Lemma 2, there exists independent r.v. {B_i} with $E\left(B_i^2\right)<\infty$ such that max_k$\{\mid \partial \widehat{f}({\zeta }_i)∕\partial {\zeta }_{\mathit{ik}}-\partial f_0({\zeta }_i)∕\partial {\zeta }_{\mathit{ik}}\mid \}\le B_i{\Vert \widehat{f}-f_0\Vert }_{L^2}$. Also note that ∥g∥_n→∥g∥_L2 a.s. by the strong law of large numbers. Therefore we have, for some constant c,

$$\begin{array}{cc}\hfill T_2& \le \frac{2}{n}\sum _{i=1}^n\mid {∊}_i\mid \sum _{k=1}^s{B}_i{\Vert \widehat{f}-f_0\Vert }_{L^2}\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid =2{\Vert \widehat{f}-f_0\Vert }_{L^2}\left(\frac{1}{n}\mid {∊}_i{B}_i\mid \sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \right)\hfill \\ \hfill & \le c{\Vert \widehat{f}-f_0\Vert }_n\sqrt{\left(\frac{1}{n}\sum _{i=1}^n{∊}_i^2{B}_i^2\right)\left(\frac{1}{n}\sum _{i=1}^n{(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )}^2\right)}={\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right).\hfill \\ \hfill T_3& =\frac{1}{n}\sum _{i=1}^n{\left(\sum _{k=1}^s\frac{\partial f_0\left({\zeta }_i\right)}{\partial {\zeta }_{\mathit{ik}}}\left\{({\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}})+o_p(\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )\right\}\right)}^2\le \frac{c}{n}\sum _{i=1}^n{(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )}^2=O_p\left(n^{-1}\right).\hfill \end{array}$$

For the remaining terms, $n^{-1}{\sum }_{i=1}^n{∊}_i{\tilde{R}}_{2i}=o_p\left(T_2\right)$, and

$$\begin{array}{cc}\hfill \frac{1}{n}\sum _{i=1}^n{\tilde{R}}_{1i}& =\frac{1}{n}\sum _{i=1}^n{o}_p(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )\left(f_0\right({\zeta }_i)-\widehat{f}({\zeta }_i\left)\right)-\frac{1}{n}\sum _{i=1}^n{o}_p(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid )D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\hfill \\ \hfill \le o_p\left(T_1\right)& +{\left\{\frac{1}{n}\sum _{i=1}^n{\left(o_p\right(\sum _{k=1}^s\mid {\widehat{\zeta }}_{\mathit{ik}}-{\zeta }_{\mathit{ik}}\mid \left)\right)}^2\frac{1}{n}\sum _{i=1}^n{\left(D\widehat{f}\left({\zeta }_i\right)({\widehat{\zeta }}_i-{\zeta }_i)\right)}^2\right\}}^{-1∕2}=o_p\left(T_1\right)+o_p\left(n^{-1}\right).\hfill \end{array}$$

We can now simplify (23) as follows:

$$\begin{array}{cc}\hfill {\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le & O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\left(\widehat{f}\right)+J\left(f_0\right)\right)}^{1∕4}\hfill \\ \hfill & +{\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)+O_p\left(n^{-1}\right)+{\tau }_n^{2}J\left(f_0\right).\hfill \\ \hfill \text{If}{O}_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\left(\widehat{f}\right)+J\left(f_0\right)\right)}^{1∕4}& \ge {\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)+O_p\left(n^{-1}\right)+{\tau }_n^{2}J\left(f_0\right),\hfill \end{array}$$

If $O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\left(\widehat{f}\right)+J\left(f_0\right)\right)}^{1∕4}\ge {\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)+O_p\left(n^{-1}\right)+{\tau }_n^{2}J\left(f_0\right)$, we have

$${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le O_p\left(n^{-\frac{1}{2}}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{\left(J\left(\widehat{f}\right)+J\left(f_0\right)\right)}^{1∕4},$$ (24)

otherwise,

$${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le {\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)+O_p\left(n^{-1}\right)+2{\tau }_n^{2}J\left(f_0\right).$$ (25)

The proof will be completed by solving them separately. For the case of (24), there are two possibilities.

1. If $J\left(\widehat{f}\right)\ge J\left(f_0\right)$, (24) implies ${\tau }_n^2{J}^{3∕4}\left(\widehat{f}\right)\le O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}$, and

   $$\begin{array}{cc}\hfill J^{1∕4}\left(\widehat{f}\right)\le {\left({\tau }_n^{-2}{O}_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}\right)}^{1∕3}& =O_p\left(n^{-1∕6}\right){\Vert \widehat{f}-f_0\Vert }_n^{1∕4}{\tau }_n^{-2∕3}.\text{Therefore},\hfill \\ \hfill {\Vert \widehat{f}-f_0\Vert }_n^2\le O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{J}^{1∕4}\left(\widehat{f}\right)& \le O_p\left(n^{-2∕3}\right){\Vert \widehat{f}-f_0\Vert }_n{\tau }_n^{-2∕3},\mathrm{i}.\mathrm{e}.\hfill \\ \hfill {\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-2∕3}\right)O_p\left({\tau }_n^{-2∕3}\right),J\left(\widehat{f}\right)& =O_p\left(n^{-4∕3}\right)O_p\left({\tau }_n^{-10∕3}\right).\hfill \end{array}$$ (26)
2. If $J\left(\widehat{f}\right)<J\left(f_0\right)$, then $J\left(\widehat{f}\right)=O_p\left(J\right(f_0\left)\right)O_p\left(1\right)$, and (24) implies that ${\Vert \widehat{f}-f_0\Vert }_n^2\le O_p\left(n^{-1∕2}\right){\Vert \widehat{f}-f_0\Vert }_n^{3∕4}{J}^{1∕4}\left(f_0\right)$, which leads to

   $${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-2∕5}\right)J^{1∕5}\left(f_0\right),J\left(\widehat{f}\right)=J\left(f_0\right)O_p\left(1\right).$$ (27)

Note that the results (26) and (27) are equivalent under the condition (7),.

For the case of (25), if $\Vert \widehat{f}-f_0\Vert O_p\left(n^{-1∕2}\right)>O_p\left(n^{-1}\right)+2{\tau }_n^{2}J\left(f_0\right)$, we have ${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le {\Vert \widehat{f}-f_0\Vert }_n{O}_p\left(n^{-1∕2}\right)$, otherwise ${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le O_p\left(n^{-1}\right)+4{\tau }_n^{2}J\left(f_0\right)$. The first inequality implies that

$${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-1∕2}\right),J\left(\widehat{f}\right)=O_p\left(n^{-1}\right)O_p\left({\tau }_n^{-2}\right).$$ (28)

For the second inequality, if $O_p\left(n^{-1}\right)<4{\tau }_n^{2}J\left(f_0\right)$, we ${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le 8{\tau }_n^{2}J\left(f_0\right)$, implying

$${\Vert \widehat{f}-f_0\Vert }_n=O_p\left({\tau }_n\right)J^{1∕2}\left(f_0\right),J\left(\widehat{f}\right)=J\left(f_0\right)O_p\left(1\right).$$ (29)

If $O_p\left(n^{-1}\right)\ge 4{\tau }_n^{2}J\left(f_0\right)$ and ${\Vert \widehat{f}-f_0\Vert }_n^2+{\tau }_n^{2}J\left(\widehat{f}\right)\le O_p\left(n^{-1}\right)$, then

$${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-1∕2}\right)J\left(\widehat{f}\right)=O_p\left(n^{-1}\right)O_p\left({\tau }_n^{-2}\right).$$ (30)

When J(f₀) > 0, given the condition (7), the rates of ${\Vert \widehat{f}-f_0\Vert }_n$ and $J\left(\widehat{f}\right)$ from (29), (26) and (27) are the same, and dominate those of (28) and (30). Therefore we have ${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-2∕5}\right)J^{1∕5}\left(f_0\right)$ and $J\left(\widehat{f}\right)=J\left(f_0\right)O_p\left(1\right)$. When J(f₀) = 0, then (24) implies (26), while (25) implies (28) and (30). The possibility (ii) of (24) does not exist, nor does the result in (29). Under condition (8), the result of (26) is the same as those of (28) and (30). Therefore ${\Vert \widehat{f}-f_0\Vert }_n=O_p\left(n^{-1∕2}\right)$ and $J\left(\widehat{f}\right)=O_p\left(n^{-1∕2}\right)$