Integrative Variable Selection via Bayesian Model Uncertainty

Abstract

We are interested in developing integrative approaches for variable selection problems that incorporate external knowledge on a set of predictors of interest. In particular, we have developed iBMU, an integrative Bayesian model uncertainty method that formally incorporates multiple sources of data via a second-stage probit model on the probability that any predictor is associated with the outcome of interest. Using simulations, we demonstrate that iBMU leads to an increase in power to detect true marginal associations over more commonly used variable selection techniques, such as lasso and elastic net. In addition, iBMU leads to a more efficient model search algorithm over the basic Bayesian model uncertainty method even when the predictor-level covariates are only modestly informative. The increase in power and efficiency of our method becomes more substantial as the predictor-level covariates become more informative. Finally, we demonstrate the power and flexibility of iBMU for integrating both gene structure and functional biomarker information into a candidate gene study investigating over 50 genes in the brain reward system and their role with smoking cessation from the Pharmacogenetics of Nicotine Addiction and Treatment Consortium.

1. Introduction

Throughout this paper we are focused on developing integrative variable selection techniques for high-dimensional problems. These problems arise in diverse areas from genetic and environmental epidemiology to predicting the stock market, wine prices and scouting professional athletes. In many of these areas, recent technological advances allow for the collection of massive datasets. Traditional analyses relied heavily on an expert to meticulously sift through the data deliberately building models for inference based on contextual knowledge. However, with the shear amount of factors available for evaluation it is often impracticable to build a model in this way. This analysis bottleneck has lead to a shift to data-driven and computer-based data mining approaches often at the expense of the context in which the statistical model may be relevant. The methods developed herein aim to integrate these approaches to allow for high-dimensional model search while incorporating multiple sources of data.

As an example, we are motivated by the application of these integrative techniques to genetic association studies. It is now feasible to obtain genotype information on millions of variants across the genome and these studies are seeing a dramatic increase in popularity for numerous complex diseases. Given the vast amount of potential predictors of interest, most analyses treat each variant as independent and limit the investigation to only marginal associations. The simplistic analyses of these studies lead to power limitations due to small marginal effect sizes for complex diseases and the strict thresholds imposed to determine marginal associations. Also, it is becoming increasingly likely that combinations of variants, including rare variant loads or interactions between variants, may be important. Thus, there is a growing interest in determining a set of genetic markers associated with an outcome of interest. While data-driven methods are available for selecting sets of markers, they ignore any prior information or fail to integrate additional data sources that may refine the set selection. Specifically, due to the power and computational limitations of genetic association studies and the increasing availability of complementary data sources, it is becoming even more necessary to integrate multiple sources of data to discover multivariate genetic profiles for complex disease.

Given the inability to quantify external information formally into prior beliefs for a large number of predictor variables of interest, external biological knowledge is often ignored completely in agnostic scans (e.g. GWAS). If the knowledge is used, it is mostly limited to the design phase of a study in which a set of candidate genes and/or variants of interest are specifically chosen to be genotyped. With this in mind, we focus on using a set of factors to help guide the selection of variables empirically. These factors can be thought of as a set of predictor-level covariates that reflect higher-level relationships between the predictors. To construct predictor-level covariates in genetic association studies, one may use previously existing and curated ontological data, such as the Gene Ontology [1], or other various pathway ontology databases such as KEGG [2], BioCyc [3], Reactome [4] and PANTHER Pathways [5]. Another example may be to construct the predictor-level covariates from high-density metabolomic, transcriptomic and proteomic data collected on individuals. In each case, collections of variables are defined as conditionally exchangeable groups based on the covariate specification and the estimated relative importance of that characterization on the outcome of interest.

Previous methods incorporating predictor-level covariates have focused on informing estimation [6–13]. Unlike these methods, we focus on model selection and hypothesis testing incorporating external information into the probability that any predictor variable is associated with the outcome of interest. Other penalized regression methods such as lasso [14] and elastic net [15] are common variable selection techniques. While elastic net does not explicitly incorporate predictor-level external information it does allow for the correlation structure of the predictors to guide the variable selection procedure by introducing a hybrid between the L₁ penalty of lasso and the L₂ penalty of ridge regression [16]. More recent methods such as the group lasso [17] and group bridge [18] explicitly allow for the inclusion of group based predictor-covariates (essentially dichotomous covariates) to inform the selection. The main critique of group lasso is that it selects all or none of the predictor variables within a group by introducing a group level penalty. The group bridge overcomes this drawback by also introducing a variable-level penalty to allow for group-level and within group variable selection.

The Bayesian model uncertainty (BMU) framework has been shown to be extremely powerful within variable selection problems. In particular, for genetic association studies Wilson et al. [19] have demonstrated that the BMU approach leads to an increase in power to detect truly associated variants over more commonly used variable selection techniques such as Lasso, stepwise regression, and marginal multiplicity adjusted approaches. Based on the power and flexibility of the Bayesian model uncertainty (BMU) framework for variable selection problems we are interested in extending this framework to incorporate external predictor-level knowledge. Within the BMU framework, Chipman [20] and Conti et al. [21, 22] describe an informative prior for related predictors that introduces dependencies between higher-order interaction terms and their ‘parent’ terms. Similarly, Stingo et al., Baurley et al. and Li and Zhang [23–25] describe methods to incorporate a known graphical structure into the prior probability that each variable is associated. We wish to build upon these priors and develop a more general approach for incorporating external information into the Bayesian model uncertainty framework by introducing iBMU. Within iBMU we introduce a second-stage hierarchical probit model on the probability that each predictor variable is associated with the outcome of interest that is a function of a set of predictor-level covariates and their empirically estimated effects. Unlike the group penalized regression approaches of Yuan and Lin [17] and Huang et al. [18] that account only for the inclusion of dichotomous covariates, our approach has been created within a general framework that allows for the integration of multiple sources of external information within the form of both continuous and dichotomous covariates.

The rest of the paper is organized as follows. Section 2 gives an overview of the Bayesian model uncertainty framework. Section 3 specifies the novel integrative Bayesian model uncertainty method as well as the model search and Markov Chain Monte Carlo algorithms used to sample from posterior distributions of interest and approximate posterior summaries. In Section 4, we describe several simulation studies in which the power of the integrative variable selection method is compared to a basic Bayesian model uncertainty method as well as several penalized regression alternatives. Finally, in Section 5 we apply our method to data from the Pharmacogenetics of Nicotine Addiction and Treatment Consortium and Section 6 concludes with a discussion.

2. Bayesian Model Uncertainty Overview

Here we give an overview of the general Bayesian model uncertainty (BMU) framework that is described in more detail in [26, 27]. In particular, we assume that our data is comprised of 1) Y, a n-dimensional outcome vector, 2) X, a (n × p) dimensional matrix comprised of the measured predictors that are included in the model search, and 3) Z, a (n × q) dimension matrix comprised of the measured confounders that will be forced into every model (such as age, race, etc..). Each model ${\mathcal{M}}_{\gamma }\in \mathcal{M}$ is specified by a p dimensional indicator vector γ where γ_j = 1 if the predictor variable X_j is included in model ${\mathcal{M}}_{\gamma }$ and γ_j = 0 if X_j is not included in ${\mathcal{M}}_{\gamma }$ . Thus, each model ${\mathcal{M}}_{\gamma }\in \mathcal{M}$ is defined by a unique subset of the p predictor variables of interest.

Given any model ${\mathcal{M}}_{\gamma }\in \mathcal{M}$, we assume that the relation between the outcome variable Y and the predictor variables can be specified as some generalized linear model with mean μ:

$${\mathcal{M}}_{\gamma }:\mu =g^{-1}[{\beta }_0+\mathbf{Z}\beta +{\mathbf{X}}_{\gamma }{\beta }_{\gamma }];$$

where g is the link function corresponding to the generalized linear model of interest, β₀ is the intercept common to every model, β are the coefficients of the confounder variables that are also common to every model, X_γ is some parametrization of the set of predictors incorporated in model ${\mathcal{M}}_{\gamma }$, and β_γ are the model specific effects of X_γ on the outcome of interest. To simplify notation throughout, we combine all regression coefficients into the vector θ_γ = (β₀, β, β_γ).

2.1. Posterior Quantities of Interest

The degree to which any model ${\mathcal{M}}_{\gamma }\in \mathcal{M}$ is supported by the data is quantified by posterior model probabilities defined as:

$$p({\mathcal{M}}_{\gamma }\mid \mathbf{Y})=\frac{p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })p\left({\mathcal{M}}_{\gamma }\right)}{{\sum }_{{\mathcal{M}}_{\gamma }\in \mathcal{M}}p(Y\mid {\mathcal{M}}_{\gamma })p\left({\mathcal{M}}_{\gamma }\right)}.$$

The posterior model probabilities are a function of 1) $p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })$, the marginal likelihood of model ${\mathcal{M}}_{\gamma }$ obtained by integrating out the model-specific parameters θ_γ with respect to their prior distribution and 2) $p\left({\mathcal{M}}_{\gamma }\right)$, the prior probability placed on model ${\mathcal{M}}_{\gamma }$. While posterior model probabilities inform us of the models that best explain Y, they do not provide formal marginal inference as to which predictor variables, if any, are associated with Y. To provide formal inference, we calculate marginal posterior inclusion probabilities and marginal Bayes Factors (MargBF) for each predictor X_j. The posterior inclusion probabilities are computed as:

$$p({\gamma }_j=1\mid \mathbf{Y})=\sum _{{\mathcal{M}}_{\gamma }\in \mathcal{M}:{\gamma }_j=1}p({\mathcal{M}}_{\gamma }\mid \mathbf{Y}),$$

which is simply the sum of the posterior model probabilities of all models that include X_j (or all models with γ_j = 1). The MargBF are defined as the posterior odds divided by the prior odds for inclusion:

$$BF[{\gamma }_j=1:{\gamma }_j=0]=\frac{p({\gamma }_j=1\mid \mathbf{Y})}{p({\gamma }_j=0\mid \mathbf{Y})}∕\frac{p({\gamma }_j=1)}{p({\gamma }_j=0)}.$$

2.2. Association Studies

Although the framework described above can be implemented for any generalized linear model, we are interested in the application of case-control association studies. Here Y is a binary outcome variable that takes on the value Y_i = 1 if individual i is a case and Y_i = 0 if individual i is a control. As presented in [19] and [28] we use logistic regression to relate Y to the subset of predictor variables, X_γ in model ${\mathcal{M}}_{\gamma }$:

$${\mathcal{M}}_{\gamma }:\mathrm{logit}(\mathbf{Y}=1)={\beta }_0+\mathbf{Z}\beta +{\mathbf{X}}_{\gamma }{\beta }_{\gamma }.$$

For the purpose of genetic association studies involving common variants, X_γ can be defined to specify the genetic parametrization of each variant included in model ${\mathcal{M}}_{\gamma }$ as in [19]. For the analysis of rare variants, X_γ can define a risk index of the rare variants included in model ${\mathcal{M}}_{\gamma }$ as in [28].

Given a prior specification for θ_γ we must obtain the marginal likelihood to calculate posterior qualities of interest:

$$p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })=\int p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma },{\theta }_{\gamma })p\left({\theta }_{\gamma }\right)d{\theta }_{\gamma }.$$

For logistic regression models this integral is intractable and Laplace approximations are commonly used to approximate $p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })$. In the supplementary materials of [19], it is shown that under a normal prior distribution for the model-specific parameters, θ_γ, the Laplace approximation of the marginal likelihood corresponds to a penalized likelihood of the form:

$$p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })\approx \exp \left[-\frac{1}{2}(\mathrm{dev}\left({\mathcal{M}}_{\gamma }\right)+\mathrm{pen}\left({\mathcal{M}}_{\gamma }\right))\right],$$

where $\mathrm{dev}\left({\mathcal{M}}_{\gamma }\right)$ is the deviance of model ${\mathcal{M}}_{\gamma }$ and $\mathrm{pen}\left({\mathcal{M}}_{\gamma }\right)$ is a penalty on model size that is induced by the choice of variance in the normal distribution. In particular, we will approximate the marginal likelihood with the Akaike information criterion (AIC) which roughly corresponds to a prior standard deviation of any standardized log odds ratio of approximately 2.5.

3. Integrative Model Uncertainty

We wish to extend upon the basic BMU framework with an itegrative Bayesian model uncertainty method (iBMU) that allows external information to guide the selection of predictors. In particular, we incorporate external information in the estimation of marginal inclusion probabilities and in turn model uncertainty probabilities by introducing a second stage regression on the probability that any given predictor variable X_j is associated. This model incorporates a set of c predictor-level covariates that is specified in a (p × c) dimensional matrix W and that quantify external information on the relationships between the p predictors. In particular, we use a probit model to relate the c predictor-level covariates for predictor X_j within the vector W_j to the probability that each predictor is associated to the outcome of interest by introducing a latent vector t. Each element of t is distributed normally as:

$$t_j\mid \alpha \sim N({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha ,1).$$

The inclusion indicator of the predictor variable X_j in model ${\mathcal{M}}_{\gamma }$ is then specified by the function γ_j = I[t_j > 0]. Here is a c-dimensional regression coefficient that quantifies the increase or decrease in probability that each variable, X_j, is associated based on the c predictor-level covariates and α₀ specifies the baseline probability of association common to all of the predictor variables. We define α₀ based on the the multiplicity corrected model space priors introduced in [19] such that the probability of the null hypothesis, H₀, that no predictors are associated is equal to the probability of the alternative hypothesis, H_A, that at least one predictor is associated with the outcome of interest at baseline (when α = 0 for all c covariates). This leads to setting α₀ = Φ⁻¹(2^−1/p). Finally, to complete the specification of the second stage model we assume that α has a prior distribution of α~ N(0, I_c). We note that when α = 0 for all c covariates iBMU is equivalent to BMU.

Based on our specification, the marginal inclusion probabilities, π_j, can be written as:

$$\begin{array}{cc}\hfill {\pi }_j\mid \alpha =& {\int }_0^{\infty }\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(t_j-{\mu }_j)}{2}}d{t}_j;\hfill \\ \hfill =& 1-\Phi ({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha ).\hfill \end{array}$$

Thus, the probability for each model in the model space ${\mathcal{M}}_{\gamma }\in \mathcal{M}$ given α is:

$$p({\mathcal{M}}_{\gamma }\mid \alpha )=\prod _{j=1}^p{[1-\Phi ({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha )]}^{{\gamma }_j}{\left[\Phi ({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha )\right]}^{1-{\gamma }_j}.$$

3.1. Posterior computation

In many studies the total number of predictor variables under investigation can be quite large, causing the model space to quickly become innumerable. In these situations a model search algorithm must be introduced to sample from the space. For our purpose, we use a simple Metropolis Hastings (MH) algorithm to sample models from the model space conditional upon . In the MH algorithm models are evaluated based on the following fitness function:

$$\text{fitness}({\mathcal{M}}_{\gamma }\mid \alpha )=p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })p({\mathcal{M}}_{\gamma }\mid \alpha ).$$

New models are proposed by randomly selecting one variant and changing the status within the current model. For example if predictor X_j is randomly selected and is included in the current model with γ_j = 1 we propose to remove predictor X_j from the new model and vice versa. The new model is then accepted with probability ${\pi }_{accept}=\min (1,\frac{\text{fitness}({\mathcal{M}}_{\text{new}}\mid \alpha )}{\text{fitness}({\mathcal{M}}_{\text{old}}\mid \alpha )})$ so that the new model is always accepted if the fitness of it is larger than that of the old model and is accepted with a probability less than 1 if the fitness of the new model is smaller than that of the old.

Given the current sampled model ${\mathcal{M}}_{\gamma }\in \mathcal{M}$, we use Gibbs sampling techniques to sample from the posterior distribution of α in the second stage model. The full conditionals that we will need to sample from are calculated as:

$$\begin{array}{cc}\alpha \mid {\mathcal{M}}_{\gamma },\mathbf{t}\sim N({\alpha }^{\ast },{\mathbf{V}}_{\alpha }^{\ast });\hfill & \hfill \\ t_j\mid {\mathcal{M}}_{\gamma },\alpha \sim N_{(-\infty ,0)}({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha ,1)\hfill & \text{if}{\gamma }_j=0;\hfill \\ t_j\mid {\mathcal{M}}_{\gamma },\alpha \sim N_{(0,\infty )}({\alpha }_0+{\mathbf{W}}_j^{\prime }\alpha ,1)\hfill & \text{if}{\gamma }_j=1.\hfill \end{array}$$

where ${\alpha }^{\ast }={\mathbf{V}}_{\alpha }^{\ast }\left[{\mathbf{W}}^{\prime }(\mathbf{t}-{\alpha }_0)\right]$ and ${\mathbf{V}}_{\alpha }^{\ast }={[I_c^{-1}+{\mathbf{W}}^{\prime }\mathbf{W}]}^{-1}$.

By iterating between the MH and Gibbs algorithms we are able to obtain a sample from the model space, denoted ${\mathcal{M}}_s$, and a sample from the posterior distribution of α, denoted α_s. Given these samples, we can approximate the posterior

$$p({\mathcal{M}}_{\gamma }\mid \mathbf{Y})\approx \frac{p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })p({\mathcal{M}}_{\gamma }\mid \widehat{\pi })}{{\sum }_{{\mathcal{M}}_{\gamma }\in {\mathcal{M}}_s}p(\mathbf{Y}\mid {\mathcal{M}}_{\gamma })p({\mathcal{M}}_{\gamma }\mid \widehat{\pi })},$$

where the posterior model probabilities are renormalized over the sum of sampled models and $\widehat{\pi }$ are the Monte Carlo (MC) estimates of the inclusion probabilities given the sampled values α_s.

4. Simulation Study

To examine the power of iBMU we have developed a set of 1000 independent simulations comprised of 500 cases and 500 controls and 100 total predictor variables. We assume conditional independence of each of the predictor variables. Also, for each simulation there is one dichotomous predictor-level covariate that assigns some of the predictors to a single group. For each simulation set, given the simulated predictor variables and predictor-level covariate, we sample a random α ∈ {0, 1, 2, 3} and calculate the probability that each predictor is associated based on the sampled α and the probit equation given in Section 3. We also assume that the baseline α₀ is defined as in Section 3. Specifically, when the total number of predictors is 100 we are assuming that the baseline probability that each predictor is associated is .007 (when α = 0 and for all predictors with W_j = 0). However, when α ≠ 0 the probability that each variant with W_j = 1 is associated increases to .072 when α = 1, .322 when α = 2, and .705 when α = 3. Based on these probabilities we assign anywhere between 0 to 10 (total number of associated predictors within each simulation is randomly assigned) predictors to be associated and if associated we assume that they have a modest odds ratio of 1.1.

We also created a set of 1000 genetic association study-based simulations formed by using the genotype data from a systems-based candidate gene study of smoking cessation as part of the Pharmacogenetics of Nicotine Addiction and Treatment Consortium (described in detail in Section 5) [29]. With these simulations, we aim to demonstrate the power of iBMU for more realistic simulations when correlation exists between the variants within each group (or gene) as well as show the power and flexibility of the method to account for continuous predictor-level covariates. To create the study-based simulations, X was formed from genotypes of 122 variants within 789 individuals. The 122 variants are from 7 unique gene regions and thus are comprised of a great deal of correlation between the markers within each gene. In particular, with the exception of 2 pairs of variants that are completely correlated, the correlation of the other variants on average across all gene regions ranges from .00 to .95 with a mean correlation of .22. We then create the predictor-level covariate matrix W by constructing dichotomous dummy variables for the assignment of each variant within a gene region as well as creating a continuous predictor-level covariate. Within the set of simulations, we select one predictor-level covariate, W* from the set of gene dummy variables and continuous covariate to have an increased probability of being associated with the outcome of interest based on randomly assigning an α* level in {0, 1, 2, 3}. The corresponding predictor-level covariate and the sampled α* were then used to assign a probability of association for each marker based on the probit equation given in Section 3. All other predictor-level covariates not equal to W^* were not used in determining the simulated set of associated markers (or equivalently their α level was assumed to be 0). Also, when α* was selected to be 0 for the candidate covariate, all associated markers were chosen at random, independent from the predictor-level covariates. Finally, based on these probabilities we assign anywhere between 0 to 10 predictors to be associated and assumed an odds ratio of 1.5 for all associated markers. The disease status, Y, was then simulated accordingly.

4.1. Comparison with Alternative Variable Selection Methods

We compare the power of our novel iBMU approach with the following commonly used variable selection methods:

• Lasso: The least absolute shrinkage and selection operator [14] introduces an L₁ penalty on the set of regression coefficients to induce sparsity and allow variable selection. Lasso was implemented in R using the glmnet package [30] that uses coordinate descent to fit the regularization path over a grid of values for the lasso tuning parameter λ.

• Elastic Net: The elastic net method [15] is a hybrid of Lasso and Ridge regression [16] that incorporates both an L₁ and L₂ penalty on the regression coefficients to obtain sparsity and to encourage a grouping effect in that strongly correlated predictors will have similarly estimated regression coefficients. The method was also implemented using the glmnet package [30] on a grid of values for λ and the mixing parameter. The optimal mixing parameter was then chosen based on using cross-validation to find the parameter that gives the smallest mean squared error.

• Group Bridge: The group bridge [18] allows for variable selection at the group level as well as within groups. The group bridge was implemented with the grpreg package in R [31] that uses the idea of locally approximated coordinate descent to fit the regularization path over a grid of values for λ. The tuning parameter of the group bridge that induces a penalty on the L₁ norm of the coefficients within a group is selected using cross-validation.

• iBMU & BMU: The novel iBMU approach with one dichotomous predictor-level covariate for the independent simulations and seven dichotomous predictor-level covariates as well as one continuous covariate for the study-based simulations. The effect of the predictor-level covariates, α, is sampled using the Gibbs sampling approach described in Section 3.1. We also implemented the basic BMU framework that is akin to iBMU with α = 0 for all predictor-level covariates. Under both methods we use the MH algorithm described in Section 3.1 to sample models from the model space. Under each method we run the MH/Gibbs algorithms for 250,000 iterations.

4.2. Variable Selection Simulation Results

For each of the above mentioned methods we calculate marginal true positive rates (TPR) and false positive rate (FPR) as the proportion of casual and non-causal predictors respectively that are selected using each method. The TPR and FPR rates are calculated across a grid of thresholds that determine which predictors are selected and these values are plotted as ROC curves. For the penalized regression methods we calculate TPR and FPR rates using varying values of λ as the threshold and for Bayesian approaches we calculate the values across varying MargBF thresholds.

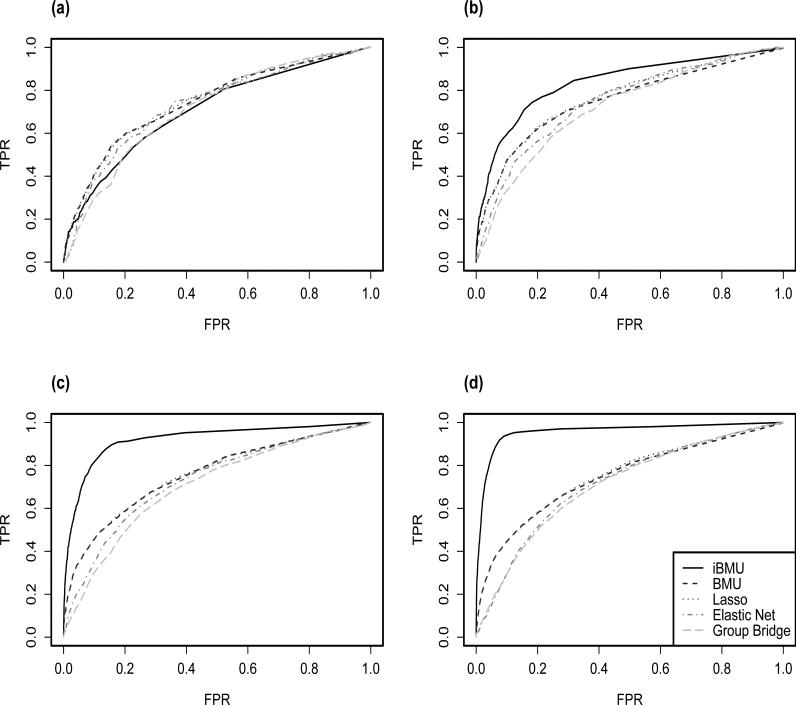
Figure 1 plots ROC curves for the independent simulations in which the informativeness of the predictor-level covariate varies from being non-informative to strongly informative based on the truly sampled α ∈ {0, 1, 2, 3}. We note that even when we assume that α = 0 and the associated predictors are completely independent from the dichotomous predictor-level covariate there is only a modest reduction in power when using iBMU over BMU, Lasso and Elastic Net. However, as increases there is a substantial increase in the power of iBMU over the other commonly used alternatives that seem to retain the same amount of power across all sets of simulations.

Figure 1.

ROC curves are calculated under BMU and iBMU by varying the MargBF threshold that determines which predictor variables are associated with the outcome of interest and are calculated under the penalized regression approaches by varying the value of λ. Given each threshold, the corresponding FPR is plotted on the x-axis and TPR is plotted on the y-axis. Plot a) corresponds to α = 0 in which the predictor-level covariate is non-informative with regards to the associated predictors and plots b), c) and d) correspond to α ∈ {1, 2, 3} respectively for varying informativeness of the covariate.

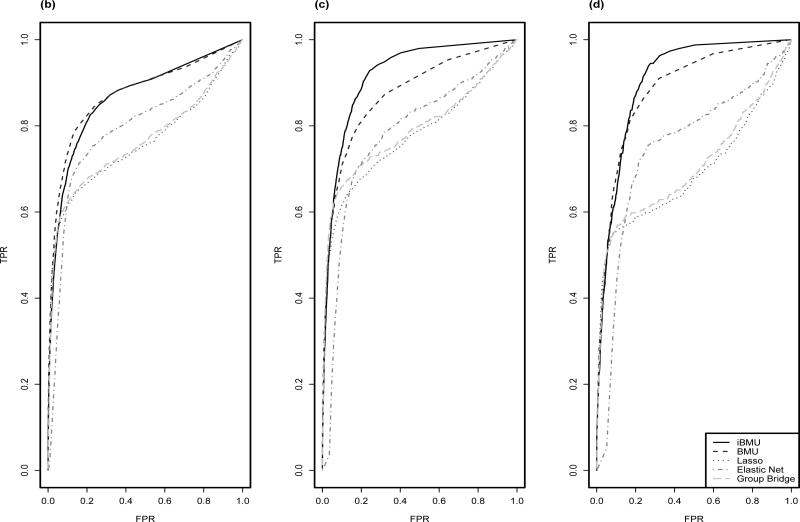
Figure 2 plots ROC curves for the study-based simulations when a) all predictor-level covariates are assumed to be non-informative, b) one gene based covariate is assumed to be informative, and c) the continuous covariate is assumed to be informative. Similarly to the previous simulations above there is an increase in power to detect marginal associations of the variants for iBMU within the informative simulations and little power reduction when the predictor-level covariates are assumed to be non-informative. Also, in the more realistic study-based simulations we see an increase in power of the BMU approach over all of the penalized regression approaches. Of the penalized regression approaches, elastic net is the most powerful. This is most likely due to the fact that elastic net takes into consideration the correlation structure of the predictors. Within Table 1 we calculate the MargBF threshold needed to achieve a FPR of .05 and .20 for iBMU and BMU and the λ threshold needed for the penalized regression methods for each simulation. We then report the average MargBF threshold and λ needed as well as the corresponding average TPR under all 1) non-informative simulations, 2) simulations informed by a dichotomous covariate and 3) simulations informed by a continuous covariate. We see that under the iBMU approach we can achieve a FPR of .05 if we use a MargBF threshold of 10 and a FPR of .20 if we use a MargBF threshold of 3.

Figure 2.

ROC curves are calculated under BMU and iBMU by varying the MargBF threshold that determines which predictor variables are associated with the outcome of interest and are calculated under the penalized regression approaches by varying the value of λ. Given each threshold, the corresponding FPR is plotted on the x-axis and TPR is plotted on the y-axis. Plot a) corresponds to α = 0 for all predictor-level covariates, b) corresponds to α > 0 for a informative gene-based dichotomous covariate and c) corresponds to α > 0 for the informative continuous covariate.

Table 1.

Estimated TPR given a FPR of .05 and .20 for iBMU versus competing methods under 1) all non-informative simulations, 2) all simulations informed by a dichotomous covariate, and 2) all simulations informed by a continuous covariate. Also reported are the average MargBF thresholds need to achieve the corresponding FPR for iBMU and BMU and the average λ thresholds needed for the penalized regression approaches.

	FPR=.10				FPR=.20
	Thresh.	α = 0	αD > 0	αC > 0	Thresh.	α = 0	αD > 0	αC > 0
iBMU	10.00	.59	.60	.51	3.00	.81	.88	.87
BMU	5.00	.61	.58	.50	.70	.82	.81	.80
Lasso	.03	.57	.52	.51	.01	.62	.64	.65
Elastic Net	.20	.29	.34	.38	.02	.70	.67	.71
Group Bridge	.02	.52	.54	.55	.01	.64	.66	.68

4.3. Sensitivity of Marginal Bayes Factors

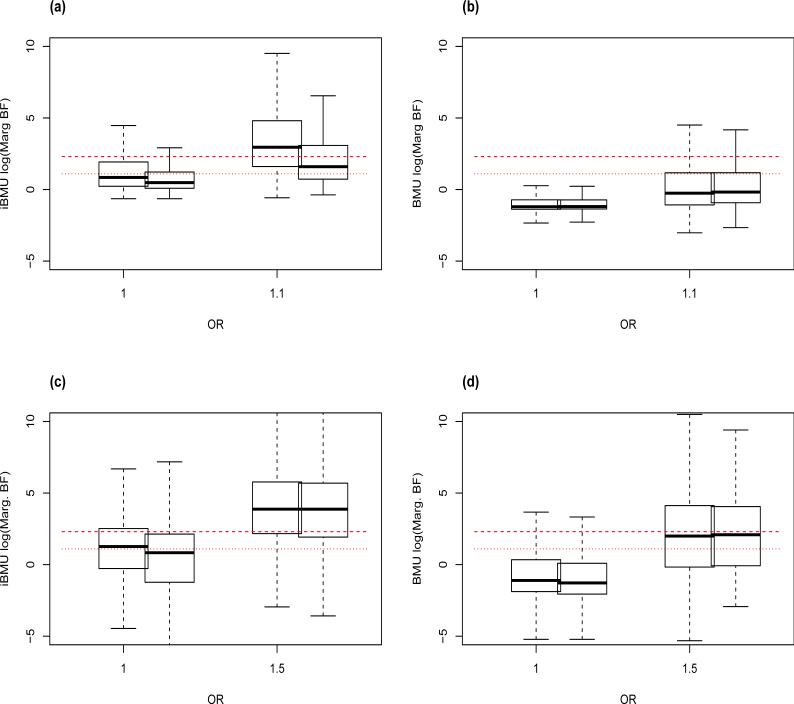
It is of interest to investigate the sensitivity of the estimated MargBF under the iBMU approach that incorporates both continuous and dichotomous predictor-level covariates. With this in mind, Figure 3 plots the log of the MargBF (log(MargBF)) for group informed predictors under iBMU and BMU. Here group informed predictors are defined as predictors that are assigned to a group based on a dichotomous predictor-level covariate that is assumed to inform the associated predictors (has an α > 0). The top plots (a and b) of Figure 3 show the log(MargBF) under iBMU and BMU respectively within the simplistic simulations and the bottom plots (c and d) show the log(MargBF) within the study-based simulations. Within all plots the log(MargBF) are plotted as a function of the true OR of each predictor. For each OR we plot the log(MargBF) for all informed predictors (on the left) and for predictors that are informed by a group where there are only one or two associated members (on the right). Here, we show that although the iBMU approach does lead to an overall increase in log(MargBF) for all predictors within an informed group when compared to the BMU approach, there is a noticeable gap between the average log(MargBF) calculated for associated and non-associated variants within the same informed group (plots a and c). When we look at the distribution of the log(MargBF) for informed predictors that are within a group with a low number of associated members in plot a) we do not see an increase in the log(MargBF) of non-associated predictors within the group. However, we do see that the log(Marg BF) of the associated variants decreases (although Marg BF > 3) such that there are less true positives. This does not appear to be a problem in plot c) for the PNAT study-based simulations where we assume a larger OR of associated variants.

Figure 3.

The log(MargBF) for informed predictors are plotted against the true OR for each predictor. Plot a) corresponds to the log(MargBF) computed under iBMU for the simplistic simulations, b) under BMU for the simplistic simulations, c) under iBMU for the study-based simulations and d) under BMU for the study-based simulations. For each OR we plot the log(MargBF) for all informed predictors on the left and for informed predictors that are within a group that has a low number of associated members (one or two). The red lines in each plot corresponds to a MargBF threshold of 10 and 3.

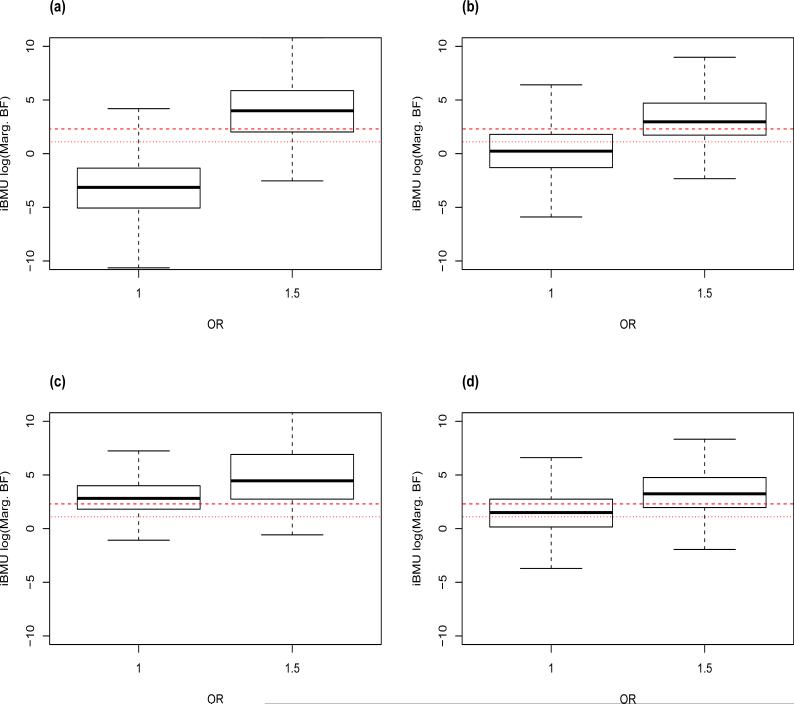
We are also interested in assessing the sensitivity of the estimated MargBF under stimulations in which a continuous predictor-level covariate informs the associations within our study-based simulations. With this in mind, Figure 4 plots the log(MargBF) under iBMU for all predictors with a continuous covariate less than 1 (the mean of the continuous covariate) in plot a), greater than 1 but less than 3 (within 2 standard deviations from the mean) in plot b) and greater than 3 (greater than 2 standard deviations from the mean) in plot c). Here, we can see that if the continuous covariate is less than 3 a large gap remains in the distribution of the log(MargBF) between associated and non-associated predictors. Furthermore, most of the MargBF of the non-associated predictors remain below the significance thresholds of 3 and 10. However, if the value of the continuous covariate is above 2 standard deviations from the mean the gap in the distribution of the log(MargBF) between associated and non-associated predictors lessens and there are a larger number of false positives. Finally, in Figure 4 plot d) we look at the log(MargBF) under iBMU for all predictors within the group corresponding to gene CHRNA5. This gene is of particular interest since there is a high correlation (.68) between the dichotomous covariate that categorizes the predictors within the gene and the continuous predictor-level covariate. Thus, value of the continuous covariate for predictors within the gene tends to be high. Here, we see that although the gap in the distribution of the log(MargBF) between the associated and non-associated predictors is smaller than that in plot a) with most of the log(MargBF) for the non-associated predictors below the threshold of 10.

Figure 4.

The log(MargBF) are plotted against the true OR for predictors in simulations that assume that associations are informed by a continuous predictor-level covariate. Plot a) corresponds to the log(MargBF) computed under iBMU for predictors with a continuous covariate less than 1, b) for predictors with a continuous covariate greater than 1 but less than 3, c) for predictors with a continuous covariate greater than 3, and d) for predictors within the group corresponding to gene CHRNA5.

4.4. Model Search Efficiency Simulations Results

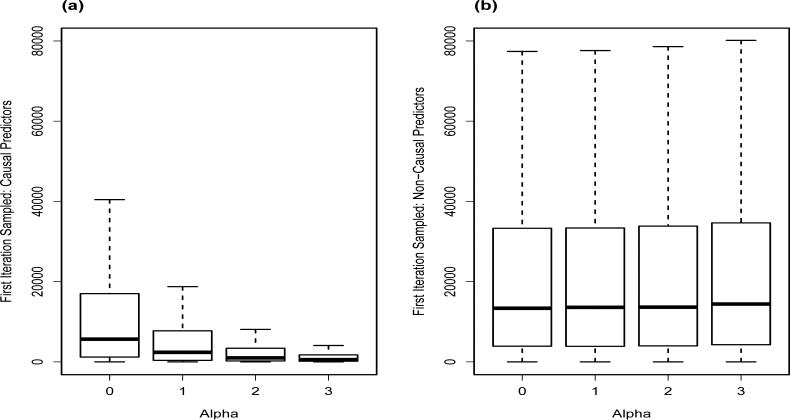
To explore the model search efficiency of the MH/Gibbs algorithm under iBMU, Figure 5 plots the first iteration of the MH/Gibbs algorithm in which a predictor variable is sampled for both causal and non-causal predictors within the independent simulations. Here, as the simulated α increases and there is a corresponding gain in information via W, the model search becomes more efficient in terms of accepting models with causal predictors earlier on in the stochastic search. Furthermore, since the iteration in which a model with a non-causal variant is first accepted remains constant as the known simulated value of α increases, the increased speed of sampling causal predictors within informative simulations does not come at the cost of also accepting non-causal predictors earlier.

Figure 5.

Number of iterations under iBMU until the first acceptance of the causal and non-causal predictors as a function of the simulated for independent simulations.

5. Genetic Association Study of Smoking Cessation

To demonstrate the applicability of iBMU we analyzed data from a systems-based candidate gene study of smoking cessation as part of the Pharmacogenetics of Nicotine Addiction and Treatment Consortium (PNAT) [29, 32]. The study combines data from two comparable pharmacogentic trials of smoking cessation treatment conducted by the University of Pennsylvania Transdisciplinary Tobacco Use Research Center. One aim of the study is to investigate the influence on smoking cessation (abstinence rates at the end of treatment and after a 6-month follow-up period) of variants within genes in the neuronal nicotinic receptor and dopamine systems, studied within a bupropion placebo-controlled randomized clinical trial and a randomized clinical trial comparing transdermal nicotine replacement therapy (patch) to nicotine nasal spray (spray). Detailed descriptions of the study design for the clinical trials were previously reported in [32], [33], [29] and [34]. Our analysis was limited to 789 persons with self-reported European ancestry. For illustrative purposes to highlight the specific influence of prior covariates, we focused on investigating possible associations within several gene regions related to nicotine processing in the body. This includes 121 SNPs within 6 unique gene regions that code for several nicotinic acetylcholine receptors (nAChRs). These receptors are involved in the dopamine reward system, a system that is stimulated by nicotine. In addition, we examine genetic variants found within the gene CYP2A6 that have been previously found to be associated with altered nicotine metabolism. CYP2A6 converts 80-90% of nicotine to cotinine and subsequently metabolizes cotinine to 3-hydroxycotinine. Additionally, we have measured the nicotine metabolite ratio (NMR),a ratio of 3-hydorxycotinine to cotinine, on all individuals. NMR has been shown to be a stable phenotypic measure of nicotine metabolism and related associations for genetic variants can serve as an biologically informative prior covariate especially for CYP2A6 as it is directly involved in nicotine metabolism. As described in [35], we collapse all variants genotyped within CYP2A6 to a single covariate. The outcome of interest is abstinence after a 6-month follow up period post-treatment. Finally, our analyses were adjusted for treatment, age, gender, and individual scores from the Fagerström Test for Nicotine Dependence (FTND) by forcing these covariates into all models.

Of particular interest in our analysis is the incorporation of additional biological covariates to aid in the selection of important genetic factors associated with smoking cessation. One such covariate is the categorization of SNPs within gene regions since we expect highly correlated variants within the same gene to show similar evidence of association. Thus, while the model selection aims at identifying single SNPs driving association, structuring the prior covariates to reflect gene regions will allow SNPs within a region to influence the probability of inclusion for other SNPs within that region and provide a summary of the overall influence of the gene via the estimated α. In addition, results from the use of these covariates will also reflect how any single associated SNP can influence the total number of SNPs (ranging from 13 to 33). To reflect potentially more biologically relevant prior information, we construct an additional continuous covariate that is a function of empirical associations of each variant to the nicotine metabolite ratio (NMR). Since it is very likely that variants associated with NMR will be more likely to influence smoking cessation, we allow for the degree to which a variant is associated with NMR to inform the prior probability that the variant will be associated with smoking cessation. Specifically, for each variant under consideration (including the covariate coded for CYP2A6) we calculate the marginal t-statistic quantifying the likelihood that each variant is associated with NMR. We then use these t-statistics as an additional prior covariate.

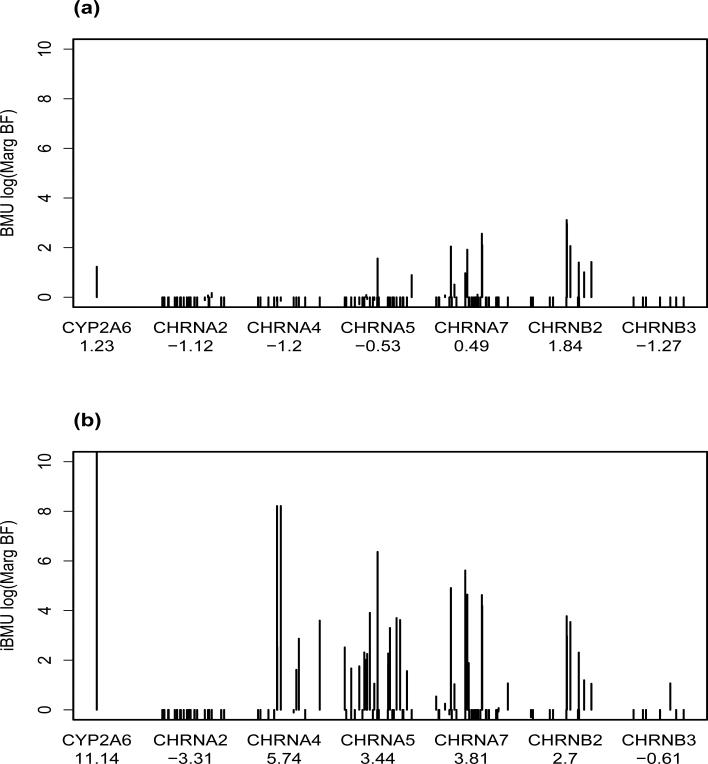
To determine the impact of incorporating informative predictor-level covariates to the analysis we applied BMU and iBMU with gene grouping and NMR-SNP associations as predictor-level covariates to the the PNAT data. MargBF were calculated under both methods based on 500,000 iterations of the combine MH/Gibbs techniques described in Section 3 (for BMU only the MH model search technique was needed). Convergence was determined based on investigating MargBF from two independent runs of the MH/Gibbs algorithms for each scenario. Gene BFs, defined as the posterior odds that at least one variant from gene G_k was associated with smoking cessation divided by the prior odds, were also calculated under each prior scenario. Figure 6 plots MargBF for all variants in the study. Each variant is grouped by gene on the x-axis and the position of the variant within the gene is relative to the chromosomal position of the variant. Plot (a) is under BMU and plot (b) under iBMU. Gene log(BFs) are reported under each gene on the x-axis. In Table 2 we provide results for the top 20 variants within the top 5 genes ranked under the iBMU approach. Under each gene we report the estimated effect (α) for the predictor-level covariate corresponding to each gene. We also note that the estimated effect for the NMR based predictor-level covariate is .79. For each variant, we report the variant specific t-statistics for NRM-SNP associations, log(MargBF) under iBMU and BMU, and marginal prior probabilities under iBMU and BMU. Also, for the alternative penalized regression methods we performed k-fold cross validation to determine the optimal value of λ with regards to mean squared error and report the variants that were determined to be associated under each approach.

Figure 6.

Each plot reports the log(MargBF) of each variant on the y-axis. The variants are organized by gene on the x-axis and the space between each variant on the x-axis within each gene is proportional to the chromosomal position. Plot (a) corresponds to log(MargBF) calculated under BMU method and plot (b) under the gene region and NMR biomarker based iBMU method. Gene log(BFs) are reported on the x-axis under each gene.

Table 2.

Top 20 variants within top 5 genes. Genes are ranked based on the Gene BF and variants within each gene are ranked based on their MargBF under iBMU. Under each gene we report the estimated effect (α) for the gene based predictor-level covariate. For each variant we report: 1) rs number, 2) NMR by variant marginal t-statistic. 3) iBMU log(MargBF), 4) iBMU Marg Prior. 5) BMU log (MargBF), 6) BMU Marg Prior., and if the variant was determined to be associated under 7) Group Bridge, 8) Elastic Net, and 9) Lasso

			iBMU		BMU		Penalized Approach
Gene	SNP	NMR	log(MargBF)	Prior	log(MargBF)	Prior	Group	Elastic Net	Lasso
CYP2A6 ($\widehat{\alpha }=.10$)	CYP2A6	6.39	11.21	.84	1.23	.01	1	1	1
CHRNA4 ($\widehat{\alpha }=.56$)	rs1044396	1.34	8.43	.24	−0.15	.01	1	1	0
	rs3787137	1.33	8.43	.24	−0.16	.01	0	0	0
	rs4809549	2.11	3.65	.22	−1.03	.01	0	0	0
	rs2273505	1.74	2.89	.32	−1.02	.01	1	1	0
	rs3787138	1.95	2.58	.37	−1.53	.01	0	0	0
CHRNA7 ($\widehat{\alpha }=.75$)	rs6494211	1.05	5.64	.20	0.97	.01	1	1	1
	rs4779969	1.15	4.91	.22	2.05	.01	1	1	1
	rs8033518	0.96	4.65	.18	1.92	.01	1	1	0
	rs16956223	0.57	4.61	.12	2.56	.01	1	1	1
	rsl392808	0.59	4.21	.12	2.01	.01	0	0	0
CHRNA5 ($\widehat{\alpha }=-.61$)	rs3743077	2.91	6.39	.27	1.56	.01	1	1	1
	rs514743	2.73	3.94	.23	−1.05	.01	0	0	0
	rs7178270	2.97	3.72	.28	−1.64	.01	0	0	0
	rs950776	2.69	3.62	.41	−0.90	.01	1	1	0
	rsl878399	3.02	3.31	.29	−0.67	.01	0	0	0
	rs4275821	3.09	2.52	.31	−0.99	.01	0	0	0
CHRNB2 ($\widehat{\alpha }=.27$)	rs2072660	0.67	3.74	.07	3.11	.01	1	1	1
	rs3811450	1.09	3.56	.12	2.07	.01	1	1	1
	rs2072661	0.83	2.97	.09	2.96	.01	0	1	0

By allowing the gene structure and NMR-SNP associations of the variants to inform the prior probability of a marginal association, the approach is able to detect various variants within the CHRNA4, CHRNA5,CHRNA7, and CHRNB2 gene regions that are likely associated with smoking cessation as well as CYP2A6. Without accounting for these biological predictor-level covariates, evidence of associations of variants within these regions is sparse and modest at best. One particular gene of interest is CHRNA4. Variants within this gene have been shown in independent studies to be associated with nicotine dependence [36]. Under the BMU and Lasso penalized regression approaches, we do not determine that any of the variants within this gene are association. However, when we incorporate gene and correlation structure within the elastic net and group bridge penalized regression approaches we deem two variants within this region to be associated. Additionally, when we incorporate NMR as well as gene structure within the iBMU approach there is strong evidence that 5 variants within this region are associated. Another gene of interest is CHRNA5. Although we do not estimate an increase in prior probability of a variant being associated based solely upon it being in the gene ($\widehat{\alpha }=-.61$) we do see several of the variants within this gene among the top 20 variants in Table 2. This is most likely due to their high values of NMR by variant t-statistic. Variants within this gene are a good example of the ability of iBMU to discern likely associated variants from likely non-associated variants within a gene that is highly correlated with the continuous predictor level covariate of NMR by variant t-statistic. This is also a good example of the difference between the empirically estimated effects of the gene-based predictor-level covariates on the prior probability of association within the iBMU approach and the posterior Gene BF's that give the weight of evidence that at least one variant within a gene is associated.

6. Discussion

The Bayesian model uncertainty framework provides an extremely powerful and flexible basis for variable selection problems. We have shown that the incorporation of informative predictor-level covariates within this framework leads to an increase in power to detect marginal associations and a more efficient model search algorithm, even when the informativeness is moderate over more commonly used variable selection techniques. By incorporating biological covariates on the gene structure and SNP-NMR associations within the PNAT study, we show strong evidence of an association with variants in CHRNA4, CHRNA5, CHRNA7,CHRNB2, and CYP2A6 and smoking cessation. Without the incorporation of these prior covariates, the posterior evidence of a marginal association for a variant within any of the gene regions of interest is modest at best. The PNAT analysis was adjusted for treatment, age, gender, and individual scores from the FTND by forcing these covariates into all models. Once we adjusted for the possible confounding variable we focused on identifying main effects within the variants of interest. It is of future interest to also investigate possible gene-treatment interactions (i.e. placebo, bupropion, patch and spray).

The integrative variable selection approach described herein has vast implications not only in genetic association studies, but also in a wide range of model choice and variable selection problems in a diverse group of interdisciplinary fields. The current implementation focuses on model uncertainty within a logistic regression framework. However, iBMU can easily be extended to other regression problems such as those with a continuous or survival outcome. Within the logistic regression framework, we assume a basic normal prior on the model specific parameters. However, other prior distributions on the model specific coefficients can be incorporated into the framework. In particular, predictor-level covariates can also be included in the prior on the coefficient of each included predictor to inform the estimation of the magnitude of the effect of each of the associated predictors. With this in mind, it is of interest in future work to explore the implications of incorporating informative predictor-level covariates on both estimation and inference via model selection.

The BMU and iBMU approaches come at a computational cost of running MH and Gibbs algorithms to sample from the high-dimensional model space and to sample the effects of the predictor-level covariates. The computational complexity of the MH algorithm needed for high-dimensional applications of both BMU and iBMU is a function of the computational cost of estimating model specific parameters and marginal likelihoods for each unique model sampled which scales linearly with n and cubically with model size. Thus, an increase in sample size will not cause a significant increase in computation time of the MH algorithm. However, as the model size of sampled models increases the computation time of the algorithm will increase substantially. The computational complexity of the Gibbs algorithm needed under the iBMU approach to sample the effects (α) of the predictor-level covariates scales linearly with respect to the number of predictor-level covariates (c) and the total number of predictor variables of interest (p). Therefore, as these parameters increase we will not see a significant increase in computation time per iteration of the Gibbs sampling algorithm. As an example of the computational cost of the BMU and iBMU algorithms, performing 100,000 iterations of the current MH/Gibbs algorithm under the iBMU approach on the PNAT data took approximately 2 hours to complete on a single processor. This can be compared to taking approximately 1.5 hours to perform 100,000 iterations of the MH algorithm under the BMU approach on the same processor. The added computational cost of iBMU over BMU is due in part to the added computational complexity of the Gibbs algorithm to sample the effects of the predictor-level covariates. However, it is more likely due to larger models being sampled when the marginal prior probabilities increase for informed predictor variables under the iBMU approach. The computational complexity of BMU and iBMU can be compared to that of the alternative penalized regression approaches which took approximately 3 seconds, 6 minutes and 30 minutes to run lasso, elastic net and the group bridge approach respectively.

These examples demonstrate the computational complexity of BMU and iBMU approaches for a set number of iterations of the MH and Gibbs algorithms. However, as the total number of predictor variables of interest increase the number of iterations of the algorithms needed for convergence of posterior quantities will also need to increase. To determine the number of iterations needed for convergence, we suggest doing two independent runs of the algorithms and comparing the global and marginal posterior quantities computed under a set number of iterations of each independent run to determine if the algorithm has converged. The current framework uses a simple MH algorithm to sample models of interest from the innumerable model space. The proposal distribution within the algorithm selects a single predictor variable at random and proposes to mutate the status of the variable in the current model, i.e. a random walk. Within this framework, the information within the predictor-level covariates comes into play only in the acceptance probability of the proposed model. However, we have shown that even when the information within the predictor level covariates is modest the random walk MH/Gibbs algorithm is more efficient in selecting casual variants over non-causal variants than when there is no prior information. Therefore the number of iterations needed to reach convergence of the algorithm may be less than that of the MH algorithm under the basic BMU approach. It is of future interest to explore alternative model search algorithms that also incorporate these predictor level covariates in the proposal distribution to increase the efficiency of the model search even further. Finally, we have investigated the estimation of marginal inclusion probabilities using both a Monte Carlo approach (calculating the proportion of times a variable is sampled) as well as our current approach of calculating them using renormalized posterior model probabilities. We have found that marginal inclusion probabilities calculated from renormalized posterior model probabilities were equally as powerful as those calculated from Monte Carlo estimates.

For ease of specification of informativeness in terms of sensitivity/specificity and for interpretation of the corresponding effect estimates, we have focused the simulations on incorporating dichotomous predictor-level covariates that specify a known group structure of the predictor variables of interest as well as a single continuous predictor-level covariate. However, the amount of information that can be incorporated into an analysis via covariates is extremely flexible. This is demonstrated in our analysis of the PNAT study where the degree to which a variant is associated with NMR (a biomarker that quantifies the rate of nicotine metabolism within an individual) was included as a predictor-level covariate and was shown to significantly inform the prior probability that the variant will be associated with smoking cessation. In particular, for our motivating application of genetic association studies, a vast amount of external biological information exists for the variants under consideration, as discussed in [22]. As one specific example, Cooper and Shendure [37] give a review of approaches to estimate the overall deleteriousness of genetic variants with the goal of prioritizing disease-causing variants. Many of the reviewed methods use a combination of evolutionary, biochemical and structural information to guide the estimation. Within our framework similar information can easily be used as predictor-level covariates or, once estimated from one of the approaches described in [37], the probability that a variant is deleterious can be used itself as a covariate within the study of interest.

7. Software

Software for the methods described herein is freely available for R within the BVS package on CRAN at the following link: http://cran.r-project.org/web/packages/BVS/.