Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jul 8;4:5618. doi: 10.1038/srep05618

Pushing the resolution of photolithography down to 15nm by surface plasmon interference

Jianjie Dong 1, Juan Liu 1,a, Guoguo Kang 1, Jinghui Xie 1, Yongtian Wang 1
PMCID: PMC4085591  PMID: 25001238

Abstract

A deep ultraviolet plasmonic structure is designed and a surface plasmon interference lithography method using the structure is proposed to generate large-area periodic nanopatterns. By exciting the anti-symmetric coupled surface plasmon polaritons in the structure, ultrahigh resolution periodic patterns can be formed in a photoresist. The resolution of the generated patterns can be tuned by changing the refractive index and thickness of the photoresist. We demonstrate numerically that one-dimensional and two-dimensional patterns with a half-pitch resolution of 14.6 nm can be generated in a 25 nm-thick photoresist by using the structure under 193 nm illumination. Furthermore, the half-pitch resolution of the generated patterns can be down to 13 nm if high refractive index photoresists are used. Our findings open up an avenue to push the half-pitch resolution of photolithography towards 10 nm.

Optical lithography is the most widely used technique for fabricating large-area integrated devices. However, the resolution of conventional photolithography techniques is limited by the diffraction of light, which makes it difficult for them to meet the demand of fabricating ultrahigh density integrated devices. To overcome this problem, surface plasmon polaritons (SPPs) have been used for lithography. The superlens imaging lithography1,2,3,4,5,6,7, which uses SPPs to amplify evanescent waves to achieve a sub-diffraction-limit resolution, is a promising plasmonic lithography technique. Although this technique has a higher resolution than conventional photolithography techniques, it still faces some obstacles such as the difficulty of fabricating ultrahigh resolution masks. Recently, a superlens system8 used for lithography was proposed to reduce the difficulty in the fabrication of masks by demagnification imaging, but its complex structure leads to an engineering challenge.

The focused plasmon beam lithography9, which uses a focused plasmon beam generated from a plasmonic lens to generate patterns, is a maskless plasmonic lithography technique and hence completely solve the problems involved with masks. By optimizing the structure of the plasmonic lens, its resolution has been improved to 22 nm10. However, it becomes difficult to further improve the resolution of this technique due to the facts that the focused spot size of a plasmonic lens increases with increasing its focal depth and the decay of SPPs increases with reducing their wavelengths.

The surface plasmon interference lithography11,12,13,14,15,16,17,18,19, which can employ the interference effect of SPPs to generate sub-diffraction-limit patterns, which is due to the fact that SPPs have a larger wave vector than light waves of the same frequency11,12, is perhaps the most promising plasmonic lithography technique for fabricating large-area periodic structures such as an array of nanoparticles20,21, an array of nanoholes22,23, and an array of nanowires24,25,26. Since dielectric-metal multilayer structures support ultra-short wavelength SPPs, the surface plasmon interference lithography method (SPILM) using an 8 pairs of GaN and Al multilayer becomes the highest-resolution SPILM among previous SPILMs15. This SPILM can produce 16.5 nm half-pitch one-dimensional (1D) patterns with an image contrast of about 0.2 under 193 nm illumination. However, because the image contrasts of the higher-resolution patterns produced by this SPILM are below 0.2, which don't satisfy the minimum requirement for photoresists, its resolution can't be further improved. It is imperative to overcome the fundamental limitations on the resolution of previous plasmonic lithography techniques for obtaining a higher resolution.

In this paper, a deep ultraviolet plasmonic structure is designed and a SPILM using this structure is proposed to produce ultrahigh resolution patterns with a sufficient image contrast for photoresists. Because the designed structure supports anti-symmetric coupled SPPs with ultra-short wavelengths, the half-pitch resolution of the produced patterns can go beyond 15 nm. Although the proposed SPILM needs a mask, the pitch resolution of the mask is at least two times lower than that of the produced patterns, which can reduce the fabrication difficulty of masks.

Results and Discussion

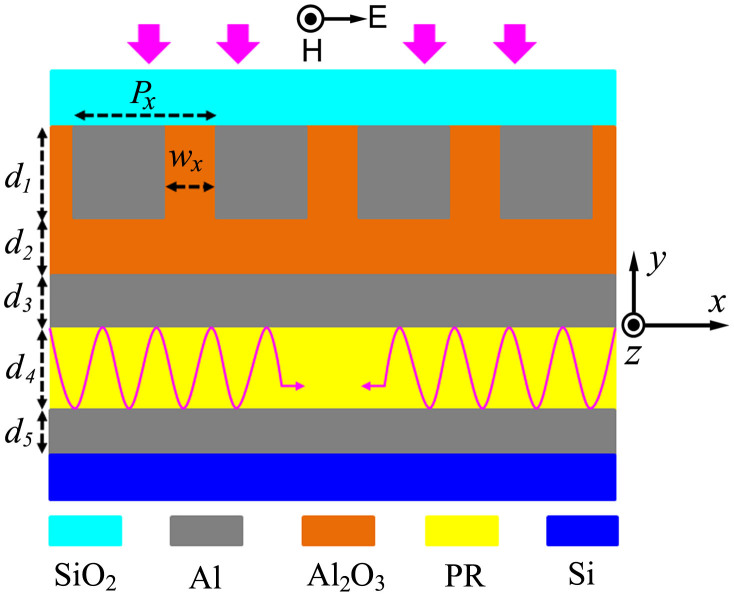
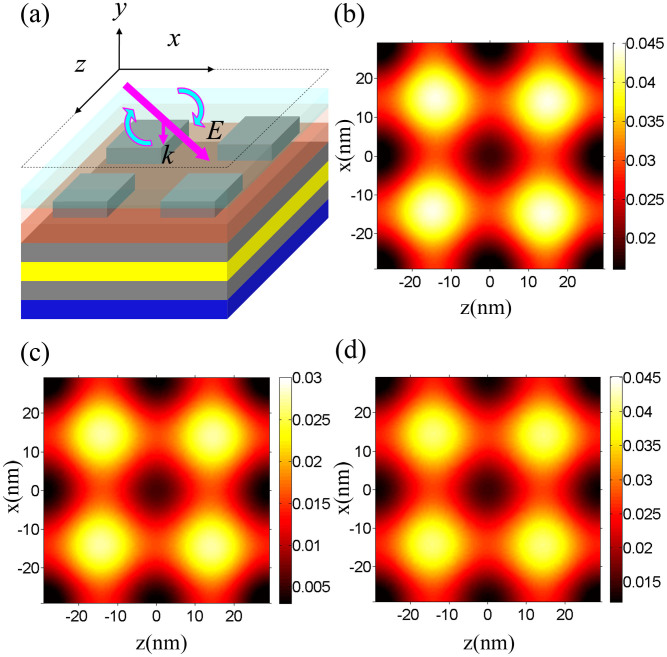
A schematic of the deep ultraviolet plasmonic structure is shown in Figure 1. This structure consists of an Al grating, an Al2O3 spacer layer, and two Al films separated by a photoresist (PR) layer. The Al grating is located at the bottom surface of a SiO2 substrate, and its openings are filled with Al2O3. The Al2O3 spacer layer is sandwiched between the Al grating and the upper Al film. The lower Al film is coated on a Si substrate. The thicknesses of the Al grating, the Al2O3 spacer layer, the upper Al film, the PR layer and the lower Al film are denoted by d1, d2, d3, d4 and d5, respectively. Al is chosen as the metal material of the plasmonic structure because its dielectric constant has a highly negative real part and its absorption is low in the deep ultraviolet band, which are beneficial to exciting SPPs.

Figure 1. Cross section of the deep ultraviolet plasmonic structure.

Figure 1

Open in a new tab

The SiO2 layer, the Al grating layer with thickness d1, the Al2O3 spacer layer with thickness d2, the upper Al film with thickness d3, the photoresist (PR) layer with thickness d4, the lower Al film with thickness d5 and the Si layer extend in both the z direction and the x direction. The pink arrows show the propagation direction of the incident plane wave. The pink curves in the PR layer represent coupled SPPs.

The Al grating is used as a mask. We use a one-dimensional (1D) grating mask to illustrate the principle of the proposed SPILM. A two-dimensional (2D) grating mask can be considered as a combination of two 1D grating masks. We assume that the openings of the 1D grating extend in the z direction. The period and opening width of the 1D grating are denoted by Px and wx, respectively. The PR layer and the two Al films form a plasmonic waveguide. The dispersion relations of the coupled SPPs whose propagation directions are perpendicular to the yz plane in the plasmonic waveguide are given by27

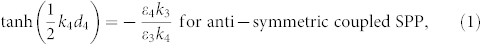graphic file with name srep05618-m1.jpg
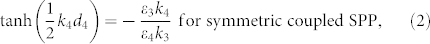graphic file with name srep05618-m2.jpg

where ε represents the dielectric constant, and 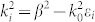Inline graphic for i = 3 (Al) and i = 4 (PR). k0 is the wavenumber of light in free space, β is the wavenumber of the coupled SPPs. Since the wavenumber of the anti-symmetric coupled SPPs is larger than that of the symmetric coupled SPPs, the anti-symmetric coupled SPPs are used for lithography.

When a TM plane wave normally illuminates the 1D grating, diffracted waves with wavenumber kg can be produced. kg is expressed as kg = 2mπ/Px, where m is the order of diffracted waves. Two anti-symmetric coupled SPPs with opposite propagation directions can be excited by the ±mth order diffracted waves when the following condition is satisfied:

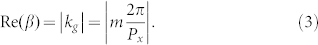graphic file with name srep05618-m3.jpg

The two anti-symmetric coupled SPPs can form interference patterns in the PR layer. The pitch resolution of the interference patterns is π/Re(β), so the pitch resolution of the mask is at least two times lower than that of the interference patterns. The interference patterns can be recorded in the PR layer and be transferred into the lower Al film. Then, the Si substrate can be patterned by using the patterned Al film as a mask.

A feasible lithography process using the deep ultraviolet plasmonic structure is described as follows. First, the Al grating mask is fabricated on the bottom surface of the SiO2 substrate by using atomic layer deposition, electronic beam lithography and reactive ion etching24,26. Second, the Al2O3 spacer layer and the upper Al film are integrated on the Al grating mask of the SiO2 substrate by using atomic layer deposition26 or E-beam evaporation28. The integrated structure consisting of the SiO2 substrate, the Al grating mask, the Al2O3 spacer layer and the upper Al film is simply called mask stack. Thirdly, the lower Al film is fabricated on the top surface of the Si substrate by using atomic layer deposition26. Fourthly, the PR layer is coated on the top surface of the lower Al film. Fifthly, the upper Al film of the mask stack is placed on the PR layer with the help of air pressure28. Sixthly, the mask stack is removed when the exposure of the PR layer is completed. After development, the patterns can be formed in the PR layer. The patterns of the PR layer can be transferred into the lower Al film on the Si substrate by using reactive ion etching24. Lastly, the patterns of the lower Al film which acts as a metal mask can be transferred into the Si substrate by using dry etching26. Similar lithography processes using metal-potoresist-metal multilayer structures were successfully realized in experiments28,29,30.

Numerical simulations with the finite-element method for 1D masks and with the finite-difference time-domain method for 2D masks are performed to demonstrate the proposed SPILM. Some key physical quantities are defined as follows. The normalized electric field intensity is defined as |E|2/|E0|2, where E0 is the incident electric field. The image contrast is defined as 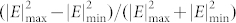Inline graphic. The wavelength of the incident light in free space is set to 193 nm. At this wavelength, the dielectric constants of SiO2, Al2O3, Al and Si are 2.44, 3.74, −4.84+0.50i and −6.94+4.91i, respectively31,32. The dielectric constant of common 193 nm PRs is 2.8933,34.

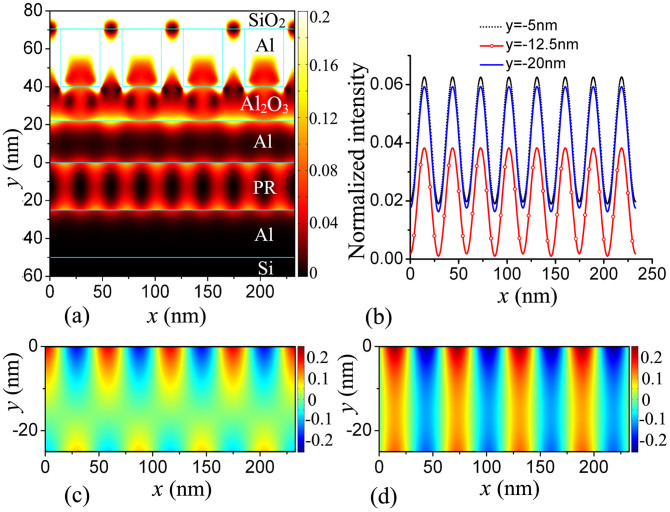
We first use a 1D grating mask to generate 1D periodic patterns. The thickness d4 of the PR layer is set to be d4 = 25 nm, which can be achieved in practical lithography10,28. We use the ±1order diffracted waves to excite the anti-symmetric coupled SPPs. According to Eq. (1), the normalized wavenumber Re(β)/k0 of the anti-symmetric coupled SPPs is 3.3171 for d4 = 25 nm. Thus, we set Px = 58.2 nm according to Eq. (3). Other parameters of the plasmonic structure are the same as in Figure 2. Figure 2(a) shows the normalized electric field intensity distribution of the plasmonic structure. It can be seen that a uniform 1D periodic pattern is formed in the PR layer. The half-pitch resolution of this pattern is 14.6 nm. The cross sections of the normalized electric field intensity at y = −5 nm, −12.5 nm and −20 nm are shown in Figure 2(b). The image contrasts at y = −5 nm, −12.5 nm and −20 nm are 0.52, 0.91 and 0.54, respectively. These image contrasts are larger than the minimum contrast (0.4) required for positive PRs and are larger than the minimum contrast (0.2) required for negative PRs15,35. Therefore, the generated 1D periodic pattern can be recorded in the PR layer.

Figure 2.

Figure 2

Open in a new tab

(a) Normalized electric field intensity distribution of the plasmonic structure. (b) Cross sections of the normalized electric field intensity at y = −5 nm, −12.5 nm and −20 nm. (c) Distribution of normalized x component of the electric field Ex/|E0|. (d) Distribution of normalized y component of the electric field Ey/|E0|. Geometric parameters of the plasmonic structure are set as follows: Px = 58.2 nm, wx = 21 nm, d1 = 30.5 nm, d2 = 18 nm, d3 = 22 nm, d4 = 25 nm and d5 = 25 nm.

The phenomenon that the interference pattern with an ultrahigh resolution formed by the anti-symmetric coupled SPPs has relatively high image contrasts in the PR layer can be explained as follows. The interference pattern of the Ex component and that of the Ey component have a half pitch shift (i.e., π/[2Re(β)]) in the x direction since the Ex component and Ey component of a SPP have a phase difference of π/2, which are reflected in Figures 2(c) and 2(d). In addition, |Ex|/|Ey| goes to 1 when the wavenumber of SPPs goes to +∞16. Therefore, the image contrast of a higher resolution plasmonic interference pattern will be very low if the lower Al film is removed. However, for the plasmonic structure, the lower Al film leads to the interference between the forward SPPs from the upper Al film and the reflected SPPs from the lower Al film in the y direction. At the interface between the PR layer and the lower Al film, the Ex component of the reflected SPPs has a π phase shift, whereas the Ey component of the reflected SPPs has no phase shift. Thus, the interference between the forward SPPs and the reflected SPPs in the PR layer is nearly destructive for the Ex component and constructive for the Ey component, as shown in Figures 2(c) and 2(d). As a result, the high resolution patterns produced by the designed plasmonic structure can have a relatively high image contrast. Since SPPs decay with the distance away from the Al-PR interfaces, the image contrast is larger at the longitudinal center of the PR layer than that near the surfaces of the PR layer.

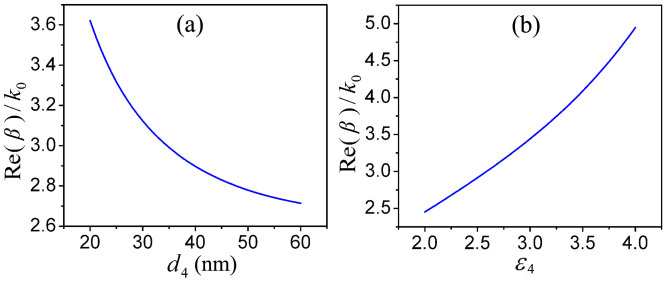
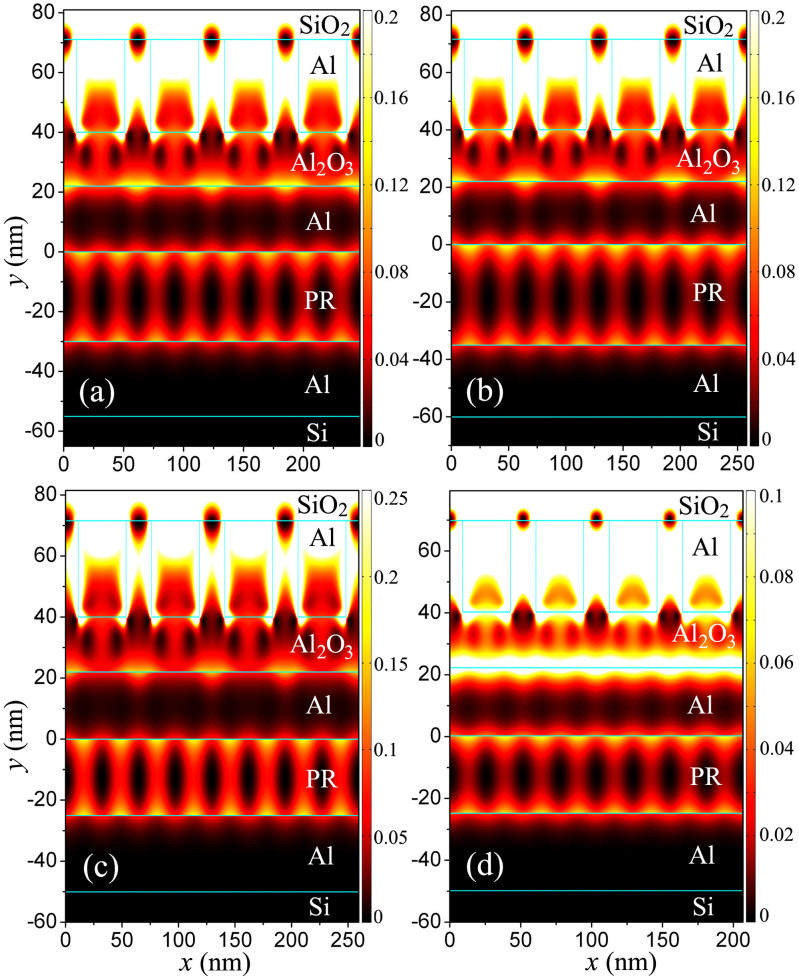
According to Eq.(1), the half-pitch resolution of the produced interference patterns can be tuned by changing the thickness and the dielectric constant (or the refractive index) of the PR layer. As shown in Figures 3(a) and 3(b), the normalized wavenumber Re(β)/k0 of the anti-symmetric coupled SPPs increases as the thickness d4 of the PR layer decreases and that increases as the dielectric constant ε4 of the PR layer increases, which mean that the half-pitch resolution of the produced interference patterns can be improved by reducing the thickness d4 of the PR layer and increasing the dielectric constant ε4 (or the refractive index n) of the PR layer. Note that the relationship between the refractive index n and dielectric constant ε4 of the PR layer is given by 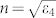Inline graphic. Figures 4(a) and 4(b) show the normalized electric field intensity distributions for d4 = 30 nm and d4 = 35 nm. The half-pitch resolutions of produced 1D periodic patterns are 15.5 nm for d4 = 30 nm and 16.1 nm for d4 = 35 nm, and the image contrasts at the longitudinal centers of PR layers are 0.89 for d4 = 30 nm and 0.84 for d4 = 35 nm. Figures 4(c) and 4(d) show the normalized electric field intensity distributions for ε4 = 2.56 (n = 1.6) and ε4 = 3.24 (n = 1.8). The half-pitch resolutions of produced 1D periodic patterns are 16.2 nm for ε4 = 2.56 and 12.9 nm for ε4 = 3.24, and the image contrasts at the longitudinal centers of PR layers are 0.96 for ε4 = 2.56 and 0.85 for ε4 = 3.24. These results verify that the half-pitch resolution of the produced patterns can be tuned while keeping the operating wavelength the same, which is useful for practical applications. These results also imply that if the refractive index n of the PR layer is larger than 1.8 for the case d4 = 25 nm, the half-pitch resolution of the produced patterns can be down to 12.9 nm.

Figure 3. The normalized wavenumber Re(β)/k0 of the anti-symmetric coupled SPPs (a) as a function of the thickness d4 of the PR layer and (b) as a function of the dielectric constant ε4 of the PR layer.

Figure 3

Open in a new tab

The operating wavelength λ0 ( = 2π/k0) is fixed at 193 nm. The dielectric constant ε4 of the PR layer is 2.89 in (a). The thickness d4 of the PR layer is 25 nm in (b).

Figure 4.

Figure 4

Open in a new tab

(a) Normalized electric field intensity distribution for d4 = 30 nm. Some parameters of the structure are set as follows: ε4 = 2.89, Px = 61.8 nm, wx = 21.5 nm, d1 = 31 nm,d2 = 18 nm, d3 = 22 nm and d5 = 25 nm. (b) Normalized electric field intensity distribution for d4 = 35 nm. Some parameters of the structure are set as follows: ε4 = 2.89, Px = 64.5 nm, wx = 22.5 nm, d1 = 31.5 nm, d2 = 18 nm, d3 = 22 nm and d5 = 25 nm. (c) Normalized electric field intensity distribution for ε4 = 2.56. Some parameters of the structure are set as follows: Px = 64.9 nm, wx = 22.5 nm, d1 = 31.5 nm, d2 = 18 nm, d3 = 22 nm, d4 = 25 nm and d5 = 25 nm. (d) Normalized electric field intensity distribution for ε4 = 3.24. Some parameters of the structure are set as follows: Px = 51.7 nm, wx = 18 nm, d1 = 29.5 nm, d2 = 18 nm, d3 = 22 nm, d4 = 25 nm and d5 = 25 nm.

We next use a 2D grating mask to generate 2D periodic patterns. A 3D View of the plasmonic structure is shown in Figure 5(a). The periods of the 2D grating are Px in the x direction and Pz in the z direction, and its opening widths are wx in the x direction and wz the z direction. For simplicity, we set Px = Pz and wx = wz. The momentum matching condition for exciting SPPs with 2D grating masks is given by

graphic file with name srep05618-m4.jpg

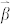where Inline graphic is the wave vector of the anti-symmetric coupled SPPs, i is the order of diffracted waves in the x direction, and j is the order of diffracted waves in the z direction. The magnitude of the wave vector β can be obtained with Eq. (1). To excite SPPs of different propagation directions, circularly polarized light is used. As shown in Figure 5(a), circularly polarized light normally illuminates the 2D grating. We set Re(β) = 2π/Px = 2π/Pz, so two coupled SPPs whose propagation directions are perpendicular to the yz plane and two coupled SPPs whose propagation directions are perpendicular to the yx plane can be excited. These four SPPs can interfere and hence generate a 2D periodic pattern in the PR layer. The thickness and dielectric constant of the PR layer are set to be d4 = 25 nm and ε4 = 2.89. Note that the PR layer is from y = −25 nm to y = 0 nm. Other parameters of the plasmonic structure are the same as in Figure 5. The normalized electric field intensity distributions in the xz plane at y = −5 nm, y = −12.5 nm and y = −20 nm are shown in Figures 5(b), 5(c) and 5(d), respectively. It can be seen that 2D patterns with a half-pitch resolution of 14.6 nm in both x and z directions are produced. Note that Figures 5(b), 5(c) and 5(d) only show two periods of patterns in both x and z directions. It can be also seen that the area between two bright spots in a row or a column is not dark, which is due to the fact that the interferences among the four SPPs are not all destructive in this area. The minimum image contrasts at y = −5 nm, y = −12.5 nm and y = −20 nm are about 0.20, 0.26 and 0.20, respectively. These mean that if the PR is a negative PR, bright spots may be recorded in the area from y = −20 nm to y = −5 nm. The maximum image contrasts at y = −5 nm, y = −12.5 nm and y = −20 nm are about 0.42, 0.66 and 0.46, respectively. These mean that if the PR is a positive PR, dark spots may be recorded in the area from y = −20 nm to y = −5 nm.

Figure 5.

Figure 5

Open in a new tab

(a) 3D view of the plasmonic structure. (b) Normalized electric field intensity distribution in the xz plane at y = −5 nm. (c) The same as in (b) but at y = −12.5 nm. (d) The same as in (b) but at y = −20 nm. Some parameters of the structure are set as follows: Px = Pz = 58.2 nm, wx = wz = 23 nm, d1 = 45 nm, d2 = 12 nm, d3 = 28 nm and d5 = 25 nm.

In summary, we have designed a deep ultraviolet plasmonic structure and proposed a SPILM using the designed structure. We have demonstrated numerically that 1D and 2D periodic patterns with a half-pitch resolution of 14.6 nm can be produced in a 25nm-thick PR layer under 193 nm illumination by using grating masks with a pitch resolution of 58.2 nm. We have also demonstrated numerically that if a 25nm-thick PR layer with a refractive index of 1.8 is used, the half-pitch resolution of the produced patterns can reach 12.9 nm. The half-pitch resolution of the proposed SPILM can be further improved by increasing the refractive index of the PR and reducing the thickness of the PR. The proposed SPILM has the potential for fabricating large-area periodic nanostructures, which were widely used in fields such as electromagnetic polarization manipulation24,25,26, strong-field emission36,37, wavelength-selective photocurrent enhancement38 and surface-enhanced Raman scattering39. Our findings open up an avenue to push the half-pitch resolution of photolithography towards 10 nm.

Methods

FEM simulations were performed with COMSOL for 1D grating masks. In the case of 1D grating masks, periodic boundary conditions are used in the x direction and perfectly matched layers are used in the y direction. FDTD simulations were performed with OptiFDTD for 2D grating masks. In the case of 2D grating masks, periodic boundary conditions are used in both the x direction and the z direction and perfectly matched layers are used in the y direction. Equation (1) was solved with MATLAB.

Author Contributions

J.D. and J.L. proposed the idea and completed the writing of the paper. J.D. performed the theoretical calculations and the numerical simulations. G.K., J.X. and Y.W. contributed to the discussion and paper writing.

Acknowledgments

This work was supported by the National Basic Research Program of China (973 program Grant Nos. 2013CBA01702 and 2013CB328801) and the National Natural Science Founding of China (Grant Nos. 61235002, 61077007 and 61205053).

References

  1. Fang N., Lee H., Sun C. & Zhang X. Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005). [DOI] [PubMed] [Google Scholar]
  2. Lee H. et al. Realization of optical superlens imaging below the diffraction limit. New J. Phys. 7, 255 (2005). [Google Scholar]
  3. Melville D. O. S. & Blaikie R. J. Super-resolution imaging through a planar silver layer. Opt. Express 13, 2127–2134 (2005). [DOI] [PubMed] [Google Scholar]
  4. Schilling A., Schilling J., Reinhardt C. & Chichkov B. A superlens for the deep ultraviolet. Appl. Phys. Lett. 95, 121909 (2009). [Google Scholar]
  5. Chaturvedi P. et al. A smooth optical superlens. Appl. Phys. Lett. 96, 043102 (2010). [Google Scholar]
  6. Liu H. et al. High aspect subdiffraction-limit photolithography via a silver superlens. Nano Lett. 12, 1549–1554 (2012). [DOI] [PubMed] [Google Scholar]
  7. Dong J. et al. Image distance shift effect of the metal superlens and its applications to photolithography. Europhys. Lett. 102, 24002 (2013). [Google Scholar]
  8. Dong J. et al. A super lens system for demagnification imaging beyond the diffraction limit. Plasmonics 8, 1543–1550 (2013). [Google Scholar]
  9. Srituravanich W. et al. Flying plasmonic lens in the near field for high-speed nanolithography. Nat. Nanotechnol. 3, 733–737 (2008). [DOI] [PubMed] [Google Scholar]
  10. Pan L. et al. Maskless plasmonic lithography at 22 nm resolution. Sci. Rep. 1, 175 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Luo X. & Ishihara T. Surface plasmon resonant interference nanolithography technique. Appl. Phys. Lett. 84, 4780–4782 (2004). [Google Scholar]
  12. Liu Z., Wei Q. & Zhang X. Surface plasmon interference nanolithography. Nano Lett. 5, 957–961 (2005). [DOI] [PubMed] [Google Scholar]
  13. Guo X., Du J. & Guo Y. Large-area surface-plasmon polariton interference lithography. Opt. Lett. 31, 2613–2615 (2006). [DOI] [PubMed] [Google Scholar]
  14. Sreekanth K. V., Murukeshan V. M. & Chua J. K. A planar layer configuration for surface plasmon interference nanoscale lithography. Appl. Phys. Lett. 93, 093103 (2008). [Google Scholar]
  15. Yang X., Zeng B., Wang C. & Luo X. Breaking the feature sizes down to sub-22 nm by plasmonic interference lithography using dielectric-metal multilayer. Opt. Express 17, 21560–21565 (2009). [DOI] [PubMed] [Google Scholar]
  16. Zeng B., Yang X., Wang C. & Luo X. Plasmonic interference nanolithography with a double-layer planar silver lens structure. Opt. Express 17, 16783–16791 (2009). [DOI] [PubMed] [Google Scholar]
  17. Sreekanth K. V. & Murukeshan V. M. Large-area maskless surface plasmon interference for one- and two-dimensional periodic nanoscale feature patterning. J. Opt. Soc. Am. A 27, 95–99 (2010). [DOI] [PubMed] [Google Scholar]
  18. He M. et al. A practical nanofabrication method: surface plasmon polaritons interference lithography based on backside-exposure technique. Opt. Express 18, 15975–15980 (2010). [DOI] [PubMed] [Google Scholar]
  19. Dong J. et al. Surface plasmon interference lithography with a surface relief metal grating. Opt. Commun. 288, 122–126 (2013). [Google Scholar]
  20. Kravets V. G., Schedin F. & Grigorenko A. N. Extremely Narrow Plasmon Resonances Based on Diffraction Coupling of Localized Plasmons in Arrays of Metallic Nanoparticles. Phys. Rev. Lett. 101, 087403 (2008). [DOI] [PubMed] [Google Scholar]
  21. Linden S., Kuhl J. & Giessen H. Controlling the interaction between light and gold nanoparticles: selective suppression of extinction. Phys. Rev. Lett. 86, 4688 (2001). [DOI] [PubMed] [Google Scholar]
  22. Brolo A. G., Arctander E., Gordon R., Leathem B. & Kavanagh K. L. Nanohole-Enhanced Raman Scattering. Nano Lett. 4, 2015–2018 (2004). [Google Scholar]
  23. MuÈller R., Malyarchuk V. & Lienau C. Three-dimensional theory on light-induced near-field dynamics in a metal film with a periodic array of nanoholes. Phys. Rev. B 68, 205415 (2003). [Google Scholar]
  24. Kang G., Vartiainen I., Bai B., Tuovinen H. & Turunen J. Inverse polarizing effect of subwavelength metallic gratings in deep ultraviolet band. Appl. Phys. Lett. 99, 071103 (2011). [Google Scholar]
  25. Kang G., Fang Y., Vartiainen I., Tan Q. & Wang Y. Achromatic polarization splitting effect of metallic gratings with sub-50nm wide slits. Appl. Phys. Lett. 101, 211104 (2012). [Google Scholar]
  26. Kang G., Rahomäki J., Dong J., Honkanen S. & Turunen J. Enhanced deep ultraviolet inverse polarization transmission through hybrid Al-SiO2 gratings. Appl. Phys. Lett. 103, 131110 (2013). [Google Scholar]
  27. Maier S. A. [Surface plasmon polaritons at metal/insulator interfaces]. Plasmonics: Fundamentals and Applications [21–34] (Springer, New York, 2007). [Google Scholar]
  28. Wang C. et al. Deep sub-wavelength imaging lithography by a reflective plasmonic slab. Opt. Express 21, 20683–20691 (2013). [DOI] [PubMed] [Google Scholar]
  29. Shao D. B. & Chen S. C. Surface-plasmon-assisted nanoscale photolithography by polarized light. Appl. Phys. Lett. 86, 253107 (2005). [Google Scholar]
  30. Shao D. B. & Chen S. C. Surface plasmon assisted contact scheme nanoscale photolithography using an UV lamp. J. Vac. Sci. Technol. B 26, 227–231 (2008). [Google Scholar]
  31. Palik E. D. [Metals, semiconductors and insulators]. Handbook of Optical Constants of Solids I [Palik, E. D. (ed.)] [275–765] (Academic, Orlando, 1985). [Google Scholar]
  32. Palik E. D. [Insulators]. Handbook of Optical Constants of Solids III [Palik, E. D. (ed.)] [653–683] (Academic, San Diego, 1998). [Google Scholar]
  33. Smith B. W., Fan Y., Slocum M. & Zavyalova L. 25 nm immersion lithography at a 193 nm wavelength. Proc. SPIE 5754, 141–147 (2005). [Google Scholar]
  34. Zhou J., Lafferty N. V., Smith B. W. & Burnett J. H. Immersion lithography with numerical apertures above 2.0 using high index optical materials. Proc. SPIE 6520, 5204T–5204T (2007). [Google Scholar]
  35. Madou M. J. [Lithography]. Fundamentals of Microfabrication [1–71] (CRC, Boca Raton, 2002). [Google Scholar]
  36. Dombi P. et al. Ultrafast strong-field photoemission from plasmonic nanoparticles. Nano Lett. 13, 674–678 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Walsh G. F. & Negro L. D. Engineering plasmon-enhanced Au light emission with planar arrays of nanoparticles. Nano Lett. 13, 786–792 (2013). [DOI] [PubMed] [Google Scholar]
  38. Lin Y. et al. Au nanocrystal array/silicon nanoantennas as wavelength-selective photoswitches. Nano Lett. 13, 2723–2731 (2013). [DOI] [PubMed] [Google Scholar]
  39. Huang J. et al. Ordered Ag/Si nanowires array: wide-range surface-enhanced Raman spectroscopy for reproducible biomolecule detection. Nano Lett. 13, 5039–5045 (2013). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES