Phonon-Electron Interactions in Piezoelectric Semiconductor Bulk Acoustic Wave Resonators

Abstract

This work presents the first comprehensive investigation of phonon-electron interactions in bulk acoustic standing wave (BAW) resonators made from piezoelectric semiconductor (PS) materials. We show that these interactions constitute a significant energy loss mechanism and can set practical loss limits lower than anharmonic phonon scattering limits or thermoelastic damping limits. Secondly, we theoretically and experimentally demonstrate that phonon-electron interactions, under appropriate conditions, can result in a significant acoustic gain manifested as an improved quality factor (Q). Measurements on GaN resonators are consistent with the presented interaction model and demonstrate up to 35% dynamic improvement in Q. The strong dependencies of electron-mediated acoustic loss/gain on resonance frequency and material properties are investigated. Piezoelectric semiconductors are an extremely important class of electromechanical materials, and this work provides crucial insights for material choice, material properties, and device design to achieve low-loss PS-BAW resonators along with the unprecedented ability to dynamically tune resonator Q.

Dynamics of acoustic waves (or phonons) trapped in resonant cavities comprised of solid elastic materials have been studied extensively¹. At an appropriate frequency that satisfies the resonance criteria, mechanical energy is confined in the form of standing waves in such an elastic cavity. This principle forms the basis of bulk acoustic wave (BAW) resonators¹,²,³. While ideal standing wave BAW resonators are lossless, the energy confinement in practical materials is not ideal due to attenuation occurring via a number of phonon-scattering processes. This attenuation limits the quality factor (Q) of such a BAW resonator. Analytical expressions for maximum Q limits for a variety of intrinsic scattering processes, such as anharmonic phonon-phonon loss and thermoelastic damping (TED), are well known and experimentally validated for commonly used acoustic materials⁴,⁵,⁶,⁷,⁸,⁹,¹⁰. An often neglected scattering process is the phonon-electron interaction¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶, which is significant in materials that have both moderate-to-high doping concentrations and a mechanism facilitating strong electromechanical interactions. Piezoelectric semiconductor (PS) materials such as ZnO, GaN and CdS fulfill both criteria and as we will show in this paper, the phonon-electron scattering can be the dominant loss mechanism in such materials. Similar to well-known lattice loss mechanisms such as the phonon-phonon loss, the phonon-electron scattering is dependent on the bulk material properties and is not design dependent. We show that phonon-electron interactions can lead to acoustic gain of standing waves in PS-BAW resonators and present, for the first time, a comprehensive model that explains the resulting enhanced mechanical Q of PS-BAW resonators under the acoustoelectric effect¹⁷,¹⁸. We evaluate the effect of phonon-electron interactions in PS-BAW resonators in context with other important acoustic loss mechanisms (such as anharmonic phonon loss and TED loss) by comparing the limiting figure of merit, the product of frequency and quality factor (f × Q product), for each interaction mechanism. We compare theoretical estimates with measured results obtained using GaN BAW resonators as test vehicles. The measured data acquired on multiple BAW resonators with resonance frequencies ranging from 37 MHz to 8.7 GHz and fabricated using multiple wafers of single-crystal wurtzite GaN are consistent with theoretical trends. We further explore the dependence of attenuation/amplification on factors such as charge carrier concentration, mobility, and resonance frequency. We show that it is practically possible to design PS-BAW resonators with (i) minimum phonon-electron scattering loss under normal operation, (ii) reduced total energy loss via acoustoelectric interaction, and (iii) acoustoelectric gain that can overcome all other losses, effectively creating a highly frequency-selective acoustoelectric resonant amplifier.

Results

Theory of acoustoelectric amplification in resonators

Acoustic waves travelling in a piezoelectric material cause local perturbations in the electric field in the material, as described by the basic piezoelectric constitutive equation T = cS − eE. Here, T, S and E are the local stress, strain, and electric field, while c and e are the stiffness coefficient and the piezoelectric coefficient, respectively. In a PS, the locally perturbed electric field causes the electrons to accumulate in the minima of the potentials of the waves, but as the wave progresses the electrons tend to lag behind¹⁴. This places more charge density in the electric field whose direction is that of wave propagation. This means that the average power transferred from acoustic phonons to electrons is positive, causing attenuation of the acoustic wave¹⁴,¹⁵. A large body of work¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸ on phonon-electron interactions proved analytically and experimentally that travelling acoustic waves in PS materials suffer attenuation due to electron-scattering. The electrons gain energy and momentum, get accelerated in the direction of the acoustic wave, and appear as a net DC current in the material (Weinreich DC current¹²). It was observed that if electrons are accelerated by applying an external electric field across the material with velocities higher than the phonon velocity, energy can be transferred from the electrons to the phonons, effectively increasing the energy of the acoustic wave¹⁴,¹⁷,¹⁸,¹⁹. This is referred to as acoustoelectric amplification and has been used to develop high-gain travelling-wave acoustic amplifiers¹⁶.

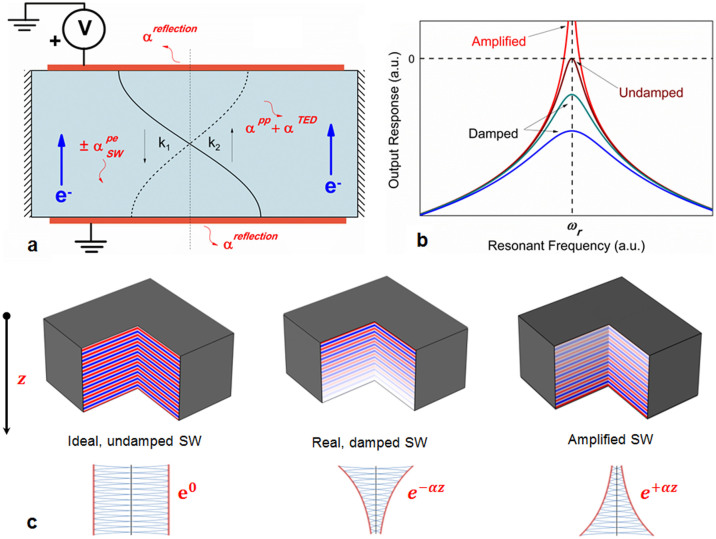
We extend the existing analysis on acoustic amplification in travelling waves¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸ to standing waves in BAW resonators, for the first time, and demonstrate that it is possible to generate acoustic gain in standing waves in PS-BAW resonators under the right conditions. We begin the analysis by solving for standing wave loss in a BAW resonator. Considering a real, elastic material of a finite thickness L, an acoustic wave travelling through this material will reflect back from the boundaries and remain confined in the material if the resonance condition nλ = 2L is satisfied, where λ is the wavelength of the n^th vibration mode. This forms a cavity resonance and is the basic operational principle of BAW resonators¹,²,³. The cavity resonance is a standing wave which is described as the superposition of two travelling waves with equal amplitudes and frequencies but opposite wave vectors³. Assuming plane acoustic waves, we can denote the standing wave in the BAW resonator as the superposition of the two waves (Fig. 1a).

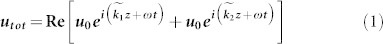or

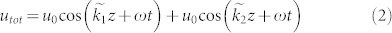For ideal elastic materials, 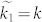and 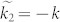which gives

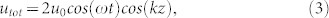which is the equation for an ideal lossless standing wave in a resonant cavity. For a real, lossy material, the wave vectors are denoted by 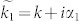and 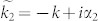where the imaginary components are the loss coefficients per unit distance travelled. The loss α is composed of all distributed sources of acoustic loss in the bulk of the material, namely, losses due to phonon-phonon interaction (α^pp), thermoelastic damping (α^TED), and phonon-electron interaction (α^pe). At this point, we assume that the boundary reflection is perfectly lossless; reflection losses (α^reflection) will be considered separately later. The superposition relation can be written as

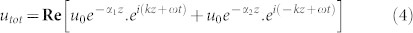or

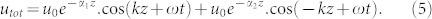The above relation can be further simplified as

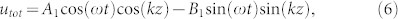where

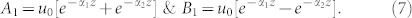This equation predicts a pseudo-standing wave, which may have non-zero amplitude at the nodes if B₁ ≠ 0. Most lossy resonant cavities are symmetric, i.e., the attenuation in each direction is equal in magnitude, as it is a result of the fundamental, non-directional loss mechanisms of the material. That is, α₁ = α₂ ≡ α. Consequently, B₁ = 0 and A₁ = 2u₀[e^−αz]. This recovers the expression for a real, damped resonant cavity, which is the most commonly encountered practical situation (Fig. 1b):

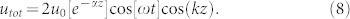The possible responses for such a standing-wave BAW resonator depend on the nature of α. Fig. 1b and Fig. 1c depict possible scenarios of damped, undamped (ideal) and amplified BAW resonators (α > 0, α = 0, and α < 0 respectively). The possibility of an amplified response with an additional external stimulus is a unique attribute of PS materials and is detailed in further discussion. In the case of a non-symmetric interaction mechanism, where the attenuation is direction-dependent (i.e., α₁ ≠ α₂), equation (6) must be considered in its entirety. We can simplify the amplitude coefficients (equation (7)) by expanding them in a Taylor series and neglecting higher powers of αz, to get

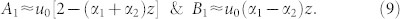For practical values of attenuation 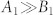and thus we can neglect the term B₁ sin (ωt)sin(kz). This assumption is valid as long as 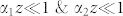and we can consider the lossy standing wave to be

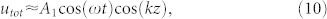where

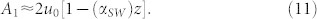The assumption 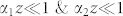is valid for any BAW resonator made with a high-quality thin-film elastic material. As an example, for a high-quality GaN film and in the absence of an external electric field, the value of 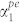and 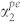is ~2500 m⁻¹ at 1.5 GHz, or an energy loss of 0.25% per micrometer of the GaN film. We define net roundtrip attenuation per unit length for the standing wave BAW resonator as,

Other distributed losses in the material of the BAW resonator (the phonon-phonon and TED losses) are symmetric, i.e., α₁ = α₂. Again, this directly implies B₁ = 0, resulting in a lossy standing wave. For phonon-electron interaction in PS materials, upon application of a DC electric field, there is a net drift of electrons in one direction. Based on the directional nature of the interaction between coherent phonons and electrons, the uni-directional drift of the electrons breaks the symmetry of attenuation, and thus 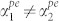. Using equation (12) and the equations for attenuation coefficients in travelling waves from the theory put forward by Hutson and White¹⁸,¹⁹, we can write effective attenuation due to phonon-electron interaction for the standing wave as

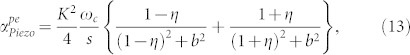where

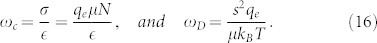Here, K is the piezoelectric coupling coefficient, μ is the electron mobility, N is the effective free electron concentration, E_D is the applied DC electric field, ν_e is the electron drift velocity, s is the acoustic velocity, η is the velocity ratio, ω_C is the carrier relaxation frequency, and ω_D is the carrier diffusion frequency. The electrical conductivity, permittivity, electronic charge, absolute temperature and Boltzmann's constant are denoted by the usual symbols σ,,q_e,T, and k_B, respectively. Equation (13) agrees with observations of Maines and Paige²⁰. Note that without applied bias, η = 0, and equation (13) reduces to the symmetric situation denoting the nominal loss due to phonon-electron interaction with piezoelectric coupling

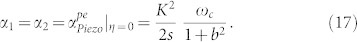Equation (13) can be physically interpreted to be the combination of the phonon-electron interaction for the travelling-wave components parallel and anti-parallel to the direction of carrier drift. Based on the theory of acoustoelectric amplification in travelling waves¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹, when the carrier drift velocity exceeds the acoustic velocity, the parallel wave component is amplified by transfer of energy from electrons to phonons, while the anti-parallel wave component is attenuated by electron-scattering. When an adequate electric field is applied to the BAW resonator and the parallel gain exceeds anti-parallel loss, 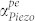can become negative, denoting net gain over the roundtrip (Fig. 1b and Fig. 1c). This is the theoretical basis for achieving a net acoustic gain in a standing wave PS-BAW resonator. Unlike the travelling wave model¹⁸,¹⁹, 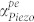is symmetric with respect to the direction of applied electric field. Further, the acoustoelectric amplification in BAW resonators can be practically observed only for those modes that fulfill the resonance condition nλ = 2L. This imparts frequency selectivity to the standing wave model in BAW resonators that is unique to it and differentiates it from the travelling wave model.

Figure 1. Theory of acoustoelectric amplification in standing waves for PS materials.

(a) Schematic cross-section of a PS-BAW resonator, depicting the fundamental thickness mode of vibration. The schematic indicates the various intrinsic loss mechanisms (phonon-phonon scattering, TED and phonon-electron scattering) in addition to the reflection losses. In the absence of other external losses, such as air damping, the total energy loss per cycle is dominated by these loss mechanisms. For a PS material, under the right conditions, the phonon-electron scattering losses can be inverted to achieve acoustoelectric gain. (b) A representative set of output responses for BAW resonators, denoting damped, undamped, and amplified responses (α > 0, α = 0, and α < 0 respectively). (c) The same responses can be visualized by the strain distribution of BAW resonator cross-sections under ideal, damped and amplified conditions (α > 0, α = 0, and α < 0 respectively). The cross-section images here show higher order standing wave BAW resonance modes, and visually exaggerated damping/amplification envelopes for clarity of concept. The color map shows areas of positive (red) and negative (blue) strain. The damped standing wave is the most commonly encountered situation in practical devices. However, this work demonstrates that it is possible to realize highly frequency-selective amplified BAW resonators using PS materials.

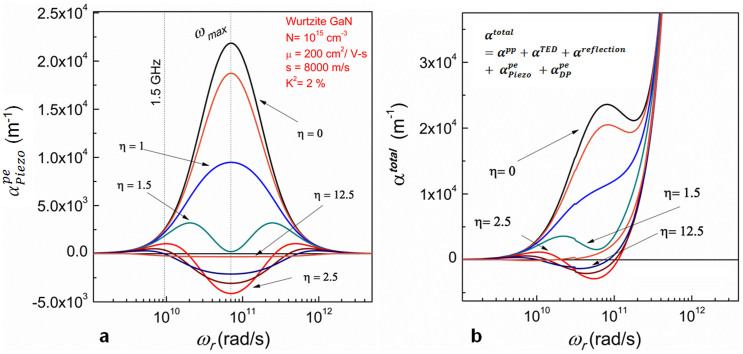
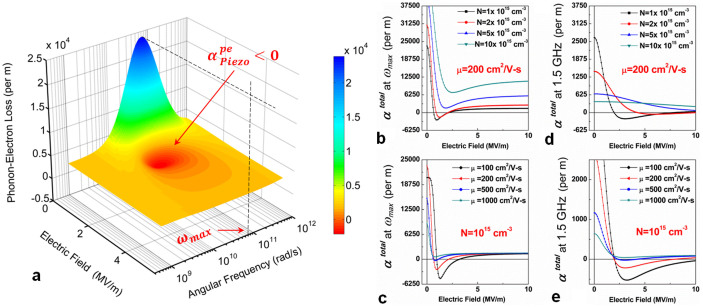
The curves for 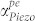as a function of frequency and velocity ratio can be obtained using equation (13) for wurtzite GaN (Fig. 2a). Here, an effective carrier concentration of 10¹⁵ cm⁻³, a carrier mobility of 200 cm²/V-s, an acoustic velocity of 8000 m/s, and a coupling coefficient of 2% are assumed. Other material properties are given in Supplementary Table S1. In addition to the frequency selectivity imposed by the mechanical resonance condition and the resonator dimensions, the phonon-electron interaction itself has strong frequency dependence (Fig. 2a). The maximum interaction of phonons and electrons is observed at the geometric mean of ω_c and ω_D (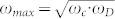). At ω_max, and without DC bias, the nominal 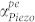is at its peak value corresponding to the maximum acoustic loss due to electron-scattering. However, the acoustic gain is also maximum at ω_max when a sufficiently large E_D is applied to the GaN film. With increasing η, the acoustic loss decreases. Above a threshold velocity ratio (η_th), 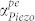becomes negative, indicating a crossover into the gain regime. The highest gain is seen for ω_max; but it is also possible to achieve acoustic gain at lower frequencies. This is a significant finding as it relaxes the design frequency range for resonators. The frequency of highest gain, ω_max tends to be high (~10 GHz or higher for most PS materials). This result indicates that it is possible to boost the Q electrically with resonators operating in the VHF/UHF ranges. In fact, given the high nominal values of loss at ω_max, it may be practically more useful to choose a frequency at which the original loss is small and yet obtain a relatively large improvement in Q with increasing E_D. Alternately, it is possible to design for lower values of ω_max by careful selection of N in the material, within reason (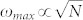). This enables higher amplification ratios at lower frequencies. The dependence of the interaction on material properties is detailed in the proceeding sections.

Figure 2. Phonon-electron interactions in PS materials and the effect on total intrinsic loss/gain.

(a) The phonon-electron loss/gain 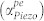in a representative GaN material system with respect to resonant frequency and the velocity ratio η. Increasing the applied electric field (and thus η) reduces the phonon-electron loss across all frequencies. Here, η = 0,1,2,… correspond to electric field values E_D = 0 kV/m, 400 kV/m, 800 kV/m… as per equation (15). Within a certain range of η, the phonon-electron loss is negative, indicating acoustic gain. The maximum effect is seen at ω_max. For lower frequencies this effect is less pronounced in absolute terms, and while the transition to the gain regime may not occur, the phonon-electron loss is clearly reduced by a significant fraction of the original value. (b) The total loss in the system (α^total) is clearly affected by phonon-phonon loss and thermoelastic damping, but still includes regions where 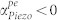, predicting the possibility of acoustoelectric amplification in the resonator that can theoretically overcomes all other intrinsic losses in the material. Note that this is the frequency dependence of 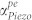and α^total for the PS material, not the resonator. The mechanics of the BAW resonator itself imposes further frequency selectivity, allowing only those modes that conform to the resonance condition nλ = 2L.

Influence on total intrinsic Q

For practical PS-BAW resonators, 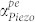needs to be seen in context with all other loss mechanisms. The total loss can be written as the sum of all contributing intrinsic and extrinsic loss mechanisms. Note that 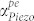can be positive (attenuation) or negative (gain), but for other loss mechanisms α > 0.

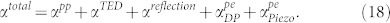The mechanical Q of the resonator is defined as the ratio of the energy conserved to the energy dissipated per cycle of operation¹,³,⁵ and is given by

We neglect other extrinsic factors, such as air damping that can be eliminated by good resonator design or by operation in vacuum. The phonon-phonon loss and the TED loss have been explored in detail and are generally considered to be the ultimate limiting factors for the Q of mechanical resonators with low-doped or dielectric materials⁸,⁹,¹⁰. The reflection losses include all interfacial losses from the body of the resonator to the surrounding media, inclusive of the loss through the supporting tethers. An important distinction between the travelling-wave amplifier and the amplified resonator arises from the selectivity afforded by α^reflection. The reflection loss is low at resonance, and extremely high at other wavelengths that do not fulfill the resonance condition mentioned earlier. The loss due to deformation-potential coupling 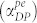is another phonon-electron interaction mechanism that is present in all semiconductors but only becomes significant at high or degenerate doping. Details of the calculation of loss factors are given in the Supplementary Section SI and Table S1. The total phonon-electron loss/gain for wurtzite GaN as a function of frequency and η is shown in Fig. 2b. It is seen that total loss is still lowered with increased E_D, and it is theoretically possible for the phonon-electron gain to overcome other loss mechanisms (α^total < 0) under the right conditions.

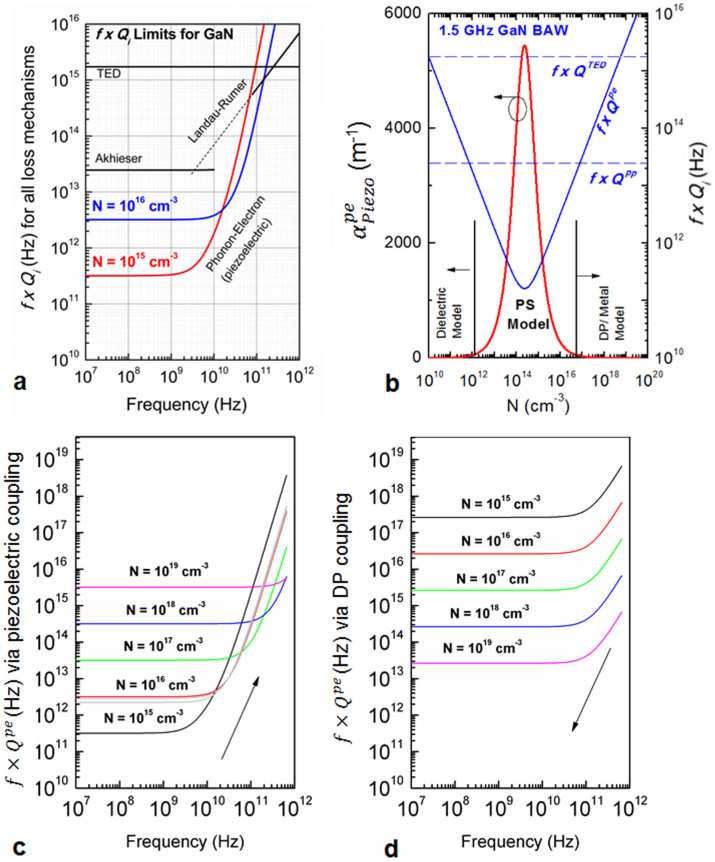
Limiting values of f × Q product

A popular figure of merit for comparing acoustic resonators and their loss mechanisms is the f × Q limit (where f = ω/2π)⁷,⁸,⁹,¹⁰. The higher the limit, the lower the loss at a particular frequency and the better the resonator performance. Fig. 3 compares the limits set by the phonon-electron interaction due to piezoelectric coupling with other limiting values for GaN (Fig. 3a). As discussed, the electromechanical interactions can be of two types: piezoelectric coupling or deformation-potential coupling. Loss due to piezoelectric interaction is given by equation (13) and the loss due to deformation-potential coupling is explained in Supplementary Section SI. Fig. 3b describes the non-monotonic dependence of the f × Q limit for phonon-electron interactions as a function of N for a particular frequency (here, 1.5 GHz). It is seen that in the moderately doped GaN, the phonon-electron loss is more significant (higher) than losses due to other mechanisms. By the same logic, significant acoustoelectric gain is only possible for moderately doped GaN. In lightly doped PS materials, the interaction between acoustic wave and charge carriers is limited due to the low density of charge carries, leading to low phonon-electron loss and consequently a high limiting value of 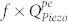. This tends towards the dielectric model, where phonon-electron losses are insignificant. As N increases to a highly-doped level, the piezoelectric interaction is screened, leading to lower phonon-electron loss due to piezoelectric coupling and again a high limiting value of 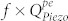. At extremely high doping levels, the material behaves similar to a metal, where acoustic loss occurs due to interaction of phonons and the free-electron gas, described by a different model⁵. For the range of doping from unintentionally doped²¹,²² to highly doped bulk GaN (10¹⁵ cm⁻³ < N < 10¹⁹ cm⁻³) the f × Q limits for both phonon-electron interaction mechanisms are depicted in Fig. 3c and Fig. 3d. The limiting value set by the piezoelectric coupling portion of the phonon-electron loss is most relevant for low to moderately doped PS resonators. In this range, the limits set by the phonon-electron interaction are lower than other intrinsic loss mechanisms and are thus the dominant limiting factors. In contrast, for highly doped or degenerately doped semiconductors (N > ~10¹⁸ cm⁻³), 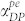becomes the significant factor. For non-piezoelectric semiconductors, deformation-potential coupling is the only form of phonon-electron interaction.

Figure 3. Limiting values for the f × Q product of BAW resonators with phonon-electron interaction.

(a) The f × Q limits for the various intrinsic loss mechanisms in PS GaN. For low to moderately doped PS GaN, the phonon-electron mechanism is the significant limiting factor, lower than the anharmonic phonon-scattering (Akhieser and Landau-Rumer losses) and thermoelastic damping (TED) loss. (b) For a representative frequency, (here, 1.5 GHz), the piezoelectrically coupled model for phonon-electron interaction is significant only for a range of values of moderate doping. Beyond this range, other interactions dominate. The f × Q limit due to phonon-electron interaction is highly dependent on the effective electron concentration. The two important mechanisms of phonon-electron interaction are (c) piezoelectric coupling and (d) deformation-potential (DP) coupling. At low to moderate doping, the piezoelectric interaction dominates, and the two loss mechanisms achieve parity only at a concentration of ~1 × 10¹⁸ cm⁻³ for GaN. Above this value, the deformation-potential coupling will dominate the phonon-electron loss. Deformation-potential coupling is more significant for weakly piezoelectric or non-piezoelectric semiconductors.

Experimental findings

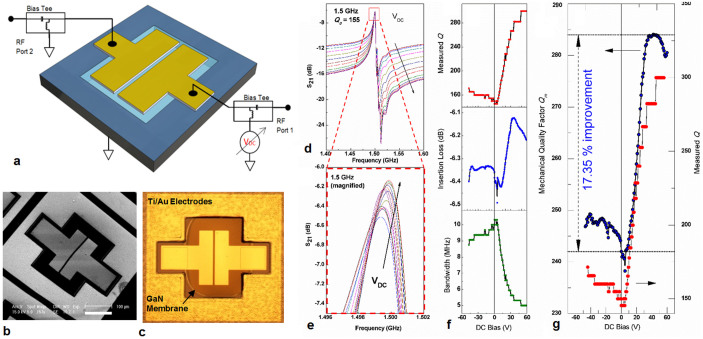
This work uses thin-film GaN-based BAW resonators as test platforms for dynamic performance enhancement via acoustoelectric amplification. The films are unintentionally doped (UID) bulk GaN. Fig. 4a–c show a schematic and images for a BAW resonator operating in the fundamental thickness extensional mode. Normal RF performance is measured using a network analyzer, and increasing DC bias is applied between the two ports using bias tees. The DC bias causes a marked change in the performance of the device (Fig. 4d–e). This change in performance can be quantified by the simultaneous improvement of the Q, lowering of the insertion loss (IL), and narrowing of the resonance bandwidth (Fig. 4f). At the same time, the off-resonance transmission decreases. The decrease in the transmission level is the result of current saturation that accompanies acoustoelectric amplification²³. The net effect of these changes is an improvement in the resonator transfer-function or a selective amplification of the energy confined in the primary resonance mode. It is to be noted that selective improvement at resonance and decrease in the off-resonance transmission distinguishes this phenomenon from a simple shift in the transmission response that can be achieved using GaN/AlGaN high electron mobility transistors (HEMTs) in conjunction with the resonator²⁴,²⁵. While the electrical contacts used in this work are non-ohmic, the non-linear nature of the contacts cannot explain the selective improvement of the transmission response at resonance. To illustrate the improvement in the purely mechanical performance of the device, electrical losses and parasitic effects are de-embedded and the mechanical (or unloaded) quality factor (Q_m) (Fig. 4g) along with the motional resistance (R_m) of the device are extracted (Supplementary Section SII, Fig. S1–Fig. S3, and Table S2). The Q_m shows clear improvement (~17.35% for this particular resonator) upon application of a DC bias, indicating that mechanical performance enhancement is significant. Various other BAW resonators operating in different modes of vibration and at different frequencies exhibit similar trends in performance (See Supplementary Section SIII and Fig. S4).

Figure 4. An exemplary PS-BAW GaN resonator with measured acoustoelectric amplification.

(a) A schematic of a two-port thin film BAW resonator made from epitaxially grown GaN. The resonator is normally driven using only an RF stimulus, but a DC bias applied across the resonant cavity causes a change in the performance. The resonator is seen in (b) a scanning electron micrograph (SEM) and (c) a microscope image that shows the edge of the released GaN membrane. Scale bar corresponds to 100 μm. (d–e) RF transmission measurements (S₂₁) of the resonator with indicating both nominal operation and the evolution of BAW resonator performance improvement with an increasing DC bias. (f) This improvement can be quantified by the improved insertion loss, decreased bandwidth, and consequently increased Q. (g) The measured Q is compared with the extracted mechanical quality factor, Q_m, which is free of all parasitic effects and quantizes the intrinsic mechanical quality factor of the BAW resonator. Q_m shows significant improvement with applied DC, demonstrating that there is a fundamental reduction in internal loss and consequently an improvement in the energy confinement in the BAW resonator.

Material dependencies for acoustoelectric loss/gain

The full model for 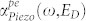presented in equation (13) and shown in Fig. 5a (for GaN) indicates that 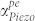is critically dependent on N, μ, K², and s. The electronic properties, N and μ especially, can be tailored by proper crystal growth and doping. These parameters influence the (i) original 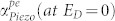, (ii) onset of gain, (iii) frequency of maximum effect ω_max, (iv) absolute magnitude of gain/loss, and (v) range of η that results in amplification. Variation of 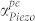with N and μ is shown in Fig. 5b–e at both ω_max (which varies with N) and at the fixed frequency of 1.5 GHz. Comparing trends at 1.5 GHz, we see that higher N screens out piezoelectric interaction, progressively decreases the nominal loss, and thus requires higher applied E_D to decrease 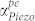(Fig. 5d). Maximum achievable gain is reduced with increasing N. Increased μ reduces the threshold E_D required for cross-over, but the minima of 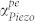is higher and does not necessarily cross over into the gain regime (Fig. 5e). Nevertheless, in all cases, applying E_D to the PS-BAW resonator results in lowered 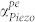and subsequently an improved Q_i^total. As discussed, the threshold velocity ratio η_th is the critical value at which 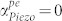. Above η_th, 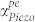is negative, leading to gain. Solving equation (13) for 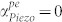gives us the critical condition

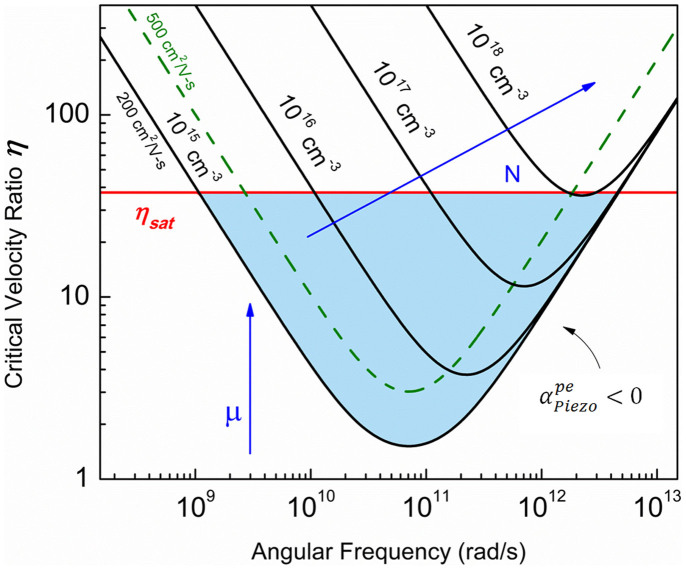
which depends on the electronic properties N and μ. The limiting values for amplification are set by the carrier saturation velocity for the particular material. Fig. 6 depicts the possible solution space for achieving phonon-electron gain. This solution space is a function of the properties N, μ, and ω, while the upper bound for amplification is set by the electron saturation velocity of the material. The parametric trends given by Fig. 5 and Fig. 6 are important rules for choosing a PS material and tailoring its properties to reduce nominal electron loss in PS-BAW resonators, or to develop PS-BAW resonant acoustoelectric amplifiers.

Figure 5. Parametric dependencies for the phonon-electron loss/gain.

(a) Phonon-electron loss/gain 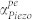as a function of frequency and applied DC electric field, for the wurtzite GaN system with a fixed carrier concentration N = 10¹⁵ cm⁻³ and carrier mobility μ = 200 cm²/V-s. The gain region 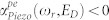is clearly seen. Subsequent plots (b)–(e) denote loss 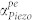as a function of E_D, at representative frequencies, ω_max and 1.5 GHz, with variations in N and μ. The nature of 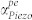is highly dependent on these parameters. A similar analysis can be carried out for other PS materials, in order to identify the optimum material properties and design for low-loss or high-gain resonant PS-BAW amplifiers.

Figure 6. Critical velocity ratio and its dependence on material properties.

The critical velocity ratio η_th is the threshold value at which 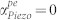. Any further increase in the velocity ratio (achieved by applying a higher electric field) would drive the resonator into the gain regime 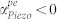. The possible solution space for the gain regime (shown shaded here for the wurtzite GaN system under consideration) is dependent on the electronic properties (N,μ) and the resonant frequency. The upper bound for amplification in any real material is set by the electron saturation velocity.

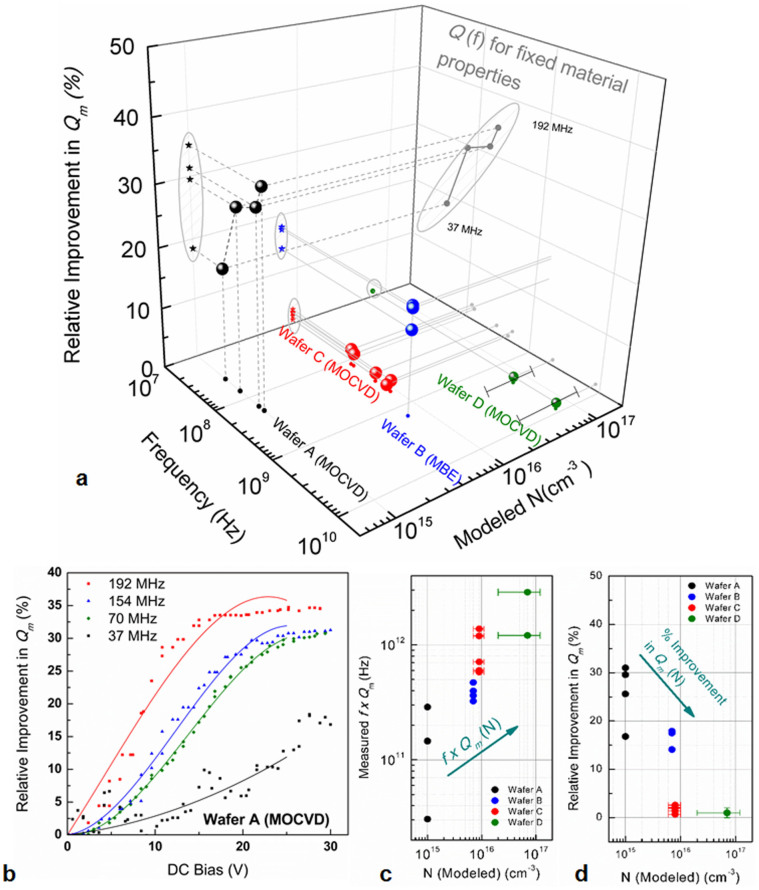
Using the theoretical model, including all loss mechanisms for GaN, we can qualitatively compare all measured devices (Supplementary Section SIII and Fig. S4) and plot relative improvement in Q_m as a function of both frequency and N (Fig. 7a). Measured f × Q values are consistent with modeled f × Q limits (Supplementary Fig. S5). For a given set of material properties, higher resonant frequencies (ω → ω_max) should result in higher relative amplification of Q_i^total. This is verified experimentally for multiple BAW resonators with increasing frequency, fabricated concurrently on the same wafer (Fig. 7b). The 192 MHz BAW resonator seen here has the dual advantage of having the highest frequency measured on the wafer with lowest N and it expectedly exhibits the highest measured improvement of ~35% in Q_m. Across all four wafers, with increasing N we also see the expected increase in the measured nominal f × Q values (Fig. 7c) and the expected decrease in relative amplification (Fig. 7d). This verifies the trends predicted in Fig. 3 and Fig. 5 and is important for the design of low-loss PS-BAW resonators, the design of highly-amplifying PS-BAW resonators, or an optimized design involving both attributes.

Figure 7. Measured results and comparison with theoretical models.

(a) Relative improvement in Q_m for multiple resonators as a function of frequency and modeled N for four GaN wafers. Planar projections indicate the trends with respect to frequency for a fixed set of material properties (Wafer A). (b) Relative improvement in experimentally measured and extracted Q_m for four BAW resonators concurrently fabricated on Wafer A (and thus possessing the same material properties). As predicted by the model, increasing the resonance frequency (ω → ω_max) increases the relative improvement in Q_m. As expected from the model, increasing electron concentration reduces piezoelectrically coupled phonon-electron interactions due to screening, and leads to (c) a higher nominal f × Q (lower loss) but also (d) a lower relative acoustoelectric improvement in Q_m.

While higher N and μ are generally reported for GaN-based HEMT electronics, the values used here more closely represent the practical values in high-quality, UID bulk GaN²¹,²². Bulk GaN has an electron saturation velocity greater than 10⁵ m/s, comfortably higher than the acoustic velocity by more than an order of magnitude²⁶,²⁷. Impact ionization effects are not expected till electric fields of at least 150 MV/m²⁸, enabling large values of η before velocity saturation or breakdown.

Experimental controls

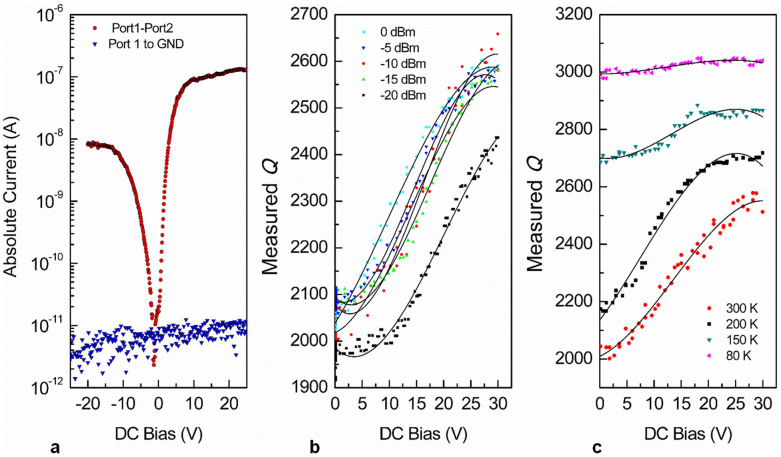
In order to validate the acoustoelectric amplification as the causal phenomenon for the improvement in observed performance of the GaN resonators, it is necessary to evaluate other possible causes. We consider non-linear current-voltage (I-V) in GaN, temperature, and RF input power. Generally, one important consideration when making electrical connections with GaN films is the contact linearity. Ti/Au is a popular combination for use with n-GaN as the barrier height for Ti to n-GaN²⁹ is one of the smallest for commonly used materials, even as-deposited without any annealing³⁰. The Au/Ti/n-GaN top contacts are not fully linear, but are expected to show only weakly-rectifying behavior³¹. The low doping expected of the UID films further means that the current transmission through the GaN is expected to be low. The bottom contact is to the AlN/AlGaN buffer layer, which can be considered to be a leaky dielectric. The two top electrodes can be considered to be back-to-back (weakly) rectifying contacts providing a leakage path through GaN, and the measured current transmission characteristics (Fig. 8a) are similar to expected trends for such a configuration with Au/Ti/n-GaN³⁰. It should be stressed however that contact non-linearity cannot explain the selective amplification of the mechanical resonance peak of the GaN resonator. Even the use of active GaN HEMTs co-fabricated with GaN resonators has been shown to only shift the entire transmission response of the resonator, without selective amplification of the mechanical peak²⁴,²⁵. It is known that mechanical resonators have a non-linear relationship between the Q and the input RF power. Increasing RF power levels improves the Q till the extreme situation of a Düffing non-linearity is achieved³². We explore the effect of input RF power on the present set of devices and observe only small improvements in the Q as we change input power from −20 dBm to 0 dBm (Fig. 8b). We do not observe the onset of non-linearity within the input range of the experiment. Increased RF power may also increase the Q due to the same mechanism as the DC bias: an interaction with RF current and the phonons, improving the acoustic performance. This is in effect, a self-actuation mechanism due to the RMS value of the RF current interacting with the acoustic phonons³³. This change is significantly lower than the improvement seen with increasing DC bias (Fig. 8b). The effect of temperature is investigated in order to gauge the effect of ambient temperature changes or any self-heating due to RF or DC currents in the device. The phonon-phonon, TED and phonon-electron loss are all expected to increase (lowering Q) at higher temperatures, and this is consistently borne out by experimental evaluation (Fig. 8c) and previous work³⁴. The data presented in Fig. 8 are elaborated on in Supplementary Section SVI and Fig. S8–S10. These control experiments do not indicate that either contact non-linearity, drive power, or self-heating could be responsible for the sharp improvements in resonator Q seen in this work.

Figure 8. Experimental Controls.

Other possible explanations for the Q amplification are explored and eliminated. (a) The DC current transmission between the two top electrodes, and through the bulk GaN can be modeled as back-to-back weakly rectifying contacts due to the non-linear nature of the Au/Ti/n-GaN contact. The leakage current from top electrodes to the bottom electrode (though GaN and buffer layer) is in pico-ampere range. The non-linear nature of the contacts cannot explain the selective amplification of the mechanical resonance peak. (b) Small improvements are seen in Q when the input RF power is increased from -20 dBm to 0 dBm; however, the changes are significantly smaller than the improvements with DC voltage. (c) As expected, increased temperature consistently decreases the resonator Q and thus self-heating or ambient heating cannot be a possible reason for the improvement in the Q.

Discussion

By definition, mechanical devices made from PS materials rely on the interactions between the electronic and mechanical domains. In practical devices, these interactions are lossy and with limited conversion efficiency. This work explores the possibility of mitigating the mechanical losses and achieving the most energy efficient devices by choosing the right material properties and designs. Furthermore, we demonstrate that it is possible to utilize the reverse effect: pumping electrical energy into the system to offset the mechanical losses. This dynamic and reversible improvement in the Q of PS-BAW resonators can be distinctly observed on applying a DC electric field. Experimental work presented here has focused on GaN as it is a high-quality acoustic PS material predicted to be optimal for demonstrating acoustoelectric amplification²⁸,³³. Measured results presented here verify these predictions. Other PS materials (CdS³⁵, ZnO³⁶,³⁷,³⁸, 4H-SiC³⁵,³⁹,⁴⁰, GaAs, InP, InGaAs, and AlAs⁴¹,⁴²) could also be potentially used to achieve Q-amplified BAW resonators (Supplementary Section SIV, Figure S6 and Table S3).

An important question arising from this work is whether one can overcome all other sources of loss in a practical PS-BAW resonator and achieve frequency-selective resonant BAW amplifiers. That is, is it possible to obtain 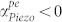and at the same time 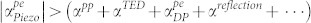in thin film PS-BAW devices? Net acoustic gain has been experimentally measured for CdS-based acoustoelectric travelling-wave amplifiers¹⁶,¹⁷. This indicates that it is possible to compensate for all loss mechanisms and further actively amplify the acoustic travelling wave. Based on the models and properties for the relevant materials, this work demonstrated that it is theoretically possible to achieve acoustic gain and high Q values exceeding the intrinsic limits of the materials for standing waves in PS-BAW resonators. If the acoustic gain via piezoelectric coupling exceeds, in absolute value, the magnitude of all losses combined, then the resonator stores acoustic energy (by consuming DC power) and the Q is undefined using conventional description given in equation (19). To demonstrate this experimentally, further investigation is necessary into PS-BAW resonators made with high-quality thin-film materials, such as GaN, CdS, or ZnO. Ideally, the resonators should be optimized for low reflection loss, operated under controlled pressure/temperature, and stimulated with continuous wave or pulsed DC excitation. This would enable exhaustive investigation into acoustoelectric interactions in PS materials and encourage the design of a new class of high-performance acoustoelectrically amplified resonant devices.

Methods

Fabrication

The BAW resonators are fabricated from wurtzite UID GaN grown by metallo-organic chemical vapor deposition (MOCVD) (Wafers A, C, and D, acquired from Nitronex Corp. NC, USA), or by molecular beam epitaxy (MBE) (Wafer B, acquired from Soitec, Bernin, France). Neither type of GaN film has the GaN/AlGaN strained interface that is used to achieve the high sheet conductivity known as the 2D electron gas (2DEG). Both types of films are thus bulk GaN, with unintentional (low) n-type doping and low mobility. Optical lithography is used to define the resonator patterns and the GaN films are etched using plasma etching with BCl₃/Cl₂ chemistry. The top electrodes are patterned using a standard liftoff process and electron beam evaporation and are comprised of 10 nm Ti and 100 nm Au. As noted before, the Au/Ti/n-GaN contacts are non-ohmic. The handle Si wafer is etched from the back using deep reactive ion etching (DRIE) to mechanically release the wafer. A thin portion of the buffer AlN/AlGaN layer is also removed in this step. The wafer is flipped and the blanket bottom electrode (10 nm/100 nm of Ti/Au) is deposited using a sputtering process to ensure good coverage in the DRIE trench. The fabrication is described in detail in previous work³⁴,⁴³ and Supplementary Section SV, Fig. S6.

Measurement procedures and controls

The RF scattering parameters of the resonators were measured using an Agilent N5241A or an Agilent E5061 network analyzer, Cascade ACP RF probes in the Ground-Signal-Ground (GSG) configuration, with 50 Ω terminations. Short-open-load-through (SOLT) calibration was performed to remove the effect of the cables and probe parasitics. DC bias is applied to the RF electrodes using bias tees. The two-port devices are fully symmetric with respect to choice of port for RF or DC stimulus. The measurements are performed with the devices in a cryogenic-capable, temperature controlled vacuum probe station (Lakeshore TTPX). Temperature of the sample stage and surrounding chamber walls is synchronously monitored and maintained at 300 K (except for the thermal testing) and monitored to within ±10 mK. Devices are measured at vacuum levels under 20 μTorr. Upper limits of RF input and DC excitation are maintained below the onset of resonator non-linearity or mechanical breakdown of the devices.

Author Contributions

V.G. designed and fabricated the resonators and conducted all experiments. Both authors contributed to the theoretical models and analysis. V.G. and M.R. wrote the manuscript. M.R. directed the project.

Supplementary Material

Supplementary Information

Supplementary Information for